2011学而思四升五超常班选拔答案

第十一届学而思综合素质测评·数学·四升五(答案版)

绝密★启用前第十一届学而思综合素质测评·数学·四升五(答案版)考试时间：90分钟考试科目：四升五数学总分：100分考生须知1．请考生务必认真填写试卷上的考生信息以方便正常通知；2．请使用蓝色或黑色签字笔或者钢笔作答；3．请将答案写在答题纸上，在试卷上作答无效；考试结束后需上交答题纸．在此特别感谢：顾伯特，李行，刘昊，邵国栋，侍春雷，苏昊，魏俐光，颜明，翟时玲，郑巍等老师（排名不分先后）为本卷所提供的试题！一、填空题．（每题4分，共60分）1.计算：201464201436⨯+⨯=________．【分析】考点：凑整运算；原式2014(6436)2014100201400=⨯+=⨯=．2.学学、而而、思思三位小朋友在一起数积分卡，学学的积分卡数量是而而的2倍多2张，而而的积分卡数量是思思的2倍，三人共有积分卡30张，则思思有________张积分卡．【分析】考点：和倍问题；思思有()()30212224-÷++⨯=张．3.如图，方形网格总面积是80平方厘米，阴影部分的两条鱼的总面积是________平方厘米．【分析】考点：毕克定理；每一个小格的面积是80801÷=(平方厘米)．由毕克定理可得一条鱼的面积是9142115+÷-=(平方厘米)，则两条鱼的总面积是15230⨯=(平方厘米)．4.20142的个位数字是________．【分析】考点：周期问题；2,4,8,6,2, ，20142的个位数字是4．5.某数加上1，再乘以2，再减去3，再除以4，其结果等于5．那么这个数是________．【分析】考点：还原问题；这个数是(543)2110.5⨯+÷-=．6.已知一个六位数2014A B 能够被104整除，则满足条件的数字,A B 的和A B +=________．【分析】考点：数的整除特征；104813=⨯，814,4B B ∴= ．13(14420),9A A -∴= ．13A B +=．7.从0~100这101个自然数中，任意取出一个数，这个数是奇数的可能性是50101．那么，任意取出一个数，这个数是质数的可能性是________．【分析】考点：质数与合数；100以内自然数中质数共有25个，可能性是25101．8.今年是2014年，由于20147+++=，人们将“7”看作今年的幸运数字．现规定，如果一个正整数除以7所得的商和余数相同，则将这样的数称为“来自星星的数”（例如32除以7商是4余数也是4，则32是一个“来自星星的数”），则在1到2014的正整数中，所有“来自星星的数”的总和是________．【分析】考点：余数问题；一个数除以7的余数只有16 这6种（商0余0的就是0，不在题目讨论范围）；因此满足条件的数只有6个．分别是：8,16,24,32,40,48，其总和为81624324048168+++++=．9.学学在做两个整数的乘法时，把其中一个因数的个位数字3误作为8，得出的乘积是2014．那么这道乘法计算，正确的乘积应该是________．【分析】考点：分解质因数；2014219533853=⨯⨯=⨯，因此正确的算式为33531749⨯=．10.在《爸爸去哪儿》节目结束后，5个明星爸爸和5个孩子想站成一排拍一个大合照，如果每一个孩子都和自己的爸爸站在一起，那么不同的拍照方法共有________种．【分析】考点：捆绑法；方法共有5222225222223840A ⨯A ⨯A ⨯A ⨯A ⨯A =种．11.如图，在梯形ABCD 中，三角形ABE 的面积是60平方厘米，AC 是AE 的3倍．则梯形ABCD 的面积为________．B 【分析】考点：等积变形；:3:1,::1:2AC AE AE EC DE EB =∴== ；21224:::1:2:2:4,2702ADE ABE DCE BCE ABE ABCD S S S S S S cm +++=∴== △△△△△梯形．单位忘记写扣一分12.在密码学中，直接可以看到的内容我们称为“明码”，对明码进行某种处理后得到的内容我们称为“密码”．现在有一种密码，将明码英文26个字母,,,,,,a b c x y z 依次对应1,2,3,,24,25,26 （见表格）．当明码对应的序号X 为奇数时，密码对应的序号()12Y X =+÷；当明码对应的序号X 为偶数时，密码对应的序号213Y X =÷+．所得序号对应的字母即为密码．字母a b c d e f g h i j k l m 序号12345678910111213字母n o p q r s t u v w x y z 序号14151617181920212223242526请你算出明码“xueersi ”译成密码是________．【分析】考点：定义新运算；明码x 对应24，为偶数，2421325÷+=，对应密码y ；明码u 对应21，为奇数，()211211+÷=，对应密码k ；明码e 对应5，为奇数，()5123+÷=，对应密码c ；明码r 对应18，为偶数，1821322÷+=，对应密码v ；明码s 对应19，为奇数，()191210+÷=，对应密码j ；明码i 对应9，为奇数，()9125+÷=，对应密码e ；因此密码是ykccvje ．13.黑板上写着1~2014这2014个自然数．小明每次擦去两个奇偶性相同的数，再写上它们的平均数．最后当黑板上只剩下一个自然数时，这个数最大是________．【分析】考点：操作中的最值问题；由于如果要平均数不小于2014，必须出现至少两个不小于2014的数，显然这是不可能的．因此平均数必定小于2014，因此是2013．具体方案：先擦1,3写2，然后擦2,2写2，然后擦2,4写3，再擦3,5写4，依此类推，最终可得2013．14.这是发生在上海学而思总部数娱大厦一件真实的故事．有A 、B 、C 、D 、E 、F 、G 七位老师乘电梯，而电梯都有其标准的载重量，当电梯里的人的总重量超出其标准载重时，电梯会发出“嘟~~”的声音．⑴当A 、B 、C 、D 这四位老师进入电梯时，电梯发出“嘟~~”的声音．⑵当A 、C 、F 、G 这四位老师进入电梯时，电梯发出“嘟~~”的声音．⑶当C 、D 、E 、G 这四位老师进入电梯时，电梯正常运行了．现在悄悄地告诉你，A 与E 一样重，而F 比G 轻．则：____________．（填“B 比D 重”、“D 比B 重”或“B 和D 一样重”）【分析】考点：逻辑推理；由⑴⑶可得，A B C D C D E G +++>+++，则A B E G +>+；因为A E =；所以B G >；由⑵⑶可得，A C F G C D E G +++>+++，A F D E +>+；因为A E =；所以F D >；又因为G F >；所以B G F D >>>，即B D >，填B 比D 重．15.在下图中，同时包含一个“马”字和一个“牛”字（同时包含两“马”的不算）的长方形有________个．【分析】考点：包含与排除；至少包含一个“马”和一个“牛”字的长方形有：36292=⨯⨯（个），而同时包含所有字的被多算了两次，有：422=⨯（个），共需要减去428⨯=（个）所以，只包含一个“马”和一个“牛”字的长方形有：36828-=（个）．二、解答题．（每题8分，共40分）16.十进制我们比较熟悉了，用0~9这九个数码来表示数，进位规则是“逢十进一”，借位规则是“借一当十”．二进制是计算机技术中广泛采用的一种数制，用0和1两个数码来表示数，进位规则是“逢二进一”，借位规则是“借一当二”．十进制和二进制可以转化，比如()()1025101=，意思是十进制中的5，在二进制中用101来表示．二进制的加、减法举例如下：1101101111000+1101101110-所以()()()2221101101111000+=，()()()2221101101110-=．请计算⑴()()2211011011⨯=________________，⑵()()2210101111÷=________________．（结果用二进制数表示）【分析】考点：二进制；（1）()222(1101)(1011)10001111⨯=；（2）()222(10101)(111)11÷=．17.一些数字如图排列，问⑴前10行的所有数的和是多少？⑵第20行左边数第14个数是多少？135717151311919212325272931494745434139373533【分析】考点：数列与数表；（1）前10行的所有数即为前100个正奇数，它们的和是210010000=；（2）首先找到第19行的最大数是第361个正奇数，即36121721⨯-=，由于第20行是从左到右由小到大排列，因此第14个数是721214749+⨯=．18.思思有四张卡片，分别印着0,1,2,4四个数字，从中任意抽出若干张就可以组成许多不同的自然数（如0,12,410,1024等）．如果将所有这些卡可能组成的自然数由小到大排列，则“2014”应该排在第几个？【分析】考点：分类枚举；用一张卡：0,1,2,4共4个；用两张卡：339⨯=（个）；用三张卡：33218⨯⨯=（个）；用四张卡千位是“1”的：3216⨯⨯=（个）；以上共有4918637+++=（个）；而四张卡千位是“2”的第1个就是“2014”，因此“2014”应该排在第38个．19.8点10分，有甲、乙两人以相同的速度分别从相距60米的,A B 两地顺时针方向沿着长方形ABCD（AD AB >）的边走向D 点．甲8点20分到达D 后，丙立即从D 点出发向A 走去，8点24分和乙相遇．8点28分甲到达C ，则此时丙距D 多少米？（甲、乙、丙在中途均未停留）DCBA【分析】考点：环道行程；由于甲乙两人速度相同且同时运动，因此两人的线上距离始终为60米；易知当8点28分甲到达C 点时，乙应该刚好到达D 点；由此可知丙从8点20分至8点24分所走的路程即为乙从8点24分至8点28分所走的路程；因此甲乙丙三人速度相同；8点28分丙与D 点的距离和甲与D 点的距离相同，即为60米．20.下图中，我们称粗实线围成的23⨯的长方形为一个“宫”．请在图中所有方格里，分别填入1~6中的某个数字，使得每行、每列和每个“宫”内，数字1~6都不重复出现．要求：任意两个相邻的方格内数字差都不为1（两个方格有共同的边称为“相邻”，只有1个共同的点不算相邻）．【分析】考点：数独；如右图所示．。

2024年超常思维(数学)五年级真题+答案

2024年第五届超常(数学)思维与创新能力测评五年级考试时间：100分钟满分：150分考试说明：(1)本试卷包括30道不定项选择题(可能有几个选项正确),每小题5分.(2)每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分.(3)请注意：试题和选项支的顺序，在学生测评系统的答题页面是随机呈现的.1.已A.0.253968D.0.253968,i,则与相等的小数为(B.0.242857E.0.1142857).C.0.2539632.给如图所示的水管注水，当水管分成两支时，水量被平均分成两份，从两边分别流下，已知给入口注水后，当D杯水量达到2升时，C杯中的水量是()升A.1B.2C.3D.4E.63.将自然数1-32排成一圈，需要满足的条件是：任何相邻两数的和均为平方数.则下图中字母a至f处应分别填入(A.15,8,24,20,11,23B.4,32,23,9,23,2C.32,4,24,23,2,6D.4,32,13,20,2,10E.4,32,24,20,2,234.如图，每个正方形的边长都是1,那么,图中面积为2的阴影长方形共有()个.A.34B.36C.38D.40E.45.如图，每个圆的面积是1平方厘米，任何一对相交圆重叠部分的面积是平方厘米，则6个圆覆)平方厘米.A.4B.C.D.6.如图，从边长为1cm的小正方形开始，以这个正方形的对角线为边作第2个正方形，再以第2个形的对角线为边作第3个正方形，如此下去，那么第13个正方形的边长是(.)cmA.16B.30 D.4C328 E.647.如图，从第二层(从下往上数了起，每个方框中的数都等于它下方两个方框中所填数的和.最上面的方框中填的数是(901670262283A.1123B.1563C.2008D.2024E.20328.老师宣布：“在下星期的某一天(星期一至星期五),将举行一场考试.”接着，他又说：“我知道你们很聪明，但是你们都无法用逻辑推理的方式推断是哪一天，只有到了考试那天早上8点钟通知下午2点钟考试，你们才能知道!”那么,这场考试将在星期()举行.A.一B.二C.三D.四E.其它选项都不对9.两支同样长度的蜡烛在同一时间被点燃，其中一支蜡烛3小时点完，另一支5小时点完.当一支蜡烛是另一支蜡烛的长度的4倍时，它们已点了()小时.B.3C. E.10.如图，把4×4方阵分成了4个2×2的实线方阵，图中阴影部分是由4条虚线围成的2×2的方阵，请在如图的4×4方阵中填入1,2,3,4,使得每行、每列以及上述5个2×2的方阵中1,2,3,4每个数字都出现.图中已经填入了3个数字，那么4×4方阵的第四行的4个数字按从左往右的顺序排列而成的四位数可能是().A.1234B.3421C.2134D.4132E.132411.如果一个正整数恰好等于它的各位数字之和的13倍，那么这样的正整数叫做超常数.超常数共有()个.A.0B.1C.2D.3E 412.有四根木料，其长度已在下图中标明，它们按图中的方式平行地摆放我们沿着与木料垂直的方向L 切割它们，使得L 左右两边的木料的总长度相等.那么最上面那根木料在L 左方的部分的长度为()m.3m2m .5mA.4.25B.3.5d4 D.3.75 E.4.12513.五个学生做加法练习，任写一个六位数，然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数，最后把这个新六位数与原数相加，分别得到172536,261589,568741,620708,845267.这五个结果中有四个肯定是错误的，那么有可能正确的结果是().A.172536B.261589C.568741D.620708E.84526714.在下午3:00,时针和分针的夹角为90°,那么,经过十二分钟后，两针所夹的锐角为().A.24°B.30°C.35°D.45°E.70°15.如图是由若干个等腰直角三角形拼成的图形，已知编号为①,②,③的三角形的面积分别是12,24和24,那么整个图形的面积是().A.110B.115C.117D.120E.1254m 4m16.现将图(a)中6块拼图板放入图(b)所示的盒子，允许翻过面来放置：拼图板中的单位正方形板放在标有字母的某个位置上，这个位置所标的字母是().(a)拼图板(b)盒子A.PB.QC.RD.SE.T17.在一村庄的赶集日，7个菠萝的价钱是9根香蕉和8个芒果的总价钱，同时5个菠萝的价钱是6根香蕉和6个芒果的总价钱.那么,在这一天，1个菠萝的价钱和()相同.A.2个芒果B.1根香蕉和2个芒果C.3根香蕉和1个芒果D.1根香蕉和1个芒果E.3根香蕉18.从0、1、2、3、4、5、6、7、8、9这个数字中，选出九个数字，组成一个两位数、一个三位数和一个四位数(每个数字恰用一次),使这三个数的和等于2028,那么其中未被选中的数字是().A.2B.4C.6D.8E.其它选项都不对19.如图，8个腰长相同的等腰三角形恰好围成一个八边形.已知八边形的8条边长分别为15,10, 10,15,15,10,10和15,则图中阴影部分与空白部分的面积差是().A.100B.125C.150D.180E.20020.鹏鹏的计算器出了故障：当打开电源时，屏幕上显示数字0.若按下“+”键，则它会加上51;若按下“-”键，则它会减去51;若按下“×”键，则它会加上85;若按下“÷”键，则它会减去85;而其他的按键无效.那么,鹏鹏打开计算器电源，任意操作上述按键，他可以得到的最接近于2024的数为().A.2025B.2024C.2023D.2004E.200621.4支足球队进行单循环赛，每两队都赛一场，每场胜者得3分，负者得0分，平局各得1分.比赛结束4支队的得分恰好是4个连续自然数，那么第四名输给了().A.第一名B.第二名C.第三名D.第四名E.无法确定22.在1000,1001,…,2000中，两个连续整数相加而不进位的整数对有()对.A.125B.150C.155D.156E.20023.从1,2,…,2024中至少需要划去(两个数的积.A.42B.43C.44)个数，才能使余下的每一个数都不等于其中另D.45E.4624.若a,b和c 是1到9(包含两端)中的不同整数，则的可能的最大值是×).A.2B.C. D.125.用8个相同的1×2的多米诺骨牌填满4×4的棋盘，则有(种不同的填法.A.36B.32C.28D.24E.2226.一个自行车轮胎，若把它安装在前轮，则自行车行驶6000km后报废；若把它安装在后轮，则自行车行驶4000km后报废，行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎，要使一辆自行车的一对新轮胎同时报废，那么,这辆车将能行驶()km.A.3000B.3750C.4000D.4800E.600027.对一个圆进行以下操作：第一次，把圆周二等分，每个分点都写上质数p,如图(a);第二次，每个基本弧(内部没有分点)的中点处写上这个弧两端所写数之和的如图(b);第三次，再在的中点处写上这个弧两端所写数之和的如图(c);第四次，再在每个基本弧的中点处个弧两端所写数之和的，如此进行了n次操作后，圆上所有数的和为2030,那么质数).号pP(a)(b)A.7B.11C.13D.23p2p p(c)E.2928.倩倩要从A地去往B地，张宇和小杰要从B地去往A地，三人同时出发.经过60分钟，倩倩和张宇相遇，相遇后倩倩立即转身要返回A地.又经过30分钟，此时张宇到达A地，而小杰恰好追上倩倩.那么,当小杰到达A地后，又经过()分钟倩倩也到达A地.A.8B.12C.18D.20E.3029.红、白、蓝、绿四个彩色的珠子放置在一个正方形的四个角上，共有()种不同的放法.(如图所示的两种放置形式被认为是同一种，因为一个正方形经旋转或翻转后放在另一个之上，此时可使上下彩珠的颜色相同.)A.2B.3C.4D.12E.2430.如图是字母“CC”,在图中的方框内填入数字1-8各1个，每个圆圈内填入“大，x,÷”之一，其中已给出两个“÷”.按“CC”的书写顺序A→B→C→D;E→F→GH前进并计算，每次算出结果之后再进行下一步计算(例如：“CC”中的第二个字母“C”,先算EOF,得到的结果为2,然后再用2÷G,……).运算过程中在箭头位置会产生“2,0,2,4”四个结果.那么在所有正确的填法中，(A+B+C+D)×(E+F+G+H)所能得到的结果是2<=G>4A.288B.308C.315D.404).E.4252024年第五届超常(数学)思维与创新能力测评五年级考试时间：100分钟满分：150分考试说明：(1)本试卷包括30道不定项选择题(可能有几个选项正确),每小题5分.(2)每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分.(3)请注意：试题和选项支的顺序，在学生测评系统的答题页面是随机呈现的.1.D16.B2.E17.AE3.E18.C4.D19.B5.E20.C6.E21.B7.E22.D8.E23.B9.E24.D10.CD25.A11.D26.D12.E27.AE13.D28.B14.A29.B15.D30.AC。

2011学而思四年级超长班试题2

第五讲简单的统计20、【例8不超过最低额度a立方米时，只付基本费3元和每户每月额定c保险费；如果每月用气量超过最低额度a立方米时，超过部分应按b元/立方米的标准付费，并知道保险费c不超过5元。

试根据以上提供的资料确定a，b，c的值。

第六讲定义新运算21、【学案4】小明来到红毛族探险，看到下面几个红毛族的算式：8×8＝8，9×9×9＝5，9×3＝3，（93＋8）×7＝837。

老师告诉他，红毛族算术中所用的符号“＋、－、×、÷、（）、＝”与我们算术中的意义相同，进位也是十进制，只是每个数字虽然与我们写法相同，但代表的数却不同。

请你按红毛族的算术规则，完成算式：89×57＝______。

22、【例7】定义a*b为a与b之间（包括a、b）所有与a奇偶性相同的自然数的平均数，例如：7*14=(7+9+11+13)÷4=10，18*10=(18+16+14+12+10)÷5=14。

在算式口*(19*99)=80的方格中填入恰当的自然数后可使等式成立，那么所填的数是多少？23、【例8】如有a#b新运算，a#b表示a、b中较大的数除以较小数后的余数。

例如：2#7=1，8#3=2，9#16=7，21#2=1。

如21#(21#x)=5，则x可以是______(x 小于50)。

第七讲游戏与策略本讲是博弈论的入门，例如：①大自然是平衡的，保护平衡就可以胜利，破坏平衡就会失败；②寻找制胜点；③当无法找到胜利的方法时保证自己不输也是对策，保证了自己不输，最终的结果就是对方输；④增强自己或者削弱对手是两种很有意思的对策，有时增强自己可以获胜，但有时增强自己却无法获胜必须削弱对手24、【作业1】甲乙二人轮流报数，报出的数只能是1～７的自然数。

同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜。

问怎样才能确保获胜？25、【学案3】15个小球围成一圈，甲、乙两人轮流从中取一个或者相邻的两个，如果两球中间有一个空位置，则不难将这两个球同时拿走，谁取走最后一个球谁就获胜，甲先拿，谁将获胜？26、【作业6】100个“+”号排成一排，甲乙轮流将“+”号改成“-”号，每次只能改一个或相邻的两个，谁将最后一个“+”改成“-”，谁获胜，获胜的策略是什么？27、【作业5】在一个6×5的棋盘上，甲乙二人轮流往棋盘的方格内放棋子。

2011学而思四升五超常班选拔答案

考试总分120分，填空题10题，每题5分1 计算：8888888888(123456787654321)⨯÷++++++++++++++=解答：123454321.2 观察下面排列的规律，第28行各个数之和与第18行各个数之和相差 (612)345512341234321(12330)(12320)255+++-+++=3 如图1所示，在长方形ABCD 中，ACB ∠等于34度。

现在将其沿对角线AC 折起，形成如图2所示的图形。

那么OCD ∠的度数是图1D C B A 图2A BC DO【分析】()29023422OCD ACD ACB BCD ACB ACB BCD ACB ∠=∠-∠=∠-∠-∠=∠-∠=-⨯=。

4 图中有个长方形。

2011学而思乐加乐超常班选拔考试（四升五）【分析】如图一、二所示各有()()+++⨯+=个长方形；12341230如图三所示，图一、图二共同构成的长方形有4312⨯=所以图中长方形总数为30+30+12=72个。

图1图2图35黑板上写有从1开始的一些连续奇数：1、3、5、7、9……擦去其中一个奇数后，剩下的所有奇数的和是2012，那么擦去的奇数是【分析】答案13 2452025=2025201213-=6某超级市场推出一个即擦即中的抽奖计划，只要购物满200元，即可获得一张抽奖券。

每张抽奖券均印上132333 (100)3其中一个数，各个数只会出现一次。

若抽奖劵上的数值的个位为7即代表中奖，那么共有张抽奖劵会中奖。

【分析】3x个位的顺序是3 9 7 1 100425÷=张7在不超过2011的正整数中，是2或11的倍数，同时不能被22整除的数有【分析】2011210051÷=10051829121005+-⨯=÷=201122919÷=20111118298改变一个数字，使970405为225的倍数，改变后的数是 .=⨯，所以要求分别能被和9整除.要能被25整除，所以最后两位只能是25或75.要能被9【分析】225259整除，所以所有数字的和是9的倍数，答案为9704259如图，一个宽为36的长方形被分为面积相等的4块.其中a是b的两倍，那么原长方形的面积是 .a b【分析】答案为：3456。

2011年学而思杯数学试题答案

1.简单小数计算2011－201.1＋20.11－2.011+0.001【解析】18282.分小四则混合运算541??1)12.3?(3.85??1854541【解析】??1)??12.3?(3.8518544?(3.85?3.6?12.3?1.8)?94????1.8?12.37.7?94?36?9?16 3 已知N*等于N的因数个数，比如4*=3，则（2011*+10*+6*）*=_______【解析】（2011*+10*+6*）*=（2+4+4）*=44用字母表示数一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k，已知k是自然数，则三角形的周长为______.【解析】k=2，周长为6+7+12=25.5基础类型应用题1红光大队用拖拉机耕地，2台3小时耕75亩，照这样计算，4台5小时耕____亩.【解析】2台1小时可耕75 ÷3＝25亩，4台5小时可耕地25×2×5＝250亩6基础类型应用题2一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。

则这个骗子一共骗了______钱？【解析】由于一开始骗子并没有骗钱，产生骗钱的是后用零钱换50元，所以共骗得50-5=45元。

7约数倍数已知A、B两数的最小公倍数是120，B、C两数的最小公倍数是180，A、C两数的最小公倍数是72，则A、B、C三数的最小公倍数是______.3×3×5【解析】120=222180=2×3×53272=2×332×3×所以最小公倍数是25=3608简单的逻辑推理2011年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。

在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。

学而思2011年暑假新四年级超常123班难题汇总

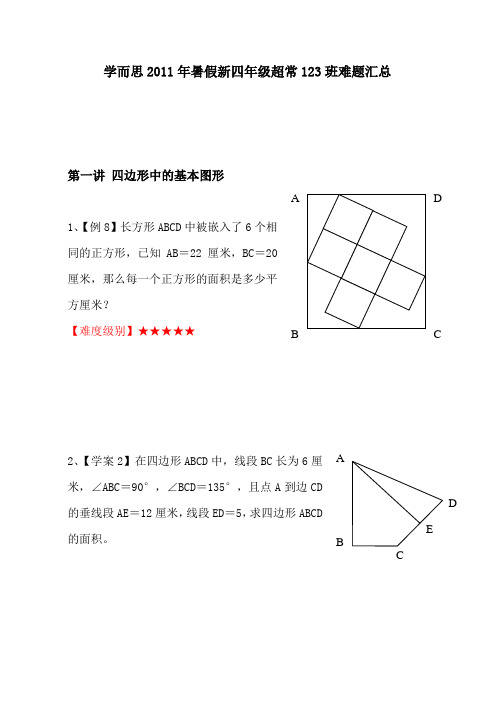
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形，已知AB＝22厘米，BC＝20厘米，那么每一个正方形的面积是多少平方厘米？【难度级别】★★★★★2、【学案2】在四边形ABCD中，线段BC长为6厘米，∠ABC＝90°，∠BCD＝135°，且点A到边CD 的垂线段AE＝12厘米，线段ED＝5，求四边形ABCD 的面积。

D C3、【学案3】等腰梯形ABCD 中，交于O 点的两条对角线互相垂直，三角形ECB 是直角三角形，OC 比AO长20厘米。

已知三角形ADE 的面积是250平方厘米，则梯形ABCD 的面积是多少平方厘米？4、【学案4】一块边长为180厘米的正方形铁片，四角各被截去一个边长为40厘米的小正方形铁片，现在要从剩下的铁片中剪出一块完整的正方形铁片来，剪出的正方形面积最大为多少平方厘米？5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形，保留必要的作图痕迹。

O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中，有多少个与5678相加时，至少发生一次进位？7、【例8】有______个四位数满足下列条件：它的各位数字都是奇数，它的各位数字互不相同，它的每个数字都能整除它本身。

8、【学案1】计算机上编程序打印出前10000个正整数：1,2,3,……,10000时，不幸打印机有毛病，每次打印数字3时，它都打印出x，问其中被错误打印的共有多少个数？9、【学案4】有9张同样大小的圆形纸片，其中标有数码“1”的有1张，标有数码“2”的有2张，标有数码“3”的有3张，标有数码“4”的有3张，把这9张圆形纸片如图所示放置在一起，但标有相同数码的纸片不许挨在一起。

(1)如果M处放标有数码“3”的纸片，一共有多少种不同的放置方法？(2)如果M处放标有数码“2”的纸片，一共有多少种不同的放置方法？10、【越玩越聪明】在例6的后面。

第十一届学而思综合素质测评·数学·四升五(答案版)

绝密★启用前第十一届学而思综合素质测评·数学·四升五(答案版)考试时间：90分钟考试科目：四升五数学总分：100分考生须知1．请考生务必认真填写试卷上的考生信息以方便正常通知；2．请使用蓝色或黑色签字笔或者钢笔作答；3．请将答案写在答题纸上，在试卷上作答无效；考试结束后需上交答题纸．在此特别感谢：顾伯特，李行，刘昊，邵国栋，侍春雷，苏昊，魏俐光，颜明，翟时玲，郑巍等老师（排名不分先后）为本卷所提供的试题！一、填空题．（每题4分，共60分）1.计算：201464201436⨯+⨯=________．【分析】考点：凑整运算；原式2014(6436)2014100201400=⨯+=⨯=．2.学学、而而、思思三位小朋友在一起数积分卡，学学的积分卡数量是而而的2倍多2张，而而的积分卡数量是思思的2倍，三人共有积分卡30张，则思思有________张积分卡．【分析】考点：和倍问题；思思有()()30212224-÷++⨯=张．3.如图，方形网格总面积是80平方厘米，阴影部分的两条鱼的总面积是________平方厘米．【分析】考点：毕克定理；每一个小格的面积是80801÷=(平方厘米)．由毕克定理可得一条鱼的面积是9142115+÷-=(平方厘米)，则两条鱼的总面积是15230⨯=(平方厘米)．4.20142的个位数字是________．【分析】考点：周期问题；2,4,8,6,2, ，20142的个位数字是4．5.某数加上1，再乘以2，再减去3，再除以4，其结果等于5．那么这个数是________．【分析】考点：还原问题；这个数是(543)2110.5⨯+÷-=．6.已知一个六位数2014A B 能够被104整除，则满足条件的数字,A B 的和A B +=________．【分析】考点：数的整除特征；104813=⨯，814,4B B ∴= ．13(14420),9A A -∴= ．13A B +=．7.从0~100这101个自然数中，任意取出一个数，这个数是奇数的可能性是50101．那么，任意取出一个数，这个数是质数的可能性是________．【分析】考点：质数与合数；100以内自然数中质数共有25个，可能性是25101．8.今年是2014年，由于20147+++=，人们将“7”看作今年的幸运数字．现规定，如果一个正整数除以7所得的商和余数相同，则将这样的数称为“来自星星的数”（例如32除以7商是4余数也是4，则32是一个“来自星星的数”），则在1到2014的正整数中，所有“来自星星的数”的总和是________．【分析】考点：余数问题；一个数除以7的余数只有16 这6种（商0余0的就是0，不在题目讨论范围）；因此满足条件的数只有6个．分别是：8,16,24,32,40,48，其总和为81624324048168+++++=．9.学学在做两个整数的乘法时，把其中一个因数的个位数字3误作为8，得出的乘积是2014．那么这道乘法计算，正确的乘积应该是________．【分析】考点：分解质因数；2014219533853=⨯⨯=⨯，因此正确的算式为33531749⨯=．10.在《爸爸去哪儿》节目结束后，5个明星爸爸和5个孩子想站成一排拍一个大合照，如果每一个孩子都和自己的爸爸站在一起，那么不同的拍照方法共有________种．【分析】考点：捆绑法；方法共有5222225222223840A ⨯A ⨯A ⨯A ⨯A ⨯A =种．11.如图，在梯形ABCD 中，三角形ABE 的面积是60平方厘米，AC 是AE 的3倍．则梯形ABCD 的面积为________．B 【分析】考点：等积变形；:3:1,::1:2AC AE AE EC DE EB =∴== ；21224:::1:2:2:4,2702ADE ABE DCE BCE ABE ABCD S S S S S S cm +++=∴== △△△△△梯形．单位忘记写扣一分12.在密码学中，直接可以看到的内容我们称为“明码”，对明码进行某种处理后得到的内容我们称为“密码”．现在有一种密码，将明码英文26个字母,,,,,,a b c x y z 依次对应1,2,3,,24,25,26 （见表格）．当明码对应的序号X 为奇数时，密码对应的序号()12Y X =+÷；当明码对应的序号X 为偶数时，密码对应的序号213Y X =÷+．所得序号对应的字母即为密码．字母a b c d e f g h i j k l m 序号12345678910111213字母n o p q r s t u v w x y z 序号14151617181920212223242526请你算出明码“xueersi ”译成密码是________．【分析】考点：定义新运算；明码x 对应24，为偶数，2421325÷+=，对应密码y ；明码u 对应21，为奇数，()211211+÷=，对应密码k ；明码e 对应5，为奇数，()5123+÷=，对应密码c ；明码r 对应18，为偶数，1821322÷+=，对应密码v ；明码s 对应19，为奇数，()191210+÷=，对应密码j ；明码i 对应9，为奇数，()9125+÷=，对应密码e ；因此密码是ykccvje ．13.黑板上写着1~2014这2014个自然数．小明每次擦去两个奇偶性相同的数，再写上它们的平均数．最后当黑板上只剩下一个自然数时，这个数最大是________．【分析】考点：操作中的最值问题；由于如果要平均数不小于2014，必须出现至少两个不小于2014的数，显然这是不可能的．因此平均数必定小于2014，因此是2013．具体方案：先擦1,3写2，然后擦2,2写2，然后擦2,4写3，再擦3,5写4，依此类推，最终可得2013．14.这是发生在上海学而思总部数娱大厦一件真实的故事．有A 、B 、C 、D 、E 、F 、G 七位老师乘电梯，而电梯都有其标准的载重量，当电梯里的人的总重量超出其标准载重时，电梯会发出“嘟~~”的声音．⑴当A 、B 、C 、D 这四位老师进入电梯时，电梯发出“嘟~~”的声音．⑵当A 、C 、F 、G 这四位老师进入电梯时，电梯发出“嘟~~”的声音．⑶当C 、D 、E 、G 这四位老师进入电梯时，电梯正常运行了．现在悄悄地告诉你，A 与E 一样重，而F 比G 轻．则：____________．（填“B 比D 重”、“D 比B 重”或“B 和D 一样重”）【分析】考点：逻辑推理；由⑴⑶可得，A B C D C D E G +++>+++，则A B E G +>+；因为A E =；所以B G >；由⑵⑶可得，A C F G C D E G +++>+++，A F D E +>+；因为A E =；所以F D >；又因为G F >；所以B G F D >>>，即B D >，填B 比D 重．15.在下图中，同时包含一个“马”字和一个“牛”字（同时包含两“马”的不算）的长方形有________个．【分析】考点：包含与排除；至少包含一个“马”和一个“牛”字的长方形有：36292=⨯⨯（个），而同时包含所有字的被多算了两次，有：422=⨯（个），共需要减去428⨯=（个）所以，只包含一个“马”和一个“牛”字的长方形有：36828-=（个）．二、解答题．（每题8分，共40分）16.十进制我们比较熟悉了，用0~9这九个数码来表示数，进位规则是“逢十进一”，借位规则是“借一当十”．二进制是计算机技术中广泛采用的一种数制，用0和1两个数码来表示数，进位规则是“逢二进一”，借位规则是“借一当二”．十进制和二进制可以转化，比如()()1025101=，意思是十进制中的5，在二进制中用101来表示．二进制的加、减法举例如下：1101101111000+1101101110-所以()()()2221101101111000+=，()()()2221101101110-=．请计算⑴()()2211011011⨯=________________，⑵()()2210101111÷=________________．（结果用二进制数表示）【分析】考点：二进制；（1）()222(1101)(1011)10001111⨯=；（2）()222(10101)(111)11÷=．17.一些数字如图排列，问⑴前10行的所有数的和是多少？⑵第20行左边数第14个数是多少？135717151311919212325272931494745434139373533【分析】考点：数列与数表；（1）前10行的所有数即为前100个正奇数，它们的和是210010000=；（2）首先找到第19行的最大数是第361个正奇数，即36121721⨯-=，由于第20行是从左到右由小到大排列，因此第14个数是721214749+⨯=．18.思思有四张卡片，分别印着0,1,2,4四个数字，从中任意抽出若干张就可以组成许多不同的自然数（如0,12,410,1024等）．如果将所有这些卡可能组成的自然数由小到大排列，则“2014”应该排在第几个？【分析】考点：分类枚举；用一张卡：0,1,2,4共4个；用两张卡：339⨯=（个）；用三张卡：33218⨯⨯=（个）；用四张卡千位是“1”的：3216⨯⨯=（个）；以上共有4918637+++=（个）；而四张卡千位是“2”的第1个就是“2014”，因此“2014”应该排在第38个．19.8点10分，有甲、乙两人以相同的速度分别从相距60米的,A B 两地顺时针方向沿着长方形ABCD（AD AB >）的边走向D 点．甲8点20分到达D 后，丙立即从D 点出发向A 走去，8点24分和乙相遇．8点28分甲到达C ，则此时丙距D 多少米？（甲、乙、丙在中途均未停留）DCBA【分析】考点：环道行程；由于甲乙两人速度相同且同时运动，因此两人的线上距离始终为60米；易知当8点28分甲到达C 点时，乙应该刚好到达D 点；由此可知丙从8点20分至8点24分所走的路程即为乙从8点24分至8点28分所走的路程；因此甲乙丙三人速度相同；8点28分丙与D 点的距离和甲与D 点的距离相同，即为60米．20.下图中，我们称粗实线围成的23⨯的长方形为一个“宫”．请在图中所有方格里，分别填入1~6中的某个数字，使得每行、每列和每个“宫”内，数字1~6都不重复出现．要求：任意两个相邻的方格内数字差都不为1（两个方格有共同的边称为“相邻”，只有1个共同的点不算相邻）．【分析】考点：数独；如右图所示．。

学而思小学四年级数学入学测试(难题)超常班选拔考试)

学校________________ 班级________________ 姓名_________________ 联系电话__________________密封线内不要答题2016年学而思数学超常班选拔考试四年级一、填空题（每题6分，共96分，将答案填在下面的空格处）1. 计算：666666666666666+-⨯÷=__________．2. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．3. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次．4.四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．5. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．6. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套．7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．8. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米.9. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手．11. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA12. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米．13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．15. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来． A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________．DCBA16. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱．二、解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1）长方形ABCD 的面积? （2）梯形ADCE 的面积?（3）阴影部分三角形AEF 的面积?D18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数．19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少．（2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密封线内不要答题321BA（1）经过多长时间，甲、乙两爬虫第一次相遇?（2）甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密封线内不要答题2016年学而思数学超常班选拔考试四年级一、填空题（每题6分，共96分，将答案填在下面的空格处）1.计算：666666666666666+-⨯÷=__________．【答案】6662. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．【答案】23. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次．【答案】304. 四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．【答案】35；81005. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．【答案】246. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套．【答案】30套7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．【答案】648. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米. 【答案】309. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．【答案】15人10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手．【答案】611. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA【答案】4812. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米．【答案】16DCBA13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．【答案】158只14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．【答案】915. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来．A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________．【答案】516. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱．【答案】700二、解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1）长方形ABCD 的面积? （2）梯形ADCE 的面积?（3）阴影部分三角形AEF 的面积?D【答案】24平方厘米；（4分）18平方厘米；（4分）（3）连接AC ，11348S AEF S ABC S ABCD D D ===正（平方厘米）．（4分） 18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数．【答案】设组成这个四位数的四个数码为a ，b ，c ，d (91a b c d ≥>>>≥)，则有383443388172abcd dcba -=+=，（4分）可得999()90()81727992180a dbc -+⨯-==+，（4分）则8ad -=，2b c -=，9a =，1d =，194338M cb =+，且M 的四位数字分别为1、c 、b 、9，由于8917+=的个位数字为7，所以b ，c 中有一个为7，但2b c -=，所以c 不能为7，故7b =，5c =，157943385917M =+=．（4分）19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少．（2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．【答案】（1）9（4分）（2）三角形三个顶点不能共线，所以不能三个点都在AB 上，一定有一个或两个点在CD 上．只含C 点：CFB △、CFA △、CEG △ 3个只含H 点：HAB △1个只含D 点：DAB △ 1个含C 、H 点：0个含H 、D 点：HDG △1个学校________________ 班级________________ 姓名_________________ 联系电话__________________密封线内不要答题共有31116+++=个．（5分）（3）只含C 点：CAE △、CFG △、CGB △ 3个只含H 点：1HAF △、HEG △、HFB △ 3个只含D 点：DAF △、DEG △、DFB △ 3个含C 、H 点：CHG △1个含H 、D 点：AHD △、FHD △2个共有3331212++++=个．（6分）20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?321BA（1）经过多长时间，甲、乙两爬虫第一次相遇?（2）甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?【答案】（1）根据题意，甲爬虫爬完半圈需要210220 5.25÷÷=分钟，乙爬虫爬完半圈需要2102157÷÷=分钟．由于甲第一次爬到1、2之间要5.25分钟，第一次爬到2、3之间要10.5分钟，乙第一次爬到2、3之间要7分钟，所以第一次相遇的地点在2号环形跑道的上半圈处．(210105)(2015)9+?=（分钟）（6分）（2）由于甲第一次爬到2、3之间要10.5分钟，第二次爬到1、2之间要15.75分钟，乙第一次爬到1、2之间要14分钟，所以第二次相遇的地点在2号环形跑道的下半圈处．第二次相遇时，两只爬虫爬了(2102105)(2015)15⨯+÷+=分钟．所以甲、乙两爬虫第二次相遇时，甲爬虫爬了2015300⨯=厘米．（8分）。

学而思超常班选拔考试(答案)

学而思六年级超常班选拔考试·答案一、简答题（共10题，每题6分，要求写出简要过程）1. 【考点】分数计算【答案】29419；111636【分析】 ⑴19101011901001190010001989810198101019801001980010001191910119191998989898981919199898398191929419⨯⨯⨯⨯⎛⎫=++⨯⨯ ⎪⨯⨯⨯⨯⎝⎭⎛⎫=++⨯⨯ ⎪⎝⎭=⨯⨯⨯=原式 ⑵()()()11199412345199219939979972399719941993199219912169979976111636=-+-+-++-+⨯-⨯=-+-++-+=+=原式2. 【考点】不定方程【答案】13平方厘米【分析】设上面长方形的未知边长为x ，下面长方形的未知边长为y ，则有：7543x y +=，由于()433mod5≡，55y ，因此有：()73mod5x ≡，又743x <，所以728x =，即4x =．代入原方程有：3y =．那么两个矩形的面积之差为：281513-=平方厘米．3. 【考点】计数【答案】12个【分析】 21世纪即为20□□年，那么这个八位数即为2002□□□□，也就是说日已经定了，接下来只要月份定下来，相应的年份也就确定了．一年12个月，所以共12个世界对称日．分别是：20100102、20200202、20300302、20400402、20500502、20600602、20700702、20800802、20900902、20011002、20111102、20211202．4. 【考点】因倍质合【答案】()A 428=；()4296B =；24【分析】分解质因数，42237=⨯⨯，即42的约数个数有2228⨯⨯=个，()A 428=，()()()()01010122337734896B n =+⨯+⨯+=⨯⨯=．由于()A 8n =，而8824222==⨯=⨯⨯，所以7n p =或13n p q =⨯或111n p q r =⨯⨯，三种情况下n 的最小值分别为128、24、30，因此n 的最小值是24．5. 【考点】等差数列【答案】4组【分析】首先1000为一个解．连续数的平均值设为x ，1000必须是x 的整数倍．假如连续数的个数为偶数个，x 就不是整数了．x 的2倍只能是5，25，125才行．因为平均值为12.5，要连续80个达不到．62.5是可以的．即62，63；61，64；…．连续数的个数为奇数时，平均值为整数．1000为平均值的奇数倍．1000=2×2×2×5×5×5；x 可以为2，4，8，40，200排除后剩下40和200是可以的．所以答案为平均值为62.5，40，200，1000的4组整数．6. 【考点】立体几何【答案】942平方厘米【分析】如下图所示将圆柱倾斜，此时可以多装一部分水．水的体积为：221π59π56300π9422V =⨯⨯+⨯⨯⨯==平方厘米．7. 【考点】概率【答案】13【分析】四人入座的不同情况有432124⨯⨯⨯=种．A 、B 相邻的不同情况，首先固定A 的座位，有4种，安排B 的座位有2种，安排C 、D 的座位有2种，一共有42216⨯⨯=种．所以A 、B 不相邻而座的概率为()12416243-÷=．8. 【考点】比例行程【答案】25:18【分析】乙45分钟的路程=丙50分钟的路程，因此有:50:4510:9v v ==乙丙，同理，甲60分钟的路程=乙75分钟的路程，因此有：:75:605:4v v ==乙甲，所以::25:20:18v v v =乙丙甲，即:25:18v v =丙甲．9. 【考点】数列数表【答案】991118590【分析】将原数列按照每组1个、2个、3个…分组，有：12132143212011201011121231234122011⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，，，，，，，，，，，，，，，我们假设第2012个数在第()1n +组，有前n 组的个数小于2012且最接近2012，即()120122n n +<，估算得62n =，此时已经有1953个数了，因此第2012个数是第63组的第59个数，即559．而倒数第2012个数就是12010．两数之差为519991592010118590-=．10. 【考点】构造与论证【答案】见分析【分析】本题答案不止一种，下面给出一种方法：二、解答题（共4题，每题10分，要求写出详细过程）11. 【考点】行程问题【答案】100米【分析】甲只可能在DC 上追上乙，当乙到达D 点时，我们可以推算一下此时甲在什么地方才有可能追上乙．如果乙走到C 点时，甲恰好追上，那么甲的追击时间就是120430÷=秒，追击路程为()305430⨯-=米．当乙第一次到达C 点时，用时180445÷=秒，甲走了455225⨯=米，甲还没有到达B 点，此时肯定追不上；当乙第二次到达C 点时，用时4804120÷=秒，甲走了1205600⨯=米，甲刚好回到A 点，此时也不可能；当乙第三次到达C 点时，用时7804195÷=秒，甲走了1955975⨯=米，此时甲从B 地返回且距离D 点25米，追及路程小于30米．可以追上．()255425÷-=秒后，甲第一次追上了乙，此时乙在距离D 点254100⨯=米处．12. 【考点】工程问题【答案】3204小时【分析】据已知条件，四管按甲乙丙丁顺序各开1小时，共开4小时，池内灌进的水是全池的11117345660-+-=，加上池内原来的水，池内有水171766060+=．再过四个4小时，即20小时后，池内有水1773460604+⨯=，还需灌水14，此时可由甲管开113434÷=小时．所以在3204小时后，水开始溢出水池．13. 【考点】逻辑推理【答案】C【分析】因为ABC 三人得分共40分，三名得分都为正整数且不等，所以前三名得分最少为6分，4058410220140=⨯=⨯=⨯=⨯，不难得出项目数只能是5．即M 5=．A 得分为22分，共5项，所以每项第一名得分只能是5，故A 应得4个一名一个二名．22542=⨯+，第二名得1分，又B 百米得第一，所以A 只能得这个第二． B 的5项共9分，其中百米第一5分，其它4项全是1分，951111=++++．即B 除百米第一外全是第三，跳高第二必定是C 所得．14. 【考点】直线型面积【答案】1:2【分析】如下图，过点E 、点F 作AD 的平行线，两条平行线间的距离为h ，∵:2:3EF FC =，∴:2:3DEF S S =乙△，∴:4:22:1DEF S S ==甲△ 又12DEF ADF ADE S S S AD h =-=⨯⨯△△△ 12BCE BCF S S S BC h =-=⨯⨯甲△△ ∴:1:2AD BC =。

2011学而思二升三超常班选拔答案

姓名_______ 联系方式：_______ 成绩_____ 考试时间：60分钟一：填空题（本小题共10小题，每小题6分，共60分，要求直接写出答案）。

1：】计算：（123+231+312）÷3=2222：】找规律填数1、3、7、15、31、（ 63 ）、（ 127 ）3：】哥哥今年18岁,妹妹今年15岁,当两人年龄和为67岁时,哥哥是（）岁。

【分析】年龄和是67，差是18-15=3.哥哥的年龄是：（67+3）÷2=35。

4：】5只猫同时吃5只老鼠用5分钟，20只猫同时吃20只老鼠用（）分钟。

【分析】共同花的时间是1只猫吃1只老鼠的时间，5分钟。

5：】30名学生报名参加兴趣小组。

其中有26人参加了美术组，17人参加了书法组。

问两个组都参加的有（）人。

（无人不参加）【分析】容斥原理，17+26-30=13（人）6：】小强的生日是6月27日，这一年的6月1日是星期六，小强的生日是星期几呢？【分析】从日历上可以看到，每个星期有7天，就是以7天为一个周期不断地重复．6月1日是星期六，那么再过7天，即6月8日，还是星期六；如果再过14天，即6月15日，还是星期六，……所以要知道6月27日是星期几，首先要求出6月27日是6月1日后的第几天，26127＝-（天）；因为每个星期都是7天，也就是周期为7，所以，53726 =÷，三星期余5天．这样，从6月1日开始经过3个星期，最后一天是星期六，从这最后一天再过5天就是星期四.所以，6月27日是星期四．7：】某科研单位每天派汽车早8点准时到工程师家接他上班。

但今天早晨，工程师临时决定提前到单位，于是他没有等汽车来接，就自己步行去单位。

步行途中遇到了前来接他的汽车，他马上上车赶到单位，结果发现比平时早到30分钟，问：工程师上车时是（）点（）分。

【分析】 7点45分2011第四届学而思·乐加乐·三年级超常班选拔8：】四个连续奇数之和是2008，则其中最小的一个奇数是（）？【分析】偶数个连续奇数求和一般先求中间一组数的和。

第六届学而思综合素质测评201109四年级答案

' ACB' __________ 7 如图，将一个三角板 ABC 绕点 C 旋转到 A' B' C' 位置，则 ACB
A A'
B'
C(C')
B
' ' 【分析】已知 ACB ACB 90
' ' ' ' ' 所以 ACB ACB' ACB B' CB ACB' ACB ACB 180
1 2 3 4 1 2 3 60 个， 1 2 3 1 2 3 36 个
1 2 3 个， 1 2 4 2 14 个， 60 36 3 14 107 个
所以，图 1 中共有 107 个长方形。 18 桌上放着这样一道算术题： 89 16 69 6A B8 88 甲、乙两位同学面对面坐在桌子两侧，而他们计算这道题的结果恰好相同，则 A 和 B 的和是 __________ 【分析】为了叙述方便，假设 A 倒过来的数字是 C ， B 倒过来的数字是 D ，一个数字倒过来看还是数字的有 0,1,6,8,9 这 5 个，其中 0 倒过来看还是 0 ，1 倒过来看还是 1 ，6 倒过来看是 9 ， 8 倒过来看还是 8 ， 9 倒过来看是 6 ，这个算式正着看是 89 16 69 6A B8 88 ，倒过来看变成了 88 8D C9 69 91 68 ，把这两个算式做如下变化， 89 16 69 6A B8 88 89 16 69 68 BA 88 88 8D C9 69 91 68 88 89 CD 69 91 68 这两个算式的结果是相等的，对于这两个算式，把两个算是中都有的数 89,88,68,69 抹掉不看，那

【六年级数学解答】超常班选拔考试样题答案

2011年秋季小学六年级超常班选拔考试样题解析一、填空题（共6题，每题5分）1、352551855612590921934833344807÷÷计算：= 。

【分析】观察约分，结果为5562、学学从1开始，按1，2，3，4，5…的顺序在黑板上写到某数为止，思思把其中一个数擦掉了，现在剩下的数的平均数是11.05，请问：思思擦掉的数是 10 .3、小明在桌面上摆了一些大小一样的正方体木块，摆完后从正面看如左下图，从侧面看如右下图，那么他最多用了__25___块木块，最少用了___9___块木块．【分析】从上往下看，分别如左下图和右下图所示(图中数字为每一格的木块数)．最多用25块，最少9块.4、从1开始的连续自然数依次写成一个多位数：A =1234567891011…200920102011，则数字A 处以9的余数是 1 。

【分析】弃九法5、在下面算式中添上运算符号或括号，使得等式成立：77 67 57 37 17=2002【分析】7653(777)772002--÷-=6、甲车从A ，乙车从B 同时相向而行，两车第一次相遇后，甲车继续行驶4小时到达B ，而乙车只行驶了1小时就到达A ，甲乙两车的速度比为 1:2 。

二、简答题（共4题，每题10分）1、“火树银花楼七层，层层红灯倍加增，共有红灯三八一，试问四层几红灯?”【分析】234561222222127++++++=，381÷127＝3，所以第一层3盏灯，第四层3×32＝24盏灯。

Q L R N M P CB A2、已知三角形的三条高交于一点.如图，在锐角三角形ABC 中，P 、Q 、R 分别为三条边的中点，由这三个点向其他两边引垂线，围成一个六边形LRMPNQ ，已知三角形ABC 的面积为a ，那么六边形LRMPNQ 的面积是多少？【分析】如图，由于L 、M 、N 三点都是中点，易知△ARQ、△BPR、△CQP 以及△PQR 四个三角形面积相同。

四升五年级2011暑期、秋季测试题

10. 某船在静水中的速度是每小时 18 千米,水速是每少小时？
新五年级诊断测试题
2
5. 王明回家,距家门 1600 米,妹妹和小狗一齐向他奔来,王明和妹妹的速度都是每分钟 50 米,小狗的速度是每分钟 100 米,小狗遇到王明后用同样的速度不停往返于王明与妹妹之间.当王明与妹妹相距 100 米时,小狗一共跑了___________米？
6. 将数字 1 至 9 分别填入右边竖式的方格内使算式成立(每个数字恰好使用一次)，那么加数中的四位数最大是__________
学理科到学而思
咨询电话：61863366
学而思 2011 暑秋四升五年级诊断测试题
姓名所在区学校年级答题计时
要求： 40 分钟完成，共 10 道题，一定要独立完成！试卷说明：答案完全正确的得分，多解、漏解、错解都不得分． 1.
20112011 2010 20102010 2011 __________。
1 2
0
0
8
1
新五年级诊断测试题
学理科到学而思
咨询电话：61863366
7. 六位数 20□□11 能被 99 整除，□□是
.
8. 右图中甲的面积比乙的面积大多少平方厘米？
4厘米
乙 8厘米
甲
6厘米
9. 小芳期末考试，语文、数学的平均成绩是 89 分，英语成绩加入以后，平均成绩上升了 3 分，问小芳英语多少分？
2. 如图，共有
个三角形，
个梯形。
3. 用长 24 米的木栅栏围成一块长方形的菜地，此菜地的面积最大是
平方米。
4. 山顶上有棵桃树，一只猴子偷吃桃子，第一天偷吃了总数的一半多 1 个，第二天又偷吃了剩下的一半多 1 个，第三天又偷吃了剩下的一半多 1 个，第四天又偷吃了剩下的一半多 1 个，这时恰好吃完所有桃子，问：树上原来有__________个桃子？

学而思小学四年级数学超常班选拔考试(难题)

第1页共4页第2页共4页2015—2016年深圳学而思超常班选拔考试四年级数学考生须知1．本试卷共4页，20道题，满分150分，考试时间90分钟． 2．在试卷上认真填写学校名称、班级和姓名．3．答案填写在答题卡上，写在试卷上无效，请用黑色字迹签字笔作答．16题，每题6分，共96分，将答案填在下面的空格处）．计算：27 3.6 6.427=⨯+⨯____________．．小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分．．4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件．．数一数，下图中共有__________个三角形．．如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF 的面积是_________平方厘米．．一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米．．如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．8．下图中包含☆的长方形有__________个.9．小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．10．用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数．11．在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）12．四位数462a 既是3的倍数，又是8的倍数，a =_________．13．1~100中，所有4的倍数的和是_________．14．一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________．15．四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．16．甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．FED CBAEDCBA☆第3页共4页第4页共4页二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分） 17．如图，长方形ABCD 的长9cm AB =，12cm CF =，阴影部分ACE ∆的面积是218cm ．（1）三角形ACF 的面积是多少平方厘米？（4分）（2）CE 的长度是多少厘米？（5分）（3）长方形ABCD 的面积是多少平方厘米？（6分）18．数列：21，34，67，210，313，616，219……按照一定的规律排列．（1）这个数列的第20个是什么？（4分）（2）数列中157□的分子是几？（5分）（3）数列中第几个数的分子和分母之和是418？（6分）19．如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里．（1）这次坐车的一共花了多少元？（4分）（2）图中三段路程，每段路程的费用分别是多少元？（6分）（3）浩浩家离学校有多少公里？（5分）20．甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1）甲、乙两人经过几分钟第一次相遇？（3分）（2）甲、丙两人经过几分钟第一次相遇？（3分）（3）甲、乙、丙三人的速度分别是多少？（6分）（4）丙沿湖边跑一圈需要多长时间？（3分）912FED CBA学校班级姓名考号指导老师密封线内禁止答题2015年深圳学而思秋季超常班选拔考试四年级考生须知1. 本试卷共4页，20题2. 本试卷满分150分，考试时间90分钟3. 在试卷密封线内填上填写学校、班级、姓名、联系电话一、填空题（共16题，每题6分，共96分，将答案填在下面的空格处）1. 计算：27 3.6 6.427=⨯+⨯____________．【解析】270．2. 小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分．【解析】()98+95+90+934=94÷分．3. 4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件．【解析】1名工人1小时做6043=5÷÷个，12名工人8小时能做5128=480⨯⨯个．4. 数一数，下图中共有__________个三角形．【解析】13个．5. 如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF的面积是_________平方厘米．【解析】38．6. 一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米．【解析】78=56⨯平方厘米．7. 如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．【解析】488=6÷平方厘米．8. 下图中包含☆的长方形有__________个.【解析】412=48⨯个．9. 小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．【解析】()288048+32=36÷分钟．10. 用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数．【解析】431+332=30⨯⨯⨯⨯．11. 在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）【解析】26a +．12. 四位数462a 既是3的倍数，又是8的倍数，a =_________．【解析】3a =．13. 1~100中，所有4的倍数的和是_________．【解析】()4+100252=1300⨯÷．14. 一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________．【解析】1+2+3+4+5+6=21，最大的数为854321．15. 四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．【解析】20名．FEDCBAECBA☆学理科到学而思16. 甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．【解析】27岁．二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分）17. 如图，长方形ABCD 的长9AB cm =，12CF cm =，阴影部分ACE ∆的面积是218cm ．（1）三角形ACF 的面积是多少平方厘米？（4分）（2） CE 的长度是多少厘米？（5分）（3）长方形ABCD 的面积是多少平方厘米？（6分）【解析】（1）29122=54cm ⨯÷．（2）()54182126CE cm =-⨯÷=．（3）1826=6AD cm =⨯÷，长方形的面积是96=54⨯平方厘米．18. 数列：21，34，67，210，313，616，219……按照一定的规律排列．（1）这个数列的第20个是什么？（4分）（2）数列中157□的分子是几？（5分）（3）数列中第几个数的分子和分母之和是418．（6分）【解析】此数列的分子是一个周期数列，分母是一个等差数列．（1）分子：203=62÷ ，分子为3；分母：1+193=58⨯，第20个是358．（2）157是这个数列的第()15713+1=53-÷个，分子是533=172÷ ，分子为3．（3）418=2+416=3+415=6+412，其中416不在分母是数列中，415是第139个，412是第138个；对于分子来说，第139个分子是2，第138个分子是6，所以6412满足要求，是第138个．19. 如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里．（1）这次坐车的一共花了多少元？（4分）（2）图中三段路程，每段路程的费用分别是多少元？（5分）（3）浩浩家离学校有多少公里？（6分）【解析】（1）6+15+21=42元．（2）第①段：63=18⨯元，第②段：()15-62=18⨯元，第③段：21156-=元．（3）前两段花的钱一样，说明前两段都是12公里，第③段花了6元，所以为123=4÷公里，浩浩家离学校有12+12+4=28公里．20. 甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1）甲、乙两人经过几分钟第一次相遇？（3分）（2）甲、丙两人经过几分钟第一次相遇？（3分）（3）甲、乙、丙三人的速度分别是多少？（6分）（4）丙沿湖边跑一圈需要多长时间？（3分）【解析】（1）5+15=20分．（2）20+5=25分．（3）甲、乙两人的速度和为800020=400÷米/分，甲的速度是乙的1.5倍，乙的速度为()4001+1.5=160÷米/分，甲的速度是160 1.5=240⨯米/分，甲、丙的速度和是800025=320÷米/分，丙的速度是32024080-=米/分．（4）800080=100÷分．912FED CBA。

学而思小学五年级数学入学考试(难度)超常班选拔考试试卷

第1页共4页第2页共4页2015—2016年深圳学而思超常班选拔考试五年级数学考生须知1．本试卷共4页，20道题，满分150分，考试时间90分钟． 2．在试卷上认真填写学校名称、班级和姓名．3．答案填写在答题卡上，写在试卷上无效，请用黑色字迹签字笔作答．6分，共96分，将答案填在下面的空格处）．计算：5.627856.2 2.2⨯+⨯=__________．．计算：412141+24+7137713⨯⨯⨯=__________．．若A 和B 都是质数，且99A B +=，则A B ⨯=__________．．若用“⊙”表示一种运算，且满足如下关系：5x y nx y =+ ，（其中n 是一个确定的数），已知3240= ，那么56= __________．．如图，长方形ABCD 的面积是32，:5:8AB BC =，将长方形沿着B 点逆时针旋转45度得到长方形BEFG ，则阴影部分的面积是__________．．小明买3支铅笔和7支钢笔需要22元，买6支铅笔和2支钢笔需要14元，则1支铅笔和1支钢笔需要__________元．．数一数，下图中有__________个正方形．．已知一个没有重复数字的四位数abcd 与它的反序数dcba 的和等于9999，这个四位数最大是__________．9．在一只口袋中装有5个红色小球、6个黄色小球、7个蓝色小球、8个黑色小球，这些小球大小一样，一次最少要从中取出__________个小球，方能保证其中至少含有2个黄球．10．把一根200厘米的木棍截成若干段，每段长度都是整数厘米，要求任意三段不能组成三角形，那么这个木棍最多可以截成__________段．11．正方形ABCD 的边长是10厘米，正方形CEFG 的边长是6厘米，连接BD 、BF ，阴影部分的面积是__________平方厘米．12．一副扑克一共有54张牌（包含大小王），从中抽取3张扑克，如果3张扑克数码是相同的，例如：3张10，或3张A ，这样的牌称为“豹子”，抽到大小王可以任意代替想要的扑克，例如：抽到大王和2张8，可以说自己的牌是“豹子”，如果从这副扑克中随机抽取3张扑克，这3张扑克是“豹子”的情况有__________种． 13．将1至2015的所有正整数按顺序排成一行123456789101112131420142015 ，再将这个多位数从左往右每三个数码一组分割开，得到一串三位数123、456、789、101、112、…，请问分割得到的第99个三位数是__________．14．有些数能表示成3个连续自然数的和，又能表示成4个连续自然数的和，还能表示成5个连续自然数的和，那么1000以内满足上述要求的数的总和是__________．15．甲、乙和丙三人沿着400米环形跑道进行1000米跑比赛，当甲跑1圈时，乙比甲多跑17圈，丙比甲少跑17圈．如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面__________米．16．小明喝一杯水，第一天喝了30毫升，第二天喝了剩下的13，第三天喝了剩下的14，第四天喝了剩下的15，…，第十天喝了剩下的111，此时还剩30毫升水没有喝，这杯水一共有__________毫升．C第3页共4页第4页共4页二、解答题（一共4题，共54分，写出必要步骤，否则不得分） 17．阅读题目，回答下面两个问题．（12分）（1）1～2000这2000个整数中是3的倍数或5的倍数或7的倍数一共有多少个？（2）1001～2000这1000个整数中，既不是3的倍数，也不是5的倍数和7的倍数的数有多少个？18．两年前，弟弟年龄占哥哥和弟弟年龄之和的411，两年后，弟弟的年龄占哥哥和弟弟年龄之和的38，回答下列两个问题．（12分）（1）求两年前弟弟与哥哥的年龄比，和两年后弟弟与哥哥的年龄比；（2）今年弟弟的年龄是多少岁？19．甲、乙两船分别在一条河的A ，B 两地同时相向而行，甲顺流而下，乙逆流而上。

四升五数学测试答案

数学测试参考答案1.答案:99980001解析:9997736=1111×1111×9×7+1111×1111×3×6=111xl11×x63+1111×1111×181111×1111x819999×999910000×9999-9999=99800012.答案:123-4-5-6-7+8-9=100,答案不唯一3.答案:2004727解析:2+7+2+7=18,18÷9=2,因此最小为20047274.答案:75解析:4@[(6*8)*(3*5)]=4@[(6+8-1)*(3+5-1)1=4@(13*7)=4@(13+7-1)=4@19=4×19-1=76-1=75。

5.答案:7(见图)（以图中的圆点为顶点的正方形）6.答案:20201解析:1002+1012=20201。

7.答案:14859解析:根据第n行最右边的数是n2,可知第19行的最右边的数是192=361,所以,第20行的最左边的数是361+1=362。

同理,第20行的最右边的数是202=400,所以第20行所有数的和为362+363+364+…+400=(362+400)×(400-362)÷1+1]÷2762×39÷2=148598.答案:0解析:因为n2与(n+7)除以7的余数相同,12、22、32、42、52、62、72分别除以7的余数为1,4 2,2,4,1,0,这七个余数为一周期,这七个余数的和为1+4+2+2+4+140=14,14÷7=2。

所以每连续7个数的和能被7整除。

20÷7=2…6;所以前14个连续自然数的和能被7整除,后六个数的和除以7的余数为1+4+2+2+4+1=14,14÷7=2-…0,即原式除以7的余数为09.答案:7.5；4.5解析:第一次顺流航行72千米,逆流航行12千米,共10小时第二次顺流航行36千米,逆流航行21千米,共10小时若第二次顺流航行72千米,逆流航行42千来共20小时所以逆流速度为:(42-12)÷(20-10)=3(千米/时),第一次顺流航行的时间:10-12÷3=6(小时),顺流速度:72÷6=12(千米/时)。

四年级超常班详解

联系电话：62164116/ 82618899
【答案】：15 【解析】：取一等奖中最后 4 名同学的平均分作为基准数．根据题目中的条件一有前六人平均分前十人平均分 2 ．这说明在计算前十人的平均分时，前六人共多出 6 2 12 (分)，用来弥补后四人的分数．因而四人的平均分比前十名的平均分少 12 4 3 (分)．根据题目中的条件二，当一等奖的后四人调整为二等奖后，二等奖者平均每人提高 2 分，这四人提供 2 （20 4）=48 分，分给二等奖的 24 人，平均每人供给 48 4 12 (分)．综上可知，原来一等奖的平均分比二等奖的平均分多 3 12 15 (分)．五、填空题（每题 12 分，共 24 分）
45 11 34 .
12. 任何大于 1 的自然数 n 阶乘表示方法为： n ! n (n 1) (n 2) 1 , 0! 1 ．现已知：
a ! b ! c ! 127 , 那么, 三位数 abc 有
【答案】：10 【解析】： 5! 120 ，
10. 一个三位数，如果它的每一位数字都不小于另一个三位数对应数位上的数字，就称它“吃掉”另一个三位数，例如： 532 吃掉 311， 123 吃掉 123，但 726 与 267 相互都不被吃掉．那么，能吃掉 678 的三位数共有【答案】：24 【解析】：即求百位数不小于 6，十位数不小于 7，个位不小于 8 的自然数．百位数不小于 6，有 4 种；十位数不小于 7，有 3 种；个位不小于 8，有 2 种．由乘法原理，能吃掉 678 的三位数共有 4 3 2 24 种． 11. 下图中不同的汉字表示不同的数字，相同的汉字表示相同的数字，那么，“四+年+级+学 +而+思+超+常”= . 个．

学而思集训队选拔考试详解

一个八位数，它被 3 除余 1 ，被 4 除余 2 ，被 11 恰好整除，已知这个八位数的前 6 位是 368755 ，那么它的后两位数是 _______ 。
【分析与解】设被 3 除余 1 ，被 4 除余 2 ，被 11 恰好整除的数为 n ；因为 n 被 3 除余 1 ；所以 n 可能是 1 ， 4 ， 7 ， 10 ，…；因为 10 4 2 2 ；所以 n 被 3, 4 12 除余 10 ；所以 n 可能是 10 ， 22 ，…；因为 22 11 2 ；所以 n 被 12,11 132 除余 22 ；因为 36875599 132 279360 79 ；所以这个八位数是 36875599 79 22 36875542 ，即这个八位数的后两位数是 42 。
上海学而思外联竞赛部
【第10题】如图， A B C D E F G H I _______ 度。
I A F B C E D H G
【分析与解】
I Q A B R J K C L D M H P O N E G F
A 180 ARJ AJR 180 180 QRJ 180 RJK QRJ RJK 180 ；
H OPQ PQR 180 ， I PQR QRJ 180 ；
A B C D E F G H I
RJK JKL KLM LMN MNO NOP OPQ PQR QRJ 2 180 9
2014 年学而思四升五集训队选拔考试
【考试说明】 1、考试时间： 2014 年 4 月 3 日 18 : 00 ~ 20 : 00 2、本试卷一共 30 题，满分 150 分。 3、请将所有答案写在答题纸上。一、填空题Ⅰ（直接写出得数。第 1 ~ 10 题，每题 3 分，共 30 分）【第1题】计算：

2011学而思四升五超常班选拔答案

第十一届学而思综合素质测评·数学·四升五(答案版)

2024年超常思维(数学)五年级真题+答案

2011学而思四年级超长班试题2

2011学而思四升五超常班选拔答案

2011年学而思杯数学试题答案

学而思2011年暑假新四年级超常123班难题汇总

第十一届学而思综合素质测评·数学·四升五(答案版)

学而思小学四年级数学入学测试(难题)超常班选拔考试)

学而思超常班选拔考试(答案)

2011学而思二升三超常班选拔答案

第六届学而思综合素质测评201109四年级答案

【六年级数学解答】超常班选拔考试样题答案

四升五年级2011暑期、秋季测试题

学而思小学四年级数学超常班选拔考试(难题)

学而思小学五年级数学入学考试(难度)超常班选拔考试 试卷

四升五数学测试答案

四年级超常班详解

学而思集训队选拔考试详解

学而思小学五年级数学入学考试(难度)超常班选拔考试试卷