数据模型与决策习题4答案
《数据模型与决策》复习题及参考答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,“s·t”表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是( A )A.销售数量 B.销售价格 C.顾客的需求 D.竞争价格2.我们可以通过( C )来验证模型最优解。
A.观察 B.应用 C.实验 D.调查3.建立运筹学模型的过程不包括( A )阶段。
A.观察环境 B.数据分析 C.模型设计 D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的( B )A数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值( D )A可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有( A )A 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
数据模型与决策试题及参考答案

数据模型与决策试题及参考答案本文为《数据模型与决策》复,共分为五个填空题。
1.已知成年男子的身高服从正态分布N(167.48,6.092),随机调查100位成年男子的身高,那么,这100位男子身高的平均数服从的分布是N(167.48,0.609)。
2.某高校想了解大学生每个月的消费情况,随机抽取了100名大学生,算得平均月消费额为1488元,标准差是2240元。
根据正态分布的“68-95-99”法则,该高校大学生每个月的消费额的95%估计区间为[1040,1936]。
3.从遗传规律看,一个产妇生男生女的概率是一样的,都是50%,但也有个人的特殊情况。
假设某人前一胎是女孩,那么她的下一胎也是女孩的概率为0.55;如果某人前一胎是男孩,那么她的下一胎还是男孩的概率为0.48.已知___第一胎是女孩,那么她的第三胎生男孩的概率是0.4653.4.调查发现,一个刚参加工作的MBA毕业生在顶级管理咨询公司的初始年薪可以用均值为9万美元和标准差是2万美元的正态分布来表示,那么一个这样的毕业生初始年薪超过9万美元的概率是0.5.5.结合生活实际,判断两个量之间的相关系数大概有多大?比如问您孩子身高与父母身高的的相关系数可能是0.6.1.孩子与父母的身高存在相关性,这个相关性可以用相关系数来衡量。
相关系数的取值范围为-1到1,绝对值越接近1表示相关性越强,绝对值越接近0表示相关性越弱。
在这个问题中,孩子与父母平均身高的相关性比较高,应该选0.9作为相关系数。
2.模拟仿真的关键步骤包括:确定仿真目标、建立仿真模型、选择仿真工具、设计实验方案、进行仿真实验、分析仿真结果、验证仿真模型。
模拟仿真是一种通过计算机模拟来研究和分析实际系统的方法,可以帮助人们更好地理解和预测系统的行为,从而提供决策支持和优化方案。
3.___某天上班路上捡到10元钱属于小概率事件。
小概率事件是指在一次试验中,出现的概率很小的事件。
通常认为,小概率事件的概率小于等于0.05.在这个问题中,其他选项中抛硬币的结果全是正面的概率都大于0.05,因此不属于小概率事件。
MBA数据模型与决策考卷及答案

MBA数据模型与决策考卷及答案一、选择题(每题1分,共5分)A. 线性模型B. 非线性模型C. 网络模型D. 层次分析法模型A. 期望收益B. 折现率C. 净现值D. 敏感性分析A. 敏感性分析B. 概率树C. 决策树D. 蒙特卡洛模拟A. 目标函数为线性函数B. 约束条件为非线性函数C. 变量之间存在相关性D. 变量取值范围为整数A. ExcelB. SPSSC. MATLABD. AutoCAD二、判断题(每题1分,共5分)1. 数据模型只能用于定量分析,不能用于定性分析。
()2. 在决策过程中,确定性决策的风险一定低于不确定性决策。
()3. 敏感性分析可以找出影响项目收益的关键因素。
()4. 多目标规划问题中,各个目标函数之间一定是相互矛盾的。
()5. 网络计划技术(PERT)是一种确定型网络图。
()三、填空题(每题1分,共5分)1. 数据模型的三个基本要素是变量、______和关系。
2. 决策树分析中,节点分为______节点和______节点。
3. 在线性规划问题中,目标函数和约束条件均为______函数。
4. 概率树分析是一种______分析工具,适用于评估项目风险。
5. 数据挖掘的五个基本步骤包括:数据准备、______、数据挖掘、结果评估和______。
四、简答题(每题2分,共10分)1. 简述蒙特卡洛模拟的基本原理。
2. 什么是网络计划技术(PERT)?它有哪些优点?3. 简述线性规划在企业管理中的应用。
4. 如何运用决策树分析解决实际问题?5. 数据挖掘技术在市场营销中的作用是什么?五、应用题(每题2分,共10分)1. 某企业生产两种产品,产品A的利润为50元/件,产品B的利润为80元/件。
生产一件产品A需要2小时,生产一件产品B需要3小时。
企业每月共有240小时的生产能力,请问如何安排生产计划,使得总利润最大化?2. 某项目有三种投资方案,方案一的投资额为100万元,收益率为10%;方案二的收益率为12%,投资额为150万元;方案三的投资额为200万元,收益率为15%。
MBA数据模型与决策考卷及答案

MBA数据模型与决策考卷及答案一、选择题(每题1分,共5分)A. 线性回归模型B. 决策树模型C. 主成分分析模型D. 聚类分析模型A. 信息增益B. 均方误差C. 相关系数D. F值A. 加权评分模型B. 层次分析法C. 数据包络分析法D. 逻辑回归分析法A. 目标函数线性B. 约束条件线性C. 变量非负D. 变量连续A. SPSSB. ExcelC. SASD. MATLAB二、判断题(每题1分,共5分)1. 数据模型可以用来描述现实世界中的数据关系和规律。
(√)2. 在决策分析中,只需要关注定量数据,无需考虑定性数据。
(×)3. 熵值法可以用于评估决策树的节点纯度。
(√)4. 线性规划问题中,目标函数和约束条件都必须是线性的。
(√)5. 数据挖掘就是从大量数据中提取有价值信息的过程。
(√)三、填空题(每题1分,共5分)1. 在决策树中,用于分割节点的属性称为______属性。
2. 多属性决策方法中,加权评分模型的核心是确定各属性的______。
3. 线性规划问题中,目标函数的取值称为______。
4. 在数据挖掘过程中,将原始数据转换为适合挖掘的格式的过程称为______。
5. ______是一种基于样本相似度的分类方法。
四、简答题(每题2分,共10分)1. 简述决策树的基本原理。
2. 什么是线性规划?它有哪些应用场景?3. 简述主成分分析的基本步骤。
4. 聚类分析的主要目的是什么?5. 请列举三种常用的多属性决策方法。
五、应用题(每题2分,共10分)1. 某企业拟投资两个项目,项目A的预期收益为100万元,风险系数为0.6;项目B的预期收益为150万元,风险系数为0.8。
请使用加权评分模型为企业选择投资项目。
2. 某公司生产两种产品,产品1的单件利润为10元,产品2的单件利润为15元。
生产一件产品1需要2小时,生产一件产品2需要3小时。
公司每月最多生产100件产品,且生产时间不超过240小时。
数据模型与决策练习题含答案
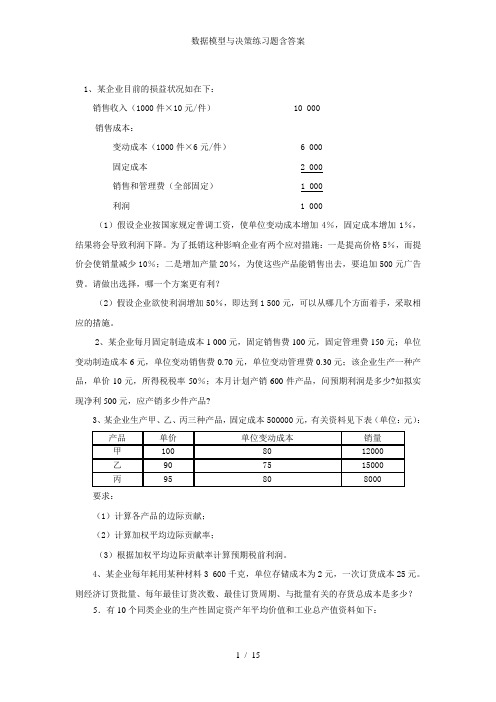
1、某企业目前的损益状况如在下:销售收入(1000件×10元/件) 10 000销售成本:变动成本(1000件×6元/件) 6 000固定成本 2 000销售和管理费(全部固定) 1 000利润 1 000(1)假设企业按国家规定普调工资,使单位变动成本增加4%,固定成本增加1%,结果将会导致利润下降。
为了抵销这种影响企业有两个应对措施:一是提高价格5%,而提价会使销量减少10%;二是增加产量20%,为使这些产品能销售出去,要追加500元广告费。
请做出选择,哪一个方案更有利?(2)假设企业欲使利润增加50%,即达到1 500元,可以从哪几个方面着手,采取相应的措施。
2、某企业每月固定制造成本1 000元,固定销售费100元,固定管理费150元;单位变动制造成本6元,单位变动销售费0.70元,单位变动管理费0.30元;该企业生产一种产品,单价10元,所得税税率50%;本月计划产销600件产品,问预期利润是多少?如拟实现净利500元,应产销多少件产品?3、某企业生产甲、乙、丙三种产品,固定成本500000元,有关资料见下表(单位:元):要求:(1)计算各产品的边际贡献;(2)计算加权平均边际贡献率;(3)根据加权平均边际贡献率计算预期税前利润。
4、某企业每年耗用某种材料3 600千克,单位存储成本为2元,一次订货成本25元。
则经济订货批量、每年最佳订货次数、最佳订货周期、与批量有关的存货总成本是多少?5.有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)估计生产性固定资产(自变量)为1100万元时总产值(因变量)的可能值。
6、某商店的成本费用本期发生额如表所示,采用账户分析法进行成本估计。
首先,对每个项目进行研究,根据固定成本和变动成本的定义及特点结合企业具体情况来判断,确定它们属于哪一类成本。
例如,商品成本和利息与商店业务量关系密切,基本上属于变动成本;福利费、租金、保险、修理费、水电费、折旧等基本上与业务量无关,视为固定成本。
数据,模型与决策练习题含答案

数据,模型与决策练习题含答案(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1、某企业目前的损益状况如在下:销售收入(1000件×10元/件) 10 000销售成本:变动成本(1000件×6元/件) 6 000固定成本 2 000销售和管理费(全部固定) 1 000利润 1 000(1)假设企业按国家规定普调工资,使单位变动成本增加4%,固定成本增加1%,结果将会导致利润下降。
为了抵销这种影响企业有两个应对措施:一是提高价格5%,而提价会使销量减少10%;二是增加产量20%,为使这些产品能销售出去,要追加500元广告费。
请做出选择,哪一个方案更有利(2)假设企业欲使利润增加50%,即达到1 500元,可以从哪几个方面着手,采取相应的措施。
2、某企业每月固定制造成本1 000元,固定销售费100元,固定管理费150元;单位变动制造成本6元,单位变动销售费元,单位变动管理费元;该企业生产一种产品,单价10元,所得税税率50%;本月计划产销600件产品,问预期利润是多少如拟实现净利500元,应产销多少件产品3、某企业生产甲、乙、丙三种产品,固定成本500000元,有关资料见下表(单位:元):要求:(1)计算各产品的边际贡献;(2)计算加权平均边际贡献率;(3)根据加权平均边际贡献率计算预期税前利润。
4、某企业每年耗用某种材料3 600千克,单位存储成本为2元,一次订货成本25元。
则经济订货批量、每年最佳订货次数、最佳订货周期、与批量有关的存货总成本是多少5.有10个同类企业的生产性固定资产年平均价值和工业总产值资料如(2)建立直线回归方程;(3)估计生产性固定资产(自变量)为1100万元时总产值(因变量)的可能值。
6、某商店的成本费用本期发生额如表所示,采用账户分析法进行成本估计。
首先,对每个项目进行研究,根据固定成本和变动成本的定义及特点结合企业具体情况来判断,确定它们属于哪一类成本。
数据、模型与决策(运筹学)课后习题和案例答案004

CHAPTER 4 LINEAR PROGRAMMING: FORMULATION AND APPLICATIONSReview Questions4.1-1 Determine which levels should be chosen of different advertising media to obtain the mosteffective advertising mix for the new cereal.4.1-2 The expected number of exposures.4.1-3 TV commercials are not being used and that is the primary method of reaching youngchildren.4.1-4 They need to check the assumption that fractional solutions are allowed and the assumptionof proportionality.4.2-1 Each functional constraint in the linear programming model is a resource constraint.4.2-2 Amount of resource used ≤ Amount of resource available.4.2-3 1) The amount available of each limited resource.2) The amount of each resource needed by each activity. Specifically, for eachcombination of resource and activity, the amount of resource used per unit of activitymust be estimated.3) The contribution per unit of each activity to the overall measure of performance.4.2-4 The three activities in the examples are determining the most profitable mix of productionrates for two new products, capital budgeting, and choosing the mix of advertising media.4.2-5 The resources in the examples are available production capacities of different plants,cumulative investment capital available by certain times, financial allocations foradvertising and for planning purposes, and TV commercial spots available for purchase. 4.3-1 For resource-allocation problems, limits are set on the use of various resources, and thenthe objective is to make the most effective use of these given resources. For cost-benefit-tradeoff problems, management takes a more aggressive stance, prescribing what benefitsmust be achieved by the activities under consideration, and then the objective is to achieve all these benefits with minimum cost.4.3-2 The identifying feature for a cost-benefit-tradeoff problem is that each functional constraintis a benefit constraint.4.3-3 Level achieved ≥ Minimum acceptable level.4.3-4 1) The minimum acceptable level for each benefit (a managerial policy decision).2) For each benefit, the contribution of each activity to that benefit (per unit of theactivity).3) The cost per unit of each activity.4.3-5 The activities for the examples are choosing the mix of advertising media, personnelscheduling, and controlling air pollution.4.3-6 The benefits for the examples are increased market share, minimizing total personnel costswhile meeting service requirements, and reductions in the emission of pollutants.4.4-1 Distribution-network problems deal with the distribution of goods through a distributionnetwork at minimum cost.4.4-2 An identifying feature for a distribution-network problem is that each functional constraintis a fixed-requirement constraint.4.4-3 In contrast to the ≤ form for resource constraints and the ≥ form for benefit constraints,fixed-requirement constraints have an = form.4.4-4 Factory 1 must ship 12 lathes, Factory 2 must ship 15 lathes, Customer 1 must receive 10lathes, Customer 2 must receive 8 lathes, and Customer 3 must receive 9 lathes.4.5-1 Two new goals need to be incorporated into the model. The first is that the advertisingshould be seen by at least 5 million young children. The second is that the advertisingshould be seen by at least 5 million parents of young children.4.5-2 Two benefit constraints and a fixed-requirement constraint are included in the new linearprogramming model.4.5-3 Management decided to adopt the new plan because it does a much better job of meeting allof management’s goals f or the campaign.4.6-1 Mixed problems may contain all three types of functional constraints: resource constraints,benefit constraints, and fixed-requirement constraints.4.6-2 The Save-It Co. problem is an example of a blending problem where the objective is to findthe best blend of ingredients into final products to meet certain specifications.4.7-1 A linear programming model must accurately reflect the managerial view of the problem.4.7-2 Large linear programming models generally are formulated by management science teams.4.7-3 The line of communication between the management science team and the manager is vital.4.7-4 Model validation is a testing process used on an initial version of a model to identify theerrors and omissions that inevitably occur when constructing large models.4.7-5 The process of model enrichment involves beginning with a relatively simple version of themodel and then using the experience gained with this model to evolve toward moreelaborate models that more nearly reflect the complexity of the real problem.4.7-6 What-if analysis is an important part of a linear programming study because an optimalsolution can only be solved for with respect to one specific version of the model at a time.Management may have “what-if” quest ions about how the solution will change givenchanges in the model formulation.4.8-1 The Ponderosa problem falls into the mixed problem category. The United Airlinesproblem is basically a cost-benefit-tradeoff problem. The Citgo problem is a distribution-network problem.4.8-2 The Ponderosa problem has 90 decision variables, the United Airlines problem has over20,000 decision variables, and the Citgo problem has about 15,000 decision variables.4.8-3 Two factors helped make the Ponderosa application successful. One is that theyimplemented a financial planning system with a natural-language user interface, with theoptimization codes operating in the background. The other success factor was that theoptimization system used was interactive.4.8-4 The most important success factor in the United Airlines application was the support ofoperational managers and their staffs.4.8-5 The factors that helped make the Citgo application successful were developing outputreports in the language of managers to mee t their needs, using “what-if” analysis, thesupport of operational managers, and, most importantly, the unlimited support provided the management science task force by top management.Problems4.1 a)Data cells: B2:E2, B6:E7, H6:H7, B13, and D13Changing cells: B11:E11Target cell: H114 5 6 7FBudgetSpent=SUMPRODUCT(B6:E6,$B$11:$E$11)=SUMPRODUCT(B7:E7,$B$11:$E$11)91011HTotal Exposures(thousands)=SUMPRODUCT(B2:E2,B11:E11)b) This is a linear programming model because the decisions are represented by changing cells that can have any value that satisfy the constraints. Each constraint has an output cell on the left, a mathematical sign in the middle, and a data cell on the right. The overall level of performance is represented by the target cell and the objective is to maximize that cell. Also, the Excel equation for each output cell is expressed as aSUMPRODUCT function where each term in the sum is the product of a data cell and a changing cell.c) Let T = number of commercials on TV M = number of advertisements in magazines R = number of commercials on radio S = number of advertisements in Sunday supplements. Maximize Exposures (thousands) = 140T + 60M + 90R + 50S subject to 300T + 150M + 200R + 100S ≤ 4,000 ($thousands) 90T + 30M + 50R + 40S ≤ 1,000 ($thousands) T ≤ 5 spots R ≤ 10 spots and T ≥ 0, M ≥ 0, R ≥ 0, S ≥ 0. 4.2b)Bestd) Let x1 = level of activity 1x2 = level of activity 2Maximize Contribution = $20x1 + $30x2subject to 2x1 + x2≤ 103x1 + 3x2≤ 202x1 + 4x2≤ 20and x1≥ 0, x2≥ 0.e) Optimal Solution: (x1, x2) = (3.333, 3.333) and Total Contribution = $166.67.4.3 a)b) Let x1 = level of activity 1x2 = level of activity 2x3 = level of activity 3Maximize Contribution = $50x1 + $40x2 + $70x3subject to 30x1 + 20x2≤ 50010x2 + 40x3≤ 60020x1 + 20x2 + 30x3≤ 1,000and x1≥ 0, x2≥ 0, x3≥ 0.4.4b) Below are five possible guesses (many answers are possible).Best4.5 a) The activities are the production rates of products 1, 2, and 3. The limited resources are hours available per week on the milling machine, lathe, and grinder.b) The decisions to be made are how many of each product should be produced per week. The constraints on these decisions are the number of hours available per week on the milling machine, lathe, and grinder as well as the sales potential of product 3. The overall measure of performance is total profit, which is to be maximized.c) milling machine: 9(# units of 1) + 3(# units of 2) + 5(# units of 3) ≤ 500 lathe: 5(# units of 1) + 4(# units of 2) ≤ 350 grinder: 3(# units of 1) + 2(# units of 3) ≤ 150 sales: (# units of 3) ≤ 20Nonnegativity: (# units of 1) ≥ 0, (# units of 2) ≥ 0, (# units of 3) ≥ 0Profit = $50(# units of 1) + $20(# units of 2) + $25(# units of 3)d)Data cells: B2:D2, B5:D7, G5:G7, and D12 Changing cells: B10:D10 Target cell: G10 Output cells: E5:E734567E Hours Used=SUMPRODUCT(B5:D5,$B$10:$D$10)=SUMPRODUCT(B6:D6,$B$10:$D$10)=SUMPRODUCT(B7:D7,$B$10:$D$10)910GTotal Prof it=SUMPRODUCT(B2:D2,B10:D10)e) Let x 1 = units of product 1 produced per weekx 2 = units of product 2 produced per week x 3 = units of product 3 produced per week Maximize Profit = $50x 1 + $20x 2 + $25x 3 subject to 9x 1 3x 2 + 5x 3 ≤ 500 hours 5x 1 + 4x 2 ≤ 350 hours 3x 1 + 2x 3 ≤ 150 hours x 3 ≤ 20 and x 1 ≥ 0, x 2 ≥ 0,x 3 ≥ 0.4.6 a) The activities are the production quantities of parts A, B, and C. The limited resourcesare the hours available on machine 1 and machine 2.c) Below are three possible guesses (many answers are possible).Beste)B = number of part B producedC = number of part C producedMaximize Profit = $50A + $40B + $30Csubject to 0.02A + 0.03B + 0.05C≤ 40 hours0.05A + 0.02B + 0.04C≤ 40 hoursand A≥ 0, B≥ 0, C≥ 0.4.74.8b)Bestd) 1x2 = level of activity 2Minimize Cost = $60x1 + $50x2subject to 5x1 + 3x2≥ 602x1 + 2x2≥ 307x1 + 9x2≥ 126and x1≥ 0, x2≥ 0.e) Optimal Solution: (x1, x2) = (6.75, 8.75) and Total Cost = $842.50.4.9b) Below are five possible guesses (many answers are possible).Best4.10b) (x1, x2, x3) = (1,2,2) is a feasible solution with a daily cost of $3.48. This diet willprovide 210 kg of carbohydrates, 310 kg of protein, and 170 kg of vitamins daily.c) Answers will vary.e) Let C = kg of corn to feed each pigT = kg of tankage to feed each pigA = kg of alfalfa to feed each pigMinimize Cost = $0.84C + $0.72T + $0.60Asubject to 90C + 20T + 40A≥ 20030C + 80T + 40A≥ 18010C + 20T + 60A≥ 150and C≥ 0, T≥ 0, A≥ 0.4.11c) (x1, x2, x3) = (100,100,200) is a feasible solution. This would generate $400 million in5 years, $300 million in 10 years, and $550 million in 20 years. The total invested willbe $400 million.d) Answers will vary.f) Let x1 = units of Asset 1 purchasedx2 = units of Asset 2 purchasedx3 = units of Asset 3 purchasedMinimize Cost = x1 + x2 + x3 ($millions)subject to 2x1 + x2 + 0.5x3≥ 400 ($millions)0.5x1 + 0.5x2 + x3≥ 100 ($millions)1.5x2 + 2x3≥ 300 ($millions)and x1≥ 0, x2≥ 0, x3≥ 0.4.12 a) The activities are leasing space in each month for a number of months. The benefit ismeeting the space requirements for each month.b) The decisions to be made are how much space to lease and for how many months. Theconstraints on these decisions are the minimum required space. The overall measure ofperformance is cost which is to be minimized.c) Month 1: (M1 1mo lease) + (M1 2mo lease) + (M1 3mo lease) + (M1 4mo lease) + (M15 mo lease) ≥ 30,000 square feet.Month 2: (M1 2mo lease) + M1 3 mo lease) + (M1 4 mo lease) + (M1 5mo lease) +(M2 1 mo lease) + (M2 2 mo lease) + (M2 3 mo lease) + (M2 4 mo lease) ≥ 20,000square feet.Month 3: (M1 3mo lease) + (M1 4mo lease) + (M1 5mo lease) + (M2 2mo lease) + (M23mo lease) + (M2 4mo lease) + (M3 1mo lease) + (M3 2mo lease) + (M3 3mo lease) ≥40,000 square feet.Month 4: (M1 4mo lease) + (M1 5mo lease) + (M2 3mo lease) + (M2 4mo lease) + (M32 mo lease) + (M3 3mo lease) + (M4 1mo lease) + (M4 2mo lease) ≥ 10,000 square feet.Month 5: (M1 5mo lease) + (M2 4mo lease) + (M3 3mo lease) + (M4 2 mo lease) +(M5 1mo lease) ≥ 50,000 square feet.Nonnegativity: (M1 1mo lease) ≥ 0, (M1 2mo lease) ≥ 0, (M1 3 mo lease) ≥ 0, (M1 4mo lease) ≥ 0, (M1 5mo lease) ≥ 0, (M2 1mo lease) ≥ 0, (M2 2mo lease) ≥ 0, (M2 3 molease) ≥ 0, (M2 4mo lease) ≥ 0, (M3 1mo lease) ≥ 0, (M3 2mo lease) ≥ 0, (M3 3molease) ≥ 0, (M4 1mo lease) ≥ 0, (M4 2mo lease) ≥ 0, (M5 1mo lease) ≥ 0.Cost = ($650)[(M1 1mo lease) + (M2 1mo lease) + (M3 1mo lease) + (M4 1mo lease) +(M5 1mo lease)] + ($1,000)[(M1 2mo lease) + (M2 2mo lease) + (M3 2mo lease) +(M4 2mo lease)] + ($1,350)[(M1 3mo lease) + (M2 3mo lease) + (M3 3mo lease)] +($1,600)[(M1 4mo lease) + (M2 4mo lease)] + ($1,900)[M1 5mo lease]d)Data cells: B4:P8, B10:P10, and S4:S8 Changing cells: B13:P13 Target cell: S13 Output cells: Q4:Q812345678QTotal Leased (sq. ft.)=SUMPRODUCT(B4:P4,$B$13:$P$13)=SUMPRODUCT(B5:P5,$B$13:$P$13)=SUMPRODUCT(B6:P6,$B$13:$P$13)=SUMPRODUCT(B7:P7,$B$13:$P$13)=SUMPRODUCT(B8:P8,$B$13:$P$13)1213STotal Cost=SUMPRODUCT(B10:P10,B13:P13)e) Let x ij = square feet of space leased in month i for a period of j months. for i = 1, ... , 5 and j = 1, ... , 6-i .Minimize C = $650(x 11 + x 21 + x 31 + x 41 + x 51) + $1,000(x 12 + x 22 + x 32 + x 42) +$1,350(x 13 + x 23 + x 33) + $1,600(x 14 + x 24) + $1,900x 15 subject to x 11 + x 12 + x 13 + x 14 + x 15 ≥ 30,000 square feet x 12 + x 13 + x 14 + x 15 + x 21 + x 22 + x 23 + x 24 ≥ 20,000 square feetx 13 + x 14 + x 15 + x 22 + x 23 + x 24 + x 31 + x 32 + x 33 ≥ 40,000 sq. feet x 14 + x 15 + x 23 + x 24 + x 32 + x 33 + x 41 + x 42 ≥ 10,000 square feet x 15 + x 24 + x 33 + x 42 + x 51 ≥ 50,000 square feet and x ij ≥ 0, for i = 1, ... , 5 and j = 1 , ... , 6-i . 4.134.14a) This is a cost-benefit-tradeoff problem because it asks you to meet minimum required benefit levels (number of consultants working each time period) at minimum cost.b)c) Let f1 = number of full-time consultants working the morning shift (8 a.m.-4 p.m.),f2 = number of full-time consultants working the afternoon shift (12 p.m.-8 p.m.),f3 = number of full-time consultants working the evening shift (4 p.m.-midnight),p1 = number of part-time consultants working the first shift (8 a.m.-12 p.m.),p2 = number of part-time consultants working the second shift (12 p.m.-4 p.m.),p3 = number of part-time consultants working the third shift (4 p.m.-8 p.m.),p4 = number of part-time consultants working the fourth shift (8 p.m.-midnight).Minimize C = ($14 / hour)(8 hours)(f1 + f2 + f3) + ($5 / hour)(4 hours)(p1 + p2 + p3 + p4)subject to f1 + p1≥ 6f1 + f2 + p2≥ 8f2 + f3 + p3≥ 12f3 + p4≥ 6f1≥ 2p1f1 + f2≥ 2p2f2 + f3≥ 2p3f3≥ 2p4and f1≥ 0, f2≥ 0, f3≥ 0, p1≥ 0, p2≥ 0, p3≥ 0, p4≥ 0.4.15 a) This is a distribution-network problem because it deals with the distribution of goodsthrough a distribution network at minimum cost.b)c) Let x ij = number of units to ship from Factory i to Customer j (i = 1,2; j = 1, 2, 3)Minimize Cost = $600x11 + $800x12 + $700x13 + $400x21 + $900x22 + $600x23subject to x11 + x12 + x13 = 400x21 + x22 + x23 = 500x11 + x21 = 300x12 + x22 = 200x13 + x23 = 400and x11≥ 0, x12≥ 0, x13≥ 0, x21≥ 0, x22≥ 0, x23≥ 0.4.16 a) Requirement 1: The total amount shipped from Mine 1 must be 40 tons.Requirement 2: The total amount shipped from Mine 2 must be 60 tons.Requirement 3: The total amount shipped to the Plant must be 100 tons.Requirement 4: For Storage 1, the amount shipped out = the amount in.Requirement 5: For Storage 2, the amount shipped out = the amount in.b)c) Let x M1S1 = number of units shipped from Mine 1 to Storage 1x M1S2 = number of units shipped from Mine 1 to Storage 2x M2S1 = number of units shipped from Mine 2 to Storage 1x M2S2 = number of units shipped from Mine 2 to Storage 2x S1P = number of units shipped from Storage 1 to the Plantx S2P = number of units shipped from Storage 2 to the PlantMinimize Cost = $2,000x M1S1 + $1,700x M1S2 + $1,600x M2S1 + $1,100x M2S2+$400x S1P + $800x S2Psubject to x M1S1 + x M1S2 = 40x M2S1 + x M2S2 = 60x M1S1 + x M2S1 = x S1Px M1S2 + x M2S2 = x S2Px S1P + x S2P = 100x M1S1≤ 30, x M1S2≤ 30, x M2S1≤ 50, x M2S2≤ 50, x S1P≤ 70, x S2P≤ 70 and x M1S1≥ 0, x M1S2≥ 0, x M2S1≥ 0, x M2S2≥ 0, x S1P≥ 0, x S2P≥ 0.4.17 a) A1 + B1 + R1 = $60,000A2 + B2 + C2 + R2 = R1A3 + B3 + R3 = R2 + 1.40A1A4 + R4 = R3 + 1.40A2 + 1.70B1A5 + D5 + R5 = R4 + 1.40A3 + 1.70B2b) Let A t = amount invested in investment A at the beginning of year t.B t = amount invested in investment B at the beginning of year t.C t = amount invested in investment C at the beginning of year t.D t = amount invested in investment D at the beginning of year t.R t = amount not invested at the beginninf of year t.Maximize Return = 1.40A4 + 1.70B3 + 1.90C2 + 1.30D5 + R5subject to A1 + B1 + R1 = $60,000A2 + B2 + C2–R1 + R2 = 0–1.40A1 + A3 + B3–R2 + R3 = 0–1.40A2 + A4– 1.70B1–R3 + R4 = 0–1.40A3– 1.70B2 + D5–R4 + R5 = 0and A t≥ 0, B t≥ 0, C t≥ 0, D t≥ 0, R t≥ 0.c)4.18 a) Let x i = percentage of alloy i in the new alloy (i = 1, 2, 3, 4, 5).(60%)x1 + (25%)x2 + (45%)x3 + (20%)x4 + (50%)x5 = 40%(10%)x1 + (15%)x2 + (45%)x3 + (50%)x4 + (40%)x5 = 35%(30%)x1 + (60%)x2 + (10%)x3 + (30%)x4 + (10%)x5 = 25%x1 + x2 + x3 + x4+ x5 = 100%b)c) Let x i = percentage of alloy i in the new alloy (i = 1, 2, 3, 4, 5).Minimize Cost = $22x1 + $20x2 + $25x3 + $24x4 + $27x5subject to (60%)x1 + (25%)x2 + (45%)x3 + (20%)x4 + (50%)x5 = 40%(10%)x1 + (15%)x2 + (45%)x3 + (50%)x4 + (40%)x5 = 35%(30%)x1+ (60%)x2 + (10%)x3 + (30%)x4 + (10%)x5 = 25% and x1≥ 0, x2≥ 0, x3≥ 0, x4≥ 0, x5≥ 0.4.19 a)b) Let x ij = number of units produced at plant i of product j (i = 1, 2, 3; j = L, M, S).Maximize Profit = $420(x1L + x2L + x3L) + $360(x1M + x2M + x3M) + $300(x1S + x2S + x3S)subject to x1L + x1M + x1S≤ 750x2L + x2M + x2S≤ 900x3L + x3M + x3S≤ 45020x1L + 15x1M + 12x1S≤ 13,000 square feet20x2L + 15x2M + 12x2S≤ 12,000 square feet20x3L + 15x3M + 12x3S≤ 5,000 square feetx1L + x2L + x3L≤ 900x1M + x2M + x3M≤ 1,200x1S + x2S + x3S≤ 750(x1L + x1M + x1S) / 750 = (x2L + x2M + x2S) / 900(x1L + x1M + x1S) / 750 = (x3L + x3M + x3S) / 450and x1L≥ 0, x1M≥ 0, x1S≥ 0, x2L≥ 0, x2M≥ 0, x2S≥ 0, x3L≥ 0, x3M≥ 0, x3S≥ 0.4.20 a)b) Let x ij = tons of cargo i stowed in compartment j (i = 1,2,3,4; j = F, C, B)Maximize Profit = $320(x1F + x1C + x1B) + $400(x2F + x2C + x2B)+ $360(x3F + x3C + x3B) + $290(x4F + x4C + x4B)subject to x1F + x2F + x3F + x4F≤ 12 tonsx1C + x2C + x3C + x4C≤ 18 tonsx1B + x2B + x3B + x4B≤ 10 tonsx1F + x1C + x1B≤ 20 tonsx2F + x2C + x2B≤ 16 tonsx3F + x3C + x3B≤ 25 tonsx4F + x4C + x4B≤ 13 tons500x1F + 700x2F + 600x3F + 400x4F≤ 7,000 cubic feet500x1C + 700x2C + 600x3C + 400x4C≤ 9,000 cubic feet500x1B + 700x2B + 600x3B + 400x4B≤ 5,000 cubic feet(x1F + x2F + x3F + x4F) / 12 = (x1C + x2C + x3C + x4C) / 18(x1F + x2F + x3F + x4F) / 12 = (x1B + x2B + x3B + x4B) / 10and x1F≥ 0, x1C≥ 0, x1B≥ 0, x2F≥ 0, x2C≥ 0, x2B≥ 0,x3F≥ 0, x3C≥ 0, x3B≥ 0, x4F≥ 0, x4C≥ 0, x4B≥ 0.4.21 a)b) Let M=number of men’s gloves to produce per week,W= number of women’s gloves to produce per week,C= number of children’s gloves to produce per week,F = number of full-time workers to employ,PT = number of part-time workers to employ.Maximize Profit = $8M + $10W + $6C– $13(40)F– $10(20)PTsubject to 2M + 1.5W + C≤ 5,000 square feet30M + 45W + 40C≤ 40(60)F + 20(60)PT hoursF≥ 20F≥ 2PTand M≥ 0, W≥ 0, C≥ 0, F≥ 0, PT≥ 0.4.224.23 a) Resource Constraints:Calories must be no more than 420.No more than 20% of total calories from fat.Benefit Constraints:Calories must be at least 380There must be at least 50 mg of vitamin content.There must be at least 2 times as much strawberry flavoring as sweetener.Fixed-Requirement Constraints:There must be 15 mg of thickeners.b)c) Let S = Tablespoons of strawberry flavoring,CR = Tablespoons of cream,V = Tablespoons of vitamin supplement,A = Tablespoons of artificial sweetener,T = Tablespoons of thickening agent,Minimize C = $0.10S + $0.08CR + $0.25V + $0.15A + $0.06Tsubject to 50S + 100CR + 120A + 80T≥ 380 calories50S + 100CR + 120A + 80T≤ 420 caloriesS + 75CR + 30T≤ 0.2(50S + 100C + 120A + 80T)20S + 50V + 2T≥ 50 mg VitaminsS≥ 2A3S + 8CR + V + 2A + 25T = 15 mg Thickenersand S≥ 0, CR≥ 0, V≥ 0, A≥ 0, T≥ 0.4.24 a) Resource Constraints:Calories must be no more than 600.No more than 30% of total calories from fat.Benefit Constraints:Calories must be at least 400There must be at least 60 mg of vitamin C.There must be at least 12 g of protein.There must be at least 2 times as much peanut butter as jelly.There must be at least 1 cup of liquidFixed-Requirement Constraints:There must be 2 slices of bread.b)c) Let B = slices of bread,P= Tablespoons of peanut butter,S = Tablespoons of strawberry jelly,G = graham crackers,M = cups of milk,J = cups of juice.Minimize C = $0.05B + $0.04P + $0.07S + $0.08G + $0.15M + $0.35Jsubject to 70B + 100P + 50S + 60G + 150M + 100J≥ 400 calories70B + 100P + 50S + 60G + 150M + 100J≤ 600 calories10B + 75P + 20G + 70M≤ 0.3(70B + 100P + 50S + 60G + 150M + 100J)3S + 2M + 120J≥ 60mg Vitamin C3B + 4P + G + 8M + J≥ 12mg ProteinB = 2 slicesP≥ 2SM + J≥ 1 cupand B≥ 0, P≥ 0, S≥ 0, G≥ 0, M≥ 0, J≥ 0.Cases4.1 a) The fixed design and fashion costs are sunk costs and therefore should not beconsidered when setting the production now in July. Since the velvet shirts have apositive contribution to covering the sunk costs, they should be produced or at leastconsidered for production according to the linear programming model. Had Ted raisedthese concerns before any fixed costs were made, then he would have been correct toadvise against designing and producing the shirts. With a contribution of $22 and ademand of 6000 units, maximum expected profit will be only $132,000. This amountwill not be enough to cover the $500,000 in fixed costs directly attributable to thisproduct.b) The linear programming spreadsheet model for this problem is shown below.67B C DMaterial Cost =SUMPRODUCT(CostOf Material,C11:C17)=SUMPRODUCT(CostOf Material,D11:D17)Net Contribution=Price-LMCost-MaterialCost =Price-LMCost-MaterialCost91011121314151617N Material Used=SUMPRODUCT(C11:M11,ItemsProduced)=SUMPRODUCT(C12:M12,ItemsProduced)=SUMPRODUCT(C13:M13,ItemsProduced)=SUMPRODUCT(C14:M14,ItemsProduced)=SUMPRODUCT(C15:M15,ItemsProduced)=SUMPRODUCT(C16:M16,ItemsProduced)=SUMPRODUCT(C17:M17,ItemsProduced)2021222324OP Total Contribution=SUMPRODUCT(NetContribution,ItemsProduced)Fixed Cost8960000Total Prof it=TotalContribution-FixedCostTrendLine should produce 4,200 Wool Slacks, 4,000 Cashmere Sweaters, 7,000 Silk Blouses, 15,000 Silk Camisoles, 8,067 Tailored Skirts, 5,000 Wool Blazers, 40,000 Cotton Minis, 6,000 Velvet Shirts, and 9,244 Button-Down Blouses. The total net contribution of all clothing items is $6,862,933. However, with the total fixed cost of $860,000 + 3($2,700,000) or $8,960,000, TrendLines actually loses $2,097,067.c) If velvet cannot be sent back to the textile wholesaler, then the whole quantity will beconsidered as a sunk cost and therefore added to the fixed costs. The objective function coefficients of items using velvet will no longer include the material cost. The netcontribution of the velvet pants and shirts are now $175 and $40, respectively. The revised spreadsheet model is as follows.20 21 22 23 24 25O PTotalContribution=SUMPRODUCT(NetContribution,ItemsProduced) Original Fixed Cost8960000Velv et Sunk Cost=B16*P16Total Prof it=TotalContribution-FixedCost-Velv etSunkCostThe production plan changes considerably. TrendLines should produce 3,178 tailored skirts (down from 8,067), 3,667 velvet pants (up from 0), 60,000 cotton minis (up from 40,000), and 15,763 button-down blouses (up from 9,244). The production decisions for all other items are unaffected by the change. The total net contribution of allclothing items equals $840,000 + $1,226,00 + $ 2,025,000 + $2,983,822.22 =$7,085,822. The sunk costs now include the material cost for velvet and totals$9,200,000. The loss now equals $2,114,178.d) When TrendLines cannot return the velvet to the wholesaler, the costs for velvet cannotbe recovered. These cost are no longer variable cost but now are sunk cost. As aconsequence the increased net contribution of the velvet items makes them moreattractive to produce. This way the revenues from selling these items can contribute to the recovery of at least some of the fixed costs. Instead of zero TrendLines nowproduces 3,667 velvet pants. These pants also require some acetate and thus theirproduction affects the production plan for all other items. Since it is not optimal to make full use of the ordered velvet in part (b) it comes as no surprise that the loss in part (c) is even bigger than in part (b).e) The unit contribution of a wool blazer changes to $75.25.TrendLines should produce 10,067 skirts (up from 8,067), the minimum of 3,000 wool blazers (down from 5,000), and 6,578 button-down blouses (down from 9,244). The production decisions for all other items are unaffected by the change. The total net contribution of all clothing items is $6,527,933.33. The total loss is $2,432,067.f) The available acetate changes from 28,000 to 38,000 square yards. The resultingspreadsheet solution is shown below.TrendLines should produce 14,733 skirts (up from 8,067) and 356 button-down blouses (down from 9,244). The production decisions for all other items are unaffected by the change. The total net contribution of all clothing items is $7,581,267. The loss is$1,378,733.g) We need to include new decision variables representing the number of clothing itemsthat are sold during the November sale. The new spreadsheet model is shown below.91011B C D Nov Discount 0.4Price (Nov )=(1-Nov Discount)*Price =(1-Nov Discount)*PriceNet Contribution (Nov )=PriceNov -LMCost-MaterialCost =PriceNov -LMCost-MaterialCost131415161718192021N Material Used=SUMPRODUCT(C15:M15,TotalSales)=SUMPRODUCT(C16:M16,TotalSales)=SUMPRODUCT(C17:M17,TotalSales)=SUMPRODUCT(C18:M18,TotalSales)=SUMPRODUCT(C19:M19,TotalSales)=SUMPRODUCT(C20:M20,TotalSales)=SUMPRODUCT(C21:M21,TotalSales)2425262728OP Total Contribution=SUMPRODUCT(NetContribution,SeptOctSales)+SUMPRODUCT(NetContributionNov ,Nov SalesFixed Cost8960000Total Prof it=TotalContribution-FixedCostIt only pays to produce 2,000 more Cashmere sweaters. The production plan for all other items is the same as in part (b). The sale of the Cashmere sweaters increases the total net contribution by $60,000 to $6,922,933, and reduces the loss to $2,037,066.67.4.2 a) We define 12 decision variables, one for each age group surveyed in each region. Rob'srestrictions are easily modeled as constraints. For example, his condition that at least 20percent of the surveyed customers have to be from the first age group requires that thesum of the variables for the age group "18 to 25" across all three regions is at least 400.All his other requirements are modeled similarly. Finally, the sum of all variables has toequal 2000, because that is the number of customers Rob wants to have interviewed.Range Name CellsCostOf Surv ey C3:F5NumberToSurv ey C9:F11PercentageRequiredInAG C15:F15PercentageRequiredInRegion J9:J11RequiredInAG C14:F14RequiredInRegion I9:I11RequiredSurv ey s J15TotalCost J17 TotalInAG C12:F12 TotalInRegion G9:G11 TotalSurv ey s J137891011G H ITotal Requiredin Region in Region =SUM(C9:F9)>==J9*RequiredSurv ey s=SUM(C10:F10)>==J10*RequiredSurv ey s =SUM(C11:F11)>==J11*RequiredSurv ey s12 13 14B C DTotal in A.G.=SUM(C9:C11)=SUM(D9:D11)>=>=Required in A.G.=C15*RequiredSurv ey s=D15*RequiredSurv ey s1314151617I JTotal Surv ey s=SUM(NumberToSurv ey)=Required Surv ey s2000Total Cost=SUMPRODUCT(CostOf Surv ey,NumberToSurv ey)The cost of conducting the survey meeting all constraints imposed by AmeriBank incurs cost of $11,200. The mix of customers is displayed in the spreadsheet above.b) Sophisticated Surveys will submit a bid of (1.15)($11,200) = $12,880.。
数据模型重点习题及答案

数据模型与决策14版重点习题与答案第4章16题:芬古森造纸公司生产用于法器、台式计算器和收银机的卷纸。
这些卷纸每卷长度为200英尺,宽度可为1.5,2.5和3.5英尺。
生产过程只能提供200英尺长和10英尺宽的卷纸。
所以,公司必须剪切卷纸以满足所需的宽度。
7种剪切方案以及每种方案造成的浪费如下表所示。
A.若公司希望使用的10英寸卷纸最少,则每一种方案应剪切多少个10英寸卷纸?总欧冠那个需要多少个?最后浪费了多少(英寸)?B.若公司希望造成的浪费最少,每一种方案应剪切多少个10另存卷纸?总共需要多少?最后浪费了多少?C.A问题和b问题有什么不同?在这个案例里,你偏好哪一种目标?请加以解释。
什么样的情况下,另一种目标更有吸引力?答案:A:根据题目要求,定义决策变量如下:X1=方案1中应剪切10英寸卷的个数X2=方案2中应剪切10英寸卷的个数X3=方案3中应剪切10英寸卷的个数X4=方案4中应剪切10英寸卷的个数X5=方案5中应剪切10英寸卷的个数X6=方案6中应剪切10英寸卷的个数X7=方案7中应剪切10英寸卷的个数如果建模目标是希望使用10英寸的卷纸数量最少,那么目标函数是:Min X1+X2+X3+X4+X5+X6+X7根据已知信息,已知模型的约束条件为:6X1+ 2X3+X5+ X6+ 4X7 ≥10004X2+ X4 +3X5+ 2X6≥20002X3+2X4 + X6+ X7 ≥4000X1,X2,X3,X4,X5,X6,X7≥0对上述模型用LINGO进行求解,结果如下:综上可得,总共需要10英寸卷纸的数量为2125个,其中每种方案所需数量为:X1=0,X2=125,X3=500,X4=1500,X5=0,X6=0,X7=0;最后浪费的尺寸为:X1+0X2+0X3+0.5X4+X5+0X6+0.5X7=750英寸;b.目标函数是:Min X1+0X2+0X3+0.5X4+X5+0X6+0.5X7=X1+0.5X4+X5+0.5X7根据已知信息,已知模型的约束条件为:6X1+ 2X3+X5+ X6+ X7 ≥10004X2+ X4 +3X5+ 2X6≥20002X3+2X4 + X6+ X7 ≥4000X1,X2,X3,X4,X5,X6,X7≥0对上述模型用LINGO求解得,无浪费,总共需要10英寸卷纸的数量为2500个,但是1.5英寸的规格多生产了3000个;第4章17题弗朗德克公司制造、组装和改造仓库和分销中心使用装卸装备。
《数据模型与决策》复习题及参考答案

二、应用各学科交叉的方法三、采用计划方法 四、为进一步研究揭露新
问题。
5、线性规划数学模型具备哪几个要素?答:(1).求一组决策变量Xi或xj
的值(i=1,2,…m j=1,2…n)使目标函数达到极大或极小;(2).表示 约束条件的数学式都是线性等式或不等式;(3).表示问题最优化指标的目 标函数都是决策变量的线性函数
17.求解线性规划问题可能的结果有无解, 有唯一最优解,有无穷多个最优解。
18.如果某个约束条件是“w”情形,若化为标准形式,需要引入一松弛变量。
19.如果某个变量X为自由变量,则应引进两个非负变量XjXj,同时令X=
20.表达线性规划的简式中目标函数为max(min)Z=ECjX』。
二、单选题
1.如果一个线性规划问题有n个变量,m个约束方程(m<n),系数矩阵的数
A.观察B.应用C.实验D.调查
3•建立运筹学模型的过程不包括(A)阶段。
A.观察环境B.数据分析C.模型设计D.模型实施
4.建立模型的一个基本理由是去揭晓那些重要的或有关的(B)
A数量B变量C约束条件D目标函数
5.模型中要求变量取值(D)
A可正B可负C非正D非负
6.运筹学研究和解决问题的效果具有(A)
的集合。
5•运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。运 筹学研究和解决问题的效果具有连续性。
6•运筹学用系统的观点研究功能之间的关系。
7•运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用
特性。
8•运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9•运筹学解决问题时首先要观察待决策问题所处的环境。
数据模型与决策 习题答案

数据模型与决策习题答案数据模型与决策习题答案在当今信息时代,数据的价值越来越受到重视。
数据模型作为一种描述和组织数据的方式,对于决策过程起着重要的作用。
本文将通过解答一些与数据模型和决策相关的习题,来探讨数据模型在决策中的应用和意义。
1. 什么是数据模型?为什么在决策过程中需要使用数据模型?数据模型是对现实世界进行抽象和描述的一种方式。
它通过定义实体、属性和关系的方式,将现实世界中的事物转化为计算机可以处理的形式。
数据模型可以帮助我们更好地理解和组织数据,为决策提供支持。
在决策过程中,数据模型的使用具有以下几个重要的作用:1) 数据模型可以帮助我们对现实世界进行建模和描述,将复杂的现实问题转化为可计算的形式,从而更好地理解问题的本质。
2) 数据模型可以帮助我们组织和管理大量的数据,使得数据更易于存储、检索和分析,为决策提供必要的信息支持。
3) 数据模型可以帮助我们对不同的决策方案进行评估和比较,通过模拟和预测的方式,帮助我们选择最佳的决策方案。
2. 数据模型的种类有哪些?请简要介绍其中的几种。
常见的数据模型包括层次模型、网状模型、关系模型和面向对象模型等。
层次模型是最早的数据模型之一,它将数据组织成一种树状结构,其中每个节点代表一个实体,每个节点之间通过父子关系连接。
层次模型的优点是结构简单,易于理解和实现,但缺点是不适合处理复杂的关系和多对多的关联。
网状模型是层次模型的扩展,它允许多个父节点指向同一个子节点,从而解决了层次模型不适合处理多对多关联的问题。
但网状模型的缺点是结构复杂,不易理解和维护。
关系模型是目前应用最广泛的数据模型,它将数据组织成一张二维表格,其中每一行代表一个实体,每一列代表一个属性。
关系模型通过定义实体间的关系和约束,实现了数据的灵活查询和操作。
面向对象模型是一种基于对象的数据模型,它将数据组织成一组对象,每个对象包含了数据和对数据的操作。
面向对象模型适用于处理复杂的关系和行为,但在实际应用中较为复杂和庞大。
《数据、模型和决策》习题解答
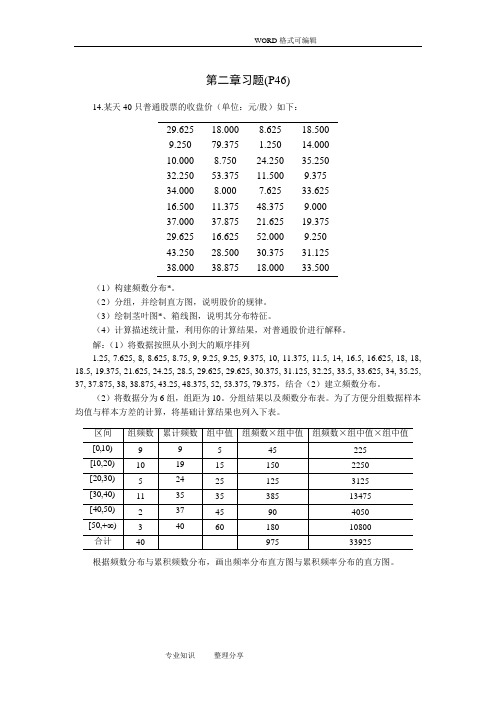
第二章习题(P46)14.某天40只普通股票的收盘价(单位:元/股)如下:29.625 18.000 8.625 18.5009.250 79.375 1.250 14.00010.000 8.750 24.250 35.25032.250 53.375 11.500 9.37534.000 8.000 7.625 33.62516.500 11.375 48.375 9.00037.000 37.875 21.625 19.37529.625 16.625 52.000 9.25043.250 28.500 30.375 31.12538.000 38.875 18.000 33.500(1)构建频数分布*。
(2)分组,并绘制直方图,说明股价的规律。
(3)绘制茎叶图*、箱线图,说明其分布特征。
(4)计算描述统计量,利用你的计算结果,对普通股价进行解释。
解:(1)将数据按照从小到大的顺序排列1.25, 7.625, 8, 8.625, 8.75, 9, 9.25, 9.25, 9.375, 10, 11.375, 11.5, 14, 16.5, 16.625, 18, 18, 18.5, 19.375, 21.625, 24.25, 28.5, 29.625, 29.625, 30.375, 31.125, 32.25, 33.5, 33.625, 34, 35.25, 37, 37.875, 38, 38.875, 43.25, 48.375, 52, 53.375, 79.375,结合(2)建立频数分布。
(2)将数据分为6组,组距为10。
分组结果以及频数分布表。
为了方便分组数据样本均值与样本方差的计算,将基础计算结果也列入下表。
根据频数分布与累积频数分布,画出频率分布直方图与累积频率分布的直方图。
频率分布直方图从频率直方图和累计频率直方图可以看出股价的规律。
股价分布10元以下、10—20元、30—40元占到60%,股价在40元以下占87.5%,分布不服从正态分布等等。
数据模型与决策试题及参考答案

《数据模型与决策》复习(附参考答案)2018.9一、填空题(五题共15分)1.已知成年男子的身高服从正态分布N(167.48,6.092),随机调查100位成年男子的身高,那么,这100位男子身高的平均数服从的分布是①。
解:N(167.48,0.609)考查知识点:已知总体服从正态分布,求样本均值的分布。
2.某高校想了解大学生每个月的消费情况,随机抽取了100名大学生,算得平均月消费额为1488元,标准差是2240元。
根据正态分布的“68-95-99”法则,该高校大学生每个月的消费额的95%估计区间为②。
解:[1040,1936]考查知识点:区间估计的求法。
正态总体均值的区间估计是[X-Z上,X + Z与] 1-a n'n1-a nn 其中X是样本平均数,s是样本的标准差,n是样本数。
详解:直接带公式得:区间估计是— s _ s2240 2240[X—Z -=, X + Z ,]= [1488 —2^^,1488 + 2^^] 山nn山.nn x100 * 100=[1040,1936]3.从遗传规律看,一个产妇生男生女的概率是一样的,都是50%,但也有个人的特殊情况。
假设某人前一胎是女孩,那么她的下一胎也是女孩的概率为0.55;如果某人前一胎是男孩,那么她的下一胎还是男孩的概率为0.48。
已知小李第一胎是女孩,那么她的第三胎生男孩的概率是③。
解p=0.4653考查知识点:离散概率计算方法。
详解:假设B1二第1胎生男孩,B2二第2胎生男孩,B3二第3胎生男孩G1二第1胎生女孩,G2=第2胎生女孩,G3=第3胎生女孩P(B3)二P(B3B2)+P(B3G2)(直观解释是:第二胎生男孩的情况下第三胎生男孩,第二胎生女孩的情况下第三胎生男孩,两个概率之和为P(B3))= P(B3|B2)P(B2)+P(B3|G2)P(G2)=0.48 义(1-0.55) + (1-0.55)义 0.55=0.46534.调查发现,一个刚参加工作的MBA毕业生在顶级管理咨询公司的初始年薪可以用均值为9万美元和标准差是2万美元的正态分布来表示,那么一个这样的毕业生初始年薪超过9万美元的概率是④。
《数据模型与决策》复习试题和参考题答案

《数据模型与决策》复习试题和参考题答案一、选择题1. 下列哪种数据模型不是数据库系统常用的数据模型?()A. 关系模型B. 层次模型C. 网状模型D. 面向对象模型2. 以下哪项不是数据库系统的主要功能?()A. 数据存储B. 数据检索C. 数据更新D. 数据加密3. 在关系数据库中,下列哪个概念表示表之间的关系?()A. 外键B. 主键C. 候选键D. 索引4. 下列哪种决策方法属于定量决策方法?()A. 直觉决策法B. 经验决策法C. 线性规划法D. 逻辑推理法5. 以下哪个概念不属于数据挖掘的范畴?()A. 关联规则B. 聚类分析C. 决策树D. 文本挖掘二、填空题6. 数据模型通常包括________、________和________三个基本要素。
7. 数据库系统的核心是________。
8. 在关系数据库中,为了实现表之间的连接,通常使用________。
9. 数据挖掘的方法主要包括________、________和________。
10. 线性规划法在决策过程中主要用于解决________问题。
三、判断题11. 数据模型是数据库设计和实现的基础,它描述了数据如何存储、组织和访问。
()12. 数据库系统只能用于存储数据,不能进行数据检索和更新操作。
()13. 在关系数据库中,主键可以唯一标识表中的每一行数据。
()14. 数据挖掘是一种从大量数据中提取有价值信息的方法,它包括关联规则、聚类分析和决策树等技术。
()15. 定量决策方法主要依赖于数学模型和算法,通常比定性决策方法更加准确和有效。
()四、简答题16. 简述数据模型的作用。
17. 简述数据库系统的四个主要功能。
18. 简述数据挖掘的主要应用领域。
19. 简述线性规划法的基本原理。
五、综合题20. 设某公司销售三种产品A、B、C,每种产品的销售价格、成本和销售量如下表所示。
请根据这些数据,计算该公司每种产品的利润,并确定哪种产品的销售利润最高。
MBA数据模型与决策考卷及答案

MBA数据模型与决策考卷一、选择题(每题2分,共20分)A. 变量B. 参数C. 数据源D. 数据分析工具A. 信息增益B. 权重C. 相关性D. 方差A. 线性回归模型B. 逻辑回归模型C. 神经网络模型D. 决策树模型A. 目标函数B. 约束条件C. 变量非负D. 变量连续A. 加权评分模型B. 层次分析法C. 数据包络分析法D. 主成分分析法A. 欧氏距离B. 曼哈顿距离C. 杰卡德距离D. 马氏距离A. 移动平均法B. 指数平滑法C. 自回归移动平均模型D. 聚类分析法A. 敏感度B. 确定性C. 稳定性D. 风险A. 数据库B. 模型库C. 知识库D. 网络库A. 净现值B. 内部收益率C. 投资回收期D. 利润率二、简答题(每题10分,共30分)1. 简述数据模型的分类及其特点。
2. 请阐述决策树的基本原理及其在商业决策中的应用。
3. 简述线性规划与非线性规划的区别。
三、计算题(每题15分,共30分)1. 某企业生产两种产品,产品A的利润为10元/件,产品B的利润为15元/件。
生产一件产品A需要2小时,生产一件产品B需要3小时。
企业每月共有240小时的生产时间,且市场需求量分别为100件和80件。
请用线性规划方法求解该企业如何分配生产时间以获得最大利润。
数据:{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}四、案例分析题(20分)某电商企业想要提高用户转化率,现有一份用户行为数据,包括用户年龄、性别、浏览时长、次数、购买次数等。
请结合数据模型与决策方法,为该企业提出一套提高用户转化率的策略。
五、论述题(10分)请结合实际案例,论述数据模型与决策在企业战略管理中的应用价值。
一、选择题答案1. D2. A3. C4. D5. D6. A7. D8. A9. D10. A二、简答题答案1. 数据模型分类及特点:统计模型:基于概率论和统计学原理,特点是可以处理不确定性数据。
优化模型:基于数学规划,特点是可以求解最优解。
《数据模型与决策》练习题及答案
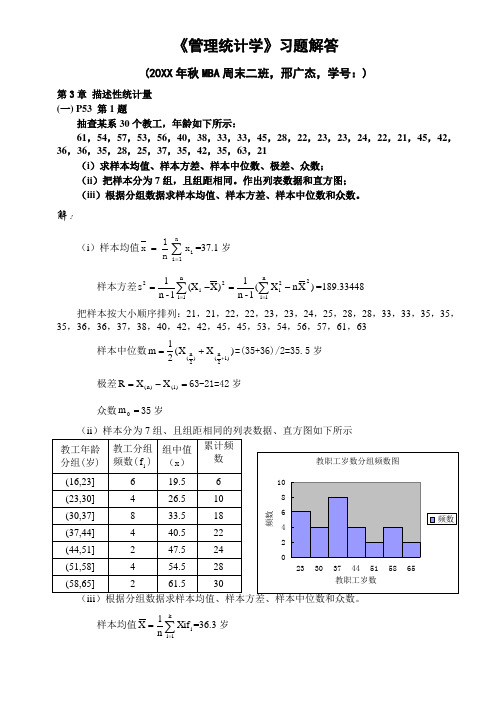
《管理统计学》习题解答(20XX 年秋MBA 周末二班,邢广杰,学号:)第3章 描述性统计量 (一) P53 第1题抽查某系30个教工,年龄如下所示:61,54,57,53,56,40,38,33,33,45,28,22,23,23,24,22,21,45,42,36,36,35,28,25,37,35,42,35,63,21(i )求样本均值、样本方差、样本中位数、极差、众数;(ii )把样本分为7组,且组距相同。
作出列表数据和直方图; (iii )根据分组数据求样本均值、样本方差、样本中位数和众数。
解:(i )样本均值∑==n1i ixn1x =37.1岁样本方差)X n X (1-n 1)X (X 1-n 1s 2n 1i 2i2n 1i i 2-=-=∑∑===189.33448 把样本按大小顺序排列:21,21,22,22,23,23,24,25,28,28,33,33,35,35,35,36,36,37,38,40,42,42,45,45,53,54,56,57,61,63样本中位数)X X (21m 1)2n ()2n (++==(35+36)/2=35.5岁极差=-=1)()n (X X R 63-21=42岁 众数=0m 35岁(ii )样本分为7组、且组距相同的列表数据、直方图如下所示样本均值i k1i f Xi n 1X ∑===36.3岁样本方差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i 2i i2k 1i i 2-=-=∑∑===174.3724 样本中位数810230730f F 2n i I m -+=-+==34.375岁 众数=--⨯-+=---+=+448248730f f 2f f f iI m 1m 1-m m 1-m m 033.5岁(二)P53 第2题某单位统计了不同级别的员工的月工资水平资料如下:解:样本均值i k1i f Xi n 1X ∑===1566.667元样本标准差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i2i i 2k 1i i -=-=∑∑===398.1751元 样本中位数在累计74人的那一组,m=1500元; 众数1500m 0=元。
《数据模型与决策》复习试题和参考题答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,“s·t”表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是( A )A.销售数量 B.销售价格 C.顾客的需求 D.竞争价格2.我们可以通过( C )来验证模型最优解。
A.观察 B.应用 C.实验 D.调查3.建立运筹学模型的过程不包括( A )阶段。
A.观察环境 B.数据分析 C.模型设计 D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的( B )A数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值( D )A可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有( A )A 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
