人教版高中数学必修2空间几何体练习题及答案全

合集下载

【三维设计】人教版高中数学必修2练习：第一章空间几何体(含答案解析)

1．1空间几何体的结构第一课时棱柱、棱锥、棱台的结构特征空间几何体与多面体[导入新知]1．空间几何体1．对于多面体概念的理解，注意以下两个方面：(1)多面体是由平面多边形围成的，围成一个多面体至少要4个面．一个多面体由几个面围成，就称为几面体．(2)多面体是一个“封闭”的几何体，包括其内部的部分． 2．棱柱具有以下结构特征和特点：(1)侧棱互相平行且相等，侧面都是平行四边形．(2)两个底面与平行于底面的截面是全等的多边形，如图a 所示．(3)过不相邻的两条侧棱的截面是平行四边形，如图b 所示．(4)有两个面平行，其余各面都是平行四边形的几何体不一定是棱柱，如图c 所示．3．对于棱锥要注意有一个面是多边形，其余各面都是三角形的几何体不一定是棱锥，必须强调其余各面是共顶点的三角形，如图d 所示．4．棱台中各侧棱延长后必相交于一点，否则不是棱台．棱柱的结构特征[例1]下列关于棱柱的说法：(1)所有的面都是平行四边形；(2)每一个面都不会是三角形；(3)两底面平行，并且各侧棱也平行；(4)被平面截成的两部分可以都是棱柱．其中正确说法的序号是________．[答案](3)(4)[类题通法]有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析．①两个面互相平行；②其余各面是四边形；③相邻两个四边形的公共边互相平行．求解时，首先看是否有两个平行的面作为底面，再看是否满足其他特征．(2)多注意观察一些实物模型和图片便于反例排除．[活学活用]下列说法正确的是()A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．各个侧面都是正方形的四棱柱一定是正方体D．九棱柱有9条侧棱，9个侧面，侧面均为平行四边形答案：D棱锥、棱台的结构特征[例2]下列关于棱锥、棱台的说法：(1)用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；(2)棱台的侧面一定不会是平行四边形；(3)棱锥的侧面只能是三角形；(4)由4个面围成的封闭图形只能是三棱锥；(5)棱锥被平面截成的两部分不可能都是棱锥．其中说法正确的序号是________．[答案](2)(3)(4)[类题通法]判断棱锥、棱台形状的两个方法(1)举反例法：结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．(2)直接法：下列说法正确的有()①由5个面围成的多面体只能是四棱锥；②仅有两个面互相平行的五面体是棱台；③两个底面平行且相似，其余各面都是梯形的多面体是棱台；④有两个面互相平行，其余4个面都是等腰梯形的六面体是棱台．A．0个B．1个C．2个D．3个答案：A多面体的平面展开图[例3]如下图是三个几何体的侧面展开图，请问各是什么几何体？[解]由几何体的侧面展开图的特点，结合棱柱，棱锥，棱台的定义，可把侧面展开图还原为原几何体，如图所示：所以①为五棱柱，②为五棱锥，③为三棱台．[类题通法]1．解答此类问题要结合多面体的结构特征发挥空间想象能力和动手能力．2．若给出多面体画其展开图时，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面．3．若是给出表面展开图，则可把上述程序逆推．[活学活用]水平放置的正方体的6个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图(图中数字写在正方体的外表面上)，若图中“0”上方的“2”在正方体的上面，则这个正方体的下面是()A．1B．5C．快D．乐答案：B1.柱、锥、台结构特征判断中的误区[典例]如下图所示，下列关于这个几何体的正确说法的序号为________．①这是一个六面体；②这是一个四棱台；③这是一个四棱柱；④此几何体可由三棱柱截去一个三棱柱得到；⑤此几何体可由四棱柱截去一个三棱柱得到．[解析]①正确，因为有6个面，属于六面体的范围；②错误，因为侧棱的延长线不能交于一点，所以不正确；③正确，如果把几何体放倒就会发现是一个四棱柱；④⑤都正确，如下图所示．[答案]①③④⑤[易错防范]1．解答过程中易忽视侧棱的延长线不能交于一点，直观感觉是棱台，而不注意逻辑推理．2．解答空间几何体概念的判断题时，要注意紧扣定义，切忌只凭图形主观臆断．[成功破障]如右图所示，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是()A．棱柱B．棱台C．棱柱与棱锥的组合体D．不能确定答案：A一、选择题1．下列图形中，不是三棱柱的展开图的是()答案：C2.如右图所示，在三棱台ABC-A′B′C′中，截去三棱锥A′-ABC，则剩余部分是()A．三棱锥B．四棱锥C．三棱柱D．组合体答案：B3．下列说法正确的是()①棱锥的各个侧面都是三角形；②三棱柱的侧面为三角形；③四面体的任何一个面都可以作为棱锥的底面；④棱锥的各侧棱长都相等．A．①②B．①③C．②③D．②④答案：B4．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有()A．20 B．15C．12 D．10答案：D5．下列命题正确的是()A．用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台B．棱柱中两个互相平行的面一定是棱柱的底面C．棱台的底面是两个相似的正方形D．棱台的侧棱延长后必交于一点答案：D二、填空题6．面数最少的棱柱为________棱柱，共有________个面围成．答案：三 57.如右图所示，M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点，沿正方体表面从点A到点M的最短路程是________ cm.答案：138．侧棱垂直于底面的棱柱叫做直棱柱．侧棱不垂直于底面的棱柱叫做斜棱柱．底面是正多边形的直棱柱叫做正棱柱．底面是平行四边形的四棱柱叫做平行六面体．侧棱与底面垂直的平行六面体叫做直平行六面体．底面是矩形的直平行六面体叫做长方体．棱长都相等的长方体叫做正方体．请根据上述定义，回答下面的问题：(1)直四棱柱________是长方体；(2)正四棱柱________是正方体．(填“一定”“不一定”或“一定不”)答案：(1)不一定(2)不一定三、解答题9．如右图所示，长方体ABCD -A1B1C1D1.(1)这个长方体是棱柱吗？如果是，是几棱柱？为什么？(2)用平面BCNM把这个长方体分成两部分，各部分形成的几何体还是棱柱吗？如果是，是几棱柱，并用符号表示；如果不是，请说明理由．解：(1)是棱柱，并且是四棱柱，因为长方体相对的两个面是互相平行的四边形(作底面)，其余各面都是矩形(作侧面)，且相邻侧面的公共边互相平行，符合棱柱的定义．(2)截面BCNM的上方部分是三棱柱BB1M-CC1N，下方部分是四棱柱ABMA1-DCND1.10．给出两块正三角形纸片(如图所示)，要求将其中一块剪拼成一个底面为正三角形的三棱锥模型，另一块剪拼成一个底面是正三角形的三棱柱模型，请设计一种剪拼方案，分别用虚线标示在图中，并作简要说明．解：如图①所示，沿正三角形三边中点连线折起，可拼得一个底面为正三角形的三棱锥．如图②所示，正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的14，有一组对角为直角，余下部分按虚线折成，可成为一个缺上底的底面为正三角形的三棱柱，而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底.第二课时圆柱、圆锥、圆台、球的结构特征简单组合体的结构特征旋转体 [导入新知]1．以直角三角形斜边所在的直线为旋转轴，其余两边旋转成的曲面围成的旋转体不是圆锥．2．球与球面是完全不同的两个概念，球是指球面所围成的空间，而球面只指球的表面部分．3．圆台也可以看作是等腰梯形以其底边的垂直平分线为轴，各边旋转半周形成的曲面所围成的几何体．简单组合体[导入新知]1．简单组合体的概念由简单几何体组合而成的几何体叫做简单组合体．2．简单组合体的构成形式有两种基本形式：一种是由简单几何体拼接而成的；另一种是由简单几何体截去或挖去一部分而成的．[化解疑难]简单组合体识别的要求(1)准确理解简单几何体(柱、锥、台、球)的结构特征．(2)正确掌握简单组合体构成的两种基本形式．(3)若用分割的方法，则需要根据几何体的结构特征恰当地作出辅助线(或面)．旋转体的结构特征[例1]给出下列说法：(1)以直角三角形的一条边所在直线为轴，其余两边旋转形成的曲面围成的几何体是圆锥；(2)以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)经过圆锥任意两条母线的截面是等腰三角形；(4)圆锥侧面的母线长有可能大于圆锥底面圆直径．其中说法正确的序号是________．[答案](2)(3)(4)[类题通法]1．判断简单旋转体结构特征的方法(1)明确由哪种平面图形旋转而成．(2)明确旋转轴是哪条直线．2．简单旋转体的轴截面及其应用(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量．(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．[活学活用]给出下列说法：(1)圆柱的底面是圆面；(2)经过圆柱任意两条母线的截面是一个矩形面；(3)圆台的任意两条母线的延长线可能相交，也可能不相交；(4)夹在圆柱的两个截面间的几何体还是一个旋转体．其中说法正确的是________．答案：(1)(2)简单组合体[例2]观察下列几何体的结构特点，完成以下问题：(1)题图①所示几何体是由哪些简单几何体构成的？试画出几何图形，可旋转该图形180°后得到几何体①.(2)题图②所示几何体的结构特点是什么？试画出几何图形，可旋转该图形360°得到几何体②.(3)题图③所示几何体是由哪些简单几何体构成的？请说明该几何体的面数、棱数、顶点数．[解](1)图①是由圆锥和圆台组合而成．可旋转如下图形180°得到几何体①.(2)图②是由一个圆台，从上而下挖去一个圆锥，且圆锥的顶点恰为圆台底面圆的圆心．可旋转如下图形360°得到几何体②.(3)图③是由一个四棱锥与一个四棱柱组合而成，且四棱锥的底面与四棱柱底面相同．共有9个面，9个顶点，16条棱．[类题通法]1．明确组合体的结构特征，主要弄清它是由哪些简单几何体组成的，必要时也可以指出棱数、面数和顶点数，如题图③所示的组合体有9个面，9个顶点，16条棱．2．会识别较复杂的图形是学好立体几何的第一步，因此我们应注意观察周围的物体，然后将它们“分拆”成几个简单的几何体，进而培养我们的空间想象能力和识图能力．[活学活用]指出图①～图③的3个几何体分别是由哪些简单几何体组成的．解：图①几何体由一个圆锥、一个圆柱和一个圆台拼接而成；图②几何体由一个六棱柱和一个圆柱拼接而成；图③几何体由一个六棱柱挖去一个圆柱而成．1.旋转体的生成过程[典例]如右图所示，四边形ABCD为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体．[解题流程][规范解答]以边AD所在直线为旋转轴旋转，形成的几何体是圆台，如图①所示．以边AB所在直线为旋转轴旋转，形成的几何体是一个圆锥和一个圆柱拼接而成的几何体，如图②所示．以边CD所在直线为旋转轴旋转，形成的几何体是一个圆柱挖掉一个圆锥构成的几何体，如图③所示．以边BC所在直线为旋转轴旋转，形成的几何体是由一个圆台挖掉一个圆锥构成的几何体和一个圆锥拼接而成，如图④所示．[活学活用]一个有30°角的直角三角板绕其各条边所在直线旋转一周所得几何体是圆锥吗？如果以斜边上的高所在的直线为轴旋转180°得到什么几何体？旋转360°又得到什么几何体？解：如图①和图②所示，绕其直角边所在直线旋转一周围成的几何体是圆锥．如图③所示，绕其斜边所在直线旋转一周所得几何体是两个同底相对的圆锥．如图④所示，绕其斜边上的高所在的直线为轴旋转180°围成的几何体是两个半圆锥，旋转360°围成的几何体是一个圆锥．一、选择题1．下列说法正确的是()A．平行于圆锥某一母线的截面是等腰三角形B．平行于圆台某一母线的截面是等腰梯形C．过圆锥顶点的截面是等腰三角形D．过圆台上底面中心的截面是等腰梯形答案：C2．将一个等腰梯形绕它的较长的底边所在的直线旋转一周，所得的几何体包括() A．一个圆台、两个圆锥B．两个圆台、一个圆柱C．两个圆柱、一个圆台D．一个圆柱、两个圆锥答案：D3．以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的几何体是() A．两个圆锥拼接而成的组合体B．一个圆台C．一个圆锥D．一个圆锥挖去一个同底的小圆锥答案：D4．下列叙述中正确的个数是()①以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥；②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台；③圆柱、圆锥、圆台的底面都是圆面；④用一个平面去截圆锥，得到一个圆锥和一个圆台．A．0 B．1C．2 D．3答案：B5.如右图所示的几何体，关于其结构特征，下列说法不正确的是()A．该几何体是由两个同底的四棱锥组成的几何体B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中一个面是四边形，其余均为三角形答案：D二、填空题6．有下列说法：①在圆柱的上、下底面的圆周上各取一点，则这两点连线是圆柱的母线；②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在直线是互相平行的．其中正确的是________(把所有正确说法的序号都填上)．答案：②④7．下面这个几何体的结构特征是_____________________________________.答案：由一个四棱锥、一个四棱柱拼接，又在四棱柱中挖去了一个圆柱而成8．如图是一个几何体的表面展成的平面图形，则这个几何体是________．答案：圆柱三、解答题9．指出如图①、图②、图③所示的图形分别是由哪些简单几何体构成的．解：分割原图，使它的每一部分都是简单几何体．图①是由一个三棱柱和一个四棱柱拼接而成的简单组合体；图②是由一个圆锥和一个四棱柱拼接而成的简单组合体；图③是由一个半球、一个圆柱和一个圆台拼接而成的简单组合体．10.如右图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的半径分别为2 cm和5 cm，圆台的母线长是12 cm，求圆锥SO的母线长．解：如右图所示，过圆台的轴作截面，截面为等腰梯形ABCD ，由已知可得上底半径O 1A ＝2 cm ，下底半径OB ＝5 cm ，且腰长AB ＝12 cm.设截得此圆台的圆锥的母线长为l ，则由△SAO 1∽△SBO ，可得l －12l ＝25，所以l ＝20 cm ，即截得此圆台的圆锥的母线长为20 cm.1．2空间几何体的三视图和直观图1.2.1 & 1.2.2 中心投影与平行投影空间几何体的三视图中心投影与平行投影 [导入新知] 1．投影的定义由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影．其中，把光线叫做投影线，把留下物体影子的屏幕叫做投影面．2．中心投影与平行投影平行投影和中心投影都是空间图形的一种画法，但二者又有区别 (1)中心投影的投影线交于一点，平行投影的投影线互相平行．(2)平行投影下，与投影面平行的平面图形留下的影子，与这个平面图形的形状和大小完全相同；而中心投影则不同．三视图 [导入新知]1．每个视图都反映物体两个方向上的尺寸．正视图反映物体的上下和左右尺寸，俯视图反映物体的前后和左右尺寸，侧视图反映物体的前后和上下尺寸．2．画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．中心投影与平行投影 [例1] 下列说法中：①平行投影的投影线互相平行，中心投影的投影线相交于一点；②空间图形经过中心投影后，直线变成直线，但平行线可能变成了相交的直线； ③两条相交直线的平行投影是两条相交直线．其中正确的个数为( ) A ．0 B ．1 C ．2 D ．3[答案] B [类题通法]1．判定几何体投影形状的方法．(1)判断一个几何体的投影是什么图形，先分清楚是平行投影还是中心投影，投影面的位置如何，再根据平行投影或中心投影的性质来判断．(2)对于平行投影，当图形中的直线或线段不平行于投影线时，平行投影具有以下性质： ①直线或线段的投影仍是直线或线段； ②平行直线的投影平行或重合；③平行于投影面的线段，它的投影与这条线段平行且等长；④与投影面平行的平面图形，它的投影与这个图形全等；⑤在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．2．画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得此图形在该平面上的投影．[活学活用]如右图所示，在正方体ABCD -A′B′C′D′中，E，F分别是A′A，C′C的中点，则下列判断正确的序号是________．①四边形BFD′E在底面ABCD内的投影是正方形；②四边形BFD′E在平面A′D′DA内的投影是菱形；③四边形BFD′E在平面A′D′DA内的投影与在平面ABB′A内的投影是全等的平行四边形．答案：①③画空间几何体的三视图[例2]画出如右图所示的四棱锥的三视图．[解]几何体的三视图如下：[类题通法]画三视图的注意事项(1)务必做到长对正，宽相等，高平齐．(2)三视图的安排方法是正视图与侧视图在同一水平位置，且正视图在左，侧视图在右，俯视图在正视图的正下方．(3)若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．[活学活用]沿一个正方体三个面的对角线截得的几何体如下图所示，则该几何体的侧视图为()答案：B由三视图还原空间几何体[例3]如下图所示的三视图表示的几何体是什么？画出物体的形状．(1)(2)(3)[解](1)该三视图表示的是一个四棱台，如右图．(2)由俯视图可知该几何体是多面体，结合正视图、侧视图可知该几何体是正六棱锥．如下图．(3)由于俯视图有一个圆和一个四边形，则该几何体是由旋转体和多面体拼接成的组合体，结合侧视图和正视图，可知该几何体上面是一个圆柱，下面是一个四棱柱，所以该几何体的形状如右图所示．[类题通法]由三视图还原几何体时，一般先由俯视图确定底面，由正视图与侧视图确定几何体的高及位置，同时想象视图中每一部分对应实物部分的形状．[活学活用]如图①、图②、图③、图④为4个几何体的三视图，根据三视图可以判断这四个几何体依次分别为()A．三棱台、三棱柱、圆锥、圆台B．三棱台、三棱锥、圆锥、圆台C．三棱柱、正四棱锥、圆锥、圆台D．三棱柱、三棱台、圆锥、圆台答案：C2.画几何体的三视图常见误区[典例]某几何体及其俯视图如下图所示，下列关于该几何体正视图和侧视图的画法正确的是()[解析]该几何体是由圆柱切割而得，由俯视图可知正视方向和侧视方向，进一步可画出正视图和侧视图(如图所示)，故选A.[答案] A[易错防范]1．易忽视该组合体的结构特征是由圆柱切割而得到，对正视方向与侧视方向的判断不正确而出错．2．三种视图中，可见的轮廓线都画成实线，存在但不可见的轮廓线一定要画出，但要画成虚线．画三视图时，一定要分清可见轮廓线与不可见轮廓线，避免出现错误．[成功破障]沿圆柱体上底面直径截去一部分后的物体如右图所示，它的俯视图是()答案：D一、选择题1．4个直立在地面上的字母广告牌在不同情况下，在地面上的投影(阴影部分)效果如图，则在字母L，K，C的投影中，与字母N属同一种投影的有()答案：A2.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为()答案：D3．若某几何体的三视图如下图所示，则这个几何体的直观图可以是()答案：B4．某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()答案：C5．将正方体(如图①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的侧视图为()答案：B二、填空题6．已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于________．答案： 27．如图甲所示，在正方体ABCD -A1B1C1D1中，E，F分别是AA1，C1D1的中点，G是正方形BCC1B1的中心，则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________．答案：(1)(2)(3)8．两条平行线在一个平面内的正投影可能是________．①两条平行线；②两个点；③两条相交直线；④一条直线和直线外的一点；⑤一条直线．答案：①②⑤三、解答题9．如下图所示，画出下列组合体的三视图．解：三视图如图①、图②所示．10．某组合体的三视图如下图所示，试画图说明此组合体的结构特征．解：该三视图表示的是组合体，如右图所示，是7个小正方体拼接而成的组合体．1．2.3空间几何体的直观图斜二测画法[导入新知]1．用斜二测画法画平面图形的步骤(1)在已知图形中取互相垂直的x轴和y轴，两轴相交于点O，画直观图时，把它们画成对应的x′轴和y′轴，两轴相交于点O′，且使∠x′O′y′＝45°(或135°)，它们确定的平面表示水平面．(2)已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段．(3)已知图形中平行于x轴的线段，在直观图中保持原长度不变，平行于y轴的线段，长度变为原来的一半．2．用斜二测画法画空间几何体的直观图的步骤(1)画底面，这时使用平面图形的斜二测画法即可．(2)画z′轴，z′轴过点O′，且与x′轴的夹角为90°，并画出高线(与原图高线相等，画正棱柱时只需要画侧棱即可)，连线成图．(3)擦去辅助线，被遮线用虚线表示．[化解疑难]1．画水平放置的平面图形的直观图，关键是确定多边形顶点的位置，借助于平面直角坐标系确定顶点后，只需把这些顶点顺次连接即可．2．用斜二测画法画直观图要掌握水平长不变，垂线长减半，直角画45°(或135°)．水平放置的平面图形的直观图[例1]按右图所示的建系方法，画水平放置的正五边形ABCDE的直观图．[解]画法：(1)在图①中作AG⊥x轴于G，作DH⊥x轴于H.(2)在图②中画相应的x′轴与y′轴，两轴相交于点O′，使∠x′O′y′＝45°.。

人教版必修二高一数学：空间几何体练习与答案

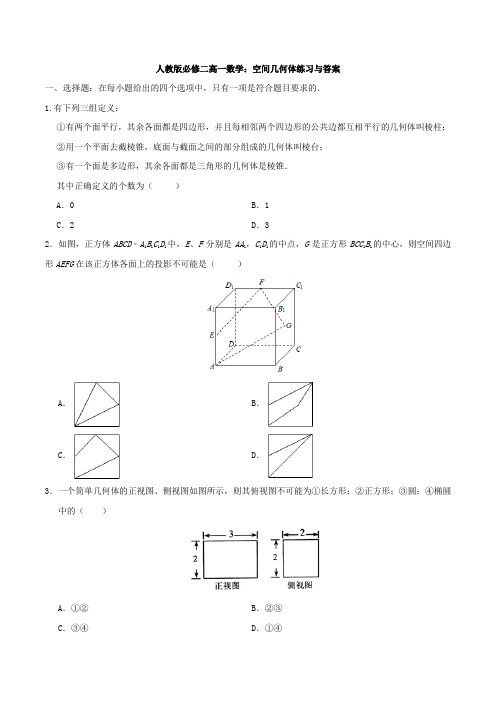
人教版必修二高一数学：空间几何体练习与答案一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.有下列三组定义：①有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱；②用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台；③有一个面是多边形，其余各面都是三角形的几何体是棱锥．其中正确定义的个数为（）A．0 B．1C．2 D．32．如图，正方体ABCD﹣A1B1C1D1中，E、F分别是AA1，C1D1的中点，G是正方形BCC1B1的中心，则空间四边形AEFG在该正方体各面上的投影不可能是（）A．B．C．D．3．一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为①长方形；②正方形；③圆；④椭圆中的（）A．①②B．②③C．③④D．①④4．用斜二测画法画出水平放置的正方形ABCD ABCD 的面积为（）A ．4B ．2C ．2D5．已知边长为1的正方体的所有顶点在一个球面上，则这个球的表面积为（）A ．43π B ．2π C ．3π D ．4π6．如图，一竖立在水平地面上的圆锥形物体的母线长为4m ，一只小虫从圆锥的底面圆上的点P 出发，绕圆锥表面爬行一周后回到点P 处，若该小虫爬行的最短路程为，则圆锥底面圆的半径等于（）A ．1mB ．3m 2C ．4m 3D ．2m7．已知圆锥的母线长为5，底面周长为8π，则它的体积为（） A ．48π B ．64π3 C ．16πD ．80π38．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是（）A．73B．143C．3 D．69．一圆锥的侧面展开图是半径为4的半圆，则该圆锥表面积为（）A．12πB．4πC．3D．16π310．已知长方体全部棱长的和为36，表面积为52，则其体对角线的长为（）A．4 B．．11．边长为）A．4B．1C．D．812．如图所示为某三棱锥的三视图，则该三棱锥外接球的表面积为（）A．B．24πC．16πD．8π二、填空题：请将答案填在题中横线上．13．下列四个平面图形都是正方体的展开图，还原成正方体后，数字排列规律完全一样的两个是________．(1) (2) (3) (4)14．棱长为a的正方体ABCD﹣A1B1C1D1的8个顶点都在球O的表面上，E、F分别是棱AA1、DD1的中点，则直线EF被球O截得的线段长为__________．15．若将边长为2 cm的正方形绕着它的一边所在的直线旋转一周，则所得圆柱的侧面积为__________ cm2．16．已知一个几何体的三视图如图所示（单位： cm），则该几何体的体积为__________．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．如图是一个正四棱台的直观图，它的上底面是边长为2的正方形，下底面是边长为4的正方形，侧棱长为2，侧面是全等的等腰梯形，求此四棱台的表面积．18．在正方形ABCD中，E、F分别为AB、BC的中点，现在沿DE、DF及EF把△ADE、△CDF和△BEF折起，使A、B、C三点重合，重合后的点记为P．问：①依据题意画出这个几何体；②这个几何体由哪几个面构成，每个面的三角形是什么三角形；③若正方形边长为2a，则每个面的三角形面积为多少．19．已知圆台的上下底面半径分别是2、5，且侧面面积等于两底面面积之和，求该圆台的母线长．20．如果一个几何体的正视图与侧视图都是全等的长方形，边长分别是4 cm与2 cm．如图所示，俯视图是一个边长为4 cm的正方形．（1）求该几何体的全面积；（2）求该几何体的外接球的体积．21．如图是一个空间几何体的三视图，试用斜二测画法画出它的直观图．（尺寸不作严格要求）22．一个几何体的三视图如图所示．已知正视图是底边长为11的矩形，俯视图为两个边长为1的正方形拼成的矩形．（1）求该几何体的体积V ；（2）求该几何体的表面积S ．1．【答案】B【解析】由棱柱的定义可知只有①正确；②截面必须平行于底面；③其余各三角形应有一个公共顶点，所以②③都不正确．故选B ． 2．【答案】B【解析】光线由上向下照射可以得到A 的投影，光线有面ABB 1A 1照射，可以得到C 的投影，光线由侧面照射可以得到D 的投影，故选B ． 3．【答案】B【解析】若俯视图为正方形，则正视图中的边长3不成立；若俯视图为圆，则正视图中的边长3也不成立．所以其俯视图不可能为②正方形；③圆，故选B ． 4．【答案】A【解析】斜二测画法画出水平放置的正方形ABCD 的直观图，如图所示，设正方形的边长为a ，则直观图的面积为a •12a •sin45° a =2，∴正方形ABCD 的面积为a 2=4．故选A ．5．【答案】C【解析】由题意，正方体的中心为其外接球的球心，∵正方体的棱长为12，∴外接球的表面积为24π3π⨯=．故选C ． 6. 【答案】C【解析】作出该圆锥的侧面展开图，如下图所示：该小虫爬行的最短路程为PP '，在OPP '△中，OP =OP '=4，P P '=120P OP '∠=．设底面圆的半径为r ，则有1202ππ4180r =⋅，∴34=r ．故C 正确．7．【答案】C【解析】∵圆锥的底面周长为8π，∴圆锥的底面半径r =4；又∵圆锥的母线长l =5，∴圆锥的高h =3，所以圆锥的体积为V 13=⨯π•42×3=16π，故选C ． 8．【答案】A【解析】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱，且三棱锥的一个侧面垂直于底面，且棱锥的高为1，棱柱的底面为等腰直角三角形，棱柱的高为2，所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+=⎪ ⎪⎝⎭⎝⎭.故选：A9．【答案】A【解析】底面圆的半径为r ，则12π2π42r =⋅⋅，所以r =2，所以圆锥的表面积为：221π2π412π2⋅+⋅=．故选A ． 10．【答案】B【解析】设长方体的三条棱的长分别为：,,x y z ，则2()524()36xy yz zx x y z ++=⎧⎨++=⎩，===．故选B ．11．【答案】C【解析】边长为(2=8，水平放置的正方形的面积与斜二测画法所得的直观图的面积之比为：1，=C ．12．【答案】B【解析】由已知中的三视图可得，该几何体的外接球，相当于一个棱长为1，1，2的长方体的外接球，故外接球直径2R ==S =4πR 2=24π，故选B ．13．【答案】（2）（3）【解析】 (2)(3)中，①④为相对的面，②⑤为相对的面，③⑥为相对的面，故它们的排列规律完全一样．14【解析】因为正方体内接于球，所以2R =R 2a =，过球心O 和点E 、F 的大圆的截面图如图所示，则直线被球截得的线段为QR ，过点O 作OP ⊥QR 于点P ，所以在△QPO 中，QR =2QP =． 15．【答案】8π【解析】将边长为2 cm 的正方形绕着它的一边所在的直线旋转一周，所得圆柱的底面圆半径为r =2 cm ，母线长为l =2 cm ．则圆柱的侧面积为S 侧=2πrl =2π×2×2=8π（ cm 2）．故答案为：8π． 16．【答案】363π2-【解析】几何体的直观图如图是一个棱柱挖去一个圆柱的几何体，几何体的体积为：213334π()232⨯⨯-⋅⋅⋅=363π2-．故答案为：363π2-．17．【答案】20+【解析】依题意，上底面和下底面的面积分别是222,4， ∵侧面是全等的等腰梯形，且侧棱长2，∴侧面高==，∴侧面面积为()1242⨯+=∴该四棱台的表面积2224420S =++=+． 18．【解析】①如图所示．②这个几何体由四个面构成，即面DEF 、面DFP 、面DEP 、面EFP ．由题意可知DE =DF ，∠DPE =∠EPF =∠DPF =90°，所以△DEF 为等腰三角形，△DFP 、△EFP 、△DEP 为直角三角形．③由②可知，DE =DF =，EF =，所以，S △DEF 32=a 2．DP =2a ，EP =FP =a ，所以S △DPE =S △DPF =a 2，S △EPF 12=a 2．19．【解析】设圆台的母线长为l ，∵圆台的上下底面半径分别是2、5，∴圆台的上底面面积：2π2S =⨯=上4π，圆台的下底面面积：2π525πS =⨯=下，∴圆台的底面面积：S =S 上+S 下=29π，又圆台的侧面积：S 侧=π（2+5）l =7πl ． ∵圆台的侧面面积等于两底面面积之和，∴7πl =29π，解得l 297=． ∴该圆台的母线长为297．20．【解析】（1）由题意可知，该几何体是长方体，底面是正方形，边长是4，高是2，因此该几何体的全面积是：2×4×4＋4×4×2=64 cm 2．所以几何体的全面积是64 cm 2．（2）由长方体与球的性质可得，长方体的对角线是球的直径，记长方体的体对角线为d ，球的半径是r ，则d =，所以球的半径r =3．因此球的体积V =344π27π36π 33r =⨯=(cm 3)，所以外接球的体积是36π cm 3．21．【解析】由题可知题目所述几何体是正六棱台，画法如下：画法：（1）画轴画x 轴、y 轴、z 轴，使∠x ′O ′y ′=45°，∠x ′O ′z ′=90°（图1）（2）画底面以O ′为中心，在XOY 坐标系内画正六棱台下底面正方形的直观图ABCDEF ．在z ′轴上取线段O ′O 1等于正六棱台的高；过O 1 画O 1M 、O 1N 分别平行O ’x ′、O ′y ′，再以O 1为中心，画正六棱台上底面正方形的直观图A ′B ′C ′E ′F ′（3）成图连接AA′、BB′、CC′、DD′、EE′、FF′，并且加以整理，就得到正六棱台的直观图（如图2）．22．【解析】（1）由三视图可知，该几何体是一个平行六面体（如图），其底面是边长为1∴V=1×1=（2）由三视图可知，该平行六面体中，A1D⊥面ABCD，CD⊥面BCC1B1，∴AA1=2，侧面ABB1A1，CDD1C1均为矩形∴S=2×（1×1+11×2）。

精品解析：人教版高一数学必修2第一章《空间几何体》专题检测(含答案)(解析版).docx

人教版高一数学必修2第一章《空间几何体》专题检测一.选择题1. 在三棱锥P-ABC 屮，PA = PB = AC = BC = 2,AB = 2A //3,PC= 1,则三棱锥P-ABC 的外接球的表而积为( )4兀 52兀 A. — B. 4兀 C. 12n D. ---------------------- 3 3【答案】D【解析】取AB 中点D,连接PD,CD,则AD = \$, PD = ^AP 2-AD 2 = h 所以ABZAPD = 60°, ^APB= 120°,设△ APB 外接圆圆心为0】，半径为「则2T = ------------ = 4 sinl20°所以r = 2.同理可得：CD = L ZACB = 120°, A ABC 的外接圆半径也为2,因为PC = PD = CD= 1,所以APCD 是等边三角形，ZPDC = 60%即二面角P-AB-C 为60。

，球心O 在平面PCD 上, 过平面PCD 的截血如图所示，则O 】D = L PD=1,所以001=^01D = —,所以OF 2 = OO J + O J F 2 = - 3 3 3D.【点睛】本小题主要考查儿何体外接球的表面积的求法，考查三角形外心的求解方法•在解决有关儿何体外接球有关的问题时，主要的解题策略是找到球心，然后通过解三角形求得半径•找球心的方法是先找到一个血的外心，再找另一个血的外心，球心就在两个外心垂线的交点位置.2.直三棱柱ABC ・AiB 】C ］的各顶点都在同一球面上，若AB=AC=AA 1=2,则此球的表面积等于()52兀52兀 A. ---- B. 20兀 C- 10n D. 9 ・ 13 _ + 4 =—— ； 3 即R 2 = -,所以外接球的表而积S = 4TT R 2 = —.故选【答案】B【解析】设三角形BAC 外接圆半径为「，则= 盂=薯・•・「= 2・・・球的半径等于、夕+ 1 = “5,表面积等于4HR 2 = 20n.选B ・3. 某几何体的三视图如图所示，则此几何体的体积为（—2—H —2T【答案】C【解析】该儿何体为三棱锥，其直观图如图所示，体枳V = 1x （lx2 ><2卜2=±.故选C.4. 已知正四棱锥P-ABCD 的顶点均在球0上，且该正四棱锥的各个棱长均为2,则球0的表面积为A. 4兀B. 6兀C. 8兀D. 16n 【答案】c【解析】设点P 在底面ABCD 的投影点为O ；贝|JAO‘=-AC = Q, PA = 2, PCT 丄平面ABCD,故 2PO = 7P A 2-AO 2 = 而底iklABCD 所在截面圆的半径AO‘ = ©，故该截血圆即为过球心的圆，则球的半径 R = &‘故球O 的表面积$ = 4?rR 2 = 87T»故选C.点睛：本题考查球的内接体的判断与应用，球的表面积的求法，考查计算能力；研究球与多面体的接、切问题主要考虑以下几个方面的问题：（1）球心与多面体中心的位置关系；（2）球的半径与多面体的棱长的A.B. 1C.-D.俯视图关系；（3）球自身的对称性与多面体的对称性；（4）能否做岀轴截面.5. 己知一个空间几何体的三视图如图，根据图中标出的尺寸（单位：cm ）,可得这个几何体的体积是6. 如图，网格纸上正方形小格的边长为1,粗线画出的是某几何体的三视图，则该几何体的最长棱的长度为【答案】D【解析】由三视图可知，该儿何体为三棱锥，如图所示:C. 6 cm 3D. 7 cm 3【答案】A 【解析】几何体如图四棱锥’体积为+ 2) x 2 = 4,选A.俯觀图A. 4cm 3B. 5 cm 3()A. 6yj2B. 6&C. 8D. 9AAB = 6, BC = 3忑,BD = CD = 3屈 AD = 9,故选：D点睛：思考三视图还原空间儿何体首先应深刻理解三视图Z间的关系，遵循“长对正，高平齐，宽相等” 的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.7.我国古代数学名箸《孙子算经》中有如下问题：“今有筑城，上广二丈，下广五丈四尺，高三丈八尺，长五千五百五十尺，秋程人功三百尺•问：须工儿何？”意思是：“现要筑造底面为等腰梯形的直棱柱的城墙，其中底面等腰梯形的上底为2丈、下底为5.4丈、高为38丈，直棱柱的侧棱长为5550尺.如果一个秋天工期的单个人可以筑出300立方尺，问：一个秋天工期需要多少个人才能筑起这个城墙？”（注：一丈等于十尺）A. 24642B. 26011C. 52022D. 78033【答案】B20 + 54【解析】根据棱柱的体积公式，可得城墙所需土方为------ x 38 x 5500 = 7803300 （立方尺），一个秋夭工期2所需人数为------- = 26011,故选B.3008.已知某儿何体是两个正四棱锥的组合体，其三视图如下图所示，则该儿何体外接球的表面积为（）A. 2兀B. 2#5兀C. 4兀D. 8兀【答案】D【解析】由已知三视图得：该几何体的直观图如下可知该儿何体外接球的半径为Q则该儿何体外接球的表而积为4兀•(厨=8TI故选D9. 在空间直角坐标系O-xyz 中，四面体ABCD 的顶点坐标分别是A(0Q2), B(220), C(1.2,l), D(222).则该四而体的体积V=()二、填空题10. 在平行六面体 ABCD —A]B]C]D]中，AB = 4 , AD = 3 , A 】A=5,厶 BAD = 90。

人教版必修二第一章-空间几何体(答案解析)

人教版必修二第一章-空间几何体-A一、选择题(共10小题)1. (2015•新课标II)已知A，B是球O的球面上两点，∠AOB=90°，C为该球面上的动点，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为()A.36πB.64πC.144πD.256π【分析】当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，利用三棱锥O﹣ABC体积的最大值为36，求出半径，即可求出球O的表面积.【解答】解：如图所示，当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，设球O的半径为R，此时V O﹣ABC=V C﹣AOB===36，故R=6，则球O的表面积为4πR2=144π，故选 C.【点评】本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大是关键.2.(2013•上海)若两个球的表面积之比为1：4，则这两个球的体积之比为()A.1：2B.1：4C.1：8D.1：16【分析】设两个球的半径分别为r1、r2，根据球的表面积公式算出它们的表面积之比为=，解之得=，由此结合球的体积公式即可算出这两个球的体积之比.【解答】解：设两个球的半径分别为r1、r2，根据球的表面积公式，可得它们的表面积分别为S1=4，S2=4∵两个球的表面积之比为1：4，∴===，解之得=(舍负)因此，这两个球的体积之比为==()3=即两个球的体积之比为1：8故选：C【点评】本题给出两个球的表面积之比，求它们的体积之比.着重考查了球的表面积公式和体积公式等知识，属于基础题.3.(2013•新课标Ⅰ)如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6cm，如不计容器的厚度，则球的体积为()A. B. C. D.【分析】设正方体上底面所在平面截球得小圆M，可得圆心M为正方体上底面正方形的中心.设球的半径为R，根据题意得球心到上底面的距离等于(R﹣2)cm，而圆M的半径为4，由球的截面圆性质建立关于R的方程并解出R=5，用球的体积公式即可算出该球的体积.【解答】解：设正方体上底面所在平面截球得小圆M，则圆心M为正方体上底面正方形的中心.如图.设球的半径为R，根据题意得球心到上底面的距离等于(R﹣2)cm，而圆M的半径为4，由球的截面圆性质，得R2=(R﹣2)2+42，解出R=5，∴根据球的体积公式，该球的体积V===.故选A.【点评】本题给出球与正方体相切的问题，求球的体积，着重考查了正方体的性质、球的截面圆性质和球的体积公式等知识，属于中档题.4. (2015•浙江)如图，某简单组合体由一个圆锥和一个圆柱组成，则该组合体三视图的俯视图为()A. B. C. D.【考点】简单空间图形的三视图.【专题】计算题；数形结合；空间位置关系与距离.【分析】直接利用三视图判断俯视图即可.【解答】解：简单组合体由一个圆锥和一个圆柱组成，左侧是圆锥，右侧是圆柱，俯视图为：三角形与矩形组成，故选：D.【点评】本题考查空间几何体的三视图的判断，是基础题.5.(2015•徐汇区模拟)长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是()A.20πB.25πC.50πD.200π【分析】设出球的半径，由于直径即是长方体的体对角线，由此关系求出球的半径，即可求出球的表面积.【解答】解：设球的半径为R，由题意，球的直径即为长方体的体对角线，则(2R)2=32+42+52=50，∴R=.∴S球=4π×R2=50π.故选C【点评】本题考查球的表面积，球的内接体，考查计算能力，是基础题.6.(2013•甘肃模拟)已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是()A.16πB.20πC.24πD.32π【分析】先求正四棱柱的底面边长，然后求其对角线，就是球的直径，再求其表面积.【解答】解：正四棱柱高为4，体积为16，底面积为4，正方形边长为2，正四棱柱的对角线长即球的直径为2，∴球的半径为，球的表面积是24π，故选 C.【点评】本题考查学生空间想象能力，四棱柱的体积，球的表面积，容易疏忽的地方是几何体的体对角线是外接球的直径，导致出错.7.(2013•广东)某四棱台的三视图如图所示，则该四棱台的体积是()A.4B.C.D.6【分析】由题意直接利用三视图的数据求解棱台的体积即可.【解答】解：几何体是四棱台，下底面是边长为2的正方形，上底面是边长为1的正方形，棱台的高为2，并且棱台的两个侧面与底面垂直，四楼台的体积为V==.故选 B.【点评】本题考查三视图与几何体的关系，棱台体积公式的应用，考查计算能力与空间想象能力.8. (2016•松江区二模)如图，圆锥形容器的高为h，圆锥内水面的高为h1，且h，若将圆锥倒置，水面高为h2，则h2等于()A.hB.C.hD.h【考点】旋转体(圆柱、圆锥、圆台).【专题】数形结合；等体积法；立体几何.【分析】根据水的体积不变列出方程解出h2.【解答】解：设圆锥形容器的底面积为S，则未倒置前液面的面积为.∴水的体积V=﹣=.设倒置后液面面积为S′，则，∴S′=.∴水的体积V==.∴，解得h2=.故选：D.【点评】本题考查了圆锥的结构特征，圆锥的体积计算，属于中档题.9.(2014•陕西)已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一球面上，则该球的体积为()A. B.4π C.2π D.【分析】由长方体的对角线公式，算出正四棱柱体对角线的长，从而得到球直径长，得球半径R=1，最后根据球的体积公式，可算出此球的体积.【解答】解：∵正四棱柱的底面边长为1，侧棱长为，∴正四棱柱体对角线的长为=2又∵正四棱柱的顶点在同一球面上，∴正四棱柱体对角线恰好是球的一条直径，得球半径R=1根据球的体积公式，得此球的体积为V=πR3=π.故选： D.【点评】本题给出球内接正四棱柱的底面边长和侧棱长，求该球的体积，考查了正四棱柱的性质、长方体对角线公式和球的体积公式等知识，属于基础题.二、填空题(共6小题)10. (2016•天津)已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图所示(单位：m)，则该四棱锥的体积为2m3【分析】由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，进而可得答案.【解答】解：由已知中的三视图可得：该几何体是一个以俯视图为底面的四棱锥，棱锥的底面是底为2，高为1的平行四边形，故底面面积S=2×1=2m2，棱锥的高h=3m，故体积V==2m3，故答案为：2【点评】本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键.11.(2013•新课标Ⅱ)已知正四棱锥O﹣ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为24π.【分析】先直接利用锥体的体积公式即可求得正四棱锥O﹣ABCD的高，再利用直角三角形求出正四棱锥O﹣ABCD 的侧棱长OA，最后根据球的表面积公式计算即得.【解答】解：如图，正四棱锥O﹣ABCD的体积V=sh=(×)×OH=，∴OH=，在直角三角形OAH中，OA===所以表面积为4πr2=24π；故答案为：24π.【点评】本题考查锥体的体积、球的表面积计算，考查学生的运算能力，属基础题.12.(2013•新课标Ⅰ)已知H是球O的直径AB上一点，AH：HB=1：2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为.【分析】本题考查的知识点是球的表面积公式，设球的半径为R，根据题意知由与球心距离为R的平面截球所得的截面圆的面积是π，我们易求出截面圆的半径为1，根据球心距、截面圆半径、球半径构成直角三角形，满足勾股定理，我们易求出该球的半径，进而求出球的表面积.【解答】解：设球的半径为R，∵AH：HB=1：2，∴平面α与球心的距离为R，∵α截球O所得截面的面积为π，∴d=R时，r=1，故由R2=r2+d2得R2=12+(R)2，∴R2=∴球的表面积S=4πR2=.故答案为：.【点评】若球的截面圆半径为r，球心距为d，球半径为R，则球心距、截面圆半径、球半径构成直角三角形，满足勾股定理，即R2=r2+d213.(2009•全国卷Ⅰ)已知OA为球O的半径，过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π，则球O的表面积等于16π.【分析】由题意求出圆M的半径，设出球的半径，二者与OM构成直角三角形，求出球的半径，然后可求球的表面积.【解答】解：∵圆M的面积为3π，∴圆M的半径r=，设球的半径为R，由图可知，R2=R2+3，∴R2=3，∴R2=4.∴S球=4πR2=16π.故答案为：16π【点评】本题是基础题，考查球的体积、表面积的计算，理解并能够应用小圆的半径、球的半径、以及球心与圆心的连线的关系，是本题的突破口，解题重点所在，仔细体会.14.(2013•湖北)我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸.若盆中积水深九寸，则平地降雨量是3寸. (注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)【分析】由题意得到盆中水面的半径，利用圆台的体积公式求出水的体积，用水的体积除以盆的上地面面积即可得到答案.【解答】解：如图，由题意可知，天池盆上底面半径为14寸，下底面半径为6寸，高为18寸.因为积水深9寸，所以水面半径为寸.则盆中水的体积为(立方寸).所以则平地降雨量等于(寸).故答案为3.【点评】本题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是基础题.15.(2014秋•扶余县校级期末)已知圆O和圆K是球O的大圆和小圆，其公共弦长等于球O的半径，，则球O的表面积等于16π.【分析】正确作出图形，利用勾股定理，建立方程，即可求得结论.【解答】解：如图所示，设球O的半径为r，AB是公共弦，∠OCK是面面角根据题意得OC=，CK=在△OCK中，OC2=OK2+CK2，即∴r2=4∴球O的表面积等于4πr2=16π故答案为16π【点评】本题考查球的表面积，考查学生分析解决问题的能力，属于中档题.三、解答题(共14小题)16. (2016•江苏)现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P﹣A1B1C1D1，下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m，PO1=2m，则仓库的容积是多少？(2)若正四棱锥的侧棱长为6m，则当PO1为多少时，仓库的容积最大？【分析】(1)由正四棱柱的高O1O是正四棱锥的高PO1的4倍，可得PO1=2m时，O1O=8m，进而可得仓库的容积；(2)设PO1=xm，则O1O=4xm，A1O1=m，A1B1=•m，代入体积公式，求出容积的表达式，利用导数法，可得最大值.【解答】解：(1)∵PO1=2m，正四棱柱的高O1O是正四棱锥的高PO1的4倍.∴O1O=8m，∴仓库的容积V=×62×2+62×8=312m3，(2)若正四棱锥的侧棱长为6m，设PO1=xm，则O1O=4xm，A1O1=m，A1B1=•m，则仓库的容积V=×(•)2•x+(•)2•4x=x3+312x，(0＜x＜6)，∴V′=﹣26x2+312，(0＜x＜6)，当0＜x＜2时，V′＞0，V(x)单调递增；当2＜x＜6时，V′＜0，V(x)单调递减；故当x=2时，V(x)取最大值；即当PO1=2m时，仓库的容积最大.【点评】本题考查的知识点是棱锥和棱柱的体积，导数法求函数的最大值，难度中档.17. (2016春•重庆校级月考)画出图中两个几何体的三视图.【分析】利用三视图的画法，直接画出几何体的三视图.【解答】解：(1)如图(2)如图【点评】本题考查三视图的画法，考查作图能力，是基础题.18. (2015秋•安阳校级期末)已知一个空间组合体的三视图如图所示，其中正视图、侧视图都是由半圆和矩形组成，请说出该组合体由哪些几何体组成，并且求出该组合体的表面积和体积.【考点】由三视图求面积、体积.【专题】数形结合；数形结合法；立体几何.【分析】根据几何体的三视图，得出该几何体是上部为半球体，下部为圆柱体的组合体；结合图中数据求出它的表面积与体积.【解答】解：根据几何体的三视图，得；该几何体是上部为半球体，下部为圆柱体的组合体；…(2分)且半球体与圆柱体的直径都是2，圆柱体的高是1，；所以，该几何体的表面积是：S=2π×12+2π×1×1+π×12=5π；…(6分)体积是：V=×π×13+π×12×1=.…(10分)【点评】本题考查了利用空间几何体的三视图求体积与表面积的应用问题，是基础题目.19. (2016春•定州市校级月考)直角梯形的一个内角为45°，下底长为上底长的，这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是(5+)π，求这个旋转体的体积.【分析】画出旋转前的图形，判断构成组合几何体的简单几何体的特征，求出相应的几何量，即可求解整体的体积. 【解答】解：如图，梯形ABCD，AB∥CD，∠A=90°，∠B=45°，绕AB边旋转一周后形成一圆柱和一圆锥的组合体.设CD=x，AB=AD=AB﹣CD=，BC=，S全面积=S圆柱底+S圆柱侧+S圆锥侧=πAD2+2πAD•CD+π•AD•BC==根据题设，∴x=2，∴旋转体体积==【点评】本题考查组合体的结构特征，几何体的体积的求法，考查空间想象能力以及计算能力.20. (2013秋•七里河区校级期末)如图是一个圆台形的纸篓(有底无盖)，它的母线长为50cm，两底面直径分别为40cm 和30cm；现有制作这种纸篓的塑料制品50m2，问最多可以做这种纸篓多少个？.【分析】利用圆台的侧面积公式与圆面积公式，算出制作一个纸篓所用的塑料制品的面积，再用50m2除以这个面积，即可得到最多可以做这种纸篓的个数.【解答】解：设圆台两底半径分别为r、r'，母线为l，可得它侧面积S侧=π(r+r')l=π(15+20)×50=1750πcm2，∵纸篓底的面积S底=πr2=225πcm2，∴纸篓的全面积为S=1750π+225π=1975πcm2═0.1975π(m2)因此，用制作这种纸篓的塑料制品50m2，最多可以做这种纸篓80(个)﹣﹣﹣﹣﹣﹣﹣(7分)答：用制作这种纸篓的塑料制品50m2，最多可以做这种纸篓约80个.【点评】本题给出实际应用问题，求制作纸篓的最多数目.着重考查了圆台的侧面积公式与圆面积，旋转体表面积公式的实际应用的知识，属于基础题.第11页（共11页）。

数学《必修2》第一章“空间几何体”测试题与答案

数学《必修2》第一章“空间几何体”测试题一、选择题：(本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符号题目要求的)１．利用斜二测画法得到的：①三角形的直观图一定是三角形；②正方形的直观图一定是正方形；③等腰梯形的直观图一定是等腰梯形；④平行四边形的直观图一定是平行四边形。

以上结论正确的是（）Ａ.①②Ｂ.①④Ｃ.③④Ｄ. ①②③④2．下列说法正确的是（）A.棱柱的侧面可以是三角形B.正方体和长方体都是特殊的四棱柱C.所有的几何体的表面都能展开成平面图形D.棱柱的各条棱都相等3．圆台的母线长为6，两底面半径分别为2、7，则圆台的侧面积为（）A.54πB.8πC.4πD.164．给出下列结论：①圆柱的母线是其上底面圆周上任意一点与下底面圆周上任意一点的连线；②圆锥的母线是圆锥顶点与底面圆周上任意一点的连线；③圆台的母线是圆台上、下底面圆周上任意两点的连线。

其中正确的是（）A.①②B.②③C.①③D.②。

5．已知底面为正方形的长方体的各顶点都在一个球面上，长方体的高为4，体积为16，则这个球的表面积是（）A.16πB.20πC.24πD.32π6．下列说法错误的是（）A.棱柱最少有5个面B.棱锥最少有4个面C.棱台的底面有2个D.棱锥的底面边数和侧棱数不一定相同7．下列四个图形不是下图1中几何体的三视图之一的是（）图1 A B C D8．下面几何体中，过轴的截面一定是圆面的是（）A.圆柱B.圆锥C.球D.圆台 9．正方体的表面积是96，则正方体的体积是（）A. B.64 C.16 D. 96 10．若某几何体的三视图如图所示，则这个几何体的直观图可以是（）二、填空题：(本大题共5个小题，每小题5分，共25分)11．半径为2的球的体积等于，表面积等于12．圆锥的侧面展开图为圆心角为120、半径为1的扇形，则圆锥的侧面积为 13．如下图所示，等腰梯形ABCD ，上底1CD =，腰AD CB ==3AB =，以下底所在直线为x 轴，则由斜二测画法画的直观图''''A B C D 的面积为 14．某几何体的三视图如下图所示, 则其体积为_______.15．某几何体的三视图如下图所示,则该几何体的体积是____________.第13题图14题图第15题图三、解答题：(本大题共6个小题，共75分，解答应写出文字说明，证明过程或演算步骤)16．求下列几何体的体积与表面积。

高中数学必修二第一章《空间几何体》单元练习题(含答案)

高中数学必修二第一章《空间几何体》单元练习题(30分钟50分)一、选择题(每小题3分,共18分)1.斜四棱柱的侧面是矩形的面最多有( )A.0个B.1个C.2个D.3个2.所给三视图表示的简单组合体的结构特征是( )A.由圆柱和圆锥组成B.由圆柱和棱锥组成C.由棱柱和圆锥组成D.由圆台和圆锥组成3.一个四面体的三视图如图所示,则该四面体的表面积是( )A.1+B.2+C.1+2D.24.圆柱的轴截面是正方形,面积是S,则它的侧面积是( )A.SB.πSC.2πSD.4πS5.若圆台两底面周长的比是1∶4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是 ( )A.B.C.1D.6.如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是 ( )二、填空题(每小题4分,共12分)7.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.8.在三棱柱ABC-A 1B 1C 1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P 分别是AB,BC,B 1C 1的中点,则三棱锥P-A 1MN 的体积是 .9.用一张4×8(cm 2)的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是 cm 2.三、解答题(每小题10分,共20分)10.已知四棱锥P-ABCD,其三视图和直观图如图,求该四棱锥的体积.11.如图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的体积是多少?高中数学必修二第一章《空间几何体》单元练习题(30分钟50分)一、选择题(每小题3分,共18分)1.斜四棱柱的侧面是矩形的面最多有( )A.0个B.1个C.2个D.3个【解析】选C.根据棱柱的结构特征不可能有奇数个,因此最多2个.2.所给三视图表示的简单组合体的结构特征是( )A.由圆柱和圆锥组成B.由圆柱和棱锥组成C.由棱柱和圆锥组成D.由圆台和圆锥组成【解析】选A.由三视图可知此组合体的上方是圆柱,下方是圆锥,故选A.3.(2015·安徽高考)一个四面体的三视图如图所示,则该四面体的表面积是( )A.1+B.2+C.1+2D.2【解析】选B.由该四面体的三视图可知,该四面体的直观图如图所示:其中侧面PAC⊥底面ABC,且△PAC≌△BAC,由三视图中所给数据可知PA=PC=AB=BC=,取AC的中点O,连接PO,BO,则在Rt△POB中,PO=BO=1,可得PB=,所以S=2××2+×2×2=2+.4.(2015·西安高一检测)圆柱的轴截面是正方形,面积是S,则它的侧面积是( )A.SB.πSC.2πSD.4πS【解析】选B.设圆柱底面半径为r,则S=4r2,S侧=2πr·2r=4πr2=πS.5.若圆台两底面周长的比是1∶4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是( )A. B. C.1 D.【解析】选D.设上、下底半径分别为r1,r2,过高中点的圆面半径为r0,由题意得r2=4r1,r0=r1,所以==.6.(2015·威海高一检测)如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为,则该几何体的俯视图可以是( )【解析】选C.当俯视图为A中正方形时,几何体为棱长为1的正方体,体积为1;当俯视图为B中圆时,几何体为底面半径为,高为1的圆柱,体积为;当俯视图为C 中三角形时,几何体为三棱柱,且底面为直角边长为1的等腰直角三角形,高为1,体积为;当俯视图为D 中扇形时,几何体为圆柱的,且体积为. 二、填空题(每小题4分,共12分)7.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.【解析】设球的半径为rcm,则πr 2×8+πr 3×3=πr 2×6r.解得r=4. 答案:48.(2015·四川高考)在三棱柱ABC-A 1B 1C 1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P 分别是AB,BC,B 1C 1的中点,则三棱锥P-A 1MN 的体积是 .【解析】V=××=.答案:9.用一张4×8(cm 2)的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是 cm 2.【解析】以4为高卷起,则2πr=8,所以2r=,所以轴截面面积为cm 2;若以8为高卷起,则2πR=4,所以2R=,所以轴截面面积为cm 2.答案:三、解答题(每小题10分,共20分)10.已知四棱锥P-ABCD,其三视图和直观图如图,求该四棱锥的体积.【解析】由三视图知底面ABCD为矩形,AB=2,BC=4.顶点P在面ABCD内的射影为BC中点E,即棱锥的高为2,则体积V P-ABCD=S ABCD×PE=×2×4×2=.11.如图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的体积是多少?【解析】设球半径为Rcm,根据已知条件知正方体的上底面与球相交所得截面圆的半径为4cm,球心到截面的距离为(R-2)cm,所以由42+(R-2)2=R2,得R=5,所以球的体积V=πR3=π×53=(cm3).。

高中数学人教课标实验A版必修2第一章《空间几何体的结构》同步练习(附答案)

《空间几何体的结构》同步练习一、考点分析三视图是新课程改革中出现的内容，是新课程高考的热点之一，几乎每年都考，同学们要予以足够的重视．在高考中经常以选择、填空题的形式出现，属于基础或中档题，但也要关注三视图以提供信息为目的，出现在解答题中．这部分知识主要考查学生的空间想象能力与计算求解能力．二、典型例题知识点一：柱、锥、台、球的结构特征例1．下列叙述正确的是（）①有两个面平行，其余各面都是平行四边形的几何体叫棱柱．②两个底面平行且相似，其余各面都是梯形的多面体是棱台．③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台．④直角三角形绕其一条边旋转得到的旋转体是圆锥．⑤直角梯形以它的一条垂直于两底边的腰所在的直线为旋转轴，其余三边旋转形成的面围成的旋转体叫圆台．⑥用一个平面去截圆锥，底面和截面之间的部分是圆台．⑦通过圆锥侧面上一点，有无数条母线．⑧以半圆的直径所在直线为旋转轴，半圆面旋转一周形成球体．A．①②③④⑤⑥⑧B．①③④⑦⑧C．①②⑤⑧D．⑤思路分析：遇到概念判断问题，一定要在理解透彻相关概念的基础上，仔细分析，如果判断它是正确的，必须能紧扣定义，而不是模棱两可地去作判断；如果判断它是错误的，只需找到一个反例即可．解答过程：如图所示，由图（1）可知①是错误的；由图（2）可知②③是错误的；由图（3）可知④是错误的；由图（4）可知⑥是错误的．因为通过圆锥侧面上一点和圆锥的顶点只能连一条射线，所以“通过圆锥侧面上一点，有无数条母线．”是错误的，即⑦是不正确的．以半圆的直径所在直线为旋转轴，半圆旋转一周形成的应该是球面，半圆面旋转一周形成的才是球体．所以⑧是错误的．所以只有⑤是正确的．故应选D．解题后的思考：在作判断的时候没有严格的根据定义进行多角度分析，而是只抓住定义中的某一点就作出判断，容易导致错误．知识点二：组合体例2．如图，下列组合体是由哪几种简单几何体组成的？解答过程：（1）由一个三棱锥和一个四棱锥组成，为左右结构（2）由两个三棱锥组成，为上下结构（3）由圆锥和圆台组成，为上下结构知识点三：柱、锥的侧面展开图例3．小明在一个正方体盒子的每个面都写有一个字母，分别是：A、B、C、D、E、F，其平面展开图如图所示，那么在该正方体盒子中，和“A”相对的面所写的字母是哪一个？思路分析：在每个格子中标明你所想象的面的位置，如将A 格标明“上”，将B格标明“前”等等．解答过程：为字母“E”解题后的思考：本题突出考查了学生将正方体各面展开图复原为正方体的空间想象能力．例4．如图所示，为一个封闭的立方体，在它的六个面上标出A ，B ，C ，D ，E ，F 这六个字母，现放成下面三种不同的位置，所看见的表面上的字母已标明，则字母A ，B ，C 对面的字母分别是（）A ．D ，E ，FB ．F ，D ，EC ．E ，F ，D D ．E ，D ，F思路分析：本题处理方法比较灵活，要将几个图结合起来一起分析．解答过程：由（1）（2）两个图知，A 与B ，C ，D 相邻，结合第（3）个图知，B ，C 与F 共顶点，所以A 的对面为F ，同理B ，C 的对面分别为D ，E ，故选择B ．解题后的思考：本题考查推理能力以及空间想象能力．也可先结合图（1）（3）进行判断．例5．用长和宽分别是π3和π的矩形硬纸卷成圆柱的侧面，求圆柱的底面半径？思路分析：要注意哪条边是圆柱的母线，哪条边是圆柱底面的圆周．解答过程：设圆柱底面圆的半径为r ，由题意可知矩形长为底面圆的周长时，r ππ23=，解得23=r ．矩形宽为底面圆的周长时，r ππ2=，解得21=r ．故圆柱的底面半径为23或21．解题后的思考：本题学生经常会丢解，即主观认为只有图中所示的情况，即以π3作为底面周长，而忽视了它也可作为母线这种情况．知识点四旋转体中的有关计算例6．一个圆台的母线长cm 12，两底面面积分别为24cm π和225cm π，求：（1）圆台的高；（2）截得此圆台的圆锥的母线长．思路分析：通过作截得此圆台的圆锥的轴截面，构造直角三角形与相似三角形求解．解答过程：（1）作OA H A ⊥1242=∴=r r ππΘ 5252=∴=R R ππΘ3=∴AH153312221=-=∴H A（2）11O VA ∆Θ与O VA ∆相似 AO O A VA VA 111=∴20=∴VA解题后的思考：通过构造旋转体的轴截面，将立体问题转化为平面问题．例7．已知球的两个平行截面的面积分别为π5和π8，且距离为3，求这个球的半径．思路分析：两截面的相互位置可能出现两种情况，一种是在球心O 的同侧，另一种是在球心O 的异侧．解答过程：（1）当两截面在球心O 的同侧时，如图所示，设这两个截面的半径分别为21,r r ，球心O 到截面的距离分别为21,d d ，球的半径为R ．8,5,8,522212221==∴=⋅=⋅r r r r ππππΘ．又222221212d r d r R +=+=Θ，321222221=-=-∴r r d d ，即3))((2121=+-d d d d ．又321=-d d Θ，⎩⎨⎧=+=-∴,1,32121d d d d 解得⎩⎨⎧-==.1,221d d又∴>,02d Θ这种情况不成立．（2）当两截面在球心O 的异侧时，321=+d d ，由上述解法可知3))((2121=+-d d d d ，⎩⎨⎧=-=+∴,1,32121d d d d 解得⎩⎨⎧==.1,221d d 3452121=+=+=∴d r R ．综上所述，这个球的半径为3．解题后的思考：同学们要注意不要只对同侧的情况进行讨论，而忽略对另一种位置关系的讨论．知识点五：画几何体的三视图例8．画出如图所示的三棱柱的三视图．思路分析：在正视图中，中间的竖线看不到，应画成虚线；侧视图是从左侧看三棱柱投射到竖直的正对着的平面上的正投影，所以不是三棱柱的一个侧面，而应该是过底面正三角形的一条高线的矩形．解答过程：解题后的思考：画三视图的时候要做到“长对正、宽相等、高平齐”，还要注意实线与虚线的区别．知识点六：三视图中的推测问题例9．根据下列三视图，说出各立体图形的形状．思路分析：三视图是从三个不同的方向看同一物体得到的三个视图．正视图反映物体的主要形状特征，主要体现物体的长和高，不反映物体的宽．而俯视图和正视图共同反映物体的长相等．侧视图和俯视图共同反映物体的宽相等．据此就不难得出该几何体的形状．解答过程：（1）圆台；（2）正四棱锥；（3）螺帽．解题后的思考：三视图的画法里要注意“长对正”，“高平齐”，“宽相等”，另外，还要熟悉基本空间几何体的三视图．知识点七：直观图的还原与计算问题例10．已知△A′B′C′是水平放置的边长为a 的正三角形ABC 的斜二测水平直观图，那么△A′B′C′的面积为_________．思路分析：先根据题意，画出直观图，然后根据△A′B′C′直观图的边长及夹角求解．解答过程：如图甲、乙所示的实际图与直观图．a OC C O a AB B A 4321,==''==''．在图乙中作C′D′⊥A′B′于D′，则a C O D C 8622=''=''．所以2166862121a a a D C B A S C B A =⨯⨯=''⋅''='''∆．故填2166a ．解题后的思考：该题求直观图的面积，因此应在直观图中求解，需先求出直观图的底和高，然后用三角形面积公式求解．本题旨在考查同学们对直观图画法的掌握情况．例11．如图所示，正方形O′A′B′C′的边长为cm 1，它是水平放置的一个平面图形的直观图，则原图形的周长是____________．思路分析：先根据题意，由直观图画出原图形解答过程：逆用斜二测画法的规则画出原图如下图所示，由BC//OA 且BC=OA ，易知OABC 为平行四边形．在上图中，易求O′B′=2，所以OB =22．又OA =1，所以在Rt △BOA 中，31)22(22=+=AB ．故原图形的周长是)cm (8)13(2=+⨯，应填cm 8．解题后的思考：该题考查的是直观图与原图形之间的关系，及逆用斜二测画法的规则．。

人教版高中数学必修二《第八章立体几何初步》同步练习及答案解析

人教版高中数学必修二《第八章立体几何初步》同步练习《8.1 基本几何图形》同步练习第1课时棱柱、棱锥、棱台一、选择题1．下图代表未折叠正方体的展开图，将其折叠起来，变成正方体后的图形是（）A．B．C．D．2．一个棱锥的各条棱都相等，那么这个棱锥必不是( )A．三棱锥B．四棱锥C．五棱锥D．六棱锥3．下列几何体中棱柱有( )A．5个B．4个C．3个D．2个4．用一个平面去截一个四棱锥，截面形状不可能的是 ( )A．四边形 B．三角形 C．五边形 D．六边形5．（多选题）给出下列命题，其中假命题是（）A.棱柱的侧棱都相等，侧面都是全等的平行四边形；B.用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台；C.若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；D.棱台的侧棱延长后交于一点，侧面是等腰梯形.6．（多选题）正方体的截面可能是（）A．钝角三角形B．直角三角形C．菱形D．正六边形二、填空题7．一棱柱有10个顶点，其所有的侧棱长的和为60 cm，则每条侧棱长为________cm.8.如图，M是棱长为2 cm的正方体ABCD－A1B1C1D1的棱CC1的中点，沿正方体表面从点A到点M的最短路程是________cm.9.下列说法中正确的为________（填序号）.（1）棱柱的侧棱长相等，侧面都是平行四边形：（2）各侧面都是正方形的四棱柱一定是正方体；（3）正棱锥的侧面是等边三角形；（4）有两个面互相平行，其余各面都是等腰梯形的几何体是棱台.10.一个棱台至少有________个面，面数最少的棱台有________个顶点，有________条棱．三、解答题11．如图所示是一个三棱台ABC－A′B′C′，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．12.如图在正方形ABCD中，E，F分别为AB，BC的中点，沿图中虚线将3个三角形折起，使点A，B，C重合，重合后记为点P.问：(1)折起后形成的几何体是什么几何体？(2)若正方形边长为2a，则每个面的三角形面积为多少？《8.1 基本几何图形》同步练习答案解析第1课时棱柱、棱锥、棱台一、选择题1．下图代表未折叠正方体的展开图，将其折叠起来，变成正方体后的图形是（）A ．B ．C ．D ．【答案】B 【解析】将其折叠起来，变成正方体后的图形中，相邻的平面中三条线段是平行线，排除A ，C ；相邻平面只有两个是空白面，排除D ；故选B2．一个棱锥的各条棱都相等，那么这个棱锥必不是( )A ．三棱锥B ．四棱锥C ．五棱锥D ．六棱锥【答案】D【解析】正六棱锥的底面是个正六边形，正六边形共由6个等边三角形构成，设每个等边三角形的边长为 r ，正六棱锥的高为h ，正六棱锥的侧棱长为 l ，由正六棱锥的高h 、底面的半径r 、侧棱长l 构成直角三角形得，222h r l += ，故侧棱长 l 和底面正六边形的边长r 不可能相等.故选D.3．下列几何体中棱柱有( )A．5个B．4个C．3个D．2个【答案】D【解析】由棱柱的定义及几何特征，①③为棱柱．故选D.4．用一个平面去截一个四棱锥，截面形状不可能的是 ( )A．四边形 B．三角形 C．五边形 D．六边形【答案】D【解析】根据一般的截面与几何体的几个面相交就得到几条交线，截面就是几边形，而四棱锥最多只有5个面，则截面形状不可能的是六边形，故选D.5．（多选题）给出下列命题，其中假命题是（）A.棱柱的侧棱都相等，侧面都是全等的平行四边形；B.用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台；C.若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；D.棱台的侧棱延长后交于一点，侧面是等腰梯形.【答案】ABD【解析】对于A，棱柱的侧面不一定全等，故错误；对于B，由棱台的定义可知只有当平面与底面平行时，所截部分才是棱台，故错误；对于C，若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直，比如正方体中共点的三个相邻平面，故正确；对于D，棱台的侧面不一定是等腰三角形，故错误；故选ABD .6．（多选题）正方体的截面可能是（）A．钝角三角形B．直角三角形C．菱形D．正六边形【答案】CD【解析】如图所示截面为三角形ABC ，OA =a ，OB =b ，OC =c ，∴222222222,,AC a c AB a b BC b c =+=+=+， ∴222202AB AC BC cos CAB AB AC +-∠==>⋅ ∴∠CAB 为锐角，同理∠ACB 与∠ABC 也为锐角，即△ABC 为锐角三角形，∴正方体的截面若是三角形，则一定是锐角三角形，不可能是钝角三角形和直角三角形，A 、B 错误；若是四边形，则可以是梯形（等腰梯形）、平行四边形、菱形、矩形、正方形，但不可能是直角梯形，C 正确；正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，如图为正六边形，故若是六边形，则可以是正六边形，D 正确.故选：CD .二、填空题7．一棱柱有10个顶点，其所有的侧棱长的和为60 cm ，则每条侧棱长为________cm.【答案】12【解析】该棱柱为五棱柱，共有5条侧棱，每条侧棱长都相等，∴每条侧棱长为12 cm.8.如图，M 是棱长为2 cm 的正方体ABCD －A 1B 1C 1D 1的棱CC 1的中点，沿正方体表面从点A 到点M 的最短路程是________cm.【答案】 13【解析】由题意，若以BC 为轴展开，则A ，M 两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm ，3 cm ，故两点之间的距离是13 cm.若以BB 1为轴展开，则A ，M 两点连成的线段所在的直角三角形的两直角边的长度分别为1，4，故两点之间的距离是17cm.故沿正方体表面从点A到点M的最短路程是13 cm.9.下列说法中正确的为________（填序号）.（1）棱柱的侧棱长相等，侧面都是平行四边形：（2）各侧面都是正方形的四棱柱一定是正方体；（3）正棱锥的侧面是等边三角形；（4）有两个面互相平行，其余各面都是等腰梯形的几何体是棱台.【答案】（1）【解析】（1）正确，由棱柱定义可知，棱柱的侧棱相互平行且相等，所以侧面均为平行四边形；（2）不正确，上、下底面是菱形，各侧面是全等的正方形的四棱柱不一定是正方体；（3）不正确，正棱锥的侧面都是等腰三角形，不一定是等边三角形；（4）不正确，用反例去检验，如图，显然错误图.故答案为：（1）10.一个棱台至少有________个面，面数最少的棱台有________个顶点，有________条棱．【答案】5 6 9【解析】面数最少的棱台是三棱台，共有5个面，6个顶点，9条棱．三、解答题11．如图所示是一个三棱台ABC－A′B′C′，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．【答案】见解析【解析】过A′，B，C三点作一个平面，再过A′，B，C′作一个平面，就把三棱台ABC －A′B′C′分成三部分，形成的三个三棱锥分别是A′－ABC，B－A′B′C′，A′－BCC′.(答案不唯一)12.如图在正方形ABCD中，E，F分别为AB，BC的中点，沿图中虚线将3个三角形折起，使点A ，B ，C 重合，重合后记为点P .问：(1)折起后形成的几何体是什么几何体？(2)若正方形边长为2a ，则每个面的三角形面积为多少？【答案】（1）三棱锥（2）见解析【解析】(1)如图折起后的几何体是三棱锥．(2)S △PEF ＝12a 2，S △DPF ＝S △DPE ＝12×2a ×a ＝a 2， S △DEF ＝32a 2.《8.1 基本几何图形》同步练习第2课时圆柱、圆锥、圆台、球一、选择题1．下列命题中，正确的是（）①在圆柱上、下底面圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．A ．①②B ．②③C ．②④D ．③④ 2．圆柱体被平面截成如图所示的几何体，则它的侧面展开图是（）A ．B ．C ．D ．3．已知圆柱的轴截面是正方形，其面积为Q ，则它的一个底面的面积为（）A ．QB ．Q πC ．4Q πD ．2Q π 4．下列平面图形中，通过围绕定直线l 旋转可得到如图所示几何体的是( )A ．B ．C ．D ．5．（多选题）下列说法中正确的是（）A ．正棱锥的所有侧棱长相等B ．圆柱的母线垂直于底面C ．直棱柱的侧面都是全等的矩形D ．用经过旋转轴的平面截圆锥，所得的截面一定是全等的等腰三角形6．（多选题）下列结论中错误的是（）A ．半圆弧以其直径为轴旋转一周所形成的曲面叫做球B ．直角三角形绕一边旋转得到的旋转体是圆锥C ．夹在圆柱的两个平行截面间的几何体还是一个旋转体D ．圆锥截去一个小圆锥后剩余的部分是圆台二、填空题7．如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得到的.现用一个竖直的平面去截这个几何体，则所截得的图形可能是______.（填序号）8．下列命题中正确的是________（填序号）.①以直角三角形的一边所在直线为旋转轴，将直角三角形旋转一周所得到的旋转体是圆锥；②以直角梯形的一腰所在直线为旋转轴，将直角梯形旋转一周所得到的旋转体是圆台； ③圆柱、圆锥、圆台的底面都是圆；④以等腰三角形的底边上的高所在直线为旋转轴，将等腰三角形旋转一周形成的几何体是圆锥；⑤半圆面绕其直径所在直线旋转一周形成球；⑥用一个平面去截球，得到的截面是一个圆面.9.如图是一个几何体的表面展开图形，则这个几何体是．10.一个半径为5 cm 的球，被一平面所截，球心到截面圆心的距离为4 cm ，则截面圆半径为 cm ，面积为 cm 2.三、解答题9．如图，四边形ABCD 为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体.10．一个圆台的母线长为12cm ，两底面面积分别为24cm π和225cm π．（1）求圆台的高；（2）求截得此圆台的圆锥的母线长．《8.1 基本几何图形》同步练习及答案解析第2课时圆柱、圆锥、圆台、球一、选择题1．下列命题中，正确的是（）①在圆柱上、下底面圆周上各取一点，则这两点的连线是圆柱的母线；②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．A．①②B．②③C．②④D．③④【答案】C【解析】①：若上下底面各取的点的连线能平行于轴，则是母线，反之则不是，错误；②：母线的定义，显然正确；③：圆台可看做是由平行于圆锥底面的平面截圆锥得到的，根据圆锥母线的定义可知错误；④圆柱的母线都平行于轴，故也相互平行，正确；只有②④两个命题是正确的.故选C.2．圆柱体被平面截成如图所示的几何体，则它的侧面展开图是（）A．B．C．D．【答案】D【解析】结合几何体的实物图，从截面最低点开始高度增加缓慢，然后逐渐变快，最后增加逐渐变慢，不是均衡增加的，所以A，B，C错误.故选：D.3．已知圆柱的轴截面是正方形，其面积为Q ，则它的一个底面的面积为（）A ．QB ．Q πC ．4Q πD ．2Q π 【答案】C【解析】圆柱的轴截面一边为高，另一边为底面的直径，由轴截面为正方形可知，高与，所以底面的面积为2ππ4Q ⋅=⎝⎭. 4．下列平面图形中，通过围绕定直线l 旋转可得到如图所示几何体的是( )A ．B ．C ．D ．【答案】B【解析】A.是一个圆锥以及一个圆柱; C.是两个圆锥; D. 一个圆锥以及一个圆柱;所以选B.5．（多选题）下列说法中正确的是（）A ．正棱锥的所有侧棱长相等B ．圆柱的母线垂直于底面C ．直棱柱的侧面都是全等的矩形D ．用经过旋转轴的平面截圆锥，所得的截面一定是全等的等腰三角形【答案】ABD【解析】对于A ,根据正棱锥的定义知,正棱锥的所有侧棱长相等,故A 正确；对于B ,根据圆柱是由矩形绕其一边旋转而成的几何体,可知圆柱的母线与底面垂直,故B 正确；对于C ,直棱柱的侧面都是矩形,但不一定全等,故C 错误；对于D ,圆锥的轴截面是全等的等腰三角形,故D 正确.故选:ABD 。

高中数学必修2(人教A版)第一章几何空间体1.3知识点总结含同步练习及答案

高中数学必修2(人教A版)知识点总结含同步练习题及答案
第一章空间几何体 1.3 空间几何体的表面积与体积
一、学习任务了解球、棱柱、棱锥、台的表面积和体积的计算公式．会求直棱柱、正棱锥、正棱台、圆柱、圆锥、圆台和球的表面积和体积．二、知识清单
表面积与体积表面距离
三、知识讲解
1.表面积与体积描述：多面体的表面积多面体的表面积等于各个面的面积之和，也就是展开图的面积．表面积公式直棱柱 S 侧 = ch ，S 全 = ch + 2S 底（其中 c 为底面周长， h 为棱柱的高）．正棱锥
− 解：√− 10 将三棱柱沿着 AA 1 展开如图所示，则线段 AD 1 即为最短路线，即 − − − − − −− − − − − −． AD 1 = √AD 2 + DD 2 1 = √10
如图，在圆锥中，其母线长为 2 ，底面半径为
面爬行一周后又回到 A 点，则这只虫子爬行的最短路程是多少？
PA = PB = PC = 2 ，求三棱锥 P − ABC 的表面积 S 与体积 V ．
P A 、P B 、P C 两两互相垂直，且 P A = P B = P C = 2，所以 AB = AC = BC = 2√2 ，可得 △ABC 的高为 √6 ．所以
解：因为
S = S △PAC + S △PAB + S △PBC + S △ABC 1 1 = 3 × × 2 × 2 + × 2√2 × √6 2 2 = 6 + 2√3 ;
四、课后作业
（查看更多本章节同步练习题，请到快乐学）
1. 正方体的内切球与其外接球的体积之比为 (
)
A．1 : √3
答案： C

高中数学必修2第一章空间几何体综合练习题及答案

AB D E F第一章空间几何体综合型训练一、选择题1．如果一个水平放置的图形的斜二测直观图是一个底面为045，腰和上底均为1的等腰梯形，那么原平面图形的面积是（）A ． 22+B ． 221+ C ． 222+ D ． 21+ 2．半径为R 的半圆卷成一个圆锥，则它的体积为（）A ． 33RB ． 33RC ． 35RD ． 35R 3．一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（）Ａ． 28cm π Ｂ． 212cmπ Ｃ． 216cm π Ｄ． 220cm π 4．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（）A ． 7 Ｂ． 6 Ｃ． 5 Ｄ． 35．棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( )A ． 1:7 Ｂ． 2:7 Ｃ． 7:19 Ｄ． 5:166．如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，//EF AB ,32EF =,且EF 与平面ABCD 的距离为2，则该多面体的体积为（） A ． 92Ｂ． 5 Ｃ． 6 Ｄ． 152 二、填空题1．圆台的较小底面半径为1，母线长为2，一条母线和底面的一条半径有交点且成060,则圆台的侧面积为____________．2． Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为____________．3．等体积的球和正方体,它们的表面积的大小关系是S 球___S 正方体4．若长方体的一个顶点上的三条棱的长分别为3,4,5，从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是______________．5．图（1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成;图（2）中的三视图表示的实物为_____________．6．若圆锥的表面积为a 平方米，且它的侧面展开图是一个半圆，则这个圆锥的底面的直径为_______________．三、解答题1．有一个正四棱台形状的油槽，可以装油190L ，假如它的两底面边长分别等于60cm 和40cm ，求它的深度为多少cm ？2．已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长．参考答案图（1）图（2）一、选择题1． A恢复后的原图形为一直角梯形1(11)222S =⨯=+ 2． A2312,,,22324R r R r h V r h R πππ===== 3． B正方体的顶点都在球面上，则球为正方体的外接球，则2R =，2412R S R ππ===4． A (3)84,7S r r l r ππ=+==侧面积5． C 中截面的面积为4个单位， 12124746919V V ++==++ 6． D 过点,E F 作底面的垂面，得两个体积相等的四棱锥和一个三棱柱，1313152323234222V =⨯⨯⨯⨯+⨯⨯⨯= 二、填空题1． 6π 画出圆台，则12121,2,2,()6r r l S r r l ππ====+=圆台侧面2． 16π 旋转一周所成的几何体是以BC 为半径，以AB 为高的圆锥，2211431633V r h πππ==⨯⨯= 3． <设334,3V R a a R π====2264S a S R π=====<正球4．从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,有两种方案==5．（1）4 （2）圆锥6．设圆锥的底面的半径为r ，圆锥的母线为l ，则由2l r ππ=得2l r =，而22S r r r a ππ=+⋅=圆锥表，即23,r a r π===，即直径为3π三、解答题1.解：'1(),3V S S h h =+= 319000075360024001600h ⨯==++数学试卷及试题2．解：2229(25)(25),7l lππ+=+=。

人教版高中数学必修2第一章空间几何体练习题及答案全

第一章空间几何体1.1 空间几何体的构造一、选择题1、以下各组几何体中是多面体的一组是〔〕A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、以下说法正确的选项是〔〕A 有一个面是多边形，其余各面是三角形的多面体是棱锥B 有两个面相互平行，其余各面均为梯形的多面体是棱台C 有两个面相互平行，其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面相互平行，侧面均为平行四边形3、下面多面体是五面体的是〔〕A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、以下说法错误的选项是〔〕A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是〔〕A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中，直角三角形最多可有几个〔〕A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面，面数最少的棱柱有————————个顶点，有—————————个棱。

8、一个棱柱有10个顶点，全部侧棱长的和为60，那么每条侧棱长为————————————9、把等腰三角形绕底边上的高旋转1800，所得的几何体是——————10、程度放置的正方体分别用“前面、后面、上面、下面、左面、右面〞表示。

图中是一个正方体的平面绽开图，假设图中的“似〞表示正方体的前面，“锦〞表示右面，“程〞表示下面。

那么“祝〞“你〞“前〞分别表示正方体的—————三、解答题：祝你前程似锦11、长方体—A 1B 1C 1D 1中，＝3，＝2，1＝1，由A 到C 1在长方体外表上的最短间隔为多少？12、说出以下几何体的主要构造特征〔1〕〔2〕〔3〕一、选择题1、两条相交直线的平行投影是〔〕A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线2、如图中甲、乙、丙所示，下面是三个几何体的三视图，相应的标号是〔〕① 长方体 ② 圆锥 ③ 三棱锥 ④ 圆柱A ②①③B ①②③C ③②④D ④③②正视图侧视图俯视图正视图侧视图俯视图正视图侧视图俯视图甲乙丙3、假如一个几何体的正视图和侧视图都是长方形，那么这个几何体可能是〔〕A 长方体或圆柱B 正方体或圆柱C 长方体或圆台D 正方体或四棱锥A A 1B 1BC C 1D 1 D4、以下说法正确的选项是〔〕A 程度放置的正方形的直观图可能是梯形B 两条相交直线的直观图可能是平行直线C 平行四边形的直观图仍旧是平行四边形D 相互垂直的两条直线的直观图仍旧相互垂直5、假设一个三角形，采纳斜二测画法作出其直观图，其直观图面积是原三角形面积的〔〕 A 21倍 B 42倍 C 2倍 D 2倍6、如图〔１〕所示的一个几何体，，在图中是该几何体的俯视图的是〔〕二、选择题7、当圆锥的三视图中的正视图是一个圆时，侧视图及俯视图是两个全等的———————三角形。

高一数学必修二第一章空间几何形状练习题及答案

高一数学必修二第一章空间几何形状练习题及答案练题1. 已知立方体$ABCD-A_1B_1C_1D_1$的棱长为$6\text{cm}$ ，点$E$恰好在 $BC$ 上，在 $DE$ 上取点 $F$，试求：(1) $\angle A_1FB_1$ 的大小；(2) $EF$ 的长度。

2. 已知底面为等腰直角梯形的四面体$S-ABC$，$AB=AC=\sqrt{3}\text{cm}$，$BC=2\text{cm}$，$SA\perp AB$，$SA=2\text{cm}$，$M$ 为 $BC$ 中点，过点 $M$ 作 $SA$ 的垂线$MH$，交 $BC$ 于点 $H$。

(1)求 $SA$ 与面 $ABC$ 的夹角；(2) 求 $MH$ 的长度。

3. 在正四面体$S-ABC$中，$M$ 为 $BC$ 中点，过 $S$，$M$ 的平面与直线 $AB$ 交于点 $E$，过 $S$，$M$ 的平面与直线$BC$ 交于点 $F$。

(1) 求 $EF$ 的长；(2) 设 $SE$ 交 $AF$ 于 $N$，求 $SN$ 的长。

4. 已知棱长为 $5\text{cm}$ 的正四棱锥 $S-ABCD$，平面$ABCD$ 与平面 $SAB$ 的夹角为 $60^{\circ}$。

设 $AD$ 与平面$SBC$ 相交于 $E$，$BE$ 交平面 $SAD$ 于点 $F$。

(1) 求过顶点 $S$ 的平面与平面 $ABCD$ 的交线段的长度；(2) 过顶点 $S$ 且垂直于平面 $ABCD$ 的直线交 $EF$ 于点$G$，求 $SG$ 的长度。

答案1.(1) $\angle A_1FB_1=45^{\circ}$(2) $EF=3\sqrt{2}\text{cm}$2.(1) $\cos \angle BSA=\dfrac{\sqrt{2}}{2}$, 则 $\angle BSA=45^{\circ}$。

(2) $MH=\dfrac{\sqrt{2}}{2}\text{cm}$3.(1) $EF= \dfrac{5\sqrt{3}}{3}$(2) $SN=\dfrac{5\sqrt{2}}{6}$4.(1) $SB=\dfrac{5\sqrt{3}}{2}$(2) $SG=\dfrac{5\sqrt{3}}{6}$以上答案仅供参考，具体求解过程需要参考相关知识点及公式计算。

高一数学人教a版必修二习题第一章空间几何体 1.2.2 含答案

(本栏目内容，在学生用书中以独立形式分册装订！)一、选择题(每小题5分，共20分)1．在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )解析：由几何体的正视图和俯视图可知，该几何体的底面为半圆和等腰三角形，其侧视图可以是一个由等腰三角形及底边上的高构成的平面图形．答案： D2．如图所示，这些几何体各自的三视图中，有且仅有两个视图相同的是( )A．①②B．①③C．①④D．②④解析：以正方体其中一面为正视方向时所得的三视图都是正方形，所以①不符合题意，排除A、B、C.答案： D3．右图是长和宽分别相等的两个矩形．给定下列三个说法：①存在三棱柱，其正视图、俯视图如右图；②存在四棱柱，其正视图、俯视图如右图；③存在圆柱，其正视图、俯视图如右图．其中正确说法的个数是( )A．3 B．2C．1 D．0解析：底面是等腰直角三角形的三棱柱，当它的一个矩形侧面放置在水平面上时，它的正视图和俯视图可以是全等的矩形，因此①正确；若长方体的高和宽相等，则存在满足题意的两个相等的矩形，因此②正确；当圆柱侧放时(即侧视图为圆时)，它的正视图和俯视图可以是全等的矩形，因此③正确．答案： A4．某四面体的三视图如图所示，该四面体四个面的面积中最大的是( )A．8 B．6 2C．10 D．8 2解析：将三视图还原成几何体的直观图如图所示．它的四个面的面积分别为8,6,10,62，故最大的面积应为10.答案：C二、填空题(每小题5分，共15分)5．已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于________．解析：由题意可知该正方体的放置如图所示，侧视图的方向垂直于面BDD1B1，正视图的方向垂直于面A1C1CA，且正视图是长为2，宽为1的矩形，故正视图的面积为 2.答案： 26．如图甲所示，在正方体ABCD－A1B1C1D1中，E，F分别是AA1，C1D1的中点，G是正方形BCC1B1的中心，则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________．解析：在面ABCD和面A1B1C1D1上的投影是图乙(1)；在面ADD1A1和面BCC1B1上的投影是图乙(2)；在面ABB1A1和面DCC1D1上的投影是图乙(3)．答案：(1)(2)(3)7．两条平行线在一个平面内的正投影可能是________．①两条平行线；②两个点；③两条相交直线；④一条直线和直线外的一点；⑤一条直线．解析：如图，在正方体A1B1C1D1－ABCD中，直线A1B1∥C1D1，它们在平面ABCD内的投影为AB，CD，且AB∥CD，故①正确；它们在平面BCC1B1内的正投影是点B1和点C1，故②正确；取A1D1的中点E，B1C1的中点F，连接EF，则EF∥D1C1且EF与D1C1在平面ABB1A1内的投影是同一直线A1B1，故⑤正确，故填①②⑤.答案：①②⑤三、解答题(每小题10分，共20分)8．画出如图所示的几何体的三视图．解析：该几何体的三视图如下：的直观图．解析：三视图对应的几何体如图所示．§4 二项分布1．掌握独立重复试验的概念及意义，理解事件在n次独立重复试验中恰好发生k次的概率公式．(重点)2．理解n次独立重复试验的模型，并能用于解一些简单的实际问题．(难点) 3．了解二项分布与超几何分布的关系．(易混点)[基础·初探]教材整理二项分布阅读教材P48～P50，完成下列问题．1．n次独立重复试验进行n次试验，如果满足以下条件：(1)每次试验只有两个相互________的结果，可以分别称为“________”和“________”；(2)每次试验“成功”的概率均为p，“失败”的概率均为；(3)各次试验是相互独立的，则这n次试验称为n次独立重复试验．【答案】(1)对立成功失败(2)1－p2．二项分布(1)若用随机变量X 表示n 次独立重复试验的次数，则P(X ＝k)＝________(k ＝0,1,2，…，n)．(2)若一个随机变量X 的分布列如(1)所述，则称X 服从参数为n ，p 的二项分布，简记为X ～________.【答案】 (1)C k np k (1－p)n －k (2)B(n ，p)1．独立重复试验满足的条件是________．(填序号) ①每次试验之间是相互独立的； ②每次试验只有发生和不发生两种情况；③每次试验中发生的机会是均等的； ④每次试验发生的事件是互斥的．【解析】由n 次独立重复试验的定义知①②③正确．【答案】 ①②③2．一枚硬币连掷三次，只有一次出现正面的概率为________．【解析】抛掷一枚硬币出现正面的概率为12，由于每次试验的结果不受影响，故由独立重复试验可知，所求概率为P ＝C 13⎝ ⎛⎭⎪⎪⎫12⎝ ⎛⎭⎪⎪⎫122＝38.【答案】38[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：解惑：疑问2：解惑：疑问3：解惑：[小组合作型]某气象站天气预报的准确率为80%，计算(结果保留到小数点后面第2位)：(1)5次预报中恰有2次准确的概率；(2)5次预报中至少有2次准确的概率；(3)5次预报中恰有2次准确，且其中第3次预报准确的概率．【精彩点拨】由于5次预报是相互独立的，且结果只有两种(即准确或不准确)，符合独立重复试验．【自主解答】(1)记预报一次准确为事件A，则P(A)＝0.8.5次预报相当于5次独立重复试验，2次准确的概率为P＝C25×0.82×0.23＝0.051 2≈0.05，因此5次预报中恰有2次准确的概率约为0.05.(2)“5次预报中至少有2次准确”的对立事件为“5次预报全部不准确或只有1次准确”，其概率为P＝C05×(0.2)5＋C15×0.8×0.24＝0.006 72≈0.01.所以所求概率为1－P＝1－0.01＝0.99.所以5次预报中至少有2次准确的概率约为0.99.(3)说明第1,2,4,5次中恰有1次准确．所以概率为P＝C14×0.8×0.23×0.8＝0.02 048≈0.02，所以恰有2次准确，且其中第3次预报准确的概率约为0.02.独立重复试验概率求法的三个步骤1．判断：依据n次独立重复试验的特征，判断所给试验是否为独立重复试验．2．分拆：判断所求事件是否需要分拆．3．计算：就每个事件依据n次独立重复试验的概率公式求解，最后利用互斥事件概率加法公式计算．[再练一题]1．(1)甲、乙两队进行排球比赛，已知在一局比赛中甲队胜的概率为23，没有平局．若进行三局两胜制比赛，先胜两局者为胜，甲获胜的概率为________．(2)在4次独立重复试验中，事件A 至少发生1次的概率为6581，则事件A 在1次试验中出现的概率为________．【解析】 (1)“甲获胜”分两类：①甲连胜两局；②前两局中甲胜一局，并胜最后一局．即P ＝⎝ ⎛⎭⎪⎪⎫232＋C 12×23×13×23＝2027.(2)由题意知，C 04p 0(1－p)4＝1－6581，p ＝13. 【答案】 (1)2027 (2)13一名学生每天骑自行车上学，从家到学校的途中有5个交通岗，假设他在各交通岗遇到红灯的事件是相互独立的，并且概率都是13.(1)求这名学生在途中遇到红灯的次数ξ的分布列；(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列．【精彩点拨】 (1)首先判断ξ是否服从二项分布，再求分布列．(2)注意“首次遇到”“或到达”的含义，并明确η的取值．再求η取各值的概率．【自主解答】 (1)ξ～B ⎝⎛⎭⎪⎪⎫5，13，ξ的分布列为P(ξ＝k)＝C k 5⎝ ⎛⎭⎪⎪⎫13k ⎝ ⎛⎭⎪⎪⎫235－k ，k ＝0,1,2,3,4,5.(2)η的分布列为P(η＝k)＝P(前k 个是绿灯，第k ＋1个是红灯)＝⎝ ⎛⎭⎪⎪⎫23k ·13，k ＝0,1,2,3,4；P(η＝5)＝P(5个均为绿灯)＝⎝ ⎛⎭⎪⎪⎫235.故η的分布列为!1．本例属于二项分布，当X 服从二项分布时，应弄清X ～B(n ，p)中的试验次数n 与成功概率p.2．解决二项分布问题的两个关注点(1)对于公式P(X ＝k)＝C k np k (1－p)n －k (k ＝0,1,2，…，n)必须在满足“独立重复试验”时才能运用，否则不能应用该公式．(2)判断一个随机变量是否服从二项分布，关键有两点：一是对立性，即一次试验中，事件发生与否两者必有其一；二是重复性，即试验是独立重复地进行了n 次．[再练一题]2．在一次数学考试中，第14题和第15题为选做题．规定每位考生必须且只需在其中选做一题．设4名考生选做每道题的可能性均为12，且各人的选择相互之间没有影响．(1)求其中甲、乙2名考生选做同一道题的概率；(2)设这4名考生中选做第15题的人数为ξ名，求ξ的分布列．【解】 (1)设事件A 表示“甲选做14题”，事件B 表示“乙选做14题”，则甲、乙2名考生选做同一道题的事件为“AB ＋A －B －”，且事件A ，B 相互独立．∴P(AB ＋A －B －)＝P(A)P(B)＋P(A )P(B ) ＝12×12＋⎝ ⎛⎭⎪⎪⎫1－12×⎝ ⎛⎭⎪⎪⎫1－12＝12.(2)随机变量ξ的可能取值为0,1,2,3,4，且ξ～B ⎝⎛⎭⎪⎪⎫4，12.∴P(ξ＝k)＝C k 4⎝ ⎛⎭⎪⎪⎫12k ⎝⎛⎭⎪⎪⎫1－124－k＝C k 4⎝ ⎛⎭⎪⎪⎫124(k ＝0,1,2,3,4)． ∴随机变量ξ的分布列为[探究共研型]探究1 王明在做一道单选题时，从A ，B ，C ，D 四个选项中随机选一个答案，他做对的结果数服从二项分布吗？两点分布与二项分布有何关系？【提示】做一道题就是做一次试验，做对的次数可以为0次、1次，它服从二项分布．两点分布就是一种特殊的二项分布，即是n ＝1的二项分布．探究2 王明做5道单选题，每道题都随机选一个答案，那么他做对的道数服从二项分布吗？为什么？【提示】服从二项分布．因为每道题都是随机选一个答案，结果只有两个：对与错，并且每道题做对的概率均相等，故做5道题可以看成“一道题”重复做了5次，做对的道数就是5次试验中“做对”这一事件发生的次数，故他做对的“道数”服从二项分布．探究3 王明做5道单选题，其中2道会做，其余3道均随机选一个答案，他做对的道数服从二项分布吗？如何判断一随机变量是否服从二项分布？【提示】不服从二项分布．因为会做的两道题做对的概率与随机选取一个答案做对的概率不同，不符合二项分布的特点，判断一个随机变量是否服从二项分布关键是看它是否是n 次独立重复试验，随机变量是否为在这n 次独立重复试验中某事件发生的次数，满足这两点的随机变量才服从二项分布，否则就不服从二项分布．(2016·泰兴高二检测)甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分．假设甲队中每人答对的概率均为23，乙队中3人答对的概率分别为23，23，12，且各人回答正确与否相互之间没有影响．用ξ表示甲队的总得分．(1)求随机变量ξ的分布列；(2)用A 表示“甲、乙两个队总得分之和等于3”这一事件，用B 表示“甲队总得分大于乙队总得分”这一事件，求P(AB)．【精彩点拨】 (1)由于甲队中每人答对的概率相同，且正确与否没有影响，所以ξ服从二项分布，其中n ＝3，p ＝23；(2)AB 表示事件A 、B 同时发生，即甲、乙两队总得分之和为3且甲队总得分大于乙队总得分．【自主解答】 (1)由题意知，ξ的可能取值为0,1,2,3，且 p(ξ＝0)＝C 03⎝ ⎛⎭⎪⎪⎫1－233＝127， P(ξ＝1)＝C 1323⎝ ⎛⎭⎪⎪⎫1－232＝29， P(ξ＝2)＝C 23⎝ ⎛⎭⎪⎪⎫232⎝ ⎛⎭⎪⎪⎫1－23＝49， P(ξ＝3)＝C 33⎝ ⎛⎭⎪⎪⎫233＝827.所以ξ的分布列为(2)用C 表示“甲得2分乙得1分”这一事件，用D 表示“甲得3分乙得0分”这一事件，所以AB ＝C ＋D ，且C ，D 互斥，又P(C)＝C 23⎝ ⎛⎭⎪⎪⎫232⎝⎛⎭⎪⎪⎫1－23⎣⎢⎢⎡23×13×12＋13×23×⎦⎥⎥⎤12＋13×13×12＝1034， P(D)＝C 33⎝ ⎛⎭⎪⎪⎫233⎝ ⎛⎭⎪⎪⎫13×13×12＝435，由互斥事件的概率公式得 P(AB)＝P(C)＋P(D) ＝1034＋435＝3435＝34243.对于概率问题的综合题，首先，要准确地确定事件的性质，把问题化归为古典概型、互斥事件、独立事件、独立重复试验四类事件中的某一种；其次，要判断事件是A ＋B 还是AB ，确定事件至少有一个发生，还是同时发生，分别运用相加或相乘事件公式，最后，选用相应的求古典概型、互斥事件、条件概率、独立事件、n 次独立重复试验的概率公式求解.[再练一题]3．(2016·余姚高二质检)为拉动经济增长，某市决定新建一批重点工程，分为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的12，13，16.现有3名工人独立地从中任选一个项目参与建设．(1)求他们选择的项目所属类别互不相同的概率；(2)记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数，求ξ的分布列．【解】记第i 名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件A i ，B i ，C i ，i ＝1,2,3.由题意知A 1，A 2，A 3相互独立，B 1，B 2，B 3相互独立，C 1，C 2，C 3相互独立，A i ，B j ，C k (i ，j ，k ＝1,2,3且i ，j ，k 互不相同)相互独立，用P(A i )＝12，P(B j )＝13，P(C k )＝16.(1)他们选择的项目所属类别互不相同的概率．P ＝3! P(A 1B 2C 3)＝6P(A 1)P(B 2)P(C 3)＝6×12×13×16＝16.(2)法一：设3名工人中选择的项目属于民生工程的人数为η，由已知，η～B ⎝⎛⎭⎪⎪⎫3，13，且ξ＝3－η，所以P(ξ＝0)＝P(η＝3)＝C 33⎝ ⎛⎭⎪⎪⎫133＝127，P(ξ＝1)＝P(η＝2)＝C 23⎝ ⎛⎭⎪⎪⎫132⎝ ⎛⎭⎪⎪⎫23＝29，P(ξ＝2)＝P(η＝1)＝C 13⎝ ⎛⎭⎪⎪⎫13⎝ ⎛⎭⎪⎪⎫232＝49，P(ξ＝3)＝P(η＝0)＝C 03⎝ ⎛⎭⎪⎪⎫233＝827. 故ξ的分布列是法二：记第i 名工人选择的项目属于基础设施工程或产业建设工程分别为事件D i ，i ＝1,2,3.由已知，D 1，D 2，D 3相互独立，且P(D i )＝P(A i ∪C i )＝P(A i )＋P(C i )＝12＋16＝23，所以ξ～B ⎝ ⎛⎭⎪⎪⎫3，23，即P(ξ＝k)＝C k 3⎝ ⎛⎭⎪⎪⎫23k ⎝ ⎛⎭⎪⎪⎫133－k ，k ＝0,1,2,3.故ξ的分布列是[构建·体系]1．(2016·桂林二模)一袋中有5个白球，3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了X 次球，则P(X ＝12)＝( )A ．C 1012⎝ ⎛⎭⎪⎪⎫3810⎝ ⎛⎭⎪⎪⎫582B ．C 912⎝ ⎛⎭⎪⎪⎫3810⎝ ⎛⎭⎪⎪⎫582C ．C 911⎝ ⎛⎭⎪⎪⎫582⎝ ⎛⎭⎪⎪⎫382 D ．C 911⎝ ⎛⎭⎪⎪⎫3810⎝ ⎛⎭⎪⎪⎫582 【解析】 “X ＝12”表示第12次取到红球，且前11次有9次取到红球，2次取到白球，因此，P(X ＝12)＝38·C 911⎝ ⎛⎭⎪⎪⎫389×⎝ ⎛⎭⎪⎪⎫582＝C 911⎝ ⎛⎭⎪⎪⎫3810⎝ ⎛⎭⎪⎪⎫582.【答案】 D2．某电子管正品率为34，次品率为14，现对该批电子管进行测试，设第ξ次首次测到正品，则P(ξ＝3)＝( )A ．C 23⎝ ⎛⎭⎪⎪⎫142×34B ．C 23⎝ ⎛⎭⎪⎪⎫342×14C.⎝ ⎛⎭⎪⎪⎫142×34D.⎝ ⎛⎭⎪⎪⎫342×14【解析】 ξ＝3表示第3次首次测到正品，而前两次都没有测到正品，故其概率是⎝ ⎛⎭⎪⎪⎫142×34.【答案】 C3．某市公租房的房源位于A ，B ，C 三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的．该市的4位申请人中恰有2人申请A 片区房源的概率为________. 【62690039】【解析】每位申请人申请房源为一次试验，这是4次独立重复试验，设申请A 片区房源记为A ，则P(A)＝13，所以恰有2人申请A 片区的概率为C 24·⎝ ⎛⎭⎪⎪⎫132·⎝ ⎛⎭⎪⎪⎫232＝827. 【答案】8274．设X ～B(4，p)，且P(X ＝2)＝827，那么一次试验成功的概率p 等于________．【解析】 P(X ＝2)＝C 24p 2(1－p)2＝827，即p 2(1－p)2＝⎝ ⎛⎭⎪⎪⎫132·⎝ ⎛⎭⎪⎪⎫232，解得p ＝13或p ＝23.【答案】13或235．甲、乙两人各射击一次击中目标的概率分别是23和34，假设两人射击是否击中目标，相互之间没有影响，每次射击是否击中目标，相互之间也没有影响．(1)求甲射击4次，至少1次未击中目标的概率；(2)求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率．【解】设“甲、乙两人各射击一次击中目标分别记为A ，B ”，则P(A)＝23，P(B)＝34.(1)甲射击4次，全击中目标的概率为 C 44P 4(A)[1－P(A)]0＝⎝ ⎛⎭⎪⎪⎫234＝1681. 所以甲射击4次至少1次未击中目标的概率为1－1681＝6581.(2)甲、乙各射击4次，甲恰好击中2次，概率为 C 24P 2(A)·[1－P(A)]2＝6×⎝ ⎛⎭⎪⎪⎫232×⎝ ⎛⎭⎪⎪⎫132＝827.乙恰好击中3次，概率为C34P3(B)·[1－P(B)]1＝27 64.故所求概率为827×2764＝18.我还有这些不足：(1)(2)我的课下提升方案：(1)(2)学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．一头病猪服用某药品后被治愈的概率是90%，则服用这种药的5头病猪中恰有3头猪被治愈的概率为( )A．0.93B．1－(1－0.9)3C ．C 35×0.93×0.12D ．C 35×0.13×0.92 【解析】由独立重复试验恰好发生k 次的概率公式知，该事件的概率为C 35×0.93×(1－0.9)2.【答案】 C2．假设流星穿过大气层落在地面上的概率为14，现有流星数量为5的流星群穿过大气层有2个落在地面上的概率为( )A.116 B.135512C.45512D.271 024【解析】此问题相当于一个试验独立重复5次，有2次发生的概率，所以P ＝C 25·⎝ ⎛⎭⎪⎪⎫142·⎝ ⎛⎭⎪⎪⎫343＝135512. 【答案】 B3．在4次独立重复试验中事件出现的概率相同．若事件A 至少发生1次的概率为6581，则事件A 在1次试验中出现的概率为( )A.13 B.25 C.56 D.34【解析】设所求概率为p ，则1－(1－p)4＝6581，得p ＝13.【答案】 A4．位于坐标原点的一个质点P 按下述规则移动：质点每次移动一个单位；移动的方向为向上或向右，并且向上、向右移动的概率都是12，质点P 移动五次后位于点(2,3)的概率是( )A.⎝ ⎛⎭⎪⎪⎫125 B ．C 25×⎝ ⎛⎭⎪⎪⎫125C ．C 35×⎝ ⎛⎭⎪⎪⎫123 D ．C 25×C 35×⎝ ⎛⎭⎪⎪⎫125【解析】如图，由题可知，质点P 必须向右移动2次，向上移动3次才能位于点(2,3)，问题相当于5次独立重复试验向右恰好发生2次的概率．所以概率为 P ＝C 25×⎝ ⎛⎭⎪⎪⎫122×⎝ ⎛⎭⎪⎪⎫123＝C 25⎝ ⎛⎭⎪⎪⎫125.故选B.【答案】 B5．若随机变量ξ～B ⎝⎛⎭⎪⎪⎫5，13，则P(ξ＝k)最大时，k 的值为( )A ．1或2B ．2或3C ．3或4D ．5【解析】依题意P(ξ＝k)＝C k 5×⎝ ⎛⎭⎪⎪⎫13k ×⎝ ⎛⎭⎪⎪⎫235－k ，k ＝0,1,2,3,4,5.可以求得P(ξ＝0)＝32243，P(ξ＝1)＝80243，P(ξ＝2)＝80243，P(ξ＝3)＝40243，P(ξ＝4)＝10243，P(ξ＝5)＝1243.故当k ＝2或1时，P(ξ＝k)最大．【答案】 A 二、填空题6．已知汽车在公路上行驶时发生车祸的概率为0.001，如果公路上每天有1 000辆汽车通过，则公路上发生车祸的概率为________；恰好发生一起车祸的概率为________．(已知0.9991 000≈0.367 70,0.999999≈0.368 06，精确到0.000 1)【解析】设发生车祸的车辆数为X ，则X ～B(1 000，0.001)． (1)记事件A ：“公路上发生车祸”，则P(A)＝1－P(X ＝0)＝1－0.9991000≈1－0.367 70＝0.632 3.(2)恰好发生一次车祸的概率为P(X ＝1)＝C 11 000×0.001×0.999999≈0.368 06≈0.368 1. 【答案】 0.632 3 0.368 17．在等差数列{a n }中，a 4＝2，a 7＝－4，现从{a n }的前10项中随机取数，每次取出一个数，取后放回，连续抽取3次，假定每次取数互不影响，那么在这三次取数中，取出的数恰好为两个正数和一个负数的概率为______．(用数字作答)【解析】由已知可求通项公式为a n ＝10－2n(n ＝1,2,3，…)，其中a 1，a 2，a 3，a 4为正数，a 5＝0，a 6，a 7，a 8，a 9，a 10为负数，∴从中取一个数为正数的概率为410＝25，取得负数的概率为12. ∴取出的数恰为两个正数和一个负数的概率为C 23×⎝ ⎛⎭⎪⎪⎫252×⎝ ⎛⎭⎪⎪⎫121＝625. 【答案】6258．下列说法正确的是________．(填序号)①某同学投篮的命中率为0.6，他10次投篮中命中的次数X 是一个随机变量，且X ～B(10,0.6)；②某福彩的中奖概率为p ，某人一次买了8张，中奖张数X 是一个随机变量，且X ～B(8，p)；③从装有5个红球、5个白球的袋中，有放回地摸球，直到摸出白球为止，则摸球次数X 是随机变量，且X ～B ⎝⎛⎭⎪⎪⎫n ，12.【解析】 ①②显然满足独立重复试验的条件，而③虽然是有放回地摸球，但随机变量X 的定义是直到摸出白球为止，也就是说前面摸出的一定是红球，最后一次是白球，不符合二项分布的定义．【答案】 ①② 三、解答题9．(2016·滨州高二检测)某市医疗保险实行定点医疗制度，按照“就近就医，方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区有A ，B ，C 三家社区医院，并且他们的选择相互独立．设4名参加保险人员选择A 社区医院的人数为X ，求X 的分布列．【解】由已知每位参加保险人员选择A 社区的概率为13，4名人员选择A 社区即4次独立重复试验，即X ～B ⎝ ⎛⎭⎪⎪⎫4，13，所以P(X ＝k)＝C k 4·⎝ ⎛⎭⎪⎪⎫13k ·⎝ ⎛⎭⎪⎪⎫234－k (k ＝0,1,2,3,4)，所以X 的分布列为10.(2016·柳州高二检测)甲、乙两队在进行一场五局三胜制的排球比赛中，规定先赢三局的队获胜，并且比赛就此结束，现已知甲、乙两队每比赛一局，甲队获胜的概率为35，乙队获胜的概率为25，且每局比赛的胜负是相互独立的．(1)求甲队以3∶2获胜的概率； (2)求乙队获胜的概率．【解】 (1)设甲队以3∶2获胜的概率为P 1，则P 1＝C 24⎝ ⎛⎭⎪⎪⎫352·⎝ ⎛⎭⎪⎪⎫252·35＝6483 125. (2)设乙队获胜的概率为P 2，则P 2＝⎝ ⎛⎭⎪⎪⎫253＋C 23⎝ ⎛⎭⎪⎪⎫252·35·25＋C 24⎝ ⎛⎭⎪⎪⎫252·⎝ ⎛⎭⎪⎪⎫352·25＝9923 125.[能力提升]1．甲、乙两人进行乒乓球比赛，比赛规则为“3局2胜”，即以先赢2局者为胜，根据经验，每局比赛中甲获胜的概率为0.6，则本次比赛甲获胜的概率是( )A ．0.216B ．0.36C ．0.432D ．0.648【解析】甲获胜有两种情况，一是甲以2∶0获胜，此时p 1＝0.62＝0.36；二是甲以2∶1获胜，此时p 2＝C 12×0.6×0.4×0.6＝0.288，故甲获胜的概率p ＝p 1＋p 2＝0.648.【答案】 D2．(2016·孝感高级中学期中)掷一枚质地均匀的骰子n 次，设出现k 次点数为1的概率为P n (k)，若n ＝20，则当P n (k)取最大值时，k 为( ) A ．3B ．4C ．8D ．10【解析】掷一枚质地均匀的骰子20次，其中出现点数为1的次数为X ，X ～B ⎝ ⎛⎭⎪⎪⎫20，16，P n (k)＝C k 20·⎝ ⎛⎭⎪⎪⎫5620－k ·⎝ ⎛⎭⎪⎪⎫16k .P n k P nk －1＝15⎝ ⎛⎭⎪⎪⎫21k －1.当1≤k ≤3时， 15⎝ ⎛⎭⎪⎪⎫21k －1>1，P n (k)>P n (k －1)．当k ≥4时，15⎝ ⎛⎭⎪⎪⎫21k －1<1，P n (k)<P n (k－1)．因此k ＝3时，P n (k)取最大值．故选A.【答案】 A3．有n 位同学参加某项选拔测试，每位同学能通过测试的概率都是p(0<p<1)，假设每位同学能否通过测试是相互独立的，则至少有一位同学通过测试的概率为________. 【62690040】【解析】所有同学都不通过的概率为(1－p)n ，故至少有一位同学通过的概率为1－(1－p)n .【答案】 1－(1－p)n4．“石头、剪刀、布”是一种广泛流传于我国民间的古老游戏，其规则是：用三种不同的手势分别表示石头、剪刀、布；两个玩家同时出示各自手势1次记为1次游戏，“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”；双方出示的手势相同时，不分胜负．现假设玩家甲、乙双方在游戏时出示三种手势是等可能的．(1)求在1次游戏中玩家甲胜玩家乙的概率；(2)若玩家甲、乙双方共进行了3次游戏，其中玩家甲胜玩家乙的次数记作随机变量X ，求X 的分布列．【解】 (1)玩家甲、乙双方在1次游戏中出示手势的所有可能结果是(石头，石头)，(石头，剪刀)，(石头，布)，(剪刀，石头)，(剪刀，剪刀)，(剪刀，布)，(布，石头)，(布，剪刀)，(布，布)，共有9个基本事件．玩家甲胜玩家乙的基本事件分别是(石头，剪刀)，(剪刀，布)，(布，石头)，共有3个．所以在1次游戏中玩家甲胜玩家乙的概率P ＝13.(2)X 的可能取值分别为0,1,2,3，X ～B ⎝ ⎛⎭⎪⎪⎫3，13，则P(X ＝0)＝C 03·⎝ ⎛⎭⎪⎪⎫233＝827， P(X ＝1)＝C 13·⎝ ⎛⎭⎪⎪⎫131·⎝ ⎛⎭⎪⎪⎫232＝49，P(X ＝2)＝C 23·⎝ ⎛⎭⎪⎪⎫132·⎝ ⎛⎭⎪⎪⎫231＝29，P(X ＝3)＝C 33·⎝ ⎛⎭⎪⎪⎫133＝127.X 的分布列如下：第2课时分类加法计数原理与分步乘法计数原理的应用1．掌握分类加法计数原理和分步乘法计数原理．(重点))2．会应用两个计数原理解决简单的实际问题．(难点[基础·初探]教材整理分类加法计数原理与分步乘法计数原理的联系与区别阅读教材P3“例1”和P4“例2”部分，完成下列问题．两个计数原理的联系与区别：【答案】分解成若干个完成独立一种中间独立地完成任何一步各个步骤1．由1,2,3,4组成没有重复数字的三位数的个数为________．【解析】由题意知可以组成没有重复数字的三位数的个数为4×3×2＝24.【答案】242．(a1＋a2＋a3)(b1＋b2＋b3)(c1＋c2＋c3＋c4)展开后共有________项．【解析】该展开式中每一项的因式分别来自a1＋a2＋a3，b1＋b2＋b3，c1＋c2＋c3＋c4中的各一项．由a1，a2，a3中取一项共3种取法，从b1，b2，b3中取一项有3种不同取法，从c1，c2，c3，c4中任取一项共4种不同的取法．由分步乘法计数原理知，该展开式共3×3×4＝36(项)．【答案】363．5名班委进行分工，其中A不适合当班长，B只适合当学习委员，则不同的分工方案种数为________．【解析】根据题意，B只适合当学习委员，有1种情况，A不适合当班长，也不能当学习委员，有3种安排方法，剩余的3人担任剩余的工作，有3×2×1＝6种情况，由分步乘法计数原理，可得共有1×3×6＝18种分工方案．【答案】184．用1,2,3三个数字组成一个四位数，规定这三个数必须全部使用，且同一数字不能相邻，这样的四位数有________个．【解析】分三步完成，第1步，确定哪一个数字被使用2次，有3种方法；第2步，把这2个相同的数字排在四位数不相邻的两个位置上，有3种方法；第3步，将余下的2个数字排在四位数余下的两个位置上，有2种方法．故有3×3×2＝18个不同的四位数．【答案】18[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：解惑：疑问2：解惑：[小组合作型](1)高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践，其中工厂甲必须有班级去，每班去何工厂可自由选择，则不同的分配方案有( )A．16种B．18种C．37种D．48种(2)甲、乙、丙、丁四人各写一张贺卡，放在一起，再各取一张不是自己的贺卡，则不同取法的种数有________．【精彩点拨】(1)由于去甲工厂的班级分配情况较多，而其对立面较少，可考虑间接法求解．(2)先让一人去抽，然后再让被抽到贺卡所写人去抽．【自主解答】(1)高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践有43种不同的分配方案，若三个班都不去工厂甲则有33种不同的分配方案．则满足条件的不同的分配方案有43－33＝37(种)．故选C.(2)不妨由甲先来取，共3种取法，而甲取到谁的将由谁在甲取后第二个来取，共3种取法，余下来的人，都只有1种选择，所以不同取法共有3×3×1×1＝9(种)．【答案】(1)C (2)9求解抽取(分配)问题的方法1．当涉及对象数目不大时，一般选用枚举法、树状图法、框图法或者图表法．2．当涉及对象数目很大时，一般有两种方法：①直接法：直接使用分类加法计数原理或分步乘法计数原理．②间接法：去掉限制条件，计算所有的抽取方法数，然后减去所有不符合条件的抽取方法数即可．[再练一题]1．3个不同的小球放入5个不同的盒子，每个盒子至多放一个小球，共有多少种方法？【解】法一(以小球为研究对象)分三步来完成：第一步：放第一个小球有5种选择；第二步：放第二个小球有4种选择；第三步：放第三个小球有3种选择．根据分步乘法计数原理得：共有方法数N＝5×4×3＝60.法二(以盒子为研究对象)盒子标上序号1,2,3,4,5，分成以下10类：第一类：空盒子标号为(1,2)，选法有3×2×1＝6(种)；第二类：空盒子标号为(1,3)，选法有3×2×1＝6(种)；第三类：空盒子标号为(1,4)，选法有3×2×1＝6(种)；分类还有以下几种情况：空盒子标号分别为(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)，共10类，每一类都有6种方法．根据分类加法计数原理得，共有方法数N＝6＋6＋…＋6＝60(种)．用0,1,2,3,4,5可以组成多少个无重复数字的(1)银行存折的四位密码．(2)四位整数．【精彩点拨】(1)用分步乘法计数原理求解(1)问；(2)0不能作首位，优先排首位，用分步乘法计数原理求解．【自主解答】(1)分步解决．第一步：选取左边第一个位置上的数字，有6种选取方法；第二步：选取左边第二个位置上的数字，有5种选取方法；第三步：选取左边第三个位置上的数字，有4种选取方法；第四步：选取左边第四个位置上的数字，有3种选取方法．由分步乘法计数原理知，可组成不同的四位密码共有6×5×4×3＝360(个)．(2)分步解决．第一步：首位数字有5种选取方法；第二步：百位数字有5种选取方法；第三步：十位数字有4种选取方法；第四步：个位数字有3种选取方法．由分步乘法计数原理知，可组成四位整数有5×5×4×3＝300(个)．1．对于组数问题，一般按特殊位置(一般是末位和首位)由谁占领分类，分类中再按特殊位置(或者特殊元素)优先的方法分步完成；如果正面分类较多，可采用间接法从反面求解．2．解决组数问题，应特别注意其限制条件，有些条件是隐藏的，要善于挖。

人教版高中数学必修2《空间几何体》章节测验(含两套,附答案)

人教版高中数学必修2《空间几何体》章节测验（含两套，附答案）（考试时间：120分钟试卷满分：150分）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．下图中的图形经过折叠不能围成棱柱的是（）2．一个几何体的三视图如图所示，则这个几何体的体积等于（）A ．4B ．6C ．8D ．123．下列命题中，正确的命题是（） A ．存在两条异面直线同时平行于同一个平面B ．若一个平面内两条直线与另一个平面平行，则这两个平面平行C ．底面是矩形的四棱柱是长方体D ．棱台的侧面都是等腰梯形4．水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图所示，是一个正方体的表面展开图，若图中“2”在正方体的上面，则这个正方体的下面是（）A ．0B ．9C ．快D ．乐5．如图，是水平放置的的直观图，则的面积是（）O A B '''△OAB △AOB △A ．6B ．C ．D ．126．下列几何图形中，可能不是平面图形的是（） A ．梯形B ．菱形C ．平行四边形D ．四边形7．如图所示，在正方体中，M 、N 分别是BB 1、BC 的中点．则图中阴影部分在平面上的正投影为（）8．若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为（）A ．B ．C ．D ．69．一正方体表面沿着几条棱裁开放平得到如图所示的展开图，则在原正方体中（）1111ABCD A B C D 11ADDAA ．AB ∥CD B ．AB ∥平面CDC ．CD ∥GH D ．10．若圆台两底面周长的比是，过高的中点作平行于底面的平面，则圆台被分成两部分的体积比是（） A ．B ．C ．1D ．11．如图所示，正四棱锥的所有棱长都等于a ，过不相邻的两条棱SA ，SC 作截面SAC ，则截面的面积为（）A ．B ．C ．D ．12．一个正方体内接于一个球，过球心作一截面，如图所示，则截面的可能图形是（）A ．①③④B ．②③④C ．①②④D ．①②③二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．已知A 、B 、C 、D 四点在同一个球面上，AB ⊥BC ，AB ⊥BD ，AC ⊥CD ，若AB ＝6，AD ＝8，则B 、C 两点间的球面距离是________． 14．若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为________． 15．下列有关棱柱的说法： ①棱柱的所有的面都是平的； ②棱柱的所有的棱长都相等；③棱柱的所有的侧面都是长方形或正方形； ④棱柱的侧面的个数与底面的边数相等； ⑤棱柱的上、下底面形状、大小相等．其中正确的有________．(填序号)16．如图，是一个正方体的展开图，在原正方体中，相对的面分别是________．AB GH ∥1:4121439129S ABCD -232a 2a 212a 213a AC =三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．(10分)画出如图所示的四边形OABC 的直观图．(要求用斜二测画法，并写出画法)18．(12分)已知四棱锥，其三视图和直观图如图，求该四棱锥的体积．P ABCD19．(12分)如图，在正三棱柱中，AB＝3，AA1＝4，M为AA1的中点，P是BC上的一点，且由P沿棱柱侧面经过棱CC1到M，设这条最短路线与CC1的交点为N．求：（1）该三棱柱的侧面展开图的对角线的长；（2）PC和NC的长．20．(12分)已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8，高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6，高为4的等腰三角形．求：（1）该几何体的体积V；（2）该几何体的侧面积S．111ABC A B C。

高中数学必修2(人教a版)第一章几何空间体1.1知识点总结含同步练习及答案

高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征，能运用这些结构特征描述现实生活中简单物体的结构．二、知识清单典型空间几何体空间几何体的结构特征组合体展开图截面分析三、知识讲解1.典型空间几何体描述：空间几何体的概念只考虑物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．例题：用一个平行于棱锥底面的平面去截棱锥，得到两个几何体，一个是______，另一个是______．解：棱锥；棱台．2.空间几何体的结构特征描述：多面体由若干个平面多边形围成的几何体叫做多面体．围成多面体的各个多边形叫做多面体的面；相邻两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点；连接不在同一个面上的两个顶点的线段叫做多面体的对角线．按多面体的面数可把多面体分为四面体、五面体、六面体．其中，四个面均为全等的正三角形的四面体叫做正四面体．旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体．这条定直线叫做旋转体的轴．棱柱的结构特征一般地，有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱（prism）．棱柱中，两个互相平行的面叫做底面，简称底；其余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧棱与底面的公共顶点叫做棱柱的顶点．底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱，可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱，如下图的六棱柱可以表示为棱柱ABCDEF − A′ B′ C ′ D′ E′ F ′或棱柱A′ D．侧棱与底面不垂直的棱柱叫做斜棱柱；侧棱与底面垂直的棱柱叫做直棱柱；底面是正多边形的直棱柱叫做正棱柱；底面是平行四边形的棱柱叫做平行六面体；侧棱与底面垂直的平行六面体叫做直平行六面体．棱锥的结构特征一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥（pyramid）．这个多边形面叫做棱锥的底面或底；有公共顶点的各个三角形面叫做棱锥的侧面；各侧面的公共顶点叫做棱锥的顶点；相邻侧面的公共边叫做棱锥的侧棱．底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体．棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示，如下图的四棱锥表示为棱锥S−ABCD或者棱锥S−AC．棱锥的底面是正多边形，且它的顶点在过底面中心且与底面垂直的直线上，这个棱锥叫做正棱锥．正棱锥各侧面都是全等的等腰三角形，这些等腰三角形底边上的高都相等，叫做棱锥的斜高．棱台的结构特征用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的多面体叫做棱台（frustum of a pyramid）．原棱锥的底面和截面分别叫做棱台的下底面和上底面；其他各面叫做棱台的侧面；相邻两侧面的公共边叫做棱台的侧棱；两底面的距离叫做棱台的高．由正棱锥截得的棱台叫做正棱台，正棱台的各个侧面都是全等的等腰梯形，这些等腰梯形的高叫做棱台的斜高．圆柱的结构特征以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱（circular cylinder）．旋转轴叫做圆柱的轴；垂直于轴的边旋转而成的圆面叫做圆柱的底面；平行于轴的边旋转而成的曲面叫做圆柱的侧面；无论旋转到什么位置，不垂直于轴的边都叫做圆柱侧面的母线．圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥（circular cone）．圆台的结构特征用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台（frustum of a cone）．棱台与圆台统称为台体．球的结构特征以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称球（solid sphere）．半圆的圆心叫做球的球心，半圆的半径叫做球的半径，半圆的直径叫做球的直径．球常用表示球心的字母O表示．例题：下列命题中，正确的是（）A．有两个面互相平行，其余各面都是四边形的几何体叫棱柱B．棱柱中互相平行的两个面叫做棱柱的底面C．棱柱的侧面是平行四边形，而底面不是平行四边形D．棱柱的侧棱长相等，侧面是平行四边形解：D如图(1)，满足 A 选项条件，但不是棱柱；对于 B 选项，如图(2)，构造四棱柱ABCD − A1 B1 C1 D1，令四边形ABCD 是梯形，可知面ABB1A1∥面DCC1D1，但这两个面不能作为棱柱的底面；C选项中，若棱柱是平行六面体，则它的底面是平行四边形．若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是（）A．三棱锥B．四棱锥C．五棱锥D．六棱锥解：D ABCDEF OA = OB =⋯= AB S − ABCDEF如下图，正六边形中，，那么正六棱锥中，SA>OA=AB，即侧棱长大于底面边长．资料内容仅供您学习参考，如有不当之处，请联系改正或者删除如图所示的几何体中，是台体的是（）A．①②B．①③C．③D．②③解：C利用棱台的定义求解．①中各侧棱的延长线不能交于一点；②中的截面不平行于底面；③中各侧棱的延长线能交于一点且截面与底面平行．有下列四种说法：①圆柱是将矩形旋转一周所得的几何体；②以直角三角形的一直角边为旋转轴，旋转所得几何体是圆锥；③圆台的任意两条母线的延长线，可能相交也可能不相交；④半圆绕其直径所在直线旋转一周形成球．其中错误的有（）A．1个B．2个C．3个D．4个解：D圆柱是矩形绕其一条边所在直线旋转形成的几何体，故①错；以直角三角形的一条直角边所在直线为轴，旋转一周，才能构成圆锥，②错；圆台是由圆锥截得，故其任意两条母线延长后一定交于一点，③错；半圆绕其直径所在直线旋转一周形成的是球面，故④错误．3.组合体描述：简单组合体的构成有两种基本形式：一种是由简单几何体拼接而成，一种是由简单几何体截去或挖去一部分而成．----完整版学习资料分享----。

2023年高一下数学必修二《空间几何体》测试试卷及答案解析

2023年高一下数学必修二《空间几何体》测试试卷一．选择题（共18小题）1．如图几何体中不是柱体的有（）A．1个B．2个C．3个D．4个2．下列说法中正确的是（）A．棱柱的侧面可以是三角形B．正方体和长方体都是特殊的四棱柱C．所有的几何体的表面都能展成平面图形D．棱柱的各条棱都相等3．在侧棱长为3的正三棱锥P﹣ABC中，∠APB＝∠BPC＝∠CPA＝40°过点A作截面AEF与PB、PC侧棱分别交于E、F两点，则截面的周长最小值为（）A．4B．2C．10D．94．如图，在三棱台ABC﹣A1B1C1中，截去三棱锥A1﹣ABC，则剩余部分是（）A．三棱锥B．四棱锥C．三棱柱D．五棱锥5．球O的半径为1，该球的一小圆O1上两点A、B的球面距离为，OO1＝，则∠AO1B ＝（）A．B．C．D．π6．若长方体的一个顶点上三条棱长分别是1、2、2，且它的八个顶点都在同一球面上，则这个球的表面积是（）A．6πB．9πC．3πD．12π7．如图，是几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）A．5B．6C．7D．88．下列光线所形成的投影不是中心投影的是（）A．太阳光线B．台灯的光线C．手电筒的光线D．路灯的光线9．如图所示，E、F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是如图中的（）A．四个图形都正确B．只有②③正确C．只有④错误D．只有①②正确10．如图所示的水平放置的平面图形的直观图，所表示的图形ABCD是（）A．任意梯形B．直角梯形C．任意四边形D．平行四边形11．如图是水平放置的△ABC按“斜二测画法”得到的直观图，其中B′O′＝C′O′＝，A′O′＝，那么△ABC的面积是（）A．B．C．D．312．若某几何体的三视图如图所示，则这个几何体的直观图可以是（）A．B．C．D．13．△OAB的直观图△O′A′B′如图所示，且O′A′＝O′B′＝2，则△OAB的面积为（）A．1B．2C．4D．814．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（）A．10cm3B．20cm3C．30cm3D．40cm315．如图所示四个几何体中，几何体只有正视图和侧视图相同的是（）A．①②B．①③C．①④D．②④16．从长32cm，宽20cm的矩形薄铁板的四角剪去相等的正方形，做一个无盖的箱子，若使箱子的容积最大，则剪去的正方形边长为（）A．4cm B．2cm C．1cm D．3cm17．若一个圆锥侧面展开图是面积为2π的半圆面，则该圆锥底面的面积为（）A．πB．2πC．3πD．4π18．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为线段B1C的中点，F是棱C1D1上的动点，若点P为线段BD1上的动点，则PE+PF的最小值为（）A．B．C．D．二．填空题（共4小题）19．下面三视图的实物图形的名称是20．下列物品：①探照灯；②车灯；③太阳；④月亮；⑤台灯中，所形成的投影是中心投影的是．（填序号）21．某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的侧面积为．22．某几何体的三视图如图所示，其中俯视图是半径为4的圆面的四分之一，则该几何体的体积为．三．解答题（共5小题）23．已知如图：四边形ABCD是矩形，BC⊥平面ABE，且AE＝EB＝BC＝2，点F为CE上一点，且BF⊥平面ACE．（1）求证：AE∥平面BFD；（2）求多面体ABCDE的表面积．24．长方体A1B1C1D1﹣ABCD中，AB＝AD＝2，A1A＝2，M为棱C1C的中点，C1D与D1C交于点N，求证：AM⊥A1N．25．有一盛满水的圆柱形容器，内壁底面半径为5，高为2．将一个半径为3的玻璃小球缓慢浸没与水中．（1）求圆柱体积；（2）求溢出水的体积．26．如图，平行四边形ABCD中，BD＝2，AB＝2，AD＝4，将△BCD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD．（I）求证：AB⊥DE（Ⅱ）求三棱锥E﹣ABD的侧面积．27．如图所示，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝1，BB1＝2，连接A1C，BD．（1）求三棱锥A1﹣BCD的体积（2）求证：BD⊥平面A1AC．2023年高一下数学必修二《空间几何体》测试试卷参考答案与试题解析一．选择题（共18小题）1．如图几何体中不是柱体的有（）A．1个B．2个C．3个D．4个【分析】可知柱体分为棱柱和圆柱，从而可判断哪些图形不是柱体，即得出不是柱体的个数．【解答】解：①是三棱柱，②的上下两个平面不平行，不是三棱柱，③是四棱柱，④是圆柱，⑤是四棱柱，⑥是四棱台，⑦三棱锥；∴不是柱体的为②⑥⑦，共3个．故选：C．【点评】考查柱体的定义，以及棱柱和圆柱的定义，棱锥的定义．2．下列说法中正确的是（）A．棱柱的侧面可以是三角形B．正方体和长方体都是特殊的四棱柱C．所有的几何体的表面都能展成平面图形D．棱柱的各条棱都相等【分析】从棱柱的定义出发判断A、B、D的正误，找出反例否定C，即可推出结果．【解答】解：棱柱的侧面都是四边形，A不正确；正方体和长方体都是特殊的四棱柱，正确；所有的几何体的表面都能展成平面图形，球不能展开为平面图形，C不正确；棱柱的各条棱都相等，应该为侧棱相等，所以D不正确；故选：B．【点评】本题考查棱柱的结构特征，考查基本知识的熟练情况，是基础题．3．在侧棱长为3的正三棱锥P﹣ABC中，∠APB＝∠BPC＝∠CPA＝40°过点A作截面AEF与PB、PC侧棱分别交于E、F两点，则截面的周长最小值为（）A．4B．2C．10D．9【分析】将三棱锥的侧面展开，则截面的周长最小值的最小值，即可转化为求AA1的长度，解三角形PAA1，即可得到答案．【解答】解：将三棱锥的侧面A展开，如图，则图中∠APA1＝120°，AA1为所求，由余弦定理可得AA1＝，故选：D．【点评】本题考查的知识点是棱锥的结构特征，其中将三棱锥的侧面展开，将空间问题转化为平面上两点间距离问题，是解答本题的关键．4．如图，在三棱台ABC﹣A1B1C1中，截去三棱锥A1﹣ABC，则剩余部分是（）A．三棱锥B．四棱锥C．三棱柱D．五棱锥【分析】画出图形，根据图形和四棱锥的结构特征，即可得出剩余几何体是什么图形．【解答】解：如图所示，三棱台A′B′C′﹣ABC中，沿A′BC截去三棱锥A′﹣ABC，剩余部分是四棱锥A′﹣BCC′B′．故选：B．【点评】本题考查了空间几何体结构特征的应用问题，是基础题目．5．球O的半径为1，该球的一小圆O1上两点A、B的球面距离为，OO1＝，则∠AO1B ＝（）A．B．C．D．π【分析】由题意知应先求出AB的长度，在直角三角形AOB中由余弦定理可得AB＝1，由此知三角形AO1B的三边长，由此可以求出∠AO1B的值．【解答】解：由题设知OO1＝，OA＝OB＝1，在圆O1中有O1A＝O1B＝，又A，B两点间的球面距离为，由余弦定理，得：AB＝1，在三角形AO1B中由勾股定理可得：∠AO1B＝，故选：B．【点评】本题的考点是球面距离及相关计算，其考查背景是球内一小圆上两点的球面距，对空间想象能力要求较高，此类题是一个基本题型，属于基础题．6．若长方体的一个顶点上三条棱长分别是1、2、2，且它的八个顶点都在同一球面上，则这个球的表面积是（）A．6πB．9πC．3πD．12π【分析】长方体的对角线的长度，就是外接球的直径，求出直径即可求出表面积．【解答】解：由题意得，此问题是球内接长方体，所以可得长方体的对角线长等于球的直径，即，所以，所以求得表面积为．故选：B．【点评】本题考查球的表面积，球的内接体，考查计算能力和空间想象力，是基础题．7．如图，是几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）A．5B．6C．7D．8【分析】根据俯视图可知这个几何体，底面是4个小正方体，根据主视图及左视图，可知里面上方有两个小正方体，从而可得结论．【解答】解：根据俯视图可知这个几何体，底面是4个小正方体，根据主视图及左视图，可知里面上方有两个小正方体，故共有6个小正方体．故选：B．【点评】本题考查三视图还原几何体，考查学生分析解决问题的能力，属于基础题．8．下列光线所形成的投影不是中心投影的是（）A．太阳光线B．台灯的光线C．手电筒的光线D．路灯的光线【分析】利用中心投影和平行投影的定义即可判断出．【解答】解：A．太阳距离地球很远，我们认为是平行光线，因此不是中心投影．B．台灯的光线是由台灯光源发出的光线，是中心投影；C．手电筒的光线是由手电筒光源发出的光线，是中心投影；D．路灯的光线是由路灯光源发出的光线，是中心投影．综上可知：只有A不是中心投影．故选：A．【点评】本题考查了中心投影和平行投影的定义，属于基础题．9．如图所示，E、F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是如图中的（）A．四个图形都正确B．只有②③正确C．只有④错误D．只有①②正确【分析】按照三视图的作法：上下、左右、前后三个方向的射影，四边形的四个顶点在三个投影面上的射影，再将其连接即可得到三个视图的形状，按此规则对题设中所给的四图形进行判断即可．【解答】解：因为正方体是对称的几何体，所以四边形BFD1E在该正方体的面上的射影可分为：自上而下、自左至右、由前及后三个方向的射影，也就是在面ABCD、面ABB1A1、面ADD1A1上的射影．四边形BFD1E在面ABCD和面ABB1A1上的射影相同，如图②所示；四边形BFD1E在该正方体对角面的ABC1D1内，它在面ADD1A1上的射影显然是一条线段，如图③所示．故②③正确故选：B．【点评】本题考查简单空间图形的三视图，考查根据作三视图的规则来作出三个视图的能力，三视图是高考的新增考点，不时出现在高考试题中，应予以重视．10．如图所示的水平放置的平面图形的直观图，所表示的图形ABCD是（）A．任意梯形B．直角梯形C．任意四边形D．平行四边形【分析】由直观图可知，BC，AD两条边与横轴平行且不等，边AB与纵轴平行，得到AB与两条相邻的边之间是垂直关系，而另外一条边CD不和上下两条边垂直，得到平面图形是一个直角梯形．【解答】解：根据直观图可知，BC，AD两条边与横轴平行且不等，边AB与纵轴平行，∴AB⊥AD，AB⊥BC，∴平面图形ABCD是一个直角梯形，故选：B．【点评】本题考查平面图形的直观图，考查有直观图得到平面图形，考查画直观图要注意到两条坐标轴之间的关系．11．如图是水平放置的△ABC按“斜二测画法”得到的直观图，其中B′O′＝C′O′＝，A′O′＝，那么△ABC的面积是（）A．B．C．D．3【分析】′O′＝C′O′＝，A′O′＝，直接计算△ABC即可．【解答】解：因为B′O′＝C′O′＝，A′O′＝，所以△ABC的面积为＝．故选：C．【点评】本题考查斜二测画法中原图和直观图面积之间的关系，属基本运算的考查．12．若某几何体的三视图如图所示，则这个几何体的直观图可以是（）A．B．C．D．【分析】根据已知中的三视图，结合三视图中有两个三角形即为锥体，有两个矩形即为柱体，有两个梯形即为台体，将几何体分解为简单的几何体分析后，即可得到答案．【解答】解：由已知中三视图的上部分有两个矩形，一个三角形故该几何体上部分是一个三棱柱下部分是三个矩形故该几何体下部分是一个四棱柱故选：A．【点评】本题考查的知识点是由三视图还原实物图，考查学生的识图能力，比较基础．13．△OAB的直观图△O′A′B′如图所示，且O′A′＝O′B′＝2，则△OAB的面积为（）A．1B．2C．4D．8【分析】由斜二测画法还原出原图，求面积．【解答】解：由斜二测画法可知原图应为：其面积为：S＝＝4，故选：C．【点评】本题考查直观图与平面图形的画法，注意两点：一是角度的变化；二是长度的变化；考查计算能力．14．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（）A．10cm3B．20cm3C．30cm3D．40cm3【分析】由三视图知几何体为直三棱柱削去一个三棱锥，且三棱柱的高为5，底面是直角三角形，两直角边长分别为3、4，代入体积公式计算．【解答】解：由三视图知几何体为直三棱柱削去一个三棱锥，且三棱柱的高为5，底面是直角三角形，两直角边长分别为3、4，∴几何体的体积V＝×3×4×5﹣××4×5＝20（cm3），故选：B．【点评】本题考查了由三视图求几何体的体积，解题的关键是由三视图判断几何体的形状及数据所对应的几何量．15．如图所示四个几何体中，几何体只有正视图和侧视图相同的是（）A．①②B．①③C．①④D．②④【分析】分别根据四个几何体的三视图进行判断．【解答】解：①正方体的正视图，侧视图和俯视图都是正方形，不满足条件．②圆锥的正视图为三角形，侧视图为三角形，俯视图为圆，满足条件．③三棱台的正视图为等腰梯形，侧视图为梯形，但正视图和侧视图不相同，不满足条件．④正四棱锥的正视图和侧视图为相同的三角形，俯视图为正方形，满足条件．故选：D．【点评】本题主要考查三视图的识别和判断，要求熟练掌握常见空间几何体的三视图，比较基础．16．从长32cm，宽20cm的矩形薄铁板的四角剪去相等的正方形，做一个无盖的箱子，若使箱子的容积最大，则剪去的正方形边长为（）A．4cm B．2cm C．1cm D．3cm【分析】设剪去的正方形的边长为xcm，（0＜x＜10），箱子的容积V＝（32﹣2x）（20﹣2x）•x＝4（x3﹣26x2+160x），V′＝12（x﹣4）（x﹣），由此利用导数性质能求出若使箱子的容积最大，则剪去的正方形边长为4cm．【解答】解：设剪去的正方形的边长为xcm，（0＜x＜10），则做成的无盖的箱子的底是长为（32﹣2x）cm，宽为（20﹣2x）cm的矩形，箱子的高为xcm，∴箱子的容积V＝（32﹣2x）（20﹣2x）•x＝4（x3﹣26x2+160x），V′＝12（x﹣4）（x﹣），当0＜x＜10时，V′＝0只有一个解x＝4，在x＝4附近，V′是左正右负，∴V有x＝4处取得极大值即为最大值，∴若使箱子的容积最大，则剪去的正方形边长为4cm．故选：A．【点评】本题考查棱柱体积的求法及应用，是中档题，解题时要注意导数性质的合理运用．17．若一个圆锥侧面展开图是面积为2π的半圆面，则该圆锥底面的面积为（）A．πB．2πC．3πD．4π【分析】通过侧面展开图的面积．求出圆锥的母线，底面的半径，求出圆锥底面的面积．【解答】解：由题意一个圆锥的侧面展开图是面积为2π的半圆面，因为4π＝πl2，所以l＝2，半圆的弧长为2π，圆锥的底面半径为2πr＝2π，r＝1，所以圆锥底面的面积为π，故选：A．【点评】本题考查旋转体的条件的求法，侧面展开图的应用，考查空间想象能力，计算能力．18．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为线段B1C的中点，F是棱C1D1上的动点，若点P为线段BD1上的动点，则PE+PF的最小值为（）A．B．C．D．【分析】连接BC1，得出点P、E、F在平面BC1D1中，问题转化为在平面内直线BD1上取一点P，求点P到定点E的距离与到定直线的距离的和的最小值问题，利用平面直角坐标系，求出点E关于直线BD1的坐标即可．【解答】解：连接BC1，则BC1∩B1C＝E，点P、E、F在平面BC1D1中，且BC1⊥C1D1，C1D1＝1，BC1＝，如图1所示；在Rt△BC1D1中，以C1D1为x轴，C1B为y轴，建立平面直角坐标系，如图2所示；则D1（1，0），B（0，），E（0，）；设点E关于直线BD1的对称点为E′，∵BD1的方程为x+＝1①，∴k EE＝﹣＝，′∴直线EE′的方程为y＝x+②，由①②组成方程组，解得，直线EE′与BD1的交点M（，）；所以对称点E′（，），∴PE+PF＝PE′+PF≥E′F＝．故选：D．【点评】本题考查了空间几何体中距离和的计算问题，解题的关键是把空间问题转化为平面问题解答，是难题．二．填空题（共4小题）19．下面三视图的实物图形的名称是四棱锥【分析】只看正视图或侧视图可以判断几何体可能是柱体或锥体，结合俯视图，即可判断几何体的形状．【解答】解：只看正视图或侧视图可以判断几何体可能是柱体或锥体，由正视图和侧视图可以判断几何体是锥体，结合俯视图，几何体是四棱锥．故答案为：四棱锥．【点评】本题是基础题，考查常见几何体的三视图复原几何体的特征，考查空间想象能力．20．下列物品：①探照灯；②车灯；③太阳；④月亮；⑤台灯中，所形成的投影是中心投影的是①②⑤．（填序号）【分析】利用中心投影和平行投影的定义即可判断出．【解答】解：探照灯、车灯、台灯的光线是由源发出的光线，是中心投影；太阳、月亮距离地球很远，我们认为是平行光线，因此不是中心投影．故答案为：①②⑤．【点评】本题考查了中心投影和平行投影的定义，属于基础题．21．某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的侧面积为12+2π．【分析】三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，该几何体已知由圆柱切割获得．【解答】解：由题意，圆柱的底面半径为2，高为3；则曲面面积为：×2×3＝2π，其他两个侧面为矩形，边长为2，3．故面积为2×3×2＝12．故该几何体的侧面积为：12+2π．故答案为：12+2π．【点评】三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．22．某几何体的三视图如图所示，其中俯视图是半径为4的圆面的四分之一，则该几何体的体积为16π．【分析】由已知中的三视图可得：该几何体是一个以俯视图为底面的柱体，代入柱体体积公式，可得答案．【解答】解：由已知中的三视图可得：该几何体是一个以俯视图为底面的柱体，其底面面积S＝＝4π，高h＝4，故几何体的体积V＝Sh＝16π，故答案为；16π【点评】本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．三．解答题（共5小题）23．已知如图：四边形ABCD是矩形，BC⊥平面ABE，且AE＝EB＝BC＝2，点F为CE上一点，且BF⊥平面ACE．（1）求证：AE∥平面BFD；（2）求多面体ABCDE的表面积．【分析】（1）线面平行转化证明线线平面即可．记AC∩BD＝M，连FM，则M为AC的中点；证明FM∥AE，可证AE∥平面BFD；（2）多面体ABCDE的表面积各面的面积之和．根据题设各边长计算即可．【解答】（1）证明：如图，记AC∩BD＝M，连FM，则M为AC的中点；而BF⊥平面ACE，∴BF⊥CE，在△BCE中，∵BE＝BC，∴F为CE的中点；从而FM是△ACE的中位线，所以FM∥AE，又FM⊂平面DBF，AE⊄平面DBF，∴AE∥平面BFD；（2）由题意：由BF⊥平面ACE，∴AE⊥BF；∵BC⊥平面ABE，∴AE⊥BC，AE⊥平面BEC，AE⊥BE，因此△ABE为直角三角形，所以，而，所以△CDE为正三角形．所以多面体ABCDE的表面积S ABCD+S△ESC+S△CFD+S AEFD＝．【点评】本题考查了线面平行的证明和多面体ABCDE的表面积的计算．属于基础题．24．长方体A1B1C1D1﹣ABCD中，AB＝AD＝2，A1A＝2，M为棱C1C的中点，C1D与D1C交于点N，求证：AM⊥A1N．【分析】两条异面直线垂直的证明，通过平行相交，求角是90°即可．或者是建立空间直角坐标系，用向量进行计算．【解答】解法一：解：由题意：M为棱C1C的中点，C1D与D1C交于点N，即N是C1D，D1C的中点．取A1B1的中点E，连接ME，MN．∵CD，A1AB，AB＝CD．∴平面MNA1E是平行四边形，则有A1N；所以：AM与A1N所成的角是∠AME．取A1A的中点F，连接NF，由A1B1C1D1﹣ABCD是长方体：∴A1FN是直角三角形，A1F＝A1A＝，FN＝＝∴A1N＝EM＝AE＝AM＝在△AME中，∵AE2＝AM2+EM2，∴△AME是直角三角形，∠AME＝90°，即AM与A1N所成的角是90°．故AM⊥A1N，得证．解法二：解：以A为原点，以为正交基底建立空间直角坐标系，∵AB＝AD＝2，A1A＝2，M为棱C1C的中点，C1D与D1C交于点N，即中点．则有A（0，0，0），，，∴，，∵，∴AM⊥A1N【点评】本题考查了两条异面直线垂直的证明，常用方法是通过平行相交，求角是90°即可．或者证明其中一条直线垂直另外一条直线所在的平面．或者是建立空间直角坐标系，用向量进行计算．属于基础题．25．有一盛满水的圆柱形容器，内壁底面半径为5，高为2．将一个半径为3的玻璃小球缓慢浸没与水中．（1）求圆柱体积；（2）求溢出水的体积．【分析】（1）利用圆柱的体积公式求圆柱体积；（2）利用球的体积公式求溢出水的体积．【解答】解：（1）∵内壁底面半径为5，高为2，∴圆柱体积V＝π•52•2＝50π；（2）溢出水的体积＝•＝12π．【点评】本题着重考查了球体积公式和圆柱体积公式等知识，考查学生的计算能力，属于基础题．26．如图，平行四边形ABCD中，BD＝2，AB＝2，AD＝4，将△BCD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD．（I）求证：AB⊥DE（Ⅱ）求三棱锥E﹣ABD的侧面积．【分析】（Ⅰ）利用面面垂直，证明线面垂直转化为线线垂直．证明AB⊥BD，在证明AB⊥平面EBD，可得AB⊥DE（Ⅱ）三棱锥E﹣ABD的侧面积等于三面之和，由（1）可得ED⊥平面ABCD，可求三个面的面积．【解答】解：（Ⅰ）证明：由题意：AB＝2，BD＝2，AD＝4，∵AB2+BD2＝AD2∴AB⊥BD；∵平面EBD⊥平面ABD，平面EBD∩平面ABD＝BD，∴AB⊥平面EBD．∵DE⊆平面EBD，∴AB⊥DE．（Ⅱ）由（Ⅰ）可知AB⊥BD，∵CD∥AB，∴CD⊥BD，从而DE⊥BD．在三角形DBE中，∵DB＝，DE＝CD＝AB＝2．∴又∵AB⊥平面EBD，EB⊂平面EBD，∴AB⊥BE．∵BE＝BC＝AD＝4，∴．又∵DE⊥BD，平面EBD⊥平面ABD，∴DE⊥平面ABD，而DE⊂平面ABD，DE⊥AD．∴综上，三个面之和为三棱锥E﹣ABD的侧面积，即为8+2．【点评】本题考查了面面垂直转化为线面垂直来证明线线垂直．以及侧面积的计算．属于基础题．27．如图所示，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝1，BB1＝2，连接A1C，BD．（1）求三棱锥A1﹣BCD的体积（2）求证：BD⊥平面A1AC．【分析】（1）以BCD为棱锥的底面，则AA1为棱锥的高，代入棱锥的体积公式计算即可；（2）连结AC，由底面正方形可知BD⊥AC，由AA1⊥平面ABCD可知AA1⊥BD，故而BD⊥平面A1AC．【解答】解：（1）在长方体ABCD﹣A1B1C1D1中，∵A1A⊥平面ABCD，即A1A是三棱锥A1﹣BCD的高，∵AA1＝BB1＝2，AB＝BC＝1，∴．∴．证明：（2）连结AC，∵A1A⊥平面ABCD，BD⊂平面ABCD，∴A1A⊥BD．又AB＝BC，∴矩形ABCD是正方形，∴BD⊥AC，∵AC⊂平面A1AC，A1A⊂平面A1AC，A1A∩AC＝A，∴BD⊥平面A1AC．【点评】本题考查了长方体的结构特征，线面垂直的判定，棱锥的体积计算，属于基础题．。

高中数学必修二第一章空间几何体课后作业(含答案)

第一章空间几何体第1课时多面体的结构特征一、基础过关1．下列说法中正确的是( )A ．棱柱的侧面可以是三角形B ．由6个大小一样的正方形所组成的图形是正方体的展开图C ．正方体的各条棱长都相等D ．棱柱的各条棱长都相等 2．棱台不具备的特点是( )A ．两底面相似B ．侧面都是梯形C ．侧棱都相等D ．侧棱延长后都交于一点3. 如图，将装有水的长方体水槽固定底面一边后倾斜一个小角度，则倾斜后水槽中的水形成的几何体是( )A ．棱柱B ．棱台C ．棱柱与棱锥的组合体D ．不能确定4．若棱台上、下底面的对应边之比为1∶2，则上、下底面的面积之比是( )A ．1∶2B ．1∶4C ．2∶1D ．4∶15．一个棱柱有10个顶点，所有的侧棱长的和为60 cm ，则每条侧棱长为________cm. 6．在下面的四个平面图形中，哪几个是侧棱都相等的四面体的展开图________(填序号)．7．如图所示为长方体ABCD —A ′B ′C ′D ′，当用平面BCFE 把这个长方体分成两部分后，各部分形成的多面体还是棱柱吗？如果不是，请说明理由；如果是，指出底面及侧棱．8．如图所示的是一个三棱台ABC —A 1B 1C 1，如何用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．二、能力提升9．下图中不可能围成正方体的是()10．在正方体上任意选择4个顶点，它们可能是如下各种几何体的4个顶点，这些几何体是________(写出所有正确结论的编号)．①矩形； ②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体； ④每个面都是等边三角形的四面体； ⑤每个面都是直角三角形的四面体．11．根据下列对于几何体结构特征的描述，说出几何体的名称．（1）由八个面围成，其中两个面是互相平行且全等的正六边形，其它各面都是矩形；（2）由五个面围成，其中一个面是正方形，其它各面都是有一个公共顶点的全等三角形．三、探究与拓展12．正方体的截面可能是什么形状的图形？第二课时旋转体与简单组合体的结构特征一、基础过关 1．下列说法正确的是( )A ．直角三角形绕一边旋转得到的旋转体是圆锥B ．夹在圆柱的两个截面间的几何体还是一个旋转体C ．圆锥截去一个小圆锥后剩余部分是圆台D ．通过圆台侧面上一点，有无数条母线 2．下列说法正确的是( )A ．直线绕定直线旋转形成柱面B ．半圆绕定直线旋转形成球体C ．有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台D ．圆柱的任意两条母线所在的直线是相互平行的3．如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面，下底面圆心为顶点的圆锥而得到的组合体，现用一个竖直的平面去截这个组合体，则截面图形可能是()A ．(1)(2)B ．(1)(3)C ．(1)(4)D ．(1)(5) 4．观察如图所示的四个几何体，其中判断正确的是()A ．a 是棱台B ．b 是圆台C ．c 是棱锥D ．d 不是棱柱5．将等边三角形绕它的一条中线旋转180°，形成的几何体是________． 6．请描述下列几何体的结构特征，并说出它的名称．（1）由7个面围成，其中两个面是互相平行且全等的五边形，其它面都是全等的矩形；（2）如右图，一个圆环面绕着过圆心的直线l 旋转180°.7. 如图所示，梯形ABCD 中，AD ∥BC ，且AD <BC ，当梯形ABCD 绕AD 所在直线旋转一周时，其他各边旋转围成了一个几何体，试描述该几何体的结构特征．二、能力提升8．下列说法正确的个数是( )①长方形绕一条直线旋转一周所形成的几何体是圆柱；②过圆锥侧面上一点有无数条母线；③圆锥的母线互相平行． A ．0B ．1C ．2D ．39．一个正方体内有一个内切球，作正方体的对角面，所得截面图形是下图中的()10．已知球O 是棱长为1的正方体ABCD —A 1B 1C 1D 1的内切球，则平面ACD 1截球O 所得的截面面积为________．11．以直角三角形的一条边所在的直线为旋转轴，其余两边旋转形成的面所围成的旋转体有哪些？三、探究与拓展12．如图所示，圆台母线AB 长为20 cm ，上、下底面半径分别为5 cm 和10 cm ，从母线AB 的中点M 拉一条绳子绕圆台侧面转到B 点，求这条绳长的最小值．§1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影 1.2.2 空间几何体的三视图一、基础过关 1．下列命题正确的是( )A ．矩形的平行投影一定是矩形B ．梯形的平行投影一定是梯形C ．两条相交直线的投影可能平行D ．一条线段中点的平行投影仍是这条线段投影的中点 2．如图所示的一个几何体，哪一个是该几何体的俯视图()3．如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A ．①②B ．①③C ．①④D ．②④4．一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图()5．根据如图所示俯视图，找出对应的物体．(1)对应________；(2)对应________；(3)对应________；(4)对应________；(5)对应________．6．若一个三棱柱的三视图如图所示，则这个三棱柱的高(两底面之间的距离)和底面边长分别是______和________．7．在下面图形中，图(b)是图(a)中实物画出的正视图和俯视图，你认为正确吗？如果不正确，请找出错误并改正，然后画出侧视图(尺寸不作严格要求)．8．画出如图所示的四棱锥和三棱柱的三视图．二、能力提升9．一个长方体去掉一角的直观图如图所示，关于它的三视图，下列画法正确的是()10．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是()A．球B．三棱锥C．正方体D．圆柱11．用若干块相同的小正方体搭成一个几何体，该几何体的三视图如图所示，则搭成该几何体需要的小正方体的块数是________．12．如图，螺栓是棱柱和圆柱的组合体，画出它的三视图．三、探究与拓展13．用小立方体搭成一个几何体，使它的正视图和俯视图如图所示，搭建这样的几何体，最多要几个小立方体？最少要几个小立方体？1.2.3空间几何体的直观图一、基础过关1．下列结论：①角的水平放置的直观图一定是角；②相等的角在直观图中仍然相等；③相等的线段在直观图中仍然相等；④两条平行线段在直观图中对应的两条线段仍然平行．其中正确的有()A．①②B．①④C．③④D．①③④2．在用斜二测画法画水平放置的△ABC时，若∠A的两边分别平行于x轴、y轴，则在直观图中∠A′等于()A．45°B．135°C．90°D．45°或135°3．下面每个选项的2个边长为1的正△ABC的直观图不是全等三角形的一组是()4．如图甲所示为一个平面图形的直观图，则此平面图形可能是图乙中的()5．利用斜二测画法得到：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形．以上结论中，正确的是______________．(填序号)6．水平放置的△ABC的斜二测直观图如图所示，已知A′C′＝3，B′C′＝2，则AB边上的中线的实际长度为____________．7．如图是一梯形OABC的直观图，其直观图面积为S.求梯形OABC的面积．8．如图所示，已知几何体的三视图，用斜二测画法画出它的直观图．二、能力提升9．如图，正方形O ′A ′B ′C ′的边长为1 cm ，它是水平放置的一个平面图形的直观图，则原图的周长是( )A ．8 cmB ．6 cmC ．2(1＋3) cmD ．2(1＋2) cm10．如图所示的是水平放置的△ABC 在直角坐标系的直观图，其中D ′是A ′C ′的中点，且∠A ′C ′B ′≠30°，则原图形中与线段BD 的长相等的线段有________条． 11．如图所示，为一个水平放置的正方形ABCO ，它在直角坐标系xOy 中，点B 的坐标为(2,2)，则在用斜二测画法画出的正方形的直观图中，顶点B ′到x ′轴的距离为________．12．如图所示，梯形ABCD 中，AB ∥CD ，AB ＝4 cm ，CD ＝2 cm ，∠DAB ＝30°，AD ＝3 cm ，试画出它的直观图．三、探究与拓展13．在水平放置的平面α内有一个边长为1的正方形A ′B ′C ′D ′，如图，其中的对角线A ′C ′在水平位置，已知该正方形是某个四边形用斜二测画法画出的直观图，试画出该四边形的真实图形并求出其面积．§1.3 空间几何体的表面积与体积第一课时柱体、锥体、台体的表面积一、基础过关1．用长为4、宽为2的矩形做侧面围成一个高为2的圆柱，此圆柱的轴截面面积为( )A ．8B ．8πC ．4πD ．2π2．一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比为 ( )A ．1＋2π2πB ．1＋4π4πC ．1＋2ππD ．1＋4π2π3．若一个圆台的正视图如图所示，则其侧面积等于()A ．6B ．6πC ．35πD ．65π 4．三视图如图所示的几何体的全面积是()A ．7＋ 2B ．112＋2C ．7＋ 3D ．325．如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是________． 6．一简单组合体的三视图及尺寸如下图所示(单位：cm)，则该组合体的表面积为________cm 2.7．表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________．8．长方体ABCD —A 1B 1C 1D 1中，宽、长、高分别为3、4、5，现有一个小虫从A 出发沿长方体表面爬行到C 1来获取食物，求其路程的最小值．二、能力提升9．已知由半圆的四分之三截成的扇形的面积为B ，由这个扇形围成一个圆锥，若圆锥的全面积为A ，则A ∶B 等于( ) A ．11∶8B ．3∶8C ．8∶3D ．13∶8 10．一个几何体的三视图如图，该几何体的表面积为()A ．372B ．360C ．292D ．28011．一个几何体的三视图如图所示，则该几何体的表面积为________．12．有一根长为3π cm ，底面半径为1 cm 的圆柱形铁管，用一段铁丝在铁管上缠绕2圈，并使铁丝的两个端点落在圆柱的同一母线的两端，求铁丝的最短长度．三、探究与拓展13．有一塔形几何体由3个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点．已知最底层正方体的棱长为2，求该塔形的表面积(含最底层正方体的底面面积)．第二课时柱体、锥体、台体、球的体积与球的表面积一、基础过关1．一个三棱锥的高和底面边长都缩小为原来的12时，它的体积是原来的( )A ．12B ．14C ．18D ．242．两个球的半径之比为1∶3，那么两个球的表面积之比为 ( )A ．1∶9B ．1∶27C ．1∶3D ．1∶1 3．已知直角三角形的两直角边长为a 、b ，分别以这两条直角边所在直线为轴，旋转所形成的几何体的体积之比为( )A ．a ∶bB ．b ∶aC ．a 2∶b 2D ．b 2∶a 24．若球的体积与表面积相等，则球的半径是( )A ．1B ．2C ．3D ．45．将一钢球放入底面半径为3 cm 的圆柱形玻璃容器中，水面升高4 cm ，则钢球的半径是________ cm. 6．如图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝AD ＝3 cm ，AA 1＝2 cm ，则四棱锥A －BB 1D 1D 的体积为______ cm 3.7．（1）表面积相等的正方体和球中，体积较大的几何体是______；（2）体积相等的正方体和球中，表面积较小的几何体是______．8．在球面上有四个点P 、A 、B 、C ，如果P A 、PB 、PC 两两垂直且P A ＝PB ＝PC ＝a ，求这个球的体积．二、能力提升9．有一个几何体的三视图及其尺寸如图(单位：cm)，则该几何体的表面积和体积分别为( )A ．24π cm 2,12π cm 3B ．15π cm 2,12π cm 3C ．24π cm 2,36π cm 3D ．以上都不正确10．圆柱的底面半径为1，母线长为2，则它的体积和表面积分别为( )A ．2π，6πB ．3π，5πC ．4π，6πD ．2π，4π11．一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________ m 3.12．有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个半径为r 的铁球，并注入水，使水面与球正好相切，然后将球取出，求这时容器中水的深度．三、探究与拓展13．有三个球，第一个球内切于正方体，第二个球与这个正方体各条棱相切，第三个球过这个正方体的各个顶点，求这三个球的表面积之比．章末检测一、选择题1．如图所示的长方体，将其左侧面作为上底面，右侧面作为下底面，水平放置，所得的几何体是 ( ) A ．棱柱B ．棱台C ．棱柱与棱锥组合体D ．无法确定1题图 2题图2．一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能．．．为：①长方形；②正方形；③圆．其中正确的是()A．①②B．②③C．①③D．①②3．如图所示的正方体中，M、N分别是AA1、CC1的中点，作四边形D1MBN，则四边形D1MBN在正方体各个面上的正投影图形中，不可能出现的是()4．如图所示的是水平放置的三角形直观图，D′是△A′B′C′中B′C′边上的一点，且D′离C′比D′离B′近，又A′D′∥y′轴，那么原△ABC的AB、AD、AC三条线段中()A．最长的是AB，最短的是AC B．最长的是AC，最短的是ABC．最长的是AB，最短的是AD D．最长的是AD，最短的是AC4题图5题图5．具有如图所示直观图的平面图形ABCD是()A．等腰梯形B．直角梯形C．任意四边形 D．平行四边形6．如图是一个几何体的三视图，则在此几何体中，直角三角形的个数是()A．1 B．2 C．3 D．47．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为()A．6 B．9 C．12 D．188．平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为2，则此球的体积为()A.6πB．43πC．46πD．63π9．如图所示，则这个几何体的体积等于()A．4 B．6 C．8 D．1210．将正三棱柱截去三个角(如图1所示，A，B，C分别是△GHI三边的中点)得到几何体如图2，则该几何体按图2所示方向的侧视图为选项图中的()11．圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为()A．120°B．150°C．180°D．240°12．已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为()A．26B．36C．23D．22二、填空题13．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号)．①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱14．已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积等于________ cm3.15．已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是________．16．一个水平放置的圆柱形储油桶(如图所示)，桶内有油部分所在圆弧占底面圆周长的14，则油桶直立时，油的高度与桶的高度的比值是________．三、解答题17．某个几何体的三视图如图所示(单位：m)，（1）求该几何体的表面积(结果保留π)；（2）求该几何体的体积(结果保留π)．18．如图是一个空间几何体的三视图，其中正视图和侧视图都是边长为2的正三角形，俯视图如图．（1）在给定的直角坐标系中作出这个几何体的直观图(不写作法)；（2）求这个几何体的体积．19．如图所示，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝22，AD＝2，求四边形ABCD 绕AD旋转一周所成几何体的表面积及体积．20．如图所示，有一块扇形铁皮OAB，∠AOB＝60°，OA＝72 cm，要剪下来一个扇形环ABCD，作圆台形容器的侧面，并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面)．试求：（1）AD的长；（2）容器的容积．第一章空间几何体参考答案第1课时多面体的结构特征参考答案1．C 2.C 3.A 4.B 5.12 6.①②7．解截面BCFE右侧部分是棱柱，因为它满足棱柱的定义．它是三棱柱BEB′—CFC′，其中△BEB′和△CFC′是底面．EF，B′C′，BC是侧棱，截面BCFE左侧部分也是棱柱．它是四棱柱ABEA′—DCFD′.其中四边形ABEA′和四边形DCFD′是底面．A′D′，EF，BC，AD为侧棱．8．解过A1、B、C三点作一个平面，再过A1、B、C1作一个平面，就把三棱台ABC—A1B1C1分成三部分，形成的三个三棱锥分别是A1—ABC，B—A1B1C1，A1—BCC1.9．D10.①③④⑤11．解(1)该几何体有两个面是互相平行且全等的正六边形，其他各面都是矩形，可满足每相邻两个面的公共边都相互平行，故该几何体是六棱柱．(2)该几何体的其中一个面是四边形，其余各面都是三角形，并且这些三角形有一个公共顶点，因此该几何体是四棱锥．12．解本问题可以有如下各种答案：①截面可以是三角形：等边三角形、等腰三角形、一般三角形；②截面三角形是锐角三角形；③截面可以是四边形：平行四边形、矩形、菱形、正方形、梯形、等腰梯形；截面为四边形时，这个四边形中至少有一组对边平行；④截面可以是五边形；⑤截面可以是六边形；⑥截面六边形可以是等角(均为120°)的六边形．特别地，可以是正六边形．截面图形举例第二课时旋转体与简单组合体的结构特征参考答案1．C 2.D 3.D 4.C 5.圆锥6．解(1)特征：具有棱柱的特征，且侧面都是全等的矩形，底面是正五边形．几何体为正五棱柱．(2)由两个同心的大球和小球，大球里去掉小球剩下的部分形成的几何体，即空心球．7．解如图所示，旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体．8．A9.B10.π611．解假设直角三角形ABC 中，∠C ＝90°.以AC 边所在的直线为旋转轴，其余两边旋转形成的面所围成的旋转体如图(1)所示．当以BC 边所在的直线为旋转轴，其余两边旋转形成的面所围成的旋转体如图(2)所示．当以AB 边所在的直线为旋转轴，其余两边旋转形成的面所围成的旋转体如图(3)所示．12．解作出圆台的侧面展开图，如图所示，由其轴截面中Rt △OP A 与Rt △OQB 相似，得OA OA ＋AB ＝510，可Q 的周长相等，求得OA ＝20 cm.设∠BOB ′＝α，由于扇形弧BB ′的长与底面圆而底面圆Q 的周长为2π×10 cm.扇形OBB ′的半径为OA ＋AB ＝20＋20＝40 cm ，扇度20π为所在圆形OBB ′所在圆的周长为2π×40＝80π cm.所以扇形弧BB ′的长周长的14.所以OB ⊥OB ′.所以在Rt △B ′OM 中，B ′M 2＝402＋302，所以B ′M ＝50 cm ，即所求绳长的最小值为50 cm.1.2.1 中心投影与平行投影1.2.2 空间几何体的三视图参考答案1．D 2.C 3.D 4．C5．(1)D (2)A (3)E (4)C (5)B 6.2 47．解图(a)是由两个长方体组合而成的，正视图正确，俯视图错误，俯视图应该画出不可见轮廓线(用虚线表示)，侧视图轮廓是一个矩形，有一条可视的交线(用实线表示)，正确画法如图所示．8．解三视图如图所示：9．A 10．D 11．612．解该物体是由一个正六棱柱和一个圆柱组合而成的，正视图反映正六棱柱的三个侧面和圆柱侧面，侧视图反映正六棱柱的两个侧面和圆柱侧面，俯视图反映该物体投影后是一个正六边形和一个圆(中心重合)．它的三视图如图所示．13．解由于正视图中每列的层数即是俯视图中该列的最大数字，因此，用的立方块数最多的情况是每个方框都用该列的最大数字，即如图①所示，此种情况共用小立方块17块．而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字，其他方框内的数字可减少到最少的1，即如图②所示，这样的摆法只需小立方块11块．1.2.3 空间几何体的直观图参考答案1．B 2.D 3.C 4.C 5.①② 6.2.57．解设O ′C ′＝h ，则原梯形是一个直角梯形且高为2h .过C ′作C ′D ′⊥O ′A ′于D ′，则C ′D ′＝22h . 由题意知12C ′D ′(C ′B ′＋O ′A ′)＝S .即24h (C ′B ′＋O ′A ′)＝S . 又原直角梯形面积为S ′＝12·2h (C ′B ′＋O ′A ′)＝h (C ′B ′＋O ′A ′)＝4S2＝22S .所以梯形OABC 的面积为22S .8．解 (1)作出长方体的直观图ABCD －A 1B 1C 1D 1，如图a 所示；(2)再以上底面A 1B 1C 1D 1的对角线交点为原点建立x ′，y ′，z ′轴，如图b 所示，在z ′上取点V ′，使得V ′O ′的长度为棱锥的高，连接V ′A 1，V ′B 1，V ′C 1，V ′D 1，得到四棱锥的直观图，如图b ； (3)擦去辅助线和坐标轴，遮住部分用虚线表示，得到几何体的直观图，如图c.9．A 10.2 11.2212．解画法：步骤：(1)如图a 所示，在梯形ABCD 中，以边AB 所在的直线为x 轴，点A 为原点，建立平面直角坐标系xOy .如图b 所示，画出对应的x ′轴，y ′轴，使∠x ′O ′y ′＝45°. (2)在图a 中，过D 点作DE ⊥x 轴，垂足为E .在图b 中，在x ′轴上取A ′B ′＝AB ＝4 cm ，A ′E ′＝AE ＝323≈2.598 cm ；过点E ′作E ′D ′∥y ′轴，使E ′D ′＝12ED ＝12×32＝0.75 cm ，再过点D ′作D ′C ′∥x ′轴，且使D ′C ′＝DC ＝2 cm.(3)连接A ′D ′、B ′C ′，并擦去x ′轴与y ′轴及其他一些辅助线，如图c 所示，则四边形A ′B ′C ′D ′就是所求作的直观图．13．解四边形ABCD 的真实图形如图所示，∵A ′C ′在水平位置，A ′B ′C ′D ′为正方形， ∴∠D ′A ′C ′＝∠A ′C ′B ′ ＝45°，∴在原四边形ABCD 中， DA ⊥AC ，AC ⊥BC ， ∵DA ＝2D ′A ′＝2， AC ＝A ′C ′＝2，∴S 四边形ABCD ＝AC ·AD ＝2 2.第一课时柱体、锥体、台体的表面积参考答案1．B 2．A 3．C 4.A 5.60° 6.12 800 7.28．解把长方体含AC 1的面作展开图，有三种情形如图所示：利用勾股定理可得AC 1的长分别为90、74、80.由此可见图②是最短路线，其路程的最小值为74. 9．A 10．B 11．3812．解把圆柱侧面及缠绕其上的铁丝展开，在平面上得到矩形ABCD (如图所示)，由题意知BC ＝3π cm ，AB ＝4π cm ，点A 与点C 分别是铁丝的起、止位置，故线段AC 的长度即为铁丝的最短长度． AC ＝AB 2＋BC 2＝5π cm ，故铁丝的最短长度为5π cm.13．解易知由下向上三个正方体的棱长依次为2，2，1.考虑该几何体在水平面的投影，可知其水平面的面积之和为下底面积最大正方体的底面面积的二倍． ∴S 表＝2S 下＋S 侧＝2×22＋4×[22＋(2)2＋12]＝36. ∴该几何体的表面积为36.第二课时柱体、锥体、台体、球的体积与球的表面积参考答案1．C 2.A 3.B 4.C 5.3 6．6 7．(1)球 (2)球8．解 ∵P A 、PB 、PC 两两垂直，P A ＝PB ＝PC ＝a .∴以P A 、PB 、PC 为相邻三条棱可以构造正方体．又∵P 、A 、B 、C 四点是球面上四点，∴球是正方体的外接球，正方体的对角线是球的直径．∴2R ＝3a ，R ＝32a ，∴V ＝43πR 3＝43π(32a )3＝32πa 3.9．A 10.A 11.9π＋1812．解由题意知，圆锥的轴截面为正三角形，如图所示为圆锥的轴截面．根据切线性质知，当球在容器内时，水深为3r ，水面的半径为3r ，则容器内水的体积为V ＝V 圆锥－V球＝13π·(3r )2·3r －43πr 3＝53πr 3，而将球取出后，设容器内水的深度为h ，则水面圆的半径为33h ，从而容器内水的体积是V ′＝13π·(33h )2·h ＝19πh 3，由V ＝V ′，得h ＝315r . 即容器中水的深度为315r .13．解设正方体的棱长为a .如图所示．(1)中正方体的内切球球心是正方体的中心，切点是正方体六个面的中心，经过四个切点及球心作截面，所以有2r 1＝a ，r 1＝a 2，所以S 1＝4πr21＝πa 2.(2)中球与正方体的各棱的切点在每条棱的中点，过球心作正方体的对角面得截面，2r 2＝2a ，r 2＝22a ，所以S 2＝4πr 22＝2πa 2.(3)中正方体的各个顶点在球面上，过球心作正方体的对角面得截面，所以有2r 3＝3a ，r 3＝32a ，所以S 3＝4πr 23＝3πa 2.综上可得S 1∶S 2∶S 3＝1∶2∶3.章末检测答案1．A 2.B 3.D 4．C 5．B 6．D 7.B 8.B 9．A 10．A 11．C 12．A 13．①②③⑤ 14．1 15.24π16.14－12π17．解由三视图可知：该几何体的下半部分是棱长为2 m 的正方体，上半部分是半径为1 m 的半球．(1)几何体的表面积为S ＝12×4π×12＋6×22－π×12＝24＋π(m 2)．(2)几何体的体积为V ＝23＋12×43×π×13＝8＋2π3(m 3)．18．解 (1)直观图如图．(2)这个几何体是一个四棱锥．它的底面边长为2，高为3，所以体积V ＝13×22×3＝433.19．解 S 表面＝S 圆台底面＋S 圆台侧面＋S 圆锥侧面＝π×52＋π×(2＋5)×5＋π×2×2 2 ＝(42＋60)π.V ＝V 圆台－V 圆锥＝13π(r 21＋r 1r 2＋r 22)h －13πr 21h ′ ＝13π(25＋10＋4)×4－13π×4×2 ＝1483π. 20．解 (1)设圆台上、下底面半径分别为r 、R ，AD ＝x ，则OD ＝72－x ，由题意得⎩⎪⎨⎪⎧2πR ＝60·π180×7272－x ＝3R，∴⎩⎪⎨⎪⎧R ＝12x ＝36.即AD 应取36 cm.(2)∵2πr ＝π3·OD ＝π3·36，∴r ＝6 cm ，圆台的高h ＝x 2－(R －r )2＝362－(12－6)2＝635. ∴V ＝13πh (R 2＋Rr ＋r 2)＝13π·635·(122＋12×6＋62)＝50435π(cm 3)．。

高中数学必修2(人教A版)第一章几何空间体1.2知识点总结含同步练习及答案

（）AC >AD >AB >则原图形的面积为______．．OABC 242√=6×4=24S OABC 2√2√例题：由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影．其中我们把光线叫做投影线，把留下物体影子的屏幕叫做投影面．平行投影投影线平行的投影称为平行投影．其中投影线与投影面垂直的平行投影叫做正投影，投影线与投影面不垂直的平行投影称为斜投影．平行投影的性质线段的平行投影是线段或点；平行直线的平行投影是平行或重合的直线；平行于投影面的线段，它的投影与这条线段平行且等长；与投影面平行的平面图形，它的投影与这个图形全等；在同一直线或平行直线上，两条线段平行投影长的比等于这两条线段长的比．中心投影投影线交于一点的投影称为中心投影．空间几何体的三视图三视图是观察者从三个不同位置观察同一个空间几何体而画出的图形．通常，总是选择三种正投影：投影线从几何体的前面向后面正投影得到投影图，这种投影称为几何体的正视图，也叫主视图；投影线从几何体的左面向右面正投影得到投影图，这种投影称为几何体的侧视图，也叫左视图；投影线从几何体的上面向下面正投影得到投影图，这种投影称为几何体的俯视图．几何体的正视图、侧视图和俯视图统称为几何体的三视图．三视图的画法一个几何体的俯视图和正视图长度一样，侧视图和主视图高度一样，侧视图和俯视图宽度一样，简称为：“长对正，高平齐，宽相等”．侧视图在正视图的右边，俯视图在正视图的下边．能看见的轮廓线和棱用实线表示，不能看见的轮廓线和棱用虚线表示．给出以下四个命题：①正方形的平行投影一定是菱形；②三角形的平行投影一定是三角形；③平行直线的平行投影仍是平行的直线；④当直线或线段不平行于投影线时，它的平行投影仍是直线或线段．其中真命题的个数是（）A． B． C． D．解：B①正方形的平行投影有三种情况：a．当正方形所在平面与投影面平行时，它的投影是正方形；b．当正方形所在平面与投射面垂直时，它的投影是一条线段；c．当正方形所在平面与投射面斜交时，它的投影是平行四边形．②三角形的平行投影可能是一条线段或三角形．③两条平行直线的平行投影为两个点或重合为一条直线或仍为两条平行直线．0123④由平行投影的性质知④是真命题．如图(1)，、分别是正方体的面，面的中心，则四边形在该正方体的面上的正投影可能是图(2)中的______．（要求把可能序号都填上）解：②③四边形在正方体的面、面、面、面上的投影是②．四边形在正方体的面、面上的投影是③．E F AD D 1A 1BC C 1B 1BF E D 1BF E D 1ABCD A 1B 1C 1D 1CD D1C 1AB B 1A 1BF E D 1BCC 1B 1AD D 1A 1下列四个几何体中，只有主视图和左视图相同的是（）A．①② B．①③ C．①④ D．②④解：D如图(1)(2)所示的是两个相同的正方体，阴影面选为正面，正方体的棱长均为，分别画出它们的三视图．解：三视图分别如下图中的(1)(2)．1一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如下图所示，则该几何体的俯视图为（）解：C由正（主）视图可知去掉的长方体在正对视线的方向，从侧（左）视图可以看出去掉的长方体在原长方体的左侧．A． B． C．862√×4×2+43√．．．．高考不提分，赔付1万元，关注快乐学了解详情。

高中数学人教A版必修2 第一章空间几何体高考复习习题(选择题1-100)含答案解析

高中数学人教A版必修2 第一章空间几何体高考复习习题（选择题1-100）含答案解析学校:___________姓名：___________班级：___________考号：___________一、单选题1．下图是某四棱锥的三视图，网格纸上小正方形的边长为1，则该四棱锥的外接球的表面积为（）A．B．C．D．2．已知三棱锥的所有顶点都在球的球面上，，，若三棱锥体积的最大值为2，则球的表面积为( )A．B．C．D．3．在正方体ABCD-A1B1C1D1中，三棱锥A1-BC1D内切球的表面积为，则正方体外接球的体积为A．B．C．D．4．已知三棱锥的所有顶点都在球的球面上，是边长为的正三角形，两两垂直，则球的体积为（）A．B．C．D．5．已知三棱锥中，，，，，且二面角的大小为，则三棱锥外接球的表面积为（）A．B．C．D．6．某棱锥的三视图如下图所示,则该棱锥的外接球的表面积为（）A．B．C．D．7．如图，网格纸上小正方形的边长为1，粗线或虚线面出的是某几何体的三视图，俯视图中的两条弧均为圆弧，则该几何体的体积为（）A．B．C．D．8．一个直三棱柱的三视图如图1所示，其俯视图是一个顶角为的等腰三角形，则该直三棱柱外接球的表面积为（）A．B．C．D．9．已知边长为的菱形，，沿对角线把折起，二面角的平面角是，则三棱锥的外接球的表面积是（）A．B．C．D．10．在三棱锥中，平面，，，，是边上的一动点，且直线与平面所成角的最大值为，则三棱锥的外接球的表面积为（）A．B．C．D．11．在三棱锥中，是边长为2的等边三角形，，，则三棱锥的外接球的表面积为（）A．B．C．D．12．已知三棱柱的六个顶点都在球的球面上，球的表面积为，平面,则直线与平面所成角的正弦值为（）A．B．C．D．13．为推导球的体积公式，刘徽制造了一个牟合方盖（在一个正方体内作两个互相垂直的内切圆柱，这两个圆柱的公共部分叫做牟合方盖），但没有得到牟合方盖的体积．200年后，祖暅给出牟合方盖的体积计算方法，其核心过程被后人称为祖暅原理：缘幂势既同，则积不容异．意思是，夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截，如果截面的面积总相等，那么这两个几何体的体积也相等．现在截取牟合方盖的八分之一，它的外切正方体的棱长为1，如图所示，根据以上信息，则该牟合方盖的体积为（）A．B．C．D．14．已知某几何体的三视图如图所示，则该几何体的外接球的表面积为A ．B ．C ．D ．15．如图，正方形1111ABCD A BC D -的棱长为 4,点P Q 、分别在底面ABCD 、棱1AA 上运动,且4PQ =，点M 为线段PQ 运动时,则线段1C M 的长度的最小值为( )A ． 2B ．C ． 6D ． 16．在长方体中，，， , 分别在线段和上，，则三棱锥的体积最小值为A ． 4B ．C ．D ．17．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A ．B ．C ．D ．18．在正方体中，为棱上一点，且，以为球心，线段的长为半径的球与棱分别交于两点，则的面积为（）A ．B ．C ．D ．19．中国古代数学家名著《九章算术》中记载了一种名为“堑堵”的几何体，其三视图如图所示，则其外接球的表面积为（）A ．B ．C ．D ．20．已知，，，四点均在以点为球心的球面上，且，，.若球在球内且与平面相切，则球直径的最大值为A．1B．2C．4D．821．四面体中，，，点是的中点，点在平面的射影恰好为的中点，则该四面体外接球的表面积为（）A．B．C．D．22．已知菱形的边长为，，沿对角线将菱形折起，使得二面角的余弦值为，则该四面体外接球的体积为（）A．B．C．D．23．如图，正三棱柱各条棱的长度均相等，为的中点，分别是线段和线段上的动点(含端点)，且满足，当运动时，下列结论中不正确的是( )A．在内总存在与平面平行的线段B．平面平面C．三棱锥的体积为定值D．可能为直角三角形24．我国古代《九章算术》将上、下两面为平行矩形的六面体称为刍童.右图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和4，高为2，则该刍童的表面积为A．B．40C．D．25．某几何体的三视图如图所示,则该几何体的体积为（）A．3+1πB．C．D．26．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图，且该几何体的体积为83，则该几何体的俯视图可以是( )A．B．C．D．27．如图是某几何体的三视图，则该几何体的外接球的表面积为（)A．B．C．D．28．用与圆柱底面成角的平面截圆柱，得到一完整的椭圆截面，则该椭圆的离心率为A．B．C．D．29．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A ． 83B ． 163C ． 323D ． 16 30．一个正三棱柱的三视图如图所示，若该三棱柱的外接球的表面积为，则侧视图中的的值为（）A ． 6B ． 4C ． 3D ． 231．三棱锥S ABC -中，侧棱SA ⊥底面ABC ， 5AB =， 8BC =， 60B ∠=︒，）A ．B ．C ．D ． 32．在长方体中，底面是边长为的正方形，侧棱，为矩形内部（含边界）一点，为中点，为空间任一点且，三棱锥的体积的最大值记为，则关于函数，下列结论确的是（）A ．为奇函数B ．在上不单调；C ．D ．33．如图是一个几何体的三视图，在该几何体的各个面中，面积最小的面的面积为（）A ． 8B ． 4C ．D ． 34．一个多面体的直观图、正视图、侧视图、俯视图如图，M ，N 分别为A 1B ，B 1C 1的中点.下列结论中正确的个数有 ( )①直线MN 与A 1C 相交.②MN ⊥BC ．③MN∥平面ACC 1A 1.④三棱锥N -A 1BC 的体积为1N A BC V -=3. A ． 4个 B ． 3个 C ． 2个 D ． 1个35．已知正中，点为的中点，把沿折起，点的对应点为点，当三棱锥体积的最大值为时，三棱锥的外接球的体积为（）A ．B ．C ．D ．36．已知三棱锥A B C D -的四个顶点,,,A B C D 都在球O 的表面上，,BC CD AC ⊥⊥平面BCD ，且2A C C D===，则球O 的表面积为（）A ． 4πB ． 8πC ． 16πD ．37．如图，网格纸上虚线围成的最小正方形边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（）A ．B ．C ．D ．38．已知三棱锥中，侧面底面，，则三棱锥外接球的体积为（）A．B．C．D．39．某简单凸多面体的三视图如图所示，其中俯视图和左视图都是直角三角形，主视图是直角梯形，则其所有表面（含底面和侧面）中直角三角形的个数为（）A．1 B．2 C．3 D．440．已知四棱锥的三视图如图所示，则四棱锥外接球的表面积是（）A．B．C．D．41．我国南北朝时间著名数学家祖暅提出了祖暅原理：“幂势既同，则积不容异”.意思是：夹在两平行平面间的两个几何体，被平行于这两个平行平面的任何平面所载，若截得的两个截面面积总相等，则这两个几何体的体积相等.为计算球的体积，构造一个底面半径和高都与球半径相等的圆柱，然后再圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥，运用祖暅原理可证明此几何体与半球体积相等（任何一个平面所载的两个截面面积都相等）.将椭圆绕轴旋转一周后得一橄榄状的几何体，类比上述方法，运用祖暅原理可求得其体积等于（）A ．B ．C ．D ．42．某三棱锥的三视图如图所示，则该三棱锥最长的棱长为A ．B ．C ．D ．43．某几何体的三视图如图所示，图中网格纸上小正方形的边长为 1，则该几何体的外接球的表面积为A ．B ．C ．D ．44．已知一个圆锥的侧面积是底面积的2倍，记该圆锥的表面积为1S ，外接球的表面积为2S ，则） A ． 3:8 B ． 9:16 C ． 1:4 D ． 1:845．四面体中，，，，则四面体外接球的表面积为（）A ．B ．C ．D ．46．在三棱锥P ABC -中，90ABC BCPPAB ∠=∠=∠=，，则三棱锥P ABC -外接球的表面积为（） A ． 5π B ． 13π C ． 6π D ． 14π47．在四面体中，，，底面，的面积是，若该四面体的顶点均在球的表面上，则球的表面积是（）A ．B ．C ．D ．48．在中，，、分别在、上，，，将沿折起，连接，，当四棱锥体积最大时，二面角的大小为（）A ．B ．C ．D ． 49．在三棱柱中，，分别为棱，的中点，过，，的截面把三棱柱分成两部分，则这两部分的体积比为（）A ． 5:3B ． 2:1C ． 17:7D ． 3:150．如图所示，正方形的边长为2，切去阴影部分围成一个正四棱锥，则当正四棱锥的侧面积取值范围为（）A ．B ．C ．D ．51．在长方体1111ABCD A BC D -中， AB =， 11BC AA ==，点M 为1AB 的中点，点P 为对角线1AC 上的动点，点Q 为底面ABCD 上的动点（点P ， Q 可以重合），则MP PQ +的最小值为（）A．B．C．34D．152．如图为一个多面体的三视图，则该多面体的体积为（）A．B．7C．D．53．如图，在矩形中，四边形为边长为的正方形，现将矩形沿过点的动直线翻折，使翻折后的点在平面上的射影落在直线上,若点在折痕上射影为，则的最小值为（）A．B．C．D．54．四棱锥P ABCD-的三视图如图所示，则该四棱锥的外接球的表面积为（）A．B．C．D．55．某棱锥的三视图如图所示，则该棱锥的外接球的表面积为（）A ． 11πB ． 12πC ． 13πD ． 14π56．在四面体ABCD 中，若 2AC BD ==，四面体ABCD 的外接球的表面积为（）A ． 2πB ． 4πC ． 6πD ． 8π57．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为A ． 163πB ． 112πC ． 173πD ． 356π 58．古希腊亚历山大时期的数学家怕普斯(Pappus, 约300~约350)在《数学汇编》第3卷中记载着一个定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交，那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以重心旋转所得周长的积”如图，半圆的直径，点是该半圆弧的中点，那么运用帕普斯的上述定理可以求得，半圆弧与直径所围成的半圆面(阴影部分个含边界)的重心位于对称轴上，且满足 = ( )A ．B ．C ．D ． 59．如图，各棱长都相等的三棱锥内接于一个球，则经过球心的一个截面图形可能是( )A．①③B．①②C．②④D．②③60．已知四棱锥的底面是边长为2的正方形，侧棱平面，，若在四棱锥的内部有一个半径为的球，则的最大值为（）A．B．1C．D．61．棱长为的正方体内有一个内切球O，过正方体中两条互为异面直线的，的中点作直线，该直线被球面截在球内的线段的长为（）A．B．C．D．62．某三棱锥的三视图如图所示，该三棱锥的表面积是（）A．B．C．D．63．四面体中，三组对棱的长分别相等，依次为5，4，，则的取值范围是A．B．C．D．64．已知,,,A B C D是球O表面上四点，点E为BC的中点，若,,120AE BC DE BC AED⊥⊥∠=︒,2AE DE BC===，则球O的表面积为（）A．73πB．283πC．4πD．16π65．在底面是正方形的四棱锥中，底面，点为棱的中点，点在棱上，平面与交于点，且，，则四棱锥的外接球的表面积为（）A．B．C．D．66．在三棱锥中，，平面和平面所成角为，则三棱锥外接球的体积为（）A．B．C．D．67．如图所示，正方体的棱长为，动点在对角线上，过点作垂直于的平面，记这样得到的截面多边形（含三角形）的面积为，设，则当时，函数的值域为（）A．B．C．D．68．多面体的三视图如图所示，则该多面体的外接球的表面积为（）A．B．C．D．69．已知顶点在同一球面上的某三棱锥三视图中的正视图，俯视图如图所示．若球的体积为，则图中的的值是（）A ．B ．C ．D ．70．如图是某几何体的三视图，其中俯视图为等边三角形，正视图为等腰直角三角形，若该几何体的各个顶点都在同一个球面上，则这个球的体积与该几何体的体积的比为（）A ．B ．C ．D ． 71．在三棱锥A BCD -中， ABC ∆与BCD ∆都是正三角形，平面ABC ⊥平面BCD ，，则ABC ∆边长为（）A ．B ．C ．D ． 672．已知球O 半径为，设S A B C 、、、是球面上四个点，其中90,AB =，则棱锥S ABC -的体积的最大值为（）A ．B ．C ．D ． 73．已知边长为2的等边三角形ABC ， D 为BC 的中点，以AD 为折痕进行折叠，，则过A ， B ， C ， D 四点的球的表面积为（）A ． 3πB ． 4πC ． 5πD ． 6π74．某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)是( )A ．＋1B ．＋3C ．＋1D ．＋375．如图，在ABC ∆中， AB BC == 90ABC ∠=︒，点D 为AC 的中点，将ABD ∆沿BD 折起到PBD ∆的位置，使PC PD =，连接PC ，得到三棱锥P BCD -，若该三棱锥的所有顶点都在同一球面，则该球的表面积是（）A ． πB ． 3πC ． 5πD ． 7π76．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A ．B ．C ．D ．77．已知表面积为100 的球内接一个圆锥，则该圆锥体积的最大值为A ．B ．C ．D ．78．一个几何体的三视图如图所示，图中的三个正方形的边长均为2，则该几何体的体积为（）A ．B ．C ．D ． 79．如图所示，在直三棱柱中， , 分别为的中点，为线段上一点，设，给出下面几个命题：① 的周长是单调函数，当且仅当时，的周长最大； ② 的面积满足等式，当且仅当时，的面积最小；③三梭锥的体积为定值.其中正确的命题个数是（）A ． 0B ． 1C ． 2D ． 380．在菱形ABCD 中， 60AB A ==，将ABD ∆沿BD 折起到PBD ∆的位置，若二面角P BD C --的大小为120，三棱锥P BCD -的外接球球心为O ， BD 的中点为E ，则OE =A ． 1B ． 2C ．D ． 81．一个底面半径为1，高为2的圆锥形工件切割成一个圆柱体，能切割出的圆柱的最大体积为()A ． π27B ． 8π27C ． π3D ． 2π982．如图，已知平面α⋂平面l β=， αβ⊥， A 、B 是直线l 上的两点， C 、D 是平面β内的两点，且DA l ⊥， BC l ⊥， 4DA =， 6AB =， 8CB =， P 是平面α上的一动点，且有APD BPC ∠=∠，则四棱锥P ABCD -体积的最大值是（）A ． 48B ． 16C ．D ． 14483．已知SC 是球O 的直径， ,A B 是球O 球面上的两点，且若三棱锥S ABC -的体积为1，则球O 的表面积为（）A ． 4πB ． 13πC ． 16πD ． 52π84．设正三棱锥P ABC -的高为H ，且此棱锥的内切球的半径（）A ．B ．C ．D ． 85．已知棱长为2的正方体1111ABCD A BC D -，球O 与该正方体的各个面相切，则平面1ACB 截此球所得的截面的面积为（）A ．B ．C ．D ． 86．三棱锥中，平面且是边长为的等边三角形，则该三棱锥外接球的表面积为( )A ．B ．C ．D ． 87．三棱锥A BCD -中， AD ⊥平面BCD ， 1AD =， BCD ∆是边长为2的等边三角形，则该几何体外接球的表面积为（）A ．B ．C ．D ． 88．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A．B．C．D．2π89．如图：AB是圆锥底面圆的直径，PA，PB是圆锥的两种母线，P'为底面圆的中心，过PB的中点D作平行于PA的平面α，使得平面α与底面圆的交线长为4，沿圆锥侧面连接A点和D点，当曲线段AD时，则该圆锥的外接球（圆锥的底面圆周及顶点均在球面上）的半径为（）A．B．C．D．90．如图，某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形．若该三棱锥的顶点都在同一个球面上，则该球的表面积为（）A．B．C．D．91．6个棱长为1的正方体在桌面上堆叠成一个几何体，该几何体的主视图与俯视图如图所示，则其侧视图不可能为（）A．B．C．D．92．形，则该三棱锥外接球的表面积为（）A．20πB．16πC．8πD．17π93．一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A. B. C. D.94．四棱锥的三视图如下图所示，四棱锥的五个顶点都在一个球面上，，分别是棱、的中点，直线被球面所截得的线段长为，则该球的表面积为（）A．B．C．D．-的度面为矩形，平面PAD⊥平面ABC D，96．如图，已知四棱锥P ABCD-的外接球的表面积为（）．===，则四棱锥P ABCD2PA PD ABA．2πB．4πC．12πD．8π97( )A．2π＋2B．2π＋1C．π＋1D．π＋2-中，E是棱AD的中点，P是棱AC上一动点，98．如图所示，在正四面体A BCD+的最小值为）BP PEA．B．6πC．D．99．如图所示，网络纸上每个小格都是边长为1的正方形，粗线画出的是一个几何体的三视图，则该几何体的表面积为（）A．B．C．D．100．某几何体的三视图如图所示，则该几何体的体积为（）A ． 64B ． 644π-C ． 648π-D ．参考答案1．C【解析】分析：还原几何体得四棱锥，根据球心到各顶点的距离相等列方程可得解.详解：根据三视图得出：该几何体是镶嵌在正方体中的四棱锥O﹣ABCD，正方体的棱长为2，A，D为棱的中点其中.根据几何体可以判断：球心应该在过A，D的平行于底面的中截面上，设球心到截面BCO的距离为x，则到AD的距离为：4﹣x，∴R2=x2+（）2，R2=22+（4﹣x）2，解得出：，该多面体外接球的表面积为：4πR2=，故选：C．点睛：对于外接球问题，若是锥体，可以先找底面外接圆的圆心，过圆心做底面的垂线，再做一条侧棱的中垂线，两条直线的交点就是球心，构造平面几何关系求半径.2．D【解析】分析：根据棱锥的最大高度和勾股定理计算球的半径，从而得出外接球的表面积．详解：因为，所以，过的中点作平面的垂下，则球心在上，设，球的半径为，则棱锥的高的最大值为，因为，所以，由勾股定理得，解得，所以球的表面积为，故选D．点睛：本题考查了有关球的组合体问题，以及三棱锥的体积的求法，解答时要认真审题，注意球的性质的合理运用，求解球的组合体问题常用方法有（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）利用球的截面的性质，根据勾股定理列出方程求解球的半径．3．B【解析】【分析】利用体积相等求出正四棱锥的高，从而可得正四棱锥的棱长，可求得正方体的棱长，利用正方体外接球直接就是正方体对角线长，可求外接球的半径，进而可得结果.【详解】设正方体的棱长为，则，因为三棱锥内切球的表面积为，所以三棱锥内切球的半径为1，设内切球的球心为，到面的距离为，则，，，又，，又因为正方体外接球直接就是正方体对角线长，正方体外接球的半径为，其体积为，故选B.【点睛】解答多面体内切球的表面积与体积问题，求出内切球半径是解题的关键，求内切球半径的常见方法有两种：一是对特殊几何体（例如正方体，正四面体等等）往往直接找出球心，求出半径即可；二是对不规则多面体，往往将多面体分成若干个以多面体的面为底面以内切球的球心为高的棱锥，利用棱锥的体积和等于多面体的体积列方程求出内切球半径.4．A【解析】分析：由题意可构造以为过一顶点的三条棱的长方体，则该三棱锥的外接球即为长方体的外接球，由于长方体的体对角线即为其外接球的直径，由此可得球半径，从而可求得球的体积．详解：∵三棱锥中两两垂直，∴以为过同一顶点的三条棱构造长方体，该长方体的外接球即为三棱锥的外接球．又是边长为的正三角形，∴，∴长方体的体对角线为，即球的直径为，∴球的体积为．故选A．点睛：关于球的内接几何体的问题，往往涉及到求球的体积或表面积，求解的关键是确定球心的位置和求出球的半径．当球外接于正方体（或长方体），即正方体（或长方体）的顶点均在球面上时，则正方体（或长方体）的体对角线长等于球的直径．5．D【解析】【分析】由题意可知，三棱锥外接球的球心在过外接圆圆心的法线上，设，由题设条件可知，外接球半径，由此解得，从而求出外接球的半径及表面积.【详解】如图，设、中点为、，过点、作面，面，过点作垂足为，交于，则为外接圆的圆心，三棱锥外接球球心在直线上，设，，，且二面角的大小为，，，，，，，,在中，；在中，；外接球半径，，解得，外接球表面积故选D.【点睛】本题考查三棱锥外接球表面的求法，涉及到棱锥的结构特征、二面角的平面角、直角三角形的性质、勾股定理和球的简单性质等知识点，解题时要认真审题，注意合理地转化空间几何问题.6．A【解析】分析：由三视图可知该几何体是如图所示的三棱锥，外接球球心在过中点且垂直于平面的直线上，可知是直线与面的交点，也是直线与直线的交点没有此可求三棱锥外接球的半径，得到棱锥的外接球的表面积详解：由三视图可知该几何体是如图所示的三棱锥，外接球球心在过中点且垂直于平面的直线上，又点到距离相等，∴点又在线段的垂直平分面上，故是直线与面的交点，可知是直线与直线的交点（分别是左侧正方体对棱的中点）∴，，故三棱锥外接球的半径，表面积为.故选A.点睛：本题考查了三棱锥的性质、空间几何位置关系、三垂线定理、球的性质，考查了推理能力与计算能力，属于中档题．7．C【解析】分析：由题意首先确定该几何体的空间结构，然后结合体积公式整理计算即可求得最终结果.详解：如图所示，在棱长为4的正方体中，分别为其对应棱上的中点，将正方体裁取四分之一圆柱和四分之一圆锥后对应的几何体即为三视图所对应的几何体，其中正方体的体积，四分之一圆柱的体积四分之一圆锥的体积，则所求组合体的体积为：.本题选择C选项.点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．8．B【解析】分析：由正弦定理求出底面三角形外接圆半径，由勾股定理可得球的半径，从而可得结果.详解：由三视图可知，该三棱柱的底面是一个顶点角为，两腰为的等腰三角形，高为，底面三角形的外接圆直径为，半径，根据三棱柱的性质可得球心在底面三角形外心连线的中点处，设该三棱柱的外接球的半径为，则，该直三棱柱外接球的表面积，故选B.点睛：本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.9．B【解析】【分析】正确作出图形，利用勾股定理建立方程，求出四面体的外接球的半径，即可求出四面体的外接球的表面积.【详解】如图所示，设菱形的对角线交于，由菱形的性质可得，二面角的平面角是因为菱形的边长为，，，设，则，由勾股定理可得，，即，解得，，四面体的外接球的表面积为，故选B.【点睛】本题主要考查三棱锥外接球表面积的求法，属于难题.要求外接球的表面积和体积，关键是求出球的半径，求外接球半径的常见方法有：①若三条棱两垂直则用（为三棱的长）；②若面（），则（为外接圆半径）；③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.10．B【解析】分析：根据题意画出图形，结合图形找出的外接圆圆心与三棱锥外接球的球心，求出外接球的半径，再计算它的表面积．详解：三棱锥中，平面，设直线与平面所成角为，如图所示；则，由题意且的最大值是，∴，，解得，即的最小值为，∴的最小值是，即点到的距离为，，，；取的外接圆圆心为，作，，解得；，为的中点，，，由勾股定理得，∴三棱锥的外接球的表面积是．点睛：本题考查了几何体外接球的应用问题，解题的关键求外接球的半径，是中档题．11．A【解析】分析：先证明面于CD中点E,再由OC=OA算出球的半径，再求球的表面积。