高中数学必修2《空间几何体》知识点
高中数学必修2知识点总结归纳整理

高中数学必修二·空间几何体1.1空间几何体的构造 棱柱定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边 形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、 五棱柱等。
表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱'''''E D C B A ABCDE - 几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形, 由这些面所围成的几何体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、 五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
棱台定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间 的局部分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、 五棱台等表示:用各顶点字母,如四棱台ABCD —A'B'C'D'几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点 圆柱定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的 曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面 圆的半径垂直;④侧面展开图是一个矩形。
圆锥定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的 曲面所围成的几何体几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面 展开图是一个扇形。
圆台定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之 间的局部几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点; ③侧面展开图是一个弓形。
必修二数学知识点整理

必修二数学知识点整理一、立体几何初步。
(一)空间几何体。
1. 结构特征。
- 棱柱。
- 有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
- 棱柱的底面、侧面、侧棱、顶点等概念。
按底面多边形的边数可分为三棱柱、四棱柱、五棱柱等。
- 棱锥。
- 有一个面是多边形,其余各面都是有一个公共顶点的三角形。
- 棱锥的底面、侧面、侧棱、顶点等概念。
按底面多边形的边数可分为三棱锥(四面体)、四棱锥等。
- 棱台。
- 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分。
- 棱台的上底面、下底面、侧面、侧棱、顶点等概念。
- 圆柱。
- 以矩形的一边所在直线为轴旋转,其余三边旋转所成的曲面所围成的几何体。
- 圆柱的轴、底面、侧面、母线等概念。
- 圆锥。
- 以直角三角形的一条直角边所在直线为轴旋转,其余两边旋转所成的曲面所围成的几何体。
- 圆锥的轴、底面、侧面、母线等概念。
- 圆台。
- 用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分。
- 圆台的上底面、下底面、侧面、母线等概念。
- 球。
- 以半圆的直径所在直线为轴,半圆面旋转一周形成的几何体。
- 球心、半径、直径等概念。
2. 三视图和直观图。
- 三视图。
- 正视图(主视图)、侧视图(左视图)、俯视图的概念。
- 画三视图的规则:长对正、高平齐、宽相等。
- 通过三视图还原空间几何体的方法:先根据视图的轮廓想象出基本的几何体形状,再根据视图中的线段长度等确定几何体的具体尺寸。
- 直观图。
- 斜二测画法的步骤:- 在已知图形中取互相垂直的x轴和y轴,两轴相交于点O。
画直观图时,把它们画成对应的x'轴和y'轴,两轴相交于点O',且∠x'O'y' = 45°(或135°)。
- 已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴或y'轴的线段。
- 已知图形中平行于x轴的线段,在直观图中长度不变;平行于y轴的线段,长度变为原来的一半。
高中数学必修2知识点总结:第一章-空间几何体

高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征 1.2空间几何体的三视图和直观图1 三视图:正视图:从前往后 侧视图:从左往右 俯视图:从上往下 2 画三视图的原则:长对齐、高对齐、宽相等 3直观图:斜二测画法 4斜二测画法的步骤:(1).平行于坐标轴的线依然平行于坐标轴;(2).平行于y 轴的线长度变半,平行于x ,z 轴的线长度不变; (3).画法要写好。
5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图1.3 空间几何体的表面积与体积 (一 )空间几何体的表面积1棱柱、棱锥的表面积: 各个面面积之和2 圆柱的表面积3 圆锥的表面积2r rl S ππ+= 4 圆台的表面积22R Rl r rl S ππππ+++= 5 球的表面积24R S π=(二)空间几何体的体积1柱体的体积 h S V ⨯=底 2锥体的体积 h S V ⨯=底313台体的体积 h S S S S V ⨯++=)31下下上上( 4球体的体积 334R V π=222r rl S ππ+=第一章空间几何体1.1 空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是()A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是()A 有一个面是多边形,其余各面是三角形的多面体是棱锥B 有两个面互相平行,其余各面均为梯形的多面体是棱台C 有两个面互相平行,其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行,侧面均为平行四边形3、下面多面体是五面体的是()A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是()A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是()A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中,直角三角形最多可有几个()A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面,面数最少的棱柱有————————个顶点,有—————————个棱。
(完整word版)人教A版高中数学必修2知识点

必修2知识点归纳第一章 空间几何体1、空间几何体的结构:空间几何体分为多面体和旋转体和简单组合体⑴常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。
简单组合体的构成形式:一种是由简单几何体拼接而成,例如课本图1.1-11中(1)(2)物体表示的几何体; 一种是由简单几何体截去或挖去一部分而成,例如课本图1.1-11中(3)(4)物体表示的几何体。
⑵棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
⑶棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
1、空间几何体的三视图和直观图把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的。
(1)定义:正视图:光线从几何体的前面向后面正投影得到的投影图; 侧视图:光线从几何体的左面向右面正投影得到的投影图; 俯视图:光线从几何体的上面向下面正投影得到的投影图。
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(2)三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”2、空间几何体的直观图(表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形.3、斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上) ②建立斜坐标系'''x O y ∠,使'''xOy∠=450(或1350),注意它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X 轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半;一般地,原图的面积是其直观图面积的22倍,即22S S 原图直观=4、空间几何体的表面积与体积⑴圆柱侧面积;l r S ⋅⋅=π2侧面⑵圆锥侧面积:l r S ⋅⋅=π侧面⑶圆台侧面积:l R lr S ⋅⋅+⋅⋅=ππ侧面⑷体积公式:h S V ⋅=柱体;h S V ⋅=31锥体;()13V h S S S S =+⋅+下下台体上上⑸球的表面积和体积:32344R V R S ππ==球球,.一般地,面积比等于相似比的平方,体积比等于相似比的立方。
高中数学必修2知识点加例题加课后习题

高中数学必修二第一章 空间几何体1.1空间几何体的结构 1、棱柱定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱'''''E D C B A ABCDE -几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
2、棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
3、棱台定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如四棱台ABCD—A'B'C'D'几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点4、圆柱定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
5、圆锥定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
6、圆台定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
高中数学必修2《空间几何体》知识点
第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体,它们都占据着空间的一部分。
如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。
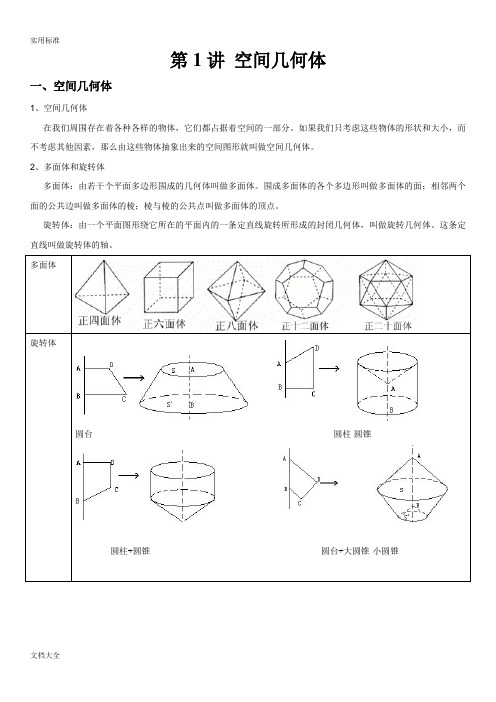
2、多面体和旋转体多面体:由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转几何体。
这条定直线叫做旋转体的轴。
多面体旋转体圆台圆柱-圆锥圆柱+圆锥圆台+大圆锥-小圆锥二、柱、锥、台、球的结构特征1.棱柱定义图形表示分类性质有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDEF-A1B1C1D1E1F1。
棱柱的分类一(底面):棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱柱的分类二(根据侧棱与底面的关系):斜棱柱: 侧棱不垂直于底面的棱柱.直棱柱: 侧棱垂直于底面的棱柱叫做直棱柱正棱柱: 底面是正多边形的直棱柱叫做正棱柱(1)上下底面平行,且是全等的多边形。
(2)侧棱相等且相互平行。
(3) 侧面是平行四边形。
三棱柱四棱柱五棱柱斜棱柱直棱柱正棱柱2.棱锥定义图形表示性质分类有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
用顶点及底面各顶点字母表示棱锥,如:棱锥S-ABC侧面是三角形,底面是多边形。
按底面多边形的边数分类可分为三棱锥、四棱锥、五棱锥等等,其中三棱锥又叫四面体。
特殊的棱锥-正棱锥定义:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心三棱锥四棱锥五棱锥直棱锥2.棱台定义图形表示分类性质用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。
高中数学必修2复习资料

必修2数学复习资料第一章 空间几何体1.1柱、锥、台、球的结构特征 1.2空间几何体的三视图和直观图1、 三视图: 正视图:从前往后; 侧视图:从左往右; 俯视图:从上往下。
2、 画三视图的原则: 长对齐、高对齐、宽相等3、直观图:斜二测画法4、斜二测画法的步骤:(1).平行于坐标轴的线依然平行于坐标轴;(2).平行于y 轴的线长度变半,平行于x ,z 轴的线长度不变; (3).画法要写好。
5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图 1.3 空间几何体的表面积与体积 (一 )空间几何体的表面积 1、棱柱、棱锥的表面积: 各个面面积之和2、圆柱的表面积3、圆锥的表面积2r rl S ππ+=4、圆台的表面积22R Rl r rl S ππππ+++=5、球的表面积24R S π=(二)空间几何体的体积 1、柱体的体积 h S V ⨯=底2、锥体的体积 h S V ⨯=底313、台体的体积h S S S S V ⨯++=)31下下上上(4、球体的体积 334R V π=第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系 2.1.11、平面含义:平面是无限延展的2、平面的画法及表示 (1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母γβα、、等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3、三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为ααα⊂⇒⎪⎪⎭⎪⎪⎬⎫∈∈∈∈L L B L A B A 公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α,222r rl S ππ+= D CBAαC · B· A·LA· α使.,,ααα∈∈∈C B A公理2作用:确定一个平面的依据。
(完整版)高中数学必修2立体几何知识点

高中数学必修 2 知识点第一章空间几何体1.1 柱、锥、台、球的构造特色(略)棱柱:棱锥:棱台:圆柱:圆锥:圆台:球:1.2 空间几何体的三视图和直观图1三视图:正视图:以前去后侧视图:从左往右俯视图:从上往下2画三视图的原则:长对齐、高对齐、宽相等3直观图:斜二测画法4斜二测画法的步骤:(1).平行于坐标轴的线依旧平行于坐标轴;(2).平行于 y 轴的线长度变半,平行于x,z 轴的线长度不变;(3).画法要写好。
5用斜二测画法画出长方体的步骤:(1)画轴( 2)画底面( 3)画侧棱( 4)成图1.3 空间几何体的表面积与体积(一)空间几何体的表面积1 棱柱、棱锥的表面积:各个面面积之和2圆柱的表面积4圆台的表面积S 2 rl2r 2 3 圆锥的表面积S rlr 2 S rl r 2Rl R2 5 球的表面积S 4R26扇形的面积公式S扇形n R21lr (此中l表示弧长,r表示半径)3602(二)空间几何体的体积1柱体的体积 V S底h 2 锥体的体积1S底h V33台体的体积V1S上h4 球体的体积V4R3(下下3S上 SS )3第二章直线与平面的地点关系2.1 空间点、直线、平面之间的地点关系1平面含义:平面是无穷延展的 , 无大小,无厚薄。
2平面的画法及表示450,且横边画成邻边的(1)平面的画法:水平搁置的平面往常画成一个平行四边形,锐角画成 2 倍长(2)平面往常用希腊字母α、β、γ等表示,如平面α、平面β等,也能够用表示平面的平行四边形的四个极点或许相对的两个极点的大写字母来表示,如平面AC、平面 ABCD等。
3三个公义:(1)公义 1:假如一条直线上的两点在一个平面内,那么这条直线在此平面内A l符号表示为B ll AB公义 1 作用:判断直线能否在平面内(2)公义 2:过不在一条直线上的三点,有且只有一个平面。
符号表示为: A、B、C 三点不共线有且只有一个平面α,使A∈α、 B∈α、 C∈α。
高中数学必修2《空间几何体》知识点(完整资料).doc

【最新整理,下载后即可编辑】第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体,它们都占据着空间的一部分。
如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。
2、多面体和旋转体多面体:由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转几何体。
这条定直线叫做旋转体的轴。
多面体旋转体圆台圆柱-圆锥圆柱+圆锥圆台+大圆锥-小圆锥二、柱、锥、台、球的结构特征1.棱柱定义图形表示分类性质有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDEF-A1B1C1D1E1F1。
棱柱的分类一(底面):棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱柱的分类二(根据侧棱与底面的关系):斜棱柱: 侧棱不垂直于底面的棱柱.直棱柱: 侧棱垂直于底(1)上下底面平行,且是全等的多边形。
(2)侧棱相等且相互平行。
(3) 侧面是平行四边形。
面的棱柱叫做直棱柱正棱柱: 底面是正多边形的直棱柱叫做正棱柱三棱柱四棱柱五棱柱斜棱柱直棱柱正棱柱2.棱锥定义图形表示性质分类有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
用顶点及底面各顶点字母表示棱锥,如:棱锥S-ABC侧面是三角形,底面是多边形。
按底面多边形的边数分类可分为三棱锥、四棱锥、五棱锥等等,其中三棱锥又叫四面体。
特殊的棱锥-正棱锥定义:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心三棱锥四棱锥五棱锥直棱锥2.棱台定义图形表示分类性质用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱棱台用表示上、下底面各顶点的字母来表示,如下图,棱台ABCD-A1B1C1D1由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…特殊的棱上下底面平行,其余各面是梯形,且侧棱延长后交于一点。
高中数学必修二最全完整笔记

高中数学必修二第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质第三章直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式第四章圆与方程4.1 圆的方程4.2 直线、圆的位置关系4.3 空间直角坐标系第一章空间几何体1.1 空间几何体的结构一、空间几何体:占据着空间的一部分,只考虑这些物体的形状和大小,那么由这些物体抽象出来的空间图形叫空间几何体。
1.多面体:一般地,我们把由若干个平面多边形围成的几何体叫做多面体。
(1)面:围成多面体的各个多边形叫做多面体的面。
(2)棱:相邻两个面的公共边叫做多面体的棱。
(3)顶点:棱与棱的公共顶点叫做多面体的顶点。
2.旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何,叫做旋转体。
(1棱3.棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
(1)底面:两个互相平行的面叫做棱柱的底面(简称底)。
(2)侧面:其余各面叫做棱柱的侧面。
(3)侧棱:相邻侧面的公共边。
(4)顶点:侧面与底面的公共顶点。
(5)简单性质:1.侧棱都相等,侧面都是平行四边形。
2.两个底面与平行于底面的截面是全等的。
3.各不相邻的侧棱所形成的斜面是平行四边形。
(6)棱柱的分类:1.按底面边多少分:n棱柱(n≥3)2.按侧棱与底面的关系分:垂直:直棱柱、正棱柱(底面为正多边形) 三棱柱四棱柱不垂直:斜棱柱1.底面为直角三角形 1.直平行六面体2.底面为等边三角形 2.正四棱柱3.底面为等腰直角三角形 3.正方体(非棱柱)4.棱锥:有一个面是多边形,其余各面都是有一公共点的三角形。
(1)底面:多边形面。
高中学必修二知识点空间几何体【共10页】

高中学必修二知识点空间几何体-----------各类专业好文档,值得你下载,教育,管理,论文,制度,方案手册,应有尽有-------------- 高中数学必修2知识点第一章空间几何体1、1柱、锥、台、球的结构特征1、2空间几何体的三视图和直观图1 三视图:正视图:从前往后侧视图:从左往右俯视图:从上往下2 画三视图的原则:长对齐、高对齐、宽相等3直观图:斜二测画法4斜二测画法的步骤:(1)、平行于坐标轴的线依然平行于坐标轴;(2)、平行于y轴的线长度变半,平行于x,z轴的线长度不变;(3)、画法要写好。
5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图1、3 空间几何体的表面积与体积(一)空间几何体的表面积1棱柱、棱锥的表面积:各个面面积之和2 圆柱的表面积3 圆锥的表面积4 圆台的表面积5 球的表面积(二)空间几何体的体积1柱体的体积2锥体的体积3台体的体积4球体的体积第二章直线与平面的位置关系2、1空间点、直线、平面之间的位置关系2、1、11 平面含义:平面是无限延展的2 平面的画法及表示 DC B A α (1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC、平面ABCD等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号表示为L A · α A∈LB∈L => L α A∈α B∈α 公理1作用:判断直线是否在平面内C · B · A · α (2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A、B、C三点不共线 => 有且只有一个平面α,使A∈α、B∈α、C∈α。
数学必修二空间几何知识点

数学必修二空间几何知识点在我们的学习时代,说到知识点,大家是不是都习惯性的重视?知识点是传递信息的基本单位,知识点对提高学习导航具有重要的作用。
掌握知识点是我们提高成绩的关键!以下是店铺为大家收集的数学必修二空间几何知识点,供大家参考借鉴,希望可以帮助到有需要的朋友。
数学必修二空间几何知识点1空间几何体表面积计算公式1、直棱柱和正棱锥的表面积设棱柱高为h、底面多边形的周长为c、则得到直棱柱侧面面积计算公式:S=ch、即直棱柱的侧面积等于它的底面周长和高的乘积、正棱锥的侧面展开图是一些全等的等腰三角形、底面是正多边形、如果设它的底面边长为a、底面周长为c、斜高为h'、则得到正n 棱锥的侧面积计算公式S=1/2xnah'=1/2xch'、即正棱锥的侧面积等于它的底面的周长和斜高乘积的一半、2、正棱台的表面积正棱台的侧面展开图是一些全等的等腰梯形、设棱台下底面边长为a、周长为c、上底面边长为a'、周长为c'、斜高为h'则得到正n棱台的侧面积公式:S=1/2xn(a+a')h'=1/2(c+c')h'、3、球的表面积S=4πR2、即球面面积等于它的大圆面积的四倍、4.圆台的表面积圆台的侧面展开图是一个扇环,它的表面积等于上,下两个底面的面积和加上侧面的面积,即S=π(r'2+r2+r'l+rl)柱、锥、台、球的结构特征(1)棱柱:几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的.比的平方。
(3)棱台:几何特征:①上下底面是相似的平行多边形;②侧面是梯形;③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
高中数学必修二空间几何体知识点

高中数学必修二第一章空间几何体一·空间几何体结构1.空间结合体:如果我们只考虑物体占用空间部分的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形,就叫做空间几何体。
2.棱柱的结构特征:有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边互相平行,由这些面围成的图形叫做棱柱。
(图如下)底面:棱柱中,两个相互平行的面,叫做棱柱的底面,简称底。
底面是几边形就叫做几棱柱。
侧面:棱柱中除底面的各个面.侧棱:相邻侧面的公共边叫做棱柱的侧棱。
顶点:侧面与底面的公共顶点叫做棱柱的顶点。
棱柱的表示:用表示底面的各顶点的字母表示。
如:棱柱ABCDEF-A’B’C’D’E’F’3.棱锥的结构特征:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥. (图如下)底面:棱锥中的多边形面叫做棱锥的底面或底。
侧面:有公共顶点的各个三角形面叫做棱锥的侧面顶点:各个侧面的公共顶点叫做棱锥的顶点。
侧棱:相邻侧面的公共边叫做棱锥的侧棱。
棱锥可以表示为:棱锥S-ABCD底面是三角形,四边形,五边形----的棱锥分别叫三棱锥,四棱锥,五棱锥---4.圆柱的结构特征:以矩形的一边所在直线为旋转轴,其余边旋转形成的面所围成的旋转体叫做圆柱。
圆柱的轴:旋转轴叫做圆柱的轴。
圆柱的底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面。
圆柱的侧面:平行于轴的边旋转而成的曲面叫做圆柱的侧面。
圆柱侧面的母线:无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示.如:圆柱O’O注:棱柱与圆柱统称为柱体5.圆锥的结构特征:以直角三角形的一条直角边所在直线为旋转轴, 两余边旋转形成的面所围成的旋转体叫做圆锥。
轴:作为旋转轴的直角边叫做圆锥的轴。
底面:另外一条直角边旋转形成的圆面叫做圆锥的底面。
侧面:直角三角形斜边旋转形成的曲面叫做圆锥的侧面。
顶点:作为旋转轴的直角边与斜边的交点母线:无论旋转到什么位置,直角三角形的斜边叫做圆锥的母线。
高中数学必修二 空间几何体知识点

空间几何体(川诚.樊培整理)一·空间几何体结构1.空间结合体:如果我们只考虑物体占用空间部分的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形,就叫做空间几何体。
2.棱柱的结构特征:有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边互相平行,由这些面围成的图形叫做棱柱。
(图如下)底面:棱柱中,两个相互平行的面,叫做棱柱的底面,简称底。
底面是几边形就叫做几棱柱。
侧面:棱柱中除底面的各个面.侧棱:相邻侧面的公共边叫做棱柱的侧棱。
顶点:侧面与底面的公共顶点叫做棱柱的顶点。
棱柱的表示:用表示底面的各顶点的字母表示。
如:棱柱ABCDEF-A’B’C’D’E’F’3.棱锥的结构特征:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥. (图如下)底面:棱锥中的多边形面叫做棱锥的底面或底。
侧面:有公共顶点的各个三角形面叫做棱锥的侧面顶点:各个侧面的公共顶点叫做棱锥的顶点。
侧棱:相邻侧面的公共边叫做棱锥的侧棱。
棱锥可以表示为:棱锥S-ABCD底面是三角形,四边形,五边形----的棱锥分别叫三棱锥,四棱锥,五棱锥---4.圆柱的结构特征:以矩形的一边所在直线为旋转轴,其余边旋转形成的面所围成的旋转体叫做圆柱。
圆柱的轴:旋转轴叫做圆柱的轴。
圆柱的底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面。
圆柱的侧面:平行于轴的边旋转而成的曲面叫做圆柱的侧面。
圆柱侧面的母线:无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示.如:圆柱O’O注:棱柱与圆柱统称为柱体5.圆锥的结构特征:以直角三角形的一条直角边所在直线为旋转轴, 两余边旋转形成的面所围成的旋转体叫做圆锥。
轴:作为旋转轴的直角边叫做圆锥的轴。
底面:另外一条直角边旋转形成的圆面叫做圆锥的底面。
侧面:直角三角形斜边旋转形成的曲面叫做圆锥的侧面。
顶点:作为旋转轴的直角边与斜边的交点母线:无论旋转到什么位置,直角三角形的斜边叫做圆锥的母线。
(完整版)高一数学必修2_第一章空间几何体知识点

第一章空间几何体1.1 空间几何体的结构1. 多面体与旋转体:(1)由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面.相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.(2)由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转体,这条定直线叫做旋转体的轴.2. 棱柱:(1)有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.棱柱中,两个互相平行的面叫做棱柱的底面(简称底),其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.(2)侧棱垂直于底面的棱柱叫直棱柱,否则斜棱柱;底面是正多边形的直棱柱叫正棱柱。
(3)棱柱的分类:按底面的多边形的边数分,有三棱柱、四棱柱、五棱柱等.按侧棱与底面的关系分为直棱柱和斜棱柱。
(4)底面是平行四边形的四棱柱叫平行六面体;侧棱与底面垂直的平行六面体叫直平行六面体;底面为矩形的直平行六面体叫长方体;底面为正方形的长方体叫正四棱柱;棱长都相等的正四棱柱叫正方体。
(5)棱柱的性质:①两底面是对应边平行的全等多边形;②侧面、对角面都是平行四边形;③侧棱平行且相等;④平行于底面的截面是与底面全等的多边形。
3. 棱锥:(1)有一个面是多边形,其余各面都是有一公共点的三角形,由这些面所围成的几何体叫做棱锥.棱锥中,这个多边形面叫做棱锥的底面或底,有公共顶点的各个三角形面叫做棱锥的侧面,各侧面的公共顶点叫做棱锥的顶点,相邻侧面的公共边叫做棱锥的侧棱.(2)底面是正多边形,顶点在底面的射影是正多边形的中心的棱锥叫正棱柱。
正棱柱顶点与底面中心的连线段叫正棱锥的高;正棱锥侧面等腰三角形底边上的高叫正棱锥的斜高。
(3)棱锥的分类:按底面的多边形的边数分,有三棱锥、四棱锥、五棱锥等.(4)棱锥的性质:①侧面、对角面都是三角形;②平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.(5)正棱锥的性质:①正棱锥各侧棱都相等,各侧面都是全等的等腰三角形。
高中数学必修2--第一章《空间几何体》知识点总结与练习

高中数学必修2__第一章《空间几何体》知识点总结与练习第一节空间几何体的结构特征及三视图和直观图[知识能否忆起]一、多面体的结构特征多面体棱柱棱锥棱台结构特征有两个面互相平行,其余各面都是四边形,并且每相邻两个面的交线都平行且相等有一个面是多边形,而其余各面都是有一个公共顶点的三角形棱锥被平行于底面的平面所截,截面和底面之间的部分二、旋转体的形成几何体圆柱圆锥圆台球旋转图形矩形直角三角形直角梯形半圆旋转轴任一边所在的直线一条直角边所在的直线垂直于底边的腰所在的直线直径所在的直线三、简单组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成;一种是由简单几何体截去或挖去一部分而成,有多面体与多面体、多面体与旋转体、旋转体与旋转体的组合体.四、平行投影与直观图空间几何体的直观图常用斜二测画法来画,其规则是:(1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.(2)原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.五、三视图几何体的三视图包括正视图、侧视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.1.正棱柱与正棱锥(1)底面是正多边形的直棱柱,叫正棱柱,注意正棱柱中 “正”字包含两层含义:①侧棱垂直于底面;②底面是正多边形.(2)底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫正棱锥,注意正棱锥中“正”字包含两层含义:①顶点在底面上的射影必需是底面正多边形的中心,②底面是正多边形,特别地,各棱均相等的正三棱锥叫正四面体.2.对三视图的认识及三视图画法(1)空间几何体的三视图是该几何体在三个两两垂直的平面上的正投影,并不是从三个方向看到的该几何体的侧面表示的图形.(2)在画三视图时,重叠的线只画一条,能看见的轮廓线和棱用实线表示,挡住的线要画成虚线.(3)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体用平行投影画出的轮廓线.3.对斜二测画法的认识及直观图的画法(1)在斜二测画法中,要确定关键点及关键线段,“平行于 x 轴的线段平行性不变,长度不变;平行于 y 轴的线段平行性不变,长度减半.”(2)按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积有以下关系:S 直观图= 2 4S 原图形,S 原图形=2 2S 直观图.空间几何体的结构特征典题导入[例 1] (2012· 哈师大附中月考)下列结论正确的是()A .各个面都是三角形的几何体是三棱锥B .以三角形的一条边所在直线为旋转轴,其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C .棱锥的侧棱长与底面多边形的边长都相等,则该棱锥可能是六棱锥D .圆锥的顶点与底面圆周上的任意一点的连线都是母线[自主解答] A 错误,如图 1 是由两个相同的三棱锥叠放在一起构成的几何体,它的各个面都是三角形,但它不是三棱锥;B错误,如图△2,若ABC不是直角三角形,或△ABC是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥;图1图2C错误,若该棱锥是六棱锥,由题设知,它是正六棱锥.易证正六棱锥的侧棱长必大于底面边长,这与题设矛盾.[答案]D由题悟法解决此类题目要准确理解几何体的定义,把握几何体的结构特征,并会通过反例对概念进行辨析.举反例时可利用最熟悉的空间几何体如三棱柱、四棱柱、正方体、三棱锥、三棱台等,也可利用它们的组合体去判断.以题试法1.(2012·天津质检)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是()A.等腰四棱锥的腰与底面所成的角都相等B.等腰四棱锥的侧面与底面所成的二面角都相等或互补C.等腰四棱锥的底面四边形必存在外接圆D.等腰四棱锥的各顶点必在同一球面上解析:选B如图,等腰四棱锥的侧棱均相等,其侧棱在底面的射影也相等,则其腰与底面所成角相等,即A正确;底面四边形必有一个外接圆,即C正确;在高线上可以找到一个点O,使得该点到四棱锥各个顶点的距离相等,这个点即为外接球的球心,即D正确;但四棱锥的侧面与底面所成角不一定相等或互补(若为正四棱锥则成立).故仅命题B为假命题.几何体的三视图典题导入[例2](2012·湖南高考)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()[自主解答]根据几何体的三视图知识求解.由于该几何体的正视图和侧视图相同,且上部分是一个矩形,矩形中间无实线和虚线,因此俯视图不可能是C.[答案]C由题悟法三视图的长度特征三视图中,正视图和侧视图一样高,正视图和俯视图一样长,侧视图和俯视图一样宽,即“长对正,宽相等,高平齐”.[注意]画三视图时,要注意虚、实线的区别.以题试法2.(1)(2012·莆田模拟)如图是底面为正方形、一条侧棱垂直于底面的四棱锥的三视图,那么该四棱锥的直观图是下列各图中的()解析:选D由俯视图排除B、C;由正视图、侧视图可排除A.= ,所以 OC ′=sin 120° a = 6a ,(2)(2012· 济南模拟)如图,正三棱柱 ABC -A 1B 1C 1 的各棱长均为 2,其正视图如图所示,则此三棱柱侧视图的面积为()A .2 2C. 3B .4D .2 3解析:选 D 依题意,得此三棱柱的左视图是边长分别为 2, 3的矩形,故其面积是2 3.几何体的直观图典题导入[例 3] 已知△ABC 的直观图 A ′B ′C ′是边长为 a 的正三角形,求原△ABC 的面积.[自主解答]建立如图所示的坐标系 xOy ′, △A ′B ′C ′的顶点 C ′在 y ′轴上,A ′B ′边在 x 轴上,OC 为△ABC 的高.把 y ′轴绕原点逆时针旋转 45°得 y 轴,则点 C ′变为点 C ,且 OC =2OC ′,A ,B 点即为 A ′,B ′点,长度不变.已知 A ′B ′=A ′C ′=△a ,在 OA ′C ′中,由正弦定理得OC ′ A ′C ′sin ∠OA ′C ′ sin 45°sin 45° 2所以原三角形 ABC 的高 OC = 6a.2 2 2S = (1+ 2+1)×2=2+ 2.V = Sh = πr 2h = πr 2 l 2-r 2所以 △S ABC =1×a ×6a = 26a 2.由题悟法用斜二测画法画几何体的直观图时,要注意原图形与直观图中的“三变、三不变”.⎧⎪坐标轴的夹角改变,“三变”⎨与y 轴平行线段的长度改变,⎪⎩图形改变;⎧⎪平行性不变,“三不变”⎨与x 轴平行的线段长度不变,⎪⎩相对位置不变.以题试法3.如果一个水平放置的图形的斜二测直观图是一个底角为 45°,腰和上底均为 1 的等腰梯形,那么原平面图形的面积是()A .2+ 22+ 2 C. 1+ 2 B.D .1+ 2解析:选 A 恢复后的原图形为一直角梯形1 2第二节空间几何体的表面积和体积[知识能否忆起]柱、锥、台和球的侧面积和体积面积体积圆柱圆锥S 侧=2πrlS 侧=πrlV =Sh =πr 2h1 1 13 3 31 V = ShV = πR 3圆台S 侧=π(r 1+r 2)l1V =3(S 上+S 下+ S 上· S 下)h1=3π(r 2+r 2+r 1r 2)h直棱柱正棱锥 正棱台球S 侧=Ch1S 侧=2Ch ′1S 侧=2(C +C ′)h ′S 球面=4πR 2V =Sh1 31V =3(S 上+S 下+ S 上· S 下)h431.几何体的侧面积和全面积:几何体侧面积是指(各个)侧面面积之和,而全面积是侧面积与所有底面积之和.对侧面积公式的记忆,最好结合几何体的侧面展开图来进行.2.求体积时应注意的几点:(1)求一些不规则几何体的体积常用割补的方法转化成已知体积公式的几何体进行解决.(2)与三视图有关的体积问题注意几何体还原的准确性及数据的准确性.3.求组合体的表面积时注意几何体的衔接部分的处理.几何体的表面积典题导入[例 1] (2012· 安徽高考)某几何体的三视图如图所示,该几何体的表面积是________.[自主解答] 由几何体的三视图可知,该几何体是底面为直角梯形的直四棱柱 (如图所示).所以其表面积为2×1×(2+5)×4+2×4+4×5+4×5+4×4=92. 视图、侧视图都是面积为 3,且一个内角为 60°的菱形,俯视图为正方面边长和侧面上的高均等于菱形的边长,因此该饰物的表面积为 8×⎝2×1×1⎭=4.在四边形 ABCD 中,作 DE ⊥AB ,垂足为 E ,则 DE =4,AE =3,则 AD =5.2[答案] 92由题悟法1.以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.2.多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.3.旋转体的表面积问题注意其侧面展开图的应用.以题试法1.(2012· 河南模拟)如图是某宝石饰物的三视图,已知该饰物的正2形,那么该饰物的表面积为()A. 3B .2 3C .4 3D .4解析:选 D 依题意得,该饰物是由两个完全相同的正四棱锥对接而成,正四棱锥的底⎛1 ⎫几何体的体积典题导入[例 2](1)(2012·广东高考)某几何体的三视图如图所示,它的体积为()V =V 半球+V 圆锥= · π·33+ ·π·32·4=30π. [答案](1)C (2)=π×32×4-1π×32×4=24π.3A .72πB .48πC .30πD .24π(2)(2012· 山东高考)如图,正方体 ABCD -A 1B 1C 1D 1 的棱长为 1,E为线段 B 1C 上的一点,则三棱锥 A -DED 1 的体积为________.[自主解答] (1)由三视图知,该几何体是由圆锥和半球组合而成的,直观图如图所示,圆锥的底面半径为 3,高为 4,半球的半径为 3.14 1 23 31 1 1 1(2)V A -DED 1=VE -ADD 1=3×△S ADD 1×CD =3×2×1=6.16本例(1)中几何体的三视图若变为:其体积为________.解析:由三视图还原几何体知,该几何体为圆柱与圆锥的组合体,其体积V =V 圆柱-V圆锥答案:24π由题悟法1.计算柱、锥、台体的体积,关键是根据条件找出相应的底面面积和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解.2.注意求体积的一些特殊方法:分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算常用的方法,应熟练掌握.3.等积变换法:利用三棱锥的任一个面可作为三棱锥的底面.①求体积时,可选择容易计算的方式来计算;②利用“等积法”可求“点到面的距离”.3 32 2 32 1 = .33和 2 个直角边分别为 3,1 的直角三角形,其底面积 S =9+2× ×3×1=12,以题试法2.(1)(2012·长春调研)四棱锥 P -ABCD 的底面 ABCD 为正方形,且 PD 垂直于底面ABCD ,N 为 PB 中点,则三棱锥 P -ANC 与四棱锥 P -ABCD 的体积比为()A .1∶2C .1∶4B .1∶3D .1∶8解析:选 C 设正方形 ABCD 面积为 S ,PD =h ,则体积比为1 11 1 11Sh - · S · h - · Sh1 4Sh(2012· 浙江模拟)如图,是某几何体的三视图,则这个几何体的体积是()A .32C .8B .2432 D.解析:选 B 此几何体是高为 2 的棱柱,底面四边形可切割成为一个边长为 3 的正方形12所以几何体体积 V =12×2=24.与球有关的几何体的表面积与体积问题典题导入[例 3] (2012·新课标全国卷)已知三棱锥 S -ABC 的所有顶点都在球 O 的球面上,△ABC是边长为 1 的正三角形,SC 为球 O 的直径,且 SC =2,则此棱锥的体积为()A.C. 2 62 3B.D. 3 62 2×AB 2=4 41 3 6=2 =2V O -ABC =2× ×34 3 6 × . b c A .2 3π8πB.[自主解答 ] 由于三棱锥 S -ABC 与三棱锥 O -ABC 底面都是△ABC ,O 是 SC 的中点,因此三棱锥 S -ABC 的高是三棱锥 O -ABC 高的 2 倍,所以三棱锥 S -ABC 的体积也是三棱锥 O -ABC 体积的 2 倍.在三棱锥 O -ABC 中,其棱长都是 1,如图所示,△S ABC = 3 3,高 OD =12-⎛ 3⎫2= 6,⎝ 3 ⎭ 3∴V S -ABC[答案] A由题悟法1.解决与球有关的“切”、“接”问题,一般要过球心及多面体中的特殊点或过线作截面,把空间问题转化为平面问题,从而寻找几何体各元素之间的关系.2.记住几个常用的结论:(1)正方体的棱长为 a ,球的半径为 R ,①正方体的外接球,则 2R = 3a ;②正方体的内切球,则 2R =a ;③球与正方体的各棱相切,则 2R = 2a.(2)长方体的同一顶点的三条棱长分别为 a ,,,外接球的半径为 R ,则 2R = a 2+b 2+c 2. (3)正四面体的外接球与内切球的半径之比为 1∶3.以题试法3.(1)(2012·琼州模拟)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为()3C .4 316πD. B 2=16π.2 故球 O 的体积 V = = 6π.3(2)(2012· 潍坊模拟)如图所示,已知球 O 的面上有四点 A 、 、C 、D ,DA ⊥平面 ABC ,AB ⊥BC ,DA =AB =BC = 2,则球 O 的体积等于________.解析:(1)由三视图可知几何体的直观图如图所示.其中侧面 DBC ⊥底面 ABC ,取 BC 的中点 O 1,连接 AO 1,DO 1 知 DO 1⊥底面 ABC 且 DO 1= 3,AO 1=1,BO 1=O 1C =1.在 △Rt ABO 1 和 Rt △ACO 1 中,AB =AC = 2,又∵BC =2,∴∠BAC =90°.∴BC 为底面 ABC 外接圆的直径,O 1 为圆心, 又∵DO 1⊥底面 ABC ,∴球心在 DO 1 上,即△BCD 的外接圆为球大圆,设球半径为 R ,则( 3-R)2+12=R 2,∴R = 2 3.⎛ 2 ⎫∴S 球=4πR 2=4π×⎝ 3⎭3(2)如图,以 DA ,AB ,BC 为棱长构造正方体,设正方体的外接球 球 O 的半径为 R ,则正方体的体对角线长即为球 O 的直径,所以|CD|= ( 2)2+( 2)2+( 2)2=2R ,所以 R =6 .4πR 33答案:(1)D (2) 6π某些空间几何体是某一个几何体的一部分,在解题时,把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积问题,这是一种重要的解题策略——补形法.常见的补形法有对称补形、联系补形与还原补形.对于还原补形,主要涉及台体中“还台为锥”问题.33=3×π×12×4=3π.1.对称补形[典例 1] (2012· 湖北高考)已知某几何体的三视图如图所示,则该几何体的体积为( )8π A.10π C.B .3πD .6π[解析]由三视图可知,此几何体是底面半径为 1,高为 4 的圆柱被从母线的中点处截去了圆柱的1,根据对称性,可补全此圆柱如图,故体积 V44[答案] B[题后悟道] “对称”是数学中的一种重要关系,在解决空间几何体中的问题时善于发现对称关系对空间想象能力的提高很有帮助.2.联系补形(2012· 辽宁高考)已知点 P ,A ,B ,C ,D 是球 O 表面上的点,PA ⊥平面 ABCD ,四边形ABCD 是边长为 2 3的正方形.若 P A =2 △6,则 OAB 的面积为________.[解析] 由 P A ⊥底面 ABCD ,且 ABCD 为正方形,故可补形为长方体如图,知球心 O 为 PC 的中点,又 PA =2 6,AB =BC =2 3,∴AC =2 6,∴PC =4 3,∴OA =OB =2 △3,即 AOB 为正三角形,∴S =3 3.[答案] 3 3[题后悟道] 三条侧棱两两互相垂直,或一侧棱垂直于底面,底面为正方形或长方形,则此几何体可补形为正方体或长方体,使所解决的问题更直观易求.练习题1.(教材习题改编)以下关于几何体的三视图的论述中,正确的是()A.球的三视图总是三个全等的圆B.正方体的三视图总是三个全等的正方形C.水平放置的正四面体的三视图都是正三角形D.水平放置的圆台的俯视图是一个圆解析:选A B中正方体的放置方向不明,不正确.C中三视图不全是正三角形.D中俯视图是两个同心圆.2.(2012·杭州模拟)用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是()A.圆柱C.球体B.圆锥D.圆柱、圆锥、球体的组合体解析:选C当用过高线的平面截圆柱和圆锥时,截面分别为矩形和三角形,只有球满足任意截面都是圆面.3.下列三种叙述,其中正确的有()①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.A.0个C.2个B.1个D.3个解析:选A①中的平面不一定平行于底面,故①错.②③可用下图反例检验,故②③不正确.4.(教材习题改编)利用斜二测画法得到的:①正方形的直观图一定是菱形;②菱形的直观图一定是菱形;③三角形的直观图一定是三角形.以上结论正确的是________.解析:①中其直观图是一般的平行四边形,②菱形的直观图不一定是菱形,③正确.答案:③5.一个长方体去掉一个小长方体,所得几何体的正视图与侧视图分别如图所示,则该几何体的俯视图为________.解析:由三视图中的正、侧视图得到几何体的直观图如图所示,所以该几何体的俯视图为③.答案:③1.(2012·青岛摸底)如图,在下列四个几何体中,其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是()A.②③④C.①③④B.①②③D.①②④解析:选A①的三个视图都是边长为1的正方形;②的俯视图是圆,正视图、侧视图都是边长为1的正方形;③的俯视图是一个圆及其圆心,正视图、侧视图是相同的等腰三角形;④的俯视图是边长为1的正方形,正视图、侧视图是相同的矩形.2.有下列四个命题:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.(其中真命题的个数是() A .1C .3B .2D .4解析:选 A 命题①不是真命题,因为底面是矩形,但侧棱不垂直于底面的平行六面体不是长方体;命题②不是真命题,因为底面是菱形 非正方形),底面边长与侧棱长相等的直 四棱柱不是正方体;命题③也不是真命题,因为有两条侧棱都垂直于底面一边不能推出侧棱与底面垂直;命题④是真命题,由对角线相等,可知平行六面体的对角面是矩形,从而推得侧棱与底面垂直,故平行六面体是直平行六面体.3.一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是()解析:选 C C 选项不符合三视图中“宽相等”的要求,故选 C.4.如图是一几何体的直观图、正视图和俯视图.在正视图右侧,按照画三视图的要求画出的该几何体的侧视图是()解析:选 B 由直观图和正视图、俯视图可知,该几何体的侧视图应为面 P AD ,且 EC投影在面 P AD 上,故 B 正确.△5.如图 A ′B ′C ′是△ABC 的直观图,那么△ABC 是()A .等腰三角形B .直角三角形解析:选 D 依题意得,该几何体的侧视图的面积等于 22+ ×2× 3=4+ 3.为 ,则这个几何体的俯视图可能是下列图形中的________.(填入所有可能的图形前的编号)角形;如图 2 所示,直三棱柱ABC -AB C 符合题设要求,此时俯视图△ABC 是直角三角形;-A B C D 符合题设要求,此时俯视图(四边形 ABCD)是正方形;若俯视图是扇形或圆,体C .等腰直角三角形D .钝角三角形解析:选 B 由斜二测画法知 B 正确.6.(2012· 东北三校一模)一个几何体的三视图如图所示,则侧视图的面积为( )A .2+ 3C .2+2 3B .1+ 3D .4+ 3127.(2012· 昆明一中二模)一个几何体的正视图和侧视图都是边长为 1 的正方形,且体积12①锐角三角形;②直角三角形;③四边形;④扇形;⑤圆.解析:如图 1 所示,直三棱柱 ABE -A 1B 1E 1 符合题设要求,此时俯视图△ABE 是锐角三1 1 1如图 3 所示,当直四棱柱的八个顶点分别是正方体上、下各边的中点时,所得直四棱柱 ABCD1 1 1 1积中会含有 π,故排除④⑤.答案:①②③8.(2013· 安徽名校模拟)一个几何体的三视图如图所示,则该几何体的体积为________.何体的体积为1×2×2sin 60°×2-1×1×2×2sin 60°×1=5 3.3解析:结合三视图可知,该几何体为底面边长为 2、高为 2 的正三棱柱除去上面的一个高为 1 的三棱锥后剩下的部分,其直观图如图所示,故该几2 3 2 35 3答案:9.正四棱锥的底面边长为 2,侧棱长均为 3,其正视图(主视图)和侧视图(左视图)是全 等的等腰三角形,则正视图的周长为________.解析:由题意知,正视图就是如图所示的截面PEF ,其中 E 、F分别是 AD 、BC 的中点,连接 AO ,易得 AO = 2,而 P A = 3,于是解得 PO =1,所以 PE = 2,故其正视图的周长为 2+2 2.答案:2+2 210.已知:图 1 是截去一个角的长方体,试按图示的方向画出其三视图;图2 是某几何体的三视图,试说明该几何体的构成.解:图 1 几何体的三视图为:图 2 所示的几何体是上面为正六棱柱,下面为倒立的正六棱锥的组合体.11.(2012· 银川调研)正四棱锥的高为 3,侧棱长为 7,求棱锥的斜高(棱锥侧面三角形在△Rt SOE 中,∵OE =1BC = 2,SO = 3,42-⎝ × ×2 3⎭2 2的高).解:如图所示,正四棱锥 S -ABCD 中,高 OS = 3,侧棱 SA =SB =SC =SD = 7,在 △Rt SOA 中,OA = SA 2-OS 2=2,∴AC =4.∴AB =BC =CD =DA =2 2.作 OE ⊥AB 于 E ,则 E 为 AB 中点.连接 SE ,则 SE 即为斜高,2∴SE = 5,即棱锥的斜高为 5.12.(2012· 四平模拟)已知正三棱锥 V -ABC 的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图; (2)求出侧视图的面积.解:(1)三棱锥的直观图如图所示.(2)根据三视图间的关系可得 BC =2 3, ∴侧视图中V A =⎛2 3 3 2⎫= 12=2 3,∴△S VBC =1×2 3×2 3=6. 1.(教材习题改编)侧面都是直角三角形的正三棱锥,底面边长为 a 时,该三棱锥的全 面积是()A. a 242 4 a 2+3× ×⎝ 2 a ⎭2= a 2.(3 2)2-⎝2×6⎭2=3,因此底面中心到各顶点的距离均等于 3,所以该四棱锥的外接球的棱锥的高是 5,可由锥体的体积公式得 V = ×8×6×5=80.3+ 3 3 B. a 2 43+ 36+ 3 C.a 2D.a 2解析:选 A ∵侧面都是直角三角形,故侧棱长等于31 ⎛2 ⎫ 3+ 3∴S 全=42422a ,2.已知正四棱锥的侧棱与底面的边长都为 3 2,则这个四棱锥的外接球的表面积为()A .12πC .72π B .36πD .108π解析: 选 B 依题意得,该正四棱锥的底面对角线长为 3 2 × 2 = 6 ,高为⎛1⎫球心为底面正方形的中心,其外接球的半径为 3,所以其外接球的表面积等于 4π×32=36π.3.某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为 5 的等腰三角形,侧视图是一个底边长为 6,高为 5 的等腰三角形,则该几何体的体积为()A .24C .64 B .80D .240解析:选 B 结合题意知该几何体是四棱锥,棱锥底面是长和宽分别为 8 和 6 的矩形,1 34.(教材习题改编)表面积为 3π 的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.解析:设圆锥的母线为 l ,圆锥底面半径为 r ,则 πrl +πr 2=3π,πl =2πr.解得 r =1,即直径为 2.答案:25.某几何体的三视图如图所示,其中正视图是腰长为 2 的等20/2733××2×2×2=.形42-⎝232+22⎭2=,所以棱锥O-A BCD的体积等于×(3×2)×51=51.________.解析:由三视图可知此几何体的表面积分为两部分:底面积即俯视图的面积,为23;侧面积为一个完整的圆锥的侧面积,且圆锥的母线长为2,底面半径为1,所以侧面积为2π.两部分加起来即为几何体的表面积,为2(π+3).答案:2(π+3)1.(2012·北京西城模拟)某几何体的三视图如图所示,该几何体的体积是()A.8 C.48 B.4 D.解析:选D将三视图还原,直观图如图所示,可以看出,这是一个底11面为正方形(对角线长为2),高为2的四棱锥,其体积V=3S正方ABCD×P A=314232.(2012·山西模拟)已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=3,BC=2,则棱锥O-ABCD的体积为()A.51 C.251B.351 D.651解析:选A依题意得,球心O在底面ABCD上的射影是矩形ABCD的中心,因此棱锥O-A BCD的高等于⎛1⎫5112323.(2012·马鞍山二模)如图是一个几何体的三视图,则它的表面积为()4 4 解析:选 D 由三视图可知该几何体是半径为 1 的球被挖出了 部分得到的几何体,故·4π·12+3· ·π·12= π.22只需求出底面积即可.由俯视图和主视图可知,底面面积为1×2+2× ×2×1=4,所以该A .4πC .5π15 B. π17 D. π18表面积为7 1 178 44 4.(2012· 济南模拟)用若干个大小相同,棱长为 1 的正方体摆成一个立体模型,其三视图如图所示,则此立体模型的表面积为()A .24C .22B .23D .21解析:选 C 这个空间几何体是由两部分组成的,下半部分为四个小正方体,上半部分为一个小正方体,结合直观图可知,该立体模型的表面积为 22.5. (2012· 江西高考)若一个几何体的三视图如下图所示,则此几何体的体积为()11 A.9 C.B .5D .4解析:选 D 由三视图可知,所求几何体是一个底面为六边形,高为1 的直棱柱,因此12几何体的体积为 4×1=4.6.如图,正方体 ABCD -A ′B ′C ′D ′的棱长为 4,动点 E ,F 在棱 AB 上,且 EF =2,动点 Q 在棱 D ′C ′上,则三棱锥 A ′-EFQ 的体积()解析:选 D 因为 V A ′-EFQ =V Q -A ′EF = ×⎝2×2×4⎭×4= ,故三棱锥 A ′-EFQ 的高为 3,连接顶点和底面中心即为高,可求得高为 2,所以体积 V =1×1×1× 2= 2.3答案: 3π⎧⎪a +b =6 ,A .与点 E ,F 位置有关B .与点 Q 位置有关C .与点 E ,F ,Q 位置都有关D .与点E ,F ,Q 位置均无关,是定值1 ⎛1 ⎫ 163 3体积与点 E ,F ,Q 的位置均无关,是定值.7.(2012· 湖州模拟)如图所示,已知一个多面体的平面展开图由一个边长为 1 的正方形和 4 个边长为 1 的正三角形组成,则该多面体的体积是________.解析:由题知该多面体为正四棱锥,底面边长为 1,侧棱长为 1,斜2 23 2 6答案:2 68.(2012· 上海高考)若一个圆锥的侧面展开图是面积为 2π 的半圆面,则该圆锥的体积为________.解析:因为半圆的面积为 2π,所以半圆的半径为 2,圆锥的母线长为 2.底面圆的周长为2π,所以底面圆的半径为 1,所以圆锥的高为 3,体积为 3π.39.(2013· 郑州模拟)在三棱锥 A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的表面积为________.解析:依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,2 2 2 设该长方体的长、宽、高分别为 a 、b 、c ,且其外接球的半径为 R ,则⎨b 2+c 2=52,⎪⎩c 2+a 2=52,得 a 2+b 2+c 2=43,即(2R)2=a 2+b 2+c 2=43,易知 R 即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为 4πR 2=43π.答案:43π10.(2012· 江西八校模拟)如图,把边长为 2 的正六边形 ABCDEF 沿对角线 BE 折起,使 AC = 6.。
高一数学必修二第一章空间几何体知识点梳理知识点总结

高一数学必修二第一章空间几何体知识点梳理知识点总结在中国古代把数学叫算术,又称算学,最后才改为数学。
小编准备了高一数学必修二第一章空间几何体知识点,具体请看以下内容。
空间几何体知识点汇总。
知识点一:空间几何体概念。
知识点二:多面体概念,多面体的面、棱和顶点。
知识点三:旋转体概念,轴。
知识点四:棱柱、棱锥、棱台结构特征。
知识点五:圆柱、圆锥、圆台结构特征。
知识点六:球结构特征。
知识点七:简单组合体的结构特征。
空间几何体的三视图和直观图知识点汇总。
知识点一:中心投影与平行投影。
知识点二:空间几何体的三视图,正视图、侧视图和俯视图。
知识点三:空间几何体的直观图,斜二测画法。
空间几何体的表面积与体积知识点汇总。
知识点一:柱体、台体、锥体的表面积。
知识点二:柱体、台体、锥体的体积。
知识点三:球体的表面积和体积。
高中是人生中的关键阶段,大家一定要好好把握高中,编辑老师为大家整理的高一数学必修二第一章空间几何体知识点,希望大家喜欢。
人教版高中数学必修二《空间几何体》基础知识要点总结

③侧面展开图为矩形。
④侧棱长等于此正棱柱的高。
(5)特殊的四棱柱
底面是四边形的棱柱叫做四棱柱。
底面的平行四边形的四棱柱叫做平行六面体。
侧棱垂直于底面的平行六面体叫做直平行六面体。
底面的矩形的直平行六面体叫做长方体。
底面是正方形的长方体叫做正四棱柱。侧棱长等于底面边长的源自四棱柱叫做正方体。2、棱锥
(1)结构特征
一般地,①有一个面是多边形,其余各面都是②有一个公共顶点的③三角形,由这些面围成的多面体叫做棱锥.
①这个多边形的面叫做棱锥的底面或底;②有公共顶点的各个三角形面叫做棱锥的侧面;③各侧面的公共顶点叫做棱锥的顶点;④相邻侧面的公共边叫做棱锥的侧棱。
(2)棱锥的性质
如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它们面积的比等于截得的棱锥的高与已知棱锥的高的平方比。
③正棱锥的高,侧棱和侧棱在底面上的射影组成一个直角三角形
(5)正四面体
正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等。
正四面体属于正三棱锥,但是正三棱锥只需要底面为正三角形,其他三个面全等且都是等腰三角形就可以,不需要四个面全等且都是等边三角形。
3、棱台
(1)结构特征
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
8、简单组合体
第一章 《空间几何体》基础知识小结
一、空间几何体的结构
空间几何体
如果我们只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体
多面体
一般地,我们把由若干个平面多边形转成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
高中数学必修2知识点总结第一章空间几何体

第一章 空间几何体
1.1柱、锥、台、球的结构特征
1.柱锥台球的机构特征
2.理解正三棱椎,正四面体、直棱柱的结构特征
1.2空间几何体的三视图和直观图
1 三视图:正视图:从前往后侧视图:从左往右俯视图:从上往下
2 画三视图的原则:长对齐、高对齐、宽相等
3直观图:斜二测画法
4斜二测画法的步骤:
(1).平行于坐标轴的线依然平行于坐标轴;
(2).平行于y 轴的线长度变半,平行于x ,z 轴的线长度不变;2=4S S 直平 5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图
1.3 空间几何体的表面积与体积
(一 )空间几何体的表面积
1棱柱、棱锥的表面积: 各个面面积之和
2 圆柱的表面积
3 圆锥的表面积2r rl S ππ+=
4 圆台的表面积22R Rl r rl S ππππ+++=
5 球的表面积24R S π=
(二)空间几何体的体积
1柱体的体积 h S V ⨯=底 2锥体的体积 h S V ⨯=底31 3台体的体积 h S S S S V ⨯++=)31下下上上( 4球体的体积 334R V π= 例1已知一个几何体的三视图(单位:cm )如右图所示,则该几何体的侧面积为_____cm 2
2.一组合体三视图如右,正视图中正方形边长为2,俯视图为正三角形及内切圆,则该组合体体积为( )
A. 23
B. 43π
C. 23+43
π D. 54343π+ 4.已知某个几何体的三视图如下,根据图中标
出的尺寸(单位:cm ),可得这个几何体的体积是
2
22r rl S ππ+=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体,它们都占据着空间的一部分。
如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。
2、多面体和旋转体多面体:由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转几何体。
这条定直线叫做旋转体的轴。
多面体旋转体圆台圆柱-圆锥圆柱+圆锥圆台+大圆锥-小圆锥二、柱、锥、台、球的结构特征1.棱柱定义图形表示分类性质有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDEF-A1B1C1D1E1F1。
棱柱的分类一(底面):棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱柱的分类二(根据侧棱与底面的关系):斜棱柱: 侧棱不垂直于底面的棱柱.直棱柱: 侧棱垂直于底面的棱柱叫(1)上下底面平行,且是全等的多边形。
(2)侧棱相等且相互平行。
(3) 侧面是平行四边形。
正棱柱: 底面是正多边形的直棱柱叫做正棱柱三棱柱四棱柱五棱柱斜棱柱直棱柱正棱柱2.棱锥定义图形表示性质分类有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
用顶点及底面各顶点字母表示棱锥,如:棱锥S-ABC侧面是三角形,底面是多边形。
按底面多边形的边数分类可分为三棱锥、四棱锥、五棱锥等等,其中三棱锥又叫四面体。
特殊的棱锥-正棱锥定义:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心三棱锥四棱锥五棱锥直棱锥2.棱台定义图形表示分类性质用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。
棱台用表示上、下底面各顶点的字母来表示,如下图,棱台ABCD-A1B1C1D1由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…特殊的棱锥-由正棱锥截得的棱台叫正棱台上下底面平行,其余各面是梯形,且侧棱延长后交于一点。
三棱台四棱台正棱台3.棱柱定义图形表示性质定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
用表示它的轴的字母表示,如圆柱OO1。
4.圆锥定义图形表示性质以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
用表示它的轴的字母表示,如圆锥SO。
6.圆台定义图形表示性质用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台。
用表示它的轴的字母表示,如圆台OO′1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。
(1)半圆的半径叫做球的半径。
(2)半圆的圆心叫做球心。
(3)半圆的直径叫做球的直径。
2、球的表示:用表示球心的字母表示,如球O3、球的性质(1)用一个平面去截球,截面是圆面;用一个平面去截球面,截线是圆。
大圆---截面过圆心,半径等于球半径;小圆---截面不过圆心。
(2)球心和截面的圆心的连线垂直于截面。
(3)球心到截面的距离d与球的半径R及截面的半径r,有下面的关系:22 r R d =-解题方法:将立体中相关问题转化为平面几何问题棱锥内由某些线段组成的直角三角形,在计算有关问题时很重要,它是将立体中相关问题转化为平面几何问题的根据,如图2-7中的△AOE,△AOC,△ACE及△OCE.这四个直角三角形中,若知道AE、AC、AO、OE、OC 及CE这六条线段中的若干条时,则可以通过这些直角三角形间的关系求出其他线段.总结三、空间几何体的三视图和直观图1、中心投影与平行投影2、三视图正视图——从正面看到的图侧视图——从左面看到的图俯视图——从上面看到的图画物体的三视图时,要符合如下原则:位置:正视图侧视图俯视图大小:长对正,高平齐,宽相等.3、直观图-----斜二测画法重点:用斜二测画法画水平放置的平面图形的直观图,步骤如下:⑴在已知图形中取互相垂直的x轴和y轴,两轴相交于点O. 画直观图时,把它们画对应的x'轴与y'轴,两轴交于点O' ,且使∠x'O'y' =45º(或135º),它们确定的平面表示水平面.⑵已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴或y'轴的线段;⑶已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的一半.例1 用斜二测画法画水平放置的正六边形的直观图.说明:1. 保持平行关系不变.2.水平长度保持不变;纵向长度取其一半.例3 用斜二测画法画长、宽、高分别是4cm、3cm、2cm的长方体ABCD-A'B'C'D'的直观图.四、 空间几何体的表面积与体积(一 )空间几何体的表面积1棱柱、棱锥的表面积: 各个面面积之和2 圆柱的表面积3 圆锥的表面积2S rl r ππ=+4 圆台的表面积22S rl r Rl R ππππ=+++5 球的表面积24SR π=6扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径)(二)空间几何体的体积 1柱体的体积 VS h =⨯底2锥体的体积 13V S h =⨯底 3台体的体积1)3V S S h =++⨯下上(222rrl S ππ+=4球体的体积343V R π=第二讲 点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示2、平面的基本性质 ①公理1:A lB l l A B ααα∈⎫⎪∈⎪⇒⊂⎬∈⎪⎪∈⎭②公理2:不共线的三点确定一个平面③公理3:二、点与面、直线位置关系1、点与平面有2种位置关系2、点与直线有2种位置关系三、空间中直线与直线之间的位置关系1、异面直线P l P l P ααββ∈⎫⇒⋂=∈⎬∈⎭则12A B αα∈⎧⎨∉⎩、、12A lB l∈⎧⎨∉⎩、、2、直线与直线的位置关系⎧⎧⎨⎪⎨⎩⎪⎩相交共面平行异面3、公理4和定理 公理4:定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤: ①作:作平行线得到相交直线;②证:证明作出的角即为所求的异面直线所成的角; ③构造三角形求出该角。
提示:1、作平行线常见方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是 。
131223l l l l l l ⎫⇒⎬⎭P P P (000,90⎤⎦四、空间中直线与平面之间的位置关系位置关系公共点 有无数个公共点有且只有一个公共点没有公共点符号表示图形表示五、空间中平面与平面之间的位置关系位置关系 两个平面平行 两个平面相交 公共点 没有公共点有一条公共直线符号表示αβPa αβ=I图形表示直线、平面平行的判定及其性质一、线面平行1、判定:a α直线与平面平行a α直线与平面相交a 直线在平面内a α⊂a αP a Aα=I b a b b a ααα⊄⎫⎪⊂⇒⎬⎪⎭P P.(线线平行,则线面平行)2、性质:(线面平行,则线线平行)二、面面平行1、判定:(线面平行,则面面平行)2、性质1:(面面平行,则线面平行) 性质2:a a ab b αβαβ⎫⎪⊂⇒⎬⎪⋂=⎭P P a b a b P a b βββααα⊂⎫⎪⊂⎪⎪⋂=⇒⎬⎪⎪⎪⎭P P P a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭P I P I.m m αββα⎫⇒⎬⊂⎭P P (面面平行,则线面平行)说明(1)判定直线与平面平行的方法:①利用定义:证明直线与平面无公共点。
②利用判定定理:从直线与直线平行等到直线与平面平行。
③利用面面平行的性质:两个平面平行,则其中一个平面内的直线必平行于另一个平面。
(2)证明面面平行的常用方法①利用面面平行的定义:此法一般与反证法结合。
②利用判定定理。
③证明两个平面垂直于同一个平面。
④证明两个平面同时平行于第三个平面。
三、线线平行、面面平行、面面平行间的关系直线与平面垂直的判定及其性质一、直线与平面所成的角00--0,180l αβ⎡⎤∈⎣⎦二、二面角三、线面垂直1、判定:2、性质1:000,90α⎡⎤∈⎣⎦,PO AO PA l αααα⊥∴∴∠Q 证明过程为在平面上的投影,为直线与平面所成的角。
,,--BO l AO l BOA l αβ⊥⊥∴∠Q 证明过程是二面角的平面角。
a b a b A l l a l b ααα⊂⎫⎪⊂⎪⎪⋂=⇒⊥⎬⎪⊥⎪⊥⎪⎭3、性质2:四、面面垂直1、判定:文字表达:一个平面过另一个平面的垂线,则这两个平面垂直。
2、性质:说明:(1)判定直线与平面垂直的方法:①利用定义(可用反证法)。
②利用判定定理。
③利用性质定理。
④结合平行关系: (2)判定平面与平面垂直的方法: l l αβαβ⊥⎫⇒⊥⎬⊥⎭AB AB AB CD αβαββα⊥⎫⎪⋂⎪⇒⊥⎬⊂⎪⎪⊥⎭,a b a b αα⊥⇒⊥P a a b b αα⊥⎫⇒⊥⎬⊂⎭①利用定义判断(证)二面角的平面角是直角。
②利用平面与平面垂直的判定定理。
