大学物理A-CH5-3、狭义相对论的时空观
大学物理2相对论基础_01_狭义相对论的时空观6.2 4.2爱因斯坦相对性原理

2
22
t t 1 u2 / c2
—— 时间变长了!运动的时钟走慢了!
第一讲 狭义相对论的时空观_20150909 XCH
20 / 38
惯性系S’ —— 同地不同时
x 0
t
2d c
相对论基础-大学物理
第一讲 狭义相对论的时空观_20150909 XCH
惯性系S —— 不同地不同时
0 2.6 108 s —— 本征时间
实验室
0
4.33108 s
1 u2 / c2
2) 在实验室中通过的平均距离 l u 10.4m
第一讲 狭义相对论的时空观_20150909 XCH
相对论基础-大学物理
05 同时性的相对性 —— 长度收缩(动尺变短)
—— 惯性参考系S’以速度相对于惯性参考系S运动 —— S’中的棒AB静止(固定在S’的x轴上)
t1)
l
v2 c2
干涉仪转动900,移过的条纹数
N
2
2l
v2 c2
0.04
???
第一讲 狭义相对论的时空观_20150909 XCH
狭义相对论的基本原理
相对论基础-大学物理
1905年爱因斯坦 —— 提出两个基本假设
假设 I 物理学定律在所有惯性参考系都是等价的 —— 爱因斯坦相对性原理
—— 两种方法测得AB的长度一样
第一讲 狭义相对论的时空观_20150909 XCH
S系中 —— AB长度的测量
相对论基础-大学物理
1) 同时测量AB两点的坐标
t
t2
t1
0
xA and xB
3狭义相对论的时空观

不同时亮。
dengyonghe1@
二.时间延缓
1.任何惯性系同一地点先后发生的两个事件之间的时间间隔为 1.任何惯性系同一地点先后发生的两个事件之间的时间间隔为 任何惯性系同一地点先后发生的两个事件之间 固有时。固有时最短。 固有时。固有时最短。 2.从惯性系中观察相对于自身运动的另一惯性系中同一地点先 2.从惯性系中观察相对于自身运动的另一惯性系中同一地点先 后发生的两事件的时间间隔拉长,即时间延缓。 后发生的两事件的时间间隔拉长,即时间延缓。时间延缓是 一种相对效应。 一种相对效应。 3.当u<<c时, ∆t≈∆t′ ,时间测量与惯性系无关,即牛顿的 . ′ 时间测量与惯性系无关, 绝对时空观。 绝对时空观。
dengyonghe1@
在S' 系中,t 1 时刻,B ' 经x1 t 1 + ∆t时刻,A ' 经x1
如图示: 如图示:
r −u
y,
y,
A'
y'
B'
在 S ' 系 , 棒是静止的 ,S 系向右运动 , x 1 相继经过 B' 与 A' 端 , 此时棒长为 L' , 故 x 1 相继经过 B' 与 A' 端两事件 的时间为 : ∆t = L' u
dengyonghe1@
例2(P123,例3.2) 宇宙射线与大气相互作用时能产生π介 ( , ) 宇宙射线与大气相互作用时能产生π
子衰变, 大气层放出µ介子, 子衰变,此衰变在 大气层放出µ介子,µ介子的速度为 u=0.998c。静止时µ介子的平均寿命为2.2×10-6s,试问 静止时µ 高空由衰变放出的µ介子,能否飞到地面。 在8000m高空由衰变放出的µ介子,能否飞到地面。
狭义相对论的三个时空观

狭义相对论的三个时空观
狭义相对论是爱因斯坦于1905年提出的一种物理学理论,它涉及到了时间和空间的观念。
狭义相对论的三个时空观如下:
1. 相对性原理:狭义相对论的第一个时空观是相对性原理,它认为物理定律在所有惯性参考系中都是相同的。
换句话说,物理定律在不同的观察者之间是不变的,无论他们的运动状态如何。
这意味着没有一个特定的参考系是绝对的,而是都是相对的。
2. 光速不变原理:狭义相对论的第二个时空观是光速不变原理,它指出光速在真空中是恒定不变的,无论观察者自身的运动状态如何。
这意味着光在不同的参考系中传播的速度始终是相同的。
这个原理对于理解狭义相对论中的时间和空间的变化至关重要。
3. 时空的相对性:狭义相对论的第三个时空观是时空的相对性。
根据狭义相对论,时间和空间是相互关联的,构成了一个四维时空的连续体。
观察者的运动状态会导致时间和空间的相对变化,即时间的流逝速度和空间的长度会随着观察者的运动状态而发生变化。
这个时空观对于理解相对论中的时间膨胀和长度收缩等效应至关重要。
狭义相对论的四维时空观

狭义相对论的四维时空观狭义相对论是建立在四维时空观上的一个理论,因此要弄清相对论的内容,要先对相对论的时空观有个大体了解。
在数学上有各种多维空间,但目前为止,我们认识的物理世界只是四维,即三维空间加一维时间。
现代微观物理学提到的高维空间是另一层意思,只有数学意义,在此不做讨论。
四维时空是构成真实世界的最低维度,我们的世界恰好是四维,至于高维真实空间,至少现在我们还无法感知。
我在一个帖子上说过一个例子,一把尺子在三维空间里(不含时间)转动,其长度不变,但旋转它时,它的各坐标值均发生了变化,且坐标之间是有联系的。
四维时空的意义就是时间是第四维坐标,它与空间坐标是有联系的,也就是说时空是统一的,不可分割的整体,它们是一种”此消彼长”的关系。
四维时空不仅限于此,由质能关系知,质量和能量实际是一回事,质量(或能量)并不是独立的,而是与运动状态相关的,比如速度越大,质量越大。
在四维时空里,质量(或能量)实际是四维动量的第四维分量,动量是描述物质运动的量,因此质量与运动状态有关就是理所当然的了。
在四维时空里,动量和能量实现了统一,称为能量动量四矢。
另外在四维时空里还定义了四维速度,四维加速度,四维力,电磁场方程组的四维形式等。
值得一提的是,电磁场方程组的四维形式更加完美,完全统一了电和磁,电场和磁场用一个统一的电磁场张量来描述。
四维时空的物理定律比三维定律要完美的多,这说明我们的世界的确是四维的。
可以说至少它比牛顿力学要完美的多。
至少由它的完美性,我们不能对它妄加怀疑。
相对论中,时间与空间构成了一个不可分割的整体——四维时空,能量与动量也构成了一个不可分割的整体——四维动量。
这说明自然界一些看似毫不相干的量之间可能存在深刻的联系。
在今后论及广义相对论时我们还会看到,时空与能量动量四矢之间也存在着深刻的联系。
--------------------------------------------------------------------------------狭义相对论基本原理物质在相互作用中作永恒的运动,没有不运动的物质,也没有无物质的运动,由于物质是在相互联系,相互作用中运动的,因此,必须在物质的相互关系中描述运动,而不可能孤立的描述运动。
大学物理(14.3.2)--狭义相对论的时空观

大学物理 第十四单元 相对论
第三讲 狭义相对论的时空观
s ys' y'v
固有时间 :同一地点
o o'
y
s
d
12
发生的两事件的时间
9
B
6
3
x' x
间隔
. (原Δt时>)Δt' Δt0
12
Dt
Dt0
9
3
6
d
1
v2 c2
x1
o 12
x2 12 x
时间延缓 :运动的
第三讲 狭义相对论的时空观
讨论
在一个惯性系同时发生的
两个事件,在另一个惯性系是否
同时 ?
Δt'
Δt
v c2
Δx
1 2
一个惯性系
另一个惯性系
1 Δx 0 Δt 0 --- -- - 不同时 同时不同地
2
Δx 0 Δt 0
同时同地 ------ 同时
同地
东北大学 理学院 物理系
的时间间隔是多少? S系
S' 系
事件 1 (x1, y1, z1,t1) (x'1 , y'1 , z'1 ,t'1 )
事件 2 (x2 , y2 , z2 ,t2 ) (x'2 , y'2 , z'2 ,t'2 )
Δt t2 t1
Δtᄁ t2ᄁ t1ᄁ
东北大学 理学院 物理系
大学物理 第十四单元 相对论
v c2
Δx Δt
� � �>
0
Δtᄁ> 0 在 S´ 系仍然 1 事件先发生
3狭义相对论的时空观

4.3 狭义相对论的时空观4.3.1 同时的相对性光速相对于所有惯性系中的观测者以不变的速率传播,其惊人的结果是:时间一定是相对的。
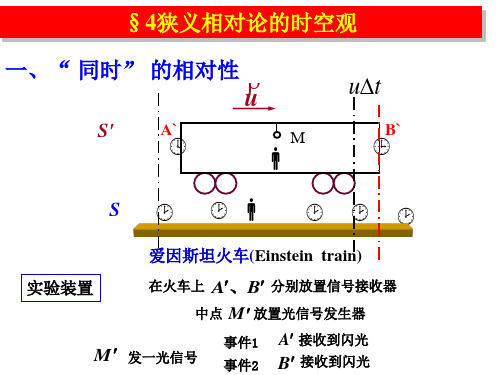
1 “同时”的定义设A 、B 两处发生两个事件,在事件发生的同时,发出两光信号,若在A 、B 的中心点同时收到两光信号,则A 、B 两事件是同时发生的。
这就是用光前进的路程来测量时间,而这样定义的理由就是光速不变,这样的定义适用于一切惯性系。
2 爱因斯坦理想的 “火车对钟实验”设有一列火车相对于站台以匀速向右运动,站台上的观测者测得当列车的首尾两点与站台上的A ,B 两点重合时,站台上的A ,B 两点同时发出一个闪光,所谓“同时”,就是两闪光同时传到站台上的中心点C 。
但对于列车来说,由于它向右行驶,车上的中点先接到来自车头方(即站台上的A 点)的闪光,后接到来自车尾方(即站台的B 点)的闪光。
于是对于列车上中点的观察者来说,A 点的闪光早于B 点。
就是说,对于站台参照系是同时的事件,对于列车参照系就不是同时的,即事件的同时性是相对的。
在一个惯性系中的两个同时事件,在另一个惯性系中观测不是同时的,这是时空均匀性和光速不变原理的一个直接结果。
3 同时的相对性设在惯性系S 中,在不同地点同时发生两事件,时空坐标分别为(x 1,0,0 ,t )和(x 2,0,0,t ),则根据洛仑兹变换式(4-4a ),有2221'11c u c ux t t --=, 2222'21c u c ux t t --=,即()0122122'1'2≠---=-cu x x c ut t 讨论 1 从上可知,在某一惯性系同时不同地发生的两个事件,在另一惯性系中观测则是不同时发生, 这就是狭义相对论的同时相对性。
同时相对性的本质在于在狭义相对论中时间和空间是相互关联的。
若u 沿x 轴正方向,且12x x ->0,则0'1'2<-t t ,可得出结论,沿两个惯性系相对运动方向发生的两个事件,在其中一个惯性系中表现为同时的,在另一惯性系中观察,则总是在前一惯性系运动的后方那一事件先发生。
狭义相对论的时空观
例3
静系中 子的平均寿命为 = 2.210-6 s。据报导,在
一组高能物理实验中,当它的速度为u = 0.9966c 时通过的 平均距离为8km。试说明这一现象。
L 解: 按经典力学: u
3 10 2.2 10 660 m
8
6
按相对论力学,地面系上测:
t g
1 u2 c 2
xA xB x A xB v t A t B v2 1 c
2
xB l0
x xB A
x A xB 1 v
2
c
2
xA
x A xB 1 v
2
xB
2
l0 1 v
2
l0 0 c
2
闪电不会击中火车。所以,无论从地面上看, 还是火车上看,闪电都不会击中火车。这个 物理事实,不因参考系而异.
l l0 1 v
2
c
2
l0
?
A a
b
B
闪电会击中火车?
请注意:从火车上看隧道B端运动到火车b 端这个事件与隧道A处发生闪电这个事件并 不是同时发生的!是B与b相遇在前,A处发 生闪电在后,因此有两种可能。 设地面为s 系,火车为s系,则 对s系 对s系 有
t A tB , xB l0 , xA 0
③用洛仑兹 变换定量计 算。
车 尾
车 头
车 尾
车 头
解:从地面上看,火车的 长度为
A a B
l l0 1 v
2
c
2
l0
b
即当火车前端 b 到达隧道 的 B端时,火车末端 a 已 A a 进入隧道内了,则 A端闪 电不能击中火车留下痕迹
大学物理学习课件-§18.3 狭义相对论的时空观

x ( x v t) t (t v x / c2 )
2.时间膨胀 在不同的惯性参照系中,同时是相对的,两事件发 生的时间间隔同样也与参照系有关。
实验:固定在小车上的光脉
s
平面镜
s
冲装置发射和接受光 脉冲的时间间隔的测 量。
o
o
x
x
S系中观测者测得光脉冲的发射与接收时间
间隔:
t 2d c
异地同时:x 0, t 0 t 0
若在 S系
即在S系不同时。
同地同时: x 0, t 0 t 0
即在S系亦同时。
结论:“异地”同时性与具体参照系有关,
即具有相对意义。
同样可证明:“同地”同时性与参照系的选择 无关,具有绝对意义。
常用的空间间隔、时间间隔的变换:
x ( x v t) t (t v x / c2)
试用洛沦兹变换证明该结论。
证明: 设两事件的坐标分别为
A
:
S S
: :
( (
x1 x1
, ,
t1 ) t1 )
B
:
S S
: :
( (
x2 x2
, ,
t2 ) 则:
t2 )
t1 (t1 vx1 / c2 ) t2 (t2 vx2 / c2 )
t t2 t1 [(t2 t1 ) v( x2 x1 ) / c2 ] (t vx / c2 )
s sv
当两坐标系原点重合时,S′系中的观 测者将S′系中所有步钟调零。
oo
x x
S系:A、B两步钟同时调到零,即Δt = tA-tB=0。
S′系:A、B两步钟调到零的时间间隔为
Δt tB tA (t vx / c2 ) vx / c2 而 Δx xB xA 0
狭义相对论的时空观20页PPT

2c 3
S S/
u
研究:天线长度,倾斜角
S ——地 S/ ——飞船
已知: S/中 L0 1m
Lx L0cos0
3 2
Ly L0si n012
S中:L xL x 1 232 1 2 31 2
Ly
Ly
1 2
L
L2xL2y
2 2
tgLy 1 45
Lx
13
S
S/ 0
u
地球
L0
恒星
飞船走比原长 L 0 短的距离就可到达恒星;
的寿命,已测得静止p-介子的平均寿命0=2×10-8s。某加速
器产生的p-介子以速度u =0.98c相对实验室运动。试求p-介子 衰变前在实验室中通过的平均距离。
S
S/ p
u 0.9c8
x/ x
研究:p 介子能走多远
S ——实验室 S/ —— p 介子
在S/ 中:p 介 子静止,经历原时,t 0 x 0
S ——长方形
3. 当 u << c 时: 1u2 c2 1 LL 0 绝 对 时 空 观
4. 如何理解:一切惯性系都是等价的?
等价并不是说我们看到的结果一样。
两个一米尺,一个静止,一个上飞船,我们看静止的一
米,飞船上的不到一米;而宇航员看飞船上的一米,我们这
里的不足一米,收缩程度一样。
12
例:飞船上的天线 L0 1m ,0 30,u
在S 中: t 0 12
xu
10
三. 空间的相对性 长度收缩
S S/
u 研究:a b的(固定在S/中x/轴上)长度
x/
S ——地
a
b
x S/ ——车
大学物理教程10.3 狭义相对论时空观

x ' 0 已知 t 0
若
t 0
不同地点发生的事件的同时性是相对的!
相同地点发生的事件的同时性是绝对的!
第10章 狭义相对论基础
10.3 狭义相对论时空观
讨论 •同时性是相对的。 •同时性的相对性是光速不变原理的直接结果。 •在一个惯性系中“看”另外一个惯性系中的钟不同步 。 •相对效应—惯性系等价、不能说哪一个正确! •当速度远远小于 c 时,两个惯性系结果相同。
第10章 狭义相对论基础
10.3 狭义相对论时空观
例 宇宙射线进入大气层(10km高)时与大气微粒碰 撞产生 μ 介子。μ 子在相对自身静止的惯性参考系中 的平均寿命大约为2.15×10–6s。试解释为什么在地平 面也能检测到大量的 μ 子?
( 2.15 106 s, mμ 207me , u 0.998 ) c
l0
S
S
事件1
( x1 , t1)
( x1 , t1 ) ( x2 , t2 )
事件2 ( x2 , t2 )
第10章 狭义相对论基础
10.3 狭义相对论时空观
直尺原长
棒静止时测得的它的长度,也称静止长度
l0 。
棒静止在 S 系中,
运动长度
l0
(静长)
l
S 系中怎么测? 两端必须同时测!
第10章 狭义相对论基础
10.3 狭义相对论时空观
二 时间间隔的相对性 研究的问题: 在某惯性系(S)中,同一地点先后发生的两 个事件的时间间隔(同一只钟测量)
与另一惯性系(S)中,两个地点发生的个事
件的时间间隔(两只钟分别测量)的关系。
第10章 狭义相对论基础
10.3 狭义相对论时空观
狭义相对论时空观

2
在不同惯性系中测量同一尺长,以原长为最长。
讨论 (1) 当v << c 时,
l l0
(2) 长度收缩效应是相对的。 (3) 长度收缩发生在物体运动的方向上。 (4) 长度收缩效应并不是视觉感受,而是测量结果。
2013-6-16
15
第14章 狭义相对论力学基础
例 地球-月球系中测得地-月距离为 3.844×108 m,一火箭以 0.8c 的速率沿着从地球到月球的方向飞行,先经过地球 (事件1),之后又经过月球 (事件2)。 求 在地球-月球系和火箭系中观测,火箭从地球飞经月球所需 要的时间。 解 取地球-月球系为 S 系,火箭系为 S' 系。则在 S 系中,地月距离为
2013-6-16 10
第14章 狭义相对论力学基础
三. 长度收缩
1. 运动长度的测量
S'
u
A
O'
S l0 x2' x1' uΔ t'
不要求同时测量
S S'
B
u t'
x1'
x2'
原长: 相对于棒 静止的惯性系测 得棒的长度
u
O'
A
B
x1
S'
O S
S l x2 x1 uΔ t
第14章 狭义相对论力学基础
狭义相对论的两个基本假设 I. 光速不变原理
在所有的惯性系中,光在真空中的传播速率具有相同的值 II. 狭义相对性原理 一切物理规律在所有惯性系中具有相同的形式
2013-6-16
1
第14章 狭义相对论力学基础
洛伦兹变换
正变换
狭义相对论的时空观

16
物理学
第五版
14-4
狭义相对论的时空观
例3 设想有一光子火箭以 v 0.95c 速率相 对地球作直线运动 ,若火箭上宇航员的计时器记录 他观测星云用去 10 min , 则地球上的观察者测得此 事用去多少时间 ? 解: 设火箭为
S' 系、地球为 S 系
10 1 0.952
迈克耳孙-莫雷实验
作为绝对参考系的以太不存在.
第十四章 相对论
6
物理学
第五版
14-4 狭义相对论的基本原理
狭义相对论的时空观
1)爱因斯坦相对性原理:物理定律在所有的 惯性系中都具有相同的表达形式 . 2)光速不变原理: 真空中的光速是常量,它 与光源或观察者的运动无关,即不依赖于惯性系的 选择. x vt x' ( x vt ) 2 1 y' y 洛伦兹变换式 z' z
y y'
o ' o
l0 15m
v x' s
x
s'
火箭参照系 地面参照系
解 :固有长度
l0 15m l '
l 15 1 0.952 m 4.68m
第十四章 相对论
11
l l' 1
2
物理学
第五版
14-4
狭义相对论的时空观
例2 一长为 1 m 的棒静止地放在 O ' x ' y ' 平面内, 在 S' 系的观察者测得此棒与 O' x' 轴成 45 角,试问从 S 系的观察者来看,此棒的长度以及棒与 Ox 轴的夹角是 多少?设想 S'系相对 S 系的运动速度 v 3c 2 . 解:在 S' 系 ' 45 , l ' 1m y y' v 2 ' l 'x' l ' y ' m ly' 2 ' ' l 2 x ' x'x 在 S 系 ly l'y' m o o' 2
2狭义相对论的时空观

假设
t 0
事件1先于事件2发生
两独立事件间的时序
u x2 x1 c 2 t2 t1
t' 0 t' 0 t' 0
时序不变 同时发生 时序颠倒
u x2 x1 c 2 t2 t1
u x2 x1 c 2 t2 t1
(1) 同时性是相对的。 (2) 同时性的相对性是光速不变原理的直接结果。 (3) 同时性的相对性否定了各个惯性系具有统一时间的可能性,
否定了牛顿的绝对时空观。
时序
t2 t1 u x2 x1 c 2 t' t ' t '
2 1
1
2
在 S 系中 在 S' 系中
y'
l
' y'
v
' l' x ' x'x
2 2
' 45 , l ' 1m 解:在 S' 系
l ' x ' l ' y ' 2 / 2m
在S系
o o'
l y l ' y ' 2 / 2m
l x l ' x ' 1 v / c 2l ' / 4
l l l 0.79m
t1 t2
(t 2 t1 ) u ( x2 x1 ) c 1
2
2
显然,在 S 系中不同地点(x2 ≠ x1) 同时发生 (t2 = t1 ) 的两个事 件,在 S' 系中观测并不同时( t'2 ≠ t'1)。
狭义相对论的时空观

讨论
(1) 同时性是相对的。 同时性是相对的。 (2) 同时性的相对性是光速不变原理的直接结果。 同时性的相对性是光速不变原理的直接结果。 (3) 同时性的相对性否定了各个惯性系具有统一时间 的可能性,否定了牛顿的绝对时空观。 的可能性,否定了牛顿的绝对时空观。
5
第6章相对论
二、 时间延缓
在S' 系的 O' 处放置一闪光光源和一信号接收器,在竖直 处放置一闪光光源和一信号接收器, 方向距离 O' 点 h' 的位置处放置一平面反射镜 M' 事件1 事件1 O' 处的闪光光源 发出一光信号 O' 处的接收器接 收到该光信号
13 第6章相对论
高速行驶时看到周围世界 的图象有什么变化呢? 的图象有什么变化呢?
“变扁了的世界”是仅考虑 变扁了的世界” 变扁了的世界 尺缩效应时物体的外形图象
高速运 动时我 们将看 到的图 像
静止或低速运动时看到的图象
14 第6章相对论
“变扁了的世界”是仅考虑尺缩效应时物体的外形图象 变扁了的世界” 变扁了的世界 物体外形图象是人们在同一时刻测量运动物体上各点 物体外形图象是人们在同一时刻测量运动物体上各点 的位置坐标( 同时到达”眼睛的光线) 的位置坐标( “同时到达”眼睛的光线)所构成的 外形图象 ---------测量形象 ---------测量形象
2 2
7
u∆ t
第6章相对论
t' t t ( c∆ ) =( c∆ ) −( u∆ )
2 2
2
∆t'(固有时) 固有时)
固有时: 固有时 在某惯性 系中,同一地点先 系中,同一地点先 后发生的两个事件 之间的时间间隔
(∆ ) =(∆ ) −(u t c) t' t ∆
狭义相对论的时空观

∆ x 12000 5 -1 ≈ ≈ 4 × 10 km ⋅ s > c 0 . 03 ∆t
事件1和事件2无因果关联,也不可能有因果关联, 事件1和事件2无因果关联,也不可能有因果关联, 可能在某个飞船上的观察者看来, 可能在某个飞船上的观察者看来,乙地小孩 B 先 出生。 出生。
动尺变短) 二 长度的收缩(动尺变短)
2 ∆x = 0 ∆t ≠ 0
------不同时 ------不同时 同地不同时
讨论
v ∆t − 2 ∆x c ∆t ′ = 1− β 2
------同时 ------同时
3 ∆x = 0 ∆t = 0
同时同地 4 ∆x ≠ 0 ∆t ≠ 0 ------不同时 ------不同时 不同时不同地
u ------同时 ∆t = 2 ∆x 时 ------同时 c
u<c
c ∆x ≤c< ∆t u
2
有因果关联的事件之间的信号速率 满足时序不变条件
有因果关联或可能有因果关联的事件时序不变, 有因果关联或可能有因果关联的事件时序不变, 时序不变 无因果关联的事件才可能发生时序变化。 无因果关联的事件才可能发生时序变化。 才可能发生时序变化 狭义相对论不违背因果律
设甲、乙两地相距12000km 设甲、乙两地相距12000km 例 事件1 在甲地出生; 事件1:某天孩子 A 在甲地出生; 飞机由甲地起飞 事件2:24小时后孩子 在乙地出生; 事件2 24小时后孩子B在乙地出生; 小时后孩子 在乙地出生 飞机抵达乙地 事件1和事件2无因果关联。 事件1和事件2无因果关联。 事件1和事件2 事件1和事件2可能有因 果关联,时序不变。 果关联,时序不变。
两参考系中各处的钟不可能同时对准, 两参考系中各处的钟不可能同时对准,在一个参考 系内各处相互对准了的钟, 系内各处相互对准了的钟,在其它参考系看来是没 有对准的, 迎面而来的钟超前。 有对准的,对 O(O′),迎面而来的钟超前。 ( ),迎面而来的钟超前
大学物理(下册) 14.2 狭义相对论的时空观

例:S’系不同空间点发生的光信号接受事件;
事件 1 :车厢后壁接收器接收到光信号; 事件 2 :车厢前壁接收器接收到光信号;
由洛伦兹变换可得时间间隔在两惯性系的变换关系:
v t ' 2 x ' c t 1 2
注意:(1)式是讨论时间关系的法则; 讨论三种情况的变换结果:
(1)
a. t ' 0;x' 0; S’系不同地点同时发生的两事件; b. t ' 0 ;x' 0; S’系同地点不同时发生的两事件;
l x2 x1
固有长度:观察者与物体相对静止时所测得的长度。
于是由(5)式得:
l0
l 1 2
l l ' 1 l0
2
(6)
l l ' 1 l0
2
(6)
洛伦兹收缩: 运动物体在 运动方向上长度收缩。
注意:长度收缩是一种相 对效应,是测量结果!
s s'
其中:
υ 0.92c, τ 2.603 10 s
解:分析 设 介子为 S 系、地球为 S 系,直 接由时间变换关系式解得地球参考系粒子的寿命 及通过的路程为:
t
τ 1 υ2 / c 2
2.603 10
8
1 (0.92) 2
6.642 108 s
L υt 0.92c 6.642 108 18.32m
1. 在S.R中,除长度不是绝对量外,时间间隔也不是 绝对量。设S’系同一地点发生两事件: S’系静止钟表记录两事件时间间隔: t ' t '2 t '1;
t t 2 t1; S 系静止钟表记录两事件时间间隔:
第06讲 狭义相对论的时空观

x 0
t 4 .0s
─固有时间
x ?
u ?
t 6 .0s
t ' t
由时间膨胀效应
6 4 3 2
u
5 3
c
由洛仑兹变换
x x ut 1 u
2
c
2
u
5 3
c
9
x 0
x
3 2
5 3
c 4 .0 1 .3 4 1 0 m
例题7 : 接上题,根据地面观察者的记录,完成这项任务需 要多长时间?在宇航员看来,这段旅程有多长? 解:
t t 1 u c
2 2
1 1 0 .9 8 0 5 8
2
5 .0 9 9 年
或者 用 u t x 可求得
t x u 5 0 .9 8 0 5 8 5 .0 9 9 年
实际上对于这样的两个惯性系来说,一旦兄弟 分开后就再也不会相遇,也就无法比较谁更年轻了。 要使哥俩能够相遇,飞船必须做变速运动。若 不考虑飞船变速运动引起的时间修正,设兄弟于20 岁分开,取γ=5 ,哥哥航行了10年,返回时是30岁, 而弟弟 天上一日, t 20 10 70 地上N年哪! 70岁了!
二者结论一致。
l
1年×0.98058c = 0.98058光年
走,樱花去! 不用花钱的吆
汉口江滩,樱花开得更鲜艳,配着沿江大 道上的老租界建筑群,情调上更胜一筹。
青山公园,原本就有千株樱花组成的樱花 林,特别是还有20余株绿樱花,当满树花 开时,可谓凝霞散景。 堤角公园,武汉第一座江南园林风格的公园。这里的樱 花美景就像苏州评弹一般柔美。园内小桥流水,仿古楼 榭。在开阔处盛开的樱花,就像一首短暂的歌曲,匆匆 而来,又匆匆离去,如同吴侬软语娓娓动听,令人动心。 光谷广场内栽有成片的樱花树。 中南民大校内樱花超过千株
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
但在地球上的人看来还不需要100年。(爱 因斯坦延缓)故可以去旅行。
8、在某惯性系中,同时、异地发生的两件事,在另外 的 惯性系中: (A)可能仍为同时,但不同地; (B)可能同时,也可能同地; (C)不可能同时,可能同地; (D)不能同时,也不可能同地。
X
设在K系X1处t1时刻发生事件“1”,(进门)
设在K系X2处t2时刻发生事件“2”,(开灯)
显然:
,“1”在先,“2”在后
,“1”,“2”同时
,“1”在后,“2”在先
但在K’系谁先谁后 呢?设K’系测得这 两件事的时间为:
则依“LT”
Y Y’ o o X1
t1
X2X’ t2
X
K’系中测得的时间差为
16、边长为a的的正方形薄板静止于惯性系K的XOY平 面内,且两边分别与X、Y轴平行,今有惯性系K’ 以0.8C(C为真空中光速)的速度相对于K系沿X轴 作匀速直线运动,则K’测得薄板面积: (A)a2;(B)0.6a2 ;(C)0.8a2 ;(D)a2/0.6 .
答案:[( B )]
解释:
解 取地球-月球系为 S 系,火箭系为 S' 系。则在 S 系中,地月距离为
火箭从地球飞径月球的时间为
设在系 S' 中,地-月距离为 l ',根据长度收缩公式有 因此,在 S' 系中火箭从地球飞径月球的时间为
另解:
例 宇宙飞船以 0.8c 速度远离地球(退行速度 u= 0.8c ),在此过
程中飞船向地球发出两光信号,其时间间隔为 tE .
求 地球上接收到它发出的两个光信号间隔 tR . 解 令宇宙飞船为 S' 系,地面为 S 系。则 S 系中测得发出两光
信号的时间间隔为
接收两光信号的时间间隔为
S
S'
S'
O
O'
O' x
ቤተ መጻሕፍቲ ባይዱ
作业
P128~130:选1~5 计1、4、7。
四)时序的相对性(时刻顺序的相对性)
Y Y’
o o X1 t1
X2X’ t2
Yd
O 用 代入上式得:
X’
X 结果 一样!
时间延缓的实验验证: 1966---1967年欧洲原子核研究中心(CERN)对 粒子进行了研究。粒子是一种基本粒子,在静 系中测得的寿命为0=2.210-6秒.当其加速到v= 0.9966C时,它漂移了八公里.
若依据“GT”,寿命不变,故漂移距离为:
依相对论:当粒子加速至於0.9966C时,寿命为:
答案:[D] 解释:
若在惯性系K中是同时、同地的两事件,由“LG”,则 K’系测则得这两件事的时间间隔和空间间隔:
即不同时。
若在惯性系K中是同时、异地的两事件,由“LG”,则 K’系则得这两件事空间间隔:
即也不同地。
9、在某惯性系中同地,先后发生两件事另外的惯性系中: (A)可能仍为同地,但不能同时; (B)可能仍为同地,但也可能同时; (C)不可能同地,也不可能同时,发生的先后顺序不 能变; (D)不可能同地,也不可能同时,发生的先后顺序也 可能变。
答案:[(D)]
3、一观察者测得的运动米尺长度为0.6米,则此尺接近观察 者的速度为:
(A)0.6C;(B)0.72C;(C)0.8C(D) C 答案:[(C) ]
解:
代入数据:
3、地球上的人,在他活到100岁以前,能否乘以光速 飞行的飞船到距离地球100光年的地方去旅行?
(A)行;(B)不行。
作匀速直线运动的惯性系中测得的长度
为本征长度的
倍。
例:一宇宙飞船静止在地面时长为20米,当其以
0.99C飞行时,地面观测者测得宇宙飞船长多少?
解:由题意,K’系中飞船静长
K’系
故K系测得的长度
K系
三)时间的延缓(膨胀)
在经典物理中,时间的测量是绝对的,一秒就是一秒, 哪个参照系测量都是一样。相对论中呢?
令:
称之为信号传递速度 时序能否颠倒呢?
甲地
t1 X1
时序能否颠倒呢?
X’
乙地Xt22X
事实上,只要有因果
关系,就必然有联系, 比如父母从甲地迁到 乙地生下自已的儿子 就必须有一迁移速度 u。 又如投球,就有球从出手到进球的速度….. 所有这些都称为信号传递速度。
甲地
t1 X1
X’
结论:有因果关系的问题的时序
出生(李小乙),且t2-t1=0.006s,(小甲先生,小
乙个飞后船生上)甲看、耒乙谁两先地出相生距?X2-X1=Y3’000km,那么在一
X’
Y
X2. t2
X1。t1
X
1)当
K’系看小 甲、小乙 同时出生
X2. t2 X’ X 2)当
Y’
Y
X1。t1
K’系看小 甲后生、 小乙先生 时序颠倒
但是有些事情时序是否也可以颠倒呢?如先播种
系中有一光源发出一光子(光速为C).求K系中测
得的该光子的光速.
C
v
X’ X
解:
思考题
1、爱田因斯坦16岁在瑞士阿劳州上中学时。曾设想过以光速C 随同光线一起运动时(如以光速运动的飞 船上)光的电磁场是 怎样的,当时他设想有两种可能:
(A)一个在空间振荡而仃止不前的电磁波; (B)观察到的电磁波与地球上观察到的电磁场一样,光速 仍为C。
、后收获,打兰球先出手后进球,乃至父母先生、 儿女后生等类似的事情时序能否颠倒呢?
五)因果性和最大信号传递速度
设K系X1处t1时刻发生 事件“1”
o
Y o
X2处t2时刻发生事件“2”
Y’
X1 t1
X2X’ t2
X
这两件事在K’系看来,发生在t’1、t’2时刻。则:
五)因果性和最大信号传递速度 这两件事在K’系看耒, Y Y’ 发生在t’1、t’2时刻。则:o o X1
生一件事情(如举手)Y
Y’
经历了 时间。
X’
(本征)O 由“LT”同样可得:
X’ O’
X
即K’系看来时间膨胀了
结论:相对物体运动的参照系 ,观测物体经历 的过程的时间延缓(膨胀)了,为本征时间的
倍。(又称爱因斯坦延缓)
在K’系中雷达信号 Y’
一来一往的时间为
d
在K系看,雷达信 O’ K'
号传播时间为:
§5.3狭义相对论的时空观
(View of Time and Space of the Special Relativity)
0)时间作为第四维
根据LT,任意两个物理事件的时空距离总满足如下
关系有:
第四维坐标——时间坐标为:
一)同时的相对性 Y Y’
设在K系中,发生两 件事:
O O’
X’ 若同时: X
答案:[(B)]飞船仍是一惯性系;由相对论计算也一样。
2、下列几种说法: 、所有惯性系对物理基本规律都是等价的; 、真空中,光的速度与光的频率、光源的运动状态无关; 、在任何惯性系中,光在真空中沿任何方向传播的速度都相
同。 以上说法哪些正确。 (A)只有、是正确的; (B)只有、是正确的; (C)只有、是正确的; (D)三种说法都是正确的。
故漂移的距离为:
与实验情况吻合得很好!
例 - 介子是一种不稳定的粒子,从它产生到它衰变 为 - 介子经历的时间即为它的寿命,已测得静
止 - 介子的平均寿命 0 = 2 10-8s. 某加速器产
生的 - 介子以速率 u = 0.98 c 相对实验室运动。 求 - 介子衰变前在实验室中通过的平均距离。
解 对实验室中的观察者来说,运动的 - 介子的寿命 为
因此, - 介子衰变前在实验室中通过的距离 d ' 为
例 地球-月球系中测得地-月距离为 3.844×108 m,一火箭以 0.8 c 的速率沿着从地球到月球的方向飞行,先经过地球 (事件1),之后又经过月球 (事件2)。
求 在地球-月球系和火箭系中观测,火箭从地球飞经月球所需 要的时间。
设地球为K系,飞船为K’系
甲乙地地((XX12))处处父儿母子出出生生((tt12)),t2>t1 现在从K’系观测,设观测的时刻分别为t’1、t’2
甲地
t1 X1
X’ t2
乙地X2X
现在从K’系观测,设观测的时刻分别为t’1、t’2
甲地
t1 X1
X’
乙地Xt22X
现在从K’系观测,设观测的时刻分别为t’1、t’2
是不能颠倒的。尽管时空是相
对的,但相对论中也有绝对的一
面。
乙地Xt22X
光速C是最大信号传递的速度。
六)狭义相对论中的速度变换(了解) 在两个惯性系中观测一个质点速度之间的关系
Y Y’ oo
X’ X 显然有:
设质点在两参照 系中的坐标为:
依“LT”
整理:
综合::
注意:1)作为一种特殊情况: 则变换只剩下X方向的分量:
t1
X2X’ t2
X
为简单设A)
B)
由此看出时序颠倒的条件为:
1)不同两件事发生在不同地点,即 2)观测事件的参照系相对事件发生的地点有 相对运动,即
例2)设父母一出世就随祖父母展转迁移从甲地 到了乙地,在乙地父母生了自已的儿子。显然 这是一个有因果关系的问题。因果关系能否颠 倒呢?
X’
X1
X2 X
依“LT”
二)长度的收缩
Y Y’
(本征长度) 杆长
O O’ 依“LT”
X’1 X’2X’
X1
X2 X
同时 测量
K系看棒缩短了,
为原长的
倍
Y
