中考数学总复习课件：1.2 整式
合集下载
北师大中考数学总复习《整式及因式分解》课件
考点聚焦 归类探究 回归教材 中考预测
(1)同类项必须符合两个条件：第一，所含字母相同； 第二，相同字母的指数相同．两者缺一不可。 (2)根据同类项概念——相同字母的指数相同列方程 (组)是解此类题的一般方法。
考点聚焦
归类探究
回归教材
中考预测
►
探究二
整式的运算
命题角度： 1．整式的加、减、乘、除运算； 2．乘法公式．
例2 [2013·泸州] 下列各式计算正确的是( D ) A．(a7)2＝a9 B．a7· a2＝a14 C．2a2＋3a3＝5a5 D．(ab)3＝a3b3
解 析 A．利用幂的乘方运算法则计算得到结果；B.利用 同底数幂的乘法法则计算得到结果；C.原式不能合并；D.利 用积的乘方运算法则计算得到结果．
先用一个多项式的每一项乘另一个多项式 的每一项，再把所得的积相加，即(m＋ n)(a＋b)＝ma ＋mb＋na＋nb
回归教材 中考预测
考点聚焦
归类探究
整式 的除 法 乘法 公式
把系数与同底数幂分别相除，作为商 单项式除以单 的因式，对于只在被除式里含有的字 项式 母，则连同它的指数作为商的一个因 式 多项式除以单 先把这个多项式的每一项分别除以这 项式 个单项式，然后把所得的商相加 a2－b2 平方差公式 (a＋b)(a－b)＝________
考点聚焦 归类探究 回归教材 中考预测
例3
[2013·娄底] 先化简，再求值：
3 3
3 (x＋y)(x－y)－(4x y－8xy )÷ 2xy，其中 x＝－1，y＝ . 3
解
原式＝x2－y2－2x2＋4y2＝－x2＋3y2. 3 当 x＝－1，y＝ 时， 3 3 2 2 2 2 －x ＋3y ＝－(－1) ＋3× 3 ＝－1＋1＝0.
(1)同类项必须符合两个条件：第一，所含字母相同； 第二，相同字母的指数相同．两者缺一不可。 (2)根据同类项概念——相同字母的指数相同列方程 (组)是解此类题的一般方法。
考点聚焦
归类探究
回归教材
中考预测
►
探究二
整式的运算
命题角度： 1．整式的加、减、乘、除运算； 2．乘法公式．
例2 [2013·泸州] 下列各式计算正确的是( D ) A．(a7)2＝a9 B．a7· a2＝a14 C．2a2＋3a3＝5a5 D．(ab)3＝a3b3
解 析 A．利用幂的乘方运算法则计算得到结果；B.利用 同底数幂的乘法法则计算得到结果；C.原式不能合并；D.利 用积的乘方运算法则计算得到结果．
先用一个多项式的每一项乘另一个多项式 的每一项，再把所得的积相加，即(m＋ n)(a＋b)＝ma ＋mb＋na＋nb
回归教材 中考预测
考点聚焦
归类探究
整式 的除 法 乘法 公式
把系数与同底数幂分别相除，作为商 单项式除以单 的因式，对于只在被除式里含有的字 项式 母，则连同它的指数作为商的一个因 式 多项式除以单 先把这个多项式的每一项分别除以这 项式 个单项式，然后把所得的商相加 a2－b2 平方差公式 (a＋b)(a－b)＝________
考点聚焦 归类探究 回归教材 中考预测
例3
[2013·娄底] 先化简，再求值：
3 3
3 (x＋y)(x－y)－(4x y－8xy )÷ 2xy，其中 x＝－1，y＝ . 3
解
原式＝x2－y2－2x2＋4y2＝－x2＋3y2. 3 当 x＝－1，y＝ 时， 3 3 2 2 2 2 －x ＋3y ＝－(－1) ＋3× 3 ＝－1＋1＝0.
2024河南中考数学专题复习 整式 课件
代 代数式 数 式 求值
(1)直接代入法：把已知字母的值代入代数式，并按原来的运算顺序 计算求值 (2)整体代入法：①观察已知条件和所求代数式的关系
(整体思想) ②将所求代数式变形后与已知代数式成倍分关 系，一般会用到提公因式法、平方差公式、完 全平方公式
整式
定义：由数或字母的 乘积 表示的式子 单独的一个数或一个字母也是单项
整式 的运 算
加减运算
1.字母和字母的 指数 不变 合并同类项
2.系数相加减作为新的系数，如2xy2＋3xy2＝ 5xy2
(实质：合
括号前是“＋”号，去括号时，括号内各项不变号：
并同类项) 去括号法则 a＋(b＋c)＝a ＋ b ＋ c
括号前是“－”号，去括号时，括号内每一项都变号：
a－(b＋c)＝a － b － c
1 考点精讲 2 河南9年真题子母题
列代数式 代数式求值
代数式
单项式 多项式 整式 同类项
整式相 关概念
整式
加减运算 整式的运算 幂的运算
乘法运算
目的 因式分解 基本方法
考点精讲
1.原价a的8.5折表示为0.85a；原价a提高20%后再打8折表示为
0.8(1＋20%)a_
2.原量a的2倍多(或少)3表示为 2a＋3(或2a－3) ，原量a增加(或减
少)数式
3.3个单价为a元的商品与2个单价为b元的商品总价为 (3a＋2b) 元 4.每天完成的工作量为a，则完成m的工作量所需时间为 m 天
a 【易错警示】
列出的代数式化为最简后，若最后一步是加、减时，有单位必
须将代数式用括号括起来再加单位
4. [2023河南16(2)题5分]化简：(x－2y)2－x(x－4y)． 解：原式＝x2－4xy＋4y2－x2＋4xy
2015年广西中考数学总复习课件第3课时 整式(共39张PPT)
解：∵a＋b＝5，ab＝3，
∴(a＋b)2＝25，
即a2＋2ab＋b2＝25，
∴a2＋b2＝25－2ab
＝25－2×3＝19.
第3课时
整式
中考预测 1．已知(m－n)2＝8，(m＋n)2＝2，则m2＋n2＝( C ) A．10 B．6
C．5
D．3
2．已知a＋b＝4，a－b＝3，则a2－b2＝________ 12 ．
B．x2＋8x＋16
D．x2＋4x＋16
5．下列式子中一定相等的是( C )
A．(a－b)2＝a2－b2
B．(a＋b)2＝a2＋b2
C．(－a＋b)2＝b2－2ab＋a2
D．(－a－b)2＝b2－2ab＋a2
第3课时 整式
1 xyz － 6 6．单项式－ 的系数是________ ，次数是________ ． 2 2
第3课时
整式
(3)多项式与多项式相乘：(m＋n)(a＋b)＝ma＋mb＋na＋nb. (a＋b)(a－b) ． (4)平方差公式：a2－b2＝________________ (5)完全平方公式：(a±b)2＝______________ a2±2ab＋b2 ．
3．整式的除法：
单项式相除，把系数与同底数幂分别相除作为商的因式，对
[2014·盐城] 先化简，再求值：(a＋2b)2＋(b＋
a)(b－a)，其中a＝－1，b＝2.
解：原式＝a2＋4ab＋4b2＋b2－a2＝4ab＋5b2. 当 a ＝－ 1 ， b ＝ 2 时，原式＝ 4×( － 1)×2 ＋ 5×22 ＝－ 8 ＋ 20 ＝12.
第3课时
整式
┃考题回归教材┃ 完全平方公式大变身 已知a＋b＝5，ab＝3，求a2＋b2的值．
中考数学专题复习：第2课 整式及其运算优质课件PPT
【答案】 2
【类题演练 4】 (2018·扬州)计算：(2x＋3)2－(2x＋3)(2x －3)．
【解析】 原式＝4x2＋12x＋9－(4x2－9)＝12x＋18．
1．整式的加减实质就是合并同类项，整式的乘除实质就 是幂的运算．
2．本课主要用到以下三种数学思想方法： (1)数形结合思想： 在列代数式时，常常会遇到一种题型：题中提供一 定的图形，要求通过对图形的观察、探索，提取图 形中反馈的信息，并根据相关的知识列出相应的代 数式，也能用图形来验证整式的乘法和乘法公式．
A．34
B．1
C．23
D．98
【答案】 D
()
题型一 幂的运算
熟记法则，依照法则进行计算.
【典例 1】 有下列运算：①a2·a3＝a6；②(a3)2＝a6；③a5
÷a5＝a；④(ab)3＝a3b3．其中结果正确的个数为 ( )
A．1
B．2
C．3
D．4
【解析】 ①a2·a3＝a5，故本项错误；②(a3)2＝a6，故本 项正确；③a5÷a5＝1，故本项错误；④(ab)3＝a3b3，故本 项正确．故选 B．
注意公式的变形及整体思想的应用．
【典例 3】 (2018·河北)将 9．52 变形正确的是 ( ) A．9．52＝92＋0．52 B．9．52＝(10＋0．5)(10－0．5) C．9．52＝102－2×10×0．5＋0．52 D．9．52＝92＋9×0．5＋0．52
【解析】 9．52＝(10－0．5)2＝102－2×10×0．5＋0．52．
【答案】 C
【类题演练 3】 (2018·乐山)已知实数 a，b 满足 a＋b＝2，
ab＝34，则 a－b＝
()
A．1
中考数学专题复习课件：整式方程
( x 2 ) 2 ( x 1 ) 2
的值.
解：根据题意得 x２+4x-5＝0，且x２-x-30=0 ∴x＝-5或x=1，且x=6或x=-5 ∴x＝-5
( x 2 ) 2 ( x 1 ) 2 ( 5 2 ) 2 ( 5 1 ) 2 3
【例5】(2008年· 绍兴)若一个三角形的三边长均满 足x2-6x+8=0，则此三角形周长为 6,10,12 .
课时训练
6.(2008年· 新疆)用配方法解方程x2+6x-7=0. 解：x2+6x-7=0 x2+6x+9=7+9 (x+3)2=16 x+3=±4 x =1，x =-7 1 2
课时训练
1. (2008年·河南省)已知一元二次方程x2-2x=0，它的 解是 ( D ) A.0 B.2 C.0，-2 D.0，2 2. (2008年· 厦门市)一元二次方程x2+x-1=0的根是.
1 5 x 2Байду номын сангаас
3. (2008年·陕西省)方程(x+1)2=9的解是 ( C ) A.x=2 B.x=-4 C.x1=2,x2=-4 D.x1=-2,x2=4
2a
④因式分解法.
课前热身
1. (2008年·黑龙江)如果代数式4y2-2y+5的值为7， 那么代数式2y2-y+1的值等于 ( A ) A.2 B.3 C.-2 D.4 2. (2008年·北京海淀区)若a的值使得x2+4x+a=(x+2)2-1 成立，则a的值为 ( C ) A.5 B.4 C.3 D.2 3.(2008年· 吉林省)已知m是方程x2-x-2=0的一个根，则 2 代数式m2-m的值等于 。
的值.
解：根据题意得 x２+4x-5＝0，且x２-x-30=0 ∴x＝-5或x=1，且x=6或x=-5 ∴x＝-5
( x 2 ) 2 ( x 1 ) 2 ( 5 2 ) 2 ( 5 1 ) 2 3
【例5】(2008年· 绍兴)若一个三角形的三边长均满 足x2-6x+8=0，则此三角形周长为 6,10,12 .
课时训练
6.(2008年· 新疆)用配方法解方程x2+6x-7=0. 解：x2+6x-7=0 x2+6x+9=7+9 (x+3)2=16 x+3=±4 x =1，x =-7 1 2
课时训练
1. (2008年·河南省)已知一元二次方程x2-2x=0，它的 解是 ( D ) A.0 B.2 C.0，-2 D.0，2 2. (2008年· 厦门市)一元二次方程x2+x-1=0的根是.
1 5 x 2Байду номын сангаас
3. (2008年·陕西省)方程(x+1)2=9的解是 ( C ) A.x=2 B.x=-4 C.x1=2,x2=-4 D.x1=-2,x2=4
2a
④因式分解法.
课前热身
1. (2008年·黑龙江)如果代数式4y2-2y+5的值为7， 那么代数式2y2-y+1的值等于 ( A ) A.2 B.3 C.-2 D.4 2. (2008年·北京海淀区)若a的值使得x2+4x+a=(x+2)2-1 成立，则a的值为 ( C ) A.5 B.4 C.3 D.2 3.(2008年· 吉林省)已知m是方程x2-x-2=0的一个根，则 2 代数式m2-m的值等于 。
中考数学专题复习专题02 代数式与整式(课件)
知识点梳理
知识点4 ：幂的运算
1. 同底数幂乘法：底数不变，指数相加，am·an= am+n ，如 a3 ·a-2= a . 2. 同底数幂除法： 底数不变，指数相减 ，am÷an= am-n （a≠0） 3. 幂的乘方： 底数不变，指数相乘 ，(am)n= amn . 4. 积的乘方： 各因式乘方的积 ，(ambn)p= ampbnp ，如(-2a2b)3= -8a6b3 ， (-ab)2= a2b2 .
典型例题
知识点4 ：幂的运算
【例12】（2022•南充）比较大小：2-2 30．（选填＞，＝，＜）
【考点】零指数幂；负整数指数幂
【解答】解：∵2-2= 1 ，30=1，
4
∴2-2＜30， 故答案为：＜． 【点评】本题考查了负整数指数幂，零指数幂，掌握负整数指数幂的意义， 零指数幂的意义是解决问题的关键．
知识点梳理
知识点5 ：整式的乘除
4.（1）乘法公式：(a+b)(a-b)= a2-b2 ； (a+b)2= a2+2ab+b2 ；
（2）常见的变形有：a2+b2=(a+b)2-2ab； (-a-b)2=(a+b)2；
(a-b)2= a2-2ab+b2 ； (a-b)2=(a+b)2-4ab； (-a+b)2=(a-b)2
“书香满校园”的读书活动．现需购买甲，乙两种读本共100本供学生阅读，
其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x
本，则购买乙种读本的费用为（ ）
A．8x元
B．10(100－x)元 C．8(100－x)元 D．(100－8x)元
【考点】列代数式． 【解答】【解答】解：设购买甲种读本x本，则购买乙种读本的费用为：8(100－x)元． 故选：C．
中考数学课件 第1章 第2节 整 式
B．10(100－x)元
• C．8(100－x)元
D．(100－8x)元
• 2．(2022·广安)已知a＋b＝1，则代数式a2－b2＋2b＋9的 值1为0 _____．
考点 幂的运算性质
• 3．(2022·台州)下列运算正确的是
• A．a2·a3＝a5
B．(a2)3＝a8
• C．(a2b)3＝a2b3
安徽十年精选
考点 幂的运算性质
• 1．(2022·安徽)下列各式中，计算结果等于a9的是 ( B )
• A．a3＋a6
B．a3·a6
• C．a10－a
D．a18÷a2
2．(2020·安徽)计算－a6÷a3 的结果是
• A．－a3
B．－a2
• C．a3
D．a2
(C )
• 3．(2018·安徽)下列运算正确的是
B
• 10．(2014·安徽)下列四个多项式中，能因式分解的是
()
• A．a2＋1
B．a2－6a＋9
• C．x2＋5y
D．x2－5y
考点 规律探究
• 11．(2022·安徽)观察以下等式： • 第1个等式：(2×1＋1)2＝(2×2＋1)2－(2×2)2； • 第2个等式：(2×2＋1)2＝(3×4＋1)2－(3×4)2； • 第3个等式：(2×3＋1)2＝(4×6＋1)2－(4×6)2； • 第4个等式：(2×4＋1)2＝(5×8＋1)2－(5×8)2；
• 8．(2018·安徽)下列分解因式正确的是 • A．－x2＋4x＝－x(x＋4)
( C)
• B．x2＋xy＋x＝x(x＋y)
• C．x(x－y)＋y(y－x)＝(x－y)2
• D．x2－4x＋4＝(x＋2)(x－2)
中考复习课件一元二次方程复习
★淄博市师德标兵 ★ 市学科带头人
★淄博市优秀教师
★淄博市优秀青年知识分子 ★县优秀校长 ★在国家级、省级、市级报刊杂志发表教育教学论文20余篇
一、考点分析
本章共有如下八大考点 1、一元二次方程的概念 2、一元二次方程的一般式 3、一元二次方程的根的意义 4、一元二次方程的解法 5、一元二次方程根的判别式 6、一元二次方程根与系数的关系 7、一元二次方程与几何、函数（一次函数、二次函数）的综合 8、一元二次方程解决实际问题
例6、已知方程2xa-xb-x2+4=0是关于x的一元二次方程，求 a、b的值。
考点2：一元二次方程的一般形式 一元二次方程的一般形式：ax2+bx+c=0，它的特征是： 等式左边是一个关于未知数x的二次多项式，等式右边 是零，其中ax2叫做二次项，a叫做二次项系数；bx叫 做一次项，b叫做一次项系数；c叫做常数项（要求能 正确找出a、b、c的值，特别注意符号不要错） 例1指出下列一元二次方程的二次项系数、一次项系数、常数项 各是多少？ （1）5x2+10x=22 （2）2x2+15=0 （3）x2=3x （4)（x+2）2=3 （5）x2-5x+1=p2 （6）x2-x-2=70 （7）4x2-5-6x=0 （8）x2+x+ 3=3-2 3 x 例2关于x的方程3x2-x-6=0中，a=（ ），b=（ ），c=（ ）
例2、已知p、q是方程x2+（2m+3）x+m2=0的两个不等的实根，且p q =-1，则m的值为（ ） A :3或-1 B :3 C :1 D：-3或1 例3、方程x2-3x=6与方程x2+3=6x的所有根的和是（ ）所有根的积是 ( )。
1
★淄博市优秀教师
★淄博市优秀青年知识分子 ★县优秀校长 ★在国家级、省级、市级报刊杂志发表教育教学论文20余篇
一、考点分析
本章共有如下八大考点 1、一元二次方程的概念 2、一元二次方程的一般式 3、一元二次方程的根的意义 4、一元二次方程的解法 5、一元二次方程根的判别式 6、一元二次方程根与系数的关系 7、一元二次方程与几何、函数（一次函数、二次函数）的综合 8、一元二次方程解决实际问题
例6、已知方程2xa-xb-x2+4=0是关于x的一元二次方程，求 a、b的值。
考点2：一元二次方程的一般形式 一元二次方程的一般形式：ax2+bx+c=0，它的特征是： 等式左边是一个关于未知数x的二次多项式，等式右边 是零，其中ax2叫做二次项，a叫做二次项系数；bx叫 做一次项，b叫做一次项系数；c叫做常数项（要求能 正确找出a、b、c的值，特别注意符号不要错） 例1指出下列一元二次方程的二次项系数、一次项系数、常数项 各是多少？ （1）5x2+10x=22 （2）2x2+15=0 （3）x2=3x （4)（x+2）2=3 （5）x2-5x+1=p2 （6）x2-x-2=70 （7）4x2-5-6x=0 （8）x2+x+ 3=3-2 3 x 例2关于x的方程3x2-x-6=0中，a=（ ），b=（ ），c=（ ）
例2、已知p、q是方程x2+（2m+3）x+m2=0的两个不等的实根，且p q =-1，则m的值为（ ） A :3或-1 B :3 C :1 D：-3或1 例3、方程x2-3x=6与方程x2+3=6x的所有根的和是（ ）所有根的积是 ( )。
1
中考数学总复习1.2代数式及整式(含因式分解)1
第二节 代数式及整式(含因式分解)11．(2019·怀化中考)单项式－5ab 的系数是( )A ．5B ．－5C ．2D ．－2 2．(2019·毕节中考)如果3ab 2m －1与9ab m ＋1是同类项，那么m 等于( )A ．2B ．1C ．－1D ．03．(2019·甘肃中考)计算(－2a)2·a 4的结果是( )A ．－4a 6B ．4a 6C ．－2a 6D ．－4a 84．(2019·本溪中考)下列计算正确的是( )A ．x 7÷x ＝x 7B ．(－3x 2)2＝－9x 4C ．x 3·x 3＝2x 6D ．(x 3)2＝x 65．已知a ＋b ＝14，则代数式4a ＋4b －3的值是( ) A ．2B ．－2C ．－4D ．－312 6．(2019·台湾中考)计算(2x －3)(3x ＋4)的结果，与下列哪一个式子相同？( )A ．－7x ＋4B ．－7x －12C ．6x 2－12D ．6x 2－x －127．(2019·甘肃中考改编)如图，每一幅图中有若干个大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，如果第n 幅图中有2 019个菱形，则n 的值为( )A ．1 009B ．1 010C ．1 011D ．1 0128．(2019·绥化中考)计算：(－m 3)2÷m 4＝________．9．(2019·桂林中考)若x 2＋ax ＋4＝(x －2)2，则a ＝________.10．(2019·赤峰中考)因式分解：x 3－2x 2y ＋xy 2＝__________________．11．(2019·乐山中考)若3m ＝9n ＝2，则3m ＋2n ＝______.12．(2019·兰州中考)化简：a(1－2a)＋2(a ＋1)(a －1)．13．(2019·宜昌中考)化简(x －3)2－x(x －6)的结果为( )A ．6x －9B ．－12x ＋9C ．9D ．3x ＋914．(2019·贺州中考)把多项式4a 2－1分解因式，结果正确的是( )A ．(4a ＋1)(4a －1)B ．(2a ＋1)(2a －1)C ．(2a －1)2D ．(2a ＋1)215．(2019·常德中考)观察下列等式：70＝1，71＝7，72＝49，73＝343，74＝2 401，75＝16 807，…，根据其中的规律可得70＋71＋72＋…＋72 019的结果的个位数字是( )A ．0B ．1C ．7D ．816．(2019·广东中考)已知x ＝2y ＋3，则代数式4x －8y ＋9的值是________．17．(2019·衢州中考)已知实数m ，n 满足⎩⎨⎧m －n ＝1，m ＋n ＝3，则代数式m 2－n 2的值为________． 18．(2019·枣庄中考)若m －1m ＝3，则m 2＋1m 2＝________. 19．(2019·长春中考)先化简，再求值：(2a ＋1)2－4a(a －1)，其中a ＝18.参考答案1．B 2.A 3.B 4.D 5.B 6.D 7.B8．m 2 9.－4 10.x(x －y)2 11.412．解：原式＝a －2a 2＋2(a 2－1)＝a －2a 2＋2a 2－2＝a －2.13．C 14.B 15.A16．21 17.3 18.1119．解：原式＝4a 2＋4a ＋1－4a 2＋4a ＝8a ＋1.当a ＝18时，原式＝8×18＋1＝2.。
中考数学复习 第一章数与式数与式 第2课 整式及其运课件
解：(2)∵(x＋y)2＝x2＋y2＋2xy， ∴2xy＝(x＋y)2－(x2＋y2)＝72－25＝24， ∴x－y)2＝x2＋y2－2xy＝25－24＝1. ∵x>y，∴x－y＝ 1 ＝1.
探究提高 1.算式中的局部直接使用乘法公式、简化运算，
任何时候都要遵循先化简，再求值的原则. 2.在利用完全平方公式求值时，通常用到以下
探究提高 整式的加减，实质上就是合并同类项，有括号的，先 去括号．只要算式中没有同类项，就是最后的结果．
知能迁移1 (1)(2011·义乌)下列计算正确的是( D )
A．x2＋x4＝x6
B．2x＋3y＝5xy
C．x6÷x3＝x2
D．(x3)2＝x6
解析：(x3)2＝x3×2＝x6.
(2)(2011·台北)化简(－4x＋8)－3(4－5x)，
题型四 整式的混合运算及求值
【例4】 (本题5分)先化简，再求值： 3x(x2－x－1)－(x＋1)(3x2－x)，其中x＝－1 . 2
解题示范——规范步骤，该得的分，一分不丢！
解：原式＝3x3－3x2－3x－(3x3－x2＋3x2－x)
[2分]
＝3x3－3x2－3x－3x3＋x2－3x2＋x
＝－5x2－2x.
3．整式： 单项式和多项式 统称为整式． 4．同类项：多项式中所含 字母 相同并且 相同字母的指数 也
相同的项，叫做同类项．
6．整式乘法： 单项式与单项式相乘，把系数、同底数幂分别相乘作为积 的因式，只在一个单项式里含有的字母，连同它的指数作 为积的一个因式． 单项式乘多项式：m(a＋b)＝ ma＋mb . 多项式乘多项式：(a＋b)(c＋d)＝ ac＋ad＋bc＋bd .
第2个图形所需的棋子数为11＝6×2－1. 第3个图形所需的棋子数为17＝6×3－1， …… 第n个图形所需的棋子数为6n－1.
2024年中考数学总复习课件第一部分第一章：2 整式与因式分解(共27张PPT)
4 851
[北师大七上P99习题3.8 T1改编] 下图是一组有规律的图案，它由若干大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片， .依此规律，第
个图案中有_________（用含的代数式表示）个白色圆片．
1.多项式各项的公因式是( )
续表
考点二 列代数式与代数式求值
1.用基本运算符号把数或表示数的字母连接起来的式子叫做代数式. 2.代数式求值 （1）直接代入法：把已知字母的值直接代入代数式，并按原来的运算顺序计算可求值. （2）整体代入法：先对比已知定值关系式与所求代数式，找出两个式子间共同的部分作为切入点，再对已知关系式与所求代数式进行变形（一般会用到提公因式法、平方差公式法、完全平方公式法），最后将已知定值关系式或变形后的式子整体代入计算可求值.
体验2 [2023·白山一模] 为了调研大众的低碳环保意识，小刚在某超市收银台出口统计后发现：一小时内使用自带环保袋的人数比使用超市塑料袋人数的2倍少4人．如果使用超市塑料袋的有人，那么使用自带环保袋的有__________（用含的代数式表示）人．
考点三 幂的运算性质
幂的运算（，，为正整数） 同底数幂相乘：底数不变，指数相加，即______. 同底数幂相除：底数______，指数______，即______. 幂的乘方：底数不变，指数______，即_____. 积的乘方：先把积中的每一个因式分别乘方，再把所得的幂______，即______.体验3 [2023·锦州] 下列运算中正确的是( )
（1） 已知实数，，满足,，则的值为___．（2） 分解因式：___________________.
6
类型三 规律探索
[北师大七上P99习题3.8 T1改编] 下图是一组有规律的图案，它由若干大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片， .依此规律，第
个图案中有_________（用含的代数式表示）个白色圆片．
1.多项式各项的公因式是( )
续表
考点二 列代数式与代数式求值
1.用基本运算符号把数或表示数的字母连接起来的式子叫做代数式. 2.代数式求值 （1）直接代入法：把已知字母的值直接代入代数式，并按原来的运算顺序计算可求值. （2）整体代入法：先对比已知定值关系式与所求代数式，找出两个式子间共同的部分作为切入点，再对已知关系式与所求代数式进行变形（一般会用到提公因式法、平方差公式法、完全平方公式法），最后将已知定值关系式或变形后的式子整体代入计算可求值.
体验2 [2023·白山一模] 为了调研大众的低碳环保意识，小刚在某超市收银台出口统计后发现：一小时内使用自带环保袋的人数比使用超市塑料袋人数的2倍少4人．如果使用超市塑料袋的有人，那么使用自带环保袋的有__________（用含的代数式表示）人．
考点三 幂的运算性质
幂的运算（，，为正整数） 同底数幂相乘：底数不变，指数相加，即______. 同底数幂相除：底数______，指数______，即______. 幂的乘方：底数不变，指数______，即_____. 积的乘方：先把积中的每一个因式分别乘方，再把所得的幂______，即______.体验3 [2023·锦州] 下列运算中正确的是( )
（1） 已知实数，，满足,，则的值为___．（2） 分解因式：___________________.
6
类型三 规律探索
第1章第2讲第1课时整式-中考数学一轮考点复习课件(共42张)
式
另一个多项式的每一项，再把所得的积相加，即(a
多项式乘
的
＋b)(p＋q)＝ ap＋aq＋bp＋bq
多项式
乘
平方差公式：(a＋b)(a－b)＝ a2－b2
法
完全平方公式：(a±b)2＝ a2±2ab＋b2
单项式除 整式的 以单项式 除法 多项式除
以单项式
把系数和同底数幂分别相除作为商的因式，对于只在被除 式里含有的字母，则连同它的指数作为商的一个因式 先把这个多项式的每一项除以这个单项式，再把所得的商 相加
能进行简单的整式乘法运算(其中多项式相乘仅 北师：七上第三章P78～P104；
指一次式之间以及一次式与二次式相乘)． 七下第一章P2～P36；
(3)能推导乘法公式：(a＋b)(a－b)＝a2－b2； 八下第四章P92～P106；
(a±b)2＝a2±2ab＋b2，了解公式的几何背景，并 华师：七上第3章P82～P118；八上第12章
(3)原式＝26＋6×25×－12＋15×24×－122＋ 20×23×－123＋15×22×－124＋6×2×－125＋－126－2－－126 ＝2－126－－126－2 ＝326－126－2 ＝323－123323＋123－2 ＝32－12×94＋34＋14×32＋12×
94－34＋14－2 ＝143×2×74－2 ＝2×131×6 7－1 ＝785.
第一章 数与式
第2讲 整式和因式分解
第1课时 整 式
忆知识·奇妙导引 过考点·夯实基础 破重难·讲透练活 练好题·课堂达标
课标要求
版本导航
(1)了解整数指数幂的意义和基本性质．
(2)理解整式的概念，掌握合并同类项和去括号 人教：七上第二章P53～P76；
中考数学复习《1.2整式与因式分解》课件
2023 ． 8．若 a ＋a－5＝0，则 2a ＋2a＋2013 的值为________
9．先化简，再求值：[(x－y) ＋(x＋y)(x－y)]÷x，其中 x＝ 1 －1
1 解：原式＝2x－2y，当 x＝－1，y＝ 时，原式＝－3 2
积 把一个多项式化为几个整式的________ 的形式 定义 叫做因式分解 提公因 m(a＋b＋c) ma＋mb＋mc＝________ 式法 方法 a＋b)(a－b) a2－b2＝(________ 公式法 (a± b )2 a2±2ab＋b2＝________ (1)一提：如果多项式各项有公因式，应先提取 公因式； (2)二套： 尝试使用公式法来分解因式； 步骤 (3)三查：要检查多项式因式是否能继续分解， 要分解到每个多项式不能再分解为止
6．下列式子中是完全平方式的是( D ) 2 2 2 A．a ＋ab＋b B．a ＋2a＋2 2 2 2 C．a －2b＋b D．a ＋2a＋1
7．下列计算结果正确的是( C ) 2 3 3 4 A．－2x y ·2xy＝－2x y 2 2 2 B．3x y－5xy ＝－2x y 4 2 3 C．28x y ÷7x y＝4xy 2 D．(－3a－2)(3a－2)＝9a －4
2
2
(1)三角形的周长为 4x ＋3 (2)19
2
mn a a ·a ＝________ ；(a ) ＝________； a n n 幂的 m m－n n n a b a a ÷a ＝________( a≠0)；(ab) ＝________. 运算
m
n
m＋n
m n
整式 的乘 法
相同字母 相乘，对 把________ 、________ 系数 单项式乘 于只在一个单项式里含有的字 以单项式 母， 则连同它的指数作为积的一 个因数 多项式乘 am＋bm＋cm (a＋b＋c)m＝____________ 以单项式 多项式乘 am＋an＋bm＋bn (a＋b)(m＋n)＝____________ 以多项式
中考数学(北京) §1.2 整 式
考点一 整式及其运算法则
教师专用题组
1.(2019安徽,2,4分)计算a3·(-a)的结果是 ( ) A.a2 B.-a2 C.a4 D.-a4 答案 D a3·(-a)=-a4,故选D.
2.(2019黑龙江齐齐哈尔,3,3分)下列计算不正确的是 ( ) A.± 9 =±3 B.2ab+3ba=5ab C.( 2 -1)0=1 D.(3ab2)2=6a2b4
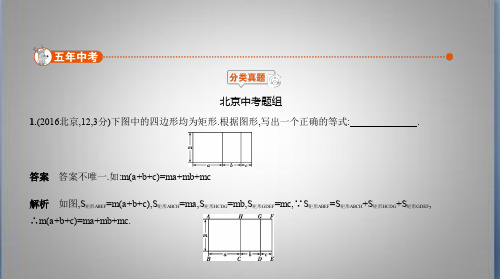
2.(2015北京,11,3分)分解因式:5x3-10x2+5x=
.
答案 5x(x-1)2 解析 5x3-10x2+5x=5x(x2-2x+1)=5x(x-1)2. 思路分析 分解因式的一般方法为“一提二套”,先提公因式,再套公式. 3.(2015北京,18,5分)已知2a2+3a-6=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值. 解析 原式=6a2+3a-4a2+1=2a2+3a+1=(2a2+3a-6)+7,∵2a2+3a-6=0,∴原式=0+7=7. 思路分析 先化简所求代数式,再整体代入求值. 方法技巧 求代数式的值的问题要先化简代数式.若由已知易得未知数的值,则代入未知数的值进行求解, 否则采用整体代入法,将所求代数式转化为含有已知代数式的形式.
答案 B 设恰好用完1 500元,可购买a个A品牌足球和b个B品牌足球. 由题意,得60a+75b=1 500,
整理得a=25- 5 b,∵a,b为正整数, 4
∴①b=4时,a=20;②b=8时,a=15; ③b=12时,a=10;④b=16时,a=5. ∴有4种方案,故选B.
7.(2018河北,13,2分)若2n+2n+2n+2n=2,则n= ( )
1.2整式PPT课件
8.(202X湖南怀化,2,4分)下列运算正确的是 ( ) A.3m-2m=1 B.(m3)2=m6 C.(-2m)3=-2m3 D.m2+m2=m4
答案 B A.原式=(3-2)m=m,故本选项错误; B.原式=m3×2=m6,故本选项正确; C.原式=(-2)3·m3=-8m3,故本选项错误; D.原式=(1+1)m2=2m2,故本选项错误.故选B.
2.(202X陕西,5,3分)下列计算正确的是 ( ) A.2a2·3a2=6a2 B.(-3a2b)2=6a4b2 C.(a-b)2=a2-b2 D.-a2+2a2=a2
答案 D 2a2·3a2 =6a4 ,选项A错误;(-3a2b)2=9a4b2,选项B错误;(a-b)2=a2-2ab+b2 ,选项C错误;-a2+2a2=a2 ,选项 D正确,故选D.
11.(202X湖南株洲,11,3分)单项式5mn2的次数为
.
答案 3
解析 单项式5mn2的次数是1+2=3. 故答案是3.
考点二 乘法公式
1.(202X湖南张家界,4,3分)下列运算正确的是 ( ) A.a2·a3=a6 B.a2+a3=a5 C.(a+b)2=a2+b2 D.(a3)2=a6
9.(2015湖南长沙,20,6分)先化简,再求值:(x+y)(x-y)-x(x+y)+2xy.其中x=(3-π)0,y=2.
解析 原式=x2-y2-x2-xy+2xy=xy-y2. 当x=(3-π)0=1,y=2时,原式=1×2-22=-2.
考点三 因式分解
1.(202X湖南株洲,8,3分)下列各选项中因式分解正确的是 ( ) A.x2-1=(x-1)2 B.a3-2a2+a=a2(a-2) C.-2y2+4y=-2y(y+2) D.m2n-2mn+n=n(m-1)2
中考数学总复习课件(完整版)
第2讲┃ 归类示例
请解答下列问题：
(1)按以上规律列出第5个等式：a5＝__9×_1_1_1___＝
___12_×__19_－_1_11_______；
(2)用含n的代数式表示第n个等式：an＝ （_2n_－__1_）_×_1_（__2_n＋__1_）__＝_12_×__2_n_1－_1_－__2_n_1＋_1___(n为正整数)；
第1讲 实数的有关概念 第2讲 实数的运算与实数的大小比较 第3讲 整式及因式分解 第4讲 分式 第5讲 数的开方及二次根式
第1讲┃ 实数的有关概念
第1讲┃ 考点聚焦
考点聚焦
考点1 实数的概念及分类
1．按定义分类：
实数
有理数
整数
分数
正整数 零 负整数
正分数 有限小数或 负分数 无限循环小数
________2．
图1－2
第1讲┃ 回归教材
2．[2011·贵阳] 如图1－3，矩形OABC的边OA长为2，
边 AB 长为1，OA 在数轴上，以原点 O 为圆心，对角线 OB
的长为半径画弧，交正半轴于一点，则这个点表示的实数是
( D) A ． 2.5
B ． 2√2
C.√3
D.√5
图1－3 [解析] 由勾股定理得 OB＝ OA2＋AB2＝ 22＋12＝ 5.
而应从最后结果去判断．一般来说，用根号表示
的数不一定就是无理数，如
是有理数，
用三角函数符号表示的数也不一定就是无理数，
如sin30°、tan45°也不是无理数，一个数是不
是无理数关键在于不同形式表示的数的最终结果
是不是无限不循环小数．
第1讲┃ 归类示例
► 类型之二 实数的有关概念