机械优化设计讲义第1讲
八章机械优化设计实例PPT课件

2)曲柄摇杆机构的传动角应在 和 之间,可得 min
max
g7
x
arccos
l2
2
l32 l1
2l2l3
l4
2
max
0
g8
x
min
arccos
l22
l32 l1
2l2l3
l4
2
0
二、曲柄摇杆机构再现已知运动轨迹的优化设计
所谓再现已知运动轨迹:是指机构的连杆曲线尽可能 地接近某一给定曲线。
第15页/共25页
不同的设计要求,目标函数不同。若减速器的中心距没有要求时,可取减速器 最大尺寸最小或重量最轻作为目标函数。
第16页/共25页
f x m min f x l r1 a r4 min
若中心距固定,可取其承载能力为目标函数。
f x 1/ min
减速器类型、结构形式不同,约束函数也不完全相同。 (1)边界约束
第14页/共25页
不同类型的减速器,选取的设计变量使不同的。
展开式圆柱齿轮减速器:齿轮齿数、模数、齿宽、 螺旋角及变位系数等。
行星齿轮减速器:除此之外,还可加行星轮个数。 设计变量应是独立参数,非独立参数不可列为设计 变量。例如齿轮齿数比为已知,一对齿轮传动中,只 能取Z1或Z2一个为设计变量。
又如中心距不可取为设计变量,因为齿轮齿数确定 后,中心距就随之确定了。
(2)性能约束
第17页/共25页
一、单级圆柱齿轮减速器的优化设计
第18页/共25页
第四节 平面连杆机构的优化设计 连杆机构的类型很多,这里只以曲柄摇杆机构两类 运动学设计为例来说明连杆机构优化设计的一般步骤 和方法。 一、曲柄摇杆机构再现已知运动规律的优化设计
机械优化设计孙靖民主编课件

航空航天
优化飞机结构,减少重量,提高燃油效率。
能源工程
优化能源装备设计,提高能量利用率。
汽车工程
优化汽车零部件设计,提高安全性和经济性。
制造工程
优化制造工艺,降低成本,提高生产效率。
机械优化设计案例分析
发动机优化
通过优化活塞、气门和燃烧室设 计,提高燃烧效率,降低排放。
涡轮叶片优化
通过优化叶片几何Байду номын сангаас状,提高涡 轮的效率和性能。
传动箱优化
通过优化齿轮和轴承设计,提高 传动效率和可靠性。
机械优化设计的挑战和未来发展
复杂性
机械系统的复杂性增加了优化设计的难度。
计算资源
优化设计需要大量的计算资源和时间。
多目标优化
考虑多个目标和约束条件的优化设计仍具挑战性。
智能化发展
人工智能和机器学习技术将推动机械优化设计的发展。
总结与展望
机械优化设计是提高机械产品性能和质量的关键技术。随着计算资源和算法 的发展,机械优化设计将在更多领域得到广泛应用,并推动机械工程的进步。
1 设计参数分析
通过分析设计参数的影响,找到关键参数并 确定其范围。
2 数学模型建立
建立机械系统的数学模型,包括力学、动力 学和材料性能等方面。
3 优化算法应用
使用优化算法(如遗传算法和粒子群算法) 搜索最佳设计方案。
4 结果评价与验证
评价设计方案的性能,并进行仿真和试验验 证。
机械优化设计的应用领域
机械优化设计孙靖民主编 课件
本课件介绍机械优化设计的原理、方法和应用领域。通过案例分析,了解机 械优化设计的挑战和未来发展。最后总结与展望。
机械优化设计的定义
机械优化设计是通过优化设计参数,提高机械产品性能和质量的过程。它综合运用数学模型、仿真和试验验证 等方法,以达到最佳设计方案。
《机械优化设计》第一章 优化设计概述

f ( x) W1 f1 ( x) W2 f2 ( x) ... Wq f q ( x)
Wq:加权因子,是个非负系数。
第一章 优化设计概述
第三节 优化设计问题的数学模型
求设计变量 x [ x1 x2 xn ]T , xn ) min , l) 使目标函数f ( x) f ( x1 , x2 , 和g j ( x) 0( j 1, 2, , m)
第一章 优化设计概述
第一节 人字架的优化设计
FL F ( B 2 h ) 钢管所受的压力F1 h h 2 EI 压杆失稳的临界压力Fe 2 L 其中,I是钢管截面惯性矩 I
1 2 2
θ
θ
L
A 2 (T D 2 ) 4 8 A是钢管截面面积A ( R 2 r 2 ) TD (R4 r 4 ) r和R分别是钢管的内半径和外半径 D=r+R而T=R-r
第一章 优化设计概述
第三节 优化设计问题的数学模型
优化设计的维数:设计变量的数目称为优化设计的维数,如 有n(n=1,2,…)个设计变量,则称为n维设计问题。
任意一个特定的向量都可以说是一个“设计”。
第一章 优化设计概述
第三节 优化设计问题的数学模型
设计空间:由n个设计向量为坐标所组成的实空间称作设计 空间。 一个“设计”,就是设计空间中的一个点,这个点可以看 成是设计变量向量的端点(始点是坐标原点),称这个点式 设计点。 设计空间的维数(设计的自由度):设计变量愈多,则设计 的自由度愈大、可供选择的方案愈多,设计愈灵活,但难度 亦愈大、求解亦愈复杂。 • 含有2—10个设计变量的为小型设计问题; • 10—50个为中型设计问题; • 50个以上的为大型设计问题。
机械优化设计方法ppt课件

f (x) f (x1, x2,...xn )
23
优化设计的目的就是要求所选择的设计变
量使目标函数达到最佳值,即使 f (x) Opt
通常 f (x) min
单目标设计问题
目标函数
多目标设计问题
目前处理多目标设计问题的方法是组合成一个 复合的目标函数,如采用线性加权的形式,即
f (x) W1 f1(x) W2 f2 (x) ... Wq fq (x)
24
四、优化问题的数学模型
优化设计的数学模型是对优化设计问题的数 学抽象。 优化设计问题的一般数学表达式为:
min f (x) x Rn
s.t. gu (x) 0 u 1, 2,..., m
hv (x) 0 v 1, 2,..., p n
4
图1-3 机械优化设计过程框图
5
优化设计与传统设计相比,具有如下三个特点:
(1)设计的思想是最优设计; (2)设计的方法是优化方法; (3)设计的手段是计算机。
二、机械优化设计的发展概况
1ቤተ መጻሕፍቲ ባይዱ优化设计的应用领域 近几十年来,随着数学规划论和电子计算机的迅 速发展而产生的,它首先在结构设计、化学工程、 航空和造船等部门得到应用。
架的高h和钢管平均直径D,使钢管总质量m为最小。
11
图2-2 人字架的受力
12
人字架的优化设计问题归结为:
x D H T 使结构质量
mx min
但应满足强度约束条件 x y 稳定约束条件 x e
13
1
钢管所受的压力
F1
FL h
F(B2 h
25
机械优化设计PPT

二、离散变量优化的主要方法及其特点、思路和步骤
表7-3 离散变量优化的主要方法及其特点和步骤
图7-8 两个目标函数的等值线和约束边界
三、协调曲线法
图7-9 协调曲线
四、分层序列法及宽容分层序列法
四、分层序列法及宽容分层序列法
采用分层序列法,在求解过程中可能会出现中断现象,使求解过程 无法继续进行下去。当求解到第k个目标函数的最优解是惟一时, 则再往后求第(k+1),(k+2),…,l个目标函数的解就完全没有意义 了。这时可供选用的设计方案只是这一个,而它仅仅是由第一个至 第k个目标函数通过分层序列求得的,没有把第k个以后的目标函数 考虑进去。尤其是当求得的第一个目标函数的最优解是唯一时,则 更失去了多目标优化的意义了。为此引入“宽容分层序列法”。这 种方法就是对各目标函数的最优值放宽要求,可以事先对各目标函 数的最优值取给定的宽容量,即ε1>0,ε2>0,…。这样,在求后一 个目标函数的最优值时,对前一目标函数不严格限制在最优解内, 而是在前一些目标函数最优值附近的某一范围内进行优化,因而避 免了计算过程的中断。
5.组合型算法终止准则
6.组合型算法的辅助功能
(1) 直线加速与二次曲线加速 当目标函数严重非线性时,即若
函数具有尖峰脊线,即存在“谷”时,则希望能沿着脊线方向进 行搜索,可迅速提高算法的寻优效率,该算法称为具有脊线加速 能力。 (2) 网格搜索法技术 将离散空间视为一网格空间,每个离散点 就是一个网格节点。 (3) 变量分解策略 将目标函数中的变量分成若干个子集合,若
离散复合形,重新进行调优搜索,直到前后两次离散复合形运算
的优化点重合,算法才最终结束。
6.组合型算法的辅助功能
图7-24 有脊线目标函数 寻优过程示意图
第一章 机械优化设计的基本问题PPT课件

10d D 0 或 10d0.62831805
n
n
该问题属于二维约束问题
12
1.1.3连杆机构优化设计
由图所示六杆机构。它是铰链四杆机构ABCD和带有 滑块5的摆杆6由连杆BE连接而成的。原动件AB逆时 针转动使从动件6绕P点往复摆动。机架AD水平置放, F点已选定。 要求: 当原动件AB转角φ0在180—300o范围内, 摆杆6处于LM位置不动, 即从动件摆杆产生间歇运动。
单价c与螺栓材料,直径d,长度l及加工状况有关。本组 螺栓取35号钢,长度l=50mm的六角头半精制螺栓,单 价见下表
直径d (mm)
单价c (元)
10 0.052
12 0.091
14 0.142
16 0.174
18 0.228
20 0.251
9
由表中数据初步画C=f(d)曲线,由下图线形回归法求得 方程:
表a,每小时生产零件利润量
零件种类
机器序号
1
2
3
4
1
5
6
4
3
2
5
4
5
4
3
6
7
2
8
表b,各机器生产零件速率
零件种类
机器序号
1
2
3
4
1
8
2
4
9
2
7
6
6
3
3
4
8
5
2
19
解:为获利润最大,需合理确定每台机器生产某种零件
若干,设xij表示第j台机器生产第i中零件的件数。
一个月内获总利润: W 5 x 1 16 x 1 24 x 1 33 x 1 45 x 2 14 x 2 25 x 2 34 x 24 6 x 3 17 x 3 22 x 3 38 x 34 且要满足以下约束条件: (1)数量需求限制
01机械优化设计第一章(哈工大—孙靖民)

哈尔滨工业大学 孙靖民 主编
2020年8月14日9时12分
课程介绍
计划学时数:26学时 使用教材
孙靖民. 机械优化设计. 北京:机械工业出版社,2003
参考书
[1]方世杰,綦耀光主编. 机械优化设计. 北京:机械工业 出版社,2003
[2] 陈立周,机械优化设计方法,北京:冶金工业出版社, 1997
Page 4
2020年8月14日9时12分
优化是万物演化的自然选择和趋势
•(1)来源:优化一语来自英文Optimization,其本意是
寻优的过程,最优化可简写为Opt;
•(2)优化过程:是寻找约束空间下给定函数取极大值或
极小值的过程。
f
例如, 在右图中,求得一维函
f(x)
数 f(x) 最小值的条件为:若
Page 13
2020年8月14日9时12分
优化设计的作用(优点):
使传统机械设计中,求解可行解上升为求解最优 解成为可能;
使传统机械设计中,性能指标的校核可以不再进 行;
使机械设计的部分评价,由定性改定量成为可能; 大大提高了产品的设计质量,从而提高了产品的
质量; 提高生产效率,降低产品开发周期; ……
3、武汉钢铁公司从德国引进的1700薄板轧机,经该公 司自主优化后,20年8月14日9时12分
4、美国波音飞机公司对大型机翼用138个设计变量进 行结构优化,使重量减少了三分之一;大型运输舰用 10个变量进行优化设计,使成本降低约10%。
实践证明,最优化设计是保证产品具有优良的性能,减轻 自重或体积,降低产品成本的一种有效设计方法。同时也可使 设计者从大量繁琐和重复的计算工作中解脱出来,使之有更多 的精力从事创造性的设计,并大大提高设计效率。
《现代机械优化设计》第1章 概述

* 最优化方法用于机械设计是从二十世纪六十年代开始的, 较早的成果主要反映在机构的优化设计方面,现已广泛用 于机械零部件设计和机械系统的优化设计。
机械优化设计的主要内容
一)优化设计概论 二)一维搜索方法 三)无约束优化方法 四)线性规划方法 五)约束优化方法 六)多目标优化方法 七)机械优化设计实例
x1
3. 步长:
(k)
4. 是否终止迭代。 --后三个问题是每次迭代都要解决的问题,
但中间两个是数学规划法的核心。
3.算法的收敛性和收敛准则
1)算法的收敛性
若由某迭代算法计算得到的近似解系列 X (k),k 0,1,2,.....
有极限 lim X (k) X *,这里X *为精确解,则称该迭代算法是 k
“所有的”可行方案中找出“最优的”设 计方案.
二.优化设计方法简介
1)古典方法: 微分法; 变分法. ---仅能解决简单的极值问题
2)现代方法: 数学规划方法 ---可求解包含等式约束和不等式约束 的复杂的优化问题.
有线性规划、非线性规划、几何规划、动态规划 和混合离散规划等。
三.最优化方法的发展概况
---是适于生产建设、计划管理、科学实验和战争的需要发展起来的。
1)二十世纪三十年代.前苏联 Канторович 根据生产组织和计划管理的需要提出线性规划问题. 在 第二次世界大战期间出于战争运输需要,提出线性规划 问题的解法;
2)二十世纪五十年代末. H.W.Kuhn & A.W.Tucker提出 非线性规划的基本定理,奠定了非线性规划的理论基础. 其求解方法在六十年代获得飞速发展;
3)二十世纪六十年代.美数学家 R.J.Duffin(卡内基工 学院的达芬教授)提出了几何规划, 可把高度非线性的 问题转化为具有线性约束的问题来求解, 使计算大为简 化; 4)动态规划由 数学家R.Bellman (University of Southern California)创立, 可解与时间有关的最优化问题;
机械优化设计第1章概述-PPT精品文档

50年代末数学规划方法被首次用于结构最优化,并成为优 化设计中求优方法的理论基础。数学规划方法是在第二次世界 大战期间发展起来的一个新的数学分支,线性规划与非线性规 划是其主要内容。
最优化设计是在数学规划方法的基础上发展起来的,是 6O年代初电子计算机引入结构设计领域后逐步形成的一种有效的 设计方法。
Evaluation only. eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 Copyright 2019-2019 Aspose Pty Ltd.
第一章 优化设计的基本概念
§1-1 绪论
Evaluation only. §1-2 优化设计问题的示例 eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 Copyright 2019-2019 Aspose Pty Ltd. §1-3 优化设计的数学模型
第三阶段 工程优化:近二十余年来,计算机技术的发展给 Evaluation only. 解决复杂工程优化问题提供了新的可能,非数学领域专家开发 了一些工程优化方法,能解决不少传统数学规划方法不能胜任 eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 的工程优化问题。在处理多目标工程优化问题中,基于经验和 Copyright 2019-2019 Aspose Pty Ltd. 直觉的方法得到了更多的应用。
机械优化设计
机械工程系 吴军 2009.8
Evaluation only. eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 Copyright 2019-2019 Aspose Pty Ltd.
机械优化设计讲义

机械优化设计讲义学院:专业:姓名:学号:第一讲绪论一、机械优化设计的基本概念1、什么是优化设计在机械产品设计过程中,根据问题的性质和给定的条件,在分析的基础上,综合各方面的要求因素,从全部可行的方案中,寻找出最优方案的方法和过程。
优化设计是利用高等数学中求极(最)值理论,以计算机为计算工具,用数值分析的方法,对机械产品设计问题求出最佳设计参数的工程方法。
“优化设计”对应的是“经验设计”.2、优化设计的过程A、分析设计任务的对象,提出设计思想B、建立优化数学模型,包括选取设计变量,建立目标函数和约束方程C、选择优化方法(自编程序或选择商品程序),上机计算D、对计算结果进行分析F、当结果不甚合理时,修改数学模型,返回B.3、优化设计的局限A、优化设计过程是人和机器合作完成的,“人”在其中起着巨大作用。
B、所谓“最优”是相对的,当设计思想、约束条件,甚C、“最优方案”是否合理、可行,还是要用经验来判断。
二、一个优化设计实例某空心圆柱压杆,压力载荷为P,长度L,截面外径D0,内径D1.变换成中径D和壁厚T;D= (D0+D1)/2T = (D0—D1)/2设材料已经选定,即材料的弹性模量E,许用应力【σ】,密度ρ等已确定。
设计要求:1、强度要求:σ压=P/(πDT)≤【σ】2、稳定要求:σ压=P/(πDT) ≤ 欧拉应力3、结构要求: D ≤ K1T ≥ K2K1,K2为定值T ≤ D/2杆的重量:W = πDTLρ整个问题可以归结为:设计一个压杆,在满足上述5个条件的前提下,使W最小.经验设计此问题,人工选取一对D和T,分别代入上述5个条件,都满足时即可。
是否重量最轻,材料最省,不予考虑,也不得而知。
用优化设计的语言表示上述问题:D,T(或者D0、D1)为设计变量,表示成: X =(x1, x2)W为目标函数,是设计变量的函数,表示成:W = F(x1, x2) = F(X)5个条件叫做约束方程,或者约束条件。
机械优化设计讲义
《机械优化设计》讲义刘长毅第一讲第一课时:机械优化设计概论课程的研究对象:根据最优化原理和方法,利用计算机为计算工具,寻求最优设计参数的一种现代设计方法。
目标:本课程目标体系可以分为三大块:理论基础、算法的分析、理解和掌握,算法的设计、实现(编程)能力的培养。
将主要是对算法的学习为主,并兼顾培养一定的解决实际问题能力、上机编程调试能力。
首先,几个概念:优化(或最优化原理、方法)、优化设计、机械(工程)优化设计。
现代的优化方法,研究某些数学上定义的问题的,利用计算机为计算工具的最优解。
优化理论本身是一种应用性很强的学科,而工程优化设计(特别是机械优化设计)由于采用计算机作为工具解决工程中的优化问题,可以归入计算机辅助设计(CAD)的研究范畴。
再,优化方法的发展:源头是数学的极值问题,但不是简单的极值问题,计算机算法和运算的引入是关键。
从理论与实践的关系方面,符合实践-理论-实践的过程。
优化原理和方法的理论基础归根结底还是来源于实际生产生活当中,特别是工程、管理领域对最优方案的寻找,一旦发展为一种相对独立系统、成熟的理论基础,反过来可以指导工程、管理领域最优方案的寻找(理论本身也在实践应用中不断进步、完善)。
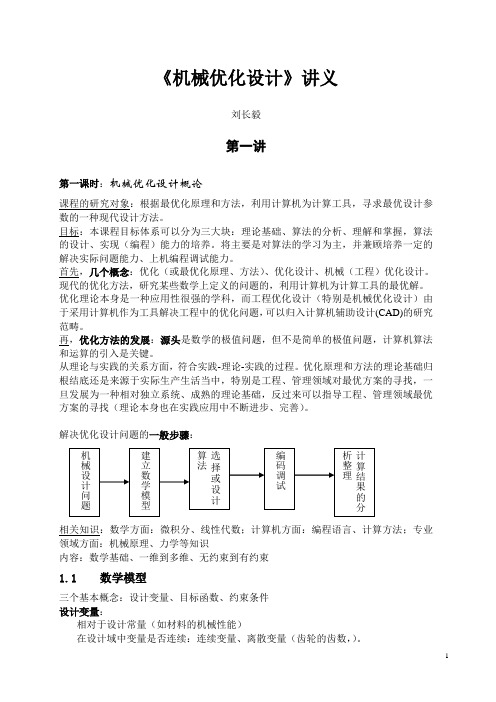
解决优化设计问题的一般步骤:相关知识:数学方面:微积分、线性代数;计算机方面:编程语言、计算方法;专业领域方面:机械原理、力学等知识内容:数学基础、一维到多维、无约束到有约束1.1数学模型三个基本概念:设计变量、目标函数、约束条件设计变量:相对于设计常量(如材料的机械性能)在设计域中变量是否连续:连续变量、离散变量(齿轮的齿数,)。
设计问题的维数,表征了设计的自由度。
每个设计问题的方案(设计点)为设计空间中的一个对应的点。
设计空间:二维(设计平面)、三维(设计空间)、更高维(超设计空间)。
目标函数:设计变量的函数。
单目标、多目标函数。
等值面的概念:设计目标为常量时形成的曲面(等值线、等值面、超等值面)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:一金属板,长为24cm,宽为50cm。要制成如图所示的对称型槽。 求斜边长a和倾角θ为多大时,容积最大。
设计变量:a,θ 目标函数: V (a, ) 1 (24 2a 24 2a
2
2a cos )a sin 50
约束条件:0≤a≤12, 0≤θ≤π
性能约束:针对性能要求而提出的约束。
边界约束:对设计变量的取值范围加以限制的约束。
2.按数学表达式的不同: 不等式约束: g j ( X ) 0
( j 1,2,, m)
等式约束: hk ( X ) 0
(k 1,2, , l )
上例中,约束条件: g1(a)=-a≤0 g2(a)=a-12≤0 g3(θ)= -θ≤0 g4(θ)=θ-π≤0
注意:
X [x1, x2 ,, xn ]T
1.向量中分量的次序是任意的,根据使用的方便任意选取。
2.由n个设计变量为坐标所组成的实空间称做设计空间, 一个“设计”对应设计空间中的一点。
3.设计变量视为连续有界的变量,机械设计中的离散性参数 以后再讨论(如模数) 。
1.2.2 约束条件 约束条件:一个可行设计必须满足的某些设计限制条件。 1.按约束的性质不同:
机
第1章 绪论
械
第2章 优化设计的数学基础
优
第3章 一维搜索方法
化
第4章 无约束优化方法
设
第5章 约束优化方法
计
第6章 多目标及离散变量优化方法
第1章 绪论
1.1 优化设计概述 1.2 优化设计问题的数学模型 1.3 优化设计问题的基本解法及收敛条件
1.1 优化设计概述
优化设计:最优化原理+计算技术 机械优化设计:是使某项机械设计在规定的各种设计限制条件下,
|| f ( X k ) || 4 (4)迭代次数作为终止原则。
迭代次数=N。
θ g1(a)=0 π
.A
0 <1>约束面:由g(X)=0的点集构成。 <2>可行域:满足所有约束条件的点的集合。 <3>可行点:可行域中的任一点。 <4>边界点:在约束边界上的点。
<5>起作用约束:边界点所在的约束。
g2(a)=0
g4(θ)=0
. B
g3(θ)=0 12 a
1.2.3 目标函数 目标函数:用以评价设计方案优劣的函数。
迭代公式: Xk+1=Xk+αkdk
1.建立搜索方向dk 2.是计算最佳步长αk
迭代终止准则: (1)相邻两设计点的移动距离达到充分小时。
‖Xk+1-Xk‖≤ε1 (2)函数值的下降量已达到充分小时。
| f ( X k1 ) f ( X k ) | 3 (3)某次迭代点的目标函数梯度已达到充分小时。
优化问题求解方法分类: (1)解析解法:根据目标函数导数的变化规律与函数极值的关系,
求目标函数的极值点。 (2)数值解法(迭代法):根据目标函数值的变化规律,以适当的步
长沿着能使目标函数值下降的方向,逐步 向目标函数值的最优点进行探索,逐步逼 近到目标函数的最优点。
迭代公式: Xk+1=Xk+αkdk
一维搜索过程:
在过点Xk和dk方向上求一元函数:f(Xk)=f(Xk+αkdk)的极值点的问题。 这里只有αk是唯一的变量。所以这个问题就是以αk为变量的一元函数 φ(αk)求极值的问题。
这种一元函数求极值的过程简称为一维搜索过程,它是确定αk的 值使f(X k+αkd k)取极值的过程。
数学规划法的核心:
V 0 a
V
0
机械优化设计包括: 1.建立优化设计问题的数学模型 2.选择恰当的优化方法与程序
1.2 优化设计问题的数学模型
数学模型:
min f (X ) s.t. g j ( X ) 0
hk ( X ) 0
X [x1, x2 ,, xn ]T Rn ( j 1, 2,, m)
(kБайду номын сангаас 1, 2,,l)
f ( X ) f (x1, x2 ,, xn )
优化设计的目的就是要求所选择的设计变量使目标函数值 达到最佳值。
即:f(X)→min
1.3 优化设计问题的基本解法及收敛条件
优化设计的全过程:
建立优化设计的数学模型 →选择适合的优化方法 →确定必要的数据和设计初始点 →编写计算机的语言程序 →通过计算机求解并输出计算结果 →对结果数据进行必要的分析
三要素: 1.设计变量 2.约束条件 3.目标函数
优化问题的分类: 1.无约束优化问题:无约束条件 2.约束优化问题 :有约束条件 1.线性规划问题:约束函数和目标函数同时为线性函数 2.非线性规划问题:约束函数和目标函数不同时为线性函数
1.2.1 设计变量
设计常数:根据实际情况预先确定
设计变量:需要优选的参数,其数值在优化设计过程中是变化的
