四年级下册运算定律汇总

四年级下-运算定律

运算定律知识集结知识元加法运算定律知识讲解加法运算定律1、加法交换律：两个数相加，交换加数的位置，它们的和不变，这叫做加法的交换律.用字母表示为：a+b=b+a 例如：3+4=4+3 5+6=6+52、加法结合律：三个数相加，先把前两个数相加，再和第三个数相加；或者先把后两个数相加，再和第一个数相加，它们的和不变，这叫做加法的结合律.用字母表示为：(a+b)+c=a+(b+c) 例如：（3+5）+5=3+（5+5）（5+6）+4=5+（6+4）例题精讲加法运算定律例1.250+300+350+400+450+500+550=（）A．250×7 B．400×7 C．550×7例2.'你能很快计算出下题的结果吗？1541+1543+1545+1550+1555+1557+1559'例3.'用简便方法计算。

500-41-1-42-2-43-3-…-48-8-49-9'例4.'用简便方法计算。

30-29+28-27+26-25+…+14-13+12-11'例5.'用简便方法计算。

9+99+999+9999+99999'例6.'用合适的方法计算。

9+99+999+9999+99999'例7.'用5、6、7、8编写4道得数相同的两位数加两位数的算式。

'例8.'用合适的方法计算。

40-39+38-37+...+24-23+22-21'例9.'用简便方法计算1+3+5+7+9+…+95+97+99。

（1）观察发现1+99=100，3+97=100，…，49+51=_____，这50个加数一共可以组成_____组，这个算式就可以转换成100×_____=_____。

（2）根据上面的解题方法，你能算出下面加法的得数吗？试一试。

2+4+6+8+10+...+96+98+100'例10.'有一群动物在渡口准备过江，现有一大一小两条渡船，这些动物能同时过江吗？如何乘船合适？'乘法运算定律知识讲解乘法交换律和结合律1.乘法交换律：两个数相乘，交换两个因数的位置，积不变。

四年级下册数学【运算律】知识点+例题解析

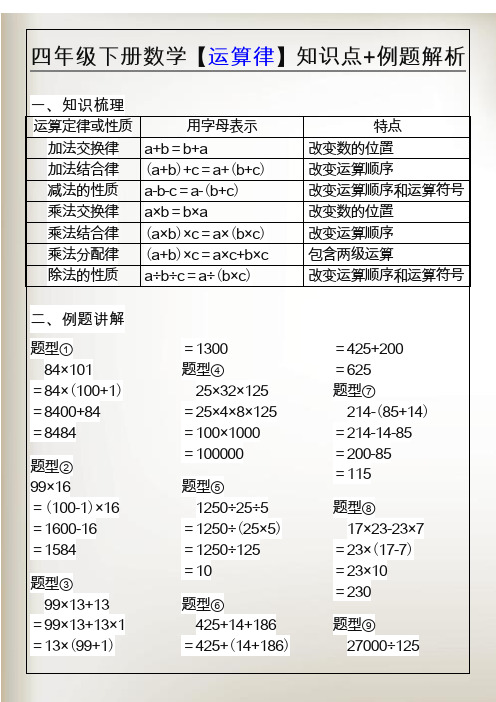
四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10＝230题型⑨27000÷125＝27×1000÷125 ＝27×8 ＝216四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10。

人教版小学数学四年级下册【运算定律与简便计算】知识篇

加、减法的速算与巧算( 基础篇 )1、加法运算定律（2个）：☆加法交换律：两个数相加，交换加数的位置，和不变。

即：a + b = b + a☆加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

即：(a + b) + c = a + (b + c)（提醒：运用加法结合律时，要注意把结合的两个数用括号括起来。

）连加的简便计算方法：①使用加法交换律、结合律凑整（把和是整十、整百、整千的数先交换再结合在一起。

）②个位：1与9，2与8，3与7，4与6，5与5，结合。

③十位：0与9，1与8，2与7，3与6，4与5，结合。

连加的简便计算例题：50+98+50 488+40+60 １６５+９３+３５ 65+28+35+72＝50+50+98 ＝488+（40+60）＝９３+１６５+３５＝（65+35）+（28+72）＝100+98 ＝488+100 ＝９３+（１６５+３５）＝ 100+100＝198 ＝588 ＝293 ＝ 2002、连减的性质：☆一个数连续减去几个数等于这个数减去这几个数的和。

即：a – b – c = a – (b + c)注：连减的性质逆用：a – (b + c) = a – b – c = a – c – b☆一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

即：a - b - c＝a - c - b连减的简便计算方法：①连续减去几个数就等于减去这几个数的和。

如：106-26-74 = 106-(26+74)②连续减去两个数可以先减去后一个数再减去前一个数。

如：226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。

如：106-(26+74) = 106-26-74连减的简便计算例题：528—65—35 528—89—128 528—（150+128）=528—（65+35） =528—128—89 =528—128—150=528—100 =400—89 =400—150=428 =311 =2503、加、减法混合运算的性质：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。

四年级下册数学运算定律分类指导举一反山

四年级下册运算定律分类指导举一反三一、加法运算定律1.加法交换律：两个数相加，交换加数的位置，和不变。

加法交换律也合用三个数连续相加。

用字母表示：a+b=b+a例：16+23=23+16做一做：75+168+252 65+73+135 88+75+122.加法结合律：三个数相加，先把前两个数相加,或者先把后两个数相加,和不变。

用字母表示;(a+b)+c=a+(b+c)例：（22＋58）+42=22+（58+42）=22+100=122做一做：425+14+186 186+38+62 155+657+2453.加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数调换位置，再将这两个加数结合起来先运算。

加法交换律和加法结合律的综合应用时，加括号可以使计算过程更清晰。

例：343+452+148+257=343+257+452+148=（343+257）+（452+148）=600+600=1200做一做：63＋71＋37＋29 67+25+33+75 129+235+171+165二、连减的简便计算1.一个数连续减去两个数,等于这个数减去后面两个数的和。

用字母表示：a-b-c=a-(b+c)例：342-28-172=342-（28+172）=342-200=142做一做：868-52-48 400-256-44 500－257－34－1432.如果一个数连续减去两个数，交换两个减数的位置，差不变。

用字母表示：a-b-c=a-c-b例：198-75-98=198-98-75=100-75=25做一做：425-74-25 515-128-215 534－257－34－1433.“同级运算”中的数字搬家。

加减法属同一级运算，交换加数或者减数的位置，结果不变。

（通常排在第一个位置上的数字不动，后面的数字在搬家时一定要带着符号搬）用字母表示：a-b＋c=a＋c-b例：384-59+16=384+16-59=400-59=341做一做：528-64+72 672-36+28 342-87+584.减号后面加括号，加变减，减变加。

四年级数学下册运算定律知识点梳理与思维导图

百、整千……的减去一个较小的数，然后利用运算定律简便计算举。例：98×250=（100-2）×250
连除的性质公式：a÷b÷c=a÷（b×c ）
拆分、凑整简便运算
描述：举当例一：个33数0÷比5整÷百2=、33整0÷千（…5…×稍2大）一些时，可以将它拆成整百、
拆分法
整千……和一个较小的数的和，然后利用运算定律简便计算。
凑整法
举例：204×25=（200+4）×25 描述：当一个数比整百、整千……稍小一些时，可以将它凑成整
加法运算定律加法交换律
定义：两个数相加，交换加数的位置，和不变。
公式：a+b=b+a 举例：40+56=56+40
加法结合律
定义：三个数相加，先把前两个数相加，或者先把后两个
数相加，和不变。公式：（a+b）+c=a+（b+c）举例：（88+104）+96=88+（104+96）
定义：两个数相乘，交换因数的位置，积不变。
公式：（a+b）×c=a × c+ b× c
举例：（4+2）×25=4×25+2×25
连减的性质
连减、连这个数减去两个数的和
公式：a-b-c=a -（b + c ）举例：234-66-34=234-（66+34）
定义：一个数连续除以两个数，等于这个数除以两个数的积。
乘法交换律公式：a×b=b×a
举例：25×4=4×25
定义：三个数相乘，先乘前两个数，或者先乘后两个数，
运
乘法运算定律乘法结合律
积不变。公式：（a×b）×c=a × （b × c ）举例：（25×5）×2=25×（5×2）

人教版四年级下册数学之运算定律

人教版四年级下册数学之运算定律一、加法运算定律1.加法交换律两个数相加,交换加数的位置,和不变。

用字母表示为a+b=b+a 。

2.加法结合律三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。

用字母表示为(a+b )+c=a+(b+c )。

加法交换律和加法结合律同样适用于计算多个数连加。

如如: 125+36+75+264=(125+75)+(36+264)=200+300=500有的算式中带有括号,先算括号里面的并不简便,根据数的特点可以先把括号去掉,再运用加法交换律和加法结合律使计算变得简便。

如:(452+36)+(48+564)=(452+48)+(36+564) =500+600 =1100注意:在计算连加算式时,不要盲目地进行计算,首先要观察算式中的数,看看有没有能凑成整十、整百、整千的数．．．．．．．．．．．．．．．．．．,．如果有．．．,．那么可以运用加法交换律或加法结合律进行计算．．．．．．．．．．．．．．．．．．．．．,．这样既简便．．．．．又准确．．．。

二、减法的运算性质1.一个数连续减去两个数,等于减去这两个数的和。

用字母表示为a-b-c=a-(b+．c )。

注意:根据数据的特点逆运用减法的性质也可以使计算变．．．．．．．．．．．．．．．．．．．．．．得简便。

括号前面是减号．．．．．．．．．．．,．去掉括号后．．．．．,．括号里面的算式要改变运．．．．．．．．．．．算符号．．．。

如:346-(146+63)=346-146-．63 =200-63 =137减法性质的逆运用:一个数减去两个数的和相当于从被减数中连续减去这两个数。

2.在连减运算中,任意交换两个减数的位置,差不变。

用字母表示为a-b-c=a-c-b 。

3.在加减混合运算中,带着数前面的运算符号交换加数、减数的位置再进行计算,其结果不变。

用字母表示为a+b-c=a-c+b (a>c )运用加法交换律可以验算加法:交换两个加数的位置再算一遍,看看和是否相等。

小学四年级数学运算定律知识点

小学四年级数学运算定律知识点归类
一、加法运算定律
1、加法交换律：两个数相加，交换加数的位置，和不变。

a+b=b+a
2、加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

(a+b)+c=a+(b+c)
3、连减的性质：一个数连续减去两个数，等于这个数减去那两个数的和。

a-b-c=a-(b+c)
二、乘法运算定律：
1、乘法交换律：两个数相乘，交换因数的位置，积不变。

a×b=b×a
2、乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变。

(a×b)×c=a×(b×c)
3、乘法分配律：两个数的和与一个数相乘，可以先把这两个数分别与这两个数相乘，再把积相加。

(a+b)×c=a×c+b×c (a-b)×c=a×c-b×c
4.一个数连续除以两个数等于这个数除以两个数的积：
a÷b÷c=a÷（c×b）
a÷（c×b）= a÷b÷c。

(完整版)人教版小学数学四年级下册【运算定律与简便计算】知识篇

加、减法的速算与巧算( 基础篇 )1、加法运算定律（2个）：☆加法交换律：两个数相加，交换加数的位置，和不变。

即：a + b = b + a☆加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

即：(a+b)+c = a+(b+c)（提醒：运用加法结合律时，要注意把结合的两个数用括号括起来。

）连加的简便计算方法：①使用加法交换律、结合律凑整（把和是整十、整百、整千的数先交换再结合在一起。

）②个位：1与9，2与8，3与7，4与6，5与5，结合。

③十位：0与9，1与8，2与7，3与6，4与5，结合。

连加的简便计算例题：50+98+50 488+40+60 165+93+35 65+28+35+72＝50+50+98 ＝488+（40+60）＝93+165+35 ＝（65+35）+（28+72）＝100+98 ＝488+100 ＝93+(165+35) ＝ 100+100＝198 ＝588 ＝293 ＝ 2002、连减的性质：☆一个数连续减去几个数等于这个数减去这几个数的和。

即：a – b – c = a – (b + c)注：连减的性质逆用：a – (b + c) = a – b – c = a – c – b☆一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

即：a-b-c＝a-c-b连减的简便计算方法：①连续减去几个数就等于减去这几个数的和。

如：106-26-74 = 106-(26+74)②连续减去两个数可以先减去后一个数再减去前一个数。

如：226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。

如：106-(26+74) = 106-26-74连减的简便计算例题：528—65—35 528—89—128 528—（150+128）=528—（65+35） =528—128—89 =528—128—150=528—100 =400—89 =400—150=428 =311 =2503、加、减法混合运算的性质：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。

四年级下册运算定侓

四年级下册运算定侓一、加法运算定律。

1. 加法交换律。

- 定义：两个数相加，交换加数的位置，和不变。

- 用字母表示：a + b=b + a。

例如：3+5 = 5+3，结果都是8。

2. 加法结合律。

- 定义：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

- 用字母表示：(a + b)+c=a+(b + c)。

例如：(2 + 3)+4=2+(3 + 4)，先算2+3 = 5，再算5+4 = 9；右边先算3+4 = 7，再算2+7 = 9。

二、乘法运算定律。

1. 乘法交换律。

- 定义：两个数相乘，交换因数的位置，积不变。

- 用字母表示：a×b = b×a。

例如：3×5=5×3 = 15。

2. 乘法结合律。

- 定义：三个数相乘，先把前两个数相乘，再和另外一个数相乘，或者先把后两个数相乘，再和另外一个数相乘，积不变。

- 用字母表示：(a×b)×c=a×(b×c)。

例如：(2×3)×4 = 2×(3×4)，左边先算2×3 = 6，再算6×4 = 24；右边先算3×4 = 12，再算2×12 = 24。

3. 乘法分配律。

- 定义：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。

- 用字母表示：(a + b)×c=a×c + b×c。

例如：(2+3)×4 = 2×4+3×4，左边先算2 + 3=5，再算5×4 = 20；右边2×4 = 8，3×4 = 12，8+12 = 20。

三、减法的性质。

1. 一个数连续减去两个数，等于这个数减去这两个数的和。

- 用字母表示：a - b - c=a-(b + c)。

例如：10-3 - 2=10-(3 + 2)，左边先算10-3 = 7，再算7-2 = 5；右边先算3+2 = 5，再算10 - 5=5。

小学数学四年级下册运算定律定义和公式

小学数学四年级下册运算定律定义和公式运算定律的定义和公式加法的交换律定义：两个数相乘，互换加数的边线，和维持不变，这叫作用法的交换律。

公式：a+b=b+a乘法的结合律定义：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变，这叫做加法的结合律。

公式（a+b)+c=a+(b+c)减法的性质定义：一个数已连续乘以两个数可以乘以这两个数的和，或者互换后两个减数的边线，高维持不变。

公式：a-b-c=a-(b+c)a-b-c=a-c-b乘法的交换律定义：两个数相加，互换因数的边线，内积维持不变，这叫作乘法的交换律。

公式：axb=bxa乘法的结合律定义：三个数相乘，先乘前两个数，或者先乘后两个数，积不变。

这叫做乘法的结合律。

公式：(axb)xc=ax(bxc)乘法的分配律定义：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加，这叫做乘法的分配律。

公式：（a+b)xc=axc+bxc定义：两个数的高与一个数相加，可以先把它们分别与这个数相加，再相乘。

公式：（a-b)xc=axc-bxc连除的性质定义：一个数已连续除以两个数，可以除以这两个数的积，或者互换后面两个除数的边线，商维持不变。

公式：a÷b÷c=a÷(bxc)a÷b÷c=a÷c÷b加法各部分间的关系：和=加数+加数加数=和-另一个加数乘法各部分间关系：积=因数x因数因数=积÷另一个因数余数各部分间关系：被除数=商x除数+余数商=（被除数-余数）÷除数除数=（被除数-余数）÷商除法各部分间的关系：商=被除数÷除数除数=被除数÷商被除数=商x除数减法各部分间的关系：差=被减数-减数减数=被减数-差被减数=减数+差。

小学四年级数学运算定律、法则与顺序大全,

小学四年级数学运算定律、法则与顺序大全，给孩子收藏！1. 加法交换律：两个数相加，交换加数的位置，它们的和不变，即a+b=b+a 。

2. 加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再和第一个数相加它们的和不变，即（a+b)+c=a+(b+c) 。

3. 乘法交换律：两个数相乘，交换因数的位置它们的积不变，即a×b=b×a。

4. 乘法结合律：三个数相乘，先把前两个数相乘，再乘以第三个数；或者先把后两个数相乘，再和第一个数相乘，它们的积不变，即(a×b)×c=a×(b×c)。

5. 乘法分配律：两个数的和与一个数相乘，可以把两个加数分别与这个数相乘再把两个积相加，即(a+b)×c=a×c+b×c 。

6. 减法的性质：从一个数里连续减去几个数，可以从这个数里减去所有减数的和，差不变，即a-b-c=a-(b+c) 。

1. 整数加法计算法则：相同数位对齐，从低位加起，哪一位上的数相加满十，就向前一位进一。

2. 整数减法计算法则：相同数位对齐，从低位加起，哪一位上的数不够减，就从它的前一位退一作十，和本位上的数合并在一起，再减。

3. 整数乘法计算法则：先用一个因数每一位上的数分别去乘另一个因数各个数位上的数，用因数哪一位上的数去乘，乘得的数的末尾就对齐哪一位，然后把各次乘得的数加起来。

4. 整数除法计算法则：先从被除数的高位除起，除数是几位数，就看被除数的前几位；如果不够除，就多看一位，除到被除数的哪一位，商就写在哪一位的上面。

如果哪一位上不够商1，要补“0”占位。

每次除得的余数要小于除数。

5. 小数乘法法则：先按照整数乘法的计算法则算出积，再看因数中共有几位小数，就从积的右边起数出几位，点上小数点；如果位数不够，就用“0”补足。

6. 除数是整数的小数除法计算法则：先按照整数除法的法则去除，商的小数点要和被除数的小数点对齐；如果除到被除数的末尾仍有余数，就在余数后面添“0”，再继续除。

四年级7个运算定律的知识点

四年级7个运算定律的知识点1. 加法交换律：就像你换座位一样，两个数相加，交换它们的位置，和不变。

比如 3 + 5 和 5 + 3，结果都是 8，不管谁在前谁在后，加起来的总数不会变。

2. 加法结合律：这就好比你和小伙伴们手拉手，先拉哪两个再拉另一个都没关系。

三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。

比如说（2 + 3）+ 4 和 2 +（3 + 4），都等于 9。

3. 乘法交换律：跟加法交换律差不多，乘法里两个数相乘，换换位置，积不变。

比如 2×3 和 3×2，积都是 6。

4. 乘法结合律：三个数相乘时，不管是先让前两个数相乘，还是先让后两个数相乘，最后的乘积都一样。

就像你穿衣服，先穿外套再穿衬衫，或者先穿衬衫再穿外套，最后的效果是一样的。

比如（2×3）×4 和 2×（3×4），乘积都是 24 。

5. 乘法分配律：这个有点像发礼物，比如有一堆礼物要分给两个小组，你可以先把礼物总数算出来再平均分，也可以先分别算出每个小组应得的，加起来也一样。

比如 5×（2 + 3） = 5×2 + 5×3 ，结果都是 25 。

6. 减法的性质：从一个数里连续减去两个数，等于减去这两个数的和。

就好像你花钱，一下子花两笔，不如把两笔加起来一起算花了多少。

比如 10 - 2 - 3 = 10 - （2 + 3），都等于 5 。

7. 除法的性质：一个数连续除以两个数，等于除以这两个数的积。

好比你分糖果，一下子分给两个小朋友，不如先算出两个小朋友一共要分多少，然后再一起分。

比如 100÷2÷5 = 100÷（2×5），结果都是 10 。

怎么样，这些运算定律是不是变得有趣多啦？。

(完整版)人教版小学数学四年级下册【运算定律与简便计算】知识篇

力口、减法的速算与巧算（基础篇）1加法运算定律（2个）：☆加法交换律：两个数相加，交换加数的位置，和不变。

即：a +b = b + a☆加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。

即：（a+b ）+c = a+（b+c ）（提醒：运用加法结合律时，要注意把结合的两个数用括号括起来。

）连加的简便计算方法：① 使用加法交换律、结合律凑整（把和是整十、整百、整千的数先交换再结合在一起。

）② 个位：1与9, 2与8, 3与7，4与6, 5与5,结合。

③ 十位：0与9，1与8, 2与7，3与6, 4与5,结合。

连加的简便计算例题：50+98+50488+40+60165+93+35 65+28+35+72=50+50+98 =488+ (40+60) =93+165+35 =(65+35) + (28+72) =100+98 =488+100 =93+(165+35) =100+100 =198=588=293=2002、连减的性质:☆一个数连续减去几个数等于这个数减去这几个数的和。

即：a - b - c = a - （b + c ）注：连减的性质逆用：a - （b + c ） = a - b - c = a - c - b ☆一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

即：a-b-c = a-c-b 连减的简便计算方法：① 连续减去几个数就等于减去这几个数的和。

如：106-26-74 = 106-（26+74）② 连续减去两个数可以先减去后一个数再减去前一个数。

如： 226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。

如: 连减的简便计算例题：3、加、减法混合运算的性质：在计算没有括号的加、减混合运算时，计算时可以带着运算符号106-(26+74) = 106-26-74528—65—35 528— 89—128 528 =528—( 65+35) =528 —128— 89=528—100=400 — 89=528 =400—(150+128) —128—150 —150=428=311=250“搬家”。

四年级下册数学运算定律与简便运算知识点归纳

四年级下册数学运算定律与简便运算知识点归纳四年级下册数学运算定律与简便运算知识点归纳上学期间，大家最不陌生的就是知识点吧！知识点是传递信息的基本单位，知识点对提高学习导航具有重要的作用。

为了帮助大家掌握重要知识点，以下是小编为大家收集的四年级下册数学运算定律与简便运算知识点归纳，欢迎大家借鉴与参考，希望对大家有所帮助。

四年级下册数学运算定律与简便运算知识点归纳篇1一、加减法运算定律1、加法交换律定义：两个加数交换位置，和不变字母表示：abba例如：16+23=23+16 546+78=78+5462、加法结合律定义：先把前两个数相加，或者先把后两个数相加，和不变。

字母表示：(ab)ca(bc)注意：加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数进行调换位置，再将这两个加数结合起来先运算。

例题：(1)50+98+50 (2)488+40+60 (3)165+93+353.减法交换律、结合律注：减法交换律、结合律是由加法交换律和结合律衍生出来的。

减法交换律：如果一个数连续减去两个数，那么后面两个减数的位置可以互换。

字母表示：abcacb例题：(1)198-75-98 (2)528—89—128 (3)226-58-26减法结合律：如果一个数连续减去两个数，那么相当于从这个数当中减去后面两个数的和。

字母表示：abca(bc)例题：(1)369-45-155 (2)896-580-120 (3)528—(150+128)(4)126-(26+88)4、加减法的“符号搬家”：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。

字母表示：abcacb例题：(1)256-58 +44 (2)123 + 38 - 23 (3)146 -78 +54二、乘除法运算定律1、乘法交换律定义：交换两个因数的位置，积不变。

字母表示：abba例如：85×18=18×85 23×88=88×232、乘法结合律定义：先乘前两个数，或者先乘后两个数，积不变。

四年级下册数学运算律

数学整理与复习知识点一：加法交换律和结合律1．加法交换律：两个数相加，交换加数的位置，和不变。

用字母表示为：a+b=b+a 。

2．加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。

用字母表示为：(a+b)+c=a+(b+c) 。

例：81 +( )= 62 + 81184 + 168 + 32 = 184 +（ + 32 ）知识点二：应用加法运算律进行简便计算口诀：连加计算仔细看，考虑加数是关键。

整十、整百与整千，结合起来更简单。

交换定律记心间，交换位置和不变。

结合定律应用广，加数凑整更简便。

例：69+75+25 78+（47+22） 387+98（多加要减）387+102（少加要加） 387﹣98（多减要加）387﹣102（少减要减）知识点三：减法的运算性质1：一个数连续减去两个数等于这个数减去这两个减数的和。

用字母表示：a-b-c=a-(b+c)减法的运算性质2：一个数减去两个数的和等于这个数连续减去和里每个加数。

例:324-58-42 670-25-75 159﹣（59+37）268﹣（35+68）加减的规律：（1）先加后减等于先减后加。

（2）先减后加等于先加后减。

例：325+41﹣25 268+45﹣68 268﹣45+32 325﹣41+75知识点四：乘法的交换律和结合律1．乘法交换律：两个数相乘，交换乘数的位置，积不变。

用字母表示为：a×b=b×a 2．乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘；或者先把后两个数相乘，再和第一个数相乘，积不变。

用字母表示为：(a×b)×c=a×(b×c) 例：16×19=19×( )35×8×4= ( )×( )× 8知识点五：应用乘法运算律进行简便计算在连乘计算中，当某两个乘数的积正好是整十、整百、整千的数时，运用乘法运算律可使计算简便。

四年级下册数学运算定律知识点

四年级下册数学运算定律知识点四年级下册数学运算定律知识点汇总导语：在真实的生命里，每桩伟业都由信心开始，并由信心跨出第一步。

下面是小编为大家整理的，数学知识，更多相关信息请关注CNFLA相关栏目!1.两个数相加，交换加数的位置，和不变。

这叫做加法交换律。

用字母表示为：a+b=b+a2.三个数相加，先把前两个数相加，再加第三个数，或者先把后两个数相加，再加第一个数，和不变。

这叫做加法结合律。

用字母表示为：(a+b)+c=a+(b+c)3.两个数相乘，交换两个因数的位置，积不变。

这叫做乘法交换律。

用字母表示为：a×b=b×a4.三个数相乘，先让前两个数相乘，再乘第三个数，或者先让后两个数相乘，再乘第一个数，积不变。

这叫做乘法结合律。

用字母表示为：(a×b) ×c=a×(b×c)5.两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

这叫做乘法分配律。

用字母表示为：(a+b)×c=a×c+b×c6. 类似于乘法分配律的简便公式;(a-b)×c=a×c-b×c (a+b)÷c=a÷c+b÷c (a-b)÷c=a÷c-b÷c10.一个数连续除以两个数，等于这个数除以另两个数的积。

这是除法的运算性质。

用字母表示为：a÷b÷c=a÷(b×c)11. 在一个带有括号的算式中，括号前面是“×”，去掉括号后，括号里面的运算符号不发生改变。

用字母表示为：a×(b×c)=a×b×c a×(b÷c)=a×b÷c12.在一个带有括号的算式中，括号前面是“÷”，去掉括号后，括号里面的运算符号发生了改变。