概率论例题与详解

合集下载

概率论·课后答案(绝对详解)

i习题一3 设,,B A 为二事件，化简下列事件：B B B A B BA B A B A B A =⋃=⋃⋃=⋃⋃)()())()(1(B B A B B A A A B A B A =⋃⋃⋃=⋃⋃)())()(2(4 电话号码由5个数字组成，每个数字可能是从0到9这10个数字中的任一个，求电话号码由5个不同数字组成的概率。

3024.010302410427210678910445==⋅=⋅⋅⋅⋅=p5 n 张奖券中有m 张有奖的，k 个人购买，每人一张，求其中至少有一人中奖的概率。

答案：.1k n k mn C C --6 从5双不同的鞋子中任取4只，这4只鞋子中“至少有两只配成一双”的概率是多少？解；将这五双靴子分别编号分组},,,,{};,,,,{5432154321b b b b b B a a a a a A ==，则C 表示：“至少有两只配成一双”；从5双不同的鞋子中任取4只，其可能选法有.45C不能配对只能是：一组中选i 只，另一组中选4-i 只，且编号不同，其可能选法为)0,1,2,3,4(;455=--i C C i i i41045341523251235451)(1)(C C C C C C C C C C P C P ++++-=-= 2113218177224161247720104060401011234789105453245224551=-=⋅⋅-=⋅++++-=⋅⋅⋅⋅⋅⋅⋅+⋅+⋅⋅+⋅⋅+-= 7在[—1，1]上任取一点，求该点到原点的距离不超过51的概率。

答案：518在长度为a 的线段内任取两点，将其分成三段，求它们可以构成三角形的概率。

,0,0a y a x <<<<且a y x <+<0，又41222,,=⎪⎪⎪⎩⎪⎪⎪⎨⎧<<>+⇒⎪⎩⎪⎨⎧--<---<--->+P ay a x a y x y x a x y y x a y x y x a y x 9在区间)1,0(内任取两个数，求这两个数的积小于41的概率。

概率论习题答案及答题范例

• 解：如图，设两船的到达时间分别为x和y，则图中着色部分为两船需要等待的时间面积，即：
P( A) 1
202 212 22
242
311 1152
5
P59，习题34
6
(N 1)! 1
P( Ai )
N!
N
P( Ai Aj )
(N 2)! N!
1 N(N
1)
,
i j
P( A1A2 A3...AN
P57，习题6
1Байду номын сангаас
P57，习题10
• 甲袋中有3只白球，7只红球，15只黑球，乙袋中有10只白球，6只红球，9只黑球，现从两袋中各取一球，求两球颜色相同的概率。
• 解：分别求出同取白、红、黑球的概率，再相加即可
P 3 10 7 6 15 9 207 25 25 25 25 25 25 625
15
P114，习题37
7
C7k 0.6k 0.47k 0.71
k 4
16
P115，习题41
P( A)
1
20 0!
e 2
5
0.484
P(B)
5 k3
C5k
1
20 0!
e 2
k
20 0!
e 2
5k
=0.98
17
P115，习题47
• 某车间宣称自己产品的合格率超过99%，检验人员从该车间的10000件产品中抽查了100件，发现有两件次品，能否据此断定该车间谎报合格率？
2
P58，习题13
• 从6双不同的手套中任取4只，问其中恰有一双配对的概率是多少？
• 解：
P C61C52C21C21 16

概率论练习题与解析

概率论练习题与解析十、概率论与数理统计一、填空题1、设在一次试验中，事件A 发生的概率为p 。

现进行n 次独立试验，则A 至少发生一次的概率为np )1(1--；而事件A 至多发生一次的概率为1)1()1(--+-n n p np p 。

2、三个箱子，第一个箱子中有4个黑球1个白球，第二个箱子中有3个黑球3个白球，第三个箱子有3个黑球5个白球。

现随机地取一个箱子，再从这个箱子中取出1个球，这个球为白球的概率等于。

已知取出的球是白球，此球属于第二个箱子的概率为。

解：用iA 代表“取第i 只箱子”，i =1，2，3，用B 代表“取出的球是白球”。

由全概率公式⋅=⋅+⋅+⋅=++=12053853*********)|()()|()()|()()(332211A B P A P A B P A P A B P A P B P由贝叶斯公式⋅=⋅==5320120536331)()|()()|(222B P A B P A P B A P3、设三次独立试验中，事件A 出现的概率相等。

若已知A 至少出现一次的概率等于19/27，则事件A 在一次试验中出现的概率为。

解：设事件A 在一次试验中出现的概率为)10(<<p p ，则有2719)1(13=--p ，从而解得31=p4、已知随机事件A 的概率5.0)(=A P ，随机事件B 的概率6.0)(=B P 及条件概率8.0)|(=A B P ，则和事件B A Y 的概率)(B A P Y = 。

7.08.05.06.05.0)|()()()()()()()(=⨯-+=-+=-+=A B P A P B P A P AB P B P A P B A P Y 5、甲、乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5。

现已知目标被命中，则它是甲射中的概率为。

用A 代表事件“甲命中目标”，B 代表事件“乙命中目标”，则B A Y 代表事件“目标被命中”，且8.06.05.06.05.0)()()()()()()()(=⨯-+=-+=-+=B P A P B P A P AB P B P A P B A P Y所求概率为75.08.06.0)()()|(===B A P A P B A A P Y Y6、设随机事件A ，B 及其和事件B A Y 的概率分别是0.4，0.3和0.6。

概率论例题解析

P ( B | A)
P ( AB ) P ( B ) m 1 P ( A) P ( A) 2M m 1
(2)设C表示“所取产品中至少有一件合格品”， D表示“所取产品中有一件合格品，一件不合格品”。则
m M m M m 1 1 2 P (C ) M 2
例12 有朋友自远方来访，他乘火车、轮船、汽车、飞机来的概率分别是0.3、0.2、0.1、0.4。如果他乘火车、轮船、汽车来的话，迟到的概率分别是1/4、1/3、1/12，而乘飞机不会迟到。结果他迟到了，试问他是乘火车来的概率是多少？解: 用A1表示“朋友乘火车来”，A2表示“朋友乘轮船来”，A3表示“朋友乘汽车来”，A4表示 “朋友乘飞机来”，B表示“朋友迟到了”。由贝叶斯公式，
(1) P ( Ak | A1 Ak 1 ) 1 1 n (k 1) n k 1
n1 n 2 1 1 n n1 n k 1 n
(2) P( Ak ) P( A1 Ak 1 Ak )
例10 某厂调进号码为1的箱子10个，号码为2 的箱子20个，其中号码为1的每个箱子有A等品10件，B等品5件；号码为2的每个箱子有A 等品10件，B等品20件，现任取1个箱子并从中任取1件物品，问取到A等品和B等品的概率分别是多少？
例题解析
例1 写出下列实验的样本空间
（1）生产产品直到得到10件正品，记录生产产品的总件数。
（2）对某工厂出厂的产品进行检查，合格的盖上正品，不合格的盖上次品，如连续查出两个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。
答案：(1) {10,11,12,} (2) {00,100,0100 ,0101 ,0111 ,0110 ,1010 ,1011 ,1100 ,1101 ,1110 ,1111 }

概率论与数理统计重点总结及例题解析

概率论与数理统计重点总结及例题解析一：全概率公式和贝叶斯公式例:某厂由甲、乙、丙三个车间生产同一种产品，它们的产量之比为3：2：1，各车间产品的不合格率依次为8％，9％， 12% 。

现从该厂产品中任意抽取一件，求:（1）取到不合格产品的概率;（2）若取到的是不合格品，求它是由甲车间生产的概率。

（同步45页三、1）解:设A1，A2,A3分别表示产品由甲、乙、丙车间生产,B表示产品不合格，则A1,A2,A3为一个完备事件组。

P（A1）=1/2, P(A2）=1/3， P(A3)=1/6，P（B｜ A1)＝0。

08，P（B｜ A2）＝0。

09，P（B｜ A3)＝0。

12.由全概率公式P（B） = P(A1)P（B｜ A1）+ P（A2)P(B| A2）+ P(A3）P(B| A3) = 0.09由贝叶斯公式：P（A1｜ B）＝P(A1B）/P(B) = 4/9练习:市场上出售的某种商品由三个厂家同时供货，其供应量第一厂家为第二厂家的2倍,第二、三两厂家相等，而且第一、二、三厂家的次品率依次为2％,2％，4％。

若在市场上随机购买一件商品为次品,问该件商品是第一厂家生产的概率是多少？(同步49页三、1）【0.4 】练习:设两箱内装有同种零件，第一箱装50件，有10件一等品，第二箱装30件，有18件一等品,先从两箱中任挑一箱,再从此箱中前后不放回地任取2个零件，求：(同步29页三、5）（1）取出的零件是一等品的概率；（2)在先取的是一等品的条件下,后取的仍是一等品的条件概率. 解：设事件i A ={从第i 箱取的零件},i B =｛第i 次取的零件是一等品｝（1）P （1B )=P(1A )P （1B |1A ）+P （2A )P(1B ｜2A )=52301821501021=+（2)P （1B 2B ）=194.02121230218250210=+C C C C ,则P （2B |1B )=)()(121B P B B P = 0.485二、连续型随机变量的综合题例:设随机变量X 的概率密度函数为⎩⎨⎧<<=others x x x f 020)(λ 求：（1)常数λ;（2）EX ；（3)P{1〈X<3｝；（4)X 的分布函数F （x)（同步47页三、2）解：(1）由⎰⎰==∞+∞-201)(xdx dx x f λ得到λ＝1/2 （2)3421)(22===⎰⎰∞+∞-dx x dx x xf EX (3)⎰⎰===<<31214321)(}31{xdx dx x f x P (4)当x<0时,⎰∞-==xdt x F 00)(当0≤x<2时，⎰⎰⎰∞-∞-=+==xxx tdt dx dt t f x F 00241210)()(当x ≥2时，F(x ）=1故201()02412x F x x x x <⎧⎪⎪=≤<⎨⎪≥⎪⎩练习：已知随机变量X 的密度函数为⎩⎨⎧≤≤+=others x b ax x f 010)(且E （X)=7/12。

概率论解题示例详解

概率论解题示例详解概率论是数学中的一个重要分支，它研究的是不确定事件的规律性。

通过概率的计算和推理，我们可以预测和评估各种事件发生的可能性。

概率论在实际生活中有着广泛的应用，比如在金融、统计、工程等领域中都能看到它的身影。

本文将通过详解一些概率论解题示例，来帮助读者更好地理解和掌握概率论的基本概念和解题方法。

示例一：抛硬币问题抛硬币是常见的概率论例题。

假设有一枚公平的硬币，正反两面出现的机会均等。

现在我们抛掷这枚硬币三次，问以下几种情况的概率是多少：1. 出现三次正面的概率2. 出现两次反面的概率3. 至少出现一次正面的概率解答：1. 出现三次正面的概率：假设硬币抛掷的结果为独立事件，每次抛掷都有两种可能的结果，即正面和反面。

因此，出现三次正面的概率可以表示为：1/2 * 1/2 * 1/2 = 1/8。

2. 出现两次反面的概率：同样地，假设硬币抛掷的结果为独立事件，每次抛掷都有两种可能的结果。

根据排列组合的原理，两次反面和一次正面可以有三种不同的组合，即反反正、反正反、正反反。

因此，出现两次反面的概率可以表示为：3 * (1/2 * 1/2 * 1/2) = 3/8。

3. 至少出现一次正面的概率：可以通过计算出至少出现一次反面的概率，然后用1减去该概率即可。

出现一次反面的概率可以表示为：(1/2 * 1/2 * 1/2) = 1/8。

因此，至少出现一次正面的概率为1 - 1/8 = 7/8。

示例二：生日悖论生日悖论是概率论中一个有趣且常见的问题。

假设有一个房间里有n个人，问至少有两个人生日相同的概率是多少？解答：假设每个人的生日是均匀分布的，即每一天出生的概率相等。

我们可以通过计算每个人生日不相同的概率，然后用1减去该概率得到至少有两个人生日相同的概率。

第一个人的生日可以是任意一天，概率为1。

第二个人的生日不能与第一个人相同，即概率为364/365。

第三个人的生日不能与前两个人相同，即概率为363/365。

高等数学(概率论)习题及解答

高等数学(概率论)习题及解答高等数学（概率论）题及解答
1. 题一
1.1. 题目
已知事件A和B的概率分别为P(A) = 0.2，P(B) = 0.3，且P(A∪B) = 0.4，求P(A∩B)。

1.2. 解答
根据概率的加法定理，有：
P(A∪B) = P(A) + P(B) - P(A∩B)
代入已知数据得：
0.4 = 0.2 + 0.3 - P(A∩B)
P(A∩B) = 0.1
所以，P(A∩B)的概率为0.1。

2. 题二
2.1. 题目
已知某城市一天中的天气分为晴天、阴天和雨天三种情况，其中晴天的概率为0.4，阴天的概率为0.3。

现已知，当下为晴天时，随后一天也是晴天的概率为0.7；当下为阴天时，随后一天为晴天的概率为0.5。

求当下为晴天时，随后一天为阴天的概率。

2.2. 解答
设事件A为当下为晴天，事件B为随后一天为阴天。

根据条件概率的定义，有：
P(B|A) = P(A∩B) / P(A)
已知 P(A) = 0.4，P(B|A) = 0.5，代入并整理得：
0.5 = P(A∩B) / 0.4
P(A∩B) = 0.5 * 0.4
P(A∩B) = 0.2
所以，当下为晴天时，随后一天为阴天的概率为0.2。

以上是高等数学（概率论）习题及解答的部分内容，如有更多问题或需要补充，请随时告知。

概率论习题及答案详解

一、填空题1. 掷21n +次硬币，则出现正面次数多于反面次数的概率是0.52. 把10本书任意的放到书架上，求其中指定的三本书放在一起的概率1153. 6．一批产品分一、二、三级，其中一级品是二级品的两倍，三级品是二级品的一半，从这批产品中随机的抽取一件，试求取到二级品的概率274. 已知()0.7,()0.3,P A P A B =-= 则()0.6.P AB =5. 已知()0.3,()0.4,()0.5,P A P B P A B === 则(|)0.8.P B A B ⋃=6. 掷两枚硬币，至少出现一个正面的概率为34.7. 设()0.4,()0.7,P A P A B =⋃= 若,A B 独立，则()0.5.P B =8. 设,A B 为两事件，11()(),(|),36P A P B P A B === 则7(|).12P A B =9. 设123,,A A A 相互独立，且2(),1,2,3,3i P A i == 则123,,A A A 最多出现一个的概率是7.2710．某人射击三次，其命中率为0.8，则三次中至多命中一次的概率为0.104二、选择题1. 下面四个结论成立的是（B ）.()().,.().()A A B C A B C B AB C A BC C A B B A D A B B A--=-⋃=∅⊂=∅⋃-=-⋃=若且则2. 设()0,P AB =则下列说法正确的是（ D ） ...()0()0.()()A AB B ABC P A P BD P A B P A ==-=和不相容是不可能事件或3. 掷21n +次硬币，正面次数多于反面次数的概率为（ C ）1..21211.0.5.21nn A B n n n C D n -++++ 4. 设,A B 为随机事件，()0,(|)1,P B P A B >= 则必有（ A ）.()()..()().()()A P AB P A B B AC P A P BD P AB P A ⋃=⊂==5. 设A 、B 相互独立，且P (A )>0，P (B )>0，则下列等式成立的是（ B ）.A ．P (AB )=0 .B P (A -B )=P (A )P (B ).C P (A )+P (B )=1 .D ．P (A |B )=06．设事件A 与B 互不相容，且P (A )>0，P (B ) >0，则有（ A ）.A P (AB )=l .B P (A )=1-P (B ) .C P (AB )=P (A )P (B ).D P (A ∪B )=17. 已知()0.5P A =，()0.4P B =，()0.6P A B +=，则(|)P A B =（ D ）.A 0.2 .B 0.45 .C 0.6 .D 0.758．同时抛掷3枚均匀的硬币，则恰好有两枚正面朝上的概率为（ C ）.A 0.125 .B 0.25 .C 0.375 .D 0.509．设事件,A B 互不相容，已知()0.4P A =，()0.5P B =，则()P AB =（ B ）.A 0.1 .B 0.4 .C 0.9 .D 110．已知事件A ，B 相互独立，且()0P A >，()0P B >，则下列等式成立的是（ B ）.A ()()()P A B P A P B ⋃=+ .B ()1()()P A B P A P B ⋃=- .C ()()()P A B P A P B ⋃=.D ()1P A B ⋃=三、计算题1. 一宿舍内住有6位同学，求他们之中至少有2个人的生日在同一个月份概率。

全概率经典例题详解

全概率经典例题详解题目：甲、乙、丙三人向同一飞机射击，设击中的概率分别为，，，若只有1人击中，则飞机被击落概率为，若2人击中，则飞机被击落的概率为，若3人击中，则飞机一定被击落，则飞机被击落的概率为多少？解：设甲、乙、丙三人击中分别为A、B、C，飞机被击落为D。

首先，我们考虑只有1人击中的情况。

这包括三种子情况：甲击中而乙丙不击中、乙击中而甲丙不击中、丙击中而甲乙不击中。

对于甲击中而乙丙不击中的情况，其概率为$P(A\overset{―}{B}\overset{―}{C}) = \times (1 - ) \times (1 - ) = \times \times = $。

对于乙击中而甲丙不击中的情况，其概率为$P(\overset{―}{A}B\overset{―}{C}) = (1 - ) \times \times (1 - ) = \times \times = $。

对于丙击中而甲乙不击中的情况，其概率为$P(\overset{―}{A}\overset{―}{B}C) = (1 - ) \times (1 - ) \times = \times \times = $。

因此，只有1人击中的总概率为 $P_1 = P(A\overset{―}{B}\overset{―}{C}) + P(\overset{―}{A}B\overset{―}{C}) + P(\overset{―}{A}\overset{―}{B}C) = + + = $。

接下来，我们考虑有2人击中的情况。

这包括三种子情况：甲乙击中而丙不击中、甲丙击中而乙不击中、乙丙击中而甲不击中。

对于甲乙击中而丙不击中的情况，其概率为 $P(AB\overset{―}{C}) =\times \times (1 - ) = \times \times = $。

对于甲丙击中而乙不击中的情况，其概率为 $P(A\overset{―}{B}C) =\times (1 - ) \times = \times \times = $。

概率论练习题与解析.

十、概率论与数理统计一、填空题1、设在一次试验中，事件A 发生的概率为p 。

现进行n 次独立试验，则A 至少发生一次的概率为np )1(1--；而事件A 至多发生一次的概率为1)1()1(--+-n n p np p 。

2、三个箱子，第一个箱子中有4个黑球1个白球，第二个箱子中有3个黑球3个白球，第三个箱子有3个黑球5个白球。

现随机地取一个箱子，再从这个箱子中取出1个球，这个球为白球的概率等于。

已知取出的球是白球，此球属于第二个箱子的概率为。

解：用iA 代表“取第i 只箱子”，i =1，2，3，用B 代表“取出的球是白球”。

由全概率公式⋅=⋅+⋅+⋅=++=12053853163315131)|()()|()()|()()(332211A B P A P A B P A P A B P A P B P由贝叶斯公式⋅=⋅==5320120536331)()|()()|(222B P A B P A P B A P3、设三次独立试验中，事件A 出现的概率相等。

若已知A 至少出现一次的概率等于19/27，则事件A 在一次试验中出现的概率为。

解：设事件A 在一次试验中出现的概率为)10(<<p p ，则有2719)1(13=--p ，从而解得31=p4、已知随机事件A 的概率5.0)(=A P ，随机事件B 的概率6.0)(=B P 及条件概率8.0)|(=A B P ，则和事件B A 的概率)(B A P = 。

7.08.05.06.05.0)|()()()()()()()(=⨯-+=-+=-+=A B P A P B P A P AB P B P A P B A P5、甲、乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5。

现已知目标被命中，则它是甲射中的概率为。

用A 代表事件“甲命中目标”，B 代表事件“乙命中目标”，则B A 代表事件“目标被命中”，且8.06.05.06.05.0)()()()()()()()(=⨯-+=-+=-+=B P A P B P A P AB P B P A P B A P所求概率为 75.08.06.0)()()|(===B A P A P B A A P 6、设随机事件A ，B 及其和事件B A 的概率分别是0.4，0.3和0.6。

概率论典型例题(稻谷书苑)

(1 p5 )[1 (1 p1 p3 )(1 p2 p4 )].
藤蔓课堂
13
三、典型例题
例1 已知离散型随机变量 X 的可能取值为 2,0,
2, 5,相应的概率依次为 1 , 3 , 5 , 7 ,试求概率 a 2a 4a 8a
P{ X 2 X 0}.
[思路] 首先根据概率分布的性质求出常数 a 的
值, 然后确定概率分布律的具体形式,最后再计
算解利用概率分布律的性质 pi 1,
条件概率.
i
藤蔓课堂
14
有
1
i
pi
1 a
3 2a
5 4a
7 8a
37 , 8a
故 a 37 , 8
因此 X 的分布律为
藤蔓课堂
7
解记 Hi {抽到地区考生的报名表 }, i 1, 2, 3;
Aj {第 j 次抽到报名表是男生的}, j 1,2,
则有
P(Hi
)
1 3
(i
1,2,3);
P(
A1
H1
)
7; 10
P(
A1
H2
)
8; 15
P( A1
H3)
20 . 25
(1)由全概率公式知
3
p P( A1 ) P(Hi )P( A1 Hi ) i 1
藤蔓课堂
3
例3 假设目标出现在射程之内的概率为0.7,这时射击命中目标的概率为0.6, 试求两次独立射击至少有一次命中目标的概率.
[思路] 引进事件 A {目标进入射程};
Bi {第i次射击命中目标}, i 1,2. 故所求概率为事件B B1 B2的概率,由于目标不在射程之内是不可能命中目标的, 因此 , 可利用全概率公式来求解.

概率论例题

解:设B 从该箱中任取4只检查, 结果都是好的 . Ai = 箱中含有i只次品 ,i 0,1,2.
据题意得：P ( A0 ) 0.8, P ( A1 ) 0.1, P ( A2 ) 0.1，
P ( B | A0 ) 1,
4 C19 4 P ( B | A1 ) 4 , C20 5 4 C18 12 P ( B | A2 ) 4 . C20 19
y 0; 0, 2 FY y P Y y lim F x, y = y , 0 y 1; x 1, y 1.
1 1 (2) P X 3, 1 Y 3 2 1 1 1 1 1 F 3, F , 1 F , F 3, 1 . 12 3 2 2 3
例3.2 :已知二维随机变量 X , Y 的联合概率分布函数为 0， 2 2 x y , 2 F ( x, y ) x , y2, 1, x 0 或 y 0; 0 x 1, 0 y 1; 0 x 1,1 y ; 1 x , 0 y 1; 1 x ,1 y .
根据题意，两人能见面 | X Y | 15 ,
y
60
y x 15
15 o 15
x y 15
x
60
所以，两人能见面的概率为阴影图像的面积 45 45 7 P | X Y | 15 1 . 3600 3600 16
例316:已知 . X , Y 的联合概率密度为 21 2 2 x y ， x y 1， f ( x, y ) 4 其他。 0，
1问至少要配备多少维修工人,才能保证当设备发生
故障时不能及时维修的概率小于0. 5%；

(完整版)概率论高等数学习题解答

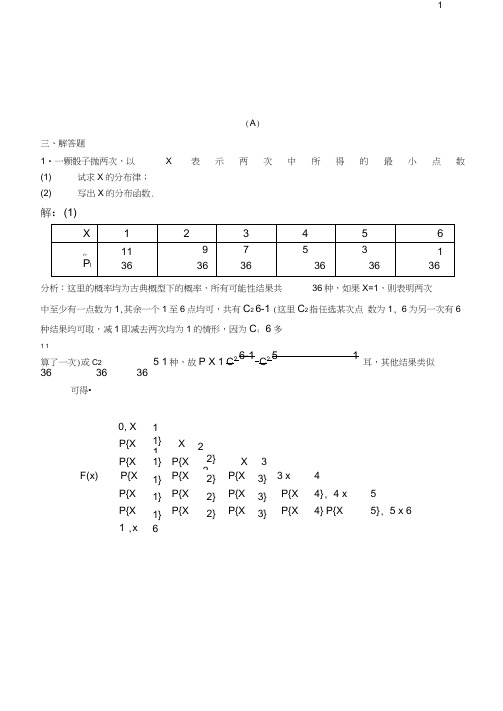
1(A )三、解答题1•一颗骰子抛两次，以 X表示两次中所得的最小点数(1) 试求X 的分布律； (2)写出X 的分布函数.解：(1)分析：这里的概率均为古典概型下的概率，所有可能性结果共 36种，如果X=1，则表明两次中至少有一点数为1,其余一个1至6点均可，共有C 2 6-1 (这里C 2指任选某次点数为1, 6为另一次有6种结果均可取，减1即减去两次均为1的情形，因为C ； 6多1 1算了一次)或C 2 5 1种，故P X 1 C 26-1C25 1耳，其他结果类似36 3636可得•0, X1P{X 1} ,1X 2P{X 1} P{X 2} ,2X3F(x)P{X 1} P{X 2} P{X 3}， 3 x 4P{X 1} P{X 2} P{X3}P{X 4}, 4 x 5 P{X1} P{X2} P{X 3} P{X4} P{X5}, 5 x 61 ,x 622 •某种抽奖活动规则是这样的：袋中放红色球及白色球各 5只，抽奖者交纳一元钱后得到一次抽奖的机会，然后从袋中一次取出 5只球，若5只球同色，则获奖100元，否则无奖,以X 表示某抽奖者在一次抽取中净赢钱数，求X 的分布律.解:注意，这里 X 指的是赢钱数，X 取0-1或100-1，显然P X 99k3.设随机变量 X 的分布律为P{X k} a ,k 0,1,2, k!k解：因为 a ae 1，所以a e k 0 k!4.设随机变量X 的分布律为X -1 2 3 p1/41/21/4(1)求X 的分布函数;1 3 512627，3 翌,4 3635,5 36x 2 x 3x 4 x 5x 6 62 1 C ；0 1260为常数，试求常数 a .3⑵求P{X 丄}，P{- X 5}，P{2 x 3}.2 2 2解:40, x -1布，而与时间间隔的起点无关(时间以小时计)(1) 求某一天中午12时至下午3时没有收到紧急呼救的概率. (2) 求某一天中午12时至下午5时至少收到一次紧急呼救的概率. 解：(1) X ~ P 0.5t P 1.5 P X 0 e 1.5. (2) 0.5t2.50, x -1P{X 1}， 1 x2(1) F (x)P{X 1} P{X 2}1, x 3⑵P 1XX1 124P 2 X 3 P X 2X 3 5.设随机变量X 的分布律为 P{X k}(1) P{X =偶数｝(2) P{ X 5}(3) P{ X=3的倍数｝2 x 33 ， ,2x341, x 33 51 P — X P X2 —222P X2 3 P X 3.4扌,k 1,2, 求：解：(1) P X 偶数丄1丄 22 221 lim i1(2) P X 51 P X 4115 1 16 16⑶P X 3的倍数23236.某公安局在长度为i123ilim123t 的时间间隔内收到的紧急呼救的次数X 服从参数为0.5t 的泊松分2.5丄，1x2 45 7.某人进行射击，每次射击的命中率为0.02，独立射击400次，试求至少击中2次的概6解：设射击的次数为 X ，由题意知X ~ B 400,0.2i k k 400 kP X 2 1 P X 11 C 4000.02 0.98k 0查表泊松分布函数表得:P{X 2} 1 0.28 0.99728.设事件A 在每一次试验中发生的概率为 0.3,当A 发生不少于3次时，指示灯发出信(1)系数a ;(2) X 落在区间(0,[)内的概率.号•现进行5次独立试验，试求指示灯发出信号的概率.解：设X 为事件A 在5次独立重复实验中出现的次数,则指示灯发出信号的概率 X ~ B 5,0.3 p P X 3 1 P X 3 1 (C 00.3°0.75 C 50.310.74 C ；0.320.73) 1 0.8369 0.1631. 9.设顾客在某银行窗口等待服务的时间 X (以分钟计) 在窗口等待服务，若超过务而离开窗口的次数.写出服从参数为 5 10分钟，他就离开.他一个月要到银行 5次，以 Y 的分布律，并求P{Y 1}.指数分布•某顾客 Y 表示他未等到服 x 解：因为X 服从参数为5的指数分布，则F(x) 1 e T , P X 10 Y~ B5, e 2 , 1 F(10) e 2 ,则 P{Y k} C5 (e 2)k (1 e 2)5k,k 0,1, 5 P{Y 1} 1- P{Y 0} 1 (1 e 2)5 0.5167 a cosx. 10.设随机变量 X 的概率密度为 f(x)0,|x|~2，试求:|x |2解：(1)由归一性知：1 f (x)dx2a cosxdx 2a ，所以 a2由于上面二项分布的概率计算比较麻烦, 所以而且X 近似服P{X 2}18k ek 0k!7⑵-11.2.P{0 X —} ； cosxdx sin x |(424 .0,x011 . 设连续随机变量X的分布函数为F(x)Ax,0x 11,x1⑶X的概率密度.试求:(1) 解系数(1)A；由⑵X落在区间(0.3, 0.7)内的概率；的连续性可得lim F(x)F(x )在x=1 lim F(x) F(1)，即A=1.x 1(2) 0.3 X 0.7 F(0.7) F(0.3) 0.4.(3) X的概率密度 f (x) F (x)2x,00,12.设随机变量X服从(0, 5)上的均匀分布，求的概率.x的方程4x2 4Xx X 0有实根解：因为X服从(0, 5)上的均匀分布，所以1f(x) 50x5其他2 2方程4x 4Xx X(x 2)( X2(4X) 16X1，所以有实根的概率为0有实根，则32 51dx2510dxX〜N(3, 4)13.设求P{2 X 5}, P{(1) X 10}, P{ X 2}, P{X解: 确定c使得P{X c}设d满足P{X d} 0.9，问d至多为多少？(1)因为X ~ N(3,4)所以P{X c};2 3P{2 X 5} P{〒穿}P{1}(1) (0.5) (1) (0.5) 1 0.8413 0.6915 0.5328P 4 X 108F(2)(2.5)经查表得1 (0)，即2专)故斗214.设随机变量1.29，解：P XF(所以(k)15.设随机变量如何变化的？(3.5)2 0.999810 3 4 3(^)2 2(3.5) 2 (3.5)1 0.99962) 1(0.5)0.1，解：X ~ N(,(0.5)0.3023F(3)，则P X2X2(2.5)0.6977(0)得c 3 ；由概率密度关于即(-d 3)20.42.X服从正态分布2 2 (k)0.95 , p XN(0,1 0.5 0.5.c 3 1F(c)(〒)-，x=3对称也容易看出。

概率论题目和问题详解

【奥鹏】[东北大学]19春学期《概率论》在线作业1试卷总分:100 得分:100第1题X 服从标准正态分布(01)，如此Y=1+2X的分布是：A、N(12)；B、N(14)C、N(24)；D、N(25)。

正确答案:B第2题下面哪一种分布没有“可加性〞？〔即同一分布类型的独立随机变量之和仍然服从这种分布〕？A、均匀分布；B、泊松分布；C、正态分布；D、二项分布。

正确答案:A第3题设电灯泡使用寿命在2000h以上的概率为0.15，如果要求3个灯泡在使用2000h以后只有一个不坏的概率，如此只需用〔〕即可算出A、全概率公式B、古典概型计算公式C、贝叶斯公式D、贝努利公式正确答案D第4题独立地抛掷一枚质量均匀硬币，连续出现了10次反面，问下一次抛掷时出现的是正面的概率是：A、1/11B、B.1/10C、C.1/2D、D.1/9正确答案:C第5题一袋中有5个乒乓球，编号分别为1，2，3，4，5从中任意去取3个，以X表示球中的最大，X=3的概率为：A、0.1B、0.4C、0.3D、0.6正确答案:A 第6题某人打靶的命中率为0.8，现独立地射击5次，那么，5次中有2次命中的概率为A、0.82 *0.2B、0.82C、0.4*0.82D、10*0.82 *0.23正确答案D第7题10个球中3个红，7个绿，随机分给10个小朋友，每人一球。

如此最后三个分到球的小朋友中恰有一个得到红球的概率为A、9/10B、147/1000C、441/1000D、21/40正确答案D第8题设X是一随机变量，E〔X〕=u，D(x)=σ2〔uσ0常数〕，如此对任意常数c，必有A、E〔X-c〕2=E(X2)-c2B、E(X-c)2=E(X-u)2C、E(X-c)2 E(X-u)2D、E(X-c)2 =E(X-u)2正确答案D第9题某人从家乘车到单位，途中有3个交通岗亭。

假设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，如此此人上班途中遇红灯的次数的期望为A、0.4B、1.2C、0.43D、0.6正确答案:B第10题设X、Y的联合分布函数是F(x，y)，如此F(+∞，y)等于：A、0；B、1；C、Y的分布函数；D、Y的密度函数。

概率论部分习题及答案

7 均匀分布·指数分布·随机变量函数的概率分布一、公共汽车站每隔5分钟有一辆汽车通过．乘客到达汽车站的任一时刻是等可能的．求乘客候车时间不超过3分钟的概率．解：设随机变量X 表示“乘客的候车时间”，则X 服从]5,0[上的均匀分布，其密度函数为⎩⎨⎧∉∈=]5,0[,0]5,0[,1)(x x x f 于是有.6.053)()30(3===≤≤⎰dx x f X P二、已知某种电子元件的使用寿命X (单位:h)服从指数分布，概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,8001)(800x x e x f x任取３个这种电子元件，求至少有１个能使用1000h 以上的概率．解：设A 表示“至少有１个电子元件能使用1000h 以上”；321A 、A 、A 分别表示“元件甲、乙、丙能使用1000h 以上”．则287.08001)1000()()()(4510008001000800321≈=-==>===-∞+-∞+-⎰e e dx e X P A P A P A P xx)()()()()()()()()(321313221321321A A A P A A P A A P A A P A P A P A P A A A P A P +---++=⋃⋃=638.0287.0287.03287.0332≈+⨯-⨯=（另解）设A 表示“至少有１个电子元件能使用1000h 以上”．则287.08001)1000(4510008001000800≈=-==>-∞+-∞+-⎰ee dx e X P xx从而有713.01)1000(1)1000(45≈-=>-=≤-eX P X P ，进一步有638.0713.01)]1000([1)(33≈-≈≤-=X P A P三、(1) 设随机变量X 服从指数分布)(λe ．证明：对于任意非负实数s 及t ，有).()(t X P s X t s X P ≥=≥+≥这个性质叫做指数分布的无记忆性．(2) 设电视机的使用年数X 服从指数分布)10(．e ．某人买了一台旧电视机，求还能使用５年以上的概率．解：（１）因为)(~λe X ，所以R x ∈∀，有xex F λ--=1)(，其中)(x F 为X 的分布函数．设t s X A +≥=，t X B ≥=．因为s 及t 都是非负实数，所以B A ⊂，从而A AB =．根据条件概率公式，我们有)(1)(1)()()()()()()()(s X P t s X P s X P t s X P B P A P B P AB P B A P s X t s X P <-+<-=≥+≥====≥+≥tst s e e e λλλ--+-=----=]1[1]1[1)(．另一方面，我们有t t e e t F t X P t X P t X P λλ--=--=-=≤-=<-=≥)1(1)(1)(1)(1)(．综上所述，故有)()(t X P s X t s X P ≥=≥+≥．（２）由题设，知X 的概率密度为⎩⎨⎧≤>=-．，；，0001.0)(1.0x x e x f x 设某人购买的这台旧电视机已经使用了s 年，则根据上述证明的（１）的结论，该电视机还能使用5年以上的概率为6065.01.0)()5()5(5.051.051.05≈=-===≥=≥+≥-∞+-∞+-∞+⎰⎰e e dx e dx xf X P s X s X P xx ．答：该电视机还能使用5年以上的概率约为6065.0．四、设随机变量X 服从二项分布)4.0 ,3(B ，求下列随机变量函数的概率分布：（1）X Y 211-=；（2）2)3(2X X Y -=．解：X 的分布律为（1）X Y 211-=的分布律为（2）2)3(2X XY -=的分布律为即五、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤>+=.0,0;0,)1(2)(2x x x x f π求随机变量函数X Y ln =的概率密度．解：因为)()()(ln )()(yX yY e F e X P y X P y Y P y F =<=<=<=所以随机变量函数X Y ln =的概率密度为)( )1(2)()()()(2''+∞<<-∞+====y e e e e f e e F y F y f y yyyyyXYY π，即)( )1(2)(2+∞<<-∞+=y e e y f yyY π．８二维随机变量的联合分布与边缘分布一、把一颗均匀的骰子随机地掷两次．设随机变量X 表示第一次出现的点数，随机变量Y 表示两次出现点数的最大值，求二维随机变量),(Y X 的联合概率分布及Y 的边缘概率分布．解：二维随机变量),(Y X 的联合概率分布为Y 的边缘概率分布为二、设二维随机变量（X ，Y ）的联合分布函数)3arctan )(2arctan(),(y C x B A y x F ++=．求：（1）系数A 、B 及C ；（2）（X ，Y ）的联合概率密度：（3）边缘分布函数及边缘概率密度．解：（1）由0)0,(,0),0(,1),(=-∞=∞+=∞+-∞F F F ，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=--=++0)2(0)2)(0(1)2)(2(πB AC πC B A πC πB A 解得2πC B ==，.12πA =（2）因为)3arctan 2)(2arctan 2(1),(2y x y x F ++=πππ，所以（X ，Y ）的联合概率密度为.)9)(4(6),(),(222"y x y x F y x f xy ++==π （3）X 及Y 的边缘分布函数分别为 xxxX xdx x dy y x f dx x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰2arctan1)4(2),()(2ππ2arctan 121x π+=yxyY ydy y dx y x f dy x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰3arctan1)9(3),()(2ππ3arctan 121y π+=X 及Y 的边缘概率密度分别为⎰⎰⎰+∞+∞∞-+∞∞-++⋅=++==0222222)9(1)4(112)9)(4(6),()(dy y x dy y x dy y x f x f X ππ )4(2)3arctan 31()4(1122022x y x +=+⋅=∞+ππ ⎰⎰⎰+∞+∞∞-+∞∞-++=++==022222241)9(12)9)(4(6),()(dx x y dx y x dx y x f y f Y ππ)9(3)2arctan 21()9(122022y x y +=+=∞+ππ三、设),(Y X 的联合概率密度为⎩⎨⎧>>=+-.,00;0,,Ae ),(3y)(2x 其它y x y x f 求：（1）系数A ；（2）),(Y X 的联合分布函数；（3）X 及Y 的边缘概率密度；（4）),(Y X落在区域R ：632 ,0 ,0<+>>y x y x 内的概率．解：（1）由1),(=⎰⎰+∞∞-+∞∞-dy dx y x f ，有16132==⎰⎰∞+∞+--A dy e dx e A y x ，解得.6=A （2）),(Y X 的联合分布函数为⎪⎩⎪⎨⎧>>==⎰⎰⎰⎰--∞-∞-其它0,06),(),(0032y x dy e dx e dy y x f dx y x F x y y x xy⎩⎨⎧>>--=--其它0,0)1)(1(32y x e e y x （3）X 及Y 的边缘概率密度分别为⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰00020006),()(2032x x ex x dye e dy y xf x f xy x X⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰0030006),()(3032y y ex x dxe e dx y xf y f yy x Y（4）⎰⎰⎰⎰---==∈x y xRdy e dx edxdy y x f R Y X P 32203326),(}),{(636271)(2---⎰-=-=e dx e e x四、设二维随机变量),(Y X 在抛物线2x y =与直线2+=x y 所围成的区域R 上服从均匀分布．求：(1) ),(Y X 的联合概率密度；(2) 概率)2(≥+Y X P ．解：(1) 设),(Y X 的联合概率密度为⎩⎨⎧∉∈=.),(, 0;),(,),(R y x R y x C y x f 则由129)322()2(21322122212==-+=-+==--+-⎰⎰⎰⎰⎰Cx x x C dx x x C dy dx C Cdxdy x x R解得92=C ．故有 ⎪⎩⎪⎨⎧∉∈=.),(, 0;),(,92),(R y x R y x y x f(2) ⎰⎰⎰⎰⎰⎰++-≥++==≥+x x x x y x dy dx dy dx dxdy y x f Y X P 2212210229292),()2(⎰⎰-++=21210)2(92292dx x x xdx2713)322(92922132102=-++=x x x x ．13 正态分布的概率密度、分布函数、数学期望与方差一、设随机变量X 服从正态分布)2,1(2N ，求（1）)8.56.1(<≤-X P ；（2）)56.4(≥X P ．解：(1) )4.2213.1()8.416.2()8.56.1(<-≤-=<-≤-=<≤-X P X P X P 8950.09032.019918.0)]3.1(1[)4.2()3.1()4.2(1,01,01,01,0=+-=--=--=ΦΦΦΦ (2) )78.12178.2(1)56.4(1)56.4(<-<--=<-=≥X P X P X P )]78.2(1)78.1(1)]78.2()78.1([11,01,01,01,0ΦΦΦΦ-+-=---= .0402.09973.09625.02=--二、已知某种机械零件的直径X （mm ）服从正态分布)6.0,100(2N ．规定直径在2.1100±（mm ）之间为合格品，求这种机械零件的不合格品率．解：设p 表示这种机械零件的不合格品率，则)2.1100(1)2.1100(≤--=>-=X P X P p ．而)26.01002()6.02.16.01006.02.1()2.1100(≤-≤-=≤-≤-=≤-X P X P X P 1)2(2)]2(1[)2()2()2(-Φ=Φ--Φ=-Φ-Φ= 9544.019772.02=-⨯= 故0456.09544.01=-=p ．三、测量到某一目标的距离时发生的误差X (m)具有概率密度3200)20(22401)(--=x ex f π求在三次测量中至少有一次误差的绝对值不超过30m 的概率．解：三次测量中每次误差绝对值都超过30米可表为}30{}30{}30{>⋃>⋃>=ξξξD 第三次第二次第一次因为)40,20(~2N ξ，所以由事件的相互独立性，有31,01,033)]25.0(1)25.1([})3030{(})30{()(ΦΦ-+-=>+-<=>=ξξP ξP D P 13025.05069.0)8944.05987.02(33≈=--= 于是有86975.013025.01)(1}30{=-=-=<D P P 米至少有一次绝对值三次测量中ξ．四、设随机变量),(~2σμN X ，求随机变量函数Xe Y =的概率密度（所得的概率分布称为对数正态分布）．解：由题设，知X 的概率密度为)(21)(222)(+∞<<-∞=--x ex f x X σμσπ从而可得随机变量Y 的分布函数为)()()(y e P y Y P y F X Y ≤=≤=．当0≤y 时，有0)(=y F Y ；此时亦有0)(='y F Y ．当0>y 时，有dx ey X P y F yx Y ⎰∞---=≤=ln 2)(2221)ln ()(σμσπ．此时亦有222)(ln 21)(σμσπ--='y Y eyy F ．从而可得随机变量Y 的概率密度为⎪⎩⎪⎨⎧>≤=--.0,21;0,0)(222)(ln y e yy y f y Y σμσπ五、设随机变量X 与Y 独立，),(~211σμN X ，),(~222σμN Y ，求： (1) 随机变量函数bY aX Z +=1的数学期望与方差，其中a 及b 为常数； (2) 随机变量函数XY Z =2的数学期望与方差．解：由题设，有211)(,)(σμ==X D X E ；222)(,)(σμ==Y D Y E ．从而有(1)211)()()()()()(μμb a Y bE X aE bY E aX E bY aX E Z E +=+=+=+=； 222212221)()()()()()(σσb a Y D b X D a bY D aX D bY aX D Z D +=+=+=+=． (2)212)()()()(μμ===Y E X E XY E Z E ；)()()()()()()()(22222222Y E X E Y E X E XY E Y X E XY D Z D -=-== )()()]()()][()([2222Y E X E Y E Y D X E X D -++= )()()()()()(22X E Y D Y E X D Y D X D ++=212222212221μσμσσσ++=．四、100台车床彼此独立地工作着，每台车床的实际工作时间占全部工作时间的80%，求：（1）任一时刻有70至86台车床在工作的概率；（2）任一时刻有不少于80台车床在工作的概率．解：设ξ表示“任一时刻正在工作的车床数”，则)8.0,100(~B ξ．808.0100=⨯=ξE ． 16)8.01(8.0100=-⨯⨯=ξD ．（1）)5.2()5.1()168070()168086()8670(1,01,01,01,0-Φ-Φ=-Φ--Φ≈<<ξP 927.019938.09332.0)]5.2(1[)5.1(1,01,0=-+=Φ--Φ=（2）)16800()168080([1)800(1)80(1,01,0-Φ--Φ-≈<<-=≥ξξP P )20()0(2)20()0(11,01,01,01,0Φ-Φ-=-Φ+Φ-=5.015.02=--=．五、在一家保险公司里有10000人参加保险，每人每年付12元保险费．在一年内一个人死亡的概率为0.006，死亡时其家属可向保险公司领得1000元．问：（1）保险公司亏本的可能性是多大？（2）保险公司一年的利润不少于50000元的概率是多少？解：设X 表示“一年内死亡的人数”，则)006.0,10000(~B X ．60006.010000=⨯=EX ． 84.59)006.01(006.010000=-⨯⨯=DX ．（1）)84.596012084.596084.59600(1)1200(1)12100001000(-≤-≤--≈≤≤-=⨯>ξP X P X P 0)7.7(22)]7.7()7.7([11,01,01,0=-=---≈ΦΦΦ．即保险公司不可能亏本．（2）)84.591084.596084.5960()700()5000010001210000(≤-≤-=≤≤=≥-⨯X P X P X P9032.01)756.7()293.1()756.7()293.1(≈-Φ+Φ=-Φ-Φ≈．即保险公司一年利润不少于50000元的概率为9032.0．。

概率论答案详解

第一章随机变量习题一7、设一个工人生产了四个零件，i A 表示事件“他生产的第i 个零件是正品”),,,(4321=i ，用1A ,2A ,3A ,4A 的运算关系表达下列事件.(1)没有一个产品是次品； (1) 43211A A A A B =(2)至少有一个产品是次品；(2) 432143212A A A A A A A A B =⋃⋃⋃= (3)只有一个产品是次品；(3) 43214321432143213A A A A A A A A A A A A A A A A B ⋃⋃⋃= (4)至少有三个产品不是次品4)432143214321432143214A A A A A A A A A A A A A A A A A A A A B ⋃⋃⋃⋃=8. 设 E 、F 、G 是三个随机事件，试利用事件的运算性质化简下列各式： (1)()()F E F E (2) ()()()E F F E （3）()()G F F E 解 :(1) 原式 ()()()()E F F F E F E E E == (2) 原式 ()()()()E F F E F F E F E F E === (3) 原式 ()()()()()G E F G F F F G E F E ==12. (1)设事件 A , B 的概率分别为 51 与 41，且 A 与 B 互斥，则 )(B A P =51. (2).一个盒中有8只红球，3只白球，9只蓝球，如果随机地无放回地摸3只球，则取到的3 只都是红球的事件的概率等于 ___14285____。

(3) 一袋中有4只白球，2只黑球，另一只袋中有3只白球和5只黑球，如果从每只袋中各摸一只球，则摸到的一只是白球，一只是黑球的事件的概率等于 ___1324___。

(4) .设 A1 , A2 , A3 是随机试验E 的三个相互独立的事件，已知P(A1) = α , P(A2) = β，P(A3) = γ ，则A1 , A2 , A3 至少有一个发生的概率是 1- (1- α)(1- β)(1- γ) .(5) ．一个盒中有8只红球，3只白球，9只蓝球，如果随机地无放回地摸3只球，则摸到的没有一只是白球的事件的概率等于 __3457____。

概率论与数理统计典型例题与解析(期末考试与考研必备的超强资料)

概率论与数理统计典型例题分析（期末考试与考研必备）1.在数学系学生中任选一名学生．设事件A ＝{选出的学生是男生}，B ＝{选出的学生是三年级学生}，C ＝{选出的学生是科普队的}．(1)叙述事件ABC 的含义．(2)在什么条件下，ABC ＝C 成立？(3)在什么条件下，C ⊂B 成立？解 (1)事件ABC 的含义是，选出的学生是三年级的男生，不是科普队员．(2)由于ABC ⊂C ，故ABC ＝C 当且仅当C ⊂ABC ．这又当且仅当C ⊂AB ，即科普队员都是三年级的男生．(3)当科普队员全是三年级学生时，C 是B 的子事件，即C ⊂B 成立．2.将一枚硬币独立地掷两次，引进事件：A ＝{掷第一次出现正面}，B ＝{掷第二次出现正面}，C ＝{正、反面各出现一次}，则事件A ，B ，C 是相互独立，还是两两独立？解由题设，可知P (AB )＝P (A )P (B )，即A ，B 相互独立．而1()(())()()(),4P AC P A AB AB P AB P A P B =+=== ()()()()()(()())P A P C P A P AB AB P A P AB P AB =+=+⋅=+⨯=41)4121(21 故A ，C 相互独立，同理B ，C 也相互独立．但是P (ABC )＝P (∅)＝0，而 ,81212121)()()(=⨯⨯=C P B P A P 即 )()()()(C P B P A P ABC P ≠,因此A ，B ，C 两两独立．问题 (1)两个事件的“独立”与“互斥”之间有没有关系？在一般情况下，即P (A )＞0，P (B )＞0时，有关系吗？为什么？(2)设0＜P (A )＜1，0＜P (B )＜1，P (B |A )＋P (B |A )＝1．问A 与B 是否独立，为什么？由此可以得到什么结论？3.设A ，B ，C 是三个随机事件，且=====)()(,41)()()(CB P AB P C P B P A p 0，81)(=AC P ,求A ，B ，C 中至少有一个发生的概率．解设D ＝{A ，B ，C 中至少有一个发生}，则D ＝A ＋B ＋C ，于是P (D )＝P (A ＋B ＋C )＝P (A )＋P (B )＋P (C )－P (AB )－P (BC )－P (AC )＋P (ABC )．又因为,41)()()(===C P B P A P ,0)()(==CB P AB P 81)(=AC P ,而由P (AB )＝0，有P (ABC )＝0，所以⋅=-=858143)(D P 问题怎样由P (AB )＝0推出P (ABC )＝0？提示利用事件的关系与运算导出．4.设事件A 与B 相互独立，P (A )＝a ，P (B )＝b ．若事件C 发生，必然导致A 与B 同时发生，求A ，B ，C 都不发生的概率．解由于事件A 与B 相互独立，因此P (AB )＝P (A )·P (B )＝a ·b ．考虑到C ⊂AB ，故有,B A B A AB C ⊃+=⊃因此).1)(1()()()()(b a B P A P B A P C B A P --===5.某地铁每隔5 min 有一列车通过，在乘客对列车通过该站时间完全不知道的情况下，求每一个乘客到站等车时间不多于2 min 的概率．解设A ＝{每一个乘客等车时间不多于2 min}．由于乘客可以在接连两列车之间的任何一个时刻到达车站，因此每一乘客到达站台时刻t 可以看成是均匀地出现在长为5 min 的时间区间上的一个随机点，即Ω＝[0，5)．又设前一列车在时刻T 1开出，后一列车在时刻T 2到达，线段T 1T 2长为5(见图1－1)，即L (Ω)＝5；T 0是T 1T 2上一点，且T 0T 2长为2．显然，乘客只有在T 0之后到达(即只有t 落在线段T 0T 2上)，等车时间才不会多于2min ，即L (A )＝2．因此图1－1⋅=Ω=52)()()(L A L A P 6.甲乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内到达的时间是等可能的，如果甲船和乙船停泊的时间都是两小时，它们同日到达时会面的概率是多少？解这是一个几何概型问题．设A ＝{它们会面}．又设甲乙两船到达的时刻分别是x ，y ，则0≤x ≤24，0≤y ≤24．由题意可知，若要甲乙会面，必须满足|x －y |≤2，即图中阴影部分．由图1－2可知：L (Ω)是由x ＝0，x ＝24，y ＝0，y ＝24图1－2所围图形面积S ＝242，而L (A )＝242－222，因此.)2422(1242224)()()(2222-=-=Ω=L A L A P7.设随机事件B 是A 的子事件，已知P (A )＝1/4，P (B )＝1/6，求P (B |A )．分析这是一个条件概率问题．解因为B ⊂A ，所以P (B )＝P (AB )，因此⋅===32)()()()()|(A P B P A P AB P A B P 8.在100件产品中有5件是不合格的，无放回地抽取两件，问第一次取到正品而第二次取到次品的概率是多少？解设事件A ＝{第一次取到正品}，B ＝{第二次取到次品}．用古典概型方法求出.010095)(=/=A P 由于第一次取到正品后不放回，那么第二次是在99件中(不合格品仍是5件)任取一件，所以⋅=995)|(A B P 由公式(1－4)， ⋅=⨯==3961999510095)|()()(A B P A P AB P9.五个人抓一个有物之阄，求第二个人抓到的概率．解这是一个乘法公式的问题．设A i ＝{第i 个人抓到有物之阄}(i ＝1，2，3，4，5)，有⋅=+∅=+=+=Ω=2121212111222)(A A A A A A A A A A A A A根据事件相同，对应概率相等有).|()()()(121212A A P A P A A P A P ==又因为,41)|(,54)(,51)(1211===A A P A P A P 所以 ⋅=⨯=514154)(2A P10.设袋中有4个乒乓球，其中1个涂有白色，1个涂有红色，1个涂有蓝色，1个涂有白、红、蓝三种颜色．今从袋中随机地取一个球，设事件A ＝{取出的球涂有白色}，B ＝{取出的球涂有红色}，C ＝{取出的球涂有蓝色}．试验证事件A ，B ，C 两两相互独立，但不相互独立．证根据古典概型，我们有n ＝4，而事件A ，B 同时发生，只能是取到的球是涂有白、红、蓝三种颜色的球，即m ＝1，因而⋅=41)(AB P 同理，事件A 发生，只能是取到的球是涂红色的球或涂三种颜色的球，因而⋅==⋅==2142)(2142)(B P A P 因此，有 ,412121)()(=⨯=B P A P 所以 P (AB )＝P (A )P (B )，即事件A ，B 相互独立．类似可证，事件A ，C 相互独立，事件B ，C 相互独立，即A ，B ，C 两两相互独立，但是由于,41)(=ABC P 而 ,4181212121)()()(=/=⨯⨯=C P B P A P 所以A ，B ，C 并不相互独立．11.加工某一零件共需经过四道工序，设第一、二、三、四道工序的次品率分别是2％、3％、5％、3％，假定各道工序是互不影响的，求加工出来的零件的次品率．答案是：0.124(或1－0.98×0.97×0.95×0.97)．12.一批零件共100个，其中有次品10个．每次从中任取一个零件，取出的零件不再放回去，求第一、二次取到的是次品，第三次才取到正品的概率．答案是：)989099910010(0084.0⨯⨯或． 13.用高射炮射击飞机，如果每门高射炮击中飞机的概率是0.6，试问：(1)用两门高射炮分别射击一次击中飞机的概率是多少？(2)若有一架敌机入侵，至少需要多少架高射炮同时射击才能以99％的概率命中敌机？分析本题既可使用加法公式，也可使用乘法公式．解 (1)令B i ＝{第i 门高射炮击中敌机}(i ＝1，2)，A ＝{击中敌机}．在同时射击时，B 1与B 2可以看成是互相独立的，从而21,B B 也是相互独立的，且有P (B 1)＝P (B 2)＝0.6，.4.0)(1)()(121=-==B P B P B P方法1(加法公式)由于A ＝B 1＋B 2，有P (A )＝P (B 1＋B 2)＝P (B 1)＋P (B 2)－P (B 1)P (B 2)＝0.6＋0.6－0.6×0.6＝0.84．方法2(乘法公式) 由于21B B A =，有,16.04.04.0)()()()(2121=⨯===B P B P B B P A P于是 .84.0)(1)(=-=A P A P(2)令n 是以99％的概率击中敌机所需高射炮的门数，由上面讨论可知，99％＝1－0.4n 即 0.4n ＝0.01，亦即.026.53979.024.0lg 01.0lg ≈--==n 因此若有一架敌机入侵，至少需要配置6门高射炮方能以99％的把握击中它．14.设某人从外地赶来参加紧急会议．他乘火车、轮船、汽车或飞机来的概率分别是31110510、、及52，如果他乘飞机来，不会迟到；而乘火车、轮船或汽车来迟到的概率分别为41、⋅12131、试问：(1)他迟到的概率；(2)此人若迟到，试推断他是怎样来的可能性最大？解令A 1＝{乘火车}，A 2＝{乘轮船}，A 3＝{乘汽车}，A 4＝{乘飞机}，B ＝{迟到}．按题意有：,103)(1=A P ,51)(2=A P ,101)(3=A P ,52)(4=A P,41)|(1=A B P ,31)|(2=A B P ,121)|(3=A B P .0)|(4=A B P (1)由全概率公式，有⋅=⨯+⨯+⨯+⨯==∑=203052121101315141103)|()()(41i i i A B P A P B P (2)由逆概率公式 ),4,3,2,1()|()()|()()|(41==∑=i A B P A P A B P A P B A P jj j i i i得到.0)|(,181)|(,94)|(,21)|(4321====B A P B A P B A P B A P 由上述计算结果可以推断出此人乘火车来的可能性最大．15.三人同时向一架飞机射击，设他们射中的概率分别为0.5，0.6，0.7．又设无人射中，飞机不会坠毁；只有一人击中飞机坠毁的概率为0.2；两人击中飞机坠毁的概率为0.6；三人射中飞机一定坠毁．求三人同时向飞机射击一次飞机坠毁的概率．解设A i ＝{第i 个人射中}(i ＝1，2，3)，有P (A 1)＝0.5， P (A 2)＝0.6， P (A 3)＝0.7．又设B 0＝{三人都射不中}，B 1＝{只有一人射中}，B 2＝{恰有两人射中}，B 3＝{三人同时射中}，C ＝{飞机坠毁}．由题设可知,0)|(0=B C P ,2.0)|(1=B C P ,6.0)|(2=B C P ,1)|(3=B C P并且.06.03.04.05.0)()()()()(3213210=⨯⨯===A P A P A P A A A P B P同理)()(3213213211A A A A A A A A A P B P ++=)()()(321321321A A A P A A A P A A A P ++=123123123()()()()()()()()()P A P A P A P A P A P A P A P A P A =++＝0.5×0.4×0.3＋0.5×0.6×0.3＋0.5×0.4×0.7＝0.29；P (B 2)＝0.44；P (B 3)＝0.21．利用全概率公式便得到)|()()(30i i i B C P B P C P ∑==＝0.06×0＋0.29×0.2＋0.44×0.6＋0.21×1＝0.532．由上面的讨论可以看出，在使用全概率公式和逆概率公式解题时，“分析题目，正确写出题设，找出(或计算)先验概率和条件概率”是十分重要的．练习：两台机床加工同样的零件，第一台出现废品的概率是0.03，第二台出现废品的概率是0.02．加工出来的零件放在一起，并且已知第一台加工的零件比第二台加工的零件多一倍，求任意取出的零件是合格品的概率；又：如果任意取出的零件经检查是废品，求它是由第二台机床加工的概率．答案是：0.973；0.25．16.某类电灯泡使用时数在1000 h 以上的概率为0.2，求三个灯泡在使用1000 h 以后最多只坏一个的概率．解这是一个n ＝3，p ＝0.8二项概型问题P 3(μ≤1)＝P (μ＝0)＋P (μ＝1)．17.袋中有10个球，其中2个为白色，从中有放回地取出3个，求这3个球中恰有2个白球的概率．解方法1 设A ＝{恰有2个白球}，由古典概型，有310=n , 8232⨯⨯=m ，因此 ⋅⨯⨯=3210823)(A P 方法2 由二项概型，有⋅⨯⨯====321223310823)108()102()2()(C P A P μ18.袋中有4个白球、6个红球，先从中任取出4个，然后再从剩下的6个球中任取一个，则它恰为白球的概率是______．分析设A i ＝{第i 次取到白球}，根据古典概型，我们有⋅==104)(110141C C A P 由于 ,)(212111222A A A A A A A ΩA A +=+==并且,94106)|()()(,93104)|()()(1212112121⨯==⨯==A A P A P A A P A A P A P A A P 因此 ⋅=⨯⨯+⨯=1049104634)(2A P 同理 ⋅=104)(5A P 19.有一批产品，其中正品有n 个，次品有m 个，先从这批产品中任意取出l 个(不知其中的次品数)，然后再从剩下的产品中任取一个恰为正品的概率为( )．方法1 设A k ＝{前l 次中恰有k 个正品}，k ＝q ，q ＋1，…，p ；其中q ＝max(l －m ，0)，p ＝min(n ，l )．又设B ＝{第l ＋1个恰为正品}，有,)(,1nm k l m k n k p q q C C C A P ΩA A A +-+==+++ 而 ,)|(11ln m k n C C A B P l n m k n k -+-==-+- 由全概率公式有⋅+==∑=nm n A B P A P B P k k p q k )|()()( 举例说明：(1)n ＝3，m ＝5，l ＝4，这时k ＝0，1，2，3．⋅=+++=8)4/()0306015()(48C B P⋅=+++=8)4/()5609020()(48C B P 方法2 利用抓阄问题的讨论，直接得到⋅+n m n 方法3 前l ＋1次取到正品的概率减去前l 次取到正品的概率(有条件限制，有时使用起来不一定方便)方法4 (全排列方法)令第l ＋1个位置上为正品，由于有n 个正品，故有n 种方法，于是⋅+=+-+=nm n n m n m n B P )!()!1()( 方法5 将第l ＋1次看成第1次，于是⋅+==+nm n C C B P n m n 11)( 20.袋中有5个球，其中1个是红球，每次取1个球，取出后不放回，前3次取到红球的概率为( )．分析设A ＝{前3次取到红球}，根据古典概型，有⋅==53)(352411C C C A P说明利用这一结论，可以计算第3次取到红球的概率：P {第3次取到红球}＝P {前3次取到红球}－P {前2次取到红球}⋅=-=-=515253251411352411C C C C C C 注意这里实际用到了互斥情况下的加法公式．21.设两两相互独立的三事件A ，B ，C ，满足：ABC ＝∅，P (A )＝P (B )＝P (C )＜21,并且169)(=++C B A P ，求事件A 的概率．分析设P (A )＝p ．由于ABC ＝∅，有P (ABC )＝0，根据三个事件两两独立．．．．情况下的加法公式，有P (A ＋B ＋C )＝P (A )＋P (B )＋P (C )－P (A )P (B )－P (B )P (C )－P (A )P (C )＋P (ABC )，即 ,1690332=+-p p 亦即 ,01632=+-p p 解得 41=p 或43(由题意舍去)．于是 ⋅=41)(A P 说明 (1)三个事件两两独立，不能推出三个事件相互独立．(2)由ABC ＝⇒∅P (ABC )＝0，反之不真．22.设P (A )＞0，P (B )＞0，证明(1)若A 与B 相互独立，则A 与B 不互斥．(2)若A 与B 互斥，则A 与B 不独立．分析 (1)由于事件A 与B 相互独立，且P (A )＞0，P (B )＞0，因此P (AB )＝P (A )P (B )＞0．可见，AB ≠∅，即事件A 与B 不互斥(相容)．(2)由于事件A 与B 互斥，即AB ＝∅，因此P (AB )＝0，而P (A )＞0，P (B )＞0，故P (AB )≠P (A )P (B )，即事件A 与B 不可能相互独立．说明 (1)事件之间相互独立，并不意味着它们互斥，反之亦然．(2)在P (A )＞0，P (B )＞0的条件下，两个事件独立与否，是在它们相容情况下讨论的．(3)事件的“互斥”与“相互独立”是没有关系的两个“关系”．23.设A ，B 是两个随机事件，且0＜P (A )＜1，P (B )＞0，)|()|(A B P A B P =，则P (AB )＝P (A )P (B )．分析由公式()()()(|),(|),()()1()P AB P AB P AB P B A P B A P A P A P A ===- 由题设 ),|()|(A B P A B P =即,)(1)()()(A P B A P A P AB P -= 于是，有 ()()(()())()()()(),P AB P A P AB P AB P A P AB AB P A P B =+=+=即A 、B 相互独立．说明 (1) )|()|(A B P A B P =是A ，B 独立的一个充要条件．(2)若此题换成下述选择题：设……，则______ (A)).|()|(B A P B A P = (B)(|)(|).P A B P A B =/(C)P (AB )＝P (A )P (B )． (D )P (AB )≠P (A )P (B )．时，能否认为(A )与(B )，或(C )与(D )之中必有一个成立．24.设两个随机事件A ，B 相互独立，已知仅有A 发生的概率为41，仅有B 发生的概率为41，则 P (A )＝______，P (B )＝______．分析方法1 因为P (A )＞0，P (B )＞0，且A 与B 相互独立，所以AB ≠∅(想一想为什么)．一方面P (A ＋B )＝P (A )＋P (B )－P (A )P (B )； (1－6)另一方面).()(21)()()()()(B P A P B P A P B A P B A P B A P +=++=+ (1－7) 由于)()(B A P B A P =，有 ),()()()(B P AB B A P AB B A P A P =+=+=于是由式(1－6)，式(1－7)有,))((21))(()(222A P A P A P +=- 即 ⋅===-21)(,21)(,41))(()(2B P A P A P A P 方法2 因为A 与B 相互独立，所以A 与B 也相互独立．由于)()(B A P B A P =，有P (A )＝P (B )，于是,41))(1)(())(1)(()()()(=-=-==A P A P B P A P B P A P B A P 因此 ⋅==21)()(B P A P 问题比较上述两种方法，哪个更简单一些，还有没有其他方法？25.设随机事件A 与B 的和事件的概率为0.6，且积事件B A ⋅的概率为0.3，则事件A 的概率P (A )＝( )．分析因为B A B A +=⋅，所以.4.06.01)(1)()(=-=+-=+=⋅B A P B A P B A P又因为,)(B A B A B B A ΩA A +=+==故 .7.04.03.0)()(=+=+=B A B A P A P26.甲、乙两封信随机地投入标号是1，2，3，4，5的五个信筒内，则第3号信筒恰好只投入一封信的概率为( )．分析这是一个古典概型问题，有1422,5C m n ⨯==，因此P (A )＝0.32．问题 (1)如何将信投入信箱转化为在信封上写号问题？ (2)本题是否可用(有放回)摸球问题来解决？27.袋中有10个球，其中有4个白球、6个红球．从中任取3个，求这3个球中至少有1个是白球的概率．分析这一个古典概型问题，样本空间中样本点的总数为⋅=310C n方法1 设A ＝{至少有1个白球}，有⋅=++=65)(310063416242614C C C C C C C A P 方法2 设B ＝{取出的全是红球}，有⋅-=-=3104361)(1)(C CC B P A P方法3 先从4个白球中任取一个，然后再从剩下的9个球(有红球又有白球)中任取2个，因此⋅=3102914)(C CC A P问题上述三种方法都对吗，为什么？28.一批产品共100件，对产品进行不放回地抽样检查，整批产品不合格的条件是：在被检查的5件产品中至少有一件是废品．如果在该批产品中有5件是废品，求该批产品被拒绝接收的概率．解设A i ＝{被检查的第i 件产品是废品}，i ＝1，2，3，4，5；B ＝{该批产品被拒绝接收}．方法1 由于,54321A A A A A B ++++=于是1234512345()1()1()P B P A A A A A P A A A A A =-++++=-1213124123512341()(|)(|)(|)(|),P A P A A P A A A P A A A A P A A A A A =-而 ,9893)|(,9994)|(,10095)(213121===A A A P A A P A P ⋅==9691)|(,9792)|(432153214A A A A A P A A A A P因此 .23.09691979298939994100951)(=⨯⨯⨯⨯-=B P方法2 .23.01)(1)(5100595=-=-=C C B P B P29.由以往记录的数据分析，某船只在不同情况下运输某种物品，损坏2％，10％，90％的概率分别为0.8，0.15和0.05．现在从中随机地取三件，发现这三件全是好的，试分析这批物品的损坏率为多少？分析设B ＝{三件都是好的}，A 1＝{损坏率为2％}， A 2＝{损坏率为10％}，A 3＝{损坏率为90％}，则A 1，A 2，A 3两两互斥，且A 1∪A 2∪A 3＝Ω．已知P (A 1)＝0.8，P (A 2)＝0.15，P (A 3)＝0.05，且3198.0)|(=A B P ， 3290.0)|(=A B P ， 3310.0)|(=A B P ．由全概率公式可知)()|()(31i i i A P A B P B P ∑==05.01.015.090.08.098.0333⨯+⨯+⨯= 8624.0≈．由贝叶斯公式，这批物品的损坏率为2％，10％，90％的概率分别是,8731.08624.08.098.0)()()|()|(3111≈⨯==B P A P A B P B A P,1268.08624.015.090.0)()()|()|(3222≈⨯==B P A P A B P B A P.0001.08624.005.01.0)()()|()|(3333≈⨯==B P A P A B P B A P由于P (A 1|B )比P (A 2|B )，P (A 3|B )大得多，因此可以认为这批货物的损坏率为2％．30.掷两枚匀称的骰子，X ＝{点数之和}，求X 的分布．答案是：⋅⎥⎦⎤⎢⎣⎡36/136/236/11232~ X 31.设⎪⎩⎪⎨⎧≤>+=,0,0,0,11)(2x x x x f f (x )是否为分布密度函数？如何改造？解由于,2πd )(=⎰+∞∞-x x f 所以f (x )不是分布密度函数．令⎪⎩⎪⎨⎧≤>+⋅==.0,0,0,11π2)(π2)(2x x x x f x p则p (x )是分布密度函数．32.设随机变量X 的分布密度函数为⎩⎨⎧≤≤=.,0,10,)(其他x Cx x p求(Ⅰ)常数C ；(Ⅱ)P (0.3≤X ≤0.7)；(Ⅲ)P (－0.5≤X ＜0.5)．解 (Ⅰ)由p (x )的性质，有,21|2d d )(110210C x C x Cx x x p =⋅===⎰⎰∞+∞-所以C ＝2．(Ⅱ).4.0|d 2)7.03.0(7.03.027.03.0===≤≤⎰x x x X P(Ⅲ).25.0|d 2d 0)5.05.0(5.0025.0005.0==+=≤≤-⎰⎰-x x x x X P问题若连续型随机变量X 的分布密度函数p (x )为不可求积函数，如何计算P (X ∈D )呢？33.从一批有13个正品和2个次品的产品中任意取3个，求抽得的次品数X 的分布列和分布函数，并求⋅≤<)2521(X P 解先求X 的分布列，X 的所有可能取值为0，1，2，由古典概型的概率计算公式知3122113213213323151********(0),(1),(2)353535C C C C C P X P X P X C C C =========⋅ 故X 的分布列为四个区间．当x ＜0时，F (x )＝P (X ≤x )＝0．当10<≤x 时，⋅===3522)0()(X P x F 当12x ≤<时，⋅==+==3534)1()0()(X P X P x F 当x ≥2时，F (x )＝P (X ＝0)＋P (X ＝1)＋P (X ＝2)＝1．综上有X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=.2,1,21,3534,10,3522,0,0)(x x x x x F由分布函数可求出⋅=-=-=≤<351335221)21()25()2521(F F X P 34.设连续型随机变量X 的分布函数⎪⎩⎪⎨⎧≤>+=-,0,0,0,e )(22x x B A x F x求系数A 和B ．解由lim ()1n F x →+∞=，知A ＝1．再由F (x )在x ＝0处的连续性可知,)e(lim )(lim 02200B A B A x F x x x +=+==-+→→故 B ＝－A ＝－1．35.设连续型随机变量X 的分布函数为()1xAF x e-=+， +∞<<∞-x ，求(Ⅰ)常数A ． (Ⅱ)X 的分布密度函数p (x )． (Ⅲ)P {X ≤0}．答案是：(Ⅰ)A ＝1．(Ⅱ)2)e 1(e )(x xx p --+= +∞<<∞-x ． (Ⅲ)⋅==<21)0()0(F X P 问题 (1)离散型随机变量的概率分布与分布函数之间有什么关系？(2)连续型随机变量的概率分布密度与分布函数之间有什么关系？ (3)如何利用分布函数计算P (X ∈D )？其中D ＝(a ，b ]． (4)如何确定分布函数中的待定常数？36.设X 服从指数分布，则Y ＝min{X ，2}的分布函数( )．(A)连续． (B)至少有两个间断点． (C)阶梯函数． (D)恰有一个间断点．答案是：D ．分析方法1 由题设可知X ～E (λ)，有⎩⎨⎧≤>=-.0,0,0,e )(x x x p x λλ 令X 1＝X ，X 2＝2，则⎩⎨⎧≥<=⎩⎨⎧>-≤=-.2,1,2,0)(;0,e 1,0,0)(21x x x F x x x F xλ于是，Y ＝min{X ，2}＝min{X 1，X 2}的分布函数为))(1))((1(1)(21y F y F y F ---=○一⎪⎩⎪⎨⎧≥<<-≤=-.2,1,20,e 1,0,0y y y y λ 可见它只有一个间断点y ＝2．方法2 从图2－1中，容易看出它只有一个间断点y ＝2．图2－137.一袋中装有5只球，编号为1，2，3，4，5．在袋中同时取3只球，用X 表示取出的3只球中的最小号码数，求X 的分布函数．解 X 的可能取值为3，2，1．,106/)1(,103/)2(,101/)3(352435233522=========C C X P C C X P C C X P 即X 的分布阵为⎥⎥⎦⎤⎢⎢⎣⎡101103106321, 从而X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=.3,1,32,109,21,106,1,0)(x x x x x F38.设X ～U (a ，b )，即⎪⎩⎪⎨⎧≤≤-=.,0,,1)(其他b x a a b x p则⎪⎩⎪⎨⎧≥<≤--<=.,1,,,,0)(b x b x a a b a x a x x F 其图形是一条连续的曲线，见图2－3．图2－339.设X ～N (0，1)，求P (X ＜2.35)，P (X ＜－1.25)以及P (|X |＜1.55)．解 P (X ＜2.35)＝Ф(2.35)查表0.9906．P (X ＜－1.25)＝Ф(－1.25)＝1－Ф(1.25)＝1－0.8944＝0.1056．P (|X |＜1.55)＝P (－1.55＜X ＜1.55)＝Ф(1.55)－Ф(－1.55)＝2Ф(1.55)－1＝2×0.9394－1＝0.8788．40.设X ～N (1，22)，求P (0＜X ≤5)．解这里μ＝1，σ＝2，β＝5，α＝0，有.5.0,2--=-σμασμβ 于是P (0＜X ≤5)＝Ф(2)－Ф(－0.5)＝Ф(2)－[1－Ф(0.5)]＝Ф(2)＋Ф(0.5)－1＝0.9772＋0.6915－1＝0.6687．41.若X ～N (μ，σ2)，求(Ⅰ)P {μ－σ＜X ＜μ＋σ}； (Ⅱ)P {μ－2σ＜X ＜μ＋2σ}； (Ⅲ)P {μ－3σ＜X ＜μ＋3σ}．解 (Ⅰ)由于X ～N (μ，σ2)，故)()(}{σμσμσμσμσμσμ----+=+<<-ΦΦX P ＝Ф(1)－Ф(－1)＝2Ф(1)－1＝0.6826≈0.68．同理有：(Ⅱ) P {μ－2σ＜X ＜μ＋2σ}＝2Ф(2)－1＝0.9545≈0.95． (Ⅲ) P {μ－3σ＜X ＜μ＋3σ}＝2Ф(3)－1＝0.9973≈0.99．42.设X ～N (2，32)，求：(Ⅰ)P {－1≤X ≤8}；(Ⅱ)P {X ≥－4}；(Ⅲ)P {X ≤11}．解由于X ～N (2，32)，即μ＝2，σ＝3，因此 (Ⅰ)P {－1≤X ≤8}＝P {2－3≤X ≤2＋2×3}＝P {2－3≤X ＜2}＋P {2≤X ≤2＋2×3}}322322{21}3232{21⨯+<≤⨯-++<≤-=X P X P.815.0295.0268.0=+≈(Ⅱ)P {X ≥－4}＝P {－4≤X ＜＋∞}＝P {2－2×3≤X ≤2}＋P {X ≥2}.975.021295.0=+≈(Ⅲ)P {X ≤11}＝P {－∞＜X ≤11}＝P {－∞＜X ≤2}＋P {2≤X ≤2＋3×3}.995.0299.021=+≈43.设X ～N (3，σ2)，并且P (3≤X ≤7)＝0.4，求P (X ≤－1)．答案是：0.1．分析(略)44.设某机器生产的螺栓的长度(cm)服从参数μ＝10.05，σ＝0.06的正态分布，规定长度在范围(10.05±0.12)cm 内为合格品，求螺栓的次品率．答案是：0．0455(或0．05)．分析(略)．求Y ＝X ＋1的概率分布．解由y i ＝2i x ＋1(i ＝1，2，…，5)及X 的分布，得到把f (x i )＝2i x ＋1相同的值合并起来，并把相应的概率相加，便得到Y 的分布，即,21)2()2()5(==+-===X P X P Y P ,103)1()1()2(==+-===X P X P Y P ⋅====51)0()1(X P Y P 所以46.设X ～U (0，1)，并且Y ＝X ，求Y 的分布密度p 2(y )．解 X 的分布密度函数为⎩⎨⎧∈=.,0],1,0[,1)(1其他x x p 对于函数y ＝x 2，当x ∈[0，1]时，α＝min{x 2}＝0，β＝max{x 2}＝1，于是⎪⎩⎪⎨⎧≥<<≤=.1,1,10*,,0,0)(y y y y F 当0＜y ＜1时)()()()(2y X P y X P y Y P y F ≤=≤=≤=.d 1d 0d )(01y x x x x p yy=+==⎰⎰⎰∞-∞-由 ,21)()()(2yy y F y p ='='=故随机变量Y 的分布密度函数为⎪⎩⎪⎨⎧<<=.,0,10,21)(2其他y yy p47.设随机变量)2π,2π(~-U X ，求随机变量Y ＝sin X 的分布密度p 2(y )．解 X 的分布密度函数为⎪⎩⎪⎨⎧-∈=.0,],2π,2π[,π1)(1其他x x p因为y ＝sin x 在)2π,2π(-内单调增加，所以存在反函数x ＝arc sin y ，其导数为 ⋅-='211yx y利用公式求出Y 的分布密度函数，首先计算,1}{sin min 2π2π-==≤≤-x x α ππ22max {sin }1,x x β-≤≤== 于是⎪⎩⎪⎨⎧<<-'⋅=-.,0,11|,|))(()(112其他y x y f p y p y⎪⎩⎪⎨⎧<<--=.,0,11,11.π12其他y y 48.X ～U (0，π)，Y ＝sin X ，求p 2(y )．解 X 的分布密度函数为⎪⎩⎪⎨⎧∈=.,0],π,0[,π1)(1其他x x p0π0πmin{sin }0,max{sin } 1.x x x x αβ≤≤≤≤====当0＜y ＜1时，F (y )＝P (Y ≤y )＝P (sin X ≤y )＝P (0≤X ≤arc sin y )＋P (π－arc sin y ≤X ≤π),sin arc π2y =所以⎪⎩⎪⎨⎧≥<<≤=1,,11,0,sin arc π20,,0)(y y y y y F 即⎪⎩⎪⎨⎧<<-=.,0,10,1π2)(22其他y yy p 49.(1).,,2,1,}{N k NAk X P ⋅⋅⋅=== (2) ,!}{k B k X P kλ⋅==k ＝0，1，2，…，λ＞0且λ为常数，试确定常数A 和B ．解 (1)由分布律的性质可知,)(111A N NAN A k X P Nk N k =⋅====∑∑== 因此，A ＝1．于是，X 的分布律为).,,2,1(1)(N k Nk X P === 称这样的分布为离散型的均匀分布．(2)由分布律的性质，有,e !!10λλλ⋅===∑∑∞=∞=B k B k Bkk kk解得B ＝e －λ．于是.e !)(λλ-==k k X P k这表明X 服从参数为λ的泊松分布．50.设平面区域D 是由x ＝1，y ＝0，y ＝x 所围成(如图2－5)，今向D 内随机地投入10个点，求这10个点中至少有2个点落在由曲线y ＝x 2与y ＝x 所围成的区域D 1内的概率．图2－5分析分两步进行．第一步：先计算任投一点落入D 1的概率．根据几何概型，有11()123()1()32L A P A L Ω-===⋅第二步：设X ＝{落入D 1内的点数}，有),31,10(~B X 于是P (X ≥2)＝1－P (X ＝0)－P (X ＝1).)32)(31()32(1911010C --=51.设随机变量X 具有连续的分布函数F 1(x )，求Y ＝F 1(X )的分布函数F 2(y )．(或证明题：设X 的分布函数F 1(x )是连续函数，证明随机变量Y ＝F 1(X )在区间(0，1)上服从均匀分布．)分析由于F 1(x )为X 的连续分布函数，可知α＝min{F 1(x )}＝F 1(－∞)＝0， β＝max{F 1(x )}＝F 1(＋∞)＝1．因为F 1(x )是单调递增函数，所以11-F (y )存在(单调函数必有单值反函数存在)，因而有⎪⎩⎪⎨⎧≥<≤<=≤.1,1,10*,,0,0)()(def2y y y y Y P y F 当0≤y ＜1时，*＝F 2(y )＝P (F 1(X )≤y )＝P (X ≤11-F (y )) ＝F 1(11-F (y ))＝y ．代入F 2(y )表达式有⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(2y y y y y F 因此，Y 的分布密度函数为⎩⎨⎧≤≤=.,0,10,1)(2其他y y p即 ).1,0(~U Y52．设X ～E (2)，证明Y ＝1－e －2X～U (0，1)分析由于X ～E (2)，因此⎩⎨⎧≤>=-.0,0,0,e 2)(21x x x p x 当x ＝0时，y ＝0＝α；当x →＋∞时，y →1＝β：因为y ＝1－e －2x单调增加，所以其反函数为)1ln(21y x --=，有 .e 21112111212x yy y x =-=---='方法1(公式法)⎩⎨⎧≤≤'=--.,0,10|,))((|))(()(1112其他y y f y f p y p⎪⎩⎪⎨⎧≤≤⋅=-.,0,10,e 21e 222其他y xx ⎩⎨⎧≤≤=.,0,10,1其他y 即Y ～U (0，1)．方法2(定义法) 由分布函数的定义⎪⎩⎪⎨⎧>≤≤<=.1,1,10*,,0,0)(2y y y y F 当0≤y ≤1时，有))1ln(21()e 1()()(22y X P y P y Y P y F X --≤=≤-=≤=-12(ln(1))211(ln(1))1e 2---=--=-y F y,)1(1y y =--=因此⎪⎩⎪⎨⎧>≤≤<=,1,1,10,,0,0)(y y y y y F即Y ～U (0，1)．53.设随机变量X 的概率密度为⎪⎩⎪⎨⎧∈=,,0],8,1[,31)(32其他x x x fF (x )是X 的分布函数．求随机变量Y ＝F (X )的分布函数．解易见，当x ＜1时，F (x )＝0；当x ＞8时，F (x )＝1．对于x ∈[1，8]，有.1d 31)(1332-==⎰xx t t x F设G (y )是随机变量Y ＝F (X )的分布函数．显然，当y ≤0时，G (y )＝0；当y ≥1时，G (y )＝1．对于y ∈(0，1)，有}1{})({}{)(3y X P y X F P y Y P y G ≤-=≤=≤=,])1[(})1({33y y F y X P =+=+≤=于是，Y ＝F (X )的分布函数为⎪⎩⎪⎨⎧≥<<≤=.1,1,10,,0,0)(y y y y y G即Y ～U (0，1)．54.设随机变量X ～U (0，5)，求方程4x 2＋4Xx ＋X ＋2＝0有实根的概率．分析因为X 在(0，5)上服从均匀分布，故X 的分布密度为⎪⎩⎪⎨⎧≤≤=.,0,50,51)(其他x x p方程4x 2＋4Xx ＋X ＋2＝0有实根的条件是∆＝16X 2－16(X ＋2)≥0，即 (X ＋1)(X －2)≥0．解得X ≤－1或X ≥2．舍去X ≤－1，最后得2≤X ≤5．因此，所求概率为⋅==≤≤⎰53d 51)52(52x X P 问题本题可否使用其他方法？55. 设随机变量X 的绝对值不大于1，即|X |≤1，且===-=)1(,81)1(X P X P41，在事件{－1＜X ＜1}出现的条件下，X 在(－1，1)内的任一子区间上取值的条件概率与该子区间长度成正比．试求X 的分布函数F (x )及P (X ＜0)(即X 取负值的概率)．分析 (1)由题设，我们有x ＜－1时，F (x )＝0；x ≥1时，F (x )＝1．以下考虑－1＜x ＜1时的情形．由于1＝P (|X |≤1)＝P (X ＝－1)＋P (－1＜X ＜1)＋P (X ＝1)，故 ⋅=--=<<-8541811)11(X P 另据条件，有),1(21)11|1(+=<<-≤<-x X x X P 于是，对于－1＜x ＜1，有(－1，x ]⊂(－1，1)，因此P (－1＜X ≤x )＝P (－1＜X ≤x ，－1＜X ＜1)＝P (－1＜X ＜1)P (－1＜X ≤x |－1＜X ＜1)),1(165)1(2185+=+⨯=x x ⋅+=≤<-+-≤=1675)1()1()(x x X P X P x F综上，有⎪⎩⎪⎨⎧≥<≤-+-<=.1,1,11,16/)75(,1,0)(x x x x x F (2)P (X ＜0)＝P (X ≤0)－P (X ＝0)＝F (0)＝7/16．56.射击用的靶子是一个半径为R 的圆盘，已知每次射击都能击中靶子，并且击中靶子上任一以靶心为圆心的圆盘的概率与该盘的面积成正比．设随机变量X 表示击中点与靶心的距离，求X 的分布密度函数．分析根据分布函数的定义及几何概型，由图2－6有图2－6),0(ππ)()(2222R x R x R x x X P x F ≤≤==≤=于是 22()(),xp x F x R='=因此⎪⎩⎪⎨⎧≤≤=.,0,0,2)(2其他R x R xx p 说明 (1)注意其分布函数应为⎪⎪⎩⎪⎪⎨⎧>≤≤<=.,1,0,,0,0)(22R x R x R x x x F 57.点随机地落在中心在原点，半径为R 的圆周上，并且对弧长是均匀地分布，求(1)落点的横坐标的概率分布密度函数p 1(x )．(2)落点与点(－R ，0)的弦长的概率分布密度函数p 2(y )． (提示：落点的极角θ均匀地分布在(0，2π)上)分析设落点的极角为Θ，落点P 的横坐标为X ，落点与(－R ，0)点的弦长为Y ，则由题设可知Θ～U (0，2π)，即()1,02π,2π0,.p θθΘ⎧≤<⎪=⎨⎪⎩其他由图2－7不难看出⋅==2cos2,cos ΘR Y ΘR X图2－7(1)定义法试求点P 的横坐标X ＝R cos Θ的密度函数．因为x ＝R cos θ(0≤θ＜2π)不是单调函数，由图2－8得到，使R cos θ≤x 成立的θ应满足⋅-≤≤Rx R x cos arc π2cosarc θ图2－8于是，对－R ≤x ≤R ，有θθθd )()cos ()()(cos ΘxR X p x ΘR P x X P x F ⎰≤=≤=≤=⋅-==⎰-Rx Rx Rx os arcc π11d 2π1arccosπ2arccosθ 对x ＜－R ，有.0)()cos ()()(=∅=≤=≤=P x ΘR P x X P x F X对x ＞R ，有,1)()cos ()()(==≤=≤=ΩP x ΘR P x X P x F X即⎪⎩⎪⎨⎧≥<<---≤=.,1,,cos arc π11,,0)(R x R x R R xR x x F X 所以X 的密度函数为⎪⎩⎪⎨⎧<<--='=.,0,,π1)()(22其他R x R x R x F x p X X(2)公式法设θ∈(－π，π)．由,2cos 2θR y =有当0≤θ≤π时，单调递减，⋅--='=2242,2cosarc 2y R R y y θθ 当－π≤θ≤0时，单调递增，2arccos,2y y R θθ=-=' 可见p Y (y )＝P θ(f －1(y ))|y y f'-))((1|⋅-=--+-=22222241π2|42|2π1422π1yR y R y R 因此⎪⎩⎪⎨⎧<≤-=.,0,20,4π2)(22其他R y y R y p Y58.设随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧∈∈=.,0],6,3[,92],1,0[,31)(其他x x x p若使得32)(=≥k X P ，则k 的取值范围是________．分析由图2－9可知图2－9,32)36(92)63(=-⨯=≤≤X P 因此k ∈[1，3]时，⋅=≤≤=≥32)63()(X P k X P 59.设随机变量X 的分布函数为F (x )，则Y ＝－2ln F (X )的概率分布密度函数P Y (y )＝______．分析用定义法求出Y 的分布，首先求出Y 的分布函数．当y ＞0时，有F (y )＝P (Y ≤y )＝P (－2ln F (X )≤y ))e )((2y X F P -≥= ))e ((21y F X P --≥= ))e ((121y F F ---=.e 12y--=当y ≤0时，F (y )＝0．因此 ⎪⎩⎪⎨⎧≤>-=-.0,0,0,e 1)(2y y y F y 再求出Y 的分布密度函数⎪⎩⎪⎨⎧≤>='=-.0,0,0,e 21)()(2y y y F y p yY60.设)2π,2π(~-U X ，并且y ＝tan x ，求Y 的分布密度函数p (y )．分析由)2π,2π(~-U X ，有⎪⎩⎪⎨⎧-∈=.,0],2π,2π[,π1)(1其他x x p 下面利用公式法求出Y ＝tan X 的分布，为此先求出：α＝－∞，β＝＋∞．,tan arc )(1y y f x ==-⋅+='='-2111))((yy f x y y 于是有121()(())|(1'())|y p y p f y f y --=⋅').(11.π12+∞<<-∞+=y y61.设二维随机向量(X ，Y )共有6个取正概率的点，它们是：(1，－1)，(2，－1)，(2，0)(2，2)，(3，1)，(3，2)，并且(X ，Y )取得它们的概率相同，则(X ，Y )的联合分布及边缘分布为62.设(X ，Y )的联合分布密度为⎩⎨⎧≥≥=+-.,0,0,0,e ),()43(其他y x C y x p y x试求：(1)常数C . (2)P {0＜X ＜1，0＜Y ＜2}． (3)X 与Y 的边缘分布密度p 1(x )，p 2(y )．解 (1)由p (x ，y )的性质，有y x C y x y x p y x d d e d d ),(1)43(0+-+∞+∞+∞∞-+∞∞-⎰⎰⎰⎰==3401e d e d ,12x y C x y C +∞+∞--=⋅⋅=⎰⎰ 即C ＝12．(2)令D ＝{(x ，y )|0＜x ＜1，0＜y ＜2}，有y x y x p D Y X P Y X P Dd d ),(}),{(}20,10{⎰⎰=∈=<<<<).e 1)(e 1(d e d e 12d d e 128342310)43(----+---===⎰⎰⎰⎰y x y x y x y x D(3)先求X 的边缘分布：①当x ＜0时，p (x ，y )＝0，于是10()(,)d 0.p x p x y y +∞==⎰②当x ≥0时，只有y ≥0时，p (x ，y )＝12e－(3x ＋4y )，于是⎰+∞∞--+-==.e 3d e 12)(3)43(1x y x y x p因此⎩⎨⎧<≥=-.0,0,0,e 3)(31x x x p x 同理⎩⎨⎧<≥=-.0,0,0,e 4)(42y y y p y 63.设二维连续型随机变量(X ，Y )在区域D 上服从均匀分布，其中D ＝{(x ，y ):|x ＋y |≤1，|x －y |≤1}，求X 的边缘密度p X (x )．解区域D 实际上是以(－1，0)，(0，1)，(1，0)，(0，－1)为顶点的正方形区域(见图3－9)，其边长为2，面积S D ＝2，因此(X ，Y )的联合密度是图3－9⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(D y x D y x y x p 11111d ,10,21()(,)d d ,01,20,.x x x X x y x p x p x y y y x +--+∞--∞-⎧-≤≤⎪⎪⎪==<≤⎨⎪⎪⎪⎩⎰⎰⎰其他即 1,10,()1,01,0,.X x x p x x x +-≤≤⎧⎪=-<≤⎨⎪⎩其他 64.设二维随机向量(X ，Y )的联合分布函数为⎩⎨⎧≥≥+--=----.,0,0,0,333),(其他y x C y x F y x y x求(1)常数C ；(2)分布密度p (x ，y )．解 (1)由性质F (＋∞，＋∞)＝1，得到C ＝1．(2)由公式：yx Fy x p ∂∂∂=2),(有3ln 33ln 3,x x y Fx--∂=-∂ .)3(ln 3)3ln 33ln 3(22y x y x x yyx F -----=-∂∂=∂∂∂故 ⎩⎨⎧≥≥=--.,0,0,0,)3(ln 3),(2其他y x y x p y x65.设D 2是x ＝0，y ＝0，y ＝2x ＋1围成的区域，ξ＝(X ，Y )在D 2上均匀分布，求F (x ，y )．答案是：⎪⎪⎪⎩⎪⎪⎪⎨⎧⋅∈∈-∈+∈-+∈=54232221),(,1,),(,2,),(,)12(,),(,)12(2,),(,0),(D y x D y x y y D y x x D y x y x y D y x y x F 其中区域D 1，D 2，D 3，D 4，D 5如图3－10所示．图3－1066.求 (1)X 与Y 的边缘分布．(2)X 关于Y 取值y 1＝0.4的条件分布． (3)Y 关于X 取值x 2＝5的条件分布．解(1)由公式),3,2,1()(====∑⋅i p x X p p ijji i),2,1()(====⋅j p y Y p p ijij j(2)计算下面各条件概率：,8380.030.0)(),()|(,16380.015.0)(),()|(1121211111======y p y x p y x p y p y x p y x p⋅===16780.035.0)(),()|(11313y p y x p y x p因此，X 关于Y(3)同样方法求出Y 关于X 取值x ＝5的条件分布为67.设二维随机向量(X ，Y )的联合分布密度为.e π1),()52(2122y xy x y x p ++-=求(1)X 与Y 的边缘分布密度； (2)条件分布密度．解 (1)由公式y y y x p x p y xy x d e π1d ),()()52(21122++-∞+∞-∞+∞-⎰⎰==)10125(d e 52e e π1222)10125(102x y x y x x +=⎰∞+∞-+-- ,e 5π2πe 52π1224.04.0x x --=⋅=这里应用了.πd e2=-+∞∞-⎰u u 同理，可求得Y 的边缘分布密度为.e π2)(222y y p -=(2)在给定Y ＝y 的条件下，X 的条件分布密度为,e 2π1)(),()|(2)(5.02y x y p y x p y x p +-==而在给定X ＝x 的条件下，Y 的条件分布密度为.e 2π5)(),()|(2)5(1.01y x x p y x p x y p +-==69.设随机变量X 与Y 相互独立，下表列出了二维随机向量(X ，Y )联合分布律及关于X和关于Y 的边缘分布律中的部分数值，试将其余数值填入下表中的空白处．分析应注意到X 与Y 相互独立．解由于P (X ＝x 1，Y ＝y 1)＝P (Y ＝y 1)－P (X ＝x 2，Y ＝y 1),2418161=-=考虑到X 与Y 相互独立，有P (X ＝x 1)P (Y ＝y 1)＝P (X ＝x 1，Y ＝y 1)，⋅===4161241}{1x X P所以同理，可以导出其他数值．故XY 的联合分布律为70.设随机变量X 以概率1取值0，而Y 是任意的随机变量，证明X 与Y 相互独立．证 X 的分布函数为⎩⎨⎧≥<=.0,1,0,0)(1时当时当x x x F 设Y 的分布函数为F 2(y )，(X ，Y )的分布函数为F (x ，y )，则当x ＜0时，对任意的y 有F (x ，y )＝P {X ≤x ，Y ≤y }＝P ({X ≤x }∩{Y ≤y })＝P (∅∩{Y ≤y })＝P (∅)＝0＝F 1(x )F 2(y )．当x ≥0时，对任意的y 有F (x ，y )＝P ({X ≤x }∩{Y ≤y })＝P {Y ≤y }＝F 2(y )＝F 1(x )F 2(y )．因此，对任意的x ，y 均有F (x ，y )＝F 1(x )F 2(y )，即X 与Y 相互独立．71.设(X ，Y )的联合分布密度为⎪⎩⎪⎨⎧<<+=.,0,1||,1||,41),(其他y x xy y x p试证明：(1)X 与Y 是相依的． (2)X 2与Y 2是相互独立的．证 (1)先求X 的边缘分布密度．当|x |＜1时，有⋅=+==⎰⎰-+∞∞-21d 41d ),()(111y xy y y x p x p当|x |≥1时，p 1(x )＝0，因此⎪⎩⎪⎨⎧<=.,0,1||,21)(1其他x x p 同理⎪⎩⎪⎨⎧<=.,0,1||,21)(2其他y y p 可见，当|x |＜1，|y |＜1时p (x ，y )≠p 1(x )·p 2(y )，所以X 与Y 不独立，即是相依的．(2)令ξ＝X 2，η＝Y 2，其分布函数分别为F 1(x )和F 2(y )，于是当0≤x ＜1时，有)()()(21x X x P x X P x F ≤≤-=≤=⎰-==x x x x ,d 21因此⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(1x x x x x F同理可求得Y 2的分布函数⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(2y y y y y F如图3－11所示，将Oxy 平面分成5块区域来讨论，并将(ξ，η)的分布函数记为F 3(x ，y )，则图3－11①当x ＜0或y ＜0时，F 3(x ，y )＝0． ②当0≤x ＜1，y ≥1时，.)(),(),(2223x x X P y Y x X P y x F =≤=≤≤=③当0≤y ＜1，x ≥1时，同理.),(3y y x F =④当0≤x ＜1，0≤y ＜1时， F 3(x ，y )＝P (X 2≤x ，Y 2≤y )),(y Y y x X x P ≤≤-≤≤-=1d 4sxs t +==⑤当x ≥1，y ≥1时，.1d d 41),(),(1111223=+=≤≤=⎰⎰--y x xyy Y x X P y x F综合起来得到⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥<≤<≤≥<≤≥<≤<<=.1,1,1,10,10,,1,10,,1,10,,00,0),(3y x y x xy x y y y x x y x y x F 或不难验证，对于所有x ，y 都有F 3(x ，y )＝F 1(x )·F 2(y )，所以ξ与η相互独立，即X 2与Y 2相互独立．72. 设(X ，Y )的联合分布为求(Ⅰ)Z 1＝X ＋Y ；23解 (Ⅰ)Z 1＝X ＋Y 的正概率点为0，1，2，3．因为。

概率论例题与详解

例题1.玻璃杯成箱出售，每箱20只，各箱次品数为0,1,2只的概率分别为0.8,0.1,0.1,一顾客欲买下一箱玻璃杯售货员随机取出一箱，顾客开箱后随机取4只进行检查，若无次品，则购买，否则退回，求（1）顾客买下该箱玻璃杯的概率？（2）在顾客买下的一箱中，确实没有次品的概率？解设),2,1,0(=i A i 表示箱中有i 件次品，B 表示顾客买下该箱玻璃杯（1）由全概率公式()()()94.01.01.018.042041842041920≈⨯+⨯+⨯=∑==C C C C A p A B P B P i i i （2）由贝叶斯公式85.0)()()()(000≈=B P A P A B P B A P2.设有两箱同类零件，第一箱内装有50件，其中10件是一等品；第二箱内装有30件，其中18件是一等品，现从两箱中任意挑出一箱，然后从该箱中依次随机地取出两个零件（取出的零件不放回），试求（1）第一次取出的零件是一等品的概率；（2）在第一次取出的零件是一等品的条件下，第二次取出的零件仍是一等品的概率.解设),2,1,0(=i A i 表示从第i 箱中取得的是一等品（取出的零件不放回），B 表示从第一箱中取零件，B 表示从第二箱中取零件（1）由全概率公式4.02130********)()()()()(111=⨯+⨯=+=B P B A P B P B A P A P （2）由全概率公式 2129173018214995010)()()()()(212121⨯⨯+⨯⨯=+=B P B A A P B P B A A P A A P 因此有 )()()(12112A P A A P A A P =4856.0)2129173018214995010(25=⨯⨯+⨯⨯= 3.某电子元件在每一次试验中发生故障的概率为0.3，当故障发生不少于3次时，指示灯发出信号（1）进行了5次重复独立试验，求指示灯发出信号的概率；（2）进行了7次重复独立试验，求指示灯发出信号的概率.解（1）进行了5次重复独立试验，指示灯发出信号的概率为163.03.07.03.07.03.054452335≈+⋅+⋅C C（2）进行了7次重复独立试验，指示灯发出信号的概率为353.07.03.07.03.07.0152276177≈⋅+⋅--C C4.甲、乙、丙3人同向一飞机射击，设击中飞机的概率分别为0.4,0.5,0.7，如果只有1人击中飞机，则飞机被击落的概率是0.2；如果有2人击中飞机，则飞机被击落的概率是0.6；如果3人都击中飞机，则飞机一定被击落，求飞机被击浇的概率.解：设321,,A A A 分别表示甲、乙、丙击中飞机，i B 表示有)3,2,1(=i i 个人击中飞机=)(1B P )()()(321321321A A A P A A A P A A A P ++)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=36.07.05.06.03.05.06.03.05.04.0=⨯⨯+⨯⨯+⨯⨯==)(2B P )()()(321321321A A A P A A A P A A A P ++)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=41.07.05.04.03.05.06.03.05.04.0=⨯⨯+⨯⨯+⨯⨯==)(3B P )(321A A A P)()()(321A P A P A P =14.07.05.04.0=⨯⨯=由全概率公式)()()(11B B P B P B P =)()(22B B P B P +)()(33B B P B P +458.0114.06.041.02.036.0=⨯+⨯+⨯=5.随机地向半圆220x ax y -<<（a 为正常数）内扔一个点，点落在半圆内任何区域内的概率与区域的面积成正比，求原点与该点的连线与x 轴的夹角小于4π的概率. 解：以D 表示半圆220x ax y -<<，由题设，点),y x （应该落在如图的阴影部分G ，G 的面积为（在极坐标系中计算）θθπθθπd r rdr d G S a a ⎰⎰⎰⎪⎭⎫ ⎝⎛==40cos 202cos 204021)( θθπd a ⎰=4022cos 22402214)2cos 1(a d a ⎪⎭⎫ ⎝⎛+=+=⎰πθθπ（或G 的面积等于一个等腰直角三角形的面积加上41个圆的面积）故πππ12121214)()()(22+=⎪⎭⎫ ⎝⎛+==a a D S G S A P 6.设1)(0<<A P ，1)(0<<B P ，证明：B A 、独立⇔1)|()|(=+B A P B A P . 证明：1)|()|(=+B A P B A P ⇔)()|(1)|(B A P B A P B A P =-= ⇔)(1)()()(B P B A P B P AB P -=⇔)()()()()(B A P B P AB P B P AB P =- ⇔)()()]()()[()(A P B P B A P AB P B P AB P =+=⇔B A 、独立7. 要验收一批100件的乐器,验收方案如下:自该批乐器中随机地取3件测试（设3件乐器的测试是相互独立的），如果3件中至少有一件被认为音色不纯，则这批乐器就被拒绝接收，设一件音色不纯的乐器经测试查出其为音色不纯的概率为0.95，而一件音色纯的乐器经测试被误认为不纯的概率为0.01，如果已知这100件乐器中恰好有4件是音色不纯的，试问这批乐器被接收的概率是多少？解：设i B ={随机地取3件乐器，其中有i 件是音色不纯的}（3,2,1,0=i ）A={这批乐器被接收}30)99.0()(=B A P ，05.0)99.0()(21⋅=B A P ，22)05.0(99.0)(⋅=B A P33)05.0()(=B A P31003960)(C C B P =，3100142961)(C C C B P =，3100241962)(C C C B P =，3100343)(C C B P = 故由全概率公式有8629.0)()()(30==∑=i i i B P B A P A P8.一猎人用猎枪射击野兔，第一枪距离200米，如果未击中就追到150米处第二次射击，如果仍未击中，再追到100米处第三次射击，此时击中的概率为0.5，如果猎人的命中率始终与距离的平方成反比，求猎人击中野兔的概率。

概率论例题讲解

2
y3 3
1
(y3)
当
(x)在区间[0，1]上的均匀分布时，
(
x)
1 0
0 x 1 否则
2
3的密度函数
( y)
y3 3
1
0
1
0 y3 1
否则
2
y 3
3
0
0 y 1 否则
七、(4 5) 求出服从在B上均匀分布的随机变量(X ,Y )的分布密度及分布函数，其中B为x轴、y轴及直线y 2x 1所围成的三角形区域。
（i=1,2,3,4,5） (3)* 若将（2）中的这个硬币再抛掷1次，又出现字面。
解：设A "任取一个硬币抛掷出现字面"事件； Bi "被选出的是第i个硬币"事件 i=1,2,3,4,5
B1 B2 B3 B4 B5 P(Bi ) 1/ 5 i=1,2,3,4,5 P( A | Bi ) pi i=1,2,3,4,5 (1) 任取一个硬币抛掷出现字面的概率=P( A)
0
1
分布函数：F
(
x)
6 2
3
1
x 1 1 x 2
2 x3 x3
五、(3 23) 设电子管的寿命具有密度的函数
100
(x)
x2
x 100
(单位：h)
0 x 100
问：在150h内：
(1)三只管子没一只损坏的概率是多少？
(2)三只管子全损坏的概率是多少？
解：设A "任抽取1只管子，该管子在150h内会损坏"
P(Ci ) P(Bi | A) i 1, 2,3, 4,5
5
5
P(D) P(Ci )P(D | Ci ) P(Bi | A)P( A | Bi )