四年级学而思_1--12讲
小学数学奥数辅导讲座(四年级)

- 1 -小学四年级奥数辅导讲座第1讲速算与巧算(一)第2讲速算与巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法(一)第15讲盈亏问题与比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算与巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
打印学而思小学奥数36个精彩讲座总汇全-90页文档资料

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×0.5.具体过程如下:原式=5919(3 5.22)19930.41.6 910() 52719950.51995 19(6 5.22)950+-⨯÷+⨯-+3.计算:1111111987 -+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少?【分析与解】方法一:1118x 68114x 112x 7111+11148x 62+214x 1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25. 方法二:有11131118821x 4+==+++,所以18222133x 4+==++;所以13x 42+=,那么x =1.25. 5.求944,43,443,...,44...43个这10个数的和.【分析与解】方法一:方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=; 再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=; 再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=; 再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=; 再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=; 再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=; 再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=; 再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为4938271591.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少? 【分析与解】 因为每个端点均有三条线段通过,所以这6条线段的长度之和为:7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○2.9=2.9○3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9=2.9△3.5=2.9.请计算:23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+ 【分析与解】原式8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1?【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如1.892915929.那么在所有这种数中。
学而思2011年暑假新四年级超常123班难题汇总
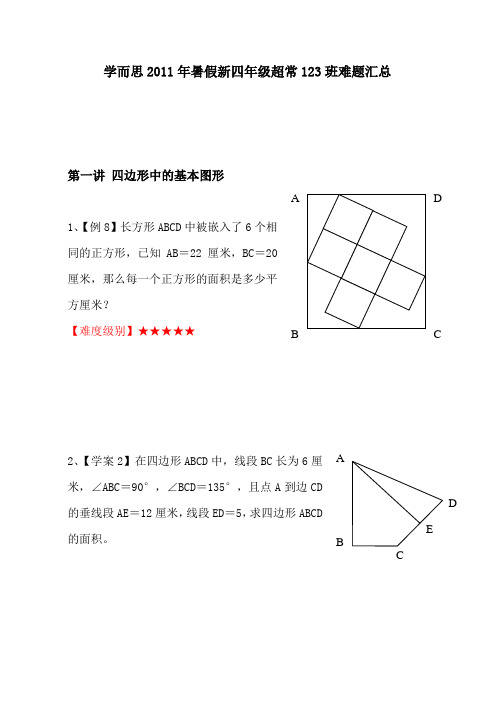
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形,已知AB=22厘米,BC=20厘米,那么每一个正方形的面积是多少平方厘米?【难度级别】★★★★★2、【学案2】在四边形ABCD中,线段BC长为6厘米,∠ABC=90°,∠BCD=135°,且点A到边CD 的垂线段AE=12厘米,线段ED=5,求四边形ABCD 的面积。
D C3、【学案3】等腰梯形ABCD 中,交于O 点的两条对角线互相垂直,三角形ECB 是直角三角形,OC 比AO长20厘米。
已知三角形ADE 的面积是250平方厘米,则梯形ABCD 的面积是多少平方厘米?4、【学案4】一块边长为180厘米的正方形铁片,四角各被截去一个边长为40厘米的小正方形铁片,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为多少平方厘米?5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形,保留必要的作图痕迹。
O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中,有多少个与5678相加时,至少发生一次进位?7、【例8】有______个四位数满足下列条件:它的各位数字都是奇数,它的各位数字互不相同,它的每个数字都能整除它本身。
8、【学案1】计算机上编程序打印出前10000个正整数:1,2,3,……,10000时,不幸打印机有毛病,每次打印数字3时,它都打印出x,问其中被错误打印的共有多少个数?9、【学案4】有9张同样大小的圆形纸片,其中标有数码“1”的有1张,标有数码“2”的有2张,标有数码“3”的有3张,标有数码“4”的有3张,把这9张圆形纸片如图所示放置在一起,但标有相同数码的纸片不许挨在一起。
(1)如果M处放标有数码“3”的纸片,一共有多少种不同的放置方法?(2)如果M处放标有数码“2”的纸片,一共有多少种不同的放置方法?10、【越玩越聪明】在例6的后面。
学而思-五年制10级思维训练体系(7级上)四年级解题能力超常班-第1讲教程文件

学而思-五年制10级思维训练体系(7级上)四年级解题能力超常班-第1讲简单的抽屉原理1.理解抽屉原理的基本含义。
2.能运用抽屉原理对一些简单问题进行说明。
3.能使用最不利原则进行分析。
知识要点最不利原则所谓“最不利原则”是指完成某一项工作先从最不利的情况下考虑,然后研究任意情况下可能的结果。
由此得到充分可靠的结论。
抽屉原理如果把n+1个苹果任意放入n个抽屉,那么必定有一个抽屉里至少有两个苹果。
抽屉原理1:如果把多于n件物品任意放到n个抽屉中,那么必有1个抽屉至少有2件物品。
抽屉原理2:如果把多于m×n件物品任意放到n个抽屉中,那么必有1个抽屉至少有m +1件物品。
例1围棋盒中装有黑子和白子各180粒,一次最少取出多少粒才能保证至少有20粒棋子颜色相同?(2007年第五届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题能力展示大赛四年级初赛第12题)袋中有外形完全一样的红、黄、蓝三种颜色的小球各15个,每个小朋友只能从中摸出2个小球。
至少有_____个小朋友摸球,才能保证一定有两个人模的球的颜色一样。
口袋里有蓝色球6个,红色球2个,黄色球19个,至少要取多少个小球才能保证至少有5个小球同色?体育用品的仓库里有许多足球、排球和篮球,有66个同学来仓库拿球,要求每个人至少拿一个,最多拿两个球,问至少有多少名同学所拿的球的种类是完全一样的?一个布袋里有大小相同颜色不同的一些木球,其中红色的有10个,黄色的有8个,蓝色的有3个,绿色的有1个。
请问:⑴一次至少要取出多少个球,才能保证取出的球至少有三种颜色?⑵一次至少要取出多少个球,才能保证其中必有红球和黄球?例6用红、蓝两种颜色将一个2×5方格图中的小方格随意涂色(见下图),每个小方格涂一种颜色。
是否存在两列,它们的小方格中涂的颜色完全相同?测试题1.要想保证至少有5个人的属相相同,但不能保证有6个人的属相相同,那么总人数应该在什么范围内?2.今有乒乓球盒22个,每个盒子内最多可放六个球,试说明这些盒子中,至少有四个盒子里所放球数相同。
学而思讲义四年级第一讲(整数与数列)

2
四年级秋季班(七级下) 1.1
2010 年四年级秋季班 第一讲 整数与数列 程雪
第 n 项=首项+公差×(n-1)
2、项数公式:什么时候用?——知道首项、末项及公差,求项数
项数=(末项-首项)÷公差+1
3、求和公式(高斯公式) :什么时候用?——任何一个等差数列求和
和=(首项+末项)×项数÷2
辅助记忆:装皮鞋 4、中项公式:什么时候用?——对于容易找到中项的等差数列求和
和=中项×项数
注意:高斯公式与中项公式的联系 高斯公式:和=(首项+末项)×项数÷2 =(首项+末项)÷2 ×项数
中项(也即平均数)
二、常用公式 2 1、从 1 开始连续奇数求和=项数 2 即:1 + 3 + 5 + 7 + … +(2n-1)= n 图示: 1 3 5 7 9
2、金字塔数列=中项 2 即:1 + 2 + 3 + … +(n-1)+ n +(n-1)+ … + 3 + 2 + 1 = n 图示:
三、平方差公式:a - b =(a+b)×(a-b) ……两数平方差=两数和×两数差 几何证明:
2Hale Waihona Puke 2b a 2 2 a - b 表示的是图中大正方形减去黑色小正方形后的空白部分的面积,沿虚线将空白部分减 成两部分再拼接起来,即为一个长方形的面积。该长方形长为 a+b,宽为 a-b,面积为(a+b) ×(a-b) ,得证。 特例: 两数相差为 1,其平方差就是两数和 2 2 37 -36 =(37+36)×(37-36)=37+36 四、平方差公式拓展: (逆向思维)既然平方差=和×差,那么两个数相乘能否转化为平方差的形式呢? 1、若两数的奇偶性相同,则这两数的乘积可化为平方差的形式。 如:41×39 41=a+b,39=a-b ,利用和差公式即可算出 a=40,b=1(a 即是 41 与 39 的平均数) 2 2 所以 41×39=(40+1)×(40-1)=40 -1 2、进而,若两数相差不大,且两数和为整十整百时,乘积改写为平方差可简化计算 2 2 如:68×72=(70-2)×(70+2)=70 -2 =4900-4=4896 五、自然数列的平方和公式 2 2 2 2 1 +2 +3 +…+n =n(n+1) (2n+1)÷6 图示证明: 1 2 3 … n n 3 2 3 … … n
四年级数学第12讲课后习题

第12讲差倍问题
1.大胖吃的包子的数量比小胖的倍还多个,已知大胖比小胖多吃了个,那么小胖吃了
________个。
A. 10
B. 45
C. 6
2.学而思网校竞赛班比启航班多名学员,而且竞赛班的人数是启航班人数的倍,那么启航班有________名学员。
A. 300
B. 100
C. 50
3.小鹿为找工作准备了中、英文两份简历。
中文简历的字数比英文简历单词数的倍多个,而且中文简历字数比英文简历单词数多。
那么,中文简历的字数是________个。
A. 100
B. 320
C. 200
4.一个车间男工人比女工人多人,其中男工人数是女工人数的倍,男工人有________人,女工人有________人。
A. 120 20
B. 20 120
5.李爷爷家养的鸭比鹅多只,鸭的只数是鹅的倍,李爷爷家养的鸭有________只,鹅有
________只。
A. 24 8
B. 12 36
C. 36 12
【答案】1. A 2. B 3. B 4. A 5. C
第 1 页,共 1 页。
完整小学新编学而思合集完整版

完整小学新编学而思合集HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】完整小学学而思合集高清无密(2013-06-02 01:18:14)转载▼分类:小学标签:教育二年级奥数和阅读写作:【2801】2011一升二年级数学竞赛班-8讲【3211】2011秋季二年级数学竞赛班-12讲【4716】2012春季二年级数学竞赛班-14讲【3746】2012寒假二年级数学竞赛班-8讲【2802】2011暑期二升三数学竞赛班-12讲【6031】糖果星球探秘:二升三年级“畅享语文”成长计划暑期班12讲【3747】精灵旅行团:2012年寒假二年级说话写话训练营10讲6531:小柿子星球探秘:二年级“畅享语文”成长计划秋季班(6级)共11讲三年级奥数和阅读写作:【3212】2011秋季三年级奥数竞赛班-16讲【3779】2012寒假三年级奥数竞赛班-10讲【4860】2012春季三年级奥数竞赛班-16讲【4861】2012春季三年级奥数零基础班-10讲【6039】三升四奥数暑期班14讲4863人教春季三年级数学同步8讲6055人教版三年级上册数学满分班16讲7429北师版三年级下册数学满分班(教材精讲+奥数知识拓展)14讲4209+2012年寒假五年制小学三年级数学超常班12讲【6032】杮子星球探秘,三升四年级畅想语文成长计划暑期班12讲【3230】精灵旅行团:2011秋季三年级阅读写作训练营12讲【3783】精灵旅行团:2012寒假三年级阅读写作训练营8讲【4865】精灵旅行团:2012春季三年级阅读写作训练营12讲四年级奥数及阅读写作:【2799】2011暑期三升四数学强化班共14讲[6040]2012四升五年级奥数暑期班18讲【3297】2011秋季四年级上册人教数学课内同步班8讲【4772】人教四年级下册数学同步8讲【3208】2011秋季四年级数学强化班,18讲【3947】2012寒假奥数强化班10讲【6057】人教版四年级上册数学满分班14讲【4770/4771】2011春季四年级数学竞赛班18讲7088第13届中环杯四年级初赛冲刺VIP班12讲3948+2012寒假四年级奥数竞赛班10讲1891:四年级奥数必考知识点系统复习全能班(上)9讲6063北师版四年级上册数学满分班(教材精讲+奥数知识拓展)17讲7431北师版四年级下册数学满分班(教材精讲+奥数知识拓展)18讲【6033】6033乐学星球探秘:四升五年级畅想语文成长计划暑期班11讲【3231】精灵旅行团:2011秋季四年级阅读写作训练营12讲【3945】精灵旅行团:2012寒假四年级阅读写作训练营10讲【4775】精灵旅行团:2012春季四年级阅读写作训练营10讲五年级奥数及阅读写作:【3209】2011秋季五年级数学强化班共20讲,【4817】2011原春季五年级奥数强化班20讲【3768】2011原寒假五年级奥数强化班共16讲【2921】2011原暑假五年级奥数强化班共18讲2925崔兆玉2011五年级奥数年卡74讲7421人教五年级下册数学满分班15讲[6059]人教版五年级上册数学满分班16讲3299+2011秋季五年级数学课内同步班(人教版)8讲4820+2012春季五年级数学课内同步班(人教版)8讲3769+2012寒假五年级数学零基础班14讲6071苏教版五年级上册数学满分班14讲(教材精讲+奥数知识拓展)7427苏教版五年级下册数学满分班(教材精讲+奥数知识拓展)14讲6065北师版五年级上册数学满分班14讲7433北师版五年级下册数学满分班13讲【6102】小升初总复习:2012五升六年级语文暑期班12讲【3232】精灵旅行团:2011秋季五年级阅读写作训练营10讲【3773】精灵旅行团:2012寒假五年级阅读写作训练营10讲【4822】精灵旅行团:2012春季五年级阅读写作训练营10讲【3058】小学语文知识大全—小学阅读技巧魔法班-4讲【2666】小学语文必学写作技巧之非常作文训练营-10讲3618小学语文知识大全——小学语文基础知识精讲(上)9讲3721:小学语文知识大全——小学语文基础知识精讲(下)8讲2515:春季五年级语文阅读课外拓展班6讲2516:春季小学语文总复习小升初冲刺班8讲3809:五年制小学五年级语文阅读写作综合提高共10讲六年级奥数及阅读写作:【2819】2011年暑期五升六数学课内预习班人教8讲上册【4851】2012春季六年级数学课内同步班人教12讲【6463】人教版六年级上册数学满分班(教材精讲)14讲【6464】人教版六年级上册数学满分班(教材精讲)18讲4【6535】2012六年级培优数学秋季班(竞赛班)22讲2974:六升初一有理数四则运算必备3讲2975-六升初一不等式(组)解法攻略3讲2976-六升初一几何证明与推理初步3讲2977-六升初一二元一次方程组全透析3讲7556北师版六年级下册数学满分班(教材精讲+奥数知识拓展)17讲4547+12华杯赛初赛六年级VIP全能班8讲8375+2013高年级华杯复赛考前冲刺班(五、六年级)10讲【3065】小学语文经典课程:精讲心理描写2讲【3371】小学语文经典课程:文章立意有深度-1讲【3372】小学语文经典课程:分析文段作用,领会句子含义1讲【3409】小学语文经典课程:叙事文阅读2讲【3629】小学语文经典课程:运用对比手法塑造人物形象1讲3057:小学语文知识大全—古诗文奥秘赏析-1讲4992:小学语文知识大全—8课时突破小学记叙文阅读考点5453:小学语文知识大全—8课时文言文轻松入门7194:小学语文知识大全—小学分类作文全攻略--9讲3059:小学语文知识大全—小学写作技巧宝典班--5讲6727:柿子星球探秘:四年级“畅享语文”成长计划秋季班12课时(14级)7、5717庄海燕考试速记系列:如何快速记忆小学语文知识4讲2、7336百变精灵阅读满分班(记叙文+说明文+文言文)共20讲六年级及小升初:【2912】2011年六-小升初年级奥数年卡{竞赛班}2806+3295+3921+4847.共70讲【2914】(3296+4857+3925+2808)2011六年级六年级语文年卡(竞赛班)-42讲[7563]小升初总复习:2013六年级语文下半学年卡24讲[2917-75] (2851+3229+3927+4853) 2011六年级小升初英语年卡6520+1+英语“坑爹”题目大汇总——小升初190多讲六年级奥数七大专题3340:组合专题3393:几何专题3656/2966:数论专题4136:行程专题八、玩转小学英语语法共30课时:【3532】六大时态6讲【3679】五大句型5讲【3822】词法大全12讲【3695】被动语态2讲【4456】三大从句5讲九、亲子英语口语【5450】和孩子一起学口语(亲子英语课程)共20讲【3914】学而思乐学口语一级7讲【3748】学而思乐学口语二级8讲【3784】学而思乐学口语三级8讲【3937】学而思乐学口语四级9讲【3772】学而思乐学口语五级10讲【3926】学而思乐学口语六级10讲[6572 ](1-10)乐学英语预备级:2012秋季听说6747 (1-17)乐学英语五级:2012秋季听说读[6746] (1-15)乐学英语四级:2012秋季听说读写6745 (1-15)乐学英语三级2012秋季听说读写训练营(三、四年级)6538 (1-15)乐学英语二级:2012秋季听说读写训练6573 (1-15)乐学英语一级:2012秋季听说读4523剑桥少儿英语预备级(上)1-7讲5325剑桥少儿英语预备级(上)8-15讲7027剑桥少儿英语预备级(下)1-8讲7082剑桥少儿英语预备级(下)9-15讲十、3225/4998:自然拼音一级二级三级和10次国际音标和自然拼音全掌握十、剑桥少儿英语一40讲、二级40讲、三级40讲新概念第一册整套编号:5501+5692+4282+3228共58讲【2183】新概念一册同步强化班 15课时【2523】新概念英语一册同步强化15讲新概念第二册整套:80讲新概念英语二册L1-L80 2185+2524+2814新概念第三册:40讲十二、单词记忆:【7044】过目不忘背单词--小学核心词汇1000词上-11讲【7103】过目不忘背单词-小学核心词汇1000词(中)11讲十二、英语阅读写作核心词:5442/3099编号共10课时一年级奥数全部国学经典各40课时6078共欠11-40讲千字文:5909欠18-40讲弟子规:6222孟子40讲:6221欠21-40讲论语:6220欠12-40讲三字经:5172--小魔方大智慧:世界冠军教你玩转异形魔方4682--小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)5532 小魔方大智慧:世界冠军庄海燕教你玩....5171--世界记忆锦标赛经典项目:超速记忆扑克牌5714---庄海燕考试速记系列:如何快速记忆英语单词5718_庄海燕考试速记系列:如何快速记忆初....。
学而思(四年级)目30讲全

合用标准准数,各数与基准数的差的和叫做累学而思(四年级)若是你需要更多的各种奥数计差。
由例 1 获取:教材,课程同步教材,同步总和数 =基准数×加数的个数+累计第 1 讲速算与巧算(一)练习题,培优练习题,期中差,第 2 讲速算与巧算(二)期末单元试卷,平均数 =基准数 +累计差÷加数的个第 3讲高斯求和各种致富管理文学作品书籍数。
第4讲4, 8, 9 整除的数的特点维修书籍大人物传记在使用基准数法时,应采用与各第 5讲弃九法都是电子档。
能够联系我数的差较小的数作为基准数,这样才第 6 讲数的整除性(二)468453607简单计算累计差。
同时考虑到基准数第 7 讲找规律(一)微信电话与加数个数的乘法能够方便地计算出第 8 讲找规律(二)来,所以基准数应尽量采用整十、整第 9 讲数字谜(一)百的数。
第 10 讲数字谜(二)例 2 某农场有 10 块麦田,每块的产量第 11 讲归一问题与归总问题以下(单位:千克):第 12 讲年龄问题462,480,443,420,473,429 ,第 13 讲鸡兔同笼问题与假设法例 1 四年级一班第一小组有10名同468, 439,475 , 461。
求平均每块麦第 14 讲盈亏问题与比较法(一)学,某次数学测试的成绩(分数)如田的产量。
第 15 讲盈亏问题与比较法(二)下:解:选基准数为 450,则第 16 讲数阵图(一)86, 78, 77, 83, 91, 74, 92,累计差 =12+ 30-7- 30+23- 21第 17 讲数阵图(二)69,84,75。
+18-11+25+11第 18 讲数阵图(三)求这 10 名同学的总分。
=50,第 19 将乘法原理解析与解:平常的做法是将这10 个数平均每块产量 =450 + 50÷ 10 =第 20 讲加法原理(一)直接相加,但这些数纷乱无章,直接455(千克)。
第 21 讲加法原理(二)相加既繁且易错。
学而思想奥数全能版目录

第一专题:计算专题共34讲【强化篇17讲竞赛篇17讲】一、计算竞赛篇共17讲竞赛1-加减法巧算之凑整与组合思想之竞赛篇(第1讲)竞赛2-乘除法巧算之提取公因式与组合思想之竞赛篇(第2讲)竞赛3-四则混合巧算只综合技巧之竞赛篇(第3讲)竞赛4-定义新运算之速算与巧算之竞赛篇(第4讲)竞赛5-数列求和与公式技巧之竞赛篇(第5讲)竞赛6-多位计算与归纳思想之竞赛篇(第6讲)竞赛7-小数计算与换元思想之竞赛篇(第7讲)竞赛8-数表计算与代数公式应用之竞赛篇(第8讲)竞赛9-循环小数互化与错位相减技巧之竞赛篇(第9讲)竞赛10-分数(繁分数)计算综合与比例转化之竞赛篇(第10讲)竞赛11-比较与估算综合技巧之竞赛篇(第11讲)竞赛12-分数计算之拆分、裂项与通项归纳之竞赛篇(第12讲)竞赛13-分数计算之换元与缩放之竞赛篇(第13讲)竞赛14-定义新运算之复杂运算与抽象运算之竞赛篇(第14讲)竞赛15-四大杯赛中的计算综合思想之竞赛篇(第15讲)竞赛16-计算综合之复杂分数裂项计算综合之复杂整数裂项之竞赛篇(第16讲) 竞赛17-计算综合之复杂公式与复杂换元计算之竞赛篇(第17讲)二、计算强化篇共17讲第一讲加减法巧算之凑整与组合思想(第18讲)第二讲乘除法巧算之提取公因式与组合思想(第19讲)第三讲四则混合巧算只综合技巧(第20讲)第四讲定义新运算之速算与巧算(第21讲)第五讲数列求和与公式技巧(第22讲)第六讲多位计算与归纳思想(第23讲)第七讲小数计算与换元思想(第24讲)第八讲数表计算与代数公式应用(第25讲)第九讲循环小数互化与错位相减技巧(第26讲)第十讲分数(繁分数)计算综合与比例转化(第27讲)第十一讲比较与估算综合技巧(第28讲)第十二讲分数计算之拆分、裂项与通项归纳(第29讲)第十三讲分数计算之换元与缩放(第30讲)第十四讲定义新运算之复杂运算与抽象运算(第31讲)第十五讲四大杯赛中的计算综合思想(第32讲)第十六讲计算综合之复杂分数裂项与整数裂项(第33讲)第十七讲计算综合之复杂公式与复杂换元计算(第34讲)第二专题数论专题计算专题共38讲【强化篇19讲竞赛篇19讲】一、数论竞赛篇第一讲奇偶数的性质与应用之竞赛篇(第35讲)第二讲有趣余数之性质与周期之竞赛篇(第36讲)第三讲整数分拆之分类与计数之竞赛篇(第37讲)第四讲整数分拆之最值与应用之竞赛篇(第38讲)第五讲数的整除之性质与求法之竞赛篇(第39讲)第六讲数的整除之代数思想与运用之竞赛篇(第40讲)第七讲数的整除之四大判断法综合运用之竞赛篇(第41讲)第八讲质数、合数与两大约数定理之竞赛篇(第42讲)第九讲因数与倍数之最大公因数与最小公倍数之竞赛篇(第43讲)第十讲因数与倍数之综合应用之竞赛(第44讲)第十一讲完全平方数之竞赛篇(第45讲)第十二讲带余除法之竞赛篇(第46讲)第十三讲同余问题之竞赛篇(第47讲)第十四讲中国剩余定理之竞赛篇(第48讲)第十五讲进制与位值原理之竞赛篇(第49讲)第十六讲四大杯赛的数论综合思想之竞赛篇(第50讲)第十七讲数论综合之整除相关问题之竞赛篇(第51讲)第十八讲数论综合之余数相关问题之竞赛篇(第52讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第53讲) 二、数论强化篇第一讲奇偶数的性质与应用(第54讲)第二讲有趣余数之性质与周期(第55讲)第三讲整数分拆之分类与计数(第56讲)第四讲整数分拆之最值与应用(第57讲)第五讲数的整除之性质与求法(第58讲)第六讲数的整除之代数思想与运用(第59讲)第七讲数的整除之四大判断法综合运用(第60讲)第八讲质数、合数与两大约数定理(第61讲)第九讲因数与倍数之最大公因数与最小公倍数(第62讲)第十讲因数与倍数之综合应用(第63讲)第十一讲完全平方数(第64讲)第十二讲带余除法(第65讲)第十三讲同余问题(第66讲)第十四讲中国剩余定理(第67讲)第十五讲进制与位值原理(第68讲)第十六讲四大杯赛中的数论综合思想(第69讲)第十七讲数论综合之整除相关问题(第70讲)第十八讲数论综合之余数相关问题(第71讲)第十九讲数论在方程、计数、最值、行程等问题中的应用之竞赛篇(第72讲) 第三专题行程专题计算专题共30讲【强化篇15讲竞赛篇15讲】一、行程竞赛篇第一讲基础行程之竞赛篇(第73讲)第二讲简单相遇、追及之竞赛篇(第74讲)第三讲复杂相遇、追及之竞赛篇(第75讲)第四讲猎狗追兔之竞赛篇(第76讲)第五讲火车过桥之竞赛篇(第77讲)第六讲多次相遇之竞赛篇(第78讲)第七讲多人行程之竞赛篇(第79讲)第八讲流水行船之竞赛篇(第80讲)第九讲简单环形之竞赛篇(第81讲) 第十讲复杂环形之竞赛篇(第82讲) 第十一讲接送问题之竞赛篇(第83讲) 第十二讲间隔发车之竞赛篇(第84讲) 第十三讲电梯问题之竞赛篇(第85讲) 第十四讲变速变道之竞赛篇(第86讲) 第十五讲综合行程之竞赛篇(第87讲) 二、行程强化篇第一讲基础行程(第88讲)第二讲简单相遇、追及(第89讲)第三讲复杂相遇、追及(第90讲)第四讲猎狗追兔(第91讲)第五讲火车过桥(第92讲)第六讲多次相遇(第93讲)第七讲多次行程(第94讲)第八讲流水行船(第95讲)第九讲简单环形(第96讲)第十讲复杂环形(第97讲)第十一讲接送问题(第98讲)第十二讲间隔发车(第99讲)第十三讲电梯问题(第100讲)第十四讲变速变道(第101讲)第十五讲综合行程(第102讲)第四专题应用题专题共16讲一应用题1和差倍问题(第103讲)盈亏问题(第104讲)二应用题2还原问题(第105讲)鸡兔同笼(第106讲)三应用题3年龄问题(第107讲)周期问题(第108讲)四应用题4平均数问题(第109讲)统筹与规划问题(第110讲)五应用题5分数百分数问题(第111讲)牛吃草(第112讲)六应用题6比和比例(第113讲)工程问题(第114讲)七应用题7经济问题(第115讲)浓度问题(第116讲)八应用题8方程解复杂应用题(第117讲)应用题综合(第118讲)第五专题:几何专题计算专题共4讲【5级2讲6级2讲】一、几何专题能力进阶五级:五大模型及常用思维与方法第一讲五大模型(第119讲)第二讲常用思维与方法(第120讲)二、几何专题能力进阶六级:曲线型与立体几何第一讲曲线型(第121讲)第二讲立体几何(第122讲)。
学而思2012年春季四年级超常123班难题汇总

学而思2012年春季四年级超常123班难题汇总第一讲小数本讲是小数的入门,主要是小数的计算,难度不大,掌握一些常用方法即可。
小数计算常用的方法有:(1)凑数、(2) 扩大再缩小、(3)提取公因数、 (4)平方和平方差公式、 (5)解方程、 (6)换元法。
希望孩子领会各种方法的要领。
作业看了一遍,没有太大难度。
在此分析几道张老师课堂上讲解的补充题目,会对大家有用途的。
11、【补充1】计算:2012×22+407×80+325612、【补充2】2012年12月21日是电影玛雅人末日,20121221这个数的数字和是11,2012年所有日期(日期用8位数字表示)中是11的倍数的有多少个?13、【补充3】1个两位数除以6余3,如果十位数字和个位数字对换后的两位数仍然除以6余3,则称这样的一对数为“学而思数”,问“学而思数”共有多少对?14、【补充4】正12边形怎么画?如果正12边形的面积是81,则图中阴影部分的面积是多少?15、【补充5】某船往返甲乙两岸,共用12小时,前6小时比后6小时多走80千米,顺水速度比逆水速度大16千米/小时,求甲乙两岸距离。
第二讲 长度与角度综合 21、【学案3】如图,正五边形ABCDE ,若△CDF 为正三角形,试求∠BFE 的度数。
22、【例4】已知一正多边形,其内角小于160°,且大于150°,试求出此多边形可能是哪几种正多边形? 23、【作业8】华罗庚爷爷说:数学是中国人民所擅长的学科。
请小朋友求解《九章算术》中一个古老问题:“今有木长二丈,围之三尺。
葛生其下,缠木七周,上与木齐。
问葛长几何?”白话译文:如图,有圆柱形木棍直立地面,高20尺,圆柱地面周长3尺。
葛藤生于圆柱底部A 点,等距缠绕圆柱七周恰好长到圆柱上底面的B 点,则葛藤的长度是__。
A BCD EF1 2 3 20 2120/7 324、【例7】如图,点P 在锐角∠AOB 的内部,在OB 边上求作一点D ,在OA 边上求作一点C ,使△PCD 的周长最小。
学而思资料_奥数_12浓度配比问题

浓度配比问题一、知识点概述在百分数应用题中有一种关于溶液浓度的计算问题,我们把它称为浓度配比问题。
这个问题主要研究溶液、溶质和溶剂之间的关系,由于浓度问题变化多,有的难度较大,计算也较复杂。
因此我们要根据题目提供的信息和问题逐一分析,也可以分步解答。
二、重点知识归纳及讲解(一)什么是浓度配比问题?有时需要研究用多少水和多少糖才能配制成某一预先给定浓度的糖水;或者两种同类不同浓度的溶液各取多少,才能配制成某一预定浓度的溶液,这就是浓度配比问题。
(二)浓度配比问题中常见的数量关系人们习惯上把像盐、糖、纯酒精、纯农药等叫做溶质,把水叫做溶剂。
把溶质与溶剂的混合液叫溶液。
它们有如下关系:溶质质量+溶剂质量=溶液质量溶液质量×浓度=溶质质量溶质质量÷浓度=溶液质量(三)浓度配比问题几种类型1、稀释浓度问题2、增加浓度问题3、两种溶液混合配制问题三、难点知识剖析例1、在浓度为35%的10千克的盐水中加入4千克的水,这时盐水浓度是多少?解析:由于加入4千克水,使得整个溶液(即盐水)重量增加为10+4=14千克,而加水前后盐的质量(即溶质)没有变化。
根据盐在整个盐水的百分比即为盐水浓度,便可求出加水稀释后的盐水浓度。
答:这时盐水浓度是25%例2、要把浓度为25%的盐水300克,加清水冲淡为浓度15%的盐水,需要加清水多少克?解析:根据“把浓度为25%的盐水300克,加清水冲淡为浓度15%的盐水”可知盐水稀释前后的盐的质量不变;由“浓度为25%的盐水300克”可以求出盐的质量,再根据冲淡后盐水的浓度15%,可以求出稀释后盐水的质量,进而求出需要加清水的质量。
解答:300×25%÷15%-300=75÷15%-300=500-300=200(克)答:需要加清水200克。
例3、有含盐8%的盐水400克,要配制含盐20%的盐水,需要加盐多少克?解析:此例是增加浓度问题,因为加盐,溶液浓度由稀变浓,其中水的质量(即溶剂)始终不变,据此可以先求出原来盐水中水的质量,再求出后来盐水的质量,进而求出需要加盐的质量。
学而思四年级英语课程

学而思四年级英语课程The four-year curriculum of Xueersi English aims to provide comprehensive language learning for fourth-grade students. Through a variety of interactive activities, engaging exercises, and diverse teaching methods, we aim to enhance students' English proficiency in listening, speaking, reading, and writing.Listening Skills:In this curriculum, students will develop their listening skills through a range of audio materials, including conversations, stories, and songs. They will learn to understand more complex instructions, answer questions accurately, and identify key details. Fun listening games and exercises are designed to improve their concentration and ability to follow spoken information.Speaking Skills:To enhance students' speaking skills, the curriculum encourages active participation in discussions and debates. They will gain confidence in expressing their thoughts and ideas fluently and accurately. Through role-plays, group activities, and presentations, students will learn to use appropriate vocabulary, grammar structures, and intonation patterns.Reading Skills:In this curriculum, reading comprehension is prioritized. Students will explore various genres of texts, including stories, poems, articles, and informational texts. They will learn effective reading strategies, such as skimming, scanning, and inferencing, to understand the main idea and key details. Vocabulary expansion activities and comprehension exercises will strengthen their reading skills.Writing Skills:Students will develop their writing skills by practicing different types of writing, such as narratives, descriptive paragraphs, and opinion essays. The curriculum emphasizes sentence structure, paragraph organization, and coherence in writing. Students will receive regular feedback on grammar, vocabulary, and overall writing style to improve their composition skills.Integrated Learning:Throughout the course, integrated learning is emphasized. Students will see connections between different language skills, promoting a holistic understanding of the English language. Vocabulary and grammar learned in lessons are reinforced through listening, speaking, reading, and writing activities. Assessment and Feedback:Regular assessments and progress tracking are conducted to evaluate students' learning outcomes. Teachers provide constructive feedback to guide student progress, focusing on areas that need improvement and recognizing achievements. This process helps students identify their strengths and weaknesses, fostering a growth mindset.In conclusion, the four-year curriculum of Xueersi English for fourth graders provides a comprehensive and engaging language learning experience. Through a balanced approach todeveloping listening, speaking, reading, and writing skills, students will enhance their English proficiency and build a strong foundation for future language learning.。
学而思小学四年级数学知识点归纳

小学四年级数学知识点归纳四年级上册知识点概括总结1.大数的认识:(1)亿以内的数的认识:十万:10个一万;一百万:10个十万;一千万:10个一百万;一亿:10个一千万;2.数级:数级是为便于人们记读阿拉伯数的一种识读方法,在位值制(数位顺序)的基础上,以三位或四位分级的原则,把数读,写出来。
通常在阿拉伯数的书写上,以小数点或者空格作为各个数级的标识,从右向左把数分开。
3.数级分类(1)四位分级法即以四位数为一个数级的分级方法。
我国读数的习惯,就是按这种方法读的。
如:万(数字后面4个0)、亿(数字后面8个0)、兆(数字后面12个0,这是中法计数)……。
这些级分别叫做个级,万级,亿级……。
(2)三位分级法即以三位数为一个数级的分级方法。
这西方的分级方法,这种分级方法也是国际通行的分级方法。
如:千,数字后面3个0、百万,数字后面6个0、十亿,数字后面9个0……。
4.数位:数位是指写数时,把数字并列排成横列,一个数字占有一个位置,这些位置,都叫做数位。
从右端算起,第一位是“个位”,第二位是“十位”,第三位是“百位”,第四位是“千位”,第五位是“万位”,等等。
这就说明计数单位和数位的概念是不同的。
5.数的产生:阿拉伯数字的由来:古代印度人创造了阿拉伯数字后,大约到了公元7世纪的时候,这些数字传到了阿拉伯地区。
到13世纪时,意大利数学家斐波那契写出了《算盘书》,在这本书里,他对阿拉伯数字做了详细的介绍。
后来,这些数字又从阿拉伯地区传到了欧洲,欧洲人只知道这些数字是从阿拉伯地区传入的,所以便把这些数字叫做阿拉伯数字。
以后,这些数字又从欧洲传到世界各国。
阿拉伯数字传入我国,大约是13到14世纪。
由于我国古代有一种数字叫“筹码”,写起来比较方便,所以阿拉伯数字当时在我国没有得到及时的推广运用。
本世纪初,随着我国对外国数学成就的吸收和引进,阿拉伯数字在我国才开始慢慢使用,阿拉伯数字在我国推广使用才有100多年的历史。
四年级学而思奥数讲义

四年级学而思奥数讲义
目录
1. 引言
2. 第一章: 基本数学运算
3. 第二章: 数字与数的关系
4. 第三章: 分数和小数
5. 第四章: 几何形状
1. 引言
学而思奥数讲义是为四年级学生设计的数学研究材料。
本讲义旨在帮助学生掌握奥数中的基础概念和解题技巧,以提升他们在数学领域的能力。
2. 第一章: 基本数学运算
这一章节将介绍四则运算,包括加法、减法、乘法和除法。
学生将研究如何进行这些运算,并通过练题加深理解。
3. 第二章: 数字与数的关系
在这一章节中,学生将研究数字的分类和排序,以及数字之间的关系。
他们将掌握如何使用大于、小于和等于符号来比较数字,并通过实例练加强掌握。
4. 第三章: 分数和小数
分数和小数是四年级数学中的重要概念。
本章将介绍如何读写分数和小数,并涵盖分数和小数之间的转换。
学生将通过实例练巩固所学知识。
5. 第四章: 几何形状
在这一章中,学生将探索不同的几何形状,包括正方形、长方形、圆形和三角形。
他们将研究如何计算这些形状的周长和面积,并通过练题应用所学知识。
本文档将作为四年级学生研究学而思奥数的参考资料。
学生可以根据讲义中的例题和练题进行实际操作和巩固知识。
希望这份讲义能够帮助学生提高数学能力,并享受数学研究的乐趣。
以上是《四年级学而思奥数讲义》的简要目录和介绍。
祝学生们研究愉快!。
学而思教材目录

学而思教材目录一年级寒假班:第一讲:突破加减竖式第二讲:巧填算符初步第三讲:剪拼图形第四讲:图文代换第五讲:巧移物体第六讲:左右脑开发3(逻辑推理)第七讲:期末测评二年级寒假班:第一讲:认识倍第二讲:带余除法初步第三讲:有趣的自然数串第四讲:分割图像第五讲:枚举法的妙用第六讲:鸡兔同笼初步第七讲:期末测评三年级寒假班:第一讲:角度初识第二讲:速算与巧算之四则运算第三讲:字母表示数第四讲:和差倍第五讲:倒退与图示第六讲:方阵第七讲:期末测评三年级春季班:第一讲:巧填算符第二讲:小数的认识第三讲:平行四边形与梯形第四讲:年龄问题第五讲:带余除法初步第六讲:简单统计第七讲:图形计数初步第八讲:组合中的点线关系第九讲:等差数列初步第十讲:页码问题第十一讲:标数法第十二讲:简易方程第十三讲:简易方程应用第十四讲:路程速度与时间第十五讲:期末测评四年级暑假班:第一讲:简单抽屉原理第二讲:奇数和偶数第三讲:二次相遇问题第四讲:应用题:假设法和还原法(鸡兔同笼,还原问题,方阵综合应用)第五讲:应用题:图示法和对应法(年龄,盈亏,平均数综合)第六讲:图形计数进阶第七讲:余数和周期第八讲:四边形中的基本图形第九讲:体育比赛中的数学第十讲:期末测评四年级秋季班:第一讲:定义新运算第二讲:体育比赛中的数学问题第三讲:图形计数进阶第四讲:多位数计算第五讲:等积变型第六讲:一半模型第七讲:最值问题初步第八讲:数阵图初步—从幻方谈起第九讲:平均数进阶第十讲:破译乘除法竖式第十一讲:方程和方程组第十二讲:方程组解应用题第十三讲:环形跑道第十四讲:火车过桥第十五讲:期末测评四年级寒假班:第一讲:小数巧算第二讲:格点与割补第三讲:数表从日历谈起第四讲:第五种运算(乘方的认识,运算性质,平方差认识)第五讲:质数合数初步第六讲:包含与排除第七讲:期末测评四年级春季班:第一讲:等积变形第二讲:整数与数列第三讲:统筹和最优化第四讲:加乘原理进阶第五讲:最值问题进阶第六讲:抽屉原理初步第七讲:流水行船第八讲:方程与方程组第九讲:一半模型第十讲:相遇与追及综合第十一讲:平移、选择和对称第十二讲:破译横式(奇偶分析,枚举试算)第十三讲:进位制初步第十四讲:数阵图进阶第十五讲:期末测评五年级暑假班:第一讲:分数乘除第二讲:分数加减第三讲:棋盘中的数学第四讲:枚举法进阶。
小学语文目录(学而思课程)

QQ:201733998 需要课程可以加QQ联系【小学语文】一年级语文【20885】2015学年新一年级“畅享语文”成长计划年卡(1-4级)【44讲-杨惠涵】【20883】2015年新一年级“畅享语文”成长计划暑期班(1级)【12讲-杨惠涵】【20884】2015学年新一年级“畅享语文”成长计划上半年卡(1-2级)【24讲-杨惠涵】【15216】2014年一年级“畅享语文”成长计划秋季班(2级)【12讲-杨惠涵】【16642】2015年一年级“畅享语文”成长计划寒假班(3级)【8讲杨惠涵】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【18005】探秘拼音王国——10课时攻破必学拼音【10讲杨惠涵】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【8710】小精灵星球探秘:一年级“畅享语文”成长计划年卡(1-4级)【40讲-王雨洁杨惠涵】【5906】新一年级“畅享语文”成长计划暑期班(1级)【10讲王雨洁】【6569=9864】一年级“畅享语文”成长计划秋季班(2级)【10讲王雨洁】【7533】小精灵星球探秘:一年级“畅享语文”成长计划寒假班(3级)【10讲杨惠涵】【7864】小精灵星球探秘:一年级“畅享语文”成长计划春季班(4级)【10讲杨惠涵】【11771】探秘图画王国——看图作文全攻略【8讲杨惠涵】【8841】2013一年级学而思杯语文真题解析【2讲杨惠涵】【5909】大语文学堂:国学经典《弟子规》【40讲王雨洁】【6222】大语文学堂:国学经典《孟子》【40讲陈双】【6221】大语文学堂:国学经典《论语》【40讲张瑾】【6220】大语文学堂:国学经典《三字经》【40讲杨惠涵】【6078】大语文学堂:国学经典《千字文》【40讲张瑾】【4682】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)【3讲庄海燕】讲【5532】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原提速+竞技叠杯教程)【4讲】讲【5172】小魔方大智慧:世界冠军教你玩转魔方(二阶魔方、金字塔魔方、镜面魔方盲拧)【4讲】【5171】世界记忆锦标赛经典项目:超速记忆扑克牌(揭示过目不忘的奥秘)【5讲庄海燕】讲二年级语文【20512】2015学年一升二年级“畅享语文”成长计划年卡(5-8级)【44讲杨惠涵】【12445】糖果星球探秘:二年级“畅享语文”成长计划暑期班(5级)【12讲杨惠涵】【15218】2014年二年级“畅享语文”成长计划秋季班(6级)【12讲杨惠涵】【20511】2015学年一升二年级“畅享语文”成长计划上半年卡(5-6级)【24讲杨惠涵】【16644】2015年二年级“畅享语文”成长计划寒假班(7级)【8讲杨惠涵】【18536】2015年二年级“畅享语文”成长计划春季班(8级)【12讲杨惠涵】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【18005】探秘拼音王国——10课时攻破必学拼音【10讲杨惠涵】【16305】【小鱼语文棒棒堂】标点符号的故事【2讲李颖瑜】【8711】小柿子星球探秘:二年级“畅享语文”成长计划年卡(5-8级)【44讲-张瑾】【6087】小柿子星球探秘一升二年级“畅享语文”成长计划暑期班(5级)【11讲张瑾】【6531】小柿子星球探秘:二年级“畅享语文”成长计划秋季班(6级)【11讲张瑾】【7534】小柿子星球探秘:二年级“畅享语文”成长计划寒假班(7级)【11讲张瑾】【7865】小柿子星球探秘:二年级“畅享语文”成长计划春季班(8级)【11讲张瑾】【11771】探秘图画王国——看图作文全攻略【8讲杨惠涵】【10624】小学语文积累必备-----天天快乐学成语【52讲张瑾】【7312】生活中的语文实验室——应用文写作【9讲张瑾】【5208=3747】精灵旅行团:2012寒假二年级说话写话训练营【10讲张瑾】【4721】精灵旅行团:2012春季二年级说话写话训练营【10讲张瑾】【8842】2013二年级学而思杯语文真题解析【2讲张瑾】【5909】大语文学堂:国学经典《弟子规》【40讲王雨洁】【6222】大语文学堂:国学经典《孟子》【40讲陈双】【6221】大语文学堂:国学经典《论语》【40讲张瑾】【6220】大语文学堂:国学经典《三字经》【40讲杨惠涵】【6078】大语文学堂:国学经典《千字文》【40讲张瑾】【4682】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)【3讲庄海燕】讲【5532】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原提速+竞技叠杯教程)【4讲】讲【5172】小魔方大智慧:世界冠军教你玩转魔方(二阶魔方、金字塔魔方、镜面魔方盲拧)【4讲】【5171】世界记忆锦标赛经典项目:超速记忆扑克牌(揭示过目不忘的奥秘)【5讲庄海燕】讲QQ:201733998 需要课程可以加QQ联系三年级语文思泉语文3-6年级系列【21067】2015学年二升三年级“畅享语文”成长计划年卡(9-12级)【44讲-杨惠涵】【21065】2015年二升三年级“畅享语文”成长计划暑期班(9级)【12讲-杨惠涵】【21066】2015学年二升三年级“畅享语文”成长计划上半年卡(9-10级)【24讲-杨惠涵】【14946】糖果星球探秘:三年级“畅享语文”成长计划秋季班(10级)【12讲-杨惠涵】【17275】糖果星球探秘:2015年三年级“畅享语文”成长计划寒假班(11级)【8讲-杨惠涵】【21072】2015学年二升三年级“畅享语文”成长计划年卡(9-12级)【44讲-张瑾】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【16174】2014学年“尔雅语文”三级成长计划秋季班【12讲-胡璟怡】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【21088】2015学年“尔雅语文”三级成长计划年卡【44讲-付泽新】【8606】糖果星球探秘:三年级“畅享语文”成长计划年卡(9-12级)【48讲-杨惠涵】【6031】糖果星球探秘:二升三年级“畅享语文”成长计划暑期班(9级)【12讲杨惠涵】【6726=9827】糖果星球探秘:三年级“畅享语文”成长计划秋季班(10级)【12讲杨惠涵】【7389】糖果星球探秘:三年级“畅享语文”成长计划寒假班(11级)【12杨惠涵】【7927】糖果星球探秘:三年级“畅享语文”成长计划春季班(12级)【12讲杨惠涵】【14913】大语文·“达语文”——“诸子”思想初涉【18讲达吾力江】【11831】小达老师语文达人秀——达人作文课堂【9达吾力江】【14515】小新国学知识大讲堂【10讲付泽新】【15396】小新国学知识大讲堂(二)-梦回大唐【10讲付泽新】【10624】小学语文积累必备-----天天快乐学成语【52讲张瑾】【15059】小帆课堂:8课时搞定成语词典【8讲王帆】【14669】小学语文必备——中年级记叙文阅读八音盒【8讲张瑾】【7359】手把手教作文:小升初作文心旅程(每月限报16人)【10陈双王雨洁】【14914】大语文·“达”语文——中国古代名家名篇导读【16讲达吾力江】【3807】五年制小学三年级语文阅读写作综合提高【10讲焦娜】【5050=3230】-精灵旅行团:2011秋季三年级阅读写作训练营【12讲杨惠涵】【3783】精灵旅行团:2012寒假三年级阅读写作训练营【8讲杨惠涵】【4865】精灵旅行团:2012春季三年级阅读写作训练营【12讲杨惠涵】【2666】小学语文知识大全——小学语文必学写作技巧之非常作文训练营【10讲王雨洁】【3618】小学语文知识大全——小学语文基础知识精讲(上)【9讲张瑾】【3721】小学语文知识大全——小学语文基础知识精讲(下)【8讲陈双】【8843】2013三年级学而思杯语文真题解析【2讲杨惠涵】【7312】生活中的语文实验室——应用文写作【9讲张瑾】【9790】小学作文入门必备-----写作七步曲【7讲张瑾】【4130】小学语文知识大全——小翰林读诗班:小学必备80首【22讲陈双】【3057】小学语文知识大全——古诗文奥秘赏析【1讲陈双】【3058】小学语文知识大全——小学阅读技巧魔法班【4讲陈双】【3059】小学语文知识大全——小学写作技巧宝典班【5讲陈双】【7194】小学语文知识大全——小学分类作文全攻略【9讲陈双】【5453】小学语文知识大全——8课时文言文轻松入门【8讲陈双】【6476】小学语文知识大全——小学语文基础知识精讲(17讲)【17讲张瑾】【3617】小学语文基础知识精讲——句式转换【2讲张瑾】【3678】小学语文基础知识精讲——修辞手法【2讲张瑾】【3719】小学语文基础知识精讲——语病修改【2讲张瑾】【3732】小学语文基础知识精讲——词语积累【2讲张瑾】【3733】小学语文基础知识精讲——词语解析【1讲陈双】【4001】小学语文基础知识精讲——标点符号【2讲陈双】【4002】小学语文基础知识精讲——趣味对联【1讲陈双】【5909】大语文学堂:国学经典《弟子规》【40讲王雨洁】【6222】大语文学堂:国学经典《孟子》【40讲陈双】【6221】大语文学堂:国学经典《论语》【40讲张瑾】【6220】大语文学堂:国学经典《三字经》【40讲杨惠涵】【6078】大语文学堂:国学经典《千字文》【40讲张瑾】【4992】小学语文知识大全8课时突破小学记叙文阅读考点【8讲陈双】【5588】大语文学堂系列课程穿越时空对话:苏轼来了【10讲】【3409】小学语文经典课程:叙事文阅读【2讲王雨洁】【3630】小学语文经典课程:唐代诗坛【1讲王雨洁】【3065】小学语文经典课程:精讲心理描写【1讲王雨洁】【3631】小学语文经典课程:宋代词坛【1讲王雨洁】【7953】看电影学写作--编剧青春,导演人生【10讲王帆】【7135】妙笔生花作文四大招【4讲马银霞】小学语文精品课程推荐【5265】读经典童话学写作系列——《安徒生童话》【4讲王雨洁张瑾陈双杨惠涵】【4539】诗仙李白系列课程——李白:绣口一吐就半个盛唐(人文素质版)8讲【4540】大语文学堂系列课程——李白:绣口一吐就半个盛唐(官网无讲义)10讲【6836】学而思教育创始人张邦鑫老师教育理念分享——如何培养优秀的孩子1讲【4756】典雅苑庄主带你走进四大名著1讲【3658】典雅苑:读《红楼梦》写人物(官网无讲义)1讲【4913】典雅苑:读《红楼梦》学语文【7讲-杨巧玲】【4682】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)【3讲庄海燕】讲【5532】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原提速+竞技叠杯教程)【4讲】讲【5172】小魔方大智慧:世界冠军教你玩转魔方(二阶魔方、金字塔魔方、镜面魔方盲拧)【4讲】【5171】世界记忆锦标赛经典项目:超速记忆扑克牌(揭示过目不忘的奥秘)【5讲庄海燕】讲【7044】过目不忘背单词--小学核心词汇1000词(上)【11讲庄海燕】讲【7103】过目不忘背单词--小学核心词汇1000词(中)【11讲庄海燕】讲【5714】庄海燕考试速记系列:如何快速记忆英语单词【2讲庄海燕】四年级语文思泉语文3-6年级系列【21073】2015学年三升四年级“畅享语文”成长计划年卡(13-16级)【44讲-张瑾】【21069】2015年三升四年级“畅享语文”成长计划暑期班(13级)【12讲-张瑾】【21071】2015学年三升四年级“畅享语文”成长计划上半年卡(13-14级)【24讲-张瑾】【14947】2014学年四年级“畅享语文”成长计划秋季班(14级)【12讲-张瑾】【17276】2015年四年级“畅享语文”成长计划寒假班(15级)【8讲张瑾】【18291】2015年四年级“畅享语文”成长计划春季班(16级))【12讲张瑾】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【8607】柿子星球探秘:四年级“畅享语文”成长计划年卡(13-16级)【48讲-张瑾】【6032】柿子星球探秘:三升四年级“畅享语文”成长计划(13级)【12讲张瑾】【6727】柿子星球探秘:四年级“畅享语文”成长计划秋季班(14级)【12讲张瑾】【7394】柿子星球探秘:四年级“畅享语文”成长计划寒假班(15级)【12张瑾】【7928】柿子星球探秘:四年级“畅享语文”成长计划春季班(16级)【12张瑾】【9829】乐学星球探秘:五年级“畅享语文”成长计划秋季班(18级)【11讲陈双】【14913】大语文·“达语文”——“诸子”思想初涉【18讲达吾力江】【11831】小达老师语文达人秀——达人作文课堂【9达吾力江】【14515】小新国学知识大讲堂【10讲付泽新】【15396】小新国学知识大讲堂(二)-梦回大唐【10讲付泽新】【10624】小学语文积累必备-----天天快乐学成语【52讲张瑾】【15059】小帆课堂:8课时搞定成语词典【8讲王帆】【14669】小学语文必备——中年级记叙文阅读八音盒【8讲张瑾】【7359】手把手教作文:小升初作文心旅程(每月限报16人)【10陈双王雨洁】【14914】大语文·“达”语文——中国古代名家名篇导读【16讲达吾力江】【16262-】小新课堂:小升初阅读满分突破班【6讲付泽新】【2666】小学语文知识大全——小学语文必学写作技巧之非常作文训练营【10讲王雨洁】【3618】小学语文知识大全——小学语文基础知识精讲(上)【9讲张瑾】【3721】小学语文知识大全——小学语文基础知识精讲(下)【8讲陈双】【6914】第七届沪港杯初赛四五年级作文辅导冲刺班【3讲程迪】【3808】五年制小学四年级语文阅读写作综合提高【10平奕杰】【3231】精灵旅行团:2011秋季四年级阅读写作训练营【12讲张瑾】【3945】精灵旅行团:2012寒假四年级阅读写作训练营【10讲张瑾】【4775】精灵旅行团:2012春季四年级阅读写作训练营【10讲张瑾】【7336】百变精灵阅读满分班(记叙文+说明文+文言文)【20讲陈双王雨洁】【8844】2013四年级学而思杯语文真题解析【2讲张瑾】【7312】生活中的语文实验室——应用文写作【9讲张瑾】【9790】小学作文入门必备-----写作七步曲【7讲张瑾】【4130】小学语文知识大全——小翰林读诗班:小学必备80首【22讲陈双】【3057】小学语文知识大全——古诗文奥秘赏析【1讲陈双】【3058】小学语文知识大全——小学阅读技巧魔法班【4讲陈双】【3059】小学语文知识大全——小学写作技巧宝典班【5讲陈双】【7194】小学语文知识大全——小学分类作文全攻略【9讲陈双】【5453】小学语文知识大全——8课时文言文轻松入门【8讲陈双】【3617】小学语文基础知识精讲——句式转换【2讲张瑾】【3678】小学语文基础知识精讲——修辞手法【2讲张瑾】【3719】小学语文基础知识精讲——语病修改【2讲张瑾】【3732】小学语文基础知识精讲——词语积累【2讲张瑾】【3733】小学语文基础知识精讲——词语解析【1讲陈双】【4001】小学语文基础知识精讲——标点符号【2讲陈双】【4002】小学语文基础知识精讲——趣味对联【1讲陈双】【5909】大语文学堂:国学经典《弟子规》【40讲王雨洁】【6222】大语文学堂:国学经典《孟子》【40讲陈双】【6221】大语文学堂:国学经典《论语》【40讲张瑾】【6220】大语文学堂:国学经典《三字经》【40讲杨惠涵】【6078】大语文学堂:国学经典《千字文》【40讲张瑾】【4992】小学语文知识大全8课时突破小学记叙文阅读考点【8讲陈双】【5588】大语文学堂系列课程穿越时空对话:苏轼来了【10讲】【3409】小学语文经典课程:叙事文阅读【2讲王雨洁】【3630】小学语文经典课程:唐代诗坛【1讲王雨洁】【3065】小学语文经典课程:精讲心理描写【1讲王雨洁】【3631】小学语文经典课程:宋代词坛【1讲王雨洁】【7953】看电影学写作--编剧青春,导演人生【10讲王帆】【7135】妙笔生花作文四大招【4讲马银霞】小学语文精品课程推荐【5265】读经典童话学写作系列——《安徒生童话》【4讲王雨洁张瑾陈双杨惠涵】【4539】诗仙李白系列课程——李白:绣口一吐就半个盛唐(人文素质版)8讲4540 大语文学堂系列课程——李白:绣口一吐就半个盛唐(官网无讲义)10讲6836 学而思教育创始人张邦鑫老师教育理念分享——如何培养优秀的孩子1讲4756 典雅苑庄主带你走进四大名著1讲【3658】典雅苑:读《红楼梦》写人物(官网无讲义)1讲【4913】典雅苑:读《红楼梦》学语文【7讲-杨巧玲】【5717】庄海燕考试速记系列:如何快速记忆小学语文知识【4讲庄海燕】【5713】世界记忆大师经典课程:全脑图像记忆法入门必备【7讲庄海燕】【4682】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)【3讲庄海燕】讲【5532】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原提速+竞技叠杯教程)【4讲】讲【5172】小魔方大智慧:世界冠军教你玩转魔方(二阶魔方、金字塔魔方、镜面魔方盲拧)【4讲】【5171】世界记忆锦标赛经典项目:超速记忆扑克牌(揭示过目不忘的奥秘)【5讲庄海燕】讲【7044】过目不忘背单词--小学核心词汇1000词(上)【11讲庄海燕】讲【7103】过目不忘背单词--小学核心词汇1000词(中)【11讲庄海燕】讲【5714】庄海燕考试速记系列:如何快速记忆英语单词【2讲庄海燕】五年级语文思泉语文3-6年级系列【20888】2015学年四升五年级“畅享语文”成长计划年卡(17-20级)【50讲达吾力江】【20886】2015年四升五年级“畅享语文”成长计划暑期班(17级)【15讲达吾力江】【14948】2014年五年级“畅享语文”成长计划秋季班(18级)【12讲达吾力江】【17277】2015年五年级“畅享语文”成长计划寒假班(19级)【8讲达吾力江】【18293】2015年五年级“畅享语文”成长计划春季班(20级)【15讲达吾力江】【18124】【小鱼语文棒棒堂】跟着动画学作文【8讲李颖瑜】【8608】乐学星球探秘:五年级“畅享语文”成长计划年卡(17-20级)【44讲-陈双】【6033】乐学星球探秘:四升五年级“畅享语文”成长计划(17级)【11讲陈双】【6728】乐学星球探秘:五年级“畅享语文”成长计划秋季班(18级)【11讲陈双】【7395】乐学星球探秘:五年级“畅享语文”成长计划寒假班(19级)【11讲陈双】【7929】乐学星球探秘:五年级“畅享语文”成长计划春季班(20级)【11讲陈双】【14913】大语文·“达语文”——“诸子”思想初涉【18讲达吾力江】【11831】小达老师语文达人秀——达人作文课堂【9达吾力江】【14515】小新国学知识大讲堂【10讲付泽新】【15396】小新国学知识大讲堂(二)-梦回大唐【10讲付泽新】【10624】小学语文积累必备-----天天快乐学成语【52讲张瑾】【15059】小帆课堂:8课时搞定成语词典【8讲王帆】【7359】手把手教作文:小升初作文心旅程(每月限报16人)【10陈双王雨洁】【14914】大语文·“达”语文——中国古代名家名篇导读【16讲达吾力江】【16262】小新课堂:小升初阅读满分突破班【6讲付泽新】【14896】百变精灵阅读满分班(记叙文+说明文+文言文)【20讲陈双达吾力江】【6914】第七届沪港杯初赛四五年级作文辅导冲刺班【3讲程迪】【3232】精灵旅行团:2011秋季五年级阅读写作训练营【10讲王雨洁】【5190=3773】精灵旅行团:2012寒假五年级阅读写作训练营【10讲王雨洁】【4822】精灵旅行团:2012春季五年级阅读写作训练营【10讲陈双】【1653】2010年秋季五年级语文百变精灵读写尖子班【16讲王雨洁】【7336】百变精灵阅读满分班(记叙文+说明文+文言文)【20讲陈双王雨洁】【2666】小学语文知识大全——小学语文必学写作技巧之非常作文训练营【10讲王雨洁】【3618】小学语文知识大全——小学语文基础知识精讲(上)【9讲张瑾】【3721】小学语文知识大全——小学语文基础知识精讲(下)【8讲陈双】【2187】2011寒假小学五年级语文强化班(官方无讲义)【8讲】【3809】五年制小学五年级语文阅读写作综合提高【10讲程迪】【2514】2011春季小学五年级语文写作课外拓展班【6讲王雨洁】【2515】2011春季五年级语文阅读课外拓展班(叙事+写人+说明文+应用文)【6讲王雨洁】【8845】2013五年级学而思杯语文真题解析【2讲陈双】【7312】生活中的语文实验室——应用文写作【9讲张瑾】【9790】小学作文入门必备-----写作七步曲【7讲张瑾】【4130】小学语文知识大全——小翰林读诗班:小学必备80首【22讲陈双】【3057】小学语文知识大全——古诗文奥秘赏析【1讲陈双】【3058】小学语文知识大全——小学阅读技巧魔法班【4讲陈双】【3059】小学语文知识大全——小学写作技巧宝典班【5讲陈双】【7194】小学语文知识大全——小学分类作文全攻略【9讲陈双】【5453】小学语文知识大全——8课时文言文轻松入门【8讲陈双】【8347】精灵教主感恩回馈——古诗文分享【3讲王雨洁】【2870】专题课程卡经典系列课程:文言文阅读与古诗词积累【3讲王雨洁】【3617】小学语文基础知识精讲——句式转换【2讲张瑾】【3678】小学语文基础知识精讲——修辞手法【2讲张瑾】【3719】小学语文基础知识精讲——语病修改【2讲张瑾】【3732】小学语文基础知识精讲——词语积累【2讲张瑾】【3733】小学语文基础知识精讲——词语解析【1讲陈双】【4001】小学语文基础知识精讲——标点符号【2讲陈双】【4002】小学语文基础知识精讲——趣味对联【1讲陈双】【5909】大语文学堂:国学经典《弟子规》【40讲王雨洁】【6222】大语文学堂:国学经典《孟子》【40讲陈双】【6221】大语文学堂:国学经典《论语》【40讲张瑾】【6220】大语文学堂:国学经典《三字经》【40讲杨惠涵】【6078】大语文学堂:国学经典《千字文》【40讲张瑾】【4992】小学语文知识大全8课时突破小学记叙文阅读考点【8讲陈双】【5588】大语文学堂系列课程穿越时空对话:苏轼来了【10讲】【3409】小学语文经典课程:叙事文阅读【2讲王雨洁】【3630】小学语文经典课程:唐代诗坛【1讲王雨洁】【3065】小学语文经典课程:精讲心理描写【1讲王雨洁】【3631】小学语文经典课程:宋代词坛【1讲王雨洁】【7953】看电影学写作--编剧青春,导演人生【10讲王帆】【7135】妙笔生花作文四大招【4讲马银霞】小学语文精品课程推荐【5265】读经典童话学写作系列——《安徒生童话》【4讲王雨洁张瑾陈双杨惠涵】【4539】诗仙李白系列课程——李白:绣口一吐就半个盛唐(人文素质版)8讲4540 大语文学堂系列课程——李白:绣口一吐就半个盛唐(官网无讲义)10讲6836 学而思教育创始人张邦鑫老师教育理念分享——如何培养优秀的孩子1讲4756 典雅苑庄主带你走进四大名著1讲【3658】典雅苑:读《红楼梦》写人物(官网无讲义)1讲【4913】典雅苑:读《红楼梦》学语文【7讲-杨巧玲】【5436=5433+5434+5435】2012年统测必备:语-数-英问鼎巅峰完美攻略【22讲】【5433】统测必备:精灵派语文探险之旅【10讲王雨洁】【5717】庄海燕考试速记系列:如何快速记忆小学语文知识【4讲庄海燕】【5713】世界记忆大师经典课程:全脑图像记忆法入门必备【7讲庄海燕】【4682】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)【3讲庄海燕】讲【5532】小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原提速+竞技叠杯教程)【4讲】讲【5172】小魔方大智慧:世界冠军教你玩转魔方(二阶魔方、金字塔魔方、镜面魔方盲拧)【4讲】【5171】世界记忆锦标赛经典项目:超速记忆扑克牌(揭示过目不忘的奥秘)【5讲庄海燕】讲【7044】过目不忘背单词--小学核心词汇1000词(上)【11讲庄海燕】讲【7103】过目不忘背单词--小学核心词汇1000词(中)【11讲庄海燕】讲【5714】庄海燕考试速记系列:如何快速记忆英语单词【2讲庄海燕】六年级语文思泉语文3-6年级系列【20530】2015学年五升六年级“畅享语文”成长计划年卡(21-24级)【49讲达吾力江】【12446】小升初总复习:2014年六年级语文暑期班(畅享语文成长计划21级)【15讲达吾力江】【15219】小升初总复习:2014年六年级语文秋季班(畅享语文成长计划22级)【12讲达吾力江】【16645】小升初总复习:2015年六年级语文寒假班(畅享语文成长计划23级)【12讲达吾力江】【18538】小升初总复习:2015年六年级语文春季班(畅享语文成长计划24级)【10讲达吾力江】【14896】百变精灵阅读满分班(记叙文+说明文+文言文)【20讲达吾力江】【8712】小升初总复习:六年级语文年卡(精灵星球探秘| 畅享语文成长计划21-24级)【40讲-王雨吉】【6100】六年级总复习:2012六年级语文年卡(精灵星球探秘| 畅享语文成长计划21-24级)【48讲,有1-42讲.王雨洁】【2914】2011六年级语文年卡(竞赛班)【42讲王雨洁】【6102=8706】小升初总复习:2012五升六年级语文暑期班(21级)【12讲王雨洁】【6532=9866】小升初总复习:2012六年级语文秋季班(畅享语文成长计划22级)【12讲王雨洁】【7535】2013六年级语文寒假班(精灵星球探秘| 畅享语文成长计划23级)【12讲王雨洁】【7866】六年级总复习:2013六年级语文春季班(畅享语文成长计划24级)【12讲陈双王雨洁】【10471】2013学年六年级上学期语文半年卡(沪教版课内梳理班)【19讲王帆】【11073】2013学年预初下学期语文半年卡(沪教版课内梳理班)【19讲王帆】【10472=12563】2014六年级新生语文年卡目标满分班(沪教版)【38讲王帆】【12562】六年级新生语文半年卡目标满分班(沪教版)【19讲王帆】【12561】六年级新生语文暑假预习领先班(沪教版)【10讲王帆】【11831】小达老师语文达人秀——达人作文课堂【9达吾力江】【14515】小新国学知识大讲堂【10讲付泽新】【15396】小新国学知识大讲堂(二)-梦回大唐【10讲付泽新】【11290】小升初语文现代文阅读短期提分全攻略【7讲达吾力江】【10624】小学语文积累必备-----天天快乐学成语【52讲张瑾】【15059】小帆课堂:8课时搞定成语词典【8讲王帆】【7359】手把手教作文:小升初作文心旅程(每月限报16人)【10陈双王雨洁】【14913】大语文·“达语文”——“诸子”思想初涉【18讲达吾力江】【14914】大语文·“达”语文——中国古代名家名篇导读【16讲达吾力江】【16262-】小新课堂:小升初阅读满分突破班【6讲付泽新】【3554】2011暑期五升六语文竞赛班【12讲王雨洁】【3296】2011秋季六年级语文竞赛班【10讲王雨洁】【3925】2012寒假六年级语文竞赛班【10讲王雨洁】【4857】2012春季六年级语文竞赛班【10讲王雨洁】【7336】百变精灵阅读满分班(记叙文+说明文+文言文)【20讲陈双王雨洁】【2666】小学语文知识大全——小学语文必学写作技巧之非常作文训练营【10讲王雨洁】【3618】小学语文知识大全——小学语文基础知识精讲(上)【9讲张瑾】【3721】小学语文知识大全——小学语文基础知识精讲(下)【8讲陈双】【1663】2010年秋季六年级语文百变精灵读写尖子班【16讲王雨洁】【2516】2011春季小学语文总复习六年级冲刺班(提分秘决+面试技巧+模拟评测)【8讲王雨洁】【8832-】2013六年级语文暑期附赠课【2讲王雨洁】【8833-】2013六年级语文秋季附赠课【2讲王雨洁】【8834-】2014六年级语文寒假附赠课【2讲王雨洁】【8835-】2014六年级语文春季附赠课【2讲王雨洁】【8846】2013六年级学而思杯语文真题解析【2讲】【7312】生活中的语文实验室——应用文写作【9讲张瑾】【9790】小学作文入门必备-----写作七步曲【7讲张瑾】【4130】小学语文知识大全——小翰林读诗班:小学必备80首【22讲陈双】。
学而思数学复习

第一讲长方形与正方形1、单位换算(1)200厘米=()分米=()米(2)5㎡=( )dm2 3dm2=( )cm2(3)()m2=800dm2=()cm2(4)10公顷=()m22、一个长方形的面积是40平方米,长是8米,宽是()米,这个长方形的周长是()。
3、一个长方形的周长是40米,长是12米,宽是()米,这个长方形的面积是()平方米。
4、如果正方形A的连长是正方形B的边长的2倍,那么正方形A的周长是正方形B的()倍;正方形A的面积是正方形B的面积的()倍。
一个小正方形的连长是3厘米,一个大正方形的面积是小正方形面积的4倍,大正方形的周长是多少?5、如图,四边形ABCDE ,DEFG 均为正方形,已知CE =14,AG =2,那么两个正方形的面积之和是多少?第二讲:奇数与偶数进阶 1、判断下面程式结果的奇偶性 3+5+7+9+11+13+15+175+7+9+11+13+15+17+19+212、判断下面各式的奇偶性12×6 37×6 52×7 31×91×3×5×7×9×11×12×13 1×3×5×7×……×1991×1993AB C D EFG3、用4、5、0可以组成多少个没有重复数字的奇数和偶数?4、有四个互不相同的自然数,最大的数与最小的数之差是4,最大的数与最小的数之积是奇数,而这四个数的和是最小的两位奇数,则这四个数分别是多少?5、有一本500页的书,从中任意撕下20X纸,这20X纸上所有页码之和能否是1999?6、沿着河岸长着8丛植物,相邻两丛植物上所结的浆果数目相差1个,问:8丛植物上能否一共结有225个浆果?说明理由。
第三讲:巧算乘法1、计算99×4×25 125×119×8125×72 25×125×162、计算125×(80+8)(100-4)×25 45×11 23×993、计算:33×66+33×44 155×83-55×8367×22+67×77+674、80×75-150+75×22 68×101 256×10015、36×219+64×220 64×75+65×256、222×555 2×3×5×5×7+3×3×3×5×7第四讲:巧算除法1、计算(140+56+350)÷7 (360-72-30)÷62、计算1÷5+2÷5+3÷5+4÷5756÷8+223÷8+21÷83、计算12200÷25 1428÷68÷7 100÷8×124、计算27000÷4÷5 11100÷3÷25÷375、8250÷(11×5)3232÷2026、42000÷(125×7)(99999+9999+999+99+9)÷9第五讲:和倍问题1、红药丸和白药丸共160颗,红药丸的颗数是白药丸的3倍,红药丸和白药丸各有多少颗?2、博士去年和今年共售书220万册,今年售书量比去年售书量的3倍还多20万册,问去年和今年各售书多少万册?3、甲、乙两观众原来共有观众430人,二十分钟后,从甲区离开50人,乙区进来20人,这时,甲区人数正好是乙区人数的3倍,问甲、乙两区原来有观众多少人?4、甲有95本书,乙有155本书,要使甲的书本数是乙的书本数的4倍,乙应该给甲多少本书?5、鸡、鸭、鹅共112只,已知鸡的只数是鸭的3倍,鹅比鸭少3只,鸡、鸭、鹅各多少只?第六讲:差倍问题1、等等要包饺子,和面需要的面粉配方是:普通面粉比饺子粉多800克,普通面粉的重量是饺子粉的3倍,问:普通面粉和饺子粉各需要多少克?2、艾迪拿来白菜和猪肉准备和馅包饺子,拿来的白菜比猪肉多1500克,白菜的重量是猪肉的4倍还多300克,问艾迪拿来的白菜和猪肉各多少克?3、有大小两个盘子,里面装的饺子一样多,如果从小盘子里拿出102上饺子到大盘子里,则大盘子里的饺子是小盘子里的5倍,那么原来大小两个盘子各有饺子多少个?4、大瓶里有可乐500毫升,小瓶里有可乐200毫升,将两个瓶子里的可乐倒出同样多以后,大瓶里剩下的可乐是小瓶的4倍,问:两个瓶子各剩可乐多少毫升?5、两根同样长的绳子,第一根剪掉31米,第二根剪掉19米,剩下的绳子第二根的长度是第一根的4倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级第一讲:乘法原理基础班1、有五顶不同的帽子,两件不同的上衣,三条不同的裤子。
从中取出一顶帽子、一件上衣、一条裤子配成一套装束。
问:有多少种不同的装束?2、四角号码字典,用4个数码表示一个汉字。
小王自编一个"密码本",用3个数码(可取重复数字)表示一个汉字,例如,用"011"代表汉字"车"。
问:小王的"密码本"上最多能表示多少个不同的汉字?3、"IMO"是国际数学奥林匹克的缩写,把这3个字母写成三种不同颜色。
现在有五种不同颜色的笔,按上述要求能写出多少种不同颜色搭配的"IMO"?4、在右图的方格纸中放两枚棋子,要求两枚棋子不在同一行也不在同一列。
问:共有多少种不同的放法?5、要从四年级六个班中评选出学习和体育先进集体各一个(不能同时评一个班),共有多少种不同的评选结果?6、甲组有6人,乙组有8人,丙组有9人。
从三个组中各选一人参加会议,共有多少种不同选法?7、如下图,在三条平行线上分别有一个点,四个点,三个点(且不在同一条直线上的三个点不共线).在每条直线上各取一个点,可以画出一个三角形.问:一共可以画出多少个这样的三角形?8、在自然数中,用两位数做被减数,用一位数做减数.共可以组成多少个不同的减法算式?9、一个篮球队,五名队员A、B、C、D、E,由于某种原因,C不能做中锋,而其余四人可以分配到五个位置的任何一个上.问:共有多少种不同的站位方法?10、由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?11、某市的电话号码是六位数的,首位不能是0,其余各位数上可以是0~9中的任何一个,并且不同位上的数字可以重复.那么,这个城市最多可容纳多少部电话机?解答1.30种。
2.1000个。
3.60种。
4.400种。
提示:第一枚棋子有25种放法,去掉这枚棋子所在的行和列,还有16个空格,所以第二枚棋子有16种放法。
5.30种。
6.432种。
7.1×4×3=12(个).8.90×9=810(个).9.4×4×3×2×1=96(种).10.①8×8×8=512(个);②4×8×8=256(个);③4×7×6=168(个);④1×7×6=42(个);⑤1×3×6=18(个).11.9×10×10×10×10×10=900000(部).提高班1.用四种颜色给右图的五块区域染色,要求每块区域染一种颜色,相邻的区域染不同的颜色。
问:共有多少种不同的染色方法?2.由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?答案1. 48种。
2.①8×8×8=512(个);②4×8×8=256(个);③4×7×6=168(个);④1×7×6=42(个);⑤1×3×6=18(个).第二讲:加法原理基础班1.南京去上海可以乘火车、乘飞机、乘汽车和乘轮船。
如果每天有20班火车、6班飞机、8班汽车和4班轮船,那么共有多少种不同的走法?2.光明小学四、五、六年级共订300份报纸,每个年级至少订99份报纸。
问:共有多少种不同的订法?3.将10颗相同的珠子分成三份,共有多少种不同的分法?4.在所有的两位数中,两位数码之和是偶数的共有多少个?5.用1,2,3这三种数码组成四位数,在可能组成的四位数中,至少有连续两位是2的有多少个?6.下图中每个小方格的边长都是1。
有一只小虫从O点出发,沿图中格线爬行,如果它爬行的总长度是3,那么它最终停在直线AB上的不同爬行路线有多少条?7.如下图,从甲地到乙地有三条路,从乙地到丙地有三条路,从甲地到丁地有两条路,从丁地到丙地有四条路,问:从甲地到丙地共有多少种走法?8.书架上有6本不同的画报和7本不同的书,从中最多拿两本(不能不拿),有多少种不同的拿法?9.如下图中,沿线段从点A走最短的路线到B,各有多少种走法?10.在1~1000的自然数中,一共有多少个数字0?11.在1~500的自然数中,不含数字0和1的数有多少个?12.十把钥匙开十把锁,但不知道哪把钥匙开哪把锁,问:最多试开多少次,就能把锁和钥匙配起来?答案1.38种。
2.10种。
提示:没有年级订99份时,只有三个年级各订100份一种订法;只有一个年级订99份时,另外两个年级分别订100份和101份,有6种订法;有两个年级订99份时,另外一个年级订102份,有3种订法。
3.8种。
4.45个。
提示:两个数码都是奇数的有5×5(个),两个数码都是偶数的有4×5(个)。
5.21个。
提示:与例5类似,连续四位都是2的只有1种,恰有连续三位是2的有4种,恰有连续两位是2的有16种。
6.10条。
提示:第一步向下有5条,第一步向上有1条,第一步向左或向右各有2条。
7.3×3+2×4=17(种).8.6+7+15+21+6×7=91(种).提示:拿两本的情况分为2本画报或2本书或一本画报一本书.9.(1)6;(2)10;(3)20;(4)35.10.9+180+3=192(个).11.8+8×8+3×8×8=264(个).12.9+8+7+6+5+4+3+2+1=45(次).我们通常解题,总是要先列出算式,然后求解。
可是对有些题目来说,这样做不仅麻烦,而且有时根本就列不出算式。
这一讲我们介绍利用加法原理在“图上作业”的解题方法。
提高班1. 用五种颜色给右图的五个区域染色,每个区域染一种颜色,相邻的区域染不同的颜色。
问:共有多少种不同的染色方法?11.小明要登15级台阶,每步登1级或2级台阶,共有多少种不同登法?12.小明要登20级台阶,每步登2级或3级台阶,共有多少种不同登法?13.有一堆火柴共10根,每次取走1~3根,把这堆火柴全部取完有多少种不同取法,答案1. 420种。
解:如上图所示,按A,B,C,D,E顺序染色。
若B,D颜色相同,则有5×4×3×1×3=180(种);若B,D颜色不同,则有5×4×3×2×2=240(种)。
共有不同的染色方法180+240=420(种)。
2. 987种。
3. 114种。
4. 274种。
提示:取走1根有1种方法,取走2根有2种方法,取走3根有4种方法。
将1,2,4作为数列的前三项,从第4项起每项都是它前三项的和,得到1,2,4,7,13,24,44,81,149,274。
第10项274就是取走10根火柴的方法数。
第三讲:排列基础班1.计算2.某铁路线共有14个车站,这条铁路线共需要多少种不同的车票.3.有红、黄、蓝三种信号旗,把任意两面上、下挂在旗杆上都可以表示一种信号,问共可以组成多少种不同的信号?4.班集体中选出了5名班委,他们要分别担任班长,学习委员、生活委员、宣传委员和体育委员.问:有多少种不同的分工方式?5.由数字1、2、3、4、5、6可以组成多少没有重复数字的①三位数?②个位是5的三位数?③百位是1的五位数?④六位数?解答1.(1)30;(2)2002;(3)156;(4)1.第四讲:组合基础班1.计算:①C315;②C19982000;③C34×C28;④P28-C68.2.从分别写有1、2、3、4、5、6、7、8的八张卡片中任取两张作成一道两个一位数的加法题.问:①有多少种不同的和?②有多少个不同的加法算式?3.某班毕业生中有10名同学相见了,他们互相都握了一次手,问这次聚会大家一共握了多少次手?4.在圆周上有12个点.①过每两个点可以画一条直线,一共可以画出多少条直线?②过每三个点可以画一个三角形,一共可以画出多少个三角形?5.如图,图上一共有六个点,且六个点中任意三个点不共线,问:①从这六个点中任意选两点可以连成一条线段,这些点一共可以连成多少条线段?②从这六个点中任意选两点可以作一条射线,这些点一共可以作成多少条射线?(射线是一端固定,经另一点可以无限延长的.)6.下图中共有4×4=16个小方格,要把A,B,C,D四个不同的棋子放在方格里,每行和每列只能出现一个棋子,共有多少种放法?解答1.①455;②1999000;③112;④28.2.①C28=28;②P28=56.3.C28=45.4.①C212=66;②C312=220.5.①C26=15;②P26=30.6.16×9×4×1=576(种)或4!×4!=576(种)提高班1. 5件不同的商品陈列在橱窗内,排成一排。
(1)如果某件商品不放在中间,有几种不同排法?(2)如果某件商品不能放在两端,有几种不同排法?2.有四封不同的信,随意投入三个信筒里,有多少种不同投法?解答1.(1)5×4×3×2×1-4×3×2×1=96;(2)3×4×3×2×1=72。
2. 34=81(种)第五讲:排列、组合基础班1.有6名同学参加象棋决赛,得冠军和亚军的名单有几种可能的情况?2.一个口袋装有6个小球,另一个口袋装有5个小球,所有小球的颜色都不相同。
(1)从两个口袋中任取一个小球,有多少种不同的取法?(2)从两个口袋中各取一个小球,有多少种不同的取法?3.某市电话号码是五位数,每一数位上的数码可以是0,l,2,…8,9中的任意一个(数字可以重复出现,如00000也算一个电话号码)那么这个城市最多有多少个电话号码?4.在“希望杯”足球赛中,共有27支小足球队参赛。
(l)如果这27个队进行单循环赛(两队间只比赛一次,称作一场),需要比赛多少场?(2)如果这27个队进行淘汰赛,最后决出冠军,共需比赛多少场?5.如上图,从A地到B地有两条路;从B地到D地有两条路;从A地到C地只有一条路;从C地到D地有3条路。
那么从A地到D地有多少种不同走法?6.5件不同的商品陈列在橱窗内,排成一排。
(1)如果某件商品不放在中间,有几种不同排法?(2)如果某件商品不能放在两端,有几种不同排法?7.有四封不同的信,随意投入三个信筒里,有多少种不同投法?8.下图中共有4×4=16个小方格,要把A,B,C,D四个不同的棋子放在方格里,每行和每列只能出现一个棋子,共有多少种放法?9.由数字0、1、2、3、4可以组成多少个①三位数?②没有重复数字的三位数?③没有重复数字的三位偶数?④小于1000的自然数?答案1.由乘法原理,有6×5种不同情况。
