上海沪教版数学2018年初三一模1-18题
上海市2018届九年级数学上学期期中阶段质量调研试题沪教版五四制

精品文档,欢迎下载如果你喜欢这份文档,欢迎下载,另祝您成绩进步,学习愉快!上海市学2018届九年级数学上学期期中阶段质量调研试题(完卷时间:100分钟 满分:150分)考生注意:答题写在答题纸上,在草稿纸、本试卷上答题一律无效。
一、选择题:(本大题共6题,每题4分,满分24分)1.在△ABC ,直线DE ∥BC ,DE 分别交边AB 、AC 于D 、E ,在下列比例式中,不能成立的是…………………………………………………( ▲ ) (A)EC AE DB AD =;(B)EC AE BC DE =;(C)AE AC AD AB =;(D)AC ABEC DB =. 2.在Rt △ABC ,∠C=90°,AC=3,BC=4,则∠A 的余切值等于( ▲ ) (A)34; (B)43; (C)54;(D)53.3.如图,在四边形ABCD 中,如果∠ADC=∠BAC ,那么下列条件中不能判定△ADC 和△BAC 相似的……………( ▲ )(A)∠DAC=∠ABC ;(B)AC 是∠BCD 的平分线; (C) AC 2=BC •CD ;(D)ACDCAB AD =. 4.下列关于向量的运算,正确的是…………( ▲ ) (A)+-=-2)2-(;(B)a a =+0;(C)0)(=-+a a ;a e =⋅ (是一个单位向量).5.已知在△ABC 中,DE //BC ,DE 分别交边AB 、AC 于D 、E ,且AD :DB=2:1,则△ADE 与△ABC 的面积比是……………………………………( ▲ ) (A)2:1;(B) 4:1;(C) 2:3; (D) 4:9.6.如图,在△ABC 中,∠C=90°,AC=8cm ,AB 的垂直平分线MN 交AC 于D ,连接BD ,若cos ∠BDC=53,则BC 的长( ▲)DCBA NMCB AD(A)4cm ; (B) 6cm ; (C) 8cm ;(D) 10cm .二、填空题:(本大题共12题,每题4分,满分48分) 7.已知43=b a ,则ba a+2的值为 ▲ . 8.已知线段AB=20cm ,点C 是线段AB 的黄金分割点,则较长线段AC 的长为 ▲ cm . 9.如图,已知AB ∥CD ,AD 与BC 相交于点O .若32=OC BO ,AD=10,则AO=▲. 10.计算:tan 45°﹣3cot 60°=▲.11.已知在Rt △ABC 中,∠C=90°,BC=6,∠A=60°,那么AB=▲.12.如图,直线a ∥b ∥c ,直线l 1,l 2与这三条平行线分别交于点A ,B ,C 和点D ,E ,F .若AB :BC=1:2,DE=3,则EF 的长为▲.13.a 的长度是单位向量e 长度的2倍,方向相反,用e 表示a ,=a ▲.14.如图,在□ABCD 中,E 是BC 上的一点,且EC=2BE ,联结DE ,若a BA =,b BC =,则DE 关于a 、b 的分解式是=DE ▲.第9题图 第12题图 第14题图 15.△ABC 中,中线AD 和BE 交于点G ,AG=6,则GD=▲.16.如果两个相似三角形的两条对应边长分别是20cm 和25cm ,其中小三角形一边上的中线长是12cm ,那么大三角形对应边上的中线长是▲cm .17.如图,在△ABC 中,AD 是BC 边上的高,∠C=45°,sinB=31,AD=1.则BC 的长▲.18.如图,矩形ABCD 中,E 是AB 上的一点,且AE :BE=3:2,DA 边上有一点F ,EF=18,将矩形沿着EF 翻折,使A 落在BC 上的G 处,则AB= ▲.EDCBAGFEDC BA OCBA Dl 2l 1FED CBA c ba DBAC第17题图 第18题图 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 已知线段a 、b 、c 满足875cb a ==,且1823=+-c b a ,求c b a 342+-的值.20.(本题满分10分)已知:如图,两个不平行的向量a 和b .先化简,再求作:)86(21)32b a b a +-+(. (不要求写作法,但要指出图中表示结论的向量)21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)如图,已知△ABC 中,点D 、E 分别在边AB 和AC 上,DE ∥BC ,点F 是DE 延长线上的点,EF DEDB AD =,联结FC ,(1)求证:AB //CF ;(2)若32=AC AE ,FC=6,求AB 的长.baFECBAD22.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图,△ABC 中,∠ACB=90°,sinA=54,BC=8,D 是AB 中点,过点B 作直线CD 的垂线,垂足为点E .(1)求线段CD 的长; (2)求cos ∠ABE 的值.23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分)如图,在△ABC 中,D 和E 分别是BC 和AB 上的点,BE=EC ,联结DE ,EC 交AD 于点F ,且FC BC DC AB ⋅=⋅. (1)求证:△FCD ∽△ABC ; (2)若AF=FD ,求证:DE ⊥BC .24.(本题满分12分,每小题4分)从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.(1)如图,在△ABC 中,AD 为角平分线,∠B=50°,∠C=30°,求证:AD 为△ABC 的优美线; (2)在△ABC 中,∠B=46°,AD 是△ABC 的优美线,且△ABD 是以AB 为腰的等腰三角形,求∠BAC 的度数;(3)在△ABC 中,AB=4,AC=2,AD 是△A B C 的优美线,且△ABD 是等腰三角形,直接..写出优美线AD 的长.E DCBAF EDCBADAC25.(本题满分14分,第一小题3分,第二小题4分,第三小题7分)在Rt △AOB 中,∠AOB=90°,OA=OB=4厘米,点P 从B 出发,以1厘米/秒的速度沿边BO 运动,设点P 运动时间为x (x >0)秒.△APC 是以AP 为斜边的等腰直角三角形,且C ,O 两点在直线AB 的同侧,连接OC . (1)当x=1时,求AOAC的值; (2)当x=2时,求tan ∠CAO 的值; (3)设△POC 的面积为y ,求y 与x的函数解析式,并写出定义域.CPOBA数学阶段质量调研参考答案一、选择题:(本大题共6题,每题4分,满分24分) 题号 1 2 3 4 5 6 答案BBCBDA二、填空题:(本大题共12题,每题4分,满分48分) 题号 789 10 1112 答案 7610510-4 0 346 题号 131415 16 1718答案e 2-b a 32-- 315122+ 65三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 解:(1)设k cb a ===875则k a 5=,k b 7=,k c 8=………………………………………………………1分 代入1823=+-c b a1881415=+-k k k ………………………………………………………………1分解得2=k …………………………………………………………………………2分所以10=a ,14=b ,16=c ……………………………………………………3分 所以12342=+-c b a ……………………………………………………………3分 20.(本题满分10分)解:)86(21)32+-+( 4-362-+=…………………………………………………………………2分 2-+=……………………………………………………………………………3分作图正确得4分,结论1分21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分) 解:(1)∵BC DE // ∴ECAEDB AD =……………………………………………………………………2分∵EFDEDB AD = ∴ECAEEF DE =……………………………………………………………………2分 ∴AB //CF …………………………………………………………………1分(2)∵DE ∥BC ,AB //CF∴四边形DBCF 是平行四边形………………………………………………1分 ∴BD=CF=6……………………………………………………………………1分 ∵AB //CF ∴AECEAD CF =…………………………………………………………………1分 ∴AD=12………………………………………………………………………1分 ∴AB=18………………………………………………………………………1分 或:先证明△FCE ∽△ABC (2分),得AC EC AB CF =(1分),得316=AB (1分) 所以AB=18(1分)22.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分) 解:(1)在△ABC 中,∵∠ACB=90°,∴sinA=AB BC…………………………………………………………………1分 ∴AB854=……………………………………………………………………1分 ∴AB=10………………………………………………………………………1分 ∵D 是AB 中点∴CD=5;………………………………………………………………………1分 (2)在Rt △ABC 中,∵AB=10,BC=8∴AC=6………………………………………………………………………1分 又∵D 是AB 中点∴CD=BD=5∴ABC BCD ∠=∠………………………………………………………………1分 ∵CE BE ⊥∴︒=∠=∠90ACB E∴△BCE ∽△ABC ………………………………………………………………1分∴ABBCAC BE =……………………………………………………………………1分 ∴524=BE ……………………………………………………………………1分∴cos ∠ABE 2524==BD BE ………………………………………………………1分 23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分) (1)证明:∵BE=EC ,∴∠ECB =∠B ………………………………………………………2分∵FC BC DC AB ⋅=⋅ ∴BCDCAB CF =…………………………………………………………2分 ∴△FCD ∽△ABC ;………………………………………………2分(2)证明:∵△FCD ∽△ABC∴BCDCAC FD =…………………………………………………………1分 ∠ADC =∠ACB ,…………………………………………………1分 ∴AD=AC ,…………………………………………………………1分 ∵AF=FD ,∴21==AC FD AD FD ………………………………………………………1分 ∴21=BC DC ……………………………………………………………1分 ∴DC BD =∵BE=EC ,(此条件不写,下列不得分)∴DE ⊥BC ……………………………………………………………1分24.(本题满分12分,每小题4分) (1)证明:∵∠B=50°,∠C=30°,∴∠BAC=100°, ∵AD 平分∠BAC ,∴∠BAD=∠DAC=50°,…………………………………………………………1分 ∴∠B=∠BAD=50°,∴DB=DA ,…………………………………………1分 ∴△ABD 是等腰三角形, ∵∠C=∠C ,∠DAC=∠B=50°,∴△CAD ∽△CBA ,………………………………………………………………1分 ∴线段AD 是△ABC 的优美线.…………………………………………………1分 (2)若AB=AD ,舍去,…………………………………………………………1分,(理由若△CAD ∽△CBA ,则∠B=∠ADB=∠CAD ,则AC ∥BC ,) 若AB=BD ,∠B=46°,∴∠BAD=∠BDA=67°,………………………………………………………1分 ∵△CAD ∽△CBA ,∴∠CAD =∠B=46°,……………………………………………………………1分 ∴∠BAC=67°+46°=113°.………………………………………………………1分 (3)334=AD 或4-24=AD ………………………………………………2分+2分25.(本题满分14分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分7分) 解:(1)当x=1时,OP=3,OA=4,在Rt △AOP 中,AP=5,…………………………………………………………1分 ∵△ACP 为等腰三角形, ∴AC=AP •cos45°=225,……………………………………………………1分 ∴825=AO AC ……………………………………………………………………1分 (2)作AB PH ⊥,交AB 于H ,垂足为H ∵△AOB ,△ACP 都是等腰三角形, ∴∠BAO=∠PAC=∠B=∠APC=45°,∴∠BAP=∠OAC ,……………………………………………………………………1分 当x=2时,BP=2,在Rt △BPH 中,∠B=45°,BP=2∴2==PH BH ………………………………1分 ∵Rt △ABO 中,AO=BO=4 ∴24=AB∴23=AH …………………………………………………………………………1分 ∴tan ∠CAO =tan ∠BAP=31…………………………………………………………1分 (3)∵∠BAO=∠PAC=∠B=∠APC =45°, ∴△BAO ∽△PAC∴AC AO AP AB =∴ACAP AO AB = ∵∠BAP=∠OAC∴△APB ∽△ACO ;…………………………………………………………………2分 ∴∠B=∠AOC=45°…………………………………………………………………1分2==AOAB OC BP ∴x OC 22=…………………………………………………………………………1分 作CM ⊥BO ,垂足为M ,则CM=OC•sin 45°=x 21………………………………………………………………1分∴4421)4(21212x x x x CM PO y -=⋅-=⋅=(0<x <4)……………………1分+1分。
沪教版-九年级(初三)数学上册-期中考试复习试卷试题及答案(Word版)

沪教版-九年级(初三)数学上册-期中考试复习试卷试题及答案(Word版)AC51.将抛物线y=x^2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为哪一个?A。
y=(x-1)^2+2B。
y=(x+1)^2+2C。
y=(x-1)^2-2D。
y=(x+1)^2-22.已知二次函数y=ax^2-1的图象经过点(1,-2),那么a的值为多少?A。
a=-2B。
a=2C。
a=1D。
a=-13.对于非零向量a、b,如果2|a|=3|b|,且它们的方向相同,那么用向量a表示向量b正确的是哪一个?A。
b=a*(3/2)B。
b=a*(2/3)C。
b=-a*(3/2)D。
b=-a*(2/3)4.在四边形ABCD中,若AB=a,AD=b,BC=c,则CD等于哪一个?A。
a-b-cB。
-a+b-cC。
a-b+cD。
-a+b+c5.在直角三角形ABC中,∠C=90°,如果∠A=α,AB=3,那么AC等于哪一个?A。
3sinαB。
3cosαC。
sinα/3D。
cosα/36.在直角三角形ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为多少?A。
3/4B。
4/3C。
5/3D。
3/57.在直角三角形ABC中,∠ACB=90°,BC=1,AC=2,则下列结论正确的是哪一个?A。
sinA=3/2B。
tanA=1/2C。
cosB=3/2D。
tanB=3/48.抛物线y=-3x^2+2x-1的图象与x轴交点的个数是多少?A。
没有交点B。
只有一个交点C。
有且只有两个交点D。
有且只有三个交点9.关于二次函数y=(x+1)^2的图象,下列说法正确的是哪一个?A。
开口向下B。
经过原点C。
对称轴右侧的部分是下降的D。
顶点坐标是(-1,0)10.在三角形ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE//BC的是哪一个?A。
DE^2/BC^2=3/2B。
2018年-上海中考数学一模-23题合集
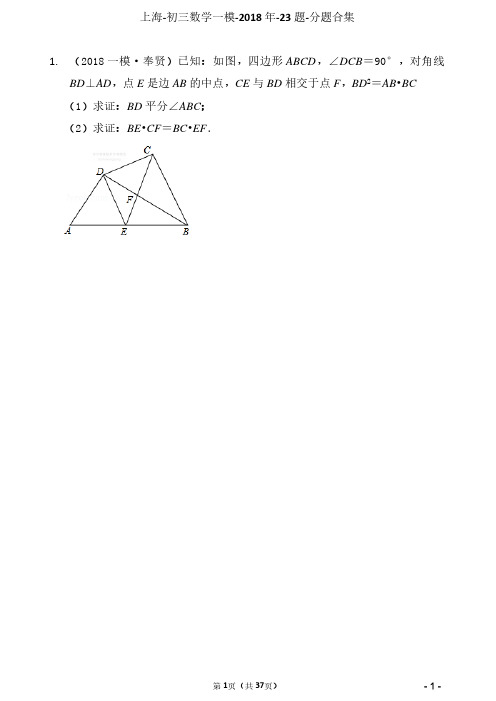
上海-初三数学一模-2018年-23题-分题合集1.(2018一模·奉贤)已知:如图,四边形ABCD,∠DCB=90°,对角线BD⊥AD,点E是边AB的中点,CE与BD相交于点F,BD2=AB•BC(1)求证:BD平分∠ABC;(2)求证:BE•CF=BC•EF.2.(2018•金山区一模)如图,已知在R t△ABC中,∠ACB=90°,AC>BC,CD是R t△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.(1)求证:DF是BF和CF的比例中项;(2)在AB上取一点G,如果AE•AC=AG•AD,求证:EG•CF=ED•DF.3.(2018•虹口区一模)如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且EF•DF=BF•CF.(1)求证:AD•AB=AE•AC;(2)当AB=12,AC=9,AE=8时,求BD的长与 △ △ 的值.4.(2018•松江区一模)已知四边形ABCD中,∠BAD=∠BDC=90°,BD2=AD•BC.(1)求证:AD∥BC;(2)过点A作AE∥CD交BC于点E.请完善图形并求证:CD2=BE•BC.5.(2018•嘉定区一模)如图,已知梯形ABCD中,AD∥BC,AB=CD,点E在对角线AC上,且满足∠ADE=∠BAC.(1)求证:CD•AE=DE•BC;(2)以点A为圆心,AB长为半径画弧交边BC于点F,联结AF.求证:AF2=CE•CA.6.(2018•黄浦区一模)如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.(1)求证:∠CDE=12∠ABC;(2)求证:AD•CD=AB•CE.7.(2018•长宁区一模)如图,在△ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DE•DF.(1)求证:△BFD∽△CAD;(2)求证:BF•DE=AB•AD.8.(2018•宝山区一模)如图,△ABC中,AB=AC,过点C作CF∥AB交△ABC的中位线DE的延长线于F,联结BF,交AC于点G.(1)求证: = ;(2)若AH平分∠BAC,交BF于H,求证:BH是HG和HF的比例中项.9.(2018•闵行区一模)如图,已知在△ABC中,∠BAC=2∠B,AD平分∠BAC,DF∥BE,点E在线段BA的延长线上,联结DE,交AC于点G,且∠E=∠C.(1)求证:AD2=AF•AB;(2)求证:AD•BE=DE•AB.10.(2018•崇明县一模)如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.(1)求证:GD•AB=DF•BG;(2)联结CF,求证:∠CFB=45°.11.(2018•青浦区一模)如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD•CA=CE•CB.(1)求证:∠CAE=∠CBD;(2)若 = ,求证:AB•AD=AF•AE.12.(2018•杨浦区一模)已知:梯形ABCD中,AD∥BC,AD=AB,对角线AC、BD交于点E,点F在边BC上,且∠BEF=∠BAC.(1)求证:△AED∽△CFE;(2)当EF∥DC时,求证:AE=DE.13.(2018•浦东新区一模)如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF•FC=FB•DF.(1)求证:BD⊥AC;(2)联结AF,求证:AF•BE=BC•EF.14.(2018•徐汇区一模)如图在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,且∠ADE=∠B,∠ADF=∠C,线段EF交线段AD于点G.(1)求证:AE=AF;(2)若 = ,求证:四边形EBDF是平行四边形.15.(2018•静安区一模)已知:如图,梯形ABCD中,DC∥AB,AD=BD,AD⊥DB,点E是腰AD上一点,作∠EBC=45°,联结CE,交DB于点F.(1)求证:△ABE∽△DBC;(2)如果 =56,求 △ △ 的值.16.(2018•普陀区一模)已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DE•DB,求证:(1)△BCE∽△ADE;(2)AB•BC=BD•BE.。
2018年上海初三年级数学各区一模压轴题汇总[15套全]
![2018年上海初三年级数学各区一模压轴题汇总[15套全]](https://img.taocdn.com/s3/m/37ab745932687e21af45b307e87101f69f31fb52.png)
2018年上海初三年级数学各区一模压轴题汇总[15套全]2016~2017学年度上海市各区初三一模数学压轴题汇总(18+24+25)共15套整理廖老师宝山区一模压轴题18(宝山)如图,D 为直角ABC D 的斜边AB 上一点,DE AB ^交AC 于E ,如果AED D 沿着DE 翻折,A 恰好与B 重合,联结CD 交BE 于F ,如果8AC =,1tan 2A =,那么:___________.CF DF =24(宝山)如图,二次函数232(0)2y ax x a =-+?的图像与x 轴交于A B 、两点,与y 轴交于点,C 已知点(4,0)A -.(1)求抛物线与直线AC 的函数解析式;(2)若点(,)D m n 是抛物线在第二象限的部分上的一动点,四边形OCDA 的面积为S ,求S 关于m 的函数关系;(3)若点E 为抛物线上任意一点,点F 为x 轴上任意一点,当以A C E F 、、、为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E 的坐标.第18题第24题25(宝山)如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P Q 、同时从点B 出发,点P 以1/cm s 的速度沿着折线BE ED DC --运动到点C 时停止,点Q 以2/cm s 的速度沿着BC 运动到点C 时停止。
设P Q 、同时出发t 秒时,BPQ D 的面积为2ycm ,已知y 与t 的函数关系图像如图(2)(其中曲线OG 为抛物线的一部分,其余各部分均为线段).(1)试根据图(2)求05t(2)求出线段BC BE ED 、、的长度;(3)当t 为多少秒时,以B P Q 、、为顶点的三角形和ABE D 相似;(4)如图(3)过点E 作EF BC ^于F ,BEF D 绕点B 按顺时针方向旋转一定角度,如果BEF D 中E F 、的对应点H I 、恰好和射线BE CD 、的交点G 在一条直线,求此时C I 、两点之间的距离.(3)(2)(1)第25题BB崇明县一模压轴题18(崇明)如图,已知 ABC ?中,45ABC ∠=o ,AH BC ⊥于点H ,点D 在AH 上,且DH CH =,联结BD ,将B H D V 绕点H 旋转,得到EHF ?(点B 、D 分别与点E 、F 对应),联结AE ,当点F 落在AC 上时,(F 不与C 重合)如果4BC =,tan 3C =,那么AE 的长为;24(崇明)在平面直角坐标系中,抛物线235y x bx c =-++与y 轴交于点(0,3)A ,与x 轴的正半轴交于点(5,0)B ,点D 在线段OB 上,且1OD = ,联结AD 、将线段AD 绕着点D 顺时针旋转90?,得到线段DE ,过点E 作直线l x ⊥轴,垂足为H ,交抛物线于点F .(1)求这条抛物线的解析式;(2)联结DF ,求cot EDF ∠的值;(3)点G 在直线l 上,且45EDG ?∠=,求点G 的坐标.25(崇明)在ABC ?中,90ACB ?∠=,3cot 2A =,AC =,以BC 为斜边向右侧作等腰直角EBC ?,P 是BE 延长线上一点,联结PC ,以PC 为直角边向下方作等腰直角PCD ?,CD 交线段BE 于点F ,联结BD .(1)求证:PC CECD BC=;(2)若PE x =,BDP ?的面积为y ,求y 关于x 的函数解析式,并写出定义域;(3)当BDF ?为等腰三角形时,求PE 的长.奉贤区一模压轴题18(奉贤)如图3,在矩形ABCD 中,AB =6,AD =3,点P 是边AD 上的一点,联结BP ,将△ABP 沿着BP 所在直线翻折得到△EBP ,点A 落在点E 处,边BE 与边CD 相交于点G ,如果CG=2DG ,那么DP 的长是__ ____.24(奉贤)如图,在平面直角坐标系中xOy 中,抛物线2y x bx c =-++与x 轴相交于点A (-1,0)和点B ,与y 轴相交于点C (0,3),抛物线的顶点为点D ,联结AC 、BC 、DB 、DC .(1)求这条抛物线的表达式及顶点D 的坐标;(2)求证:△ACO ∽△DBC ;(3)如果点E 在x 轴上,且在点B 的右侧,∠BCE=∠ACO ,求点E 的坐标。
上海-初三数学一模-2018年-24题-分题合集

上海-初三数学一模-2018年-24题-分题合集1.如图,在平面直角坐标系xOy中,已知抛物线y=38 2+bx+c与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y 轴相交于点E,与抛物线的另一个交点为F,且 =13.(1)求这条抛物线的表达式,并写出它的对称轴;(2)求∠FAB的余切值;(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.2.(2018•虹口区一模)如图,在平面直角坐标系x O y中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.(1)求该抛物线的表达式,并直接写出点D的坐标;(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标.3.(2018•金山区一模)平面直角坐标系x O y中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.(1)求这条抛物线的表达式和顶点P的坐标;(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.4.(2018•黄浦区一模)在平面直角坐标系x O y中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).(1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.5.(2018•深圳模拟)抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(32,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.6.(2018•深圳模拟)在直角坐标平面内,直线y=12x+2分别与x轴、y轴交于点A、C.抛物线y=﹣12 2+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.(1)求上述抛物线的表达式;(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.7.(2018•松江区一模)如图,在平面直角坐标系x O y中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.(1)求点A的坐标和抛物线的表达式;(2)当AE:EP=1:2时,求点E的坐标;(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.8.(2018•嘉定区一模)已知在平面直角坐标系x O y(如图)中,已知抛物线y=23 2+bx+c点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D 的坐标;(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.9.(2018•宝山区一模)设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.(1)反比例函数y=2018 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k 和t的值;(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.10.(2018•马边县模拟)如图,抛物线y=﹣43 2+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x 轴的直线与直线AB和抛物线分别交于点P、N.(1)求直线AB的解析式和抛物线的解析式;(2)如果点P是MN的中点,那么求此时点N的坐标;(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.11.(2018•徐汇区一模)如图,在平面直角坐标系x O y中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.(1)求直线BC及该抛物线的表达式;(2)设该抛物线的顶点为D,求△DBC的面积;(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.12.(2018•长春模拟)如图,在平面直角坐标系x O y中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.(1)求点C的坐标(用含a的代数式表示);(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.13.(2018•杨浦区一模)在平面直角坐标系x O y中,抛物线y=﹣x2+2mx﹣m2﹣m+1交y轴于点为A,顶点为D,对称轴与x轴交于点H.(1)求顶点D的坐标(用含m的代数式表示);(2)当抛物线过点(1,﹣2),且不经过第一象限时,平移此抛物线到抛物线y=﹣x2+2x的位置,求平移的方向和距离;(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.14.(2018•静安区一模)在平面直角坐标系x O y中(如图),已知抛物线y=ax2+bx ﹣53,经过点A(﹣1,0)、B(5,0).(1)求此抛物线顶点C的坐标;(2)联结AC交y轴于点D,联结BD、BC,过点C作CH⊥BD,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.15.(2018•浦东新区一模)已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.(1)求抛物线的表达式;(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,求tan∠CPA的值;(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB?若存在,求出点E的坐标;若不存在,请说明理由.16.(12分)(2018•普陀区一模)如图,已知在平面直角坐标系中,已知抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A,它的坐标是(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4(1)求抛物线的表达式;(2)求∠CAB的正切值;(3)如果点P是抛物线上的一点,且∠ABP=∠CAO,试直接写出点P 的坐标.。
2018年上海初三年级数学一模压轴题汇总[各区23~25题]
![2018年上海初三年级数学一模压轴题汇总[各区23~25题]](https://img.taocdn.com/s3/m/88aaccf789eb172ded63b7b5.png)
崇明23.(本题满分12分,每小题各6分)如图,点E 是正方形ABCD 的边BC 延长线上一点,联结DE ,过顶点B 作BF DE ⊥,垂足为F ,BF 交边DC 于点G . (1)求证:GD AB DF BG ⋅=⋅; (2)联结CF ,求证:45CFB ∠=︒.(第23题图)ABDECGF崇明24.(本题满分12分,每小题各4分)如图,抛物线24yx bx c =-++过点(3,0)A ,(0,2)B .(,0)M m 为线段OA 上一个动点(点N .(((△(第24题图) (备用图)崇明25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知ABC △中,90ACB ∠=︒,8AC =,4cos 5A =,D 是AB 边的中点,E 是AC 边上一点,联结DE ,过点D 作DF DE ⊥交BC 边于点F ,联结EF .(1)如图1,当DE AC ⊥时,求EF 的长;(2)如图2,当点E 在AC 边上移动时,DFE ∠的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出DFE ∠的正切值;(3)如图3,联结CD 交EF 于点Q ,当CQF △是等腰三角形时,请直接写出....BF 的长.(第25题图1) ABCD FE BD FE CA(第25题图2)BDFECA(第25题图3)如图,已知在Rt△ABC中,∠ACB=90°,AC>BC,CD是Rt△ABC的高,E是AC 的中点,ED的延长线与CB的延长线相交于点F.(1)求证:DF是BF和CF的比例中项;(2)在AB上取一点G,如果AE:AC=AG:AD,求证:EG:CF=ED:DF.平面直角坐标系xOy 中(如图),已知抛物线23y ax bx =++与y 轴相交于点C ,与x 轴正半轴相交于点A ,OA OC =,与x 轴的另一个交点为B ,对称轴是直线1x =,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)抛物线的对称轴与x 轴相交于点M ,求∠PMC 的正切值;(3)点Q 在y 轴上,且△BCQ 与△CMP 相似,求点Q 的坐标.金山25. (本题满分14分,第(1)小题3分,第(2)小题5分,第(3)小题6分)如图,已知在△ABC中,45,cos5AB AC B===,P是边AB一点,以P为圆心,PB为半径的Pe与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB =x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.青浦23.(本题满分12分,第(1)小题4分,第(2)小题8分)如图8,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD CA CE CB⋅=⋅.(1)求证:∠CAE=∠CBD;(2)若BE ABEC AC=,求证:AB AD AF AE⋅=⋅.ABDEF图8如图9,在平面直角坐标系xOy 中,抛物线()20y ax bx c a =++>与x 轴相交于点A (-1,0)和点B ,与y 轴交于点C ,对称轴为直线1x =.(1)求点C 的坐标(用含a 的代数式表示);(2)联结AC 、BC ,若△ABC 的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q 为x 轴正半轴上一点,点G 与点C ,点F 与点A 关于点Q 成中心对称,当△CGF 为直角三角形时,求点Q 的坐标.图9如图10,在边长为2的正方形ABCD 中,点P 是边AD 上的动点(点P 不与点A 、点 D 重合),点Q 是边CD 上一点,联结PB 、PQ ,且∠PBC =∠BPQ . (1)当QD =QC 时,求∠ABP 的正切值; (2)设AP =x ,CQ =y ,求y 关于x 的函数解析式;(3)联结BQ ,在△PBQ 中是否存在度数不变的角,若存在,指出这个角,并求出它的度数;若不存在,请说明理由.图10QP D C BA备用图A BCD黄浦23、(本题满分12分)如图,BD 是ABC △的角平分线,点E 位于边BC 上,已知BD 是BA 与BE 的比例中项.(1)求证:12CDE ABC ∠=∠(2)求证:AD CD AB CE ⋅=⋅ED CBA在平面直角坐标系xOy 中,对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-. (1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y 方向平移若干个单位,所得抛物线的顶点为D ,与y 轴的交点为B ,与x 轴负半轴交于点A ,过点B 作x 轴的平行线交所得抛物线于点C ,若A C B D ∥,试求平移后所得抛物线的表达式.如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积; (2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域.PDBA P EDC BA已知四边形ABCD中,∠BAD=∠BDC=90°,2=⋅.BD AD BC(1)求证:AD∥BC;(2)过点A作AE∥CD交BC于点E.请完善图形并求证:2=⋅.CD BE BC如图,在平面直角坐标系xOy 中,抛物线2y x bx c =++的对称轴为直线x =1,抛物线与x 轴交于A 、B 两点(点A 在点B 的左侧),且AB =4,又P 是抛物线上位于第一象限的点,直线AP 与y 轴交于点D ,与对称轴交于点E ,设点P 的横坐标为t . (1)求点A 的坐标和抛物线的表达式; (2)当AE :EP =1:2时,求点E 的坐标;(3)记抛物线的顶点为M ,与y 轴的交点为C ,当四边形CDEM是等腰梯形时,求t 的值.松江25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠P AB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.如图,已知在△ABC 中,∠BAC =2∠B ,AD 平分∠BAC , DF //BE ,点E 在线段BA 的延长线上,联结DE ,交AC 于点G ,且∠E =∠C .(1)求证:2AD AF AB =⋅; (2)求证:AD BE DE AB ⋅=⋅.(第23题图)ABDCEFG抛物线23(0)y ax bx a=++≠经过点A(1-,0),B(3 2且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求∠ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.(第24题图)闵行25.(共3小题,第(1)小题4分,第(2)小题6分,第(3)小题4分,满分14分)如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,CD 是斜边上中线,点E 在边AC 上,点F 在边BC 上,且∠EDA =∠FDB ,联结EF 、DC 交于点G . (1)当∠EDF =90°时,求AE 的长;(2)CE = x ,CF = y ,求y 关于x 的函数关系式,并指出x 的取值范围; (3)如果△CFG 是等腰三角形,求CF 与CE 的比值.(备用图)ABDC(第25题图)AB DCEFG浦东23.(本题满分12分,其中第(1)小题6分,第(2)小题6分)如图,已知,在锐角△ABC 中,CE ⊥AB 于点E ,点D 在边AC 上, 联结BD 交CE 于点F ,且DF FB FC EF ⋅=⋅. (1)求证:BD ⊥AC ;(2)联结AF ,求证:AF BE BC EF ⋅=⋅.A (第23题图)DEFBC浦东24.(本题满分12分,每小题4分)已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.(1)求抛物线的表达式;(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,求tan∠CPA的值;(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E(第24题图)浦东25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知在△ABC 中,∠ACB=90°,BC =2,AC =4,点D 在射线BC 上,以点D 为圆心,BD 为半径画弧交边AB 于点E ,过点E 作EF ⊥AB 交边AC 于点F ,射线ED 交射线AC 于点G . (1)求证:△EFG ∽△AEG ;(2)设FG =x ,△EFG 的面积为y ,求y 关于x 的函数解析式并写出定义域; (3)联结DF ,当△EFD 是等腰三角形时,请直接..写出FG 的长度.(第25题备用图)ABC(第25题备用图)ABC虹口23.(本题满分12分,第(1)题满分6分,第(2)题满分6分)如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且EF DF BF CF⋅=⋅.(1)求证AD AB AE AC⋅=⋅;(2)当AB=12,AC=9,AE=8时,求BD的长与△△ADE ECFSS的值.分4分)如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.(1)求该抛物线的表达式,并直接写出点D的坐标;(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F的坐标.分4分)已知AB=5,AD=4,AD∥BM,3cos5B=(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,AFy AC=.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.普陀23. (本题满分12分)已知:如图9,四边形ABCD 的对角线AC 和BD 相交于点E ,2,AD DC DC DE DB ==⋅.求证:(1)BCE ADE ∽;(2)··AB BC BD BE =.图9Bx普陀24.(本题满分12分,每小题满分各4分)如图10,在平面直角坐标系中,已知抛物线22y ax ax c +=+(其中a c 、为常数,且0a <)与x 轴交于点A ,它的坐标是()3, 0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4.(1)求该抛物线的表达式; (2)求CAB ∠的正切值;(3)如果点P 是抛物线上的一点,且ABP CAO ∠=∠,试直接写出点P 的坐标.普陀25.(本题满分14分,第(1)小题满分3分,第(1)小题满分5分,第(1)小题满分6分)如图11,BAC ∠的余切值为2,AB =D 是线段AB 上的一动点(点D 不与点A B 、重合),以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上,且点F 在点E 的右侧.联结BG ,并延长BG ,交射线EC 于点P .(1)点D 在运动时,下列的线段和角中,______是始终保持不变的量(填序号);①AF ; ②FP ; ③BP ; ④BDG ∠; ⑤GAC ∠; ⑥BPA ∠; (2)设正方形的边长为x ,线段AP 的长为y ,求y 与x 之间的函数关系式,并写出定义域; (3)如果PFG 与AFG 相似,但面积不相等,求此时正方形的边长.备用图图11P ACC E F嘉定23.(本题满分12分,每小题6分)如图6,已知梯形ABCD 中,AD ∥BC ,CD AB =,点E 在对角线AC 上,且满足BAC ADE ∠=∠.(1)求证:BC DE AE CD ⋅=⋅;(2)以点A 为圆心,AB 长为半径画弧交边BC 于点F ,联结AF .求证:CA CE AF ⋅=2.图6嘉定24.(本题满分12分,每小题4分)已知在平面直角坐标系xOy (如图7)中,已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .(1)求该抛物线的表达式;(2)设该抛物线的对称轴与x 轴的交点为C , 第四象限内的点D 在该抛物线的对称轴上,如果 以点A 、C 、D 所组成的三角形与△AOB 相似, 求点D 的坐标;(3)设点E 在该抛物线的对称轴上,它的纵坐标是1, 联结AE 、BE ,求ABE ∠sin .嘉定25.(满分14分,第(1)小题4分,第(2)、(3)小题各5分)在正方形ABCD 中,8=AB ,点P 在边CD 上,43tan =∠PBC ,点Q 是在射线BP 上的一个动点,过点Q 作AB 的平行线交射线AD 于点M ,点R 在射线AD 上,使RQ 始终与直线BP 垂直.(1)如图8,当点R 与点D 重合时,求PQ 的长; (2)如图9,试探索:MQRM的比值是否随点Q 的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图10,若点Q 在线段BP 上,设x PQ =,y RM =,求y 关于x 的函数关系式,并写出它的定义域.图8图9图10静安23. (本题满分12分,其中第1小题6分,第2小题6分)已知:如图,梯形ABCD 中,//,,DC AB AD BD AD DB =⊥,点E 是腰AD 上一点,作45EBC ∠=,联结CE ,交DB 于点F . (1)求证:ABE ∽DBC ;(2)如果56BC BD =,求BCE BDAS S 的值.静安24. (本题满分12分,第1小题4分,第2小题8分)在平面直角坐标系xOy中(如图),已知抛物线25 3y ax bx=+-经过点(1,0)A-、(5,0)B.(1)求此抛物线顶点C的坐标;(2)联结AC交y轴于点D,联结BD、BC,过点C作CH BD⊥,垂足为点H,抛物线对称轴交x轴于点G,联结HG,求HG的长.静安25. (本题满分14分,第1小题4分,第2小题6分,第3小题4分)已知:如图,四边形ABCD 中,090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠.(1)求证:四边形ABCD 是菱形;(2)如果点E 在对角线AC 上,联结BE 并延长,交边DC 于点G ,交线段AD 的延长线于点F (点F 可与点D 重合),A F B A C B∠=∠,设AB 长度是a (a 实常数,且0a >),,A C xA F y ==,求y 关于x 的函数解析式,并写出定义域;(3)在第(2)小题的条件下,当CGE 是等腰三角形时,求AC 的长.(计算结果用含a 的代数式表示)长宁23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,在∆ABC 中,点D 在边BC 上,联结AD ,∠ADB=∠CDE , DE 交边AC 于点E ,DE 交BA 延长线于点F ,且DF DE AD ⋅=2. (1)求证:BFD ∆∽CAD ∆; (2)求证:AD AB DE BF ⋅=⋅.F EDA第23题图长宁24.(本题满分12分,每小题4分)在直角坐标平面内,直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ,且与x 轴的另一个交点为点B . 点D 在该抛物线上,且位于直线AC 的上方.(1)求上述抛物线的表达式;(2)联结BC 、BD ,且BD 交AC 于点E ,如果∆ABE 的面积与∆ABC 的面积之比为4:5,求∠DBA 的余切值;(3)过点D 作DF ⊥AC ,垂足为点F ,联结CD . 若∆CFD 与∆AOC 相似,求点D 的坐标.备用图第24题图长宁25.(本题满分14分,第(1)小题3分,第(2)小题6分,第(3)小题5分) 已知在矩形ABCD 中,AB =2,AD =4. P 是对角线BD 上的一个动点(点P 不与点B 、D 重合),过点P 作PF ⊥BD ,交射线BC 于点F . 联结AP ,画∠FPE =∠BAP ,PE 交BF 于点E .设PD=x ,EF =y .(1)当点A 、P 、F 在一条直线上时,求 ABF 的面积;(2)如图1,当点F 在边BC 上时,求y 关于x 的函数解析式,并写出函数定义域; (3)联结PC ,若∠FPC =∠BPE ,请直接写出PD 的长.备用图 备用图图1DCBA DCBA F EP D CB A 第25题图徐汇23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分) 如图在△ABC 中,AB =AC ,点D 、E 、F 分别在边BC 、AB 、AC 上,且∠ADE =∠B , ∠ADF =∠C ,线段EF 交线段AD 于点G . (1)求证:AE =AF ;(2)若DF CFDE AE,求证:四边形EBDF 是平行四边形.徐汇24.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线2=++过点B、C且与x轴的另一个交y x bx c点为A.(1)求直线BC及该抛物线的表达式;(2)设该抛物线的顶点为D,求△DBC的面积;(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.徐汇25.(本题满分14分,第(1)小题3分,第(2)小题7分,第(3)小题4分)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M 的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.杨浦23.(本题满分12分,第(1)小题5分,第(2)小题7分)已知:梯形ABCD中,AD//BC,AD=AB,对角线AC、BD交于点E,点F在边BC上,且∠BEF=∠BAC.(2)当EF//DC时,求证:AE=DE.(第23题图)杨浦24.(本题满分12分,第(1)小题3分,第(2)小题5分,第(3)小题4分)在平面直角坐标系xOy 中,抛物线2221y x mx m m =-+--+交 y 轴于点为A ,顶点为D ,对称轴与x 轴交于点H .(1)求顶点D 的坐标(用含m 的代数式表示);(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线22y x x =-+的位置,求平移的方向和距离;(3)当抛物线顶点D 在第二象限时,如果∠ADH =∠AHO ,求m 的值.(第24题图)杨浦25.(本题满分14分,第(1)、(2)小题各6分,第(3)小题2分)已知:矩形ABCD 中,AB =4,BC =3,点M 、N 分别在边AB 、CD 上,直线MN 交矩形对角线AC 于点E ,将△AME 沿直线MN 翻折,点A 落在点P 处,且点P 在射线CB 上. (1)如图1,当EP ⊥BC 时,求CN 的长; (2)如图2,当EP ⊥AC 时,求AM 的长;(3)请写出线段CP 的长的取值范围,及当CP 的长最大时MN 的长.(备用图)(图1) A B C D NP ME(图2) A B C D N P M E (第25题图)A B C D奉贤23.(本题满分 12 分,每小题满分各 6 分)已知:如图 8,四边形90ABCD DCB ∠=︒,,对角线 BD ⊥AD ,点 E 是边 AB 的中点,CE 与 BD 相交于点 F ,2·BD AB BC =.(1) 求证:BD 平分∠ABC ;(2) 求证:··BE CF BC EF =.奉贤24. (本题满分 12 分,每小题满分各 4 分)如图9,在平面直角坐标系xOy 中,抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ,与y 轴相交于点(0,3)C -,经过点A 的射线AM 与y 轴相交于点E ,与抛物线的另一个交点为点F ,且13AE EF =. (1)求这条抛物线的表达式,并写出它的对称轴; (2)求FAB ∠的余切值; (3)点D 是点C 关于抛物线对称轴的对称点,点 P 是 y 轴上一点,且AFP DAB ∠=∠,求点 P 的坐标.奉贤25.(本题满分 14 分,第(1)小题满分 3 分,第(1)小题满分 5 分,第(1)小题满分 6 分)已知:如图10,在梯形ABCD 中,//,90,2AB CD D AD CD ∠===,点E 在边AD上(不与点A 、D 重合),45,C E B E B ∠=与对角线AC 相交于点F ,设DE x =.(1)用含x 的代数式表示线段CF 的长; (2)如果把CAE 的周长记作CAE C,BAF 的周长记作BAF C,设CAE BAFCy C=,求y 关于x 的函数关系式,并写出它的定义域; (3)当ABE ∠的正切值是35时,求AB 的长.如图,ABC 中,AB AC =,过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ,联结BF ,交AC 于点G . (1)求证:AE EGAC CG=; (2)若AH 平分BAC ∠,交BF 于H ,求证:BH 是HG 和HF 的比例中项.设,a b 是任意两个不等实数,我们规定:满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间,表示为[],a b ,对于一个函数,如果它的自变量x 与函数值y 满足:当m x n ≤≤时,有m y n ≤≤,我们就此称此函数是闭区间[],m n 上的“闭函数”。
【初三英语试题精选】2018届中考数学一模试卷分类汇编:选择题(上海市16区含答案)

2018届中考数学一模试卷分类汇编:选择题(上海市16区
含答案)
上海市16区2);(B)(-2,0); ( C) (0,-1) ; ( D)(0,0)
4 如图1,在平行四边形ABCD中,点E在边DC上,联结AE并延长交BC的延长线于点F,若AD=3CF,那么下列结论中正确的是()(A)FCFB=13 (B)CECD=13
(C)CEAB=14 (D)AEAF=12
A D
EB C F
5 已知矩形ABCD的对角线AC与BD相交于点O,如果,,那么等于()
(A)(B)
(C)(D)
6 下列四个命题中,真命题是()
(A)相等的圆心角所对的两条弦相等(B)圆既是中心对称图形也是轴对称图形
(C)平分弦的直径一定垂直于这条弦(D)相切两圆的圆心距等于这两圆的半径之和
金区
1.已知a、b是不等于0的实数,2a=3b,那么下列等式中正确的是()
(A);(B);(C);(D).
2.在Rt△ABC中,,,,,下列各式中正确的是()
(A);(B);(C);(D).
3.将抛物线平移,使平移后所得抛物线经过原点,那么平移的过程为()
(A)向下平移3个单位;(B)向上平移3个单位;
(C)向左平移4个单位;(D)向右平移4个单位.。
最新上海市2018届中考一模数学试卷分类汇编:平面向量(Word版,含答案)

九年级上学期期末(一模)数学试卷分类汇编平面向量专题20.(本题满分10分,每小题各5分)如图,AB ∥CD ∥EF ,而且线段AB 、CD 、EF 的长度分别为5、3、2. (1)求AC :CE 的值;(2)如果AE 记作a ,BF 记作b ,求CD (用a 、b表示).20.(本题满分10分,第(1)小题5分,第(2)小题5分)如图,在∆ABC 中,点D 在边AB 上,DE //BC ,DF //AC ,DE 、DF 分别交边AC 、BC于点E 、F ,且23=EC AE . (1)求BCBF的值;(2)联结EF ,设=,=,用含、的式子表示EF . 20.(本题满分10分,每小题各5分) 如图,在ABC △中,BE 平分ABC ∠交AC 于点E ,过点E 作ED BC ∥交AB 于点D ,已知5AD =,4BD =.(1)求BC 的长度;(2)如果AD a = ,AE b = ,那么请用a 、b 表示向量CB.第20题图AD E ADE20.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)已知:如图,在平行四边形ABCD 中,AD =2,点E 是边BC 的中点,AE 、BD 想交于点F ,过点F 作FG ∥BC ,交边DC 于点G . (1)求FG 的长;(2)设AD a = ,DC b = ,用、a b 的线性组合表示AF.如图,在△ABC 中,点E 在边AB 上,点G 是△ABC 的重心,联结AG 并延长交BC 于点D .(1)若AB a = ,AC b = ,用向量、a b 表示向量AG; (2)若∠B =∠ACE ,AB =6,AC =,BC =9,求EG 的长.如图,已知平行四边形ABCD ,点M 、N 分别是边DC 、BC 的中点,设=AB a ,=AD b ,求向量MN关于a 、b 的分解式.20.(本题满分10分,每小题5分)第20题图且DE 经过△ABC 的重心,设BC a =. (1)=DE ▲ (用向量a表示);(2)设AB b = ,在图中求作12b a +.(不要求写作法,但要指出所作图中表示结论的向量.)22.(本题满分10分)下面是一位同学做的一道作图题:. ON 于点D .(1)试将结论补完整:线段 ▲ 就是所求的线段x . (2)这位同学作图的依据是 ▲ ;(3)如果4OA =,5AB =,AC m = ,试用向量m表示向量DB .20.(本题满分10分,每小题各5分)如图,已知△ABC 中,D 、E 、F 分别是边AB 、BC 、CA 上的点,且EF //AB ,2CF ADFA DB==. (1)设AB a = ,AC b = .试用、表示AE(2)如果△ABC 的面积是9,求四边形ADEF 的面积.MO ABCDab cN(第20题图)CE F B19.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图,在△ABC 中,∠ACD =∠B ,AD =4,DB =5. (1)求AC 的长(2)若设,CA a CB b ==u u r r u u r r,试用、的线性组合表示向量CD uu u r.20.(本题满分10分,第(1)、(2)小题各5分) 已知:如图,Rt △ABC 中,∠ACB =90°,sin B =35,点D 、E 分别在边AB 、BC 上,且AD ∶DB =2∶3,DE ⊥BC . (1)求∠DCE 的正切值; (2)如果设AB a = ,CD b = ,试用a 、b 表示AC.参考答案20.(本题满分10分,第(1)小题5分,第(2)小题5分)解:(1)∵23=EC AE ∴52=AC EC (1分) ∵DE //BC ∴52==AC EC AB BD (2分)(第20题图)又∵DF //AC ∴52==AB BD BC BF (2分) (2)∵52=BC BF ∴53=BC FC ∵a BC =,CF 与BC 方向相反 ∴a CF 53-= (2分)同理:b EC 52= (2分)又∵→+=CF ∴→-=a b EF 5352 (1分)20、(1)∵BE 平分ABC ∠ ∴ABE CBE =∠∠ ∵ED BC ∥ ∴DEB CBE =∠∠∴ABE DEB =∠∠ ………………………………………………………2分 ∴4BD DE == ∵ED BC ∥ ∴DE AD BC AB= ……………………………………1分 又∵5AD =,4BD = ∴9AB =∴459BC = ∴365BC = ………………………………………2分 (2)∵ED BC ∥ ∴5=9DE AD BC AB = ∴95BC DE = …………………………………………………………1分又∵ED 与CB同向 ∴95CB ED = ………………………………1分∵AD a = ,AE b = ∴ED a b =-……………………………1分∴9955CB a b =-…………………………………………………………2分20.(本题共2小题,第(1)小题4分,第(2)小题6分,满分10分)如图,已知向量a r 、b r 和p u r,求作:(1)向量132a b -+r r. (2)向量p u r分别在a r 、b r 方向上的分向量.20.解:(1)作图.…………………………………………………………………………(3分)结论. …………………………………………………………………………(1分) (2)作图.…………………………………………………………………………(4分)结论. …………………………………………………………………………(2分)a r p u r (第20题图)b r20.解:(1)=23a.……………………………(5分)(2)图正确得4分,结论:AF 就是所要求作的向量. …(1分).22.解:(1)CD ; ·························································································································· (2分) (2)平行线分线段成比例定理(两条直线被三条平行的直线所截,截得的对应线段成比例);或:三角形一边的平行线性质定理(平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例). ··············································································································································· (2分)(3)∵BD ∥AC ,∴AC OABD OB=. ················································································ (1分) ∵4OA =,5AB =,∴49AC BD =. ········································································· (2分) 得94BD AC =. ········································································································· (1分)∵94BD AC = ,AC m = ,DB 与AC反向,∴94DB m =- . ·········································································································· (2分)20.解:(1)∵EF //AB∴CF CEFA EB = 又CF AD FA DB = ∴CE AD EB DB=…………………………………………(1分) ∴DE ∥AC , ………………………………………(1分) ∴四边形ADEF 是平行四边形………………………(1分)AE AF AD =+……………………………………(1分)∵2CF ADFA DB ==,AB a = ,AC b = ∴13AF b = , 23A D a= 2133AE a b =+………………………………………(1分)(2)∵EF //AB ,2CFFA=(第20题图)B∴9:4:=∆∆ABC CEF S S ………………………………(1分) ∵△ABC 的面积是9,∴4=∆CEF S ……………………………………………(1分) 由(1)得DE ∥AC , 且2ADDB= ∴9:1:=∆∆ABC BD E S S ………………………………(1分) ∴1=∆BDE S …………………………………………(1分) ∴四边形ADEF 的面积=9-4-1=4……………………(1分) 19.(1)在△ABC 中,∠ACD =∠B ,∠A =∠A ,∴ ACD ABC ∆:V . ……………………………………………………(2分)∴AD ACAC AB=,即2AC AD AB =g ∴249AC =⨯, 6.AC = ……………………………………………(2分) (2) 49CD CA AD a AB =+=+uu u r uu r uuu r r uu u r……………………………………………(2分)4()9a AC CB =++r uuu r uu r 4()9a a b =+-+r r r………………………………(2分)5499a b =+r r………………………………………………………(2分)20.(本题满分10分,第(1)、(2)小题各5分) 解:(1)∵∠ACB =90°,sin B =35,∴35AC AB =. -------------------------(1分) ∴设AC =3a ,AB =5a . 则BC =4a .∵AD :DB =2:3,∴AD =2a ,DB =3a .∵∠ACB =90°即AC ⊥BC ,又DE ⊥BC ,∴AC//DE. ∴DE BD AC AB =, CE ADCB AB=. ∴335DE a a a =, 245CE a a a =. ∴95DE a =,85CE a =.----------(2分) ∵DE ⊥BC ,∴9tan 8DE DCE CE ∠==.-----------------------------(2分) (2)∵AD :DB =2:3,∴AD :AB =2:5. ------------------------------------------------(1分)∵AB a = ,CD b = ,∴25AD a = . DC b =-.--------------------(2分)∵AC AD DC =+,∴25AC a b =- .-----------------------------------(2分)。
2018上海初三数学一模卷

2018上海初三数学一模卷全文共四篇示例,供读者参考第一篇示例:2018年上海初三数学一模卷是学生们备战中考的第一道考题,这份试卷的设计和命题将直接影响着学生们的中考成绩。
数学作为中考科目之一,在学生们的中考成绩中占据着重要的比例,因此对于这份试卷的复习和备考是至关重要的。
2018年上海初三数学一模卷的命题从往年来看会有所变化,但它会涵盖初中阶段所学的各个知识点,涉及到的题型会比较多样化,涉及的难度也会有一定的提升。
数学考试的命题会分为选择题和解答题两部分,选择题考查学生对知识点的掌握和运用能力,解答题则考查学生们的解决问题的能力和思维逻辑能力。
在备考这份试卷的过程中,学生们需要系统地复习和总结初中数学的知识点,包括代数、几何、数学应用等各个方面。
针对选择题的备考,学生们需要熟练掌握各种题型的解题方法和技巧,提高解题速度和准确率;针对解答题的备考,学生们需要多做一些综合性的练习题,培养自己的解决问题的能力和思维逻辑能力。
2018年上海初三数学一模卷的命题具有一定的难度和挑战性,对学生们的综合能力和解决问题的能力提出了较高的要求。
在备考这份试卷的过程中,学生们需要克服困难,坚持不懈地努力学习,保持积极的心态和良好的学习状态,相信自己能够取得优异的成绩。
2018年上海初三数学一模卷是学生们备战中考的第一道考题,对学生们的数学综合能力和解决问题的能力提出了一定的挑战。
在备考这份试卷的过程中,学生们需要系统地复习和总结数学知识点,注重解题方法和技巧的掌握,提升解题思维和逻辑推理能力。
相信只要学生们保持努力和坚持,认真备考,一定能够取得令人满意的成绩,实现自己的中考梦想。
希望各位学生都能在这份试卷上取得理想的成绩,为自己的中考之路打下坚实的基础。
加油!第二篇示例:2018年上海初三数学一模卷是对初中生进行数学学科综合能力和知识掌握情况的考核。
本次考试分为选择题和主观题两个部分,旨在通过考试内容的涵盖全面,考查学生对数学理论知识的掌握能力,解题技巧的运用和灵活应用能力。
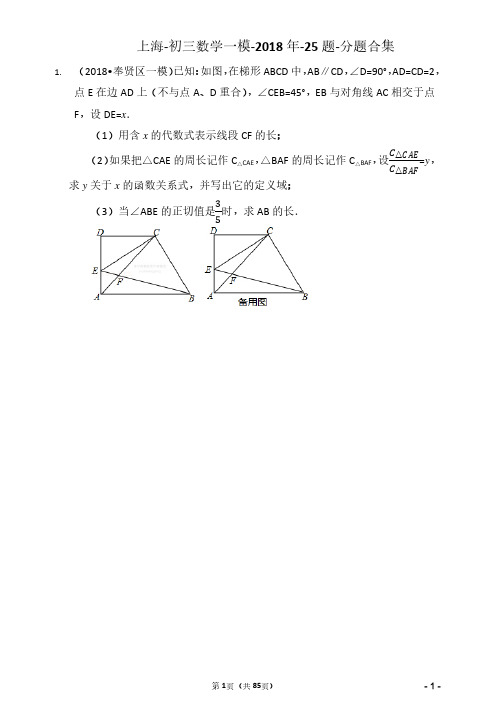
上海-初三数学一模-2018年-25题-分题合集
上海-初三数学一模-2018年-25题-分题合集1.(2018•奉贤区一模)已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.(1)用含x的代数式表示线段CF的长;(2)如果把△CAE的周长记作C△CAE ,△BAF的周长记作C△BAF,设 =y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是 时,求AB的长.2.(2018•虹口区一模)已知AB=5,AD=4,AD∥BM,cos B= (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x, =y.(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.3.(2018•浦东新区一模)如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E 作EF⊥AB交边AC于点F,射线ED交射线AC于点G.(1)求证:△EFG∽△AEG;(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.4.(2018•静安区一模)已知:如图,四边形ABCD中,0°<∠BAD≤90°,AD=DC,AB=BC,AC平分∠BAD.(1)求证:四边形ABCD是菱形;(2)如果点E在对角线AC上,联结BE并延长,交边DC于点G,交线段AD的延长线于点F(点F可与点D重合),∠AFB=∠ACB,设AB长度是a (a是常数,且a>0),AC=x,AF=y,求y关于x的函数关系式,并写出定义域;(3)在第(2)小题的条件下,当△CGE是等腰三角形时,求AC的长(计算结果用含a的代数式表示)5.(2018•杨浦区一模)已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.(1)如图1,当EP⊥BC时,求CN的长;(2)如图2,当EP⊥AC时,求AM的长;(3)请写出线段CP的长的取值范围,及当CP的长最大时MN的长.6.(2018•徐汇区一模)已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).(1)当BM的长为10时,求证:BD⊥DM;(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x 的函数关系式,并写出它的定义域;(3)如果△DMN是等腰三角形,求BN的长.7.(2018•青浦区一模)如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.(1)当QD=QC时,求∠ABP的正切值;(2)设AP=x,CQ=y,求y关于x的函数解析式;(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.8.(2018•市中区二模)如图,已知△ABC中,∠ACB=90°,AC=8,cos A= ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.(1)如图1,当DE⊥AC时,求EF的长;(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.9.(2018•闵行区一模)如图,在R t△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边上中线,点E在边AC上,点F在边BC上,且∠EDA=∠FDB,联结EF、DC交于点G.(1)当∠EDF=90°时,求AE的长;(2)CE=x,CF=y,求y关于x的函数关系式,并指出x的取值范围;(3)如果△CFG是等腰三角形,求CF与CE的比值.10.(2018•宝山区一模)如图,等腰梯形ABCD中,AD∥BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点且AE:BE=1:2,F为BC一动点,∠FEG=∠B,EG 交射线BC于G,直线EG交射线CA于H.(1)求sin∠ABC;(2)求∠BAC的度数;(3)设BF=x,CH=y,求y与x的函数关系式及其定义域.11.(2018•长宁区一模)已知在矩形ABCD中,AB=2,AD=4.P是对角线BD上的一个动点(点P不与点B、D重合),过点P作PF⊥BD,交射线BC于点F.联结AP,画∠FPE=∠BAP,PE交BF于点E.设PD=x,EF=y.(1)当点A、P、F在一条直线上时,求△ABF的面积;(2)如图1,当点F在边BC上时,求y关于x的函数解析式,并写出函数定义域;(3)联结PC,若∠FPC=∠BPE,请直接写出PD的长.12.(2018•黄浦区一模)如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;(2)当△ABE与△BCE相似时,求线段CD的长;(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.(C)13.(2018•松江区一模)如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.(1)求线段CD的长;(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.14.(2018•嘉定一模)在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;(2)如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.15.(14分)(2018•普陀区一模)如图1,∠BAC的余切值为2,AB=2 ,点D是线段AB上的一动点(点D不与点A、B重合),以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上,且点F在点E的右侧,联结BG,并延长BG,交射线EC于点P.(1)点D在运动时,下列的线段和角中,是始终保持不变的量(填序号);①AF;②FP;③BP;④∠BDG;⑤∠GAC;⑥∠BPA;(2)设正方形的边长为x,线段AP的长为y,求y与x之间的函数关系式,并写出定义域;(3)如果△PFG与△AFG相似,但面积不相等,求此时正方形的边长.16.(2018•金山一模)如图,已知在△ABC中,AB=AC=5,cos B= ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.(1)求△ABC的面积;(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△APD是直角三角形,求PB的长.。
2018年上海市黄浦区中考数学一模试卷附答案解析

2018年上海市黄浦区中考数学一模试卷一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.(4分)已知二次函数y=ax2+bx+c的图象大致如图所示,则下列关系式中成立的是( )A.a>0B.b<0C.c<0D.b+2a>02.(4分)若将抛物线向右平移2个单位后,所得抛物线的表达式为y=2x2,则原来抛物线的表达式为( )A.y=2x2+2B.y=2x2﹣2C.y=2(x+2)2D.y=2(x﹣2)23.(4分)在△ABC中,∠C=90°,则下列等式成立的是( )A.B.C.D.4.(4分)如图,线段AB与CD交于点O,下列条件中能判定AC∥BD的是( )A.OC=1,OD=2,OA=3,OB=4B.OA=1,AC=2,AB=3,BD=4C.OC=1,OA=2,CD=3,OB=4D.OC=1,OA=2,AB=3,CD=4.5.(4分)如图,向量与均为单位向量,且OA⊥OB,令,则=( )A.1B.C.D.26.(4分)如图,在△ABC中,∠B=80°,∠C=40°,直线l平行于BC.现将直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN与△ABC相似,则旋转角为( )A.20°B.40°C.60°D.80°二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)已知a、b、c满足,a、b、c都不为0,则= .8.(4分)如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC= .9.(4分)已知向量为单位向量,如果向量与向量方向相反,且长度为3,那么向量= .(用单位向量表示)10.(4分)已知△ABC∽△DEF,其中顶点A、B、C分别对应顶点D、E、F,如果∠A=40°,∠E=60°,那么∠C= 度.11.(4分)已知锐角α,满足tanα=2,则sinα= .12.(4分)已知点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 千米.13.(4分)已知二次函数的图象开口向下,且其图象顶点位于第一象限内,请写出一个满足上述条件的二次函数解析式为 (表示为y=a(x+m)2+k的形式).14.(4分)已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N 两点,那么线段MN的长度随直线向上平移而变 .(填“大”或“小”)15.(4分)如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC 上.已知AC=6,AB=8,BC=10,设EF=x,矩形DEFG的面积为y,则y关于x的函数关系式为 .(不必写出定义域)16.(4分)如图,在△ABC中,∠C=90°,BC=6,AC=9,将△ABC平移使其顶点C位于△ABC的重心G处,则平移后所得三角形与原△ABC的重叠部分面积是 .17.(4分)如图,点E为矩形ABCD边BC上一点,点F在边CD的延长线上,EF与AC交于点O,若CE:EB=1:2,BC:AB=3:4,AE⊥AF,则CO:OA= .18.(4分)如图,平面上七个点A、B、C、D、E、F、G,图中所有的连线长均相等,则cos∠BAF= .三、解答题:(本大题共7题,满分78分)19.(10分)计算:2cos230°+﹣sin60°.20.(10分)用配方法把二次函数y=﹣2x2+6x+4化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.21.(10分)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.(1)求tan∠ACE的值;(2)求AE:EB.22.(10分)如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.(1)试问坡AB的高BT为多少米?(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米,≈1.73,≈1.41)23.(12分)如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.(1)求证:∠CDE=∠ABC;(2)求证:AD•CD=AB•CE.24.(12分)在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).(1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.25.(14分)如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;(2)当△ABE与△BCE相似时,求线段CD的长;(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.2018年上海市黄浦区中考数学一模试卷参考答案与试题解析一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.(4分)已知二次函数y=ax2+bx+c的图象大致如图所示,则下列关系式中成立的是( )A.a>0B.b<0C.c<0D.b+2a>0【解答】解:∵抛物线开口向下,对称轴大于1,与y轴交于正半轴,∴a<0,﹣>0,c>0,∴b>﹣2a,∴b+2a>0.故选:D.2.(4分)若将抛物线向右平移2个单位后,所得抛物线的表达式为y=2x2,则原来抛物线的表达式为( )A.y=2x2+2B. y=2x2﹣2C.y=2(x+2)2D.y=2(x﹣2)2【解答】解:∵将抛物线向右平移2个单位后,所得抛物线的表达式为y=2x2,∴原抛物线可看成由抛物线y=2x2向左平移2个单位可得到原抛物线的表达式,∴原抛物线的表达式为y=2(x+2)2,故选:C.3.(4分)在△ABC中,∠C=90°,则下列等式成立的是( )A.B.C.D.【解答】解:如图所示:sinA=.故选:B.4.(4分)如图,线段AB与CD交于点O,下列条件中能判定AC∥BD的是( )A.OC=1,OD=2,OA=3,OB=4B.OA=1,AC=2,AB=3,BD=4C.OC=1,OA=2,CD=3,OB=4D.OC=1,OA=2,AB=3,CD=4.【解答】解:A、∵≠,∴本选项不符合题意.B、无法判断=,∴本选项不符合题意;C、∵OC=1,OA=2,CD=3,OB=4,∴=,∴AC∥BD,∴本选项符合题意;D、∵≠,∴本选项不符合题意.故选:C.5.(4分)如图,向量与均为单位向量,且OA⊥OB,令,则=( )A.1B.C.D.2【解答】解:∵向量与均为单位向量,∴||=1,||=1,∵OA⊥OB,∴AB==,∵,∴=AB=,故选:B.6.(4分)如图,在△ABC中,∠B=80°,∠C=40°,直线l平行于BC.现将直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN与△ABC相似,则旋转角为( )A.20°B.40°C.60°D.80°【解答】解:如图,直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN∽△ACB,则∠AMN=∠C=40°,又∵直线l平行于BC,∴∠ADE=∠B=80°,∴∠DFM=∠ADE﹣∠AMN=80°﹣40°=40°,即直线l旋转前后的夹角为40°,∴旋转角为40°,故选:B.二、填空题:(本大题共12题,每题4分,满分48分)7.(4分)已知a、b、c满足,a、b、c都不为0,则= .【解答】解:设=k,可得:a=3k,b=4k,c=6k,把a=3k,b=4k,c=6k代入=,故答案为:;8.(4分)如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC= 3:2 .【解答】解:解:∵DE∥BC,∴=,∵AD:DB=3:2,AB=AD+DB,∴=,∴=,∵DE∥BC,EF∥AB,∴四边形DEBF是平行四边形,∴DE=BF,∵BC=BF+CF, =,∴=,∴BF:CF=3:2,故答案为3:2;9.(4分)已知向量为单位向量,如果向量与向量方向相反,且长度为3,那么向量= ﹣3 .(用单位向量表示)【解答】解:∵向量为单位向量,向量与向量方向相反,∴=﹣3.故答案为﹣3.10.(4分)已知△ABC∽△DEF,其中顶点A、B、C分别对应顶点D、E、F,如果∠A=40°,∠E=60°,那么∠C= 80 度.【解答】解:∵△ABC∽△DEF,∴∠B=∠E=60°,∴∠C=180°﹣∠A﹣∠B=180°﹣40°﹣60°=80°故答案为80;11.(4分)已知锐角α,满足tanα=2,则sinα= .【解答】解:如图,由tanα==2,得a=2b,由勾股定理,得c==b,sinα===,故答案为:.12.(4分)已知点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 8 千米.【解答】解:依照题意画出图形,如图所示.(方法一)∵∠BAD=30°,∠CAD=30°,∴∠BAC=∠BAD+∠CAD=60°.又∵AB=AC,∴△ABC为等边三角形,∴BC=AC=8千米.故答案为:8.(方法二)在Rt△ABD中,∠BAD=30°,AB=8千米,∴BD=4千米.同理,CD=4千米,∴BC=BD+CD=8千米.故答案为:8.13.(4分)已知二次函数的图象开口向下,且其图象顶点位于第一象限内,请写出一个满足上述条件的二次函数解析式为 y=﹣(x﹣1)2+1(答案不唯一) (表示为y=a(x+m)2+k的形式).【解答】解:∵二次函数的图象开口向下,且其图象顶点位于第一象限内,∴满足上述条件的二次函数解析式为y=﹣(x﹣1)2+1等.故答案为:y=﹣(x﹣1)2+1(答案不唯一).14.(4分)已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N 两点,那么线段MN的长度随直线向上平移而变 大 .(填“大”或“小”)【解答】解:设平行于x轴的直线直线y=h,根据题意得:ax2+bx+c=h,则ax2+bx+c﹣h=0,设M(x1,h),N(x2,h),∴x1•x2=﹣,x1+x2=﹣,∴MN2=(x1﹣x2)2=(x1+x2)2﹣4xx=﹣+,∵a,b,c是常数,∴MN2是h得一次函数,∵>0,∴MN随h的增而增大,∵直线向上平移h变大,∴线段MN的长度随直线向上平移而变大,故答案为:大;15.(4分)如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC 上.已知AC=6,AB=8,BC=10,设EF=x,矩形DEFG的面积为y,则y关于x的函数关系式为 y=4.8x﹣0.48x2 .(不必写出定义域)【解答】解:作AH为BC边上的高,AH交DG于点P,∵AC=6,AB=8,BC=10,∴三角形ABC是直角三角形,∴△ABC的高=,∵矩形DEFG的边EF在△ABC的边BC上,∴DG∥BC,∴△ADG∽△ABC,∵AH⊥BC,∴AP⊥DG∴,∴,∴AP=∴PH=4.8﹣,∴y=x(4.8﹣)=4.8x﹣0.48x2故答案为:y=4.8x﹣0.48x2;16.(4分)如图,在△ABC中,∠C=90°,BC=6,AC=9,将△ABC平移使其顶点C位于△ABC的重心G处,则平移后所得三角形与原△ABC的重叠部分面积是 3 .【解答】解:设平移后直角边交斜边AB于M、N,延长CG交AB于H.∵G是重心,∴HG:HC=1:3,∵GN∥AC,AC=9,∴GN:AC=HG:HC,∴GN=3,同法可得MG=2,∴S△MGN=×2×3=3.故答案为3;17.(4分)如图,点E为矩形ABCD边BC上一点,点F在边CD的延长线上,EF与AC交于点O,若CE:EB=1:2,BC:AB=3:4,AE⊥AF,则CO:OA= 11:30 .【解答】解:由BC:AB=3:4,设BC=3a,AB=4a,则CE=a,BE=2a,∵四边形ABCD是矩形,∴AB=CD=4a,BC=AD=3a,∠B=∠BCD=∠DAB=∠ADF=90°,∵EA⊥AF,∴∠BAD=∠EAF=90°,∴∠BAE=∠DAF,∵∠B=∠ADF=90°,∴△BAE∽△DAF,∴==,∴DF=a,在Rt△ECF中,EF==,在Rt△ABC中,AC==5a,在Rt△ADF中,AF==a,∵∠ECF+∠EAF=180°,∴A、E、C、F四点共圆,∴∠ECO=∠AFO,∵∠EOC=∠AOF,∴△EOC∽△AOF,∴===,设EO=x则AO=x,设OC=y,则OF=y,则有,解得,∴OC=a,OA=a,∴CO:OA=a: a=11:30.故答案为:11:30;18.(4分)如图,平面上七个点A、B、C、D、E、F、G,图中所有的连线长均相等,则cos∠BAF= .【解答】解:连接AC、AD,过点D作DM⊥AC,垂直为M.设AE的长为x,则AB=AG=BG=CG=CB=AF=AE=EF=x,∴△ABG、△AEF、△CBG和△DEF都是等边三角形,四边形ABCG、四边形AEDF是菱形,∴∠BAC=∠EAD=30°∴AC=AD=2×cos∠BAC×AB=2×x=x∵∠CAD=∠BAE﹣∠BAC﹣∠EAD=∠BAE﹣60°,∠BAF=∠BAE﹣∠EAF=∠BAE﹣60°,∴∠BAF=∠CAD在Rt△AMD中,因为DM=sin∠CAD×x,AM=coa∠CAD×x,CM=x﹣cos∠CAD×x,在Rt△CMD中,CD2=CM2+MD2,即x2=(x﹣cos∠CAD×x)2+(sin∠CAD×x)2整理,得5x2=6x2cos∠CAD∴cos∠CAD=∴cos∠BAF=.故答案为:三、解答题:(本大题共7题,满分78分)19.(10分)计算:2cos230°+﹣sin60°.【解答】解:原式=2×()2+﹣,=+﹣,=3﹣.20.(10分)用配方法把二次函数y=﹣2x2+6x+4化为y=a(x+m)2+k的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.【解答】解:y=﹣2x2+6x+4=,=,开口向下,对称轴为直线,顶点.21.(10分)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.(1)求tan∠ACE的值;(2)求AE:EB.【解答】解:(1)由∠ACB=90°,CE⊥BD,得∠ACE=∠CBD在△BCD中,BC=3,CD=AC=2,∠BCD=90°,得tan∠CBD=,即tan∠ACE=,(2)过A作AC的垂线交CE的延长线于P,则在△CAP中,CA=4,∠CAP=90°,tan∠ACP=,得AP=,又∠ACB=90°,∠CAP=90°,得BC∥AP,得AE:EB=AP:BC=8:9.22.(10分)如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.(1)试问坡AB的高BT为多少米?(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米,≈1.73,≈1.41)【解答】解:(1)在△ABT中,∠ATB=90°,BT:AT=1:2.4, AB=130米,令TB=h,则AT=2.4h,有h2+(2.4h)2=1302,解得h=50(舍负),答:坡AB的高BT为50米;(2)作DK⊥MN于K,作DL⊥CH于L,在△ADK中,AD=AB=65,KD=BT=25,得AK=60,在△DCL中,∠CDL=30°,令CL=x,得LD=,易知四边形DLHK是矩形,则LH=DK,LD=HK,在△ACH中,∠CAH=60°,CH=x+25,得AH=,所以,解得,则CH=64.4+25=89.4≈89,答:建筑物高度为89米.23.(12分)如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.(1)求证:∠CDE=∠ABC;(2)求证:AD•CD=AB•CE.【解答】证明:(1)∵BD是AB与BE的比例中项,∴,又BD是∠ABC的平分线,则∠ABD=∠DBE,∴△ABD∽△DBE,∴∠A=∠BDE.又∠BDC=∠A+∠ABD,∴∠CDE=∠ABD=∠ABC;(2)∵∠CDE=∠CBD,∠C=∠C,∴△CDE∽△CBD,∴.又△ABD∽△DBE,∴,∴,∴AD•CD=AB•CE.24.(12分)在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).(1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.【解答】解:(1)由题意得:,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)解得:,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)所以抛物线的表达式为y=﹣x2+2x+8,其顶点为(1,9).﹣﹣﹣﹣﹣(5分)(2)令平移后抛物线为y=﹣(x﹣1)2+k,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)易得顶点D(1,k),B(0,k﹣1),且k﹣1>0,由BC平行于x轴,知点C与点B关于对称轴x=1对称,得C(2,k﹣1).(7分)∴DH=k﹣(k﹣1)=1,BH=1,当y=0时,0=﹣(x﹣1)2+k,解得:x=1±,即.﹣﹣﹣﹣(8分)作DH⊥BC于H,CT⊥x轴于T,则在△DBH中,HB=HD=1,∠DHB=90°,∴∠BHD=∠ATC=90°又AC∥BD,∴∠DBC=∠BCA=∠CAT∴△CTA∽△DHB,所以CT=AT,即,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)解得k=4,所以平移后抛物线表达式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.﹣﹣﹣﹣﹣(10分)25.(14分)如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;(2)当△ABE与△BCE相似时,求线段CD的长;(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.【解答】解:(1)过C作CH⊥AB与H,由∠A=90°,DP∥AB,得四边形ADCH为矩形,在△BCH中,CH=AD=4,∠BHC=90°,tan∠CBH=2,得HB=CH÷2=2,所以CD=AH=5﹣2=3,则四边形ABCD的面积=.(2)由BE平分∠ABC,得∠ABE=∠EBC,①∠BCE=∠BAE=90°,由BE=BE,得△BEC≌△BEA,得BC=BA=5,于是在△BCH中,BH=,所以CD=AH=5﹣3=2.②∠BEC=∠BAE=90°,延长CE交BA延长线于T,由∠ABE=∠EBC,∠BEC=∠BET=90°,BE=BE,得△BEC≌△BET,得BC=BT,且CE=TE,又CD∥AT,得AT=CD.令CD=x,则在△BCH中,BC=BT=5+x,BH=5﹣x,∠BHC=90°,所以BC2=BH2+CH2,即(5+x)2=(5﹣x)2+42,解得.综上,当△ABE∽△EBC时,线段CD的长为2或.(3)延长BE交CD延长线于M.由AB∥CD,得∠M=∠ABE=∠CBM,所以CM=CB.在△BCH中,.则DM=CM﹣CD=,又DM∥AB,得,即,解得y=(0<x<4.1).。
2018届黄浦区中考数学一模及答案

第 1 页黄浦区2017学年度第一学期九年级期终调研测试 数学试卷 2018.1(考试时间:100分钟 总分:150分)考生注意:1. 本试卷含三个大题,共25题;2. 答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1、已知二次函数2y ax bx c =++的图像大致如图所示,则下列关系式中成立的是( ) (A )0a >; (B )0b <; (C )0c <; (D )20b a +>.222y x =,则原来抛物线的表达式为( )(222x -; (C )()222y x =+; (D )()222y x =-.3 ) (AB BC A AB =; (C )sin AC A BC =; (D )sin BCA AC=. 4、如图,线段AB 与CD 交于点O ,下列条件中能判定AC BD ∥的是( )(A )1OC =,2OD =,3OA =,4OB =; (B )1OA =,2AC =,3AB =,4BD =; (C )1OC =,2OA =,3CD =,4OB =; (D )1OC =,2OA =,3AB =,4CD =. 5、如图,向量OA 与OC 均为单位向量,且OA OB ⊥,令n OA OB =+,则||n =( )(A )1; (B (C (D )2.6、如图,在ABC △中,80B ∠=︒,40C ∠=︒,直线l 平行于BC ,现将直线l 绕点A 逆时针旋转,所得直线分(第1题)第 2 页别交边AB 和AC 于点M 、N ,若AMN △和ABC △相似,则旋转角为( ) (A )20︒; (B )40︒; (C )60︒; (D )80︒. 二、填空题(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置】 7、已知a 、b 、c 满足346a b c ==,则a bc b+-= . 8、如图,点D 、E 、F 分别位于ABC △的三边上,满足DE BC ∥,EF AB ∥,如果:3:2AD DB =,那么:BF FC = .9、已知向量e 为单位向量,如果向量n 与向量e 方向相反,且长度为3,那么向量n = .(用单位向量e 表示)10、已知ABC DEF △∽△,其中顶点A 、B 、C 分别对应顶点D 、E 、F ,如果40A ∠=︒,60E ∠=︒,那么C ∠= 度.11、已知锐角α,满足tan 2α=,则sin α= .12、已知点B 位于点A 北偏东30︒方向,点C 位于点A 北偏西30︒方向,且8AB AC ==千米,那么 BC = 千米.13、已知二次函数的图像开口向下,且其图像顶点位于第一象限,请写出一个满足上述条件的二次函数解析式为 (表示为()2y a x m k =++的形式)14、已知抛物线2y ax bx c =++开口向上,一条平行于x 轴的直线截此抛物线于M 、N 两点,那么线段MN 的长度随直线向上平移而变 .(填“大”或“小”)15、如图,矩形DEFG 的边EF 在ABC △的边BC 上,顶点D 、G 分别在边AB 、AC 上.已知6AC =,8AB =,10BC =,设EF x =,矩形DEFG 的面积为y ,则y 关于x 的函数关系式为 (不必写出定义域).16、如图,在ABC △中,90C ∠=︒,6BC =,9AC =,将ABC △平移使其顶点C 位于ABC △的重心G 处,则平移后所得三角形与原ABC △的重叠部分面积是 .17、如图,点E 为矩形ABCD 边BC 上一点,点F 在边CD 的延长线上,EF 与AC 交于点O ,若:1:2C E E B =,:3:4BC AB =,AE AF ⊥,则:CO OA = .18、如图,平面上七个点A 、B 、C 、D 、E 、F 、G ,图中所有的连线长均相等,则cos BAF ∠= .三、解答题(本大题共7题,满分78分) 19、(本题满分10分) 计算:2cot 452cos 30sin60tan301︒︒+-︒︒+.20、(本题满分10分)用配方法把二次函数2264y x x =-++化为()2y a x m k =++的形式,再指出该函数图像的开口方向、对称轴和顶点坐标.21、(本题满分10分)如图,在ABC △中,90ACB ∠=︒,4AC =,3BC =,D 是边AC 的中点,CE BD ⊥交AB 于点E . (1)求tan ACE ∠; (2)求:AE EB . 22、(本题满分10分)如图,坡AB 的坡比为1:2.4,坡长130AB =米,坡AB 的高为BT .在坡AB 的正面有一栋建筑物CH ,点H 、A 、T 在同一条地平线MN上.(1)试问坡AB 的高BT 为多少米?(2)若某人在坡AB 的坡脚A 处和中点D 处,观测到建筑物顶部C 处的仰角分别为60︒和30︒,试求建筑物的高度CH . 1.73≈ 1.41)23、(本题满分12分)如图,BD 是ABC △的角平分线,点E 位于边BC 上,已知BD 是BA 与BE 的比例中项.(1)求证:12CDE ABC ∠=∠(2)求证:AD CD AB CE ⋅=⋅ 24、(本题满分12分)的抛在平面直角坐标系xOy 中,对称轴为直线1x =EDCBA第 4 页物线28y ax bx =++过点()2,0-.(1)求抛物线的表达式,并写出其顶点坐标;(2)现将此抛物线沿y 方向平移若干个单位,所得抛物线的顶点为D ,与y 轴的交点为B ,与x 轴负半轴交于点A ,过点B 作x 轴的平行线交所得抛物线于点C ,若AC BD ∥,试求平移后所得抛物线的表达式.25、(本题满分14分)如图,线段5AB =,4AD =,90A ∠=︒,DP AB ∥,点C 为射线DP 上一点,BE 平分ABC ∠交线段AD 于点E (不与端点A 、D 重合).(1)当ABC ∠为锐角,且tan 2ABC ∠=时,求四边形ABCD 的面积; (2)当ABE △与BCE △相似时,求线段CD 的长;(3)设DC x =,DE y =,求y 关于x 的函数关系式,并写出定义域.参考答案1-6、DCBCBB7、738、3:2 9、3e - 10、80 1112、813、()211y x =--+ 14、大 15、21224255y x x =-+ 16、3 17、113018、56 19、320、2317222y x ⎛⎫=--+ ⎪⎝⎭,对称轴32x =,开口向下,顶点317,22⎛⎫ ⎪⎝⎭21、(1)23(2)8:9 22、(1)50米;(2)89米 23、(1)证明略;(2)证明略24、(1)228y x x =-++,顶点()1,9;(2)223y x x =-++25、(1)16;(2)2或45;(3)41541410xy x--⎫=<<⎪⎝⎭第5 页。
