数学名题:圆圈标数经典系列
初中数学圆形专题训练50题含答案
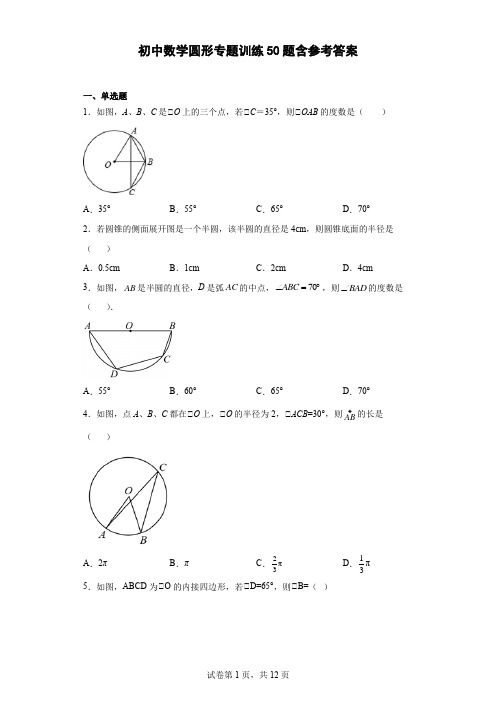
初中数学圆形专题训练50题含参考答案一、单选题1.如图,A 、B 、C 是⊙O 上的三个点,若⊙C =35°,则⊙OAB 的度数是( )A .35°B .55°C .65°D .70° 2.若圆锥的侧面展开图是一个半圆,该半圆的直径是4cm ,则圆锥底面的半径是( )A .0.5cmB .1cmC .2cmD .4cm 3.如图,AB 是半圆的直径,D 是弧AC 的中点,70ABC ∠=︒,则BAD ∠的度数是( ).A .55°B .60°C .65°D .70° 4.如图,点A 、B 、C 都在⊙O 上,⊙O 的半径为2,⊙ACB =30°,则AB 的长是( )A .2πB .πC .2π3 D .1π35.如图,ABCD 为⊙O 的内接四边形,若⊙D=65°,则⊙B=( )A .65°B .115°C .125°D .135° 6.如图,AB 、AC 是O 的两条切线,切点为B 、C , ∠BAC =30°,则∠BAO 度数为( )A .60B .45C .30D .15 7.如图,已知⊙O 的半径为1,锐角△ABC 内接于⊙O ,BD ⊙AC 于点D ,OM ⊙AB 于点M ,OM =13,则sin⊙CBD 的值等于( )A B .13 C D .128.如图,在Rt⊙ABC 中,⊙C =90°,AC =8,BC =6,两等圆⊙A ,⊙B 外切,图中阴影部分面积为( )A .25244π-B .25248π-C .252416π-D .252432π- 9.如图,AB 为⊙O 的切线,A 为切点,OB 交⊙O 于点D ,C 为⊙O 上一点,若42ABO ∠=︒,则ACD ∠的度数为( )A .48°B .24°C .36°D .72° 10.如图,点A ,B ,C 在O 上,//BC OA ,20A ∠=︒,则B ∠的度数为( )A .10︒B .20︒C .40︒D .50︒ 11.如图,⊙O 是⊙ABC 的外接圆,已知AD 平分⊙BAC 交⊙O 于点D ,连结CD ,延长AC ,BD ,相交于点F.现给出下列结论:⊙若AD=5,BD=2,则DE=25; ⊙ACB DCF ∠=∠;⊙FDA ∆⊙FCB ∆;⊙若直径AG⊙BD 交BD 于点H ,AC=FC=4,DF=3,则cosF=4148; 则正确的结论是( )A .⊙⊙B .⊙⊙⊙C .⊙⊙D .⊙⊙⊙ 12.下列说法中,正确的是( )A .垂直于半径的直线一定是这个圆的切线B .任何三角形有且只有一个内切圆C .所有的正多边形既是轴对称图形也是中心对称图形D .三角形的内心到三角形的三个顶点的距离相等13.如图,ABC 中,30C ∠=,90B ∠=,8AC =,以点A 为圆心,半径为4的圆与BC 的位置关系是( )A .相交B .相离C .相切D .不能确定 14.如图,⊙O 的半径长6cm ,点C 在⊙O 上,弦AB 垂直平分OC 于点D ,则弦AB 的长为( )A .9 cmB .cmC .92 cmD .cm 15.如图,正ABC 的边长为3cm ,边长为1cm 的正RPQ 的顶点R 与点A 重合,点P ,Q 分别在AC ,AB 上,将RPQ 沿着边AB ,BC ,CA 连续翻转(如图所示),直至点P 第一次回到原来的位置,则点P 运动路径的长为( )A .cm πB .2cm πC .3cm πD .6cm π 16.如图,两个半径都为1的圆形纸片,固定⊙O 1,使⊙O 2沿着其边缘滚动回到原来位置后运动终止,则⊙O 2上的点P 运动的路径长为( )A .2πB .4πC .6πD .无法确定 17.下列五个说法:⊙近似数3.60万精确到百分位;⊙三角形的外心一定在三角形的外部;⊙内错角相等;⊙90°的角所对的弦是直径;⊙函数y =x 的取值范围是2x ≥-且1x ≠.其中正确的个数有( )A .0个B .1个C .2个D .3个 18.下列命题正确的有( )A .在同圆或等圆中,等弦所对的弧相等B .圆的两条不是直径的相交弦,不能互相平分C .正多边形的中心是它的对称中心D .各边相等的圆外切多边形是正多边形 19.若扇形的面积是56cm 2,周长是30cm ,则它的半径是( )A .7cmB .8cmC .7cm 或8cmD .15cm 20.如图,在ABC 中,3AB =,6BC =,60ABC ∠=︒,以点B 为圆心,AB 长为半径画弧,交BC 于点D ,则图中阴影部分的面积是( )A .3πB 2π-C πD 32π二、填空题21.在圆O 中,弦AB 的长为6,它所对应的弦心距为4,那么半径OA =___. 22.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O 为圆心,5m 为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB 长为8m ,则筒车工作时,盛水桶在水面以下的最大深度为_____m .23.用一个圆心角为90°半径为32cm 的扇形作为一个圆锥的侧面(接缝处不重叠),则这个圆锥的底面圆的半径为___cm .24.如图,一块三角形透明胶片刚好在量角器上的位置,点A 、B 的读数分别是80︒、30︒,则ACB =∠________.25.如图,点I 为ABC 的三个内角的角平分线的交点,4AB =,3AC =,2BC =,将ACB ∠平移使其顶点与I 重合,则图中阴影部分的周长为______.26.已知⊙O 1和⊙O 2的半径长分别为3和4,若⊙O 1和⊙O 2内切,那么圆心距O 1O 2的长等于_____.27.已知一个圆锥的底面半径为5cm ,则这个圆锥的表面积为___________28.如图,在⊙O 中,AB 为直径,CD 为弦,已知⊙BAD=60°,则⊙ACD=______度.29.正十二边形的中心角是_____度.30.如图,A 、D 是半圆O 上的两点,BC 是直径,若⊙D =35°,则⊙AOB =_____°.31.如图,四边形ABCD 内接于O ,1079,,BD CD AB AC ====,则AD 的长为 ___________.32.如图,已知⊙P的半径为1,圆心P在抛物线22=-上运动,当⊙P与x轴相切y x时,圆心P的坐标是___________________.33.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____34.如图,AB为⊙O的直径,弦CD⊙AB于点E,若AE=8,BE=2,则CD=_______________.35.如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为________.36.一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上.木工师傅想到了一个巧妙的办法,他测量了PQ 与圆洞的切点K 到点B 的距离及相关数据(单位:cm )后,从点N 沿折线NF FM NF BC FM AB -(∥,∥)切割,如图1所示.图2中的矩形EFGH 是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则CN AM ,的长分别是_______.37.如图,菱形ABCD 的对角线AC 与BD 相交于点O ,分别以点A 、C 为圆心,OA 长为半径作OE 、OF 交AD 于点E 、BC 于点F .若6AC =,50∠=°ACB ,则阴影部分图形的面积为__________.(结果保留π)38.如图,在直角坐标系中,点A 坐标为(2,0),点B 的坐标为(6,0),以B 点为圆心,2长为半径的圆交x 轴于C 、D 两点,若P 是⊙B 上一动点,连接P A ,以P A 为一直角边作Rt ⊙P AQ ,使得1tan 2APQ ∠=,连接DQ ,则DQ 的最小值为_____39.如图,点O 为以AB 为直径的半圆的圆心,点M ,N 在直径AB 上,点P ,Q 在AB 上,四边形MNPQ 为正方形,点C 在QP 上运动(点C 与点P ,Q 不重合),连接BC 并延长交MQ 的延长P 线于点D ,连接AC 交MQ 于点E ,连接OQ ,则sin⊙AOQ =__________,若圆半径为R ,则DM ·EM =_______.40.已知Rt △ABC 中,⊙A =90°,M 是BC 的中点.如图,(1)以M 为圆心,MB 为半径,作半圆M ;(2)分别B ,C 为圆心,BA ,CA 为半径作弧,两弧交于D 点;(3)连接AM ,AD ,CD ;(4)作线段CD 的中垂线,分别交线段CD 于点F ,半圆M 于点G ,连接GC ;(5)以点..G 为圆心...,线段GC 为半径,作弧.CD .根据以上作图过程及所作图形,下列结论中:⊙点A 在半圆M 上;⊙AC =CD ;⊙弧AC =弧CD ;⊙△ABM ⊙△ACD ;⊙BC =GC ;⊙⊙BAM =⊙CGF .一定正确的是_______.三、解答题41.如图,⊙O 的半径OA 、OB 分别交弦CD 于点E 、F ,且CE =DF .求证:⊙OEF 是等腰三角形.42.如图,Rt ABC 中90BAC ∠=︒,2AE AD AC =⋅,点D 在AC 边上,以CD 为直径画O 与AB 交于点E .(1)求证:AB 是O 的切线;(2)若1==,求BE的长度.AD DO43.如图,AC是⊙O的直径,AD是⊙O的切线.点E在直径AC上,连接ED交⊙O于点B,连接AB,且AB=BD.(1)求证:AB=BE;(2)若⊙O的半径长为5,AB=6,求线段AE的长.44.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,求球的半径长.45.如图,⊙ABC内接于⊙O,AB=AC,P为⊙O上一动点(P,A分别在直线BC的两侧),连接PC.(1)求证:⊙P=2⊙ABC;(2)若⊙O的半径为2,BC=3,求四边形ABPC面积的最大值.46.如图,AB是⊙O的直径,过点A作⊙O切线AP,点C是射线AP上的动点,连接CO交⊙O于点E,过点B作BD//CO,交⊙O于点D,连接DE、OD、CD.(1)求证:CA=CD;(2)填空:⊙当⊙ACO的度数为时,四边形EOBD是菱形.⊙若BD=m,则当AC=(用含m的式子表示)时,四边形ACDO是正方形.47.如图,已知△ABC为直角三角形,⊙C=90°,边BC是⊙O的切线,切点为D,AB 经过圆心O并与圆相交于点E,连接AD.(1)求证:AD平分⊙BAC;(2)若AC=8,tan⊙DAC=34,求⊙O的半径.48.已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.(⊙)如图⊙,求⊙ADC的大小;(⊙)如图⊙,经过点O作CD的平行线,与AB交于点E,与AB交于点F,连接AF,求⊙F AB的大小.49.(1)小迪同学在学习圆的内接正多边形时,发现:如图1,若P是圆内接正三角形ABC的外接圆的BC上任一点,则60APB∠=︒,在PA上截取PM PC=,连接MC,可证明MCP∆是_______(填“等腰”、“等边”或“直角”)三角形,从而得到=PC MC,再进一步证明PBC≅_______,得到=PB MA,可证得:.(2)小迪同学对以上推理进行类比研究,发现:如图2,若P是圆内接正四边形ABCD的外接圆的BC上任一点,则APB APD∠=∠=°,分别过点,B D作BM AP⊥于M、⊥DN AP于N.(3)写出,PB PD与PA之间的数量关系,并说明理由.50.某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知⊙CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm,(1)用含x的代数式表示扇形O2CD的半径;(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2,当⊙O1的半径为多少时,该玩具的制作成本最小?参考答案:1.B【分析】根据“同一条弧所对的圆周角等于它所对的圆心角的一半”求出⊙AOB 的度数,再根据等腰三角形的性质求解即可.【详解】⊙⊙AOB 与⊙C 是同弧所对的圆心角与圆周角,⊙⊙AOB =2⊙C =2×35°=70°,⊙OA =OB ,⊙⊙OAB =⊙OBA =180AOB 2︒-∠=180702︒︒-=55°. 故选:B .【点睛】本题考查的是圆周角定理,掌握圆周角定理及等腰三角形的性质是关键. 2.B【分析】根据圆锥侧面展开图的半圆的周长等于圆锥底面的周长,从而求出底面半径; 【详解】解:由题意,底面圆的周长为:1422ππ⨯⨯=, ⊙底面圆的半径为:212ππ=(cm ), 故选:B【点睛】此题考查立体图形的侧面展开;圆锥的侧面展开图为扇形,扇形的半径为圆锥的母线,扇形的弧长为圆锥的底面周长.3.A【分析】连接BD ,由于点D 是AC 的中点,即CD AD =,根据圆周角定理得ABD CBD ∠=∠,则35ABD ∠=︒,再根据直径所对的圆周角为直角得到90ADB ∠=︒,然后利用三角形内角和定理可计算出BAD ∠的度数.【详解】解:连接BD ,如图,⊙点D 是AC 的中点,即CD AD =,⊙ABD CBD ∠=∠,而70ABC ∠=︒,⊙170352ABD ∠=⨯︒=︒, ⊙AB 是半圆的直径,⊙90ADB ∠=︒,⊙903555BAD ∠=︒-︒=︒.故选:A .【点睛】本题考查了圆周角定理及其推论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直径所对的圆周角为直角.4.C【详解】⊙点A 、B 、C 都在⊙O 上,⊙ACB =30°,⊙⊙AOB =60°,⊙OA =2,⊙AB =6022=1801803n r πππ⨯=︒ 故选:C .5.B【分析】根据圆内接四边形的对角互补可得答案.【详解】⊙⊙B +⊙D =180°,⊙⊙B =180°﹣65°=115°.故选B .【点睛】本题主要考查了圆内接四边形的性质,关键是掌握圆内接四边形的对角互补. 6.D【分析】根据切线长定理即可求解.【详解】⊙AB 、AC 是O 的两条切线,切点为B 、C ,⊙AO 平分⊙BAC ,⊙∠BAO =12⊙BAC=15°, 故选D.【点睛】此题主要考查圆内角度求解,解题的关键是熟知切线长定理的性质.7.B【分析】根据锐角⊙ABC 内接于⊙O ,BD ⊙AC 于点D ,OM ⊙AB 于点M ,得出sin ⊙CBD =sin ⊙OBM 即可得出答案.【详解】连接AO ,⊙OM⊙AB于点M,AO=BO,⊙⊙AOM=⊙BOM,⊙⊙AOB=2⊙C⊙⊙MOB=⊙C,⊙⊙O的半径为1,锐角⊙ABC内接于⊙O,BD⊙AC于点D,OM=13,⊙sin⊙CBD=sin⊙OBM=13113 MOOB==则sin⊙CBD的值等于13.故选B.【点睛】此题主要考查了垂径定理以及锐角三角函数值和圆周角定理等知识,根据题意得出sin⊙CBD=sin⊙OBM是解决问题的关键.8.A【分析】设等圆⊙A,⊙B外切于O点,如图,利用两圆相切的性质得到O点在AB上,再利用勾股定理计算出AB,则OA=OB=5,然后根据扇形的面积公式,利用S阴影=S△ABC一2S扇形进行计算,即可求解.【详解】解:设两等圆⊙A,⊙B外切于点O,则点O在AB上,⊙⊙C=90°,AC=8,BC=6,⊙10AB,⊙A+⊙B=90°,⊙OA =OB =5,⊙S 阴影=S △ABC -2S 扇形2190525682423604ππ⨯⨯=⨯⨯-=-. 故选:A .【点睛】本题考查了相切两圆的性质:如果两圆相切,那么连心线必经过切点.也考查了勾股定理和扇形面积的计算.9.B【分析】连结OA ,由切线定理和直角三角形性质可得⊙AOB=48°,再由圆周角定理可得⊙ACD=24°.【详解】解:如图,连结OA ,则由切线定义可得:⊙OAB=90°,⊙⊙AOB=90°-⊙ABO=90°-42° =48°,⊙根据圆周角定理可得:⊙ACD=12⊙AOB=24°, 故选B .【点睛】本题考查圆的应用,综合运用圆周角定理、切线的性质定理和直角三角形的性质求解是解题关键.10.C【分析】由//BC OA 得20C A ∠=∠=︒,由圆心角和圆周角的关系得40O ∠=︒,再利用平行线的性质可得结论.【详解】解:如图,⊙//BC OA ,20A ∠=︒⊙20C A ∠=∠=︒⊙240O C ∠=∠=︒//,BC OA⊙40B O ∠=∠=︒故选:C【点睛】此题考查了圆周角定理与平行线的性质.此题难度不大,注意掌握数形结合思想的应用.11.C【详解】试题分析:此题主要考查圆的综合问题,熟悉圆的相关性质,会证明三角形相似并解决相关问题,能灵活运用垂径定理和三角函数是解题的关键.⊙只需证明⊙BDE⊙⊙ADB ,运用对应线段成比例求解即可; ⊙连接CD ,假设⊙ACB=⊙DCF ,推出与题意不符即可判断; ⊙由公共角和同弧所对的圆周角相等即可判断; ⊙先证明⊙FCD⊙⊙FBA ,求出BD 的长度,根据垂径定理求出DH ,结合三角函数即可求解.⊙如图1,⊙AD 平分⊙BAC ,⊙⊙BAD=⊙CAD ,⊙⊙CAD=⊙CBD ,⊙⊙BAD=⊙CBD ,⊙⊙BDE=⊙BDE ,⊙⊙BDE⊙⊙ADB , ⊙BD DE AD BD=, 由AD=5,BD=2,可求DE=45, ⊙不正确;⊙如图2,连接CD ,⊙FCD+⊙ACD=180°,⊙ACD+⊙ABD=180°,⊙⊙FCD=⊙ABD ,若⊙ACB=⊙DCF ,因为⊙ACB=⊙ADB ,则有:⊙ABD=⊙ADB ,与已知不符,故⊙不正确;⊙如图3,⊙⊙F=⊙F,⊙FAD=⊙FBC,⊙⊙FDA⊙⊙FCB;故⊙正确;⊙如图4,连接CD,由⊙知:⊙FCD=⊙ABD,又⊙⊙F=⊙F,⊙⊙FCD⊙⊙FBA,⊙FC FD FB FA=,由AC=FC=4,DF=3,可求:AF=8,FB=323,⊙BD=BF-DF=233,⊙直径AG⊙BD,⊙DH=233,⊙FG=416,⊙cosF=FGAF=4148,故⊙正确.故选C.考点:圆的综合题.12.B【分析】经过半径的外端并且垂直于这条半径的直线是圆的切线,所以A不正确;三角形的内切圆的圆心是三个内角平分线的交点,而交点只有一个,所以B是对的;一个图形绕中心旋转180度能与自身重合则称此图形为中心对称图形,正五边形不是,所以C不正确;三角形的内心是三个内角平分线的交点,根据角平分线上的点的特点,D是错误的.【详解】解:A.经过半径的外端并且垂直于这条半径的直线是圆的切线,故A错误;B.三角形的内切圆的圆心是三个内角平分线的交点,而交点只有一个,故B正确;C.一个图形绕中心旋转180度能与自身重合则称此图形为中心对称图形,正五边形不是,故C错误;D.三角形的内心是三个内角平分线的交点,到三边的距离相等,故D错误.故选B.【点睛】本题考查了圆的切线的判定,三角形的内心及轴对称和中心对称的概念,要求学生对这些概念熟练掌握.13.C【分析】由已知条件易求AB的长,和圆的半径4比较大小即可得知与BC的位置关系.【详解】⊙⊙C =30°,⊙B =90°,AC =8,⊙AB =12AC =4. ⊙以点A 为圆心,半径为4画圆,⊙d =r ,即以点A 为圆心,半径为4的圆与BC 的位置关系是相切.故选C .【点睛】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.14.B【分析】弦AB 垂直平分OC 于点D ,得OD=3,由勾股定理得AD ,由垂径定理得AB=2AD ,可得答案.【详解】⊙⊙O 的半径长6cm ,弦AB 垂直平分OC ,⊙OD=3,由勾股定理得:,⊙OC 过O ,OC⊙AB ,⊙AB=2AD=,故选B .【点睛】本题主要考查了垂径定理,勾股定理,利用弦AB 垂直平分OC 得OD 是解答此题的关键.15.B【分析】从图中可以看出在AB 边,翻转的第一次是一个120度的圆心角,半径是1,第二次是以点P 为圆心,所以没有路程,同理在AC 和BC 上也是相同的情况,由此求解即可.【详解】解:从图中可以看出在AB 边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=1201180⨯π,第二次是以点P 为圆心,所以没有路程,在BC 边上,第一次1201180⨯π,第二次同样没有路程,AC 边上也是如此,点P 运动路径的长为1201180⨯π×3=2π. 故选:B .【点睛】本题主要考查了等边三角形的性质,求弧长,解题的关键在于能够根据题意得到P 点的运动轨迹.16.B【分析】由⊙O 2上的点P 运动的路径长=点O 2运动的路径长可求解.【详解】解:⊙⊙O 2沿着其边缘滚动回到原来位置后运动终止,⊙⊙O 2上的点P 运动的路径长=点O 2运动的路径长,⊙⊙O 2上的点P 运动的路径长=2π(1+1)=4π故选:B .【点睛】本题考查了轨迹问题,掌握⊙O 2上的点P 运动的路径长=点O 2运动的路径长是本题的关键.17.B【分析】根据近似数3.60万精确到百位可判断⊙,根据三角形的外心是三角形外接圆的圆心,是三角形三边中垂线的交点,锐角三角形在形内,直角三角形在斜边中点上,钝角三角形在形外可判断⊙,根据两直线平行,内错角相等可判断⊙; 90°的圆周角性质可判断⊙,函数y =0,可判断⊙即可得出答案.【详解】解:⊙近似数3.60万精确到百位,故⊙近似数3.60万精确到百分位错误; ⊙三角形的外心是三角形外接圆的圆心,是三角形三边中垂线的交点,锐角三角形在形内,直角三角形在斜边中点上,钝角三角形在形外,故⊙三角形的外心一定在三角形的外部错误;⊙两直线平行,内错角相等;故⊙内错角相等错误;⊙90°的圆周角性质是90°的圆周角所对的弦是直径,故⊙90°的角所对的弦是直径不正确;;⊙函数y = 2010x x +≥⎧⎨-≠⎩, 解得2x ≥-且1x ≠,⊙函数y =x 的取值范围是2x ≥-且1x ≠正确. 正确的个数有一个⊙.故选择:B .【点睛】本题考查基本技能,精确度,三角形外心,内错角,90°圆周角的性质,函数的自变量取值范围,熟练掌握精确度,三角形外心,内错角,90°圆周角的性质,函数的自变量取值范围是解题关键.18.B【分析】根据垂径定理和正多边形的相关知识判断.【详解】解:A 、错误.因为一条弦对应着两条弧;B 、正确.只有垂直于弦的直径才能平分弦;C 、错误.正多边形的中心是它的外接圆的圆心;D 、错误.各边相等的圆外切多边形不一定是正多边形,因为角不一定相等.故选:B.【点睛】本题比较复杂,涉及到垂径定理,圆心角、弧、弦的关系,正多边形和圆的关系,是中学阶段的难点.19.C【分析】设扇形的半径为Rcm ,求出扇形的弧长为(30-2R )cm ,根据扇形的面积是56cm 2得出12R (30-2R )=56,求出即可. 【详解】解:设扇形的半径为R ,⊙扇形周长是30cm ,⊙扇形的弧长为(30-2R )cm ,⊙扇形的面积是56cm 2, ⊙12R (30-2R )=56,解得:R=7或8,故答案为C .【点睛】本题考查了扇形的面积的有关应用,注意:扇形的面积等于弧和半径积的一半. 20.D【分析】连接AD ,根据等边三角形的性质得到3AD AB ==,60ADB ∠=︒,根据勾股定理得到AC =【详解】解:连接AD ,3AB BD ==,60ABC ∠=︒,ABD ∴是等边三角形,3AD AB ∴==,60ADB ∠=︒,6BC =,3CD ∴=,AD CD ∴=,C CAD ∴∠=∠,60C CAD ADB ∠+∠=∠=︒,30C ∴∠=︒,90BAC ∴∠=︒,AC ∴=∴图中阴影部分的面积2160313332360222AB AC πππ⋅⨯=⋅-=⨯⨯=, 故选:D .【点睛】本题考查了扇形面积公式,等边三角形的判定和性质,直角三角形的性质,勾股定理,推出ABD △是等边三角形是解题的关键.21.5【详解】如图,OC 是弦AB 的弦心距,⊙AC =116322AB =⨯=,⊙5OA =.22.2【分析】过O 点作半径OD⊙AB 于E ,如图,由垂径定理得到AE =BE =4,再利用勾股定理计算出OE ,然后即可计算出DE 的长.【详解】解:过O 点作半径OD⊙AB 于E ,如图,⊙AE =BE =12AB =12×8=4,在Rt⊙AEO 中,OE 3,⊙ED =OD ﹣OE =5﹣3=2(m ),答:筒车工作时,盛水桶在水面以下的最大深度为2m .故答案为:2.【点睛】本题考查了垂径定理,垂直于弦的直径平分弦,并且平分弦所对的两条弧,能熟练运用垂径定理是解题的关键.23.8【详解】试题分析:⊙扇形的圆心角为90°半径为32cm ,⊙根据扇形的弧长公式,扇形的弧长为()9032=16cm 180ππ⋅⋅. ⊙圆锥的底面周长等于它的侧面展开图的弧长,⊙根据圆的周长公式,得2r=16ππ,解得()r=8cm .24.25°【分析】首先设半圆的圆心为O ,连接OA ,OB ,由A 点的读数为80°,B 点的读数为30°,即可求得圆心角⊙AOB 的度数,又由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得⊙ACB 的大小.【详解】解:设半圆的圆心为O ,连接OA ,OB ,⊙A 点的读数为80°,B 点的读数为30°,⊙⊙AOB=80°-30°=50°, ⊙⊙ACB=12⊙AOB=25°.故答案为:25°.【点睛】此题考查了圆周角定理.此题难度不大,正确的作出辅助线是解题的关键.25.4【分析】连接AI,BI,由点I为⊙ABC的内心,得到AI平分⊙CAB,根据角平分线的定义得到⊙CAI=⊙BAI.根据平移的性质得到AC⊙DI,由平行线的性质和等角对等边得到AD=DI,BE=EI,根据三角形的周长公式进行计算即可得到答案.【详解】解:连接AI,BI,⊙点I为⊙ABC的内心,⊙AI平分⊙CAB,⊙⊙CAI=⊙BAI.由平移得:AC⊙DI,⊙⊙CAI=⊙AID.⊙⊙BAI=⊙AID,⊙AD=DI.同理可得:BE=EI,⊙⊙DIE的周长=DE+DI+EI=DE+AD+BE=AB,因为4AB ,即图中阴影部分的周长为4.故答案为:4.【点睛】本题考查角平分线的定义、平移的性质、等腰三角形的判定和平行线的性质,解题的关键是掌握角平分线的定义、平移的性质和平行线的性质和等角对等边.26.1【分析】根据两圆内切,圆心距等于半径之差.【详解】解:⊙⊙O1和⊙O2的半径长分别为3和4,⊙O1和⊙O2内切,⊙圆心距O1O2的长=4﹣3=1,故答案为:1.【点睛】本题考查了圆与圆的位置关系,掌握圆与圆之间的位置关系是解题的关键.27.255cmπ【分析】首先求得底面的周长、面积,利用勾股定理求得圆锥的母线长,然后利用扇形的面积公式即可求得圆锥的侧面积,加上底面面积就是表面积.【详解】解:底面周长是2×5π=10πcm,底面积是:5²π=25πcm².(cm),则圆锥的侧面积是:12×10π×6=30π(cm²),则圆锥的表面积为25π+30π=55π(cm²).故答案为:255cmπ.【点睛】本题考查了圆锥的计算,勾股定理,圆的面积公式,圆的周长公式和扇形面积公式求解.注意圆锥表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2的应用.28.30【分析】由在⊙O中,AB为直径,根据直径所对的圆周角是直角,可求得⊙ADB=90°,又由圆周角定理,可求得⊙ACD=⊙B=90°-⊙BAD,继而求得答案.【详解】⊙在⊙O中,AB为直径,⊙⊙ADB=90°,⊙⊙ACD=⊙B=90°-⊙BAD=30°,故答案为:30.【点睛】此题考查了圆周角定理.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角.29.30【分析】根据正多边形的中心角公式:360n计算即可【详解】正十二边形的中心角是:360°÷12=30°.故答案为30.【点睛】本题的关键是掌握正多边形中心角的计算公式30.70【分析】根据圆周角定理即可求出.【详解】⊙⊙D =35°,⊙⊙AOB =2⊙D =70°,故答案为70【点睛】本题考查了圆周角定理:在同圆和等圆中,同弧所对的圆心角是圆周角的2倍.31【分析】过点A 作AF BD ⊥,垂足为F ,过点A 作AE CD ⊥,交CD 的延长线于点E ,根据已知易证ADB ADE ∠=∠,从而证明证明AFD AED △≌△,可得,DF DE AF AE ==,然后再证明Rt Rt BAF CAE ≌,可得BF CE =,最后进行计算即可求出DF ,从而求出,,BF AF AD ,即可解答.【详解】解:过点A 作.AF BD ⊥,垂足为F ,过点A 作AE CD ⊥,交CD 的延长线于点E ,⊙AB AC =,⊙ABC ACB ∠=,⊙四边形ABCD 是圆内接四边形,⊙180ABC ADC ∠+∠=︒,⊙180ADC ADE ∠+∠=︒,⊙ABC ADE ∠=∠,⊙ADB ACB ∠=∠,⊙ADB ADE ∠=∠,⊙90,AFD AED AD AD ∠=∠=︒=,⊙(AAS)AFD AED ≌,⊙.,DF DE AF AE ==,⊙90AFB AEC ∠=∠=︒,⊙Rt Rt (HL)BAF CAE ≌,⊙.BF CE =,⊙BD DF CD DE -=+,⊙107DF DE -=+, ⊙32DF DE ==, ⊙3171022BF BD DF =-=-=,⊙AF ===⊙AD = ⊙AD【点睛】本题考查了全等三角形的判定与性质,圆内接四边形的性质,勾股定理,圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.32.或(或(1,-1)或(1,-1)-【分析】根据圆与直线的位置关系可知,当⊙P 与x 轴相切时,P 点的纵坐标为1或-1,把1或-1代入到抛物线的解析式中求出横坐标即可.【详解】⊙⊙P 的半径为1,⊙当⊙P 与x 轴相切时,P 点的纵坐标为1或-1.当1y =时,221y x =-=,解得x =,⊙此时P 的坐标为或(;当1y =-时,221y x =-=-,解得1x =± ,⊙此时P 的坐标为(1,1)-或(1,1)--;故答案为:或(或(1,-1)或(1,-1)-.【点睛】本题主要考查直线与圆的位置关系和已知函数值求自变量,根据圆与x 轴相切找到点P的纵坐标的值是解题的关键.33.(﹣2,﹣1)【分析】根据外心的定义作图即可.【详解】如图:分别作AC与AB的垂直平分线,相交于点O,则点O即是该圆弧所在圆的圆心.⊙点A的坐标为(﹣3,2),⊙点O的坐标为(﹣2,﹣1).【点睛】本题考查了三角形外心,熟练掌握外心的定义,准确求作线段的垂直平分线是解题的关键.34.8【详解】连接OC,因为AE=8,BE=2,所以AB=10,则OB=12AB=5,所以OE=OB-BE=5-2=3,在Rt⊙OEC中,由勾股定理可得:CE4=,则CD=8,故答案为:8.35.【详解】解:设圆的圆心是O,连接OD,作DE⊙AB于E,OF⊙AC于F.根据题意知,⊙OF⊙AC,⊙AF=12AC=3,⊙⊙CAD=⊙BAD,⊙CD BD=,⊙点D是弧BC的中点.⊙⊙DOB=⊙OAC=2⊙BAD,在⊙AOF和⊙OED中,⊙⊙OFA=⊙OED,⊙FAO=⊙EDO,AO=DO,⊙⊙AOF⊙⊙OED(AAS),⊙OE=AF=3,⊙DO=5,⊙DE=4,=故答案为【点睛】本题考查翻折变换(折叠问题);勾股定理.36.18cm , 31cm .【分析】如图,延长OK 交线段MF 于点1M ,延长PQ 交BC 于点G ,交FN 于点2N ,设圆孔半径为r .根据勾股定理,得222BH KH BK +=.从而得16r =.根据题意知,12111122ON KN AB OM KM r CB ===+=,.则根据图中相关线段间的和差关系求得CN =QH -QN 2=44-26=18, AM =BC -PD -KM 1=130-50-49=31 ( cm).【详解】解:作辅助线如图所示,设圆孔半径为r ,根据勾股定理,得222BH KH BK +=.⊙()()2221305044100r -++=, 16r ∴=.按题意要求,切割后,以圆O 为中心,到两对边的距离相等, 即:12111122ON KN AB OM KM r CB ===+=,. ⊙21422KN AB ==, ⊙ QN 2+r =42,即QN 2=42-16=26.⊙CN =QH -QN 2=44-26=18.又⊙112KM r CB +=,即 11161302KM +=⨯, ⊙ KM 1=49.⊙AM =BC -PD -KM 1=130-50-49=31.⊙CN =18cm ,AM =31cm .故答案为:18cm ,31cm【点睛】本题考查了矩形、直角三角形及圆等相关知识,将实际问题转化为数学问题经验,利用图形变换思想是解题的关键,体现了数学思想方法在现实问题中的应用价值. 37.52π 【分析】每个扇形的圆心角是50°,半径为3,根据扇形面积计算公式计算即可.【详解】⊙菱形ABCD,⊙AD∥BC,OA=OC=12AC=3,⊙⊙ACB=⊙EAO=50°,⊙阴影部分的面积为50952=3602ππ⨯⨯⨯,故答案为:52π.【点睛】本题考查了菱形的性质,扇形的面积公式,熟练掌握菱形的性质,灵活运用扇形面积公式是解题的关键.38.1##1-+【分析】由题意根据“瓜豆原理-主从联动”可得Q的点轨迹也是一个圆,找到此圆即可解决问题.【详解】解:如图,取点M(2,-2),连接AM,MQ、PB,⊙⊙MAB=⊙QAP=90°,⊙⊙MAQ=⊙BAP,⊙12 AM AQAB AP==,⊙⊙MAQ⊙⊙BAP,⊙MQ=12PB=1,⊙Q点在以M为圆心,以1为半径的圆上,由图象可得:DQ的最小值为:DM-MQ,AD=OD-OA=6+2-2=6,由勾股定理可得:DM =⊙DQ 的最小值等于:故答案为:.【点睛】本题考查轨迹圆问题,熟悉掌握利用相似三角形的性质解决动点的轨迹是快速解题的关键.39. 245R 【分析】利用全等三角形的性质证明OM =ON ,设OM =ON =m ,则MQ =2m ,求出OQ ,可得结论. 再证明⊙AME ⊙⊙DMB ,可得AM EM DM BM,由此构建关系式,可得结论. 【详解】解:如图,连接OP .⊙四边形MNPQ 是正方形,⊙⊙OMQ =⊙ONP =90°,MQ =PN ,⊙OQ =OP ,⊙Rt ⊙OMQ ⊙Rt ⊙ONP (HL ),⊙OM =ON , 设OM =ON =m ,则MQ =2m ,225OQOM MQ m , ⊙sin⊙AOQ =22555MQ m OQ m . ⊙AB =2R ,⊙OA =OB =OQ =R ,⊙QM =2MO , ⊙525sin ,55R R OM OQ AOQ MQ ,55555,,555RAM R R BM R⊙AB 是直径,⊙⊙ACB =⊙DCE =90°,⊙⊙CED =⊙AEM ,⊙⊙A =⊙D ,⊙⊙AME =⊙DMB =90°,⊙⊙AME ⊙⊙DMB ,⊙ AM EM DM BM, 255554.555R DM EMR R245R 【点睛】本题考查了圆周角定理,全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,解直角三角形等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.40.⊙⊙【分析】根据圆周角定理,弧、弦、圆心角的关系定理,相似三角形的判定方法,以及其他与圆有关的性质及定理即可判断.【详解】⊙由作图可知,以M 为圆心,BC 为直径的半圆是Rt⊙ABC 的外接圆, ⊙⊙BAC=90°,⊙⊙BAC 是直径所对的圆周角,⊙点A 在半圆M 上,故⊙正确;⊙由分别以B ,C 为圆心,BA ,CA 为半径作弧,两弧交于点D 可知,CA 、CD 是以圆C 的半径,⊙AC=CD ,故⊙正确; ⊙⊙AC 在以M 为圆心、BM 为半径的圆中,CD 在以G 为圆心,以CG 为半径的圆中, ⊙AC CD ,故⊙错误;。
初三数学圆典型难题及答案
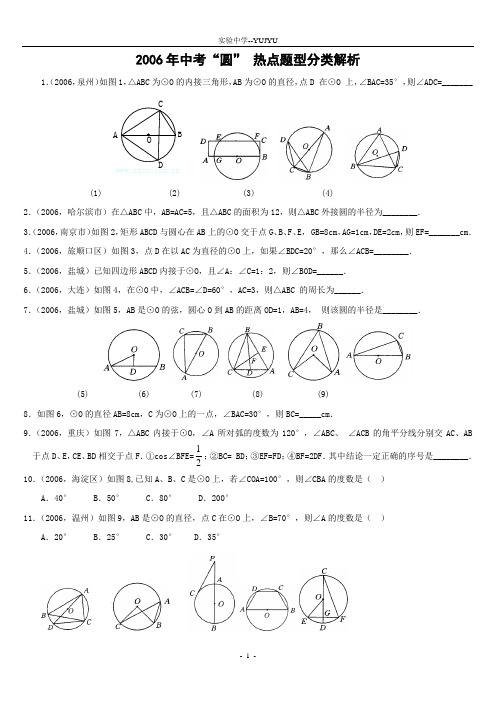
2006年中考“圆” 热点题型分类解析1.(2006,泉州)如图1,△ABC 为⊙O 的内接三角形,AB 为⊙O 的直径,点D•在⊙O 上,∠BAC=35°,则∠ADC=_______BA(1) (2) (3) (4)2.(2006,哈尔滨市)在△ABC 中,AB=AC=5,且△ABC 的面积为12,则△ABC 外接圆的半径为________.3.(2006,南京市)如图2,矩形ABCD 与圆心在AB 上的⊙O 交于点G 、B 、F 、E ,•GB=8cm ,AG=1cm ,DE=2cm ,则EF=_______cm .4.(2006,旅顺口区)如图3,点D 在以AC 为直径的⊙O 上,如果∠BDC=20°,那么∠ACB=________.5.(2006,盐城)已知四边形ABCD 内接于⊙O ,且∠A :∠C=1:2,则∠BOD=______.6.(2006,大连)如图4,在⊙O 中,∠ACB=∠D=60°,AC=3,则△ABC•的周长为______.7.(2006,盐城)如图5,AB 是⊙O 的弦,圆心O 到AB 的距离OD=1,AB=4,•则该圆的半径是________.(5) (6) (7) (8) (9)8.如图6,⊙O 的直径AB=8cm ,C 为⊙O 上的一点,∠BAC=30°,则BC=_____cm .9.(2006,重庆)如图7,△ABC 内接于⊙O ,∠A 所对弧的度数为120°,∠ABC 、•∠ACB 的角平分线分别交AC 、AB 于点D 、E ,CE 、BD 相交于点F .①cos ∠BFE=12;②BC=•BD ;③EF=FD ;④BF=2DF .其中结论一定正确的序号是________. 10.(2006,海淀区)如图8,已知A 、B 、C 是⊙O 上,若∠COA=100°,则∠CBA 的度数是( )A .40°B .50°C .80°D .200°11.(2006,温州)如图9,AB 是⊙O 的直径,点C 在⊙O 上,∠B=70°,则∠A 的度数是( )A .20°B .25° C.30° D .35°(10) (11) (12) (13) (14)12.(2006,陕西)如图10,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接CD ,若⊙O 的半径r=32,AC=2,则cosB 的值是( )A .32BCD .2313.(2006,浙江)如图11,A 、B 、C 是⊙O 上的三点,∠BAC=45°,则∠BOC•的大小是( )A .90°B .60°C .45°D .22.5°14.(2006,浙江台州)我们知道,“两点之间线段最短”,“直线外一点与直线上各点连线的所有线段中,垂线段最短”.在此基础上,人们定义了点与点的距离,•点到直线的距离.类似地,如图12,若P 是⊙O 外一点,直线PO 交⊙O 于A 、B 两点,PC•切⊙O 于点C ,则点P 到⊙O 的距离是( )A .线段PO 的长度;B .线段PA 的长度;C .线段PB 的长度;D .线段PC 的长度15.(2006,绵阳)如图13,AB 是⊙O 的直径,BC 、CD 、DA 是⊙O 的弦,且BC=CD=•DA ,则∠BCD=( )A .100°B .110°C .120°D .135°16.(2006,重庆)如图14,⊙O 的直径CD 过弦EF 的中点G ,∠EOD=40°,•则∠DCF 等于( )A .80°B .50°C .40°D .20°17.(2006,广安)用一把带有刻度尺的直角尺,①可以画出两条平行的直线a•和b ,如 图(1);②可以画出∠AOB 的平分线OP ,如图(2);•③可以检验工件的凹面是否为半圆,如图(3);④可以量出一个圆的半径,如图(4).这四种说法正确的有( )A .4个B .3个C .2个D .1个18.(2006,攀枝花)图16中∠BOD 的度数是( )A .55°B .110°C .125°D .150°(16) (17) (18)19.(2006,攀枝花)如图17,AB是⊙O的直径,弦AC、BD相交于点E,则CDAB等于()A.tan∠AED B.cot∠AED C.sin∠AED D.cos∠AED20.(2006,浙江舟山)如图18已知A、B、C是⊙O上的三点,若∠ACB=44°,•则∠AOB的度数为()A.44° B.46° C.68° D.88°21.(2006,浙江台州)如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,•交边BC于点E,连结BD.(1)根据题设条件,请你找出图中各对相似的三角形;(2)请选择其中的一对相似三角形加以证明.22.(2006,黄冈)如图,AB,AC分别是⊙O的直径和弦,点D为劣弧AC上一点•弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过点C的切线交ED的延长线于点P.(1)若PC=PF;求证:AB⊥ED.(2)点D在劣弧AC的什么位置时,才能使AD=DE.DF,为什么?23.(2006,广东课改区)如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE 与OF的数量关系,并给予证明.24.(2006,上海市)本市新建的滴水湖是圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,•并测得BC长为240米,A到BC的距离为5米,如图所示,•请你帮他们求出滴水湖的半径.1.(2006,温州)已知∠ABC=60°,点O在∠ABC的平分线上,OB=5cm,以O为圆心,•3cm为半径作圆,则⊙O与BC 的位置关系是________.2.(2006,大连)如图1,AB是⊙O的切线,OB=2OA,则∠B的度数是_______.(1)(2)(3)3.(2006,天津)已知⊙O中,两弦AB和CD相交于点P,若AP:PB=2:3,CP=2cm,DP=•12cm,则弦AB的长为_______cm.4.(2006,天津)如图2,已知直线CD与⊙O相切于点C,AB为直径,若∠BCD=•40°,则∠ABC的大小等于_______(度).5.(2006,上海市)已知圆O的半径为1,点P到圆心O的距离为2,过点P•作圆的切线,那么切线长是________.6.(2006,哈尔滨)如图3,PB为⊙O的切线,B为切点,连结PO交⊙O于点A,PA=2,PO=5,则PB的长为()A.4 B. D.7.(2006,旅顺口区)如图4,AB与⊙O切于点B,AO=6cm,AB=4cm,则⊙O•的半径为()A...(4)(5)(6)8.(2006,浙江绍兴)如图5,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC•与AB的延长线交于点P,那么∠P等于()A.15° B.20° C.25° D.30°9.(2006,浙江台州)如图6,已知⊙O中弦AB,CD相交于点P,AP=6,BP=2,CP=•4,则PD的长是()A.6 B.5 C.4 D.310.(2006,重庆)⊙O的半径为4,圆心O到直线L的距离为3,则直线L与⊙O•的位置关系是()A.相交 B.相切 C.相离 D.无法确定11.(2006,白云区)如图,A是⊙O外一点,B是⊙O上一点,AO•的延长线交⊙O 于点C,连结BC,∠C=22.5°,∠A=45°.求证:直线AB是⊙O的切线.12.(2006,陕西)如图,⊙O的直径AB=4,∠ABC=30°,D是线段BC•的中点.(1)试判断点D与⊙O的位置关系,并说明理由;(2)过点D作DE⊥AC,垂足为点E,求证直线DE是⊙O的切线.13.(2006,攀枝花)如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=•80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.14.(2006,绵阳)已知在Rt△ABC中,AD是∠BAC的角平分线,以AB上一点O•为圆心,AD为弦作⊙O.(1)在图中作出⊙O;(不写作法,保留作图痕迹)(2)求证:BC为⊙O的切线;(3)若AC=3,tanB=34,求⊙O的半径长.15.(2006,天津)如图,已知⊙O的割线PAB交⊙O于A、B两点,PO与⊙O•交于点C,且PA=AB=6cm,PO=12cm.(1)求⊙O的半径;(2)求△PBO的面积.(结果可带根号)16.(2006,海淀区)如图,在⊙O中,弦AC与BD交于E,AB=6,AE=8,ED=4,•求CD的长.17.(2006,盐城)如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB•于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.(1)求证:点F是BD中点;(2)求证:CG是⊙O的切线;(3)若FB=FE=2,求⊙O的半径.1.(2006,攀枝花市)如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O 于B、C,则BC=_______.2.(2006,淄博市)要在一个矩形纸片上画出半径分别是4cm和1cm•的两个外切圆,该矩形长的最小值是_______.3.(2006,哈尔滨)已知⊙O与⊙O半径的长是方程x2-7x+12=0的两根,且O1O2=12,则⊙O1与⊙O2的位置关系是()A.相交 B.内切 C.内含 D.外切4.(2006,白云山区)已知两圆的半径分别为1和4,圆心距为3,则两圆的位置关系是()A.外离 B.外切 C.相交 D.内切5.(2006,南安市)已知⊙O1和⊙O2的半径分别为2cm和3cm,两圆的圆心距是1cm,则两圆的位置关系是() A.外离 B.外切 C.相交 D.内切6.(2006,烟台市)已知:关于x的一元二次方程x2-(R+r)x+14d2=0无实数根,其中R、•r分别是⊙O1、⊙O2的半径,d为此两圆的圆心距,则⊙O1,⊙O2的位置关系为()A.外离 B.相切 C.相交 D.内含7.(2006,哈尔滨市)下列命题中,正确命题的个数是()①垂直于弦的直径平分这条弦;②平行四边形对角互补;③有理数与数轴上的点是一一对应的;④相交两圆的公共弦垂直平分两圆的连心线.A.0个 B.1个 C.2个 D.3个8.(2006,浙江)如果两圆半径分别为3和4,圆心距为8,那么这两圆的位置关系是()A.内切 B.相交 C.外离 D.外切9.(2006,广安)若⊙A和⊙B相切,它们的半径分别为8cm和2cm,则圆心距AB为( • )A.10cm B.6cm C.10cm或6cm D.以上都不对10.(2006,攀枝花)在等边三角形、正五边形、正六边形、正七边形中,既是轴对称又是中心对称的图形是() A.等边三角形 B.正五边形 C.正六边形 D.正七边形11.(2006,哈尔滨市)已知:如图,⊙O1与⊙O2外切于点P,经过⊙O1上一点A•作⊙O1的切线交⊙O2于B、C两点,直线AP交⊙O2于点D,连结DC、PC.(1)求证:D C2=DP·DA;(2)若⊙O1与⊙O2的半径之比为1:2,连结BD,,PC=12,求AB的长.12.(2006,成都)已知:如图,⊙O与⊙A相交于C、D两点,A、O分别是两圆的圆心,△ABC内接于⊙O,弦CD交AB 于点G,交⊙O的直径AE于点F,连结BD.(1)求证:△ACG∽△DBG;(2)求证:AC2=AC·AB;(3)若⊙A、⊙O的直径分别为15,且CG:CD=1:4,求AB和BD的长.13.(2006,盐城)已知:AB为⊙O的直径,P为AB弧的中心.(1)若⊙O′与⊙O外切于点P(见图甲),AP、BP的延长线分别交⊙O′于点C、D,•连接CD,则△PCD是________.(2)若⊙O′与⊙O相交于点P、Q(见图乙),连接AQ、BQ并延长分别交⊙O•′于点E、F,请选择下列两个问题中的一个作答:问题1:判断△PEF的形状,并证明你的结论;问题2:判断线段AE与BF的关系,并证明你的结论.我选择问题______,结论:___________.证明:1.(2006,浙江)如图1,圆锥的底面半径为6cm,高为8cm,•那么这个圆锥的侧面积是________c m2.(1)(2)(3)(4)2.(2006,泉州)已知圆柱的底面半径为2cm,母线长为3cm,•则该圆柱的侧面展开图的面积为_____cm2.3.(2006,黄冈)如图2,将边长为8cm的正方形ABCD的四边沿直线L向右滚动(不滑动),当正方形滚动两周时,正方形的顶点A所经过的路线的长是_____cm.4.(2006,广州)如图3,从一块直径为a+b的圆形纸板上挖去直径分别为a•和b 的两个圆,则剩下的纸板面积为________.5.(2006,旅顺口)若圆锥的底面周长为20 ,•侧面展开后所得扇形的圆心角为120°,则圆锥的侧面积为________.6.(•2006,•晋江)•若圆锥的底面半径为3,•母线长为8,•则这个圆锥的全面积是_____平方单位.7.(2006,哈尔滨市)已知矩形ABCD的一边AB=5cm,另一边AD=3cm,则以直线AB•为轴旋转一周所得到的圆柱的表面积为______c m2.8.(2006,晋江)正十二边形的每一个外角等于______度.9.(2006,黄冈)已知圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径长的比是________.10.(2006,广东课改实验区)如图4,已知圆柱体底面圆的半径为2π,高为2,•AB 、CD 分别是两底面的直径,AD 、BC 是母线.若一只小虫从A 点出发,从侧面爬地到C 点,则小虫爬行的最短路线的长度是_______(结果保留根式).11.(2006,广安)将一个弧长为12πcm ,半径为10cm 的扇形铁皮围成个圆锥形容器(不计接缝),那么这个圆锥形容器的高为_______cm .12.(2006,•重庆)•圆柱的底面周长为2π,•高为1,•则圆柱的侧面展开图的面积为______.13.(•2006,•浙江舟山)•已知正六边形的外接圆的半径是a ,•则正六边形周长是_____.14.(2006,浙江台州)如图5,已知圆锥的母线长为5cm ,底面半径为3cm ,则此圆锥的侧面积为( )A .15πcm 2B .20πcm 2C .12πcm 2D .30πcm 2(5) (6) (7)15.(2006,浙江)在△ABC 中,斜边AB=4,∠B=60°,将△ABC 绕点B 旋转60°,•顶点C 运动的路线长是( )A .24 (333)B C D ππππ 16.(2006,成都)如图6,小丽要制作一个圆锥模型,要求圆锥的母线长9cm ,•底面圆的直径为10cm ,•那么小丽要制作的这个圆锥模型的侧面展开扇形的纸片的圆心角度数是( )A .150°B .200°C .180°D .240°17.(2006,广州)一个圆柱的侧面展开图是相邻边长分别为10和16的矩形,•则该圆柱的底面圆半径是( )A .58581016...B C D ππππππ或或18.(2006,天津)若同一个圆的内接正三角形、正方形、正六边形的边心距分别为r 3,r 4,r 6,则r 3:r 4:r 6等于( )A .1:1 C .1:2:3 D .3:2:119.(2006,青岛市)如图7,在△ABC 中,BC=4,以点A 为圆心、2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交AC 于F ,点P 是⊙A 上的一点,且∠EPF=40°,则图中阴影部分的面积是( )A .4-49πB .4-89πC .8-49πD .8-89π 20.(2006,南安)如图,半圆M 的直径AB 为20cm ,现将半圆M 绕着点A 顺时针旋转180°.(1)请你画出旋转后半圆M 的图形;(2)求出在整个旋转过程中,半圆M 所扫过区域的面积(结果精确到1c m 2)21.(2006,海淀区)如图,已知⊙O 的直径AB 垂直弦CD 于E ,连结AD ,BD ,OC ,•OD ,且OD=5,(1)若sin ∠BAD=35,求CD 的长; (2)若∠ADO :∠EDO=4:1,求扇形OAC (阴影部分)的面积(结果保留π).22.(2006,烟台市)如图a ,O 为圆柱形木块底面的圆心,过底面的一条弦AD ,•沿母线AB 剖开,得剖面矩形ABCD ,AD=24cm ,AB=25cm ,若AmD 的长为底面周长的23,•如图b 所示. (1)求⊙O 的半径;(2)求这个圆柱形木块的表面积.(结果可保留π和根号)(a ) (b )23.(2006,攀枝花市)如图,圆锥的底面半径r=3cm ,高h=4cm ,求这个圆锥的表面积(π取3.14).1.(2006,福建泉州)如图,已知O 为原点,点A 的坐标为(4,3),⊙A•的半径为2,过A 作直线L 平行于x 轴,点P 在直线L 上运动.(1)当点P 在⊙O 上时,请你直接写出它的坐标;(2)设点P的横坐标为12,试判断直线OP与⊙A的位置关系,并说明理由.2.(2006,广安市)已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于点E.(1)求证:DE⊥BC;(2)如果CD=4,CE=3,求⊙O的半径.3.(2006,广安市)如图,已知AB是⊙O的直径,直线L与⊙O相切于点C且AC AD,弦CD交AB于E,BF⊥L,垂足为F,BF交⊙O于G.(1)求证:CE2=FG·FB;(2)若tan∠CBF=12,AE=3,求⊙O的直径.4.(2006,苏州市)如图①,△ABC内接于⊙O,且∠ABC=∠C,点D在弧BC•上运动,过点D作DE∥BC,DE交直线AB 于点E,连结BD.(1)求证:∠ADB=∠E;(2)求证:A D2=AC·AE;(3)当点D运动到什么位置时,△DBE∽△ADE.请你利用图②进行探索和证明.5.(2006,晋江)街道旁边有一根电线杆AB和一块半圆形广告牌.有一天,•小明突然发现,在太阳光照射下,电线杆的顶端A的影子刚好落在半圆形广告牌的最高处G,•而半圆形广告牌的影子刚好落在地面上一点E,已知BC=5米,半圆形的直径为6米,•DE=2米.(1)求电线杆落在广告牌上的影长(即CG的长度,精确到0.1米).(2)求电线杆的高度.6.(2006,深圳)如图①,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x 轴于A、B两点,交y轴于C、D两点,且C为AE的中点,AE交y轴于G点.若点A•的坐标为(-2,0),AE=8.(1)求点C的坐标;(2)连结MG、BC,求证:MG∥BC;(3)如图②,过点D作⊙M的切线,交x轴于点P.动点F在⊙M的圆周上运动时,OFPF的比值是否发生变化,若不变,求出比值;若变化,请说明变化规律.①②7.(2006,烟台市)如图,从⊙O 外一点A 作⊙O 的切线AB 、AC ,切点分别为B 、C ,且⊙O 直径BD=6,连结CD 、AD . (1)求证:CD ∥AO ;(2)设CD=x ,AO=y ,求y 与x 之间的函数关系式,并写出自变量x 的取值范围;(3)若AO+CD=11,求AB 的长.8.(2006,上海市)已知点P 在线段AB 上,点O 在线段AB 延长线上,以点O 为圆心,•OP 为半径作圆,点C 是圆O 的一点.(1)如图,如果AP=2PB ,PB=BO,求证:△CAO ∽△BCO ;(2)如果AP=m (m 是常数,且m>1),BP=1,OP 是OA 、OB 的比例中项,当点C 在圆O•上运动时,求AC :BC 的值(结果用含m 的式子表示);(3)在(2)的条件下,讨论以BC 为半径的圆B 和以CA 为半径的圆C 的位置关系,并写出相应m 的取值范围.1.(2006,浙江市)在平面直角坐标系xOy 中,直线L 1经过点A (-2,0)和点B (0),•直线L 2的函数表达式为y=-3x+3,L 1与L 2相交于点P .⊙C 是一个动圆,圆心C 在直线L 1上运动,设圆心C 的横坐标是a ,过点C 作CM ⊥x 轴,垂足是点M .(1)填空:直线L 1的函数表达式是________,交点P 的坐标是______,∠FPB•的度数是_______.(2)当⊙C 和直线L 2相切时,请证明点P 到直线CM 的距离等于⊙C 的半径R ,•并写出时a 的值.(3)当⊙C 和直线L 2不相离时,已知⊙C 的半径-2,记四边形NMOB 的面积为S (•其中点N 是直线CM 与L 2的交点),S 是否存在最大值?若存在,求出这个最大值及此时a 的值;若不存在,请说明理由.2.(2006,浙江舟山)如图10-62①,在直角坐标系中,点A 的坐标为(1,0),以OA•为边在第四象限内作等边△AOB ,点C 为x 轴的正半轴上一动点(OC>1),连结BC ,以BC 为边在第四象限内作等边△CBD ,直线DA 交y 轴于点E . (1)试问△OBC 与△ABD 全等吗?并证明你的结论.(2)随着点C 位置的变化,点E 的位置是否发生变化,若没有变化,求出点E 的坐标;若有变化,请说明理由. (3)如图10-62②,以OC 为直径作圆,与直线DE 分别交于点F 、G ,设AG=m ,AF=n ,•用含n 的代数式表示m .圆难题整理:爱我在春天1.如图,BC 是圆O 的直径,AD 垂直BC 于D ,弧BA 等于弧AF ,BF 与AD 交于E , 求证:(1)∠BAD=∠ACB ;(2)AE=BE . 证明:(1)∵BC 是圆O 的直径, ∴∠BAC=90°, ∴∠BAD+∠CAD=90°, 又AD ⊥BC , ∴∠ACB+∠CAD=90°, ∴∠BAD=∠ACB ; (2)∵弧BA 等于弧AF , ∴∠ACB=∠ABF , ∵∠BAD=∠ACB , ∴∠ABF=∠BAD ,∴AE=BE .N所以OC=OB=AC=AB。
(精选)2021-2022学年人教版三年级上册数学竞赛培优专题:寻找隐藏周期(含答案)

2021-2022学年人教版三年级上册数学竞赛培优专题----寻找隐藏周期姓名:___________班级:___________考号:___________一、解答题1.如图,电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈。
现在,一只红跳蚤从标有数“1”的圆圈按顺时针方向跳了100步,落在一个圆圈里。
一只黑跳蚤也从标有数“1”的圆圈起跳,但它是沿着逆时针方向跳了200步,落在另一个圆圈里。
这两个圆圈里的数的乘积是多少?2.钟表上现在时针正对着数字2,那么121小时后时针正对着数字几?3.如图,伸出左手,估后从大拇指起开始数,当数到200的时候,正好数到哪根手指?4.如图,在A,B两地之间有11个站,一辆车不停的往返于两地之间。
从A出发,每天走到下一站,到达B地后的第二天又回到11号站,第1天的时候它在A站,那么第100天时它在哪个站?5.100位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,然后从第二位同学开始,每位同学都把前一位同学所报的数乘以7,再报出乘积的个位来。
请问:第100个同学报的是几?6.同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报6,然后从第二位同学开始,每位同学都把前一位同学所报的数乘2,再报出乘积的个位来。
请问:第50个同学报的是几?7.84位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,第二位同学报3,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来。
请问:最后一名同学报的是几?总共有多少个人报的数是3?8.50位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报4,第二位同学报9,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来。
请问:最后一名同学报的是几?9.甲、乙、丙、丁兄弟四人各收藏一些宝石。
每天早上他们都要聚在一起,重新分配宝石,分配的规则是:拥有宝石最多的人分给其他三人每人1颗。
数学名题:圆圈标数经典系列

[阅读材料] 圆圈标数经典系列在教学过程中一些同类型的题见得多了,可以挖掘一下,整理出来,供读者参考。
现给大家献上在直线与圆圈上写数以及二者之间关系的系列名题。
题目1. 今要在一个圆周上标出一些数,第一次先把圆周二等分,在两个分点旁分别标上3121和,第二次把两段半圆弧二等分,在分点旁标上相邻两分点旁所标两数的和312165+=,第三次把4段圆弧二等分,并在4个分点旁标上相邻两分点旁所标两数的和6531611,6521311+=+=如此继续下去,当第八次标完数以后,圆周上所有已标数的总和是多少? 解析:碰到这样的题,可先把3121和改作A 与B ,整个探索过程不把每一个复杂的和算出,只是数出A 与B 的总个数。
这样第一次为A 与B 和的一倍,第二次后为3A+ 3B ,第三次标完后为9A+9B ,……… 这样能较容易地发现规律:每次新的结果总是原来的3倍。
正是因为增加的每个数都是原来相邻两个数之和,所以每次增加数的总和恰好是原来所有数总和的2倍,也就是说每次标完数后圆周上所有数的总和是前一步标完数后圆周上所有数的总和的3倍,例如:二分之一它在左边算了一次,在右边算了一次,本身一次,所以二分之一在下次标完后已成为原为的3倍了,其它数也是如此。
于是第八次标完数后圆周上所有数的总和是:7111()31822232+⨯=.变化一题目2. 今要在一条线段上标出一些数,第一次在两个端点旁分别标上3121和,第二次把线段二等分,在中点旁标上两边所标两数的和312165+=,第三次把2段线段各二等分,并在2个分点旁标上相邻两分点旁所标两数的和6531611,6521311+=+=,即每次都在已写上的两个相邻数之间,写上这两个相邻数之和,如此继续下去,当第八次标完数以后,线段上所有已标数的总和是多少? 解析:与上题一样先把11和改作A 与B ,次数与A+B 的个数填入下表:这串数有什么规律吗?可以看出后一数总是前一个数的3倍减1,则可算出第八次为:1094个A+B,代入计算可得32911。
把1-10十个数分别填入下图圆圈内,使每个四边形顶点的圆圈内四个数的和都相等,且和最大)
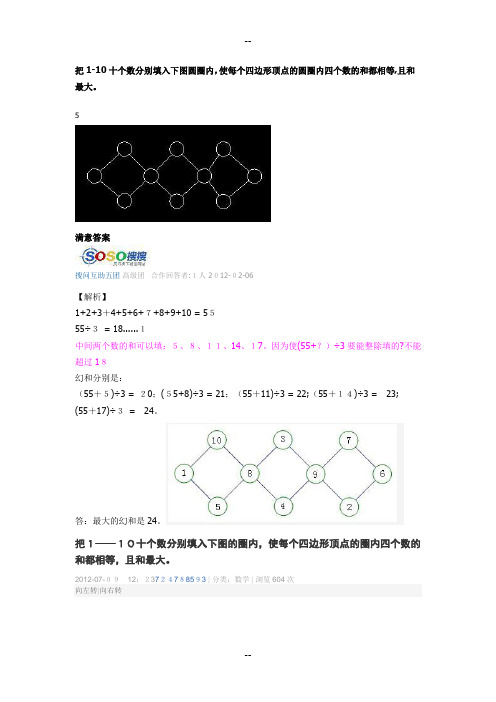
把1-10十个数分别填入下图圆圈内,使每个四边形顶点的圆圈内四个数的和都相等,且和最大。
5满意答案搜问互助五团高级团合作回答者:1人 2012-02-06【解析】1+2+3+4+5+6+7+8+9+10 = 5555÷3= 18......1中间两个数的和可以填:5、8、11、14、17。
因为使(55+?)÷3要能整除填的?不能超过18幻和分别是:(55+5)÷3 = 20;(55+8)÷3 = 21;(55+11)÷3 = 22;(55+14)÷3 =23; (55+17)÷3=24。
答:最大的幻和是24。
把1——10十个数分别填入下图的圈内,使每个四边形顶点的圈内四个数的和都相等,且和最大。
2012-07-0912:23724788593|分类:数学|浏览604次向左转|向右转过程详细清楚明白分享到:2012-07-0912:47提问者采纳..... 2 .. (3)19 710 8ﻫ645ﻫ1----10的和为55ﻫ有两个数加两次ﻫ55+10+9=74不能够被3整除最大只能是72,选10,7这2个数确定后其他就可以添入把1-8这八个数分别填如图中的正方形的各个圆圈中,使正方形每条边上的三个数的和相等满意答案佐手青春↗佑 4级2011-02-241''''''4''''''87'''''''''''''''35''''''6''''''2ﻫﻫ没有太多技巧。
注意角上的四个数。
1到8所有数字之和+ 角上4数之和= 每边之和【四边都相等的】×4ﻫ因此角上4数之和必是4的倍数。
ﻫ挑出角上4数,即可算出边和,验证一下即可1 8 35 76 4 21 83ﻫ57ﻫ6 4 2每一条边之和都是121''''''4''''''87'''''''''''''''35''''''6''''''2 ﻫ没有太多技巧。
(专题精选)初中数学圆的经典测试题及答案解析

(专题精选)初中数学圆的经典测试题及答案解析一、选择题1.如图,点,,A B S 在圆上,若弦AB 的长度等于圆半径的2倍,则ASB ∠的度数是( ).A .22.5°B .30°C .45°D .60°【答案】C【解析】【分析】 设圆心为O ,连接OA OB 、,如图,先证明OAB V 为等腰直角三角形得到90AOB ∠=︒,然后根据圆周角定理确定ASB ∠的度数.【详解】解:设圆心为O ,连接OA OB 、,如图,∵弦AB 的长度等于圆半径的2倍,即2AB OA =,∴222OA OB AB +=,∴OAB V 为等腰直角三角形,90AOB ∠=︒ ,∴1452ASB AOB ∠=∠=°. 故选:C .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.2.如图,已知AB 是⊙O 的直径,CD 是弦,且CD ⊥AB ,BC=3,AC=4,则sin ∠ABD 的值是( )A.43B.34C.35D.45【答案】D【解析】【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC,再根据勾股定理求得AB=5,即可求sin∠ABD 的值.【详解】∵AB是⊙O的直径,CD⊥AB,∴弧AC=弧AD,∴∠ABD=∠ABC.根据勾股定理求得AB=5,∴sin∠ABD=sin∠ABC=45.故选D.【点睛】此题综合考查了垂径定理以及圆周角定理的推论,熟悉锐角三角函数的概念.3.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为()A.3B.36ππC.312πD.48336ππ【答案】C【解析】【分析】易得AD长,利用相应的三角函数可求得∠ABD的度数,进而求得∠EOD的度数,那么一个阴影部分的面积=S△ABD-S扇形DOE-S△BOE,算出后乘2即可.【详解】连接OE,OF.∵BD=12,AD :AB=1:2,∴AD=43 ,AB=83,∠ABD=30°,∴S △ABD =×43×12=243,S 扇形=603616,633933602OEB S ππ⨯==⨯⨯=V ∵两个阴影的面积相等,∴阴影面积=()224369330312ππ⨯--=- .故选:C【点睛】本题主要是理解阴影面积等于三角形面积减扇形面积和三角形面积.4.如图,正方形ABCD 内接于⊙O ,AB=22,则»AB 的长是( )A .πB .32πC .2πD .12π 【答案】A【解析】 【分析】连接OA 、OB ,求出∠AOB=90°,根据勾股定理求出AO ,根据弧长公式求出即可.【详解】连接OA 、OB ,∵正方形ABCD 内接于⊙O ,∴AB=BC=DC=AD ,∴»»»»AB BCCD DA ===, ∴∠AOB=14×360°=90°,在Rt△AOB中,由勾股定理得:2AO2=(22)2,解得:AO=2,∴»AB的长为902 180π´=π,故选A.【点睛】本题考查了弧长公式和正方形的性质,求出∠AOB的度数和OA的长是解此题的关键.5.如图,在扇形OAB中,120AOB∠=︒,点P是弧AB上的一个动点(不与点A、B重合),C、D分别是弦AP,BP的中点.若33CD=,则扇形AOB的面积为()A.12πB.2πC.4πD.24π【答案】A【解析】【分析】如图,作OH⊥AB于H.利用三角形中位线定理求出AB的长,解直角三角形求出OB即可解决问题.【详解】解:如图作OH⊥AB于H.∵C、D分别是弦AP、BP的中点.∴CD是△APB的中位线,∴AB=2CD=63∵OH⊥AB,∴BH=AH=33∵OA=OB,∠AOB=120°,∴∠AOH=∠BOH=60°,在Rt△AOH中,sin∠AOH=AH AO,∴AO=336sin3AHAOH==∠,∴扇形AOB的面积为:2120612360ππ=g g,故选:A.【点睛】本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.6.如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB 相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于()A.20°B.25°C.30°D.32.5°【答案】A【解析】【分析】连接OD,根据三角形内角和定理和等边对等角求出∠DOB=40°,再根据圆周角定理即可求出∠BAD的度数.【详解】解:连接OD,∵OC⊥AB,∴∠COB=90°,∵∠AEC=65°,∴∠OCE=180°﹣90°﹣65°=25°,∵OD=OC,∴∠ODC=∠OCD=25°,∴∠DOC=180°﹣25°﹣25°=130°,∴∠DOB=∠DOC﹣∠BOC=130°﹣90°=40°,∴由圆周角定理得:∠BAD=12∠DOB=20°,故选:A.【点睛】本题考查了圆和三角形的问题,掌握三角形内角和定理、等边对等角、圆周角定理是解题的关键.7.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.4 B.22C.3D.23【答案】B【解析】【分析】根据垂径定理得到CH=BH,»»AC BC=,根据圆周角定理求出∠AOB,根据正弦的定义求出BH,计算即可.【详解】如图BC与OA相交于H∵OA⊥BC,∴CH=BH,»»AC AB=,∴∠AOB=2∠CDA=60°,∴BH=OB⋅sin∠3,∴BC=2BH=23,故选D.【点睛】本题考查的是垂径定理、圆周角定理,熟练掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.8.已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为()A.60πcm2B.65πcm2C.120πcm2D.130πcm2【答案】B【解析】【分析】先利用三视图得到底面圆的半径为5cm,圆锥的高为12cm,再根据勾股定理计算出母线长为13cm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.【详解】根据三视图得到圆锥的底面圆的直径为10cm,即底面圆的半径为5cm,圆锥的高为12cm,所以圆锥的母线长=225+12=13,所以这个圆锥的侧面积=12×2π×5×13=65π(cm2).故选B.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.9.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则⊙O的半径为()A .3B .23C .32D .233【答案】A【解析】连接OC ,∵OA=OC ,∠A=30°,∴∠OCA=∠A=30°,∴∠COB=∠A+∠ACO=60°,∵PC 是⊙O 切线,∴∠PCO=90°,∠P=30°,∵PC=3,∴OC=PC •tan30°=3,故选A10.已知线段AB 如图,(1)以线段AB 为直径作半圆弧»AB ,点O 为圆心;(2)过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、,交»AB 于点E F 、;(3)连接,OE OF .根据以上作图过程及所作图形,下列结论中错误的是( )A .CE DF =B .»»AE BF =C .60EOF ∠=︒D . =2CE CO【答案】D【解析】【分析】 根据作图可知AC CO OD DB ===,据此对每个选项逐一判断即可.【详解】根据HL 可判定ECO FDO ≅V V ,得CE DF =,A 正确;∵过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、,连接AE ,CE 为OA 的中垂线,AE OE =在半圆中,OA OE =∴OA OE AE ==,AEO △为等边三角形,60EOF =o ∠AOE=∠FOD=∠, C 正确;∴圆心角相等,所对应的弧长度也相等,»»AE BF=,B 正确 ∵60,90EOC =o o ∠AOE=∠, ∴=3CE CO ,D 错误【点睛】本题考查了全等三角形的判定和性质,勾股定理等知识点,解题的关键在于证明60o ∠AOE=.11.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,连接OC 交⊙O 于点D ,连接BD ,∠C=40°.则∠ABD 的度数是( )A .30°B .25°C .20°D .15°【答案】B【解析】 试题分析:∵AC 为切线 ∴∠OAC=90° ∵∠C=40° ∴∠AOC=50°∵OB=OD ∴∠ABD=∠ODB ∵∠ABD+∠ODB=∠AOC=50° ∴∠ABD=∠ODB=25°. 考点:圆的基本性质.12.如图,在矩形ABCD 中,6AB =,对角线10AC =,O e 内切于ABC ∆,则图中阴影部分的面积是( )A .24π-B .242π-C .243π-D .244π-【答案】D【解析】【分析】 先根据勾股定理求出BC ,连接OA 、OB 、OC 、过点O 作OH ⊥AB ,OE ⊥BC ,OF ⊥AC ,设O e 的半径为r ,利用面积法求出r=2,再利用三角形ABC 的面积减去圆O 的面积得到阴影的面积.【详解】∵四边形ABCD 是矩形,∴∠B=90°,∵6AB =,10AC =,∴BC=8,连接OA 、OB 、OC 、过点O 作OH ⊥AB ,OE ⊥BC ,OF ⊥AC ,设O e 的半径为r ,∵O e 内切于ABC ∆,∴OH=OE=OF=r , ∵11()22ABC S AB BC AB AC BC r =⋅=++⋅V , ∴1168(6108)22r ⨯⨯=++⋅, 解得r=2,∴O e 的半径为2,∴2168-2224-4ABC O S S S ππ=-=⨯⨯⨯=V e 阴影, 故选:D .【点睛】此题考查矩形的性质,勾股定理,三角形内切圆的定义,阴影面积的求法,添加合适的辅助线是解题的关键.13.如图,点I 是Rt △ABC 的内心,∠C =90°,AC =3,BC =4,将∠ACB 平移使其顶点C 与I 重合,两边分别交AB 于D 、E ,则△IDE 的周长为( )A .3B .4C .5D .7【答案】C【解析】【分析】 连接AI 、BI ,根据三角形的内心的性质可得∠CAI =∠BAI ,再根据平移的性质得到∠CAI =∠AID,AD=DI,同理得到BE=EI,即可解答.【详解】连接AI、BI,∵∠C=90°,AC=3,BC=4,∴AB=22AC BC+=5∵点I为△ABC的内心,∴AI平分∠CAB,∴∠CAI=∠BAI,由平移得:AC∥DI,∴∠CAI=∠AID,∴∠BAI=∠AID,∴AD=DI,同理可得:BE=EI,∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=5故选C.【点睛】此题考查了平移的性质和三角形内心的性质,解题关键在于作出辅助线14.如图,已知⊙O的半径是4,点A,B,C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为()A.8833π-B.16833π-C.16433π-D.8433π-【答案】B【解析】【分析】连接OB和AC交于点D,根据菱形及直角三角形的性质先求出AC的长及∠AOC的度数,然后求出菱形ABCO及扇形AOC的面积,则由S扇形AOC-S菱形ABCO可得答案.【详解】连接OB和AC交于点D,如图所示:∵圆的半径为4,OB=OA=OC=4,又四边形OABC是菱形,∴OB⊥AC,OD=12OB=2,在Rt△COD中利用勾股定理可知:CD=224223,243AC CD-===,∵sin∠COD=3, CDOC=∴∠COD=60°,∠AOC=2∠COD=120°,∴S菱形ABCO=1144383 22OB AC⨯=⨯⨯=,∴S扇形=2 1204163603ππ⨯⨯=,则图中阴影部分面积为S扇形AOC-S菱形ABCO=1683 3π-.故选B.【点睛】考查扇形面积的计算及菱形的性质,解题关键是熟练掌握菱形的面积=12a•b(a、b是两条对角线的长度);扇形的面积=2 360 n r π.15.如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )A.10 B.9 C.8 D.7【答案】D【解析】分析:先根据多边形的内角和公式(n﹣2)•180°求出正五边形的每一个内角的度数,再延长五边形的两边相交于一点,并根据四边形的内角和求出这个角的度数,然后根据周角等于360°求出完成这一圆环需要的正五边形的个数,然后减去3即可得解.详解:∵五边形的内角和为(5﹣2)•180°=540°,∴正五边形的每一个内角为540°÷5=108°,如图,延长正五边形的两边相交于点O,则∠1=360°﹣108°×3=360°﹣324°=36°,360°÷36°=10.∵已经有3个五边形,∴10﹣3=7,即完成这一圆环还需7个五边形.故选D.点睛:本题考查了多边形的内角和公式,延长正五边形的两边相交于一点,并求出这个角的度数是解题的关键,注意需要减去已有的3个正五边形.16.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为()A.2 B3C2D.1 2【答案】B【解析】【分析】连接OA,由圆周角定理可求出∠AOC=60°,再根据∠AOC的正切即可求出PA的值.【详解】连接OA,∵∠ABC=30°,∴∠AOC=60°,∵PA是圆的切线,∴∠PAO=90°,∵tan∠AOC =PA OA,∴PA= tan60°3.故选B.【点睛】本题考查了圆周角定理、切线的性质及锐角三角函数的知识,根据圆周角定理可求出∠AOC=60°是解答本题的关键.17.如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO,则图中阴影部分的面积之和为()A.10﹣32πB.14﹣52πC.12 D.14【答案】B【解析】【分析】根据勾股定理求出AB,求出△ABC的内切圆的半径,根据扇形面积公式、三角形的面积公式计算,得到答案.【详解】解:设⊙O与△ABC的三边AC、BC、AB的切点分别为D、E、F,连接OD、OE、OF,在Rt△ABC中,AB22AC BC+10,∴△ABC的内切圆的半径=68102+-=2,∵⊙O是△ABC的内切圆,∴∠OAB=12∠CAB,∠OBA=12∠CBA,∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣12(∠CAB+∠CBA)=135°,则图中阴影部分的面积之和=222902113525 21021436023602πππ⨯⨯-+⨯⨯-=-,故选B.【点睛】本题考查的是三角形的内切圆与内心、扇形面积计算、勾股定理,掌握扇形面积公式是解题的关键.18.如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为()A.23B.13C.4 D.32【答案】B【解析】【分析】如下图,作AD⊥BC,设半径为r,则在Rt△OBD中,OD=3-1,OB=r,BD=3,利用勾股定理可求得r.【详解】如图,过A作AD⊥BC,由题意可知AD必过点O,连接OB;∵△BAC是等腰直角三角形,AD⊥BC,∴BD=CD=AD=3;∴OD=AD-OA=2;Rt△OBD中,根据勾股定理,得:OB= 22+=BD OD13故答案为:B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用,解题关键是利用等腰直角三角形ABC判定点O在AD上.19.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为()A.91cm B.8cm C.6cm D.4cm【答案】B【解析】【分析】由于⊙O的直径CD=10cm,则⊙O的半径为5cm,又已知OM:OC=3:5,则可以求出OM=3,OC=5,连接OA,根据勾股定理和垂径定理可求得AB.【详解】解:如图所示,连接OA.⊙O的直径CD=10cm,则⊙O的半径为5cm,即OA=OC=5,又∵OM:OC=3:5,所以OM=3,∵AB⊥CD,垂足为M,OC过圆心∴AM=BM,在Rt△AOM中,22AM=5-3=4,∴AB=2AM=2×4=8.故选:B.【点睛】本题考查了垂径定理和勾股定理的应用,构造以半径、弦心距和弦长的一半为三边的直角三角形,是解题的关键.20.如图,7×5的网格中的小正方形的边长都为1,小正方形的顶点叫格点,△ABC的三个顶点都在格点上,过点C作△ABC外接圆的切线,则该切线经过的格点个数是()A.1 B.2 C.3 D.4【答案】C【解析】【分析】作△ABC的外接圆,作出过点C的切线,两条图象法即可解决问题.【详解】如图⊙O即为所求,观察图象可知,过点C作△ABC外接圆的切线,则该切线经过的格点个数是3个,选:C.【点睛】考查三角形的外接圆与外心,切线的判定和性质等知识,解题的关键是理解题意.。
圆圈里数字相等类型的题

圆圈里数字相等类型的题
这类题目的规则可以有多种,下面我将从几个不同的角度来解
释和回答这类题目。
1. 等差数列规律:
在某些题目中,圆圈的数字满足等差数列的规律。
也就是说,每个圆圈内的数字之间的差值是相同的。
通过观察已知的数字,我
们可以根据等差数列的性质推测出其他圆圈内的数字,从而填写空
缺的圆圈。
2. 等比数列规律:
另一种常见的规律是等比数列。
在这种情况下,每个圆圈内
的数字之间的比值是相同的。
通过观察已知的数字,我们可以根据
等比数列的性质推测出其他圆圈内的数字。
3. 递归规律:
有些题目中,圆圈内的数字之间存在递归的规律。
也就是说,
每个圆圈内的数字可以通过前一个或多个圆圈内的数字计算得出。
通过观察已知的数字,我们可以找到递归的规律,从而填写其他圆圈内的数字。
4. 数字排列规律:
还有一些题目中,圆圈内的数字之间存在特定的数字排列规律,例如按照某种顺序排列、按照某种模式交替排列等。
通过观察已知的数字,我们可以找到数字排列的规律,从而填写其他圆圈内的数字。
需要注意的是,每个题目的规律可能不同,解题的方法也会因题目而异。
在解决这类问题时,我们通常需要观察已知的数字,寻找数字之间的关系和规律,然后根据这些规律推测出其他圆圈内的数字。
同时,我们还可以通过试错的方法来验证我们的推测,确保填写的数字满足题目要求。
总之,圆圈里数字相等类型的题目是一种需要观察和推理的数学题目,通过寻找数字之间的规律,我们可以填写空缺的圆圈内的数字。
希望以上解释能够帮助到你。
九年级数学上册第二十三章旋转经典大题例题(带答案)

九年级数学上册第二十三章旋转经典大题例题单选题1、如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4√2,DE=4,则BC的长是()A.1B.√2C.2D.4答案:C分析:根据垂径定理求出OD的长,再根据中位线求出BC=2OD即可.设OD=x,则OE=OA=DE-OD=4-x.∵AB是⊙O的直径,OD垂直于弦AC于点,AC=4√2∴AD=DC=1AC=2√22∴OD是△ABC的中位线∴BC=2OD∵OA2=OD2+AD2∴(4−x)2=x2+(2√2)2,解得x=1∴BC=2OD=2x=2故选:C小提示:本题考查垂径定理、中位线的性质,根据垂径定理结合勾股定理求出OD的长是解题的关键.2、如图,有①~⑤5个条形方格图,每个小方格的边长均为1,则②~⑤中由实线围成的图形与①中由实线围成的图形全等的有()A.②③④B.③④⑤C.②④⑤D.②③⑤答案:C分析:根据旋转变换及全等图形的定义对应边相等,对应角相等的图形是全等图形对个图进行一一分析判断即可解:②以右下角顶点为定点顺时针旋转90°后,两个实线图形刚好重合,③中为平行四边形,而①中为梯形,所以不能和①中图形完全重合,④可上下反转成②的情况,然后旋转可和①中图形完全重合,⑤可旋转180°后可和①中图形完全重合,∴与①中由实线围成的图形全等的有②④⑤.故选择C.小提示:本题考查多边形全等的判定,掌握全等图形的定义,关键是会通过图形的旋转使它们全等.3、在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,﹣b),则ab的值为()A.﹣4B.4C.12D.﹣12答案:D分析:首先根据关于原点对称的点的坐标特点可得a+2+4=0,2−b=0,可得a,b的值,再代入求解即可得到答案.解:∵点(a+2,2)关于原点的对称点为(4,﹣b),∴a+2+4=0,2−b=0,解得:a=−6,b=2,∴ab=−12,故选D小提示:本题主要考查了关于原点对称的点的坐标特点:两个点关于原点对称时,它们的横纵坐标都互为相反数.4、如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,当点O的对应点C落在OB上时,点D的坐标为()A.(7,3√3)B.(7,5)C.(5√3,5)D.(5√3,3√3)答案:A分析:如图,过点D作DE⊥x轴于点E.证明△AOC是等边三角形,解直角三角形求出DE,CE,可得结论.解:如图,过点D作DE⊥x轴于点E.∵B(6,0),∴OB=6,由旋转的性质可知AO=AC=4,OB=CD=6,∠ACD=∠AOB=60°,∵∠AOC=60°,∴△AOC是等边三角形,∴OC=OA=4,∠ACO=60°,∴∠DCE=60°,∴CE=1CD=3,DE=√CD2−CE2=3√3,2∴OE=OC+CE=4+3=7,∴D(7,3√3),故选:A.小提示:本题考查了旋转变换,含30度角的直角三角形的性质,勾股定理,等边三角形的判定和性质等知识,解题的关键是掌握旋转变换的性质.5、如图,在由小正方形组成的网格图中再涂黑一个小正方形,使它与原来涂黑的小正方形组成的新图案为轴对称图形,则涂法有()A.1种B.2种C.3种D.4种答案:C分析:根据轴对称图形的概念,找到对称轴即可得答案.解:如下图,∵图形是轴对称图形,对称轴是直线AB,∴把1、2、3三个正方形涂黑,与原来涂黑的小正方形组成的新图案仍然是轴对称图形,故选:C.小提示:本题考查了轴对称图形的概念,解题的关键是找到对称轴.6、连接正八边形的三个顶点,得到如图所示的图形,下列说法不正确的是()A.四边形ABCH与四边形EFGH的周长相等B.连接HD,则HD平分∠CHEC.整个图形不是中心对称图形D.△CEH是等边三角形答案:D分析:根据正八边形和圆的性质进行解答即可.解:A.∵根据正八边形的性质,四边形ABCH与四边形EFGH能够完全重合,即四边形ABCH与四边形EFGH 全等∴四边形ABCH与四边形EFGH的周长相等,故选项正确,不符合题意;B.连接DH,如图1,∵正八边形是轴对称图形,直线HD是对称轴,∴HD平分∠CHE故选项正确,不符合题意;C.整个图形是轴对称图形,但不是中心对称图形,故选项正确,不符合题意;D.∵八边形ABCDEFGH是正八边形,∴B=BC=CD=DE=EF=FG=GH,CH=EH,设正八边形的中心是O,连接EO、DH,如图2,∠DOE=360°=45°8∵OE=OH∠DOE=22.5°∴∠OEH=∠OHE=12∴∠CHE=2∠OHE=45°∴∠HCE=∠HEC=1(180°-∠CHE)=67.5°2∴△CEH不是等边三角形,故选项错误,符合题意.故选:D.小提示:本题考查了正多边形和圆,熟记正八边形与等腰三角形的性质是解题的关键.7、平面直角坐标系中,O为坐标原点,点A的坐标为(−5,1),将OA绕原点按逆时针方向旋转90°得OB,则点B 的坐标为()A.(−5,1)B.(−1,−5)C.(−5,−1)D.(−1,5)答案:B分析:根据题意证得△AOC≌△OBD,可得结论.解:如图,根据题意得∶∠AOB=90°,∠ACO=∠BDO=90°,OA=OB,∴∠AOC+∠BOD=90°,∠AOC+∠OAC=90°,∴∠BOD=∠OAC,∴△AOC≌△OBD,∴BD=OC,OD=AC,∵点A的坐标为(−5,1),∴BD=OC=1,OD=AC=5,∴B(−1,−5).故选:B.小提示:本题考查坐标与图形变化−旋转,解题的关键是熟练掌握旋转的性质,属于中考常考题型.8、如图,正方形OABC的边长为√2,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为()A.(−√2,0)B.(−√2,0)C.(0,√2)D.(0,2)答案:D分析:连接OB,由正方形ABCD绕原点O顺时针旋转45°,推出∠A1OB1=45°,得到△A1OB1为等腰直角三角形,点B1在y轴上,利用勾股定理求出O B1即可.解:连接OB,∵正方形ABCD绕原点O顺时针旋转45°,∴∠AOA1=45°,∠AOB=45°,∴∠A1OB1=45°,∴△A1OB1为等腰直角三角形,点B1在y轴上,∵∠B1A1O=90°,A1B1=OA1=√2,∴OB1=√A1B12+OA12=√2+2=2,∴B1(0,2),故选:D.小提示:本题考查了正方形的性质,旋转的性质,特殊三角形的性质.关键是根据旋转角证明点B1在y轴上.9、在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是()A.(2,3)B.(−3,2)C.(−3,−2)D.(−2,−3)答案:C分析:根据坐标系中对称点与原点的关系判断即可.关于原点对称的一组坐标横纵坐标互为相反数,所以(3,2)关于原点对称的点是(-3,-2),故选C.小提示:本题考查原点对称的性质,关键在于牢记基础知识.10、已知两点M1(x1,y1),M2(x2,y2),若x1+x2=0,y1+y2=0,则点M1与M2()A.关于y轴对称B.关于x轴对称C.关于原点对称D.以上均不对答案:C分析:首先利用等式求出x1=−x2,y1=−y2,然后可以根据横纵坐标的关系得出结果.∵x1+x2=0,y1+y2=0,∴x1=−x2,y1=−y2,∵两点M1(x1,y1),M2(x2,y2),∴点M1与M2关于原点对称,故选:C.小提示:本题主要考查平面直角坐标系中关于原点对称的点,属于基础题,利用等式找到点M1与M2横纵坐标的关系是解题关键.填空题11、如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,AB=5,BC=9,则BD=______.答案:√106分析:连接BE,如图,根据旋转的性质得∠BCE=60°,CB=CE,BD=AE,再判断△BCE为等边三角形得到BE=BC=9,∠CBE=60°,从而有∠ABE=90°,然后利用勾股定理计算出AE即可.解:连接BE,如图,∵△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,∴∠BCE=60°,CB=CE,BD=AE,∴△BCE为等边三角形,∴BE=BC=9,∠CBE=60°,∵∠ABC=30°,∴∠ABE=90°,在Rt△ABE中,AE=√52+92=√106.所以答案是:√106.小提示:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.12、以原点为中心,把M(3,4)逆时针旋转90°得到点N,则点N的坐标为______.答案:(−4,3)分析:建立平面直角坐标系,根据旋转的性质得出N点坐标,由此即可得出答案.解:如图:由旋转的性质可得:M点横坐标等于N点纵坐标的值,M点纵坐标的值等于N点横坐标的绝对值,又∵M(3,4),∴N(-4,3),所以答案是:(-4,3).小提示:此题考查有关点的坐标旋转的性质,结合坐标轴和旋转的特点确定坐标即可.13、如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是__________.答案:2分析:点F 运动所形成的图象是一条直线,当OF ⊥F 1F 2时,垂线段OF 最短,当点F 1在x 轴上时,由勾股定理得:P 1O =F 1O =4√33,进而得P 1A =P 1F 1=AF 1=8√33,求得点F 1的坐标为(4√33,0),当点F 2在y 轴上时,求得点F 2的坐标为(0,-4),最后根据待定系数法,求得直线F 1F 2的解析式为y =√3x -4,再由线段中垂线性质得出F 1F 2=AF 1=8√33,在Rt △OF 1F 2中,设点O 到F 1F 2的距离为h ,则根据面积法得12×OF 1×OF 2=12×F 1F 2×ℎ,即12×4√33×4=12×8√33×ℎ,解得h =2,根据垂线段最短,即可得到线段OF 的最小值为2.解:∵将线段PA 绕点P 顺时针旋转60°得到线段PF ,∴∠APF =60°,PF =PA ,∴△APF 是等边三角形,∴AP =AF ,如图,当点F 1在x 轴上时,△P 1AF 1为等边三角形,则P 1A =P 1F 1=AF 1,∠AP 1F 1=60°,∵AO ⊥P 1F 1,∴P 1O =F 1O ,∠AOP 1=90°,∴∠P 1AO =30°,且AO =4,由勾股定理得:P 1O =F 1O =4√33, ∴P 1A =P 1F 1=AF 1=8√33, ∴点F 1的坐标为(4√33,0), 如图,当点F 2在y 轴上时,∵△P 2AF 2为等边三角形,AO ⊥P 2O ,∴AO =F 2O =4,∴点F 2的坐标为(0,-4),∵tan∠OF 1F 2=OF 2OF 1=4√33=√3,∴∠OF 1F 2=60°,∴点F 运动所形成的图象是一条直线,∴当OF ⊥F 1F 2时,线段OF 最短,设直线F 1F 2的解析式为y =kx +b , 则{4√33k +b =0b =−4,解得{k =√3b =−4, ∴直线F 1F 2的解析式为y =√3x -4,∵AO =F 2O =4,AO ⊥P 1F 1,∴F 1F 2=AF 1=8√33, 在Rt △OF 1F 2中,OF ⊥F 1F 2,设点O 到F 1F 2的距离为h ,则12×OF 1×OF 2=12×F 1F 2×ℎ,∴12×4√33×4=12×8√33×ℎ,解得h =2,即线段OF的最小值为2,故答案为2.小提示:本题属于三角形的综合题,主要考查了旋转的性质,勾股定理的应用,等边三角形的性质以及待定系数法的运用等,解决问题的关键是作辅助线构造等边三角形以及面积法求最短距离,解题时注意勾股定理、等边三角形三线合一以及方程思想的灵活运用.14、已知点P(m−2,m)关于原点对称的点在第三象限,则m的取值范围是_______.答案:m>2分析:根据关于原点对称的点的性质可得点P在第一象限,进而得出不等式组,再解不等式组即可.解:∵点P(m−2,m)关于原点对称的点在第三象限,∴点P(m−2,m)在第一象限,∴{m−2>0,m>0解得:m>2,所以答案是:m>2.小提示:此题主要考查了关于原点对称的点的坐标特点,解一元一次不等式组,关键是掌握各象限内点的坐标符号.15、如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,将△AOB绕顶点O,按顺时针方向旋转到△AB,则线段B1D的长度为______.A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,OD=12答案:1.5cm##3cm2分析:先在直角△AOB中利用勾股定理求出AB=5cm,再利用直角三角形斜边上的中线等于斜边的一半得出ODAB=2.5cm.然后根据旋转的性质得到OB1=OB=4cm,则问题得解.=12∵在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,∴AB=√OA2+OB2=5cm,∴OD=1AB=2.5cm,2∵将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,∴OB1=OB=4cm,∴B1D=OB1-OD=1.5cm.所以答案是:1.5cm.小提示:本题主要考查勾股定理和直角三角形的性质以及图形旋转的性质,掌握勾股定理是解题的关键.解答题16、如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(﹣1,4),B(﹣3,1).(1)画出线段AB向右平移4个单位后的线段A1B1;(2)画出线段AB绕原点O旋转180°后的线段A2B2.答案:(1)画图见解析,(2)画图见解析分析:(1)分别确定A,B向右平移4个单位后的对应点A1,B1,再连接A1B1即可;(2)分别确定A,B绕原点O旋转180°后的对应点A2,B2,再连接A2B2即可.解:(1)如图,线段A1B1即为所求作的线段,(2)如图,线段A2B2即为所求作的线段,小提示:本题考查的是平移的作图,中心对称的作图,掌握平移的性质与中心对称的性质是解题的关键. 17、如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.(1)写出△OAB各顶点的坐标;(2)以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,写出A′,B′的坐标.答案:(1)A(-2,0),B(-1,√3),C(0,0)(2)A′(−1,√3),B′(1,√3)分析:(1)作高线BC,根据等边三角形的性质和勾股定理求OC和BC的长,写出三点的坐标,注意象限的符号问题;(2)如图2,由旋转可知:A′与B重合,B与B′关于y轴对称,可得:A′,B′的坐标.(1)解:如图1,过B作BC⊥OA于C,∵△AOB是等边三角形,且OA=2,OA=1,∴OC=12由勾股定理得:BC=√22−12=√3,∴A(−2,0),B(−1,√3),O(0,0);(2)解:如图2,∵∠AOB=60°,OA=OB,∴A′与B重合,∴A′(−1,√3),由旋转得:∠BOB′=60°,OB=OB′,∵∠AOD=90°,∴∠BOD=30°,∴∠DOB′=30°,∴BB′⊥OD,DB=DB′,∴B′(1,√3).小提示:本题考查了坐标与图形变换、等边三角形的性质、旋转的性质,熟练掌握旋转和等边三角形的性质是关键,并注意点所在象限的符号问题.18、如图,一伞状图形,已知∠AOB=120°,点P是∠AOB角平分线上一点,且OP=2,∠MPN=60°,PM与OB交于点F,PN与OA交于点E.(1)如图一,当PN与PO重合时,探索PE,PF的数量关系(2)如图二,将∠MPN在(1)的情形下绕点P逆时针旋转α度(0<α<60°),继续探索PE,PF的数量关系,并求四边形OEPF的面积.答案:(1)PE=PF,证明详见解析;(2)PE=PF,√3分析:(1)根据角平分线定义得到∠POF=60°,推出△PEF是等边三角形,得到PE=PF;(2)过点P作PQ⊥OA,PH⊥OB,根据角平分线的性质得到PQ=PH,∠PQO=∠PHO=90°,根据全等三角形的性质得到PE=PF,S四边形OEPF=S四边形OQPH,求得OQ=1,QP=√3,根据三角形的面积公式即可得到结论.解:(1)∵∠AOB=120°,OP平分∠AOB,∴∠POF=60°,∵∠MPN=60°,∴∠MPN=∠FOP=60°,∴ΔPEF是等边三角形,∴PE=PF;(2)过点P作PQ⊥OA,PH⊥OB,∵OP平分∠AOB,∴PQ=PH,∠PQO=∠PHO=90°,∵∠AOB=120°,∴∠QPH=60°,∴∠QPE+∠FPH+∠EPH,∴∠QPE=∠EPF,在ΔQPE与ΔHPF中{∠EQP=∠FHP ∠QPE=∠HPFPQ=PH,∴ΔQPE≌ΔHPF(AAS),∴PE=PF,S四边形OEPF =S四边形OQPH,∵PQ⊥OA,PH⊥OB,OP平分∠AOB,∴∠QPO=30°,∴OQ=1,QP=√22−12=√3,∴SΔOPQ=12×1×√3=√32,∴四边形OEPF的面积=2SΔOPQ=√3小提示:本题考查了旋转的性质,角平分线的性质,全等三角形的判定和性质,三角形的面积,正确的作出辅助线是解题的关键.。
初中数学圆形专题训练50题答案

初中数学圆形专题训练50题含参考答案一、单选题1.函数233y x =--自变量x 的取值范围是( ). A .0x ≠ B .1x ≠ C .1x > D .1x <2.反比例函数y=kx的图象经过点(-1,2),k 的值是( ) A .-1 B . 1 C .-2 D .2 3.如图,A ,B ,C 是O 上的三个点,若66B ︒∠=,则OAC ∠的度数为( )A .24︒B .29︒C .33︒D .132︒ 4.如图,在同一平面直角坐标系中,一次函数(0)y ax b ab =+≠的图象与反比例函数(0)ab y ab x=≠的图象大致可以是( ) A . B .C .D .5.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 的夹角为150°,AB 的长为30cm,BD的长为15cm,则DE的长为()A.254cmπB.252cmπC.25cmπD.50cmπ6.已知点A(3a+1,﹣4a﹣2)在第二、四象限角平分线上,则a2009+a2010的值为()A.﹣1B.0C.1D.27.小芳步行上学,最初以某一速度匀速前进,中途遇红灯,稍作停留后加快速度跑步去上学,到校后,她请同学们画出她行进路程s(米)与行进时间t(分钟)的函数图象的示意图.你认为正确的是()A.B.C.D.8.如图是我们学过的反比例函数图象,它的函数解析式可能是()A.2y x B.4yx=C.3yx=-D.12y x=9.如图,点P为反比例函数myx=上的一点,PA x⊥轴于点A,C为y轴上一点.如果PCA 的面积为2,则二次函数()221y m x mx =--+的顶点在第( )象限A .一B .二C .三D .四 10.对于圆的周长公式C =2πR ,下列说法错误的是( )A .π是变量B .R、C 是变量 C .R 是自变量D .C 是因变量 11.已知圆O 的半径是3,A ,B ,C 三点在圆O 上,∠ACB=60°,则弧AB 的长是( )A .2πB .πC .32πD .12π 12.在圆柱形油槽内装有一些油.截面如图,油面宽AB 为60cm ,如果再注入一些油后,油面AB 上升10cm ,油面宽变为80cm ,则该圆柱形油槽直径MN 为( )A .55cmB .60cmC .80cmD .100cm 13.下列一次函数中,y 随x 增大而减小的是( )A .3y x =B .32y x =-C .32y x x =+D .32y x =-- 14.一次函数y =mx +n 的图象经过一、二、四象限,点A (1,y 1),B (3,y 2)在该函数图象上,则( )A .y 1>y 2B .y 1≥y 2C .y 1<y 2D .y 1≤y 215.已知抛物线()2210y ax ax a =-+<,当12x -≤≤时,y 的最大值为2,则当12x -≤≤时,y 的最小值为( )A .1B .0C .1-D .2- 16.如图,O 的半径为6,将劣弧沿弦AB 翻折,恰好经过圆心O ,点C 为优弧AB 上的一个动点,则ABC 面积的最大值是( )A.B.C.D.18+17.关于二次函数223y x x=-++,下列说法中不正确...的是()A.图象开口向下B.图象的对称轴是1x=C.当1x>时,y随x的增大而增大D.函数的最大值为418.若点B(a,0)在以点A(1,0)为圆心,以3为半径的圆内,则a的取值范围是()A.-2<a<4B.a<4C.a>-2D.a>4或a<-219.二次函数y=ax2+bx+c(abc≠0)的图象如图所示,反比例函数y=cx与正比例函数y=bx在同一坐标系内的大致图象是()A.B.C.D.20.给出下列函数:∠y=31(1)31(1)x xx x-≥⎧⎨--<⎩;∠y=3x;∠y=3x2.从中任取一个函数,取出的函数符合条件“当x>1时,函数值y随x增大而减小”的概率是()A .1B .23 C .13 D .0二、填空题21.若点P (a ,a ﹣4)在第四象限,则点N (﹣a ,4﹣a )在第 _____象限. 22.已知一次函数32y x =-+,那么y 的值随x 的增大而________.23.如图,抛物线2y ax bx c =++与x 轴交于点A ,B ,若对称轴为直线=1x -,点A 的坐标为(-3,0),则不等式20ax bx c ++>的解集为______.24.若点A (2,n )在x 轴上,则点B (n+2,n-5)位于第______象限.25.抛物线244y x x =-+与坐标轴有_______个交点.26.若一个扇形的圆心角为60︒,面积为26cm π,则这个扇形的弧长为__________ cm(结果保留π)27.已知二次函数y =x 2﹣2x +m 的图象与x 轴交于A ,B 两点,若点A 坐标为(﹣1,0),则点B 的坐标为_____.28.点()1,23A m m --在第一、三象限夹角的角平分线上,则m 的值为_________.29.把函数22y x x =-化为2()y a x h k =-+的形式为________.30.已知点(32,4)N a a --到x 轴的距离等于到y 轴的距离的2倍,则a 的值为__________.31.抛物线2y ax bx c =++上部分点的横坐标x ,纵坐标y 的对应值如表所示,则抛物线的对称轴是____.32.如图,这是一个铅皮做成的无盖半圆锥状容器,它是由半个圆锥侧面和一个等腰三角形围成的.若不考虑容器厚度、接缝以及余料等因素,则根据图中给出的尺寸,制造这样一个容器需要铅皮____cm 2.33.若抛物线 ()22y a x =- 的开口向上,则 a 的取值范围是________.34.如图,圆锥的母线长为10,侧面展开图的面积为60π,则圆锥主视图的面积为__________.35.如图,Rt △ABC 中,∠C =90°,AC =3,AB =5.则△ABC 的内切圆半径r =____.36.用半径为6的半圆围成一个圆锥的侧面,则圆锥的底面半径为________. 37.我们规定:平面内点A 到图形G 上各个点的距离的最小值称为该点到这个图形的最小距离d ,点A 到图形G 上各个点的距离的最大值称为该点到这个图形的最大距离D ,定义点A 到图形G 的距离跨度为R =D -d .在平面直角坐标系xOy 中,图形G 为以原点O 为圆心,2为半径的圆,则点A(1,-1)到图形G 的距离跨度是_______. 38.如图,点、、A B C 在半径为8的O 上,过点B 作//BD AC ,交OA 延长线于点D .连接BC ,且30BCA OAC ︒∠=∠=,则图中阴影部分的面积为__________.39.一圆锥的侧面展开图的圆心角为90︒,底面半径为3,则该圆锥的侧面积为_______.40.在平面直角坐标系中,已知点()4,0A -,点()0,4B ,点()4,4C -,动点D 从A 点出发,以每秒1个单位的速度水平向右运动,动点E 从点B 出发,以每秒1个单位的速度竖直向上运动,过点A 作AG CE ∥交CD 于点G ,当线段OG 的值最小时,则运动时间t 的值为 _____.三、解答题41.如图,以四边形ABCD 的对角线BD 为直径作圆,圆心为O ,过点A 作AE CD ⊥的延长线于点E ,已知DA 平分BDE ∠.(1)求证:AE 是O 的切线;(2)若4AE =,6CD =,求O 的半径和AD 的长.42.如图,∠ABC 内接于∠O ,AB 是∠O 的直径,I 是∠ABC 内一点,AI 的延长线交BC 于点D ,交∠0于点E ,连接BE ,BI ,若IB 平分∠ABC ,EB =EI .(1)求证:AE 平分∠BAC ;(2)若BD OI ∠AD 于点I ,求BE 的长.43.如图,O 是ABC 的外接圆,点O 在BC 边上,BAC ∠的平分线交O 于点D ,连接,BD CD ,过点D 作DP BC ∥,与AC 的延长线交于点P .(1)求证:DP 是O 的切线;(2)当3cm,4cm AB AC ==时,求线段PC 的长.44.如图,一条直线11y k x b =+与反比例函数22k y x=的图象交于A (1,5)、B (5,n )两点,与x 轴交于C 点.(1)求反比例函数的解析式;(2)求C 点坐标(3)请直接写出当12y y <时,x 的取值范围;45.如图,已知AB 是O 直径,且8AB =,C ,D 是O 上的点,OC BD ∥,交AD于点E,连接BC,30CBD∠=︒.(1)求COA∠的度数;(2)求图中弧BD与弦BD围成的阴影部分的面积(结果保留π).46.小明准备给长16米,宽12米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形ABCD和EFGH均为正方形,且各有两边与长方形边重合;矩形MFNC(区域II)是这两个正方形的重叠部分,如图所示.(1)若花卉均价为300元2/米,种植花卉的面积为S()2米,草坪均价为200元2/米,且花卉和草坪栽种总价不超过43600元,求S的最大值.(2)若矩形MFNC满足:1:2MF FN=.∠求MF,FN的长.∠若甲、乙、丙三种花卉单价分别为180元2/米,90元2/米,180元2/米,且边BN的长不小于边ME长的54倍.求图中I、II、III三个区域栽种花卉总价W的最大值.47.如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中(1)A→C(,),B→D(,),C→ (+1,);(2)若甲虫A的爬行路线为A→B→C→D,请计算甲虫A爬行的路程;(3)若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.48.如图,O是ABC∆的外接圆,AB是O的直径,点D在O上,AC平分BAD∠,过点C的切线交直径AB的延长线于点E,连接AD、BC.(1)求证:BCE=∠∠CAD.(2)若O的半径长为r,AD m=,写出求线段CE长的思路(不用求出结果).49.如图,点P是∠O直径AB上的一点,过P作直线CD∠AB,分别交∠O于C、D两点,连接AC,并将线段AC绕点A逆时针旋转90°,得到AE,连接ED,分别交∠O和A、B于F、G,连接FC,(1)求证:∠ACF=∠AED;(2)若点P在直径AB上运动(不与点A,B重合)其他条件不变,请问EGAP是否为定值?若是,请求出其值,若不是,请说明理由.50.已知△ABC内接于∠O,CD为直径,CD交AB边于点E,且CE=AC.(1)如图1,求证∠ACD=2∠BCD;(2)如图2,过点O作OF∠AC,过点B作BH∠CD,求证:AC=2OH;(3)如图3,在(2)的条件下,过点E作AB的垂线交BC于点K,连接EF,AD,若AD+AC=14,且∠AFE+∠CEF=90°,求CK的长.参考答案:1.B【分析】根据分式的分母不为零进行求解即可.【详解】根据题意,330x -≠,解得1x ≠,故选:B.【点睛】本题主要考查了反比例函数自变量的取值范围,熟练掌握分式的性质是解决本题的关键.2.C【详解】∠反比例函数y=kx经过(-1,2),∠k=-1×2=-2.故选C. 3.A【分析】根据圆周角定理得到2132AOC B ∠=∠=︒,再根据等腰三角形的性质及三角形内角和求解即可.【详解】解:66B ∠=︒,2132AOC B ∴∠=∠=︒,OA OC =,OAC OCA ∴∠=∠,11(180)(180132)2422OAC AOC ∴∠=︒-∠=⨯︒-︒=︒, 故选:A .【点睛】此题考查了圆周角定理,解题的关键是熟记圆周角定理.4.C【分析】根据一次函数图象所在象限,确定出a ,b 的符号,再根据反比例函数图象所在的象限,确定出a ,b 的符号,至此找出一次函数和反比例函数a ,b 的符号一致的选项即可.【详解】解:A.由一次函数图象知a ,b 异号,由反比例函数图象知a ,b 同号,故该选项错误,不符合题意;B.由一次函数图象知a ,b 同号,由反比例函数图象知a ,b 异号,故该选项错误,不符合题意;C.由一次函数图象知a ,b 异号,由反比例函数图象知a ,b 异号,故该选项正确,符合题意;D.由一次函数图象知a ,b 异号,由反比例函数图象知a ,b 同号,故该选项错误,不符合题意.故选:C .【点睛】本题考查了一次函数,反比例函数图象与系数的关系.解题的关键在于确定出a ,b 的符号,明确系数与函数图象的关系.5.B【分析】根据AB =30cm ,BD =15cm ,可以得到AD 的长,然后根据AB ,AC 夹角为150°和弧长计算公式可以得到DE 的长.【详解】∠AB =30cm ,BD =15cm ,AB ,AC 夹角为150°,∠AD =AB ﹣BD =15cm ,∠DE 的长为:15015180π⨯⨯=252π(cm ), 故选:B .【点睛】本题考查了弧长的计算,掌握计算公式是解题关键.6.B【分析】根据角平分线上的点到角的两边的距离相等,以及第二、四象限点的横坐标与纵坐标的符号相反列出方程求解即可.【详解】解:∠点A (3a +1,﹣4a ﹣2)在第二、四象限的角平分线上,∠3a +1=﹣(﹣4a ﹣2),解得a =﹣1,∠a 2009+a 2010=﹣1+1=0.故选:B【点睛】本题考查了角平分线的性质和平面直角坐标系各象限的点的坐标特征,熟知两个知识点是解题关键.7.C【详解】试题分析:运用排除法解答本题,中间的停留路程不变,可排除BD 两项,最后的加速图象应为比最初的路程增加直线增速更快的图象,排除A ,故选C.考点:函数的图象.8.B【分析】此题考查反比例函数图象的性质;【详解】反比例函数(0)k y k x=≠,当0k >时,图像分布在第一、三象限; 当0k <时,图像分布在第二、四象限;所以选B9.D【分析】先根据反比例函数比例系数的几何意义求出m 的值,然后求出二次函数的顶点坐标即可得到答案.【详解】解:∠点P 为反比例函数m y x=上的一点,PA x ⊥轴于点A ,C 为y 轴上一点,PCA 的面积为2, ∠24PCA m S ==△,又∠反比例函数图象经过第一象限,∠4m =,∠二次函数解析式为()22241211y x x x =-+=--, ∠二次函数的顶点坐标为()11-,, ∠二次函数()221y m x mx =--+的顶点在第四象限,故选:D .【点睛】本题主要考查了反比例函数比例系数的几何意义,二次函数图象的性质,判断点所在的象限,正确求出m 的值是解题的关键.10.A【详解】解:A .π是一个常数,是常量,故选项符合题意;B .R 、C 是变量,故选项不符合题意;C .R 是自变量,故选项不符合题意;D .C 是因变量,故选项不符合题意.故选:A .11.A【详解】分析:先根据同弧所对的圆心角是其所对圆周角的2倍求出∠AOB 的度数,再根据扇形的弧长公式计算.详解:如图,∠∠AOB 与∠ACB 对的弧相同,∠ACB =60°,∠∠AOB =2∠ACB =120°, ∠12032180180n R l πππ⨯⨯===. 故选A .点睛:本题考查了圆周角定理和弧长的计算公式,熟记弧长计算公式是解答本题的关键,如果扇形的圆心角是n º,扇形的半径是R ,则扇形的弧长l 的计算公式为:180n R l π=. 12.D【分析】若油面AB 上升后到达油面CD ,过圆心O 作圆的半径OE 垂直于AB ,设垂足为H ,交CD 于点G ,连接OA 、OC ,设出OG 的长度,在两直角三角形中利用勾股定理分别可得OA 、OC 的长度,利用圆的半径相等,即OA=OC 可求得OG ,进而可求MN 的长度【详解】解:如图:若油面AB 上升后到达油面CD ,过圆心O 作圆的半径OE 垂直于AB ,设垂足为H ,交CD 于点G ,连接OA 、OC ,由垂径定理可得:CG=40,AH=30设OG=x ,则OH=x+10在直角三角形OGC 中:22240OC x =+在直角三角形OHA 中:()2221030OA x =++OC OA =()2222401030x x ∴+=++ 解得x=30代入22240OC x =+可得22500OC =0OC >50OC ∴=2100MN OC ∴==故选:D【点睛】本题考查垂径定理的应用及勾股定理,根据垂径定理构造直角三角形是解决本题的关键13.D【详解】∠A ,B ,C 中,自变量的系数大于0,∠y 随x 增大而增大;∠D 中,自变量的系数小于0,∠y 随x 增大而减小;故选D.14.A【分析】先根据图象在平面坐标系内的位置确定m 、n 的取值范围,进而确定函数的增减性,最后根据函数的增减性解答即可.【详解】解:∠一次函数y =mx +n 的图象经过第一、二、四象限,∠m <0,n >0∠y 随x 增大而减小,∠1<3,∠y 1>y 2.故选:A.【点睛】本题主要考查一次函数图象在坐标平面内的位置与k 、b 的关系、一次函数的增减性等知识点,图象在坐标平面内的位置确定m 、n 的取值范围成为解答本题的关键. 15.D【分析】根据抛物线的解析式可得其对称轴为直线x =1,从而当x =1时,y 有最大值2,此时可求得a 的值,再根据抛物线的增减的性质求得y 在所给范围内的最小值.【详解】∠212a x a-=-=,即抛物线的对称轴为直线x =1 ∠当x =1时,y 有最大值,且1在12x -≤≤范围内∠a -2a +1=2解得:a =-1即2+21y x x =-+当1<1x ≤-时,函数值y 随x 的增大而增大,此时函数在x =-1处取得最小值,且最小值为1212y =--+=-当12x <≤时,函数值y 随x 的增大而减小,此时函数在x =2处取得最小值,且最小值为42211y =--⨯+=∠-2<1∠当12x -≤≤时,y 的最小值为−2故选:D .【点睛】本题考查了二次函数的增减性质、求函数解析式,关键是确定抛物线的对称轴,根据对称轴的位置便可确定函数的增减的范围,解答函数在某个自变量的范围的最值问题时,最好借助图象,利用数形结合的思想能帮助解决问题.16.A【分析】如图,过点C 作CT ∠AB 于点T ,过点O 作OH ∠AB 于点H ,交∠O 于点K ,连接AO ,AK .解直角三角形求出AB ,求出CT 的最大值,可得结论.【详解】解:如图,过点C 作CT ∠AB 于点T ,过点O 作OH ∠AB 于点H ,交∠O 于点K ,连接AO ,AK .由题意AB 垂直平分线段OK ,∠AO =AK ,∠OA =OK ,∠OA =OK =AK ,∠∠OAK =∠AOK =60°.∠AH =OA •sin60°=∠OH ∠AB ,∠AH =BH ,∠AB =2AH =∠OC +OH ≥CT ,∠CT ≤6+3=9,∠CT 的最大值为9,∠∠ABC 的面积的最大值为192⨯=, 故选:A .【点睛】本题考查垂径定理,勾股定理,三角形的面积,垂线段最短等知识,解题的关键是求出CT 的最大值,属于中考常考题型.17.C【分析】根据题目中的函数解析式,利用二次函数的性质可以判断各个选项中的说法是否正确. 【详解】解:二次函数()222314y x x x =-++=--+,∴该函数的图象开口向下,故选项A 的说法正确,不符合题意; 对称轴是直线()2121x =-=⨯-,故选项B 中的说法正确,不符合题意; 当1x >时,y 随x 的增大而增小,故选项C 中的说法错误,符合题意;函数图象的顶点坐标为()1,4,则函数的最大值为4,故选项D 中的说法正确,不符合题意;故选:C .【点睛】本题考查抛物线的开口方向,对称轴,顶点坐标,增减性,解答本题的关键是明确题意,利用二次函数的性质解答.18.A【详解】试题解析:∠点B (a ,0)在以点A (1,0)为圆心,以3为半径的圆内, ∠|a-1|<3,∠-2<a <4.故选A .点睛:点与圆的位置关系:设∠O 的半径为r ,点P 到圆心的距离OP=d ,则有:点P 在圆外⇔d >r ;点P 在圆上⇔d=r ;点P 在圆内⇔d <r .19.D【分析】先根据二次函数的图象可得,b c 的符号,再根据反比例函数的图象、正比例函数的图象特点即可得. 【详解】解:抛物线的开口向上,与y 轴的交点位于y 轴的正半轴,0,0a c ∴>>,抛物线的对称轴位于y 轴的右侧,02b x a∴=->, 0b ∴<,由0c >可知,反比例函数c y x=的图象位于第一、三象限, 由0b <可知,正比例函数y bx =的图象经过原点,且经过第二、四象限,观察四个选项可知,只有选项D 符合,故选:D .【点睛】本题考查了二次函数、反比例函数和正比例函数的图象,熟练掌握各函数的图象特点是解题关键.20.C【分析】分别求各函数在X 大于1时的单调性以得到在X 大于1时递减的函数的个数,再求其概率.【详解】∠X 大于1时,系数3大于0,函数递增.∠K=3时,反比例函数在第一象限递减.∠二次函数系数3大于0,在第一象限递增.综上所述,三个函数中,只有第二个函数满足条件,所以概率为13.即答案选C. 【点睛】熟练掌握各种函数的图像单调性是本题解答的关键.21.二【分析】根据各象限内点的坐标特征解答即可.【详解】解:∠点P (a ,a ﹣4)在第四象限,∠a >0,a -4<0,∠0<a <4,∠-a <0,4-a >0,∠点N (﹣a ,4﹣a )在第二象限,故答案为:二.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).22.减小【分析】根据一次函数图象与系数的关系可判断.【详解】解:∠一次函数的0k <,∠y 的值随x 的增大而减小,故答案为减小.【点睛】本题考查了一次函数图象与系数的关系:对于一次函数y =kx +b :当k >0,y 的值随x 的增大而增大;k <0,y 的值随x 的增大而减小.23.31x -<<【分析】函数的对称轴为直线=1x -,与x 轴交点(3,0)A -,则另一个交点(1,0)B ,进而求解.【详解】解:函数的对称轴为直线=1x -,与x 轴交点(3,0)A -,则另一个交点(1,0)B , 观察函数图象知,不等式20ax bx c ++>的解集为:31x -<<,故答案为:31x -<<.【点睛】本题考查了抛物线与x 轴的交点,主要考查函数图象上点的坐标特征,解题的关键是要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.24.四【分析】直接利用x 轴上点的坐标特点得出n 的值,进而得出答案.【详解】∠点A (2,n )在x 轴上,∠n =0,则点B (n +2,n ﹣5)的坐标为:(2,﹣5)位于第四象限.故答案为四.【点睛】本题考查了点的坐标,正确得出n 的值是解题的关键.25.2【分析】根据二次函数的图像与系数的关系直接进行求解即可.【详解】解:由抛物线244y x x =-+可得与y 轴的交点坐标为()0,4,与x 轴只有一个交点其坐标为()2,0,所以与坐标轴的交点有2个;故答案为2.【点睛】本题主要考查二次函数的图像与系数的关系,熟练掌握二次函数的图像与系数的关系是解题的关键.26.3π 【分析】先利用扇形的面积公式求出扇形的半径,再利用弧长公式即可得.【详解】设扇形的半径为rcm 则2603606πr π= 解得1()r cm =或1()r cm =-(不符题意,舍去) 则这个扇形的弧长为601()1803ππcm ⨯= 故答案为:3π. 【点睛】本题考查了扇形的面积公式、弧长公式,熟记公式是解题关键.27.(3,0).【分析】根据二次函数y =x 2﹣2x +m 的图象与x 轴交于A ,B 两点,点A 坐标为(﹣1,0),可以求得m 的值,从而可以得到该函数的解析式,进而求得点B 的坐标.【详解】∠二次函数y =x 2﹣2x +m 的图象与x 轴交于A ,B 两点,点A 坐标为(﹣1,0), ∠0=(﹣1)2﹣2×(﹣1)+m ,解得,m =﹣3,∠y =x 2﹣2x ﹣3,当y =0时,0=x 2﹣2x ﹣3=(x ﹣3)(x +1),解得,x 1=3,x 2=﹣1,∠点B 的坐标为(3,0),故答案为(3,0).【点睛】本题考查抛物线与x 轴的交点,解答本题的关键是明确题意,利用二次函数的性质解答.28.2【分析】根据第一、三象限角平分线上点的坐标特点列式计算即可.【详解】解:∠点A (m -1,2m −3)在第一、三象限夹角的平分线上,∠m -1=2m −3,解得m =2,故答案为:2.【点睛】本题主要考查点的坐标,解题的关键是掌握第一、三象限角平分线上点的横纵坐标相等.29.2(1)1y x =--【分析】由于二次项系数为1,利用配方法直接加上一次项系数的一半的平方配成完全平方式,可把一般式转化为顶点式.【详解】y =x 2﹣2x =x 2﹣2x +1﹣1=(x ﹣1)2﹣1.故答案为y =(x ﹣1)2﹣1.【点睛】本题主要考查了利用配方法将一般式转化为顶点式的方法.二次函数的解析式有三种形式:(1)一般式:y =ax 2+bx +c (a ≠0,a 、b 、c 为常数);(2)顶点式:y =a (x ﹣h )2+k ;(3)交点式(与x 轴):y =a (x ﹣x 1)(x ﹣x 2).30.87或0 【详解】解:由题可知: ∠4232a a -=-,∠当42(32)a a -=-时,得:87a =; ∠当42(23)a a -=-时,得0a =, 故答案为:87a =或0. 31.x =12 【分析】利用y 值相等的x 值,根据抛物线对称性即可求解.【详解】解:∠x =0,x =1时,y=6,∠对称轴为x =0+11=22. 故答案为x =12.【点睛】本题考查表格信息获取问题,抛物线对称轴,掌握表格信息获取方法,抛物线对称性求对称轴方法是解题关键.32.(240+130π)【详解】由题意得圆锥的侧面展开图面积为S=11202626022LR ππ=⨯⨯=但是图中的是圆锥的一半所以为了130π,而三角形的面积为240.故为(240+130π).33.a >2【分析】利用二次函数图像的性质直接求解.【详解】解:∠抛物线()22y a x =-的开口向上, ∠a-2>0,∠a >2,故答案为a >2.【点睛】本题考查二次函数图像的性质,掌握二次项系数决定开口方向是本题的解题关键. 34.48【分析】圆锥的主视图是等腰三角形,根据圆锥侧面积公式S=πrl 代入数据求出圆锥的底面半径长,再由勾股定理求出圆锥的高即可.【详解】根据圆锥侧面积公式:S=πrl ,圆锥的母线长为10,侧面展开图的面积为60π, 故60π=π×10×r ,解得:r=6.由勾股定理可得圆锥的高∠圆锥的主视图是一个底边为12,高为8的等腰三角形,∠它的面积=1128=482⨯⨯, 故答案为:48【点睛】本题考查了三视图的知识,圆锥侧面积公式的应用,正确记忆圆锥侧面积公式是解题关键.35.1【分析】设AB 、BC 、AC 与∠O 的切点分别为D 、E 、F ;易证得四边形OECF 是正方形;那么根据切线长定理可得:CE=CF=12(AC+BC-AB ),由此可求出r 的长.【详解】如图,在Rt△ABC,∠C=90°,AC=3,AB=5,根据勾股定理,四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,∠四边形OECF是正方形,由切线长定理,得:AD=AF,BD=BE,CE=CF,∠CE=CF=1(AC+BC-AB),2(3+4-5)=1.即:r=12故答案为1【点睛】此题考查了三角形内切圆的性质.注意切线长定理,还要注意直角三角形的内切圆中,如果连接过切点的半径,可以得到一个正方形,借助于方程即可求得半径.36.3cm.【详解】解:由题意知:底面周长=6πcm,∠底面半径=6π÷2π=3cm.故答案为:3cm.【点睛】本题考查圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.37.【分析】先根据跨度的定义先确定出点到圆的最小距离d和最大距离D,即可得出跨度;【详解】解:如图,过点A作圆O的直径EF,则EF=4,d=AF,D=EA∠A(1,-1),=,∠R=D -d=故答案为:【点睛】本题主要考查了点和圆的位置关系,理解和应用新定义解决问题,还涉及到平面坐标系内,两点间的距离公式,由已知点的坐标计算距离跨度是解本题的关键.38.323π 【分析】连接OB ,证明∠OBD=90°,再由//BD AC 得到∠D=∠OAC=30°,求出BD ,分别求出∠BOD 的面积和扇形AOB 的面积,再相减即可得出答案.【详解】解:证明:连接OB ,交CA 于E ,∠∠C=30°,∠C=12∠BOA , ∠∠BOA=60°,又//BD AC ,∠∠D=∠OAC=30°∠∠DBO=180°-∠D-∠BOA=180°-30°-60°=90°,∠∠D=30°,∠BD∠2211132==882360263阴影扇形πππ∆-⨯⨯-⨯=⨯-⨯=BOD BOA n S S S BD OB OB .故答案为323π. 【点睛】本题考查了平行线的性质,圆周角定理,扇形的面积,三角形的面积,解直角三角形等知识点的综合运用,题目比较好,难度适中.39.36π【分析】由题意知圆锥展开扇形的弧长为9023180r ππ⨯⨯=⨯⨯,求出r 的值,然后根据圆锥的侧面积为290360r π⨯⨯计算求解即可. 【详解】解:由题意知圆锥展开扇形的弧长为9023180r ππ⨯⨯=⨯⨯ 解得12r =∠圆锥的侧面积为2901236360ππ⨯⨯= 故答案为:36π.【点睛】本题考查了扇形的面积与弧长.解题的关键在于求出圆锥展开图的半径.40.2##2-+【分析】如图,连接CA ,CB ,取AC 的中点Q ,连接QG ,QO ,证明四边形ACBO 为正方形,可得90ACB ∠=︒,证明CAD CBE ≌,可得90AGC DCE ∠=∠=︒,则G 在以AC 为直径的圆上运动,可得当Q ,G ,O 三点共线时,OG 最短,OG 最短时,2OG =,再证明OGD OAG ∽,从而可得答案.【详解】解:如图,连接CA ,CB ,取AC 的中点Q ,连接QG ,QO ,∠点()4,0A -,点()0,4B ,点()4,4C -,∠4OA OB AC BC ====,CB OE ⊥,CA OA ⊥,∠90CBE CAD ∠==∠︒,∠四边形ACBO 为正方形,∠90ACB ∠=︒,∠动点D 从A 点出发,以每秒1个单位的速度水平向右运动,动点E 从点B 出发,以每秒1个单位的速度竖直向上运动,∠AD BE =,∠CAD CBE ≌,∠ACD BCE ∠=∠,∠90DCE DCB BCE DCB ACD ∠=∠+∠=∠+∠=︒,∠AG CE ∥,∠90AGC DCE ∠=∠=︒,∠G 在以AC 为直径的圆上运动,当Q ,G ,O 三点共线时,OG 最短,∠4AC =,则2AQ =,∠OQ =∠OG 最短时,2OG =,∠QC QG =,∠QCG QGC ∠=∠,而DGO QGC ∠=∠,∠QCG DGO ∠=∠,∠90QCG CAG CAG OAG ∠+∠=︒=∠+∠,∠QCG OAG ∠=∠,∠OAG DGO ∠=∠,∠GOD GOA ∠=∠,∠OGD OAG ∽, ∠OG OD OA OG=,∠()22264OG OD OA ===-,∠462AD =-+,∠2t ==.故答案为:2.【点睛】本题考查的是坐标与图形,全等三角形的判定与性质,相似三角形的判定与性质,圆周角定理的应用,证明G 在以AC 为直径的圆上运动是解本题的关键. 41.(1)见解析(2)5,【分析】(1)连接OA ,根据已知条件证明OA AE ⊥即可解决问题;(2)取CD 中点F ,连接OF ,根据垂径定理可得OF CD ⊥,所以四边形AEFO 是矩形,利用勾股定理即可求出结果.【详解】(1)证明:如下图,连接OA ,∠AE CD ⊥,∠90DAE ADE ∠+∠=︒.∠DA 平分BDE ∠,∠ADE ADO ∠=∠.又∠OA OD =,∠OAD ADO ∠=∠,∠90DAE OAD ∠+∠=︒,∠OA AE ⊥,∠OA 是半径,∠AE 是O 切线;(2)解:如上图,取CD 中点F ,连接OF ,∠OF CD ⊥于点F ,∠四边形AEFO 是矩形.∠6CD =,∠3DF FC ==.在Rt ∠OFD 中,4OF AE ==,∠5OD =,在Rt ∠AED 中,4AE =,532ED EF DF OA DF OD DF =-=-=-=-=,∠AD =,∠AD 的长是【点睛】本题考查了切线的判定与性质,垂径定理,圆周角定理,勾股定理,解决本题的关键是掌握切线的判定与性质.42.(1)见解析(2)2【分析】(1)根据角平分线的性质得到∠ABI =∠CBI ,由等腰三角形的性质得到∠EBI =∠EIB ,通过三角形外角的性质和圆周角定理即可得到结论;(2)由AB 是∠O 的直径,得到AE ∠BE ,推出OI ∠BE ,根据三角形的中位线的性质得到AI =IE =BE ,推出AE =2BE ,根据相似三角形的性质得到12DE BE BE AE ==,求得BE =2,DE =1,AE =4,AD =3,由于∠ACD ∠∠BDE ,得到EC CD A BE D =即可求得BE 的长. (1)证明:∠IB 平分∠ABC ,∠∠ABI =∠CBI ,∠EB =EI ,∠∠EBI =∠EIB ,∠∠EIB =∠BAI +∠IBA ,∠EBI =∠IBC +∠CBE ,∠∠BAE =∠CBE ,∠∠CBE =∠EAC ,∠∠BAE =∠CAE ,∠AE 平分∠BAC ;(2)如图,∠AB 是∠O 的直径,∠AE ∠BE ,∠OI ∠AE ,∠OI ∠BE ,∠AO =BO ,∠AI =IE =BE ,∠AE =2BE ,∠∠EBC =∠BAE ,∠∠BDE ∠∠ABE , ∠12DE BE BE AE ==,∠BD∠BE =2,DE =1,∠∠E =∠C ,∠EBC =∠DAC∠∠ACD ∠∠BDE , ∠EC CD A BE D ==2, ∠22BE DE ==【点睛】本题考查了三角形的外接圆和外心,垂径定理,圆周角定理,三角形外角性质,等腰三角形的性质,能正确作出辅助线并求出AE =2BE 是解此题的关键.43.(1)证明见解析 (2)25cm 6PC =【分析】(1)连接OD .根据角平分线的定义,圆周角定理的推论确定BD CD =,根据垂。
一年级下册数学思维图填在圆圆圈10.20.30.40.50

一年级下册数学思维图填在圆圆圈10.20.30.40.50 题目
把10、20、30、40、50填在圈里,使每条直线上三个数的和相等.
答案
答案解析
中间圆圈的数很特殊,横行的三个数有它,竖列的三个数也有它,也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次.因为横行的三个数之和与竖列的三个数之和都等于(10+20+30+40+50
)+重叠数=每条直线上三数之和×2,所以,每条直线上三数之和=(150+重叠数)÷2
,因为每条直线上的三数之和是整数,所以重叠数只可能是10,30或50.。
一年级1到9填入圆圈题目

一年级1到9填入圆圈题目把1 9这9个数字分别填入下面的圆圈中,使每条线上的三个数相加的和都相等。
(三角形每条边上有三个圆圈)解析1. 1+2+3+4+5+6+7+8 + 9=(1 + 9)+(2+8)+(3 + 7)+(4+6)+5 = 45。
2. 因为三角形每条边上的三个数相加和相等,设这个和为S。
三条边数字之和为3S,但在计算三条边数字之和时,三个顶点的数字被重复计算了一次。
3. 我们假设三个顶点的数字分别为a、b、c。
则3S=45 + a + b+ c。
由于S为整数,a + b + c必须是3的倍数。
4. 可以先尝试把1、2、3放在顶点。
那么1+2+3 = 6。
此时3S=45+6 = 51,S = 17。
那么对于含1的这条边,剩下两个数之和为17 1=16,可以是7和9。
对于含2的这条边,剩下两个数之和为17 2 = 15,可以是6和9(9已用,舍去)或者5和10(10超出范围,舍去)或者4和11(超出范围,舍去)或者3和14(超出范围,舍去)或者2和15(超出范围,舍去)或者1和16(超出范围,舍去),所以这种顶点放置1、2、3不合适。
5. 再尝试把1、5、9放在顶点,1+5+9 = 15。
此时3S=45+15 = 60,S = 20。
对于含1的这条边,剩下两个数之和为20 1 = 19,可以是9和10(10超出范围,舍去)或者8和11(超出范围,舍去)或者7和12(超出范围,舍去)或者6和13(超出范围,舍去)或者5和14(超出范围,舍去)或者4和15(超出范围,舍去)或者3和16(超出范围,舍去)或者2和17(超出范围,舍去),所以这种顶点放置1、5、9不合适。
6. 尝试把1、4、7放在顶点,1+4+7 = 12。
此时3S=45+12 = 57,S = 19。
对于含1的这条边,剩下两个数之和为19 1 = 18,可以是9和9(重复,舍去)或者8和10(10超出范围,舍去)或者7和11(11超出范围,舍去)或者6和12(超出范围,舍去)或者5和13(超出范围,舍去)或者4和14(超出范围,舍去)或者3和15(超出范围,舍去)或者2和16(超出范围,舍去),所以这种顶点放置1、4、7不合适。
与圆有关的最值(取值范围)问题,附详细答案

与圆有关的最值(取值范围)问题,附详细答案1.在坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2.设tan∠BOC=m,则m的取值范围是____ _____.2.如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.(1)求证:AE=b+a;(2)求a+b的最大值;(3)若m是关于x的方程:x2+ax=b2+ab的一个根,求m的取值范围.3.如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为( ).A.3 B.6 C 33D.33BACMD 4.如图,A 点的坐标为(﹣2,1),以A 为圆心的⊙A 切x 轴于点B ,P (m ,n )为⊙A 上的一个动点,请探索n +m 的最大值.5.如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,点D 是平面内的一个动点,且AD =2,M 为BD 的中点,在D 点运动过程中,线段CM 长度的取值范围是 .6.如图是某种圆形装置的示意图,圆形装置中,⊙O 的直径AB =5,AB 的不同侧有定点C 和动点P ,tan ∠CAB =.其运动过程是:点P 在弧AB上滑动,过点C 作CP 的垂线,与PB 的延长线交于点Q . (1)当PC = 时,CQ 与⊙O 相切;此时CQ = . (2)当点P 运动到与点C 关于AB 对称时,求CQ 的长; (3)当点P 运动到弧AB 的中点时,求CQ 的长.(4)在点P 的运动过程中,线段CQ 长度的取值范围为 。
7.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=22D是线段BC上的一个动点,以AD为直径作⊙O分别交AB,AC于E,F两点,连接EF,则线段EF长度的最小值为.8.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD 的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,则PM长度的最大值是.9.如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x <4),则当x= 时,PD•CD的值最大,且最大值是为 .ODCEABE BODO BC10.如图,线段AB =4,C 为线段AB 上的一个动点,以AC 、BC 为边作等边△ACD 和等边△BCE ,⊙O 外接于△CDE ,则⊙O 半径的最小值为( ). A.4 23 C.322D. 211.在平面直角坐标系中,以坐标原点O 为圆心,2为半径画⊙O ,P 是⊙O 上一动点,且P 在第一象限内,过点P 作⊙O 的切线与x 轴相交于点A ,与y 轴相交于点B ,线段AB 长度的最小值是 .12.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,D 为AB 边上一点,过点D 作CD 的垂线交直线BC 于点E ,则线段CE 长度的最小值是 .13.如图,Rt △ABC 中,∠C =90°,∠A =30°,AB =4,以AC 上的一点O 为圆心OA 为半径作⊙O ,若⊙O 与边BC 始终有交点(包括B 、C 两点),则线段AO 的取值范围是 .14.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为()A.B.C.3 D.215.(2015•)抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),交y轴于点C.(1)求抛物线的函数表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.O ABDC P16.如图,已知A、B是⊙O与x轴的两个交点,⊙O的半径为1,P是该圆上第一象限内的一个动点,直线PA、PB分别交直线x=2于C、D两点,E为线段CD的中点.(1)判断直线PE与⊙O的位置关系并说明理由;(2)求线段CD长的最小值;(3)若E点的纵坐标为m,则m的范围为.17.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( ).(A)4 (B)215(C)358(D)174CQ PO AEFAQC PB18.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( ).A.194B.245C.5 D.4219.如图,在等腰Rt△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E在AB边上运动(点E不与点A重合),过A、D、E三点作⊙O,⊙O交AC于另一点F,在此运动变化的过程中,线段EF长度的最小值为.20.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,⊙C的半径为1,点P在斜边AB上,PQ切⊙O于点Q,则切线长PQ长度的最小值为( ).7 B.22 C. 3 D.421.在平面直角坐标系中,M(3,4),P是以M为圆心,2为半径的⊙M上一动点,A(-1,0)、B(1,0),连接PA、PB,则PA2+PB2最大值是 .参考答案引例1. 解:C 在以A 为圆心,以2为半径作圆周上,只有当OC 与圆A 相切(即到C 点)时,∠BOC 最小,AC =2,OA =3,由勾股定理得:OC =,∵∠BOA =∠ACO =90°,∴∠BOC +∠AOC =90°,∠CAO +∠AOC =90°,∴∠BOC =∠OAC ,tan ∠BOC =tan ∠OAC ==,随着C 的移动,∠BOC 越来越大,∵C 在第一象限,∴C 不到x 轴点,即∠BOC <90°, ∴tan ∠BOC ≥,故答案为:m ≥.引例1图引例2图引例2.2a b +≤;原题:(2013•武汉模拟)如图,在边长为1的等边△OAB 中,以边AB 为直径作⊙D ,以O 为圆心OA 长为半径作圆O ,C 为半圆AB 上不与A 、B 重合的一动点,射线AC 交⊙O 于点E ,BC =a ,AC =b .(1)求证:AE =b +a ;(2)求a +b 的最大值; (3)若m 是关于x 的方程:x 2+ax =b 2+ab 的一个根,求m 的取值范围.【考点】圆的综合题.【分析】(1)首先连接BE,由△OAB为等边三角形,可得∠AOB=60°,又由圆周角定理,可求得∠E的度数,又由AB为⊙D的直径,可求得CE的长,继而求得AE=b+a;(2)首先过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,可得(a+b)2= a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,即可求得答案;(3)由x2+ax=b2+ab,可得(x﹣b)(x+b+a)=0,则可求得x的值,继而可求得m的取值范围.【解答】解:(1)连接BE,∵△OAB为等边三角形,∴∠AOB=60°,∴∠AEB=30°,∵AB为直径,∴∠ACB=∠BCE=90°,∵BC=a,∴BE=2a,CE=a,∵AC=b,∴AE=b+a;(2)过点C作CH⊥AB于H,在Rt△ABC中,BC=a,AC=b,AB=1,∴a2+b2=1,∵S△ABC=AC•BC=AB•CH,∴AC•BC=AB•CH,∴(a+b)2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2,∴a+b≤,故a+b的最大值为,(3)∵x2+ax=b2+ab,∴x2﹣b2+ax﹣ab=0,∴(x+b)(x﹣b)+a(x﹣b)=0,∴(x﹣b)(x+b+a)=0,∴x=b或x=﹣(b+a),当m=b时,m=b=AC<AB=1,∴0<m<1,当m=﹣(b+a)时,由(1)知AE=﹣m,又∵AB<AE≤2AO=2,∴1<﹣m≤2,∴﹣2≤m<﹣1,∴m的取值范围为0<m<1或﹣2≤m<﹣1.【点评】此题考查了圆周角定理、等边三角形的性质、完全平方公式的应用以及一元二次方程的解法.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.引例3.解:连接EP,DP,过P点作PM垂直DE于点M,过O做OF⊥AC与F,连接AO,如图,∵∠BAC=60°,∴∠DPE=120°.∵PE=PD,PM⊥DE,∴∠EPM=60°,∴ED=2EM=2EP•sin60°=EP=P A.当P与A、O共线时,且在O点右侧时,⊙P直径最大.∵⊙O与∠BAC两边均相切,且∠BAC=60°,∴∠OAF=30°,OF=1,∴AO==2,AP=2+1=3,∴DE=PA=3.故答案为:D。
圆的认识与圆周率专项练习30题(有答案)ok

圆的认识与圆周率专项练习30题(有答案)一.选择题(共19小题)1.所有的车轮都做成圆形是利用了圆的()特性.A.曲线图形B.容易加工C.圆心到圆上任意一点的距离相等2.圆的半径决定圆的()A.大小B.位置C.形状3.圆周率表示()A.圆的周长B.圆的面积与直径的倍数关系C.圆的周长与直径的倍数关系4.圆的周长与直径的比值是一个()A.无限小数B.有限小数C.无限不循环小数5.以一点为圆心可以画出()个圆.A.1B.2C.无数D.无答案6.下列说法正确的是()A.用圆规画圆时.若圆规两脚间的距离是3cm,则所画圆的直接为3cmB.用4个圆心角都是90°的扇形,一定可以拼成一个圆C.圆的半径扩大到原来的2倍,周长也扩大到原来的2倍D.小明身高1m,爸爸身高180cm,小明和爸爸身高的比是1:1807.下列说法错误的是()A.半径一定比直径短B.圆具有对称性C.圆是曲线图形8.下面几种说法中正确的是()A.圆周率表示圆的周长B.圆周率表示圆的周长与它直径的比的比值C.圆周率表示π保留两位小数的近似值9.关于圆周率的说法错误的是()A.是圆的直径与周长的比值B.是一个无限不循环小数C.计算时通常取3.1410.两个圆的面积不相等,是因为()不同.A.圆心的位置B.半径C.圆周率11.大圆的周长除以它的直径()小圆的周长除以它的直径.A.大于B.小于C.等于12.下列说法错误的是()A.同一个圆的直径为半径的二倍B.圆有无数条对称轴C.圆锥的体积是圆柱体积的三分之一D.圆柱的侧面展开图为长方形13.下面各数中,用()表示圆周率更精确.A.B.3.14 C.D.314.关于圆周率π说法正确的是()A.π是直径和圆周长的比B.圆周长是半径的π倍C.π是一个无限不循环小数D.π=3.1415.一个长方形的长是4厘米,宽是2厘米,在长方形内画一个最大的圆,圆的直径长是()厘米.A.4B.1.25 C.2.5 D.216.半径3厘米的圆的圆周率()半径5厘米的圆的圆周率.A.大于B.小于C.等于17.圆周率是()A.圆的周长÷直径 B.圆的周长÷半径 C.圆的面积÷直径 D.圆的面积÷半径18.下列说法中不正确的是()A.圆周率π的值是圆周长与直径的比值B.圆周率π的值是圆面积与直径的比值C.圆周率π的值与圆的大小无关D.圆周率π的值是一个无限不循环小数19.圆的周长与它的直径的商是()A.3.14 B.3C.π20.在一张长32cm,宽16cm的长方形纸内画半径是4cm的圆,这样的圆最多能画_________个.21.同一个圆内直径与半径的比是_________:_________.22.在一个圆里挖去一个小圆就得到一个圆环._________.23.把一张圆形纸对折一次,这条折痕是圆的_________.24.如图由一个正方形、一个大圆和两个相等的小圆组成,如果正方形的边长是8厘米,那么小圆的半径是_________厘米.25.圆是_________图形,圆的任意一条_________所在的直线都是圆的对称轴.26.如图,一个圆有无数条对称轴,对折后的折痕所在的直线都是对称轴,它们都交于一点,这个点就是_________,这些折痕就是_________.27.到圆上各点的距离相等的点只有圆心一个点._________.28.图中,圆的半径是多少厘米?圆的直径是多少厘米?29.看一看,填一填.(1)圆的直径是_________,正方形的边长是_________.(2)大圆的直径是_________,小圆的半径是_________.(3)圆的直径是_________,圆的半径是_________.(4)圆的直径是_________,圆的半径是_________.30.你能用直角三角板或直尺找出一个圆的圆心吗?简要地写出你的解决问题的想法或在图中画出你的思路.(一种方法的5分)参考答案:1.由分析得出:所有的车轮都做成圆形是利用了圆的圆心到圆上任意一点的距离相等特性.故选:C.2.根据圆的特征可知:圆的半径决定圆的大小;故选:A.3.由圆周率的含义可知:圆周率π表示圆的周长与直径的倍数关系;故选:C4.由分析知:圆的周长与直径的比值是一个无限不循环小数;故选:C5.以一点为圆心,以任意长为半径可以画无数个同心圆,故选C.6.A、用圆规画圆时.若圆规两脚间的距离是3cm,则所画圆的直径为3cm,说法错误,应为6厘米;B、用4个圆心角都是90°的扇形,一定可以拼成一个圆,说法错误,必须是4个完全一样圆心角为90度的扇形;C、根据圆的周长计算公式C=πd可知:圆的半径扩大到原来的2倍,周长也扩大到原来的2倍;D、小明身高1m,爸爸身高180cm,小明和爸爸身高的比是1:180,说法错误,应统一单位;故选:C7.A、半径一定比直径短,说法错误,如一个圆的半径是5厘米,另一个圆的直径是4,前提是必须是在同圆或等圆中,半径一定比直径短;B、圆是轴对称图形,具有对称性,故B说法正确;C、圆是曲线图形,说法正确;故选:A8.根据圆周率的含义可知:A、圆周率表示圆的周长,说法错误;B、圆周率表示圆的周长与它直径的比的比值,说法正确;C、圆周率表示π保留两位小数的近似值,说法错误;故选:B9.A、圆周率是圆的周长和它直径的比值,故圆周率是圆的直径与周长的比值的说法错误,符合题意;B、圆周率是一个无限不循环小数的说法正确,不符合题意;C、因为圆周率的近似值是3.14,所以计算时通常取3.14的说法正确,不符合题意;故选:A10.由“圆的面积=πr2”可知:圆的面积和半径、圆周率有关系,因为圆周率不变,所以只与半径有关,即:两个圆的面积不相等,是因为半径不同;故选:B.11.根据圆周率的含义可知:大圆的周长除以它的直径等于小圆的周长除以它的直径;故选:C.12.(1)在同一个圆中,直径等于半径的2倍,正确;(2)圆的直径所在的直线就是圆的对称轴,因为圆有无数条直径,所以圆有无数条对称轴,正确;(3)等底等高的圆锥体的体积是圆柱体体积的三分之一,所以原题说法错误;(4)圆柱的侧面展开图为长方形,圆柱的高等于长方形的宽,底面周长等于长方形的长,原题说法正确.故选:C13.=3.4285;=3.1415929203539…;π的取值在3.1415926至3.1415927之间,所以表示圆周率更精确;故答案选:C14.A、π是直径和圆周长的比,说法错误,应为π是圆的周长和它直径的比值;B、圆周长是直径的π倍,而不是半径的π倍,故B说法错误;C、π是一个无限不循环小数,说法正确;D、π=3.14,说法错误,因为π的近似值是3.14;故选:C15.一个长方形的长是4厘米,宽是2厘米,在长方形内画一个最大的圆,圆的直径长是2厘米;故选:D.16.根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率”可知:半径3厘米的圆的圆周率等于半径5厘米的圆的圆周率;故选:C17. 圆的周长÷直径=圆周率(π);故选:A.18.A、由圆周率的含义可知:圆周率π的值是圆周长与直径的比值;进而得出A正确;B、圆周率π的值是圆面积与直径的比值,说法错误,即B错误;C、圆周率π的值是圆周长与直径的比值,所以周率π的值与圆的大小无关,C说法正确;D、圆周率=3.1415926…,是一个无限不循环小数,所以D说法正确;故选:B19.圆的周长与它的直径的比值是:π,即圆的周长与它的直径的商是π;故选:C.20.R=2×4=8(厘米),32÷8=4(个),16÷8=2(个),4×2=8(个),故答案为:821. 通过圆的直径和半径的定义可知,直径:半径=2:1.故答案为:2,122.在圆内剪去一个小圆便成为圆环.说法错误,因为只有当大圆和小圆是同一个圆心时,从大圆中减去一个小圆,才能成为圆环;故答案为:错误.23.由直径的含义可知:把一张圆形纸对折一次,这条折痕是圆的直径;故答案为:直径.24.8÷2÷2,=4÷2,=2(厘米);答:小圆的半径是2厘米;故答案为:225.圆是轴对称图形,圆的任意一条直径所在的直线都是圆的对称轴.26.如图,一个圆有无数条对称轴,对折后的折痕所在的直线都是对称轴,它们都交于一点,这个点就是圆心,这些折痕就是直径.27.圆上任意一点到圆心的距离都是半径,在同圆中,所有的半径都相等;反之也是正确的.故答案为:正确.28.12÷3=4(厘米);4×2=8(厘米);答:圆的半径是4厘米,圆的直径是8厘米29.看一看,填一填.(1)圆的直径是10厘米,正方形的边长是10厘米.(2)大圆的直径是3厘米,小圆的半径是2厘米.(3)圆的直径是6厘米,圆的半径是3厘米.(4)圆的直径是 4.5厘米,圆的半径是 2.25厘米.30.(1)选择合适的直角三角板,用等腰直角三角板;(2)用直角三角板的直角和圆上一点重合,沿两直角边划直线,连接两条直线与圆的交点,两圆之间的线段即为⊙O的直径;(3)因为直角三角板上角的度数是一定的,所以过直角三角形的顶点向斜边作垂线即可.斜边与垂线的交点即为该圆的圆心。
数字推理圆圈题

数字推理圆圈题一、什么是数字推理圆圈题数字推理圆圈题啊,就是那种在圆圈里有数字,然后通过这些数字之间的关系来找出规律的题目。
比如说,可能是圆圈里几个数字进行加减乘除运算能得到另一个数字,或者是数字之间有等差、等比之类的关系,只不过这些数字都在圆圈这个特定的形式里呈现出来啦。
二、做数字推理圆圈题的小技巧1. 先整体看把整个圆圈里的数字都看一遍,大概感受一下这些数字是大是小,是整数还是小数之类的。
有时候从整体上就能发现一些比较明显的规律,像如果所有数字都是偶数,那说不定规律就和偶数的一些性质有关呢。
2. 找特殊数字在圆圈里的数字中,有些数字可能比较特殊。
比如是0啊,1啊,或者是和题目给出的一些限制条件相关的数字。
像如果题目说所有数字都是某个数的倍数,那这个倍数数字就是很关键的特殊数字啦。
如果有0的话,那和0相关的运算规则就很值得思考,像任何数乘以0都得0这种。
3. 尝试运算从简单的运算开始尝试,先加减,再乘除。
看看相邻的数字之间做这些运算能不能得到什么规律。
要是相邻数字不行,就再看看间隔数字之间的运算关系。
比如说,第一个圆圈里的数字1和3,先算 1 + 3 = 4,再看看这个4和圆圈里其他数字或者整个题目有没有什么联系。
如果没有,再试试1 - 3或者1 × 3之类的运算。
三、数字推理圆圈题示例比如说有这样一个数字推理圆圈题,一个圆圈被分成了三部分,上面部分数字是2,左边部分数字是3,右边部分数字是6。
那我们就可以先按照刚刚说的小技巧来做。
整体看这几个数字都是比较小的整数。
特殊数字呢,2是最小的质数,3也是质数。
然后我们尝试运算,2 × 3 = 6,正好就是右边的数字。
这可能就是这道题的规律啦。
四、答案和解析1. 答案就像上面那道示例题,答案就是通过前面数字的乘法运算得到后面的数字。
2. 解析我们先整体看数字,确定数字的范围和大致特征。
然后发现2和3都是质数这个特殊之处,再尝试不同的运算,当尝试到乘法时,发现 2 × 3 = 6,符合这个圆圈里数字之间的关系。
一年级数学画圈题

一年级数学画圈题通常是为了锻炼学生的观察和思维能力,同时也是为了加强学生对数学知识的理解和记忆。
以下是一些一年级数学画圈题的示例:
1.在下列数字中,把相同的数字圈起来:
35 46 53 64 78 89 97
2.在下列图形中,把相同数量的圆圈圈起来:
○ ○ △△☆☆ □ □
3.在下列数字中,把比30大的数字圈起来:
20 35 40 15 50
4.在下列图形中,把三角形圈起来:
○ △☆ □
5.在下列数字中,把比50小的数字圈起来:
40 55 60 70 80
这些题目可以让学生更好地理解数字、图形等基本数学概念,并且通过画圈的方式加强记忆和理解。
同时,这些题目也可以培养学生的观察和思维能力,提高他们的注意力和专注力。
趣味数学19张圆卡片涂色解题

趣味数学19张圆卡片涂色解题【原创版】目录1.趣味数学的概述2.19 张圆卡片的解题思路3.涂色解题的技巧和方法4.解题过程中需要注意的细节5.趣味数学的启示和价值正文【提纲】1.趣味数学的概述趣味数学是一种将数学知识和趣味性结合在一起的数学游戏,旨在让人们在轻松愉快的氛围中学习数学,提高数学思维能力和解决实际问题的能力。
在趣味数学中,题目往往以一些幽默、巧妙或者奇特的方式呈现,引人入胜,让人乐此不疲。
2.19 张圆卡片的解题思路19 张圆卡片是一种经典的趣味数学题目。
题目中给出了 19 张圆形卡片,每张卡片上都有一个数字,要求通过移动这些卡片,使得每张卡片上的数字按照一定的顺序排列,而且移动的次数要尽可能地少。
3.涂色解题的技巧和方法涂色解题是一种常见的趣味数学解题方法。
在涂色解题中,我们需要根据题目的要求,将一些图形或者卡片涂上特定的颜色,以满足题目的条件。
涂色解题的技巧和方法主要包括以下几点:(1)观察题目中的规律和特点,找出解题的关键所在;(2)充分利用题目中给出的条件,尝试从不同的角度去解决问题;(3)注意涂色的顺序和方法,避免重复劳动和无效的尝试;(4)保持耐心和细心,不要轻易放弃,相信自己一定能够找到解决问题的方法。
4.解题过程中需要注意的细节在解题过程中,我们需要注意以下几个细节:(1)仔细阅读题目,理解题目的要求和条件;(2)在涂色解题中,要注意颜色的排列和搭配,避免出现重复或者错误的颜色;(3)在移动卡片解题中,要注意卡片的顺序和位置,确保移动的次数最少;(4)在解题过程中,要保持良好的心态,不要因为遇到困难而灰心丧气。
5.趣味数学的启示和价值趣味数学不仅能够帮助我们增强数学思维能力,提高解决实际问题的能力,还能够激发我们对数学的兴趣和热情。
数学题圆圈里面数字规律_解释说明

数学题圆圈里面数字规律解释说明1. 引言1.1 概述本文将探讨数学题中关于圆圈内数字的规律和变化,旨在解释说明这些数字规律的背后原理以及应用领域。
在数学问题中,我们常会遇到给定一组数字并要求找出它们之间的规律或预测下一个满足条件的数字等情况。
而圆圈里面数字的排列规律是其中一种常见形式,通过深入分析和解释这种数学现象,可以帮助读者更好地理解这类题目。
1.2 文章结构本文按照以下结构进行讲述:首先,在第二部分将介绍圆圈里面数字的排列规律、数字之间的关系以及圆圈中数字的变化规律;然后,在第三部分将具体解释说明如何通过参照数值对应关系进行推理解释、运算规则对数字产生影响以及给定数字求下一个满足条件的数值等问题;接着,在第四部分将应用和拓展这些数字规律,并阐述其在数学题中的应用和其他领域中可能涉及到的应用场景;最后,在结论部分对整篇文章进行总结归纳。
1.3 目的本文主要目的是通过解释和说明圆圈数字规律的背后原理,帮助读者更好地理解数学题中这一类特殊的问题。
同时,我们还将探讨该数字规律在其他领域的应用,并展示如何拓展和扩展这些规律。
尽管本文使用了圆圈内数字规律作为案例进行说明,但读者可以将所学到的方法和思路应用到更广泛的数学问题中,提高自己的解题能力和思维逻辑。
2. 数字规律的介绍:2.1 圆圈里面数字的排列规律在圆圈中,数字的排列遵循一定的规律。
通常情况下,相邻数字之间存在一定的关系,这种关系可以是递增、递减或者其他特定的变化方式。
圆圈中的数字通常按照某种规则进行排列,比如从左上角开始顺时针方向排列,或者从外层开始逐渐向内部移动。
这样的排列方式使得我们能够更好地理解和解读数字之间的关系。
2.2 数字之间的关系在圆圈中,数字之间可能存在多种不同的关系。
其中一种常见的关系是相邻数字之间差值恒定。
例如,在一个由1到10组成的圆圈里,相邻两个数字之间都相差1。
另一种常见的关系是相邻两个数字之和恒定。
例如,在一个由1到9组成的圆圈里,任意两个相邻数字之和都为10。
初三年级数学圆经典例题
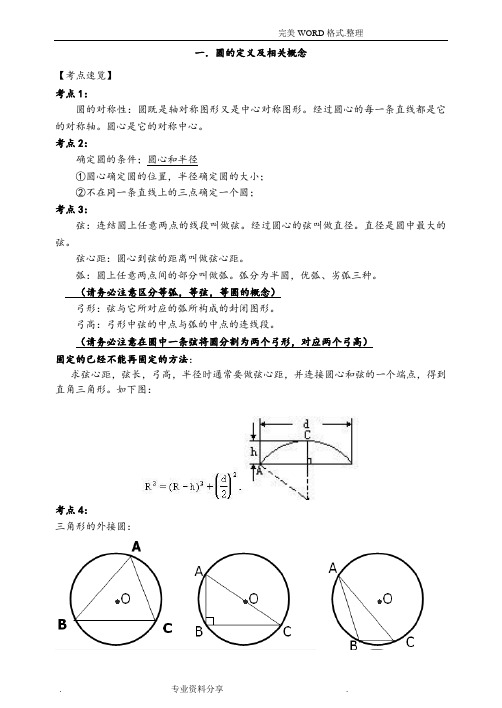
一.圆的定义及相关概念【考点速览】考点1:圆的对称性:圆既是轴对称图形又是中心对称图形。
经过圆心的每一条直线都是它的对称轴。
圆心是它的对称中心。
考点2:确定圆的条件;圆心和半径①圆心确定圆的位置,半径确定圆的大小;②不在同一条直线上的三点确定一个圆;考点3:弦:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
直径是圆中最大的弦。
弦心距:圆心到弦的距离叫做弦心距。
弧:圆上任意两点间的部分叫做弧。
弧分为半圆,优弧、劣弧三种。
(请务必注意区分等弧,等弦,等圆的概念)弓形:弦与它所对应的弧所构成的封闭图形。
弓高:弓形中弦的中点与弧的中点的连线段。
(请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高)固定的已经不能再固定的方法:求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。
如下图:考点4:三角形的外接圆:锐角三角形的外心在 ,直角三角形的外心在 ,钝角三角形的外心在 。
考点5点和圆的位置关系 设圆的半径为r ,点到圆心的距离为d , 则点与圆的位置关系有三种。
①点在圆外⇔d >r ;②点在圆上⇔d=r ;③点在圆内⇔ d <r ;【典型例题】例1 在⊿ABC 中,∠ACB =90°,AC =2,BC =4,CM 是AB 边上的中线,以点C 为圆心,以5为半径作圆,试确定A,B,M 三点分别与⊙C 有怎样的位置关系,并说明你的理由。
例2.已知,如图,CD 是直径,︒=∠84EOD ,AE 交⊙O 于B ,且AB=OC ,求∠A 的度数。
例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ,最大为8cm ,则这圆的半径是_________cm 。
例4 在半径为5cm 的圆中,弦AB ∥CD ,AB=6cm ,CD=8cm ,则AB 和CD 的距离是多少? 例5 如图,⊙O 的直径AB 和弦CD 相交于点E ,已知AE=6cm ,EB=2cm,30=∠CEA , 求CD 的长.例6.已知:⊙O 的半径0A=1,弦AB 、AC 的长分别为3,2,求BAC ∠的度数.AB DCO· EMABCDOEBACACBD例7.如图,已知在ABC ∆中,︒=∠90A ,AB=3cm ,AC=4cm ,以点A 为圆心,AC 长为半径画弧交CB 的延长线于点D ,求CD 的长.例8、如图,有一圆弧开桥拱,拱的跨度AB =16cm ,拱高CD =4cm ,那么拱形的半径是__m 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学名题:圆圈标数经典系列
————————————————————————————————作者:————————————————————————————————日期:
[阅读材料] 圆圈标数经典系列
在教学过程中一些同类型的题见得多了,可以挖掘一下,整理出来,供读者参考。
现给大家献上在直线与圆圈上写数以及二者之间关系的系列名题。
题目1. 今要在一个圆周上标出一
些数,第一次先把圆周二等分,在两个分点旁分别标上
3
1
21和,第二次把两段半圆弧二等分,在分点旁标上相邻两分点旁所标两数的和
3
1
2165+=,
第三次把4段圆弧二等分,并在4个分点旁标上相邻两分点旁所标两数的和6
5
31611,6521311
+=+=如此继续下去,当第八次标完数以后,圆周上所有已标数的总和是多少?
解析:碰到这样的题,可先把
3
1
21和改作A 与B ,整个探索过程不把每一个复杂的和算出,只是数出A 与B 的总个数。
这样第一次为A 与B 和的一倍,第二次后为3A+ 3B ,第三次标完后为9A+9B ,……… 这样能较容易地发现规律:每次新的结果总是原来的3倍。
正是因为增加的每个数都是原来相邻两个数之和,所以每次增加数的总和恰好是原来所有数总和的2倍,也就是说每次标完数后圆周上所有数的总和是前一步标完数后圆周上所有数的总和的3倍,例如:二分之一它在左边算了一次,在右边算了一次,本身一次,所以二分之一在下次标完后已成为原为的3倍了,其它数也是如此。
于是第八次标完数后圆周上所有数的总和是:
7111()31822232
+⨯=. 变化一
题目2. 今要在一条线段上标出一些数,第一次在两个端点旁分别标上
3
1
21和,第二次把线段二等分,在中点旁标上两边所标两数的和
3
1
2165+=,第三次把2段线段各二等分,并在2个分点旁标上相邻两分点旁所标两数的和
6
5
31611,6521311+=+=,即每次都在已写上的两个相邻数之间,写上这两个相邻数之和,如此继续下去,当第八次标完数以后,线段上所有已标数的总和是多少?
解析:与上题一样先把
3
1
21和改作A 与B ,次数与A+B 的个数填入下表: 写数的次数 1 2 3 4 5 A+ B 的个数
1
3
9
27
81
写数的次数 1 2 3 4 5 A+ B 的个数
1
2
5
14
41
这串数有什么规律吗?可以看出后一数总是前一个数的3倍减1,则可算出第八次为:1094个A+B,代入计算可得3
2911。
为什么是3倍减一的关系呢? 这是因为这种标数方法每一次除了两端的数算两次外,其余每数都要算3次,因此乘3后得减去1个A+B 。
寻求最佳解法:可借助上题的结论。
再取一条本题所说的线段同样标数,这样把两条线段两端对接围成一个圆圈,这个圆圈的和比上题多出了一个
3
1
21和,反过来,给上题的圆圈在3121和旁边再各补上一个3
1
21和,然后切成两段,其中的一段就是第二题的结论。
因此可用上题的结论来列式:7115152
(()3)2(1822)2911236263
+⨯+÷=+÷=也得到同样结果。
变化二:
题目3. 在2,3两数之间,第一次写上5(5=2+3),第二次在2,5和5,3之间分别
写上7(7=2+5),8(8=5+3),即每次都在已写上的两个相邻数之间,写上这两个相邻数之和,这样的过程共重复6次,问所有数之和是 。
2...7...5...8 (3)
用找规律的办法,列出数据, 写数的次数 原始 1 2 3 4 每次的总和
5
10
25
70
205
有上两题的经验,这里也是3倍减1的递推关系。
可求得1825。
模仿第二题的最佳解法试试:5
((23)35)21825+⨯+÷=,也就是先把本题当成类似题1的圆圈上标数后再多加上2与3,然后切成两条线,其中的一条是本题所求。
这一思路可能对其它类似题目有所帮助。
在实际教学中发现很多学生拿不准次数,总要算成数列中的前一个或后一个,这里要提醒大家对原始状态与第一次一定要区分开。
变化三:
题目4. 在一个圆上标出一些数:第一次先把圆周二等分,在两个分点分别标上2和4。
第二次把两段半圆弧分别二等分,在分点标上相邻两分点两数的平均数3(见右图)。
第三次把四段弧再分别二等分,在四个分点分别标上相邻两分点两数的平均数。
如此下去,当第8次标完后,圆周上所有标出的数的总和是多少?
提示:第一次标完数后,以后每次标上的数字之和都等于上次圆周上的所有数字之和,即每次标完数后,圆周上的所有数字之和是原来的2倍。
第8次标完后的总和是
6×28-1=6×27=768。
变化四:
第一次操作,在圆上两个不同的点上分别写上数4和3,第二次操作,在数字3,4 将圆周分成的两条圆弧的中点处分别写上3与4的和,第三次操作,在四个四分之一圆弧的中点处分别写上每条弧的两端点上的数之和;……;如图1所示,每次都在由数字划分出的圆弧的中点处分别写上这条弧的两端点上的两个数的和。
(1)操作了10次后,圆周上的所有数的和
是。
(2)20次操作后圆周上的所有数的和与22次操作后
圆周上的所有数的和的比是。
(第十届华杯赛试题)
提示:设第K次操作后圆周上的数字的和是S,则
S1=7,并且,第K+1次操作后圆周上新写上的数字的和是2k S,因此
(1)当K+1=10时,
10
S=7×103=7×3×81×81=137781
(2)20
221 9
S
S
答:(1)操作了10次后,圆周上的所有数的和是137781,(2)20次操作后圆周上的所有数
的和与22次操作后圆周上的所有数的和的比是1
9。
评注:这是一道简单的推进归纳的题目,如果将本题中的圆周改成直线段,问题会复杂一些,而且可以编出更为新颖和难度更高的问题,例如:
在4,3 两数之间,第一次写上7,第二次在4和7之间,7和3之间分别写上11和10,如下所示:第0次操作:4 3
第1次操作:4 7 3
第2次操作:4 11 7 10 3
以后每次操作都在两个相邻数之间写上这两个相邻数之和,小明将这样的过程共操作了M 次,并写上所有数的和,小华将这样的过程共操作了N次,并写下所以数的和,若二人的和数之差是1000的倍数,问小明至少比小华多操作多少次?
变化五:
题目5.一条直径将圆周分成两个半圆周,在每个分点标上质数P,第二次将两个半圆
周分别分成两个相等的
41圆周,在新产生的分点标上相邻两数和的2
1
,第三次将四个41圆周分别分成两个相等的81
圆周,在新产生的分点标上相邻两数和的
3
1
;……;如此进行了N 次,最后,圆周上所有数的和为11130,求N ,和P 的值各为多少?
参考答案:104与3
变化六:
题目6. 在数3与7之间第一次写上10 ,第二次分别在3与10 ,10与7之间写上
310107,
22++,第三次分别在3与132,132与10,10与172, 17
2
与7之间写上1131131171173,10,10,7,
32323232⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭
,第N 次在每
相邻的两数之间写上这两数和的
1
n
倍(N=1,2,3,……)。
求第10次写完数后该行所有数之和。
(如下所示)
初始:3,7
第一次后:3,10,7
第二次后:3,132,10,17
2,7,
第三次后:191311371731
3,,,,10,,,,7622626
(2007 Enjoy Mathematics Camp )
参考答案:335。
