中考数学专题复习 专题八 图形折叠问题训练
中考数学八大题型集训:专题复习(5)图形的折叠问题含解析

专题复习(五) 图形的折叠问题折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中,其实质是轴对称性质的应用.解题的关键利用轴对称的性质找到折叠前后不变量与变量,运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.类型1 三角形中的折叠问题(·宜宾)如图,一次函数的图象与x 轴、y 轴分别相交于点A 、B ,将△AOB 沿直线AB 翻折,得△ACB.若C(32,32),则该一次函数的解析式为________.【思路点拨】 利用翻折变换的性质结合锐角三角函数关系得出CO ,AO 的长,进而得出A 、B 两点的坐标,再利用待定系数法求出直线AB 的解析式.【解答】 连接OC ,过点C 作CD⊥x 轴于点D ,∵将△AOB 沿直线AB 翻折,得△ACB,C(32,32),∴AO =AC ,OD =32,DC =32,BO =BC ,则tan ∠COD =CD OD =33,故∠COD=30°,∠BOC =60°,∴△BOC 是等边三角形,且∠CAD=60°. 则sin60°=CD AC ,则AC =DCsin60°=1,故A(1,0),sin30°=CD CO =32CO =12.则CO =3,故BO =3,B 点坐标为(0,3),设直线AB 的解析式为y =kx +3,把A(1,0)代入解析式可得k =- 3. ∴直线AB 的解析式为y =-3x + 3.折叠(翻折)意味着轴对称,会生成相等的线段和角,这样便于将条件集中.如果题目中有直角,则通常将条件集中于较小的直角三角形,利用勾股定理求解.1.(·绵阳)如图,D 是等边△ABC 边AB 上的一点,且AD∶DB=1∶2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE∶CF=( )A.34B.45C.56D.672.(·德阳)如图,△ABC 中,∠A =60°,将△ABC 沿DE 翻折后,点A 落在BC 边上的点A′处.如果∠A′EC =70°,那么∠A′DE 的度数为________.3.(·宜宾)如图,在Rt△ABC 中,∠B =90°,AB =3,BC =4,将△ABC 折叠,使点B 恰好落在边AC 上,与点B′重合,AE 为折痕,则EB′=________.4.(·滨州)如图,在平面直角坐标系中,将矩形AOCD 沿直线AE 折叠(点E 在边DC 上),折叠后顶点D 恰好落在边OC 上的点F 处,若点D 的坐标为(10,8),则点E 的坐标为________.类型2 四边形及其他图形中的折叠问题(·南充)如图,在矩形纸片ABCD 中,将△AMP 和△BPQ 分别沿PM 和PQ 折叠(AP >AM),点A 和点B 都与点E 重合;再将△CQD 沿DQ 折叠,点C 落在线段EQ 上点F 处.(1)判断△AMP,△BPQ ,△CQD 和△FDM 中有哪几对相似三角形?(不需说明理由)(2)如果AM =1,sin ∠DMF =35,求AB 的长.【思路点拨】 (1)由矩形的性质得∠A =∠B =∠C =90°,由折叠的性质和等角的余角相等,可得∠BPQ =∠AMP =∠DQC ,所以△AMP∽△BPQ∽△CQD ;(2)设AP =x ,由折叠关系可得:BP =AP =EP =x ,AB =DC =2x ,AM =1,根据△AMP∽△BPQ 得:AMBP=AP BQ ,即BQ =x 2,根据△AMP∽△CQD 得:AP CD =AM CQ ,即CQ =2,从而得出AD =BC =BQ +CQ =x 2+2,MD =AD -AM =x 2+2-1=x 2+1,根据Rt △FDM 中∠DMF 的正弦值得出x 的值,从而求出AB 的值.【解答】 (1)有三对相似三角形,即△AMP∽△BPQ∽△CQD. 理由如下:∵四边形ABCD 是矩形, ∴∠A =∠B=∠C=90°.根据折叠可知:∠APM=∠EPM,∠EPQ =∠BPQ,∴∠APM +∠BPQ=∠EPM+∠EPQ=90°. ∵∠APM +∠AMP=90°,∴∠BPQ =∠AMP,∴△AMP ∽△BPQ , 同理:△BPQ∽△CQD. ∴△AMP ∽△BPQ ∽△CQD. (2)设AP =x ,∴由折叠关系,BP =AP =EP =x ,AB =DC =2x.由△AMP∽△BPQ 得,AM BP =AP BQ ,即1x =xBQ ,得BQ =x 2.由△AMP∽△CQD 得,AP CD =AM CQ ,即x 2x =1CQ ,得CQ =2.∴AD =BC =BQ +CQ =x 2+2.∴MD =AD -1=x 2+1.∵在Rt△FDM 中,sin ∠DMF =35,∴2x x 2+1=35.解得x 1=3,x 2=13(不合题意,舍去). 即AB =6.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数,或者利用折叠性质以及勾股定理求线段长度.矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图),从而构造相似三角形,利用相似三角形求边或者角的度数.1.(·南充)如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′处,若AE =2,DE =6,∠EFB =60°,则矩形ABCD 的面积是( )A .12B .24C .12 3D .16 32.(·泸州)如图,在△ABC 中,AB =AC ,BC =24,tanC =2,如果将△ABC 沿直线l 翻折后,点B 落在边AC 的中点E 处,直线l 与边BC 交于点D ,那么BD 的长为( )A.13 B.152C.272D.123.(·德阳)将抛物线y=-x2+2x+3在x轴上方的部分沿x轴翻折至x轴下方,图象的剩余部分不变,得到一个新的函数图象,那么直线y=x+b与此新图象的交点个数的情况有()A.6种 B.5种 C.4种 D.3种4.(·成都)如图,在□ABCD中,AB=13,AD=4,将ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为________.5.(·内江)如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为________.6.(·南充)如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是________.7.(·绵阳)如图1,在矩形ABCD中,AB=4,AD=3,将矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,顶点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.参考答案类型1 三角形中的折叠问题1.B 提示:∵△ABC 为等边三角形,∴∠A =∠B=∠C=60°.又∵折叠△ABC,使得点C 恰好与边AB 上的点D 重合,折痕为EF ,∴∠EDF =∠C=60°,CE =DE ,CF =DF.∴∠ADE+∠FDB=120°.∴∠AED =∠FDB.∴△AED∽△BDF.∴AE BD =AD BF =DEFD .设等边△ABC 边长为6个单位,CE =x ,CF =y ,AE =6-x ,BC =6-y ,∴6-x 4=26-y =x y ,解得x =145,y =72.∴x ∶y =4∶5,故选择B.2.65°3.1.54.(10,3)类型2 四边形及其他图形中的折叠问题1.D 2.A3.B 提示:由题意,易知y =-x 2+2x +3与x 轴的两个交点坐标分别为(3,0)和(-1,0),顶点坐标为(1,4),顶点关于x 轴对称点的坐标为(1,-4).当直线y =x +b 过(-1,0)时,b =1,此时直线与新的函数图象只有一个交点;当b>1时,此时直线与新的函数图象无交点;当直线y =x +b 过(3,0)时,b =-3,此时直线与新的函数图象有三个交点;观察图象,易知:当-3<b<1时,此时直线与新的函数图象有三个交点;当直线y =x +b 过(1,-4)时,b =-5,此时直线与新的函数图象有三个交点;观察图象,易知:当-5≤b<-3时,此时直线与新的函数图象有四个交点;观察图象,易知:当b<-5时,此时直线与新的函数图象有二个交点;综上,直线y =x +b 与此新图象的交点的个数的情况有5种,故选B.4.35. 6 提示:作AH⊥BC 于H.∵分别以AE ,BE 为折痕将两个角(∠D,∠C)向内折叠,点C ,D 恰好落在AB 边的点F 处,∴DE =EF ,CE =EF ,AF =AD =2,BF =CB =3.∴DC=2EF ,AB =5.∵AD∥BC,∠C =90°, ∴四边形ADCH 为矩形,∴AH =DC =2EF ,HB =BC -CH =BC -AD =1.在Rt△ABH 中,AH =AB 2-BH 2=26,∴EF = 6. 6.2≤x≤87.(1)证明:由矩形的性质可知△ADC≌△CEA,∴AD =CE ,DC =EA ,∠ACD =∠CAE. 在△CED 与△ADE 中,⎩⎪⎨⎪⎧CE =AD ,DE =ED ,DC =EA ,∴△DEC ≌△EDA.(2)∵∠ACD=∠CAE,∴AF =CF.设DF =x ,则AF =CF =4-x ,在Rt△ADF 中,AD 2+DF 2=AF 2,即32+x 2=(4-x)2,解得x =78,即DF =78.(3)由矩形PQMN 的性质得PQ∥CA, ∴PE CE =PQCA. 又∵CE=3,AC =AB 2+BC 2=5.设PE =x(0<x <3),则x 3=PQ 5,即PQ =53x.过E 作EG⊥AC 于G ,则PN∥EG,∴CP CE =PN EG. 又∵在Rt△AEC 中,EG ·AC =AE·CE,解得EG =125.∴3-x 3=PN 125,即PN =45(3-x).设矩形PQMN 的面积为S ,则S =PQ·PN=-43x 2+4x =-43(x -32)2+3(0<x <3).∴当x =32,即PE =32时,矩形PQMN 的面积最大,最大面积为3.。
专题八 三角形的折叠问题 2020年中考数学冲刺难点突破 图形折叠问题(原卷版)
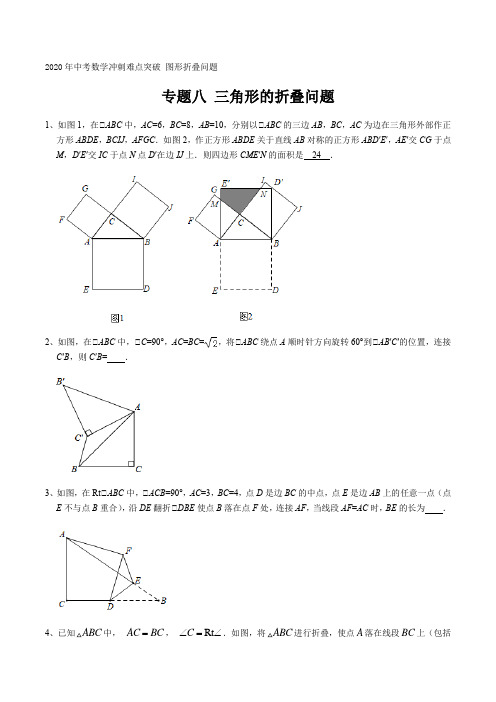
2020年中考数学冲刺难点突破 图形折叠问题专题八 三角形的折叠问题1、如图1,在△ABC 中,AC =6,BC =8,AB =10,分别以△ABC 的三边AB ,BC ,AC 为边在三角形外部作正方形ABDE ,BCIJ ,AFGC .如图2,作正方形ABDE 关于直线AB 对称的正方形ABD ′E ′,AE ′交CG 于点M ,D ′E ′交IC 于点N 点D ′在边IJ 上.则四边形CME ′N 的面积是 24 .2、如图,在△ABC 中,△C =90°,AC =BC =,将△ABC 绕点A 顺时针方向旋转60°到△AB ′C ′的位置,连接C ′B ,则C ′B = .3、如图,在Rt△ABC 中,△ACB =90°,AC =3,BC =4,点D 是边BC 的中点,点E 是边AB 上的任意一点(点E 不与点B 重合),沿DE 翻折△DBE 使点B 落在点F 处,连接AF ,当线段AF =AC 时,BE 的长为 .4、已知ABC 中, AC BC =, Rt C ∠=∠.如图,将ABC 进行折叠,使点A 落在线段BC 上(包括点B 和点C ),设点A 的落点为D ,折痕为EF ,当DEF 是等腰三角形时,点D 可能的位置共有( ).A .2种B .3种C .4种D .5种5、如图,在Rt △ABC 中,△A =90°,△B =30°,BC ,点E 、F 分别是BC 、AC 边上的动点,沿E 、F 所在直线折叠△C ,使点C 的落对应点C '始终落在边AB 上,若△BEC '是直角三角形时,则BC '的长为6、如图,矩形ABCD 中,点E 为射线BC 上的一个动点,连接AE ,以AE 为对称轴折叠△AEB ,得到△AEB ′,点B 的对称点为点B ′,若AB =5,BC =3,当点B ′落在射线CD 上时,线段BE 的长为 .7、如图例3-1,在Rt △ABC 中,△ACB =90°,△B =30°,BC =3,点D 是BC 边上一动点(不与点B 、C 重合),过点D 作DE △BC 交AB 边于点E ,将△B 沿直线DE 翻折,点B 落在射线BC 上的点F 处,当△AEF 为直角三角形时,BD 的长为图例3-1图例3-2 图例3-38、如图例5-1,在Rt ABC ∆中,90A ∠=︒,AB AC =,1BC =,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠B ∠,使点B 的对应点'B 始终落在边AC 上.若'MB C ∆为直角三角形,则BM 的长为 .图例5-1图例5-2图例5-39、如图例6-1,在△MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A’BC与△ABC 关于BC所在直线对称. D、E分别为AC、BC的中点,连接DE并延长交A’B所在直线于点F,连接A’E. 当△A’EF为直角三角形时,AB的长为.图例6-1图例6-2图例6-310、如图,在Rt△ABC中,△A=90°,△B=30°,BC,点E、F分别是BC、AC边上的动点,沿E、F 所在直线折叠△C,使点C的落对应点C'始终落在边AB上,若△BEC'是直角三角形时,则BC'的长为。
中考数学专题复习图形的折叠型题PPT课件

(2)请你通过操作和猜想,将第3、第4和第n次裁剪后
所得扇形的总个数(S)填入下表.
等分圆及扇形面的次数(n) 1 2 3 4 **** n
所得扇形的总个数(S)
47
***
(3)请你推断,能不能按上述操作过程,将本来的圆形 纸板剪成33个扇形?为什么?
例26、如图,若把边长为1的正方形ABCD的四个
例25、如图,⊙O表示一圆形纸板,根
O
据要求,需通过多次剪裁,把它剪成若 干个扇形面,操作过程如下:第1次剪,
第25题图
将圆形纸板等分为4个扇形;第2次剪裁,将上次得的
扇形面中的一个再等分成4个扇形;以后按第2次剪裁
的作法进行下去.(1)请你在⊙O中,用尺规作出第2次
剪裁后得到的7个扇形(保留痕迹不写作法).
角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎 样剪,才能使剩下的图形仍为正方形,且剩下图
形的面积为原正方形面积的 5 ,请说明理由(写
出证明及计算过程).
9
E
A M DA M
例22、电脑CPU蕊片由一种叫“单晶硅”的材料制
成,未切割前的单晶硅材料是一种薄型圆片,叫 “晶圆片”。现为了生产某种CPU蕊片,需要长、 宽都是1cm 的正方形小硅片若干。如果晶圆片的直 径为10.05cm。问一张这种晶圆片能否切割出所需尺 寸的小硅片66张?请说明你的方法和理由。(不计 切割损耗)
典例精析
一.折叠后求度数 例1、将一张长方形纸片按如图所示的方式折 叠,BC、BD为折痕,则∠CBD的度数为( ) A.600 B.750 C.900 D.950
例2、如图,把一个长方形纸片沿EF折叠后,点D、C
分别落在D′、C′的位置,若∠EFB=65°,则 ∠AED′等于( ) A.50° B.55° C.60° D.65°
浙江省2019届中考数学专题复习专题八图形折叠问题训练2

专题八 图形折叠问题类型一 折叠三角形(2018·浙江台州中考)如图,等边三角形ABC 边长是定值,点O 是它的外心,过点O 任意作一条直线分别交AB ,BC 于点D ,E.将△BDE 沿直线DE 折叠,得到△B′DE,若B′D,B′E 分别交AC 于点F ,G ,连结OF ,OG ,则下列判断错误的是( )A .△ADF≌△CGEB .△B′FG 的周长是一个定值C .四边形FOEC 的面积是一个定值D .四边形OGB′F 的面积是一个定值【分析】A .根据等边三角形ABC 的外心的性质可知AO 平分∠BAC,根据角平分线的定理和逆定理得FO 平分∠DFG,由外角的性质可证明∠DOF=60°,同理可得∠EOG=60°,∠FOG=60°=∠DOF=∠EOG,再根据三角形全等的性质可得△ADF≌△CGE;B .根据△DOF≌△GOF≌△GOE,得DF =GF =GE ,所以△ADF≌△B′GF≌△CGE,可得结论;C .根据S 四边形FOEC =S △OCF +S △OCE 判断即可;D .将S 四边形OGB′F =S △OAC -S △OFG ,根据S △OFG =12·FG·OH,FG 变化,故△OFG 的面积变化,从而四边形OGB′F的面积也变化,可作判断. 【自主解答】三角形的折叠问题一般考查轴对称的性质、勾股定理和线段的性质等,解题的关键是抓住折叠的本质是轴对称,轴对称是全等变换,找出相等的角和线段.类型二折叠平行四边形(2018·山东淄博中考)在如图所示的平行四边形ABCD中,AB=2,AD=3,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处,且AE过BC的中点O,则△ADE的周长等于________.【分析】要计算周长首先需要证明E,C,D共线,DE可求,问题得解.【自主解答】关于平行四边形折叠问题,解答时需要关注:在折叠前后,折痕两边能够完全重合的部分是全等图形,它们的对应线段、对应角相等,与特殊的平行四边形相比,它缺少了特殊的条件.1.(2018·甘肃兰州中考)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD=48°,∠CFD=40°,则∠E为( )A .102°B .112°C .122°D .92° 类型三 折叠菱形(2018·山东烟台中考)对角线长分别为6和8的菱形ABCD 如图所示,点O 为对角线的交点,过点O 折叠菱形,使B ,B′两点重合,MN 是折痕.若B′M=1,则CN 的长为( )A .7B .6C .5D .4【分析】连结AC ,BD ,利用菱形的性质得OC =12AC =3,OD =12BD =4,∠COD=90°,再利用勾股定理计算出CD =5,接着证明△OBM≌△ODN 得到DN =BM ,然后根据折叠的性质得BM =B′M=1,从而有DN =1,于是计算CD -DN 即可. 【自主解答】折叠是轴对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.对于菱形的折叠,还要明确菱形的基本性质,在解题过程中要抓住菱形的性质进行分析.2.(2018·贵州遵义中考)如图,在菱形ABCD 中,∠ABC=120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B ,D 重合),折痕为EF ,若DG =2,BG =6,则BE 的长为__________.3.如图,在菱形ABCD 中,tan A = 43,M ,N 分别在边AD ,BC 上,将四边形AMNB 沿MN 翻折,使AB 的对应线段EF 经过顶点D ,当EF⊥AD 时, BNCN的值为____.类型四 折叠矩形(2018·浙江杭州中考)折叠矩形纸片ABCD 时,发现可以进行如下操作:①把△ADE 翻折,点A 落在DC 边上的点F 处,折痕为DE ,点E 在AB 边上;②把纸片展开并铺平;③把△CDG 翻折,点C 落在线段AE 上的点H 处,折痕为DG ,点G 在BC 边上.若AB =AD +2,EH =1,则AD =________.【分析】设AD =x ,则AB =x +2,利用折叠的性质得DF =AD ,EA =EF ,∠DFE =∠A=90°,则可判断四边形AEFD 为正方形,所以AE =AD =x ,再根据折叠的性质得DH =DC =x +2,则AH =AE -HE =x -1,然后根据勾股定理得到x 2+(x -1)2=(x +2)2,再解方程求出x 即可. 【自主解答】此类问题中,运用的知识点比较多,综合性强,如轴对称性、全等、相似、勾股定理、转换思想、与其他图形(圆)结合等,抓住翻折前后两个图形是全等的,把握翻折前后不变的要素是解决此类问题的关键.4.(2018·湖北宜宾中考)如图,在矩形ABCD 中,AB =3,CB =2,点E 为线段AB 上的动点,将△CBE 沿CE 折叠,使点B 落在矩形内点F 处,下列结论正确的是__________(写出所有正确结论的序号). ①当E 为线段AB 中点时,AF∥CE; ②当E 为线段AB 中点时,AF =95;③当A ,F ,C 三点共线时,AE =13-2133;④当A ,F ,C 三点共线时,△CEF≌△AEF.类型五 折叠正方形(2018·江苏宿迁中考)如图,在边长为1的正方形ABCD 中,动点E ,F 分别在边AB ,CD 上,将正方形ABCD 沿直线EF 折叠,使点B 的对应点M 始终落在边AD 上(点M 不与点A ,D 重合),点C 落在点N 处,MN 与CD 交于点P ,设BE =x. (1)当AM =13时,求x 的值;(2)随着点M 在边AD 上位置的变化,△PDM 的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(3)设四边形BEFC 的面积为S ,求S 与x 之间的函数表达式,并求出S 的最小值.【分析】(1)利用勾股定理构建方程,即可解决问题;(2)设AM=y,则BE=EM=x,MD=1-y,在Rt△AEM中,由勾股定理得出x,y的关系式,可证Rt△AEM∽Rt△DMP,根据相似三角形的周长比等于相似比求△DMP的周长;(3)作FH⊥AB于H.则四边形BCFH是矩形.连结BM交EF于O,交FH于K.根据梯形的面积公式构建二次函数,利用二次函数的性质解决最值问题即可.【自主解答】正方形的折叠同其他图形一样,要关注勾股定理、全等图形、相似等相关知识,但由于正方形的特点,所以有关正方形的折叠问题有着其他图形没有的特殊性,解题时应关注正方形本身具有的特点.5.综合与实践问题背景折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):操作1:将正方形ABCD 对折,使点A 与点D 重合,点B 与点C 重合.再将正方形ABCD 展开,得到折痕EF ; 操作2:再将正方形纸片的右下角向上翻折,使点C 与点E 重合,边BC 翻折至B′E 的位置,得到折痕MN ,B′E 与AB 交于点P.则P 即为AB 的三等分点,即AP∶PB=2∶1.解决问题(1)在图1中,若EF 与MN 交于点Q ,连结CQ.求证:四边形EQCM 是菱形; (2)请在图1中证明AP∶PB=2∶1. 发现感悟若E 为正方形纸片ABCD 的边AD 上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:(3)如图2.若DE AE =2.则APBP =________;(4)如图3,若DE AE =3,则APBP=________;(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.类型六 折叠圆(2018·湖北武汉中考)如图,在⊙O 中,点C 在优弧AB ︵上,将BC ︵沿BC 折叠后刚好经过AB 的中点D.若⊙O 的半径为5,AB =4,则BC 的长是( )A .2 3B .3 2 C.532D.652【分析】连结OD ,AC ,DC ,OB ,OC ,作CE⊥AB 于E ,OF⊥CE 于F ,利用垂径定理、勾股定理、折叠的性质、圆周角定理、等腰三角形的性质及正方形的性质即可求解. 【自主解答】6.如图,将半径为4 cm 的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )A .2 3 cmB .4 3 cm C. 3 cmD. 2 cm参考答案类型一【例1】 A .如图,连接OA ,OC. ∵点O 是等边三角形ABC 的外心, ∴AO 平分∠BAC,∴点O 到AB ,AC 的距离相等. 由折叠得DO 平分∠BDB′, ∴点O 到AB ,DB′的距离相等, ∴点O 到DB′,AC 的距离相等,∴FO 平分∠DFG,∠DFO=∠OFG=12(∠FAD+∠ADF).由折叠得∠BDE=∠ODF=12(∠DAF+∠AFD),∴∠OFD+∠ODF=12(∠FAD+∠ADF+∠D AF +∠AFD)=120°,∴∠DOF=60°. 同理可得∠EOG=60°, ∴∠FOG=60°=∠DOF=∠EOG, ∴△DOF≌△GOF≌△GOE,∴OD=OG ,OE =OF ,∠OGF=∠ODF=∠ODB,∠OFG=∠OEG=∠OEB, ∴△OAD≌△OCG,△OAF≌△OCE,∴AD=CG ,AF =CE ,∴△ADF≌△CGE,故选项A 正确; B .∵△DOF≌△GOF≌△GOE, ∴DF=GF =GE ,∴△ADF≌△B′GF≌△CGE,∴B′G=AD ,∴△B′FG 的周长=FG +B′F+B′G=FG +AF +CG =AC(定值),故选项B 正确; C .S 四边形FOEC =S △OCF +S △OCE =S △OCF +S △OAF =S △AOC =13(定值),故选项C 正确;D .S 四边形OGB′F =S △OFG +S △B′GF =S △OFD +S △ADF =S 四边形OFAD =S △OAD +S △OAF =S △OCG +S △OAF =S △OAC -S △OFG . 如图,过O 作OH⊥AC 于H , ∴S △OFG =12·FG·OH,由于OH 是定值,FG 变化,故△OFG 的面积变化,从而四边形OGB′F 的面积也变化,故选项D 不一定正确.故选D.类型二【例2】 ∵四边形ABCD 是平行四边形, ∴AD∥BC,CD =AB =2. 由折叠知∠DAC=∠EAC.∵∠DAC=∠ACB,∴∠ACB=∠EAC, ∴OA=OC.∵AE 过BC 的中点O , ∴AO=12BC ,∴∠BAC=90°, ∴∠ACD=90°. 由折叠知∠ACE=90°, ∴E,C ,D 共线,则DE =4, ∴△ADE 的周长为3+3+4=10.故答案为10.变式训练1.B类型三【例3】 如图,连结AC ,BD.∵点O 为菱形ABCD 的对角线的交点, ∴CD=32+42=5.∵AB∥CD,∴∠MBO=∠NDO.在△OBM 和△ODN 中,⎩⎪⎨⎪⎧∠MBO=∠NDO,OB =OD ,∠BOM=∠DON,∴△OBM≌△ODN,∴DN=BM.∵过点O 折叠菱形,使B ,B′两点重合,MN 是折痕,∴BM=B′M=1,∴DN=1,∴CN=CD -DN =5-1=4.故选D.变式训练2.2.8 3.27类型四【例4】 设AD =x ,则AB =x +2.∵把△ADE 翻折,点A 落在DC 边上的点F 处,∴DF=AD ,EA =EF ,∠DFE=∠A=90°,∴四边形AEFD 为正方形,∴AE=AD =x.∵把△CDG 翻折,点C 落在线段AE 上的点H 处,折痕为DG ,点G 在BC 边上, ∴DH=DC =x +2.∵HE=1,∴AH=AE -HE =x -1.在Rt△ADH 中,∵AD 2+AH 2=DH 2,∴x 2+(x -1)2=(x +2)2,整理得x 2-6x -3=0,解得x 1=3+23,x 2=3-23(舍去),即AD 的长为3+2 3.故答案为3+2 3.变式训练4.①②③类型五【例5】 (1)在Rt△AEM 中,AE =1-x ,EM =BE =x ,AM =13. ∵AE 2+AM 2=EM 2,∴(1-x)2+(13)2=x 2,∴x=59. (2)△PDM 的周长不变为定值2.理由如下:设AM =y ,则BE =EM =x ,AE =1-x.在Rt△AEM 中,由勾股定理得AE 2+AM 2=EM 2,(1-x)2+y 2=x 2,解得1+y 2=2x ,∴1-y 2=2(1-x).∵∠EMP=90°,∠A=∠D,∴Rt△AEM∽Rt△DMP,∴AE +EM +AM DM +MP +DP =AE DM , 即1-x +x +y DM +MP +DP =1-x 1-y, 解得DM +MP +DP =1-y 21-x=2, ∴△DMP 的周长为2.(3)如图,作FH⊥AB 于H.则四边形BCFH 是矩形.连结BM 交EF 于O ,交FH 于K.在Rt△AEM 中,AM =x 2-(1-x )2=2x -1.∵B,M 关于EF 对称,∴BM⊥EF,∴∠KOF=∠KHB.∵∠OKF=∠BKH,∴∠KFO=∠KBH.∵AB=BC =FH ,∠A=∠FHE=90°,∴△ABM≌△HFE,∴EH=AM =2x -1,∴CF=BH =x -2x -1,∴S=12(BE +CF)·BC =12(x +x -2x -1) =12[(2x -1)2-2x -1+1] =12(2x -1-12)2+38. 当2x -1=12时,S 有最小值为38. 变式训练5.解:(1)由折叠可得CM =EM ,∠CMQ=∠EMQ,四边形CDEF 是矩形, ∴CD∥EF,∴∠CMQ=∠EQM,∴∠EQM=∠EMQ,∴ME=EQ =MC ,又∵MC∥QE,∴四边形EQCM 是平行四边形.又∵CM=EM ,∴四边形EQCM 是菱形.(2)如图1,设正方形ABCD 的边长为1,CM =x ,则EM =x ,DM =1-x.图1在Rt△DEM 中,由勾股定理可得EM 2=ED 2+DM 2,即x 2=(12)2+(1-x)2, 解得x =58,∴CM=58,DM =38. ∵∠PEM=∠D=90°,∴∠AEP+∠DEM=90°,∠DEM+∠EMD=90°,∴∠AEP=∠DME.又∵∠A=∠D=90°,∴△AEP∽△DME,∴AP AE =DE DM ,即AP 12=1238,解得AP =23, ∴PB=13,∴AP∶PB=2∶1. (3)4 (4)6(5)根据问题(2),(3),(4),可得当DE AE =n(n 为正整数)时,则AP BP=2n. 理由:设正方形ABCD 的边长为1,CM =x ,则EM =x ,DM =1-x. 在Rt△DEM 中,由勾股定理可得EM 2=ED 2+DM 2,即x 2=(n n +1)2+(1-x)2, 解得x =(n +1)2+n 22(n +1)2, ∴DM=1-CM =2n +12(n +1)2, 由△AEP∽△DME 可得AP AE =DE DM, 即AP 1n +1=nn +12n +12(n +1)2,解得AP =2n 2n +1, ∴PB=12n +1,∴AP BP =2n. 类型六【例6】 如图,连结OD ,AC ,DC ,OB ,OC ,作CE⊥AB 于E ,OF⊥CE 于F.∵D 为AB 的中点,∴OD⊥AB,∴AD=BD =12AB =2. 在Rt△OBD 中,OD =(5)2-22=1.∵将BC ︵沿BC 折叠后刚好经过AB 的中点D ,∴AC ︵和CD ︵所在的圆为等圆,∴AC ︵=CD ︵,∴AC=DC ,∴AE=DE =1,易得四边形ODEF 为正方形,∴OF=EF =1.在Rt△OCF 中,CF =(5)2-12=2,∴CE=CF +EF =2+1=3,而BE =BD +DE =2+1=3,∴BC=3 2.故选B. 变式训练6.B。
2024年中考数学压轴突破【几何中的折叠】题型汇编(解析版)

几何中的折叠问题一、单选题1如图,在菱形ABCD中,AD=5,tan B=2,E是AB上一点,将菱形ABCD沿DE折叠,使B、C的对应点分别是B 、C ,当∠BEB =90°时,则点C 到BC的距离是()A.5+5B.25+2C.6D.35【答案】D【分析】过C作CH⊥AD于H,C 作C F⊥AD于F,HD=5,HC=25,再由折叠证明∠BED=∠B ED=135°,∠EDC=∠EDC =45°,△CHD≌△DFC ,C F= HD=5,【C作CH⊥AD于H,C 作C F⊥AD于F,由已知AD=5,tan B=2,=2,∴CD=5,tan∠CDH=HCHD∴设HD=x,HC=2x,∴在Rt△HDC中HC2+HD2=CD2,2x2+x2=52,解得x=5,∴HD=5,HC=25,由折叠可知∠BED=∠B ED,∠EDC=∠EDC ,CD=C D∵∠BEB =90°,∴∠BED=∠B ED=135°,∵AB∥DC,∴∠EDC=180°-∠BED=45°,∴∠EDC=∠EDC =45°∴∠CDC =90°∵∠CHD =∠C AD =90°,∴∠CDH +C DF =90°,∵∠CDH +∠HCD =90°,∴∠C DF =∠HCD ,∴△CHD ≌△DFC ,∴C F =HD =5,∴点C 到BC 的距离是C F +CH =5+25=35.故选:D .【点睛】本题考查了全等三角形的性质和判定、菱形的性质、图形的折叠以及正切定义的应用,解答关键是根据折叠的条件推出∠BED =∠B ED =135°.2如图,将△ABC 折叠,使AC 边落在AB 边上,展开后得到折痕l 与BC 交于点P ,且点P 到AB 的距离为3cm ,点Q 为AC 上任意一点,则PQ 的最小值为()A.2cmB.2.5cmC.3cmD.3.5cm【答案】C【分析】由折叠可得:PA 为∠BAC 的角平分线,根据垂线段最短即可解答.【详解】解:∵将△ABC 折叠,使AC 边落在AB 边上,∴PA 为∠BAC 的角平分线,∵点Q 为AC 上任意一点,∴PQ 的最小值等于点P 到AB 的距离3cm .故选C .【点睛】本题主要考查了折叠的性质、角平分线的性质定理等知识点,掌握角平分线上的点到两边距离相等是解答本题的关键.3如图,在▱ABCD 中,BC =8,AB =AC =45,点E 为BC 边上一点,BE =6,点F 是AB 边上的动点,将△BEF 沿直线EF 折叠得到△GEF ,点B 的对应点为点G ,连接DE ,有下列4个结论:①tan B =2;②DE =10;③当GE ⊥BC 时,EF =32;④若点G 恰好落在线段DE 上时,则AF BF=13.其中正确的是()A.①②③B.②③④C.①③④D.①②④【答案】D【分析】过点A 作AH ⊥BC 于点H ,利用三线和一以及正切的定义,求出tan B ,即可判断①;过点D 作DK ⊥BC 于点K ,利用勾股定理求出DE ,判断②;过点F 作FM ⊥BC 于点M ,证明△EMF 为等腰直角三角形,设EM =FM =x ,三角函数求出BM 的长,利用BE =BM +EM ,求出x 的值,进而求出EF 的长,判断③;证明△AND ∽△CNE ,推出∠ENC =∠ECN ,根据折叠的性质,推出EF ∥CA ,利用平行线分线段成比例,即可得出结论,判断④.【详解】解:①过点A 作AH ⊥BC 于点H ,∵BC =8,AB =AC =45,∴BH =12BC =4,∴AH =AB 2-BH 2=8,∴tan B =AHBH=2;故①正确;②过点D 作DK ⊥BC 于点K ,则:四边形AHKD 为矩形,∴DK =AH =8,HK =AD =BC =8,∵BE =6,∴CE =2,∵CH =12BC =4,∴CK =4,∴EK =CE +CK =6,∴DE =EK 2+DK 2=10;故②正确;③过点F 作FM ⊥BC 于点M ,∵GE ⊥BC ,∴∠BEG =90°,∵翻折,∴∠BEF =∠GEF =45°,∴∠EFM =∠BEF =45°,∴EM =FM ,设EM =FM =x ,∵tan B =FMBM =2,∴BM =12FM =12x ,∴BE =BM +EM =12x +x =6,∴x =4,∴EM =FM =4,∴EF =2EM =42;故③错误;④当点G 恰好落在线段DE 上时,如图:设AC 与DE 交于点N ,∵▱ABCD ,∴AD ∥BC ,∴△AND ∽△CNE ,∴EN DN =CE AD=28=14,∴EN DE =15,∴EN =15DE =2=CE ,∴∠ENC =∠ECN ,∴∠BEN =∠ENC +∠ECN =2∠ECN ,∵翻折,∴∠BEN =2∠BEF ,∴∠BEF =∠ECN ,∴EF ∥AC ,∴AF BF =CE BE=26=13;故④正确,综上:正确的是①②④;故选D .【点睛】本题考查平行四边形的折叠问题,同时考查了解直角三角形,相似三角形的判定和性质,等腰三角形的判定和性质,勾股定理.本题的综合性强,难度较大,是中考常见的压轴题,熟练掌握相关性质,添加合适的辅助线,构造特殊三角形,是解题的关键.4如图,AB 是⊙O 的直径,点C 是⊙O 上一点,将劣弧BC 沿弦BC 折叠交直径AB 于点D ,连接CD ,若∠ABC =α0°<α<45° ,则下列式子正确的是()A.sin α=BCABB.sin α=CD ABC.cos α=AD BDD.cos α=CD BC【答案】B【分析】连AC ,由AB 是⊙O 的直径,可知∠ACB =90°,由折叠,AC和CD所在的圆为等圆,可推得AC =CD ,再利用正弦定义求解即可.【详解】解:连AC ,∵AB 是⊙O 的直径,∴∠ACB =90°,由折叠,AC 和CD所在的圆为等圆,又∵∠CBD =∠ABC ,∴AC和CD所对的圆周角相等,∴AC=CD,∴AC =CD ,在Rt △ACB 中,sin α=AC AB =CDAB,故选:B .【点睛】本题考查圆周角定理和圆心角、弦、弧之间的关系以及正弦、余弦定义,解答关键是通过折叠找到公共的圆周角推出等弦.5如图,在平面直角坐标系中,OA 在x 轴正半轴上,OC 在y 轴正半轴上,以OA ,OC 为边构造矩形OABC ,点B 的坐标为8,6 ,D ,E 分别为OA ,BC 的中点,将△ABE 沿AE 折叠,点B 的对应点F 恰好落在CD 上,则点F 的坐标为()A.3213,3013B.3013,3213C.3013,2013D.2013,3013【答案】A【分析】先求得直线CD 的解析式,过点F 作FM ⊥CE 于点M ,过点F 作FN ⊥OC 于点N ,设点F m ,-32m +6 ,在Rt △EMF 中,再利用勾股定理得到关于m 的方程,解方程即可.【详解】解:∵点B 的坐标为8,6 ,四边形OABC 是矩形,D ,E 分别为OA ,BC 的中点,∴C 0,6 ,D 4,0 ,E 4,6 ,由折叠的性质可得:EF =BE =4,设直线CD 的解析式为y =kx +b ,则6=b 4k +b =0 ,解得:k =-32b =6,∴直线CD 的解析式为y =-32x +6,过点F 作FM ⊥CE 于点M ,过点F 作FN ⊥OC 于点N ,设点F m,-32m+6,则MF=CN=6--32m+6=32m,EM=4-m,在Rt△EMF中,EM2+MF2=EF2,∴4-m2+32m2=42,解得:m=3213或m=0(不合题意,舍去),当m=3213时,y=-32×3213+6=3013,∴点F的坐标为3213,30 13,故选:A.【点睛】本题是一次函数与几何综合题,考查了求一次函数解析式,勾股定理,翻折的性质,矩形的性质,中点的性质,熟练掌握知识点并灵活运用是解题的关键.6综合与实践课上,李老师让同学们以矩形纸片的折叠为主题开展数学活动.如图,将矩形纸片ABCD对折,折痕为EF,再把点A折叠在折痕EF上,其对应点为A ,折痕为DP,连接A B,若AB=2,BC =3,则tan∠A BF的值为()A.33B.3 C.32D.12【答案】A【分析】先证明EF=AB=CD=2,CF=BF=DE=32,∠DEA=90°,∠A FB=90°,AD=A D=3,可得A E=A D2-DE2=32,AF=2-32=12,再利用正切的定义求解即可.【详解】解:∵矩形纸片ABCD对折,折痕为EF,AB=2,BC=3,∴EF=AB=CD=2,CF=BF=DE=32,∠DEA=90°,∠A FB=90°,由折叠可得:AD=A D=3,∴A E=A D2-DE2=32,∴A F=2-32=12,∴tan ∠A BF =1232=33.故选A【点睛】本题考查的是轴对称的性质,矩形的性质,勾股定理的应用,求解锐角的正切,熟记轴对称的性质是解本题的关键.7如图,矩形ABCD 中,AB =2,BC =3,P 是边BC 中点,将顶点D 折叠至线段AP 上一点D ,折痕为EF ,此时,点C 折叠至点C .下列说法中错误的是()A.cos ∠BAP =45B.当AE =53时,D E ⊥AP C.当AE =18-65时,△AD E 是等腰三角形 D.sin ∠DAP =45【答案】C【分析】根据矩形的性质,直角三角形的性质,三角函数,勾股定理,折叠的性质计算判断即可.【详解】∵矩形ABCD 中,AB =2,BC =3,P 是边BC 中点,∴BP =12BC =32,∠B =90°,∴AP =AB 2+BP 2=22+32 2=52,∴cos ∠BAP =AB AP=252=45,故A 正确;∵矩形ABCD ,∴AD ∥BC ,∴∠DAP =∠APB ,∴sin ∠DAP =sin ∠APB =cos ∠BAP =45,故D 正确;设DE =D E =x ,根据题意,得AE =AD -DE =3-x ,sin ∠DAP =45,∵D E ⊥AP ,∴sin ∠DAP =D E AE=x 3-x =45,解得x =43,∴AE =AD -DE =3-x =53,故B 正确;当D E =AE 时,∴x =3-x ,解得x =32;此时D ,A 重合,三角形不存在,不符合题意;当D E =AD 时,过点D 作D N ⊥AD 于点N ,则AN =NE ;∵矩形ABCD ,∴AD ∥BC ,∴∠DAP =∠APB ,∴cos ∠DAP =cos ∠APB =3252=35,设DE =D E =x ,根据题意,得AE =AD -DE =3-x ,D E =AD =x ,∴AN AD=AN x =35,解得AN =35x ;∴AE =AD -DE =3-x =2AN =65x ,解得x =1511;∴AE =65×1511=1811;当AE =AD 时,过点D 作D H ⊥AD 于点H ,设DE =D E =x ,根据题意,得AE =AD =AD -DE =3-x ,∴D H =AD sin ∠DAP =453-x ,AH =AD cos ∠DAP =353-x ,∴HE =AE -AH =3-x -353-x =253-x ,根据勾股定理,得HE 2+D H 2=D E 2,∴253-x 2+453-x2=x 2解得x =65-12;∴AE =3-x =15-65;综上所述,AE =15-65或AE =1811,故C 错误,故选C .【点睛】本题考查了矩形的性质,直角三角形的性质,三角函数,勾股定理,折叠的性质,熟练掌握三角函数,勾股定理,矩形的性质,折叠的性质是解题的关键.8如图,AB 为半圆O 的直径,点O 为圆心,点C 是弧上的一点,沿CB 为折痕折叠BC交AB 于点M ,连接CM ,若点M 为AB 的黄金分割点(BM >AM ),则sin ∠BCM 的值为()A.5-12B.5+12C.5-14D.12【答案】A【分析】过点M作MD⊥CB,垂足为D,延长MD交半⊙O于点M′,连接CM ,BM′,根据折叠的性质可得:∠CMB=∠CM′B,BC⊥MM′,从而可得∠BDM=90°,再根据黄金分割的定义可得BMAB =5-12,然后利用直径所对的圆周角是直角可得∠ACB=90°,从而证明A字模型相似三角形△DBM∽△CBA,进而利用相似三角形的性质可得DMAC=BMAB=5-12,最后根据圆内接四边形对角互补以及平角定义定义可得:∠A=∠AMC,从而可得CA=CM,再在Rt△CDM中,利用锐角三角函数的定义进行计算,即可解答.【详解】解:过点M作MD⊥CB,垂足为D,延长MD交半⊙O于点M′,连接CM ,BM′,由折叠得:∠CMB=∠CM′B,BC⊥MM′,∴∠BDM=90°,∵点M为AB的黄金分割点(BM>AM),∴BMAB =5-12,∵AB为半圆O的直径,∴∠ACB=90°,∴∠ACB=∠MDB,∵∠DBM=∠CBA,∴△DBM∽△CBA,∴DMAC =BMAB=5-12,∵四边形ACM′B是半⊙O的内接四边形,∴∠A+∠CM′B=180°,∵∠AMC+∠CMB=180°,∠CMB=∠CM′B,∴∠A=∠AMC,∴CA=CM,在Rt△CDM中,sin∠BCM=DMCM=DMAC=5-12.故选:A.【点睛】本题考查了相似三角形的判定与性质,黄金分割,解直角三角形,翻折变换(折叠问题),圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.二、填空题9如图,将一张矩形纸片ABCD折叠,折痕为EF,折叠后,EC的对应边EH经过点A,CD的对应边HG交BA的延长线于点P.若PA=PG,AH=BE,CD=3,则BC的长为.【答案】43【分析】本题考查了矩形与折叠问题,全等三角形的判定和性质,勾股定理.连接PF ,设BC =2x ,AH =BE=a ,证明Rt △PAF ≌Rt △PGF HL ,求得FA =FG =FD =x ,由折叠的性质求得BE =12x ,在Rt △ABE中,利用勾股定理列式计算,即可求解.【详解】解:连接PF ,设BC =2x ,AH =BE =a ,由矩形的性质和折叠的性质知FG =FD ,∠G =∠FAP =90°,AB =CD =3,AD =BC ,∵PA =PG ,PF =PF ,∴Rt △PAF ≌Rt △PGF HL ,∴FA =FG =FD =12AD =12BC =x ,由矩形的性质知:AD ∥BC ∴∠AFE =∠FEC ,折叠的性质知:∠FEA =∠FEC ,∴∠FEA =∠AFE ,∴AE =FA =x ,由折叠的性质知EC =EH =AE +AH =x +a ,∴BC =BE +EC =a +x +a =2x ,∴a =12x ,即BE =12x ,在Rt △ABE 中,AB 2+BE 2=AE 2,即32+12x 2=x 2,解得x =23,∴BC =2x =43,故答案为:4310如图,在矩形ABCD 中,AB =3,AD =6,M 为AD 的中点,N 为BC 边上一动点,把矩形沿MN 折叠,点A ,B 的对应点分别为A ,B ,连接AA '并延长交射线CD 于点P ,交MN 于点O ,当N 恰好运动到BC 的三等分点处时,CP 的长为.【答案】1或5【分析】分两种情况:①当CN =2BN 时.过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形;②当BN =2CN 时,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,根据矩形的性质得GM =AM -AG =1.再由折叠的性质可得∠AOM =90°,然后根据相似三角形的判定与性质可得答案.【详解】解:①当CN =2BN 时.如图1,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,∴NG =AB =3,AG =BN =2.∵M 为AD 的中点,∴AM =3,∴GM =AM -AG =1.由折叠A 与A 对应,∴∠AOM =90°,∵∠MAO +∠APD =90°,∠MAO +∠AMO =90°,∴∠AMO =∠APD ,即∠GMN =∠APD .又∵∠NGM =∠ADP =90°,∴△ADP ∽△NGM ,∴NG AD=GM DP =12,解得DP =2,∴CP =CD -DP =1.②当BN =2CN 时,如图2,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,∴NG =AB =3,AG =BN =4.∵M 为AD 的中点,∴AM =3,∴GM =AG -AM =1.由折叠A 与A 对应,∴∠AOM =90°∠MAO +∠AMO =90°,∠MAO +∠APD =90°,∴∠AMO =∠APD ,即∠GMN =∠APD .又∠ADP =∠NGM =90°,∴△ADP ∽△NGM ,∴NG AD=GM DP =12,解得DP =2,∴CP =CD +DP =5.综上,CP 的长为1或5.故答案为:1或5.【点睛】此题考查的是翻折变换-折叠问题、矩形的性质,正确作出辅助线是解决此题的关键.11如图,DE 平分等边△ABC 的面积,折叠△BDE 得到△FDE ,AC 分别与DF ,EF 相交于G ,H 两点.若DG =m ,EH =n ,用含m ,n 的式子表示GH 的长是.【答案】m 2+n 2【分析】先根据折叠的性质可得S △BDE =S △FDE ,∠F =∠B =60°,从而可得S △FHG =S △ADG +S △CHE ,再根据相似三角形的判定可证△ADG ∽△FHG ,△CHE ∽△FHG ,根据相似三角形的性质可得S △ADG S △FHG =DG GH2=m 2GH 2,S △CHE S △FHG =EH GH 2=n 2GH 2,然后将两个等式相加即可得.【详解】解:∵△ABC 是等边三角形,∴∠A =∠B =∠C =60°,∵折叠△BDE 得到△FDE ,∴△BDE ≌△FDE ,∴S △BDE =S △FDE ,∠F =∠B =60°=∠A =∠C ,∵DE 平分等边△ABC 的面积,∴S 梯形ACED =S △BDE =S △FDE ,∴S △FHG =S △ADG +S △CHE ,又∵∠AGD =∠FGH ,∠CHE =∠FHG ,∴△ADG ∽△FHG ,△CHE ∽△FHG ,∴S △ADG S △FHG =DG GH 2=m 2GH 2,S △CHE S △FHG =EH GH 2=n 2GH 2,∴S △ADG S △FHG +S △CHE S △FHG =m 2+n 2GH 2=S △ADG +S △CHE S △FHG =1,∴GH 2=m 2+n 2,解得GH =m 2+n 2或GH =-m 2+n 2(不符合题意,舍去),故答案为:m 2+n 2.【点睛】本题考查了等边三角形的性质、折叠的性质、相似三角形的判定与性质等知识点,熟练掌握相似三角形的判定与性质是解题关键.12在矩形ABCD 中,点E 为AD 边上一点(不与端点重合),连接BE ,将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,连接并延长EF ,BF 分别交BC ,CD 于G ,H 两点.若BA =6,BC =8,FH =CH ,则AE 的长为.【答案】92【分析】连接GH ,证明Rt △FHG ≅Rt △CHG (HL ),可得FG =CG ,设FG =CG =x ,在Rt △BFG 中,有62+x 2=(8-x )2,可解得CG =FG =74,知BG =254,由矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,得∠AEB =∠FEB ,可得∠FEB =∠EBG ,EG =BG =254,故EF =EG -FG =92,从而得到AE =92.【详解】连接GH ,如图:∵四边形ABCD 是矩形,∴∠A =∠C =90°,∵将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,∴BF =AB =6,AE =EF ,∠BFE =∠A =90°,∴∠GFH =90°=∠C ,∵GH =GH ,FH =CH ,∴Rt △FHG ≅Rt △CHG (HL ),∴FG =CG ,设FG =CG =x ,则BG =BC -CG =8-x在Rt △BFG 中,BF 2+FG 2=BG 2∴62+x 2=(8-x )2,解得:x =74,∴CG =FG =74,∴BG =8-x =25x,∵将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,∴∠AEB =∠FEB ,∵AD ⎳BC ,∴∠AEB =∠EBG ,∴∠FEB =∠EBG ,∴EG =BG =254,∴AE =92,故答案为:92.【点睛】本题考查矩形中的翻折变换,涉及三角形全等的判定与性质,勾股定理及应用,掌握相关知识是解题的关键.13如图,在矩形ABCD 中,AD =23,CD =6,E 是AB 的中点,F 是线段BC 上的一点,连接EF ,把△BEF 沿EF 折叠,使点B 落在点G 处,连接DG ,BG 的延长线交线段CD 于点H .给出下列判断:①∠BAC =30°;②△EBF ∽△BCH ;③当∠EGD =90°时,DG 的长度是23 ④线段DG 长度的最小值是21-3;⑤当点G 落在矩形ABCD 的对角线上,BG 的长度是3或33;其中正确的是.(写出所有正确判断的序号)【答案】①②③【分析】利用正切函数的定义即可判断①正确;利用同角的余角相等推出∠HBC =∠BEF ,可判断②正确;推出点D 、G 、F 三点共线,证明Rt △EAD ≌Rt △EGD HL ,可判断③正确;当点D 、G 、E 三点共线,线段DG 长度的最小值是21-3,由于F 是线段BC 上的一点,不存在D 、G 、E 三点共线,可判断④不正确;证明△BGE 是等边三角形,可判断⑤.【详解】解:连接AC ,∵矩形ABCD 中,AD =23,CD =6,∴tan ∠ACD =AD CD=236=33,∴∠ACD =30°,∴∠BAC =30°,故①正确;由折叠的性质知EF 是BG 的垂直平分线,∴∠HBC +∠BFE =90°=∠BEF +∠BFE ,∴∠HBC =∠BEF ,∴△EBF ∽△BCH ,故②正确;由折叠的性质知∠EGF =∠ABC =90°,∵∠EGD =90°,∴点D 、G 、F 三点共线,连接DE ,在Rt △EAD 和Rt △EGD 中,AE =BE =EG ,DE =DE ,∴Rt △EAD ≌Rt △EGD HL ,∴DG =AD =23,故③正确;∵AE =BE =EG ,∴点A 、G 、B 都在以E 为圆心,3为半径的圆上,DE =23 2+32=21,∴当点D 、G 、E 三点共线,线段DG 长度的最小值是21-3,但F 是线段BC 上的一点,∴D 、G 、E 三点不可能共线,故④不正确;当点G 落在矩形ABCD 的对角线AC 上时,由折叠的性质知BE =EG ,∵E 是AB 的中点,由①知∠BAC =30°,∴BE =EG =EA ,∠BAC =∠EGA =30°,∴∠BEG =∠BAC +∠EGA =60°,∴△BGE 是等边三角形,∴BG 的长度是3;由于F 是线段BC 上的一点,则点G 不会落在矩形ABCD 的对角线BD 上,故⑤不正确;综上,①②③说法正确,故答案为:①②③.【点睛】本题考查了矩形与折叠问题,正切函数,相似三角形的判定,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.14如图,将矩形ABCD沿BE折叠,点A与点A 重合,连接EA 并延长分别交BD、BC于点G、F,且BG=BF.(1)若∠AEB=55°,则∠GBF=;(2)若AB=3,BC=4,则ED=.【答案】40°/40度5-10/-10+5【分析】(1)先证明∠DEF=180°-2×55°=70°,∠BFG=∠DEF=70°,利用BG=BF,可得答案;(2)如图,过F作FQ⊥AD于Q,可得CF=DQ,FQ=CD=3,同理可得:∠BGF=∠BFG,∠DEG=∠BFG,而∠DGE=∠BGF,则∠DEG=∠DGE,设DE=DG=x,而BD=32+42=5,则BG=BF=5-x,CF=4-5-x=1,再求解EF=12+32=10,由折叠可得:A E=AE=4 =x-1,EQ=x-x-1-x,AF=10-4+x,利用cos∠BFA=cos∠FEQ,再建立方程求解即可.【详解】解:(1)∵∠AEB=55°,结合折叠可得:∠AEB=∠A EB=55°,∴∠DEF=180°-2×55°=70°,∵矩形ABCD,∴AD∥BC,∴∠BFG=∠DEF=70°,∵BG=BF,∴∠BGF=∠BFG=70°;∴∠GBF=180°-2×70°=40°;故答案为:40°.(2)如图,过F作FQ⊥AD于Q,∴四边形FCDQ是矩形,则CF=DQ,FQ=CD=3,同理可得:∠BGF=∠BFG,∠DEG=∠BFG,而∠DGE=∠BGF,∴∠DEG=∠DGE,∴设DE=DG=x,∵矩形ABCD,AB=3,BC=4,∴BD=32+42=5,∴BG=BF=5-x,∴CF=4-5-x=x-1,∴EQ=x-x-1=1,∴EF=12+32=10,由折叠可得:A E=AE=4-x,∴AF =10-4+x,∵∠QEF=∠BFA ,∴cos∠BFA =cos∠FEQ,∴EQEF=A FBF,∴110=10-4+x5-x,解得:x=5-10,经检验符合题意;∴DE=5-10.故答案为:5-10.【点睛】本题考查的是轴对称的性质,矩形的性质与判定,勾股定理的应用,锐角三角函数的应用,等腰三角形的判定与性质,熟练的利用以上知识解题是关键.三、解答题15综合与实践课上,老师让同学们以“正方形的折叠”为主题开展实践活动.(1)操作判断操作一:如图(1),正方形纸片ABCD,点E是BC边上(点E不与点B,C重合)任意一点,沿AE折叠△ABE到△AFE,如图(2)所示;操作二:将图(2)沿过点F的直线折叠,使点E的对称点G落在AE上,得到折痕MN,点C的对称点记为H,如图(3)所示;操作三:将纸片展平,连接BM,如图(4)所示.根据以上操作,回答下列问题:①B,M,N三点(填“在”或“不在”)一条直线上;②AE和BN的位置关系是,数量关系是;③如图(5),连接AN,改变点E在BC上的位置,(填“存在”或“不存在”)点E,使AN平分∠DAE.(2)迁移探究苏钰同学将正方形纸片换成矩形纸片ABCD,AB=4,BC=6,按照(1)中的方式操作,得到图(6)或图(7).请完成下列探究:①当点N在CD上时,如图(6),BE和CN有何数量关系?并说明理由;②当DN的长为1时,请直接写出BE的长.【答案】(1)①在,②AE⊥BN,相等;③不存在;(2)①BECN =23,理由见解析;②BE=2或165.【分析】(1)①E的对称点为E ,BF⊥EE ,MF⊥EE ,即可判断;②由①AE⊥BN,由同角的余角相等得∠BAE=∠CBN,由AAS可判定△ABE≌△BCN,由全等三角形的性质即可得证;③由AAS可判定△DAN≌△MAN,由全等三角形的性质得AM=AD,等量代换得AB=AM,与AB>AM矛盾,即可得证;(2)①由(1)中的②可判定△ABE∽△BCN,由三角形相似的性质即可求解;②当N在CD上时,△ABE∽△BCN,由三角形相似的性质即可求解;当N在AD上时,同理可判定△ABE∽△NAB,由三角形相似的性质即可求解.【详解】(1)解:①E的对称点为E ,∴BF⊥EE ,MF⊥EE ,∴B、F、M共线,故答案为:在;②由①知:B、F、M共线,N在FM上,∴AE⊥BN,∴∠AMB=90°,∴∠ABM+∠BAE=90°,∵四边形ABCD是正方形,∴∠ABC=∠BCN=90°,AB=BC,∴∠CBN+∠ABM=90°,∴∠BAE=∠CBN,在△ABE和△BCN中,∠BAE=∠CBN ∠ABC=∠BCN AB=BC,∴△ABE≌△BCN(AAS),∴AE=BN,故答案为:相等;③不存在,理由如下:假如存在,∵AN平分∠DAE,∴∠DAN=∠MAN,∵四边形ABCD是正方形,AM⊥BN,∴∠D=∠AMN=90°,在△DAN和△MAN中,∠D=∠AMN∠DAN=∠MAN AN=ANN∴△DAN≌△MAN(AAS),∴AM=AD,∵AD=AB,∴AB=AM,∵AB是Rt△ABM的斜边,∴AB>AM,∴AB =AM 与AB >AM 矛盾,故假设不成立,所以答案为:不存在;(2)解:①BE CN=23,理由如下:由(1)中的②得:∠BAE =∠CBN ,∠ABE =∠C =90°,∴△ABE ∽△BCN ,∴BE CN =AB BC=23;②当N 在CD 上时,CN =CD -DN =3,由①知:△ABE ∽△BCN ,∴BE CN =AB BC =23,∴BE =23CN =2,当N 在AD 上时,AN =AD -DN =5,∵∠BAE =∠CBN =∠ANB ,∠ABE =∠BAN =90°,∴△ABE ∽△NAB ,∴BE AB =AB AN ,∴BE 4=45,∴BE =165,综上所述:BE =2或165.【点睛】本题考查了折叠的性质,矩形的性质,正方形的性质,全等三角形的判定及性质,三角形相似的判定及性质,掌握相关的判定方法及性质,“十字架”典型问题的解法是解题的关键.16在矩形ABCD 中,AD =2AB =8,点P 是边CD 上的一个动点,将△BPC 沿直线BP 折叠得到△BPC .(1)如图1,当点P 与点D 重合时,BC ′与AD 交于点E ,求BE 的长度;(2)当点P 为CD 的三等分点时,直线BC ′与直线AD 相交于点E ,求DE 的长度;(3)如图2,取AB 中点F ,连接DF ,若点C ′恰好落在DF 边上时,试判断四边形BFDP 的形状,并说明理由.【答案】(1)BE 的长度为5;(2)DE 的长度为113或83;(3)四边形BFDP 是平行四边形(理由见解析)【分析】本题利用了折叠的知识(折叠后的两个图形全等)以及矩形的性质(矩形的对边相等,对角相等),以及平行四边形的判定有关知识.(1)利用矩形性质和折叠的性质可推出BE=DE,设BE=x,则DE=x,AE=8-x,利用勾股定理建立方程求解即可得出答案;(2)设DE=m,则AE=m+8,设BE交CD于G,可证得△AEB∽△CBG,得出CGAB =BCAE,即CG4=8m+8,求得CG=32m+8,分两种情况:当PC=13CD=43时,当PC=23CD=83时,分别添加辅助线构造相似三角形,利用相似三角形性质建立方程求解即可得出答案;(3)由中点定义可得AF=BF,过点C 作C M∥AD交AB于点M,过点F作FN⊥BC 于点N,由矩形性质和翻折的性质可得∠C BP=∠CBP=12∠C BC,可证得△FC M∽△FDA,得出FMAF=C MAD,再证得△BFN∽△BC M,进而推出FM=FN,利用角平分线的判定定理可得∠BC F=∠MC F=12∠BC M推出∠BC F=∠C BP,再由平行线的判定定理可得DF∥BP,运用平行四边形的判定定理即可证得四边形BFDP是平行四边形.【点睛】点睛片段【详解】(1)解:∵AD=2AB=8,∴AB=4,∵四边形ABCD是矩形,∴∠A=90°,AD∥BC,∴∠ADB=∠DBC,由折叠得:∠DBC=∠DBC ,∴∠ADB=∠DBC ,即∠EDB=∠EBD,∴BE=DE,设BE=x,则DE=x,AE=8-x,在Rt△ABE中,AE2+AB2=BE2,∴(8-x)2+42=x2,解得:x=5,∴BE的长度为5;(2)设DE=m,则AE=m+8,设BE交CD于G,∵四边形ABCD是矩形,∴BC=AD=8,CD=AB=4,AD∥BC,∠A=∠BCG=90°,∴∠AEB=∠CBG,∴△AEB∽△CBG,∴CG AB =BCAE,即CG4=8m+8,∴CG=32m+8,当PC=13CD=43时,BP=BC2+PC2=82+432=4373,连接CC ,过点C 作C H⊥CD于点H,如图,∵将△BPC沿直线BP折叠得到△BPC ,∴CC ⊥BP,△BPC ≌△BPC,∴S四边形BCPC =2S△BPC,∴1BP⋅CC =2×1BC⋅PC,即12×4373CC =2×12×8×43,∴CC =163737,∵∠C CH +∠BPC =90°,∠PBC +∠BPC =90°,∴∠C CH =∠PBC ,∵∠CHC =∠BCP =90°,∴△CC H ∽△BPC ,∴C H PC =CH BC =CC BP ,即CH 43=CH 8=1637374373,∴C H =1637,CH =9637,∵∠C HG =∠EDG =90°,∴C H ∥AE ,∴∠GC ′H =∠AEB ,∴△C GH ∽△EBA ,∴GH AB =C H AE ,即GH 4=1637m +8,∴GH =6437(m +8),∵CH +GH =CG ,∴9637+6437(m +8)=32m +8,解得:m =113,经检验,m =113是该方程的解,∴DE =113;当PC =23CD =83时,BP =BC 2+PC 2=82+83 2=8103,连接CC ,过点C 作C H ⊥CD 交CD 的延长线于点H ,作C G ⊥AD 于点G ,如图,同理可得:CC =8105,同理△CC H ∽△BPC ,∴C H PC =CH BC =CC BP ,即CH 83=CH 8=81058103,∴C H =85,CH =245,∴DH =CH -CD =245-4=45,∵∠HDG =∠H =∠C GD =90°,∴四边形DGC H 是矩形,∴C G =DH =45,DG =C H =85,∵∠C GE =∠A =90°,∠C EG =∠BEA ,∴△C EG ∽△BEA ,∴EG AE =C G AB =454=15,∴AE =5EG ,∵AE +EG =AG =AD -DG =8-85=325,∴5EG +EG =325,∴EG =1615,∴DE =DG +EG =85+1615=83,综上所述,DE 的长度为113或83;(3)四边形BFDP 是平行四边形,理由如下:∵点F 是AB 的中点,∴AF =BF ,过点C 作C M ∥AD 交AB 于点M ,过点F 作FN ⊥BC 于点N ,如图,则∠FC M =∠ADF ,∵四边形ABCD 是矩形,∴AD ∥BC ,AB ∥CD ,∴C M ∥BC ,∴∠BC M =∠C BC ,由翻折得:∠C BP =∠CBP =12∠C BC ,BC =BC =8,∵C M ∥AD ,∴△FC M ∽△FDA ,∴FM AF =C M AD ,∴FM BF =C MBC ,∵∠BNF =∠BMC =90°,∠FBN =∠C BM ,∴△BFN ∼△BC M∴FN BF =C MBC ,∴FM BF =FN BF ,∴FM =FN ,又∵FM ⊥C M ,FN ⊥C B ,∴∠BC F =∠MC F =12∠BC M ,∴∠BC F =∠C BP ,∴DF ∥BP ,∴四边形BFDP 是平行四边形.17矩形ABCD 中,AB =6,AD =8,点E 为对角线AC 上一点,过点E 作EF ⊥AD 于点F ,EG ⊥AC 交边BC 于点G ,将△AEF 沿AC 折叠得△AEH ,连接HG .(1)如图1,若点H 落在边BC 上,求证:AH =CH ;(2)如图2,若A ,H ,G 三点在同一条直线上,求HG 的长;(3)若△EHG 是以EG 为腰的等腰三角形,求EF 的长.【答案】(1)见解析(2)HG =94(3)EF =103或4【分析】(1)根据矩形的性质和翻折的性质证明∠ACH =∠HAC ,即可解决问题;(2)结合(1)的方法AG =CG ,解Rt △AEG ,Rt △HEG 分别求得EG ,HG ;(3)当△EHG 是以EG 为腰的等腰三角形时,分两种情况:①当EG =EH ,②当EG =HG ,结合(2)的方法,利用全等三角形的判定与性质和相似三角形的判定与性质即可解决问题.【详解】(1)∵四边形ABCD 是矩形,∴AD ∥BC .∴∠DAE =∠ACH .∵△AHE 由△AFE 折叠得到,∴∠HAC =∠DAE ,∴∠HAC =∠ACH ,∴AH =CH ;(2)∵矩形ABCD 中,AB =6,AD =8.∴AC =10.当A ,H ,G 三点在同一条直线上时,∠EHG =90°.同(1)可得AG =CG .又∵EG ⊥AC ,∴AE =12AC =5.∵∠AEH +∠HEG =90°,∠AEH +∠HAE =90°,∴∠HEG =∠HAC =∠CAD .∵在Rt △AEG 中,tan ∠EAG =EG AE =34,∴EG =34AE =154.∵在Rt △HEG 中,sin ∠HEG =HG EG =35,∴HG =35EG =94.(3)①若EH =EG ,如图3①设EF =EH =EG =x ,∵EF ⊥AD ,∴EF ∥CD ,∴△AEF ∽△ACD ,∴AE AC =AF AD =EF CD ∴AE 10=AF 8=x 6∴AE =53x ,AF =43x ,∴AH =AF =43x ,∵∠AHE =∠CEG =90°,∠HAE =∠GCE ,EH =EH ,∴△AHE ≌△CGE AAS ,∴AH =CE ,∴43x =10-53x ,∴x =103∴EF =103.②若HG =GE ,如图3②.(图3②)过点G 作GM ⊥HE ,设EF =a ,∵EC =10-53a ,∵∠AHE =∠CEG =90°,∠HAE =∠GCE ,∴△AHE ∽△CGE ,∴EG =34EC =3410-53a =152-54a ,∵∠GME =∠EHA ,∠MGE =90°-∠MEG =∠HAE ,∴△MGE ∽△HEA ,∴ME AH =EG AE ,∵AH AE =AD AC =45,∴AH =45AE ,∴ME =45EG =45152-54a =6-a ,∴HE =2ME =12-2a =EF ,∴12-2a =a ,∴a =4,∴EF =4,综上,EF =103或4.【点睛】本题考查了矩形的性质,解直角三角形,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰三角形的性质,翻折的性质,解决本题的关键是综合运用以上知识.18综合与实践【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.【初步尝试】把正方形对折,折痕为EF,然后展开,沿过点A与点E所在的直线折叠,点B落在点B 处,连接 B C,如图1,请直接写出∠AEB 与∠ECB 的数量关系.【能力提升】把正方形对折,折痕为EF,然后展开,沿过点A与BE上的点G所在的直线折叠,使点B落在EF上的点P处,连接PD,如图2,猜想∠APD的度数,并说明理由.【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A ,连接PA ,BA ,AC,如图3,求∠PA B的度数.【答案】初步尝试:∠AEB =∠ECB ;能力提升:猜想:∠APD=60°,理由见解析;拓展延伸:∠PA B=15°【分析】初步尝试:连接BB ,由折叠的性质可知,BE=CE,BE=BE ,∠AEB=∠AEB ,BB ⊥AE,根据等边对等角的性质和三角形内角和定理,得出∠BB C=90°,推出AE∥CB ,即可得出答案;能力提升:根据正方形的性质和折叠的性质,易证△AFP≌△DFP SAS,从而证明△APD是等边三角形,即可得到答案;拓展延伸:连接A C、AA ,由(2)得△APD是等边三角形,进而得出∠PDC=30°,再结合等边对等角的性质和三角形内角和定理,求得∠PAC=15°,∠ACP=30°,由对称性质得:AC=A C,∠ACP=∠A CP=30°,证明△AA B≌△CA B SSS,得到∠CA B=30°,再由∠CA P=∠CAP=15°,即可求出∠PA B的度数.【详解】解:初步尝试:∠AEB =∠ECB ,理由如下:如图,连接BB ,由折叠的性质可知,BE=CE,BE=BE ,∠AEB=∠AEB ,BB ⊥AE,∴BE=CE=BE ,∴∠EBB =∠EB B,∠ECB =∠EB C,∵∠EBB +∠EB B+∠EB C+∠ECB =2∠EB B+∠EB C=180°,∴∠BB C=90°,即BB ⊥CB ,∴AE∥CB ,∴∠AEB=∠ECB ,∴∠AEB =∠ECB ;解:能力提升:猜想:∠APD=60°,理由如下:理由:∵四边形ABCD是正方形,∴AB=AD,∠ADC=90°,由折叠性质可得:AF =DF ,EF ⊥AD ,AB =AP ,在△AFP 和△DFP 中,AF =DF∠AFP =∠DFP =90°FP =FP,∴△AFP ≌△DFP SAS ,∴AP =PD ,∴AP =AD =PD ,∴△APD 是等边三角形,∴∠APD =60°;解:拓展延伸:如图,连接A C 、AA ,由(2)得△APD 是等边三角形,∴∠PAD =∠PDA =∠APD =60°,AP =DP =AD ,∵∠ADC =90°,∴∠PDC =30°,又∵PD =AD =DC ,∴∠DPC =∠DCP =12×180°-30° =75°,∠DAC =∠DCA =45°,∴∠PAC =∠PAD -∠DAC =60°-45°=15°,∠ACP =∠DCP -∠DCA =75°-45°=30°,由对称性质得:AC =A C ,∠ACP =∠A CP =30°,∴∠ACA =60°,∴△ACA 是等边三角形,在△AA B 与△CA B 中,A A =A CA B =A B AB =BC,∴△AA B ≌△CA B SSS ,∴∠AA B =∠CA B =12∠AA C =30°,又∵∠CA P =∠CAP =15°,∴∠PA B =∠CA B -∠CA P =15°.【点睛】本题考查了折叠的性质,等腰三角形的判定和性质,三角形内角和定理,正方形的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,作辅助线构造全等三角形是解题关键.19综合与实践数学活动课上,数学老师以“矩形纸片的折叠”为课题开展数学活动:将矩形纸片ABCD 对折,使得点A ,D 重合,点B ,C 重合,折痕为EF ,展开后沿过点B 的直线再次折叠纸片,点A 的对应点为点N ,折痕为BM . (1)如图(1)若AB =BC ,则当点N 落在EF 上时,BF 和BN 的数量关系是,∠NBF 的度数为.思考探究:(2)在AB=BC的条件下进一步进行探究,将△BMN沿BN所在的直线折叠,点M的对应点为点M .当点M 落在CD上时,如图(2),设BN,BM 分别交EF于点J,K.若DM =4,请求出三角形BJK的面积.开放拓展:(3)如图(3),在矩形纸片ABCD中,AB=2,AD=4,将纸片沿过点B的直线折叠,折痕为BM,点A的对应点为点N,展开后再将四边形ABNM沿BN所在的直线折叠,点A的对应点为点P,点M的对应点为点M ,连接CP,DP,若PC=PD,请直接写出AM的长.(温馨提示:12+3=2-3,12+1=2-1)【答案】(1)BF=12BN,60°(2)2+2(3)4-23【分析】(1)根据折叠的性质得:AB=BN,BF=CF=12BC,根据直角三角形的性质可得∠BNF=30°,由直角三角形的两锐角互余可得结论;(2)由折叠得:BM=BM ,证明Rt△ABM≌Rt△CBM (HL),可知AM=CM ,∠ABM=∠CBM ,得△BFJ是等腰直角三角形,再证明四边形ABCD是正方形,分别计算BF=FJ=12BC=2+2,JK=2,由三角形面积公式可得结论;(3)如图(3),过点P作PG⊥BC于G,PH⊥CD于H,根据等腰三角形的三线合一可得DH=CH=12CD=12AB=1,由折叠的性质和矩形的性质可得PG=CH=1,BN=BP=AB=2,∠NBP=∠ABN,设PL=x,则M L=2x,M P=3x,根据NL=233=NM +M L,列方程可解答.【详解】(1)解:由折叠得:AB=BN,BF=CF,∠BFN=90°,∵AB=BC,∴BF=12BN,∴∠BNF=30°,∴∠NBF=90°-30°=60°,故答案为:BF=12BN,60°;(2)由折叠得:BM=BM ,∵四边形ABCD是矩形,∴∠A=∠C=90°,∵AB=BC,∴Rt△ABM≌Rt△CBM (HL),∴AM=CM ,∠ABM=∠CBM ,∴∠ABM=∠MBN=∠NBM =∠CBM ,∴∠FBJ=45°,∴△BFJ是等腰直角三角形,∵四边形ABCD是矩形,AB=BC,∴矩形ABCD是正方形,∴AD=CD,∠D=90°,∴DM=DM =4,∴MM =42,∵AM=MN=M N=CM ,∴CM =22,∴BC =CD =4+22,∴BF =FC =2+2,∵FK ∥CM ,∴BK =KM ,∴FK =12CM =2,∵△BFJ 是等腰直角三角形,∴BF =FJ =12BC =2+2,∴JK =2+2-2=2,∴S △BJK =12⋅JK ⋅BF =12×2×(2+2)=2+2;(3)如图,过点P 作PG ⊥BC 于G ,PH ⊥CD 于H ,∵PC =PD ,∴DH =CH =12CD =12AB =1,∵∠PGC =∠PHC =∠BCH =90°,∵四边形PGCH 是矩形,∴PG =CH =1,由折叠得:BN =BP =AB =2,∠NBP =∠ABN ,Rt △BPG 中,∠PBG =30°,∴∠ABN =∠NBP =90°-30°2=30°,延长NM ,BP 交于L ,Rt △BNL 中,BN =2,∠NBL =30°,∴NL =2×33=233,Rt △M PL 中,∠M LP =90°-30°=60°,∴∠PM L =30°,设PL =x ,则M L =2x ,M P =3x ,∵NL =233=NM +M L ,∴3x +2x =233,∴x =433-2,∴AM =3x =3×433-2 =4-23.【点睛】本题是四边形的综合题,考查了折叠的性质,含30°角的直角三角形的性质,矩形的性质和判定,正方形的判定和性质,三角函数等知识,掌握折叠的性质和正确作辅助线是解题的关键,题目具有一定的综合性,比较新颖.20综合与实践综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.(1)操作判断如图1,先用对折的方式确定矩形ABCD 的边AB 的中点E ,再沿DE 折叠,点A 落在点F 处,把纸片展平,延长DF ,与BC 交点为G .。
八年级数学勾股定理的应用——折叠问题(专题)(含答案)

勾股定理的应用——折叠问题(专题)一、单选题(共10道,每道10分)1.如图,长方形纸片ABCD中,AB=12,AD=5,折叠纸片使AD边与线段BD重合,折痕为DG,则AG的长为( )A. B.6C. D.答案:D解题思路:由题意得,BD=13;由折叠知D=AD=5,G=AG,∠DA′G=∠A=90°.∴B=8.设AG=x,则,BG=12-x.在Rt△BG中,∠BA′G=90°,由勾股定理得,,即,解得,.故选D.试题难度:三颗星知识点:略2.如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EF=( )A.4cmB.3cmC.5cmD.6cm答案:C解题思路:如图,AF=AD=BC=10,在Rt△ABF中,由勾股定理得,BF=6,所以FC=4,设EF=DE=x,则CE=8-x,在Rt△ECF中,∠C=90°,由勾股定理得,,解得,x=5.故选C.试题难度:三颗星知识点:略3.如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则AE的长为____,△ABE的周长为____.( )A.,7B.,7C.,D.,答案:A解题思路:解:由题意知,在Rt△ABC中,∠B=90°,AB=3,AC=5由勾股定理得,BC=4由折叠知,AE=EC设AE=EC=x,则BE=4-x在Rt△ABE中,∠B=90°由勾股定理得,解得,则AE=,BE=∴△ABE的周长为3+x+(4-x) =3+4=7综上,AE的长为,△ABE的周长为7故选A试题难度:三颗星知识点:略4.如图,将一长方形纸片ABCD折叠,使两个顶点A,C重合,折痕为EF.若AB=4,BC=8,则△ABF的面积为( )A.6B.12C.10D.20答案:A解题思路:解:由题意知,将长方形纸片ABCD折叠,使两个顶点A,C重合,折痕为EF,∴AF=CF,∵在长方形ABCD中,AB=4,BC=8∴设BF=x,则AF=FC=8-x,在Rt△ABF中,∠B=90°,AB=4,BF=x,AF=8-x,由勾股定理得,AB2+BF2=AF2,42+x2=(8-x)2,解得,x=3,即BF=3,∴△ABF的面积为故选A.试题难度:三颗星知识点:略5.如图,长方形纸片ABCD中,AD=4,CD=3,折叠纸片使AB边与线段AC重合,折痕为AE,记与点B重合的点为F,则△CEF的面积与纸片ABCD的面积的比为( )A. B.C. D.答案:B解题思路:如图,在长方形ABCD中,AB=CD=AF=3,AD=BC=4,在Rt△ABC中,∠B=90°由勾股定理得,∴∴AC=5由折叠知,EF=BE,∠AFE=∠B=90°,设BE=x,则EF=BE=x在Rt△EFC中,∠CFE=90°,CF=AC-AF=2,EC=4-x,根据勾股定理得,∴解得,x=1.5∴∵∴故选B.试题难度:三颗星知识点:略6.如图,将边长为16cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F 处,折痕为MN,则CN=_____cm,AM=_____cm.( )A.6,2B.8,3C.10,2D.12,3答案:A解题思路:∵点E是BC边的中点,∴EC BC=8,设CN=x,则EN=DN=16-x,在Rt△ECN中,∠C=90°,由勾股定理得,EC2+CN2=EN2解得,x=6如图,连接DM,EM,则DM=EM,设AM=y,则BM=16-y,在Rt△ADM中,∠A=90°,由勾股定理得,在Rt△BEM中,∠B=90°,由勾股定理得,,∵DM=ME,∴解得,y=2故选A.试题难度:三颗星知识点:略7.如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的点E处,折痕为MN.若CE的长为8cm,则AM=_____cm,BN=_____cm.( )A.,1B.,C.,D.,1答案:C解题思路:如图,设AM=x,在Rt△MED中,∠D=90°,由勾股定理,得解得,x=,即AM=,MD=,连接AN,NE,则AN=NE,设BN=y,则CN=12-y,在Rt△ABN中,∠B=90°,由勾股定理,在Rt△CEN中,∠C=90°,由勾股定理,,∵AN=NE,∴解得,故选C.试题难度:三颗星知识点:略8.如图,把长方形ABCD沿AC折叠,AD落在处,交BC于点E,已知AB=2cm,BC=4cm,则EC的长为( )A.2cmB.cmC.5cmD.cm答案:D解题思路:如图,由折叠知,∠DAC=∠EAC,∵AD∥BC,∴∠DAC=∠ECA,∴∠EAC=∠ECA,∴AE=EC设EC=x,则AE=EC=x∵BC=4,∴BE=4-x在Rt△ABE中,∠B=90°,AB=2,BE=4-x,AE=x,由勾股定理得,解得,即EC的长为cm故选D.试题难度:三颗星知识点:略9.把长方形纸片ABCD按如图所示的方式折叠,使点B与点D重合,折痕为EF.若BC=5cm,CD=3cm,则DE=( )cm.A. B.C. D.答案:B解题思路:如图,由折叠知,∠BFE=∠DFE,BF=DF,∵AD∥BC,∴∠BFE=∠DEF,∴∠DFE=∠DEF,∴DE=DF设DF=x,则BF=DF=x∵BC=5,∴CF=5-x在Rt△CDF中,∠C=90°,CD=3,CF=5-x,DF=x,由勾股定理得,解得,∴DE=DF=故选B.试题难度:三颗星知识点:略10.如图,长方形ABCD中,AB=4,BC=3,点E是CD边上一点,连接BE,把∠C沿BE折叠,使点C落在点F处.当△DEF为直角三角形时,DE的长为( )A.1B.1或C. D.3或答案:B解题思路:∵四边形ABCD是长方形,∴AB=CD=4,AD=BC=3,分两种情况讨论:①当∠FED=90°时,如图所示,则∠CEF=90°,由折叠的性质得:CE=FE=BC=3,∴DE=CD-CE=1;②当∠DFE=90°时,如图所示,在Rt△ABD中,∠A=90°,AB=4,AD=3,∴BD=5,由折叠的性质得:∠BFE=∠C=90°,BF=BC=3,EF=EC,∴∠DFE=∠BFE=90°,即点B,F,D三点共线,点F在BD上,∴DF=BD-BF=5-3=2,设DE=x,则EF=CE=4-x在Rt△DEF中,∠EFD=90°,DE=x,EF=4-x,DF=2,由勾股定理得,解得,综上所述,DE的长为1或;故选B.试题难度:三颗星知识点:略第11页共11页。
常考压轴08 折叠问题-2020年中考数学特训营(解析版)

【十大常考压轴题特训】特训08——折叠问题题量﹕25题;分值﹕共计100分;推荐时间﹕60分钟问题1.(2019 甘肃省兰州市)如图,ABCD 的对角线AC 与BD 交于点O ,将正方形ABCD 沿直线DF 折叠,点C 落在对角线BD 上的点E 处,折痕DF 交AC 于点M ,则(OM = )ABC DEFMOA .12BC .1-D 1【分析】根据正方形的性质得到AB =AD =BC =CD =2,∠DCB =∠COD =∠BOC =90°,OD =OC ,求得BD =2AB =2,得到OD =BO =OC =1,根据折叠的性质得到DE =DC =2,DF ⊥ CE ,求得OE = 2 -1,根据全等三角形的性质即可得到结论. 【解析】四边形ABCD 是正方形,∴AB =AD =BC =CD =2,∠DCB =∠COD =∠BOC =90°,OD =OC , ∴BD =2AB =2, ∴OD =BO =OC =1,∵将正方形ABCD 沿直线DF 折叠,点C 落在对角线BD 上的点E 处, ∴DE =DC =2,DF ⊥ CE ,∴OE = 2 -1,∠EDF +∠FED =∠ECO +∠OEC =90°, ∴∠ODM =∠ECO ,在△OEC 与△OMD 中,⎩⎪⎨⎪⎧∠EOC =∠DOC =90 °OD =OC ∠OCE =∠ODM ,∴△OEC ≌ △OMD , ∴OM =OE = 2 -1,故选:D .【点评】本题考查了翻折变换(折叠问题),全等三角形的判定和性质,正方形的性质,正确的识别图形是解题的关键.问题2.(2019 广西桂林市)将矩形ABCD 按如图所示的方式折叠,BE ,EG ,FG 为折痕,若顶点A ,C ,D 都落在点O 处,且点B ,O ,G 在同一条直线上,同时点E ,O ,F 在另一条直线上,则ADAB的值为( ) ABCDEFG OA .65BC .32D【分析】由折叠可得,E ,G 分别为AD ,CD 的中点,设CD =2a ,AD =2b ,根据Rt △BCG 中,CG 2+BC 2=BG 2,可得即a 2+(2b )2=(3a )2,进而得出ADAB 的值. 【解析】由折叠可得,AE =OE =DE ,CE =OG =DG , ∴,G 分别为AD ,CD 的中点,设CD =2a ,AD =2b ,则AB =2a =OB ,DG =OG =CG =a ,BG =3a ,BC =AD =2b , ∵∠C =90°,∴Rt △BCG 中,CG 2+BC 2=BG 2, 即a 2+(2b )2=(3a )2, ∴b 2=2a 2, 即b =2a , ∴ba =2, ∴ADAB 的值为 2 , 故选:B .【点评】本题主要考查了折叠问题,解题时,我们常常设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.问题3.(2019 贵州省铜仁地区)如图,正方形ABCD 中,6AB =,E 为AB 的中点,将ADE ∆沿DE 翻折得到FDE ∆,延长EF 交BC 于G ,FH BC ⊥,垂足为H ,连接BF 、DG .以下结论:①//BF ED ;②DFG DCG ∆≅∆;③FHB EAD ∆∆∽;④4tan 3GEB ∠=;⑤ 2.6BFG S ∆=;其中正确的个数是( ) ABCDEFG HA .2B .3C .4D .5【分析】根据正方形的性质以及折叠的性质依次对各个选项进行判断即可. 【解析】∵正方形ABCD 中,AB =6,E 为AB 的中点∴AD =DC =BC =AB =6,AE =BE =3,∠A =∠C =∠ABC =90° ∵△ADE 沿DE 翻折得到△FDE∴∠AED =∠FED ,AD =FD =6,AE =EF =3,∠A =∠DFE =90° ∴BE =EF =3,∠DFG =∠C =90° ∴∠EBF =∠EFB∵∠AED +∠FED =∠EBF +∠EFB ∴∠DEF =∠EFB ∴BF //ED 故结论①正确;∵AD =DF =DC =6,∠DFG =∠C =90°,DG =DG ∴△ DFG ≌ △DCG∴结论②正确;FH ⊥ BC ,∠ABC =90° ∴AB //FH ,∠FHB =∠A =90° ∵∠EBF =∠BFH =∠AED ∴△FHB ∽ △EAD∴结论③正确;∵△ DFG ≌ △DCG ∴FG =CG设FG =CG =x ,则BG =6-x ,EG =3+x在Rt △BEG 中,由勾股定理得:32+(6-x )2=(3+x )2 解得:x =2 ∴BG =4∴tan ∠GEB =BG BE =43 故结论④正确;∵△FHB ∽ △EAD ,且AE AD =12 ∴BH =2FH设FH =a ,则HG =4-2a在Rt △FHG 中,由勾股定理得:a 2+(4-2a )2=22 解得:a =2(舍去)或a =65 ∴S △BFG =12×4×65=2.4 故结论⑤错误; 故选:C .【点评】本题主要考查了正方形的性质、折叠的性质、全等三角形的判定与性质、相似三角形的判定与性质、平行线的判定、勾股定理、三角函数,综合性较强.问题4.(2019 湖北省荆州市)如图,点C 为扇形OAB 的半径OB 上一点,将△OAC 沿AC 折叠,点O 恰好落在⌒AB 上的点D 处,且⌒BD :⌒AD =1:3(⌒BD 表示⌒BD 的长),若将此扇形OAB 围成一个圆锥,则圆锥的底面半径与母线长的比为()A .1:3B .1:πC .1:4D .2:9【分析】连接OD,能得∠AOB的度数,再利用弧长公式和圆的周长公式可求解.【解析】连接OD交OC于M.由折叠的知识可得:OM=12OA,∠OMA=90°,∴∠OAM=30°,∴∠AOM=60°,∵且⌒BD:⌒AD=1:3,∴∠AOB=80°设圆锥的底面半径为r,母线长为l,80πl180=2πr,∴r:i=2:9.故选:D.【点评】本题运用了弧长公式和轴对称的性质,关键是运用了转化的数学思想.问题5.(2019山东省泰安市)如图,将⊙O沿弦AB折叠,⌒AB恰好经过圆心O,若⊙O的半径为3,则⌒AB的长为()A.12πB.πC.2πD.3π【分析】连接OA、OB,作OC⊥AB于C,根据翻转变换的性质得到OC=12OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据弧长公式计算即可.【解析】连接OA、OB,作OC⊥AB于C,由题意得,OC=12OA,∴∠OAC=30°,∵OA=OB,∴∠OBA=∠OAC=30°,∴∠AOB=120°,∴⌒AB的长=120π×3180=2π,故选:C.【点评】本题考查的是弧长的计算、直角三角形的性质、翻转变换的性质,掌握弧长公式是解题的关键.问题6.(2019重庆市)如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB 交于点E,连结AC′,若AD=AC′=2,BD=3,则点D到BC′的距离为()A.332B.3217C.7 D.13【分析】分析连接CC′,交BD于点M,过点D作DH⊥BC′于点H,由翻折知,△BDC≌△BDC′,BD垂直平分CC′,证△ADC′为等边三角形,利用解直角三角形求出DM=1,C′M= 3 DM=3,BM=2,在Rt△BMC′中,利用勾股定理求出BC′的长,在△BDC′中利用面积法求出DH的长.【解析】如图,连接CC′,交BD于点M,过点D作DH⊥BC′于点H,∵AD=AC′=2,D是AC边上的中点,∴DC=AD=2,由翻折知,△BDC≌△BDC′,BD垂直平分CC′,∴DC=DC′=2,BC=BC′,CM=C′M,∴AD=AC′=DC′=2,∴△ADC′为等边三角形,∴∠ADC′=∠AC′D=∠C′AC=60°,∵DC=DC′,∴∠DCC ′=∠DC ′C =12×60°=30°, 在Rt △C ′DM 中,∠DC ′C =30°,DC ′=2, ∴DM =1,C ′M =3DM =3, ∴BM =BD ﹣DM =3﹣1=2, 在Rt △BMC ′中,BC ′=BM 2+C 'M 2=22+(3)2=7, ∵S △BDC ′=12BC ′•DH =12BD •CM , ∴7DH =3×3, ∴DH =3217, 故选:B .【点评】点评本题考查了轴对称的性质,解直角三角形,勾股定理等,解题关键是会通过面积法求线段的长度.问题7.(2019 辽宁省大连市)如图,将矩形纸片ABCD 折叠,使点C 与点A 重合,折痕为EF ,若4AB =,8BC =.则D F '的长为( )A .5B .4C .3D .2【分析】连接AC 交EF 于点O ,由矩形的性质得出AD =BC =8,∠B =90°,由勾股定理得出AC =AB 2+BC 2=45,由折叠的性质得出EF ⊥ AC ,AO =CO =12 AC =25,证出Rt △FOA ∽ Rt △ADC ,则AO AF =ADAC ,求出AF =5,即可得出结果. 【解析】连接AC 交EF 于点O ,如图所示: ∵四边形ABCD 是矩形,∴ AD =BC =8,∠B =∠ D =90°, AC =AB 2+BC 2=45,∵折叠矩形使C 与A 重合时,EF ⊥ AC ,AO =CO =12 AC =25, ∴ ∠ AOF =∠ D =90°,∠ OAF =∠ DAC , ∴则Rt △FOA ∽ Rt △ADC , ∴AO AF = ADAC ,即:25AF =845, 解得:AF =5,∴D ′F =DF =AD -AF =8-5=3, 故选:C .【点评】本题考查了折叠的性质、矩形的性质、勾股定理、相似三角形的判定与性质等知识,熟练掌握折叠的性质,证明三角形相似是解题的关键.问题8.(2019 四川省攀枝花市)如图,在正方形ABCD 中,E 是BC 边上的一点,4BE =,8EC =,将正方形边AB 沿AE 折叠到AF ,延长EF 交DC 于G ,连接AC ,现在有如下4个结论: ①45EAC ∠=︒;②FG FC =;③//FC AG ;④14GFC S ∆=. 其中正确结论的个数是( )A.1 B.2 C.3 D.4【分析】①正确.证明∠GAF=∠GAD,∠EAB=∠EAF即可.②错误.可以证明DG=GC=FG,显然△GFC不是等边三角形,可得结论.③正确.证明CF⊥DF,AG⊥DF即可.④错误.证明FG﹕EG=3﹕5,求出△ECG的面积即可.【解析】如图,连接DF.∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠ABE=∠BAD=∠ADG=∠ECG=90°,由翻折可知:AB=AF,∠ABE=∠AFE=∠AFG=90°,BE=EF=2,∠BAE=∠EAF,∵∠AFG=∠ADG=90°,AD=AG,AD=AF,∴Rt△AGD≌Rt△AGF,∴DG=FG,∠GAF=∠GAD,,设GD=GF=x,∴∠EAG=∠EAF+∠GAF=12(∠BAF+∠DAF)=45 °,故①正确,在Rt△ECG中,∵EG2=EC2+CG2,∴(2+x)2=82+(12-x)2,∴x=6,∵CD=BC=BE+EC=12,∴DG=CG=6,∴FG=GC,易知△GFC不是等边三角形,显然FG≠FC,故②错误,∵GF=GD=GC,∴∠DFC=90°,∴CF⊥DF,∵AD=AF,GD=GF,∴AG⊥DF,∴CG//AG,故③正确,∵S△ECG=12×6×8=24,FG:FE=6:4=3:2,∴FG:EG=3:5,∴S△GFC=35×24=725,故④错误,故选:B.【点评】本题考查翻折变换,正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.问题9.(2019甘肃省天水市)如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为.【分析】先根据矩形的性质得AD=BC=5,AB=CD=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt △ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF 中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到x,进一步得到EF的长,再根据正弦函数的定义即可求解.【解析】∵四边形ABCD为矩形,∴AD=BC=5,AB=CD=3,∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,∴AF=AD=5,EF=DE,在Rt△ABF中,∵BF=AF2-AB2=4,∴CF =BC ﹣BF =5﹣4=1, 设CE =x ,则DE =EF =3﹣x 在Rt △ECF 中,∵CE 2+FC 2=EF 2, ∴x 2+12=(3﹣x )2,解得x =43,∴EF =3﹣x =53, ∴sin ∠EFC =CE EF =45. 故答案为:45.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理.问题10.(2019 广东省深圳市)如图,在正方形ABCD 中,1BE =,将BC 沿CE 翻折,使B 点对应点刚好落在对角线AC 上,将AD 沿AF 翻折,使D 点对应点刚好落在对角线AC 上,求EF = .ABCDEFXY【分析】作FM ⊥ AB 于点M .根据折叠的性质与等腰直角三角形的性质得出EX =EB =AX =1,∠EXC =∠B =90°,AM =DF =YF =1,由勾股定理得到AE =AX 2+EX 2=2.那么正方形的边长AB =FM =2+1,EM =2-1,然后利用勾股定理即可求出EF . 【解析】如图,作FM ⊥ AB 于点M . ∵四边形ABCD 是正方形, ∴ ∠BAC =∠CAD =45 °.∵将BC 沿CE 翻折,B 点对应点刚好落在对角线AC 上的点X , ∴ EX =EB =AX =1,∠EXC =∠B =90°, ∴ AE =AX 2+EX 2=2.∵将AD沿AF翻折,使D点对应点刚好落在对角线AC上的点Y,∴ AM=DF=YF=1,∴正方形的边长AB=FM=2+1,EM=2-1,∴ EF=EM2+FM2=(2-1)2+(2+1)2=6.故答案为6.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质以及勾股定理.求出EM与EM是解题的关键.问题11.(2019贵州省遵义市)如图,平行四边形纸片ABCD的边AB,BC的长分别是10cm和7.5cm,将其四个角向内对折后,点B与点C重合于点C',点A与点D重合于点A'.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=cm.【分析】先根据有三个角是直角的四边形是矩形证明四边形EHFG是矩形,再证明△FCH≌△EAG,可得CF =AE=FC',可知EF=AB,即可得结论.【解析】如图中,由翻折可知:∠CHF=∠FHC’,∠BHE=∠EHC',∴ ∠FHE=∠FHC’+∠EHC’=12(∠CHC’+∠BHC’)=90°,同法可证:∠HFG=∠GEH=90°,∴四边形EHFG是矩形.∴FH=EG,FH//EG,∴∠HFC’=∠FEG,∵∠CFH=∠HFC’,∠AEG=∠GEA’,∴∠CFH=∠AEG,∵四边形ABCD是平行四边形,∴∠C=∠A,BC=AD,由翻折得:CH=C'H=BH=12BC,AG=A'G=DG=12AD,∴CH=AG,∴△HCF≌ △GAE,∴CF=AE,∴EF=FC'+EC'=AE+BE=AB=10cm,故答案为:10.【点评】本题考查了平行四边形的性质,翻折变换,矩形的判定和性质,三角形全等的性质和判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题.问题12.(2019吉林省长春市)如图,有一张矩形纸片ABCD,AB=8,AD=6.先将矩形纸片ABCD折叠,使边AD落在边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF翻折,AF与BC相交于点G,则△GCF的周长为.【分析】根据折叠的性质得到∠DAF=∠BAF=45°,根据矩形的性质得到FC=ED=2,根据勾股定理求出GF,根据周长公式计算即可.【解析】由折叠的性质可知,∠DAF=∠BAF=45°,∴AE=AD=6,∴EB=AB﹣AE=2,由题意得,四边形EFCB为矩形,∴FC=ED=2,∵AB∥FC,∴∠GFC =∠A =45°, ∴GC =FC =2,由勾股定理得,GF =FC 2+GC 2=22, 则△GCF 的周长=GC +FC +GF =4+22, 故答案为:4+22.【点评】本题考查的是翻折变换的性质、矩形的性质一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.问题13.(2019 江苏省淮安市)如图,在矩形ABCD 中,AB =3,BC =2,H 是AB 的中点,将△CBH 沿CH 折叠,点B 落在矩形内点P 处,连接AP ,则tan ∠HAP = .【分析】连接PB ,交CH 于E ,依据轴对称的性质以及三角形内角和定理,即可得到CH 垂直平分BP ,∠APB =90°,即可得到AP ∥HE ,进而得出∠BAP =∠BHE ,依据Rt △BCH 中,tan ∠BHC =BC BH =43,即可得出tan ∠HAP =43.【解析】如图,连接PB ,交CH 于E , 由折叠可得,CH 垂直平分BP ,BH =PH , 又∵H 为AB 的中点, ∴AH =BH , ∴AH =PH =BH ,∴∠HAP =∠HP A ,∠HBP =∠HPB ,又∵∠HAP +∠HP A +∠HBP +∠HPB =180°, ∴∠APB =90°, ∴∠APB =∠HEB =90°, ∴AP ∥HE , ∴∠BAP =∠BHE ,又∵Rt△BCH中,tan∠BHC=BCBH=43,∴tan∠HAP=4 3,故答案为:4 3.【点评】本题考查的是翻折变换的性质和矩形的性质,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.问题14.(2019山东省青岛市)如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD=4cm,则CF的长为cm.【分析】设BF=x,则FG=x,CF=4﹣x,在Rt△GEF中,利用勾股定理可得EF2=(25﹣4)2+x2,在Rt △FCE中,利用勾股定理可得EF2=(4﹣x)2+22,从而得到关于x方程,求解x,最后用4﹣x即可.【解析】设BF=x,则FG=x,CF=4﹣x.在Rt△ADE中,利用勾股定理可得AE=25.根据折叠的性质可知AG=AB=4,所以GE=25﹣4.在Rt△GEF中,利用勾股定理可得EF2=(25﹣4)2+x2,在Rt△FCE中,利用勾股定理可得EF2=(4﹣x)2+22,所以(25﹣4)2+x2=(4﹣x)2+22,解得x=25﹣2.则FC=4﹣x=6﹣25.故答案为6﹣25.【点评】本题主要考查了折叠的性质、勾股定理.折叠问题主要是抓住折叠的不变量,在直角三角形中利用勾股定理求解是解题的关键.问题15.(2019 山东省泰安市)如图,矩形ABCD 中,AB =36,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .【分析】连接EC ,利用矩形的性质,求出EG ,DE 的长度,证明EC 平分∠DCF ,再证∠FEC =90°,最后证△FEC ∽△EDC ,利用相似的性质即可求出EF 的长度. 【解析】如图,连接EC , ∵四边形ABCD 为矩形,∴∠A =∠D =90°,BC =AD =12,DC =AB =3 6 , ∵E 为AD 中点, ∴AE =DE =12AD =6 由翻折知,△AEF ≌△GEF ,∴AE =GE =6,∠AEF =∠GEF ,∠EGF =∠EAF =90°=∠D , ∴GE =DE , ∴EC 平分∠DCG , ∴∠DCE =∠GCE ,∵∠GEC =90°﹣∠GCE ,∠DEC =90°﹣∠DCE , ∴∠GEC =∠DEC ,∴∠FEC =∠FEG +∠GEC =12×180°=90°, ∴∠FEC =∠D =90°, 又∵∠DCE =∠GCE , ∴△FEC ∽△EDC , ∴FE DE =EC DC ,∵EC=DE2+DC2=62+(36)2=310,∴FE6=31036,∴FE=215,故答案为:215.【点评】本题考查了矩形的性质,轴对称的性质,相似三角形的判定与性质等,解题关键是能够作出适当的辅助线,连接CE,构造相似三角形,最终利用相似的性质求出结果.问题16.(2019山东省潍坊市)如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A′,折痕为DE.若将∠B沿EA′向内翻折,点B恰好落在DE上,记为B′,则AB=.【分析】利用矩形的性质,证明∠ADE=∠A′DE=∠A′DC=30°,∠C=∠A′B′D=90°,推出△DB′A′≌△DCA′,CD=B′D,设AB=DC=x,在Rt△ADE中,通过勾股定理可求出AB的长度.【解析】∵四边形ABCD为矩形,∴∠ADC=∠C=∠B=90°,AB=DC,由翻折知,△AED≌△A′ED,△A′BE≌△A′B′E,∠A′B′E=∠B=∠A′B′D=90°,∴∠AED=∠A′ED,∠A′EB=∠A′EB′,BE=B′E,∴∠AED=∠A′ED=∠A′EB=13×180°=60°,∴∠ADE=90°﹣∠AED=30°,∠A′DE=90°﹣∠A′EB=30°,∴∠ADE=∠A′DE=∠A′DC=30°,又∵∠C=∠A′B′D=90°,DA′=DA′,∴△DB′A′≌△DCA′(AAS),∴DC=DB′,在Rt△AED中,∠ADE=30°,AD=2,∴AE=23=233,设AB=DC=x,则BE=B′E=x﹣23 3∵AE2+AD2=DE2,∴(233)2+22=(x+x﹣233)2,解得,x1=-33(负值舍去),x2=3,故答案为:3.【点评】本题考查了矩形的性质,轴对称的性质等,解题关键是通过轴对称的性质证明∠AED=∠A′ED=∠A′EB=60°.问题17.(2019上海市)如图,在正方形ABCD中,E是边AD的中点.将ABE∆沿直线BE翻折,点A落在点F处,联结DF,那么EDF∠的正切值是.【分析】由折叠可得AE=FE,∠AEB=∠FEB,由折叠的性质以及三角形外角性质,即可得到∠AEB=∠EDF,进而得到tan∠EDF=tan∠AEB=ABAE=2.【解析】如图所示,由折叠可得AE=FE,∠AEB=∠FEB=12∠AEF,∵正方形ABCD中,E是AD的中点,∴AE=DE=12AD=12AB,∴DE=FE,∴∠EDF=∠EFD,又∵∠AEF是△DEF的外角,∴∠AEF=∠EDF+∠EFD,∴∠EDF=12∠AEF,∴∠AEB=∠EDF,∴tan∠EDF=tan∠AEB=ABAE=2.故答案为:2.【点评】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.问题18.(2019天津市)如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G 点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为.【分析】由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,先证△ABF≌△DAE,推出AF的长,再利用勾股定理求出BF的长,最后在Rt△ADF中利用面积法可求出AH的长,可进一步求出AG的长,GE的长.【解析】∵四边形ABCD为正方形,∴AB=AD=12,∠BAD=∠D=90°,由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,∴BF⊥AE,AH=GH,∴∠F AH+∠AFH=90°,又∵∠F AH+∠BAH=90°,∴∠AFH=∠BAH,∴△ABF≌△DAE(AAS),∴AF=DE=5,在Rt△ADF中,BF=AB2+AF2=122+52=13,S△ABF=12AB•AF=12BF•AH,∴12×5=13AH,∴AH=60 13,∴AG=2AH=120 13,∵AE=BF=13,∴GE=AE﹣AG=13﹣12013=4913,故答案为:49 13.【点评】本题考查了正方形的性质,轴对称的性质,全等三角形的判定与性质,勾股定理,面积法求线段的长度等,解题关键是能够灵活运用正方形的性质和轴对称的性质.问题19.(2019浙江省杭州市)如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C 落在AD边上同一点P处,A点的对称点为A′点,D点的对称点为D′点,若∠FPG=90°,△A′EP的面积为4,△D′PH的面积为1,则矩形ABCD的面积等于.【分析】设AB=CD=x,由翻折可知:P A′=AB=x,PD′=CD=x,因为△A′EP的面积为4,△D′PH的面积为1,推出A′E=4D′H,设D′H=a,则A′E=4a,由△A′EP∽△D′PH,推出D'HP A'=PD'EA',推出ax=x4a,可得x=2a,再利用三角形的面积公式求出a即可解决问题.【解析】∵四边形ABCD是矩形,∴AB=CD,AD=BC,设AB=CD=x,由翻折可知:P A′=AB=x,PD′=CD=x,∵△A′EP的面积为4,△D′PH的面积为1,∴A′E=4D′H,设D′H=a,则A′E=4a,∵△A′EP∽△D′PH,∴D'HP A'=PD'EA',∴ax=x4a,∴x2=4a2,∴x=2a或﹣2a(舍弃),∴P A′=PD′=2a,∵12•a•2a=1,∴a=1,∴x=2,∴AB=CD=2,PE=22+42=25,PH=12+22=5,∴AD=4+25+5+1=5+35,∴矩形ABCD的面积=2(5+35).故答案为2(5+35)【点评】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.问题20.(2019 河南省)如图,在矩形ABCD 中,AB =1,BC =a ,点E 在边BC 上,且BE =35α.连接AE ,将△ABE 沿AE 折叠,若点B 的对应点B ′落在矩形ABCD 的边上,则a 的值为 .【分析】分两种情况:①点B ′落在AD 边上,根据矩形与折叠的性质易得AB =BE ,即可求出a 的值;②点B ′落在CD 边上,证明△ADB ′∽△B ′CE ,根据相似三角形对应边成比例即可求出a 的值. 【解析】分两种情况:①当点B ′落在AD 边上时,如图1. ∵四边形ABCD 是矩形, ∴∠BAD =∠B =90°,∵将△ABE 沿AE 折叠,点B 的对应点B ′落在AD 边上, ∴∠BAE =∠B ′AE =12∠BAD =45°, ∴AB =BE , ∴35a =1, ∴a =53;②当点B ′落在CD 边上时,如图2. ∵四边形ABCD 是矩形,∴∠BAD =∠B =∠C =∠D =90°,AD =BC =a . ∵将△ABE 沿AE 折叠,点B 的对应点B ′落在CD 边上, ∴∠B =∠AB ′E =90°,AB =AB ′=1,EB =EB ′=35a , ∴DB ′=B 'A 2-AD 2=1-a 2,EC =BC ﹣BE =a ﹣35a =25a .在△ADB ′与△B ′CE 中,⎩⎨⎧∠B 'AD =∠EB 'C =90°-∠AB 'I ∠D =∠C,∴△ADB′∽△B′CE,∴DB'CE=AB'B'E,即1-a225a=135a,解得a1=53,a2=0(舍去).综上,所求a的值为53或53.故答案为53或53.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.问题21.(2019江苏省常州市)如图,把平行四边形纸片ABCD沿BD折叠,点C落在点C′处,BC′与AD相交于点E.(1)连接AC′,则AC′与BD的位置关系是;(2)EB与ED相等吗?证明你的结论.【分析】(1)根据AD=C′B,ED=EB,即可得到AE=C′E,再根据三角形内角和定理,即可得到∠EAC′=∠EC′A=∠EBD=∠EDB,进而得出AC′∥BD;(2)依据平行线的性质以及折叠的性质,即可得到∠EDB=∠EBD,进而得出BE=DE.【解析】(1)连接AC′,则AC′与BD的位置关系是AC′∥BD,故答案为:AC′∥BD;(2)EB与ED相等.由折叠可得,∠CBD=∠C′BD,∵AD∥BC,∴∠ADB=∠CBD,∴∠EDB=∠EBD,∴BE=DE.【点评】本题主要考查了折叠问题以及平行四边形的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.问题22.(2019江苏省徐州市)如图,将平行四边形纸片ABCD沿一条直线折叠,使点A与点C重合,点D落在点G处,折痕为EF.求证:(1)∠ECB=∠FCG;(2)△EBC≌△FG C.【分析】(1)依据平行四边形的性质,即可得到∠A=∠BCD,由折叠可得,∠A=∠ECG,即可得到∠ECB=∠FCG;(2)依据平行四边形的性质,即可得出∠D=∠B,AD=BC,由折叠可得,∠D=∠G,AD=CG,即可得到∠B =∠G,BC=CG,进而得出∠EBC≌△FG C.【解析】(1)∵ 四边形ABCD是平行四边形,∴∠A=∠BCD,由折叠可得,∠A=∠ECG,∴∠BCD=∠ECG,∴∠BCD-∠ECF=∠ECG-∠ECF,∴∠ECB=∠FCG;(2)∵四边形ABCD是平行四边形,∴∠D=∠B,AD=BC,由折叠可得,∠D=∠G,AD=CG,∴ ∠ B=∠ G,BC=CG,又∵∠ECB=∠FCG,∴ △EBC≌ △FG C.【点评】本题主要考查了平行四边形的性质,平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.问题23.(2019山东省滨州市)如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG ∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.【分析】(1)根据题意和翻着的性质,可以得到△BCE≌△BFE,再根据全等三角形的性质和菱形的判定方法即可证明结论成立;(2)根据题意和勾股定理,可以求得AF的长,进而求得EF和DF的值,从而可以得到四边形CEFG的面积.【解析】(1)证明:由题意可得,△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE,∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形,又∵CE=FE,∴四边形CEFG是菱形;(2)∵矩形ABCD中,AB=6,AD=10,BC=BF,∴∠BAF=90°,AD=BC=BF=10,∴AF=8,∴DF=2,设EF=x,则CE=x,DE=6﹣x,∵FDE=90°,∴22+(6﹣x)2=x2,解得,x=10 3,∴CE=10 3,∴四边形CEFG的面积是:CE•DF=103×2=203.【点评】本题考查翻折变化、菱形的性质和判定、矩形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.问题24.(2019山东省烟台市)如图,在矩形ABCD中,CD=2,AD=4,点P在BC上,将△ABP沿AP折叠,点B恰好落在对角线AC 上的E点.O为AC上一点,⊙O经过点A,P.(1)求证:BC是⊙O的切线;(2)在边CB上截取CF=CE,点F是线段BC的黄金分割点吗?请说明理由.B【分析】(1)切线的判定重点是证明垂直;(2)判定黄金分割点其实就是证明CF2=BF•BC成立.【解析】(1)证明:如图,连接OP,则OA=OP,∴∠OAP=∠OP A.B由折叠知∠BAP=∠OAP,∴∠OP A=∠BAP.∴AB∥OP.又∵AB⊥BC,∴OP⊥B C.∴BC是⊙O的切线.(2)点F是线段BC的黄金分割点,理由如下:在矩形ABCD中,∵AB=CD=2,BC=AD=4,∴AC=AB2+BC2=22+42=25.又∵AE=AB=2,∴CE=CF=25-2.∴BF=BC-CF=6-25.∵CF2=(25-2)2=24-85,BF•BC=4(6-25)=24-85,∴CF2=BF•B C.∴点F是线段BC的黄金分割点.【点评】本题重点考查了矩形、圆的切线的判定定理、轴对称的性质、黄金分割点的概念,很巧妙地将图形的折叠问题融入其中,是一道非常好的题目.问题25.(2019山东省临沂市)如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE 是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.【分析】过点H作HN⊥BM于N,利用正方形的性质及轴对称的性质,证明△ABG≌△AFG,可推出AG是∠BAF的平分线,GA是∠BGF的平分线;证明△ABG≌△GNH,推出HN=CN,得到∠DCH=∠NCH,推出CH 是∠DCN的平分线;再证∠HGN=∠EGH,可知GH是∠EGM的平分线.【解析】过点H作HN⊥BM于N,则∠HNC=90°,∵四边形ABCD为正方形,∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°,①∵将△ADE沿AE所在的直线折叠得到△AFE,∴△ADE≌△AFE,∴∠D=∠AFE=∠AFG=90°,AD=AF,∠DAE=∠F AE,∴AF=AB,又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL),∴∠BAG=∠F AG,∠AGB=∠AGF,∴AG是∠BAF的平分线,GA是∠BGF的平分线;②由①知,∠DAE=∠F AE,∠BAG=∠F AG,又∵∠BAD=90°,∴∠GAF+∠EAF=12×90°=45°,即∠GAH=45°,∵GH⊥AG,∴∠GHA=90°﹣∠GAH=45°,∴△AGH为等腰直角三角形,∴AG=GH,∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,∴∠BAG=∠NGH,又∵∠B=∠HNG=90°,AG=GH,∴△ABG≌△GNH(AAS),∴BG=NH,AB=GN,∴BC=GN,∵BC﹣CG=GN﹣CG,∴BG=CN,∴CN=HN,∵∠DCM=90°,∴∠NCH=∠NHC=12×90°=45°,∴∠DCH=∠DCM﹣∠NCH=45°,∴∠DCH=∠NCH,∴CH是∠DCN的平分线;③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,由①知,∠AGB=∠AGF,∴∠HGN=∠EGH,∴GH是∠EGM的平分线;综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,GH是∠EGM的平分线.【点评】本题考查了正方形的性质,轴对称的性质,全等三角形的判定与性质等,解题关键是能够灵活运用轴对称的性质及全等的判定方法.。
(完整版)中考数学几何图形折叠试题典题及解答
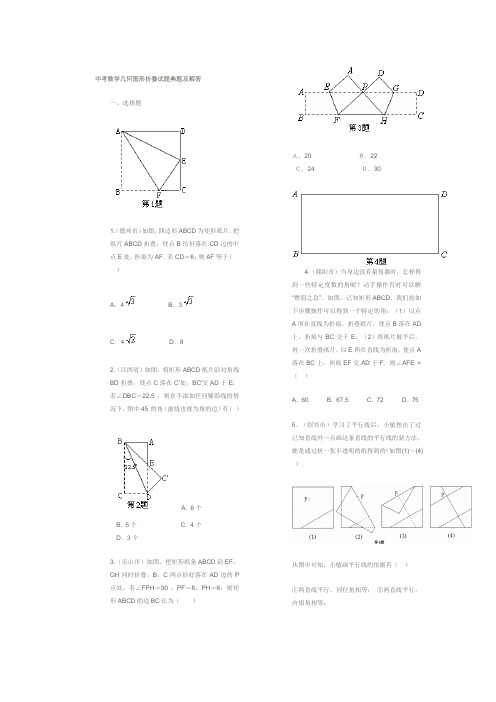
中考数学几何图形折叠试题典题及解答一、选择题1.(德州市)如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()A.4B.3C.4D.82.(江西省)如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC′交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有()A.6个B.5个C.4个D.3个3.(乐山市)如图,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为()A.20B.22C.24D.304.(绵阳市)当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD 上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A 落在BC上,折痕EF交AD于F.则∠AFE =()A.60°B.67.5°C.72°D.75°5. (绍兴市)学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A.①②B.②③C.③④D.①④6.(贵阳市)如图6-1所示,将长为20cm,宽为2cm的长方形白纸条,折成图6-2所示的图形并在其一面着色,则着色部分的面积为()A.34cm2 B.36cm2C.38cm2 D.40cm2二、填空题7.(成都市)如图,把一张矩形纸片ABCD沿E F折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠B EG°.8. (苏州市)如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.三、解答题9.(荆门市)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;在(2)的情况下,在该抛物线上是否存在点Q,使△P EQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.10. (济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;如果沿直线EB折叠纸片,点A是否能叠在直线EC 上?为什么?11.(威海市)如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.已知CE⊥AB.(1)求证:EF∥BD;(2)若AB=7,CD=3,求线段EF的长.12. (烟台市)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).13. 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.14.(孝感市)在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).请解答以下问题:(1)如图2,若延长MN交BC于P,△BMP 是什么三角形?请证明你的结论.(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系. 设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点)?为什么?15.(邵阳市)如图①,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C 重合(图②).(1)在图①中画出折痕所在的直线l.设直线l 与AB,AC分别相交于点D,E,连结CD.(画图工具不限,不要求写画法)(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(不要求证明)16.(济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ. 求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如补相似请说明理由;(3)如果直线EB折叠纸片,点A是否能叠在直线EC上?为什么?17.(临安市)如图,△OAB 是边长为的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E//x轴时,求点A′和E的坐标;(2)当A′E//x轴,且抛物线经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.18.(南宁市)如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AH=6,点D为AB边上的任意一点,过点D作DE∥BC,交AC于点E.设△ADE的高AF为x(0<x<6),以DE为折线将△ADE翻折,所得的△A′DE与梯形DBCE重叠部分的面积记为y(点A关于DE的对称点A′落在AH所在的直线上).(1)分别求出当0<x≤3与3<x<6时,y与x 的函数关系式;(2)当x取何值时,y的值最大?最大值是多少?19.(宁夏回族自治区)如图,将矩形纸片ABCD沿对角线B D折叠,点C落在点E处,BE交AD于点F,连结AE.证明:(1)BF=DF;(2)AE∥BD.参考答案一、1.A 2.B 3.C 4.B 5.C 6.B二、7.648.50°三、9. 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠OPE+∠APB= 90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA.∴Rt△POE∽Rt△BPA.∴.即.∴.且当x=2时,y 有最大值.由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).……6分设过此三点的抛物线为y=ax2+bx+c ,则∴y=.由(2)知∠EPB=90°,即点Q与点B重合时满足条件.直线PB为y=x-1,与y轴交于点(0,-1).将PB向上平移2个单位则过点E(0,1),∴该直线为y=x+1.由得∴Q(5,6).故该抛物线上存在两点Q(4,3)、(5,6)满足条件.10. 证明:(1)∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB=90°,∴△PBE~△QAB.(2)∵△PBE~△QAB ,∴∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能叠在直线EC上.由(2)得,∠AE B=∠CEB,∴EC和折痕AE重合.11. 解:(1)证明:过C点作CH∥BD,交AB的延长线于点H;连结AC,交EF于点K,则AK=CK.∵AB∥CD,∴BH=CD,BD=CH.∵AD=BC,∴AC=BD=CH.∵CE⊥AB,∴AE=EH.∴EK是△AHC的中位线.∴EK∥CH.∴EF∥BD.(2)解:由(1)得BH∥CD,EF∥BD,∴∠AEF=∠ABD.∵AB=7,CD=3,∴AH=10.∵AE=CE,AE=EH,∴AE=CE=EH=5.∵CE⊥AB,∴CH=5=BD.∵∠EAF=∠BAD,∠AEF=∠ABD,∴△AFE∽△ADB.∴.∴.12. 解:(1)由折纸过程知0<5x<26,,0<x <.(2)图④为轴对称图形,∴A M =.即点M与点A的距离是(13-x)cm.13. 证明:⑴由折叠可知:∠D=∠D′,CD=A D′,∠C=∠D′AE.∵四边形ABCD是平行四边形,∴∠B=∠D,AB=CD,∠C=∠BAD.∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.∴∠1=∠3.∴△ABE ≌△AD′F.⑵四边形AECF是菱形.由折叠可知AE=EC,∠4=∠5.∵四边形ABCD是平行四边形,∴AD∥BC.∴∠5=∠6.∴∠4=∠6.∴AF=AE.∵AE=EC,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.∵AF=AE,∴四边形AECF是菱形.14. 解:(1)△BMP是等边三角形.证明:连结AN.∵EF垂直平分AB,∴AN = BN.由折叠知AB = BN ,∴AN = AB = BN,∴△ABN为等边三角形.∴∠ABN =60°. ∴∠PBN =30°.又∵∠ABM =∠NBM =30°,∠BNM =∠A =9 0°.∴∠BPN =60°.∠MBP =∠MBN +∠PBN =60°.∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°.∴△BMP为等边三角形 .(2)要在矩形纸片ABCD上剪出等边△BMP,则BC ≥BP.在Rt△BNP中,BN = BA =a,∠PBN =30°,∴BP =. ∴b≥. ∴a≤b .∴当a≤b时,在矩形上能剪出这样的等边△BMP.(3)∵∠M′BC =60°,∴∠ABM′=90°-60°= 30°.在Rt△ABM′中,tan∠ABM′ =. ∴tan3 0°=. ∴AM′ =.∴M′(,2). 代入y=kx中,得k== .设△ABM′沿BM′折叠后,点A落在矩形ABCD 内的点为A′.过A′作AH ⊥BC交BC于H.∵△A′BM′ ≌△ABM′,∴∠A′BM′=∠ABM′=3 0°, A′B = AB =2.∴∠A′BH=∠M′BH-∠A′BM′=30°.在Rt△A′BH中,A′H =A′B =1 ,BH=,∴.∴A'落在EF上.(图2)(图3)15.解:(1)如图.等腰三角形DAC.16.(1)证明:∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB,∴△PBE∽△QAB.(2)∵△PBE∽△QAB,∴. ∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能折叠在直线EC上.由(2)得,∠AEB=∠CEB,∴EC和折痕AE 重合.17. 解:(1)由已知可得∠A'OE=60o , A'E= AE.由A′E//x轴,得△OA'E是直角三角形.设A′的坐标为(0,b),则AE=A'E=b,OE=2b.∵b+2b=2+,∴b=1.∴A'、E的坐标分别是(0,1)与(,1).(2)因为A'、E在抛物线上,所以所以函数关系式为y =.由=0得,.与x轴的两个交点坐标分别是(-,0)与(,0).(3)不可能使△A'EF成为直角三角形.∵∠FA'E=∠FAE=60o,若△A'EF成为直角三角形,只能是∠A'EF=90o或∠A'FE=90o.若∠A'EF=90o,利用对称性,则∠AEF=90o, A'、E、A三点共线,O与A重合,与已知矛盾.同理若∠A'FE=90o也不可能.所以不能使△A′EF成为直角三角形.18. 解:(1)①当0<x≤3时,由折叠得到的△A'ED落在△ABC内部如图10(1),重叠部分为△A'ED.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC.∴.∴,即.又∵FA'=FA=x,∴y=DE·A'F=·x·x.∴(0<x≤3).②当3<x<6时,由折叠得到的△A'ED有一部分落在△ABC外,如图10(2),重叠部分为梯形EDPQ.∵FH=6-AF=6-x, A'H=A'F-FH=x-(6-x)=2x-6,又∵DE∥PQ,∴△A'PQ∽△A'DE.∴.∴∴.(2)当0<x≤3时,y的最大值;当3<x<6时,由,可知当x=4时,y的最大值y2=9.∵y1<y2,∴当x=4时,y有最大值y最大=9.19. 证明:(1)能正确说明∠ADB=∠EBD(或△ABF≌△EDF),∴BF=DF.(2)能得出∠AEB=∠DBE(或∠EAD=∠BD A),∴AE∥BD.。
初中数学专题:折叠问题

For personal use only in study and research; not for commercial use专题八折叠问题学习要点与方法点拨:出题位置:选择、填空压轴题或压轴题倒数第二题折叠问题中,常出现的知识时轴对称。
折叠对象有三角形、矩形、正方形、梯形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;轴对称性质-----折线,是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。
压轴题是由一道道小题综合而成,常常伴有折叠;解压轴题时,要学会将大题分解成一道道小题;那么多作折叠的选择题填空题,很有必要。
基本图形:在矩形ABCD中,将△ABF沿BE折叠至△FBE,可得何结论?(1)基本图形练习:如图,将三角形纸片ABC沿过点A的直线折叠,使得AC落在AB上,折痕为AD,展开纸片;再次折叠,使得A 和D点重合,折痕为EF,展开纸片后得到△AEF,则△AEF是等腰三角形,对吗?(2)折叠中角的考法与做法:将矩形纸片ABCD沿过点B的直线折叠,使得A落在BC边上的点F处,折痕为BE(图1);再沿过点E的直线折叠,使点D落在BE边上的点D’,折痕为EG(图2),再展开纸片,求图(3)中角a的大小。
(3)折叠中边的考法与做法:如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是多少?模块精讲例1.(2014•扬州)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长;(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(3)如图2,,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.例2.(2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若=,则=用含k的代数式表示).例3、(2013•苏州)如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB′为正方形;(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.例4、如图,已知矩形纸片ABCD ,AD=2,AB=4.将纸片折叠,使顶点A 与边CD 上的点E 重合,折痕FG 分别与AB ,CD 交于点G ,F ,AE 与FG 交于点O .(1)如图1,求证:A ,G ,E ,F 四点围成的四边形是菱形;(2)如图2,当△AED 的外接圆与BC 相切于点N 时,求证:点N 是线段BC 的中点; (3)如图2,在(2)的条件下,求折痕FG 的长.例5、已知AD ∥BC ,AB ⊥AD ,点E ,点F 分别在射线AD ,射线BC 上.若点E 与点B 关于AC 对称,点E 与点F 关于BD 对称,AC 与BD 相交于点G ,则( )A .1+tan ∠ADB=B .2BC=5CFC .∠AEB+22°=∠DEFD .4cos ∠AGB=26课堂练习1、2、(2014连云港)如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=_________.图3 图43、(2014•徐州)如图3,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=_________°.4、(2014•扬州)如图4,△ABC的中位线DE=5cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为_________cm2.5、(2013•扬州)如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.(1)求y与x的函数关系式;(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.课后巩固习题1、(2014•淮安)如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.2、(2013•宿迁)如图,在梯形ABCD中,AB∥DC,∠B=90°,且AB=10,BC=6,CD=2.点E从点B出发沿BC 方向运动,过点E作EF∥AD交边AB于点F.将△BEF沿EF所在的直线折叠得到△GEF,直线FG、EG分别交AD 于点M、N,当EG过点D时,点E即停止运动.设BE=x,△GEF与梯形ABCD的重叠部分的面积为y.(1)证明△AMF是等腰三角形;(2)当EG过点D时(如图(3)),求x的值;(3)将y表示成x的函数,并求y的最大值.3、如图,在矩形ABCD中,AB=6,BC=8,把△BCD沿着对角线BD折叠,使点C落在C'处,BC交AD于点G,E,F,分别是C'D 和BD上的点,线段EF交AD于点H,把△FDE沿着EF折叠,使点D落在D'处,点D'恰好与点A重合.(1)求证:三角形ABG≌△C'DG(2)求tan∠ABG的值;(3)求EF的长。
最新初二年级八年级数学图型折叠类型题目汇总
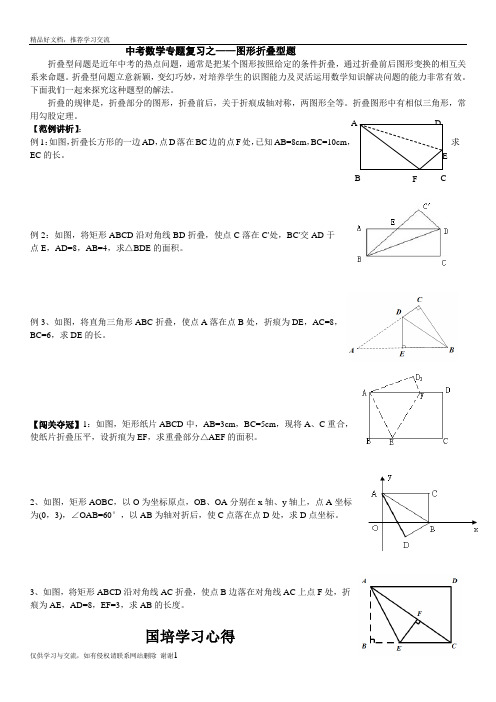
A BD FEC中考数学专题复习之——图形折叠型题折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。
折叠型问题立意新颖,变幻巧妙,对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。
下面我们一起来探究这种题型的解法。
折叠的规律是,折叠部分的图形,折叠前后,关于折痕成轴对称,两图形全等。
折叠图形中有相似三角形,常用勾股定理。
【范例讲析】:例1:如图,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长。
例2:如图,将矩形ABCD沿对角线BD折叠,使点C落在C'处,BC'交AD于点E,AD=8,AB=4,求△BDE的面积。
例3、如图,将直角三角形ABC折叠,使点A落在点B处,折痕为DE,AC=8,BC=6,求DE的长。
【闯关夺冠】1:如图,矩形纸片ABCD中,AB=3cm,BC=5cm,现将A、C重合,使纸片折叠压平,设折痕为EF,求重叠部分△AEF的面积。
2、如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在点D处,求D点坐标。
3、如图,将矩形ABCD沿对角线AC折叠,使点B 边落在对角线AC上点F处,折痕为AE,AD=8,EF=3,求AB的长度。
国培学习心得通过这次培训让我对新课程理念下的教学方式与学习方式的变革有了新的理解;让我对做一个富有人格魅力的教师充满了希望;解开了我在教学中的很多方面的迷惑,让我知道了如何有效的开发课程资源,更好的利用课程资源进行教学,为培养我们中学英语教师的专业能力指明了方向,并学会了实现自我的价值,改变自己的心态,用阳光灿烂的心态面对工作和生活。
尤其是参加了11月23号的视频答疑学习,更觉醍醐灌顶、受益匪浅。
“国培计划”真是一次难得的机会。
经过这一阶段的学习,我主要有以下几点深刻的心得:一、“国培”学习使我们更加全面深刻地理解了新课标理念,为实施素质教育奠定了基础。
轴对称的性质—折叠问题(专项培优训练)2023-2024学年八年级数学上册(人教版)(解析版)

轴对称的性质—折叠问题(专项培优训练)试卷满分:100分 考试时间:120分钟 试卷难度:较难试卷说明:本套试卷结合人教版数学八年级上册同步章节知识点,精选易错,常考,压轴类问题进行专题汇编!题目经典,题型全面,解题模型主要选取热点难点类型!同步复习,考前强化必备!适合成绩中等及偏上的学生拔高冲刺。
一、选择题:本大题共10小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(本题2分)(2022秋·天津津南·八年级校考期中)如图,把一张长方形纸片ABCD ,沿对角线AC 折叠,点B 的对应点为B ',AB '与DC 相交于点E ,则下列结论正确的有( )①ABC AB C ≅';②AE CE =;③ADE CB E ≅';④B CE EAB ∠'=∠.A .1个B .2个C .3个D .4个【答案】C 【分析】由折叠的性质可得ABC AB C ≅',,BAC CAB '∠=∠,AD BC B C =='由平行线的性质和等腰三角形的性质可得 ,ECA EAC AE CE ∠=∠=,由“HL ”可证()Rt ADE Rt CB E HL '≅,可得 ED EB =' ,即可进行判断;【详解】∵矩形纸片 ABCD 沿对角线 AC 折叠,点B 的对应点为 B '∴ABC AB C '≅,故①正确;,BAC CAB '∴∠=∠,AD BC B C =='∵AB CD ∥,BAC ACD ∴∠=∠,ACD CAB ∴∠=∠',ECA EAC ∴∠=∠∴AE CE =,故②正确;,,AE CE AD BC B C ==='在Rt ADE △ 和 Rt CB E '中,AE CE AD CB =⎧⎨=⎩∴()Rt ADE Rt CB E HL '≅故③正确;,DEA B CE '∴∠=∠,DEA EAB ∠≠∠,B CE EAB ∴∠'≠∠故④不正确;∴结论正确的有①②③共3个故选:C【点睛】本题考查了翻折变换,矩形的性质,全等三角形的性质,证明 AE EC = 是本题的关键.A .①②B .①②③C .①③④D .①②③④【答案】D 【分析】先求出点A ,点B 坐标,由勾股定理可求AB 的长,可判断①;由折叠的性质可得6OB BD ==,OC CD =,90BOC BDC ∠=∠=︒,由勾股定理可求OC 的长,可得点C 坐标,利用待定系数法可求BC 解析式,可判断②;由面积公式可求DH 的长,代入解析式可求点D 坐标,可判断③;分别讨论P 点在C 、B 点的情况,比较AP DP +值的情况,得出当P 点在C 点时,使得AP DP +的值最小可判断④,即可求解. 【详解】解:直线3=+64y x −分别与x 、y 轴交于点A 、B ,∴点()8,0A ,点()0,6B ,8OA ∴=,6OB =,10AB ∴=,故①正确;线段OB 沿BC 翻折,点O 落在AB 边上的点D 处,6OB BD ∴==,OC CD =,90BOC BDC ∠=∠=︒,4AD AB BD ∴=−=,222AC AD CD =+,()22816OC OC ∴−=+,3OC ∴=,∴点()3,0C ,设直线BC 解析式为:6y kx =+,036k ∴=+,2k ∴=−,∴直线BC 解析式为:26y x =−+,故②正确;如图,过点D 作DH AC ⊥于H ,3CD OC ==,5CA ∴=,1122ACD S AC DH CD AD =⋅=⋅△, 341255DH ⨯∴==,∴当125y =时,123654x =−+, 245x ∴=,∴点2412,55D ⎛⎫ ⎪⎝⎭,故③正确;直线BC 上存在一点P ,当P 点在C 点时,()OC DC P =,∴AP DP AC OC OA +=+=,当P 点在B 点时,AP DP AD DB AB +=+=,在Rt OAB 中,AB OA >∴当P 点在C 点时,使得AP DP +的值最小,则点P 的坐标是()3,0,故④正确;综上分析可知,正确的结论为①②③④,故D 正确.故选:D .【点睛】本题是一次函数综合题,考查了利用待定系数法求解析式,折叠的性质,面积法,勾股定理等知识,灵活运用这些性质解决问题是本题的关键. 3.(本题2分)(2023春·福建厦门·八年级厦门市湖滨中学校考期末)如图,在ABC 中,D 是AC 边上的中点,连接BD ,把BDC 沿BD 翻折,得到BDC ',DC '与AB 交于点E ,连接AC ',若2AD AC '==,3BD =,则C 到BD 的距离为( )【答案】B【分析】连接CC ',交BD 于点M ,由翻折知,BDC BDC '≌,BD 垂直平分CC ',证ADC '为等边三角形,利用含30度的直角三角形性质及勾股定理求出1DM =,CM =【详解】解:如图,连接CC ',交BD 于点M ,∵2AD AC ='=,D 是AC 边上的中点,∴2DC AD ==,由翻折知,BDC BDC '≌,BD 垂直平分CC ',∴2DC DC '==,BC BC '=,CM C M '=,∴2AD AC DC ''===,∴ADC '为等边三角形,∴60ADC AC D C AC ∠'=∠'=∠'=︒,∵DC DC =', ∴160302DCC DC C ∠'=∠'=⨯︒=︒,在Rt CDM △中,30DCC ∠'=︒,2DC =,∴1DM =,CM C M '∴=∴C 到BD故选B .【点睛】本题考查了等边三角形的判定及性质、含30度角的直角三角形的性质、勾股定理、折叠的性质、全等三角形的性质,熟练掌握性质定理是解题的关键. 4.(本题2分)(2020秋·广东广州·八年级校考期中)如图1,长方形ABCD 中,E 点在AD 上,且30ABE ∠︒=.分别以BE 、CE 为折线,将A 、D 向BC 的方向折过去,如图2,若图2中15AED ∠=︒,则BCE ∠度数为( )A .30︒B .32.5︒C .35︒D .37.5︒【答案】D 【分析】根据长方形的性质与三角形内角和定理,得到60AEB ∠=︒,再根据折叠的性质,得到A EB AEB '∠=,DEC D EC '∠=∠,由105AED '∠=︒,进而得到37.5DEC ∠=︒,最后根据平行线的性质,即可求出BCE ∠度数.【详解】解:四边形ABCD 是长方形,AD BC ∴∥,90A ∠=︒,30ABE ∠︒=,18060AEB A ABE ∴∠=︒−∠−∠=︒,由折叠的性质可知,60A EB AEB ∠=∠='︒,DEC D EC '∠=∠,15A ED ''∠=︒,606015105AED AEB A EB A ED ''''∴∠=∠+∠−∠=︒+︒−︒=︒,18075DED AED ''∴∠=︒−∠=︒,137.52DEC D EC DED ''∴∠=∠=∠=︒,AD BC ∥,37.5BCE DEC ∴∠=∠=︒,故选:D .【点睛】本题考查了折叠的性质,三角形内角和定理,平行线的性质,熟练掌握折叠的性质是解题关键.5.(本题2分)(2023春·陕西榆林·八年级校考期末)如图,在等腰ABC 中,AB AC =,50BAC ∠=︒,BAC ∠的平分线与AB 的垂直平分线交于点O ,点C 沿EF 折叠后与点O 重合,则CEF ∠的度数是( )A .55︒B .50︒C .45︒D .40︒【答案】B 【分析】连接OB ,OC ,先求出25BAO ∠=︒,进而求出40OBC ∠=︒,求出40COE OCB ∠=∠=︒,由三角形内角和定理和12CEF OEF CEO ∠=∠=∠即可求得答案. 【详解】解:如图,连接OB ,50BAC ∠=︒,AO 为BAC ∠的平分线,11502522BAO BAC ∴∠=∠=⨯︒=︒.又AB AC =,()1180652ABC ACB BAC ∴∠=∠=︒−∠=︒.DO 是AB 的垂直平分线,OA OB ∴=,25ABO BAO ∴∠=∠=︒,652540OBC ABC ABO ∴∠=∠−∠=︒−︒=︒.AO 为BAC ∠的平分线,AB AC =,∴直线AO 垂直平分BC ,OB OC ∴=,40OCB OBC ∴∠=∠=︒,点C 沿EF 折叠后与点O 重合,OE CE ∴=,12CEF OEF CEO ∠=∠=∠,40COE OCB ∴∠=∠=︒;在OCE △中,1801804040100CEO COE OCB ∠=︒−∠−∠=︒−︒−︒=︒,1502CEF CEO ∴∠=∠=︒.故选:B .【点睛】本题主要考查了等腰三角形的性质以及翻折变换及其应用,解题的关键是根据翻折变换的性质,找出图中隐含的等量关系,灵活运用有关知识来分析、判断. .将AFG 沿AG A .1B .32 【答案】C 【分析】由正方形的性质可得AD AB =,设BF CF a ==,则2CD a =,24DG CD CG a =−=−,由题意知,90ADE ABF ∠=∠=︒,由折叠的性质可得HG EF ⊥,AE AF =,GE GF =,证明()Rt Rt HL ADE ABF ≌,则DE BF a ==,2434GF GE a a a ==+−=−,由勾股定理得222GF CF DG −=,即()222344a a −−=,解得3a =,0a =(舍去),则3CF =,5EG =,9EC =,由勾股定理得EF ,根据1122CEF S EG CF EF HG =⨯=⨯,即115322HG ⨯⨯=⨯,计算求解即可.【详解】解:由正方形的性质可得AD AB =,设BF CF a ==,则2CD a =,24DG CD CG a =−=−, 由题意知,90ADE ABF ∠=∠=︒,由折叠的性质可得HG EF ⊥,AE AF =,GE GF =,∵AE AF =,AD AB =,∴()Rt Rt HL ADE ABF ≌,∴DE BF a ==,2434GF GE a a a ==+−=−,由勾股定理得222GF CF CG −=,即()222344a a −−=,解得3a =,0a =(舍去),∴3CF =,5EG =,9EC =,由勾股定理得EF ∵1122GEF S EG CF EF HG =⨯=⨯,∴115322HG ⨯⨯=⨯,解得HG =, 故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定与性质,折叠的性质,勾股定理等知识.解题的关键在于对知识的熟练掌握与灵活运用.A .65︒B .62.5︒C .55︒D .52.5︒【答案】B 【分析】根据折叠得出90OB C B ''∠=∠=︒,求出55OB G '∠=︒,根据平行线的性质得出18055125B OB '∠=︒−︒=︒.根据折叠得出162.52BOG B OB '∠=∠=︒.【详解】解:根据折叠可知,90OB C B ''∠=∠=︒,∵35GB C ''∠=︒,∴55OB G '∠=︒,∵AB CD ∥,∴18055125B OB '∠=︒−︒=︒. 由折叠可知,162.52BOG B OB '∠=∠=︒,故B 正确. 故选:B .【点睛】本题主要考查了折叠的性质,平行线的性质,解题的关键是熟练掌握两直线平行,同旁内角互补. 8.(本题2分)(2023·浙江·八年级假期作业)如图,现有一块三角板ABC ,其中90ABC ︒∠=,60CAB ︒∠=,8AB =,将该三角板沿BC 边翻转得到A BC '△,再将A BC '△沿A C '边翻转得到A B C ''△,则A 与B '两点之间的距离为( )【答案】C 【分析】连接AB ',作B D AA ''⊥,交AA '延长线于点D ,在Rt A B D ''中求得B D '、A D '的长度,在Rt AB D '中,即可求得AB '.【详解】解:连接AB ',作B D AA ''⊥,交AA '延长线于点D ,如下图:由折叠的性质可得:8AB A B A B '''===,60CAB CA B CA B '''∠=∠=∠=︒∴60B A D ''∠=︒∵B D AA ''⊥,∴90D Ð=°,∴30A B D ''∠=︒, ∴142A D A B '''==,∴B D '==,20AD =,∴AB '=故选:C【点睛】此题考查了勾股定理,折叠的性质,含30︒直角三角形的性质,解题的关键是熟练利用相关性质进行求解.A .①②④B .①②③C .①③④D .①②③④【答案】D 【分析】作FM BC ⊥于M (见详解图),①根据翻折变换的性质和正方形的性质可证ABG AFG △△≌;②设BG GF x ==,在Rt EGC △中,根据勾股定理可证3BG GC ==;③通过tan 2AB AGB BG ∠==,tan 2FM FCM CM ∠==,证明AGB FCM ∠=∠,由平行线的判定定理可得AG CF ∥;④由②得到3GC =,由③得到125FM =,根据12FCG S GC FM =△即可计算面积.【详解】解:作FM BC ⊥于M ,四边形ABCD 是正方形,∴6AB BC CD DA ====,90B D BCD ∠=∠=∠=︒,AFE △是由ADE V 翻折,∴AD AF AB ==,90ADE AFE AFG ∠=∠=∠=︒,在Rt AGF 和Rt AGB 中,AG AG AF AB =⎧⎨=⎩,∴ABG AFG △△≌.故①正确.∴BG GF =,设BG GF x ==,在Rt EGC △中,90ECG ∠=︒,2DE =,6CD =,4EC =,2EG x =+,6GC x =−,∴()()222246x x +=+−,∴3x =,∴3BG GC ==,故②正确.FM BC ⊥,CD BC ⊥∴FM EC ∥ ∴GF FM GM GE ECGC ==,3GF =,5GE =,4EC =,3GC =∴125FM =,95GM =,65CM GC GM =−=, ∴6tan 23AGB ∠==, tan 2FM FCM CM ∠==,∴AGB FCM ∠=∠,∴AG CF ∥,故③正确. ∴112183255FCG S ==△,故④正确.综上,选项D 符合题意.故选:D .【点睛】本题考查了正方形的性质、全等三角形的判定和性质、翻折变换、勾股定理的应用等知识,熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键. 为对称轴将CDE 折叠得到CHE ,使得点 A .90CEF ∠=︒ B .CE 【答案】D 【分析】A.由折叠的性质可以知道EF 和CE 分别是AEG ∠和DEG ∠的平分线,同时AED ∠是平角,所以可知90CEF ∠=︒,故选项A 正确;B.由题意和折叠的性质可以知道EF AG ⊥、EF CE ⊥,就可以得到CE AG ∥,选项B 正确;C 和D.过点C 作C M A B ⊥于点M ,120CBA ∠=︒,可得2BM =,CM =BF a =,可以得到4FG AF a ==−,2FM BF BM a =+=+.根据折叠的性质可得4CG CD ==,根据勾股定理,求得2.4a =,即可得到 1.6FG =, 5.6CF =,所以5.6745CF AB ==.故选项C 正确,选项D 错误. 【详解】解:A.由折叠可知EF 和CE 分别是AEG ∠和DEG ∠的平分线. 又180AED ∠=︒,111809022CEF CEG FEG AED ∴∠=∠+∠=∠=⨯︒=︒, 故选项A 正确.B.又点A 与点G 关于EF 对称,∴EF AG ⊥, 又EF CE ⊥,∴CE AG ∥,故选项B 正确.C 和D.如答图,过点C 作C M A B ⊥于点M .120CBA ∠=︒,∴60CBM ∠=︒,4BC =,∴易知2BM =,CM =设BF a =,∴4FG AF a ==−,2FM BF BM a =+=+,点E 是AD 的中点,折叠后点H 落到EG 上,∴点G 与点H 重合,4CG CD ==.易知点C G F ,,共线,∴448CF FG CG a a =+=−+=−.222FM CM CF +=,()(()22228a a ∴+=−+,解得 2.4a =. ∴4 2.4 1.6FG =−=,88 2.4 5.6CF a =−=−=,5.6745CF AB ∴==,故选项C 正确,选项D 错误.综上,故选:D .【点睛】本题考查翻折变换(折叠问题)、菱形的性质、勾股定理,熟练掌握翻折的性质是解答本题的关键.二、填空题:本大题共10小题,每小题2分,共20分. 11.(本题2分)(2023春·河北承德·八年级统考期末)如图,小宇将一张平行四边形纸片折叠,使点A 落在长边CD 上的点1A 处,并得到折痕DE ,小宇测得长边6CD =,则四边形1A EBC 的周长为 .【答案】12【分析】根据折叠的性质,得到DA DA '=,EA EA '=,结合平行四边形的性质,得到DA DA BC '==,代入计算即可.【详解】根据折叠的性质,得到DA DA '=,EA EA '=,∵四边形ABCD 是平行四边形,∴DA DA BC '==,6AB CD ==,∴四边形1A EBC 的周长为1111212BC BE A E AC A D AC AE BE AB CD CD +++=+++=+==.故答案为:12.【点睛】本题考查了折叠的性质,平行四边形的性质,熟练掌握性质是解题的关键.12.(本题2分)(2023春·上海浦东新·八年级统考期末)如图,在ABC 中,90A ∠=︒,28BC AC ==,点M 在边BC 上,过点M 作MN BC ⊥,垂足为点M ,交边AB 于点N ,将ABC 沿直线MN 翻折,点A 、C 分别与点D 、E 对应,如果四边形ADBE 是平行四边形,那么CM 的长是 .【答案】3【分析】当点E 在线段BC 上时,连接DE 交AB 于点O ,过点O 作OH BC ⊥于点H ,则90BHO ∠=︒,求出AB =30ABC ∠=︒,由轴对称可得4DE AC ==,得OB =2OD OE ==,OH =,求出6CE =,由折叠可知,3CM =;假设点E 在线段CB 的延长线上,得到)4AN AF x ==−,与)2AN x =−矛盾,故点E 不可能在线段CB 的延长线上,即可确定CM 的长.【详解】解:当点E 在线段BC 上时,如图,连接DE 交AB 于点O ,过点O 作OH BC ⊥于点H ,则90BHO ∠=︒,∵90BAC ∠=︒,28BC AC ==,∴AB ==30ABC ∠=︒,∵将ABC 沿直线MN 翻折,点A 、C 分别与点D 、E 对应,∴4DE AC ==,∵四边形ADBE 是平行四边形,∴1122OB AB ==⨯=122OD OE DE ===,∴12OH OB ==∴3BH ==,∴1EH ==,∴312BE BH EH =−=−=,∴826CE BC BE =−=−=,由折叠可知,132CM EM CE ===,假设点E 在线段CB 的延长线上,延长MN 交AD 于点F ,则AD FM ⊥,12AF DF AD ==,∵90BAC ∠=︒,28BC AC ==,∴AB ==30ABC ∠=︒,设CM EM x ==,则8BM x =−,∴()828BE x x x AD=−−=−=, ∴142AF DF AD x ===−, 在Rt BMN △中,30ABC ∠=︒,90BMN ∠=︒, ∴1MN BN 2=,∴222BM MN BN +=,即22212BM BN BN ⎛⎫+= ⎪⎝⎭,则)8BN x ==−,))82AN BN x x ==−==−,在Rt ANF △中,142AF DF AD x ===−,30NAF ABC ∠=∠=︒,90AFN ∠=︒, ∴12FN AN =,∴222AF FN AN +=,即22212AF AN AN ⎛⎫+= ⎪⎝⎭,)4AN AF x ==−,与)2AN x =−矛盾,故点E 不可能在线段CB 的延长线上,综上可知,3CM =,故答案为:3【点睛】此题考查了勾股定理、平行四边形的性质、含30︒角的直角三角形的性质等知识, 分类讨论是解题的关键. 13.(本题2分)(2023春·北京丰台·八年级统考期末)如图,在Rt ABC △中,90B Ð=°,3AB =,4BC =,将ABC 折叠,使点B 恰好落在边AC 上,与点B '重合,AE 为折痕,则BE 的长等于 .【答案】1.5【分析】根据折叠得到BE EB '=,AB AB 3'==,设BE EB x '==,则4EC x =−,根据勾股定理求得AC 的值,再由勾股定理可列方程求解即可.【详解】解:根据折叠可得BE EB '=,AB AB 3'==,设BE EB x '==,则4EC x =−,在Rt ABC △中,90B Ð=°,3AB =,4BC =5AC ∴=532B C AC AB ''∴=−=−=在Rt B EC '△中,由勾股定理得,()222x 24x +=− 解得 1.5x =故答案为:1.5【点睛】本题考查的是翻折变换的性质,解题的关键是掌握折叠前后图形的形状和大小不变,对应边和对应角相等,能熟练运用勾股定理列方程解决问题.14.(本题2分)(2023春·四川达州·八年级统考期末)如图,在ABC 和DCB △中,90A D ∠=∠=︒,AC ,BD 相交于点E ,AE DE =.将CDE 沿CE 折叠,点D 落在点D ¢处,若40BED '∠=︒,则BCD '∠的大小为 .【答案】15︒/15度【分析】根据全等三角形的判定和性质得出BE CE =,再由等边对等角确定EBC ECB ∠∠=,利用折叠的性质及三角形内角和定理求解即可.【详解】解:在AEB 和DEC 中,90A D AE DE AEB DEC ∠∠∠∠==︒⎧⎪=⎨⎪=⎩,∴(ASA)AEB DEC ≌,∴BE CE =,∴EBC ECB ∠∠=,∵40BED '∠=︒,CDE 沿CE 折叠,点D 落在点D ¢处,∴70D EC DEC ︒'∠=∠=,∴180110BEC DEC ∠=︒−∠=︒,790200DCE ︒−︒=︒∠=,∴180110352EBC ECB ︒−∠︒=∠==︒,20DCE D CE ︒'∠=∠=,∴15BCD ECB D CE ''∠=∠−∠=︒,故答案为:15︒.【点睛】题目主要考查折叠的性质及全等三角形的判定和性质,三角形内角和定理及等腰三角形的判定和性质,理解题意,综合运用这些知识点是解题关键.15.(本题2分)(2023·浙江·八年级假期作业)折纸是一项有趣的活动,如图所示,一张长方形纸片()90ABCD A B C ∠=∠=∠=︒,先将纸片沿EF 折叠,再将折叠后的纸片沿GH 折叠,使得GD '与A B ''重合,展开纸片后若62BFE ∠=︒,则DGH ∠= ︒.【答案】17【分析】由平行线的性质得到62GEF BFE ∠=∠=︒,由平角定义得到180118AEF GEF ∠=︒−∠=︒,由轴对称的性质得到:90A A '∠=∠=︒,118A EF AEF '∠=∠=︒,DGH D GH '∠=∠,求出A EG '∠,由直角三角形的性质求出'∠A GE ,由对顶角的性质得到DGD A GE ''∠=∠,即可求出12DGH DGD '∠=.【详解】解:四边形ABCD 是矩形, AD BC ∴∥,90A ∠=︒,62GEF BFE ∴∠=∠=︒,180118AEF GEF ∴∠=︒−∠=︒,由题意得:90A A '∠=∠=︒,118A EF AEF '∠=∠=︒,DGH D GH '∠=∠,1186256A EG A EF GEF ''∴∠=∠−∠=︒−︒=︒,9034A GE A EG ''∴∠=︒−∠=︒,34DGD A GE ''∴∠=∠=︒,1172DGH DGD '∴∠==︒.故答案为:17.【点睛】本题考查轴对称的性质,平行线的性质,余角的计算,对顶角的性质,解题的关键是掌握轴对称的性质.16.(本题2分)(2023·浙江·八年级假期作业)如图,在△ABC 中,AB AC =,30C ∠=︒,将纸片沿DE 折叠,使点B 落到点A 处,若6BC =,则DE = .【答案】1【分析】利用等腰三角形的性质得到30B C ∠=∠=︒,则120BAC ∠=︒,再由折叠性质得BD AD =,30BAD B ∠=∠=︒,90AED ∠=︒,进而得到90DAC ∠=︒,再根据含30度角的直角三角形的性质求解即可.【详解】解:∵AB AC =,30C ∠=︒∴30B C ∠=∠=︒,则3018030120BAC ∠=−︒−︒=︒,由折叠性质得BD AD =,30BAD B ∠=∠=︒,90AED ∠=︒,∴1309020DAC ︒−︒=∠=︒,12DE AD =,∴2CD AD =,又6BC =,∴236BC BD CD AD AD AD =+=+==,∴2AD =, ∴112DE AD ==, 故答案为:1.【点睛】本题考查等腰三角形的性质、折叠性质、三角形的内角和定理、含30度角的直角三角形的性质,熟练掌握折叠性质和直角三角形的性质是解答的关键. 上一动点,把CDE 沿直线,若D BC '为等边三角形,【答案】1或4/4或1【分析】依据折叠的性质、菱形的性质以及等边三角形的性质,分两种情况得到DE 的长即可.【详解】解:由折叠及菱形的性质可得CD CD CB '==,故D BC '是以BD '底的等腰三角形,故当60D BC '∠=︒,D BC '为等边三角形,分以下两种情况讨论,1)如图(1),当点D ¢点A 重合时,60D BC '∠=︒,此时点E 为AD 的中点,故1DE =,2)如图(2),当点D ¢与点A 关于直线BC 对称时,D ¢,C ,D 三点共线,EC DC ⊥,故24DE DC ==, 综上所述,1DE =或4,故答案为:1或4.【点睛】本题考查了菱形的性质,折叠问题及等边三角形的性质等知识的综合运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等. 如图,ABC 中,【答案】108【分析】连接OB 、OC ,根据角平分线的定义求出BAO ∠,根据等腰三角形两底角相等求出ABC ∠,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA OB =,根据等边对等角可得ABO BAO ∠=∠,再求出OBC ∠,证明 OB OC =,再根据等边对等角求出OCB OBC ∠=∠,根据翻折的性质可得OE CE =,然后根据等边对等角求出COE ∠,再利用三角形的内角和定理列式计算即可.【详解】解:如图,连接OB 、OC ,54BAC ∠=︒Q ,AO 为BAC ∠的平分线,11542722BAO BAC ∴∠=∠=⨯︒=︒,又AB AC =,11(180)(18054)6322ABC BAC ∴∠=︒−∠=︒−︒=︒, DO 是AB 的垂直平分线,OA OB ∴=,27ABO BAO ∴∠=∠=︒,632736OBC ABC ABO ∴∠=∠−∠=︒−︒=︒, AO 为BAC ∠的平分线,AB AC =,∴点O 在BC 的垂直平分线上,∴OB OC =,36OCB OBC ∴∠=∠=︒,将C ∠沿(EF E 在BC 上,F 在AC 上)折叠,点C 与点O 恰好重合,OE CE ∴=,36COE OCB ∴∠=∠=︒,在OCE △中,1801803636108OEC COE OCB ∠=︒−∠−∠=︒−︒−︒=︒,故答案为:108.【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,等边对等角的性质,以及翻折变换的性质,三角形内角和定理等等,熟知相关知识是解题的关键.19.(本题2分)(2023春·辽宁沈阳·八年级统考期末)如图,在ABC ∆中,90A ∠=︒,30C ∠=︒,3AB =,点D 为AC 的中点,点E 是BC 边上一个动点,将CDE ∆沿着DE 翻折,使得点C 落在点F 处,当FE AC ⊥时,EF 的长为 .【答案】32或92【分析】根据题意,分两种情况:①当E 在D 的右侧时;②当E 在D 的左侧时,由翻折性质,结合含30︒的直角三角形边的关系列方程求解即可得到答案.【详解】解:在ABC 中,90A ∠=︒,30C ∠=︒,3AB =,点D 为AC 的中点,AC ∴=12CD AB =, 当E 在D 的右侧时,延长FE 交AC 于H ,如图所示:FE AC ⊥,90EHC ∴∠=︒,由翻折的性质知,CD DF ==,30C DFH∠=∠=︒, 设EF x =,则CE EF x ==,1122EH EC x ==, 32FH x ∴=,在直角三角形DFH 中,30DFH ∠=︒,则FH =,∴32x =,32x ∴=;当E 在D 的左侧时,如图所示:由翻折性质知,CD DF ==,30C EFD ∠=∠=︒,CE EF x ==,EF AC ⊥,90FHD ∴∠=︒,1122EH EC x ∴==,1122FH x x x =−=,在直角三角形FHD 中,HF =,∴12x =,解得92x =, 故答案为:32或92.【点睛】本题考查翻折性质,充分利用翻折性质及含30︒的直角三角形边的关系分情况讨论是解决问题的关键. 20.(本题2分)(2023春·重庆忠县·八年级统考期末)如图,在正方形ABCD 中,点E 是BC 上一点,连接DE ,将BDE 沿DE 翻折得到GDE ,连接CG .若CG BD ∥,则CEG ∠= .【答案】60︒/60度【分析】根据直角三角形斜边中线的性质得出CH DH HB ==,1=2CH DB ,由折叠的性质得DB DG =,∠=∠BDE GDE ,利用辅助线构造矩形并由其性质得出CH GK =,再由等量代换得出12GK DG =,最后由特殊直角三角形的性质得出30GDK ∠=︒,利用折叠的性质及正方形的性质即可求解. 【详解】解:如图,过点C 作直线CH DB ⊥于点H ,过点G 作直线GK DB ⊥于点K ,正方形ABCD 中,DC CB =,90452CDB ︒∠==︒,CH DH HB ∴==,1=2CH DB . GDE △由BDE 沿DE 翻折得到,GDE BDE ∴≌△△, DB DG ∴=,∠=∠BDE GDE ,CH DB ⊥,GK DB ⊥,CG BD ∥,CH GK ∴∥,90CHK ∠=︒,∴四边形CHKG 是矩形.CH GK ∴=, ∴11=22GK CH DB DG ==,90GKD ∠=︒,∴30GDK ∠=︒.11=30=1522BDE GDK ∴∠=∠⨯︒︒.∵正方形ABCD ,∴45DBE ∠=︒,∴1804515120BED ∠=︒−︒−︒=︒,60CED ∠=︒,∵BDE 沿DE 翻折得到GDE ,∴120BED DEG ∠=∠=︒,∴12060CEG DEC ∠=︒−∠=︒,故答案为:60︒.【点睛】本题考查正方形—翻折问题.具体考查正方形的性质,折叠的性质,全等三角形的性质,特殊直角三角形的性质,矩形的判定和性质等的综合运用能力.灵活添加辅助线是解本题的关键.三、解答题:本大题共7小题,21-25题每小题8分,26-27题每小题10分,共60分. 若将DAB 沿直线 (1)求点A B 、的坐标.(2)求三角形ACE 的面积.(3)求直线CD 的解析式.【答案】(1)()3,0A ,()0,4B(2)6(3)364y x =−【分析】(1)当0x =,4043y =−⨯+,解得4y =,则()0,4B ,当0y =,4043x =−+,解得3x =,则()3,0A ;(2)由折叠的性质可知AB AC =,OBA ECA ∠=∠,证明()AAS ABO ACE ≌,根据12ACE ABO S S OA OB ==⨯,计算求解即可;(3)由勾股定理得,5AB ,则8OC OA AC =+=,()80C ,,待定系数法求直线CD 的解析式即可.【详解】(1)解:当0x =,4043y =−⨯+,解得4y =,则()0,4B ,当0y =,4043x =−+,解得3x =,则()3,0A ,∴()3,0A ,()0,4B ;(2)解:由折叠的性质可知AB AC =,OBA ECA ∠=∠,∵OBA ECA ∠=∠,OAB EAC ∠=∠,AB AC =,∴()AAS ABO ACE ≌, ∴1134622ACE ABO S S OA OB ==⨯=⨯⨯=,∴三角形ACE 的面积为6;(3)解:由勾股定理得,5AB ==,由(2)可知5AC AB ==,8OC OA AC =+=,∴()80C ,,设直线CD 的解析式为y kx b =+,将()0,6D −,()80C ,,代入y kx b =+得,680b k b =−⎧⎨+=⎩,解得346k b ⎧=⎪⎨⎪=−⎩,∴直线CD 的解析式为364y x =−. 【点睛】本题考查了一次函数的解析式,勾股定理,折叠的性质,全等三角形的判定与性质,一次函数的图象坐标轴的交点.解题的关键在于对知识的熟练掌握与灵活运用. 22.(本题8分)(2023春·吉林长春·八年级统考期末)将边长为2的正方形纸片ABCD 按如下操作:【操作一】如图①,将正方形纸片ABCD 对折,使点A 与点B 重合,点D 与点C 重合,再将正方形纸片ABCD 展开,得到折痕EF .则点B 、点F 之间的距离为_____________.【操作二】如图②,G 为正方形ABCD 边BC 上一点,连接AG ,将图①的正方形纸片沿AG 翻折,使点B 的对称点H 落在折痕EF 上.连接BH .(1)求证:ABH 是等边三角形.(2)求四边形CFGH 的周长.(1)证明见解析;(2)5【分析】操作一:由题知,4BC =,122CF DF CD ===,利用勾股定理可得BF =操作二:(1)由翻折得EF 是AB 的垂直平分线,故BH AH =,又AB AH =,即AB BH AH ==,即得ABH 是等边三角形;(2)由ABH 是等边三角形,可得2AH AB ==,1AE =.HE ==可得2FH EF HE =−=即可得出四边形ABGH 的周长.【详解】解:操作一:如图,连接BF ,由题知2BC CD ==,由翻折,知112CF DF CD ===,由勾股定理,得BF操作二:(1)由翻折知EF 是AB 的垂直平分线,BH AH ∴=,又AB AH =,AB BH AH ∴==,ABH ∴是等边三角形;(2)∵ABH 是等边三角形.∴2AH AB ==,1AE =.∴HE =∴2FH EF HE =−=∴四边形CFHG 的周长CF HF HG CG CF HF CB +++=++122=+5=【点睛】本题主要考查四边形的综合题,涉及勾股定理,等边三角形的判定和性质,正方形的性质等知识点,熟练掌握轴对称的性质与勾股定理的应用是解题的关键. (1)试判断重叠部分BED 的形状,并证明你的结论;(2)若BE 平分ABD ∠,12BC =,求BED 的面积.【答案】(1)BED 是等腰三角形,证明见解析(2)BED 的面积【分析】(1)根据折叠性质得出EBD DBC ∠=∠,进而得出EDB EBD ∠=∠,可得EB ED =,根据等角对等边即可得证;(2)根据含30度角的直角三角形的性质,勾股定理得出DE ,进而根据三角形的面积公式即可求解.【详解】(1)BED 是等腰三角形,证明:四边形ABCD 是长方形,AD BC ∴∥,EDB DBC ∴∠=∠,由折叠可知:EBD DBC ∠=∠,EDB EBD ∴∠=∠,EB ED ∴=,BED ∴是等腰三角形;(2)四边形ABCD 是长方形,AB DC ∴=,12AD BC ==,90A ABC C ∠=∠=∠=︒, BE 平分ABD ∠,ABE EBD ∴∠=∠,30ABE EBD DBC ∴∠=∠=∠=︒,2,BC CD BC ∴==,DC BC ∴==AB ∴=EB ED =,12AE AD DE DE ∴=−=−,在Rt ABE △中,根据勾股定理,得222AE AB BE +=,222(12)DE DE ∴−+=,解得8DE =,BED ∴的面积11822DE AB =⨯⋅=⨯⨯=【点睛】本题考查了勾股定理,折叠问题,含30度角的直角三角形的性质,熟练掌握勾股定理与折叠的性质是解题的关键. 24.(本题8分)(2023春·山西阳泉·八年级统考期末)综合与实践问题情境:在综合实践活动课上,同学们以“平行四边形纸片的折叠”为主题开展数学活动.在平行四边形纸片ABCD 中,E 为CD 边上任意一点,将ADE V 沿AE 折叠,点D 的对应点为D ¢.分析探究:(1)如图1,当点D ¢恰好落在AB 边上时,四边形D BCE '的形状为 .问题解决:(2)如图2,当E ,F 为CD 边的三等分点时,连接FD '并延长,交AB 边于点G .试判断线段AG 与BG 的数量关系,并说明理由.(3)如图3,当60ABC ∠=︒,45DAE =︒∠时,连接DD '并延长,交BC 边于点H .若ABCD Y 的面积为24,4=AD ,请直接写出线段D H '的长.【答案】(1)平行四边形;(2)2BG AG =,理由见解析;(3)D H '=【分析】(1)利用平行四边形的性质及折叠的性质可得ABCD ,AD DE AD '==,可得四边形ADED '是菱形,可知DE AD =',继而可知BD CE '=,即可求解;(2)利用折叠的性质可得AED AED '∠=∠,ED ED ¢=,结合三等分点可知ED ED EF '==,进而可得ED F EFD ''∠=∠,利用三角形外角性质可得AED ED F ''∠=∠,进而可知AE FG ∥,可得四边形AEFG 是平行四边形,再结合平行四边形的性质即可得AG 与BG 的数量关系;(3)由折叠可知:45DAE D AE '∠=∠=︒,AD AD =',易知DAD '△为等腰直角三角形,延长AD '交BC 于M ,可知45MD H AD D ''∠=∠=︒,由平行四边形的性质可得,45BHM ADH MD H '∠=∠=︒=∠,AM AD ⊥,进而可知MD MH '=由ABCD Y 的面积为24,4=AD ,得24AD AM ⋅=,求得6AM =,可得2MD AM AD ''=−=,再利用勾股定理即可求解.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AB CD ,AB CD =则D AE AED '∠=∠由折叠可知:AD AD =',DAE D AE '∠=∠,∴DAE AED ∠=∠,∴AD DE AD '==,∴四边形ADED '是平行四边形,又∵AD AD =',∴四边形ADED '是菱形,∴DE AD =',∴BD CE '=,∴四边形D BCE '是平行四边形,故答案为:平行四边形;(2)2BG AG =,理由如下:∵四边形ABCD 是平行四边形,∴AB CD ,AB CD =,又∵E ,F 为CD 边的三等分点, ∴13DE EF CF DC ===,由折叠可知:ED ED ¢=,AED AED '∠=∠,则ED ED EF '==,∴ED F EFD ''∠=∠,由三角形外角可知:DED ED F EFD AED AED ''''∠=∠+∠=∠+∠,∴AED ED F ''∠=∠,∴AE FG ∥,∴四边形AEFG 是平行四边形,∴EF AG =, ∵13EF DC =,AB CD =, ∴13AG AB =,则23BG AB =,∴2BG AG =;(3)由折叠可知:45DAE D AE '∠=∠=︒,AD AD =',∴90DAD '∠=︒,则DAD '△为等腰直角三角形,∴45ADH AD D '∠=∠=︒,延长AD '交BC 于M ,则45MD H AD D ''∠=∠=︒∵四边形ABCD 是平行四边形,∴AD BC ∥,∴45DHM ADH MD H ∠=∠=∠'︒=,90AMH DAD '∠=∠=︒,即AM AD ⊥,∴MD MH '=∵ABCD Y 的面积为24,4=AD ,即:24AD AM ⋅=,∴6AM =,则2MD AM AD AM AD ''=−=−=,∴D H '【点睛】本题考查平行四边形的判定及性质,菱形的判定,翻折的性质,等腰直角三角形的判定及性质,勾股定理等知识点,熟练掌握相关性质定理是解决问题的关键. 轴的负半轴上,若将DAB 沿直线(1)求线段AB 的长(2)求直线CD 的函数表达式;(3)点P 在直线CD 上,使得2PAC OAB SS =,求点【答案】(1)5AB =(2)364y x =− (3)7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭【分析】(1)先根据点,A B 的坐标可得3,4OA OB ==,再利用勾股定理可得5AB =;(2)设点D 的坐标为()0,D m ,则4,BD m OD m =−=−,先根据折叠的性质可得4CD BD m ==−,再在Rt COD 中,利用勾股定理可得6m =−,从而可得()0,6D −,然后利用待定系数法即可得;(3)设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭,根据2PAC OAB S S =建立方程,解方程可得n 的值,由此即可得出答案.【详解】(1)解:()3,0A ,()0,4B , 3,4OA OB ∴==, x 轴y ⊥轴,5AB ∴=.(2)解:设点D 的坐标为()0,D m ,则4,BD m OD m =−=−,由折叠的性质得:4CD BD m ==−,5AC AB ==,8OC OA AC ∴=+=,∴点C 的坐标为()8,0,在Rt COD 中,222OD OC CD +=,即()()22284m m −+=−,解得:6m =−,()0,6D ∴−,设直线CD 的函数表达式为y kx b =+,将点()()8,0,0,6C D −代入得:806k b b +=⎧⎨=−⎩,解得346k b ⎧=⎪⎨⎪=−⎩,则直线CD 的函数表达式为364y x =−.(3)解:由题意,设点P 的坐标为3,64P n n ⎛⎫− ⎪⎝⎭, 3,4OA OB ==,162OAB S OA OB ∴=⋅=,2PAC OAB S S =,61562342n −∴⨯=⨯, 解得725n =或85n =, 当725n =时,732364424655n −=−=⨯,即此时7224,55P ⎛⎫ ⎪⎝⎭, 当85n =时,83246534564n =−=−−⨯,即此时824,55P ⎛⎫− ⎪⎝⎭, 综上,点P 的坐标为7224,55⎛⎫ ⎪⎝⎭或824,55⎛⎫− ⎪⎝⎭. 【点睛】本题考查了勾股定理、折叠的性质、求一次函数的解析式、一次函数的几何应用,熟练掌握折叠的性质和待定系数法是解题关键. 26.(本题10分)(2023春·江苏苏州·八年级星海实验中学校考期中)如图1,四边形ABCD 中,AD BC ∥,90ADC ∠=︒,8AD =,6BC =,点M 从点D 出发,以每秒2个单位长度的速度向点A 运动,同时,点N 从点B 出发,以每秒1个单位长度的速度向点C 运动.其中一个动点到达终点时,另一个动点也随之停止运动,过点N 作NP AD ⊥于点P ,连接AC 交NP 于点Q ,连接MQ .设运动时间为t 秒.(1)AM =______,AP =______.(用含t 的代数式表示)(2)当四边形ANCP 为平行四边形时,求t 的值;(3)如图2,将AQM 沿AD 翻折,得AKM ,是否存在某时刻t ,使四边形AQMK 为为菱形,若存在,求出t 的值;若不存在,请说明理由.【答案】(1)82t −,2t +(2)2t =(3)存在,1t =【分析】(1)由2DM t =,根据AM AD DM =−即可求出82AM t =−;先证明四边形CNPD 为矩形,得出6DP CN t ==−,则2AP AD DP t =−=+;(2)根据四边形ANCP 为平行四边形时,可得68(6)t t −=−−,解方程即可;(3)由NP AD ⊥,QP PK =,可得当PM PA =时有四边形AQMK 为菱形,列出方程628()6t t t −−=−−,求解即可.【详解】(1)解:如图1.2DM t =,82AM AD DM t ∴=−=−.在直角梯形ABCD 中,AD BC ∥,90ADC ∠=︒,NP AD ⊥于点P ,∴四边形CNPD 为矩形,6DP CN BC BN t ∴==−=−,8(6)2AP AD DP t t ∴=−=−−=+;故答案为:82t −,2t +.(2)四边形ANCP 为平行四边形时,CN AP =,68(6)t t ∴−=−−,解得:2t =;(3)存在时刻1t =,使四边形AQMK 为菱形.理由如下:NP AD ⊥,QP PK =,∴当PM PA =时有四边形AQMK 为菱形,628(6)t t t ∴−−=−−,解得1t =.【点睛】本题主要考查了四边形综合题,其中涉及到直角梯形的性质,矩形的判定与性质,等腰直角三角形的性质,轴对称的性质,等腰三角形的性质,正方形的性质等知识,综合性较强,难度适中.运用数形结合、方程思想是解题的关键.(1)BQ = ______ (含t 的代数式表示);(2)如图2,连接AD ,PF ,PQ ,当AD PQ ∥时,求PQF △的面积;(3)如图3,连接PF ,PQ ,D 点关于直线PF 的对称点为D '点,若'D 落在PQB △的内部则t 的取值范围为______.【答案】(1)4(02)t t −<≤(2)PQFS = (3)4453t <<【分析】(1)根据几何动点的速度和时间可得结论;(2)根据四边形BPDQ 是平行四边形,证明四边形APQD 是平行四边形,可得1t =,再证明EFD ≌△CFQ ,最后利用三角形的面积公式可解答;(3)先证明DF FQ =,再计算两个边界点时点t 的值;①如图3,点D '与Q 重合,②如图4,D '在斜边AB 上,由此可得结论.【详解】(1)解:在Rt ABC △中,90830C AB A ∠∠=︒==︒,,,142BC AB AC ∴===,由题意,CQ t =,()402BQ t t ∴=−<≤. 故答案为:()402t t −<≤; (2)如图2中,四边形BPDQ 是平行四边形,∴DQ AB ∥,BP DQ BQ PD ==,,。
中考数学专题训练:图形的折叠问题(附参考答案)

中考数学专题训练:图形的折叠问题(附参考答案)1.如图,在平面直角坐标系中,矩形ABCD的边AD=5,OA∶OD=1∶4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1处,则点E的坐标是( )A.(1,2) B.(-1,2)C.(√5-1,2) D.(1-√5,2)2.如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=30°,则∠α的度数是( )A.30°B.45°C.74°D.75°3.如图,在矩形ABCD中,AB=2,BC=2√5,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos ∠ECF的值为( )A.23B.√104C.√53D.2√554.把一张矩形纸片ABCD按如图所示方法进行两次折叠,得到等腰直角三角形BEF.若BC=1,则AB的长度为( )A.√2B.√2+12C.√5+12D.435.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC 上,连接DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上.若FD平分∠EFB,则AD的长为( )A.259B.258C.157D.2076.如图,在Rt△ABC中,∠C=90°,CA=CB=3,点D在边BC上.将△ACD沿AD折叠,使点C落在点C′处,连接BC′,则BC′的最小值为__________.7.如图,在Rt△ABC纸片中,∠ACB=90°,CD是边AB上的中线,将△ACD沿CD折叠,当点A落在点A′处时,恰好CA′⊥AB.若BC=2,则CA′=_______.8.如图,点E在矩形ABCD的边CD上,将△ADE沿AE折叠,点D恰好落在边BC 上的点F处.若BC=10,sin ∠AFB=45,则DE=_____.9.如图,在扇形AOB中,点C,D在AB⏜上,将CD⏜沿弦CD折叠后恰好与OA,OB 相切于点E,F.已知∠AOB=120°,OA=6,则EF⏜的度数为________;折痕CD 的长为_______.10.如图,在矩形ABCD中,AB=5,AD=4,M是边AB上一动点(不含端点),将△ADM沿直线DM对折,得到△NDM.当射线CN交线段AB于点P时,连接DP,则△CDP的面积为______;DP的最大值为_______.11.如图,在矩形ABCD中,AB=2,AD=√7,动点P在矩形的边上沿B→C→D →A运动.当点P不与点A,B重合时,将△ABP沿AP对折,得到△AB′P,连接CB′,则在点P的运动过程中,线段CB′的最小值为_________.12.如图,DE平分等边三角形ABC的面积,折叠△BDE得到△FDE,AC分别与DF,EF相交于G,H两点.若DG=m,EH=n,用含m,n的式子表示GH的长是______.13.如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,将△DEC沿DE折叠得到△DEF,DF交AC于点G.若AGGE =73,则tan A=______.14.如图,在等边三角形ABC中,过点C作射线CD⊥BC,点M,N分别在边AB,BC上,将△ABC沿MN折叠,使点B落在射线CD上的点B′处,连接AB′,已知AB=2.给出下列四个结论:①CN+NB′为定值;②当BN=2NC时,四边形BMB′N为菱形;③当点N与C重合时,∠AB′M=18°;④当AB′最短时,MN=7√21.20其中正确的结论是__________.(填序号)15.将一个矩形纸片OABC放置在平面直角坐标系中,点O(0,0),点A(3,0),点C(0,6),点P在边OC上(点P不与点O,C重合),折叠该纸片,使折痕所在的直线经过点P,并与x轴的正半轴相交于点Q,且∠OPQ=30°,点O的对应点O′落在第一象限.设OQ=t.(1)如图1,当t=1时,求∠O′QA的大小和点O′的坐标;(2)如图2,若折叠后重合部分为四边形,O′Q,O′P分别与边AB相交于点E,F,试用含有t的式子表示O′E的长,并直接写出t的取值范围;(3)若折叠后重合部分的面积为3√3,则t的值可以是__________________________________________.(请直接写出两个不同....的值即可)16.如图,已知△ABC,AB=AC,BC=16,AD⊥BC,∠ABC的平分线交AD于点E,且DE=4.将∠C沿GM折叠使点C与点E恰好重合.下列结论正确的有________.(填序号)①BD=8;②点E到AC的距离为3;③EM=103;④EM∥AC.17.综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动,有一位同学操作过程如下:操作一:对折正方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;操作二:在AD上选一点P,沿BP折叠,使点A落在正方形内部点M处,把纸片展平,连接PM,BM,延长PM交CD于点Q,连接BQ.(1)如图1,当点M在EF上时,∠EMB=________;(填度数)(2)改变点P在AD上的位置(点P不与点A,D重合)如图2,判断∠MBQ与∠CBQ 的数量关系,并说明理由.参考答案1.D 2.D 3.C 4.A 5.D6. 3√2-3 7.2√3 8.5 9.60°4√6 10.10 2√511.-2 12.√m2+n2 13.3√7714.①②④15.(1)∠O′QA=60°点O′的坐标为(32,√32)(2)O′E=3t-6,其中t的取值范围是2<t<3 (3)3或103(答案不唯一,满足3≤t<2√3即可) 16.①④17.(1)30°(2)∠MBQ=∠CBQ,理由略。
2019-2020学年浙江省中考数学(浙教版)专题复习八: 图形折叠问题训练(含答案)

∴∠DOF=60°.
同理可得∠EOG=60°,
∴∠FOG=60°=∠DOF=∠EOG,
∴△DOF≌△GOF≌△GOE,
∴OD=OG,OE=OF,∠OGF=∠ODF=∠ODB,∠OFG=∠OEG=∠OEB,
∴△OAD≌△OCG,△OAF≌△OCE,
∴AD=CG,AF=CE,∴△ADF≌△CGE,故选项 A 正确;
DC 边上的点 F 处,折痕为 DE,点 E 在 AB 边上;②把纸片展开并铺平;③把△CDG 翻折,点 C 落在线 段 AE 上的点 H 处,折痕为 DG,点 G 在 BC 边上.若 AB=AD+2,EH=1,则 AD=________.
【分析】设 AD=x,则 AB=x+2,利用折叠的性质得 DF=AD,EA=EF,∠DFE=∠A=90°,则可判断 四边形 AEFD 为正方形,所以 AE=AD=x,再根据折叠的性质得 DH=DC=x+2,则 AH=AE-HE=x- 1,然后根据勾股定理得到 x2+(x-1)2=(x+2)2,再解方程求出 x 即可. 【自主解答】
计算出 CD=5,接着证明△OBM≌△ODN 得到 DN=BM,然后根据折叠的性质得 BM=B′M=1,从而有
DN=1,于是计算 CD-DN 即可.
【自主解答】
折叠是轴对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.对于菱形的折 叠,还要明确菱形的基本性质,在解题过程中要抓住菱形的性质进行分析. 2.(2018·贵州遵义中考)如图,在菱形 ABCD 中,∠ABC=120°,将菱形折叠,使点 A 恰好落在对角线 BD 上的点 G 处(不与 B,D 重合),折痕为 EF,若 DG=2,BG=6,则 BE 的长为__________.
∠MBO=∠NDO, OB=OD, ∠BOM=∠DON,
初三几何专题练习折叠问题

初三几何专题练习折叠问题折叠问题实际上是轴对称问题的应用,解题关键是抓住对称的性质1)关于同一条直线对称的图形全等; 2)对称轴是轴对称点连线的垂直平分线。
1、矩形ABCD 中,AB =6cm ,BC =5cm ,若将矩形折叠,使B 、D 重合,则折痕EF 长为?2一面积为1的正方形纸片ABCD ,M 、N 分别为AD 、BC 边的中点,将点C 折致MN 上,落在P 点位置,折痕为BQ ,连结PQ 。
1)求MP 的长;2)求证:以PQ 为边长的正方形面积=313、矩形ABCD 中,AB =1,点M 在对角线AC 上,AM =41AC ,直线L 过M 点且与AC 垂直与边AD 交于点E 。
1)、若AD =3,求证:点B 在直线L 上。
A D CBMN P2)、若L 与BC 交于H ,且把矩形的面积分成72的两部分,求AD 长。
若L 与AD 、AB 交于点E 、G (包括G 与C 重合),设AD长为x (33≤x ≤3)找出x 的取值范围。
4、把矩形纸片放入直角坐标系中,使OA 、OC 与X 轴、Y 轴正半轴重合,连AC 将△ABC 沿AC 翻折,点B 落在该坐标系内,设落点为D ,CD 交X 轴于E ,若CE =5,OE 、OC 长是方程x 2+(m -1)x +12=0的两根,且OC >OE ;1)求点D 坐标;2)若点F 是AC 中点,判断(8,-20)是否在过D 、F 两点的直线上。
5、ABCD 为一矩形纸,E 是AB 上一点,且BE ∶AE =5∶3,EC =15,把△BCE 沿折痕EC 向上翻折,若点B 恰好落在AD 边上,设为F 点; 求:1)AB 与BC 长;2)若☉O 内切于以F 、E 、B 、C 为顶点的四边形,求⊙O 的面积。
6、矩形纸片OABC 放入直角坐标系XOY 中,使OA 、OC 分别与X 轴、Y 轴正半轴上,连结AC 、且AC=45。
Tan ∠1) 求A 、C 两点坐标 2) 求AC 所在直线的解析式3) 将纸片OABC 折叠,使点A 与点C 重合(折痕为EF),求折叠后纸片重叠部分面积。
2022年中考数学专题复习 折叠题(含解析)

2022年中考数学专题复习:折叠题1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF 折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有以下四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是〔〕A.①②③B.①②④C.②③④D.①②③④解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF〔ASA〕,∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.应选B.点评:此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,假设EB为∠AEG的平分线,EF和BC的延长线交于点H.以下结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤假设,那么.以上命题,正确的有〔〕A.2个B.3个C.4个D.5个解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,那么G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,那么有y2+〔2y﹣2x〕2=〔2y﹣x〕2,解得x1=y〔不合题意舍去〕,x2=y.那么,故正确.故正确的有3个.应选B.点评:此题考查了翻折变换,解答过程中涉及了矩形的性质、勾股定理,属于综合性题目,解答此题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD 于F点,假设CF=1,FD=2,那么BC的长为〔〕A.3B.2C.2D.2解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM〔AAS〕,∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.应选B.点评:此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.4.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.那么以下结论:①BG=DE且BG⊥DE;②△ADG 和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的选项是〔〕A.③④B.①②③C.①②④D.①②③④解答:解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,∴可得BG与DE相交的角为90°,∴BG⊥DE.①正确;如图,延长AK,使AK=KQ,连接DQ、QG,∴四边形ADQG是平行四边形;作CW⊥BE于点W,FJ⊥BE于点J,∴四边形CWJF是直角梯形;∵AB=DA,AE=DQ,∠BAE=∠ADQ,∴△ABE≌△DAQ,∴∠ABE=∠DAQ,∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.∴△ABH是直角三角形.易证:△CWB≌△BHA,△EJF≌△AHE;∴WB=AH,AH=EJ,∴WB=EJ,又WN=NJ,∴WN﹣WB=NJ﹣EJ,∴BN=NE,③正确;∵MN是梯形WGFC的中位线,WB=BE=BH+HE,∴MN=〔CW+FJ〕=WC=〔BH+HE〕=BE;易证:△ABE≌△DAQ〔SAS〕,∴AK=AQ=BE,∴MN∥AK且MN=AK;四边形AKMN为平行四边形,④正确.S△ABE=S△ADQ=S△ADG=S▱ADQG,②正确.所以,①②③④都正确;应选D.点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.5.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,MN∥AB,MC=6,NC=,那么四边形MABN的面积是〔〕A.B.C.D.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18.应选C.点评:此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质.此题难度适中,解此题的关键是注意折叠中的对应关系,注意数形结合思想的应用.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,那么∠A′的大小是〔〕A.40°B.36°C.32°D.30°解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.应选B.点评:此题考查了折叠的性质,解答此题的关键是掌握翻折前后的对应角相等,注意此题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.7.如图,△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD翻折使AB 与AC重合,得△AB′D,那么△ABC与△AB′D重叠局部的面积为〔〕A.B.C.3﹣D.解答:解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2,∴AC=BC,∴AF=AB=,∴AC===2,由折叠的性质得:AB′=AB=2,∠B′=∠B=30°,∵∠B′CD=∠CAB+∠B=60°,∴∠CDB′=90°,∵B′C=AB′﹣AC=2﹣2,∴CD=B′C=﹣1,B′D=B′C•cos∠B′=〔2﹣2〕×=3﹣,∴DE===,∴S阴影=AC•DE=×2×=.应选A.点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.8.如图,△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD翻折,使AB与AC重合,得△AED,那么BD的长度为〔〕A.B.C.D.解答:解:作CF⊥AB于点F.∵∠CAB=∠B∴AC=BC,∴BF=AB=,在直角△BCF中,BC==2,在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,∴∠CDE=90°,设BD=x,那么CD=DE=2﹣x,在直角△CDE中,tanE===tan30°=,解得:x=3﹣.应选B.点评:此题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是〔〕A.1 B.C.D.解答:解:∵∠C=90°,AC=,BC=1,∴AB==2,∴∠BAC=30°∵△ADB沿直线BD翻折后,点A落在点E处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,∵AD⊥ED,∴BC∥DE,∴∠CBF=∠BED=30°,在Rt△BCF中,CF==,BF=2CF=,∴EF=2﹣,在Rt△DEF中,FD=EF=1﹣,ED=FD=﹣1,∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC•AD+AD•ED=2××1×〔﹣1〕+×〔﹣1〕〔﹣1〕=1.应选A.点评:此题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.。
中考数学复习《折叠问题》

EF 6 72 ∴S△BEF=EG· S△BEG=10×24= 5
14.如图,已知在矩形 ABCD 中,点 E 在边 BC 上,BE=2CE,将矩形 沿着过点 E 的直线翻折后,点 C,D 分别落在边 BC 下方的点 C′,D′处,且 点 C′,D′,B 在同一条直线上,折痕与边 AD 交于点 F,D′F 与 BE 交于点 G.设 AB=t,那么△EFG 的周长为 2 3t .(用含 t 的代数式表示)
13.如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE
折叠到DF,延长EF交AB于点G,连结DG,求△BEF的面积. 【解析】由折叠和正方形的性质,在Rt△BEG中,由勾股定理求出AG后再 求△BGE的面积,最后由△BEF与△BGE的面积关系求△BEF的面积.
解:DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°. 又∵DG=DG,∴△ADG≌△FDG(HL).∵正方形 ABCD 的边长为 12, BE=EC,∴BE=EC=EF=6.设 AG=FG=x,则 EG=x+6, BG=12-x,在 Rt△BEG 中,由勾股定理,得 EG2=BE2+BG2, 1 1 即(x+6) =6 +(12-x) ,解得 x=4.∵S△BEG=2· BE· BG=2×6×8=24,
(1)求证:△DEC≌△EDA;
(2)求DF的值; (3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶
点Q落在线段AE上,顶点M,N落在线段AC上,当线段PE的长为何值时,
矩形PQMN的面积最大?并求出其最大值.
解:(1)由矩形的性质可知△ADC≌△CEA,∴AD=CE,DC=EA, ∠ACD=∠CAE.在△DEC 与△EDA 中, CE=AD, ∵DE=ED, ∴△DEC≌△EDA(SSS) DC=EA,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题八 图形折叠问题类型一 折叠三角形(2018·浙江台州中考)如图,等边三角形ABC 边长是定值,点O 是它的外心,过点O 任意作一条直线分别交AB ,BC 于点D ,E.将△BDE 沿直线DE 折叠,得到△B ′DE ,若B ′D ,B ′E 分别交AC 于点F ,G ,连结OF ,OG ,则下列判断错误的是( )A .△ADF ≌△CGEB .△B ′FG 的周长是一个定值C .四边形FOEC 的面积是一个定值D .四边形OGB ′F 的面积是一个定值【分析】A .根据等边三角形ABC 的外心的性质可知AO 平分∠BAC ,根据角平分线的定理和逆定理得FO 平分∠DFG ,由外角的性质可证明∠DOF =60°,同理可得∠EOG =60°,∠FOG =60°=∠DOF =∠EOG ,再根据三角形全等的性质可得△ADF ≌△CGE ;B .根据△DOF ≌△GOF ≌△GOE ,得DF =GF =GE ,所以△ADF ≌△B ′GF ≌△CGE ,可得结论;C .根据S 四边形FOEC =S △OCF +S △OCE 判断即可;D .将S 四边形OGB ′F =S △OAC -S △OFG ,根据S △OFG =12·FG ·OH ,FG 变化,故△OFG 的面积变化,从而四边形OGB ′F 的面积也变化,可作判断. 【自主解答】三角形的折叠问题一般考查轴对称的性质、勾股定理和线段的性质等,解题的关键是抓住折叠的本质是轴对称,轴对称是全等变换,找出相等的角和线段.类型二折叠平行四边形(2018·山东淄博中考)在如图所示的平行四边形ABCD中,AB=2,AD=3,将△ACD沿对角线AC 折叠,点D落在△ABC所在平面内的点E处,且AE过BC的中点O,则△ADE的周长等于________.【分析】要计算周长首先需要证明E,C,D共线,DE可求,问题得解.【自主解答】关于平行四边形折叠问题,解答时需要关注:在折叠前后,折痕两边能够完全重合的部分是全等图形,它们的对应线段、对应角相等,与特殊的平行四边形相比,它缺少了特殊的条件.1.(2018·甘肃兰州中考)如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F.若∠ABD =48°,∠CFD=40°,则∠E为( )A.102°B.112°C.122°D.92°类型三折叠菱形(2018·山东烟台中考)对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B′M=1,则CN的长为( )A.7 B.6 C.5 D.4【分析】连结AC ,BD ,利用菱形的性质得OC =12AC =3,OD =12BD =4,∠COD =90°,再利用勾股定理计算出CD =5,接着证明△OBM ≌△ODN 得到DN =BM ,然后根据折叠的性质得BM =B ′M =1,从而有DN =1,于是计算CD -DN 即可. 【自主解答】折叠是轴对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.对于菱形的折叠,还要明确菱形的基本性质,在解题过程中要抓住菱形的性质进行分析.2.(2018·贵州遵义中考)如图,在菱形ABCD 中,∠ABC =120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B ,D 重合),折痕为EF ,若DG =2,BG =6,则BE 的长为__________.3.如图,在菱形ABCD中,tan A=43,M,N分别在边AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,BNCN的值为____.类型四折叠矩形(2018·浙江杭州中考)折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上.若AB=AD+2,EH=1,则AD=________.【分析】设AD=x,则AB=x+2,利用折叠的性质得DF=AD,EA=EF,∠DFE=∠A=90°,则可判断四边形AEFD为正方形,所以AE=AD=x,再根据折叠的性质得DH=DC=x+2,则AH=AE-HE=x -1,然后根据勾股定理得到x2+(x-1)2=(x+2)2,再解方程求出x即可.【自主解答】此类问题中,运用的知识点比较多,综合性强,如轴对称性、全等、相似、勾股定理、转换思想、与其他图形(圆)结合等,抓住翻折前后两个图形是全等的,把握翻折前后不变的要素是解决此类问题的关键.4.(2018·湖北宜宾中考)如图,在矩形ABCD 中,AB =3,CB =2,点E 为线段AB 上的动点,将△CBE 沿CE 折叠,使点B 落在矩形内点F 处,下列结论正确的是__________(写出所有正确结论的序号). ①当E 为线段AB 中点时,AF ∥CE ; ②当E 为线段AB 中点时,AF =95;③当A ,F ,C 三点共线时,AE =13-2133;④当A ,F ,C 三点共线时,△CEF ≌△AEF.类型五 折叠正方形(2018·江苏宿迁中考)如图,在边长为1的正方形ABCD 中,动点E ,F 分别在边AB ,CD 上,将正方形ABCD 沿直线EF 折叠,使点B 的对应点M 始终落在边AD 上(点M 不与点A ,D 重合),点C 落在点N 处,MN 与CD 交于点P ,设BE =x. (1)当AM =13时,求x 的值;(2)随着点M 在边AD 上位置的变化,△PDM 的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(3)设四边形BEFC 的面积为S ,求S 与x 之间的函数表达式,并求出S 的最小值.【分析】(1)利用勾股定理构建方程,即可解决问题;(2)设AM =y ,则BE =EM =x ,MD =1-y ,在Rt △AEM 中,由勾股定理得出x ,y 的关系式,可证Rt △AEM ∽Rt △DMP ,根据相似三角形的周长比等于相似比求△DMP 的周长;(3)作FH ⊥AB 于H.则四边形BCFH 是矩形.连结BM 交EF 于O ,交FH 于K.根据梯形的面积公式构建二次函数,利用二次函数的性质解决最值问题即可. 【自主解答】正方形的折叠同其他图形一样,要关注勾股定理、全等图形、相似等相关知识,但由于正方形的特点,所以有关正方形的折叠问题有着其他图形没有的特殊性,解题时应关注正方形本身具有的特点.5.综合与实践问题背景折纸是一种许多人熟悉的活动,将折纸的一边二等分、四等分都是比较容易做到的,但将一边三等分就不是那么容易了,近些年,经过人们的不懈努力,已经找到了多种将正方形折纸一边三等分的精确折法,最著名的是由日本学者芳贺和夫发现的三种折法,现在被数学界称之为芳贺折纸三定理.其中,芳贺折纸第一定理的操作过程及内容如下(如图1):操作1:将正方形ABCD对折,使点A与点D重合,点B与点C重合.再将正方形ABCD展开,得到折痕EF;操作2:再将正方形纸片的右下角向上翻折,使点C与点E重合,边BC翻折至B′E的位置,得到折痕MN,B′E与AB交于点P.则P即为AB的三等分点,即AP∶PB=2∶1.解决问题(1)在图1中,若EF 与MN 交于点Q ,连结CQ.求证:四边形EQCM 是菱形; (2)请在图1中证明AP ∶PB =2∶1. 发现感悟若E 为正方形纸片ABCD 的边AD 上的任意一点,重复“问题背景”中操作2的折纸过程,请你思考并解决如下问题:(3)如图2.若DE AE =2.则APBP =________;(4)如图3,若DE AE =3,则APBP=________;(5)根据问题(2),(3),(4)给你的启示,你能发现一个更加一般化的结论吗?请把你的结论写出来,不要求证明.类型六 折叠圆(2018·湖北武汉中考)如图,在⊙O 中,点C 在优弧AB ︵上,将BC ︵沿BC 折叠后刚好经过AB 的中点D.若⊙O 的半径为5,AB =4,则BC 的长是( )A .2 3B .32C.532D.652【分析】连结OD ,AC ,DC ,OB ,OC ,作CE ⊥AB 于E ,OF ⊥CE 于F ,利用垂径定理、勾股定理、折叠的性质、圆周角定理、等腰三角形的性质及正方形的性质即可求解. 【自主解答】6.如图,将半径为4 cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )A.2 3 cm B.4 3 cmC. 3 cmD. 2 cm参考答案类型一【例1】 A .如图,连接OA ,OC.∵点O 是等边三角形ABC 的外心,∴AO 平分∠BAC ,∴点O 到AB ,AC 的距离相等.由折叠得DO 平分∠BDB ′,∴点O 到AB ,DB ′的距离相等,∴点O 到DB ′,AC 的距离相等,∴FO 平分∠DFG ,∠DFO =∠OFG =12(∠FAD +∠ADF). 由折叠得∠BDE =∠ODF =12(∠DAF +∠AFD), ∴∠OFD +∠ODF =12(∠FAD +∠ADF +∠DAF +∠AFD)=120°, ∴∠DOF =60°.同理可得∠EOG =60°,∴∠FOG =60°=∠DOF =∠EOG ,∴△DOF ≌△GOF ≌△GOE ,∴OD =OG ,OE =OF ,∠OGF =∠ODF =∠ODB ,∠OFG =∠OEG =∠OEB ,∴△OAD ≌△OCG ,△OAF ≌△OCE ,∴AD =CG ,AF =CE ,∴△ADF ≌△CGE ,故选项A 正确;B .∵△DOF ≌△GOF ≌△GOE ,∴DF =GF =GE ,∴△ADF ≌△B ′GF ≌△CGE ,∴B ′G =AD ,∴△B ′FG 的周长=FG +B ′F +B ′G =FG +AF +CG =AC(定值),故选项B 正确;C .S 四边形FOEC =S △OCF +S △OCE =S △OCF +S △OAF =S △AOC =13(定值),故选项C 正确;D .S 四边形OGB ′F =S △OFG +S △B ′GF =S △OFD +S △ADF=S 四边形OFAD =S △OAD +S △OAF=S △OCG +S △OAF =S △OAC -S △OFG .如图,过O 作OH ⊥AC 于H ,∴S △OFG =12·FG ·OH , 由于OH 是定值,FG 变化,故△OFG 的面积变化,从而四边形OGB ′F 的面积也变化,故选项D 不一定正确.故选D.类型二【例2】 ∵四边形ABCD 是平行四边形,∴AD ∥BC ,CD =AB =2.由折叠知∠DAC =∠EAC.∵∠DAC =∠ACB ,∴∠ACB =∠EAC ,∴OA =OC.∵AE 过BC 的中点O ,∴AO =12BC , ∴∠BAC =90°,∴∠ACD =90°.由折叠知∠ACE =90°,∴E ,C ,D 共线,则DE =4,∴△ADE 的周长为3+3+4=10.故答案为10.变式训练1.B类型三【例3】 如图,连结AC ,BD.∵点O 为菱形ABCD 的对角线的交点,∴CD=32+42=5.∵AB ∥CD ,∴∠MBO =∠NDO.在△OBM 和△ODN 中,⎩⎪⎨⎪⎧∠MBO =∠NDO ,OB =OD ,∠BOM =∠DON ,∴△OBM ≌△ODN ,∴DN =BM.∵过点O 折叠菱形,使B ,B ′两点重合,MN 是折痕,∴BM =B ′M =1,∴DN =1,∴CN =CD -DN =5-1=4.故选D.变式训练2.2.8 3.27类型四【例4】 设AD =x ,则AB =x +2.∵把△ADE 翻折,点A 落在DC 边上的点F 处,∴DF =AD ,EA =EF ,∠DFE =∠A =90°,∴四边形AEFD 为正方形,∴AE =AD =x.∵把△CDG 翻折,点C 落在线段AE 上的点H 处,折痕为DG ,点G 在BC 边上, ∴DH =DC =x +2.∵HE =1,∴AH =AE -HE =x -1.在Rt △ADH 中,∵AD 2+AH 2=DH 2,∴x 2+(x -1)2=(x +2)2,整理得x 2-6x -3=0,解得x 1=3+23,x 2=3-23(舍去),即AD 的长为3+23. 故答案为3+23. 变式训练4.①②③类型五【例5】 (1)在Rt △AEM 中,AE =1-x ,EM =BE =x ,AM =13. ∵AE 2+AM 2=EM 2,∴(1-x)2+(13)2=x 2,∴x =59. (2)△PDM 的周长不变为定值2.理由如下:设AM =y ,则BE =EM =x ,AE =1-x.在Rt △AEM 中,由勾股定理得AE 2+AM 2=EM 2,(1-x)2+y 2=x 2,解得1+y 2=2x ,∴1-y 2=2(1-x).∵∠EMP =90°,∠A =∠D ,∴Rt △AEM ∽Rt △DMP ,∴AE +EM +AM DM +MP +DP =AE DM,即1-x +x +y DM +MP +DP =1-x 1-y, 解得DM +MP +DP =1-y 21-x=2, ∴△DMP 的周长为2.(3)如图,作FH ⊥AB 于H.则四边形BCFH 是矩形.连结BM 交EF 于O ,交FH 于K.在Rt △AEM 中,AM =x 2-(1-x )2=2x -1.∵B ,M 关于EF 对称,∴BM ⊥EF ,∴∠KOF =∠KHB.∵∠OKF =∠BKH ,∴∠KFO =∠KBH. ∵AB =BC =FH ,∠A =∠FHE =90°,∴△ABM ≌△HFE ,∴EH =AM =2x -1,∴CF =BH =x -2x -1,∴S =12(BE +CF)·BC=12(x +x -2x -1)=12[(2x -1)2-2x -1+1]=12(2x -1-12)2+38.当2x -1=12时,S 有最小值为38. 变式训练5.解:(1)由折叠可得CM =EM ,∠CMQ =∠EMQ ,四边形CDEF 是矩形, ∴CD ∥EF ,∴∠CMQ =∠EQM , ∴∠EQM =∠EMQ ,∴ME =EQ =MC , 又∵MC ∥QE ,∴四边形EQCM 是平行四边形.又∵CM =EM ,∴四边形EQCM 是菱形.(2)如图1,设正方形ABCD 的边长为1,CM =x ,则EM =x ,DM =1-x.图1在Rt △DEM 中,由勾股定理可得EM 2=ED 2+DM 2,即x 2=(12)2+(1-x)2, 解得x =58,∴CM =58,DM =38. ∵∠PEM =∠D =90°,∴∠AEP +∠DEM =90°,∠DEM +∠EMD =90°,∴∠AEP =∠DME.又∵∠A =∠D =90°,∴△AEP ∽△DME ,∴AP AE =DE DM ,即AP 12=1238,解得AP =23, ∴PB =13,∴AP ∶PB =2∶1.(3)4 (4)6(5)根据问题(2),(3),(4),可得当DE AE =n(n 为正整数)时,则AP BP =2n.理由:设正方形ABCD 的边长为1,CM =x ,则EM =x ,DM =1-x.在Rt △DEM 中,由勾股定理可得EM 2=ED 2+DM 2,即x 2=(nn +1)2+(1-x)2, 解得x =(n +1)2+n 22(n +1)2, ∴DM =1-CM =2n +12(n +1)2, 由△AEP ∽△DME 可得AP AE =DE DM, 即AP1n +1=nn +12n +12(n +1)2,解得AP =2n2n +1, ∴PB =12n +1,∴AP BP=2n. 类型六【例6】 如图,连结OD ,AC ,DC ,OB ,OC ,作CE ⊥AB 于E ,OF ⊥CE 于F.∵D 为AB 的中点,∴OD ⊥AB ,∴AD =BD =12AB =2. 在Rt △OBD 中,OD =(5)2-22=1.∵将BC ︵沿BC 折叠后刚好经过AB 的中点D ,∴AC ︵和CD ︵所在的圆为等圆,∴AC ︵=CD ︵,∴AC =DC ,∴AE =DE =1,易得四边形ODEF 为正方形,∴OF =EF =1. 在Rt △OCF 中,CF =(5)2-12=2,∴CE =CF +EF =2+1=3,而BE =BD +DE =2+1=3,∴BC =32.故选B. 变式训练6.B。
