第五章 图 习题
杨老记 机械制图习题集第2版-第5章组合体视图-完整答案

退出
第42页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第42页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第42页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第43页 5-10 根据视图构思物体形状
转到:第5章 组合体视图
转到:第5章 组合体视图
退出
第36页 续5-8 补画视图中的漏线
转到:第5章 组合体视图
退出
第36页 续5-8 补画视图中的漏线
转到:第5章 组合体视图
退出
第36页 续5-8 补画视图中的漏线
转到:第5章 组合体视图
退出
第37页 5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第43页 5-10 根据视图构思物体形状
转到:第5章 组合体视图
退出
第43页 5-10 根据视图构思物体形状
转到:第5章 组合体视图
退出
第43页 5-10 根据视图构思物体形状
转到:第5章 组合体视图
退出
第44页 5-11 根据组合体的立体图和尺寸绘制三
视图草图,任选其中两个画在A3图纸上,并标注尺寸
退出
第39页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第40页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第40页 续5-9 根据已知的两视图,补画第三视图
转到:第5章 组合体视图
退出
第40页 续5-9 根据已知的两视图,补画第三视图
心电图检查习题

第五章心电图检查习题(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第五章心电图检查习题一.选择题【A1型题】1.哪种疾病用心电图检查诊断价值最大A. 左心室肥大B. 心肌炎C. 心包炎D. 二度房室传导阻滞E. 高血钾*2. 由心房除极所产生的波是A. P波B. Q波C. R波D. S波E. T波*3. 反映心室除极过程中的电位与时间变化的是A. P波B. QRS波C. T波D. U波E. ST段4. 描记aVR导联时,探查电极应连接于A. 左上肢B. 右上肢C. 左下肢D. 右下肢E. 胸骨右缘第4肋间*5. 按照惯例,连接右上肢的导联线颜色应为A. 红色B. 黄色C. 绿色D. 黑色E. 白色6. 若QRS波群主波方向I导联向下,III导联向上,则心电轴A. 不偏B. 左偏C. 右偏D. 轻度左偏E. 极度右偏*7. 心电轴右偏是指心电轴度数在A. -30°~ +90°B. -30°~ -90°C. +90°~+180° D. -90°~ -180° E. 0°~ -30°8. 当心电图纸移动速度为25mm/s时,纸上每小格的横向距离代表A. B. C. l s D. E.9. 正常P波在哪个导联必定倒置A. I导联B. III导联C. aVR导联D. aVL导联E. V5导联10. 心电图各波命名的论述哪项错误A. P波是心房除极波B. QRS波是心室除极波C. QRS波群中第一个向上的波为R波D. R波后面向下的波称S波E. S波后面向上的波称T波11. 下列心电图各波段的时间哪项不正常A. P波<B. QRS波群~C. Q波<D. P-R间期~E. V1导联VAT≤**12. 提示心脏发生逆钟向转位的是A. V3导联R/S≈1 导联R/S<1 C. V3导联R/S>1D. V5导联呈qRs型 E. V1导联呈rS型13. 关于正常Q波的描述哪项错误A. 时间<B. 振幅<同导联R波的1/4C.时间≥D. aVR导联Q波的振幅较R波大E. V1、V2导联偶可呈QS型14. 关于ST段的描述哪项错误A. 在任何导联下移不应超过B. 除V1~V3外,任何导联上抬不应超过C. ST段抬高应从参考水平线上缘垂直量到ST段上缘D. ST段下移应从参考水平线上缘垂直量到ST段下缘E. ST段上抬常见于急性心肌梗塞15. 关于T波的描述错误的是A. 为心室复极的波形B. 方向多与其QRS主波方向一致C. 振幅应低于同导联R波的1/10D. 心肌缺血时T波常低平或倒置E. 高血钾时T波常显著增高*16. P波形态高尖,电压≥常提示A. 左房肥大B. 右房肥大C. 左室肥大D. 右室肥大E.双心房肥大**17. 下列哪一项是诊断左室肥大最基本的条件A. QRS时间达~B. V5导联VAT> C. 心电轴左偏D. ST-T改变E. Rv5>,Rv5+Sv1>~18. 诊断右室肥大的条件是A. Rv1+Sv5> B. V1导联R/S<1 C. RaVR<D. Rv1< E. 心电轴左偏19. 慢性冠状动脉供血不足,在R波占优势的导联上,ST段呈缺血型下移应A. >B. <C. =D. ≥E. >20. 下壁心肌梗塞出现特征性心电图改变的导联是A. V1~V3B. V3~V5C. II、III、aVFD. V1~V6E. I、aVL、V 5、V6*21. 哪一项符合窦性P波的形态方向A. PII 倒置,PaVR直立 B. PII直立,PaVR倒置C. PIII 倒置,PaVR直立 D. PaVF倒置,PaVR直立E. PaVR 直立,PI倒置22. 哪项不是室性早搏的心电图特征A. 提前出现的QRS波群,时限>B. QRS波形态正常C. 提前出现的QRS之前无P波D. T波方向多与QRS主波方向相反E. 代偿间歇完全**23. 房性早搏与交界性早搏的主要区别是A. 有无P波B. P波是否倒置C. QRS波形态是否正常D. P′–R间期的时间E. 代偿间歇是否完全24. 哪项不符合心房颤动的心电图特征A. P波消失,f波替代波大小、形态、间隔不一C. f波频率350~600次/minD. QRS波宽大畸形E. QRS波间隔不规则**25. 哪项不是二度I型房室传导阻滞的表现A. P波规律出现B. P-R间期逐渐延长C. 有QRS波群脱落D. QRS脱落后,P-R间期又缩短,再逐渐延长,周而复始E. QRS波群宽大畸形【A2型题】26. 男18岁,突发心悸半小时,以往有类似发作史,常突发突止。
自动控制原理第五章习题及答案

第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。
u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解(a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图:⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++=="5-2某系统结构图如题5-2图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(tcs和稳态误差)(tes(1)tt r2sin)(=(2))452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=-系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时,2=ω,r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ (2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ>)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应 h t e e t tt()..=-+≥--11808049试求系统频率特性。
工程图学基础习题集第五章答案

这道题考查了立体几何中关于点、线、面位置关系的判 断,但题目中没有给出足够的信息来确定点、线、面的 位置关系,因此无法判断答案是否正确。
习题3答案
正确 错误 不适用
这道题考查了工程图学中关于剖面图的概念,根据剖面 图的知识,剖面图可以用来表示物体的内部结构。因此 ,答案正确。
习题1答案
错误
这道题考查了平面几何中关于角度的概念,题目中的角度是锐角,但答案给出的是直角,因此答案错 误。
习题1答案
不适用
这道题考查了立体几何中关于点、线、面位置关系的判断,但题目中没有给出足够的信息来确定点、线、面的位置关系,因 此无法判断答案是否正确。
习题2答案
正确 错误 不适用
这道题考查了立体几何中关于三视图的概念,根据三视 图的知识,主视图、左视图和俯视图可以确定一个物体 的位置和方向。因此,答案正确。
该题考查了平面的投影特性,根据平面的投影特性,当平面垂直于投影面时, 其正面投影和侧面投影均与该平面重合,因此该题答案正确。
解题思路
首先判断平面与投影面的关系,然后根据平面的投影特性进行作答。
03
第五章习题易错点总结
习题1易错点总结
总结词
投影关系混淆
详细描述
部分学生在解答这道题时,容易将物 体的投影关系混淆,导致作答错误。 正确的做法是理解并掌握物体的投影 规律,根据题目给出的视图,正确判 断出物体的形状和尺寸。
感谢您的观看
THANKS
这道题考查了工程图学中关于尺寸标注的概念,题目中 的尺寸标注是正确的,但答案给出的标注方式是错误的 ,因此答案错误。
这道题考查了工程图学中关于视图和剖面图的关系,但 题目中没有给出足够的信息来确定视图和剖面图的关系 ,因此无法判断答案是否
第五章 铁碳相图习题参考答案

第五章铁碳相图习题参考答案一、解释下列名词答:1、铁素体:碳溶入α-Fe中形成的间隙固溶体。
奥氏体:碳溶入γ-Fe中形成的间隙固溶体。
渗碳体:铁与碳形成的具有复杂晶体结构的金属化合物。
珠光体:铁素体和渗碳体组成的机械混合物。
莱氏体:由奥氏体和渗碳体组成的机械混合物。
2、Fe3CⅠ:由液相中直接析出来的渗碳体称为一次渗碳体。
Fe3CⅡ:从A中析出的Fe3C称为二次渗碳体。
Fe3CⅢ:从铁素体中析出的Fe3C称为三次渗碳体。
·共析Fe3C :经共析反应生成的渗碳体即珠光体中的渗碳体称为共析渗碳体。
共晶Fe3C:经共晶反应生成的渗碳体即莱氏体中的渗碳体称为共晶渗碳体。
3、钢:含碳量大于%,小于%的铁碳合金。
白口铸铁:含碳量大于%的铁碳合金。
二、填空题1、常温平衡状态下,铁碳合金基本相有铁素体(F)、渗碳体(Fe3C)等两个。
2、Fe-Fe3C相图有4个单相区,各相区的相分别是液相(L)、δ相、铁素体(F)、奥氏体(A)。
3、Fe-Fe3C 相图有三条水平线,即HJB、ECF和PSK线,它们代表的反应分别是包晶反应、共晶反应和共析反应。
4、工业纯铁的含碳量为≤%,室温平衡组织为F+ Fe3CⅢ。
5、共晶白口铁的含碳量为%,室温平衡组织P占%,Fe3C共晶占%,Fe3CⅡ占%。
(6、一钢试样,在室温平衡组织中,珠光体占60%,铁素体占40%,该钢的含碳量为。
7、钢的组织特点是高温组织为奥氏体(A),具有良好的塑、韧性,因而适于热加工成形。
8、白口铸铁的特点是液态结晶都有共晶转变,室温平衡组织中都有莱氏体,因而适于通过铸造成形。
三、简答题1、为什么γ-Fe 和α- Fe 的比容不同一块质量一定的铁发生(γ-Fe →α-Fe )转变时,其体积如何变化答:因为γ-Fe和α- Fe原子排列的紧密程度不同,γ-Fe的致密度为74%,α- Fe的致密度为68%,因此一块质量一定的铁发生(γ-Fe →α-Fe )转变时体积将发生膨胀。
理论力学(周衍柏)习题答案,第五章

第五章习题解答5.1解如题5.1.1图杆受理想约束,在满足题意的约束条件下杆的位置可由杆与水平方向夹角所唯一确定。
杆的自由度为1,由平衡条件:即mg y =0①变换方程y=2rcos sin-= rsin2②故③代回①式即因在约束下是任意的,要使上式成立必须有:rcos2-=0④又由于cos=故cos2=代回④式得5.2解如题5.2.1图三球受理想约束,球的位置可以由确定,自由度数为1,故。
得由虚功原理故①因在约束条件下是任意的,要使上式成立,必须故②又由得:③由②③可得5.3解如题5.3.1图,在相距2a的两钉处约束反力垂直于虚位移,为理想约束。
去掉绳代之以力T,且视为主动力后采用虚功原理,一确定便可确定ABCD的位置。
因此自由度数为1。
选为广义坐。
由虚功原理:w①又取变分得代入①式得:化简得②设因在约束条件下任意,欲使上式成立,须有:由此得5.4解自由度,质点位置为。
由①由已知得故②约束方程③联立②③可求得或又由于故或5.5解如题5.5.1图按题意仅重力作用,为保守系。
因为已知,故可认为自由度为1.选广义坐标,在球面坐标系中,质点的动能:由于所以又由于故取Ox为零势,体系势能为:故力学体系的拉氏函数为:5.6解如题5.6.1图.平面运动,一个自由度.选广义坐标为,广义速度因未定体系受力类型,由一般形式的拉格朗日方程①在广义力代入①得:②在极坐标系下:③故将以上各式代入②式得5.7解如题5.7.1图又由于所以①取坐标原点为零势面②拉氏函数③代入保守系拉格朗日方程得代入保守系拉格朗日方程得5.8解:如图5.8.1图.(1)由于细管以匀角速转动,因此=可以认为质点的自由度为1.(2)取广义坐标.(3)根据极坐标系中的动能取初始水平面为零势能面,势能:拉氏函数①(4),代入拉氏方程得:(5)先求齐次方程的解.②特解为故①式的通解为③在时:④⑤联立④⑤得将代回式③可得方程的解为:5.9解如题5.9.1图.(1)按题意为保守力系,质点被约束在圆锥面内运动,故自有度数为2. (2)选广义坐标,.(3)在柱坐标系中:以面为零势能面,则:拉氏函数-①(4)因为不显含,所以为循环坐标,即常数②对另一广义坐标代入保守系拉氏方程③有得④所以此质点的运动微分方程为(为常数)所以5.10解如题5.10.1图.(1)体系自由度数为2.(2)选广义坐标(3)质点的速度劈的速度故体系动能以面为零势面,体系势能:其中为劈势能.拉氏函数①(4)代入拉格郎日方程得:②代入拉格郎日方程得③联立②,③得5.11 解如题5.11.1图(1)本系统内虽有摩擦力,但不做功,故仍是保守系中有约束的平面平行运动,自由度(2)选取广义坐标(3)根据刚体力学其中绕质心转动惯量选为零势面,体系势能:其中C为常数.拉氏函数(4)代入保守系拉氏方程得:对于物体,有5.12解如题5.12.1图.(1)棒作平面运动,一个约束,故自由度. (2)选广义坐标(3)力学体系的动能根据运动合成又故设为绕质心的回转半径,代入①得动能②(4)由③(其中)则④因为、在约束条件下任意且独立,要使上式成立,必须:⑤(5)代入一般形式的拉氏方程得:⑥又代入一般形式的拉氏方程得:⑦⑥、⑦两式为运动微分方程(6)若摆动角很小,则,代入式得:,代入⑥⑦式得:⑧又故代入⑧式得:(因为角很小,故可略去项)5.13解如题5.13.1图(1)由于曲柄长度固定,自由度.(2)选广义坐标,受一力矩,重力忽略,故可利用基本形式拉格朗日方程:①(3)系统动能②(4)由定义式③(5)代入①得:得5.14.解如题5.14.1图.(1)因体系作平面平行运动,一个约束方程:(2)体系自由度,选广义坐标.虽有摩擦,但不做功,为保守体系(3)体系动能:轮平动动能轮质心转动动能轮质心动能轮绕质心转动动能.①以地面为零势面,体系势能则保守系的拉氏函数②(1)因为不显含,得知为循环坐标.故=常数③开始时:则代入得又时,所以5.15解如题5.15.1图(1)本系统作平面平行运动,干限制在球壳内运动,自由度;选广义坐标,体系摩擦力不做功,为保守力系,故可用保守系拉氏方程证明①(2)体系动能=球壳质心动能+球壳转动动能+杆质心动能+杆绕中心转动动能②其中代入②得以地面为零势面,则势能:(其中为常数)(3)因为是循环坐标,故常熟③而代入①式得④联立③、④可得(先由③式两边求导,再与④式联立)⑤⑤试乘并积分得:又由于当5.16解如题图5.16.1.(1)由已知条件可得系统自由度.(2)取广义坐标.(3)根据刚体力学,体系动能:①又将以上各式代入①式得:设原点为零势能点,所以体系势能体系的拉氏函数②(1)因为体系只有重力势能做工,因而为保守系,故可采用③代入③式得即(5)解方程得5.17解如题5.17.1图(1)由题设知系统动能①取轴为势能零点,系统势能拉氏函数②(2)体系只有重力做功,为保守系,故可采用保守系拉氏方程.代入拉氏方程得:又代入上式得即③同理又代入上式得④令代入③④式得:欲使有非零解,则须有解得周期5.18解如题5.18.1图(1)系统自由度(2)取广义坐标广义速度(3)因为是微震动,体系动能:以为势能零点,体系势能拉氏函数(4)即①同理②同理③设代入①②③式得欲使有非零解,必须解之又故可得周期5.19解如题5.19.1图(1)体系自由度(2)取广义坐标广义速度(3)体系动能体系势能体系的拉氏函数(4)体系中只有弹力做功,体系为保守系,可用①将以上各式代入①式得:②先求齐次方程③设代入③式得要使有非零,必须即又故通解为:其中又存在特解有②③式可得式中及为积分常数。
数据结构第五章图习题

05 图【单选题】1. 设无向图G 中有五个顶点,各顶点的度分别为2、4、3、1、2,则G 中边数为(C )。
A、4条 B、5条 C、6条 D、无法确定2. 含n 个顶点的无向完全图有(D )条边;含n 个顶点的有向图最多有(C )条弧;含n 个顶点的有向强连通图最多有(C )条弧;含n 个顶点的有向强连通图最少有(F)条弧;设无向图中有n 个顶点,则要接通全部顶点至少需(G )条边。
A 、n 2B 、n(n+1)C 、n(n-1)D 、n(n-1)/2E 、n+1F 、nG 、n-13. 对下图从顶点a 出发进行深度优先遍历,则(A )是可能得到的遍历序列。
A 、acfgdebB 、abcdefgC 、acdgbefD 、abefgcd对下图从顶点a 出发进行广度优先遍历,则(D )是不可能得到的遍历序列。
A 、abcdefgB 、acdbfgeC 、abdcegfD 、adcbgef4. 设图G 的邻接矩阵A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010101010,则G 中共有(C )个顶点;若G 为有向图,则G 中共有(D )条弧;若G 为无向图,则G 中共有(B )条边。
A 、1B 、2C 、3D 、4E 、5F 、9G 、以上答案都不对5. 含n 个顶点的图,最少有(B )个连通分量,最多有(D )个连通分量。
A 、0B 、1C 、n-1D 、n6. 用邻接表存储图所用的空间大小(A )。
A 、与图的顶点数和边数都有关B 、只与图的边数有关C 、只与图的顶点数有关D 、与边数的平方有关7. n 个顶点的无向图的邻接表最多有(B )个表结点。
A 、n 2B 、n(n-1)C 、n(n+1)D 、n(n-1)/28. 无向图G=(V ,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是(D )。
电工技术第五章 三相电路习题解答

139第五章 三相电路[练习与思考]5-1-1 对称三相电源的三相绕组作星形联接时,设线电压uAB=380sin(ωt+30o)V ,试写出相电压uB 的三角函数式及相量式。
解:V t u B )120sin(220︒-=ωV U B ︒-∠=∙1202110 5-1-2 三角形联接的对称三相电源,空载运行时三相电源会不会在三相绕组所构成的闭合回路中产生电流?如果一相电源电压极性接反,则闭合回路中是否有电流通过?解:空载运行时,电源回路中无电流通过。
如果一相电源电压极性接反,则闭合回路中有电流通过。
5-2-1 为什么电灯开关一定要接在相线(火线)上?解:因为电灯是单相负载,当开关断开时,电灯灯头不带电,以便于安全维修和更换。
如果开关接在零线上,当其断开时,电灯灯头依然带电(接在火线上),作业时会造成触电事故。
5-2-2 三相四线制电路中,中线阻抗为零。
若星形负载不对称,则负载相电压是否对称?如果中线断开,负载电压是否对称?解:三相四线制电路中,若星形负载不对称,负载相电压仍然对称;如果中线断开,负载电压将不对称。
5-2-3 三相四线制电路中,电源线的中性线上规定不得加装保险丝,这是为什么? 解:如果电源线的中性线上加装保险丝,一旦由于某种原因造成保险丝熔断,接成Y 型的各组单相负载上的各相相电压将不会对称,有的相电压可能会超过单相负载的额定电压,造成损坏;有的相电压可能会低于额定电压,使得负载不能正常工作。
因此源线的中性线上规定不得加装保险丝。
5-3-1 三相负载对称是指下述三种情况下的哪一种:⑴|Z AB |=|Z BC |=|Z CA |;⑵φAB =φBC =φCA ;⑶Z AB =Z BC =Z CA 。
、解:三相负载对称是指(3),阻抗模相等,阻抗角相等。
5-3-2 已知对称三角形联接的三相电路中A 相负载线电流A 010∠=∙A I ,试写出其余各相线电流与相电流。
解:A I B ︒-∠=∙12010 A I C ︒+∠=∙12010140A I AB ︒∠=∙308.5 A I BC ︒-∠=∙908.5 A I CA ︒∠=∙1508.55-4-1 同一三相负载,采用三角形联接和星形联接接于线电压相同的三相电源上,试求这两种情况下负载的线电流、相电流及有功功率的比值。
电路与模拟电子技术(第二版第五章习题解答

第五章 电路的暂态分析5.1 题5.1图所示各电路在换路前都处于稳态,求换路后电流i 的初始值和稳态值。
解:(a )A i i L L 326)0()0(===-+,换路后瞬间 A i i L 5.1)0(21)0(==++ 稳态时,电感电压为0, A i 326==(b )V u u C C 6)0()0(==-+, 换路后瞬间 02)0(6)0(=-=++C u i 稳态时,电容电流为0, A i 5.1226=+=(c )A i i L L 6)0()0(11==-+,0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路,故 0=i(d )2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+(a)(b)(d)(c)C2ΩL 2+6V -题5.1图i稳态时电容相当于开路,故 A i 12226=++=5.2 题5.2图所示电路中,S 闭合前电路处于稳态,求u L 、i C 和i R 的初始值。
解:换路后瞬间 A i L 6=,V u C 1863=⨯= 06=-=L R i i031863=-=-=C L C u i i0==+R C L Ri u u ,V u u C L 18-=-=5.3 求题5.3图所示电路换路后u L 和i C 的初始值。
设换路前电路已处于稳态。
解:换路后,0)0()0(==-+L L i i ,4mA 电流全部流过R 2,即(0)4C i mA +=对右边一个网孔有:C C L u i R u R +⋅=+⋅210由于(0)(0)0C C u u +-==,故2(0)(0)3412L C u R i V ++==⨯=5.4 题5.4图所示电路中,换路前电路已处于稳态,求换路后的i 、i L 和 u L 。
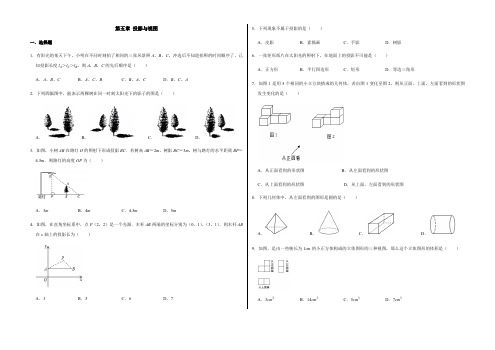
_北师大版九年级数学上册第五章 投影与视图练习题
第五章投影与视图一.选择题1.有阳光的某天下午,小明在不同时刻拍了相同的三张风景照A,B,C,冲选后不知道拍照的时间顺序了,已知投影长度l A>l C>l B,则A,B,C的先后顺序是()A.A、B、C B.A、C、B C.B、A、C D.B、C、A2.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是()A.B.C.D.3.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为()A.3m B.4m C.4.5m D.5m4.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB 在x轴上的投影长为()A.3B.5C.6D.75.下列现象不属于投影的是()A.皮影B.素描画C.手影D.树影6.一张矩形纸片在太阳光的照射下,在地面上的投影不可能是()A.正方形B.平行四边形C.矩形D.等边三角形7.如图1是用5个相同的小立方块搭成的几何体,若由图1变化至图2,则从正面、上面、左面看到的形状图发生变化的是()A.从正面看到的形状图B.从左面看到的形状图C.从上面看到的形状图D.从上面、左面看到的形状图8.下列几何体中,从左面看到的图形是圆的是()A.B.C.D.9.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的体积是()A.3cm3B.14cm3C.5cm3D.7cm310.如图是由几个大小相同的小立方块搭成的几何体从上面看到的形状图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体从正面看到的形状图是( )A .B .C .D .二.填空题11.一天下午,小红先参加了校运动会女子200m 比赛,然后又参加了女子400m 比赛,摄影师在同位置拍摄了她参加这两场比赛的照片,如图所示,则小红参加200m 比赛的照片是 .(填“图1”或“图2”)12.如图,一棵树(AB )的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE )为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多离开树干 米才可以不被阳光晒到?13.如图,甲楼AB 高18米,乙楼CD 坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE=米.(结果保留根号)14.如图,物体在灯泡发出的光照射下形成的影子是 投影.(填“平行”或“中心”).15.由若干个相同的小正方体搭成的几何体的三视图相同,如图所示.至少再加 个小正方体,该几何体可成为一个正方体.16.如图所示是若干个大小相同的小正方体搭成的几何体从三个不同方向看到的图形,则搭成这个几何体的小正方体的个数是 .17.如图,是一个实心圆柱体的三视图(单位:cm ),根据图中数据计算这个圆柱体的体积是 cm 3.(圆柱体体积公式:πr 2h ,r 为底面圆的半径,h 为圆柱体的高)18.一个几何体从正面和上面看到的图形如图所示,若这个几何体最多有a 个小正方体组成,最少有b 个小正方体组成,则a +b = .三.解答题19.画出如图所示几何体的三视图.20.如图,在平整的地面上,由若干个完全相同小正方体堆成一个几何体,请在网格中画出它的三视图.21.由几个相同的棱长的小正方体搭成的几何体的俯视图如图所示,正方形中的数字表示该位置上小正方体的个数,在网格中画出这个几何体的主视图和左视图.(注:网格中小正方形的边长等于小正方体的棱长)22.画出下面几何体的三视图.23.如图1,在平整的地面上,用8个棱长都为1cm的小正方体堆成一个几何体.(1)请利用图2中的网格画出这个几何体从正面看、从左面看和从上面看到的形状图.(一个网格为小立方体的一个面)(2)图1中8个小正方体搭成的几何体的表面积(包括与地面接触的部分)是cm2.24.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.25.如图,在地面上竖直安装着AB、CD、EF三根立柱,在同一时刻同一光源下立柱AB、CD形成的影子为BG 与DH.(1)填空:判断此光源下形成的投影是:投影.(2)作出立柱EF在此光源下所形成的影子.。
第5章现代工程图学习题集(第三版)答案

6.
参考答案
A面是 正垂 面 B面在C面之 下方 DE是 侧垂 线
5-6 补画视图中所缺图线
1
2
3答案方法ຫໍສະໝຸດ 4答案方法
5
答案
方法
6
答案
方法
5-7 读懂两视图后,补画第三视图(一)
1
答案 方法
2
答案 方法
3
答案 方法
4
答案 方法
5
答案
方法
6
答案
方法
5-8 读懂两视图后,补画第三视图(二)
1.
参考答案
CD是 正平 线 A面是 正垂 面 B面是 正平 面
2.
参考答案
A面是 正平 面
B面在C面之 下方
DE是 正平
线
3.
参考答案
A面是 侧平 面 B面是 正垂 面 B面在A面之 右方
4.
参考答案
AB是一般位置直 线 P面是 正垂 面 Q面是 水平 面
5.
参考答案
AB是 正平 线 P面是 水平 面 Q面是 正垂 面
1
答案
方法
2
答案
方法
3
答案
方法
4 答案
方法
5
答案
方法
6
答案
方法
5-9 读懂两视图后,补画第三视图(三)
1
答案
方法
2
答案 方法
3 答案
方法
4
答案
方法
4
答案
方法
5 答案
方法
6
答案
方法
5-10 尺寸4-标10注尺寸标注
1.根据轴测图在视图中标注尺寸。
2.标注组合体的尺寸,尺寸数值按1:1从图中量取(取整)。
现代工程图学习题集答案第5章

1
5-4 根据轴测图上所注尺寸,用1:1画出组合体三视图
2
5-5 标出指定的图线和线框在其他视图上的投影,并填空
1
2
3
答案
方法
4
答案
方法
答案
方法
6
答案
方法
5-7 读懂两视图后,补画第三视图(一)
答案
贰
1
壹
方法
叁
答案
方法
2பைடு நூலகம்
答案
方法
3
答案
方法
4
方法
答案
5
6
答案
方法
5-8 读懂两视图后,补画第三视图(二)
1
01
答案
02
方法
03
2
方法
答案
3
答案
方法
答案
方法
4
答案
方法
5
6
答案
方法
答案
1
方法
2
答案
方法
答案
方法
3
答案
方法
4
方法
答案
4
答案
方法
5
6
答案
5-11 标注组合体尺寸,尺寸从图上量取(取整数)
5-12 第二次制图作业指示——组合体视图
第5章 组合体视图
CONTENTS
单击此处添加标题
02
单击此处添加标题
01
5-1 根据轴测图补画视图中所缺图线
答案
1
方法
2
答案
方法
3
方法
4
3
答案
方法
5
6
答案
方法
建筑工程制图(第三版)第五章习题答案.doc

@:5-2. 画全建筑形体的六面基本视图。
5-3 改正剖面图中的错误(将缺的线补上,多余的线上打“╳”)。
1 2 3 45 6 8100 5-4 补全剖面图中所缺的线。
1 23 4101 第五章建筑形体的表达方法班级学号姓名5-5-1、作1-1剖面图。
5-5-2.补绘W投影,并将V、W投影改作合适的剖面。
材料混凝土。
5-5-3、作组合体的1-1剖视。
5-5-4、补绘W 投影,并将V 、W 投影改作合适的剖面。
材料混凝土。
102第五章 建筑形体的表达方法 班级 学号 姓名5-6. 将形体的正立面图改画为全剖面图。
5-7. 根据三视图将正面图、左侧面图改为全剖面图。
@:103 第五章建筑形体的表达方法班级学号姓名5-8. 将形体的正立面图改画为半剖面图。
5-9. 完成半剖面的正面图,求作全剖面的左侧立面图。
@:第五章建筑形体的表达方法班级学号姓名5-8、作建筑形体的2-2、3-3剖面。
5-9、求作正面图(取全剖面图)。
5-10、作2-2剖面图。
5-11、画出水平面图(全剖)。
5-12、将左侧面图改成剖面。
画出水平面图。
5-13、作建筑形体的2-2、3-3剖面。
5-14、作支架的1-1、2-2剖面图。
5-15、将形体的正立面图改画为全剖面图,左侧立面图画为半剖面。
第五章 建筑形体的表达方法 班级 学号 姓名5-16、在适当位置作局部剖面图。
5-17、作建筑形体局部剖面图。
5-18.在适当位置作局部剖面图。
5-19.分析建筑形体局部剖面图中的错误,在右侧作出正确局部剖面图。
材料混凝土。
第五章 建筑形体的表达方法 班级 学号 姓名5-22、作建筑形体的2-2、3-3剖面。
5-23、用阶梯剖面将正面图画成全剖面。
多孔材料。
并加标注。
5-24.将正立面图改为1—1剖面。
画在图形的右边。
材料钢筋混凝土。
第五章建筑形体的表达方法班级学号姓名5-25、根据给出的三视图,作出1-1、2-2剖面图。
5-26、在上方画出过滤池1-1旋转剖面图(展开)。
哈工大集合论习题课-第五章 图的基本概念习题课(学生)

第五章 图的基本概念习 题 课 11. 画出具有 6、8、10、…、2n 个顶点的三次图;是否有7个顶点的三次图?2. 无向图G 有21条边,12个3度数顶点,其余顶点的度数均为2,求G 的顶点数p 。
解:设图的顶点为p ,根据握手定理:1deg()2pi i v q ==∑,有212)12(2312⨯=-⨯+⨯p ,得15302==p p ,。
3. 下列各无向图中有几个顶点?(1)16条边,每个顶点的度为2;(2)21条边,3个4度顶点,其余的都为3度数顶点;(3)24条边,各顶点的度数相同。
解: 设图的顶点为p ,根据握手定理:(1)1deg()2pi i v q ==∑,即2221632p q ==⨯=;所以16p =,即有16个顶点。
(2)1deg()2p i i v q ==∑,即433(3)222142p q ⨯+⨯-==⨯=,所以13p =。
(3)各点的度数为k ,则1deg()2i pi v q ==∑,即222448k p q ⨯==⨯=,于是① 若1k =,48p =; ② 若2k =,24p =;③ 若3k =,16p =;④ 若4k =,12p =; ⑤ 若6k =,8p =;⑥ 若8k =,16p =; ⑦ 若12k =,4p =; ⑧ 若16k =,3p =;⑨ 若24k =,2p =; ⑩ 若48k =,1p =。
4.设图G 中9个顶点,每个顶点的度不是5就是6。
证明G 中至少有5个6度顶点或至少有6个5度顶点。
证:由握手定理的推论可知,G 中5度顶点数只能是0,2,6,8五种情况,此时6度顶点数分别为9,7,5,3,1个。
以上五种情况都满足至少5个6度顶点或至少6个5度顶点的情况。
5.有n 个药箱,若每两个药箱里有一种相同的药,而每种药恰好放在两个药箱中,问药箱里共有多少种药?[就是求一个完全图n K 的边数(1)(2)/2q p p =--]6.设G 是有p 个顶点,q 条边的无向图,各顶点的度数均为3。
第5章 MATLAB绘图_习题答案

第5章 MATLAB绘图习题5一、选择题1.如果x、y均为4×3矩阵,则执行plot(x,y)命令后在图形窗口中绘制()条曲线。
DA.12 B.7 C.4 D.32.下列程序的运行结果是()。
Ax=0:pi/100:2*pi;for n=1:2:10plot(n*sin(x),n*cos(x))hold onendaxis squareA.5个同心圆B.5根平行线C.一根正弦曲线和一根余弦曲线D.5根正弦曲线和5根余弦曲线3.命令text(1,1,'{\alpha}+{\beta}')执行后,得到的标注效果是()。
CA.{\alpha}+{\beta} B.{\α}+{\β} C.α+βD.\α+\β4.subplot(2,2,3)是指()的子图。
AA.两行两列的左下图B.两行两列的右下图C.两行两列的左上图D.两行两列的右上图5.要使函数y=2e x的曲线绘制成直线,应采用的绘图函数是()。
CA.polar B.semilogx C.semilogy D.loglog6.下列程序的运行结果是()。
B[x,y]=meshgrid(1:5);surf(x,y,5*ones(size(x)));A.z=x+y平面B.与xy平面平行的平面C.与xy平面垂直的平面D.z=5x平面7.下列函数中不能用于隐函数绘图的是()。
DA.ezmesh B.ezsurf C.ezplot D.plot38.下列程序运行后,看到的图形()。
Ct=0:pi/20:2*pi;[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);surf(x,y,z)view(0,90);axis equalA.像墨西哥帽子B.是空心的圆C.边界是正方形D.是实心的圆9.下列程序运行后得到的图形是()。
A[x,y]=meshgrid(-2:2);z=x+y;i=find(abs(x)<1 & abs(y)<1);z(i)=NaN;surf(x,y,z);shading interpA.在一个正方形的正中心挖掉了一个小的正方形B.在一个正方形的正中心挖掉了一个小的长方形C.在一个正方形的上端挖掉了一个小的正方形D.在一个正方形的下端挖掉了一个小的正方形10.在使用MA TLAB“绘图”选项卡中的命令按钮绘图之前,需要()。
现代工程图学(第四版)习题答案第5章

参考答案
现代工程图学习题集(第4版)
第5章 组合体视图
5-11.1 标注组合体尺寸,尺寸从图上量取(取整数)
参考答案
现代工程图学习题集(第4版)
第5章 组合体视图
5-11.2 标注组合体尺寸,尺寸从图上量取(取整数)
参考答案
现代工程图学习题集(第4版)
第5章 组合体视图
5-11.3标注组合体尺寸,尺寸从图上量取(取整数)
y2 y1
现代工程图学习题集(第4版)
5-7.3 读懂两视图后,补画第三视图(一)
第5章 组合体视图
参考答案
现代工程图学习题集(第4版)
5-7.4 读懂两视图后,补画第三视图(一)
第5章 组合体视图
参考答案
现代工程图学习题集(第4版)
5-7.5 读懂两视图后,补画第三视图(一)
第5章 组合体视图
现代工程图学习题集(第4版)
5-7.2 读懂两视图后,补画第三视图(一)
第5章 组合体视图
y1 y2
y2 y1
现代工程图学习题集(第4版)
5-7.3 读懂两视图后,补画第三视图(一)
第5章 组合体视图
现代工程图学习题集(第4版)
5-7.4 读懂两视图后,补画第三视图(一)
第5章 组合体视图
现代工程图学习题集(第4版)
现代工程图学习题集(第4版)
5-1.1 根据轴测图补画视图中所缺图线
第5章 组合体视图
答案
y
现代工程图学习题集(第4版)
5-1.2 根据轴测图补画视图中所缺图线
y
第5章 组合体视图
答案
现代工程图学习题集(第4版)
5-1.3 根据轴测图补画视图中所缺图线
第五章习题解答
θ
6
B
D 球对 A 球的压力大小也是 F,该力在水平面上分量为
A
C
F1 = F ⋅ sinθ =
2P 6
现在将球 A 及与其接触的绳段一起作为研究对象,其受力图在
水平面内投影如图(b)所示。列写平衡方程:
(a)
S
S
求解出 S = 6 P = 0.136P 18
2S cos 30o = F1 =
2P 6
FC C
PB
C FD
D A
FD
FA
(1)
(2)
解:对CD杆进行受力分析,由于CD杆是在两个力作用下保持平衡,所以这两个力一定 是大小相等( FC = FD ),方向相反,且作用线相同,如图(1)。再对ABC进行受力分析,由 于是三力平衡,所以FA必通过的P和FD的交点C,如图(2)所示,列出平衡方程:
A
F1
(b)
均质长方形薄板重Q=200N,用球铰链A和蝶铰链B固定在墙上,并用绳子CE拉住以维持在 水平位置。绳子CE缚在薄板上的C点,并挂在钉子E上,钉子钉入墙内,并和A点在同一铅 垂墙上,如图所示。∠ECA=∠BAC=300。求绳子的张力和支座的反力。
解:列写平衡方程如下:
RAx + RBx − T cos 30o sin 30o = 0
yA = L sinα xB = 2L cosα δyA = L cosαδα
由虚位移原理 即
由δα 的任意性有,
δxB = −2L sinαδα PδyA + QδxB = 0 PL cosαδα − 2QL sin αδα = 0 Q = (P / 2) cot α
直角弯杆 ABC 由直杆 CD 支撑,如图 2-26 所示。若∠ADC=60°,力 P=60N,沿 BC(水 平)方向,且各杆重量不计,试求铰链 A 及 D 的反力。
画法几何及工程制图第五章习题详解

a
e d
c
m
还有其他求解办法?
换面法
M f F
L
6
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-圆柱
a
c (d)
b
d
a (b) c
D A
B
C
a
c (d) d
b
d a (b)
c
A
C
a c
b
AA — 最左素线, BB — 最右素线 CC — 最前素线, DD — 最后素线
m
m ) (
m
辅助圆法
m M m
13
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
Z
V
W
X
Y
14
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
b
a
d
c
15
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
m (n') (n )
s
p 完了吗? S
31
§5.2 平面与立体相交-作图方法-平面与球相交
32
§5.2 平面与立体相交-作图方法-平面与球相交
2'
2"
7' 8' 3'4' 5'6'
1 '
8" 4"
6"
7" 3" 5"
1"
6
4 8
1
2
7 5 3
33
§5.2 平面与立体相交-作图方法-平面与环面相交
p
34
§5.2 平面与立体相交-作图方法-平面与环相交
现代工程图学习题集第四版答案 主编杨裕根第5章

第5章 组合体视图
5-2 看懂两视图,找出对应的立体图,并画出第三视图
答案
() ()
() ()
现代工程图学习题集(第4版)
第5章 组合体视图
5-2 看懂两视图,找出对应的立体图,并画出第三视图
答案
() ()
() ()
现代工程图学习题集(第4版)
第5章 组合体视图
5-3.1 根据轴测图画出组合体y 三视图(尺寸从图中直
第5章 组合体视图
5-5.3 标出指定的图线和线框在其他视图上的投影,并填空
3.
A面是
面
B面是
面
B面在A面之
现代工程图学习题集(第4版)
第5章 组合体视图
4. 5-5.4 标出指定的图线和线框在其他视图上的投影,并填空
AB是
线
P面是
面
Q面是
面
现代工程图学习题集(第4版)
第5章 组合体视图
5.5-5.5 标出指定的图线和线框在其他视图上的投影,并填空
现代工程图学习题集(第4版)
第5章 组合体视图
5-7.1 5-7.2 5-7.3 5-7.4 5-7.5 5-7.6 5-8.1 5-8.2 5-8.3 5-8.4 5-8.5 5-8.6 5-9.1 5-9.2 5-9.3 5-9.4 5-9.5 5-9.6 5-10.1 5-10.2 5-10.3 5-11.1 5-11.2 5-11.3 5-12.1 5-12.2 5-12.3
第5章 组合体视图
参考答案
现代工程图学习题集(第4版)
5-10.1根据轴测图在视图中标注尺寸。
第5章 组合体视图
参考答案
现代工程图学习题集(第4版)
第5章 组合体视图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、关于树的描述,________是错误的。 a 连通的无环图 b 有n-1条边的连通图 c 边数最少的连通图 d 有一个顶点入度为0,其他顶点入度为1
b 5、任何一个无向连通图的最小生成树_____。 a 只有一棵 b 有一棵或多棵 c 一定有多棵 d 可能不存在
d
二、判断题
1、对于无向图,顶点Vi的度是其邻接矩阵中第i行 (或第i列)的元素个数。( √ ) 2、一个带权图的最小生成树是唯一的。( ×) 3、对任何一个有向图,它的全部顶点一定可以排 成一个拓扑序列。( ×) 4、有向图g中的顶点v的出度等于其邻接矩阵第v行 中的l的个数。(√ )
三、填空题
n 1、有n个顶点的强连通有向图G至少有____条弧。
2、有n个顶点的无向图至多有____________边。 n*(n-1)/2 3、有n个选手参加的双循环赛中(即分主客场),总
n*(n-1) 共将进行________________场比赛。 n-1 4、n个顶点的连通图的生成树有_________条边。
(1)画出这个图; (2)以V1为出发点,对图进行深度优先搜索, 写出深度优先搜索访问序列。
1 2
v1 v2
2 5 4 3
4 ^ v4 5 v5 ^
2
4
5
3
以V1为出发点的深度优先搜索访问序列如下: 1-2-5-4-3
3、求下图的所有的拓扑序列。
第五章 图 习题
一、选择题
1、带权有向图G用邻接矩阵A存储,则顶点i 的 d 入度等于A中______. a 第i 行非0的元素之和 b 第i 列非0的元素之和 c 第i 行非0的元素个数 d 第i 列非0的元素个数
b 2、有n个顶点的连通无向图,最少有_____条 边。 a n b n-1 c 2n d 不确定 a 3、下面选项中,_____________不是图的存 储方法。 a 孩子兄弟链表 b 邻接链表 c 逆邻接链表 d 邻接矩阵
2 5
1 3 4
1
2 3
3 2 4
4 4 2
5 5 5
第五章 图 习题结束
5、设有向图G的邻接矩阵为A,如果图中不存在弧 <Vi,Vj>,则A[i,j]的值为_________。 0或∞
四、应用题
1、求下图的最小生成树。
1 3 2 5 4 4 3 3 3 4 2 4 1
2、已知一个无向图的邻接表为
1 2 3 4 5 v1 v2 v3 v4 v5 ^ 2 5 4 3 4 4 5 2 1 ^ ^ 1 ^
