阻尼比的取值
查阻尼比的标准

阻尼比的标准因不同的领域和应用而有所差异。
在土木、机械、航天等领域中,阻尼比指阻尼系数与临界阻尼系数之比,表达结构体标准化的阻尼大小。
它是一个无量纲的单位,用来描述结构在受激振后振动的衰减形式。
阻尼比可分为等于1、等于0、大于1、0~1之间4种,其中阻尼比=0即不考虑阻尼系统,而结构常见的阻尼比都在0~1之间。
对于小阻尼情况,阻尼比可以用定义来计算,即ζ=C/C0;也可以用ζ=C/(2mw)来计算,其中w为结构圆频率;还可以用ζ=ita/2来计算,ita 为材料损耗系数;另外,ζ=1/2/Qmax也是一个计算方法,其中Qmax为共振点放大比,无量纲。
在《建筑抗震设计规范》中,对不同类型的结构有不同的阻尼比规定。
例如,钢筋混凝土结构的阻尼比一般在0.03-0.08之间,而对于钢-混凝土结构则根据钢和混凝土对结构整体刚度的贡献率取为0.025-0.035。
以上的典型阻尼比的值即为结构动力学在等效秥滞模态阻尼中采用的阻尼比的值。
该阻尼比即为各阶振型的阻尼比的值。
阻尼比一般取值范围

阻尼比一般取值范围
阻尼比是指振动系统中阻尼和惯性的相对影响程度。
它通常用
希腊字母ζ(zeta)表示。
阻尼比的一般取值范围取决于振动系统
的特性和所处的工程领域。
在工程实践中,阻尼比的典型取值范围
可以分为以下几种情况:
1. 零阻尼(ζ=0),在没有阻尼的情况下,振动系统会产生持
续的振荡,这种情况在理论上较为理想,但在实际工程中很少出现。
2. 低阻尼(ζ<0.2),低阻尼条件下,振动系统的振荡衰减较慢,振幅变化较大。
这种情况通常出现在需要保持振动能量的系统中,如桥梁和建筑物的结构振动。
3. 中等阻尼(0.2<ζ<0.7),在这个范围内,系统的振动会逐
渐衰减,振幅逐渐减小。
这种情况在大多数工程应用中都是较为理
想的。
4. 高阻尼(ζ>0.7),高阻尼条件下,振动系统的振荡会迅速
衰减,振幅几乎不会有明显的变化。
这种情况在需要快速消除振动
能量的系统中比较常见。
总的来说,阻尼比的一般取值范围在0到1之间,具体取值取决于具体的工程需求和系统特性。
在工程设计中,合理选择阻尼比是非常重要的,它直接影响着振动系统的稳定性、能量耗散和响应特性。
特征方程阻尼比

特征方程阻尼比Damping ratio is a crucial concept in engineering and physics. It plays a significant role in controlling the behavior of systems and ensuring their stability. 阻尼比被广泛运用在振动和控制系统中,对系统的稳定性起着至关重要的作用。
The damping ratio is a measure of how fast the oscillations in a system decay after a disturbance. 阻尼比是一个衡量系统在遭受干扰后振荡衰减速度的指标。
It is used to quantify the level of damping present in a system and is crucial in understanding the dynamics of a system. 它用于量化系统中的阻尼水平,对于理解系统动力学至关重要。
The damping ratio is usual ly denoted by the Greek letter ζ (zeta) and is a dimensionless quantity that ranges from 0 to 1. 阻尼比通常用希腊字母ζ(zeta)表示,是一个无量纲的量,取值范围从0到1。
A damping ratio of 0 indicates no damping, meaning the system will oscillate indefinitely when disturbed. 阻尼比为0表示没有阻尼,也就是说当系统受到干扰时,它将无限振荡。
On the other hand, a damping ratio of 1 signifies a critically damped system, where the oscillations decay as quickly as possible without oscillating. 另一方面,阻尼比为1表示系统临界阻尼,振荡以尽可能快的速度衰减而不再振荡。
加速度放大系数理论解的分析过程(3质点)
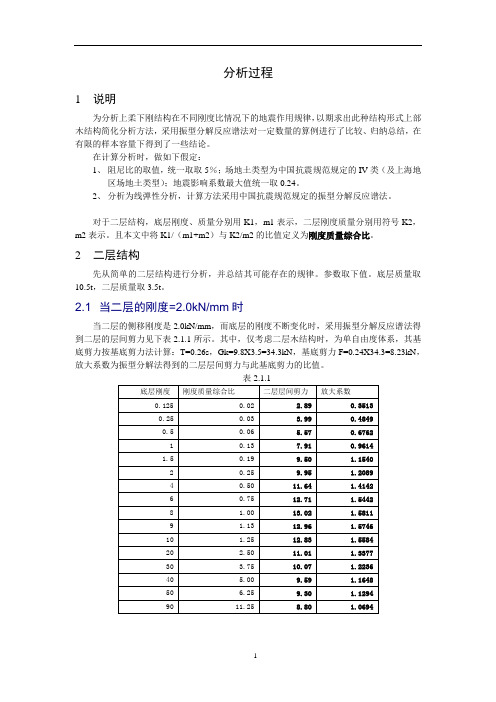
分析过程1说明为分析上柔下刚结构在不同刚度比情况下的地震作用规律,以期求出此种结构形式上部木结构简化分析方法,采用振型分解反应谱法对一定数量的算例进行了比较、归纳总结,在有限的样本容量下得到了一些结论。
在计算分析时,做如下假定:1、阻尼比的取值,统一取取5%;场地土类型为中国抗震规范规定的IV类(及上海地区场地土类型);地震影响系数最大值统一取0.24。
2、分析为线弹性分析,计算方法采用中国抗震规范规定的振型分解反应谱法。
对于二层结构,底层刚度、质量分别用K1,m1表示,二层刚度质量分别用符号K2,m2表示。
且本文中将K1/(m1+m2)与K2/m2的比值定义为刚度质量综合比。
2二层结构先从简单的二层结构进行分析,并总结其可能存在的规律。
参数取下值。
底层质量取10.5t,二层质量取3.5t。
2.1 当二层的刚度=2.0kN/mm时当二层的侧移刚度是2.0kN/mm,而底层的刚度不断变化时,采用振型分解反应谱法得到二层的层间剪力见下表2.1.1所示。
其中,仅考虑二层木结构时,为单自由度体系,其基底剪力按基底剪力法计算:T=0.26s,Gk=9.8X3.5=34.3kN,基底剪力F=0.24X34.3=8.23kN,放大系数为振型分解法得到的二层层间剪力与此基底剪力的比值。
由表1、表2可知,放大系数在底层刚度为8kN/mm、刚度比为4、刚度质量综合比为1.0时,产生最大值1.58。
底层刚度为20kN/mm、刚度比为10、刚度质量综合比为2.5时,放大系数为1.34。
2.2 当二层的刚度=4.0kN/mm、16 kN/mm时当二层的侧移刚度是4.0kN/mm时,而底层的刚度不断变化时,采用振型分解反应谱法得到二层的层间剪力见下表2.2.1所示。
其中,仅考虑二层木结构时,为单自由度体系,其基底剪力按基底剪力法计算:T=0.19s,Gk=9.8X3.5=34.3kN,基底剪力F=0.24X34.3=8.23kN,放大系数为振型分解法得到的二层层间剪力与此基底剪力的比值。
阻尼比定义

阻尼比定义
阻尼比是一个物理量,通常用来描述振动系统的阻尼程度。
它定义为振动系统的阻尼系数与临界阻尼系数的比值。
临界阻尼系数是指当振动系统的阻尼系数等于等效质量与弹性系数的平方根时,系统的阻尼被称为临界阻尼。
在这种情况下,振动系统的振幅会最快地衰减到零。
阻尼比可以是小于1的任何值,表示系统的阻尼程度低于临界阻尼,或者是大于1的任何值,表示系统的阻尼程度高于临界阻尼。
阻尼比等于1时,表示系统处于临界阻尼状态。
在实际应用中,阻尼比对于振动系统的设计和分析非常重要。
较小的阻尼比通常会导致系统在振动中保持较高的能量,而较高的阻尼比则可以减少系统的振动幅度和能量损失。
根据具体的应用场景和要求,合适的阻尼比可以通过系统参数设计和控制手段来实现。
- 1 -。
风荷载计算阻尼比

风荷载计算阻尼比
风荷载计算中的阻尼比通常表示为ξ(ksi),它是结构系统的
阻尼与临界阻尼(即无阻尼系统的阻尼)之比。
阻尼比的取值范围通常为0到1之间。
通常情况下,阻尼比的大小会对结构的应力响应、位移响应和稳定性等方面产生影响。
当阻尼比为0时,结构处于无阻尼状态,这意味着没有任何阻尼力可以减缓结构的振动,其响应会保持振幅恒定,并且可能产生共振。
当阻尼比为1时,结构处于临界阻尼状态,这意味着阻尼力与反弹力之间的比例为1:1,这是结构受到最大减振作用的状态。
在实际的工程设计中,根据结构的特点和工程要求,通常会选择合适的阻尼比来平衡结构的减振效果和经济性。
常用的阻尼比范围通常为0.02到0.1之间。
需要注意的是,风荷载计算中阻尼比的取值通常是经验性的,并且不同的计算方法和规范可能会有不同的建议值。
因此,在具体的工程设计中,需要参考当地的设计规范和准则,并结合结构的特点和工程要求来确定适当的阻尼比值。
模态阻尼和阻尼损耗因子

模态阻尼和阻尼损耗因子引言:在物理学和工程领域中,阻尼是一个重要的概念,它描述了系统在受到外界干扰时能够减少振动或衰减的能力。
模态阻尼和阻尼损耗因子是两个与阻尼相关的重要概念,它们在结构分析和振动控制中具有重要的意义。
本文将对模态阻尼和阻尼损耗因子进行详细的介绍和分析。
一、模态阻尼的概念模态阻尼是指结构振动中的能量损耗程度。
当结构受到外力激励时,会发生振动,而模态阻尼描述了这种振动在时间上的衰减过程。
模态阻尼通常用一个无量纲参数来表示,称为阻尼比。
阻尼比越大,说明结构的能量损耗越快,振动衰减得越迅速。
阻尼比的取值范围为0到1之间,分别对应无阻尼和临界阻尼。
二、阻尼损耗因子的概念阻尼损耗因子是用来描述材料或结构的阻尼能力的一个参数。
它是指当结构振动时,由于结构内部摩擦和材料吸能等原因导致的能量衰减程度。
阻尼损耗因子是一个无量纲参数,用ξ表示。
阻尼损耗因子越大,说明结构的能量损耗越快,振动衰减得越迅速。
阻尼损耗因子的取值范围为0到正无穷,分别对应无阻尼和无穷大阻尼。
三、模态阻尼和阻尼损耗因子的关系模态阻尼和阻尼损耗因子是描述阻尼特性的两个重要参数,它们之间存在一定的关系。
在一般情况下,模态阻尼和阻尼损耗因子之间的关系可以用以下公式表示:ξ = 2πζ其中,ξ为阻尼损耗因子,ζ为模态阻尼。
四、模态阻尼和阻尼损耗因子的应用模态阻尼和阻尼损耗因子在结构分析和振动控制中有广泛的应用。
在结构分析中,通过计算模态阻尼和阻尼损耗因子,可以评估结构的稳定性和安全性。
在振动控制中,通过增加结构的阻尼能力,可以减小结构的振动响应,提高结构的抗震能力。
结论:模态阻尼和阻尼损耗因子是描述结构阻尼特性的两个重要参数。
模态阻尼描述了结构振动的能量损耗程度,阻尼损耗因子描述了结构的阻尼能力。
它们之间存在一定的关系,可以通过公式进行转化。
模态阻尼和阻尼损耗因子在结构分析和振动控制中具有重要的应用价值,可以评估结构的稳定性和抗震能力。
测试橡胶件阻尼比方法

测试橡胶件阻尼比方法-概述说明以及解释1.引言1.1 概述橡胶件阻尼比是描述橡胶材料在振动过程中的能量耗散能力的重要指标,它对于橡胶材料的应用和设计具有重要的指导意义。
随着工程和科学领域对高性能橡胶件的需求日益增加,测试橡胶件阻尼比的方法也得到了广泛关注。
本文旨在介绍几种常用的测试橡胶件阻尼比的方法,并探讨其可行性和适用范围。
在背景介绍部分,将详细阐述橡胶件阻尼比的概念和定义,以及其在工程领域中的重要性。
针对目前测试橡胶件阻尼比的方法,本文将分别介绍方法1和方法2,并对它们的优缺点进行比较和讨论。
通过实验结果分析部分,将对测试结果进行详细解读和分析,探索不同测试方法的可靠性和准确性。
结果的意义与启示部分将探讨橡胶件阻尼比对橡胶材料性能和结构设计的影响,以及其在降低噪声和振动方面的应用潜力。
讨论与比较部分将对不同方法的测试结果进行比较,并分析其适用范围和局限性。
最后,我们将在结论部分总结本文的研究意义和贡献,同时也会指出本研究的局限性,并对未来的研究方向进行展望。
通过本文的研究,我们希望为橡胶件阻尼比的测试提供一些借鉴和参考,同时也为橡胶材料的应用和设计提供一些指导和思路。
我们相信,通过不断完善测试方法和扩大应用范围,橡胶件阻尼比的研究将为工程和科学领域的发展做出积极贡献。
1.2文章结构文章结构部分的内容可以按照以下方式进行编写:本文共分为以下几个部分。
首先,在引言部分,将对本文的概述进行介绍,包括研究领域的背景和研究的意义,以及文章的结构和目的。
接下来,正文部分将详细介绍橡胶件阻尼比方法的测试方法。
首先,在背景介绍中,将对橡胶件阻尼比的定义进行阐述,以及相关研究的现状和问题。
然后,将介绍两种测试橡胶件阻尼比的方法,包括方法1和方法2,分别对其原理、步骤和注意事项进行说明。
在结果与讨论部分,将对实验结果进行分析,探讨结果的意义和启示,并进行讨论和比较。
最后,在结论部分,将总结本文的研究成果和贡献,同时指出研究的局限性,并对未来的研究方向进行展望。
混凝土结构阻尼比取值

混凝土结构阻尼比取值
混凝土结构阻尼比是指结构在地震作用下的阻尼值与结构动力
特性的比值。
混凝土结构的阻尼比取值是影响结构抗震性能的重要因素之一,通常需要根据具体结构的情况进行评估和确定。
混凝土结构的阻尼比与许多因素有关,如结构形式、材料性质、结构质量等。
一般来说,混凝土结构的阻尼比应该在5%~10%之间,过高或过低都会对结构的抗震性能造成不利影响。
在实际工程设计中,混凝土结构的阻尼比通常是通过结构动力分析来确定的。
结构动力分析可以采用有限元方法、模态分析法等多种方法进行,通过对结构在地震作用下的动力响应进行分析,可以得到结构的阻尼比。
在评估混凝土结构的阻尼比时,还需要考虑结构的抗震等级、地震烈度、结构设计参数等因素,以确定合适的阻尼比取值,从而确保结构的抗震安全性和可靠性。
- 1 -。
阻尼比的概念

阻尼就是使自由振动衰减的各种摩擦和其他阻碍作用。
阻尼比在土木、机械、航天等领域是结构动力学的一个重要概念,指阻尼系数与临界阻尼系数之比,表达结构体标准化的阻尼大小。
阻尼比是无单位量纲,表示了结构在受激振后振动的衰减形式。
可分为等于1,等于0, 大于1,0~1之间4种,阻尼比=0即不考虑阻尼系统,结构常见的阻尼比都在0~1之间.ζ <1的单自由度系统自由振动下的位移 u(t) = exp(-ζwn t)*A cos (wd t - Φ ),其中wn 是结构的固有频率,wd = sqrt(1-ζ^2) ,Φ为相位移.Φ和常数A由初始条件决定.阻尼比的来源及阻尼比影响因素主要针对土木、机械、航天等领域的阻尼比定义来讲解。
阻尼比用于表达结构阻尼的大小,是结构的动力特性之一,是描述结构在振动过程中某种能量耗散的术语,引起结构能量耗散的因素(或称之为影响结构阻尼比的因素)很多,主要有[1](1)材料阻尼、这是能量耗散的主要原因。
(2)周围介质对振动的阻尼。
(3)节点、支座联接处的阻尼(4)通过支座基础散失一部分能量。
阻尼比的计算对于小阻尼情况[2]:1) 阻尼比可以用定义来计算,及ksai=C/C0;2) ksai=C/(2*m*w) % w为结构圆频率3) ksai=ita/2 % ita 为材料损耗系数4) ksai=1/2/Qmax % Qmax 为共振点放大比,无量纲5) ksai=delta/2/pi % delta是对数衰减率,无量纲6) ksai=Ed/W/2/pi % 损耗能与机械能之比再除以2pi阻尼比的取值对结构基本处于弹性状态的的情况,各国都根据本国的实测数据并参考别国的资料,按结构类型和材料分类给出了共一般分析采用的所谓典型阻尼比的值。
综合各国情况,钢结构的阻尼比一般在0.01-0.02之间(虾肝蚁胆:单层钢结构厂房可取0.05),钢筋混凝土结构的阻尼比一般在0.03-0.08之间。
阻尼比的条文规定

《高规11.3.5》、混合结构在多遇地震作用下的阻尼比可取为0.04。
风荷载作用下楼层位移验算和构件设计时,阻尼比可取为0.02~0.04。
《附录A》,人行走作用力及楼盖结构阻尼力
住宅/办公/教堂0.02~0.05
商场0.02
室内人行天桥0.01~0.02
室外人行天桥0.01
《荷载规范8.4.4》
高耸有,
《烟囱规范》:
此外,
《抗规》的5.1.5,见规范
9.2.5,单层厂房的阻尼比,可依据屋盖和围护墙的类型,取0.045~0.05。
附录G.1.4中1,钢支撑-混凝土框架结构的抗震计算,结构的阻尼比不应大于0.045,也可按混凝土框架部分和钢支撑部分在结构总变形能所占的比例折算为等效阻尼比。
《砼规》第11.8.3条,预应力混凝土框架结构的阻尼比宜取0.03,。
浅谈建筑结构的阻尼与阻尼比

浅谈建筑结构的阻尼与阻尼比浅谈建筑结构的阻尼与阻尼比摘要:阻尼是建筑结构进行动力分析一个重要的参数。
文章首先简要介绍阻尼的实质、表达方法及其对反应谱的影响,重点对空间结构弹性分析时的阻尼比取值进行讨论,并给出了阻尼比的建议值,可供设计分析参考。
关键词:阻尼;阻尼比;空间结构;反应谱1 阻尼1.1 阻尼的实质阻尼是反映结构体系振动过程中能量耗散的特征参数。
实际结构的振动耗能是多方面的,具体形式相当复杂,且耗能不具有构件尺寸、结构质量、刚度等有明确的、直接的测量手段和相应的分析方法,使得阻尼问题难以采用精细的理论分析方法。
阻尼的表达方法主要分为两大类:(1)粘滞阻尼,即假定阻尼力与速度成正比,无论对简谐振动还是非简谐振动得到的振动方程均是线性方程。
(2)滞回阻尼,即假定应力应变间存在一相位差,从而振动一周有耗能发生,其特点是可以得到不随频率而改变的振型阻尼比。
1.2 阻尼的表达方法传统上,总是将系统假定为比例阻尼来处理,应用最为广泛有:(1)Rayleigh 阻尼C = αM + βK;(2)Clough 广义阻尼C =ΣCb = MΣab ( M-1 K)b,(-∞<b<∞)。
其中M、K分别为系统的质量与刚度矩阵,α、β分别为质量与刚度比例系数,Cb=abM(M-1K)b,ab为系数,以上两种阻尼均只能描述比例阻尼。
然而,实际结构均为非比例阻尼。
自70 年代以来,研究者对如何处理非比例阻尼问题做了许多探索,提出了各种方法,如等效阻尼法、拟力实模态叠加法、非比例阻尼分析法和滞变阻尼法等。
但他们都存在共同问题:所获得的阻尼矩阵无明确的物理意义,也不存在带状稀疏特性,对工程应用十分不方便。
1992 年,美国国家地震研究中心Liang博士等人提出了一种阻尼矩阵的一般表达方式,该表达能导出复模态,即Cs = β0I+β1M +β2K+β3A。
其中下标S 表示近似的阻尼矩阵C,I 为单位矩阵,A 为M、K的某种组合。
阻尼比与固有频率的关系

阻尼比与固有频率的关系介绍阻尼比(damping ratio)是描述振动系统中阻尼效应大小的一个参数,它与固有频率(natural frequency)之间存在着密切的关系。
本文将就阻尼比与固有频率之间的关系展开探讨,由浅入深地介绍相关概念,并分析其物理机制和数学描述。
什么是阻尼比和固有频率?在开始讨论阻尼比和固有频率之间的关系之前,我们先来了解一下这两个概念的含义。
阻尼比阻尼比是振动系统中的一个重要参数,它描述了振动系统在受到外界干扰或能量耗散时的阻尼效应大小。
阻尼比通常用符号ζ(zeta)来表示,取值范围为0到1。
当阻尼比为0时,振动系统是无阻尼振动;当阻尼比为1时,振动系统是临界阻尼;当阻尼比大于1时,振动系统是过阻尼;当阻尼比小于1时,振动系统是欠阻尼。
固有频率固有频率是指振动系统在无外界干扰和阻尼的情况下,自发地以一定频率振动的频率。
固有频率通常用符号ω(omega)来表示,单位是弧度每秒。
固有频率是振动系统的本征特性,也是振动系统的固有属性。
阻尼比与固有频率的关系阻尼比与固有频率之间存在着一定的关系,它们的变化会相互影响,并决定了振动系统的行为。
阻尼比对固有频率的影响当阻尼比增大时,阻尼效应增强,振动系统的振幅逐渐减小,并且振动系统的固有频率也会有所改变。
具体来说,阻尼比增大会导致固有频率减小。
这是因为阻尼比的增大意味着系统在振动过程中受到的耗散力增大,能量的损失增加。
振动系统的固有频率是由系统的质量和刚度决定的,而阻尼比的增大会引入额外的耗散,并减小振动系统的有效刚度。
因此,阻尼比增大会导致固有频率的降低。
固有频率对阻尼比的影响相反地,固有频率也会对阻尼比产生影响。
固有频率的变化会改变振动系统的特性,进而影响到阻尼比的大小。
具体来说,当固有频率增大时,振动系统的阻尼比减小。
这是因为固有频率的增大意味着振动系统的刚度增大或质量减小,这使得振动系统对阻尼的依赖程度减小,从而导致阻尼比的减小。
阻尼 阻尼系数 阻尼比

阻尼阻尼系数阻尼比
阻尼是指物体在振动或运动过程中受到的阻力或阻碍,阻碍物体继续振动或运动的力量。
阻尼能使振动或运动逐渐减弱并停止。
阻尼系数是用来描述阻尼效果大小的物理量。
它表示单位时间内物体振动或运动的能量损失或减弱的比例。
阻尼系数通常用字母“c”表示。
阻尼比是比较阻尼系数和临界阻尼系数的大小关系的比值。
临界阻尼系数是指使物体振动停止所需的最小阻尼系数。
如果阻尼比小于1,则物体会发生过阻尼,振动或运动相对较慢;如果阻尼比等于1,则物体发生临界阻尼,振动或运动停止所需时间最短;如果阻尼比大于1,则物体发生欠阻尼,振动或运动相对较快。
阻尼比范围

阻尼比范围阻尼比是一个重要的概念,用于描述振动系统的阻力大小。
在工程中,阻尼比的范围非常重要。
在本文中,我们将探讨阻尼比的范围,以及这个范围对工程设计和性能的影响。
阻尼比是一个无量纲的物理量,定义为振动系统的阻力与其临界阻力的比值。
临界阻力是系统固有频率下的阻力。
当阻尼比为零时,振动系统没有任何阻力,它是一个无阻尼谐振态。
当阻尼比为一时,系统的阻力等于其临界阻力,达到临界阻尼状态。
当阻尼比大于一时,振动系统变成了过阻尼系统。
大部分情况下,我们关心的是振动系统在阻尼比小于一时的行为,因为它们更接近无阻尼的谐振态。
事实上,工程系统往往被设计成接近无阻尼谐振态的模式,这是因为这种振动状态能够产生最大的能量传输和最高的性能。
在实际情况中,我们会面对振动系统在不同阻尼比下的行为。
当阻尼比很小,系统处于无阻尼谐振状态,能量在系统内无限传递,系统会发生共振,这对工程系统来说往往是不利的。
在阻尼比逐渐增加时,振动系统的能量逐渐减小,系统的波形变得更加平缓,响应时间变得更长,这种情况对于多数系统来说是极其重要的。
然而,当阻尼比变得过大时,系统的反应速度会变得非常缓慢,反应时间增加,系统性能也会显著下降,这对于某些工程来说也是不利的。
因此,阻尼比的范围对于工程系统的设计和性能至关重要。
如果阻尼比过大,系统的灵敏度会下降,导致系统不能快速响应。
如果阻尼比过小,系统可能会失控,发生共振,并在远离设计过程的情况下发生损坏。
在工程中,我们往往使用数值模拟和试验来测量阻尼比的范围,并确定系统的最佳设计。
经验表明,通常将阻尼比限定在0.1到0.5之间,可以达到最佳的系统性能。
当阻尼比过高或过低时,系统的性能和稳定性都会受到影响。
总之,阻尼比是一个重要的工程参数,它能够影响系统的性能和稳定性。
在工程设计中,阻尼比需要被正确地估计和控制,以确保系统能够达到最佳性能。
导线 阻尼比

导线阻尼比
导线的阻尼比是指传输信号时,导线内部电流振荡的能量损失与储存能量的比值。
阻尼比可用以下公式表示:阻尼比(Damping Ratio)= (电流振荡的能量损失) / (储存能量)
阻尼比反映了导线内能量损失的程度。
具体来说,当阻尼比为0时,没有能量耗散,电流将以振荡的方式无限制地在导线中流动;当阻尼比为1时,电流将被完全吸收和耗散,不会发生振荡。
在实际应用中,通常会使用具有合适阻尼比的电路来确保信号的稳定传输。
阻尼比的值取决于电路的电阻、电感和电容等参数。
较低的阻尼比可能导致振荡信号失真或干扰,而较高的阻尼比可能导致信号衰减。
因此,根据具体的电路要求和信号特性,需要选择适当的阻尼比值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并非是钢结构都取0.02.要视结构形式而定.上海浦东国际机场工程对该航站楼屋盖钢结构模型作过地震振动台试验,得出结果,取0.035与实际符合较好.个人认为大跨空间钢结构应取0.035为宜;多高层钢结构应取0.02或0.035合适.建筑结构抗震规范 GB 50011-2001的8.2.2条也有说明,全文如下:钢结构在多遇地震下的阻尼比,对不超过12层的钢结构可采用0.035,对超过12层的钢结构可采用0.02;在罕遇地震下的分析,阻尼比可采用0.05.
所以,钢结构的阻尼系数为多少不仅与其工作状态有关,还与结构分析时使用的模型有关。 概括起来说, 如果材料采用线性模型,构件工作在弹性阶段,阻尼系数取0.02~0.05,当应力较小时取偏小值,应力较大时取偏大值。 采用线性模型,构件工作在弹塑性阶段,阻尼系数取0.1~0.2,进入塑性化程度较浅时取小值,进入塑性化程度较深时取大值。 如果材料采用非线性模型,阻尼系数取0.01。
阿修罗 发表于 2004-6-14 19:36
具体取多少值主要判别条件应该是看结构所处的阶段,对高层建筑钢结构在弹性阶段,当房屋层数在12一下时取0.035,在12层以上时取0.020,在弹塑性阶段取0.05。对钢混组合结构取0.035。 在日本道路公团2005年版的设计要领中,关于阻尼做如下规定: 对于直接承受动荷载的桥梁上部结构,一般不希望其工作在弹塑性阶段,阻尼系数取0.02~0.03。 对于在大地震时可能工作在弹塑性阶段的钢下部结构,当其在弹性域范围内工作时,阻尼系数取0.03~0.05, 当其工作在弹塑性域,且采用等价线性化模型解析时,阻尼系数取0.1~0.2, 需要特别注意的是:采用非线性模型解析时,由于在恢复力模型中已经采用了非线性,材料非线性引起的能量耗散已自动被考虑,这时的阻尼系数为0.01。
