利用MATLAB实现Dijkstra算法
最短路dijkstra算法Matlab程序

function [c0,c,path0,path]=dijkstra(s,t,C,flag)% Use the Dijkstra's algorithm to find the shortest path from% s to t and can also find the shortest path between s and all% the other points.% Reference: Graph Theory with Applications by J. A. Bondy and% U. S. R. Murty.% Input -- s is the starting point and also is the point s.% -- t is the given terminal point and is the point t.% -- C \in R^{n \times n}is the cost matrix, where% C(i,j)>=0 is the cost from point i to point j.% If there is no direct connection between point i and% j, C(i,j)=inf.% -- flag: if flag=1, the function just reports the% shortest path between s and t; if flag~=1, the% function reports the shortest path between s and t,% and the shortest paths between s and other points.% Output -- c0 is the minimal cost from s to t.% -- path0 denotes the shortest path form s to t.% -- c \in R{1\times n} in which the element i is the% minimal cost from s to point i.% -- path \in R^{n \times n} in which the row i denotes% the shortest path from s to point i.% Copyright by MingHua Xu(徐明华), Changhzou University, 27 Jan. 2014. s=floor(s);t=floor(t);n=size(C,1);if s<1 || t < 1 || s > n || t > nerror(' The starting point and the terminal point exceeds the valid range');endif t==sdisp('The starting point and the terminal point are the same points');endlabel=ones(1,n)*inf;label(s)=0;S=[s];Sbar=[1:s-1,s+1:n];c0=0;path=zeros(n,n);path(:,1)=s;c=ones(1,n)*inf;parent=zeros(1,n);i=1; % number of points in point set S.while i<n% for each point in Sbar, replace label(Sbar(j)) by% min(label(Sbar(j)),label(S(k))+C(S(k),Sbar(j)))for j=1:n-ifor k=1:iif label(Sbar(j)) > label(S(k))+C(S(k),Sbar(j))label(Sbar(j))=label(S(k))+C(S(k),Sbar(j));parent(Sbar(j))=S(k);endendend% Find the minmal label(j), j \in Sbar.temp=label(Sbar(1));son=1;for j=2:n-iif label(Sbar(j))< temptemp=label(Sbar(j));son=j;endend% update the point set S and SbarS=[S,Sbar(son)];Sbar=[Sbar(1:son-1),Sbar(son+1:n-i)];i=i+1;% if flag==1, just output the shortest path between s and t.if flag==1 && S(i)==tson=t;temp_path=[son];if son~=swhile parent(son)~=sson=parent(son);temp_path=[temp_path,son];endtemp_path=[temp_path,s];endtemp_path=fliplr(temp_path);m=size(temp_path,2);path0(1:m)=temp_path;c_temp=0;for j=1:m-1c_temp=c_temp+C(temp_path(j),temp_path(j+1));endc0=c_temp;path(t,1:m)=path0;c(t)=c0;returnendend% Form the output resultsfor i=1:nson=i;temp_path=[son];if son~=swhile parent(son)~=sson=parent(son);temp_path=[temp_path,son];endtemp_path=[temp_path,s];endtemp_path=fliplr(temp_path);m=size(temp_path,2);path(i,1:m)=temp_path;c_temp=0;for j=1:m-1c_temp=c_temp+C(temp_path(j),temp_path(j+1));endc(i)=c_temp;c0=c(t);path0=path(t,:);endreturn。
Dijkstra、Floyd算法Matlab_Lingo实现

Dijkstra算法Matlab实现。
%求一个点到其他各点的最短路径function [min,path]=dijkstra(w,start,terminal)%W是邻接矩阵%start是起始点Array %terminal是终止点%min是最短路径长度%path是最短路径n=size(w,1);label(start)=0;f(start)=start;for i=1:nif i~=startlabel(i)=inf;endends(1)=start;u=start;while length(s)<nfor i=1:nins=0;forif i==s(j)ins=1;endendif ins==0v=i;if label(v)>(label(u)+w(u,v))label(v)=(label(u)+w(u,v));f(v)=u;endendendv1=0;k=inf;for i=1:nins=0;for j=1:length(s)if i==s(j)ins=1;endend-if ins==0v=i;if k>label(v)k=label(v);v1=v;endendends(length(s)+1)=v1;u=v1;endmin=label(terminal);path(1)=terminal;i=1;while path(i)~=startpath(i+1)=f(path(i));i=i+1 ;endpath(i)=start;L=length(path);path=path(L:-1:1);Floyd算法:matlab程序:%floyd算法,function [D,path,min1,path1]=floyd(a,start,terminal)%a是邻接矩阵%start是起始点%terminal是终止点%D是最小权值表D=a;n=size(D,1);path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)-D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendif nargin==3min1=D(start,terminal);m(1)=start;i=1;path1=[ ];while path(m(i),terminal)~=terminalk=i+1;m(k)=path(m(i),terminal);i=i+1;endm(i+1)=terminal;path1=m;end1 6 5 5 5 66 2 3 4 4 65 2 3 4 5 45 2 3 4 5 61 4 3 4 5 11 2 4 4 1 6Floyd算法:Lingo程序:!用LINGO11.0编写的FLOYD算法如下;model:sets:nodes/c1..c6/;link(nodes,nodes):w,path; !path标志最短路径上走过的顶点;endsetsdata:path=0;w=0;@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):-@format(w(i,j),' 10.0f')),@newline(1));@text(mydata1.txt)=@write(@newline(1));@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),' 10.0f')),@newline(1));enddatacalc:w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;w(2,3)=15;w(2,4)=20;w(2,6)=25;w(3,4)=10;w(3,5)=20;w(4,5)=10;w(4,6)=25;w(5,6)=55;@for(link(i,j):w(i,j)=w(i,j)+w(j,i));@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j)));@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));w(i,j)=tm)));endcalcend无向图的最短路问题Lingomodel:sets:cities/1..5/;roads(cities,cities):w,x;endsetsdata:w=0;enddatacalc:w(1,2)=41;w(1,3)=59;w(1,4)=189;w(1,5)=81;w(2,3)=27;w(2,4)=238;w(2,5)=94;w(3,4)=212;w(3,5)=89;w(4,5)=171;@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));endcalcn=@size(cities); !城市的个数;min=@sum(roads:w*x);@for(cities(i)|i #ne#1 #and# i #ne#n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));@sum(cities(j):x(1,j))=1;-@sum(cities(j):x(j,1))=0; !不能回到顶点1;@sum(cities(j):x(j,n))=1;@for(roads:@bin(x));endLingo编的sets:dian/a b1 b2 c1 c2 c3 d/:;link(dian,dian)/a,b1 a,b2 b1,c1 b1,c2 b1,c3 b2,c1 b2,c2 b2,c3 c1,d c2,d c3,d/:x,w;endsetsdata:w=2 4 3 3 1 2 3 1 1 3 4;enddatamin=@sum(link:w*x);@for(link:@bin(x));n=@size(dian);@sum(link(i,j)|i#eq#1:x(i,j))=1;@sum(link(j,i)|i#eq#n:x(j,i))=1;@for(dian(k)|k#ne#1#and#k#ne#n:@sum(link(i,k):x(i,k))=@sum(link(k,i):x(k,i)));- sets:dian/1..5/:level; !level(i)表示点i的水平,用来防止生产圈;link(dian,dian):d,x;endsetsdata:d=0 41 59 189 8141 0 27 238 9459 27 0 212 89189 238 212 0 17181 94 89 171 0;enddatan=@size(dian);min=@sum(link(i,j)|i#ne#j:d(i,j)*x(i,j));@sum(dian(j)|j#gt#1:x(1,j))>1;@for(dian(i)|i#gt#1:@sum(dian(j)|j#ne#i:x(j,i))=1);@for(dian(i)|i#gt#1:@for(dian(j)|j#ne#i#and#j#gt#1:level(j)>level(i)+x(i,j)-(n-2)*(1-x(i,j))+(n-3)*x(j, i)));@for(dian(i)|i#gt#1:level(i)<n-1-(n-2)*x(1,i));@for(dian(i)|i#gt#1:@bnd(1,level(i),100000));@for(link:@bin(x));。
matlab计算两个区域的最小距离函数

一、概述MATLAB是一种流行的数学软件,用于进行数值计算和数据可视化。
在许多科学和工程领域,MATLAB都被广泛地应用。
其中一个非常有用的功能就是计算两个区域的最小距离函数。
这个功能在图像处理、计算几何学和机器人学等领域都有着广泛的应用。
二、MATLAB中的最小距离函数在MATLAB中,可以使用内置函数或编写自定义函数来计算两个区域的最小距离。
下面我们将介绍MATLAB中计算最小距离的几种常见方法。
1. 使用内置函数MATLAB提供了一些内置函数来计算两个区域之间的最小距离,比如pdist2函数和bwdist函数。
pdist2函数可以用来计算两个不同数据集之间的距离,而bwdist函数则可以计算二进制图像中每个像素到最近的非零像素的距离。
这两个函数都是非常高效、准确的计算最小距离的工具。
2. 编写自定义函数除了使用内置函数,我们还可以编写自定义函数来计算两个区域的最小距离。
这种方法可以根据具体的问题需求进行灵活的定制,但是需要一定的编程能力。
通常可以使用广度优先搜索、最短路径算法或者动态规划等方法来编写自定义函数。
三、最小距离函数的应用最小距离函数在许多领域都有着重要的应用。
下面将介绍一些常见的应用场景。
1. 图像处理在图像处理中,最小距离函数可以用来计算图像中不同物体或区域之间的距离。
比如在医学图像中,可以用最小距离函数来计算肿瘤与周围组织的距离,以辅助医生进行诊断。
2. 计算几何学在计算几何学中,最小距离函数可以用来计算两个几何体之间的最短距离,比如计算两个多边形之间的最小距离。
这对于设计和制造工程师来说是非常重要的。
3. 机器人学在机器人学中,最小距离函数可以用来规划机器人的路径,以避免障碍物或与其他机器人发生碰撞。
这对于自动驾驶车辆和工业机器人来说有着重要的意义。
四、总结在MATLAB中,计算两个区域的最小距离函数是非常有用的功能,它可以用来解决许多现实生活中的问题。
通过内置函数或编写自定义函数,我们可以轻松地实现这一功能。
matlab图论程序算法大全

图论算法matlab实现求最小费用最大流算法的 MATLAB 程序代码如下:n=5;C=[0 15 16 0 00 0 0 13 140 11 0 17 00 0 0 0 80 0 0 0 0]; %弧容量b=[0 4 1 0 00 0 0 6 10 2 0 3 00 0 0 0 20 0 0 0 0]; %弧上单位流量的费用wf=0;wf0=Inf; %wf 表示最大流量, wf0 表示预定的流量值for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流while(1)for(i=1:n)for(j=1:n)if(j~=i)a(i,j)=Inf;end;end;end%构造有向赋权图for(i=1:n)for(j=1:n)if(C(i,j)>0&f(i,j)==0)a(i,j)=b(i,j); elseif(C(i,j)>0&f(i,j)==C(i,j))a(j,i)=-b(i,j);elseif(C(i,j)>0)a(i,j)=b(i,j);a(j,i)=-b(i,j);end;end;end for(i=2:n)p(i)=Inf;s(i)=i;end %用Ford 算法求最短路, 赋初值for(k=1:n)pd=1; %求有向赋权图中vs 到vt 的最短路for(i=2:n)for(j=1:n)if(p(i)>p(j)+a(j,i))p(i)=p(j)+a(j,i);s( i)=j;pd=0;end;end;endif(pd)break;end;end %求最短路的Ford 算法结束if(p(n)==Inf)break;end %不存在vs 到vt 的最短路, 算法终止. 注意在求最小费用最大流时构造有向赋权图中不会含负权回路, 所以不会出现k=ndvt=Inf;t=n; %进入调整过程, dvt 表示调整量while(1) %计算调整量if(a(s(t),t)>0)dvtt=C(s(t),t)-f(s(t),t); %前向弧调整量elseif(a(s(t),t)<0)dvtt=f(t,s(t));end %后向弧调整量if(dvt>dvtt)dvt=dvtt;endif(s(t)==1)break;end %当t 的标号为vs 时, 终止计算调整量t=s(t);end %继续调整前一段弧上的流fpd=0;if(wf+dvt>=wf0)dvt=wf0-wf;pd=1;end%如果最大流量大于或等于预定的流量值t=n;while(1) %调整过程if(a(s(t),t)>0)f(s(t),t)=f(s(t),t)+dvt; %前向弧调整elseif(a(s(t),t)<0)f(t,s(t))=f(t,s(t))-dvt;end %后向弧调整if(s(t)==1)break;end %当t 的标号为vs 时, 终止调整过程t=s(t);endif(pd)break;end%如果最大流量达到预定的流量值wf=0; for(j=1:n)wf=wf+f(1,j);end;end %计算最大流量zwf=0;for(i=1:n)for(j=1:n)zwf=zwf+b(i,j)*f(i,j);end;end%计算最小费用f %显示最小费用最大流图 6-22wf %显示最小费用最大流量zwf %显示最小费用, 程序结束__Kruskal 避圈法:Kruskal 避圈法的MATLAB 程序代码如下:n=8;A=[0 2 8 1 0 0 0 02 0 6 0 1 0 0 08 6 0 7 5 1 2 01 0 7 0 0 0 9 00 1 5 0 0 3 0 80 0 1 0 3 0 4 60 0 2 9 0 4 0 30 0 0 0 8 6 3 0];k=1; %记录A中不同正数的个数for(i=1:n-1)for(j=i+1:n) %此循环是查找A中所有不同的正数if(A(i,j)>0)x(k)=A(i,j); %数组x 记录A中不同的正数kk=1; %临时变量for(s=1:k-1)if(x(k)==x(s))kk=0;break;end;end %排除相同的正数k=k+kk;end;end;endk=k-1 %显示A中所有不同正数的个数for(i=1:k-1)for(j=i+1:k) %将x 中不同的正数从小到大排序if(x(j)<x(i))xx=x(j);x(j)=x(i);x(i)=xx;end;end;endT(n,n)=0; %将矩阵T 中所有的元素赋值为0q=0; %记录加入到树T 中的边数for(s=1:k)if(q==n)break;end %获得最小生成树T, 算法终止for(i=1:n-1)for(j=i+1:n)if(A(i,j)==x(s))T(i,j)=x(s);T(j,i)=x(s); %加入边到树T 中TT=T; %临时记录Twhile(1)pd=1; %砍掉TT 中所有的树枝for(y=1:n)kk=0;for(z=1:n)if(TT(y,z)>0)kk=kk+1;zz=z;end;end %寻找TT 中的树枝if(kk==1)TT(y,zz)=0;TT(zz,y)=0;pd=0;end;end %砍掉TT 中的树枝if(pd)break;end;end %已砍掉了TT 中所有的树枝pd=0; %判断TT 中是否有圈for(y=1:n-1)for(z=y+1:n)if(TT(y,z)>0)pd=1;break;end;end;end if(pd)T(i,j)=0;T(j,i)=0; %假如TT 中有圈else q=q+1;end;end;end;end;endT %显示近似最小生成树T, 程序结束用Warshall-Floyd 算法求任意两点间的最短路.n=8;A=[0 2 8 1 Inf Inf Inf Inf2 0 6 Inf 1 Inf Inf Inf8 6 0 7 5 1 2 Inf1 Inf 7 0 Inf Inf 9 Inf Inf 1 5 Inf 0 3 Inf 8 Inf Inf 1 Inf 3 0 4 6Inf Inf 2 9 Inf 4 0 3Inf Inf Inf Inf 8 6 3 0]; % MATLAB 中, Inf 表示∞D=A; %赋初值for(i=1:n)for(j=1:n)R(i,j)=j;end;end %赋路径初值for(k=1:n)for(i=1:n)for(j=1:n)if(D(i,k)+D(k,j)<D(i,j))D(i,j )=D(i,k)+D(k,j); %更新dijR(i,j)=k;end;end;end %更新rijk %显示迭代步数D %显示每步迭代后的路长R %显示每步迭代后的路径pd=0;for i=1:n %含有负权时if(D(i,i)<0)pd=1;break;end;end %存在一条含有顶点vi 的负回路if(pd)break;end %存在一条负回路, 终止程序end %程序结束利用 Ford--Fulkerson 标号法求最大流算法的MATLAB 程序代码如下:n=8;C=[0 5 4 3 0 0 0 00 0 0 0 5 3 0 00 0 0 0 0 3 2 00 0 0 0 0 0 2 00 0 0 0 0 0 0 40 0 0 0 0 0 0 30 0 0 0 0 0 0 50 0 0 0 0 0 0 0]; %弧容量for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流for(i=1:n)No(i)=0;d(i)=0;end %No,d 记录标号图 6-19while(1)No(1)=n+1;d(1)=Inf; %给发点vs 标号while(1)pd=1; %标号过程for(i=1:n)if(No(i)) %选择一个已标号的点vifor(j=1:n)if(No(j)==0&f(i,j)<C(i,j)) %对于未给标号的点vj, 当vivj 为非饱和弧时No(j)=i;d(j)=C(i,j)-f(i,j);pd=0;if(d(j)>d(i))d(j)=d(i);endelseif(No(j)==0&f(j,i)>0) %对于未给标号的点vj, 当vjvi 为非零流弧时No(j)=-i;d(j)=f(j,i);pd=0;if(d(j)>d(i))d(j)=d(i);end;end;end;end;endif(No(n)|pd)break;end;end%若收点vt 得到标号或者无法标号, 终止标号过程if(pd)break;end %vt 未得到标号, f 已是最大流, 算法终止dvt=d(n);t=n; %进入调整过程, dvt 表示调整量while(1)if(No(t)>0)f(No(t),t)=f(No(t),t)+dvt; %前向弧调整elseif(No(t)<0)f(No(t),t)=f(No(t),t)-dvt;end %后向弧调整if(No(t)==1)for(i=1:n)No(i)=0;d(i)=0; end;break;end %当t 的标号为vs 时, 终止调整过程t=No(t);end;end; %继续调整前一段弧上的流fwf=0;for(j=1:n)wf=wf+f(1,j);end %计算最大流量f %显示最大流wf %显示最大流量No %显示标号, 由此可得最小割, 程序结束图论程序大全程序一:关联矩阵和邻接矩阵互换算法function W=incandadf(F,f)if f==0m=sum(sum(F))/2;n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=i:nif F(i,j)~=0W(i,k)=1;W(j,k)=1;k=k+1;endendendelseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);W(a(1),a(2))=1;W(a(2),a(1))=1;endelsefprint('Please imput the right value of f');endW;程序二:可达矩阵算法function P=dgraf(A) n=size(A,1);P=A;for i=2:nP=P+A^i;endP(P~=0)=1;P;程序三:有向图关联矩阵和邻接矩阵互换算法function W=mattransf(F,f)if f==0m=sum(sum(F));n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=i:nif F(i,j)~=0W(i,k)=1;W(j,k)=-1;k=k+1;endendendelseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);if F(a(1),i)==1W(a(1),a(2))=1;elseW(a(2),a(1))=1;endendelsefprint('Please imput the right value of f');endW;第二讲:最短路问题程序一:Dijkstra算法(计算两点间的最短路)function [l,z]=Dijkstra(W)n = size (W,1); for i = 1 :nl(i)=W(1,i);z(i)=0;endi=1;while i<=nfor j =1 :nif l(i)>l(j)+W(j,i)l(i)=l(j)+W(j,i);z(i)=j-1;if j<ii=j-1;endendendi=i+1;end程序二:floyd算法(计算任意两点间的最短距离)function [d,r]=floyd(a)n=size(a,1);d=a;for i=1:nfor j=1:nr(i,j)=j;endendr;for k=1:nfor i=1:nfor j=1:nif d(i,k)+d(k,j)<d(i,j)d(i,j)=d(i,k)+d(k,j);r(i,j)=r(i,k);endendendend程序三:n2short.m 计算指定两点间的最短距离function [P u]=n2short(W,k1,k2)n=length(W);U=W;m=1;while m<=nfor i=1:nfor j=1:nif U(i,j)>U(i,m)+U(m,j)U(i,j)=U(i,m)+U(m,j);endendendm=m+1;endu=U(k1,k2);P1=zeros(1,n);k=1;P1(k)=k2;V=ones(1,n)*inf;kk=k2;while kk~=k1for i=1:nV(1,i)=U(k1,kk)-W(i,kk);if V(1,i)==U(k1,i)P1(k+1)=i;kk=i;k=k+1;endendendk=1;wrow=find(P1~=0);for j=length(wrow):-1:1P(k)=P1(wrow(j));k=k+1;endP;程序四、n1short.m(计算某点到其它所有点的最短距离)function[Pm D]=n1short(W,k)n=size(W,1);D=zeros(1,n);for i=1:n[P d]=n2short(W,k,i);Pm{i}=P;D(i)=d;end程序五:pass2short.m(计算经过某两点的最短距离)function [P d]=pass2short(W,k1,k2,t1,t2)[p1 d1]=n2short(W,k1,t1);[p2 d2]=n2short(W,t1,t2);[p3 d3]=n2short(W,t2,k2);dt1=d1+d2+d3;[p4 d4]=n2short(W,k1,t2);[p5 d5]=n2short(W,t2,t1);[p6 d6]=n2short(W,t1,k2);dt2=d4+d5+d6;if dt1<dt2d=dt1;P=[p1 p2(2:length(p2)) p3(2:length(p3))];elsed=dt1;p=[p4 p5(2:length(p5)) p6(2:length(p6))];endP;d;第三讲:最小生成树程序一:最小生成树的Kruskal算法function [T c]=krusf(d,flag)if nargin==1n=size(d,2);m=sum(sum(d~=0))/2;b=zeros(3,m);k=1;for i=1:nfor j=(i+1):nif d(i,j)~=0b(1,k)=i;b(2,k)=j;b(3,k)=d(i,j);k=k+1;endendendelseb=d;endn=max(max(b(1:2,:)));m=size(b,2);[B,i]=sortrows(b',3);B=B';c=0;T=[];k=1;t=1:n;for i=1:mif t(B(1,i))~=t(B(2,i))T(1:2,k)=B(1:2,i);c=c+B(3,i);k=k+1;tmin=min(t(B(1,i)),t(B(2,i)));tmax=max(t(B(1,i)),t(B(2,i)));for j=1:nif t(j)==tmaxt(j)=tmin;endendendif k==nbreak;endendT;c;程序二:最小生成树的Prim算法function [T c]=Primf(a)l=length(a);a(a==0)=inf;k=1:l;listV(k)=0;listV(1)=1;e=1;while (e<l)min=inf;for i=1:lif listV(i)==1for j=1:lif listV(j)==0 & min>a(i,j)min=a(i,j);b=a(i,j);s=i;d=j;endendendendlistV(d)=1;distance(e)=b;source(e)=s;destination(e)=d;e=e+1;endT=[source;destination]; for g=1:e-1c(g)=a(T(1,g),T(2,g));endc;另外两种程序最小生成树程序1(prim 算法构造最小生成树)a=[inf 50 60 inf inf inf inf;50 inf inf 65 40 inf inf;60 inf inf 52 inf inf 45;...inf 65 52 inf 50 30 42;inf 40 inf 50 inf 70 inf;inf inf inf 30 70 inf inf;...inf inf 45 42 inf inf inf];result=[];p=1;tb=2:length(a);while length(result)~=length(a)-1temp=a(p,tb);temp=temp(:);d=min(temp);[jb,kb]=find(a(p,tb)==d);j=p(jb(1));k=tb(kb(1));result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];endresult最小生成树程序2(Kruskal 算法构造最小生成树)clc;clear;a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40;a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;a(4,7)=42; a(5,6)=70;[i,j,b]=find(a);data=[i';j';b'];index=data(1:2,:);loop=max(size(a))-1;result=[];while length(result)<looptemp=min(data(3,:));flag=find(data(3,:)==temp);flag=flag(1);v1=data(1,flag);v2=data(2,flag);if index(1,flag)~=index(2,flag)result=[result,data(:,flag)];endindex(find(index==v2))=v1;data(:,flag)=[];index(:,flag)=[];endresult第四讲:Euler图和Hamilton图程序一:Fleury算法(在一个Euler图中找出Euler环游)注:包括三个文件;fleuf1.m, edf.m, flecvexf.mfunction [T c]=fleuf1(d)%注:必须保证是Euler环游,否则输出T=0,c=0 n=length(d);b=d;b(b==inf)=0;b(b~=0)=1;m=0;a=sum(b);eds=sum(a)/2;ed=zeros(2,eds);vexs=zeros(1,eds+1);matr=b;for i=1:nif mod(a(i),2)==1m=m+1;endendif m~=0fprintf('there is not exit Euler path.\n')T=0;c=0;endif m==0vet=1;flag=0;t1=find(matr(vet,:)==1);for ii=1:length(t1)ed(:,1)=[vet,t1(ii)];vexs(1,1)=vet;vexs(1,2)=t1(ii);matr(vexs(1,2),vexs(1,1))=0;flagg=1;tem=1;while flagg[flagg ed]=edf(matr,eds,vexs,ed,tem); tem=tem+1;if ed(1,eds)~=0 & ed(2,eds)~=0T=ed;T(2,eds)=1;c=0;for g=1:edsc=c+d(T(1,g),T(2,g));endflagg=0;break;endendendendfunction[flag ed]=edf(matr,eds,vexs,ed,tem)flag=1;for i=2:eds[dvex f]=flecvexf(matr,i,vexs,eds,ed,tem);if f==1flag=0;break;endif dvex~=0ed(:,i)=[vexs(1,i) dvex];vexs(1,i+1)=dvex;matr(vexs(1,i+1),vexs(1,i))=0;elsebreak;endendfunction [dvex f]=flecvexf(matr,i,vexs,eds,ed,temp) f=0;edd=find(matr(vexs(1,i),:)==1);dvex=0;dvex1=[];ded=[];if length(edd)==1dvex=edd;elsedd=1;dd1=0;kkk=0;for kk=1:length(edd)m1=find(vexs==edd(kk));if sum(m1)==0dvex1(dd)=edd(kk);dd=dd+1;dd1=1;elsekkk=kkk+1;endendif kkk==length(edd)tem=vexs(1,i)*ones(1,kkk);edd1=[tem;edd];for l1=1:kkklt=0;ddd=1;for l2=1:edsif edd1(1:2,l1)==ed(1:2,l2)lt=lt+1;endendif lt==0ded(ddd)=edd(l1); ddd=ddd+1;endendendif temp<=length(dvex1)dvex=dvex1(temp);elseif temp>length(dvex1) & temp<=length(ded)dvex=ded(temp);elsef=1;endend程序二:Hamilton改良圈算法(找出比较好的Hamilton路)function [C d1]= hamiltonglf(v)%d表示权值矩阵%C表示算法最终找到的Hamilton圈。
MATLAB解决最短路径问题代码

默认是Dijkstra 算法是有权的, 我想如果把权都赋1的话, 就相当于没权的了参数是带权的稀疏矩阵及结点看看这两个例子(一个有向一个无向), 或许你能找到你想知道的% Create a directed graph with 6 nodes and 11 edgesW = [.41 .99 .51 .32 .15 .45 .38 .32 .36 .29 .21]; %这是权DG = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],W) %有权的有向图h = view(biograph(DG,[],'ShowWeights','on')) %画图, 这个好玩% Find shortest path from 1 to 6[dist,path,pred] = graphshortestpath(DG,1,6) %找顶点1到6的最短路径% Mark the nodes and edges of the shortest pathset(h.Nodes(path),'Color',[1 0.4 0.4]) %上色edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));set(edges,'LineColor',[1 0 0]) %上色set(edges,'LineWidth',1.5) %上色下面是无向图的例子% % Solving the previous problem for an undirected graph% UG = tril(DG + DG')% h = view(biograph(UG,[],'ShowArrows','off','ShowWeights','on')) % % Find the shortest path between node 1 and 6% [dist,path,pred] = graphshortestpath(UG,1,6,'directed',false)% % Mark the nodes and edges of the shortest path% set(h.Nodes(path),'Color',[1 0.4 0.4])% fowEdges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));% revEdges = getedgesbynodeid(h,get(h.Nodes(fliplr(path)),'ID')); % edges = [fowEdges;revEdges];% set(edges,'LineColor',[1 0 0])% set(edges,'LineWidth',1.5)clc;close all; clear;load data;% global quyu;quyu = [2,3];%一片区域z_jl = lxjl(jdxx,lxxh);%计算路线的距离z = qyxz(jdxx,quyu,z_jl);% 根据节点信息,从z中将y区域的节点和路线选出所有点的信息hzlx(z);%绘制Z的图像[qypt, nqypt] = ptxzm(xjpt,quyu);changdu = length(bhxz(jdxx,1:6));%选出x中y区的标号,只是分区域,求长度并绘制它tt = z(:,[1,2,end])';k = min(min(tt(1:2,:)));%求两次最小值t = tt(1:2,:) ;xsjz = sparse(t(2,:),t(1,:),tt(3,:),changdu,changdu);%产生稀疏矩阵[dist, path, pred] = zdljxz(xsjz, qypt, k );%三个原包矩阵通过zdljxz计算得到最短路径hold onfor j = 1:nqyptcolors = rand(1,3);%产生随机数并用颜色标记hzptxc(path{j},jdxx,colors)endhold offaxis equal%把坐标轴单位设为相等zjd = jdfgd( path, quyu);function z = lxjl(x, y)%计算路线的距离[m n] = size(y);for i = 1:myy(i,1:2) = x(y(i,1),2:3);yy(i,3:4) = x(y(i,2),2:3);endz = sqrt((yy(:,3) - yy(:,1)).^2 + (yy(:,2) - yy(:,4)).^2);y = sort(y');y = y';z = [y yy z];z = sortrows(z);function [z lz] = ptxz(xjpt,y)pt = xjpt(:,2);wei = ismember(xjpt(:,1),y);z = pt(wei);lz = length(z);unction hzptxc(path,jdxx,colors)n = length(path);% hold onfor i = 1:nhzptjd(jdxx, path{i},colors)end% hold offunction hzptjd(jdxx,x,colors)% m = length(x);% x = x';hold onplot(jdxx(x,2),jdxx(x,3),'o','LineStyle' ,'-' ,...'Color',colors,'MarkerEdgeColor',colors)plot(jdxx(x(1),2),jdxx(x(1),3),'*','MarkerFaceColor',colors)hold offfunction hzlx(x)%绘制x的图像[m n] = size(x);hold onfor i = 1:mplot([x(i,3) x(i,5)],[x(i,4) x(i,6)],'k:')endhold offfunction z = bhxz(x,y)%选出x中y区的标号,只是分区域xzq = x(:,4);xzr = ismember(xzq,y);z = x(xzr,:);z = z(:,1);。
加权聚类系数和加权平均路径长度matlab代码

加权聚类系数和加权平均路径长度matlab代码加权聚类系数和加权平均路径长度是图论中一对重要的指标,用于评价网络图中节点之间的连接密度和通信效率。
在本文中,我将重点介绍加权聚类系数和加权平均路径长度的概念,并提供相应的Matlab代码来计算这些指标。
1. 加权聚类系数加权聚类系数是一种度量网络图中节点局部连接密度的指标。
对于一个节点而言,它的聚类系数定义为该节点的邻居节点之间实际存在的边数与可能存在的边数的比值。
在加权网络图中,我们需要考虑边的权重。
对于给定的节点i,其邻居节点集合定义为Ni,该节点的聚类系数Ci可以通过以下步骤计算得到:1. 对于节点i的每对邻居节点j和k,计算其边的权重wij和wik。
2. 对于每对邻居节点j和k,计算其边的权重的乘积相加,即sum =Σ(wij * wik)。
3. 计算节点i的邻居节点之间可能的边数,即possible_edges = (|Ni| * (|Ni| - 1)) / 2。
4. 计算节点i的加权聚类系数Ci = 2 * sum / possible_edges。
下面是使用Matlab实现计算加权聚类系数的代码:```matlabfunction weighted_clustering_coefficient =compute_weighted_clustering_coefficient(adjacency_matrix) num_nodes = size(adjacency_matrix, 1);weighted_clustering_coefficient = zeros(num_nodes, 1);for i = 1:num_nodesneighbors = find(adjacency_matrix(i, :) > 0);num_neighbors = length(neighbors);if num_neighbors >= 2weights = adjacency_matrix(i, neighbors);weighted_sum = 0;for j = 1:num_neighbors-1for k = j+1:num_neighborsweighted_sum = weighted_sum + (weights(j) * weights(k));endendpossible_edges = (num_neighbors * (num_neighbors - 1)) / 2;weighted_clustering_coefficient(i) = 2 * weighted_sum / possible_edges;endendend```在上述代码中,我们首先根据给定的邻接矩阵的大小确定节点数量。
迪杰斯特拉算法计算最短路径

利用Dijkstra算法计算最短路径摘要福格环游地球问题是一个十分典型的最短路径求解问题,题设给出了当时世界上主要交通网络图及交通通畅的城市之间来往所需时长,并限定了福格的出行方向(福格选择的是往东走),给出起止地点后要求找出福格环游世界天数最短的最佳路径。
我们认为,这个问题的实质在于最短路径的求解和优化。
我们对比图论中的多种最短路径算法,决定利用Dijkstra算法解决这个问题。
由于Dijkstra算法要求输入图G的关联矩阵,且图G为二维赋权图,而题中给出的地图可看成是三维环状地图,因此,我们对题设地图做相关处理,将其从起点处“切断”并展开为二维图,然后根据此图建立关联矩阵。
同时,我们考虑到最短路径可能会与切断线有交点,在切断线以西找出若干地点一分为二,修改关联矩阵。
对于题目中缺失的两处数据,本文将以当时的交通数据为基础,经过合理的数据处理,结合Google Earth测距软件与题目数据的合理类比,补充缺失数据,完成关联矩阵。
得到关联矩阵后,我们分别以伦敦、纽约和上海作为起点,调整关联矩阵起点和终点,用matlab编程进行求解得到最短环游时间和最短路径,进而判断出所选择的路径是否能让他赢得赌注。
根据我们的求解结果,在这三个城市,福格均能在80天内环游地球,赢得赌注。
本文进一步对此种算法的优缺点、灵敏度与推广性进行了分析,同时初步提出了两种优化方法。
关键词:最短路径算法 dijkstra算法算法优化一、问题重述儒勒•凡尔纳的著名小说《环游世界80天》中,英国绅士福格在伦敦与人打赌能够在80天内环游世界,这在当时的1872年是一个了不起的壮举。
当时最快的旅行方式是火车和轮船,然而世界上大部分地区还是靠马车、大象、驴子或者步行来旅行。
下面是一个从伦敦环游世界不同路线的交通网络图,福格选择的是往东走,每段路线所需要的天数显示在图上(见附录一),旅行的时间基于1872年能采用的旅行方式以及距离。
我们将解决以下问题:1.我们将设计一个算法为福格选择一条最佳路径,即环游世界天数最短,并判断所选择的路径是否能让他赢得赌注。
matlab实现dijkstra算法

matlab实现dijkstra算法Matlab实现Dijkstra算法第一段:什么是Dijkstra算法,为什么它重要?Dijkstra算法是一种用于解决最短路径问题的经典算法。
它由荷兰计算机科学家Edsger Dijkstra在1956年提出,被广泛应用于网络路由、地图导航和图论等领域。
该算法的核心思想是在给定的带权图中找到从起点到终点的最短路径,通过迭代的方式逐步推进,直到找到最短路径或处理完所有节点。
Dijkstra算法被广泛认为是一种高效、可靠的解决方案,具有良好的理论基础和实际应用性。
第二段:如何在Matlab中实现Dijkstra算法?在Matlab中实现Dijkstra算法,可以分为以下几个步骤:1. 创建带权图:我们需要将问题转化为带权图的形式。
在Matlab中,可以使用邻接矩阵来表示图的连接关系,其中每个边的权重存储在矩阵中的对应位置。
2. 初始化距离和路径:将起点到每个节点的距离初始化为无穷大,并为每个节点设置一个空路径。
将起点的距离设置为0,表示起点到自身的距离为0。
3. 遍历节点:循环遍历所有节点,找到距离起点最近的节点,并标记为已访问。
更新与该节点相邻节点的距离和路径信息。
如果经过当前节点到达某个相邻节点的距离更短,则更新该节点的距离和路径。
4. 重复步骤3,直到所有节点都被遍历为止。
这样,我们就能得到从起点到其他节点的最短路径信息。
第三段:个人观点和理解Dijkstra算法是解决最短路径问题的经典算法之一,它具有广泛的应用价值。
在日常生活中,我们经常需要找到最佳的路径规划,例如快递员送货时选择最短路径、地铁或公交车乘客选择最快到达目的地的路线等。
对于这些问题,Dijkstra算法可以提供一个可靠、高效的解决方案。
在使用Matlab实现Dijkstra算法时,我们可以利用Matlab强大的矩阵运算能力和易用的函数库来简化算法的实现过程。
Matlab还提供了丰富的可视化工具,可以帮助我们直观地展示算法执行过程和结果。
一种基于改进Dijkstra的物流网络路径优化算法分析

一种基于改进Dijkstra的物流网络路径优化算法分析袁彬;刘建胜;钱丹;罗大海【摘要】路径优化是物流网络规划的关键问题,针对经典Dijkstra路径优化算法在大规模网络计算中存在时间复杂度难题,改进其对未标记节点遍历过程,直接寻求在遍历范围和方向上趋向目标节点,使得搜索过程不必全部遍历或只较少地遍历未标记结点,将时间复杂度从O(n^2)降低为O(n),提高算法的运行效率。
采用mATLAB编程,给出基于改进Dijkstra 算法的最优路径的快速求解仿真程序。
基于测试数据实验对比分析,结果表明了改进算法的有效性,特别是随着网络规模不断扩大,算法效率更加明显,具有较好的适用性。
【期刊名称】《制造业自动化》【年(卷),期】2014(000)009【总页数】4页(P86-88,105)【关键词】物流;网络分析;最优路径;改进迪杰斯特拉算法【作者】袁彬;刘建胜;钱丹;罗大海【作者单位】南昌大学机电工程学院,南昌330031;南昌大学机电工程学院,南昌330031;南昌大学机电工程学院,南昌330031;南昌大学机电工程学院,南昌330031【正文语种】中文【中图分类】TP3910 引言随着现代制造业竞争加剧,物流在整个制造业供应链管理中的作用日益凸显重要。
企业管理者开始从战略高度关注制造物流管理,旨在通过控制物流成本来降低产品总成本,提高产品竞争力。
研究人员也纷纷对制造物流网络的管理与规划问题开展研究,如文献[1]研究应用改进蚁群算法解决物流配送问题。
路径优化是物流网络规划的关键问题,目前,迪杰斯特拉(Dijkstra)算法是目前公认的较好的路径优化算法之一。
但是由于Dijkstra 算法频繁遍历所有的临时标记结点,明显降低了算法的运行速度和效率,特别是随着网络节点规模的增大,将导致算法运行时间长,难以在实际工程项目中满足使用性能要求。
许多研究人员开始对Dijkstra算法进行改进以提高算法的运行效率[2~8],其中胡树玮从限制搜索范围和限定搜索方向两方面着手,在扇形区域内寻找最短路径,对Dijkstra 算法优化改进,李元臣采用二叉树结构来改进Dijkstra 算法,张福浩提出一种基于邻接结点算法的Dijkstra优化算法,刘建美基于每个时段内的历史平均速度给出了改进的Dijkstra优化算法,王树西对Dijkstra标号法进行了改进,为解决最短路径问题提供了切实可行的算法。
基于MATLAB的最短路径算法分析

基于MATLAB的最短路径算法分析周志进(贵阳学院贵州贵阳550005)摘要:随着社会快速发展,人们生活水平提高,很多需求都在向着最优化、最快捷、最高效的方向延伸,而最短路径算法则是图论研究中的典型问题。
该文简要概述MATLAB软件,分析基于MATLAB的4种用于解决最短路径问题的算法,并研究基于MATLAB的最短路径算法的实际应用状况,以期对最短路径算法的应用提供一定借鉴意义。
关键词:MATLAB最优路径Dijkstra算法Floyd算法Bellman-Ford算法SPFA算法中图分类号:TP301.6文献标识码:A文章编号:1672-3791(2022)08(a)-0217-03最短路径算法就是用于计算一个节点到其他节点的最短路径问题,一般是指确定起点的最短路径问题,求起始节点到某一终点的最短路径问题,也常用于已知起点和终点,求解两节点之间的最短路径。
1MATLAB程序概述MATLAB是由美国MathWorks公司出品的数学软件,MATLAB意为矩阵工程,将用于一维、二维与三维数值积分的函数进行了统一,并经过基本数学和内插函数的辅助,提供数值分析、矩阵计算等诸多功能,为应用数学、工程设计和数值计算提供全方位的解决方案,很大程度上摆脱了传统程序设计语言的编辑模式。
其高效的数值及符号计算功能,可以帮助用户快速处理繁杂的数学运算问题,具备的图形处理功能可以实现计算结果和编程的可视化。
MATLAB本身是一个高级的矩阵语言,包括诸多算法、控制语句、函数等面向基本对象或问题的应用程序[1]。
比如:在最短路径计算中可以利用矩阵运算和线性方程组的求解或是数据的统计分析来优化相关问题。
2基于MATLAB的4种最短路径算法2.1Dijkstra算法Dijkstra(迪杰斯特拉)算法是最经典的单源最短路径算法,也就是用于计算一个节点到其他所有节点最短路径的算法。
Dijkstra算法采用贪心算法策略,每次遍历与起点距离最近且未访问过的节点,直至扩展到终点。
Dijkstra、Floyd算法Matlab_Lingo实现

Dijkstra算法Matlab实现。
%求一个点到其他各点的最短路径function [min,path]=dijkstra(w,start,terminal)%W是邻接矩阵%start是起始点Array %terminal是终止点%min是最短路径长度%path是最短路径n=size(w,1);label(start)=0;f(start)=start;for i=1:nif i~=startlabel(i)=inf;endends(1)=start;u=start;while length(s)<nfor i=1:nins=0;forif i==s(j)ins=1;endendif ins==0v=i;if label(v)>(label(u)+w(u,v))label(v)=(label(u)+w(u,v));f(v)=u;endendendv1=0;k=inf;for i=1:nins=0;for j=1:length(s)if i==s(j)ins=1;endend-if ins==0v=i;if k>label(v)k=label(v);v1=v;endendends(length(s)+1)=v1;u=v1;endmin=label(terminal);path(1)=terminal;i=1;while path(i)~=startpath(i+1)=f(path(i));i=i+1 ;endpath(i)=start;L=length(path);path=path(L:-1:1);Floyd算法:matlab程序:%floyd算法,function [D,path,min1,path1]=floyd(a,start,terminal)%a是邻接矩阵%start是起始点%terminal是终止点%D是最小权值表D=a;n=size(D,1);path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)-D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendif nargin==3min1=D(start,terminal);m(1)=start;i=1;path1=[ ];while path(m(i),terminal)~=terminalk=i+1;m(k)=path(m(i),terminal);i=i+1;endm(i+1)=terminal;path1=m;end1 6 5 5 5 66 2 3 4 4 65 2 3 4 5 45 2 3 4 5 61 4 3 4 5 11 2 4 4 1 6Floyd算法:Lingo程序:!用LINGO11.0编写的FLOYD算法如下;model:sets:nodes/c1..c6/;link(nodes,nodes):w,path; !path标志最短路径上走过的顶点;endsetsdata:path=0;w=0;@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):-@format(w(i,j),' 10.0f')),@newline(1));@text(mydata1.txt)=@write(@newline(1));@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),' 10.0f')),@newline(1));enddatacalc:w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;w(2,3)=15;w(2,4)=20;w(2,6)=25;w(3,4)=10;w(3,5)=20;w(4,5)=10;w(4,6)=25;w(5,6)=55;@for(link(i,j):w(i,j)=w(i,j)+w(j,i));@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j)));@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));w(i,j)=tm)));endcalcend无向图的最短路问题Lingomodel:sets:cities/1..5/;roads(cities,cities):w,x;endsetsdata:w=0;enddatacalc:w(1,2)=41;w(1,3)=59;w(1,4)=189;w(1,5)=81;w(2,3)=27;w(2,4)=238;w(2,5)=94;w(3,4)=212;w(3,5)=89;w(4,5)=171;@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));endcalcn=@size(cities); !城市的个数;min=@sum(roads:w*x);@for(cities(i)|i #ne#1 #and# i #ne#n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));@sum(cities(j):x(1,j))=1;-@sum(cities(j):x(j,1))=0; !不能回到顶点1;@sum(cities(j):x(j,n))=1;@for(roads:@bin(x));endLingo编的sets:dian/a b1 b2 c1 c2 c3 d/:;link(dian,dian)/a,b1 a,b2 b1,c1 b1,c2 b1,c3 b2,c1 b2,c2 b2,c3 c1,d c2,d c3,d/:x,w;endsetsdata:w=2 4 3 3 1 2 3 1 1 3 4;enddatamin=@sum(link:w*x);@for(link:@bin(x));n=@size(dian);@sum(link(i,j)|i#eq#1:x(i,j))=1;@sum(link(j,i)|i#eq#n:x(j,i))=1;@for(dian(k)|k#ne#1#and#k#ne#n:@sum(link(i,k):x(i,k))=@sum(link(k,i):x(k,i)));- sets:dian/1..5/:level; !level(i)表示点i的水平,用来防止生产圈;link(dian,dian):d,x;endsetsdata:d=0 41 59 189 8141 0 27 238 9459 27 0 212 89189 238 212 0 17181 94 89 171 0;enddatan=@size(dian);min=@sum(link(i,j)|i#ne#j:d(i,j)*x(i,j));@sum(dian(j)|j#gt#1:x(1,j))>1;@for(dian(i)|i#gt#1:@sum(dian(j)|j#ne#i:x(j,i))=1);@for(dian(i)|i#gt#1:@for(dian(j)|j#ne#i#and#j#gt#1:level(j)>level(i)+x(i,j)-(n-2)*(1-x(i,j))+(n-3)*x(j, i)));@for(dian(i)|i#gt#1:level(i)<n-1-(n-2)*x(1,i));@for(dian(i)|i#gt#1:@bnd(1,level(i),100000));@for(link:@bin(x));。
Dijkstra算法

Dijkstra算法定义G=(V,E),定义集合S存放已经找到最短路径的顶点,集合T存放当前还未找到最短路径的顶点,即有T=V-SDijkstra算法描述如下:(1) 假设用带权的邻接矩阵edges来表示带权有向图,edges[i][j]表示弧<Vi, Vj>上的权值。
若<Vi, Vj>不存在则置edges[i][j]=∞(计算机上用一个允许的最大值代替)。
S为已经找到的从Vs出发的最短路径的终点集合,它初始化为空集。
那么,从Vs出发到图上其余各顶点(终点)Vi可能达到的最短路径长度的初值为:D[i]=deges[s][i] Vi∈V(2) 选择Vj,使得D[j]=Min{D[i]|Vi∈V-S},Vj就是当前求得的一条从Vs出发的最短路径的终点。
令S=S∪{Vj}(3) 修改从Vs出发到集合V-S上任一顶点Vk可达的最短路径长度。
如果D[j]+edges[j][k]<D[k]则修改D[k]为D[k]=D[j]+edges[j][k]重复操作(2)(3)共n-1次。
由此求得从Vs到图上其余各顶点的最短路径。
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用O PEN, CLOSE表方式,Drew为了和下面要介绍的A* 算法和D* 算法表述一致,这里均采用OPEN,CLOSE表的方式。
其采用的是贪心法的算法策略大概过程:创建两个表,OPEN, CLOSE。
OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
(图论)matlab模板程序

第一讲:图论模型程序一:可达矩阵算法%根据邻接矩阵A〔有向图〕求可达矩阵P〔有向图〕function P=dgraf<A>n=size<A,1>;P=A;for i=2:nP=P+A^i;endP<P~=0>=1; %将不为0的元素变为1P;程序二:无向图关联矩阵和邻接矩阵互换算法F表示所给出的图的相应矩阵W表示程序运行结束后的结果f=0表示把邻接矩阵转换为关联矩阵f=1表示把关联矩阵转换为邻接矩阵%无向图的关联矩阵和邻接矩阵的相互转换function W=incandadf<F,f>if f==0 %邻接矩阵转换为关联矩阵m=sum<sum<F>>/2; %计算图的边数n=size<F,1>;W=zeros<n,m>;k=1;for i=1:nfor j=i:nif F<i,j>~=0W<i,k>=1; %给边的始点赋值为1W<j,k>=1; %给边的终点赋值为1k=k+1;endendendelseif f==1 %关联矩阵转换为邻接矩阵m=size<F,2>;n=size<F,1>;W=zeros<n,n>;for i=1:ma=find<F<:,i>~=0>;W<a<1>,a<2>>=1; %存在边,则邻接矩阵的对应值为1 W<a<2>,a<1>>=1;endelsefprint<'Please imput the right value of f'>;W;程序三:有向图关联矩阵和邻接矩阵互换算法%有向图的关联矩阵和邻接矩阵的转换function W=mattransf<F,f>if f==0 %邻接矩阵转换为关联矩阵m=sum<sum<F>>;n=size<F,1>;W=zeros<n,m>;k=1;for i=1:nfor j=i:nif F<i,j>~=0 %由i发出的边,有向边的始点W<i,k>=1; %关联矩阵始点值为1W<j,k>=-1; %关联矩阵终点值为-1k=k+1;endendendelseif f==1 %关联矩阵转换为邻接矩阵m=size<F,2>;n=size<F,1>;W=zeros<n,n>;for i=1:ma=find<F<:,i>~=0>; %有向边的两个顶点if F<a<1>,i>==1W<a<1>,a<2>>=1; %有向边由a<1>指向a<2>elseW<a<2>,a<1>>=1; %有向边由a<2>指向a<1>endendelsefprint<'Please imput the right value of f'>;endW;第二讲:最短路问题程序0:最短距离矩阵W表示图的权值矩阵D表示图的最短距离矩阵%连通图中各项顶点间最短距离的计算function D=shortdf<W>%对于W<i,j>,若两顶点间存在弧,则为弧的权值,否则为inf;当i=j时W<i,j>=0 n=length<W>;m=1;while m<=nfor i=1:nfor j=1:nif D<i,j>>D<i,m>+D<m,j>D<i,j>+D<i,m>+D<m,j>; %距离进行更新 endendendm=m+1;endD;程序一:Dijkstra算法〔计算两点间的最短路〕function [l,z]=Dijkstra<W>n = size <W,1>;for i = 1 :nl<i>=W<1,i>;z<i>=0;endi=1;while i<=nfor j =1 :nif l<i>>l<j>+W<j,i>l<i>=l<j>+W<j,i>;z<i>=j-1;if j<ii=j-1;endendendi=i+1;end程序二:floyd算法〔计算任意两点间的最短距离〕function [d,r]=floyd<a>n=size<a,1>;d=a;for i=1:nfor j=1:nr<i,j>=j;endendr;for k=1:nfor i=1:nfor j=1:nif d<i,k>+d<k,j><d<i,j>d<i,j>=d<i,k>+d<k,j>; r<i,j>=r<i,k>;endendendend程序三:n2short.m 计算指定两点间的最短距离function [P u]=n2short<W,k1,k2>n=length<W>;U=W;m=1;while m<=nfor i=1:nfor j=1:nif U<i,j>>U<i,m>+U<m,j>U<i,j>=U<i,m>+U<m,j>;endendendm=m+1;endu=U<k1,k2>;P1=zeros<1,n>;k=1;P1<k>=k2;V=ones<1,n>*inf;kk=k2;while kk~=k1for i=1:nV<1,i>=U<k1,kk>-W<i,kk>;if V<1,i>==U<k1,i>P1<k+1>=i;kk=i;k=k+1;endendendk=1;wrow=find<P1~=0>;for j=length<wrow>:-1:1P<k>=P1<wrow<j>>;k=k+1;endP;程序四、n1short.m<计算某点到其它所有点的最短距离> function[Pm D]=n1short<W,k>n=size<W,1>;D=zeros<1,n>;for i=1:n[P d]=n2short<W,k,i>;Pm{i}=P;D<i>=d;end程序五:pass2short.m<计算经过某两点的最短距离> function [P d]=pass2short<W,k1,k2,t1,t2>[p1 d1]=n2short<W,k1,t1>;[p2 d2]=n2short<W,t1,t2>;[p3 d3]=n2short<W,t2,k2>;dt1=d1+d2+d3;[p4 d4]=n2short<W,k1,t2>;[p5 d5]=n2short<W,t2,t1>;[p6 d6]=n2short<W,t1,k2>;dt2=d4+d5+d6;if dt1<dt2d=dt1;P=[p1 p2<2:length<p2>> p3<2:length<p3>>]; elsed=dt1;p=[p4 p5<2:length<p5>> p6<2:length<p6>>]; endP;d;第三讲:最小生成树程序一:最小生成树的Kruskal算法function [T c]=krusf<d,flag>if nargin==1n=size<d,2>;m=sum<sum<d~=0>>/2;b=zeros<3,m>;k=1;for i=1:nfor j=<i+1>:nif d<i,j>~=0b<1,k>=i;b<2,k>=j;b<3,k>=d<i,j>;k=k+1;endendendelseb=d;endn=max<max<b<1:2,:>>>;m=size<b,2>;[B,i]=sortrows<b',3>;B=B';c=0;T=[];k=1;t=1:n;for i=1:mif t<B<1,i>>~=t<B<2,i>>T<1:2,k>=B<1:2,i>;c=c+B<3,i>;k=k+1;tmin=min<t<B<1,i>>,t<B<2,i>>>; tmax=max<t<B<1,i>>,t<B<2,i>>>; for j=1:nif t<j>==tmaxt<j>=tmin;endendendif k==nbreak;endendT;c;程序二:最小生成树的Prim算法function [T c]=Primf<a>l=length<a>;a<a==0>=inf;k=1:l;listV<k>=0;listV<1>=1;e=1;while <e<l>min=inf;for i=1:lif listV<i>==1for j=1:lif listV<j>==0 & min>a<i,j>min=a<i,j>;b=a<i,j>;s=i;d=j;endendendendlistV<d>=1;distance<e>=b;source<e>=s;destination<e>=d;e=e+1;endT=[source;destination];for g=1:e-1c<g>=a<T<1,g>,T<2,g>>;endc;第四讲:Euler图和Hamilton图程序一:Fleury算法〔在一个Euler图中找出Euler环游〕注:包括三个文件;fleuf1.m, edf.m, flecvexf.mfunction [T c]=fleuf1<d>%注:必须保证是Euler环游,否则输出T=0,c=0n=length<d>;b=d;b<b==inf>=0;b<b~=0>=1;m=0;a=sum<b>;eds=sum<a>/2;ed=zeros<2,eds>;vexs=zeros<1,eds+1>;matr=b;for i=1:nif mod<a<i>,2>==1m=m+1;endendif m~=0fprintf<'there is not exit Euler path.\n'>T=0;c=0;endif m==0vet=1;flag=0;t1=find<matr<vet,:>==1>;for ii=1:length<t1>ed<:,1>=[vet,t1<ii>];vexs<1,1>=vet;vexs<1,2>=t1<ii>;matr<vexs<1,2>,vexs<1,1>>=0;flagg=1;tem=1;while flagg[flagg ed]=edf<matr,eds,vexs,ed,tem>;tem=tem+1;if ed<1,eds>~=0 & ed<2,eds>~=0T=ed;T<2,eds>=1;c=0;for g=1:edsc=c+d<T<1,g>,T<2,g>>;endflagg=0;break;endendendendfunction[flag ed]=edf<matr,eds,vexs,ed,tem>flag=1;for i=2:eds[dvex f]=flecvexf<matr,i,vexs,eds,ed,tem>;if f==1flag=0;break;endif dvex~=0ed<:,i>=[vexs<1,i> dvex];vexs<1,i+1>=dvex;matr<vexs<1,i+1>,vexs<1,i>>=0;elsebreak;endendfunction [dvex f]=flecvexf<matr,i,vexs,eds,ed,temp> f=0;edd=find<matr<vexs<1,i>,:>==1>;dvex=0;dvex1=[];ded=[];if length<edd>==1dvex=edd;elsedd=1;dd1=0;kkk=0;for kk=1:length<edd>m1=find<vexs==edd<kk>>;if sum<m1>==0dvex1<dd>=edd<kk>;dd=dd+1;dd1=1;elsekkk=kkk+1;endendif kkk==length<edd>tem=vexs<1,i>*ones<1,kkk>;edd1=[tem;edd];for l1=1:kkklt=0;ddd=1;for l2=1:edsif edd1<1:2,l1>==ed<1:2,l2>lt=lt+1;endendif lt==0ded<ddd>=edd<l1>;ddd=ddd+1;endendendif temp<=length<dvex1>dvex=dvex1<temp>;elseif temp>length<dvex1> & temp<=length<ded>dvex=ded<temp>;elsef=1;endend程序二:Hamilton改良圈算法〔找出比较好的Hamilton路〕function [C d1]= hamiltonglf<v>%d表示权值矩阵%C表示算法最终找到的Hamilton圈.%v =[ 51 67;37 84;41 94;2 99;18 54;4 50;24 42;25 38;13 40;7 64;22 60;25 62;18 40;41 26];n=size<v,1>;subplot<1,2,1>hold on;plot <v<:,1>,v<:,2>,'*'>; %描点for i=1:nstr1='V';str2=num2str<i>;dot=[str1,str2];text<v<i,1>-1,v<i,2>-2,dot>; %给点命名endplot <v<:,1>,v<:,2>>;%连线plot<[v<n,1>,v<1,1>],[v<n,2>,v<1,2>]>;for i =1:nfor j=1:nd<i,j>=sqrt<<v<i,1>-v<j,1>>^2+<v<i,2>-v<j,2>>^2>;endendd2=0;for i=1:nif i<nd2=d2+d<i,i+1>;elsed2=d2+d<n,1>;endendtext<10,30,num2str<d2>>;n=size<d,2>;C=[linspace<1,n,n> 1];for nnn=1:20C1=C;if n>3for m=4:n+1for i=1:<m-3>for j=<i+2>:<m-1>if<d<C<i>,C<j>>+d<C<i+1>,C<j+1>><d<C<i>,C<i+1>>+d<C<j>,C<j+1>>>C1<1:i>=C<1:i>;for k=<i+1>:jC1<k>=C<j+i+1-k>;endC1<<j+1>:m>=C<<j+1>:m>;endendendendelseif n<=3if n<=2fprint<'It does not exist Hamilton circle.'>; elsefprint<'Any cirlce is the right answer.'>;endendC=C1;d1=0;for i=1:nd1=d1+d<C<i>,C<i+1>>;endd1;endsubplot<1,2,2>;hold on;plot <v<:,1>,v<:,2>,'*'>; %描点for i=1:nstr1='V';str2=num2str<i>;dot=[str1,str2];text<v<i,1>-1,v<i,2>-2,dot>; %给点命名endv2=[v;v<1,1>,v<1,2>];plot<v<C<:>,1>,v<C<:>,2>,'r'>;text<10,30,num2str<d1>>;第五讲:匹配问题与算法程序一:较大基础匹配算法function J=matgraf<W>n=size<W,1>;J=zeros<n,n>;while sum<sum<W>>~=0a=find<W~=0>;t1=mod<a<1>,n>;if t1==0t1=n;endif a<1>/n>floor<a<1>/n>t2=floor<a<1>/n>+1;elset2=floor<a<1>/n>;endJ<t1,t2>=1,J<t2,t1>=1;W<t1,:>=0;W<t2,:>=0;W<:,t1>=0;W<:,t2>=0;endJ;程序二:匈牙利算法〔完美匹配算法,包括三个文件fc01,fc02,fc03〕function [e,s]=fc01<a,flag>if nargin==1flag=0;endb=a;if flag==0cmax=max<max<b>'>;b=cmax-b;endm=size<b>;for i =1:m<1>b<i,:>=b<i,:>-min<b<i,:>>;endfor j=1:m<2>b<:,j>=b<:,j>-min<b<:,j>>;endd=<b==0>;[e,total]=fc02<d>;while total~=m<1>b=fc03<b,e>;d=<b==0>;[e,total]=fc02<d>;endinx=sub2ind<size<a>,e<:,1>,e<:,2>>;e=[e,a<inx>];s=sum<a<inx>>;function [e,total]=fc02<d>total=0;m=size<d>;e=zeros<m<1>,2>;t=sum<sum<d>'>;nump=sum<d'>;while t~=0[s,inp]=sort<nump>;inq=find<s>;ep=inp<inq<1>>;inp=find<d<ep,:>>;numq=sum<d<:,inp>>;[s,inq]=sort<numq>;eq=inp<inq<1>>;total=total+1;e<total,:>=[ep,eq];inp=find<d<:,eq>>;nump<inp>=nump<inp>-1;nump<ep>=0;t=t-sum<d<ep,:>>-sum<d<:,eq>>+1;d<ep,:>=0*d<ep,:>;d<:,eq>=0*d<:,eq>;endfunction b=fc03<b,e>m=size<b>;t=1;p=ones<m<1>,1>;q=zeros<m<1>,1>;inp=find<e<:,1>~=0>;p<e<inp,1>>=0;while t~=0tp=sum<p+q>;inp=find<p==1>;n=size<inp>;for i=1:n<1>inq=find<b<inp<i>,:>==0>;q<inq>=1;endinp=find<q==1>;n=size<inp>;for i=1:n<1>if all<e<:,2>-inp<i>>==0inq=find<<e<:,2>-inp<i>>==0>;p<e<inq>>=1;endendtq=sum<p+q>;t=tq-tp;endinp=find<p==1>;inq=find<q==0>;cmin=min<min<b<inp,inq>>'>;inq=find<q==1>;b<inp,:>=b<inp,:>-cmin;b<:,inq>=b<:,inq>+cmin;第六讲:最大流最小费用问题程序一:2F算法<Ford-Fulkerson算法>,求最大流%C=[0 5 4 3 0 0 0 0;0 0 0 0 5 3 0 0;0 0 0 0 0 3 2 0;0 0 0 0 0 0 2 0; %0 0 0 0 0 0 0 4;0 0 0 0 0 0 0 3;0 0 0 0 0 0 0 5;0 0 0 0 0 0 0 0 ] function [f wf]=fulkersonf<C,f1>%C表示容量%f1表示当前流量,默认为0%f表示最大流±íʾ×î´óÁ÷%wf表示最大流的流量n=length<C>;if nargin==1;f=zeros<n,n>;elsef=f1;endNo=zeros<1,n>;d=zeros<1,n>;while <1>No<1>=n+1;d<1>=Inf;while <1>pd=1;for <i=1:n>if <No<i>>for <j=1:n>if <No<j>==0 & f<i,j><C<i,j>>No<j>=i;d<j>=C<i,j>-f<i,j>;pd=0;if <d<j>>d<i>>d<j>=d<i>;endelseif <No<j>==0 & f<j,i>>0>No<j>=-i;d<j>=f<j,i>;pd=0;if <d<j>>d<i>>d<j>=d<i>;endendendendendif <No<n>|pd>break;endendif <pd>break;enddvt=d<n>;t=n;while <1>if<No<t>>0>f<No<t>,t>=f<No<t>,t>+dvt;elseif <No<t><0>f<No<t>,t>=f<No<t>,t>-dvt;endif <No<t>==1>for <i=1:n>No<i>=0;d<i>=0;endbreakendt=No<t>;endendwf=0;for <j=1:n>wf=wf+f<1,j>;endf;wf;程序二:Busacker-Gowan算法<求最大流最小费用>%C=[0 15 16 0 0;0 0 0 13 14;0 11 0 17 0;0 0 0 0 8;0 0 0 0 0] %b=[0 4 1 0 0;0 0 0 6 1;0 2 0 3 0;0 0 0 0 2;0 0 0 0 0]%function [f wf zwf]=BGf<C,b>%C表示弧容量矩阵%b表示弧上单位流量的费用%f表示最大流最小费用矩阵%wf最大流量%zwf表示最小费用n=size<C,2>;wf=0;wf0=inf;f=zeros<n,n>;while <1>a=ones<n,n>*inf;for <i=1:n>a<i,i>=0;endfor <i=1:n>for <j=1:n>if<C<i,j>>0 & f<i,j>==0>a<i,j>=b<i,j>;elseif <C<i,j>>0 & f<i,j>==C<i,j>>a<j,i>=-b<i,j>;elseif <C<i,j>>0>a<i,j>=b<i,j>;a<j,i>=-b<i,j>;endendendfor <i=2:n>p<i>=inf;s<i>=i;endfor <k=1:n>pd=1;for <i=2:n>for <j=1:n>if <p<i>>p<j>+a<j,i>>p<i>=p<j>+a<j,i>;s<i>=j;pd=0; endendendif <pd>break;endendif <p<n>==inf>break;enddvt=inf;t=n;while <1>if <a<s<t>,t>>0>dvtt=C<s<t>,t>-f<s<t>,t>;elseif <a<s<t>,t><0>dvtt=f<t,s<t>>;endif <dvt>dvtt>dvt=dvtt;endif <s<t>==1>break;endt=s<t>;endpd=0;if <wf+dvt>=wf0>dvt=wf0-wf;pd=1;endt=n;while <1>if <a<s<t>,t>>0>f<s<t>,t>=f<s<t>,t>+dvt; elseif <a<s<t>,t><0>f<<t>,s<t>>=f<t,s<t>>-dvt; endif <s<t>==1>break;endt=s<t>;endif <pd>break;endwf=0;for <j=1:n>wf=wf+f<1,j>;endendzwf=0;for <i=1:n>for <j=1:n>zwf=zwf+b<i,j>*f<i,j>;endendf;。
最短路径问题(Dijkstra算法)和最小生成树(Kruskal算法和Prim算法)

t(j)=tmin;
end
end
end
ifk==n
break;
end
end
T;
c;
Prim算法程序:
function[T c] =Primf(a)
%a表示权值矩阵
%c表示生成树的权和
%T表示生成树的边集合
l=length(a);
a(a==0)=inf;
k=1:l;
listV(k)=0;
上机实验1、2
1.最短路径问题(Dijkstra算法)
2.最小生成树(Kruskal算法和Prim算法)
一、最短路径问题(Dijkstra算法)
实验问题描述:如图的交通网络,每条弧上的数字代表车辆在该路段行驶所需的时间,有向边表示单行道,无向边表示可双向行驶。若有一批货物要从1号顶点运往11号顶点,问运货车应沿哪条线路行驶,才能最快地到达目的地。
listV(1)=1;
e=1;
while(e<l)
min=inf;
fori=1:l
iflistV(i)==1
forj=1:l
iflistV(j)==0&min>a(i,j)
min=a(i,j);b=a(i,j);
s=i;d=j;
end
end
end
end
listV(d)=1;
distance(e)=b;
T =
3 4 1 2
4 5 3 5
c =
10
>> a=[0 5 3 7 inf;5 0 8 inf 4;3 8 0 1 6;7 inf 1 0 2;inf 4 6 2 0];
>> [T c] =Primf(a)
Dijkstra算法,最短路径路由算法matlab代码

Dijkstra算法,最短路径路由算法matlab代码Dijkstra算法是⼀种最短路径路由算法,⽤于计算⼀个节点到其他所有节点的最短路径。
主要特点是以起始点为中⼼向外层层扩展,直到扩展到终点为⽌。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率较低。
算法详细解释各⽹站都有,不太难。
下边是对下图从D开始到A节点寻找最短路径的matlab代码,个⼈原创。
%% Dijkstra算法%by Jubobolv369 at 2022/1/22clc;clear;close all;%% 初始化带权邻接矩阵,起点、终点等initRoute=[0 12 inf inf inf 16 14;12 0 10 inf inf 7 inf;inf 10 0 3 5 6 inf;inf inf 3 0 4 inf inf;inf inf 5 4 0 2 8;16 7 6 inf 2 0 9;14 inf inf inf 8 9 0;];[row,column]=size(initRoute);start_node=4;end_node=1;close_list=[];open_list=[];%closelist中加⼊初始节点close_list=[start_node,start_node,0];%% 如果closelist中没有终点,则遍历节点,通过⽐较逐渐加⼊节点到closelist。
while isempty(find(close_list(:,1) == end_node))[last1,~]=size(close_list);%获取closelist的最后⼀⾏的索引now_node=close_list(last1,1);%当前节点编号now_length=close_list(last1,3);%当前最优长度[last2,~]=size(open_list); %%获取openlist的最后⼀⾏的索引now_list=initRoute(now_node,:); %从原始矩阵中取初当前节点的边权值i=1;%% 更新openlistfor j=1:column%如果第j个节点可达、不是⾃⾝且不在close_list中,该点可能需要改动或添加到openlist中if now_list(j)~=inf && now_list(j)~=0 && isempty(find(close_list(:,1) == j))if last1==1open_list(i,1)=j;open_list(i,2)=now_node;open_list(i,3)=now_list(j);i=i+1;%如果不在openlist中,就将其添加到其中,否则将通过当前⽗节点到此节点的权值与之前的作⽐较elsek=find(open_list(:,1) == j);if isempty(k)open_list(last2+i,1)=j;open_list(last2+i,2)=now_node;open_list(last2+i,3)=now_list(j)+now_length;i=i+1;elseif open_list(k,3)>(now_list(j)+now_length) %若現在的路徑⾧度⼩,則更新路徑open_list(k,1)=j;open_list(k,1)=j;open_list(k,2)=now_node;open_list(k,3)=now_list(j)+now_length;endendendend%% 更新closelist和openlist。
dijkstra算法

1、(求两点之间的最短路程)Dijkstra算法的MATLAB程序dijkstra.m如下:% Dijkstra’s Algorithmfunction [S, D]= dijkstra (i,m,W)% i为最短路径的起始点,m为图顶点数,W为图的带权邻接矩阵% 不构成边的两顶点之间用inf 表示% S的每一列从上到下记录了从始点到终点的最短路径所经顶点的序号% D是一个行向量,记录了S中所示路径的大小dd=[ ];tt=[ ];ss=[ ];ss(1,1)=i; v=1:m; v(i)=[ ];dd=[0;i];% dd的第二行是每次求出的最短路径的终点,第一行是最短路径的值kk=2; [mdd,ndd]=size(dd);while ~isempty(v)[tmpd,j]=min(W(i,v));tmpj=v(j);for k=2:ndd[tmp1,jj]=min(dd(1,k)+W(dd(2,k),v));tmp2=v(jj);tt(k-1,:)=[tmp1,tmp2,jj];endtmp=[tmpd,tmpj,j;tt]; [tmp3,tmp4]=min(tmp(:,1));if tmp3==tmpd,ss(1:2,kk)=[i;tmp(tmp4,2)];else, tmp5=find(ss(:,tmp4)~=0); tmp6=length(tmp5);if dd(2,tmp4)==ss(tmp6,tmp4)ss(1:tmp6+1,kk)=[ss(tmp5,tmp4); tmp(tmp4,2)];else, ss(1:3,kk)=[i; dd(2,tmp4); tmp(tmp4,2)];endenddd=[dd,[tmp3;tmp(tmp4,2)]];v(tmp(tmp4,3))=[ ];[mdd,ndd]=size(dd);kk=kk+1;endS=ss;D=dd(1,: );。
图论MATLAB算法

第一章:Dijkstra 算法开始?dot i ≤输入,确定邻接矩阵a 确定邻接矩阵a 的节点数dot1=i算每一个节点到U 中每一个节点的最小值 输出第n i 个节点到第一个节点的最小距离i L ,i=1∧dot结束算这dot 个最小值的最小值l ,并确定其节点位置i nl L i n =将第一个节点放入集合U 中将已经确定的第i n 节点到所有节点的权值赋为∞ 将所有节点到第i n 节点的权值加上l 并代替之 ?2>i1+=i i将第i n 节点放入集合U 中 YESNOYESNO求下面赋权图(左图)中顶点u0到其余顶点的最短路。
其邻接矩阵W 为:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞=024782063446046340357630135102273201847210W)(i u l迭 代 次 数0u 1u 2u 3u 4u 5u 6u 7u1 2 3 4 5 6 7 8 0 ∞ ∞ ∞ ∞ ∞ ∞ ∞1 2 ∞ 7 ∞ 4 82 4 7 ∞ 4 83 7 ∞4 86 9 4 86 9 69 6 9 最后标记)(v l )(v z0 1 2 3 6 9 4 6 0u 0u 0u 2u 3u 3u 0u 6u1u 2u 3u 4u 5u 6u 7u 0ufunction dijkstra%注:此程序仅作参考,欢迎批评指正。
clcclear%Dijkstra算法:%%%%给邻接矩阵赋值%%%%%%%%%%%%a=[0,1,2,inf,7,inf,4,8;1,0,2,3,inf,inf,inf,7;0,0,0,1,5,inf,inf,inf;0,0,0,0,3,6,inf,inf;0,0,0,0,0,4,3,inf;0,0,0,0,0,0,6,4;0,0,0,0,0,0,0,2;];for i=2:8for j=1:i-1a(i,j)=a(j,i);endenddot=size(a,1);%节点数fprintf('\t邻接矩阵的标准形式:');afuquantu=a;%在赋权图中用到fprintf('\t其中,inf代表无穷大∞,a(i,j)代表第i个节点到第j个节点的权。
应用Dijkstra算法求赋权图最短路径
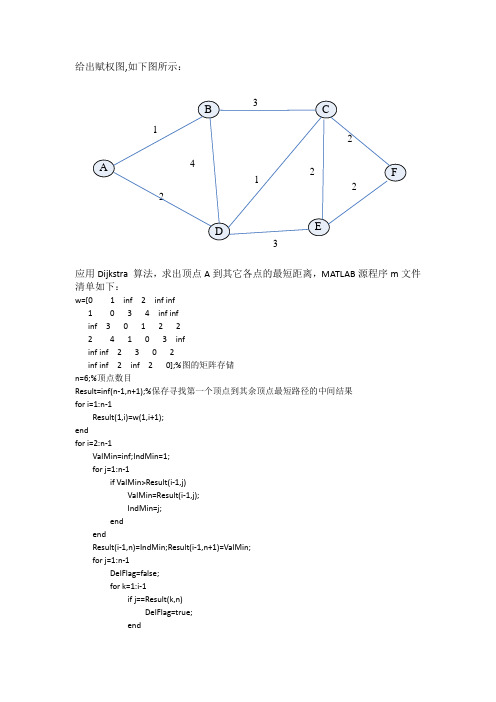
给出赋权图,如下图所示:应用Dijkstra 算法,求出顶点A到其它各点的最短距离,MATLAB源程序m文件清单如下:w=[0 1 inf 2 inf inf1 0 3 4 inf infinf 3 0 1 2 22 4 1 03 infinf inf 2 3 0 2inf inf 2 inf 2 0];%图的矩阵存储n=6;%顶点数目Result=inf(n-1,n+1);%保存寻找第一个顶点到其余顶点最短路径的中间结果for i=1:n-1Result(1,i)=w(1,i+1);endfor i=2:n-1ValMin=inf;IndMin=1;for j=1:n-1if ValMin>Result(i-1,j)ValMin=Result(i-1,j);IndMin=j;endendResult(i-1,n)=IndMin;Result(i-1,n+1)=ValMin;for j=1:n-1DelFlag=false;for k=1:i-1if j==Result(k,n)DelFlag=true;endif DelFlag==falseif Result(i-1,j)>Result(i-1,n+1)+w(Result(i-1,n)+1,j+1)Result(i,j)=Result(i-1,n+1)+w(Result(i-1,n)+1,j+1);elseResult(i,j)=Result(i-1,j);endendendendValMin=inf;IndMin=1;for j=1:n-1if ValMin>Result(n-1,j)ValMin=Result(n-1,j);IndMin=j;endendResult(n-1,n)=IndMin;Result(n-1,n+1)=ValMin;ValueRoute=inf(n-1,n);%保存用标号表示的第一个顶点到其余顶点的最短路径和最短距离for i=1:n-1j=1;while Result(j,n)~=ij=j+1;endIndRoute=n-1;ValueRoute(i,IndRoute)=Result(j,n);ValueRoute(i,n)=Result(j,n+1);ValMin=Result(j,n+1);IndMin=Result(j,n);IndRoute=IndRoute-1;while Result(j,n)>1j=j-1;if Result(j,IndMin)>ValMin;ValueRoute(i,IndRoute)=Result(j,n);IndRoute=IndRoute-1;ValMin=Result(j,n+1);IndMin=Result(j,n);endendendStringRoute.Route='A ';%结构StringRoute的Route域依次临时存储从第一个顶点到其余顶点的最短路径StringRoute.Distance=0;%结构StringRoute的Route域依次临时存储从第一个顶点到其余顶点的最短距离k=2;for i=1:n-1switch ValueRoute(1,i)StringRoute.Route(k)='B';k=k+1;case 2StringRoute.Route(k)='C';k=k+1;case 3StringRoute.Route(k)='D';k=k+1;case 4StringRoute.Route(k)='E';k=k+1;case 5StringRoute.Route(k)='F';k=k+1;otherwisecontinue;end%对于顶点数目不同并且顶点表示方式不同的图要相应修改CASE语句个数和分支语句endStringRoute.Distance=ValueRoute(1,n);CharRoute=[StringRoute];for j=2:n-1StringRoute.Route='A ';%结构StringRoute的Route域依次临时存储从第一个顶点到其余顶点的最短路径k=2;for i=1:n-1switch ValueRoute(j,i)case 1StringRoute.Route(k)='B';k=k+1;case 2StringRoute.Route(k)='C';k=k+1;case 3StringRoute.Route(k)='D';k=k+1;case 4StringRoute.Route(k)='E';k=k+1;case 5StringRoute.Route(k)='F';k=k+1;otherwisecontinue;end%对于顶点数目不同并且顶点表示方式不同的图要相应修改CASE语句个数和分支语句endStringRoute.Distance=ValueRoute(j,n);CharRoute=[CharRoute;StringRoute];endfprintf('A点到其余5个顶点的最短距离和最短路径如下:\n')for i=1:n-1disp(CharRoute(i))end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用计算机语言编程实现D算法
一:实验目的
本实验课程主要目的是让学生够熟练掌握图论中的D算法。
二:实验方法
选择MATLAB语言编程实现D算法。
三:实验要求
1.输入必要参数,包括:节点个数、节点间路径长度、给定节点;
2.输出给定节点到其它各节点的最短路径、径长;
3.节点间路径长度用矩阵形式表示。
四:实验内容
无向图共有7个节点,如下图所示。
v1
45
7
计算机输入的节点间路径长度为7×7矩阵:
1234567
1 2 3 4 5 6 7
0123
106
2054
304
5407 6408
780⎡⎤
∞∞∞⎢⎥
∞∞∞∞⎢⎥
⎢⎥∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞
⎢⎥∞∞∞
⎢⎥⎢⎥∞∞∞∞
⎣⎦v v v v v v v
v
v
v
v
v
v
v
若
1
v为指定节点,则1v到其它各节点的最短路径及径长的计算机计算结果为:
提示:不相邻的两个节点间∞可以用相对较大的数代替(如输入100表示∞)
五:实验原理
1. D 算法原理
已知图G=(V,E),将其节点集分为两组:置定节点集p G 和未置定节点集
p G G -。
其中p G 内的所有置定节点,是指定点s v 到这些节点的路径为最短(即
已完成最短路径的计算)的节点。
而p G G -内的节点是未置定节点,即s v 到未置定节点距离是暂时的,随着算法的下一步将进行不断调整,使其成为最短径。
在调整各未置定节点的最短径时,是将p G 中的节点作为转接点。
具体地说,就是将p G 中的节点作为转接点,计算(s v ,j v )的径长(j p v G G ∈-),若该次计算的径长小于上次的值,则更新径长,否则,径长不变。
计算后取其中径长最短者,之后将j v 划归到p G 中。
当(p G G -)最终成为空集,同时p G G =,即求得s v 到所有其他节点的最短路径。
j w 表示s v 与其他节点的距离。
在p G 中,i w 表示上一次划分到p G 中的节点i
v 到s v 得最短路径。
在 p G G -中,表示s v 到j v (j p v G G ∈-)仅经过p G 中的节点作为转接点所求得的该次的最短路径的长度。
如果s v 与j v 不直接相连,且无置定节点作为转接点,则令j w =∞。
2. D 算法实现流程
D 算法流程如下图所示。
六:例题的计算过程
表1 D算法计算过程
v到其他各节点的最短路径和径长
表2
1
七:仿真过程
1. 输入参数:
a. 输入无向图的节点个数
提示:‘Please input number of the notes: k=’
输入:7;
b. 输入对应节点个数的k×k大小的矩阵,并且具有检测能力,如果矩阵大小不匹配,提示重新输入
提示:‘Note: If there is no direct link between notes, use 100 to reprsent infinite Please input the k*k matrix of the length of path: M=’
输入:[0,1,2,3,100,100,100;
1,0,100,100,100,6,100;
2,100,0,100,5,4,100;
3,100,100,0,4,100,100;
100,100,5,4,0,100,7;
100,6,4,100,100,0,8;
100,100,100,100,7,8,0]
若输入错误,提示:‘please input the correct size of the matrix,Please input the k*k matrix of the length of path: M=’
c. 输入起始节点
提示:‘Please identify the initial note: s’
输入:1。
2. 输出结果
a. 输出最短路径矩阵(起始节点为
v)
1
s =
1 1 1 1 1 1 1
0 2 3 4 3 3 3
0 0 0 0 6 5 6
0 0 0 0 0 0 7
c. 输出对应的路径长度(与s顺序对应)
d =
0 1 2 3 6 7 14
3.运行结果截屏。
