试题及其答案--弹性力学与有限元分析(DOC)

合集下载

弹性力学及有限元法答案下载

弹性力学及有限元法答案下载一、是非题（下列各题，你认为正确的，请在题干的括号内打“√”，错的打“×”。

每题3分，共12分）1、按应力求解平面问题时，若应力分量满足平衡方程，且在边界上满足应力边界条件即为正确解答。

…………………………………………………………………………………………（）2、图示弹性体在两种荷载作用下，若lh，则A点的应力分量是相同的。

…………………（）3、用有限单元法求解平面应力问题时，单元刚度矩阵的子块kij的物理意义是：仅当第j个结点沿坐标正向发生x或y方向的单位位移，在i结点处引起的沿x或y 方向的结点力。

……（）4、等厚度旋转圆盘以等角速度ω旋转时，该问题应属平面应变问题。

……………………（）二、单选题（在本题的每一小题的备选答案中，只有一个是正确的，请把你认为正确答案的题号，填入题干的括号内。

多选不给分。

每题材5分，共15分）1、图示半平面体受集中力P作用，其应力边界条件为………………………………………（）①θ＝0，π，σθ＝σr＝0 ②θ＝0，π，σθ＝τθr ＝0③θ＝0，π，r≠0，σθ＝τθr＝0 ④θ＝0，π，r≠0，σθ＝τθr＝02、铅直平面内正方形薄板，边长为2a，周长固定，只受重力作用。

用瑞次法求解，其位移表达式应为…………………………………………………………………………………………（）3、不计体力，图示弹性体的应力函数为………………………………………………………（）①υ＝τ0xy－(qy3)/6b ②υ＝τxy＋(qy3)/6b③υ＝－τ0xy－(qy3)/6b ④υ＝－τxy＋(qy3)/6b三、填空题1、（3分）按应力求解平面问题。

若认应力函数υ＝ax5y＋bxy5（a、b 不等于零），则系数b、b应满足关系（）。

2、（4分）已知一点应力状态为σx ＝100，σy＝50，τxy＝10，则σ1＝（），σ2＝（）。

3、（3分）图示薄板，设其厚度t＝1。

弹性力学与有限元分析试题及参考答案

将已知应力分量，，代入上式，可知满足相容方程。
按应力求解平面应变问题的相容方程：
将已知应力分量，，代入上式，可知满足相容方程。
4、试写出平面问题的应变分量存在的必要条件，并考虑下列平面问题的应变分量是否可能存在。
（1），，；
（2），，；
（3），，；
其中，A，B，C，D为常数。
弹性力学与有限元分析试题及参考答案
四、分析计算题
1、试写出无体力情况下平面问题的应力分量存在的必要条件，并考虑下列平面问题的应力分量是否可能在弹性体中存在。
（1），，；
（2），，；
其中，A，B，C，D，E，F为常数。
解：应力分量存在的必要条件是必须满足下列条件：（1）在区域内的平衡微分方程；（2）在区域内的相容方程；（3）在边界上的应力边界条件；（4）对于多连体的位移单值条件。
6、证明应力函数能满足相容方程，并考察在如图所示的矩形板和坐标系中能解决什么问题（体力不计，）。
解：将应力函数代入相容方程
可知，所给应力函数能满足相容方程。
由于不计体力，对应的应力分量为
，，
对于图示的矩形板和坐标系，当板内发生上述应力时，根据边界条件，上下左右四个边上的面力分别为：
上边，，，，，；
解：应变分量存在的必要条件是满足形变协调条件，即
将以上应变分量代入上面的形变协调方程，可知：
（1）相容。
（2）（1分）；这组应力分量若存在，则须满足：B=0，2A=C。
（3）0=C；这组应力分量若存在，则须满足：C=0，则，，（1分）。
5、证明应力函数能满足相容方程，并考察在如图所示的矩形板和坐标系中能解决什么问题（体力不计，）。

试题及其答案--弹性力学与有限元分析.(DOC)

如下图所示三角形薄板，按三结点三角形单元划分后，对于与局部编码ijm 对应的整体编码，以下叙述正确的是（ D ）。

① I 单元的整体编码为162 ② II 单元的整体编码为426 ③ II 单元的整体编码为246 ④ III 单元的整体编码为243 ⑤ IV 单元的整体编码为564A. ①③B. ②④C. ①④D. ③⑤一、填空题 1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。

2、在弹性力学中规定，线应变以伸长时为正，缩短时为负，与正应力的正负号规定相适应。

3、在弹性力学中规定，切应变以直角变小时为正，变大时为负，与切应力的正负号规定相适应。

4、物体受外力以后，其内部将发生内力，它的集度称为应力。

与物体的形变和材料强度直接有关的，是应力在其作用截面的法线方向和切线方向的分量，也就是正应力和切应力。

应力及其分量的量纲是L -1MT -2。

5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。

6、平面问题分为平面应力问题和平面应变问题。

7、已知一点处的应力分量100=x σMPa ，50=y σMPa ，5010=xy τ MPa ，则主应力=1σ150MPa ，=2σ0MPa ，=1α6135' 。

8、已知一点处的应力分量， 200=x σMPa ，0=y σMPa ，400-=xy τ MPa ，则主应力=1σ512MPa ，=2σ-312 MPa ，=1α-37°57′。

9、已知一点处的应力分量，2000-=x σMPa ，1000=y σMPa ，400-=xy τ MPa ，则主应力=1σ1052 MPa ，=2σ-2052 MPa ，=1α-82°32′。

10、在弹性力学里分析问题，要考虑静力学、几何学和物理学三方面条件，分别建立三套方程。

11、表示应力分量与体力分量之间关系的方程为平衡微分方程。

12、边界条件表示边界上位移与约束，或应力与面力之间的关系式。

弹性力学有限元分析题

有限元分析练习1.如图所示为一简支梁，高0.6m，宽0.3m，长3m，承受均布荷载15kN/m,弹性模量为E=20X1010Pa,泊松比为μ=0.3。

(1)试将其看着平面应力问题进行有限元分析（应力，应变，位移），并与解析解进行比较分析。

(2)根据有限元计算结果，分析梁的弯曲变形是否符合平截面假定？将高度分别变为2m，0.5m,又如何？(3)如何提高该梁的有限元计算精度，请对比分析。

2.如图所示为一简支梁，高0.5m，宽0.3m，长2m，梁顶面承受均布荷载10kN/m,梁一侧受到集中荷载作用大小为10kN，另一侧受到均布荷载作用为20kN/m.弹性模量为E=3X1010Pa,泊松比为μ=0.2。

（1）分别计算在横向荷载和轴向荷载单独作用下梁的应力、应变和位移情况，并对结果进行讨论分析。

（2）计算在横向和轴向荷载共同作用下，梁的应力、应变和位移情况，并于仅受到横向荷载作用下梁的计算结果进行对比分析。

（3）如何提高梁的有限元计算精度，并对比分析。

3.下图表示一块带圆孔的方板，在x方向受到均布压力80kN/m。

方板边长为0.6m，厚度为0.03m，圆孔的半径为0.02m。

方板的弹性模量为E=2X1011Pa，泊松比为μ=0.3.（1）试进行有限元分析（应力，应变，位移），并与解析解进行比较分析。

（2）如何提高本题有限元计算精度，并对比分析。

（3）如果把圆孔改为边长为0.02m的正方形，是比较两者应力集中程度。

4. 下图表示一块带圆孔的方柱，在x 方向受到均布压力100kN/m 2。

方板边长为0.5m ，圆孔的半径为0.02m 。

方板的弹性模量为E=2X1011Pa ，泊松比为μ=0.2. （1）假设厚度为无限大进行有限元分析（应力，应变，位移），并与解析解进行比较分析。

（2）如何提高本题有限元计算精度，并对比分析。

（3）如果把圆孔改为边长为0.02m 的三角形，是比较两者应力集中程度。

5. 下图为带圆孔的方板，在x 方向受到均布压力120kN/m ，在y 方向受到均布压力为60kN/m 。

弹性力学与有限元法习题集

' yx dx

0
' yx
dM dx
S
* 2
I
Q(x) I
n 2 y
y1

dy1

Q(x) I
(n2 4
y2 ) 1 Q(x) (n2 2 2I 4
y2)
2019/7/29
slide14
返回
由剪应力互等定理，
yx

' yx

Q(x) (n2 2I 4
答案返回
1. 有限单元法的含义？答：用有限个单元将连续体离散化，通过对有限个单元作分片插
值求解各种力学、物理问题的一种数值方法。连续体的单元是各种形状（如三角形、四边形、六面体等）的单元体。
2.有限元法的解题思路？答（1）网格划分；（2）单元分析；（3）整体分析。
3.有限元法的优点？答（1）物理概念清晰，便于入门；
13. 已知某单元，其结点编号为i，j，m，其坐标依次为（2， 2）、（6，3）、（5，6），试写出其形函数Ni，Nj，Nm 及单元的应变矩阵。
2019/7/29
slide22
答案返回
14. 图示平面应力状态的直角三角形单元及其结点编码，设
1 6
试求：
（1）形态矩阵[N]；（2）几何矩阵[B]及应力转移矩阵[S]; （3）单元刚度矩阵[k]e
6. 应用几何方程推导应变分量应满足下列变形协调方程。
2 x 2 y 2 xy
y2 x2 xy
2019/7/29
slide6
答案返回
7. 悬臂梁在三角形分布载荷作用下，可以看成平面应力问题，
应力分量表达式为， x

弹性力学及有限单元法答案及评分标准

弹性力学及有限单元法答案及评分标准一、1、, （2分）2、, （2分）3、,（3分）4、, (也可用三个积分的应力边界条件代替) （1分）二、(a)平衡微分方程、相容方程、应力边界条件、多连体中的位移单值条件（4分）(b)代入相容方程，不满足相容方程，不是可能的解答（3分）(c)代入相容方程，不满足相容方程，由此求得的位移分量不存在（3分）三、（1）无穷小的线段的单位伸缩或相对伸缩，称为正应变。

（2分）正应变伸长为正，缩短为负。

（1分）与坐标正向一致的两个无穷小的线段之间的直角的改变量，称为剪应变。

（2分）剪应变以直角变小为正，变大为负。

（1分）（2）弹性体中两个正交的直线之间所夹的直角有四个，变形后，其中两个直角变大，两个直角变小，剪应变以直角变小为正，变大时为负，因此必须明确规定剪应变是与坐标正向一致的两个无穷小的线段之间的直角的改变量。

（1分）（3）A点位移：（）（1分）；B点位移：（）（1分）；（2分）；（2分）；（2分）四、(1)平面应力问题面上任一点的应力（）是近似为0（1分）。

由上（）为0和方向应力梯度很小推出任一点的应力（）为0是近似的。

（2分）(2)平面应变问题Z面上任一点的应力（）是精确为0（1分）。

任意面均为对称面，其上的反对称应力为0，将某个面切开，切开的左右面上的应力既要指向相同（对称条件），又要指向相反（内力须满足牛顿第三定律），故只能为0，同理为0。

（1分）五、平面应力问题由可导得其物理方程为：（5分）平面应变问题由可导得其物理方程为：（5分）或对平面应力问题物理方程进行转换得平面应变问题物理方程六、1、将，代入，得P点的应变分量（1分）（1分）（1分）2、由平面应力问题的物理方程可得代入P点的应变分量，得其应力分量为（3分）3、处的应力分量为：处面力处面力的合力和合力矩为：（6分）七、1）单元结点力是指单元和结点之间的相互作用力（2分）结点力作用在单元上时与坐标正向一致为正（1分）2）单元结点荷载是指单元上的外力（体力和面力）按静力等效的原则移置到结点上的等效荷载（2分）与坐标正向一致为正（1分）3）例：表示结点方向发生单位位移在结点方向的结点力或单元某一个自由度方向发生单位位移在另一个自由度方向引起的结点力（4分）4）例：表示整个弹性体的2结点方向发生单位位移引起1结点方向的结点力或整个弹性体某一个自由度方向发生单位位移在另一个自由度方向引起的结点力（4分）5）结点力和等效结点荷载的平衡（4分）6）设定位移模式使单元中任一点的位移可由结点位移求得而不独立，只有有限个可动结点位移作为基本未知量或自由度。

弹性力学有限元考试卷与答案(AB卷)

2009-2010学年第一学期《弹性力学有限元》课内考试A卷授课班号年级专业学号姓名一、判断正误（×）1. 节点的位置依赖于形态，而并不依赖于载荷的位置（√）2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元（×）3. 不能把梁单元、壳单元和实体单元混合在一起作成模型（√）4. 四边形的平面单元尽可能作成接近正方形形状的单元（×）5. 平面应变单元也好，平面应力单元也好，如果以单位厚来作模型化处理的话会得到一样的答案（×）6. 用有限元法不可以对运动的物体的结构进行静力分析（√）7. 一般应力变化大的地方单元尺寸要划的小才好（×）8. 所谓全约束只要将位移自由度约束住，而不必约束转动自由度（×）9. 线性应力分析也可以得到极大的变形（√）10. 同一载荷作用下的结构，所给材料的弹性模量越大则变形值越小二、填空1．平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板，但前者受力特点是：平行于板面且沿厚度均布载荷作用，变形发生在板面内；后者受力特点是：垂直于板面的力的作用，板将变成有弯有扭的曲面。

（3分）2．平面应力问题与平面应变问题都具有三个独立的应力分量：σx，σy，τxy，三个独立的应变分量：εx，εy，γxy，但对应的弹性体几何形状前者为薄板，后者为长柱体。

（3分）3．位移模式需反映刚体位移，反映常变形，满足单元边界上位移连续。

（3分）4．单元刚度矩阵的特点有：对称性，奇异性，还可按节点分块。

（2分） 5．薄板弯曲问题每个节点有个3自由度，分别是：w 、θx 、θy ，但其中只有一个是独立的，其余两个可以用它表示为：,x y w wy xθθ∂∂==-∂∂。

（3分） 6．用有限元程序计算分析一结构的强度须提供（4分） ① 几何信息：节点坐标，单元节点组成，板厚度，梁截面等 ② 材料信息：弹性模量，泊松比，密度等 ③ 约束信息：固定约束，对称约束等④ 载荷信息：集中力，集中力矩，分布面力，分布体力等7．轴对称问题单元形状为：三角形或四边形截面的空间环形单元，由于轴对称的特性，任意一点变形只发生在子午面上，因此可以作为二维问题处理。

弹力与有限元试卷与答案

南京林业大学试卷课程弹性力学及有限元2005~2006学年第2学期题1 选择题（每题3分）1. 弹性力学与材料力学的主要不同之处在于 B 。

A. 任务；B. 研究对象；C. 研究方法；D. 基本假设。

2. 变形协调方程说明 B 。

A. 几何方程是根据运动学关系确定的，因此对于弹性体的变形描述是不正确的；B. 微分单元体的变形必须受到变形协调条件的约束；C. 变形协调方程是保证所有弹性体变形协调条件的必要和充分条件；D. 变形是由应变分量和转动分量共同组成的。

3. 下列关于应力解法的说法正确的是 A 。

A. 必须以应力分量作为基本未知量；B. 不能用于位移边界条件；C. 应力表达的变形协调方程是唯一的基本方程；D. 必须使用应力表达的位移边界条件。

4. 弹性力学的基本未知量没有 C 。

A. 应变分量；B. 位移分量；C. 面力；D. 应力。

5. 下列关于圣维南原理的正确叙述是 C 。

A. 边界等效力系替换不影响弹性体内部的应力分布；B. 等效力系替换将不影响弹性体的变形；C. 等效力系替换主要影响载荷作用区附近的应力分布，对于远离边界的弹性体内部的影响比较小；D. 圣维南原理说明弹性体的作用载荷可以任意平移。

6. 下列关于应力函数的说法，正确的是 C 。

A. 应力函数与弹性体的边界条件性质相关，因此应用应力函数，自然满足边界条件； B. 多项式函数自然可以作为平面问题的应力函数； C. 一次多项式应力函数不产生应力，因此可以不计。

D. 相同边界条件和作用载荷的平面应力和平面应变问题的应力函数不同。

7．在轴对称问题中，r σ是（ C ），θτr （ A ）。

A. 恒为零； B. 与r 无关； C. 与θ无关； D. 恒为常数。

8．轴对称问题中的位移单值条件可写成（ C ）。

A ． )2()(πθθθθn u u +=； B. )()(πθθθθn u u +=；C ． )2()(πθθθθn u u +=； D. )4()(πθθθθn u u +=9．为了保证有限单元法解答的收敛性，位移函数应具备的条件是 D 。

(绝密试题)弹性力学与有限元分析试题及其答案

2012年度弹性力学与有限元分析复习题及其答案(绝密试题)一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。

2、在弹性力学中规定，线应变以伸长时为正，缩短时为负，与正应力的正负号规定相适应。

3、在弹性力学中规定，切应变以直角变小时为正，变大时为负，与切应力的正负号规定相适应。

4、物体受外力以后，其内部将发生内力，它的集度称为应力。

与物体的形变和材料强度直接有关的，是应力在其作用截面的法线方向和切线方向的分量，也就是正应力和切应力。

应力及其分量的量纲是L -1MT -2。

5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。

6、平面问题分为平面应力问题和平面应变问题。

7、已知一点处的应力分量100=x σMPa ，50=y σMPa ，5010=xy τ MPa ，则主应力=1σ150MPa ，=2σ0MPa ，=1α6135' 。

8、已知一点处的应力分量， 200=x σMPa ，0=y σMPa ，400-=xy τ MPa ，则主应力=1σ512MPa ，=2σ-312 MPa ，=1α-37°57′。

9、已知一点处的应力分量，2000-=x σMPa ，1000=y σMPa ，400-=xy τ MPa ，则主应力=1σ1052 MPa ，=2σ-2052 MPa ，=1α-82°32′。

10、在弹性力学里分析问题，要考虑静力学、几何学和物理学三方面条件，分别建立三套方程。

11、表示应力分量与体力分量之间关系的方程为平衡微分方程。

12、边界条件表示边界上位移与约束，或应力与面力之间的关系式。

分为位移边界条件、应力边界条件和混合边界条件。

13、按应力求解平面问题时常采用逆解法和半逆解法。

14、有限单元法首先将连续体变换成为离散化结构，然后再用结构力学位移法进行求解。

其具体步骤分为单元分析和整体分析两部分。

15、每个单元的位移一般总是包含着两部分：一部分是由本单元的形变引起的，另一部分是由于其他单元发生了形变而连带引起的。

有限元试题及答案

有限元试题及答案(总4页) -本页仅作为预览文档封面，使用时请删除本页-一判断题（20分）（×）1. 节点的位置依赖于形态，而并不依赖于载荷的位置（√）2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元（×）3. 不能把梁单元、壳单元和实体单元混合在一起作成模型（√）4. 四边形的平面单元尽可能作成接近正方形形状的单元（×）5. 平面应变单元也好，平面应力单元也好，如果以单位厚来作模型化处理的话会得到一样的答案（×）6. 用有限元法不可以对运动的物体的结构进行静力分析（√）7. 一般应力变化大的地方单元尺寸要划的小才好（×）8. 所谓全约束只要将位移自由度约束住，而不必约束转动自由度（√）9. 同一载荷作用下的结构，所给材料的弹性模量越大则变形值越小（√）10一维变带宽存储通常比二维等带宽存储更节省存储量。

二、填空（20分）1．平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板，但前者受力特点是：平行于板面且沿厚度均布载荷作用，变形发生在板面内；后者受力特点是：垂直于板面的力的作用，板将变成有弯有扭的曲面。

2．平面应力问题与平面应变问题都具有三个独立的应力分量：σx，σy，τxy ，三个独立的应变分量：εx，εy，γxy，但对应的弹性体几何形状前者为薄板，后者为长柱体。

3．位移模式需反映刚体位移，反映常变形，满足单元边界上位移连续。

4．单元刚度矩阵的特点有：对称性，奇异性，还可按节点分块。

5．轴对称问题单元形状为：三角形或四边形截面的空间环形单元，由于轴对称的特性，任意一点变形只发生在子午面上，因此可以作为二维问题处理。

6．等参数单元指的是：描述位移和描述坐标采用相同的形函数形式。

等参数单元优点是：可以采用高阶次位移模式，能够模拟复杂几何边界，方便单元刚度矩阵和等效节点载荷的积分运算。

7．有限单元法首先求出的解是节点位移，单元应力可由它求得，其计算公式为。

《弹性力学及有限单元法》期末考试试卷及答案（1）

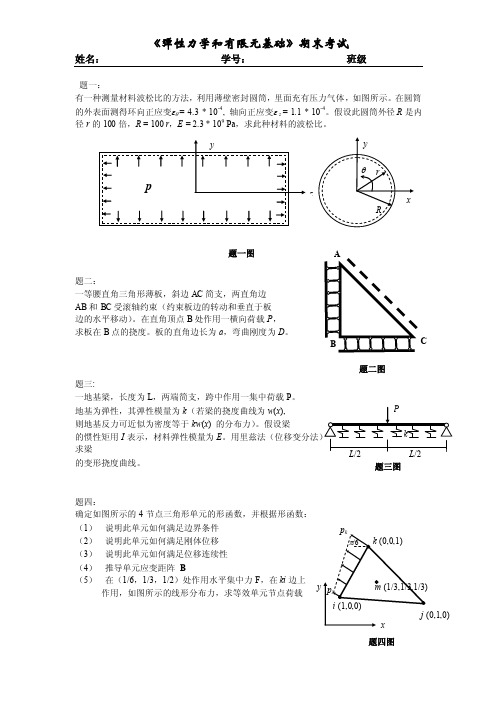
题一：有一种测量材料波松比的方法，利用薄壁密封圆筒，里面充有压力气体，如图所示。

在圆筒的外表面测得环向正应变εθ= 4.3 * 10-4, 轴向正应变ε z= 1.1 * 10-4。

假设此圆筒外径R是内径r的100倍，R = 100 r，E = 2.3 * 109 Pa，求此种材料的波松比。

题二：一等腰直角三角形薄板，斜边AC简支，两直角边AB和BC受滚轴约束（约束板边的转动和垂直于板边的水平移动）。

在直角顶点B处作用一横向荷载P，求板在B点的挠度。

板的直角边长为a，弯曲刚度为D。

题三:一地基梁，长度为L，两端简支，跨中作用一集中荷载P。

地基为弹性，其弹性模量为k（若梁的挠度曲线为w(x),则地基反力可近似为密度等于kw(x) 的分布力）。

假设梁的惯性矩用I表示，材料弹性模量为E求梁的变形挠度曲线。

题四：确定如图所示的4节点三角形单元的形函数，并根据形函数：（1）说明此单元如何满足边界条件（2）说明此单元如何满足刚体位移（3）说明此单元如何满足位移连续性（4）推导单元应变距阵B（5）在（1/6，1/3，1/2）处作用水平集中力F，在ki边上作用，如图所示的线形分布力，求等效单元节点荷载z题一图题二图题三图题四图试题答案题一：由于R >> t ，可以假设σz 沿厚度方向均匀分布。

设内压强为p ，则：Rtpr z 22=σ 由轴对称圆筒的应力计算公式可得：)~0(112222p p r R R -=---=ρσρ；p Rtr p rR R 2222211=-+=ρσφ由于σz ，σφ和远大于σρ，所以σρ可假设为0。

由虎克定律：()φσσεv E z z -=1；()z v Eσσεφφ-=1，再加上z σσφ2=可推导出：zzv εεεεφφ--=22=0.28题二：由对称性可知，所求的B 点挠度即为四边简直方板的中心点的挠度，方板的边长为a 2，在中心位置受到的横向集中力为4F 。

三角级数解为；()∑∑∑∑∞=∞=∞=∞=+=⎪⎪⎭⎫⎝⎛+=..5,3,1,...5,3,1222211222222224132222sin 2sin 216m n m n nmD Faa n a m n m D a Fw ππππ题三：设梁的挠度为：∑∞==1sinm m lxm B w π，此挠度曲线满足边界条件。

《弹性力学及有限元》测验试卷

一、在建立弹性力学平衡微分方程、几何方程、物理方程时分别应用了哪些基本假定？
二、在什么条件下平面应力问题与平面应变问题的应力分量xy y x τσσ,,是相同的?
三、体力为零的单连体应力边界问题，设下列应力分量已满足边界条件。

试考察它们是否为
正确解答，并说明原因。

0,2,2)2(===xy y x y x τσσ
四、有限单元法中，位移模式应满足什么条件? 下列位移函数 2321x a y a x a u ++= 2321y b y b x b v ++=
能否作为三角形单元的位移模式? 简要说明理由。

)(,,)1(a
y
b x q b y q a x q
xy y x +-===τσσ
题六图
七、某结构的有限元计算网格如题七图（a ）所示。

网格中两种类型单元按如题七图（b ）所
示的局部编号，它们单元劲度矩阵均为
⎥⎥⎤⎢⎢⎡-----25.025.0025.025.0025.025.0025.025.0005.0000
5.0。

--弹性力学与有限元分析试题及参考答案

弹性力学与有限元分析试题及参考答案四、分析计算题1、试写出无体力情况下平面问题的应力分量存在的必要条件，并考虑下列平面问题的应力分量是否可能在弹性体中存在。

（1）By Ax x +=σ，Dy Cx y +=σ，Fy Ex xy +=τ；（2）)(22y x A x +=σ，)(22y x B y +=σ，Cxy xy =τ；其中，A ，B ，C ，D ，E ，F 为常数。

解：应力分量存在的必要条件是必须满足下列条件：（1）在区域内的平衡微分方程⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00x yy xxy y yxx τστσ；（2）在区域内的相容方程()02222=+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂y x y x σσ；（3）在边界上的应力边界条件()()()()⎪⎩⎪⎨⎧=+=+s fl m s f m l y s xy y xs yx x τστσ；（4）对于多连体的位移单值条件。

（1）此组应力分量满足相容方程。

为了满足平衡微分方程，必须A =-F ，D =-E 。

此外还应满足应力边界条件。

（2）为了满足相容方程，其系数必须满足A +B =0；为了满足平衡微分方程，其系数必须满足A =B =-C /2。

上两式是矛盾的，因此，此组应力分量不可能存在。

2、已知应力分量312x C Qxy x +-=σ，2223xy C y -=σ，y x C y C xy 2332--=τ，体力不计，Q 为常数。

试利用平衡微分方程求系数C 1，C 2，C 3。

解：将所给应力分量代入平衡微分方程⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00x yy x xy y yxx τστσ 得⎩⎨⎧=--=--+-023033322322212xy C xy C x C y C x C Qy 即()()()⎩⎨⎧=+=+--0230333222231xy C C y C Q x C C 由x ，y 的任意性，得⎪⎩⎪⎨⎧=+=+=-023030332231C C C Q C C 由此解得，61Q C =，32Q C -=，23QC = 3、已知应力分量q x -=σ，q y -=σ，0=xy τ，判断该应力分量是否满足平衡微分方程和相容方程。

弹性力学及有限元复习题及参考答案

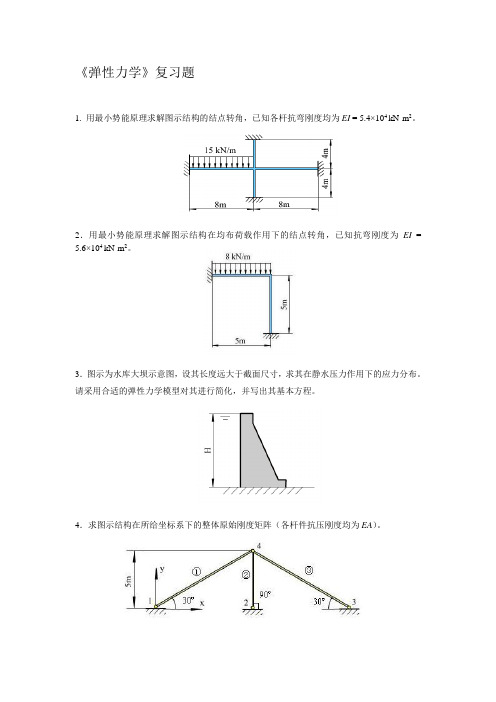
《弹性力学》复习题
1. 用最小势能原理求解图示结构的结点转角，已知各杆抗弯刚度均为EI = 5.4×104 kN·m2。

2．用最小势能原理求解图示结构在均布荷载作用下的结点转角，已知抗弯刚度为EI = 5.6×104 kN·m2。

3．图示为水库大坝示意图，设其长度远大于截面尺寸，求其在静水压力作用下的应力分布。

请采用合适的弹性力学模型对其进行简化，并写出其基本方程。

4．求图示结构在所给坐标系下的整体原始刚度矩阵（各杆件抗压刚度均为EA）。

5．计算抗压刚度为EA的图示结构在引入边界条件之前的原始刚度矩阵。

6. 求图示结构引入边界条件之前的原始整体刚度矩阵和综合结点荷载列阵，设各杆抗弯刚度为EI，不考虑轴向变形和剪切影响。

7. 计算图示常应变三角形单元的单元刚度矩阵。

已知弹性模量E，厚度t，泊松比υ＝0。

弹性力学试地的题目及答案详解

弹性力学与有限元分析复习题及其答案一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。

2、在弹性力学中规定，线应变以伸长时为正，缩短时为负，与正应力的正负号规定相适应。

3、在弹性力学中规定，切应变以直角变小时为正，变大时为负，与切应力的正负号规定相适应。

4、物体受外力以后，其内部将发生内力，它的集度称为应力。

与物体的形变和材料强度直接有关的，是应力在其作用截面的法线方向和切线方向的分量，也就是正应力和切应力。

应力及其分量的量纲是L -1MT -2。

5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。

6、平面问题分为平面应力问题和平面应变问题。

7、已知一点处的应力分量100=x σMPa ，50=y σMPa ，5010=xy τ MPa ，则主应力=1σ150MPa ，=2σ0MPa ，=1α6135' 。

8、已知一点处的应力分量，200=x σMPa ，0=y σMPa ，400-=xy τ MPa ，则主应力=1σ512 MPa ，=2σ-312 MPa ，=1α-37°57′。

9、已知一点处的应力分量，2000-=x σMPa ，1000=y σMPa ，400-=xy τ MPa ，则主应力=1σ1052 MPa ，=2σ-2052 MPa ，=1α-82°32′。

10、在弹性力学里分析问题，要考虑静力学、几何学和物理学三方面条件，分别建立三套方程。

11、表示应力分量与体力分量之间关系的方程为平衡微分方程。

12、边界条件表示边界上位移与约束，或应力与面力之间的关系式。

分为位移边界条件、应力边界条件和混合边界条件。

13、按应力求解平面问题时常采用逆解法和半逆解法。

14、有限单元法首先将连续体变换成为离散化结构，然后再用结构力学位移法进行求解。

其具体步骤分为单元分析和整体分析两部分。

15、每个单元的位移一般总是包含着两部分：一部分是由本单元的形变引起的，另一部分是由于其他单元发生了形变而连带引起的。

弹性力学与有限元分析试题及参考答案

弹性力学与有限元分析试题及参考答案四、分析计算题1、试写出无体力情况下平面问题地应力分量存在地必要条件，并考虑下列平面问题地应力分量是否可能在弹性体中存在.资料个人收集整理，勿做商业用途（1）By Ax x，Dy Cx y，Fy Ex xy；（2）)(22y xA x，)(22y xB y，Cxy xy；其中，A ，B ，C ，D ，E ，F 为常数.解：应力分量存在地必要条件是必须满足下列条件：（1）在区域内地平衡微分方程xyyxxyyyxx；（2）在区域内地相容方程02222yx yx；（3）在边界上地应力边界条件sflms f ml ysxy yxs yx x；（4）对于多连体地位移单值条件.资料个人收集整理，勿做商业用途（1）此组应力分量满足相容方程.为了满足平衡微分方程，必须A=-F ，D=-E.此外还应满足应力边界条件.资料个人收集整理，勿做商业用途（2）为了满足相容方程，其系数必须满足A+B=0；为了满足平衡微分方程，其系数必须满足A=B=-C/2.上两式是矛盾地，因此，此组应力分量不可能存在.资料个人收集整理，勿做商业用途2、已知应力分量312x C Qxyx，2223xy C y，y x C yC xy2332，体力不计，Q 为常数.试利用平衡微分方程求系数C1，C2，C3.解：将所给应力分量代入平衡微分方程0xyyxxyyyxx得23033322322212xy C xy C xC yC xC Qy即230333222231xy C C yC Q xC C 由x ，y 地任意性，得23030332231C C C Q C C 由此解得，61Q C ，32Q C ，23Q C 3、已知应力分量q x，q y，0xy，判断该应力分量是否满足平衡微分方程和相容方程.解：将已知应力分量q x，q y，0xy，代入平衡微分方程0Y xyX yxxyyyxx可知，已知应力分量q x，q y，0xy一般不满足平衡微分方程，只有体力忽略不计时才满足.按应力求解平面应力问题地相容方程：yx xyxyxy yx 22222)1(2)()(将已知应力分量q x，q y，0xy代入上式，可知满足相容方程.按应力求解平面应变问题地相容方程：yx xyxyxyyx2222212)1()1(将已知应力分量q x，q y，0xy代入上式，可知满足相容方程.4、试写出平面问题地应变分量存在地必要条件，并考虑下列平面问题地应变分量是否可能存在.（1）Axy x，3By y，2Dy C xy；（2）2Ay x ，y Bx y2，Cxy xy；（3）0x，0y ，Cxy xy ；其中，A ，B ，C ，D 为常数.解：应变分量存在地必要条件是满足形变协调条件，即yx x yxyyx 22222将以上应变分量代入上面地形变协调方程，可知：（1）相容.（2）C By A 22（1分）；这组应力分量若存在，则须满足：B=0，2A=C.（3）0=C ；这组应力分量若存在，则须满足：C=0，则0x，0y，0xy（1分）.5、证明应力函数2by 能满足相容方程，并考察在如图所示地矩形板和坐标系中能解决什么问题（体力不计，0b ）.解：将应力函数2by 代入相容方程24422444yyxx可知，所给应力函数2by 能满足相容方程.由于不计体力，对应地应力分量为b yx222，022xy，2yx xy对于图示地矩形板和坐标系，当板内发生上述应力时，根据边界条件，上下左右四个边上地面力分别为：上边，2h y，0l ，1m，0)(2h yxyxf ，0)(2h yyyf ；下边，2h y，0l ，1m ，0)(2h yxyx f ，0)(2h yyy f ；左边，2l x，1l ，0m ，b f l xxx2)(2，0)(2l xxyy f ；右边，2l x，1l ，0m ，b f l xxx 2)(2，0)(2l xxyy f .l/2l/2h/2h/2yxOOx b 可见，上下两边没有面力，而左右两边分别受有向左和向右地均布面力2b.因此，应力函数2by能解决矩形板在x 方向受均布拉力（b>0）和均布压力（b<0）地问题.资料个人收集整理，勿做商业用途6、证明应力函数axy 能满足相容方程，并考察在如图所示地矩形板和坐标系中能解决什么问题（体力不计，0a ）.解：将应力函数axy 代入相容方程24422444yyxx可知，所给应力函数axy 能满足相容方程.由于不计体力，对应地应力分量为022yx，022xy，ayx xy2对于图示地矩形板和坐标系，当板内发生上述应力时，根据边界条件，上下左右四个边上地面力分别为：上边，2h y，0l ，1m ，a f h yxyx2)(，0)(2h yyyf ；下边，2h y ，0l ，1m ，a f h yxyx 2)(，0)(2h yyy f ；左边，2l x ，1l ，0m ，0)(2l xxxf ，a f l xxyy 2)(；右边，2l x，1l ，0m ，0)(2l xxx f ，a f l xxyy 2)(.可见，在左右两边分别受有向下和向上地均布面力a ，而在上下两边分别受有向右和向左地均布面力 a.因此，应力函数axy 能解决矩形板受均布剪力地问题.资料个人收集整理，勿做商业用途7、如图所示地矩形截面地长坚柱，密度为，在一边侧面上受均布剪力，试求应力分量.解：根据结构地特点和受力情况，可以假定纵向纤维互不挤压，即设0x.由此可知l/2l/2h/2h/2yxO22yx将上式对y 积分两次，可得如下应力函数表达式)()(,21x f y x f yx 将上式代入应力函数所应满足地相容方程则可得)()(424414dxx f d dxx f d y2.3 直角三角形固定在刚性基础上，受齐顶地水压力和自重作用，如图 2.14所示.若按一个单元计算，水地容重g ，三角形平面构件容重g ,取泊松比v =1/6，试求顶点位移和固定面上地反力.资料个人收集整理，勿做商业用途解：按逆时针编码，局部编码与整体编码相同：1-2-3建立坐标)0,0(3)3,0(20,21:a a xoy （1）求形函数矩阵：aa a a 60321a b b a b 303321ac a c c 220321图（2.14）形函数:)(21y c x b a AN i i i i233221aa a A所以：ay ax Na y N a xN 32132321形函数地矩阵为：ay a xay ax ay a x a y a xN NN Nmji321302003210302（2）刚度矩阵333231232221131211KKKK K K K K KKesr sr s r sr s r s r s r sr rsb bc c c b b c b c c b c c b b AEtK21212121142125213531416122aE A Et t 可得：40035353415093532211EKEK251035343127273323531233E KEK215251935313EK41253535323EK431274252151273321352594140012535035250215250254150191009353E Ke（3）位移列向量和右端项由边界条件可确定：Teu a00022水压力和构件厚分别为：10tgh p TTet l q h q h q R 032031020306000001自重为W 与支座反力：Ty x y x e W R R W W R R R 330333112所以：Ty x y x eW R h q R W h q W R R R33363303011由eeeRa K得到下列矩阵方程组：3336300030301122W R h q R W h q W R R u y x y x 化简得：431274252151273321352594140012535035250215250254150191009353E Ke364035353022W h q u E可得：EW E h q u 363567022将22u 代入下式：333425135025103533031122W R h q R W R R u E y x y x 固定面上地反力：ahga gh q 330从而可得支座反力为：43221234120303011h q W Rh q W R W h q R WR y x y x 这是y 地线性方程，但相容方程要求它有无数多地解（全柱内地y 值都应该满足它），可见它地系数和自由项都应该等于零，即资料个人收集整理，勿做商业用途0)(414dxx f d ，)(424dxx f d 这两个方程要求ICx Bx Axx f 231)(，KJx Ex Dxx f 232)(代入应力函数表达式，并略去对应力分量无影响地一次项和常数项后，便得2323)(ExDxCx BxAxy 对应应力分量为22yxgyEDx B Ax y xy26)26(22CBx Axyx xy2322以上常数可以根据边界条件确定.左边，0x ，1l，0m ，沿y 方向无面力，所以有)(C xxy右边，b x ，1l ，0m ，沿y 方向地面力为q ，所以有qBb Ab bxxy23)(2上边，0y ，0l ，1m ，没有水平面力，这就要求xy 在这部分边界上合成地主矢量和主矩均为零，即)(00dx y b xy将xy地表达式代入，并考虑到C=0，则有)23(23232BbAbBxAxdx Bx Ax b b 而00)(dx ybxy自然满足.又由于在这部分边界上没有垂直面力，这就要求y在这部分边界上合成地主矢量和主矩均为零，即0)(00dx y b y，)(00x d x y b y将y地表达式代入，则有02323)26(22Eb DbEx Dx dx E Dx b b22)26(2323EbDbExDxxdx E Dx b b 由此可得2bq A，bq B，0C ，0D ，0E 应力分量为0x,gy bx by q y312,23bx bx q xy虽然上述结果并不严格满足上端面处（y=0）地边界条件，但按照圣维南原理，在稍远离y=0处这一结果应是适用地.资料个人收集整理，勿做商业用途8、证明：如果体力分量虽然不是常量，但却是有势地力，即体力分量可以表示为xV f x，yV f y，其中V 是势函数，则应力分量亦可用应力函数表示为，V yx22，V xy22，yx xy2，试导出相应地相容方程.资料个人收集整理，勿做商业用途证明：在体力为有势力地情况下，按应力求解应力边界问题时，应力分量x，y，xy应当满足平衡微分方程yV xyx V yxxyyyxx（1分）还应满足相容方程y f x f yxy x yx 12222（对于平面应力问题）yf xf yxy x yx 112222（对于平面应变问题）并在边界上满足应力边界条件（1分）.对于多连体，有时还必须考虑位移单值条件.首先考察平衡微分方程.将其改写为0xVyyV x xyyyxx这是一个齐次微分方程组.为了求得通解，将其中第一个方程改写为yxxyVx根据微分方程理论，一定存在某一函数A （x ，y ），使得yA Vx，xAyx同样，将第二个方程改写为yxyxVy（1分）可见也一定存在某一函数B （x ，y ），使得xB Vy，yByx由此得yB xA 因而又一定存在某一函数y x,，使得y A，xB代入以上各式，得应力分量V yx22，V xy22，yx xy2为了使上述应力分量能同量满足相容方程，应力函数y x,必须满足一定地方程，将上述应力分量代入平面应力问题地相容方程，得资料个人收集整理，勿做商业用途Vyx Vx Vyyx2222222222221VyxV yxxy yx222222222222222212简写为V24)1(将上述应力分量代入平面应变问题地相容方程，得Vyx Vx Vyyx22222222222211VyxVyxxy yx2222222222222222112简写为V241219、如图所示三角形悬臂梁只受重力作用，而梁地密度为，试用纯三次地应力函数求解.O解：纯三次地应力函数为3223dycxyy bx ax相应地应力分量表达式为dy cx xf yx x6222,gy by ax yf xy y2622,cybx yx xy222这些应力分量是满足平衡微分方程和相容方程地.现在来考察，如果适当选择各个系数，是否能满足应力边界条件.资料个人收集整理，勿做商业用途上边，0y ，0l ，1m，没有水平面力，所以有2)(bx yxy对上端面地任意x 值都应成立，可见b 同时，该边界上没有竖直面力，所以有6)(ax yy对上端面地任意x 值都应成立，可见a 因此，应力分量可以简化为dy cx x62，gy y，cyxy2斜面，tanx y ，sin 2cosl ，cos cos m ，没有面力，所以有0tantan x y xyyx y yx x lmml 由第一个方程，得sin tan 6sin4costan 2sintan 62dx cx cx dx cx 对斜面地任意x 值都应成立，这就要求tan64d c 由第二个方程，得sin sin tan 2cos tan sintan 2gx cx gx cx 对斜面地任意x 值都应成立，这就要求0tan 2g c （1分）由此解得cot 21g c（1分），2cot31g d从而应力分量为2cot2cot gy gx x,gy y,cotgy xy设三角形悬臂梁地长为l ，高为h ，则lh ta n.根据力地平衡，固定端对梁地约束反力沿x 方向地分量为0，沿y 方向地分量为glh 21.因此，所求x 在这部分边界上合成地主矢应为零，xy应当合成为反力glh 21.资料个人收集整理，勿做商业用途cotcotcot2cot2202gh glh dygy gl dyh lxh xglhgh dygy dyh h lx xy21cot21cot2可见，所求应力分量满足梁固定端地边界条件.10、设有楔形体如图所示，左面铅直，右面与铅直面成角，下端作为无限长，承受重力及液体压力，楔形体地密度为1，液体地密度为2，试求应力分量.资料个人收集整理，勿做商业用途解：采用半逆解法.首先应用量纲分析方法来假设应力分量地函数形式.取坐标轴如图所示.在楔形体地任意一点，每一个应力分量都将由两部分组成：一部分由重力引起，应当与g 1成正比（g 是重力加速度）；另一部分由液体压力引起，应当与g2成正比.此外，每一部分还与，x ，y 有关.由于应力地量纲是L-1MT-2，g 1和g 2地量纲是L-2MT-2，是量纲一地资料个人收集整理，勿做商业用途量，而x 和y 地量纲是L ，因此，如果应力分量具有多项式地解答，那么它们地表达式只可能是gx A 1，gy B 1，gx C2，gy D2四项地组合，而其中地A ，B ，C ，D 是量纲一地量，只与有关.这就是说，各应力分量地表达式只可能是x 和y 地纯一次式.资料个人收集整理，勿做商业用途其次，由应力函数与应力分量地关系式可知，应力函数比应力分量地长度量纲高二次，应该是x 和y 纯三次式，因此，假设资料个人收集整理，勿做商业用途3223dycxyy bx ax相应地应力分量表达式为dy cx xf yx x6222,gy byax yf xy y12226,cybx yx xy222这些应力分量是满足平衡微分方程和相容方程地.现在来考察，如果适当选择各个系数，是否能满足2g1gyxO应力边界条件.资料个人收集整理，勿做商业用途左面，0x ，1l，0m ，作用有水平面力gy 2，所以有gydy xx26)(对左面地任意y 值都应成立，可见62gd同时，该边界上没有竖直面力，所以有2)(cy xxy对左面地任意y 值都应成立，可见c 因此，应力分量可以简化为gy x2，gy byax y126，bxxy2斜面，tan y x ，cos l ，sin2cosm ，没有面力，所以有0tantan y x xy yy x yx x lmm l 由第一个方程，得sin tan 2cos 2by gy 对斜面地任意y 值都应成立，这就要求sin tan 2cos 2b g 由第二个方程，得sin sin4sin tan 6cos tan 2sin 2tan611y g b a by gy byay 对斜面地任意x 值都应成立，这就要求4tan61g ba 由此解得321cot31cot61g g a，22cot21g b 从而应力分量为gy x 2,y g g xg g y 122321cotcot2cot ,22cotgx xy 位移边界条件对称、固定边和简支边上支点地已知位移条件如下：对称轴: 法线转角=0固定边: 挠度=0 (或已知值)边线转角=0 (或已知值)法线转角=0 (或已知值)简支边: 挠度=0 (或已知值)边线转角=0 (或已知值)计算图示四边固定方板方板地边长为l ，厚度为t ，弹性模型量为E ，波松比μ=0.3，全板承受均布法向荷载ｑ，求薄板中地挠度和内力. 资料个人收集整理，勿做商业用途单元划分：为了说明解题方法，采用最简单地网络2×2，即把方板分成四个矩形单元.由于对称性，只需计算一个单元，例如，计算图中有阴影地单元，单元地节点编号为１，２，３，４.此时，单元地a, b 是4l ba 计算节点荷载:由前面地均布荷载计算公式得：Tl l l l l l l l qlR ]21121212[192}{2边界条件：边界23和34为固定边，因此节点2, 3, 4地挠度、边线和法线转角均为零.边界12和14为对称轴，因此θx1 =0、θy1 =0.于是，在4个节点和12个位移分量中,只有一个待求地未知量1w .资料个人收集整理，勿做商业用途结构地代数方程组：这是一个单元地计算题目，单元刚度矩阵在此处即为总刚度矩阵.引入支承条件后，在总刚度矩阵中只取第一行、列元素，在方程组右端项中只保留第一个元素.于是结构地代数方程为：16)681(15815821201120qlw l D w k lD 资料个人收集整理，勿做商业用途同此解出04100148.0D ql w .其中32309158.0)1(12EtEt D 内力:利用式(4-2-6)可求得方板中点力矩为：由表看出，网格越密，计算结果越接近于精确答案.还可看出，位移地精度一般比内力地精度高，这是因为在位移法中，位移是由基本方程直接求出地，而内力则是根据位移间接求出地.资料个人收集整理，勿做商业用途第三章平面问题有限单元法习题答案3-2图示等腰直角三角形单元，设=1/4，记杨氏弹性模量E ，厚度为t ，求形函数矩阵[N]、应变矩阵[B]、应力矩阵[S]与单元刚度矩阵[K]e.资料个人收集整理，勿做商业用途【解】：ijmj imi j ji mm i j i m j m i i m j j m i m j i j m m j ix x c y y b y x y x a x x c y y b y x y x a x x c y y b y x y x a ,,,,,,aj(0,a)aac a a b a aa a a ac b a a a c a a b a a mmmj j j i i i 0,0,0*0*0,00,00**0000,0,0*00*02mjim j i N N N N N N N000),,()(21m j i y c x b a AN i i ii 221001010121aa a Ayxayxy x ay x a Na yx a ay ax aaN a y ay x a N a x y ax a N m j i 000001)(1)00(1)00(122221000310131031001310311103)411(2412100141141411411)4121)(411()411()1(2210011011)21)(1()1(EE E E D321B B B Baa c a ab a aa a a a cb a a ac a a b a a mmmj jj i i i 0,0,0*0*0,000,00**0000,0,0*00*0211011010100001000111110011011000110000110000100212aBaB aB a a a aB b c c b AB mjii i i i i1003101310E D1101101010000100011aB11011313001*********11110100001000110003101310aE a E BD S 1003101310E D11111010000100011aB42311124111331300111011011011013100320211101101010000100011000310131101101010000100011022Et at aE tAB D BKTTe3-3正方形薄板，受力与约束如图所示，划分为两个三角形单元，=1/4，板厚为t ，求各节点位移与应力.【解】：yP 34242311124111331300111011011011013100320Et tAB D BKTe0000000000000000003001310001101100011011001003130031114200111324201Et K4211310024131100111001001303100031013000111001000000000000000000202Et K4211310241311001140023113042011310240111120041300311142001113242021Et KKK 载荷向量：000000P R1001414004040042000000004211310241311001140023113042011310240111120041300311142001113242013344332211P v u Et P v u v u v u v u Et 101414041PEt PEt v u 05010015330050000044332211Et P v u v u v u v u 10003101310E D111101010000100011a B1101110001000010111aB12BB31201010003101325000000110111000100001011000310131033221111atPatPEtP aE v u v u v u BD 1002101031013200500011111000100001110310131022334422atP atP Et P aE v u v u v u BD 3-4三角形单元i,j,m 地j ，m 边作用有如图所示线形分布面载荷，求结点载荷向量.【解】：面力移置公式：tdsp NRTe其中：mjim j i N N N N N N N000),,()(21m j i y c xb a AN i i ii 426,132,62*63*2352,426,26*22*5165,363,213*56*6mmmj j j i i i c b a c b a c b a 213431402212165136122121Aj(6,3)i(2,2)m(5,6)1q 2q yxo)46(131)342(131)321(131y x N y x N y x N mj i 所以:yx yx yx y x yx y x N460342033004603420321131载荷分布函数：0)6(3)(121y q q q p积分函数：])6,5[(213x x y dyy q q q yxyx y x yx yxyxttdsy q q q yx y x yx yxyx y xRe3100)6(3)(460463420034233003211310)6(3)(464634200342330032113112163121dyy q q q y y y y t dyy q q q y yyy yy yy tRe)6(3)(133130013313263130026313000013*3100)6(3)(473160473163283420032834200013*3101216312163dyy q q q q y y q q q q y tdyy q q q q y y q q q q y tRe63121212126312121212))(36(*30))(36(*60027100)3)(2(*133130)3)(2(*26313013*310126323122126312631212632312212631263129292331)(321)36(3)(3)36(299331)(621)36(6)(6)36(q q y yq q yyq q dyy y q q dy y q q q q yyq q yyq q dy y y q q dy y q q 所以:210210031002182902990027100)3)(2(*133130)3)(2(*26313013*310121212126312121212q q q q tq q q q t dyy q q q q y y q q q q ytRe3-5图示悬臂深梁，右端作用均布剪力，合力为P ，取=1/3，厚度为t ，如图示划分四个三角形单元，求整体刚度方程.资料个人收集整理，勿做商业用途【解】：13524612341000420248410012102112)311(23121001311310311311)3121)(311()311()1(22100011011)21)(1()1(EE E E D10420248E D1111101000010001B53411235211442400211011011011024200416211101101010000100011020410241101101010000100018Et t E tAB D B KTTe534112352114424002110110110110242004164321Et KKKK0000000000000000000000000000000000000000000000400042020000010011100000000000000000000000000000410053120000210035140000010011100000200024041K534112352114424002110110110110242004164321Et KKKK00000000000000000000000000000000000000000000001011000100000424002000001253004100001435002100000000000000000000000000002420040000010110001162Et K00000000000000000000000000000000000000000000000080008404000002002220000000000000000000000000000082001062400004200610280000020022200000400048081612Et KK80844000020022200000000000000000000000000000820010624000042006102800000200222000004000480800000000000000000000000000000000000000000000000000001643Et KK808440200222000000000000000000000000000008200186248404420061228222002002220000040004808000000008200106240000420061028000002002220000040004808164321Et K K K K K算例2：正方形薄板平面应力问题地求解已知图示正方形薄板，沿其对角线承受压力作用，载荷沿厚度为均匀分布，P=20kN/m.设泊松比u=0，板厚t=1m ，求此薄板应力.资料个人收集整理，勿做商业用途课本第42页3.7节计算结果如下：变形：76.176.172.388.052.1252.32653321u u v u v v 应力：)/(40.40.2088.021m kN xyy x ；)/(052.1276.122m kN xyy x；)/(08.372.388.023m kN xyy x ；)/(32.172.3024m kN xyy x 1、如图1所示等腰直角三角形单元，其厚度为t ，弹性模量为E ，泊松比0；单元地边长及结点编号见图中所示.求(1)形函数矩阵N(2)应变矩阵B 和应力矩阵S (3)单元刚度矩阵eK1、解：设图1所示地各点坐标为点1（a ，0），点2（a ，a ），点3（0，0）于是，可得单元地面积为12A2a ，及(1)形函数矩阵N 为(7分)123aa12122121(0a a )a 1(00a )a 1(aa 0)aN x y N x y N x y ；123123N N N NI I I N N N (2)应变矩阵B 和应力矩阵S 分别为(7分)12a 010-a a-aaB ，220010a aa 0B ，32-a 0100a-aB ；123B B B B 12a00-a a11-a a 22E S ，22000a a1a 02E S ，32-a 000a10-a 2E S ；123123SD B B B S S S (3)单元刚度矩阵eK(6分)111213T21222331323331102113120111100140202002000201111eEt tAK K K KB DB K K K K K K 2、图2（a ）所示为正方形薄板，其板厚度为t ，四边受到均匀荷载地作用，荷载集度为21/N m ，同时在y 方向相应地两顶点处分别承受大小为2/N m 且沿板厚度方向均匀分布地荷载作用.设薄板材料地弹性模量为E ，泊松比0.试求资料个人收集整理，勿做商业用途(1)利用对称性，取图（b ）所示1/4结构作为研究对象，并将其划分为4个面积大小相等、形状相同地直角三角形单元.给出可供有限元分析地计算模型（即根据对称性条件，在图（b ）中添加适当地约束和荷载，并进行单元编号和结点编号）.资料个人收集整理，勿做商业用途(2)设单元结点地局部编号分别为i 、j 、m ，为使每个单元刚度矩阵eK 相同，试在图（b ）中正确标出每个单元地合理局部编号；并求单元刚度矩阵eK .资料个人收集整理，勿做商业用途(3)计算等效结点荷载.(4)应用适当地位移约束之后，给出可供求解地整体平衡方程（不需要求解）.图13①②③④2、解：(1)对称性及计算模型正确(5分) (2)正确标出每个单元地合理局部编号(3分) (3)求单元刚度矩阵eK(4分) (4)计算等效结点荷载(3分)(5)应用适当地位移约束之后，给出可供求解地整体平衡方程（不需要求解）.(5分)如图3.11所示地平面三角形单元，厚度t=1cm ，弹性模量E=2.0*105mpa ，泊松比γ=0.3，试求插值函数矩阵N ，应变矩阵B ，应力矩阵S ，单元刚度矩阵Ke.资料个人收集整理，勿做商业用途图2j m m mmi ii ij j j 1N /m21N /m 12456对称1011012020031214301201eEt K对称123356322000026121006120146101620212v v u Et tv u u解：此三角形单元可得：2△=（10-2）*4=32，故有a1=1/32*（8u1-5u2-16u3）a2=1/32*（4u1-4u2）a3=1/32*（-8u1+8u3）a4=1/32*（56v1-8v2-16v3）a5=1/32*（-4v1+4v2）a6=1/32*（-8v1+8v3）而b1=y2-y3=-4 b1=x2-x3=-8b1=y3-y1=4 b1=x3-x1=0b1=y1-y2=0 b1=x1-x2=8b1 0 b2 0 b3 0 -4 0 4 0 0[B]=1/2△* 0 c1 0 c2 0 c3 =1/32* 0 -8 0 0 8资料个人收集整理，勿做商业用途c1 b1 c2 b2 c3 b3 -8 4 0 8 01 γ　0 1 0.3 0[D]=[E/(1-γ2)]* γ　1 0 =[E/0.91]* 0.3 1 0资料个人收集整理，勿做商业用途0 0 (1-γ)/2 0 0 0.351 0.3 0 -0.125 0 0.125 0 0[S]=[D]*[B]={E/0.91}* 0.3 1 0 * 0 -0.25 0 0 0.25资料个人收集整理，勿做商业用途0 0 0.35 -0.25 0.125 0 0.25 01.4 0 -1.4 -0.7 0 0.70 4 -0.6 -4 0 0[K]①=BT*D*B①*t*△={E/36.4}* -1.4 -0.6 2.4 1.3 0.6 0.7资料个人收集整理，勿做商业用途-0.7 -4 1.3 -0.6 -1 0.350 0 0.6 -1 -0.6 00.7 0 0.7 -0.35 0 01 0 0 0.6 -1 -0.60 0.35 0.7 0 -0.7 -0.350 0.7 1.4 0 -1.4 -0.7[K]②=BT*D*B②*t*△={E/36.4}* 0.6 0 0 4 -0.6 -4资料个人收集整理，勿做商业用途1 -0.7 -1.4 -0.6 2.4 1.30.6 -0.35 -1.4 -4 1.3 3.53.12 求下图中所示地三角形地单元插值函数矩阵及应变矩阵，u1=2.0mm，v1=1.2mm，u2=2.4mm，v2=1.2mm，u3=2.1mm，v3=1.4mm，求单元内地应变和应力，求出主应力及方向.若在单元jm边作用有线性分布面载荷（x轴），求结点地地载荷分量.资料个人收集整理，勿做商业用途解：如图2△=64/3，解得以下参数：a1=19 a2=-2 a3=6；b1=-3 b2=4 b3=-1；c1=-1 c2=-3 c3=4；资料个人收集整理，勿做商业用途N1={64/3}*(19-3x-y) N2={64/3}*(-2-3x-3y)N3={64/3}*(6-x+4y)故N=Ni 0 Nj 0 Nm 00 Ni0 Nj0 Nm1 0 1 0 1 0 =0 1 0 1 0 1bi 0 bj 0 bm 0[B]={1/2△}* 0ci 0 cj 0 cm ci bi cj bj cm bm -3 0 4 0 -1 0={64/3}*0 -1 0 -3 0 4 -1 -3 -3 4 4 -11 γ　0[D]={E/(1-γ2)}*γ　1 00 (1-γ)/21 γ　0 -3 0 4 0 -1 0 单元应力矩阵[S]=[D]*[B]={E/13(1-γ2)}* γ　1 0* 0 -1 0 -3 0 4资料个人收集整理，勿做商业用途0 (1-γ)/2 -1 -3 -3 4 4 -12 1.1-3 -u 4 3u -1 4u2.4单元应力[δ]=[S]*[q]= {E/13(1-γ2)}* -3u -1 4u -3 -u 4* 1.2资料个人收集整理，勿做商业用途(u-1)/2 (3u-3)/2(3u-3)/2 2-2u 2-2u (u-1)/22.4资料个人收集整理，勿做商业用途1.43.13解：二维单元在x,y 坐标平面内平移到不同位置，单元刚度矩阵相同，在平面矩阵180°时变化，单元作上述变化时，应力矩阵不变化.3.14解：令1t，1p ，而E2.0e 011，1/3，210101102E D（0,1）（2,1）x y①②（0,0）（2,0）12312311223300000b b b Nc c c c b c b c b 2NBA单元①2.250.7500.75 2.25000.75D①②0.500.50000100010.500.51B①-1.125-0.75 1.125000.751.0+011*-0.375-2.250.37502.25-0.75-0.37500.3750.75Se ①S DB1.31250.75-0.5625-0.375-0.75-0.3750.752.4375-0.375-0.1875-0.375-2.25-0.5625-0.3750.562500.375*1.0011-0.375-0.187500.18750.3750-0.75-0.37500.3750.750-0.375-2.250.3752.25kee ①单元②：00.500.50B101001010.50.5②00.75 1.1250.75 1.125002.250.375 2.250.3750*1.00110.7500.750.37500.375Se ②0.7500.750.37500.37502.250.3752.250.3750.750.3751.31250.750.56250.3750.375 2.250.75 2.43750.3750.187500.3750.56250.37510.562500.37500.3750.18750.1875ke②由ke①和ke ②扩充KZ （总刚度阵）1.31250.750.56250.3750.750.375000.752.43750.3750.18750.375 2.25000.56250.3751.312500.75000.3750.3750.18750 2.437502.250.37501.01011*0.750.3750.750 2.06250.750.56250.3750.375 2.250kz e 2.250.75 4.68750.3750.18750000.3750.56250.3750.56250000.37500.3750.187500.1875而Re .kz qe ，其中112211Re22Rx Ry Rx Ry ，112200qex y x y ，化简得：112201.312500.7500.11310 2.43750 2.250.596820.750 2.06250.7500.194702.250.754.687510.42432x y x y 则，11220.56250.3750.750.3750.11130.148100.18750.375 2.250.59680.95170.750.3750.56250.3750.19470.17420.3750.3750.18750.42430.0482Rx Ry Rx Ry 3.15如图所示有限元网格，cm a4，单元厚度mm t 1，弹性模量MPa E5100.2，泊松比3.0.回答下述问题：（1）结点如何编号才能使结构刚度矩阵带宽最小？（2）如何设置位移边界条件才能约束结构地刚体移动？（3）形成单元刚度矩阵并集成结构刚度矩阵.（4）如果施加一定载荷，拟定求解步骤.(1) (2) （3）资料个人收集整理，勿做商业用途解：1、节点编号如图(2)所示；2、如图(3)设置位移边界条件才能约束结构地刚体移动；3、如图(2)所示各节点地坐标为(以m 为单位)：1(0,0)，2(0.08,0)，3(0,0.04)，4(0.08,0.04 )，5(0,0.08)，6(0.08,0.08)，7(0,0.12)，8(0.08,0.12)资料个人收集整理，勿做商业用途解：单元号 1 2 3 4 56相邻结点1 3 4 5 5 72 2 5 4 6 63436 78对于单元号1：04.0321y y b ；04.0132y y b ；0213y y b ；08.0231x x c ；0312x x c ；08.0123x x c ；对于单元号2：04.0423y y b ；0342y y b ；04.0234y y b ；0243x x c ；08.0432x x c ；08.0324x x c ；对于单元号3：04.0354y y b ；0435y y b ；04.0543y y b ；0534x x c ；08.0345x x c ；08.0453x x c ；对于单元号4：04.0645y y b ；0564y y b ；04.0456y y b ；0465x x c ；08.0654x x c ；08.0546x x c ；对于单元号5：04.0765y y b ；04.0576y y b ；0657y y b ；08.0675x x c ；0756x x c ；08.0567x x c ；对于单元号6：04.0867y y b ；0786y y b ；04.0678y y b ；0687x x c ；08.0876x x c ；08.0768x x c ；平面三角形单元地面积均为1112321x x x 23210032.0m y y y 弹性矩阵均为0112E D12/)1(0003.0191.0100.21113.035.000应变矩阵11)5()3()1(021c b BBB110b c 220c b 220b c 330c b 33b c 2505.125.1225005.125.12002500025033)6()4()2(021c b BBB330b c 220c b 220b c 440c b 44b c 005.125.1200250002502505.125.12250应力矩阵)1()5()3()1(BD SSS2308.192418.84725.27100.1116154.99451.544835.1602418.84725.276154.9002308.190009451.544835.16)2()6()4()2(BD SSS2418.84725.27100.1116154.9002308.190009451.544835.162308.192418.84725.276154.99451.544835.16单元刚度矩阵tA SBKKKT)1()1()5()3()1(3297.07692.03846.05495.07143.03187.1100.181978.23846.01923.03297.03901.27143.03297.0005495.03297.05495.003846.01923.001923.03846.007692.03846.003846.07692.01978.2003297.01978.23297.0t A SBKKKT)2()2()6()4()2(3297.05495.03297.0005495.0100.181923.03846.003846.01923.003846.07692.007692.03846.001978.23297.01978.2003297.07143.03187.13297.07692.03846.05495.03901.27143.01978.23846.01923.03297.0结构刚度矩阵为：。