信号分析与处理(杨育霞许珉廖晓辉著)中国电力出版社习题2
信号分析与处理答案第二版完整版

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。
(1)解当激励为时,响应为,即:由于方程简单,可利用迭代法求解:,,…,由此可归纳出的表达式:利用阶跃响应和冲激响应的关系,可以求得阶跃响应:(2)解 (a)求冲激响应,当时,。
特征方程,解得特征根为。
所以:…(2.1.2.1)通过原方程迭代知,,,代入式(2.1.2.1)中得:解得,代入式(2.1.2.1):…(2.1.2.2)可验证满足式(2.1.2.2),所以:(b)求阶跃响应通解为特解形式为,,代入原方程有,即完全解为通过原方程迭代之,,由此可得解得,。
所以阶跃响应为:(3)解(4)解当t>0时,原方程变为:。
…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程,比较两边的系数得:阶跃响应:求下列离散序列的卷积和。
(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。
当时:当时:当时:当时:当时:(7) ,解参见右图:当时:当时:当时:当时:当时:(8) ,解参见右图当时:当时:当时:当时:(9) ,解(10),解或写作:求下列连续信号的卷积。
(1) ,解参见右图:当时:当时:当时:当时:当时:当时:(2) 和如图2.3.2所示解当时:当时:当时:当时:当时:(3) ,解(4) ,解(5) ,解参见右图。
当时:当时:当时:当时:(6) ,解(7) ,解(8) ,解(9) ,解试求题图示系统的总冲激响应表达式。
解已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;解,,(2) ;,解,,,,可定出(3) ;,解,,,可定出某一阶电路如题图所示,电路达到稳定状态后,开关S 于时闭合,试求输出响应。
解由于电容器二端的电压在t=0时不会发生突变,所以。
信号分析与处理2-4

Ts 2 T s 2
p( t )e
jn s t
1 dt Ts
s
1 X s ( ) Ts
n
X ( n
)
18
冲激抽样信号的频谱是原连续信号频谱在频率轴上 的周期延拓,其延拓周期为抽样频率s ,但与矩形脉冲 抽样信号相区别的是频谱幅度将不再随频率的增加而衰 减,而是保持不变。
P ( ) 2
n
P ( n
n
s
)
13
1 Pn Ts
Ts 2 T s 2
p( t )e jn s t dt
根据频域卷积定理
1 X s ( ) X ( ) P ( ) 2
n
:信号在时域被抽样后,它的频谱Xs()是 连续信号频谱X()的形状以抽样频率s 为间隔周期地重 复而得到,在重复过程中幅度被p(t)的傅里叶系数Pn所加 权。
X ( )
n
0
T1
t
jn1t e
X
n
2 ( n 1 )
n 1 E 1 Sa ( n 1 ) 2 n
9
x0(t) E
E
X0() 2/
0
t E/T1 x(t) E Xn
2/
这是由于傅里叶变换反映的是频谱密度概念,周期 信号在各谐振点上,具有有限幅度,说明在这些谐振频 点上其频谐密度趋于无限大,所以变成冲激函数。 这也说明了傅里叶级数可看作傅里叶变换的一种特 例。 三、周期信号与单周期信号频谱间的关系 周期信号x(t)在时域上可以看作是它的单周期信号 xd(t)的周期延拓。已知周期信号的傅里叶级数为:
信号分析与处理(杨育霞许珉廖晓辉著)中国电力出版社习题2

⎡⎛ T ⎞⎤ 0 ⎞ ⎛ ⎢⎜ cos kω t ⎥ = A ⎡ 2 − 2 cos ⎛ kω1T ⎞ ⎤ ⎟ ⎜ ( 1 ) T ⎟ − ⎜ cos ( kω1t ) 2 ⎟ ⎜ ⎟⎥ ⎢ ⎢⎜ ⎥ ⎟ − ⎟ ⎜ ⎝ 2 ⎠⎦ ⎜ ⎟ ⎥ 2 kπ ⎣ 0 ⎢ 2⎠ ⎝ ⎠⎦ ⎣⎝ A ⎡ A ⎡ k ⎛ kω T ⎞ ⎤ A = = 1 − cos ⎜ 1 ⎟ ⎥ = 1 − cos ( kπ ) ⎤ 1 − ( −1) ⎤ ⎡ ⎢ ⎣ ⎦ ⎣ ⎦ kπ ⎣ kπ ⎝ 2 ⎠ ⎦ kπ
(c) x (t ) = ( t + 2 ) [ε (t + 2) − ε (t + 1)] + [ε (t + 1) − ε (t − 1)] + ( −t + 2 ) [ε (t − 1) − ε (t − 2)]
6
课后答案网
x (t )
1 1 1 2 t -2 -1
(3)
X 1k X 2k
A1τ 1 kπτ 1 A1τ 1 kπ sinc( ) sinc( ) T T1 T 2 A 1 = 1 = 1 = 1 = A2τ 2 kπτ 2 A2τ 2 kπ sinc( ) sinc( ) A2 3 T2 T2 T2 2
5
课后答案网
| X 11 | 1 = | X 21 | 3
A = kω1T
1
课后答案网
x ( t ) = a0 + ∑ ( ak cos ( kω1t ) + bk sin ( kω1t ) )
k =1
∞
∞
= ∑ bk sin ( kω1t )
k =1
∞
A k =1 kπ ∞ A =∑ k =1 kπ
信号分析与处理 杨西侠 第2章习题答案

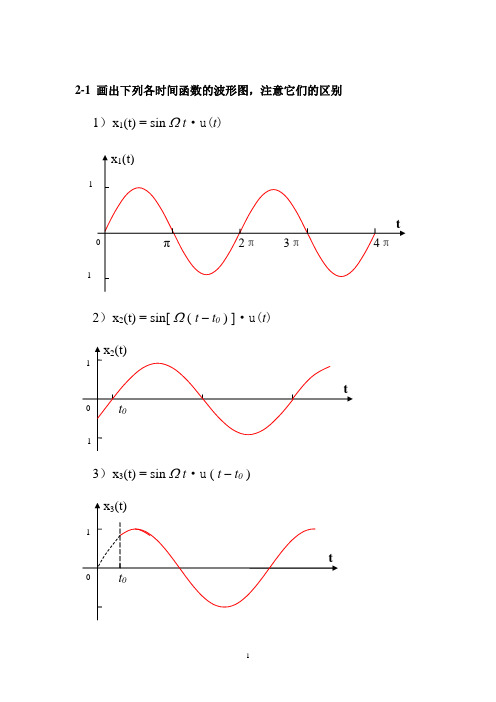
2-1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t) = sin[ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )-14)x2(t) = sin[ ( t – t0) ]·u( t – t0)2-2 已知波形图如图2-76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x ( t/2 )(5)x (-t)(6)x (-t-2)(7)x ( -t/2-2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(0t t x δ(t) dt = x(-t 0) (2)⎰+∞∞--)(0t t x δ(t) dt = x(t 0) (3)⎰+∞∞--)(0t t δ u(t -20t ) dt = u(2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u(-t 0) (5)()⎰+∞∞--+t etδ(t+2) dt = e 2-2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7) ()()[]⎰+∞∞-Ω---dt t t t e tj 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1-0t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02-4 求下列各函数x 1(t)与x 2(t) 之卷积,x 1(t)* x 2(t) (1) x 1(t) = u(t), x 2(t) = e -at · u(t) ( a>0 ) x 1(t)* x 2(t) =⎰+∞∞---ττττd t ue u a )()( =⎰-ta d e 0ττ = )1(1ate a--x 1(t)* x 2(t) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos[Ω(t+1)+4π]u(t+1) – cos[Ω(t-1)+4π]u(t-1)(3) x 1(t) = u(t) – u(t-1) , x 2(t) = u(t) – u(t-2) x 1(t)* x 2(t) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t <0时,x 1(t)* x 2(t) = 0 当 0<t <1时,x 1(t)* x 2(t) =0td τ⎰ = t 当 1<t <2时,x 1(t)* x 2(t) =21d τ⎰= 1当 2<t<3时,x 1(t)* x 2(t) = 12t d τ-⎰=3-t 当 3<t 时,x 1(t)* x 2(t) = 0(4) x 1(t) = u(t-1) , x 2(t) = sin t · u(t) x 1(t)* x 2(t) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos(t-1)2-5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t)在一个周期( 0<t<T )的波形(1) x(t)是偶函数,只含有偶次谐波分量f(t) = f(-t), f(t) = f(t ±T/2)(2) x(t)是偶函数,只含有奇次谐波分量 f(t) = f(-t), f(t) = -f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(-t)(4) x(t)是奇函数,只含有奇次谐波分量f(t) = -f(-t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(-t), f(t) = f(t±T/2)(6) x(t)是奇函数,含有偶次和奇次谐波分量f(t) = -f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
信号分析与处理 杨西侠 第2章习题答案
2-1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t) = sin[ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )-14)x2(t) = sin[ ( t – t0) ]·u( t – t0)2-2 已知波形图如图2-76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x ( t/2 )(5)x (-t)(6)x (-t-2)(7)x ( -t/2-2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(0t t x δ(t) dt = x(-t 0) (2)⎰+∞∞--)(0t t x δ(t) dt = x(t 0) (3)⎰+∞∞--)(0t t δ u(t -20t ) dt = u(2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u(-t 0) (5)()⎰+∞∞--+t etδ(t+2) dt = e 2-2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7) ()()[]⎰+∞∞-Ω---dt t t t e tj 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1-0t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02-4 求下列各函数x 1(t)与x 2(t) 之卷积,x 1(t)* x 2(t) (1) x 1(t) = u(t), x 2(t) = e -at · u(t) ( a>0 ) x 1(t)* x 2(t) =⎰+∞∞---ττττd t ue u a )()( =⎰-ta d e 0ττ = )1(1ate a--x 1(t)* x 2(t) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos[Ω(t+1)+4π]u(t+1) – cos[Ω(t-1)+4π]u(t-1)(3) x 1(t) = u(t) – u(t-1) , x 2(t) = u(t) – u(t-2) x 1(t)* x 2(t) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t <0时,x 1(t)* x 2(t) = 0 当 0<t <1时,x 1(t)* x 2(t) =0td τ⎰ = t 当 1<t <2时,x 1(t)* x 2(t) =21d τ⎰= 1当 2<t<3时,x 1(t)* x 2(t) = 12t d τ-⎰=3-t 当 3<t 时,x 1(t)* x 2(t) = 0(4) x 1(t) = u(t-1) , x 2(t) = sin t · u(t) x 1(t)* x 2(t) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos(t-1)2-5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t)在一个周期( 0<t<T )的波形(1) x(t)是偶函数,只含有偶次谐波分量f(t) = f(-t), f(t) = f(t ±T/2)(2) x(t)是偶函数,只含有奇次谐波分量 f(t) = f(-t), f(t) = -f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(-t)(4) x(t)是奇函数,只含有奇次谐波分量f(t) = -f(-t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(-t), f(t) = f(t±T/2)(6) x(t)是奇函数,含有偶次和奇次谐波分量f(t) = -f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
信号分析与处理课程习题2参考解答-2010(共5篇)

信号分析与处理课程习题2参考解答-2010(共5篇)第一篇:信号分析与处理课程习题2参考解答-2010P57-101Ω-j52-j5Ω(1)方法1:先时移→F[x(t-5)]=X(Ω)e,后尺度→F[x(2t-5)]=X()eΩt05Ω-j-j1Ω1Ω方法2:P40时移+尺度→F[x(at-t0)]=X()ea→F[x(2t-5)]=X()e2 |a|a221Ω-j(2)方法2:P40时移+尺度→F[x(at-t0)]=X()e|a|aΩt0aΩ→F[x(-t+1)]=X(-Ω)ejΩ(3)P42频域卷积定理→F[x1(t)⋅x2(t)]=X1(Ω)*X2(Ω)2π→F[x(t)⋅cos(t)]=X(Ω)*[πδ(Ω+1)+πδ(Ω-1)]=X(Ω+1)+X(Ω-1)2π22P57-12F[x(t)]=⎰x(t)e-∞∞-jΩtdt=⎰τ-2E(t+)eτ2ττdt+⎰22Eτ8ωττωτ(-t+)e-jΩtdt=2sin2()=Sa2()τ2424ωτP57-13假设矩形脉冲为g(t)=u(t+)-u(t-),其傅里叶变换为G(Ω),则22F[x(t)]=F[E⋅g(t+)-E⋅g(t-)]=E⋅G(Ω)eEΩτ=⋅G(Ω))2j2P57-15ττττjΩτ-E⋅G(Ω)e-jΩτ=E⋅G(Ω)(ejΩτ-e-jΩτ)图a)X(Ω)=|X(Ω)|e-1jΩ⎧AejΩt0,|Ω|<Ω0=⎨|Ω|>Ω0⎩0,→x(t)=F[X(Ω)]=2π⎰Ω0AejΩt0ejΩtdΩ=AΩ0Asin(Ω0(t+t0))=Sa(Ω0(t+t0))π(t+t0)π图b)X(Ω)=|X(Ω)|ejΩ⎧-jπ⎪Ae,-Ω0<Ω<0⎪jπ⎪=⎨Ae2,0<Ω<Ω0⎪0,|Ω|>Ω0⎪⎪⎩→x(t)=F[X(Ω)]=2π-1⎰-Ω0Ae-jπejΩt1dΩ+2π⎰Ω0Ae2ejΩtdΩ=jπA2A2Ω0t(cos(Ω0t-1))=-sin()πtπt2第二篇:高频电子信号第四章习题解答第四章习题解答4-1 为什么低频功率放大器不能工作于丙类?而高频功率放大器则可工作于丙类?分析:本题主要考察两种放大器的信号带宽、导通角和负载等工作参数和工作原理。
第二章 信号分析与处理-2

相关函数一般和 t1 和 t2 时刻有关。
当 t1 t2 t 时,
均方值为:
Rxx (t, t)
D
2 x
(t)
方差为:
2 x
(t)
Cx
(t , t )
Rxx (t,
t)
u x2
(t)
例: 随机相位正弦波 x(t) a sin(0t ) ,式
中,a ,0 均为常数, 是一随机变量,在0~2
对能量信号定义的自相关函数和互相关函
数将会出现无穷大。
因此对于功率信号,按下式定义:
Rxy (m)
lim
N
1 2N 1
N
x(n)
nN
y(n
m)
Rxx (m)
lim
N
1 2N 1
N
x(n)x(n
nN
m)
对应于上述情况,连续信号的相关函数为
Rxy ()
如果信号 x(t) 的总能量为E,且
2
E x(t) dt
(1)
则称 x(t) 是能量有限信号,简称能量信号。一般
实际信号都是实函数,上式可写成:
E x2 (t) dt
(2)
如果上式不满足,即信号 x(t) 的能量为无穷大,
例如 x(t) 为周期信号、阶跃信号、随机信号等等,
Rxy x(n) y(n)
n
(6)
下面讨论 Rxy
和
的含义,定义:
xy
2
x(n) ay(n) / x2 (n)
信号分析与处理课后习题答案

1 信号分析与处理课后习题答案第五章快速傅里叶变换1.1.如果一台通用计算机的速度为平均每次复乘需要如果一台通用计算机的速度为平均每次复乘需要50us 50us,每次复加需要,每次复加需要10us 10us,,用来就散N=1024点的DFT DFT,问:,问:(1)直接计算需要多少时间?用FFT 计算呢?(2)照这样计算,用FFT 计算快速卷积对信号进行处理是,估计可实现实时处理的信号最高频率?解:分析:直接利用DFT 计算:复乘次数为N 2,复加次数为N(N-1);利用FFT 计算:复乘次数为20.5log N N ,复加次数为2log N N ;(1)直接DFT 计算:复乘所需时间2215010245052.4288T N us us s=´=´=复加所需时间2(1)101024(10241)1010.47552T N N us us s=-´=-´=所以总时间1262.90432DFT T T T s=+=FFT 计算:复乘所需时间3220.5log 500.51024log 1024500.256T N N us us s =´=´´´=复加所需时间422log 101024log 1024100.1024T N N us us s =´=´´=所以总时间为340.3584FFT T T T s =+=(2)假设计算两个N 长序列1()x n 和2()x n 的卷积计算过程为如下:第一步:求1()X k ,2()X k ;所需时间为2FFTT ´第二步:计算12()()()X k X k X k =·,共需要N 次复乘运算所需时间为501024500.0512To N us us s=´=´=第三步:计算(())IFFT X k ,所需时间为FFTT 所以总时间为230.35840.0512 1.1264FFT T T To s s s=´+=´+=容许计算信号频率为N/T=911.3Hz 2.2.设设x(n)x(n)是长度为是长度为2N 的有限长实序列,()X k 为x(n)x(n)的的2N 点得DFT DFT。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
1 -1 2 t -2
1 -1 O 1
(1)
2 t
-2
-1
O
O
( −1)
( −1)
τ τ ⎤ ⎡ ⎛ ωτ ⎞ E ⎢ε (t + ) − ε (t − )⎥ ↔ EτSa⎜ ⎟ 2 2 ⎦ ⎣ ⎝ 2 ⎠
�
利用一次微分求解: x′(t ) = [ε (t + 2) − ε (t − 1)] − [ε (t − 1) − ε (t − 2)]
(3)
X 1k X 2k
A1τ 1 kπτ 1 A1τ 1 kπ sinc( ) sinc( ) T T1 T 2 A 1 = 1 = 1 = 1 = A2τ 2 kπτ 2 A2τ 2 kπ sinc( ) sinc( ) A2 3 T2 T2 T2 2
5
课后答案网
| X 11 | 1 = | X 21 | 3
−
Aτ T1
Xk
2π τ
O ω1
2π τ
ω
ω1
Aτ kπτ sinc( ) T T
(1) 谱线间隔为基波角频率
ω1 =
带宽 (2)
2π 2π = rad/s, f1 = 1 MHz T 1× 10−6 2π 2π Bw = = rad/s, f w = 2 MHz τ 0.5 × 10−6 2π 2π 1 ω1 = = rad/s, f1 = MHz −6 T 3 ×10 3 2π 2π 2 Bw = = rad/s, f w = MHz −6 τ 1.5 ×10 3
(c) x (t ) = ( t + 2 ) [ε (t + 2) − ε (t + 1)] + [ε (t + 1) − ε (t − 1)] + ( −t + 2 ) [ε (t − 1) − ε (t − 2)]
6
课后答案网
x (t )
1 1 1 2 t -2 -1
③利用时域移位性质求解。
A jA [1 − cos( kπ )] = − [1 − cos( kπ )] jkω 0T 2kπ
3
课后答案网
A
题 5-3 图 2 参考图 2,有
x (t ) = −
X0 = − A ⎛ kπ sinc ⎜ 2 ⎝ 2
A T + x1 (t − ) 2 4
−1
(1)
τ
t
(1)
τ
t
−τ O
( −2 )
x′(t ) = δ (t + τ ) − 2δ ( t ) + δ (t − τ ) ωτ ) 2
jω X (ω ) = e jωτ − 2 + e − jωτ = 2 cos (ωτ ) − 2 = −4sin 2 ( X (ω ) =
(b) x (t ) =
指数形式:
1 j ( ak − jbk ) = − bk 2 2 − jA = ⎡1 − cos ( kπ ) ⎤ ⎦ 2kπ ⎣ − jA ⎡ k 1 − ( −1) ⎤ = ⎦ 2kπ ⎣
Xk =
=
jA ⎡ k −1) − 1⎤ ( ⎦ 2kπ ⎣
1 T
T 2 T − 2
T A − jkω1t ⎤ 1 ⎡ 0 ⎛ A ⎞ − jkω1t 2 − + e dt e dt ⎥ ⎢ ∫− T ⎜ ⎟ ∫ ∫ 0 2 T ⎣ 2⎝ 2 ⎠ ⎦ T ⎤ A ⎡ 2 − jkω1t = − e jkω1t ) dt ⎥ ⎢ ∫0 ( e 2T ⎣ ⎦ ⎤ − jA ⎡ T 2 = ⎢ ∫0 sin ( kω1t ) dt ⎥ T ⎣ ⎦ ⎛ T⎞ − jA ⎜ = − cos ( kω1t ) 2 ⎟ ⎜ ⎟ kω1T ⎜ ⎟ 0 ⎝ ⎠
d [cos(2t )ε (t )] = −2sin(2t )ε (t ) + cos(2t )δ (t ) = −2sin(2t )ε (t ) + δ (t ) dt
x (t )
A 2
求题 2.2 图示对称周期矩形信号的傅里叶级数(三角形式与指数形式) ,并画出幅度频谱。
−T
−
T 2
O
A − 2
d [cos(2t )ε (t )] dt
(1)
d −t [e δ (t )] dt
解: (2)
∫
∞ −∞
etδ (t − 3)dt = e3 = ∫ π sin c(t )δ (t ) dt = π sin c(0) = π
−∞ ∞
∫
sin(π t ) δ (t )dt −∞ t
∞
(4)
∫
∞ −∞
(4)
| X 13 | 1 = | X 23 | 3
2.10 利用傅里叶变换的性质,求题 2.10 图所示各信号的傅里叶变换。
x (t )
x (t )
x (t )
1
1
−τ O
−1
1
τ
t
−2τ
−1
O
2τ
t
-2 -1
O
1
2 t
(a)
(b) 题 2.10 图
(c)
解:(a)
x (t )
x ' (t )
1
−τ O
∞
2.3 如图 2.3 所示的周期单位冲激序列 δ T (t ) = 数。
k =−∞
∑ δ (t − kT ) ,求其指数形式和三角形式的傅里叶级
(1)
-2T -T
o
T
2T
t
题 2.3 图 解:
2 T (1)因为周期冲激序列是偶函数,则 bk = ∫ 2T δ (t − kT ) sin(kωt )dt = 0 T −2
e jωτ − 2 + e − jωτ 2 cos (ωτ ) − 2 4 ωτ = = j sin 2 ( ) jω jω ω 2
1 t[ε (t + 2τ ) − ε (t − 2τ )] 2τ
x(t )
1 2τ
x ' (t )
x′(t ) =
利用时域微
1 1 [ε (t + 2τ ) − ε (t − 2τ )] − [δ (t + 2τ ) + δ (t − 2τ )] O O 2τ −2τ −2τ t 2τ −1
A 1 + 2 T
∫
T 4 T − 4
Adt = 0
⎞ −j 2 ⎟e ⎠
kπ
Xk =
2π T ⎞ − jk T × 4 A ⎛ kπ e = sinc ⎜ ⎟ 2 ⎠ ⎝ 2
当 k 为偶数时 X k = 0 ;当 k 为奇数时 X k = − j
A 。 kπ
x(t ) 是奇对称奇谐函数,傅里叶级数中只含有奇次谐波。
k =1
∞
1 2 ∞ + ∑ cos( kωt ) T T k =1
4
课后答案网
(2)①定义法: X k =
1 T
∫
T
x ( t ) e − jkω1t dt =
1 T
∫
T 2 T − 2
δ ( t ) e − jkω1t dt =
1 T
②利用三角式系数 X k =
1 1 ( ak − jbk ) = 2 T
课后答案网
习题 2
2.1 化简以下各信号的表达式。 (1)
∫
∞
−∞
etδ (t − 3)dt
(2)
∫
sin(π t ) δ (t )dt −∞ t
∞
(3) (5)
∫
∞
−∞
ε (t + 1)δ (t − 1)dt
(4) (6)
∫
∞
−∞
e −2t [δ ′(t ) + δ (t )]dt
a0 =
1 T
∫
T
x(t )dt =
1 T
∫
T 2 T − 2
δ (t ) dt =
1 2 T 2 , ak = ∫ 2T δ (t − kT ) cos( kωt ) dt = . T T −2 T
其三角形式的傅里叶级数为:
x ( t ) = a0 + ∑ ( ak cos ( kω1t ) + bk sin ( kω1t ) ) =
Xk =
x ( t ) e − jkω1t dt =
− jA ⎡ ⎛ kω T ⎞ ⎤ 1 − cos ⎜ 1 ⎟ ⎥ ⎢ 2k π ⎣ ⎝ 2 ⎠⎦ jA = ⎡cos ( kπ ) − 1⎤ ⎦ 2k π ⎣ jA ⎡ k = −1) − 1⎤ ( ⎦ 2kπ ⎣ =
(二)利用一个周期的傅里叶变换求傅里叶级数的系数。 ① 取 ( − T 2, T 2) 区间的 x ( t ) 构成单周期信号,其傅里叶变换
⎡ ⎛ kω0T ⎢ cos ⎜ 2 ⎣ ⎝
⎞ ⎤ ⎟ − 1⎥ ⎠ ⎦
jA ⎡ cos ( kπ ) − 1⎤ ⎦ 2 kπ ⎣ jA 2 kπ =− sin ( ) kπ 2 (k为偶数) ⎧0, ⎪ = ⎨ jA − , (k为奇数) ⎪ ⎩ kπ
则傅里叶级数为:
x (t ) = −
jA jkω0t e k为奇数 kπ
T 2
T
t
题 2.2 图
解: (一)定义式求解 三角形式:信号奇对称 a0 = ak = 0
bk =
T ⎤ A 2 T 2 ⎡ 0 ⎛ A⎞ 2 2 x t k ω t dt k ω t dt = − + sin sin sin ( kω1t ) dt ⎥ ( ) ( ) ( ) T⎜ T ⎢ 1 1 ⎟ ∫ ∫ ∫ 0 2 T −2 T ⎣ −2 ⎝ 2 ⎠ ⎦
