改进欧拉格式的matlab实现
MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名:樊元君学号:02 日期:一、实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
:二、实验内容1、分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
求,步长h=。
*2、实验注意事项的精确解为,通过调整步长,观察结果的精度的变化^)三、程序流程图:●改进欧拉格式流程图:~|●四阶龙格库塔流程图:]四、源程序:●改进后欧拉格式程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');…x0=input('x0=');y0=input('y0=');disp('输入的范围是:');X=input('X=');Y=input('Y=');n=round((Y-X)/h);\i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);%·yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);%y1=(yp+yc)/2;x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y);:endend●四阶龙格库塔程序源代码:function [] = LGKT(h,x0,y0,X,Y)。
format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是:');"X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:n~x1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);% k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);% k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);%…y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4);%x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.7f,%.7f\n',x1,y1,y);end·end*五、运行结果:改进欧拉格式结果:;}四阶龙格库塔结果:步长分别为:和时,不同结果显示验证了步长减少,对于精度的提高起到很大作用,有效数字位数明显增加。
欧拉法(euler)求解常微分方程的matlab程序及案例

欧拉法(euler)求解常微分方程的matlab程序及案例欧拉方法是最初用于求解常微分方程的数值方法之一,它是一种显式的一步法,具有易于实施的优点,特别适合初学者使用。
本文将介绍欧拉法的原理和使用MATLAB求解常微分方程的具体方法,同时给出一个简单的实例进行说明。
一、欧拉法原理考虑一个一阶常微分方程y'=f(t,y),欧拉法的基本思想是将时间步长Δt均分成n个小步长,从y(t0)开始依次计算每个时刻的值,得到一列估计值y1, y2, …, yn。
欧拉法的计算公式为:(1)y1=y(t0+Δt)=y(t0)+Δtf(t0, y0)(2)y2=y(t0+2Δt)=y(t0+Δt)+Δtf(t0+Δt, y1)(3)yn=y(t0+nΔt)=y(t0+(n-1)Δt)+Δtf(t0+(n-1)Δt, yn-1)可以看出,欧拉法的核心在于利用已知的t和y计算f(t,y),从而获得y的逼近值。
但是需要注意的是,步长Δt越小,计算所需的时间和内存就越多,而精度却并不一定提高。
因此在实际应用中需要结合具体问题选择合适的步长。
二、MATLAB求解常微分方程的具体方法(1)定义常微分方程我们以一个简单的例子开始,考虑求解y'=1-y,y(0)=0.5在[0,1]区间内的积分。
首先定义匿名函数dydt,将其传到ode45中求解:dydt=@(t,y)1-y;[t,y]=ode45(dydt,[0 1],0.5);plot(t,y,'-o')运行以上代码可以得到结果,其中plot函数用于绘制图像。
但是,由于求解过程中计算机执行到ode45函数时可能需要很长时间,因此需要更快捷的方法。
(2)利用欧拉法求解方程欧拉法求解方程首先需要定义步长Δt,这里设Δt为0.1。
定义起始值y=[0.5]、时间向量t=0:Δt:1,然后计算列向量y的估计值:t=0:0.1:1;y=zeros(size(t));y(1)=0.5;for n=1:length(t)-1y(n+1)=y(n)+0.1*(1-y(n));endplot(t,y,'-o')以上代码的执行结果与前面的ode45方法相同,但是速度更快。
四阶龙格库塔和向前欧拉方法和隐式欧拉法以及改进欧拉法教材

实验九欧拉方法信息与计算科学金融崔振威201002034031一、实验目的:1、掌握欧拉算法设计及程序实现二、实验内容:1、p364-9.2.4、p386-9.5.6三、实验要求:主程序:欧拉方法(前项):function [x,y]=DEEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0;for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*feval(f,x(i),y(i));endformat short欧拉方法(后项):function [x,y]=BAEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0;for i=1:nx(i+1)=x(i)+h;y1=y(i)+h*feval(f,x(i),y(i));y(i+1)=y(i)+h*feval(f,x(i+1),y1);endformat short梯形算法:function [I,step,h2] = CombineTraprl(f,a,b,eps)%f 被积函数%a,b 积分上下限%eps 精度%I 积分结果%step 积分的子区间数if(nargin ==3)eps=1.0e-4;endn=1;h=(b-a)/2;I1=0;I2=(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsym(sym(f)),b))/h;while abs(I2-I1)>epsn=n+1;h=(b-a)/n;I1=I2;I2=0;for i=0:n-1x=a+h*i;x1=x+h;I2=I2+(h/2)*(subs(sym(f),findsym(sym(f)),x)+subs(sym(f),findsym(sym(f)),x1));endendI=I2;step=n;h2=(b-a)/n;改进欧拉方法:function [x,y]=MoEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0; for i=1:nx(i+1)=x(i)+h;y1=y(i)+h*feval(f,x(i),y(i)); y2=y(i)+h*feval(f,x(i+1),y1); y(i+1)=(y1+y2)/2; endformat short四阶龙格-库塔法:function y = DELGKT4_lungkuta(f, h,a,b,y0,varvec) %f:一阶常微分方程的一般表达式的右端函数 %h:积分步长%a :自变量的取值下限 %b:自变量的取值上限%varvec :常微分方程的变量组 format long; N = (b-a)/h;y = zeros(N+1,1); y(1) = y0; x = a:h:b;var = findsym(f); for i=2:N+1K1 = Funval(f,varvec,[x(i-1) y(i-1)]);%Funval 为程序所需要的函数 K2 = Funval(f,varvec,[x(i-1)+h/2 y(i-1)+K1*h/2]); K3 = Funval(f,varvec,[x(i-1)+h/2 y(i-1)+K2*h/2]); K4 = Funval(f,varvec,[x(i-1)+h y(i-1)+h*K3]); y(i) = y(i-1)+h*(K1+2*K2+2*K3+K4)/6; endformat short;p364-9.2.4欧拉方法(前项):1、22)(,1)0(,22'+-+-==-=-t t e t y y y t y t解:执行20步时:编写函数文件doty.m 如下: function f=doty(x,y); f=x^2-y;在Matlab 命令窗口输入:>> [x1,y1]=DEEuler('doty',0,2,1,20)可得到结果:x1 =0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.70000.8000 0.9000 1.0000 1.1000 1.2000 1.3000 1.4000 1.50001.6000 1.7000 1.8000 1.90002.0000y1 =1.0000 0.9000 0.8110 0.7339 0.6695 0.6186 0.5817 0.55950.5526 0.5613 0.5862 0.6276 0.6858 0.7612 0.8541 0.96471.0932 1.2399 1.4049 1.5884 1.7906在Matlab 命令窗口输入:>> y3=-exp(-x1)+x1.^2-2*x1+2求得解析解:y3 =1.0000 0.9052 0.8213 0.7492 0.6897 0.6435 0.6112 0.59340.5907 0.6034 0.6321 0.6771 0.7388 0.8175 0.9134 1.02691.1581 1.3073 1.4747 1.6604 1.8647输入:>> plot(x1,y1,'o');hold on>> plot(x1,y3,'*');hold on可得近似值与解析解的图像比较:执行40步时:在Matlab 命令窗口输入:>> [x1,y1]=DEEuler('doty',0,2,1,40)可得到结果:x1 =0 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000 0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500 0.7000 0.75000.8000 0.8500 0.9000 0.9500 1.0000 1.0500 1.1000 1.15001.2000 1.2500 1.3000 1.3500 1.4000 1.4500 1.5000 1.55001.6000 1.6500 1.7000 1.7500 1.8000 1.8500 1.9000 1.95002.0000y1 =1.0000 0.9500 0.9026 0.8580 0.8162 0.7774 0.7417 0.7091 0.6798 0.6538 0.6312 0.6121 0.5967 0.5848 0.5767 0.5724 0.5719 0.5753 0.5826 0.5940 0.6094 0.6290 0.6526 0.68050.7126 0.7490 0.7897 0.8347 0.8841 0.9379 0.9961 1.05881.1260 1.1977 1.2739 1.3547 1.4401 1.5301 1.6247 1.7240 1.8279在Matlab 命令窗口输入:>> y3=-exp(-x1)+x1.^2-2*x1+2求得解析解:y3 =1.0000 0.9513 0.9052 0.8618 0.8213 0.7837 0.7492 0.7178 0.6897 0.6649 0.6435 0.6256 0.6112 0.6005 0.5934 0.5901 0.5907 0.5951 0.6034 0.6158 0.6321 0.6526 0.6771 0.70590.7388 0.7760 0.8175 0.8633 0.9134 0.9679 1.0269 1.09031.1581 1.2305 1.3073 1.3887 1.4747 1.5653 1.6604 1.7602 1.8647输入:>> plot(x1,y1,'o');hold on>> plot(x1,y3,'*');hold on可得近似值与解析解的图像比较:从上面结果可以看出,执行40步时近似解的值要接近于解析解,误差更小,结果更精确。
用MATLAB程序生动地演示欧拉公式

⽤MATLAB程序⽣动地演⽰欧拉公式下⾯的MA TLAB 程序⽣动地演⽰欧拉公式Exp(t) = cos(t) + j sin(t)% Henry-104% 本程序演⽰欧拉公式% Jan.25th,2012%h_fig1 = figure;set(h_fig1, 'unit', 'normalized', 'position', [0.1, 0.1, 0.9, 0.9]);set(h_fig1, 'defaultuicontrolunits', 'normalized');h_text1 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.73, 0.25, 0.05],... % 创建⽂本框'String', '▲是cos 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_text2 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.78, 0.25, 0.05],... % 创建⽂本框'String', 'Δ是sin 和exp 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_pushbutton1 = uicontrol(h_fig1, 'Style', 'PushButton', 'Position', [0.82, 0.12, 0.07, 0.06],...'string', '退出', 'BackgroundColor', [0.8 0.9 0.8], 'ForegroundColor', 'r', 'FontSize', 14, 'FontWeight', 'Bold',...'callback', 'delete(h_fig1),')h_axes0 = axes('Box', 'on', 'Position', [0.15, 0.18, 0.56, 0.68], 'FontSize', 8)set(gcf,'color','w');w = 0.1*pit = 0:40; % 在前进⽅向绕了2 圈%a = -ones(1,length(t));plot3(cos(w*t),t,sin(w*t),'b', 'LineWidth', 2);grid on; hold on;hc = plot3(cos(w*t),t,a,'k--'); hold on;set(hc, 'Color', 'r', 'LineWidth', 2);a=-a;hs = plot3(a,t,sin(w*t),'r-.'); hold on;set(hs, 'Color', 'k', 'LineWidth', 2);text(0.7,0.3,0.6, ' <-- CCW', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,-1, ' ▲Cos', 'Color', 'r', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,0, ' Δ Sin', 'FontSize', 14, 'FontWeight', 'Bold');%xlabel('x', 'FontSize', 14, 'FontWeight', 'Bold');ylabel('t', 'FontSize', 14, 'FontWeight', 'Bold');zlabel('y', 'FontSize', 14, 'FontWeight', 'Bold');title('演⽰欧拉公式y = exp(jwt) = cos(wt) + jsin(wt)', 'Color', 'b', …'FontSize', 18, 'FontWeight', 'Bold');%line([-1,-1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,40],[-1,-1],'LineWidth',3, 'Color', 'k');line([-1,1],[0,0],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,0],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[40,40],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');line([-1,1],[40,40],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');text(0,0,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'r') text(0,40,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'b')程序运⾏结果如下所⽰。
MATLAB常微分方程数值解——欧拉法、改进的欧拉法与四阶龙格库塔方法

MATLAB常微分⽅程数值解——欧拉法、改进的欧拉法与四阶龙格库塔⽅法MATLAB常微分⽅程数值解作者:凯鲁嘎吉 - 博客园1.⼀阶常微分⽅程初值问题2.欧拉法3.改进的欧拉法4.四阶龙格库塔⽅法5.例题⽤欧拉法,改进的欧拉法及4阶经典Runge-Kutta⽅法在不同步长下计算初值问题。
步长分别为0.2,0.4,1.0.matlab程序:function z=f(x,y)z=-y*(1+x*y);function R_K(h)%欧拉法y=1;fprintf('欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K=f(x,y);y=y+h*K;fprintf('欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%改进的欧拉法y=1;fprintf('改进的欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h,y+h*K1);y=y+(h/2)*(K1+K2);fprintf('改进的欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%龙格库塔⽅法y=1;fprintf('龙格库塔法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h/2,y+(h/2)*K1);K3=f(x+h/2,y+(h/2)*K2);K4=f(x+h,y+h*K3);y=y+(h/6)*(K1+2*K2+2*K3+K4);fprintf('龙格库塔法:x=%f, y=%f\n',x+h,y);end结果:>> R_K(0.2)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.200000, y=0.800000欧拉法:x=0.400000, y=0.614400欧拉法:x=0.600000, y=0.461321欧拉法:x=0.800000, y=0.343519欧拉法:x=1.000000, y=0.255934改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.200000, y=0.807200改进的欧拉法:x=0.400000, y=0.636118改进的欧拉法:x=0.600000, y=0.495044改进的欧拉法:x=0.800000, y=0.383419改进的欧拉法:x=1.000000, y=0.296974龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.200000, y=0.804636龙格库塔法:x=0.400000, y=0.631465龙格库塔法:x=0.600000, y=0.489198龙格库塔法:x=0.800000, y=0.377225龙格库塔法:x=1.000000, y=0.291009>> R_K(0.4)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.400000, y=0.600000欧拉法:x=0.800000, y=0.302400改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.400000, y=0.651200改进的欧拉法:x=0.800000, y=0.405782龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.400000, y=0.631625龙格库塔法:x=0.800000, y=0.377556>> R_K(1)欧拉法:x=0.000000, y=1.000000欧拉法:x=1.000000, y=0.000000改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=1.000000, y=0.500000龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=1.000000, y=0.303395注意:在步长h为0.4时,要将for i=1:1/h改为for i=1:0.8/h。
欧拉方法及其改进的欧拉方法的Matlab实现

11( n n y x y ++−。为了估计它,由Taylor展开得到的精确值1( n y x +是
2'
''
31( ( ( ( ( 2
n n n n h y x y x hy x y x O h +=+++ (5
2.欧拉方法、改进的欧拉方法及Matlab实现
下面主要讨论一阶常微分方程的初值问题,其一般形式为:
' 00
(,
( y f x y y x y ⎧=⎨
=⎩ (1我们知道,只要函数(, f x y适当光滑——譬如关于y满足利普希茨(Lipschitz条件
(, (, f x y f x y L y y −≤−
改进的欧拉方法是先用欧拉公式求1( n y x +的一个近似值1n y +,称为预测值,然后用梯形公式进行矫正并求得近似值1n y +。即
1111(, [(, (, ]
2n n n n n n n n n n y y f x y h h
y y f x y f x y ++++⎧=+⎪
⎨=++⎪⎩
(8 2.2.2改进的欧拉方法的误差估计
方法是一阶方法,因此它的精度不高。
2.2改进的欧拉方法
2.2.1改进的欧拉方法
用数值积分方法离散化问题(1,两端积分可得
1
1( ( (, ( (0,1, 2, n n
x n n x y x y x f x y x dx n ++−==∫
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
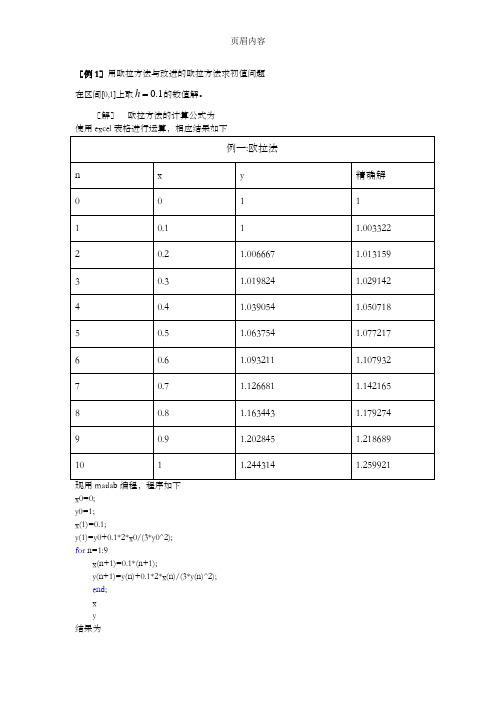
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
数值分析考试

桂林理工大学考试(考查)试卷( 学年度 第一学期)课程名称:数值分析考核专业班级:学号: 姓名: 成绩:﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍一、 简答题(4分×5=20分)1、病态线性方程组的主要判断依据有哪些?答:(1)系数矩阵的某两行(列)几乎近似相关(2)系数矩阵的行列式的值很小(3)用主元消去法解线性方程组时出现小主元(4)近似解x*已使残差向量r=b-Ax*的范数很小,但该近似解仍不符合问题要求。
2、数值计算中如何避免不稳定的算法,防止有效数字的损失?答:(1)简化计算过程,减少运算次数;(2)避免两个相近的数相减;(3)避免除数的绝对值远小于被除数的绝对值;(4)防止大数“吃掉”小数的现象;(5)使用数值稳定的算法,设法控制误差的传播。
3、解释龙格现象。
答:增加插值节点,提高插值多项式的次数,可以使插值函数在更多的点与所逼近的函数取相同的值,但会使插值函数在两端发生激烈的振荡,这就是插值计算的龙格现象。
4、阐述迭代法的基本思想。
答:就是用某种极限过程去逐步逼近线性方程组精确解得方法。
其基本思想为:先任取一组近似解初值X 0,然后按照某种迭代原则,由X 0计算新的近似解X 1,以此类推,可计算出X 2,X 3,…X K ,。
,如果{X }收敛,则取为原方程组的解。
5、叙述QR 算法的步骤。
答:对于给定的n 阶实对称矩阵A 与迭代次数M ;(1)令A 1=A ,对于k=1,2,…,M ;(2)迭代计算下一个矩阵:A k =Q k R k (对A k 作QR 分解),(3)A k =RQ(交换乘法次序),令k=k+1,A k+1=Q k T A K Q K(4)返回到2,直到k=M,输出A 的主对角元素。
二、 计算型编程题(20分×3=60分)1、 用Newton 插值拟合[0, 2*pi]上函数()sin x f x e x 。
答:function [yt,N] = NewtInterp(x,y,xt)% 已知数据点的牛顿插值% x,y:插值条件% xt:要计算的插值点,可以是多个% yt:用牛顿插值函数出xt对应的函数值数组% N: 牛顿插值多项式表达式syms t;n=length(x);ny=length(y);if n~=nyerror('插值节点x与函数值y维数不一致'); enda=zeros(1,n);N = y(1);w = 1;for k=1:n-1yy=zeros(1,n); % 记录差商for j=k+1:nyy(j) = (y(j)-y(k))/(x(j)-x(k));enda(k) = yy(k+1);w = w*(t-x(k));N = N + a(k)*w;y = yy;endyt = subs(N,'t',xt);simplify(N);N = collect(N); % 将插值多项式展开N = vpa(N, 6); % 系数转化为6位精度输入:x=[0:pi/10:2*pi];y=exp(x).*sin(x);xt=pi;[yt,N] = NewtInterp(x,y,xt)% 画图z=0:pi/20:2*pi;yz= subs(N,'t',z); %计算插值点处的函数值figure;plot(z,exp(z).*sin(z),'--r',z,yz,'-b')hold onplot(x,y,'marker','+')hold onplot(xt,yt,'marker','o')h=legend('$\exp{x}.*sin{x}$','Newton','$(x_k,y_k)$','$x=pi$');set(h,'Interpreter','latex')xlabel('x')ylabel('y')yt =7.1684e-015N =.159313e-14*t^20-.178421e-12*t^19+.578696e-11*t^18-.993977e-10*t^17+.1179 00e-8*t^16-.101872e-7*t^15+.640214e-7*t^14-.340920e-6*t^13+.131789e-5*t^12-.33 7754e-5*t^11+.19392e-4*t^10+.22800e-4*t^9+.33873e-4*t^8-.162956e-2*t^7-.110707 e-1*t^6-.333620e-1*t^5+.1611e-4*t^4+.333328*t^3+1.00000*t^2+.999992*t2、利用龙贝格算法程序计算积分x。
matlab求解微分方程数值解与解析解

matlab求解微分方程数值解与解析解微分方程是数学中的重要内容,它描述了物理、工程、经济等领域中的许多现象和问题。
在实际应用中,我们经常需要求解微分方程的解析解或数值解。
本文将以Matlab为工具,探讨如何求解微分方程并对比解析解与数值解的差异。
一、引言微分方程是描述自然界中许多现象和问题的数学语言,它包含了未知函数及其导数与自变量之间的关系。
微分方程的求解可以帮助我们了解问题的性质和变化规律,并为实际应用提供参考。
在许多情况下,微分方程的解析解很难求得,这时我们可以利用计算机进行数值求解。
二、微分方程的数值解法1.欧拉法欧拉法是最简单的数值求解微分方程的方法之一。
它通过将微分方程转化为差分方程,然后利用离散的点逼近连续的解。
具体步骤如下:(1)将微分方程转化为差分方程,即用近似的导数代替真实的导数;(2)选择初始条件,即确定初始点的值;(3)选择步长和求解区间,即确定求解的范围和步长;(4)使用迭代公式计算下一个点的值;(5)重复步骤(4),直到达到指定的求解区间。
2.改进的欧拉法欧拉法存在精度较低的问题,为了提高精度,可以使用改进的欧拉法。
改进的欧拉法是通过使用两次导数的平均值来计算下一个点的值,从而提高了数值解的精度。
3.龙格-库塔法龙格-库塔法是一种常用的数值求解微分方程的方法,它通过使用多个点的导数来逼近连续解。
龙格-库塔法的步骤如下:(1)选择初始条件和步长;(2)使用迭代公式计算下一个点的值;(3)计算下一个点的导数;(4)根据导数的值和步长计算下一个点的值;(5)重复步骤(3)和(4),直到达到指定的求解区间。
龙格-库塔法的精度较高,适用于求解一阶和高阶微分方程。
三、微分方程的解析解解析解是指能够用公式或函数表示的方程的解。
有些微分方程具有解析解,可以通过数学方法求得。
例如,一阶线性常微分方程和某些特殊类型的二阶微分方程等。
解析解的优势在于精确性和直观性,能够帮助我们深入理解问题的本质。
欧拉法

欧拉法的MATLAB实现班级:123082--04 姓名:应业敏学号:20081001088摘要:在数学和计算机科学中,欧拉方法(Euler method)命名自它的发明者莱昂哈德·欧拉,是一种一阶数值方法,用以对给定初值的常微分方程(即初值问题)求解。
它是一种解决常微分方程数值积分的最基本的一类显型方法(Explicit method)。
欧拉法(euler method)是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法。
它不直接追究质点的运动过程,而是以充满运动液体质点的空间——流场为对象。
研究各时刻质点在流场中的变化规律。
将个别流体质点运动过程置之不理,而固守于流场各空间点。
通过观察在流动空间中的每一个空间点上运动要素随时间的变化,把足够多的空间点综合起来而得出的整个流体的运动情况。
基本思想:基本思想是迭代。
其中分为前进的EULER法、后退的EULER法、改进的EULER法。
所谓迭代,就是逐次替代,最后求出所要求的解,并达到一定的精度。
误差可以很容易的计算出来。
特点:单步,显式,一阶求导精度,截断误差贰阶缺点:欧拉法简单地取切线的端点作为下一步的起点进行计算,当步数增多时,误差会因积累而越来越大。
因此欧拉格式一般不用于实际计算。
改进欧拉格式:为提高精度,需要在欧拉格式的基础上进行改进。
采用区间两端的函数值的平均值作为直线方程的斜率。
改进欧拉法的精度为二阶。
算法为:微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值,这个过程称为离散化。
实现离散化的基本途径是用向前差商来近似代替导数,这就是欧拉算法实现的依据。
欧拉(Euler)算法是数值求解中最基本、最简单的方法,但其求解精度较低,一般不在工程中单独进行运算。
所谓数值求解,就是求问题的解y(x)在一系列点上的值y(xi)的近似值yi。
对于常微分方程:,x∈[a,b]y(a) = y0可以将区间[a,b]分成n段,那么方程在第x i点有y'(x i) = f(x i,y(x i)),再用向前差商近似代替导数则为:,在这里,h是步长,即相邻两个结点间的距离。
matlab实例讲解欧拉法求解微分方程

欧拉法是数值分析中常用的一种方法,用于求解常微分方程的数值解。
在MATLAB中,可以通过编写相应的代码来实现欧拉法求解微分方程。
下面我们将通过具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
我们要了解欧拉法的基本原理。
欧拉法是一种通过迭代逼近微分方程解的方法,它基于微分方程的定义,通过离散化的方法逼近微分方程的解。
其基本思想是利用微分方程的导数定义,将微分方程以差分形式进行逼近。
具体而言,欧拉法通过将微分方程转化为差分方程的形式,然后通过迭代逼近得到微分方程的数值解。
接下来,我们通过一个具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
假设我们要求解以下的一阶常微分方程:(1) dy/dx = x + y(2) y(0) = 1现在我们来编写MATLAB代码来实现欧拉法求解这个微分方程。
我们需要确定微分方程的迭代步长和迭代范围。
假设我们将x的范围取为0到10,步长为0.1。
接下来,我们可以编写MATLAB代码如下:```matlab欧拉法求解微分方程 dy/dx = x + y定义迭代步长和范围h = 0.1;x = 0:h:10;初始化y值y = zeros(1,length(x));y(1) = 1;使用欧拉法迭代求解for i = 1:(length(x)-1)y(i+1) = y(i) + h * (x(i) + y(i));end绘制图像plot(x,y,'-o');xlabel('x');ylabel('y');title('欧拉法求解微分方程 dy/dx = x + y');```在这段MATLAB代码中,我们首先定义了迭代的步长和范围,并初始化了微分方程的初始值y(0) = 1。
然后通过for循环使用欧拉法进行迭代求解微分方程,最后绘制出了微分方程的数值解的图像。
通过以上的实例讲解,我们可以看到,在MATLAB中使用欧拉法求解微分方程是非常简单而直观的。
matlab用欧拉法求常微分方程初值

Matlab中欧拉法求解常微分方程初值问题一、概念介绍在数学和工程领域,常微分方程初值问题是一个广泛应用的数学概念。
它描述了一个未知函数在给定初始条件下的行为。
而欧拉法则是一种常用的数值方法,用来解决常微分方程初值问题。
在Matlab中,我们可以利用欧拉法来求解常微分方程问题,从而得到函数在给定初始条件下的近似解。
二、欧拉法的基本原理欧拉法的基本思想是通过离散化微分方程,将其转化为递推的差分方程。
考虑一个一阶常微分方程初值问题:\[ \frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0 \]在欧拉法中,我们采用递推的方式,根据已知的初始条件和微分方程的性质,通过迭代来得到逼近解的数值结果。
具体地,我们首先将自变量$x$的范围进行等间距分割,得到$x_0, x_1, x_2, ..., x_n$,并将步长记为$h$。
根据微分方程的性质,我们可以根据已知的初始条件$y(x_0) = y_0$,通过迭代计算得到近似解$y(x_1), y(x_2), ..., y(x_n)$。
三、Matlab中的欧拉法求解在Matlab中,我们可以利用欧拉法来求解常微分方程初值问题。
以求解一阶常微分方程为例,假设我们需要求解以下的常微分方程初值问题:\[ \frac{dy}{dx} = -2xy, \quad y(0) = 1 \]我们可以利用欧拉法的思想,将自变量$x$的范围进行离散化,然后根据欧拉法的递推公式,利用迭代的方式得到近似解的数值结果。
具体地,在Matlab中,我们可以编写如下代码来实现欧拉法的求解过程:```matlabfunction y = euler_method(f, x0, y0, h, n)% 初始化存储结果的数组x = zeros(1, n+1);y = zeros(1, n+1);% 将初始条件存入数组x(1) = x0;y(1) = y0;% 利用欧拉法进行迭代for i = 1:nx(i+1) = x(i) + h;y(i+1) = y(i) + h * f(x(i), y(i));end% 返回近似解的数值结果plot(x, y); % 绘制解的图像end```在上述代码中,我们定义了一个名为`euler_method`的函数,其中包含了欧拉法的计算过程。
欧拉改进法matlab实现

end
%% ===初始化数据 ===
x = x0:h:xn ;% == 计算节点 ==
y = y0 ;
N = length(x) ;% == 节点数 ==
for k = 1:N-1
y(k+1) = y(k) + h*f( x(k) , y(k) ) ; %==欧拉向前公式==
y(k+1) = y(k) + h* f( x(k+1) , y(k+1) ) ; %==欧拉向后公式==
function [ yy ] = Euler_correct( f , y0 , x0 , xn , hh )
% f是inline function 的句柄
% y0是初值
%[x0 xn] 是范围
% hh是步长
%% ===输入判断 ===
if (4 == nargin)
h = 0.1 ;
elseif (5 == nargin)
end
elseif (1 == nargout)
yy = y ;
else
disp('error : please check your input') ;
return ;
end
end
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考
n1yk1可编辑修改yk1欧拉向后公式yk1endelseifnargoutyyelsedisp?errorpleasecheckyourinput?endend可编辑修改thanks致力为企业和个人提供合同协议策划案计划书学习课件等等打造全网一站式需求欢迎您的下载资料仅供参考
matlab软件欧拉算法教程

改进Euler方法计算框图 开始
输入x0 , y0 , h, b
n 1
x1 x0 h y p y0 hf ( x0 , y0 ) yc y0 hf ( x1 , y p ) 1 y1 ( yc y p ) 2
输出x1 , y1
n n 1 x0 x1 , y0 y1
用三个点x n , x n p , x nq的斜率K 1 , K 2 , K 3 加权平均得出 平均斜率K 的近似值,计算格式具有
*
yn1 yn h(1 )K1 K2 K3
K1 , K2为二阶Runge-Kutta格式的表达式 如何预报K3?
在区间[xn ,xn+q ]已知两个斜率值K1,K2,对K1,K2加权 平均得出此区间的平均斜率,从而得到y(xn+q )的预报 值yn+q
Step 1: 将 K2 在 ( xn , yn ) 点作 Taylor 展开
K 2 f ( xn ph , yn phK1 ) f ( xn , yn ) phf x ( xn , yn ) phK1 f y ( xn , yn ) O( h2 )
y( xn ) phy( xn ) O(h2 )
ynq yn qh(1 )K1 K2
K 3 f ( x n q , yn q )
因此K 3为:
利用Taylor展开法选择参数p, q, , , ,使此计算格式 具有三阶精度这类格式统称为三阶Runge-Kutta格式
R-K法的常用公式
常用的三阶R-K方法.
经典R-K公式 每一步计算需 要四个函数值
注意的问题
Runge-Kutta法的主要运算在于计算 Ki 的值,即计算 f 的值。计算量与可达到的最高精度阶数的关系:
matlab改进欧拉法求解转子运动方程

matlab改进欧拉法求解转子运动方程欧拉法是一种常用的数值计算方法,适用于求解微分方程问题。
在转子运动方程中,我们通常通过欧拉法来模拟转子的运动状态,以了解其运动轨迹和相关参数的变化。
转子运动方程描述了转子在给定的初始条件下的运动状态。
它包含了转子的质量、惯性矩阵、刚度矩阵以及施加在其上的外力。
通过数值方法来求解这些微分方程,我们可以获得转子的角位移、角速度等相关信息。
下面我们将介绍如何使用改进的欧拉法来求解转子的运动方程。
首先,我们需要将转子的运动方程转化为适合数值计算的形式。
通常,在转子运动方程中,我们可以使用角位移和角速度来描述转子的状态。
通过求解转子的运动方程,我们可以得到转子在不同时间点的角位移和角速度。
接下来,我们需要将时间进行离散化,以便在数值计算中使用。
我们可以将整个运动过程划分为许多小的时间步长,然后使用欧拉法逐步求解转子的运动状态。
在标准的欧拉法中,我们使用当前时间点的状态来估计下一个时间点的状态。
但是,这种方法存在精度不高的问题,特别是对于非线性和高阶微分方程。
因此,我们引入改进的欧拉法。
改进的欧拉法使用当前时间点和下一个时间点的状态来进行估计。
具体步骤如下:1. 使用欧拉法计算当前时间点的估计状态。
2. 使用当前时间点的估计状态和下一个时间点的状态进行插值,得到改进的估计状态。
3. 使用改进的估计状态来更新下一个时间点的状态。
通过使用改进的欧拉法,我们可以更准确地估计转子的运动状态,并减小数值计算误差。
为了求解转子的运动方程,我们需要选择合适的时间步长和初始条件。
时间步长应足够小,以保证数值计算的精度,但也不能过小,以充分考虑计算效率。
初始条件应符合实际物理情况,并且应该与欧拉法的初始状态相匹配。
最后,我们使用Matlab编程来实现转子运动方程的求解。
Matlab是一种强大的数值计算工具,提供了许多函数和工具箱,方便我们进行数值计算和可视化。
通过使用改进的欧拉法求解转子运动方程,我们可以更准确地了解转子的运动状态和相关参数的变化。
matlab改进的欧拉方法计算一阶常微分方程

matlab改进的欧拉方法计算一阶常微分方程一阶常微分方程可以使用改进的欧拉方法进行数值求解。
假设要求解的方程为dy/dx=f(x,y),初值为y(x0)=y0,步长为h,则改进的欧拉方法的数值迭代公式为:
yn+1 = yn + h/2[f(xn,yn) + f(xn+1, yn + hf(xn, yn))] 其中,yn表示第n步的近似解,yn+1表示第n+1步的近似解,f(xn,yn)表示在点(xn,yn)处的斜率。
以下是MATLAB代码实现该方法:
```matlab
function y = improved_euler(f, x0, y0, h, xn)
% 输入参数:
% f: 常微分方程右端函数
% x0: 自变量初始值
% y0: 因变量初始值
% h: 步长
% xn: 自变量终止值
% 输出参数:
% y: 自变量对应的因变量值
x = x0:h:xn;
y = zeros(1,length(x));
y(1) = y0; % 初值
for i = 1:length(x)-1
y(i+1) = y(i) + h/2*(f(x(i),y(i)) + f(x(i+1),
y(i)+h*f(x(i),y(i))));
end
end
```
这个函数的输入参数包括常微分方程右端函数f,自变量初始值x0,因变量初始值y0,步长h和自变量终止值xn。
输出参数为自变量对应的因变量值y。
常微分方程数值解法-欧拉方法(1)

课题报告题目:常微分方程的数值解法-欧拉方法院 (系):理学院专业:数学与信息专业指导教师:***组员:艾佳欢(组长) 邓云娜柏茜钟岩刘磊2015 年 5 月 11 日常微分方程数值解法-欧拉方法摘要:从常微分方程数值解的基本概念入手,了解最基本的数值解法--欧拉方法。
并利用欧拉方法显式隐式的特点探究如何求解微分方程,以及欧拉方法的误差分析及校正。
关键词:数值解,欧拉方法,误差,校正ABSTRACT: From the basic concept of numerical solution of ordinary differential equations, and understand the most basic numerical solution of euler method. And by using euler explicitly implicit characteristics and explore how to solve differential equations and the error analysis and correction of euler method.KEYWORDS :arithmetic solution,Euler's method,error,revise1.初值问题数值解基本概念初值问题的数值解法,是通过微分方程离散化而给出解在某些节点上的近似值。
在[]b a ,上引入节点{}),,1(,:1100n k x x h b x x x a x k k k n nk k =-==<<<=-=称为步长。
在多数情况下,采用等步长,即),1,0(,n k kh a x nab h k =+=-=。
记准确解为)(x y ,记)(k x y 的近似值为k y ,记),(k k y x f 为k f .一阶常微分方程的初值问题⎩⎨⎧=∈=')2.1()()()1.1(),())(,()(0 x y a y b a x x y x f x y , 若f 在{}〈+∞≤≤=y b x a D ,内连续,且满足Lip 条件:0≥∃L 使2121),(),(y y L y x f y x f -≤-,则初值问题的连续可微解)(x y 在],[b a 上唯一存在,称解)(x y 在节点i x 处的近似值)(i i x y y =为其数值解,该方法称为数值方法。
