聚类分析 PPT
合集下载
聚类分析及其应用实例ppt课件

在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
聚类分析详解ppt

编号
购物环境
样本
A商厦
73
B商厦
66
C商厦
84
D商厦
91
E商厦
94
服务质量 68 64 82 88 90
• 把商厦分成两类:A、B为一类,C、D、E为一类 • 把商厦分为三类:A、B为一类,C为一类,D、E为一类 • 没有指定分类标准,大家为什么会这么分呢? • 从数据出发,根据性质上的亲疏程度进行分类!
(3) 计算新类G M 与任一G 类J
之间距离的递
推公式为 D M Ji G m M ,ijn G Jdij m ini G m K,ijn G Jdij,i G m L,ijn G Jdij
m inD K J,D L J
-
最短距离法的聚类步骤
在D 0 中G ,K G L 和
所在的行和列合并成一
个新行新G列M ,对应
,该行列上的新距离值由
(6.3.2)式求得,其余行列上的距离值不变,这
样就得到新的距离矩D 阵1 ,记作
。
(4) 对D 1
重复上述D 0对
的D两 2 步得
,
如此下去直至所有元素合并成一类为止。
如果某一步D m 中最小的元素不止一个,则称 此现象为结(tie),对应这些最小元素的类可以任 选一对合并或同时合并。
xiaxjb,a(0) b i, j i, j
cij 1
-
相似系数
c ij 1 cij c ji
xiaxjb,a(0) b i, j i, j
cij 1
-
相似系数
编号 A商厦
B商厦
购物环境 73 66
服务质量 68 64
-
相似系数
参考教材:《应用多元统计分析》高惠璇,北京大学出版社
聚类分析 PPT课件
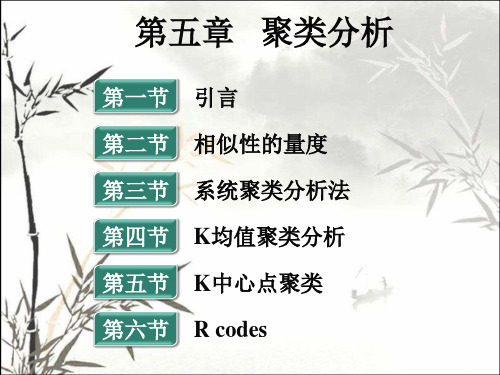
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析(共8张PPT)
第4页,共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析详解ppt课件

以上我们对例6.3.1采用了多种系统聚类法进行聚类,其结果 都是相同的,原因是该例只有很少几个样品,此时聚类的过 程不易有什么变化。一般来说,只要聚类的样品数目不是太 少,各种聚类方法所产生的聚类结果一般是不同的,甚至会 有大的差异。从下面例子中可以看到这一点。
动态聚类法(快速聚类)
(4) 对D1 重复上述对D0 的两步得 D2,如此下去 直至所有元素合并成一类为止。
如果某一步Dm中最小的元素不止一个,则称此现 象为结(tie),对应这些最小元素的类可以任选一对 合并或同时合并。
27
二、最长距离法
类与类之间的距离定义为两类最远样品间的距离, 即
DKL
max
iGK , jGL
聚类分析应注意的问题
(1)所选择的变量应符合聚类的要求
如果希望依照学校的科研情况对高校进行分类,那么可以 选择参加科研的人数、年投入经费、立项课题数、支出经 费、科研成果数、获奖数等变量,而不应选择诸如在校学 生人数、校园面积、年用水量等变量。因为它们不符合聚 类的要求,分类的结果也就无法真实地反映科研分类的情 况。
主要内容
引言 聚类分析原理 聚类分析的种类 聚类分析应注意的问题 聚类分析应用 聚类分析工具及案例分析
聚类分析的种类
(1)系统聚类法(也叫分层聚类或层次聚类) (2)动态聚类法(也叫快速聚类) (3)模糊聚类法 (4)图论聚类法
系统聚类法
对比
常用的系统聚类方法
一、最短距离法 二、最长距离法 三、中间距离法 四、类平均法 五、重心法 六、离差平方和法(Ward方法)
对比
k均值法的基本步骤
(1)选择k个样品作为初始凝聚点,或者将所有样品分成k 个初始类,然后将这k个类的重心(均值)作为初始凝聚点。
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析 PPT课件

• 在饮料数据中,每种饮料都有四个变量值。这 就是四维空间点的问题了。
7
两个距离概念
• 按照远近程度来聚类需要明确两个概念: 一个是点和点之间的距离,一个是类和类 之间的距离。
• 点间距离有很多定义方式。最简单的是歐 氏距离。
• 当然还有一些和距离相反但起同样作用的 概念,比如相似性等,两点越相似度越大, 就相当于距离越短。
18
• 有了上面的点间距离和类间距离的概念, 就可以介绍聚类的方法了。这里介绍两个 简单的方法。
Cxy(2)rxy
i
(xi x)2 (yi y)2
i
i
当变量的测量值相差悬殊时,要先进行标准化. 如R为极差,
s 为标准差, 则标准化的数据为每个观测值减去均值后再除
以R或s. 当观测值大于0时, 有人采用Lance和Williams的距
离
1 | xi yi |
p i xi yi
10
类Gp与类Gq之间的距离Dpq (d(xi,xj)表示点xi∈ Gp和xj ∈ Gq之间的距离)
3
k-means算法
k-means算法,也被称为k-均值或k-平均。 该算法首先随机地选择k个对象作为初始的k个簇的质心; 然后对剩余的每个对象,根据其与各个质心的距离,将它赋 给最近的簇,然后重新计算每个簇的质心;这个过程不断重 复,直到准则函数收敛。通常采用的准则函数为平方误差和 准则函数,即 SSE(sum of the squared error),其定义如 下:
D 12
(xkx)'(xi x) DpqD 12D 1D 2
xk Gp G q
(中间距离, 可变平均法,可变法等可参考各书). 在用欧氏距离时, 有统一的递推公式
7
两个距离概念
• 按照远近程度来聚类需要明确两个概念: 一个是点和点之间的距离,一个是类和类 之间的距离。
• 点间距离有很多定义方式。最简单的是歐 氏距离。
• 当然还有一些和距离相反但起同样作用的 概念,比如相似性等,两点越相似度越大, 就相当于距离越短。
18
• 有了上面的点间距离和类间距离的概念, 就可以介绍聚类的方法了。这里介绍两个 简单的方法。
Cxy(2)rxy
i
(xi x)2 (yi y)2
i
i
当变量的测量值相差悬殊时,要先进行标准化. 如R为极差,
s 为标准差, 则标准化的数据为每个观测值减去均值后再除
以R或s. 当观测值大于0时, 有人采用Lance和Williams的距
离
1 | xi yi |
p i xi yi
10
类Gp与类Gq之间的距离Dpq (d(xi,xj)表示点xi∈ Gp和xj ∈ Gq之间的距离)
3
k-means算法
k-means算法,也被称为k-均值或k-平均。 该算法首先随机地选择k个对象作为初始的k个簇的质心; 然后对剩余的每个对象,根据其与各个质心的距离,将它赋 给最近的簇,然后重新计算每个簇的质心;这个过程不断重 复,直到准则函数收敛。通常采用的准则函数为平方误差和 准则函数,即 SSE(sum of the squared error),其定义如 下:
D 12
(xkx)'(xi x) DpqD 12D 1D 2
xk Gp G q
(中间距离, 可变平均法,可变法等可参考各书). 在用欧氏距离时, 有统一的递推公式
聚类分析专题教育课件

❖ 由距离来构造相同系数总是可能旳,如令
cij
1 1 dij
这里dij为第i个样品与第j个样品旳距离,显然cij满足 定义相同系数旳三个条件,故可作为相同系数。
❖ 距离必须满足定义距离旳四个条件,所以不是总能 由相同系数构造。高尔(Gower)证明,当相同系 数矩阵(cij)为非负定时,如令
dij 2 1 cij
0
2
0
5
3
D(2) G7
0 3
G5 0 G5 0
表
D(3)
G6
G8
G6
0
G8
4
0
其中G6= G1∪G2
图6.3.2 最短距离法树形图
二、最长距离法
❖ 类与类之间旳距离定义为两类最远样品间旳 , jGL
dij
图6.3.3 最长距离法: DKL=d15
❖ 最长距离法与最短距离法旳并类环节完全相同,只 是类间距离旳递推公式有所不同。
注:
❖ 假如某一步D(m)中最小旳元素不止一种,相应这些 最小元素旳类能够同步合并。
❖ 因为最短距离法是用两类之间近来样本点旳距离来 聚旳,所以该措施不适合对分离得很差旳群体进行 聚类
❖ D(0)等均为对称阵 ❖ 一般距离采用绝对距离或欧氏距离
❖ 例6.3.1 设有五个样品,每个只测量了一种指标, 分别是1,2,6,8,11,试用最短距离法将它们分 类。
❖ 递推公式:
DMJ maxDKJ , DLJ
❖ 对例采用最长距离法,其树形图如图所示,它与图 有相同旳形状,但并类旳距离要比图大某些,仍提 成两类为宜。
图6.3.4 最长距离法树形图
三、中间距离法
❖ 类与类之间旳距离既不取两类近来样品间旳距离,也不取两 类最远样品间旳距离,而是取介于两者中间旳距离,称为中
聚类分析ppt课件

第七章 聚类分析
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与另一些同学却很少来往,关系比较疏远。
为了研究 课余爱好、性格、家庭情况、学习成绩 等是
否会成为划分学生小群体的主要决定因素 ,可以从有关 这些方面的数据入手,进行客观分组,然后比较所得的
分组是否与实际相吻合。对学生的客观分组就可采用聚
类分析方法。
聚类分析无处不在
谁经常光顾商店,谁买什么东西,买多少? 按会员卡记录的光临次数、光临时间、性别、年龄、职业、 购物种类、金额等变量分类
10
聚类分析无处不在
谁是银行信用卡的黄金客户?
利用储蓄额、刷卡消费金额、诚信度等变量对客户分类,
找出“黄金客户”!
这样银行可以…… 制定更具吸引力的服务,留住客户!比如:
一定额度和期限的免息透支服务!
赠送百盛的贵宾打折卡! 在他或她生日的时候送上一个小蛋糕!
11
聚类的应用领域
对基因分类,获得对种群的认识
数据挖掘领域
作为其他数学算法的预处理步骤,获得数据分布状况,集中对特定
的类做进一步的研究
12
例 对10位应聘者做智能检验。3项指标X,Y
和Z分别表示数学推理能力、空间想象能力和语
言理解能力。得分如下,选择合适的统计方法 对应聘者进行分类。
应聘者 X Y Z 1 28 29 28 2 18 23 18 3 11 22 16 4 21 23 22 5 26 29 26 6 20 23 22 7 16 22 22 8 14 23 24 9 24 29 24 10 22 27 24
聚类分析无处不在
如想把中国的县分成若干类,
可以按照自然条件来分:考虑降水、土地、日照、 湿度等各方面; 也可以考虑收入、教育水准、医疗条件、基础设施 等指标。 为了研究不同地区城镇居民生活中的收入和消费情 况,往往需要划分不同的类型去研究。
聚类分析无处不在
学校里有些同学经常在一起,关系比较密切,而他们
这样商店可以……
识别顾客购买模式(如喜欢一大早来买酸奶和鲜肉,习惯
周末时一次性大采购)
刻画不同的客户群的特征
9
聚类分析无处不在
挖掘有价值的客户,并制定相应的促销策略:
如,对经常购买酸奶的客户 对累计消费达到12个月的老客户
针对潜在客户派发广告,比在大街上乱发传单命中 率更高,成本更低!
他们的数学成绩,则只好按照数学成绩来分类
如果还知道他们的物理成绩,那么怎么对他们分 类? 如果还知道他们的语文成绩、外语成绩等,我们 怎么来对他们分类?
分类
由于不同的指标项对重要程度或依赖关系是相 互不同的,所以也不能用平均的方法,因为这 样会忽视相对重要程度的问题。
所以需要进行多元分类,即聚类分析。
聚类分析
聚类分析是一种 建立分类 的多元统计分析方法,它能够
将一批样本(或变量)数据根据其诸多特征, 按照在性
质上的亲疏程度 (各变量取值上的总体差异程度) 在没 有先验知识(没有事先指定的分类标准)的情况下 进行 自动分类,产生多个分类结果。
类内部的个体在特征上具有相似性,不同类间个体特征 的差异性较大。
样本或变量间亲疏程度的测度
研究样本或变量的亲疏程度的数量指标有两种:
一种叫 相似系数 ,性质越接近的变量或样本,它 们的相似系数越接近于 1 或一 l ,而彼此无关的变量 或样本它们的相似系数则越接近于 0,相似的为一类, 不相似的为不同类。
另一种叫 距离 ,它是将每一个样本看作 p 维空间的 一个点,并用某种度量测量点与点之间的距离,距 离较近的归为一类,距离较远的点应属于不同的类。
13
14
15
聚类分析
对于一批数据,人们既可以对变量(指标)进行 分类(相当于对数据中的列分类),也可以对观测 值(事件,样品)来分类(相当于对数据中的行 分类)。
表1 姓 名
学生的四门课程的成绩 数 学 物 理 语 文 政 治
hxh
yaju yu
99.00
88.00 79.00
98.00
89.00 80.00
聚类分析Biblioteka 分类物以类聚,人以群分。 日常生活中,我们 不自觉地用定性方法将人分为“好人”、 “坏人”;按熟悉程度分为 “朋友”、 “熟人”、“陌生人” 等等。
我们究竟是如何分类的呢?
分类
当有一个分类指标时,分类比较容易。 但是当有多个指标,要进行分类就不是很容易了。 如果想要对100个学生进行分类,如果仅仅知道
50.00
88.00 89.00
51.00
89.00 90.00
Iiakii
100.00
100.00
85.00
84.00
聚类分析
Q型和R型(根据分类对象的不同)
Q型是对样本进行分类处理,使具有相似特征的样
本聚集在一起,差异性大的样本分离开来。
R型是对变量进行分类处理,使具有相似性的变量 聚集在一起,差异性大的变量分离开来,可在相 似变量中选择少数具有代表性的变量参与其他分 析,实现减少变量个数,达到变量降维的目的。
经济领域:
帮助市场分析人员从客户数据库中发现不同的客户群,并且用购买
模式来刻画不同的客户群的特征。 谁喜欢打国际长途,在什么时间,打到那里? 对住宅区进行聚类,确定自动提款机ATM的安放位置 股票市场板块分析,找出最具活力的板块龙头股 企业信用等级分类 ……
生物学领域
推导植物和动物的分类;
21
相似性度量
如果想要对 100 个学生进行分类,如果仅仅知道他们 的数学成绩,则只好按照数学成绩来分类;这些成绩 在直线上形成 100 个点。这样就可以把接近的点放到 一类。 如果还知道他们的物理成绩,这样数学和物理成绩就 形成二维平面上的 100 个点,也可以按照距离远近来
相似性度量
样本的相似性度量
变量的相似性度量
聚类分析
聚类分析中,个体之间的“亲疏程度”是极为重 要的,它将直接影响最终的聚类结果。对“亲疏” 程度的测度一般有两个角度:第一,个体间的相 似程度;第二,个体间的差异程度。衡量个体间 的相似程度通常可采用简单相关系数等,个体间
的差异程度通常通过某种距离来测度。
78.00
89.00 95.00
80.00
90.00 97.00
shizg
hah john
89.00
75.00 60.00
78.00
78.00 65.00
81.00
95.00 85.00
82.00
96.00 88.00
watet
jess wish
79.00
75.00 60.00
87.00
76.00 56.00
