中位线的定理
三角形中位线定理

三角形中位线定理
三角形中位线定理是平面三角形几何学中的重要定理,它可以帮助我们解决三角形的几何推理问题。
本文将介绍三角形中位线定理的证明过程及其应用情况。
首先,让我们来看一下三角形中位线定理的证明。
三角形中位线定理主要讲的是,如果有一个三角形ABD,则其中的位线AC分别与
端点BD,AD的延长线相交于点C,则一定有|AB|/|BC|=|AB|/|AC|=1/2。
证明这一结论的具体看法是,如果延长线ACD的斜角的度数为120度,则ABD和ACD就会相交,因此,ABD和ACD就构成了一个等腰三角形,即|AB|/|BC|=|AB|/|AC|=1/2。
接下来,让我们来看一下三角形中位线定理的应用。
相信大家对三角函数都有所耳闻,三角函数都是利用三角形中位线定理而引起的。
我们可以利用中位线定理推出三角函数的关系式,比如y = sin x + cos x、y = tan x等,这些关系式可以帮助我们解决不等式,做函
数曲线投影,以及解决一些复杂的数学问题。
此外,三角形中位线定理还有一些实际应用,比如在机械等领域,我们可以利用中位线定理来确定轴承支撑的位置,以确保轴承正常工作。
此外,我们还可以利用中位线定理来设计复杂的制图模式,使图形具有良好的外观和稳定性。
综上所述,三角形中位线定理在几何学和实际应用中都有着重要的作用,利用它可以帮助我们更加精准的解决一些复杂的数学问题,也有助于我们设计出美观又稳定的图形。
当然,关于三角形中位线定
理的应用还有很多,这里只是简单提到两个典型的应用场景,以说明其重要性。
平行四边形中位线定理

平行四边形中位线定理平行四边形中位线定理平行四边形是指有两组对边分别平行的四边形。
在平行四边形中,连接相邻顶点的线段称为对角线,且对角线互相平分。
定义平行四边形中位线是指连接相邻顶点的中点所构成的线段。
定理在平行四边形中,两条对角线互相平分,且它们的交点是它们的共同中心。
证明设ABCD为平行四边形,E、F、G、H分别为AB、BC、CD、DA上的中点。
连接EG和FH,并延长至交于点O。
因为AB∥CD,所以∠BAC=∠ADC;同理可得∠CBD=∠CDA。
又因为AE=EB,AD=DG,所以△AED≌△GBD(SAS);同理可得△FHC≌△CHD(SAS)。
因此AE=BG,CF=DH。
又因为AF∥DC,所以∠FAH=∠DCH;同理可得∠EBG=∠FCD。
但是由于ABCD是一个平行四边形,所以AD=BC。
因此,在△AED和△FHC中:AE+ED+CF+CH=AD+FC+DG+GBBG+ED+AH+CH=AD+AF+DG+FC将AE=BG,CF=DH代入上式,得:ED+CH=DG+AFBG+ED=AF+DG因此,△AEG≌△DFH(SAS),所以EG=FH。
因此,EG和FH互相平分。
又因为E、F、G、H是ABCD的中点,所以OE=OF=OG=OH。
因此,O在EG和FH的交点处,且它们的交点是它们的共同中心。
应用平行四边形中位线定理可以用来证明两条对角线互相平分的性质,并且可以用来求解平行四边形各个部分的长度。
例如,在平行四边形ABCD中,已知AD=6cm,DC=8cm,AC=10cm。
连接AC并延长至交于点E。
由于AE=EC(垂直平分线段),所以AE=5cm。
又因为AB∥DC(对角线互相平分),所以BE/ED=BA/AD;同理可得CE/EB=CD/BA。
将已知数据代入上式可得BE/ED=4/3,CE/EB=5/2。
因此BE=(4/7)AC=(4/7)×10cm≈5.71cm,ED=(3/7)AC=(3/7)×10cm≈4.29cm。
八年级数学中位线定理

∴CF∥DA,且CF=DA.
∴CF∥DB,且CF=DB ∴四边形DBCF是平行四边形.
∴DF=BC.
∴DE=
1BC. 2
定义:连接三角形两边中点的线段叫做三角形的 中位线
中位线定理:三角形的中位线平行于三角形的 第三边,且等于第三边的一半.
一个三角形有 几条中位线? 中位线和三角 形的中线一样 吗?
小结
三角形的中位线有哪些作用?
位置关系:可以证明两条直线平行. 数量关系:可以证明线段的倍分关系.
微信群 微信群
wrg52xua
改,也很不容易啊。“总之,一定要努力啊,能考进前三最好。”为何感觉这话只有家长才会说呢……简直是古代版的家长寄语。“白 姑娘真是见多识广,在下佩服。”张祁渊云淡风轻的一笑,似乎没想到慕容凌娢会知道这么多,“留在这里,实在是有些大材小用 啊。”“我确实不准备在这里多呆。”鬼才愿意呆在这个连信号都没有的年代。“那姑娘下一步准备怎么办?”“我?当然是……存点 钱,搞清楚形式,然后就去闯荡江湖……”“原来是这样……”张祁渊沉思了片刻,起身到,“我这里有一物赠与姑娘,倘若就此别过, 再无相见之日,也好……”“别别别!”还没等他拿出东西,就被慕容凌娢激动的拍案而起阻止了,整天有人往外掉装备,她都搞不清 是线索还是道具了,这回要是收下,那真是神都救不活的作死了。“白绫不过是烟尘女子,公子注定是有大作为的人,怎敢求得公子的 挂念……”先拍马屁,然后给个台阶下,成功几率会高很多。“公子的东西白凌绝不收,请回吧……”“既然如此……也罢,就此别过, 有缘再见。”张祁渊居然向慕容凌娢拱手施了一礼,把慕容凌娢吓了一大跳。虽然这只能算是古代人告别的普通礼仪,但来这醉影楼中 的人,能把这里的歌伎平等对待的,又有多少呢?至少慕容凌娢之前从未遇到过。她只得以同样的方式回礼。……繁华街道的另一边, 一条静谧的河流缓缓流淌,水面映照下的灯光,流光逸彩。河边站着一个男子,剑眉星眸,风 流倜傥,衣着华丽。他望向河对岸的灯 火阑珊之处,像是在等待什么。“辰耀,我回来了。”张祁渊的声音从他身后响起。“怎么样?你的定情信物送出去了?”被叫做辰耀 的男子扬唇一笑,半开玩笑的说,“那女子有没有哭得泪流满面?”“别乱说!她连东西都没见,就坚决不要……”张祁渊拿出了一支 做工精致的梳子,叹了口气道,“既然如此,这东西留着也没什么用了。”说罢,他轻轻一抬手,梳子便被抛到水中,激起一圈圈的涟 漪,沉入水中便没了踪影。“喂,那么好的东西,干嘛扔了!”辰耀没来得及拦住他,只得惋惜。“你不是挑了好久吗?”“她不 要……难不成给你啊!”“给我也没问题啊。”辰耀并未生气,双手环胸一副自信满满的样子,“反正有那么多女人争着抢着,想要我 的定情之物……倒是你,在这方面简直是一窍不通。第一次去那种地方,就被那个带面纱的女子迷的神魂颠倒。你也不想想,要是她真 的倾国倾城,怎么会在独自见你时也不肯摘下面纱。”“这不重要。”“不重要?兄弟你是在开玩笑吧!”辰耀仿佛听到了世上最不可 思议的言论,“女人最重要的当然是脸啊!”“这种话你还是回去给家里那位说吧。”(古风一言)那年风华月下,谁琴曲声声惊了古刹, 谁歌舞似仙数
八年级数学中位线定理

E F
H
2
A
B
思考
下列说法是否正确? 1.三角形三条中位线组成一个三角形,其周长为 原三角形周长的一半. 2.三角形三条中位线将原三角形分割为四个全 等的三角形. 3.三角形三条中位线三角形三条中位线可从原 三角形中划分出面积相等的三个平行四边形. 4.三角形任两条中位线的夹角与这个夹角所对 的三角形的顶角相等.
8.4中位线定理
小明家的村 头有一大水 塘,要量出池 塘两端点 A,B之间的 距离,你能想 出几种方法?
A
B
C
D
E
下面的方法是不是更简单?
A
B
D
E
C
已知:点D,E分别是△ABC的边 AB,AC的中点. 1 求证:DE= BC DE∥BC
2
B
A D E
F
C
证明:延长DE到F,使EF=DE.连接FC,DC,AF. ∵AE=EC, ∴四边形ADCF是平行四边形, DE和BC 有什么位 置关系?
பைடு நூலகம்结
三角形的中位线有哪些作用?
位置关系:可以证明两条直线平行. 数量关系:可以证明线段的倍分关系.
武汉搬家公司 武汉搬家 武汉搬家公司 武汉搬家
bth53dwb
请少爷示下,是看看差不多,收了,发付外头人回去呢,还是真要在这儿装起来,扰少奶奶姑奶奶 们清赏。”这话一出,众人再不放过, 都问什么东西。明柯拉了拉那青翘双髻底梳在耳边的小辫子:“就你嘴快。”青翘不但嘴快,而且甜:“少爷若不想小姑奶奶 们看,巴巴 的叫送到这儿做什么?运回去,婢子们收着,您慢慢儿验看不成?您有了好琴,便想给小姑奶奶 们看,婢子能不揣摩您的心意吗?”苏含 萩笑道:“果然是个好丫头!五小子,你就快叫把那琴搬进来!哎哟!连我都心痒痒了。”明柯道声:“得令!”果然传命下去。俩力大 的小厮把那口大箱子吭哧吭哧搬到外头,换了腰圆膀粗的婆子接手,且喜那箱子下是装轮子的,半抬半推的弄进了暖阁里,拆开了。先见 着上头是几片雕花榆木板,花色倒也巧妙新奇。这几片木板拿出来,可以勾连组合在一起,成了个落地架子,再下头方是那琴,倒也有琴 弦、琴轴,只不过跟通行的琴都长得不一样。明柯在旁边跳来跳去的献宝:“不错吧?听说是古物哦!传说中的古琴就是这样子的吧?” 苏含萩好气又好笑道:“老五,你且数数这琴板上有多少弦呢!”明柯“呃”一声,看那宽阔琴板上,密密排着,一时也数不清,但三四 十根总有的。“我们妇道人家都晓得,如今的琴叫‘文武七弦琴’,是从前圣人加了文武二弦,传为定式。那末再古之前的琴,形状且不 论,弦数最多不过五根。”苏含萩道,“你且把这密麻麻的东西叫什么?”明柯“哎呀”一声:“那天杀的戎商跟我说是古琴,指天誓日 的!回去看我不拆了他那店!”北胡、南蛮、西戎。戎商便是西边来的商人。那里的人,个子比中原人健壮、肤色比中原人深、鼻子比中 原人挺、眉睫都比中原人浓重,说起话来,舌头都好像比中原人硬朗一点。如果一个戎人穿起汉人衣冠,乍看是不容易分辨的,但细细察 认,也总能认出些端倪,就好像——对了!就好像苏明远的影子一样!那被戏称为“明犬”的大汉,实在是很具备戎人特征的。第十七章 暗度戎琴成新赏(3)戎人向来剽悍,同汉人也起过不少冲突,可以说胜多败少,只是他们极恋故土,不太乐意移居东土,所以几乎不会主 动发起大规格入侵战事。近百年来,中原力量强盛,一发压住了他们。他们不再与汉人征战、每年向汉人朝廷朝拜纳贡,还有一些头脑灵 活的戎人,到中原来做生意,做得比北胡好得多,仅次于南蛮,但异域风致更胜于南蛮,成了中原街头一大风景。四 明秀一直凝神端详那 琴,听得“戎商”二字,点头向明柯道:“他未必是骗了你。你且看,这琴架虽然新些,琴身上木头的光泽,却显是有年头了。并琴钉等 处,光泽温润如一,应不是新做出来的。又看它纹饰风格,敢问何尝是我们中土偏好?琴上
中位线定理怎么证明

中位线定理怎么证明
中位线可以通过测量的手段而得知,也就是通过测量证明中位线。
连接三角形两边中点的线段叫做三角形的中位线,两线平行且等于第二边的一半。
若在一个三角形中,一条线段是平行于一条边,且等于平行边的一半(这条线段的端点必须是交于另外两条边上的中点),这条线段就是这个三角形的中位线。
三条中位线形成的三角形的面积是原三角形的四分之一,三条中位线形成的三角形的周长是原三角形的二分之一。
中位线的其他知识
要把三角形的中位线与三角形的中线区分开。
三角形中线是连接一顶点和它对边的中点,而三角形中位线是连接三
角形两边中点的线段。
梯形的中位线是连接两腰中点的线段而不是连接两底中点的线段。
两个中位线定义间的联系:可以把三角形看成是上底为零时的梯形,这时梯形的中位线就变成三角形的中位线。
中位线定理
△ ADB ≌ △ ADN A
12
18
N
D
6
B
3
M
C
归纳小结
知识方面:三角形中位线概念; 三角形中位线定理.
思想方法方面:转化思想.
证明:
∴DF // BC .
D
又 ∴
DE 1 DF , DE∥B2C,DE
1
B
BC .
2
A
A
延长DE到F,使EF=DE. D
连接FC.
B
∵∠AED=∠CEF,AE=CE,
∴△ADE≌△CFE.
∴∠ADE=∠F ,AD // CF.
∴BD // CF.
∴四边形BCFD是平行四边形.
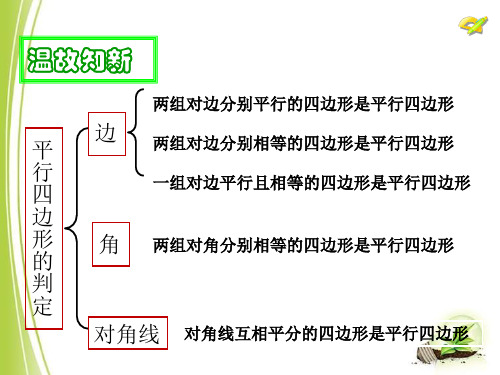
温故知新
两组对边分别平行的四边形是平行四边形
平
边 两组对边分别相等的四边形是平行四边形
行 四
一组对边平行且相等的四边形是平行四边形
边
形
角 两组对角分别相等的四边形是平行四边形
的
判
定
对角线 对角线互相平分的四边形是平行四边形
探究思考
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.
(3) 若DE+BC=12,则BC= 8 .
x+2x=12
C
x=4
E
x 2x
A
D
B
学以致用
练2. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
A
M
C
N
B
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN. 根据是三角形中位线定理.
初二数学上册知识点:三角形中位线定理

初二数学上册知识点:三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线.(1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。
(2)要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用:位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
常用结论:任一个三角形都有三条中位线,由此有:结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形.结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等.三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.一个三角形共有三条中位线.三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
如图已知△AB中,D,E分别是AB,A两边中点。
则DE平行于B且等于B/2三角形中位线逆定理:逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//B,DE=B/2,则D是AB的中点,E是A的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//B,则E是A的中点,DE=B/2 区分三角形的中位线和中线:三角形的中位线是连结三角形两边中点的线段;三角形的中线是连结一个顶点和它的对边中点的线段。
中位线,勾股定理

中位线定理和直角三角形知识点:一、中位线三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.逆定理一:三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
二、直角三角形勾股定理:直角三角形两直角边的平方和等于斜边的平方;如果直角三角形的两直角边分别为a,b,斜边为c,那么a2+b2=c2.勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方。
勾股定理的逆定理:如果三角形的三边长a、b、c满足:a2+b2=c2,那么这个三角形是直角三角形,并且c是直角三角形的斜边.【典例】例1. 证明中位线定理如图,已知△ABC 中,D ,E 分别是AB ,AC 两边中点。
求证:DE 平行且等于21BC证明:过C 作AB 的平行线交DE 的延长线于F 点。
∵CF ∥AD ∴∠A=∠ACF∵AE=CE 、∠AED=∠CEF ∴△ADE ≌△CFE ∴AD=CF∵D 为AB 中点 ∴AD=BD ∴BD=CF ∴BCFD 是平行四边形∴DF ∥BC 且DF=BC ∴DE=BC/2例2. 如图,△ABC 的三边长分别为AB =14,BC =16,AC =26,P 为∠A 的平分线AD 上一点,且BP ⊥AD ,M 为BC 的中点,求PM 的长。
例3. 证明勾股定理例2图Q P M D C B A。
3角形中位线定理

3角形中位线定理三角形中位线定理,是在三角形中,与三条相邻边的中点相连的线段,它们构成的三个交点都在同一点上。
本文将从定理的证明、推广应用、例题等三个方面进行阐述。
一、定理的证明证明思路:设三角形ABC的三边分别为a、b、c,D为BC的中点,E为AC的中点,F 为AB的中点,则连接AD、BE、CF的交点为G。
则需证明AD、BE、CF三条线段的交点G是一个固定点。
证明:由于D、E、F都是各边中点,可得:∵ D是BC的中点,∴ BD = DC;又∵ G是AD与BE的交点,故可以得出:∵ D、E分别为BC和AC的中点,∴ DE // AC,同时AE = EC,∴ △AED与△CEB 相似。
$\frac{GA}{BD}=\frac{GC}{CE}$又 $\because BD=DC$ , $\therefore GA=GC$同理可得:于是,我们得到了两个相等的值:GA=GC,GB=GC。
由此,可知三角形GAC是一个等腰三角形,且AG与CF之间的线段垂直于CF,同理可得:因为三角形GAC、GBA、CBG均拥有最长边CG,所以它们就构成了一个共同的圆,而这个圆的中心就是点G。
因此可以得知:三角形ABC的三边中位线的交点G是一个固定点。
二、推广应用利用中位线定理,我们可以推导容易证明的三条定理和一个相关问题:中位线长定值定理、七分线长定值定理、以及在四边形中应用中位线定理、解决中位线问题。
1. 中位线长定值定理在三角形中,如果其中一条中位线相等,那么这个三角形就是等边三角形。
设△ABC为等边三角形,则BD、AE、CF三条中位线的长度均为$\frac{1}{2}$边长,又 $\because BD=AE=CF$ ,所以可以得到:BD=AE=CF=$\frac{1}{2}$a=a,同理可得:b=c=a。
在三角形中,三条中位线可将它们所在线段的长分为1:2:3的比例。
首先,由于三角形的三角形内部对角线互不交于同一点,那么三角形内部的线段AB、AC、BC是不会共线的。
中位线定理不同证明方法

中位线定理不同证明方法中位线定理,又称中线定理,是几何中的一个基本定理。
它指出,在一个三角形中,三条中线交于一点,这个交点被称为三角形的质心。
中位线定理的证明有多种方法,下面我将介绍其中的一些方法。
一、初级证明方法在这个证明方法中,我们将使用简单的几何知识来证明中位线定理。
让我们回顾一下中位线的定义。
中位线是连接一个三角形的一个顶点和对边中点的线段。
根据中位线的定义,我们可以得出结论:三条中位线交于一点。
为了方便说明,我们设这个三角形的三个顶点为A、B、C,对边分别为BC、CA和AB。
设M是BC的中点,N是CA的中点,P是AB的中点。
根据中位线的定义,线段AM是连接顶点A和对边BC的中点M的线段。
现在我们来证明中位线AM和BN的交点在CP上。
设交点为D。
根据三角形中位线的性质,AD和BC互相平分。
我们可以得出以下结论:AM = MD 和 BN = ND。
然后我们来看三角形ADM和三角形BND。
根据两个三角形的边长比较,我们可以得出:AD = ND 和 AM = MD。
根据边边边相似的性质,我们可以得出结论:三角形ADM和三角形BND全等。
根据全等三角形的性质,我们可以得出:∠DMA = ∠DNB。
因为∠DMA是三角形ADC的外角,所以∠DMA = ∠ADC + ∠ACD =∠ANB + ∠ACD。
同样的道理,∠DNB = ∠ANB + ∠BCD。
我们可以得出结论:∠ANB + ∠ACD = ∠ANB + ∠BCD。
根据等式两边相等的性质,我们可以得出:∠ACD = ∠BCD。
我们可以得出结论:CD || AB。
根据平行线的性质,我们可以得出:∠BDC = ∠ACB。
因为∠BDC是三角形BDC的内角,所以∠BDC + ∠BCD = 180°。
代入之前的等式,我们可以得出:∠ACB + ∠BCD = 180°。
我们可以得出结论:∠ACB+ ∠BCD = 180°。
根据三角形内角和的性质,我们可以得出:∠ACB + ∠BCA + ∠ABC = 180°。
中位线的三种证明方法

中位线的三种证明方法
中位线是指在一组数据中,数据的中间值,即有序数据中处于中间位置的值,它可以用来描述数据的中间水平。
中位线的证明方法有三种:算术中位数定理、几何中位数定理和绘图法。
第一种证明方法是算术中位数定理。
算术中位数定理指出,给定一组数据,按照从小到大的顺序排列,如果数据的个数为奇数,则中位数是数据集合的中间值,如果数据的个数为偶数,则中位数是数据集合中间两个值的平均值。
根据这个定理,我们可以通过对数据按照大小排序,然后求出数据的中间值,就可以求出中位数。
第二种证明方法是几何中位数定理。
几何中位数定理是指,若将一组数据按照从小到大的顺序排列,将这些数据在一个数轴上画出,则从数轴的中点出发向两边等距离延伸出两条线,这两条线上的点分别是数据的最大值和最小值,中位数就是这两条线的交点,即数轴的中点。
所以,只要将一组数据画出来,就可以求出中位数。
第三种证明方法是绘图法。
绘图法是指将一组数据用频率柱状图和频率折线图等图表的形式表示出来,然后根据图表上的信息,求出中位数。
频率柱状图可以清楚地表示出数据的分布情况,而频率折线图则可以精确地给出中位数的值。
总之,中位线的三种证明方法分别是算术中位数定理、几何中位数定理和绘图法,它们都可以用来求出中位数。
在实际应用中,可以根据具体情况,选择合适的方法来求出中位数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中位线的定理
中位线定理又称为中位定理,是指一条直线将一个图形分成两边,其中左边的面积与右边面积相等。
它可应用到多边形,圆,椭圆等图形上,它是由荷兰数学家乔治·杰斐森(George-Jouffroy)于1860年提出,现在它在数学的图形学中运用较为广泛。
中位线定理可以用如下方法来证明:
(1)绘制一个带有任意多个边的多边形,用线段l连接该多边形runing顶点,于此同时将其分为两部分,所构成的新多边形称为原多边形的子多边形。
(2)分别计算子多边形左边和右边的面积,然后将它们相加再各自除以2,余下的面积就是原多边形的1/2面积。
(3)将l line向右移动,然后重复上述步骤,得出的结论是不论移动的位置如何,左边的面积仍然等于右边的面积,从而得出中位线定理——原多边形的1/2面积等同于所有可能的两个子多边形的1/2面积之和。
中位线定理的最重要的应用之一就是计算多边形的面积,通过运用中位线定理可以把多边形的面积分成多个面积相等的子多边形,然后再求出每个小子多边形的面积,最后再把它们累加起来,就可以求出原多边形的面积了。
因此,大多数多边形的面积计算都是建立在中位线定理之上的。
此外,由于多边形可以把一个图形分割成两部分,因此中位线定理还可以用来求出扇形和圆周的面积。
我们可以把一个扇形或圆周等分成相等的子扇形或者子圆周,再用中位线定理求出每个小子扇形或子圆周的面积,最后累加起来,就可以得出扇形或圆周的面积了。
总之,中位线定理是数学中一个很好用的定理,其应用非常广泛,既可用于多边形面积计算,也可用于求出扇形或圆周的面积。
虽然这一定理已经存在了150多年,但是它仍然对现在的数学学习、研究和应用都有着重要的意义。
