四年级奥数-等量代换

四年级奥数之等量代换(含答案)

1、已知：.☆+△=18☆+☆+△+△+△=40求☆和△。

△=40-2x18=4☆=18-4=142、百货店运来300双球鞋，分别装在2个木箱、6个纸箱里。

如果2个纸箱同1个木箱装的球鞋一样多，那么每个木箱和每个纸箱各装多少双球鞋？6个纸箱相当于木箱个数是6÷2＝3个共相当于木箱的个数是2＋3＝5个每个木箱装300÷5＝60(双)每个纸箱装60÷2＝30(双)每个木箱比每个纸盒多装的球鞋60-30=30(双)3、20千克苹果与30千克梨共计132元，2千克苹果的价钱与2.5千克的梨的价钱相等，求苹果和梨的单价。

20千克的苹果看成是25千克的梨,也就是说（30+25）千克的梨是132元,可以求出梨的单价.列式：132÷（30+25）=2.4(元)苹果的总价列式：132-30×2.4=60（元）苹果的单价列式：60÷20=3（元）答：苹果的价钱是3元,梨的价钱是2.4元.4、中华学校买来史地书、科技书、文艺书共456本。

其中科技书是史地书的1.2倍，文艺书比科技书多31本。

三种书各买了多少本？456-31=425史地书425÷（1.2×2+1）=125科技书 1.2×125=150文艺书150+31=1815、一件工作，甲做5小时以后由乙来做，3小时可以完成；乙做9小时以后由甲来做，也是3小时可以完成。

那么甲做1小时以后由乙来做几小时可以完成？an dAh i ng si n(9-3)÷(5-3)=3甲的效率是乙的3倍，做相同的工作量，乙用时是甲的3倍9+3×3=18(小时)如果全部由乙来做，需要18小时18-1×3=15(小时)甲做1小时后由乙来做，需要15小时6、5辆玩具汽车与3架飞机玩具的价钱相等，每架飞机玩具比每辆玩具汽7、慧月和慧琴上街买铅笔和练习本。

慧月买6支铅笔和7本练习本，共用去2.32元；慧琴买了同样的3支铅笔和9本练习本，共用去2.37元。

(完整word版)四年级奥数教材

第一课时等量代换第一站：倒酒例1：群宴时，曹丞相让曹冲给大家倒酒。

于是，曹冲就把720毫升酒倒入6个小杯和1个大杯，正好倒满。

大杯的容量是小杯的3倍，小杯和大杯各可以装多少毫升酒思路点拨：一个大杯的容量可以换成3个小杯，“把720毫升酒倒入6个小杯和1个大杯”，就可以替换成“把720毫升酒倒入（）个小杯”。

尝试解答：第二站：奖赏例2：曹操为了把宴会搞得更加隆重，他对每个大臣都进行了赏赐。

他给每个文官奖励4只羊，每个武官奖励2头猪。

如果6只同样的小猪和18只同样的小羊总共价值648文钱，且2只小猪和三只小羊的价钱相等。

问：每只小猪和每只小羊各是多少文钱思路点拨：已知2只小猪和3只小羊的价钱相等，如果把小猪替换成小羊，那么6只小猪的价钱= 只小羊的价钱。

尝试解答：第三站：取剑例3：宴会结束后，曹操把曹冲带到一个藏宝室。

曹操对曹冲说：“这里有很多宝剑和宝刀，你可以任选一样，但得回答我的一个问题。

”曹冲说：“没问题！”曹操说：“3把同样的宝刀和20把同样的宝剑，一共价值134两银子；同样的3把宝刀和16把宝剑，一共价值118两银子。

宝刀和宝剑的单价各是多少两银子”思路点拨：把两组条件进行比较，可以发现，第一组比第二组多两银子，是因为第一组比第二组多了把宝剑的价钱。

尝试解答：大胆闯关1、曹冲把40个同样质量的苹果和5个同样质量的西瓜一起称了一下，一共重12千克，并且每个西瓜的质量是每个苹果质量的8倍。

问每个苹果和每个西瓜各重多少克2、一个大臣先取出5个同样质量的橙子和6个同样质量的梨子，一共重3120克；又取出5个同样质量的橙子和9个同样质量的梨子，一共重4080克。

你知道每个橙子和每个梨子的质量分别是多少克吗3、曹冲用大小两种车运石头，大车运了9次，小车运了10次，一共运了132吨，大车3次运的石头等于小车4次运的石头。

大、小车的载重量各是多少吨4、小强在3个同样的大盒和5个同样的小盒里装满乒乓球，正好是98个。

四年级奥数等量代换教案(可以直接下载使用)

等量代换
知识结构
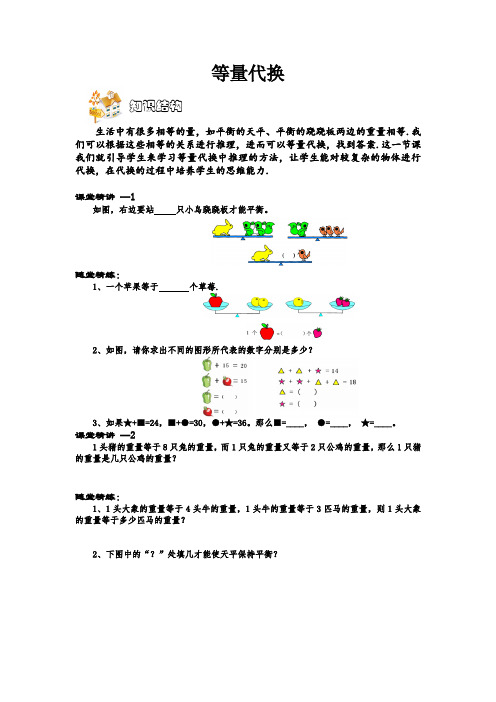
生活中有很多相等的量，如平衡的天平、平衡的跷跷板两边的重量相等.我们可以根据这些相等的关系进行推理，进而可以等量代换，找到答案.这一节课我们就引导学生来学习等量代换中推理的方法，让学生能对较复杂的物体进行代换，在代换的过程中培养学生的思维能力.
课堂精讲━1
如图，右边要站只小鸟跷跷板才能平衡。

随堂精练：
1、一个苹果等于个草莓.
2、如图，请你求出不同的图形所代表的数字分别是多少？
3、如果★+■=24，■+●=30，●+★=36。

那么■=____，●=____，★=____。

课堂精讲━2
1头猪的重量等于8只兔的重量，而1只兔的重量又等于2只公鸡的重量，那么1只猪的重量是几只公鸡的重量？
随堂精练：
1、1头大象的重量等于4头牛的重量，1头牛的重量等于3匹马的重量，则1头大象的重量等于多少匹马的重量？
2、下图中的“？”处填几才能使天平保持平衡？。

四年级奥数教材第33讲等量代换

第33讲等量代换同学们都知道曹冲称象的故事吧。

曹冲让大象上船，看船被河水水面淹没到什么位置，然后刻上记号。

再把大象赶上岸，把这条船装上石块，当水面淹没到记号的位置时，就可以知道，船上的石块菜有多重，大象就有多重。

曹冲称象就是运用了“等量代换”的方法：两个相等的量，可以互相代换。

解数学题，经常要用到这种思考方法。

例1．下面的四只天平都保持平衡。

想一想：一个西瓜和几根香蕉的重量相等？例2．已知一只狗重8千克，请你根据下图推出一只小猴和一只小兔共重多少千克。

例3．一头猪可以换3只羊，1只羊可以换2只狗，1只狗可以换4只兔子，1头猪可以换几只兔子？例4．百货商店运来300双球鞋，分别装在2个木箱和6个纸箱里。

如果2个纸箱同1个木箱装的球鞋一样多，想一想；每个木箱和每个纸箱各装多少双球鞋？例5 如右图，阴影部分BDFE 是正方形，求长方形ACGH的周长。

？根香蕉练习与思考1．○+○=△△+△+△=□□=（）个○2．下面图中每只梨重500克，那么，1根香蕉比1个苹果轻多少千克？3．已知1头猪=2只羊，1只羊=8只兔子。

1头猪=（）只兔子；2头猪=（）只兔子；3只羊=（）只兔子；24只兔子=（）只羊；32只兔子=（）头猪。

4．已知20只鸡可以换2条狗，6条狗可以换2头猪，10头猪可以换2头牛。

那么，5头牛可以换多少只鸡？5．已知3个苹果和重量加上一个梨子的重量等于14个桔子的重量，6个桔子的重量加上1个苹果的重量等于1个梨子的重量。

问：1个梨子的重量等于多少个桔子的重量？6．已知1筐梨+2筐桔子=130千克；2筐苹果+2筐桔子=160千克；3筐梨+2筐苹果=310千克。

求 1筐梨=（）千克；1筐苹果=（）千克；1筐桔子=（）千克。

7．买6千克荔枝和8千克桂圆，共付312元。

已知5千克荔枝的价钱等于2千克桂圆的价钱。

荔枝的单价是多少元？桂圆的单价是多少元？8．甲、乙二人共同生产一种零件，甲生产了8小时，乙生产了6小时，一共生产了312个零件。

（完整word版）四年级奥数之等量代换（含答案）

（完整word版）四年级奥数之等量代换（含答案）1、已知：.☆+△=18 ☆+☆+△+△+△=40 求☆和△。

△=40-2x18=4☆=18-4=142、百货店运来300双球鞋，分别装在2个木箱、6个纸箱里。

如果2个纸箱同1个木箱装的球鞋一样多，那么每个木箱和每个纸箱各装多少双球鞋？6个纸箱相当于木箱个数是6÷2＝3个共相当于木箱的个数是2＋3＝5个每个木箱装300÷5＝60(双)每个纸箱装60÷2＝30(双)每个木箱比每个纸盒多装的球鞋60-30=30(双)3、20千克苹果与30千克梨共计132元，2千克苹果的价钱与2.5千克的梨的价钱相等，求苹果和梨的单价。

20千克的苹果看成是25千克的梨,也就是说（30+25）千克的梨是132元,可以求出梨的单价.列式：132÷（30+25）=2.4(元)苹果的总价列式：132-30×2.4=60（元）苹果的单价列式：60÷20=3（元）答：苹果的价钱是3元,梨的价钱是2.4元.4、中华学校买来史地书、科技书、文艺书共456本。

其中科技书是史地书的1.2倍，文艺书比科技书多31本。

三种书各买了多少本？456-31=425史地书425÷（1.2×2+1）=125科技书1.2×125=150文艺书150+31=1815、一件工作，甲做5小时以后由乙来做，3小时可以完成；乙做9小时以后由甲来做，也是3小时可以完成。

那么甲做1小时以后由乙来做几小时可以完成？(9-3)÷(5-3)=3甲的效率是乙的3倍，做相同的工作量，乙用时是甲的3倍9+3×3=18(小时)如果全部由乙来做，需要18小时18-1×3=15(小时)甲做1小时后由乙来做，需要15小时6、5辆玩具汽车与3架飞机玩具的价钱相等，每架飞机玩具比每辆玩具汽车贵8元。

这两种玩具的单价各是多少元？第一种解题方法：第二种解法：5辆玩具汽车和5架玩具飞机相差多少钱？3架玩具飞机比3辆玩具汽车贵多少元？8元x5=40元8元x3=24元每架玩具飞机多少钱？每辆玩具汽车多少元？40元/2=20元24元/2=12元每辆玩具汽车是多少元？每辆玩具飞机是多少元20元—8元=12元 12元+8元=20元7、慧月和慧琴上街买铅笔和练习本。

小学奥数专题--等量代换

等量代换例题精讲题型一、看的见的等量代换例1 看下图，右边要站几只小鸟跷跷板才能平衡.解析：1只小兔的重量等于6只鸟的重量，右边要放6只鸟，跷跷板才能保持平衡.变式训练1 下图中第三个盘子应放几个小方块才能保持平衡?解析：1个香蕉的重量=3个方块的重量，右边要放3个方块天平才能保持平衡.变式训练2 下图中0，1，2，3，4，5，6，7，8，9十个兄弟玩跷跷板，8和6先坐在一头，让哪两个兄弟坐在另一头，才能使跷跷板平衡？解析：右边8+6=14，左边只能放9和5，9+5=14.变式训练 3 一个苹果等于（）个草莓.解析：一个苹果等于4个草莓.变式训练4 第三个盘子应放几个玻璃球才能保持平衡．解析:第三个盘子应放6个玻璃球才能保持平衡．例2 水果兄弟们也组成了各种不同的图文算式，它们各代表一个数，你能猜出它们各代表几吗？解析：这是一个很基础的题，通过这个题的练习，可让学生初步掌握代换的方法，为后面的学习打下基础.（1）因为，所以，又因为3+3+3=9，所以=3.（2）根据，想12+8=20，那么可以推出，因为4+4=8，所以可以得出一个=4.（3）因为，，这样我们可以得出=5+5+5+5=20.（4）根据得，观察算式，就相当于没加也没减还得0，这样我们就可以得出=25.变式训练1 下面的花朵各表示什么数？解析：=9，=3.变式训练2 有一天，小狗老师要在动物学校挑选队员参加数学竞赛，小松鼠很高兴也跑来了.小狗老师说：“那我就来考考你！你把下面的题做对了就可以参加了.”小松鼠看了半天说：“老师，你写的这是什么？”小狗老师说：“哈哈！看来你要好好学一学图文算式了，欢迎你下次再来.”小朋友们，上面的题你会吗？解析：通过这个故事引入新课，在这里不要求学生能马上做出来，可放在最后来解决.如果学生的能力较强，也可把这两个题作为引入新课的切入点进行讲解.（1）因为，所以=5，又因为，把=5替换，就变成，这样我们就可以得出=10.（2）我们把上下两个算式进行比较，我们发现下面比上面多了一个，得数多了18-14=4，所以我们可以推断出=4，，根据第一个算式我们可以得出；那么=5.变式训练3 下面的符号各代表一个数，相同的符号代表相同的数，它们各代表几呢？解析：根据两个算式来进行推理，通常我们要先根据一个算式的得数推理出其中一个符号表示的数，然后再把这个得数代换到另一个算式里，求出另外一个符号表示的数.具体分析如下：（1）根据●+●=6，想3+3=6，可推出●=3，把●=3替换▲+●=8，可得到新的算式▲+3=8，这样我们就可得出▲=5.（2）根据第二个算式12-■=5，可得■=7；把■=7替换第一个算式◆+■=15的◆+7=15，可以得出◆=8.变式训练4 下面的符号各代表一个数，相同的符号代表相同的数，它们各代表几呢？解析：根据两个算式来进行推理，通常我们要先根据一个算式的得数推理出其中一个符号表示的数，然后再把这个得数代换到另一个算式里，求出另外一个符号表示的数.具体分析如下：（1）根据●+●=6，想3+3=6，可推出●=3，把●=3替换▲+●=8，可得到新的算式▲+3=8，这样我们就可得出▲=5.（2）根据第二个算式12-■=5，可得■=7；把■=7替换第一个算式◆+■=15的◆+7=15，可以得出◆=8.变式训练5 根据下面的算式，你知道、、各代表数字几？解析：根据第三个算式：圆柱体+圆柱体=球，我们可以替换第一个算式中的球可得：正方体+圆柱体+圆柱体=10，我们把这个算式和第二个算式：圆柱体+正方体=8进行比较，发现多了一个圆柱体，而得数多了10-8=2，这样我们就可以得出：圆柱体=2，根据第三个算式就得：球=2+2=4，根据第一个算式得：正方体+4=10，于是可推出：正方体=6.答案：正方体=6，球=4，圆柱体=2.变式训练6 根据下面算式，算出△、○、□各表示几？解析：根据三个算式的等量关系通过等量代换，分别算出△、○、□的得数，△=2、○=3、□=1.变式训练7 下面的图形各表示什么数？解析：（1）○=11，□=2；（2）○=4，△=5；（3）△=6，□=2.变式训练8 求下面图形所表示的数.解析：（1）△=( 9 )，○=( 6 )，☆=( 7 )；（2）△=( 3 )，□=( 4 ).例3 你能根据下面的三个算式，算出●、▲、■各代表什么数吗？解析：根据第一个算式11-4=●，我们可以得出●=7；把●=7代入到第二个算式●-5=▲，可得7-5=▲，这样可以得出▲=2，最后根据第三个算式我们就能得出■=7+2=9.变式训练和是一对好朋友，它们各代表一个数，你知道它们是几吗？解析：从第一个算式可以看出西瓜比菠萝大6，而菠萝加上西瓜又得12，我们把10以内符合要求的数分组列举：10和4，9和3，8和2，7和1，发现只有9+3=12符合要求，所以西瓜=9，菠萝=3.题型二、简单的等量代换例4 1头大象的重量等于头牛的重量，头牛的重量等于匹马的重量，则头大象的重量等于多少匹马的重量？解析：因为头大象的重量=头牛的重量，头牛的重量=匹马的重量，那么头牛的重量=匹马的重量，所以头大象的重量等于匹马的重量．变式训练1 头猪的重量等于8只兔的重量，而1只兔的重量又等于2只公鸡的重量，那么1只猪的重量是几只公鸡的重量？解析：头猪的重量等于只兔子的重量，而只兔子的重量又等于只公鸡的重量．那么只兔子的重量就等于 (只)公鸡的重量，而头猪的重量等于只兔子也就是只公鸡的重量．所以头猪的重量等于只公鸡的重量．变式训练2 已知买个汉堡包的钱可以买个冰激凌，买个冰激凌的钱可以买杯牛奶：求：（1）买杯牛奶的钱可以买几个汉堡包？4l 3114134121121181282816⨯=1816l 16121360（2）买个汉堡包的钱可以买多少杯牛奶？解析：可引导学生读题、审题，找三者之间的数量关系，再通过倍数关系进行求解．可得出： (杯)，即买个汉堡包的钱和买杯牛奶的钱一样多．由此可以进行推算．⑴杯牛奶是杯牛奶的倍．所以杯牛奶的钱可以买个汉堡包．⑵60个汉堡包相当于个杯牛奶的钱．(杯)或（杯），所以买个汉堡包的钱可以买杯牛奶．例5 巳知＝克，求＝？克．解析：从左边的图可得：个白球=个黑球的重量，也就是等于（克），（克），所以每个白球的重量等于克．从右图可得：个正方体=个白球的重量，一个白球的重量等于克，个正方体的重量就是：（克）．变式训练第三个盘子应放几个玻璃球才能保持平衡？解析：⑴个， ⑵个．例6 下面的天平是不平衡的，但除了天平上的砝码，周围已找不到别的砝码了．你能通过移动天平上的砝码，使天平平衡吗？解析：我们可先看看天平两边各有多少克：天平左边：(克)．天平右边： (克)．显然，天平左边如果减少克，放到天平右边，(克)，(克)，天平两边就都平衡了，但天平左边没有克的砝码，怎么办？可以用天平左边克的砝码和天平右边克的砝码交换一下，就可以达到要求了．这样天平左边是(克)．右边是(克)．变式训练1 你能通过移动天平上的砝码，使下面的天平平衡吗？60236⨯=1660610601066060+60+60+60+60+60=360660360⨯=6036060326060120+＝120340÷=4014401404160⨯=415551020++=10421118++++=120119-=18+1=19l 54541019++=10521119++++=解析：可引用线段图帮助学生理解多的部分给少的部分多少，可达到一样多，然后再讲解此题.左边=克，右边=克，左边比右边多克．只有从左边拿克到右边，两边的重量才一样多．这样可以把左边克的砝码和右边克的砝码互换一下，左右两边重量都是克，天平平衡．变式训练2 你能通过移动天平上的砝码，使下面的天平平衡吗？解析：把左边的克和右边的克对换．或把左边的克和右边的克对换．例7 只小花猫的重量等于只狗的重量，1只小花猫等于3只鸭的重量，1只狗重千克，只猫与只鸭各重多少千克？解析：抓住突破口，利用倒推逐步推理．只猫等于只狗的重量，只狗重千克，只猫也就重千克，（千克），所以只猫就等于千克．只猫等于只鸭的重量，只猫重千克，只鸭也就重千克．（千克），所以只鸭等于千克．变式训练 1 如果个笔记本的价钱等于块橡皮的价钱，个文具盒的价钱等于块橡皮的价钱．已知个笔记本的价钱是元，那么个文具盒的价钱是多少？解析：由个文具盒等于块橡皮知：个文具盒=块橡皮，又由个笔记本=块橡皮知个笔记本=块橡皮，所以，个文具盒=个笔记本．个笔记本的价钱是元，那么个文具盒的价钱是（元）．变式训练2 1串葡萄的重量等于3个梨的重量，2个梨的重量等于80克，串葡萄重多少克？解析：个梨的重量是克，那么个梨的重量就是克，串葡萄的重量等于个梨的重量，串葡萄就是克．例8 如果只兔子可换只羊，只羊可换头猪，头猪可换头牛，那用头牛可换多少只兔子？解析：把题目条件列出来：只兔=只羊，只羊=头猪，头猪=头牛，头牛=几只兔．从这几个式子可得出：头牛=头猪，头猪=只羊，只羊=只兔．因为头牛可换头猪，头猪换只羊，头猪就换(只)羊，只羊可换只兔，只羊可换(只)兔．说明头牛可换只兔．变式训练只兔子可以换只鹅，只鹅可以换只羊，只兔子重千克，只羊重几千克？解析：只羊重千克．1020838++=1016430++=848434364731911311939933÷=131********÷=11154401314401101521012131326⨯=1280140131403120⨯=20293821202938211413110141344312⨯=110121012120⨯=112010*********例9 1个苹果和1个香蕉的重量是7个小铁块的重量，而1个苹果的重量是4个小铁块的重量，1个香蕉的重量是多少个小铁块的重量？解析：简单的代换，可通过画图对学生进行讲解，利用拓展加强学生的认识．题中告诉我们一个苹果和一个香蕉的重量等于个小正方体的重量．且一个苹果的重量等于个小正方体的重量，通过比较，我们知道一个香蕉的重量就应该是个小正方体的重量．变式训练 1瓶可乐等于1杯茶和1杯奶的重量，2杯奶的重量等于1杯茶的重量，瓶可乐相当于多少杯牛奶的重量？解析：因为瓶可乐=杯茶+杯牛奶，且杯茶=杯牛奶，两式联合起来：瓶可乐=杯牛奶+杯牛奶=杯牛奶．例10 个的重量等于个小的重量，个的重量等于个大和个小的重量和，1个大等于几个小的重量？解析：因为个=个小，那么个=个小，又因为个=个大+个小，所以个大=个小－个小=个小，个大=个小．例11 只鸡的重量等于只小鸭的重量，只鸡的重量等于只小鸭和1只小猪的重量，1只小熊等于只小猪的重量，算一算只小熊的重量与几只小鸭的重量一样重？解析：引导学生，根据条件适当扩大鸡的倍数，使前后数目一致，进行计算．因为只鸡的重量等于只小鸭的重量，所以可以变成只鸭的重量等于1只小鸭和1头小猪的重量；这样我们就可以算出头小猪的重量等于只小鸭的重量．我们又知道只小熊的重量等于头小猪的重量，因为头小猪的重量等于只小鸭的重量，所以只小熊的重量等于只小鸭的重量．变式训练1 只猴子的体重等于只猫的体重，只狗的体重等于只猫的体重．如果只猴子重千克，请问只狗重多少千克？解析：由只狗的体重=只猫的体重，得只狗的体重=只猫的体重．又只猴子的体重=只猫的体重，只狗的体重=只猴子的体重．只猴子重千克，只狗重千克．变式训练2 观察下图，看看谁最重．解析：从第一个图中可以看出只兔子的重量=只兔子+只鸡的重量．从这个等式可推出只兔子=只鸡的重量．说明兔子比鸡重；而第二个图可以看出只鸡=只鸭的重量，从而可推出鸭的重量大于鸡的重量．那么兔子和鸭哪一个更重呢？我们不妨把兔和鸭都转化成相当于几只鸡来比较．刚才我们由第个图看出：只鸭=只鸡，那么只兔等于几只鸡74311111212131322213262222624121231211261512210110133913139131311131321212322232的重量呢？因为只兔=只鸡，所以只兔的重量=只鸡的重量，而只鸭的重量=只鸡的重量．兔和鸭同样都是只，但前者相当于只鸡重，后者相当于只鸡重．显然，这里兔子的重量最重．一旦遇到不好比较的情况，我们可以将它们转化成相当于几个同一种事物，这样就便于比较了．变式训练3 个桃子等于个玻璃球的重量，个桃子和个梨的重量等于个玻璃球的重量，1个梨等于几个玻璃球？解析：个桃子=个玻璃球的重量，个桃子+个梨=个玻璃球的重量，那么个梨=个玻璃球的重量．变式训练4 只鹅可以换千克鱼，而千克鱼可以换个鸡蛋，个鸡蛋可以换个鹅蛋．一只鹅可以换多少个鹅蛋？解析：一只鹅可以换个鹅蛋．变式训练5 个足球等于几个皮球的价钱？解析：个足球等于个皮球的价钱．例12 个西瓜的重量等于个哈密瓜的重量，个哈密瓜的重量等于个苹果的重量，个苹果的重量等于个柿子的重量，那么个西瓜的重量等于几个柿子的重量？解析：因为个苹果的重量等于个柿子的重量，所以个苹果的重量等于个柿子的重量．又因为个哈密瓜的重量等于个苹果的重量，所以个哈密瓜的重量等于个柿子的重量．而个西瓜的重量等于个哈密瓜的重量，因此个西瓜的重量=个柿子的重量．变式训练1 2只兔子的重量等于6只小鸡的重量，只袋鼠的重量相当于只兔子的重量，那么只袋鼠的重量相当于多少只小鸡的重量？解析：只兔相当于只小鸡的重量，那么只兔相当于只小鸡的重量．只袋鼠的重量相当于只兔子的重量，所以只袋鼠相当于只小鸡的重量．，即只袋鼠相当于只小鸡的重量．变式训练2 一只小猴重4千克，一只小猴的重量等于两只小兔的重量，两只小兔的重量等于4只小猫的重量．一只小兔和一只小猫的重量共多少千克？解析：一只小猴的重量等于两只兔子的重量，这样可以求出一只兔子的重量．而两只兔子的重量等于4只小猫的重量，可以求出一只小猫的重量．最后一只小兔和一只小猫的总重量就求出来了．一只兔子的重量：(千克，)一只小猫的重量：(千克)，一只小兔和12242324315111115111111156-=18450103301151218231238121811212112224⨯=34126412343121234÷=14422÷=441÷=一只小猫的总重量：(千克)题型三、利用对比分析、和差倍分、整体看问题的思想解题例13 ★+■=24，■+●=30，●+★=36．■=_________ ●=________ ★=_______. 解析：，所以■表示的数为：，●表示的数为：，★表示的数为：．变式训练图书室里的故事书与科技书共有720本，又知故事书比科技书多160本，这两种图书各有多少本？解析：题目中给出了两个未知量“故事书”和“科技书”的数量关系，即已知故事书与科技书共有720本和故事书与科技书本数之差，属于典型应用题中的“和差问题”，一般用消去法来解．消去科技书本数后，可先求出故事书的本数．列式：(本)……故事书，(本)……科技书．也可以先求出科技书的本数．例14 学校第一次买了3个水瓶和20个茶杯，共用去134元；第二次又买了同样的3个水瓶和16个茶杯，共用去118元．问水瓶和茶杯的单价各是多少元？解析：引导学生学会审题，找出两次购买的相同点及差异，让学生思考解决．我们用数量关系式来比较对应的未知数量的情况：比较上面两个等式，我们可以看出，134元和118元的差正好是4个茶杯的价钱．利用这一条件，把3个水瓶的价钱消去，先求出每个茶杯的价钱，再求出每个水瓶的价钱．每个茶杯的价钱：(元)每个水瓶的价钱：(元)或(元)变式训练1 奶奶去买水果，如果她买4千克梨和5千克荔枝，需要花掉58元；如果她买6千克梨和5千克荔枝，需要花掉62元．问1千克梨和1千克荔枝各多少元？解析：我们可以把两次的情况进行比较：4千克梨的价钱千克荔枝的价钱(元) ⑴ 6千克梨的价钱千克荔枝的价钱(元) ⑵比较⑴和⑵式，发现两式中荔枝的千克数相等．⑵式比⑴式多了千克梨，213+=(243036)245++÷=45369-=452421-=453015-=7201602880++-故事书本数科技书本数本故事书本数科技书本数本倍故事书本数本(720160)2440+÷=440160280-=320134316118416+=+==个水瓶的价钱个茶杯的价钱元-个水瓶的价钱个茶杯的价钱元个茶杯的价钱元(134118)(2016)-÷-164=÷4=(134420)318-⨯÷=(118416)318-⨯÷=5+58=5+62=642-=也就是元，说明1千克梨的价钱为元．那么1千克荔枝的价钱也就好求了．(元)，(元)或(元)变式训练2 小芳在文具店买了5枝彩色铅笔和6个练习本，共用去17元．小花买了同样的铅笔8枝和6个练习本，共用去20元．一枝彩色铅笔和一个练习本的价格各是多少？解析：从题设条件进行比较，小芳和小花都买了6个练习本(同样多)，只是买的彩色铅笔枝数不同，引起付款多少不同．因此我们可以采用消去法先消去购买练习本的钱数而只剩下买彩色铅笔的钱数，从而先求出彩笔的单价．列式：(元)……一枝彩笔价格，(元)……一个练习本的价格．例15 李老师第一次买回5个篮球和3个排球，用去318元．第二次又买回7个篮球和6个排球，用去510元．问：一个篮球和一个排球的价格各是多少元？解析：可引导学生读题、审题，找出此题与例7的不同之处,并转化成例7的模型．此题有篮球单价与排球单价两个未知数量，而从题里所给条件分析，两次购买篮球与排球的数量各不相同，不能直接用消去法消去哪一个未知数，所以解题关键是使篮球或排球中的某一对未知数变换得相同，则可消去其中一个．通过比较，第一次购买的排球为3个；第二次购买的排球为6个，恰为第一次的2倍．若将第一次购买的排球、篮球各扩大2倍，付的钱也扩大2倍，则能使购买的排球个数与第二次购买的排球个数相同，从而设法消去排球这个未知数量，先求出每个篮球的价格，再求每一个排球的价格．列式：(元)……篮球的单价．(元)……排球的单价．变式训练1 学校要买足球和排球．买3个足球和4个排球共需190元，如果买6个足球和2个排球需要230元．一个足球和一个排球各需要多少元？解析：我们可以把两次情况进行比较；3个足球的价钱个排球的价钱(元)⑴ 6个足球的价钱个排球的价钱(元) ⑵我们发现两组条件不管相加还是相减，都不可能求出足球和排球的单价，因为这里62584-=422÷=(6258)(64)2-÷-=(5824)510-⨯÷=(6226)510-⨯÷=86205617303-枝彩色铅笔个练习本共价元枝彩色铅笔个练习本共价元枝彩色铅笔个练习本共价元(2017)(85)1-÷-=(2018)62-⨯÷=533182106636⨯个篮球个排球元个篮球个排球元106636765103126-个篮球个排球元个篮球个排球元个篮球元(3182510)(527)⨯-÷⨯-126342=÷=(318425)3-⨯÷108336=÷=4+190=2+230=没有一个相同的条件可减去．再观察，我们发现，如果把⑴式扩大2倍，可以得到6个足球和8个排球共380元，即⑴：6个足球的价钱个排球的价钱元 ⑶⑶⑵，可知6个排球的价钱元．容易得出排球和足球的价钱各是多少．排球：(元)，足球：(元)变式训练2 3头牛和8只羊每天共吃青草93千克，5头牛和15只羊每天共吃青草165千克．问一头牛和一只羊每天各吃青草多少千克？解析： 3头牛吃草的重量只羊吃草的重量千克 ⑴5头牛吃草的重量只羊吃草的重量千克 ⑵如果把⑴式扩大5倍，⑵式扩大3倍，那么两个式子中牛的数量就一样多了．这样就得到：⑴：15头牛吃草的重量只羊吃草的重量千克⑶ ⑵：15头牛吃草的重量只羊吃草的重量千克⑷ ⑷⑶：5只羊吃草的重量千克1只羊吃草的重量千克1头牛每天吃草的重量：(千克)例16 李宁的妈妈去菜市场买菜，买了斤土豆和斤柿子椒，共花了元角．己知斤土豆的价钱与斤柿子椒的价钱相等．那么斤土豆和斤柿子椒各多少钱？解析：可引导学生读题、审题，让学生自己思考解答．老师可以画图进行分析，已知条件为：斤土豆+斤柿子椒=元角．斤土豆=斤柿子椒．从第一个式子不能算出斤土豆、斤柿子椒的价钱．若把土豆转化成柿子椒或把柿子椒转化成土豆的价钱就可求该种菜的价钱了．由第二个式子知斤土豆=斤柿子椒，则斤土豆应等于斤柿子椒的价钱．即：斤土豆+斤柿子椒=元角，斤土豆=斤柿子椒．斤柿子椒+斤柿子椒=元角，斤柿子椒=元角．元角等于角，角买了斤柿子椒，所以斤柿子椒的价钱为：(角)= 元角．斤柿子椒的价钱为： (角)=(元)．斤土豆的价钱为：(元)．所以斤土豆的价钱为元，斤柿子椒的价钱为元角．变式训练 3米绵绸的价格与6米花布的价格相等．王云买了6米绵绸和18米花布，共花费了120元．棉绸和花布的单价各是多少？2⨯8+380=-150=150625÷=(190254)330-⨯÷=8+93=15+165=5⨯40+465=3⨯45+495=-30=6=(9368)3-⨯÷453=÷15=6513532116513532113264651356445135913513513513591135915÷=15415460⨯=61661÷=11115解析：由题意可知3米棉绸与6米花布的价格相等，由此可推知1米棉绸与2米花布的价格相等．因此可用花布的价格去替换棉绸的价格，而使棉绸价格转变为花布的价格．消去棉绸价格这个未知数量可以先求出花布的单价，进而求出棉绸的单价．(元)……每米花布的单价 (元)……每米棉绸的单价．例17 学校买2张桌子和3把椅子共用90元钱，每张桌子的价钱是每把椅子价钱的3倍．每张桌子多少钱？解析：引导学生读题、审题，让学生自己思考解答，教师集体订正．2张桌子的价钱把椅子的价钱(元) ⑴1张桌子的价钱把椅子的价钱 ⑵将⑵代入⑴式，消去桌子这个未知量，问题就可以解决．()把椅子的价钱把椅子的价钱(元)把椅子的价钱(元)1把椅子的价钱(元)1张桌子的价钱(元)变式训练红、黄、蓝三个纸盒里共有彩票56张，其中红色纸盒里的彩票是黄色纸盒里彩票张数的2倍，蓝色纸盒里的彩票是红色纸盒里彩票张数的2倍．红、黄、蓝三个纸盒里各有多少张彩票？解析：以黄色纸盒里的彩票张数为1倍数．红纸盒里的彩票张数是这样的2倍．蓝纸盒是红纸盒里彩票张数的2倍，也就是黄纸盒里彩票张数的4倍．一共是倍．这样就可以消去两个未知量而先求出黄纸盒里彩票的张数，再分别求出红色和蓝色盒子里彩票的张数．(张)……黄盒里的彩票张数，(张)……红盒里的彩票张数，(张)……蓝盒里的彩票张数．例18 甲、乙两人共储蓄32元，乙、丙两人共储蓄30元，甲、丙两人共储蓄22元．三人各储蓄多少元？解析：可先让学生自己去思考，教师巡视指正．此题要求三个未知数，甲储蓄多少元？乙储蓄多少元？丙储蓄多少元？关系较为复杂，为了化繁为简，采用消去法来解．首先用加减消去法消去乙和丙，只剩下甲，然后求出甲储蓄多少元，再求乙、丙各储蓄多少元．解法1：由2倍甲储蓄为24元，可求出甲储蓄多少元．列表：(元)……甲储蓄款．(元)……乙储蓄款，120(2618)÷⨯+120304=÷=428⨯=3+90=3=32⨯3+90=990=10=10330=⨯=(124)++56(124)÷++567=÷8=8216⨯=8432⨯=（）甲乙→32元+甲丙→22元2甲乙丙→54元-乙丙→30元2甲→24元(322230)2+-÷24212=÷=321220-=(元)……丙储蓄款．此题也可用另一种方法求解．解法2：甲乙乙丙+甲丙(元)，即2倍的(甲乙丙)等于84元．甲乙丙(元)．(元)……丙储蓄款，(元)……甲储蓄款，(元)……乙储蓄款．变式训练已知个排球和个足球共重千克．个排球和个篮球共重千克．个足球和个篮球共重千克．求每一种球各重多少千克？解析：由(千克)知：个排球+个足球+个篮球=千克，那么有个排球+个足球+个篮球=千克．(千克)……篮球的重量, (千克)……足球的重量(千克)……排球的重量题型四、利用生活中的逻辑推理解题例19 有两只大小相同的杯子，各加入了不等量的水，一多一少．李林将这两只杯子里各滴入了一滴墨水，使两只杯子里的水变黑了，请问，哪只杯子里的水更黑些？如果把较多的那杯水再倒掉一些，使两只杯子中的水一样多，这时，是否两只杯子的水一样黑？解析：因为两杯水不一样多，但同时加入的墨水是同样的．那么水少的那杯加入一滴墨水后颜色更黑一些．杯子中的水变的一样多，也不会改变杯中水的颜色的深浅．所以，即使把较多的那杯水倒掉一些，两杯水同样多了，两只杯子的水仍不一样黑．例20 已知同样大小的木块比冰块轻，铁块比冰块重，铜块与木块的重量之和与冰块与铁块的重量之和同样多，四种物品谁最重?解析：因为铜块与木块的重量之和与铁块与冰块的重量之和同样多，木块又比冰块轻，所以铜块就比铁块重．又因为铁块比冰块重，当然也比木块重，所以铜块最重．铜块重量>铁块重量>冰块重量>木块重量例21 池塘里的莲花繁殖得特别快，每天增多倍．到第天的时候长了半个池塘，那么第几天能长满整个池塘呢？解析：天还是天呢？有的同学认为天长了半个池塘，当然天长满整个池塘了．其实不然，因为池塘的莲花每天增多倍，所以在长满全池塘的前一天就是半个池塘．天长302010-=+32223084=++=++++84242=÷=423210-=423012-=422220-=1151161175+6+7=18222181119954-=963-= 972-=11516301530115。

春季五年制小学奥数四年级数学方法与思想—等量代换

数学方法与思想—等量代换生活中有很多相等的量,如平衡的天平、平衡的跷跷板两边的重量相等。

我们可以根据这些相等的关系进行推理,进而可以等量代换,找到答案。

这一节课我们就引导学生来学习等量代换中推理的方法,让学生能对较复杂的物体进行代换,在代换的过程中培养学生的思维能力。

例1第一只茶壶能装10大杯水,第二只茶壶可以装15小杯水。

已知5大杯水与9小杯水同样多,哪个茶壶大？例2已知13个李子的重量等于2个苹果和1个桃子的重量,而4个李子和1个苹果的重量等于1个桃子的重量。

问多少个李子的重量等于1个桃子的重量？例3如果鱼尾重4公斤,鱼头重量等于鱼尾加上鱼身一半的重量,而鱼身重量等于鱼头加鱼尾的重量。

问这条鱼有多少公斤重？例4阴影部分是正方形,求出最大的长方形的周长。

例5如图所示,两个相同的直角三角形重叠在一起,求阴影部分的面积。

例6下图中正方形的边长是4厘米,长方形的长是5厘米,长方形的宽是多少？测试题1．如图,第一只壶里的茶只有一半,小华倒出了5大杯,第二只壶里的茶是一满壶,小明倒出了15小杯。

已知3小杯的茶与2大杯的茶同样多,现在问你哪个壶大？2．已知1个排球和1个足球共重5千克。

1个排球和1个篮球共重6千克。

1个足球和1个篮球共重7千克。

求每一种球各重多少千克？3．学校要买足球和排球。

买3个足球和4个排球共需190元,如果买6个足球和2个排球需要230元。

一个足球和一个排球各需要多少元？4．梯形的下底是6厘米,高3厘米,DF＝2厘米,求阴影部分面积。

5．正方形ABCD的边长是8厘米,DEFG是一个长方形,宽DE＝6.4厘米,梯形AFGD比三角形ADE的面积大33.28厘米。

求AE的长？答案1．我们可以按以下三个步骤来思考：⑴第二只壶满壶茶倒出15小杯,而每3小杯可以倒满2杯,所以第二只壶可以装茶10大杯。

⑵一只壶的一半倒出了5大杯,则满壶茶可以倒出10大杯。

由⑴⑵可知,两个茶壶一样大。

2．由5+6+7=18<千克>知：2个排球＋2个足球＋2个篮球＝18千克,则有1个排球＋1个足球＋1个篮球＝9千克。

四年级奥数_等量代换

四年级奥数_等量代换学科教师辅导讲义第一讲简单枚举【专题简析】枚举是一种常见的分析问题、解决问题的方法。

一般地，要根据问题要求，一一列举问题解答。

运用枚举法解应用题时，必须注意无重复、无遗漏，因此必须有次序、有规律地进行枚举。

运用枚举法解题的关键是要正确分类，要注意以下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件的对象都列举出来。

【典型例题】【例1】从小华家到学校有3条路可以走，从学校到岐江公园有4条路可以走，从小华家到岐江公园，有几种不同的走法？【试一试】1. 从甲地到乙地，有3条公路直达，从乙地到丙地有2条铁路可以直达，从甲地到丙地有多少种不同的走法？2. 新华书店有3种不同的英语书，4种不同的数学读物销售，小明想买一种英语书和一种数学读物，共有多少种不同的买法？【例2】把4个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？【试一试】1．把5个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？2．把7个同样的苹果放在三个同样的盘子里，不允许有的盘子空着不放，问共有多少种不同的分法？【例3】从1～6这六个数字中，每次取2个数字，这两个数字的和都必须大于7，能有多少种取法？【试一试】1．从1～9这九个数字中，每次取2个数字，这两个数字的和都必须大于10，能有多少种取法？2．从1～19这十九个数字中，每次取2个数字，这两个数字的和都必须大于20，能有多少种取法？【例4】一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能值？【试一试】1．一个长方形的周长是30厘米，如果它的长和宽都是整厘米数，那么这个长方形的面积有多少种可能值？2．把15个玻璃球分成数量不同的4堆，共有多少种不同的分法？【例5】有4位小朋友，寒假中互相通一次电话，他们一共打了多少次电话？【试一试】1．6个小队进行排球比赛，每两队比赛一场，共要进行多少次比赛？2．有8位小朋友，要互通一次电话，他们一共打了多少次电话？【※例6】一条铁路，共有10个车站，如果每个起点站到终点站只用一种车票（中间至少相隔5个车站），那么这样的车票共有多少种？【※试一试】1.上海、北京、天津三个城市分别设有一个飞机场，它们之间通航一共需要多少种不同的机票？2. 一条公路上，共有8个站点，如果每个起点到终点只用一种车票（中间至少相隔3个车站），那么共有多少种不同的车票？【※例7】在1～49中，任取两个和小于50的数，共有多少种不同的取法？【※试一试】1.在两位整数中，十位数字小于个位数字的共有多少个？2.从1～99这九个数中，每次取2个数，这两个数的和都必须大于100，能有多少种取法？我的学习收获：..第二讲等量代换【专题简析】“等量代换”是解数学题时常用的一种思考方法，即两个相等的量，可以互相代换。

小学四年级奥数知识点和典型题型解答

第一课时等量代换第一站：倒酒例1：群宴时，曹丞相让曹冲给大家倒酒。

于是，曹冲就把720毫升酒倒入6个小杯和1个大杯，正好倒满。

大杯的容量是小杯的3倍，小杯和大杯各可以装多少毫升酒？思路点拨：一个大杯的容量可以换成3个小杯，“把720毫升酒倒入6个小杯和1个大杯”，就可以替换成“把720毫升酒倒入（）个小杯”。

尝试解答：第二站：奖赏例2：曹操为了把宴会搞得更加隆重，他对每个大臣都进行了赏赐。

他给每个文官奖励4只羊，每个武官奖励2头猪。

如果6只同样的小猪和18只同样的小羊总共价值648文钱，且2只小猪和三只小羊的价钱相等。

问：每只小猪和每只小羊各是多少文钱？思路点拨：已知2只小猪和3只小羊的价钱相等，如果把小猪替换成小羊，那么6只小猪的价钱= 只小羊的价钱。

尝试解答：第三站：取剑例3：宴会结束后，曹操把曹冲带到一个藏宝室。

曹操对曹冲说：“这里有很多宝剑和宝刀，你可以任选一样，但得回答我的一个问题。

”曹冲说：“没问题！”曹操说：“3把同样的宝刀和20把同样的宝剑，一共价值134两银子；同样的3把宝刀和16把宝剑，一共价值118两银子。

宝刀和宝剑的单价各是多少两银子?”思路点拨：把两组条件进行比较，可以发现，第一组比第二组多两银子，是因为第一组比第二组多了把宝剑的价钱。

尝试解答：大胆闯关1、曹冲把40个同样质量的苹果和5个同样质量的西瓜一起称了一下，一共重12千克，并且每个西瓜的质量是每个苹果质量的8倍。

问每个苹果和每个西瓜各重多少克？2、一个大臣先取出5个同样质量的橙子和6个同样质量的梨子，一共重3120克；又取出5个同样质量的橙子和9个同样质量的梨子，一共重4080克。

你知道每个橙子和每个梨子的质量分别是多少克吗？3、曹冲用大小两种车运石头，大车运了9次，小车运了10次，一共运了132吨，大车3次运的石头等于小车4次运的石头。

大、小车的载重量各是多少吨？4、小强在3个同样的大盒和5个同样的小盒里装满乒乓球，正好是98个。

小学四年级奥数题等量代换、填算式、归一问题

小学四年级奥数题等量代换、填算式、归一问题1.小学四年级奥数题等量代换篇一10个杏子的重量等于1个梨子和2个橘子的重量，4个杏子和1个橘子的重量等于1个梨子的重量。

1个梨子的重量等于几个杏子的重量？分析：我们用梨与杏的重量表示出橘子的重量，即，1个橘子的。

重量=一个梨子的重量-4个杏子的重量，然后再用杏表示出梨的重量。

解答：解：1个梨子+2个橘子=10个杏子的重量，又因，一个梨子的重量=4个杏子+1个橘子的重量，即，1个橘子的重量=一个梨子的重量-4个杏子的重量，所以，1个梨子+（1个梨子-4个杏子的重量）×2=10个杏子的重量，3个梨子的重量-8个杏子的重量=10个杏子的重量，3个梨子的重量=18个杏子的重量，3个梨子的重量÷3=18个杏子的重量÷3，一个梨子的重量=6个杏子的重量。

答：一个梨子的重量等于6个杏子的重量。

2.小学四年级奥数题填算式篇二1.两个数之间填上合适的运算符号，使等式成立3333=13333=23333=33333=92.在合适的地方添上运算符号，使等式成立444444444444=10003.在合适的地方添上+或-，使等式成立123456789=81123456789=904.在下列各数间添上+或-，使等式成立987654321=215.在合适的地方添上运算符号65432=106.在下面算式適當的地方添上加號,使算式成立88888888=10007.在下面算式中適當的地方添上+、-、?,使算式成立987654321=19938.在下面算式合適的地方添上+、-、?,使算式成立3333333333333333=19929.在下面算式合適的地方添上+、-、?,使算式成立12345678=110.在下列算式中合適的地方,添上(),使等式成立1+2（）3+4（）5+6（）7+8（）9=3033.小学四年级奥数题归一问题篇三1、一列火车3小时行240千米，照这样算，7小时行_________千米。

等量代换的小学奥数题及解题方法

等量代换的小学奥数题及解题方法
等量代换的小学奥数题及解题方法
“曹冲称象”是运用了“等量代换”的'思考方法：两个完全相等的量，可以互相代换。

解数学题，经常会用到这种思考方法。

百货商店运来300双球鞋，分别装在2个木箱、6个纸箱里。

如果2个纸箱同1个木箱装的球鞋一样多，每个木箱和每个纸箱各装多少双球鞋?
提示：我们根据“2个纸箱同一个木箱装的球鞋一样多”，把木箱换成纸箱，也就是说，把300双球鞋全部用纸箱装，不用木箱装。

根据已知条件，2个木箱里的球鞋刚好装满4个纸箱，再加上原来已装好的6个纸箱，一共是10个纸箱。

这样，题目就变为“把300双球鞋平均装在10个纸箱里，平均每个纸箱装多少双球鞋?”可以求出每个纸箱装多少双球鞋。

也就能求出一个木箱装多少双球鞋。

用两台水泵抽水，小水泵抽6小时，大水泵抽8小时，一共抽水312立方米。

小水泵5小时的抽水量等于大水泵2小时的抽水量，两种水泵每小时各抽水多少立方米?
5小=2大大换小：8 ÷ 2 × 5=20 (时) 小：312 ÷(20+6)=12(立方米) 大：12 × 5 ÷ 2=30(立方米)。

四年级奥数-等量代换讲课教案

四年级奥数-等量代换学科教师辅导讲义学员编号：年级：新小五奥数课时数：学员姓名：辅导科目：数学学科教师：C等量代换授课类型C简单枚举授课日期及时段教学内容第一讲简单枚举【专题简析】枚举是一种常见的分析问题、解决问题的方法。

一般地，要根据问题要求，一一列举问题解答。

运用枚举法解应用题时，必须注意无重复、无遗漏，因此必须有次序、有规律地进行枚举。

运用枚举法解题的关键是要正确分类，要注意以下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件的对象都列举出来。

【典型例题】【例1】从小华家到学校有3条路可以走，从学校到岐江公园有4条路可以走，从小华家到岐江公园，有几种不同的走法？【试一试】1. 从甲地到乙地，有3条公路直达，从乙地到丙地有2条铁路可以直达，从甲地到丙地有多少种不同的走法？2. 新华书店有3种不同的英语书，4种不同的数学读物销售，小明想买一种英语书和一种数学读物，共有多少种不同的买法？【例2】把4个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？【试一试】1．把5个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？2．把7个同样的苹果放在三个同样的盘子里，不允许有的盘子空着不放，问共有多少种不同的分法？【例3】从1～6这六个数字中，每次取2个数字，这两个数字的和都必须大于7，能有多少种取法？【试一试】1．从1～9这九个数字中，每次取2个数字，这两个数字的和都必须大于10，能有多少种取法？2．从1～19这十九个数字中，每次取2个数字，这两个数字的和都必须大于20，能有多少种取法？【例4】一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能值？【试一试】1．一个长方形的周长是30厘米，如果它的长和宽都是整厘米数，那么这个长方形的面积有多少种可能值？2．把15个玻璃球分成数量不同的4堆，共有多少种不同的分法？【例5】有4位小朋友，寒假中互相通一次电话，他们一共打了多少次电话？【试一试】1．6个小队进行排球比赛，每两队比赛一场，共要进行多少次比赛？2．有8位小朋友，要互通一次电话，他们一共打了多少次电话？【※例6】一条铁路，共有10个车站，如果每个起点站到终点站只用一种车票（中间至少相隔5个车站），那么这样的车票共有多少种？【※试一试】1.上海、北京、天津三个城市分别设有一个飞机场，它们之间通航一共需要多少种不同的机票？2. 一条公路上，共有8个站点，如果每个起点到终点只用一种车票（中间至少相隔3个车站），那么共有多少种不同的车票？【※例7】在1～49中，任取两个和小于50的数，共有多少种不同的取法？【※试一试】1.在两位整数中，十位数字小于个位数字的共有多少个？2.从1～99这九个数中，每次取2个数，这两个数的和都必须大于100，能有多少种取法？我的学习收获：..第二讲等量代换【专题简析】“等量代换”是解数学题时常用的一种思考方法，即两个相等的量，可以互相代换。

小学四年级奥数题自然数列、等量代换、方阵问题

小学四年级奥数题自然数列、等量代换、方阵问题1.小学四年级奥数题自然数列篇一1、小明从1写到100,他共写了多少个数字T?解：分类计算：“1”出现在个位上的数有：1,11,21,31,41,51,61,71,81,91共10个；“1”出现在十位上的数有：10,11,12,13,14,15,16,17,18,19共10个；“1”出现在百位上的数有：100共I个；共计10+10+1=21个。

2、一本小人书共100页，排版时一个铅字只能排一位数字，请你算一下，排这本书的页码共用了多少个铅字？解：分类计算：从第1页到第9页，共9页，每页用1个铅字，共用1X9=9（个）；从第10页到第99页，共90页，每页用2个铅字，共用2X90=180（个）；第100页，只1页共用3个铅字，所以排100页书的页码共用铅字的总数是:9+180+3=192（个）o2.小学四年级奥数题等量代换篇二1、一头牛一天吃草的重量和一只兔子9天吃草的重量相等，也和6只羊一天吃草的重量相等，已知一头牛一天吃青草18千克，一只兔子和一只羊一天共吃青草多少千克？因为一头牛一天吃草的重量和一只兔子9天吃草的重量相等，也就是一只兔子9天吃草的重量是18千克，即一只兔子一天共吃青草18÷9=2千克；又因为头牛一天吃草的重量也和6只羊一天吃草的重量相等，也就是6只羊一天吃草的重量是18千克，即一只羊一天共吃青草18÷6=3千克，所以一只兔子和一只羊一天共吃青草2+3=5千克。

2、有6个筐里放着同样多的鸡蛋，如果从每个筐里拿出50个鸡蛋，则6个筐里剩下的鸡蛋个数的总和等于原来两个筐里鸡蛋个数的总和，原来每个筐里有鸡蛋多少个？【思路】根据“6个筐里剩下的鸡蛋个数的总和等于原来两个筐里鸡蛋个数的总和”，说明6个筐里取出的鸡蛋个数的总和等于原来6-2=4（筐）里鸡蛋个数的总和，用取出的50X6=300（个）鸡蛋除4就可以求出原来每个筐里鸡蛋的个数。

四年级奥数-等量代换讲课教案

四年级奥数-等量代换学科教师辅导讲义学员编号：年级：新小五奥数课时数：学员姓名：辅导科目：数学学科教师：C等量代换授课类型C简单枚举授课日期及时段教学内容第一讲简单枚举【专题简析】枚举是一种常见的分析问题、解决问题的方法。

一般地，要根据问题要求，一一列举问题解答。

运用枚举法解应用题时，必须注意无重复、无遗漏，因此必须有次序、有规律地进行枚举。

运用枚举法解题的关键是要正确分类，要注意以下两点：一是分类要全，不能造成遗漏；二是枚举要清，要将每一个符合条件的对象都列举出来。

【典型例题】【例1】从小华家到学校有3条路可以走，从学校到岐江公园有4条路可以走，从小华家到岐江公园，有几种不同的走法？【试一试】1. 从甲地到乙地，有3条公路直达，从乙地到丙地有2条铁路可以直达，从甲地到丙地有多少种不同的走法？2. 新华书店有3种不同的英语书，4种不同的数学读物销售，小明想买一种英语书和一种数学读物，共有多少种不同的买法？【例2】把4个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？【试一试】1．把5个同样的苹果放在两个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？2．把7个同样的苹果放在三个同样的盘子里，不允许有的盘子空着不放，问共有多少种不同的分法？【例3】从1～6这六个数字中，每次取2个数字，这两个数字的和都必须大于7，能有多少种取法？【试一试】1．从1～9这九个数字中，每次取2个数字，这两个数字的和都必须大于10，能有多少种取法？2．从1～19这十九个数字中，每次取2个数字，这两个数字的和都必须大于20，能有多少种取法？【例4】一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能值？【试一试】1．一个长方形的周长是30厘米，如果它的长和宽都是整厘米数，那么这个长方形的面积有多少种可能值？2．把15个玻璃球分成数量不同的4堆，共有多少种不同的分法？【例5】有4位小朋友，寒假中互相通一次电话，他们一共打了多少次电话？【试一试】1．6个小队进行排球比赛，每两队比赛一场，共要进行多少次比赛？2．有8位小朋友，要互通一次电话，他们一共打了多少次电话？【※例6】一条铁路，共有10个车站，如果每个起点站到终点站只用一种车票（中间至少相隔5个车站），那么这样的车票共有多少种？【※试一试】1.上海、北京、天津三个城市分别设有一个飞机场，它们之间通航一共需要多少种不同的机票？2. 一条公路上，共有8个站点，如果每个起点到终点只用一种车票（中间至少相隔3个车站），那么共有多少种不同的车票？【※例7】在1～49中，任取两个和小于50的数，共有多少种不同的取法？【※试一试】1.在两位整数中，十位数字小于个位数字的共有多少个？2.从1～99这九个数中，每次取2个数，这两个数的和都必须大于100，能有多少种取法？我的学习收获：..第二讲等量代换【专题简析】“等量代换”是解数学题时常用的一种思考方法，即两个相等的量，可以互相代换。

小学四年级等量代换奥数题【五篇】

【导语】明天，这是个美丽灿烂、辉映着五光⼗⾊的迷⼈的字眼。

愿你的明天⽆限美丽、⽆限灿烂、⽆限迷⼈！以下是为⼤家整理的《⼩学四年级等量代换奥数题【五篇】》供您查阅。

【篇⼀】难度：★★★★ ⼀只⼩猪的重量等于6只鸡的重量，3只鸡的重量等于4只鸭的重量。

⼀只⼩猪的重量等于⼏只鸭的重量？【答案】因为3只鸡的重量等于4只鸭的重量，所以6只鸡的重量等于8只鸭的重量，⼜因为⼀只⼩猪的重量等于6只鸡的重量，所以⼀只⼩猪的重量等于8只鸭的重量【篇⼆】⼀头⽜⼀天吃草的重量和⼀只兔⼦9天吃草的重量相等，也和6只⽺⼀天吃草的重量相等，已知⼀头⽜⼀天吃青草18千克，⼀只兔⼦和⼀只⽺⼀天共吃青草多少千克？【答案】因为⼀头⽜⼀天吃草的重量和⼀只兔⼦9天吃草的重量相等，也就是⼀只兔⼦9天吃草的重量是18千克，即⼀只兔⼦⼀天共吃青草18÷9=2千克；⼜因为头⽜⼀天吃草的重量也和6只⽺⼀天吃草的重量相等，也就是6只⽺⼀天吃草的重量是18千克，即⼀只⽺⼀天共吃青草18÷6=3千克，所以⼀只兔⼦和⼀只⽺⼀天共吃青草2+3=5千克.【篇三】⼀只⼩猪的重量等于6只鸡的重量，3只鸡的重量等于4只鸭的重量。

⼀只⼩猪的重量等于⼏只鸭的重量? 答案与解析：因为3只鸡的重量等于4只鸭的重量，所以6只鸡的重量等于8只鸭的重量，⼜因为⼀只⼩猪的重量等于6只鸡的重量，所以⼀只⼩猪的重量等于8只鸭的重量【篇四】 1.请你根据上⾯的两个天枰判断，下⾯的青苹果左边括号中应该填数字（）2.请问，根据下图括号中应该填（） 1、【解析】考察天平代换。

天平平衡就说明两边是相等的，第⼀个天平表明两个红苹果等于四个青苹果，稍稍转换⼀下，⼀个红苹果等于两个青苹果；第⼆个天平表明⼀个梨等于⼀个红苹果加⼀个青苹果；第三个天平问的是梨和青苹果的关系，所以需要把红苹果转换成苹果。

1红=2青，1梨=1红+1青，所以1梨=2青+1青，即1梨=3青【答案】3 2、【解析】考察天平代换。

苏教版四年级上册同步奥数培优第十六讲等量代换

苏教版四年级上册奥数培优第十六讲等量代换【知识概述】小朋友们一定都知道曹冲(曹操的小儿子)称象的故事吧!曹冲用一条船，让大象先上船，看船被河水水面淹没到什么位置，然后刻上记号。

把大象赶上岸，再把这条船装上石块，当船被水面淹没到记号的位置时，就可以判断:船上的石块共有多重，大象就有多重。

为什么大象的重量可以换成一船石块的重量呢?因为两次船下沉后被水面所淹没的深度一样，只有当大象与一船石头一样重(重量相等)时才会淹没得一样深。

“曹冲称象”不是瞎称的，而是运用了“等量代换”的思考方法:两个完全相等的量，可以互相代换。

解数学题，经常会用到这种思考方法。

例1：下面的四只天平都保持平衡。

想一想:1个西瓜和几根香蕉的重量相等?练习一：1.下图中每只梨重500克，那么，1根香蕉比1个苹果轻多少克?2.已知1头猪＝2只羊，1只羊＝8只兔子。

1头猪＝( )只兔子； 2头猪＝( )只兔子；3只羊＝( )只兔子； 24只兔子＝( )只羊；32只兔子＝( )头猪。

3.假若20只兔子可换2只羊，9只羊可换3头猪，8头猪可换2头牛，那么用5头牛可换多少只兔子?例2：△、○、口分别表示三个数，并且(1)△+△＝□+□+□，(2)□+□+□=○+○+○+○(3)△+□+○+○=400，则△＝( )，○＝( )，□＝( )。

练习二：1.△+☆+○＝24 ○+△＝15 ☆+○＝17☆＝( ) ○=( ) △＝( ）2.1筐梨+1筐苹果＝120千克 1筐梨＝( ）千克1筐梨+1筐橘子＝100千克 1筐苹果＝( )千克1筐苹果+1筐橘子＝80千克 1筐橘子＝( )千克3.1头大象的重量等于4头牛的重量，1头牛的重量等于3匹小马的重量，1匹小马的重量等于3头小猪的重量，1头大象的重量等于几头小猪的重量?例3：百货商店运来300双球鞋，分別装在2个木箱、6个纸箱里。

如果2个纸箱同1个本箱装的球鞋一样多，想一想:每个木箱和每个纸箱各装多少双球鞋?练习三：1.买6千克荔枝和8千克桂圆，共付312元。

四年级奥数-等量代换

四年级奥数之等量代换(含答案)

(完整word版)四年级奥数教材

四年级奥数 等量代换 教案(可以直接下载使用)

四年级奥数教材第33讲 等量代换

（完整word版）四年级奥数之等量代换（含答案）

小学奥数专题--等量代换

春季五年制小学奥数四年级数学方法与思想—等量代换

最新四年级奥数-等量代换

四年级奥数_等量代换

小学四年级奥数知识点和典型题型解答

小学四年级奥数题等量代换、填算式、归一问题

等量代换的小学奥数题及解题方法

四年级奥数-等量代换讲课教案

小学四年级奥数题自然数列、等量代换、方阵问题

四年级奥数-等量代换讲课教案

小学四年级等量代换奥数题【五篇】

苏教版四年级上册同步奥数培优 第十六讲 等量代换

四年级奥数等量代换教案(可以直接下载使用)

四年级奥数教材第33讲等量代换

苏教版四年级上册同步奥数培优第十六讲等量代换