第13章 非平稳时间序列模型
第十三讲 非平稳时间序列

问题2:t统计量的非正态分布
若回归变量中包含随机性趋势,则常用的OLS t统计量在原假设成立时即使在大样本下也服 从非正态分布。这意味着常用的置信区间是不 正确的,也不能像往常一样进行假设检验。由 于这个t统计量的分布依赖于有问题的回归变 量和其他回归变量之间的关系,因此一般无法 列表给出其分布。
E (Yt ) E (Yt s ) Y
Var (Yt ) Var (Yt s)
2
COV (Yt, Yt s) E[(Yt Y )(Yt s Y )] s
非平稳时间序列
非平稳时间序列:常规假设检验、置信区间、 预测均失效。 非平稳时间序列的两个例子: 1. 趋势 2. 突变
随机游走的基本思想是序列明天的取值就是它今天的取值再加上一个不可测变化因为随机游走的基本思想是序列明天的取值就是它今天的取值再加上一个不可测变化因为yt前进的路径是由随机项前进的路径是由随机项ut组成的所以这一路径为一个随机游走
时间序列回归
平稳性时间序列的条件
平稳时间序列的期望、方差、自协方差、自相关系数 等数字特征均不随时间推移而改变。
一种确保某些基于回归的方法可靠的特例是 两个序列的趋势成分相同,即序列中包含了 共同的随机性趋势。如果是这样的话,序列 称为是协整的。
随机性趋势探测:单位AR根的检验
因此,针对式 Yt=β0+Yt-1+t 我们关心的检验为:零假设 H0:=0。 备择假设 H1:<0 上述检验可通过OLS法下的t检验完成。
L Yt Yt 2
2
L Yt Yt p
p
Yt 1Yt 1 2Yt 2 pYp 1 ut
LYt Yt 1 L Yt Yt 2 将滞后算子带入到方程,得: p L Yt Yt p
非平稳时序 计量经济学 EVIEWS建模课件

20
15
10
5
0
-5
50
100
150
200
250
确定性趋势过程中的趋势可以是线性的也可以是 非线性的,如:Yt = β0 +β1t + εt;Yt = β0 +β1t + β2t2 + εt; Yt = β0 +β1t + β2t2 + β3t3 + εt等等。
对于线性趋势模型而言,其均值是时间的线性函 数,方差是固定的常数,具体形式如下:
在社会经济现象中,多数是非平稳过程。但是它 们经过一、两次的差分之后,基本上就可以转化为平 稳的序列了。
ARIMA(p,d,q) 的不同表现形式: ⑴当p>0、d=0、q = 0时,为AR(p)过程; ⑵当p = 0、d>0、q = 0时,为I(d)过程; ⑶当p = 0、d=0、q>0时,为MA(q)过程; ⑷当p>0、d=0、q>0时,为ARMA(p,q)过程; ⑸当p>0、d>0、q = 0时,为ARI(p,d)过程; ⑹当p=0、d>0、q>0时,为IMA(d,q)过程; ⑺当p>0、d>0、q>0时,为ARIMA(p,d,q)过程;
⒈AR(p)过程中的平稳条件是p个自相关系数及 其各系数之和都要小于1;
⒉MA(q)过程的平稳条件是q个移动平均系数及 其各系数之和都要小于1;
⒊当基础模型中的上述两类系数有大于等于1 的时候,就会使时序的变化趋势不平稳。
㈡ 单位根过程
将AR⑴模型写成自回归的形式:A(L)Yt=εt;其 中滞后多项式为A(L)=1- α1L的特征根,即1- α1L=0的 根为L=1/α1;存在单位特征根的过程就叫单位根过程, 对其理解可以从如下两个方面着手:
非平稳时间序列模型

(二)随机趋势模型
随机趋势模型又称齐次非平稳ARMA模型。 为理解齐次非平稳ARMA模型,可先对 ARMA模型的性质作一回顾。
假设有一个ARMA( p, q)模型如下:
(B)xt (B)at 其中:(B) 11B 2B2 Bp
(B) 11B 2B2 qBq
at为白噪声序列.
为满足平稳,性 则必须有:(B) 0的
(二)非参数检验方法在检验序列平稳性中的应用
1.游程检验方法 (1)什么是游程 一个游程定义为一个具有相同符号的连续
串,在它前后相接的是与其不同的符号 或完全无符号。
例如,观察的结果用加、减标志表示,得 到一组这样的记录顺序:
++---+----++-+ 这个样本的观察结果共有7个游程。
(2)用游程检验方法检验时间序列平稳性
非参数检验可以很方便的通过SPSS软件进行, 游程检验可见操作。
实例:用游程检验S&T数据的平稳性; 步骤如下:
1.打开SPSS输入数据 2.依次单击Analyze—Nonparmetric Tests—Runs; 打开Runs对话框。 3.在源变量对话框中选择“stpoor”进入“Test Variable list”栏内 4.选中“cut point”栏中“mean”选项 5.单击“OK”按纽,开始进行统计分析。
上一页 下一页 返回本节首页
假设序列 yt可由下式描述 : yt yt1 ut 其中 ut为白噪声 (零均值 , 恒定方差点 , 无自相关 ), 这时我们就遇到了所谓 的单位根问题 .它是一种 非平稳的情况 . 如果我们作如下回归 :
yt yt1 ut 并确实发现 1, 那么就说随机变量 yt有一个单位
[经济学]Slides_非平稳时间序列
![[经济学]Slides_非平稳时间序列](https://img.taocdn.com/s3/m/fef4a037a300a6c30c229fcd.png)
40
协整关系
41
协整关系
42
协整关系
43
教学内容结束,谢谢同学们
祝同学们圣诞节快乐!让平安夜的钟声伴 随同学们渐渐地踏入崭新的一年,祝同学 们心想事成,新年快乐。 谢谢同学们对我教学的支持。 祝福大家2011年完事如意,心想事成!更 帅,更靓,更开心。 希望大家不要忘记“计量经济学”,请大 家多多使用计量经济学。
项来控制高阶序列相关
y t y t 1 i y t i u t
i 1
p
(5.3.11)
y t y t 1 a i y t i u t
i 1
p
(5.3.12)
yt yt 1 a t i yt i ut
性的序列称为单整(integration)序列。定义如下:
定义:如果序列 yt ,通过 d 次差分成为一个平稳序列,而 这个序列差分 d – 1 次时却不平稳,那么称序列 yt为 d 阶 单整序列,记为 yt ~ I(d)。特别地,如果序列 yt本身是 平稳的,则为零阶单整序列,记为 yt ~ I(0)。
6
非平稳序列和单整
1.确定性时间趋势和单位根过程 描述类似图 5.9 形式的非平稳经济时间序列有两种方法, 一种方法是包含一个确定性时间趋势
yt a t ut
(5.3.1)
其中 ut 是平稳序列;a + t 是线性趋势函数。这种过程 也称为趋势平稳的,因为如果从式(5.3.1)中减去 a + t, 结果是一个平稳过程。注意到像图5.9一类的经济时间序 列常呈指数趋势增长,但是指数趋势取对数就可以转换
协整的检验
双变量:Engle-Granger检验;多变量:Johansen检验。 步骤:(1)协整回归: ˆ ˆ ˆ 估计 y β x u , 得到u y β x (2)对ut进行平稳性检验:平稳则存在协整关系。
16.第十三讲 非平稳时间序列解析

非平稳时间序列
非平稳时间序列:常规假设检验、置信区间、 预测均失效。
非平稳时间序列的两个例子:
1. 趋势 2. 突变
一个平稳的时间序列在图形上往往表现出 一种围绕其均值不断波动的过程;
而非平稳序列则往往表现出在不同的时间 段具有不同的均值(如持续上升或持续下 降)。
什么是趋势
趋势(trend)是指变量随时间持续长期的运动。
Yt 1Yt 1 2Yt 2 L pYp 1 ut
LYt Yt 1 L2Yt Yt 2 LpYt Yt p
Yt 1Yt 1 2Yt 2 L pYp 1 ut
LYt Yt 1 L2Yt Yt 2 将滞后算子带入到方程,得: LpYt Yt p
随机性趋势、自回归模型和单位根
对于AR(1)来说,时间序列平稳的条件 是|β1| <1。 对于AR(p)来说,需要引入滞后算子: 定义一阶滞后算子L为:
Lxt = xt -1 k阶滞后算子定义为
Lkxt = xt - k
由于常数项与是否平稳无关,因此,原方程可 以写为:
Yt 1Yt 1 2Yt 2 L pYp 1 ut
时间趋势中有确定性和随机性两种类型的趋势。其中确 定性趋势是时间的非随机函数。例如,确定性趋势为时 间的线性函数,若通货膨胀中有每季度上升0. 1个百分 点的确定性时间趋势,则该趋势可表为0.1t,其中t表示 季度。
随机性趋势是随机的且随时间变化的趋势。
例如通货膨胀中的随机性趋势显示出较长时间 的下降之后伴随着较长时间的上升。
渐近正态分布,甚至不是对称分布,即使是在大样 本下,而是向左偏向于0。这是因为,由于{Yt} 不 是平稳序列,中心极限定理不再适用。
非平稳时间序列模型讲义

Yt Yt1 t
(2.6)
Yt t Yt1 t
(2.7)
方程(2.6)称为带漂移的单位根过程,方程
(2.7)称为带漂移和时间趋势的单位根过程。
认识数据特征:平稳数据和几种单位跟数据
图2.1: Yt 0.6Yt1 t
图2.2: Yt Yt1 t
图2.3: Yt 1 Yt1 t
图2.4: Yt 1 0.3t Yt1 t
3. 趋势平稳和差分平稳过程
一、趋势平稳和差分平稳的数据生成过程
图1.1中我国的名义GDP表现出很强的趋势,这 种趋势是随机性的还是确定性的呢?还是两者兼而有 之呢?为清楚理解这一问题的含义,考虑如下模型:
Yt 0 1t 2Yt1 t
(3.1)
金融时间序列分析
第六讲:非平稳时间序列模型
第六讲 非平稳时间序列模型
内容结构
1.认识非平稳的数据特征 2.非平稳时间序列与单位根过程 3.趋势平稳和差分平稳过程 4.单位根检验 5 .ARIMA模型 6.伪回归 7.协整与误差校正模型 8 .实证案例
前言
在前面的章节中,所阐述的有关时间序列数据模 型的内容都假定数据是平稳的,那么,实际经济中的 数据有没有可能是非平稳的?如何检验时间序列数据 的非平稳性?
5.两个或多个单位根变量之间可能存在协整关系,协整关 系表明它们之间存在长期均衡。可通过检验方程残差的平稳性 实现协整检验。
6.误差校正模型是协调协整变量短期动态变化及其长期关 系的一种方法。
1.认识非平稳的数据特征
我们以中国国内生产总值(GDP),经济 增长率(g)的数据为基础分析相关概念,具体 数据如图:
一旦知道了 , 的值,就可以准确预测 01
Yt
的均值及其
非平稳时间序列解析

动态乘子的比较
趋势平稳过程 动态乘子:
xt t+( B) t
xt s t
2 趋势平稳过程满足 j 0 j , 所以
xt s lims 0. t
单整序列
差分一次变为平稳过程,记为I(1) 平稳过程记为I(0) 如果差分n-1次不平稳,差分n次平稳,称 为n阶单整的,记为I(n)
趋势平稳过程和单位根过程比较
预测比较
H 0 : xt xt 1 t H1 : xt t ( xt 1 t ) t ,| | 1
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B) xt t 1 t 1
其中
(B) t
(1) 0, j 0 2 j , (u ) 0根在单位圆外.
单位根过程对时间序列的增量进行刻画,增 量平稳,但水平变量不平稳。
2.方差有界并且不随时间变化,是常数. 称为方差齐性
平稳ARMA模型, 可表示为
xt t 1 t 1
,
i 0
| i |
t WN (0, )
2
此类模型的特点 3. 长期预测趋于无条件均值 4. 预测误差的方差有界
序列分解
xt l t l 1 t l 1 et (l )
预测误差
l 1 t 1 l t l 1 t 1 ˆt (l ) x
预测值
ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]
非平稳时序计量经济学EVIEWS建模课件

丰富的模型估计方法
EViews提供了多种回归分析、时间序 列分析和计量经济学模型估计方法, 满足用户不同需求。
自动化的统计检验
EViews能够自动进行各种统计检验, 如单位根检验、协整检验等,帮助用 户快速验证模型的有效性。
EViews的基本操作界面
菜单栏
包含文件、编辑、视图、图表等常用菜单选项,方便用户进行基本操作。
EViews中的模型选择与估计
模型选择
根据数据特征和经济学理论,选择合适的非 平稳时序计量经济学模型,如ARIMA、 SARIMA、VAR等。
参数估计
利用EViews软件提供的工具,对选定的模型进行参 数估计,包括自回归系数、差分阶数、移动平均系 数等。
模型适用性检验
通过残差分析、ACF图、PACF图等手段, 检验模型是否符合数据特征,判断模型是否 合适。
THANKS
感谢观看
描述性统计分析
提供各种描述性统计指标,帮助用户了解数 据的基本特征和分布情况。
高级统计分析
支持回归分析、时间序列分析、计量经济学 等多种高级统计分析方法。
03
CATALOGUE
非平稳时序计量经济学模型构建
ARIMA模型及其扩展
ARIMA模型
自回归积分滑动平均模型,通过差分 将非平稳时序转化为平稳时序,再利 用ARMA模型进行拟合。
EViews中的模型检验与诊断
平稳性检验
利用ADF检验、PP检验等方法, 对原始序列和残差序列进行平稳 性检验,确保模型适用于非平稳
时序数据。
残差诊断
通过计算残差的ACF图、PACF图 、QQ图等,诊断模型的残差是否 符合白噪声假设,判断模型是否合 适。
非平稳时间序列

首先定义序列 yt 的拟差分序列如下:
d ( yt
|
a)
yt yt
ayt 1
if t 1 if t 1
并且构造如下回归方程:
t = 1, 2, , T
d ( yt | a) d ( xt | a) δ(a) ut t = 1, 2, , T (5.3.14)
§5. 3 非平稳时间序列建模
前述的AR(p)、MA(q) 和ARMA(p,q) 三个模型只适 用于刻画一个平稳序列的自相关性。一个平稳序列的数 字特征,如均值、方差和协方差等是不随时间的变化而 变化的,时间序列在各个时间点上的随机性服从一定的 概率分布。也就是说,对于一个平稳的时间序列可以通 过过去时间点上的信息,建立模型拟合过去信息,进而 预测未来的信息。
其中: = -1。
(5.3.10)
14
其中: = -1,所以原假设和备选假设可以改写为
H0 H1
: :
0 0
可以通过最小二乘法得到 的估计值ˆ,并对其进行
显著性检验的方法,构造检验 ˆ 显著性的 t 统计量。
但是,Dickey-Fuller研究了这个t 统计量在原假设下 已经不再服从 t 分布,它依赖于回归的形式(是否引进了 常数项和趋势项) 和样本长度T 。
16
2. ADF检验
考虑 yt 存在p阶序列相关,用p阶自回归过程来修正,
yt a 1 yt1 2 yt2 p yt p ut
在上式两端减去 yt-1,通过添项和减项的方法,可得
其中
p 1
Δ yt a yt1 i Δ yti ut i 1
11
非平稳金融时间序列模型

张成思
► 最简单的线性确定性趋势模型可以写成
yt ctut t 1,2,L
(6.1)
其中表示均值为0的平稳随机变量。
对(6.1)两边同取期望,可得
E(yt)ct
(6.2)
(6.2)说明,只要系数不为0,则序列的 均值随时间推移而不断增大。正因为这个
特点,确定性趋势模型也称为“均值非平 稳”过程
4
2
0
-2 10 20 30 40 50 60 70 80 90 100
6
4
AR(1): alpha=0.9
2
0
-2
-4
-6 10 20 30 40 50 60 70 80 90 100
1.00 0.75 0.50 0.25 0.00 -0.25
0
ACF: Random Walk
5
10
15
20
25
于随机游走过程的一次差分 y t是一
个平稳的随机时序变量,因为 t 等于
平稳白噪音过程。
图6-4 RWD及其 一次差分后序列
200 y(t)=2+y(t-1)+e
160
120
80
40
0
25
50
75
100
5
first difference 4
3
2
1
0
-1
25
50
75
100
以上处理方法很容易拓展到高阶 单整序列。例如,假设 y t 是一个I(2) 过程,那么对其二次差分就可以获得 平稳序列,即:
E(t2j
2 tj1
L
12)
(t j)2
进而,可以获得自相关函数的表达式:
线性非平稳模型

线性非平稳模型一、非平稳时间序列与单位根过程定义:如果一个时间序列的均值或方差随时间而变化,那么,这个时间序列数据就是非平稳的时间序列数据;如果一个序列是非平稳的序列,常常称这一序列具有非平稳性。
如果时间序列t X 不满足如下平稳性定义中的一条或几条,则t X 是非平稳的序列。
平稳性定义有如下几条:(1)t X 的均值不随时间变化,()t E X =μ;(2)t X 的方差不随时间变化,22()()t t var X E X =-=μσ;(3)任何两期的t X 与t k X -之间的协方差仅依赖于这两期间隔的距离或滞后长度(k ),而不依赖于其他变量(对所有的k ),即t X 与t k X -的协方差表述为[()()]k t t k E X X +=--γμμ。
所谓时间序列的随机游走(random walk )即指下一期的值等于当期的值加上随机误差项。
我们把随机游走划分为带漂移的随机游走和不带漂移的随机游走。
非平稳性和随机游走的关系:假设t Y 由一阶自回归过程所生成:1t t t Y Y -=+γε,将1=γ代入上述方程:1t t t Y Y -=+ε, 这样定义的Y 被称为随机游走,假定时间序列从第0期开始,我们就有:01t i t i Y Y ==+∑ε001()()tt i i E Y E Y Y ==+=∑ε2()t var Y t =σ若在方程中分别加入漂移项和时间趋势项,可得到另外两种随机游走方程:1t t t Y Y -=++δε(带漂移的单位根过程),1t t tY t Y -=+++δβε(带漂移和时间趋势的单位根过程)。
二、单位根检验数据的非平稳性可能归因于一个确定性时间趋势,也可能是源自于数据生成过程中的随机游走,也许两者兼而有之,区分非平稳数据的这两种特征非常重要。
Nelson,Plosser(1982)等认为很多经济时间序列都是由单位根而不是由确定性时间趋势来更好地近似描述。
第13章单位根与协整13.1非平稳序列如果时间序列不平稳,则称为非

1© 陈强,《计量经济学及Stata 应用》,2014年。
请勿上传或散发。
第13章 单位根与协整13.1 非平稳序列如果时间序列不平稳,则称为“非平稳序列”(non-stationary time series),包括以下几种情况。
(1) 确定性趋势:如果时间序列有“确定性趋势”(deterministic trend),则为非平稳序列。
比如,01t t y t ββε=++,则01E()t y t ββ=+随时间而改变,故不是平2稳序列。
只要把时间趋势去掉,就变成平稳序列,故称为“趋势平稳”(trend stationary)序列。
(2) 结构变动(structural break):如果一个时间序列存在结构变动,则为非平稳序列。
对此,可用邹检验(Chow test)进行检验,参见第8章。
(3) 随机趋势:另一种导致非平稳的趋势为“随机趋势”(stochastic trend)。
比如,随机游走模型(random walk): 1t t t y y ε-=+其中,{}t ε为白噪声。
由于t t y ε∆=,故来自{}t ε的任何扰动3对{}t y 都具有永久性的冲击,其影响力不随时间而衰减,故称{}t ε为这个模型的“随机趋势”。
在上式中,如果包含常数项,则为“带漂移的随机游走”(random walk with drift):010,0t t t y y βεβ-=++≠其中,0β为每个时期的平均“漂移”(drift),因为01E()E()t t y y β-=+。
随机游走是AR(1)的特例。
对于AR(1),011t t t y y ββε-=++,如果11β=,则为随机游走。
只要对随机游走进行一阶差分,即可得到平稳序列,故也称为“差分平稳”(difference stationary)序列。
定义称平稳的时间序列为“零阶单整”(Integrated of order zero),记为I(0)。
非平稳时间序列分析
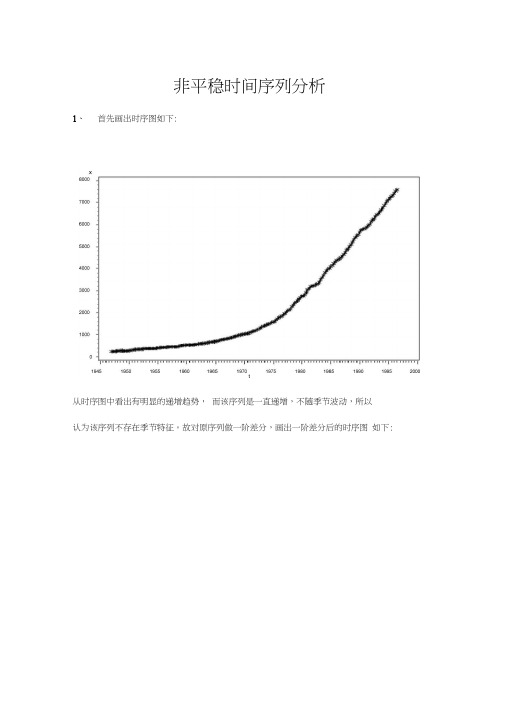
非平稳时间序列分析1、首先画出时序图如下:t从时序图中看出有明显的递增趋势,而该序列是一直递增,不随季节波动,所以认为该序列不存在季节特征。
故对原序列做一阶差分,画出一阶差分后的时序图如下:difx140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 -10从中可以看到一阶差分后序列仍然带有明显的增长趋势,再做二阶差分:dif2x90 80 70 60 50 40 30 20 10 0 -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 -110做完二阶差分可以看到,数据的趋势已经消除,接下来对二阶差分后的序列进行194519501945 19551960196519701975198019851990199520001950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000检验:AutocorrelationsLag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error0 577.333 1.00000 | |********************| 01 -209.345 -.36261 | *******| . | 0.0712472 -52.915660 -.09166 | .**| . | 0.0800693 9.139195 0.01583 | . | . | 0.0806004 15.375892 0.02663 . |* . | 0.0806155 -59.441547 -.10296 .**| . | 0.0806606 -23.834489 -.04128 | . *| . | 0.0813247 100.285 0.17370 | . |*** | 0.0814318 -146.329 -.25346 | *****| . | 0.0832909 52.228658 0.09047 | . |**. | 0.08711810 21.008575 0.03639 | . |* . | 0.08759311 134.018 0.23213 | . |***** | 0.08767012 -181.531 -.31443 | ******| . | 0.09073613 23.268470 0.04030 | . |* . | 0.09610814 71.112195 0.12317 | . |** . | 0.09619415 -105.621 -.18295 | ****| . | 0.09699116 37.591996 0.06511 . |* . | 0.09872717 23.031506 0.03989 | . |* . | 0.09894518 45.654745 0.07908 | . |** . | 0.09902719 -101.320 -.17550 | ****| . | 0.09934720 127.607 0.22103 | . |**** | 0.10090821 -61.519663 -.10656 | . **| . | 0.10333722 35.825317 0.06205 | . |* . | 0.10389323 -93.627333 -.16217 | .***| . | 0.10408124 55.451208 0.09605 | . |** . |从其自相关图中可以看出二阶差分后的序列自相关系数很快衰减为零,且都在两倍标准差范围之内,所以认为平稳,白噪声检验结果:Autocorrelation Check for White NoiseTo Chi- Pr >Lag Square DF ChiSq------------------- Autocorrelations -------------------6 30.70 6 <.0001 -0.363 -0.092 0.016 0.027 -0.103 -0.04112 84.54 12 <.0001 0.174 -0.253 0.090 0.036 0.232 -0.31418 97.98 18 <.0001 0.040 0.123 -0.183 0.065 0.040 0.07924 126.99 24 <.0001 -0.175 0.221 -0.107 0.062 -0.162 0.096P 值都小于 0.05 ,认为不是白噪声。
9时间序列模型非平稳
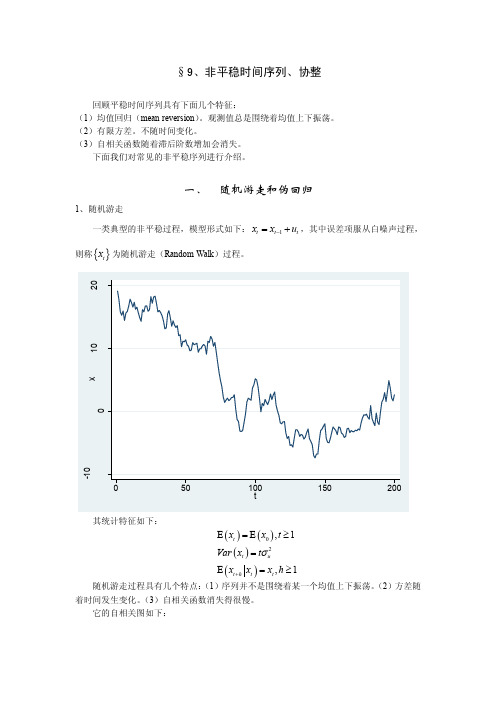
§9、非平稳时间序列、协整回顾平稳时间序列具有下面几个特征: (1)均值回归(mean reversion )。
观测值总是围绕着均值上下振荡。
(2)有限方差。
不随时间变化。
(3)自相关函数随着滞后阶数增加会消失。
下面我们对常见的非平稳序列进行介绍。
一、 随机游走和伪回归1、随机游走一类典型的非平稳过程,模型形式如下:1t t t x x u -=+,其中误差项服从白噪声过程,则称{}t x 为随机游走(Random Walk )过程。
其统计特征如下:()()()()02,1,1t t u t h t t x x t Var x t x x x h σ+E =E ≥=E =≥随机游走过程具有几个特点:(1)序列并不是围绕着某一个均值上下振荡。
(2)方差随着时间发生变化。
(3)自相关函数消失得很慢。
它的自相关图如下:下面我们来看带飘移项(drift )的随机游走过程:()2010,0,,0t t t t u x x u u WN ασα-=++~>它具有下面的统计特征:()()()020t t u t h t tx t Var x t x x h x ασα+E ==E =+2、单整如果一个平稳时间序列{}t x 经过d 次差分后才能变换为一个平稳的、可逆的ARMA 时间序列,那么我们称{}t x 具有d 阶单整性,记为:()t x d ~I 。
平稳序列,是I(0)的。
单整序列一般指单整阶数大于0的序列。
如果时间序列()(),t x a y b ~I ~I ,则[]()max ,t t t z cx dy a b =+~I 。
一般来说,()(),t x a y a ~I ~I ,()t t t z cx dy a =+~I如果z 的单整阶数小于a 时,称这两个序列存在着协整(cointegration )关系。
3.随机游走过程的统计特征()210,0,0,t t t t u x x u x u IN σ-=+=~其中u 为白噪声序列,服从独立的正态分布。
第13章非平稳时间序列模型

(13.4.3)
这里 1,因此,检验Y t 是否为单位根过 程就转而检验原假设 =0。
若 =0,则 =1,Y t 为一个单位根过程;若
<0,则 <1,Y t 是平稳的。于是我们构造原 假设H 0 : =0,备择假设H 1 : <0。
如何检验模型(13.4.3)的原假设是否成立?
p
Yt 01tYt1i Ytiut i1
(13.4.8) (13.4.9)
上述检任然是都是基于 的估计。
三、ADF检验的实例
(一)我们选择了1978~2019年江西省的商品零售价格
指数( P )和1989~2019年江西省净出口总额( EX )数
据,数据图形如图13.4.1和13.4.2。
Nelson,Plosser(1982)等认为很多经济时间序列 都是由单位根而不是由确定性时间趋势来更好 地近似描述。因此,近期广受欢迎的一种非平 稳性检验就是所谓的单位根检验。
回忆我们曾讨论方程(13.2.1)中的 值,它帮 助我们确定Y是平稳还是非平稳:
Yt Yt1t
(13.4.1)
我们已在13.2节中定义, 如果 <1时,Y t 是平
稳的;当 >1时,Y t 趋于以更快的速度爆炸性 增长,此时 Y t 称为发散过程;但当 =1,Y t 是 非平稳的且被称为单位根过程。
因此,迪基-富勒(DF)单位根检验的原理: 估计方程(13.4.1),并确定是否有 <1, 从 而判定Y t 是否是平稳的,
25 P
20
1200000 EX
1000000
15
800000
10
600000
5
400000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§13.2 非平稳时间序列与单位根过程
定义:如果一个时间序列的均值或方差随时间而 变化,那么,这个时间序列数据就是非平稳的时 间序列数据;如果一个序列是非平稳的序列,常 常称这一序列具有非平稳性。 如果时间序列 X t不满足如下平稳性定义中的一条 或几条,则 X t 是非平稳的序列。
平稳性定义 X (1) t 的均值不随时间变化,
(13.3.8)
可以看出, Yt含有时间趋势,因此 Yt的均值随时间而 变化, Yt是非平稳的。要使 Yt 变成平稳,需要对其 进行除趋势处理。也就是说,Yt 是趋势平稳过程。
二、趋势平稳的检验方法
实际研究中一个简单的区分趋势平稳和差分平稳的 方法,就是从数据中去除其所含有的确定性部分, 然后检验其剩余部分是单位根过程还是平稳过程。 如果剩余部分是单位根过程,则说明该数据本身是 差分平稳,否则该数据就是趋势平稳过程。 例如,对如下模型做回归:
Yt 0 Yt 1 t
(13.3.4)
这是一个带漂移的随机游走过程,是非平稳的单位 根过程,将其写成差分的形式:
Yt ( Yt Yt 1 ) 0 t
0
(13.3.5)
这意味着时间序列的变化( Y t )除了受 的影响外, 还受误差项 t 的影响,并且 Y t 将把以前时期的 t 值 累积起来,随机误差项对 Y t 的这种累积效应被称为 随机趋势。 带漂移的单位根过程也是差分平稳的。
k E [( X t )( X t k )]
所谓时间序列的随机游走(random walk)即指下一期 的值等于当期的值加上随机误差项。我们把随机游走划 分为带漂移的随机游走和不带漂移的随机游走。 非平稳性和随机游走的关系 : 假设 Y t 由一阶自回归过程所生成:
i 1
t
i
) Y0
(13.2.4) (13.2.5)
var (Yt ) t
2
方程(13.2.2)中没有截距项(这里称为漂移项) 和时间趋势项,若在方程中分别加入漂移项 和时间趋势项,可得到另外两种随机游走方 程:
Yt Yt 1 t Yt t Yt 1 t
Y t Y t 1 i Y t i u t
i 1 p
Y t 0 Y t 1 i Y t i u t
i 1 p
(13.4.8)
Y t 0 1t Y t 1 i Y t i u t
E(Xt)
(2)X t 的方差不随时间变化,
va r ( X t ) E ( X t )
2 2
(3)任何两期的 X t 与 X t k 之间的协方差仅依赖于这 两期间隔的距离或滞后长度( k),而不依赖于其他 变量(对所有的 k),即 X t与 X t k 的协方差表述为
回忆我们曾讨论方程(13.2.1)中的 值,它帮 助我们确定Y是平稳还是非平稳:
Yt Yt 1 t
(13.4.1)
Y 我们已在13.2节中定义, 如果 <1时, t 是平 Y 稳的;当 >1时,t 趋于以更快的速度爆炸性 增长,此时 Y t 称为发散过程;但当 =1,t 是 Y 非平稳的且被称为单位根过程。 因此,迪基-富勒(DF)单位根检验的原理: 估计方程(13.4.1),并确定是否有 <1, 从 而判定 Y t 是否是平稳的,
Yt ( Yt Yt 1 ) t
(13.3.3)
由于随机误差项( t)是平稳的,因此, Y t 是平稳的。 换言之,一个不带漂移的随机游走是一个差分平稳 过程。
(2)在模型(13.3.1)中,若 0 0 , 1 0 , 2 1, 则 可以得到:
0 1
0 1
t
(4)在模型(13.3.1)中,若 0 0 , 1 0 , 2 1, 则 可以得到:
Yt 0 1t Yt 1 t
(13.3.7)
这是一个带漂移和时间趋势的随机游走,将模型 (13.3.7)转化成差分的形式:
Yt 0 1 t t
第十三章
非平稳时间序列模型
13.1 认识非平稳的数据特征 13.2 非平稳时间序列与单位根过程 13.3. 趋势平稳和差分平稳过程 13.4 单位根检验 13.5 ARIMA模型 13.6 谬误回归 13.7 协整与误差校正模型 13.8 我国商业银行利率的协整分析
前言
在前面的章节中,所阐述的有关时间序列数据模型 的内容都假定数据是平稳的,那么,实际经济中的 数据有没有可能是非平稳的?如何检验时间序列数 据的非平稳性? 特别是,如果我们面对的是非平稳的数据,原有的 基于平稳数据而建立的分析方法是否仍然适用?如 果不适用,我们就应该针对非平稳数据的特征,提 出新的分析方法。本章我们将系统阐述非平稳性的 概念、估计与检验方法。
Yt 0 1t 2 Yt 1 t
(13.3.1)
(1)在模型(13.3.1)中,若 0 0 , 1 0 , 2 1, 则 可以得到:
Yt Yt 1 t
(13.3.2)
模型(13.3.2)是一个不带漂移和时间趋势项的随机游 走,是非平稳的单位根过程,对其取差分的形式, 得到:
首先,在方程(13.4.1)两边同时减去Y t 1 , 得到:
Yt Yt 1 Yt 1 Yt 1 t ( 1)Yt 1 t
t t t 1
(13.4.2)
定义 Y Y Y ,我们就得到迪基-富勒 (DF)检验最简单的表达式:
i 1
(13.4.9)
上述检任然是都是基于 的估计。
三、ADF检验的实例
(一)我们选择了1978~2007年江西省的商品零售价格 指数( P )和1989~2007年江西省净出口总额( EX )数 据,数据图形如图13.4.1和13.4.2。
图13.4.1:商品零售价格指数
图13.4.2:净出口总额
Yt Yt 1 v t
(13.4.3)
这里 1 ,因此,检验 Y t 是否为单位根过 程就转而检验原假设 =0。 Y 若 =0,则 =1, t 为一个单位根过程;若 Y <0,则 <1,t 是平稳的。于是我们构造原 假设 H 0 : =0,备择假设 H 1 : <0。
二、扩展的迪基-富勒(ADF)检验
考虑误差项存在序列相关,对迪基-富勒检验方程的设定形 式进行相应修正:将 Y t若干阶差分的滞后项作为迪基-富 勒检验方程中的解释变量,这种情形的DF检验被称为增广的 迪基-富勒(ADF)检验。对应三种不同形式的DF检验,ADF检 p 验为: (13.4.7)
(13.2.6)
(13.2.7)
方程(13.2.6)称为带漂移的单位根过程,方程 (13.2.7)称为带漂移和时间趋势的单位根过程。
认识数据特征:平稳数据和几种单位跟数据
图13.2.1: Yt 0.6 Yt 1 t
图13.2.2: t Yt 1 t Y
Y 图13.2.3: t 1 Yt 1 t
与三种随机游走时间序列相对应的三种形式的 DF检验形式:
Yt Yt 1 u t
(13.4.4) (13.4.5) (13.4.6)
Yt 0 Yt 1 u t
Yt 0 1 t Yt 1 u t
不论我们采用哪种形式的迪基-富勒检验,判 断法则都是基于 的估计。 注意:检验原假设 =0的 检验随DF检验形式 的不同而不同,所对应统计量的临界值也不相 同,认识这点非常重要。
Yt 0 1t t
t t 0 1
(13.3.9) ˆ t ,再检验 ˆ 的平稳性, 基于检验结果判断 Y 是否趋势平稳。
t
§13.4 单位根检验
一、迪基-富勒(DF)检验
数据的非平稳性可能归因于一个确定性时间趋 势,也可能是源自于数据生成过程中的随机游 走,也许两者兼而有之,区分非平稳数据的这 两种特征非常重要。 Nelson,Plosser(1982)等认为很多经济时间序列 都是由单位根而不是由确定性时间趋势来更好 地近似描述。因此,近期广受欢迎的一种非平 稳性检验就是所谓的单位根检验。
如何检验模型(13.4.3)的原假设是否成立?
在原假设 H 0下,估计的Y t 1的回归系数的t统计值即 使在大样本下也不服从t分布,因此,使用通常的t 检验无法检验原假设是否成立。 迪基-富勒的解决办法:在原假设 <0下,使用模 型(13.4.3)中系数 的通常t型统计量,但极限分布 不同于t分布,将这时的t统计量称之为 统计量。 迪基-富勒使用蒙特卡罗仿真实验计算了 统计量 极限分布的临界值,麦金农(MacKinnon)计算了更 为全面的极限分布临界值表,常用的计量软件都 带有。
Y 图13.2.4: t 1 0.3 t Yt 1 t
§13.3. 趋势平稳和差分平稳过程
一、趋势平稳和差分平稳的数据生成过程
图13.1.1中我国的名义GDP表现出很强的趋势,这 种趋势是随机性的还是确定性的呢?还是两者兼而 有之呢?为清楚理解这一问题的含义,考虑如下模 型:
针对商品零售价格指数没有明显确定趋势的数据特征,设定ADF 检验模型为: p p p u (13.4.10)
q t t 1 i ti t i 1
使用Eviews5对 P 进行ADF检验,其中滞后期q是根据最小AIC准则 确定为0,检验方程估计得到: ˆ Pt 0 .2 4 Pt 1 u t t = (-1.946) Eviews5检验结果输出表为:
