时间序列分析模型实例
《时间序列分析 》课件

详细描述
股票价格时间序列数据具有波动性和趋势性,通过计算 相关统计量,如均值、方差、自相关图等,可以分析股 票价格的变动规律。同时,利用ARIMA、SVM、LSTM 等时间序列分析模型,可以对股票价格进行预测,为投 资者提供决策依据。
04
时间序列的预测
预测的种类和步骤
种类
时间序列预测可以根据不同的标准进行分类,如预测方法的性质可以分为定量预测和定性预测,预测 的时间跨度可以分为长期预测、中期预测和短期预测等。
步骤
时间序列预测通常包括以下几个步骤:数据收集和整理、数据分析和处理、模型选择和建立、模型评 估和优化、预测结果分析和应用。
人口数量时间序列分析
总结词
人口数量时间序列分析是研究人口数量 随时间变化的过程,通过分析历史数据 来预测未来人口走势。
VS
详细描述
人口数量时间序列数据具有趋势性和周期 性,通过计算相关统计量,如增长率、年 龄结构、性别比例等,可以分析人口数量 的变动规律。同时,利用ARIMA、 Logistic模型等时间序列分析模型,可以 对人口数量进行预测,为政策制定和资源 分配提供决策依据。
要点二
实例2
气候变化预测:利用时间序列分析方法,对历史气候数据 进行分析,建立气候变化的时间序列模型,对未来的气候 变化趋势进行预测。
05
时间序列分析软件介绍
EViews软件介绍
总结词
EViews是一款专门用于时间序列分析和预测的软件,具有强大的数据处理和模型估计 功能。
详细描述
EViews提供了丰富的计量经济学模型和统计方法,包括ARIMA、SARIMA、VAR、 VECM等时间序列分析模型,以及回归分析、方差分析、假设检验等统计方法。它还支 持多种数据导入导出格式,如Excel、CSV、Stata等,方便用户进行数据管理和分析。
时间序列分析 滑动平均模型和自回归滑动平均模型

定义1.1 设{t }是 WN(0, 2) ,如果实数
b1, b2 , bq (bq 0) 使得
则称
q
B(z) 1 bj z j 0,| z | 1, j 1
q
X t t bjt j , t Z
(1.2)
j 1
是q阶滑动平均模型,简称为MA(q)模型;
称由(1.2)决定的平均序列 {Xt} 是滑动平 均模型,简称为MA(q)序列。
自相关系数
1 2 (b1 b1b2 ), k 0, k 2
1
1
b1 b12
b1b2 b22
, 2
1
b2 b12
b22
, k
0, k
2.
谱密度
f
()
2 2
|1 b1ei
b2ei2
|2
MA(2)序列的实际例子
MA(2)的实际例子:
Xt t 0.36t1 0.85t2
特征根为 1.084652ei1.374297 。
滑动平均模型的例子
每隔两小时记录的化学反应数据时间序 列{Xt ,t 1, 2, 197}。
一阶差分得
yt xt xt1,t 2, ,197
{yt}的样本自相关系数列呈现截尾性。
可以拟合
^
Yt t b t1, t Z
模型特点是k } 1步截尾
(1.1)
MA(q)模型和MA(q)序列
单位圆上可能有根的一般情况可以用 hilbert空间预测的方法证明。
MA(q)系数的计算
MA(q)序列的系数 (b1,b2, ,bq )及 2可以被
数 0 ,1, , q 唯一确定。 可以用文献 [5]方法计算模型参数。
MA(q)系数的计算
利用时间序列分析预测股票价格

利用时间序列分析预测股票价格预测股票价格是股市参与者一直以来的关注焦点之一。
通过利用时间序列分析,我们可以借助过去的股票数据,揭示股票价格的趋势和模式,并进一步预测未来股票价格的走势。
本文将介绍时间序列分析在股票价格预测中的应用,并提供几种常用的时间序列模型以及实际应用案例来支持我们的讨论。
时间序列分析是一种通过观察值随时间变化的模式来分析数据的方法。
对于股票价格预测,我们需要的数据是按时间顺序记录的股票价格。
这些价格可能显示出趋势(如上涨或下跌)、季节性变化或其他周期性模式。
我们将使用这些数据来构建模型,然后使用该模型来预测未来股票价格。
在时间序列分析中,我们将首先检查数据是否呈现趋势或季节性变化。
如果数据具有明显的趋势,我们可以使用移动平均方法或指数平滑方法来去除趋势。
移动平均方法通过计算在一段时间内的平均值来估计趋势。
指数平滑方法则更加关注最近的数据,并使用指数加权平均值来估计趋势。
这些方法都可以有效地消除趋势并揭示数据中的其他模式。
在处理季节性数据时,我们可以使用季节性分解。
这种方法将数据分解成趋势、季节性和残差三个部分。
趋势部分代表长期变化趋势,季节性部分代表短期循环变化,而残差部分则是未被趋势和季节性解释的部分。
通过分析这三个部分,我们可以更好地理解数据中的季节性模式,并使用它们来进行预测。
除了趋势和季节性模式,时间序列数据还可能包含随机波动和自相关结构。
为了捕捉这些特征,我们可以使用自回归移动平均模型(ARMA)或自回归积分移动平均模型(ARIMA)。
这些模型考虑了过去时点的观察值与当前时点观察值之间的关系,并使用这些关系来预测未来的观察值。
除了上述基本模型之外,时间序列分析还包括更复杂的模型,如季节性自回归整合移动平均模型(SARIMA),以及自回归条件异方差模型(ARCH)和广义自回归条件异方差模型(GARCH)。
这些模型考虑了数据中的非线性、异方差性和不同尺度的波动,并更准确地预测股票价格的变动。
金融时间序列分析-ARIMA模型建模实验报告
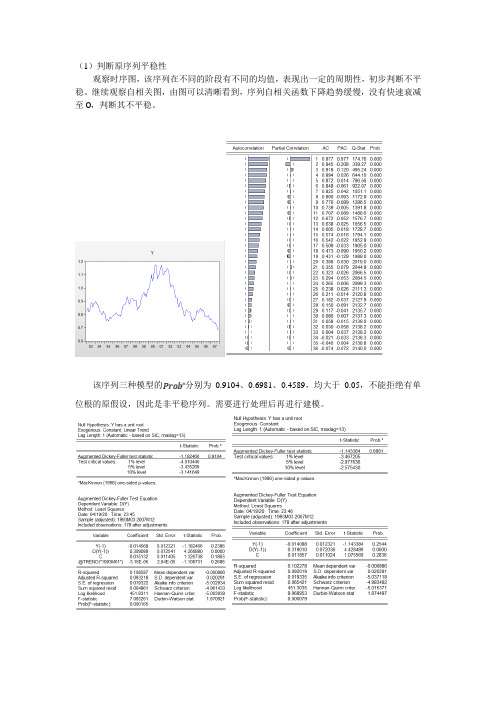
(1)判断原序列平稳性观察时序图,该序列在不同的阶段有不同的均值,表现出一定的周期性,初步判断不平稳。
继续观察自相关图,由图可以清晰看到,序列自相关函数下降趋势缓慢,没有快速衰减至0,判断其不平稳。
该序列三种模型的分别为0.9104、0.6981、0.4589,均大于0.05,不能拒绝有单位根的原假设,因此是非平稳序列。
需要进行处理后再进行建模。
(2)差分序列平稳性检验对原序列进行一次差分,再对其进行平稳性检验。
观察其时序图,该序列的时序图都表现出围绕其水平均值不断波动的过程,没有明显的趋势或周期性,粗略估计是平稳时间序列。
再观察其自相关函数图。
自相关系数快速衰减到0,在虚线范围内波动,没有明显的波动、发散,判断为平稳序列。
模型3与模型2的伴随概率为0,拒绝有单位根的原假设,说明序列是平稳的。
但模型3的时间趋势项的伴随概率为0.1789,常数项的伴随概率0.3504,在显著性水平0.05情况下不显著,故不选用。
而模型2的常数项的伴随概率为0.6608,也不显著,不选用。
因此模型1是最合适的模型,不含有常数项和时间趋势项。
(3)模型的参数估计及模型的诊断检验观察自相关图最后两列可以看到,Q检验的伴随概率均小于0.05,拒绝没有自相关性的原假设,因此该序列不是白噪声序列,没有把信息都提取出来。
接下来将尝试使用AR(1)、AR(2)、AR(3)、MA(1)、ARMA(1,1)、ARMA(2,1)模型进行拟合。
(1)AR(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,拒绝没有自相关性的原假设,不是白噪声序列,不选用。
(2)AR(2):。
该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列,可以选用。
(3)AR(3):该模型各项不显著,不选用。
(4)MA(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列,可以选用。
时间序列的分解分析

时间序列的分解分析时间序列分解分析是一种对时间序列数据进行分析和预测的方法,能够揭示时间序列数据中的趋势、季节性和不规则成分。
本文将介绍时间序列分解分析的基本原理、方法和应用,并结合实例进行详细阐述。
一、时间序列分解分析的基本原理时间序列是指按照时间顺序排列的一系列观测数据。
时间序列分解分析是将时间序列数据分解为趋势、季节性和不规则成分,以便更好地了解和预测数据的变化规律。
时间序列分解分析的基本原理是将时间序列数据表示为多个相互独立的成分之和,即y(t) = T(t) + S(t) + I(t)其中,y(t)表示时间序列数据,在某一时间点t的取值;T(t)表示趋势成分,描述数据随时间的长期变化趋势;S(t)表示季节性成分,描述数据在一定周期内的周期性变化;I(t)表示不规则成分,描述数据中的随机波动。
二、时间序列分解分析的方法1. 加法模型和乘法模型时间序列分解分析可以采用加法模型或乘法模型。
加法模型适用于季节性变化相对稳定、幅度相对固定的数据;乘法模型适用于季节性变化幅度随时间变化的数据。
加法模型可以表示为y(t) = T(t) + S(t) + I(t)乘法模型可以表示为y(t) = T(t) × S(t) × I(t)2. 移动平均和中心移动平均时间序列分解分析中常用的方法是移动平均和中心移动平均。
移动平均是用一组连续的数据点的平均值来代表该数据点,以平滑数据的波动;中心移动平均是将每个数据点替换为该数据点前后一段时间内数据的平均值。
通过移动平均和中心移动平均可以得到趋势成分的估计值。
3. X-11分析X-11分析是一种常用的季节性调整方法,适用于季节性变化相对稳定的时间序列数据。
X-11分析逐步消除季节性、趋势和不规则成分,得到经过季节性调整后的时间序列数据。
三、时间序列分解分析的应用时间序列分解分析是一种重要的时间序列分析方法,被广泛应用于经济学、金融学、气象学、环境科学等领域。
时间序列分析模型——ARIMA模型

时间序列分析模型——ARIMA模型时间序列分析模型——ARIMA模型⼀、研究⽬的传统的经济计量⽅法是以经济理论为基础来描述变量关系的模型。但经济理论通常不⾜以对变量之间的动态联系提供⼀个严密的说明,⽽且内⽣变量既可以出现在⽅程的左端⼜可以出现在⽅程的右端使得估计和推断变得更加复杂。为了解决这些问题⽽出现了⼀种⽤⾮结构⽅法来建⽴各个变量之间关系的模型,如向量⾃回归模型(vector autoregression,VAR)和向量误差修正模型(vector error correctionmodel,VEC)。
在经典的回归模型中,主要是通过回归分析来建⽴不同变量之间的函数关系(因果关系),以考察事物之间的联系。本案例要讨论如何利⽤时间序列数据本⾝建⽴模型,以研究事物发展⾃⾝的规律,并据此对事物未来的发展做出预测。研究时间序列数据的意义:在现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其⾃⾝发展的规律。在现实中很多问题,如利率波动、收益率变化、反映股市⾏情的各种指数等通常都可以表达为时间序列数据,通过研究这些数据,发现这些经济变量的变化规律(对于某些变量来说,影响其发展变化的因素太多,或者是主要影响变量的数据难以收集,以⾄于难以建⽴回归模型来发现其变化发展规律,此时,时间序列分析模型就显现其优势——因为这类模型不需要建⽴因果关系模型,仅需要其变量本⾝的数据就可以建模),这样的⼀种建模⽅式就属于时间序列分析的研究范畴。⽽时间序列分析中,ARIMA模型是最典型最常⽤的⼀种模型。
⼆、ARIMA模型的原理1、ARIMA的含义。ARIMA包含3个部分,即AR、I、MA。AR——表⽰auto regression,即⾃回归模型;I——表⽰integration,即单整阶数,时间序列模型必须是平稳性序列才能建⽴计量模型,ARIMA模型作为时间序列模型也不例外,因此⾸先要对时间序列进⾏单位根检验,如果是⾮平稳序列,就要通过差分来转化为平稳序列,经过⼏次差分转化为平稳序列,就称为⼏阶单整;MA——表⽰moving average,即移动平均模型。可见,ARIMA模型实际上是AR模型和MA模型的组合。
时间序列分析教程(四)AR与MA模型详细分析(公式推导慎入)

时间序列分析教程(四)AR与MA模型详细分析(公式推导慎入)时间序列分析中,AR模型(Autoregressive Model)和MA模型(Moving Average Model)是两种常用的模型类型。
本教程将详细介绍AR和MA模型的公式推导,让读者更好地理解其原理和应用。
首先,我们先来解释AR和MA模型的概念。
AR模型是一种基于时间序列过去的值来预测未来值的模型。
AR模型的基本思想是当前值与过去若干个时间点的值相关,即当前值是过去值的加权和。
AR模型的表示形式为AR(p),其中p表示过去时间点的数量。
MA模型是一种基于时间序列过去的误差项来预测未来值的模型。
MA 模型的基本思想是当前值与过去若干个时间点的误差项相关,即当前值是过去误差的加权和。
MA模型的表示形式为MA(q),其中q表示过去误差的数量。
下面我们将对AR和MA模型的公式进行推导。
一、AR模型的公式推导假设我们有一个时间序列{Y_t},其中Y_t表示时间点t的值。
AR(p)模型的一般形式为:Y_t=c+ϕ₁Y_(t-1)+ϕ₂Y_(t-2)+...+ϕ_pY_(t-p)+ε_t其中c是常数项,ϕ₁、ϕ₂、..、ϕ_p是过去时间点的权重系数,ε_t 是一个白噪声误差项。
为了方便推导,我们将AR(p)模型简化为AR(1)模型,即只考虑过去一个时间点的值。
即:Y_t=c+ϕY_(t-1)+ε_t我们首先假设时间序列{Y_t}是平稳的,即均值和方差不随时间变化。
然后,我们将AR(1)模型代入Y_(t-1)的表达式中,得到:Y_t=c+ϕ(c+ϕY_(t-2)+ε_(t-1))+ε_t展开后整理得:Y_t=c(1+ϕ)+ϕ²Y_(t-2)+ϕε_(t-1)+ε_t再次代入Y_(t-2)的表达式中,得到:Y_t=c(1+ϕ+ϕ²)+ϕ³Y_(t-3)+ϕ²ε_(t-2)+ϕε_(t-1)+ε_t以此类推,我们可以得到AR(1)模型的一般表达式:Y_t=c(1+ϕ+ϕ²+...+ϕ^p-1)+ϕ^pY_(t-p)+ϕ^(p-1)ε_(t-p+1)+...+ϕ²ε_(t-2)+ϕε_(t-1)+ε_t其中,c(1+ϕ+ϕ²+...+ϕ^p-1)是常数项,ϕ^pY_(t-p)是过去p个时间点的加权和,ϕ^(p-1)ε_(t-p+1)、..、ϕ²ε_(t-2)、ϕε_(t-1)和ε_t是误差项。
时间序列建模案例VAR模型分析报告与协整检验

传统的经济计量方法是以经济理论为基础来描述变量关系的模型。
但是,经济理论通常并不足以对变量之间的动态联系提供一个严密的说明,而且内生变量既可以出现在方程的左端又可以出现在方程的右端使得估计和推断变得更加复杂。
为了解决这些问题而出现了一种用非结构性方法来建立各个变量之间关系的模型。
本章所要介绍的向量自回归模型(vector autoregression ,VAR)和向量误差修正模型(vector error correction model ,VEC)就是非结构化的多方程模型。
向量自回归(VAR)是基于数据的统计性质建立模型,VAR 模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。
VAR 模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,并且在一定的条件下,多元MA 和ARMA 模型也可转化成VAR 模型,因此近年来VAR 模型受到越来越多的经济工作者的重视。
VAR(p ) 模型的数学表达式是t=1,2,…..,T其中:yt 是 k 维内生变量列向量,xt 是d 维外生变量列向量,p 是滞后阶数,T 是样本个数。
k ⨯k 维矩阵Φ1,…, Φp 和k ⨯d 维矩阵H 是待估计的系数矩阵。
εt 是 k 维扰动列向量,它们相互之间可以同期相关,但不与自己的滞后值相关且不与等式右边的变量相关,假设 ∑ 是εt 的协方差矩阵,是一个(k ⨯k )的正定矩阵。
11t t p t p t t --=+⋅⋅⋅+++y Φy Φy Hx ε注意,由于任何序列相关都可以通过增加更多的yt 的滞后而被消除,所以扰动项序列不相关的假设并不要求非常严格。
以1952一1991年对数的中国进、出口贸易总额序列为例介绍VAR 模型分析,其中包括;① VAR模型估计;②VAR模型滞后期的选择;③VAR模型平隐性检验;④VAR模型预侧;⑤协整性检验VAR模型佑计数据Lni(进口贸易总额), ,Lne的时间序列见图。
时间序列分析模型

时间序列分析模型时间序列分析是一种广泛应用于统计学和经济学领域的建模方法,用于研究随时间变化的数据。
它的目的是揭示和预测数据中隐含的模式和关系,以便更好地理解和解释现象,并做出相应的决策。
时间序列分析模型可以分为统计模型和机器学习模型两类。
一、统计模型1.平稳时间序列模型:平稳时间序列是指在统计学意义上均值和方差都是稳定的序列。
常用的平稳时间序列模型包括:自回归移动平均模型(ARMA)、自回归整合移动平均模型(ARIMA)和季节性自回归整合移动平均模型(SARIMA)等。
-自回归移动平均模型(ARMA)是根据时间序列数据的自相关和移动平均性质建立的模型。
它将序列的当前值作为过去值的线性组合来预测未来值。
ARMA(p,q)模型中,p表示自回归项的阶数,q表示移动平均项的阶数。
-自回归整合移动平均模型(ARIMA)在ARMA模型基础上引入差分操作,用于处理非平稳时间序列。
ARIMA(p,d,q)模型中,d表示差分的次数。
-季节性自回归整合移动平均模型(SARIMA)是ARIMA模型的扩展,在存在季节性变化的时间序列数据中应用。
SARIMA(p,d,q)(P,D,Q)s模型中,s表示季节周期。
2.非平稳时间序列模型:非平稳时间序列是指均值和/或方差随时间变化的序列。
常用的非平稳时间序列模型包括:趋势模型、季节性调整模型、自回归积分滑动平均模型(ARIMA)和季节性自回归积分滑动平均模型(SARIMA)等。
- 趋势模型用于描述数据中的趋势变化,例如线性趋势模型(y = ax + b)和指数趋势模型(y = ab^x)等。
-季节性调整模型用于调整季节性变化对数据的影响,常见的方法有季节指数调整和X-12-ARIMA方法。
-自回归积分滑动平均模型(ARIMA)和季节性自回归积分滑动平均模型(SARIMA)在非平稳时间序列中引入差分操作进行模型建立。
二、机器学习模型机器学习模型在时间序列分析中发挥了重要作用,主要应用于非线性和高维数据的建模和预测。
时间序列分析:方法与应用(第二版)传统时间序列分析模型

型。
例1.1
9
例1.1
Y
3,000 2,500 2,000 1,500 1,000
500 0 1955 1960 1965 1970 1975 1980
社会商品零售总额时序图 10
例1.2
Y
9,000 8,000 7,000 6,000 5,000 4,000 3,000 2,000 1,000
10,000
9,000
8,000
7,000
6,000
5,000
4,000 1995
1996
1997
1998
1999
2000
Y
YY
37
为评价模型的预测效果,也可以象例1.12一样, 预留部分数据作为试测数据,评价模型的适用性。
38
fi 为季节指数
T为季节周期的长度,4或12
26
2. 适用条件:
既有季节变动,又有趋势变动 且波动幅度不断变化的时间序列
至少需要5年分月或分季的数据
3. 应用
例1.12 我国工业总产值序列
27
1)时序变化分析 绘制时序曲线图
明显的线性增长趋势、季节波动,且波动幅度随趋 势的增加而变大。
Y
6,000
3. 应用
例1.13 我国社会商品零售总额的分析预测
33
1)时序变化分析 绘制时序曲线图
明显的线性增长趋势、季节波动,且波动幅度随趋势 的增加基本不变。
Y
10,000
9,000
8,000
7,000
6,000
5,000
4,000
1995
1996
python arima应用实例

标题:Python ARIMA 应用实例一、简介1.1 ARIMA 模型概述自回归综合移动平均模型(Autoregressive Integrated Moving Average,ARIMA)是一种用于时间序列预测和分析的经典统计模型。
ARIMA 模型能够较好地拟合时间序列数据,并对未来的走势进行预测,因此在金融、经济、气象等领域被广泛应用。
1.2 Python 中的 ARIMA 实现Python 提供了丰富的工具包,如 statsmodels 和 pmdarima,用于实现 ARIMA 模型。
这些工具包能够帮助我们进行时间序列分析,提供了方便的函数和方法来拟合 ARIMA 模型并进行预测。
二、实例分析2.1 数据准备我们以股票价格时间序列数据为例,演示如何使用 Python 中的ARIMA 模型进行分析和预测。
我们需要准备相关的股票价格数据,可以从各大财经全球信息站或数据接口获取。
2.2 模型拟合接下来,我们使用Python 中的工具包对股票价格时间序列进行拟合。
通过选择合适的 ARIMA 模型阶数(p, d, q),并使用最小二乘法进行参数估计,可以得到拟合后的模型。
2.3 模型诊断拟合完成后,需要对模型进行诊断,检验是否满足模型假设和条件。
我们可以通过观察残差序列、自相关性和偏自相关性等统计指标,来评估模型的拟合效果。
2.4 预测应用我们使用拟合好的 ARIMA 模型进行未来股票价格的预测。
通过将历史数据传入模型,并调用预测函数,可以得到未来一段时间内股票价格的预测值。
三、实践及效果3.1 实际案例我们可以选择一只具有代表性的股票,如腾讯、阿里巴巴等,进行实际应用。
通过历史数据的拟合和预测,可以观察模型的效果和准确性,评估其在实际应用中的表现。
3.2 效果评估在实际应用中,我们可以使用一些指标来评估 ARIMA 模型的预测效果,如均方根误差(RMSE)、平均绝对误差(MAE)等。
这些指标可以帮助我们了解模型的预测精度和稳定性。
宁波市镇海区伤寒疫情ARIMA时间序列模型分析

! : , … 一 { ' ~
….… ‘
~ … …
. 一
:
’
釜 溪 :曼 篓 鼎 ;茹 箍鎏繁强 臻 饕 ’ 叠 囊 嚣 量 餐
结 果
1 分 析 前 数 据 处 理 由 于 18 ~20 9 5 05年 宁 波 市 镇 海 区 伤 寒 疫情 数据 没有 出 现 丢 失 现 象 ,又 考 虑 到 伤 寒 疫 情 的 发 病 跟 该 区 的发 病 率 有 季 节 上 的 联 系 , 因 此 考 虑 采 用 季 节 发 病 率 进 行 时 问 序 列 分 析 。对 该数 据 按 季 节 进 行 建 立 时 间 变 量 。 由于 部 分 季 节 的 发 病 率 为 0 ,故 把 所 有 的 发 病 率 均 加 0 0 . 5
疫情 发展 拟合 度 欠 佳 ,如 19 第 二 季 度 伤 寒 的 实 际 发 病 90年 率为 179 /0万 ,但 是 实 际 拟 合 为 37/0万 , 相 差 了 2 .4 1 .6 1 3 .3 ,误 差 比较 大 ,从 图形 上 看 但 是 对 19 —20 30 倍 91 03年 间 的伤 寒 吻合 率 较 高 ,能 够 较 好 的 反 映 真 实 情 况 ,但 是 当 疫 情 有 大 的 波 动 时 ,预 测 也 发 生 了一 定 的 偏 差 。 在 应用 A I RMA模 型 中 ,对 各 种 具 体 的 A I RMA要 进 行 多 次 核 算 ,不 能 一 次 确定 具 体 的 模 型 。模 型 识 别 、参 数 估 计 、 检 验 修 正 三 个 过 程 之 间 相 互 作 用 、相 互 影 响 ,有 时 需 要 交 叉 进 行 、反 复 实 验 ,才 能 最 终 确 定 模 型 形 式 ,这 对 应 用 A I A模 型 在 传 染 病 疫 情 中 的 预 测 带 来 了一 定 的 困 难 。 但 RM 是 随 着 这 些 A I A模 型 不 断 地 正 确 应 用 ,相 信 ,A I RM RMA数
应用Excel进行时间序列分析

三、移动平均模型和指数平滑模型
指数平滑得叠代算法
Ft1 Yt (1 )Ft
Yt : 时间序列观测值
Ft : 时间序列预测值
Ft1 Ft (Yt Ft )
Yt : 时间序列观测值
Ft : 时间序列预测值
实例:指数平滑模型
【例2】利用例1得数据在Excel工作表中建立一个 指数平滑预测模型来预测第13周得汽油销量。
将包括当前时刻在内得N个时间点上得观测值得平均值作 为对于下一时刻得预测值(N应选择得使MSE极小化)
Ft 1
1 N
N
Yt i 1
i 1
实例:移动平均模型
【例1】某汽油批发商在过去12周内汽油得销售数量如 表所示:
周 销量(千加仑) 周 销量(千加仑)
1
17
7
22
2
21
8
18
3
19
9
22
4
23
第三步,评价模型准确性,确定最优模型参数
MSE
1 n
n t 1
et2
1 n
n t 1
(Yt
Ft )2
第四步,按要求进行预测
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
三、移动平均模型和指数平滑模型
适用于围绕一个稳定水平上下波动得时间序列。
1、移动平均模型
利用平均使各个时间点上得观测值中得随机因素互相抵消 掉,以获得关于稳定水平得预测
实例:季节指数模型
【例7】某工厂过去4年得空调机销量如下表所示,这
些数据有明显得季节性波动,试建立一个季节指数模 型来预测第5年每个季度得空调机销量 。
四年内每季度得电视机销量表
年 季度 销量(千台) 年 季度 销量(千台)
时间序列分析VAR模型实验精修订

时间序列分析V A R模型实验GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-基于VAR模型的我国房地产市场与汇率波动的因果关系————VAR模型实验第一部分实验分析目的及方法现选取人民币对美元汇率以及商品房房价作为变量构建VAR模型。
对于不满足单位根检验的序列采取对数化或差分处理,使其成为平稳序列再进行模型的拟合。
对于商品房房价这一变量,由于全国各省市差异较大,故此处采用全国房地产开发业综合景气指数这一变量。
此外,为了消除春节假期不固定因素带来的影响,增强数据的可比性,按照国家统计制度,从2012年起,不单独对1月份统计数据进行调查,1-2月份数据一起调查,一起发布。
所以国房景气指数p这一序列缺少每年一月份的相关数据,属于非随机、不可忽略缺失,在此采用平均值填充的方法,补足数据。
第二部分实验样本2.1数据来源数据来源于中经网统计数据库。
具体数据见附录表。
2.2所选数据变量由于我国于2005年7月实行第二次汇改,此次汇改以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度取代了过去人民币汇率长达10年的紧盯美元的固定汇率体制。
故本实验拟选取2005年07月到2014年10月我国以月为单位的数据。
,用以上两个变量来构建VAR模型,并利用该模型进行分析预测。
第四部分模型构建4.1判断序列的平稳性首先绘制出E的折线图,结果如下图:图4.1 汇率E的曲线图从图中可以看出,汇率E序列较强的趋势性,由此可以初步判断该序列是非平稳的。
为了减少m的变动趋势以及异方差性,先对m进行对数化处理,记为lm,其时序图如下:图4.2 lm的曲线图对数化后的趋势性减弱,但仍存在一定的趋势性,下面对lm进行一阶差分处理,去除趋势性,得到新变量dlm,观察dlm的曲线图。
图4.3 DLE的曲线图从图中可以看出,dle序列的趋势性基本已经消除,且新变量dle基本围绕0上下波动,因此选择形式为yt =yt-1+ut进行单位根检验:表4.1 单位根输出结果Null Hypothesis: DLE has a unit rootExogenous: ConstantLag Length: 2 (Automatic - based on SIC,maxlag=12)t-Statistic Prob.*Augmented Dickey-Fuller teststatistic-3.0316730.0351Test criticalvalues:1% level-3.4919285% level-2.88841110%level-2.581176*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test Equation Dependent Variable: D(DLE)Method: Least SquaresDate: 11/15/14 Time: 20:20Sample (adjusted): 2005M11 2014M10Included observations: 108 after adjustmentsVariable CoefficientStd.Errort-Statistic Prob.DLE(-1)-0.3530050.116439-3.0316730.0031D(DLE(-1))-0.5027300.115417-4.3557680.0000D(DLE(-2))-0.3115310.093265-3.3402580.0012C-0.0008880.000470-1.8875920.0619R-squared0.450240M ean dependent var 1.15E-05Adjusted R-squared0.434382S.D. dependent var 0.005058S.E. ofregression0.003804Akaike infocriterion-8.269046Sum squared 0.001505S chwarz criterion-8.16970resid8Log likelihood450.5285Hannan-Quinncriter.-8.228768F-statistic28.39119D urbin-Watson stat 2.061613Prob(F-statistic)0.000000单位根统计量ADF=-3.031673小于临界值,且P为0.0351,因此该序列不是单位根过程,即该序列是平稳序列。
时间序列分析模型

时间序列分析模型时间序列分析是一种用来处理时间变化数据的统计分析方法。
它将观测数据按照时间顺序进行排列,并利用过去的数据来预测未来的发展趋势。
在时间序列分析中,通常会使用一些常见的模型,如自回归(AR)、移动平均(MA)和自回归移动平均(ARMA)模型。
自回归模型(AR)是时间序列分析中最基本的模型之一。
它假设未来的观测值可以通过当前和过去的观测值来预测。
AR 模型的数学表达式为:Y_t = c + ∑(φ_i * Y_t-i) + ε_t其中,Y_t表示第t个观测值,c表示常数,φ_i表示第i个滞后的自回归系数,ε_t表示误差项。
通过对AR模型进行参数估计,可以得到最优的系数估计值,从而进行未来观测值的预测。
移动平均模型(MA)是另一种常见的时间序列分析模型。
它假设未来的观测值可以通过当前和过去的误差项来预测。
MA 模型的数学表达式为:Y_t = μ + ∑(θ_i * ε_t-i) + ε_t其中,Y_t表示第t个观测值,μ表示均值,θ_i表示第i个滞后的移动平均系数,ε_t表示误差项。
通过对MA模型进行参数估计,可以得到最优的系数估计值,从而进行未来观测值的预测。
自回归移动平均模型(ARMA)是将AR模型和MA模型结合起来的一种复合模型。
它假设未来的观测值可以通过当前观测值、滞后观测值和误差项来预测。
ARMA模型的数学表达式为:Y_t = c + ∑(φ_i * Y_t-i) + ∑(θ_i * ε_t-i) + ε_t其中,Y_t表示第t个观测值,c表示常数,φ_i表示第i个滞后的自回归系数,θ_i表示第i个滞后的移动平均系数,ε_t表示误差项。
通过对ARMA模型进行参数估计,可以得到最优的系数估计值,从而进行未来观测值的预测。
总之,时间序列分析模型是一种通过利用过去数据来预测未来数据的统计分析方法。
其中,自回归模型、移动平均模型和自回归移动平均模型是一些常见的时间序列分析模型。
通过对这些模型进行参数估计,可以得到最优的预测结果。
时间序列分析与的基本模型

时间序列分析与的基本模型时间序列分析是一种重要的统计学方法,用于预测和解释时间序列的行为。
它可以应用于各种领域,如经济学、金融学、气象学等。
本文将介绍时间序列分析的基本模型及其应用。
一、时间序列分析概述时间序列分析是指通过对时间序列数据进行建模和分析,来研究时间序列的特征、趋势和周期性等。
它可以帮助我们理解时间序列中的规律,并进行预测和决策。
二、基本模型1. 自回归模型(AR)自回归模型是一种线性模型,它假设当前观测值与过去的观测值之间存在关系。
自回归模型的一般形式为AR(p),其中p表示过去p个观测值对当前观测值的影响程度。
AR模型可以用公式表示为:```X(t) = c + Σ(φ(i) * X(t-i)) + ε(t)```其中,X(t)表示当前观测值,φ(i)表示对应滞后期的系数,ε(t)表示误差项。
2. 移动平均模型(MA)移动平均模型是一种线性模型,它假设当前观测值与过去观测值的误差之间存在关系。
移动平均模型的一般形式为MA(q),其中q表示过去q个观测误差对当前观测值的影响程度。
MA模型可以用公式表示为:```X(t) = μ + Σ(θ(i) * ε(t-i)) + ε(t)```其中,μ表示均值,θ(i)表示对应滞后期的系数,ε(t)表示误差项。
3. 自回归移动平均模型(ARMA)自回归移动平均模型是自回归模型和移动平均模型的结合。
ARMA模型的一般形式为ARMA(p,q),其中p表示自回归项数,q表示移动平均项数。
ARMA模型可以用公式表示为:```X(t) = c + Σ(φ(i) * X(t-i)) + Σ(θ(i) * ε(t-i)) + ε(t)```4. 自回归积分移动平均模型(ARIMA)自回归积分移动平均模型是自回归模型、差分和移动平均模型的结合。
ARIMA模型的一般形式为ARIMA(p,d,q),其中p表示自回归项数,d表示差分次数,q表示移动平均项数。
ARIMA模型可以用公式表示为:```(1-B)^d * X(t) = c + Σ(φ(i) * X(t-i)) + Σ(θ(i) * ε(t-i)) + ε(t)```其中,B是滞后算子。
报告中的时间序列模型与ARIMA分析

报告中的时间序列模型与ARIMA分析时间序列模型是一种用于分析和预测时间序列数据的统计模型。
ARIMA(自回归移动平均)是常用的时间序列模型之一,可以用于描述和预测时间序列数据中的趋势、季节性和随机性成分。
在本文中,我们将对报告中的时间序列模型与ARIMA分析进行详细讨论,包括其基本原理、建模方法和应用案例。
一、时间序列模型的基本原理时间序列模型是基于时间序列数据的统计模型,其基本原理是假设数据中存在一定的内在结构和规律,可以通过建立数学模型来揭示和利用这些结构和规律。
时间序列模型通常用于分析和预测具有时间先后顺序的数据,如股票价格、气温变化等。
它可以帮助我们理解数据的变化趋势、周期性和随机性,并提供预测未来数值的方法。
二、ARIMA模型的基本原理ARIMA模型是一种广泛应用的时间序列模型,其基本原理是通过自回归(AR)、差分(I)和移动平均(MA)的组合来描述和预测时间序列数据。
ARIMA模型假设时间序列数据既受到其自身过去值的影响,又受到随机误差的影响,通过建立自回归项、差分项和移动平均项的组合来捕捉这些影响。
三、ARIMA建模方法ARIMA建模包括模型识别、参数估计和模型检验三个步骤。
模型识别主要是通过观察时间序列图和自相关函数(ACF)和偏自相关函数(PACF)图来确定模型的阶数。
参数估计采用最大似然估计方法来估计模型的参数。
模型检验主要包括残差的白噪声检验和模型拟合程度的评估。
四、ARIMA模型的应用案例ARIMA模型在各个领域都有广泛应用。
例如,在经济学中,ARIMA模型可以用于预测经济指标的变化,如 GDP、通货膨胀率等。
在环境学中,ARIMA模型可以用于预测大气污染物浓度的变化。
在医学中,ARIMA模型可以用于预测传染病的发展趋势。
在金融领域,ARIMA模型可以用于预测股票价格变动。
这些应用案例充分展示了ARIMA模型在时间序列分析和预测中的重要作用。
五、ARIMA模型的改进和扩展ARIMA模型在实际应用中存在一些局限性,如对数据的平稳性要求较高、无法很好地处理长期依赖等。
