图论第5章
合集下载
图论第5、6章

第5章 对集
算法用生长“以u为根的M交错树”的 方法 ,来系统地搜索M可扩路. 树中除 u外都是M饱和的,直到碰到第一个 M 不饱和的顶点时,即得一M可扩路.当树 不能再生长下去时,即有N(S)=T.
本算法是个‘好’算法: 从一个M到 下一个,至多进行X次搜索运算;M 至多扩大X次.
例:
5.5 最优分派问题
第5章 对集
构作一个具有二分类(X, Y)的偶图G,其中 X={X1, X2, …, Xn},Y={Y1, Y2, …, Yn}, 并且Xi与Yj相连当且仅当工人Xi胜任工作Yj. 于是问题转化为确定G是否有完美对集的问 题.
下面给出的算法称为匈牙利算法,对任意 一个具有二分类(X, Y)的偶图G,它寻找G 的一个饱和X中所有顶点对集,或找到X的 一个子集S,使|N(S)| < |S| .
第5章 对集
若G有正常的k边着色,则称G是k边可着色的. 每个无环图都是ε边可着色的; 若G是k边可着色的,则一定是k+1边可着色的. 使G为k边可着色的最小整数k称为G的边色数, 记为χ’(G) . 若G的边色数为k,也称G是k边色的. 下图的边色数是多少?
第5章 对集
显然,在任何正常边着色中,和任一顶 点关联的边必须分配以不同的颜色,因 此
第5章 对集
定理5.2(Hall 1935) 设G是具有二分类(X,Y) 的偶图,则G包含饱和X的每个顶点的对集当 且仅当
|NG(S)|≥|S| 对所有S ⊆ X成立.
❖Hall定理是图论中最有用的定理之一,它 在数学及其他许多学科中都有应用.
Hall定理的证明
第5章 对集
必要性 假设G包含对集M,它饱和X的每个顶 点,并设S是X的子集. 由于S的顶点在M下和 N(S)中相异顶点配对,显然有|N(S)| ≥ |S| .
图论第5章

例如:
上图是3-正则图,且可以1-因子分解,但不存在Hamilton圈。
定理9 若3-正则图有割边,则不可1-因子分解。 证明 若3-正则图G可1-因子分解,因去掉G的不含割边的1-因子 后,图中每个点均为2度,从而每条边均在回路中,特别地割边 也在回路中,矛盾。 注:没有割边的3-正则图可能也没有1-因子分解,如彼得森图。
因与 S 中的顶点关联的边必与 N(S) 中的顶点关联,所以 我们可以推出E1 E2。 因此
k N S E2 E1 k S
由此可知
N S S
再根据Hall定理,可知G有一个饱和X的每个顶点的匹配M,
由于|X| = |Y|,所以M是完美匹配。
图G的一个覆盖: 指V(G)的一个子集 K,使得G的每条边都至 少有一个端点在 K 中。 G的最小覆盖: G中点数最少的覆盖。 例
|M|≤|M*|≤|
~ |≤|K|。 K
~ 由于|M|=|K |,所以 |M| = |M*|, | K | = |K|。
定理4(Kǒnig, 1931) 在偶图中,最大匹配的边数等于最小 覆盖的顶点数。 证明 设G 是具有二分类(X, Y)的偶图,M*是G的最大 匹配,用U 表示 X 中的 M* 非饱和顶点的集,用 Z 表示 由 M*交错路连接到 U 中顶点的所有顶点的集。
所以,G有完美匹配。
例 彼得森图满足推论的条件(即没有割边的 3-正则图),故它有完美匹配.
注: 有割边的3正则图不一定就没有完美匹配 。
有完美匹配
没有完美匹配
§5.4 因子分解
图G的因子: G的一个至少有一条边的生成子图; G的因子分解: 将G分解为若干个边不重的因子之并。 n-因子:指n度正则的因子。 例:1-因子的边集构成一个完美匹配。 2-因子的连通分支为一个圈。
第五章 图论

第五章 图论
图论可应用于多个领域,如信息论,控制论, 运筹学,运输网络,集合论等(如用关系图来 描述一个关系)。
计算机领域,其可应用于人工智能,操作系统, 计算机制图,数据结构)
§1
图论基本概念
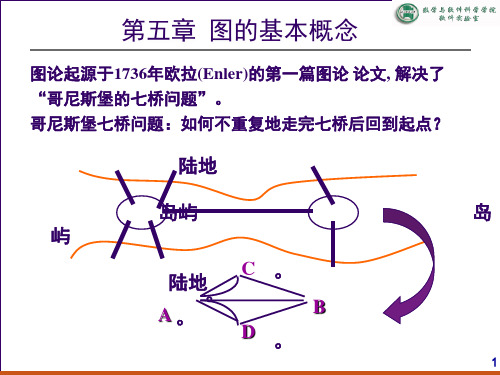
1-1 图的实例 问题1、哥尼斯堡桥问题
A C B D C B A D
问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点?
同理,结点间按别的对应方式,便都不存在一一对应
关系。
所以G1,G2不同构。
两图同构有必要条件:
(1)结点数相同; (2)边数同; (3)次数相同的结点数目相等。
1-5 多重图与带权图
1.5.1 多重图 定义11、一个结点对对应多条边,称为多重边。
包含多重边的图称为多重图,否则,成为简单图。
如:
如:基本通路:p1,p2,p3.
简单通路:p1,p2,p3,p5,p6. p4,p7既不是基本通路,也不是简单通路。
定义3、起始结点和终止结点相同的通路称为回路。 各边全不同的回路称为简单回路,各点全不同 的回路称为基本回路。
例2、上例中,1到1的回路有: c1: (1,1,),c2: (1,2,1),c3: (1,2,3,1), 1 2
例2、设有四个城市c1,c2,c3,c4;其中c1与c2间, c1与c4间,c2与c3间有高速公路直接相连,用图表 示该事实。 解:G=<V,E>,其中:V={c1,c2,c3,c4}, E={l1,l2,l3}={(c1,c2),(c1,c4),(c2,c3)} 例3、有四个程序p1,p2,p3,p4,其间调用关系为p1 p2, p1 p4,p2 p3,用图表示该事实。 解:G=<V,E>,V={p1,p2,p3,p4}, E={l1,l2,l3}={(p1,p2),(p1,p4),(p2,p3)}
图论可应用于多个领域,如信息论,控制论, 运筹学,运输网络,集合论等(如用关系图来 描述一个关系)。
计算机领域,其可应用于人工智能,操作系统, 计算机制图,数据结构)
§1
图论基本概念
1-1 图的实例 问题1、哥尼斯堡桥问题
A C B D C B A D
问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点?
同理,结点间按别的对应方式,便都不存在一一对应
关系。
所以G1,G2不同构。
两图同构有必要条件:
(1)结点数相同; (2)边数同; (3)次数相同的结点数目相等。
1-5 多重图与带权图
1.5.1 多重图 定义11、一个结点对对应多条边,称为多重边。
包含多重边的图称为多重图,否则,成为简单图。
如:
如:基本通路:p1,p2,p3.
简单通路:p1,p2,p3,p5,p6. p4,p7既不是基本通路,也不是简单通路。
定义3、起始结点和终止结点相同的通路称为回路。 各边全不同的回路称为简单回路,各点全不同 的回路称为基本回路。
例2、上例中,1到1的回路有: c1: (1,1,),c2: (1,2,1),c3: (1,2,3,1), 1 2
例2、设有四个城市c1,c2,c3,c4;其中c1与c2间, c1与c4间,c2与c3间有高速公路直接相连,用图表 示该事实。 解:G=<V,E>,其中:V={c1,c2,c3,c4}, E={l1,l2,l3}={(c1,c2),(c1,c4),(c2,c3)} 例3、有四个程序p1,p2,p3,p4,其间调用关系为p1 p2, p1 p4,p2 p3,用图表示该事实。 解:G=<V,E>,V={p1,p2,p3,p4}, E={l1,l2,l3}={(p1,p2),(p1,p4),(p2,p3)}
运筹学-图论

以可允许的10个状态向量作为顶点,将可能互相转移的状态用线段连接起 来构成一个图。
根据此图便可找到渡河方法。
(1,1,1,1) (1,1,1,0) (1,1,0,1) (1,0,1,1) (1,0,1,0) (0,0,0,0) (0,0,0,1) (0,0,1,0) (0,1,0,0) (0,1,0,1)
简单链:(v1 , v2 , v3 , v4 ,v5 , v3 )
v2
简单圈: (v4 , v1 , v2 , v3 , v5 , v7 , v6 ,v3 , v4 )
v6
v4
v5
v3
v7
连通图:图中任意两点之间均至少有一条通路,否则称为不连通 图。
v1 v5
v1
v6
v2
v2
v4
v3
v5
v4
v3
连通图
以后除特别声明,均指初等链和初等圈。
不连通图
有向图:关联边有方向 弧:有向图的边 a=(u ,v),起点u ,终点v; 路:若有从 u 到 v 不考虑方向的链,且 各方向一致,则称之为从u到v 的 路; 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 连通图: 若不考虑方向是
无向连通图; 强连通图:任两点有路;
端点的度 d(v):点 v 作为端点的边的个数 奇点:d(v)=奇数;
偶点:d(v) = 偶数; 悬挂点:d(v)=1; 悬挂边:与悬挂点连接的边; 孤立点:d(v)=0; 空图:E = ,无边图
v1
v3
v5 v6
v2
v4
图 5.7
v5
v4
V={v1 , v2 , v3 , v4 , v5 ,v6 , v7 }
圈:若 v0 ≠ vn 则称该链为开链,否则称为闭链或 回路或圈;
根据此图便可找到渡河方法。
(1,1,1,1) (1,1,1,0) (1,1,0,1) (1,0,1,1) (1,0,1,0) (0,0,0,0) (0,0,0,1) (0,0,1,0) (0,1,0,0) (0,1,0,1)
简单链:(v1 , v2 , v3 , v4 ,v5 , v3 )
v2
简单圈: (v4 , v1 , v2 , v3 , v5 , v7 , v6 ,v3 , v4 )
v6
v4
v5
v3
v7
连通图:图中任意两点之间均至少有一条通路,否则称为不连通 图。
v1 v5
v1
v6
v2
v2
v4
v3
v5
v4
v3
连通图
以后除特别声明,均指初等链和初等圈。
不连通图
有向图:关联边有方向 弧:有向图的边 a=(u ,v),起点u ,终点v; 路:若有从 u 到 v 不考虑方向的链,且 各方向一致,则称之为从u到v 的 路; 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 连通图: 若不考虑方向是
无向连通图; 强连通图:任两点有路;
端点的度 d(v):点 v 作为端点的边的个数 奇点:d(v)=奇数;
偶点:d(v) = 偶数; 悬挂点:d(v)=1; 悬挂边:与悬挂点连接的边; 孤立点:d(v)=0; 空图:E = ,无边图
v1
v3
v5 v6
v2
v4
图 5.7
v5
v4
V={v1 , v2 , v3 , v4 , v5 ,v6 , v7 }
圈:若 v0 ≠ vn 则称该链为开链,否则称为闭链或 回路或圈;
第五章_图论2

6
通路定理
[定理]通路定理 在n阶图G中,如果有顶点u到v (u v) 的通路,那么u到v必有一条长度小于等
于n1的基本通路。
7
通路定理证明
定理:在有n个顶点的图G中,如果有顶点u到v的通路,必有长 度不大于n-1的基本通路。
证明:(1)先证明u和v之间存在基本通路 若uv之间的通路P中有相同的顶点,则从P中删除相同顶点之间
路径,直到P中没有相同顶点,这样得到的路径为u和v之间的基 本通路。
(2) 再证基本通路长度不大于n-1 (反证法)设u和v之间的基本通路的长度≥n。 ∵ 一条边关联两个顶点, ∴长度≥n的基本通路上至少有n+1个顶点。 ∴至少有两个相同顶点在u和v之间的基本通路上,这与基本通路 的性质“任意两个顶点不同”相矛盾。
图G从vi点到vj点有通路当且仅当?
bij = 1
21
图的连通性与可达矩阵
有向图的连通性(n1): 设有向图G的可达矩阵为B
(1) G强连通 B中元素全为1 (2) G是单向连通的 B中所有关于主对角线对称
的两个元素中至少一个值为1
无向图的连通性(n1): 设无向图G的可达矩阵为B
G连通 B中元素全为1
[定义]基本通(回)路
结点各不相同的通路称为基本通路。 中间结点各不相同的回路称为基本回路。
A
基本通路:ACEBD
B
E
基本回路:ABCDEA
C
D
5
有向通(回)路
[定义]有向通(回)路 若通路v0v1 … vn各边是有向边,且vi-1和vi 分别是有向边的始点与终点,则称该通路为 有向通(回)路。
通路uxv相连。
由u和v的任意性,可知~G是连通的。
27
通路定理
[定理]通路定理 在n阶图G中,如果有顶点u到v (u v) 的通路,那么u到v必有一条长度小于等
于n1的基本通路。
7
通路定理证明
定理:在有n个顶点的图G中,如果有顶点u到v的通路,必有长 度不大于n-1的基本通路。
证明:(1)先证明u和v之间存在基本通路 若uv之间的通路P中有相同的顶点,则从P中删除相同顶点之间
路径,直到P中没有相同顶点,这样得到的路径为u和v之间的基 本通路。
(2) 再证基本通路长度不大于n-1 (反证法)设u和v之间的基本通路的长度≥n。 ∵ 一条边关联两个顶点, ∴长度≥n的基本通路上至少有n+1个顶点。 ∴至少有两个相同顶点在u和v之间的基本通路上,这与基本通路 的性质“任意两个顶点不同”相矛盾。
图G从vi点到vj点有通路当且仅当?
bij = 1
21
图的连通性与可达矩阵
有向图的连通性(n1): 设有向图G的可达矩阵为B
(1) G强连通 B中元素全为1 (2) G是单向连通的 B中所有关于主对角线对称
的两个元素中至少一个值为1
无向图的连通性(n1): 设无向图G的可达矩阵为B
G连通 B中元素全为1
[定义]基本通(回)路
结点各不相同的通路称为基本通路。 中间结点各不相同的回路称为基本回路。
A
基本通路:ACEBD
B
E
基本回路:ABCDEA
C
D
5
有向通(回)路
[定义]有向通(回)路 若通路v0v1 … vn各边是有向边,且vi-1和vi 分别是有向边的始点与终点,则称该通路为 有向通(回)路。
通路uxv相连。
由u和v的任意性,可知~G是连通的。
27
第五章图论树

条边,要使G成为树,G中只应留下5条边,故应删去
10条边,选C。
4。最小生成树 在带权图G中所生成的总权数最小的生成树称为
最小生成树。 5。最小生成树的求法
选取权数最大的边所在的回路,去掉其中权数 最大的边,如此做下去,直到求出生成树为止。这 样求出的生成树一定是最小生成树。
还有一种方法称为克鲁斯特尔算法。先去掉所有 的边,然后从权数最小的边的开始,从小到大逐步选 取,如果所选取的边和已选取的边构成了回路,则不 选取这条边重新选取,直到连接完所有的结点。这样 求出的树就是最小生成树。
3。任何非平凡树中至少有2片树叶。
二、生成树
1。生成树 若图G的生成子图是一棵树,则称此树是G的生
成树。
2。树的补 图G中不属于生成树T的边的集合称为树T的补。
3。生成树的求法 一般可用破圈法做,即把图G中的回路去掉一
条边,使它不再是回路。如此做下去,直到恰好把
所有的回路都破坏掉,就得到了生成树。
用破圈法一共要去掉
条边。
e 1v
[例题]
设G=<V,E>是有p个结点,s条边的连通图,则从G
中删去
条边,才能确定G的一棵生成树。
解:设要删去k条边,s k v 1, k s 1 v
[例题]
设G是有6个结点的完全图,从G中删去 C 条
边则能得到树。
A) 6
B) 9
C) 10
D) 15
解:∵G是有6个结点的完全图,∴G中共有6×5/2=15
a
1e 2
d
T=<{a,b,c,d,e},{(c,b),(b,e),(e,a),(e,d)}>。 3 b
c
1
[例题]
图论5-8章-习题课

6. 设 G 是连通的平面图,证明:G 为二部图当且仅当 G 的对偶图为欧 拉图。
证明:设 G 的对偶为 G*,则 G* 是连通的。必要性: G 为二部图,则 G 中无奇数长度回路,故 G* 中无奇数度顶点,因此 G* 是一个欧拉 图。充分性:G* 是一个欧拉图,则 G* 中无奇数度顶点,故 G 中 无奇数长度回路,因此 G 为一个二部图。
第二十八页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
14. 匈牙利算法求二部图的可增广道:如图,设初始匹配 {(x2, y2), (x3, y3), (x5, y5)},求其最大匹配。
x1
x2
x3
x4
x5
y1
y2
y3
y4
y5
28
第二十九页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
12
第十三页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图 G 中至少有 k(k1)/2 条边。
13
第十四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图G中至少有 k(k1)/2 条边。 证明:按 G 的一个 k 正常着色方案划分 G 的顶点为 k 个集合 V1,
第四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
2. 证明:Perterson 图不是平面图。
证二:反证。设其为平面图。由图示,每个面至少有5条边,即 l=5,代 入:
m (n 2)l l2
得: 3m 5(n2) 将 n =10, m =15 代入得 45 40,矛盾。
4
第五页,编辑于星期六:八点 分。
v1
v2
证明:设 G 的对偶为 G*,则 G* 是连通的。必要性: G 为二部图,则 G 中无奇数长度回路,故 G* 中无奇数度顶点,因此 G* 是一个欧拉 图。充分性:G* 是一个欧拉图,则 G* 中无奇数度顶点,故 G 中 无奇数长度回路,因此 G 为一个二部图。
第二十八页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
14. 匈牙利算法求二部图的可增广道:如图,设初始匹配 {(x2, y2), (x3, y3), (x5, y5)},求其最大匹配。
x1
x2
x3
x4
x5
y1
y2
y3
y4
y5
28
第二十九页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
12
第十三页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图 G 中至少有 k(k1)/2 条边。
13
第十四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图G中至少有 k(k1)/2 条边。 证明:按 G 的一个 k 正常着色方案划分 G 的顶点为 k 个集合 V1,
第四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
2. 证明:Perterson 图不是平面图。
证二:反证。设其为平面图。由图示,每个面至少有5条边,即 l=5,代 入:
m (n 2)l l2
得: 3m 5(n2) 将 n =10, m =15 代入得 45 40,矛盾。
4
第五页,编辑于星期六:八点 分。
v1
v2
图论第五章

Ch.5. Coloring of Graphs
4
Graph Theory
Clique number
5.1.6
The clique number of a graph G, written ω(G), is the maximum size of a set of pairwise adjacent vertices (clique) in G.
Ch.5. Coloring of Graphs
11
Graph Theory
Proposition 5.1.16. If G is an interval graph, then (G) =ω(G)
Proof: Order the vertices according to the left endpoints of the intervals in an interval representation. Apply greedy coloring, and suppose that x receives k, the maximum color assigned. Since x does not receive a smaller color, the left endpoint a of its interval belongs also to intervals that already have colors 1 through k-1. These intervals all share the point a, so we have a k-clique consisting of x and neighbors of x with colors 1 through k-1. Hence ω(G) ≥ k ≥ (G). Since (G) ≥ ω(G) always, this coloring is optimal.
第5章图的基本概念
3
此后的50年,
图论经历了一场爆炸性的发展, 成为数学科学中 一门独立的学科。主要分支有图论、超图理论、极值图论、算 法图论、网络图论和随机图论等。
几十年来图论在理论上和应用上都得到很大的发展,
特别是在 近30多年来由于计算机的广泛应用而又得到飞跃的发展。在计 算机科学、运筹学、化学、物理和社会 科学等方面都取得了不 少成果,对计算机学 科中的操作系统研究、编译技术、人工智 能 和计算机网络等方面都有广泛的应用。 这里主要讨论图的基本概念和算法 , 为今后的 学习和研究打 下基础。
9
第5章 图的基本概念
定义5.1 一个无向图G是一个二元组<V,E>,即G=<V,E>, 其中(1) V≠φ 称为顶点集, 其元素称为顶点或结点(2) E称 为边集,它是无序积V&V的多重子集,其元素称为无向边,简 称为边。 设A,B为任意的两个集合,称{(a,b)|a∈A∧b∈B},为A与
B的无序积,记作A&B.
27
如: d
c
含平行边的图称为多重图, 既不含平行边也不 含环的图称为简单图。
a
e2
v2
v1 v5
e1
e
b
e3
e4
e5 e7 e6 v4
e8
v3
28
定义5.7无向完全图 设G为n阶无向简单图,若G中每个顶点均与其余的 n-1个顶点相邻,则称G为n阶无向完全图,简称n阶完 全图,记作Kn(n≥1) 。
e1 v1 v3
e2 e4 e7
e3
v2 e5 e6
用图形表示无向图时, 常用小圆圈或实心点表示 顶点,用顶点之间的连线 表示无向边
v4
v5
11
第五章 图论

例16. 在任何聚会中,与奇数个人握过手的人必定有偶数 个。 证明: 我们用点来表示聚会中的人,若两个人有握手, 则我们用一条边把表示这两个人的点连接起来。与奇数个 人握过手的那个人,在图上表示为他的度为奇数。由握手 定理,则可知这样的点应该有偶数个,所以与奇数个人握 过手的人必定有偶数个。
(2)有向图
证明: 用6个点v1,v2,v3,v4,v5,v6来表示六个 人,互相认识的两个人用实现相连,否则用虚线相连。这 就产生了一个任何两个顶点间必有连线的图,称为完全图。 因此,问题就归结为:在一个具有六个顶点的完全图中, 至少存在一个实线三角形或虚线三角形。 任取一个顶点vi,则vi与其他五点的连线中,至少有三条 是实线或三条是虚线。不妨设为实线,其相应的顶点为vj, vk,vl,这三个顶点形成的三角形,若是实线或虚线三角 形,则问题得解;否则,至少有一条边是实线的,不妨设 为vj vk,那么三角形vjvivk便是实线三角形了。 定理1 握手定理:
5.2.3 图的运算 旧图→新图 定义6 子图:(G1G2)原图的一部分 定义7 并图:(G1∪G2)两个图的综合 定义8 补图: 对于完全图的边集的补 例14 图7-23所示的图G是K5的子图。
例15 求图a)所示的图G1和G2的并图。
习题 1.对哪些n值来说下列图是偶图? a) Kn b) Cn c) Wn d) Qn 2.至少带有一个顶点的W3 的子图有多少个? 3.证明:若G是有v个顶点和e条边的简单偶图,则ev2/4 。
一个重要类型的互联网络是超立方体。对这样的网络来 说,处理器数是2的幂, n=2m。n个处理器标记成P0, P1,…, Pn-1。每个处理器都有到m个其他处理器的双向连 接。处理器Pi与下标的二进制表示与i的二进制表示恰恰相 差1位的处理器相连接。超立方体网络在每个顶点的直接连 接数与保证处理器通信的中间连接数之间取得了平衡。已 经用超立方体网络建造了许多计算机,而且用超立方体网 络设计了许多算法。n立方体图Qn表示带n个处理器的超立 方体网络。图7-22显示8个处理器的超立方体网络。
图论第五章答案

解:由题:边 q 30, 面r 30, 故由欧拉公式得:点 p q r 2 12.
10 . 假定一个连通的平面性 二部图有 v个顶点和 e条边.证明:若 v 3,则 e 2v 4.
证:由“连通平面二部 图”知:该图每个面的 边数至少为4.(推论5.7的相关讲解注 释). 1 则由面的度数关系得: 4r 2e,即r e.又由欧拉公式知: v e r 2, 则e v r 2 2 1 v e 2,即e 2v 4. 2
2, n为偶数; 20. 对于圈图Cn (n 3),证明: ' (Cn ) { 3, n为奇数. 证:此题是讲义第五章 P1 例5.1(3.)的变式. 对圈图Cn (n 3)的边着色 对圈图Cn (n 3)的顶点着色 .
21 . 证明:每一简单、 3 正则、 Hamilton图,都有 ’ 3.
11 . 平面上有 n个点,其中任两个点之 间的距离至少是 1.证明:在这 n个点中,距 离恰好为1的点对数至多是 3n 6.
证:此题同讲义第五章 P10 例5.4. 首先建立图G (V , E ), 其中V就取平面上给定的 n个点(位置也不变),两点间距离 为1时,该两顶点之间用一 条直线段连接.只要证明G是平面图即可 . 由平面图定义(如图G能示画在曲面S上且使G的边仅在端点处相交 ),可反设在G 中存在相交的两条边 . 不妨设不同的边 uv和xy相交于非端点处 o,其夹角为 (0 ). 若 (或0),则如图(a.)所示,存在两点 (点u和x, 或点y和v)距离小于 1,矛盾. 若0 , 则如图(b.)所示,由边uv和xy的距离均为 1可知,在u, v, x, y中至少有两 1 1 1 点使从交点o到这两点的距离不超过 .不妨设这两点为u和x,则 ou , ox . 2 2 2 1 1 此时,在uox中, ux ou ox 1.因而,点u与x之间的距离小于 1,矛盾. 2 2 因此G为平面图. 从而由推论5.6知,图G的边不会超过3n 6. 故在这n个点中,距离恰好为 1的点对数至多是 3n 6.
10 . 假定一个连通的平面性 二部图有 v个顶点和 e条边.证明:若 v 3,则 e 2v 4.
证:由“连通平面二部 图”知:该图每个面的 边数至少为4.(推论5.7的相关讲解注 释). 1 则由面的度数关系得: 4r 2e,即r e.又由欧拉公式知: v e r 2, 则e v r 2 2 1 v e 2,即e 2v 4. 2
2, n为偶数; 20. 对于圈图Cn (n 3),证明: ' (Cn ) { 3, n为奇数. 证:此题是讲义第五章 P1 例5.1(3.)的变式. 对圈图Cn (n 3)的边着色 对圈图Cn (n 3)的顶点着色 .
21 . 证明:每一简单、 3 正则、 Hamilton图,都有 ’ 3.
11 . 平面上有 n个点,其中任两个点之 间的距离至少是 1.证明:在这 n个点中,距 离恰好为1的点对数至多是 3n 6.
证:此题同讲义第五章 P10 例5.4. 首先建立图G (V , E ), 其中V就取平面上给定的 n个点(位置也不变),两点间距离 为1时,该两顶点之间用一 条直线段连接.只要证明G是平面图即可 . 由平面图定义(如图G能示画在曲面S上且使G的边仅在端点处相交 ),可反设在G 中存在相交的两条边 . 不妨设不同的边 uv和xy相交于非端点处 o,其夹角为 (0 ). 若 (或0),则如图(a.)所示,存在两点 (点u和x, 或点y和v)距离小于 1,矛盾. 若0 , 则如图(b.)所示,由边uv和xy的距离均为 1可知,在u, v, x, y中至少有两 1 1 1 点使从交点o到这两点的距离不超过 .不妨设这两点为u和x,则 ou , ox . 2 2 2 1 1 此时,在uox中, ux ou ox 1.因而,点u与x之间的距离小于 1,矛盾. 2 2 因此G为平面图. 从而由推论5.6知,图G的边不会超过3n 6. 故在这n个点中,距离恰好为 1的点对数至多是 3n 6.
图论第5章 独立集与匹配

独立集
设G=<V,E>是简单图无向图, SV, S, 若S 中任何两个顶点都不相邻,则称这个顶点集合S 为图G的独立集。 若S是图G的独立集,但是任意增加一个顶点 就破坏它的独立性,则称这个独立集S为极大独 立集。 独立集S称为最大独立集,如果不存在独立集S’, 使 S’> S ,其中S为集合S的数。 G的最大独立集S的基数称为G的独立数,记作 (G)。
他指出在一个的棋盘具有处在配置下的64个格子在所给某个位置的皇后控制着同行同列以及包含这个格子的两条斜线上的所有格子这种皇后的最少个数为个格子在所给某个位置的皇后控制着同行同列以及包含这个格子的两条斜线上的所有格子这种皇后的最少个数为5左图显示了一种放置方法
第五章 独立集与匹配
独立集、支配集、覆盖集、匹配
点覆盖
设G=<V,E>, V*V, (1) V*是点覆盖(点覆盖集)——eE,vV*,使e 与v关联; (2) V*是极小点覆盖——V*的任何真子集都不是点覆 盖集; (3) 最小点覆盖——顶点数最少的点覆盖集; (4) 点覆盖数——(G)——最小点覆盖的元素个数。
图中,点覆盖数依次为3,4,7。
证明: 设S1是G的最大独立集, S2是G的最小点覆 盖,由前面的定理知V(G)-S1是点覆盖,V(G)-S2是 独立集。因而 V(G)- (G)= V(G) -S1 (G) V(G)- (G)= V(G) –S2 (G) 所以 (G)+(G)=V(G)。
边覆盖
{y2,x1} {y3,x3}
{x4}
{y2,y3} {y2,y3} {y2,y3}
y2饱和 y3饱和
{x4,x1} {y2} {x4,x1, x 3} {y2, y3}Βιβλιοθήκη 注意:不是每个支配集都是独立集;
图论 第5章

u
例: v v1v2…vm u, 其中u为非饱和点
T
由于M*是最大匹配,从上节定理1可知:u为Z中唯一的M* 非饱和点 (否则将含 M * 可扩路) 。且任意一对配对点v和w, 若 v∈S, 则必w∈T, 反之亦然. 因此 | T |= |S |-1 而且 T N(S ) 。 下证N(S ) T (2.2)
19
(3) 定理5(Kǒnig,哥尼,1931) 偶图中,最大匹配的边 数等于最小覆盖的顶点数。 证明 设G 是具有二分类(X, Y)的偶图,M*是G的最大 匹配,用U 表示 X 中的 M* 非饱和顶点的集,用 Z 表示 由 M* 交错路连接到 U 中顶点的所有顶点的集。置 S = Z∩X , T = Z∩Y。
若图G中的点均为 M 饱和点,则称M为G的完美匹配。 若G中没有另外的匹配M’,使得|M|<|M’|, 则称M为G
的最大匹配(含边数最多的匹配)。
2
例1 设图G 为: G的匹配有: M1 = {v1v8}
v1
v8
v7
v6
v2
v3
v4
v5
M2 = {v1v3,v8v4,v7v5} M3 = {v1v2,v8v3,v7v4,v6v5} 等等 对 M2,点v1是饱和点,点v2是非饱和点。
2 1 3
12
由(2.2)式和(2.3)式推出
|N(S )| = | T |= |S |-1< |S | 这与假定(2.1)式矛盾。 所以M*饱和X的所有顶点. 推论 若G是k正则偶图(k>0),则G有完美匹配。 证明 设G是具有二分类(X, Y)的k正则偶图 (k>0)。首先有 |X| = |Y| (习题1的9). 任取X的一个子集S ,令 E1={e | e∈E,并且 e 与 S 中的顶点关联}
《图论课件第五章匹配与因子分解》课件

二、因子分解
2.1 定义
因子分解是将图进行拆分,使得每个因子都是图的 一个子图。
2.2 贪心算法
贪心算法用于在因子分解时选择边或顶点。
2.3 DAG上的匈牙利算法
用于在有向无环图上寻找因子分解的算法。
2.4 Tutte定理
用于判断一个图是否存在完美匹配。
三、应用实例
1
3.1 二分图最大匹配的应用
《图论课件第五章匹配与 因子分解》PPT课件
图论课件第五章匹配与因子分解
一、匹配
1.1 定义
匹配指的是图中的一组边,这些边不相交并且 没有公共顶点。
1.3 最大匹配
最大匹配是图中包含边数最多的匹配。
1.2 匹配的分类
分类包括完美匹配、最大匹配和最小匹配。
1.4 匈牙利算法
匈牙利算法用于寻找二分图的最大匹配。
应用于任务分配、婚姻匹配等场景。
3.2 带权二分图匹配的应用
2
应用于资源分配、工作调度等场景。
3
3.3 双倍经验的关卡通关问题
使用匹配算法解决游戏中的关卡设计问
3.4 理发店问题
4
题。
利用匹配算法解决顾客理发需要和理发 师时间安排的问题。
四、参考资料
4.1 书籍
《图论导论》、《算法导论》等
4.3 网站
Grap h Alg orithm s, Grap h Theo ry Online等
4.2 论文
Graph Matching Alg orithm s: A C om prehensive C om parison
4.4 其他资源
相关研究报告、课程讲义等
第二篇 图论-习题

习题3 习题3
为正整数, 例1 设p,q为正整数,则 为何值时,无向完全图Kp是欧拉图? Kp是欧拉图 (1)p为何值时,无向完全图Kp是欧拉图?p为何值 Kp为半欧拉图 为半欧拉图? 时Kp为半欧拉图? (2)p,q为何值时Kp,q为欧拉图? p,q为何值时Kp,q为欧拉图? 为何值时Kp,q为欧拉图 p,q为何值时Kp,q为哈密顿图 为何值时Kp,q为哈密顿图? (3)p,q为何值时Kp,q为哈密顿图? 为何值时,轮图Wp为欧拉图? Wp为欧拉图 (4)p为何值时,轮图Wp为欧拉图? 判断如图所示的图是否为哈密顿图, 例2 判断如图所示的图是否为哈密顿图,若是写出哈 密顿圈,否则证明其不是哈密顿图。 密顿圈,否则证明其不是哈密顿图。
e
c b a
f a g j
d
d
j i
h
i
e h
b
c
f
g
给出一个10个顶点的非哈密顿图的例子, 10个顶点的非哈密顿图的例子 例3 给出一个10个顶点的非哈密顿图的例子,使得每 一对不邻接的顶点u和v,均有degu+degv≥9。 一对不邻接的顶点u 均有degu+degv≥9。 degu+degv≥9 证明:完全图K 例4 证明:完全图K9中至少存在彼此无公共边的两条 哈密顿回路和一条哈密顿路? 哈密顿回路和一条哈密顿路? 试求Kp中不同的哈密顿圈的个数。 Kp中不同的哈密顿圈的个数 例5 试求Kp中不同的哈密顿圈的个数。 证明具有奇数顶点的偶图不是哈密顿图; 例6(1) 证明具有奇数顶点的偶图不是哈密顿图;用 此结论证明如图所示的图不是哈密顿图。 此结论证明如图所示的图不是哈密顿图。 完全偶图K 为哈密顿图的充要条件是什么? (2) 完全偶图Km,n为哈密顿图的充要条件是什么 菱形12面体的表面上有无哈密顿回路? 12面体的表面上有无哈密顿回路 例7 菱形12面体的表面上有无哈密顿回路? G=(V,E)是连通图且顶点数为p,最小度数为 是连通图且顶点数为p,最小度数为δ 例8设G=(V,E)是连通图且顶点数为p,最小度数为δ, p>2δ 中有一长至少为2 的路。 若p>2δ,则G中有一长至少为2δ的路。 证明:彼德森图不是哈密顿图。 例9 证明:彼德森图不是哈密顿图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如, Г1 Г2 Г3
M 可扩路
取M = {红边}
M 交 错 路
可看出:对Г3 ,若取Г3中非 M 的边再连同 M 的不在 Г3中的边组成 M’,则 M’ 的边数比 M的边数多,这 表明 M 不是该图的最大匹配。
定理1(Berge, 1957)G的匹配 M是最大匹配当且仅当G不含 M 可扩路 。 证明 设M是G的匹配,并假设G 包 含M可扩充路 v0v1…v2m+1 , 定义M′ E 为 M′= (M\{ v1v2, v3v4,…,v2m-1 v2m})∪{ v0v1, v2v3,…,v2m v2m+1} 则M′是G的匹配,且 | M′| = |M| +1,因而M就不是最大匹 配。 反之,假设M不是最大匹配,且令M′是G的最大匹配,则 | M′| > |M| 置H = G[M△M′],这里M△M′表示M和M′的对称差。
于是 K 是G的覆盖,并且显然有
~ |M*|= | K |
~ 由定理3,是 K 最小覆盖。
~
例1 矩阵的一行或一列统称为一条线。证明:包含了一个 (0,1)矩阵中所有“1”的线的最小条数,等于具有性质“ 任意两个1都不在同一条线上”的“1”的最大个数。
一个覆盖
一个最小覆盖
设K是G的覆盖,M是G的匹配,由于K至少包含M中每条边 的一个端点,所以 |M|≤| K |。 特别地,若M*是最大匹配,且 K 是最小覆盖,则
| M * | K
定理3 设M是匹配,K是覆盖,若|M|=|K|,则M是最大匹配, 且K是最小覆盖。
~ 是最小覆盖,则, 证明 设M*是最大匹配 , K
又因N(S)中每个顶点v 均由一个M*交错路连接于u,故v∈Z, 从而v∈T, 这表明N(S ) T , 于是有T = N(S )。
由| T |= |S |-1 和T =N(S )推出
|N(S )| = | T |= |S |-1< |S |
这与假定(2.1)式矛盾。 所以M*饱和X的所有顶点。 推论 若G是k正则偶图(k>0),则G有完美匹配。 证明 G是具有二分类(X, Y)的k正则偶(k>0)。 由于G是k正则的,所以k|X|=|E(G)|=k|Y|,所以|X| = |Y| 。 任取X的一个子集S ,令 E1={e | e∈E, 并且 e 与 S 中的顶点关联} E2={e | e∈E, 并且 e 与 N(S) 中的顶点关联}。
|M|≤|M*|≤|
~ |≤|K|。 K
~ | = |K|。 由于|M|=|K |,所以 |M| = |M*|, | K
定理4(Kǒnig, 1931) 在偶图中,最大匹配的边数等于最小 覆盖的顶点数。 证明 设G 是具有二分类(X, Y)的偶图,M*是G的最大 匹配,用U 表示 X 中的 M* 非饱和顶点的集,用 Z 表示 由 M*交错路连接到 U 中顶点的所有顶点的集。
H 的每个顶点在H中具有的度是1或2,因为它最多只 能和M的一条边以及 M′的一条边相关联。 因此 H 的每个分支或是由M和M′中的边交错组成的偶 圈,或是由M和M′中的边交错组成的路。 由于 M′包含的边多于M的边,因而H中必定有的一条 路P,其边始于M′且终止于M′,因此P的起点和终点在 H中被M′所饱和,在图G中就是M非饱和的。
关系:
(1) 完美匹配必是最大匹配,而最大匹 配不一定是完美匹配。 (2) 一个图的最大匹配必存在,但完美 匹配不一定存在。 (3) 图G 存在完美匹配的一个必要条件 是 G 的点数为偶。
设M 为图G的一个匹配 M 交错路:G 中由M中的边与非M 中的边交替组成的路。 M 可扩路:起点与终点均为M 非饱和点的M交错路。
置S =Z∩X ,T= Z∩Y。
类似于Hall定理的证明,可知T中的每个顶点都是M*饱和 的,并且N(S)=T。 S
定义 K ( X \ S ) T。
U X \S
T=N (S)
~ 中,因为否则就存在 则G的每条边必然至少有一个端点在 K 一条边,其一个端点在S中,而另一个端点在Y\T中,这与 N(S)=T相矛盾。
因与 S 中的顶点关联的边必与 N(S) 中的顶点关联,所以 我们可以推出E1 E2。 因此
k N S E2 E1 k S
由此可知
N S S
再根据Hall定理,可知G有一个饱和X的每个顶点的匹配M,
由于|X| = |Y|,所以M是完美匹配。
图G的一个覆盖: 指V(G)的一个子集 K,使得G的每条边都至 少有一个端点在 K 中。 G的最小覆盖: G中点数最少的覆盖。 例
于是P是G的一条M可扩路。
§5.2 偶图的匹配与覆盖
取图 G 的一个顶点子集S,令 N (S) = { v | 存在 u∈S,且v与u 相邻} 称 N (S) 为 S 的邻集。
v1
例如在右图中
v8
v7
v6
v2
v3
v4
v5
取 S = {v1, v2},则 N (S) = {v8, v3, v1, v2}
定理2(Hall,1935) 设G为具有二分类(X, Y)的偶图,则 G包含饱和X的每个顶点的匹配当且仅当 |N(S)|≥|S| (2.1) 对所有 S X 成立. 证明 假设G包含匹配M,它饱和X的每个顶点,并设S是X 的子集。由于S的顶点在 M 下和N(S)中的相异顶点配对, 显然有 |N(S)|≥|S| 。 反之,假设G是满足(2.1)式的偶图, M*是G的最大匹配。 假定M*不饱和X的所有顶点。 设 u 是X的一个M* 非饱和点,并设
Z={ v | v∈V,且v通过M*交错路与u连接 }。
S
置S = Z∩X 和 T = Z∩Y。
u
T=N (S)
由于M*是最大匹配,从Berge定理可知:u为Z中唯一的M*非 饱和点(否则将含 M * 可扩路)。且任意一对配对点v和w, 若v∈S,则必w∈T,反之亦然。
因此,| T |= |S |-1 而且 T N(S ) 。
例1 设图G 为: G的匹配有: M1 = {v1v8}
v1
v8
v7
v6
v2
v3
v4
v5
M2 = {v1v3,v8v4,v7v5} M3 = {v1v2,v8v3,v7v4,v6v5} 等等 对 M2,点v1是的饱和点,点v2是非饱和点。
M1 和M2既不是最
M 可扩路
取M = {红边}
M 交 错 路
可看出:对Г3 ,若取Г3中非 M 的边再连同 M 的不在 Г3中的边组成 M’,则 M’ 的边数比 M的边数多,这 表明 M 不是该图的最大匹配。
定理1(Berge, 1957)G的匹配 M是最大匹配当且仅当G不含 M 可扩路 。 证明 设M是G的匹配,并假设G 包 含M可扩充路 v0v1…v2m+1 , 定义M′ E 为 M′= (M\{ v1v2, v3v4,…,v2m-1 v2m})∪{ v0v1, v2v3,…,v2m v2m+1} 则M′是G的匹配,且 | M′| = |M| +1,因而M就不是最大匹 配。 反之,假设M不是最大匹配,且令M′是G的最大匹配,则 | M′| > |M| 置H = G[M△M′],这里M△M′表示M和M′的对称差。
于是 K 是G的覆盖,并且显然有
~ |M*|= | K |
~ 由定理3,是 K 最小覆盖。
~
例1 矩阵的一行或一列统称为一条线。证明:包含了一个 (0,1)矩阵中所有“1”的线的最小条数,等于具有性质“ 任意两个1都不在同一条线上”的“1”的最大个数。
一个覆盖
一个最小覆盖
设K是G的覆盖,M是G的匹配,由于K至少包含M中每条边 的一个端点,所以 |M|≤| K |。 特别地,若M*是最大匹配,且 K 是最小覆盖,则
| M * | K
定理3 设M是匹配,K是覆盖,若|M|=|K|,则M是最大匹配, 且K是最小覆盖。
~ 是最小覆盖,则, 证明 设M*是最大匹配 , K
又因N(S)中每个顶点v 均由一个M*交错路连接于u,故v∈Z, 从而v∈T, 这表明N(S ) T , 于是有T = N(S )。
由| T |= |S |-1 和T =N(S )推出
|N(S )| = | T |= |S |-1< |S |
这与假定(2.1)式矛盾。 所以M*饱和X的所有顶点。 推论 若G是k正则偶图(k>0),则G有完美匹配。 证明 G是具有二分类(X, Y)的k正则偶(k>0)。 由于G是k正则的,所以k|X|=|E(G)|=k|Y|,所以|X| = |Y| 。 任取X的一个子集S ,令 E1={e | e∈E, 并且 e 与 S 中的顶点关联} E2={e | e∈E, 并且 e 与 N(S) 中的顶点关联}。
|M|≤|M*|≤|
~ |≤|K|。 K
~ | = |K|。 由于|M|=|K |,所以 |M| = |M*|, | K
定理4(Kǒnig, 1931) 在偶图中,最大匹配的边数等于最小 覆盖的顶点数。 证明 设G 是具有二分类(X, Y)的偶图,M*是G的最大 匹配,用U 表示 X 中的 M* 非饱和顶点的集,用 Z 表示 由 M*交错路连接到 U 中顶点的所有顶点的集。
H 的每个顶点在H中具有的度是1或2,因为它最多只 能和M的一条边以及 M′的一条边相关联。 因此 H 的每个分支或是由M和M′中的边交错组成的偶 圈,或是由M和M′中的边交错组成的路。 由于 M′包含的边多于M的边,因而H中必定有的一条 路P,其边始于M′且终止于M′,因此P的起点和终点在 H中被M′所饱和,在图G中就是M非饱和的。
关系:
(1) 完美匹配必是最大匹配,而最大匹 配不一定是完美匹配。 (2) 一个图的最大匹配必存在,但完美 匹配不一定存在。 (3) 图G 存在完美匹配的一个必要条件 是 G 的点数为偶。
设M 为图G的一个匹配 M 交错路:G 中由M中的边与非M 中的边交替组成的路。 M 可扩路:起点与终点均为M 非饱和点的M交错路。
置S =Z∩X ,T= Z∩Y。
类似于Hall定理的证明,可知T中的每个顶点都是M*饱和 的,并且N(S)=T。 S
定义 K ( X \ S ) T。
U X \S
T=N (S)
~ 中,因为否则就存在 则G的每条边必然至少有一个端点在 K 一条边,其一个端点在S中,而另一个端点在Y\T中,这与 N(S)=T相矛盾。
因与 S 中的顶点关联的边必与 N(S) 中的顶点关联,所以 我们可以推出E1 E2。 因此
k N S E2 E1 k S
由此可知
N S S
再根据Hall定理,可知G有一个饱和X的每个顶点的匹配M,
由于|X| = |Y|,所以M是完美匹配。
图G的一个覆盖: 指V(G)的一个子集 K,使得G的每条边都至 少有一个端点在 K 中。 G的最小覆盖: G中点数最少的覆盖。 例
于是P是G的一条M可扩路。
§5.2 偶图的匹配与覆盖
取图 G 的一个顶点子集S,令 N (S) = { v | 存在 u∈S,且v与u 相邻} 称 N (S) 为 S 的邻集。
v1
例如在右图中
v8
v7
v6
v2
v3
v4
v5
取 S = {v1, v2},则 N (S) = {v8, v3, v1, v2}
定理2(Hall,1935) 设G为具有二分类(X, Y)的偶图,则 G包含饱和X的每个顶点的匹配当且仅当 |N(S)|≥|S| (2.1) 对所有 S X 成立. 证明 假设G包含匹配M,它饱和X的每个顶点,并设S是X 的子集。由于S的顶点在 M 下和N(S)中的相异顶点配对, 显然有 |N(S)|≥|S| 。 反之,假设G是满足(2.1)式的偶图, M*是G的最大匹配。 假定M*不饱和X的所有顶点。 设 u 是X的一个M* 非饱和点,并设
Z={ v | v∈V,且v通过M*交错路与u连接 }。
S
置S = Z∩X 和 T = Z∩Y。
u
T=N (S)
由于M*是最大匹配,从Berge定理可知:u为Z中唯一的M*非 饱和点(否则将含 M * 可扩路)。且任意一对配对点v和w, 若v∈S,则必w∈T,反之亦然。
因此,| T |= |S |-1 而且 T N(S ) 。
例1 设图G 为: G的匹配有: M1 = {v1v8}
v1
v8
v7
v6
v2
v3
v4
v5
M2 = {v1v3,v8v4,v7v5} M3 = {v1v2,v8v3,v7v4,v6v5} 等等 对 M2,点v1是的饱和点,点v2是非饱和点。
M1 和M2既不是最
