直线与圆的位置关系-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(原卷版)

合集下载

苏科版数学九年级上册直线与圆的位置关系课件

(1)r＝2cm；(2)r＝2.4cm；(3)r＝3cm．
2.5 直线与圆的位置关系（1）
六、拓展提升，储备能量
在平面直角坐标系中有一点A(－3，－4)，以点A
为圆心，r长为半径时，思考：随着r的变化，⊙A
与坐标轴交点的变化情况．
y
解：当0≤ r＜3时，⊙A与x轴、y轴都相离.
当 r = 3时，⊙A与x轴相离，与y轴相切.
直线与⊙O 有_____个公共点.
2.5 直线与圆的位置关系（1）
小试牛刀
r = 5cm
2．已知⊙O的直径为10cm，点O到直线l的距离为d
，根据条件填写d的范围：
(1)若直线l与⊙O相离，则 d ＞ 5cm ； (2)若直线l与⊙O相切，则 d ＝ 5cm ； (3)若直线l与⊙O相交，则 0cm ≤ d＜5cm．
2.5 直线与圆的位置关系（1）
五、随堂检测，自我肯定
2．（2017湖南衡阳）已知⊙O的半径为5，点A在直
线l上，OA=5，则直线l 与⊙O的位置关系是（ D
） A.相离 B.相切 C.相交 D.相切或相交
2.5 直线与圆的位置关系（1）
五、随堂检测，自我肯定
3．在Rt△ABC中，∠C＝90°，AC＝3cm， BC＝4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
2.5 直线与圆的位置关系（1）
总结
判定直线与圆的位置关系的方法有_两___种：
（1）根据定义，由_直_线__与__圆__的__公__共__点__的个数来判断；
（2）根据性质，由_圆__心__到__直__线__的__距__离__d_与__半__径__r___ 的关系来判断．
在实际应用中，当无法确定公共点个数时常采用第二种方法判定.

2.5 直线与圆的位置关系苏科版九年级数学上册课件

B
练习
1.如图，点P在⊙O上，过点P西⊙O的切线
P
●
解:如图所示,连接 OP,过点 P
作直线l⊥OP,
O
则l为过点 P的⊙O 的切线.
●
练习
2.如图，AB是⊙O的直径，
B
∠ABC=45°,AB=AC，直
线AC与⊙O有怎样的位置关
O●
系?为什么?
C
A
练习
解:直线 AC 与以AB 为直径的⊙O 相切
(1)r=2 (2)r=2 3 (3)r=3
例1答案
解:过点C作CD⊥AB，垂足为D，在Rt△ACD中
∵∠A=45°
∴∠ACD=∠A,CD – AD
又∵ 2 + 2 = 2 ，AC = 4,
2
∴ =16, CD=2
即圆心C到AB所在直线的距离d=2
相离
(1)当r-2时,d>r，⊙C与AB所在直线相离
∵AB=AC,
∴∠C=∠ABC=45°
∴∠BAC=180°-∠ABC-∠C=90°
∴AB⊥AC∴AC 与以AB 为直径的⊙O 相切
练习
*3，如图，在以点O为圆心的
两个同心圈中，大圈的弦AB
切小圆于点P。PA与PB相等
●O
吗?为什么?
A
P
B
练习
解:PA=PB.
连接 OP(图略).
●O
∵AB 切小圆于点 P，
已知△ABC。根据下列作法，用直尺和圆规作⊙ O，使
它与△ ABC的各边都相切？
作法
图形
1.分别作∠ABC、∠ACB 的平分线
A
BM、CN，BM与CN 的交点为ห้องสมุดไป่ตู้.

苏科版九年级上册 2.5直线与圆的位置关系(2)(17张PPT)

（3）经过半径外端并且垂直于这条半径的直线
是圆的切线.
O
l
A
2.5 直线与圆的位置关系（2）
请你想一想
直线l与⊙O相切于点A，你能得到哪些结论？
切线的性质：圆的切线垂直于经过切点的半径. 反证法：
（1）假设直线l与OA不垂直．
（2）作OB⊥ l，垂足为点B．
O
（3）OB＜OA，即d ＜ r．
（4）直线l与圆相交，与
时,AB与⊙C相切?
A
解:(1)过点C作CD⊥AB于D.
D
∵AB=8cm,AC=4cm.
┐
C
B
∴ B8C 2-42= =4 3
4×43 CD=4 =23 因此,当半径长为第1题
１．过圆上一点画一条圆的切线，并说明理由，与你的同学交流你的想法.
P
O
请你议一议
2．请你将上面发现的结论进行归纳总结．定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．判定定理的2个条件： ①直线与圆有公共点； ②直线与过公共点的半径垂直．
2.5 直线与圆的位置关系（2）
请你议一议
直线与圆相切的判定方法：（1）与圆有惟一公共点的直线是圆的切线.
（2）与圆心的距离等于半径的直线是圆的切线.
的切线.
2.切线的性质定理
圆的切线垂直于过切点的半径.
3.证明一条直线是圆的切线时
证明一条直线是圆的切线时（1）直线与圆有交点时，连接交点与圆心，证垂直；
（2）直线与圆“无”交点时，过圆心作直线的垂线，证明垂线段的长等于半径.
初中数学九年级上册（苏科版）
2.5 直线与圆的位置关系（二）
回顾
直线与圆的位置关系
r ●O ┐d

九年级数学上册第21讲直线与圆的位置关系讲义新版苏科版

第21讲直线与圆的位置关系
新知新讲
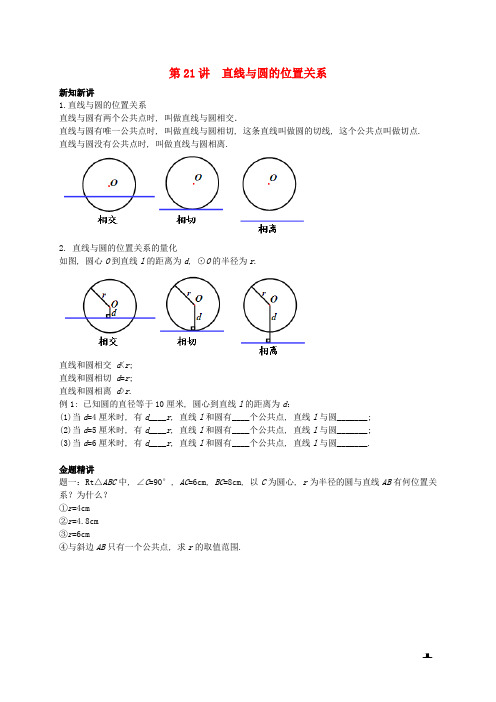
1.直线与圆的位置关系
直线与圆有两个公共点时, 叫做直线与圆相交．
直线与圆有唯一公共点时, 叫做直线与圆相切, 这条直线叫做圆的切线, 这个公共点叫做切点.
.
直线与圆没有公共点时, 叫做直线与圆相离
2. 直线与圆的位置关系的量化
如图, 圆心O到直线l的距离为d, ⊙O的半径为r
.
直线和圆相交d<r;
直线和圆相切d=r;
直线和圆相离d>r.
例1: 已知圆的直径等于10厘米, 圆心到直线l的距离为d：
(1)当d=4厘米时, 有d____r, 直线l和圆有____个公共点, 直线l与圆_______;
(2)当d=5厘米时, 有d____r, 直线l和圆有____个公共点, 直线l与圆_______;
(3)当d=6厘米时, 有d____r, 直线l和圆有____个公共点, 直线l与圆_______.
金题精讲
题一：Rt△ABC中, ∠C=90°, AC=6cm, BC=8cm, 以C为圆心, r为半径的圆与直线AB有何位置关系？为什么？
①r=4cm
②r=4.8cm
③r=6cm
④与斜边AB只有一个公共点, 求r的取值范围.
1
小初高试题、试卷、习题、复习、教案精选资料
2 第21讲直线与圆的位置关系
新知新讲
例1：(1)<, 2, 相交；(2) =, 1, 相切；(3) >, 0, 相离. 金题精讲
题一：①相离 ②相切 ③相交 ④6cm<r 8cm 或r =4.8cm。

直线与圆的位置关系课件苏科版数学九年级上册

证半径.
感悟新知
例3 如图2.5-4，在Rt△ABC中，∠B＝90°，∠BAC的平
分线交BC于点D，以点D为圆心，DB长为半径作
⊙D. 求证：AC与⊙D相切.
感悟新知
解题秘方：利用“无切点，作垂直，证半径”判
定圆的切线.
证明：如图2.5-4，过点D作DF⊥AC，垂足为F.
∵∠B＝90°，
∴ DB⊥AB.
知识点 1 直线与圆的位置关系
直线与圆的位置关系
直线与圆的位置关系
相交
相切
相离
2
1
0
图形
公共点个数
感悟新知
续表
直线与圆的位置关系
公共点名称
直线名称
圆心O到直线l的距离d
与半径r的关系
等价关系
相交
交点
割线
相切
切点
切线
相离
d<r
d=r
d>r
d<r
直线l与
⊙O相交
d=r
直线l与
⊙O相切
d>r
第2章对称图形——圆
2.5 直线与圆的位置关系
学习目标
直线与圆的位置关系
切线的判定
切线的性质
三角形内切圆
切线长定理
课时导入
山水相接的地方出现了一道红霞，过了一会儿，那
里出现了太阳的小半边脸，慢慢儿，一纵一纵地使劲儿
向上升.到了最后，它终于冲破了云霞，完全跳出了海面。
——巴金
感悟新知
直线l与
⊙O相离
要点提醒
感悟新知
“圆心到直线的距离与半径的数量关系”与
“直线与圆的位置关系”反应了图形的数量关
系与图形的位置关系之间的内在联系，这里的

圆综合练习(提优)-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

圆综合练习（提优）一．选择题1．如图，⊙O是△ABC的外接圆，半径为2cm，若BC＝2cm，则∠A的度数为（）A．30°B．25°C．15°D．10°【解答】A【解析】连接OB和OC，∵圆O半径为2，BC＝2，∴△OBC为等边三角形，∴∠BOC＝60°，∴∠A＝30°，故选A．2．刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积，设圆O的半径为1，若用圆O的外切正六边形的面积来近似估计圆O的面积，那么圆O的面积估计值是（）A．√3B．2√3C．πD．2π【解答】B【解析】根据题意画出图形，如图所示，∵六边形ABCDEF为正六边形，∴△ABO是等边三角形，∵圆O的半径为1，∴OM＝1，∴BM＝AM=√33，∴AB=2√33，∴S＝6S△ABO＝6×12×2√33×1＝2√3．答：圆O的面积估计值是2√3．故选B．3．如图，将边长为3的正方形铁丝框ABCD，变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得的扇形ADB的面积为（）A．3 B．6 C．9 D．3π【解答】C【解析】∵正方形ABCD的边长为3，∴AB＝BC＝CD＝AD＝3，即DCB̂的长是3+3＝6，∴扇形DAB的面积是12×6×3＝9，故选C．4．如图，⊙O中，若OA⊥BC、∠AOB＝66°，则∠ADC的度数为（）A．33°B．56°C．57°D．66°【解答】A【解析】如图，连接OC，OB．∵OA⊥BC，̂=AĈ，∴AB∴∠AOC＝∠AOB＝66°，∠AOC＝33°，∴∠ADC=12故选A．5．如图，已知⊙O的半径为5，弦AB、CD所对的圆心角分别是∠AOB、∠COD，若∠AOB与∠COD互补，弦CD＝6，则点O到弦AB的距离为（）A．6 B．8 C．3 D．4【解答】C【解析】延长CO交⊙O于E，连接DE，过O作OF⊥DE于F，OH⊥CD于H，OG⊥AB于G，线段OG的长是点O 到弦AB的距离，∵∠COD和∠DOE互补，∠COD和∠AOB互补，∴∠DOE＝∠AOB，∴DE＝AB，OF＝OG，∵OH⊥DC，CD＝6，OH过O，DC＝3，∠OHD＝∠OHC＝90°，∴DH＝HC=12由勾股定理得：OH=√OD2−DH2=√52−32=4，∵OC＝OE，DH＝HC，OH＝4，∴DE＝2OH＝8，∵OF⊥DE，OF过O，DE＝4，∴DF＝EF=12在Rt△DFO中，由勾股定理得：OF=√OD2−DF2=√52−42=3，∴OG＝OF＝3，即点O到AB的距离是3，故选C．6．如图，△ABC是等腰直角三角形，AC＝BC＝2，以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F，与AB分别相交于点G、H，且EH的延长线与CB的延长线交于点D，则CD的长为（）A．2√2−1 B．2√2C．√2+1 D．2√2−12【解答】C【解析】如右图所示，连接OE、OF，∵⊙O与AC、BC切于点E、F，∴∠OEC＝∠OFC＝90°，OE＝OF，又∵△ABC是等腰直角三角形，∴∠C＝90°，∴四边形CEOF是正方形，∴OE∥BC，又∵以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F，OE＝OF，∴O在∠ACB的角平分线上，∵AC＝BC，∴O是AB中点，∴AE＝CE，又∵AC＝2，∴AE＝CE＝1，∴OE＝OF＝CE＝1，∴OH＝1，∵OE∥CD，∴△OEH∽△BDH，∴OEOH =DBBH，又∵AB=√AC2+BC2=2√2，∴OB=√2，∴11=√2−1，∴BD=√2−1，∴CD＝2+BD=√2+1，故选C．7．如图，四边形ABCD内接于⊙O，AB＝CB，∠BAC＝30°，BD=√3，则AD+CD的值为（）A ．3B ．2√3C ．√3+1D ．不能确定【解答】A【解析】如图，过点B 作BE ⊥AD 于E ，BF ⊥DC 交DC 的延长线于F ．∵AB ＝BC ，∴AB̂=BC ̂， ∴∠BDE ＝∠BDF ，∵∠DEB ＝∠DFB ＝90°，DB ＝DB ，∴△BDE ≌△BDF （AAS ），∴BE ＝BF ，DE ＝DF ，∵∠AEB ＝∠F ＝90°，BA ＝BC ，BE ＝BF ，∴Rt △BEA ≌Rt △BFC （HL ），∴AE ＝CF ，∴AD +DC ＝DE +AE +DF ﹣CF ＝2DF ，∵∠BDF ＝∠BAC ＝30°，BD =√3，∴BF =12BD =√32， ∴DF =√BD 2−BF 2=√(√3)2−(√32)2=32，∴DA +DC ＝3，故选A ．8．如图，Rt △ACB 中，∠C ＝90°，AC ＝6，BC ＝8，半径为1的⊙O 与AC ，BC 相切，当⊙O 沿边CB 平移至与AB 相切时，则⊙O 平移的距离为（）A．3 B．4 C．5 D．6【解答】B【解析】∵Rt△ACB中，∠C＝90°，AC＝6，BC＝8，∴AB＝10，设⊙O与AC相切于D，与BC相切于H，平移后的⊙O′与AB相切于F，与BC相切于E，连接OH，O′D，则点O在O′D上，连接O′F，EO′并延长交AB于G，∴四边形CDOH是正方形，四边形OHEO′是矩形，∴OD＝OH＝O′E＝O′F＝CD＝CH＝1，OO′＝HE，∴EG⊥BC，∵∠C＝90°，∴EG∥AC，∴∠FGE＝∠A，∵∠GFO′＝∠C＝90°，∴∠O′FG∽∠BCA，∴O′FBC =O′GAB，∴18=O′G10，∴O′G=54，∴EG=94，∵GE∥AC，∴△BGE∽△BAC，∴BEBC =EGAC，∴BE8=946，∴BE＝3，∴OO′＝HE＝BC﹣CH﹣BE＝8﹣1﹣3＝4，∴⊙O平移的距离为4，故选B．9．如图，已知⊙O的半径为10，A、B是⊙O上的两点，∠AOB＝90°，C是射线OB上一个动点，连结AC 并延长交⊙O于点D，过点D作DE⊥OD交OB的延长线于点E．当∠A从30°增大到60°时，弦AD在圆内扫过的面积是（）A．100π3−25√3B．50π3C．64π3−16√3D．50π3−25√3【解答】B【解析】过点D作AO的垂线，交AO的延长线于F．当∠A＝30°时，∠DOF＝60°，DF＝OD•sin60°＝10×√32=5√3，S弓形ABD=120π⋅102360−12×10×5√3=1003π﹣25√3，当∠A＝60°时，过点D'作D'F⊥OA于F'，连接OD'，∠D 'OF '＝60°，D 'F '＝5√3，S 弓形ABD '=60⋅π⋅102360−12×10×5√3=503π﹣25√3， ∴S =1003π﹣25√3−（503π﹣25√3）=503π．故选B ．10．如图，在 O 中，AB̂=AC ̂，BC ＝6．AC ＝3√10，I 是△ABC 的内心，则线段OI 的值为（）A ．1B ．√10−3C ．5−√10D ．13√10【解答】C【解析】如图，连接AO ，延长AO 交BC 于H ，连接OB ．∵AB ̂=AC ̂，∴AB ＝AC ，AH ⊥BC ，∴BH ＝CH ＝3，∴AH =√AC 2−CH 2=√(3√10)2−32=9，设OA ＝OB ＝x ，在Rt △BOH 中，∵OB 2＝OH 2+BH 2，∴x 2＝（9﹣x ）2+32，∴x ＝5，∴OH ＝AHAO ＝9﹣5＝4，∵S △ABC =12•BC •AH =12•（AB +AC +BC ）•IH ，=√10−1，∴IH=6+6√10∴OI＝OH﹣IH＝4﹣（√10−1）＝5−√10，故选C．11．如图，在等腰直角△ABC中，斜边AB的长度为8，以AC为直径作圆，点P为半圆上的动点，连接BP，取BP的中点M，则CM的最小值为（）A．3√5B．2√5−√3C．√10−√2D．3√2−√5【解答】C【解析】如图，连接PA、PC，取AB、BC的中点E、F，连接EF、EM、FM，取EF的中点O，连接OM，OC，CM．∵AC是直径，∴∠APC＝90°，∵BE＝EA，BM＝MP，∴EM∥PA，同理FM∥PC，∴∠BME＝∠BPA，∠BMF＝∠BPC，∴∠BME+∠BMF＝∠BPA+∠BPC＝90°，∴∠EMF＝90°，̂，（EF为直径的半圆，图中红线部分）∴点M的轨迹是EF∵BC＝AC，∠ACB＝90°，AB＝8，∴AC＝BC＝4√2，∵AE＝EB，BF＝CF＝2√2，∴EF=12AC＝2√2，EF∥AC，∴∠EFB＝∠EFC＝∠ACB＝90°，OE＝OF＝OM=√2，∴OC=√OF2+CF2=√(√2)2+(2√2)2=√10，∵CM≥OC﹣OM，∴CM≥√10−√2故选C．12．如图，AB是⊙O的直径，点D，C在⊙O上，∠DOC＝90°，AD=√2，BC＝1，则⊙O的半径为（）A．√3B．√52C．√102D．√2+12【解答】C【解析】如图延长DO交⊙O于E，作EF⊥CB交CB的延长线于F，连接BE、EC．∵∠AOD＝∠BOE，∴AD̂=BÊ，∴AD＝BE=√2，∵∠DOC＝∠COE＝90°，OC＝OB＝OE，∴∠OCB＝∠OBC，∠OBE＝∠OEB，∴∠CBE=12（360°﹣90°）＝135°，∴∠EBF＝45°，∴△EBF是等腰直角三角形，∴EF＝BF＝1，在Rt△ECF中，EC=√EF2+CF2=√12+22=√5，∵△OCE 是等腰直角三角形，∴OC =√2=√102．故选C ．二．填空题13．如图，在矩形ABCD 中，AB ＝1，AD =√3，连接BD ，以点C 为圆心，CD 为半径作弧DF ，与BD 交于点E ，则图中阴影部分的面积是．【解答】112π−2−√34【解析】连接CE ，过C 作CF ⊥DE 于F ，∵在矩形ABCD 中，AB ＝1，AD =√3，∴∠A ＝∠DCF ＝90°，DC ＝AB ＝1，BC ＝AD =√3，∴tan ∠BDC =BC CD =√31=√3，∴∠BDC ＝60°，∵CD ＝CE ，∴△DCE 是等边三角形，∴∠DCE ＝60°，DE ＝CD ＝CE ＝1，∵CF ⊥DE ，∴DF ＝EF =12DE =12×1=12，由勾股定理得：CF =√CD 2−DF 2=√12−(12)2=√32， ∴扇形DCE 和△DCE 围成的弓形的面积S ＝S 扇形DCE ﹣S △DCE =60π×12360−12×1×√32=16π−√34，∴阴影部分的面积＝S 扇形DCF ﹣S △DCF ﹣S 弓形=90π×12360−12×1×1−（16π−√34）=112π−2−√34，故答案为112π−2−√34．14．如图，在正方形ABCD 中，AB ＝2，分别以B 、C 为圆心，以AB 的长为半径作弧，则阴影部分的面积为．【解答】2√3−23π【解析】∵在正方形ABCD 中，AB ＝2，分别以B 、C 为圆心，以AB 的长为半径作弧，∴∠DCB ＝90°，BC ＝AB ＝2，弧对应的半径是2，如图，连接BE 、CE ，∵BC ＝CE ＝BE ＝2，∴△BEC 是等边三角形，∴∠EBC ＝∠ECB ＝60°，∴∠DCE ＝30°，S 弓形＝S 扇形EBC ﹣S △EBC =60π×22360−12×2×√3=23π−√3， ∴阴影部分的面积S ＝2（S 扇形DCE ﹣S 弓形）＝2×[30π×22360−（23π−√3）]＝2√3−23π．15．如图，点P 为⊙O 外一点，过点P 作⊙O 的切线PA 、PB ，点A 、B 为切点，连接AO 并延长交PB 的延长线于点C ，过点C 作CD ⊥PO ，交PO 的延长线于点D ．已知PA ＝6，AC ＝8，则CD 的长为．【解答】2√5【解析】连接OB，如图，∵PA、PB为⊙O的切线，∴PB＝PA＝6，OB⊥PC，OA⊥PA，∴∠CAP＝∠CBO＝90°，在Rt△APC中，PC=√62+82=10，∴BC＝PC﹣PB＝4，设⊙O的半径为r，则OA＝OB＝r，OC＝8﹣r，在Rt△BCO中，42+r2＝（8﹣r）2，解得r＝3，∴OA＝3，OC＝5，在Rt△OPA中，OP=√32+62=3√5，∵CD⊥PO，∴∠CDO＝90°，∵∠COD＝∠POA，∠CDO＝∠PAO，∴△COD∽△POA，∴CD：PA＝OC：OP，即CD：6＝5：3√5，∴CD＝2√5．故答案为2√5．16．如图，AB是⊙O的直径，点C，D，E都在⊙O上，∠1＝55°，则∠2＝°．【解答】35【解析】如图，连接AD．∵AB是直径，∴∠ADB＝90°，∵∠1＝∠ADE，∴∠1+∠2＝90°，∵∠1＝55°，∴∠2＝35°，故答案为35．17．如图，正方形ABCD的边长为4，点E是AB边上一个动点，点F是CD边上一个动点，且AE＝CF，过点B作BG⊥EF于点G，连接AG，则AG长的最小值是．【解答】√10−√2【解析】设正方形的中心为O，可证EF经过O点．连结OB，取OB中点M，连结MA，MG，则MA，MG为定长，过点M作MH⊥AB于H．则MH＝BH＝1，AH＝3，OB=√2，由勾股定理可得MA=√10，MG=12∵AG≥AM﹣MG=√10−√2，当A，M，G三点共线时，AG最小=√10−√2，故答案为√10−√2．18．如图，正五边形ABCDE内接于半径为4的圆O，作OF⊥BC交⊙O于点F，连结FA，FB，则FA•FB的值为．【解答】16【解析】连接OA，OB，OB交AF于J．∵OF⊥BC，̂=CF̂，∴BF∵五边形ABCDE是正五边形，∴∠AOB＝72°，∠BOF＝36°，∴∠AOF＝108°，∵OA＝OF，∴∠OAF＝∠OFA＝∠FOJ＝36°，∴OJ＝JF，∵AO＝AJ，OB＝OF，∠OAJ＝∠FOB，∴△AOJ≌△OFB（SAS），∴OJ＝BF，∵∠OFJ＝∠AFO，∠FOJ＝∠OAF，∴△FOJ∽△FAO，∴FOFA =FJOF，∴OF2＝FJ•FA，∵FJ＝OJ＝FB，∴FA•FB＝OF2＝16．故答案为16．19．如图，在平面直角坐标系xOy中，与y轴相切的⊙M与x轴交于A、B两点，AC为⊙M直径，AC＝10，AB＝6，连结BC，点P为劣弧BĈ上点，点Q为线段AB上点，且MP⊥MQ，MP与BC交于点N．则当NQ平分∠MNB时，点P坐标是．【解答】（495，135）【解析】设⊙M与y轴相切于E，连接EM并延长交BC于H，过P作PF⊥x轴于F，延长FP交EH于D，∵AC为⊙M直径，∴BC⊥AB，∵AC＝10，AB＝6，∴BC＝8，∵⊙M与y轴相切，∴EM⊥y轴，∴四边形OEDF是矩形，∴OE ＝BH ＝DF ，ED ＝OF ，ED ∥OF ，∵AM ＝CM ，∴MH =12AB ＝3，BH ＝DF ＝4，∵MP ⊥MQ ，NQ 平分∠MNB ，∴MN ＝BN ，设MN ＝BN ＝x ，∴NH ＝4﹣x ，∵MH 2+HN 2＝MN 2，∴x 2＝32+（4﹣x ）2，解得：x =258，∴MN ＝BN =258， ∴HN =78， ∵HN ∥PD ，∴△MHN ∽△MDP ，∴MH MD =HN PD =MN MP ， ∴3MD =78PD =2585， ∴MD =245，PD =75， ∴DE ＝EM +MD =495，PF ＝DF ﹣PD =135， ∴点P 坐标是（495，135），故答案为（495，135）．20．如图，PA 、PB 切⊙O 于A 、B 两点，连接OP 交AB 于点C ，交弧AB 于点D ，∠APB ＝70°，点Q 为优弧AmB上一点，OQ∥PB，则∠OQA的大小为．【解答】10°【解析】如图，连接OA．∵PA，PB是⊙O的切线，∴∠OPB＝∠OPA=1∠APB＝35°，PA⊥OA，2∴∠OAP＝90°，∴∠POA＝90°﹣35°＝55°，∵OQ∥PB，∴∠POQ＝180°﹣∠OPB＝145°，∴AOQ＝360°﹣145°﹣55°＝160°，∵OQ＝OA，（180°﹣∠AOQ）＝10°，∴∠OQA＝∠OAQ=12故答案为10°．21．如图，等边△ABC中，AB＝2，点D是以A为圆心，半径为1的圆上一动点，连接CD，取CD的中点E，连接BE，则线段BE的最大值与最小值之和为．【解答】2√3【解析】延长CB到T，使得BT＝BC，连接AT，DT，AD．∵△ABC是等边三角形，∴BA＝BC＝AC＝BT＝2，∠ACB＝60°，∴∠CAT＝90°，∴AT＝CT•sin60°＝2√3，∵AD＝1，∴2√3−1≤DT≤2√3+1，∵CB＝BT，CE＝DE，∴BE=12DT，∴2√3−12≤BE≤2√3+12，∴线段BE的最大值与最小值之和为2√3，故答案为2√3．22．如图，等腰△ABC中，底边BC长为8，腰长为6，点D是BC边上一点，过点B作AC的平行线与过A、B、D三点的圆交于点E，连接DE，则DE的最小值是．【解答】2√5【解析】如图，连接AE，AD，OE，OD，作AJ⊥BC于J，OK⊥DE于K．∵BE∥AC，∴∠EBC+∠C＝180°，∵∠EBC+∠EAD＝180°，∴∠EAD＝∠C，∵∠EOD＝2∠EAD，∴∠EOD＝2∠C＝定值，∴⊙O的半径最小时，DE的值最小，∴当AB是⊙O的直径时，DE的值最小，∵AB＝AC＝6，AJ⊥BC，∴BJ＝CJ＝4，∴AJ=√AC2−CJ2=√62−42=2√5，∵OK⊥DE，∴EK＝DK，∵AB＝6，∴OE＝OD＝3，∵∠EOK＝∠DOK＝∠C，∴sin∠EOK＝sin∠C=√53，∴EK3=√53，∴EK=√5，∴DE＝2√5，∴DE的最小值为2√5．故答案为2√5．三．解答题23．如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，交BC于F．（1）若∠ABC＝40°，∠C＝80°，求∠CBD的度数；（2）求证：DB＝DE；（3）若AB＝6，AC＝4，BC＝5，求DE的长．【解答】（1）30°；（2）见解析；（3）2√2【解析】（1）∵∠ABC＝40°，∠C＝80°，∴∠BAC＝180°﹣40°﹣80°＝60°，∵点E是△ABC的内心，∠BAC＝30°，∴∠CAD＝∠BAD=12∴∠CBD＝∠CAD＝30°．答：∠CBD的度数为30°；（2）证明：如图，连接BE，∴∠1＝∠2，∠3＝∠4，∵∠2＝∠6，∴∠1＝∠6，∵∠5＝∠1+∠3，∠DBE＝∠6+∠4＝∠1+∠3，∴∠5＝∠DBE，∴DB＝DE；（3）∵∠1＝∠2，AB＝6，AC＝4，BC＝5，∴ABAC =BFCF=32，∴BF＝3，CF＝2，∵∠6＝∠2，∠D＝∠C，∴△BDF∽△ACF，∴BDDF =ACCF=42=2，BFAF=DFCF，∴DF=12BD，DF•AF＝BF•CF＝6，∵∠1＝∠2＝∠6，∠BDF＝∠ADB，∴△DBF∽△DAB，∴BDDA =DFBD，∴BD2＝DF•DA＝DF（AF+DF）＝DF•AF+DF2＝6+（12BD）2，解得BD＝2√2，∴DE＝BD＝2√2．答：DE的长为2√2．24．如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF＝DA，AE ∥BC交CF于E．（1）求证：EA是⊙O的切线；（2）判断BD与CF的数量关系？说明理由．【解答】（1）见解析；（2）BD＝CF 【解析】（1）证明：如图，连接AO，∵⊙O是等边三角形ABC的外接圆，∴AO平分∠BAC，∴∠OAC=12∠BAC=30°，∵AE∥BC，∴∠CAE＝∠BCA＝60°，∴∠OAE＝∠OAC+∠CAE＝90°，∴OA⊥AE，∴EA为⊙O的切线；（2）BD＝CF，理由如下：∵△ABC为正三角形，∴AB＝AC，∠BAC＝∠ABC＝60°；∵A、B、C、D四边共圆，∴∠ADF＝∠ABC＝60°，∵DF＝DA，∴△ADF为正三角形，∴∠DAF＝60°＝∠BAC，∴∠BAC+∠CAD＝∠DAF+∠CAD，即∠BAD＝∠CAF，在△BAD与△CAF中，{BA=CA∠BAD=∠CAF AD=AF，∴△BAD≌△CAF（SAS），∴BD＝CF．所以BD与CF的数量关系为相等．25．如图，AB为⊙O的直径，C、D为圆上的两点，OC∥BD，弦AD与BC，OC分别交于E、F．（1）求证：AĈ=CD̂；（2）若CE＝1，EB＝3，求⊙O的半径．【解答】（1）见解析；（2）√5【解析】（1）证明：∵AB是圆的直径，∴∠ADB＝90°，∵OC∥BD，∴∠AFO＝∠ADB＝90°，∴OC⊥AD∴AĈ=CD̂．（2）连接AC，如图，∵AĈ=CD̂，∴∠CAD＝∠ABC，∵∠ECA＝∠ACB，∴△ACE∽△BCA，∴ACBC =CEAC，∴AC2＝CE•CB，即AC2＝1×（1+3），∴AC＝2，∵AB是圆的直径，∴∠ACB＝90°，∴AB=√AC2+BC2=√22+42=2√5，∴⊙O的半径为√5．26．如图，在△ABC中，AC＝BC，以BC为直径作⊙O，交AC于点M，作CD⊥AC交AB延长线于点D，E为CD 上一点，且BE＝DE．（1）证明：BE为⊙O的切线；（2）若AM＝8，AB＝8√5，求BE的长．【解答】（1）见解析；（2）BE＝15【解析】（1）证明：∵CD⊥AC，∴∠ACD＝90°，∴∠A+∠D＝90°，∵AC＝BC，BE＝DE，∴∠A＝∠ABC，∠D＝∠DBE，∴∠ABC+∠DBE＝90°，∴∠CBE＝180°﹣90°＝90°，∴CB⊥BE，∴BE为⊙O的切线；（2）连接BM，∵BC为⊙O的直径，∴BM⊥AC，∵AM＝8，AB＝8√5，∴BM=√AB2−AM2=16，∵AC＝BC，∴CM＝BC﹣AM＝BC﹣8，∵BC2＝BM2+CM2，∴BC2＝162+（BC﹣8）2，∴BC＝20，∴AC＝BC＝20，∵BM⊥AC，AC⊥CD，∴BM∥CD，∴∠MBC＝∠BCE，∵∠BMC＝∠CBM＝90°，∴△BMC∽△CBE，∴CMBE =BMBC，∴12BE =1620，∴BE＝15．27．如图，在平行四边形ABCD中，AC是对角线，∠CAB＝90°，以点A为圆心，以AB的长为半径作⊙A，交BC边于点E，交AC于点F，连接DE．（1）求证：DE与⊙A相切；（2）若∠ABC＝60°，AB＝4，求阴影部分的面积．【解答】（1）见解析；（2）4√3−4π3【解析】（1）证明：连接AE，∵四边形ABCD是平行四边形，∴AD ＝BC ，AD ∥BC ，∴∠DAE ＝∠AEB ，∵AE ＝AB ，∴∠AEB ＝∠ABC ，∴∠DAE ＝∠ABC ，∴△AED ≌△BAC （SAS ），∴∠DEA ＝∠CAB ，∵∠CAB ＝90°，∴∠DEA ＝90°，∴DE ⊥AE ，∵AE 是⊙A 的半径，∴DE 与⊙A 相切；（2）∵∠ABC ＝60°，AB ＝AE ＝4，∴△ABE 是等边三角形，∴AE ＝BE ，∠EAB ＝60°，∵∠CAB ＝90°，∴∠CAE ＝90°﹣∠EAB ＝90°﹣60°＝30°，∠ACB ＝90°﹣∠B ＝90°﹣60°＝30°，∴∠CAE ＝∠ACB ，∴AE ＝CE ，∴CE ＝BE ，∴S △ABC =12AB •AC =12×4×4√3=8√3，∴S △ACE =12S △ABC =12×8√3=4√3， ∵∠CAE ＝30°，AE ＝4，∴S 扇形AEF =30π×AE 2360=30π×42360=4π3，∴S 阴影＝S △ACE ﹣S 扇形AEF ＝4√3−4π3．28．如图，四边形ABCD中，∠B＝∠D＝90°，∠C＝60°，⊙O过点D，与AB相切于点A，与CD相交于点E，且AB＝DE．（1）求证：BC与⊙O相切；（2）若⊙O的半径为5，求四边形ABCD的面积．【解答】（1）见解析；（2）50+50√33【解析】（1）连接AE，∵∠D＝90°，∴AE是⊙O的直径，过O作OF⊥BC于F，∵AB是⊙O的切线，∴∠OAB＝90°，∵∠B＝90°，∴∠OAB＝∠B＝∠OFB＝90°，∴四边形ABFO是矩形，∴AB＝OF，∵∠B＝∠D＝90°，∠C＝60°，∴∠DAB＝120°，∴∠DAE＝30°，∴DE =12AE ＝AO ， ∵AB ＝DE ，∴OF ＝OA ，∴BC 与⊙O 相切；（2）由（1）知，AB ＝AO ＝5，AE ＝10，过E 作EH ⊥BC 于H ，则BH ＝AE ＝10，EH ＝AB ＝5，∵∠C ＝60°，∴CH =√33EH =5√33， ∴BC ＝10+5√33，在Rt △ADE 中，∵DE ＝AB ＝5，∴AD =√3DE ＝5√3，∴四边形ABCD 的面积=12×5√3×5+12（10+10+5√33）×5＝50+50√33．29．如图，Rt △ABC 中，∠ABC ＝90°，以AB 为直径的⊙O 交AC 于点D ，E 是BC 的中点，连接DE 、OE ．（1）判断DE 与⊙O 的位置关系并说明理由．（2）若⊙O 半径r ＝3，DE ＝4，求AD 的长．【解答】（1）相切；（2）AD =185【解析】（1）连接OD 、BD ，如图所示．∵点O 为AB 的中点，点E 为BC 的中点，∴OE∥AC，且AC＝2OE，∴∠A＝∠BOE．又∵∠BOD＝2∠A，∴∠DOE＝∠A＝∠BOE．在△BOE和△DOE中，{OB=OD∠BOE=∠DOE OE=OE，∴△BOE≌△DOE（SAS），∴∠ODE＝∠OBE＝90°，∴DE与⊙O相切；（2）∵AB为⊙O的直径，∴BD⊥AC，∴∠ADB＝∠BDC＝90°，∴∠ADB＝∠ABC，∴∠A+∠ABD＝∠A+∠C＝90°，∴∠ABD＝∠C，∴△ABD∽△ACB，∴ABAD =ACAB，∵AB＝6，BC＝2DE＝8，∴AC＝10，∴AB2＝AD•AC，∴62＝AD×10，∴AD=185．30．如图，⊙O为△ABC的外接圆，D为OC与AB的交点，E为线段OC延长线上一点，且∠EAC＝∠ABC．（1）求证：直线AE是⊙O的切线．（2）若D为AB的中点，CD＝6，AB＝16①求⊙O的半径；②求△ABC的内心到点O的距离．【解答】（1）见解析；（2）①25；②53【解析】（1）证明：连接AO，并延长AO交⊙O于点F，连接CF∵AF是直径∴∠ACF＝90°∴∠F+∠FAC＝90°，∵∠F＝∠ABC，∠ABC＝∠EAC∴∠EAC＝∠F∴∠EAC+∠FAC＝90°∴∠EAF＝90°，且AO是半径∴直线AE是⊙O的切线．（2）①如图，连接AO，∵D为AB的中点，OD过圆心，∴OD⊥AB，AD＝BD=12AB＝8，∵AO2＝AD2+DO2，∴AO2＝82+（AO﹣6）2，∴AO=253，∴⊙O的半径为253；②如图，作∠CAB的平分线交CD于点H，连接BH，过点H作HM⊥AC，HN⊥BC，∵OD⊥AB，AD＝BD∴AC＝BC，且AD＝BD∴CD平分∠ACB，且AH平分∠CAB∴点H是△ABC的内心，且HM⊥AC，HN⊥BC，HD⊥AB∴MH＝NH＝DH在Rt△ACD中，AC=√AD2+CD2=√82+62=10=BC，∵S△ABC＝S△ACH+S△ABH+S△BCH，∴12×16×6=12×10×MH+12×16×DH+12×10×NH，∴DH=83，∵OH＝CO﹣CH＝CO﹣（CD﹣DH），∴OH=253−（6−83）═5．。

2.5 第1课时直线与圆的位置关系-2020秋苏科版九年级数学上册课件(共22张PPT)

随堂练习
6.如图，在Rt△ABC中，∠A=90°，∠B=30°，点O为BC上
一点，OB=2，AC=3，以点O为圆心，r为半径的⊙O与
△ABC的一边相切，求r的值.
解 ∵∠A=90°，∠B=30°，AC=3，
∴BC=2AC=6.
D
∵OB=2，∴OC=4.
当⊙O与AB相切时，过点O作
OD⊥AB于点D，
2 直线与圆的位置关系的性质
例已知∠BAC=45°，点O在AC上，且AO=4，以点O为
圆心，r为半径画圆.根据下列r的值，判断AB所在直线与
⊙O的位置关系：
C
(1)r=2;
(2)r= 2 2;
(3)r=3.
解: 过点O作OD⊥AB，垂足为D.
O
在Rt△AOD中，∵∠A=45°，
∴∠AOD=∠A，OD=AD.
例 (1)r=2;
(2)r=2 2 ;
(3)r=3.
(2)当r= 2 2时，d=r，AB所在直线与⊙O 相切（如图） C
O
A
D
B
课程讲授
2 直线与圆的位置关系的性质
例 (1)r=2;
(2)r=2 2 ;
(3)r=3.
(3)当r=3时，d＜r，AB所在直线与⊙O 相交（如图） C
O
A
D
B
课程讲授
2 直线与圆的位置关系的性质
课程讲授
1 直线与圆的位置关系
O O
直线和圆有一个公共点
定义：直线和圆有一个公共点，这时我们说这条直
线和圆相切，这条直线叫做圆的切线，这个公共点叫做圆的切点.
课程讲授
1 直线与圆的位置关系
O
O
直线和圆没有公共点

直线与圆的位置关系-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

直线与圆的位置关系知识点一、直线与圆的位置关系直线与圆有三种位置关系，如下所示：判定直线与圆的位置关系通常有以下两种方法：（1）根据直线与圆的公共点的个数判断；（2）根据圆心到直线的距离与半径的大小关系判断. 知识点二、切线的判定定理与切线的性质定理1. 切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.如图所示，OA 的一条半径，直线l 经过点A 且OA ⊥l ，则l 的切线.判定一条直线是否是圆的切线共有以下三种方法：（1）定义法：当直线与圆有且只有一个公共点时，直线与圆相切；（2）数量关系法：当圆心到直线的距离等于半径时，直线与圆相切；（3）判定定理法：经过半径的外端，并且垂直于这条半径的直线是圆的切线.2.切线的性质定理：圆的切线垂直于经过切点的半径.如图所示：直线l的切线，切点为点A，则OA⊥l.例：如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB．（1）求证：PB是的切线．（2）若PB=6，DB=8，求⊙O的半径.【解答】（1）见解析；（2）3【解析】（1）证明：∵在△DEO和△PBO中，∠EDB=∠EPB，∠DOE=∠POB，∴∠OBP=∠E=90°，∵OB为圆的半径，∴PB为圆O的切线；（2）在Rt△PBD中，PB=6，DB=8，根据勾股定理得，∵PD与PB都为圆的切线，∴PC=PB=6，∴DC=PD﹣PC=10﹣6=4，在Rt△CDO中，设OC=r，则有DO=8﹣r，根据勾股定理得：（8﹣r）2=r2+42，解得：r=3，则圆的半径为3.知识点三、三角形的内切圆1.定义：与三角形各边都相切的圆叫做三角形的内切圆.三角形内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.2.性质：三角形的内心就是三角形三条内角平分性的交点，内心到三角形各边的距离相等，任意三角形的内心都在三角形的内部.3.三角形的内切圆的作法：作三角形任意两个内角平分线，它们的交点就是内切圆的圆心，过圆心向任意一条边作垂线，垂线段的长度就是内切圆的半径.补充：三角形外心与内心对比：例：直角三角形的两条直角边分别为8和15，那么这个直角三角形最大能容纳一个直径为几的圆？【解答】6【解析】如图所示：由勾股定理可求出三角形斜边AB＝17，设三角形的内切圆的半径为r即，解得半径，则直径为6.知识点四、切线长及切线长定理1.切线长定义：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长；2.切线长定理：过圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.外一点P引两条切线PA、PB，切点分别为A、B，连接OA、OB、AB，延长PO并延长交圆于点E，则：①垂直：OA⊥PA，OB⊥PB，OD⊥AB；②全等：△OAP≌△OBP，△OCA≌△OCB，△ACP≌△BCP；③弧相等：.巩固练习一．选择题1．如图，PA、PB分别与⊙O相切于A、B两点，点C为⊙O上一点，连接AC、BC，若∠C＝65°，则∠P的度数为（）A．50°B．65°C．70°D．80°【解答】A【解析】连接OA 、OB ，∵PA 、PB 是⊙O 切线， ∴PA ⊥OA ，PB ⊥OB ， ∴∠PAO ＝∠PBO ＝90°，∵∠P +∠PAO +∠AOB +∠PBO ＝360°， ∴∠P ＝180°﹣∠AOB ， ∵∠ACB ＝65°，∴∠AOB ＝2∠ACB ＝130°， ∴∠P ＝180°﹣130°＝50°，故选A ．2．平面直角坐标系中，⊙P 的圆心坐标为（﹣4，﹣5），半径为5，那么⊙P 与y 轴的位置关系是（） A ．相交 B ．相离 C ．相切 D ．以上都不是【解答】A【解析】∵⊙P 的圆心坐标为（﹣4，﹣5）， ∴⊙P 到y 轴的距离d 为4 ∵d ＝4＜r ＝5 ∴y 轴与⊙P 相交故选A ．3．三角形的三边长分别为6，8，10，则它的边与半径为2的圆的公共点个数最多为（） A ．3 B ．4 C ．5 D ．6【解答】B【解析】∵62+82＝100，102＝100， ∴三角形为直角三角形，设内切圆半径为r ，则12（6+8+10）r =12×6×8，解得r ＝2，所以应分为五种情况：当一条边与圆相离时，有0个交点，当一条边与圆相切时，有1个交点，当一条边与圆相交时，有2个交点，当圆为三角形内切圆时，有3个交点，当两条边与圆同时相交时，有4个交点，故公共点个数可能为0、1、2、3、4个．∴则它的边与半径为2的圆的公共点个数最多为4个，故选B．4．如图，AB是圆O的直径．点P是BA延长线上一点，PC与圆O相切，切点为C，连接OC，BC，如果∠P ＝40°，那么∠B的度数为（）A．40°B．25°C．35°D．45°【解答】B【解析】∵PC与圆O相切，切点为C，∴OC⊥PC，∴∠OCP＝90°，∵∠P＝40°，∴∠POC＝90°﹣∠P＝90°﹣40°＝50°，∵OB＝OC，∴∠B＝∠OCB，∵∠POC＝∠B+∠C，∠POC＝25°．∴∠B=12故选B．5．如图，已知PA，PB是⊙O的两条切线，A，B为切点，线段OP交⊙O于点M．给出下列四种说法：①PA＝PB；②OP⊥AB；③四边形OAPB有外接圆；④M是△AOP外接圆的圆心．其中正确说法的个数是（）A．1 B．2 C．3 D．4【解答】C【解析】∵PA，PB是⊙O的两条切线，A，B为切点，∴PA＝PB，所以①正确；∵OA＝OB，PA＝PB，∴OP垂直平分AB，所以②正确；∵PA，PB是⊙O的两条切线，A，B为切点，∴OA⊥PA，OB⊥PB，∴∠OAP＝∠OBP＝90°，∴点A、B在以OP为直径的圆上，∴四边形OAPB有外接圆，所以③正确；∵只有当∠APO＝30°时，OP＝2OA，此时PM＝OM，∴M不一定为△AOP外接圆的圆心，所以④错误．故选C．6．如图，点D是△ABC中BC边的中点，DE⊥AC于E，以AB为直径的⊙O经过D，连接AD，有下列结论：AC；④DE是⊙O的切线．其中正确的结论是（）①AD⊥BC；②∠EDA＝∠B；③OA=12A．①②B．①②③C．②③D．①②③④【解答】D【解析】∵AB是⊙O直径，∴∠ADB＝90°，∴AD⊥BC，选项①正确；连接OD，如图，∵D为BC中点，O为AB中点，∴DO为△ABC的中位线，∴OD∥AC，又DE⊥AC，∴∠DEA＝90°，∴∠ODE＝90°，∴DE为圆O的切线，选项④正确；又OB＝OD，∴∠ODB＝∠B，∵AB为圆O的直径，∴∠ADB＝90°，∵∠EDA+∠ADO＝90°，∠BDO+∠ADO＝90°，∴∠EDA＝∠BDO，∴∠EDA＝∠B，选项②正确；由D为BC中点，且AD⊥BC，∴AD垂直平分BC，AB，∴AC＝AB，又OA=12AC，选项③正确；∴OA=12则正确的结论为①②③④．故选D．7．如图，在矩形ABCD中，AB＝5，BC＝4，以CD为直径作⊙O．将矩形ABCD绕点C旋转，使所得矩形A'B'C'D'的边A'B'与⊙O相切，切点为E，边CD'与⊙O相交于点F，则CF的长为（）A．2.5 B．1.5 C．3 D．4【解答】D【解析】如图，连接OE并延长交CF于点H，∵矩形ABCD 绕点C 旋转得矩形A 'B 'C 'D '， ∴∠B ′＝∠B ′CD ′＝90°，A ′B ′∥CD ′，BC ＝B ′C ＝4，∵边A 'B '与⊙O 相切，切点为E ， ∴OE ⊥A ′B ′，∴四边形EB ′CH 是矩形， ∴EH ＝B ′C ＝4，OH ⊥CF ，∵AB ＝5，∴OE ＝OC =12AB =52， ∴OH ＝EH ﹣OE =32，在Rt △OCH 中，根据勾股定理，得CH =√OC 2−OH 2=√(52)2−(32)2=2，∴CF ＝2CH ＝4．故选D ．8．如图，△ABC 内接于⊙O ，BD 切⊙O 于点B ，AB ＝AC ，若∠CBD ＝40°，则∠ABC 等于（）A ．40°B ．50°C ．60°D ．70°【解答】D【解析】∵BD 切⊙O 于点B ， ∴∠DBC ＝∠A ＝40°， ∵AB ＝AC ， ∴∠ABC ＝∠C ，∴∠ABC ＝（180°﹣40°）÷2＝70°．故选D．9．如图，PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D．若△PCD的周长等于3，则PA 的值是（）A．32B．23C．12D．34【解答】A【解析】∵PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D，∴AC＝EC，DE＝DB，PA＝PB∵△PCD的周长等于3，∴PA+PB＝3，∴PA=32．故选A．10．如图，A、B、C、D为⊙O上的点，直线BA与DC相交于点P，PA＝2，PC＝CD＝3，则PB＝（）A．6 B．7 C．8 D．9【解答】D【解析】∵PB，PD是⊙O的割线，∴PA•PB＝PC•PD，∵PA＝2，PC＝CD＝3，∴2PB＝3×6解得：PB＝9．故选D．11．如图，这条花边中有4个圆和4个正三角形，且这条花边的总长度AB为4，则花边上正三角形的内切圆半径为（）A．√33B．23√3C．1 D．√3【解答】A【解析】如图，选择一个等边三角形和其内切圆，圆O是等边三角形ACE的内切圆，圆O切三角形的边CE于点D，∵这条花边的总长度AB为4，∴CE＝2，连接OC，AD，则AD过点O，∴CD＝DE=12CE＝1，∵△ACE是等边三角形，∴∠ACE＝60°，∵圆O是等边三角形ACE的内切圆，∴∠OCD＝30°，∴OD＝CD•tan30°=√33．∴花边上正三角形的内切圆半径为√33．故选A．二．填空题12．在矩形ABCD中，AB＝6，BC＝8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是．【解答】103＜AO＜203【解析】在矩形ABCD中，∵∠D＝90°，AB＝6，BC＝8，∴AC＝10，如图1，设⊙O与AD边相切于E，连接OE，则OE⊥AD，∴OE∥CD，∴△AOE∽△ACD，∴OECD =AOAC，∴AO10=26，∴AO=103，如图2，设⊙O与BC边相切于F，连接OF，则OF⊥BC，∴OF∥AB，∴△COF∽△CAB，∴OCAC =OFAB，∴OC10=26，∴OC=103，∴AO=203，∴如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是103＜AO＜203，故答案为103＜AO＜203．13．如图，⊙O的半径为6cm，B为⊙O外一点，OB交⊙O于点A，AB＝OA，动点P从点A出发，以πcm/s 的速度在⊙O上按逆时针方向运动一周回到点A立即停止．当点P运动的时间为时，BP与⊙O相切．【解答】2秒或10秒【解析】连接OP∵当OP⊥PB时，BP与⊙O相切，∵AB＝OA，OA＝OP，∴OB＝2OP，∠OPB＝90°；∴∠B＝30°；∴∠O＝60°；∵OA＝6cm，=2π，弧AP=60π×6180∵圆的周长为：12π，∴点P运动的距离为2π或12π﹣2π＝10π；∴当t＝2秒或10秒时，有BP与⊙O相切．故答案为2秒或10秒．14．在Rt△ABC中，∠C＝90°，AC＝BC，若以点C为圆心，以2cm长为半径的圆与斜边AB相切，那么BC的长等于．【解答】2√2cm【解析】过C点作CD⊥AB于D，如图，∵⊙C与AB相切，∴CD为⊙C的半径，即CD＝2，∵∠C＝90°，AC＝BC，∴∠B＝45°，∴△CDB为等腰直角三角形，∴BC=√2CD＝2√2（cm）．故答案为2√2cm．15．如图，在矩形ABCD中，已知AB＝6，BC＝4，以CD为直径作⊙O，将矩形ABCD绕点C旋转，使所得矩形A′B′C′D′的边A′B′与⊙O相切，切点为M，边CD′与⊙O相交于点N，则CN的长为．【解答】4√2【解析】连接OM，延长MO交CD于点G，作OH⊥B′C于点H，则∠OMB′＝∠OHB′＝90°，∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′，∴∠B′＝∠B′CD′＝90°，AB＝CD＝6，BC＝B′C＝4，∴四边形OMB′H和四边形MB′CG都是矩形，OE＝OD＝OC＝3，∴B′H＝OM＝3，∴CH＝B′C﹣B′H＝1，∴CG＝B′M＝OH=√OC2−CH2=2√2，∵四边形MB′CG是矩形，∴∠OGC＝90°，即OG⊥CD′，∴CN＝2CG＝4√2，故答案为4√2．16．如图，正方形ABCD的边长为8，E为AB中点，F为BC边上的动点，连接EF，以点F为圆心，EF长为半径作⊙F．当⊙F与AD边相切时，CF的长为．【解答】8﹣4√3【解析】当⊙F与直线AD相切时．设切点为K，连接FK，如图：则FK⊥AD，四边形FKDC是矩形．∴FE＝FK＝CD＝2BE，∴BE＝4，FE＝8，在Rt△FBE中，FB=√FE2−BE2=√82−42=4√3，∴CF＝BC﹣FB＝8﹣4√3．故答案为8﹣4√3．17．一个菱形的周长是20cm，两对角线之比是4：3，则该菱形的内切圆的半径是cm．【解答】125【解析】如图所示：菱形ABCD，对角线AC，BD，可得菱形内切圆的圆心即为对角线交点，设AB与圆相切于点E，可得OE⊥AB，∵一个菱形的周长是20cm，两对角线之比是4：3，∴AB＝5cm，设BO＝4x，则AO＝3x，故（4x）2+（3x）2＝25，解得：x＝1，则AO＝3，BO＝4，故EO•AB＝AO•BO，解得：EO=12．5．故答案为12518．以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点F，交AB边于点E，若△CDE的周长为12，则直角梯形ABCE周长为．【解答】14【解析】设AE的长为x，正方形ABCD的边长为a，∵CE与半圆O相切于点F，∴AE＝EF，BC＝CF，∵EF+FC+CD+ED＝12，∴AE+ED+CD+BC＝12，∵AD＝CD＝BC＝AB，∴正方形ABCD的边长为4；在Rt△CDE中，ED2+CD2＝CE2，即（4﹣x）2+42＝（4+x）2，解得：x＝1，∵AE+EF+FC+BC+AB＝14，∴直角梯形ABCE周长为14．故答案为14．19．如图，在△ABC中，∠C＝90°，AC＝3，BC＝4，则△ABC的内切圆半径r＝．【解答】1【解析】在△ABC中，∠C＝90°，AC＝3，BC＝4，根据勾股定理，得AB＝5，如图，设△ABC的内切圆与三条边的切点分别为D、E、F，连接OD、OE、OF，∴OD⊥AB，OE⊥BC，OF⊥AC，∵∠C＝90°，∴四边形EOFC是矩形，根据切线长定理，得CE＝CF，∴矩形EOFC是正方形，∴CE＝CF＝r，∴AF＝AD＝AC﹣FC＝3﹣r，BE＝BD＝BC﹣CE＝4﹣r，∵AD+BD＝AB，∴3﹣r+4﹣r＝5，解得r＝1．则△ABC的内切圆半径r＝1．故答案为1．20．已知△ABC的三边a、b、c满足b+|c﹣3|+a2﹣8a＝4√b−1−19，则△ABC的内切圆半径＝．【解答】1【解析】∵b+|c﹣3|+a2﹣8a＝4√b−1−19，∴|c﹣3|+（a﹣4）2+（√b−1−2）2＝0，∴c＝3，a＝4，b＝5，∵32+42＝25＝52，∴c2+a2＝b2，∴△ABC是直角三角形，∠ABC＝90°，设内切圆的半径为r，根据题意，得S△ABC=12×3×4=12×3×r+12×4×r+12×r×5，∴r＝1，故答案为1．21．如图，在Rt△AOB中，OB＝2√3，∠A＝30°，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O 的一条切线PQ（其中点Q为切点），则线段PQ长度的最小值为．【解答】2√2【解析】连接OP、OQ，作OP′⊥AB于P′，∵PQ是⊙O的切线，∴OQ⊥PQ，∴PQ=√OP2−OQ2=√OP2−1，当OP最小时，线段PQ的长度最小，当OP⊥AB时，OP最小，在Rt△AOB中，∠A＝30°，=6，∴OA=OBtanA在Rt△AOP′中，∠A＝30°，OA＝3，∴OP′=12∴线段PQ长度的最小值=√32−1=2√2，故答案为2√2．三．解答题22．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【解答】（1）BC与⊙O相切，理由见解析；（2）BD=1207【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AEAD =ADAC，10 8=8AC，∴AC =325，∴CD =√AD 2−AC 2=√82−(325)2=245， ∵OD ⊥BC ，AC ⊥BC ，∴OD ∥AC ，∴△OBD ∽△ABC ，∴OD AC=BD BC ， ∴5325=BD BD+245， ∴BD =1207．23．如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为H ，P 是CD 延长线上一点，DE ⊥AP ，垂足为E ，∠EAD ＝∠HAD ．（1）求证：AE 为⊙O 的切线；（2）已知PA ＝2，PD ＝1，求⊙O 的半轻和DE 的长．【解答】（1）见解析；（2）DE 的长为35，⊙O 的半径为32 【解析】（1）证明：连接AO 并延长交⊙O 于点M ，连接MD ，如图，∵AB ⊥CD ，∴AD̂=BD ̂， ∴∠M ＝∠BAD ，∵∠EAD ＝∠HAD ．∴∠M ＝∠EAD ，∵AM 为直径，∴∠ADM ＝90°，∴∠M +∠MAD ＝90°，∴∠EAD +∠MAD ＝90°，即∠MAE ＝90°，∴AM ⊥AE ，∴AE 为⊙O 的切线；（2）∵∠EAD ＝∠HAD ，DH ⊥AH ，DE ⊥AE ，AD ＝AD ，∴△AHD ≌△AED （AAS ）∴DE ＝DH ，AH ＝AE ，设DE ＝x ，AH ＝y ，则DH ＝x ，AE ＝y ，∵∠EPD ＝∠HPA ，∠PED ＝∠PHA ＝90°，∴Rt △PED ∽Rt △PHA ，∴DE AH =PE PH =PD PA ，即x y =2−y 1+x =12， ∴解得x =35，y =65，即DE 的长为35，AH =65，设圆的半径为r ，则OH ＝r −35，在Rt △OAH 中，（r −35）2+（65）2＝r 2，解得r =32，即⊙O 的半径为32．答：⊙O 的半轻和DE 的长分别为：32，35．24．如图，AB 是⊙O 的直径，AB ＝6，OC ⊥AB ，OC ＝5，BC 与⊙O 交于点D ，点E 是BD ̂的中点，EF ∥BC ，交OC 的延长线于点F ．（1）求证：EF 是⊙O 的切线；（2）CG∥OD，交AB于点G，求CG的长．【解答】（1）见解析；（2）CG=173【解析】证明：（1）连接OE，交BD于H，∵点E是BD̂的中点，OE是半径，∴OE⊥BD，BH＝DH，∵EF∥BC，∴OE⊥EF，又∵OE是半径，∴EF是⊙O的切线；（2）∵AB是⊙O的直径，AB＝6，OC⊥AB，∴OB＝3，∴BC=√OB2+OC2=√9+25=√34，∵S△OBC=12×OB×OC=12×BC×OH，∴OH=√34=15√3434，∵cos∠OBC=OBBC =BHOB，∴√34=BH3，∴BH=9√3434，∴BD＝2BH=9√3417，∵CG∥OD，∴ODCG =BDBC，∴3CG =9√3417√34，∴CG=173．25．如图，△ABC中，BC＝14，AC＝9，AB＝13，它的内切圆分别和BC，AB，AC切于点D，E，F，求AE，BD 和CF的长．【解答】AE＝4，BD＝9，CF＝5【解析】设AE＝x，∵△ABC的内切圆分别和BC，AB，AC切于点D，E，F，∴AF＝AE＝x，BE＝BD，CD＝CF，而BE＝BA﹣AE＝13﹣x，CF＝CA﹣AF＝9﹣x，∴BD＝13﹣x，CD＝9﹣x，而BD+CD＝BC，∴13﹣x+9﹣x＝14，解得x＝4，∴AE＝4，BD＝9，CF＝5．26．已知PA、PB分别切⊙O于A、B，E为劣弧AB上一点，过E点的切线交PA于C、交PB于D．（1）若PA＝6，求△PCD的周长．（2）若∠P＝50°求∠DOC．【解答】（1）△PCD的周长＝12；（2）∠COD＝65°【解析】（1）连接OE，∵PA、PB与圆O相切，∴PA＝PB＝6，同理可得：AC＝CE，BD＝DE，△PCD的周长＝PC+PD+CD＝PC+PD+CE+DE＝PA+PB＝12；（2）∵PA PB与圆O相切，∴∠OAP＝∠OBP＝90°∠P＝50°，∴∠AOB＝360°﹣90°﹣90°﹣50°＝130°，在Rt△AOC和Rt△EOC中，{OA=OEOC=OC，∴Rt△AOC≌Rt△EOC（HL），∴∠AOC＝∠COE，同理：∠DOE＝∠BOD，∠AOB＝65°．∴∠COD=1227．已知PA、PB、DE是⊙O的切线，切点分别为A、B、F，PO＝13cm，⊙O的半径为5cm，求△PDE的周长．【解答】24cm【解析】连接OA，则OA⊥PA．在直角三角形APO中，PO＝13cm，OA＝5cm，根据勾股定理，得AP＝12cm．∵PA、PB、DE是⊙O的切线，切点分别为A、B、F，∴PA＝PB，DA＝DF，EF＝EB，∴△PDE的周长＝2PA＝24cm．28．如图，⊙O是梯形ABCD的内切圆，AB∥DC，E、M、F、N分别是边AB、BC、CD、DA上的切点．（1）求证：AB+CD＝AD+BC；（2）求∠AOD的度数．【解答】（1）见解析；（2）∠AOD＝90°【解析】（1）证明：∵⊙O切梯形ABCD于E、M、F、N，由切线长定理：AE＝AN，BE＝BM，DF＝DN，CF＝CM，∴AE+BE+DF+CF＝AN+BM+DN+CM，∴AB+DC＝AD+BC；（2）连OE、ON、OM、OF，∵OE＝ON，AE＝AN，OA＝OA，∴△OAE≌△OAN，∴∠OAE＝∠OAN．同理，∠ODN＝∠ODF．∴∠OAN+∠ODN＝∠OAE+∠ODE．又∵AB∥DC，∠EAN+∠CDN＝180°，×180°＝90°，∴∠OAN+∠ODN=12∴∠AOD＝180°﹣90°＝90°．。

圆-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

圆知识点一、圆的定义及表示1.圆的定义定义一、如图所示，将线段OP的一个端点O固定，使线段OP绕端点O在平面上旋转一周，另一个端点P运动所形成的图形叫做圆，其中，点O叫做圆心，线段OP叫做半径.定义二、圆是到定点的距离等于定长的点的集合，其中，定点叫做圆心，定长叫做半径.（1）圆上的各点到定点（圆心）的距离都等于定长（半径）；（2）到定点的距离等于定长的点都在同一个圆上.O”，读作“圆O”.2.圆的表示方法：以点OPS：确定一个圆需要两个要素，一个是圆心（确定圆的位置），一个是半径（确定圆的大小）.例：以已知点O为圆心，可以画个圆，以已知线段AB的长为半径，可以画个圆，以已知点O为圆心，已知线段AB的长为半径，可以画个圆.【解答】无数；无数；一【解析】确定一个圆的条件有两个，圆心和半径，缺一不可，前两问都只有一个条件，无法确定圆，最后一问两个条件都确定了，所以圆也就确定了.知识点二、点和圆的位置关系点和圆共有三种位置关系，分别是点在圆内，点在圆上，点在圆外，如下表所示：注：1.“”读作“等价于”，它表示从符号“”的左端可以推出右端，从右端也可以推出左端.2.点在圆上，指的是点在圆周上，而不是点在圆面上. 例：如图所示，已知矩形ABCD 的边AB ＝3，AD ＝4. （1）以点A 为圆心，4，则点B 、C 、D A 的位置关系如何？（2）若以点A 为圆心作，使B 、C 、D 的半径r 取值范围如何？【解答】见解析【解析】（1）连接AC ，如图所示：∵AB ＝3＜4，AD ＝4，由勾股定理得AC ＝5＞4， ∴点B 内，点D 上，点C 在A 外；（2）当点B在上时，r＝AB＝3，当点C上时，r＝AC＝5，∴3＜r＜5.知识点三、与圆有关的概念.1.弦：连接圆上任意两点的线段叫做弦，如图所示的弦AC；直径：经过圆心的弦叫做直径，如图所示的直径AB.弦与直径的关系：直径是圆中最长的弦，但弦不一定是直径；2.弧、半圆、优弧、劣弧（1）弧：圆上任意两点间的部分叫做圆弧，简称为弧；（2）半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆；（3）优弧：大于半圆的弧叫做优弧，用三个字母表示，如图所示的（绿色部分）；（4）劣弧：小于半圆的弧叫做劣弧，用两个字母表示，如图所示的（蓝色部分）.①弧与弦的区别：弧上圆上两点间的部分，是一条曲线，弦是圆上两点间的线段；②半圆是弧，但弧不一定是半圆.3.圆心角：定点在圆心的角叫做圆心角，如图所示的∠AOB.（1）在同一个圆中，圆的两条半径所夹的角就是圆心角；（2）一条弧所对的圆心角只有一个.4.等圆：能够重合的两个圆叫做等圆（半径相等的两个圆就是等圆），等圆和圆心的位置无关；5.等弧：能够互相重合的弧叫做等弧（长度相等的弧不一定是等弧）.中，AB的弦，C、D是直线AB上的两点，且AC＝BD，求证：△OCD为等腰三角形.【解答】见解析【解析】连接OA、OB，如图所示：∵OA、OB O的半径，∴OA＝OB，∴∠OAB＝∠OBA，∴∠OAC＝∠OBD，在△OAC与△OBD中，，∴△OAC≌△OBD，∴OC＝OD，即△OCD是等腰三角形.巩固练习一．选择题1．到定点的距离等于定长的点的集合是（）A．圆的外部B．圆的内部C．圆D．圆的内部和圆【解答】C【解析】圆可以看做是所有到定点O的距离等于定长r的点的集合．故选C．2．到圆心的距离大于半径的点的集合是（）A．圆的内部B．圆的外部C．圆D．圆的外部和圆【解答】B【解析】根据点和圆的位置关系，知圆的外部是到圆心的距离大于的所有点的集合；故选B．3．下列说法正确的是（）A．弦是直径B．弧是半圆C．直径是圆中最长的弦D．半圆是圆中最长的弧【解答】C【解析】A、直径是弦，但弦不一定是直径，故错误，不符合题意；B、半圆是弧，但弧不一定是半圆，故错误，不符合题意；C、直径是圆中最长的弦，正确，符合题意；D、半圆是小于优弧而大于劣弧的弧，故错误，不符合题意，故选C．4．下列说法中，正确的是（）A．弦是直径B．半圆是弧C．过圆心的线段是直径D．圆心相同半径相同的两个圆是同心圆【解答】B【解析】A、直径是弦，但弦不一定是直径，故错误；B、半圆是弧，正确；C、过圆心的弦是直径，故错误；D、圆心相同半径不同的两个圆是同心圆，故错误，故选B．5．下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆．正确的说法有（）A．1个B．2个C．3个D．4个【解答】C【解析】①直径是弦，正确，符合题意；②弦不一定是直径，错误，不符合题意；③半径相等的两个半圆是等弧，正确，符合题意；④能够完全重合的两条弧是等弧，故原命题错误，不符合题意；⑤半圆是弧，但弧不一定是半圆，正确，符合题意，正确的有3个，故选C．6．已知⊙O中最长的弦长8cm，则⊙O的半径是（）A．2cm B．4cm C．8cm D．16cm【解答】B【解析】∵⊙O中最长的弦为8cm，即直径为8cm，∴⊙O的半径为4cm．故选B．7．已知⊙O的半径是5cm，则⊙O中最长的弦长是（）A．5cm B．10cm C．15cm D．20cm【解答】B【解析】∵⊙O的半径是5cm，∴⊙O中最长的弦，即直径的长为10cm，故选B．8．如图，图中的弦共有（）A．1条B．2条C．3条D．4条【解答】B【解析】图形中有弦AB和弦CD，共2条，故选B．9．对于以下图形有下列结论，其中正确的是（）A．如图①，AC是弦̂组成半圆B．如图①，直径AB与ABC．如图②，线段CD是△ABC边AB上的高D．如图②，线段AE是△ABC边AC上的高【解答】C【解析】A、AC不是弦，故错误；B、半圆是弧，不包括弧所对的弦，故错误；C、线段CD是△ABC边AB上的高，正确；D、线段AE不是△ABC边AC上的高，故错误，故选C．10．如图，⊙O的直径BA的延长线与弦DC的延长线交于点E，且CE＝OB，已知∠DOB＝72°，则∠E等于（）A．36°B．30°C．18°D．24°【解答】D【解析】如图：CE＝OB＝CO，得∠E＝∠1．由∠2是△EOC的外角，得∠2＝∠E+∠1＝2∠E．由OC＝OD，得∠D＝∠2＝2∠E．由∠3是三角形△ODE的外角，得∠3＝E+∠D＝∠E+2∠E＝3∠E．由∠3＝72°，得3∠E＝72°．解得∠E＝24°．故选D．11．如图，在⊙O中，弦的条数是（）A．2 B．3C．4 D．以上均不正确【解答】C【解析】如图，在⊙O中，有弦AB、弦DB、弦CB、弦CD．共有4条弦．故选C．12．如图，AB是⊙O的直径，半径OC⊥AB，点D是弧ACB上的动点（不与A、B、C重合），DE⊥OC，DF⊥AB，垂足分别是E、F，则EF长度（）A．变大B．变小C．不变D．无法确定【解答】C【解析】连接OD，如图，∵OC⊥AB，DE⊥OC，DF⊥AB，∴∠EOF＝∠DEO＝∠DFO＝90°，∴四边形DEOF为矩形，∴EF＝OD．故选C．13．如图，在平面直角坐标系中，C（0，4），A（3，0），⊙A半径为2，P为⊙A上任意一点，E是PC的中点，则OE的最小值是（）C．2 D．√2A．1 B．32【解答】B【解析】如图，连接AC，取AC的中点H，连接EH，OH．∵CE＝EP，CH＝AH，PA＝1，∴EH=12∴点E的运动轨迹是以H为圆心半径为1的圆，∵C（0，4），A（3，0），∴H（1.5，2），∴OH=√22+1．52=2.5，∴OE的最小值＝OH﹣EH＝2.5﹣1＝1.5，故选B．二．填空题14．参加篝火晚会时，人们会自然围成一个圆，这是因为圆上任意一点到圆心的距离都，这个距离就是这个圆的．【解答】相等，半径【解析】参加篝火晚会时，人们会自然围成一个圆，这是因为圆上任意一点到圆心的距离都相等，这个距离就是这个圆的半径．故答案为相等，半径．15．圆的半径为3cm，则该圆的周长是cm．【解答】6π【解析】圆的周长＝2πr＝2×π×3＝6π（cm），故答案为6π．16．平面内，到定点O的距离等于3 cm的点集合是．【解答】以点O为圆心，3cm为半径的圆【解析】根据圆的定义可知，到定点O的距离等于3cm的点的集合是以点O为圆心，3cm为半径的圆．故答案为以点O为圆心，3cm为半径的圆.17．过圆内一点（非圆心）有条弦，有条直径．【解答】无数，1【解析】过圆内一点（非圆心）有无数条弦，有1条直径．故答案为无数，1．18．两端都在圆上的线段叫做直径．（判断对错）【解答】错误【解析】两端都在圆上的线段叫做直径，（错误），缺少条件：过圆心．故答案为错误．19．如图，在⊙O 中，是直径，是弦，以E 为端点的劣弧有，以A 为端点的优弧有．【解答】见解析【解析】在⊙O 中，AB 是直径，CD 、EF 、AB 是弦，以E 为端点的劣弧有AÊ、EB ̂、EF ̂、ED ̂、EC ̂，以A 为端点的优弧有ADĈ、ADE ̂；故答案为AB ；CD 、EF 、AB ；AÊ、EB ̂、EF ̂、ED ̂、EC ̂，ADC ̂、ADE ̂． 20．如图，OA 、OB 是⊙O 的半径，C 是⊙O 上一点，∠AOB ＝40°，∠OBC ＝50°，则∠OAC ＝ °．【解答】30°【解析】连接OC ，∵OC ＝OB ，∴∠OCB ＝∠OBC ＝50°，∴∠BOC ＝180°﹣50°×2＝80°，∴∠AOC ＝80°+40°＝120°，∵OC ＝OA ，∴∠OAC ＝∠OCA ＝30°，故答案为30．21．如图，若点O 为⊙O 的圆心，则线段是圆O 的半径；线段是圆O 的弦，其中最长的弦是；是劣弧；是半圆．【解答】OA 、OB 、OC ；AC 、AB 、BC ；AC ；AB̂、BC ̂；ADC ̂、ABC ̂ 【解析】如图，若点O 为⊙O 的圆心，则线段OA 、OB 、OC 是圆O 的半径；线段AC 、AB 、BC 是圆O 的弦，其中最长的弦是AC ；BĈ、AB ̂是劣弧；ADC ̂、ABC ̂是半圆．故答案为OA 、OB 、OC ；AC 、AB 、BC ；AC ；AB̂、BC ̂；ADC ̂、ABC ̂；三．解答题22．如图所示，AB 为⊙O 的直径，CD 是⊙O 的弦，AB 、CD 的延长线交于点E ，已知AB ＝2DE ，∠AEC ＝20°．求∠AOC 的度数．【解答】60°【解析】连接OD ，如图，∵AB ＝2DE ，而AB＝2OD，∴OD＝DE，∴∠DOE＝∠E＝20°，∴∠CDO＝∠DOE+∠E＝40°，而OC＝OD，∴∠C＝∠ODC＝40°，∴∠AOC＝∠C+∠E＝60°．23．已知，如图，CD为⊙O的直径，∠A＝22°，AE交⊙O于点B、E，且AB＝OC，求：∠EOD的度数．【解答】66°【解析】连接OB．∵AB＝OC＝OB，∴∠BOC＝∠A＝22°，∠EBO＝2∠A＝44°，∵OE＝OC，∴∠E＝∠EBO＝44°，∴∠EOD＝∠A+∠E＝22°+44°＝66°．24．如图，⊙O的半径r＝5，圆心O到直线l的距离OD＝3，在直线1上有P，Q，R三点，并且PD＝4，QD ＞4，RD＜4，点P，Q，R与圆的位置关系分别是怎样的？【解答】点P在圆上，点Q在圆内，点R在圆外【解析】如图，连接AO，则AO＝5，∵OD＝3，∴AD＝4，∵PD＝4，QD＜4，RD＞4，∴点P在圆上，点Q在圆内，点R在圆外．25．如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E．已知AB＝2DE，∠AEC＝25°，求∠AOC的度数．【解答】∠AOC＝75°【解析】连接OD，∵AB＝2DE＝2OD，∴OD＝DE，又∵∠E＝25°，∴∠DOE＝∠E＝25°，∴∠ODC＝50°，同理∠C＝∠ODC＝50°∴∠AOC＝∠E+∠OCE＝75°．26．如图所示，线段AD过圆心O交⊙O于D，C两点，∠EOD＝78°，AE交⊙O于B，且AB＝OC，求∠A的度数．【解答】∠A＝26°【解析】如右图所示，连接OB，∵AB＝OC，OB＝OC，∴AB＝OB，∠1＝∠A，又OB＝OE，∠E＝∠2＝∠1+∠A＝2∠A，∴∠EOD＝∠E+∠A＝3∠A，即3∠A＝78°，∴∠A＝26°．27．已知：如图，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB＝2DE，∠C＝40°，求∠E及∠AOC的度数．【解答】∠E＝20°；∠AOC＝60°【解析】连接OD，∵OC＝OD，∠C＝40°，∴∠ODC＝∠C＝40°，AB，∵AB＝2DE，OD=12∴OD＝DE，∵∠ODC是△DOE的外角，∠ODC＝20°，∴∠E＝∠EOD=12∵∠AOC是△COE的外角，∴∠AOC＝∠C+∠E＝40°+20°＝60°．。

苏科版数学九年级上册第二章《直线与圆的位置关系》专题解析

《直线与圆的位置关系》专题解析【考点图解】【技法透析】1．判定直线与圆的位置关系的方法有两种：一是从直线与圆的公共交点的个数来进行判断，另一种是根据圆心到直线的距离与圆的半径之间的大小关系来判断．2．切线的判定方法有三种：一是根据定义，直线与圆只有一个公共点；二是圆心到直线的距离等于半径的直线是圆的切线；三是切线的判定定理，当已知条件中明确指出圆与直线有公共点时，常用“连半径证垂直”的方法，当已知条件中没有指出圆与直线有公共点时，常用“作垂直证半径”的方法．3．切线的性质定理有：①切线与圆只有唯一的公共点；②切线和圆心的距离等于圆的半径；③切线垂直于过切点的半径；④经过圆心垂直于切线的直线必过切点；⑤经过切点垂直于切线的直线必过圆心．4．涉及切线的重要性质还有切线长定理和弦切角定理，其中切线长定理及其对应的基本图形、以及圆的外切三角形、外切四边形所存在的线段之间的关系也是解决问题常用的依据租方法，弦切角定理更是转化圆中相关角的重要定理．5．和圆有关的比例线段定理包括相交弦定理、切割线定理及其推论，统称圆幂定理，它揭示了直线与圆相交后所存在的线段间的比例关系．利用这些定理，可直接进行线段的等积式的变换，或比例线段的转化．【名题精讲】考点1直线与圆的位置关系例1 如图10－1，在△ABC中，∠C＝90°，∠A＝30°，O为AB上一点，OB＝m，⊙O的半径为r＝12，当m在什么范围内取值时，BC与⊙O相离、相切、相交？【切题技巧】要判断OB＝m在什么范围内取值时，BC与⊙O相离、相切、相交，就是要判断圆心O到BC的距离d与⊙O的半径r之间的大小关系．【切题技巧】作OD⊥BC于点Ｄ【借题发挥】判断直线与圆的位置关系，根据圆心到直线的距离与圆的半径的大小确定：①若d<r，直线与圆相交；②若d＝r，直线与圆相切；③若d>r，直线与圆相离．【同类拓展】1．在Rt△ABC中，∠C＝90°，∠B＝30°；BC＝4cm，以2cm的长为半径作圆，则⊙C与AB的位置关系是( )A．相离B．相切C．相交D．相切或相交2．如图10－2，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB＝45°，点P 在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP＝x，则x的取值范围是( )A．－1≤x≤1 B．－2≤x≤2C．0≤x≤2D．x>2考点2直线与圆相切的综合问题例2 如图10－3，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC＝PC，∠COB＝2∠PCB．(1)求证：PC是⊙O的切线(2)求证：BC＝12AB(3)点M是AB的中点，CM交AB于点N，若AB＝4，求MN·MC的值．【切题技巧】(1)证∠OCP＝∠ACB＝90°即可得PC是⊙O的切线，(2)证∠CBO＝∠COB得BC＝OC，从而有BC＝12AB，(3)连MA，MB，先证△BMN∽△CMB得MN·MC＝BM2，再在Rt△ABM中求出BM长即可求值．【规范解答】【借题发挥】切线的证明有两种方法：一种是已知切点，连接圆心和切点证垂直；另一种是不知切点，过圆心向已知直线作垂线，证垂线段长等于半径．【同类拓展】3．如图10－4，△ABC中，AB＝AC，以AB为直径的半圆O交BC于D，交AC于点E，连接AD，BE交于点M，过点D作DF⊥AC于点F，DH⊥AB于点H，交BE于点G，则以下正确的结论是_______（填序号）①BD＝CD ②DF是⊙O的切线③∠DAC＝∠BDH ④DG＝12BM4．如图10－5，已知Rt△ABC中，∠ABC＝90°，以直角边AB为直径作⊙O，交斜边AC 于点D，连接BD．(1)若AD＝3，BD＝4，求边BC的长；(2)取BC的中点E，连接ED，试证明ED与⊙O相切．考点3线段相等的证明例3 如图10－6，已知AB为⊙O的直径，C为⊙O上一点，延长BC至D，使CD＝BC，CE⊥AD，垂足为E，BE交⊙O于F，AF交CE于P，求证：PE＝PC【切题技巧】由切割线定理得PC2＝PF·PA，要证明PE＝PC，只需证明PE2＝PF·PA，这样通过圆幂定理把线段相等问题转化为线段等积式的证明，由三角形相似可完成，【规范解答】延长DA交⊙O于K，连结BK，OC．【借题发挥】证比例式或平方法是圆中证线段相等的重要方法，证比例式常通过相似三角形或平行线性质得到，当要证相等的线段中有一条是圆的切线时，常采用平方法，而线段的平方常由切割线定理，相似三角形的性质来证，值得注意的是，几何图形中有直径这一条件，常添加辅助线，构成直径上的圆周角是直角，使其杓成直角三角形．【同类拓展】5．如图10－7，AB是半圆的直径，AC⊥AB，在半圆上任取一点D，过点D 作DE⊥CD，交直径AB于点E，BF⊥AB，交线段AD的延长线于点F，问图中除了AB＝AC外，是否还有其它两条线段相等，如果有，指出这两条相等的线段，并给出证明：如果没有，也要说明理由．6．如图10－8，四边形ABCD为正方形，00过正方形的顶点A和对角线的交点P，分别交AB、AD于点F、E．(1)求证：DE＝AF；(2)若⊙O的半径为32，AB＝2＋1，求AEED的值．考点4多边形的切圆问题例4 如图10－9，有一个⊙O和两个正六边形T1，T2．T1的6个顶点都在圆周上，T2的6条边都和⊙O相切（我们称T1，T2分别为⊙O的内接正六边形和外切正六边形）．(1)设T1，T2的边长分别为a，b，⊙O的半径为r，求r：a及r：b的值；(2)求正六边形T1，T2的面积比S1：S2的值．【切题技巧】(1)由圆内接正六边形的特点可知，相邻两个顶点与圆心构造的三角形是等边三角形，所以它的外接圆半径与边长相等，由此不难得出它们的比值；(2)由相切关系和等边三角形的性质可求得它们之间的比值．【规范解答】(1)如图10－10，连接圆心O和Ｔ1的6个顶点可得6个全等的正三角形，且OC⊥AB．∴OA＝AB=b，AC=12 b．【借题发挥】解决正多边形外切圆和内接圆问题的一般方法是转化为等腰三角形或直角三角形问题，特别地，对于三角形的内切圆问题，有一条很有用的结论：如图10－11，⊙O切△ABC 的三边于点D，E，F，则AE＝AF＝12(AB＋AC－BC)，BD＝BF＝12(BC＋AB－AC)，CD＝CE＝12(AC＋BC－AB)．【同类拓展】7．如图10－12，在Rt△ABC中，∠A＝90°，以BC边上的点O为圆心作圆，分别与AB、AC相切于E，F两点，设AB＝a，AC＝b，则⊙O的半径等于_______．8．如图10－13，△ABC是正三角形，点C在矩形ABDE的边DE上，△ABC的内切圆半径是1，则矩形ABDE的外接圆直径是_______．考点5 直线与圆的动态问题例5 如图10－14，形如量角器的半圆O的直径DE＝12cm，形如三角板的△ABC中，∠ACB ＝90°，∠ABC＝30°，BC＝12 cm．半圆O以2cm/s的速度从左向右运动，在运动过程中，点D，E始终在直线BC上，设运动时间为ts，当t＝0s时，半圆O在△ABC的左侧，OC＝8cm．(1)当t为何值时，△ABC的一边所在的直线与半圆O所在的圆相切？(2)当△ABC的一边所在的直线与半圆O所在的圆相切时，如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．【切题技巧】对于(1)按半圆与直线AC，AB相切分两大类，每一大类又可分两小类：①与线段AC相切，切点为E；②与线段AC相切，切点为D；③与线段AB相切，切点为F；④与线段AB的延长线相切，切点为Q．【规范解答】(1)在图10－15中，①如图10－15①，当点E与点C重合时，AC⊥OE，OC＝OE＝6cm．所以AC与半圆O所在的圆相切．此时点O运动了2cm，所求运动时间为：t＝22＝1(s．)②如图10－15②，当点O运动到点C时，过点O作OF⊥AB，垂足为F．在Rt△FOB中，∠FBO＝30°，OB＝12 cm．则OF＝6cm，即OF等于半圆O的半径，所以AB与半圆O所在的圆相切．此时点O运动了8cm，所求运动时间为：t＝82＝4(s)．③如图10－15③，当点O运动到BC的中点时，AC⊥OD，OC＝OD＝6cm，所以AC与半圆O所在的圆相切．此时点O运动了14cm，所求运动时间为：t＝142＝7(s)．④如图10－15④，当点O运动到B点的右侧，且OB＝12cm时，过点O作⊙O上直线AB，垂足为Q．在Rt△QOB中，∠OBQ＝30°，则OQ＝6cm，即OQ等于半圆O所在的圆的半径．所以直线AB与半圆O所在的圆相切．此时点O运动了32cm，所求运动时间为：t＝322＝16 (s)．因为半圆O在运动中，它所在的圆与AC所在的直线相切只有上述①、③两种情形；与AB 所在的直线相切只有上述②、④两种情形；与BC所在直线始终相交，所以只有当t为1s，4s，7s，16s时，△ABC的一边所在的直线与半圆O所在的圆相切．(2)当△ABC的一边所在的直线与半圆O所在圆相切时，半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图②与图③所示的两种情形．①如图10－15②，设OA与半圆O的交点为M，易知重叠部分是圆心角为90°，半径为6cm的扇形，所求重叠部分面积为：s扇形EOM＝14π×62＝9(cm2)．②如图10－15③，设AB与半圆O的交点为P，连接OP，过点O作OH⊥AB，垂足为H，则PH＝BH．Rt△OBH中，∠OBH＝30°，OB＝6cm，则OH＝3cm，BH＝33cm，BP＝63cm．S△POB＝12×63×3＝93(cm2)．又因为∠DOP＝2∠DBP＝60°，所以S扇形DOP＝16π×62＝6π(cm2)．所求重叠部分面积为：S△POB＋S扇形DO P＝（93＋6π）(cm2)．【同类拓展】9．如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝12cm，AD＝8cm，BC＝22cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以2cm/s的速度运动，点P，Q分别从点A，C同时出发，当其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t(s)．(1)当t为何值时，四边形PQCD为平行四边形？(2)当t为何值时，PQ与⊙O相切？参考答案1. B2. C3.①②③④4．(1)203(2)略5．BF＝BE 6．(1)略227．aba b219．(1)t＝83（s）(2)t＝2。

初中数学苏科版九年级上册直线与圆的三种位置关系

B
d=2.4c m
2、当r满足_r_=__2_.4__c_m____ 时，
⊙C与直线AB相切．
5
3、当r满足__r_＞___2_.4__c_m__时，
⊙C与直线AB相交．
4
D
C
A
3
小结：
判定直线与圆的位置关系的方法有__两__种：（1）根据定义，由___直_线__与__圆__的__公_共__点___的个数来判断；（2）根据性质，_____圆__心__到__直_线__的__距__离__d_ ____与_半__径__r_____的关系来判断。
.O
r d .A .B
H.
.O
d r .D
.
2
C
l 相切
d .Or
.E . N .F
Q.
3
相交
相离
1、直线与圆相离 <=> d>r
想一想
你当能直根线据与d圆与r
2、直线与圆相切 <=> d=r 的相大离小、关相系切确、
3、直线与圆相交 <=> d<r
定相直交线时与，圆d的与位r有置何关关系系吗？?
BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
分析（1）r=2cm；（2）r=2.4cm (3)r=3cm。
B
2.4cm
解根：据过直C线作与C圆D⊥的A位B置，关垂系足的为数D。量
特征，必须在用Rt圆△心AB到C直中线，的距离d与
半径r的大小进行比较；
AB=
2
2=
2
4
关键=是5（确c定m）圆心C到直线AB的距离d，根这据个三距角离形是面什积么公呢式？有怎么求这

苏科版九年级数学上册《2.5直线与圆的位置关系(一)》教学课件

y
B
A. P.
C
O
x
小结
直线与圆的位置关系
直线与圆的位置关系
相交相切
相离
图形
公共点个数
公共点名称直线名称
圆心到直线距离d与半径r的
关系
O
dr
l
2个交点割线
d<r
O dr
l
1个切点切线
d=r
O r
d l
没有
d>r
2、判定直线与圆的位置关系的方法有__两__种：（1）根据定义，由_直__线___与__圆__的__公__共__点__的个数来判断；
.
o
C l2
A B
l1 l2
654321
在直角坐标系中，点A的坐标为（1，2），⊙A的半径为3，求（4）若要使⊙A经过 O点，则圆心A应当移到什么位置？即圆心A在怎样的∧y图形上？圆心A在以O为圆心， 3为半径的圆上。
A
-6 -5 -4 - 3 -2 -1
012 3 4 5 6
＞ x
-1
-2
＞ x
-1
-2
-3
A
-4
-5
⊙A的半径为3，求（3）若要使⊙A与x 轴、y 轴都相切，则圆心A应移到什么位置？请写出A 所有可能位置坐标。 ∧y
654321
A(-3,3)
A(3,3) A
-6 -5 -4 - 3 -2 -1
012 3 4 5 6
＞ x
-1
-2 A(-3,-3)
-3
A(3,-3)
1.如图，以O为圆心的两个同心圆的半径分别为5和3，大圆的弦AB 交小圆于点C、D，则弦AB的取值范围是____。

九年级数学上册2.5直线与圆的位置关系直线和圆有几种位置关系？素材苏科版(new)

直线和圆有几种位置关系？难易度：★★★关键词：位置关系答案：直线和圆有三种位置关系：相离、相切、相交.【举一反三】典题：在△ABC中,∠C=90°，AC=3cm，BC=4cm,以点C为圆心，分别以2cm、2。

4cm、3cm为半径作圆，那么直线AB与圆的交点个数分别是＿＿、＿＿、＿＿。

思路导引:圆心与直线的距离为d，半径为r，当d＞r时，直线与圆的位置关系是相离,无交点;当d=r时，直线与圆的位置关系是相切,有一个交点；当d＜r时，直线与圆的位置关系是相交,有两个交点。

利用面积相等，得CD=2.4cm，因为2＜2.4，所以直线AB与圆相离，无交点；2。

4=2。

4，所以直线AB与圆相切，有一个交点;3＞2。

4，直线与圆相交,有两个交点。

标准答案：无交点;一个交点；两个交点。

尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

苏教科版初中数学九年级上册直线与圆的位置关系

苏教科版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！苏科版初中数学和你一起共同进步学业有成！直线与圆的位置关系课前参与姓名：________一、预习提纲（一）预习内容：课本P68—70；（二）问题探究：1.作图（1）如图，点P在⊙O上，过点P作⊙O的切线。

（2）如图，点D,E,F在⊙O上，分别过点D,E,F作⊙O的切线,3条切线两两相交于点A,B,C。

（3）如图是一块三角形木料，木工师傅要从中裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？在上图中作出来。

2.知识整理（1）叫做三角形的内切圆。

（2）叫做三角形的内心。

（3）叫做圆的外切三角形。

3.思考一下，你通过预习还存在哪些疑惑？写在下面吧！课中参与例1．如图，⊙O 是△ABC 的内切圆，切点分别为D 、E 、F, ∠B=50°，∠C=70°，求∠EDF 的度数。

例2　已知：点I 是△ABC 的内心，AI 的延长线交外接圆于D ．则DB 与DI 相等吗？为什么？例3．如图，在Rt △ABC 中，∠C=90°，AB=5，6=∆ABC S ,求△ABC 的内切圆半径r 。

例4．如图，等边△ABC 的边长为4，⊙O 是等边△ABC 的内切圆，求⊙O 的半径。

课堂检测1．下列说法中，正确的是（）A 、垂直于半径的直线一定是这个圆的切线B 、圆有且只有一个外切三角形C 、三角形有且只有一个内切圆D 、三角形的内心到三角形的3个顶点的距离相等2．已知点I 为△ABC 的内心，且∠ABC=50°,∠ACB=60°,∠BIC= 。

3．在⊿ABC 中，∠A=50°F B （1）若点O 是⊿ABC 的外心，则∠BOC= .(2) 若点O 是⊿ABC 的内心，则∠BOC= .4．已知直角三角形两直角边长为5、12，则它的外接圆半径R ＝，内切圆半径r ＝．5．如图，OA 、OB 是两条射线，点C 、D 分别在OA 、OB 上。

2-5直线与圆的位置关系苏科版数学九年级上册课件1

数形结合：位置关系 <=> 数量关系
2.5 直线与圆的位置关系（1）
同学们，在我们的生活中到处都蕴含着数学
知识，下面老师请同学们欣赏美丽的海上日出
从海上日出这种自然想象中可以抽象出哪些基本的几何图形呢？
初中数学九年级(上册)
直线与圆的位置关系
2.5 直线与圆的位置关系（1）
二、小组合作，交流展示
直线与⊙O 有__0___个公共点. ．
2.5 直线与圆的位置关系（1）
小试牛刀
r = 5cm
2．已知⊙O的直径为10cm，点O到直线l的距离为d，
根据条件填写d的范围：
(1)若直线l与⊙O相离，则 d ＞ 5cm ； (2)若直线l与⊙O相切，则 d ＝ 5cm ； (3)若直线l与⊙O相交，则 0cm ≤ d＜5cm．
当 3＜r ＜4 时，⊙A与x轴相离，与y轴相交.
x
当 r = 4时，⊙A与x轴相切，与y轴相交.
．
当 r ＞ 4时，⊙A与x轴、y轴都相交.
A
2.5 直线与圆的位置关系（1）
人生感悟
你们是圆，父母是直线，你们一生都是相交的，谁也离不开谁！
你们是圆，要解决的问题是直线，你们的相遇是相切的，切点找对，什么困难都迎刃而解！
A
C
O 30° ．
B
M
2.5 直线与圆的位置关系（1）
四、归纳新知，颗粒归仓
2.5 直线与圆的位置关系（1）
图形
直线与圆的位置关系
公共点的个数圆心到直线的距离 d 与
半径 r 的关系公共点的名称
Ｏ
r d ┐A
相离
0 d＞r
直线名称
．ｏ
r d┐

苏科版数学九年级上册直线与圆的位置关系课件

尝试练习
2.已知⊙O的半径为5cm，圆心O与直线AB的距离为
d，根据条件填写d的范围:
d > 5cm
(1)若AB和⊙O相离，则
；
d = 5cm
(2)若AB和⊙O相切，则
；
0cm≤d < 5cm
(3)若AB和⊙O相交，则
.
圆的切线直线和圆有唯一的公共点（即直线和圆相切）时，这条直线叫做圆的切线（如图直线l），这个唯一的公共点叫做切点（如图点A）.
DC与⊙O相切于点C，∠DAC=30°，若⊙O的半
径长1cm，则CD= c3m.
C
A
O
D B
巩固练习 1.如图，在平面直角坐标系中，
半径为2的⊙P的圆心P的坐标
y
为（-3，0），将⊙P沿x轴正
方向平移，使⊙P与y轴相切，则平移的距离为 1或5 .
POx
2.如图，已知AB是⊙ O的切线，半径OC的延长线与
探索新知
1．尝试（1）P为⊙O外一点，如何用直角三角板经过点P作⊙O的切线？这样的切线能作几条？
（2）如图PA、PB是⊙O的两条切线，切点分别是A、B，沿直线
OP将图形对折，你发现了哪些等量关系？
你能通过证明
验证这些关系吗？

A
O•
P
B
概括
定义：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长性质：从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。
直线和圆的位置关系
位置关系
公共点个数
直线和圆的位置关系
o
o
dr
r d
o r
d
∟

直线与圆的位置关系-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(原卷版)

苏科版数学九年级上册直线与圆的位置关系课件

2.5 直线与圆的位置关系 苏科版九年级数学上册课件

苏科版九年级上册 2.5直线与圆的位置关系(2)(17张PPT)

九年级数学上册第21讲直线与圆的位置关系讲义新版苏科版

直线与圆的位置关系课件苏科版数学九年级上册

圆综合练习(提优)-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

2.5 第1课时 直线与圆的位置关系-2020秋苏科版九年级数学上册课件(共22张PPT)

直线与圆的位置关系-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

圆-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

苏科版数学九年级上册第二章《直线与圆的位置关系》专题解析

初中数学苏科版九年级上册直线与圆的三种位置关系

苏科版九年级数学上册《2.5直线与圆的位置关系(一)》教学课件

九年级数学上册2.5直线与圆的位置关系直线和圆有几种位置关系？素材苏科版(new)

苏教科版初中数学九年级上册直线与圆的位置关系

2-5直线与圆的位置关系 苏科版数学九年级上册 课件1

苏科版数学九年级上册直线与圆的位置关系课件

2.5 直线与圆的位置关系苏科版九年级数学上册课件

2.5 第1课时直线与圆的位置关系-2020秋苏科版九年级数学上册课件(共22张PPT)

2-5直线与圆的位置关系苏科版数学九年级上册课件1