数学物理方程期末试卷
数学物理方程与特殊函数试题及答案

数学物理方程与特殊函数试题及答案猜你喜欢: 1. 2. 3. 4. 5.数学物理方程与特殊函数是一门专业性比拟强的课程,要学好这门课程,同学们还是要用心去学才能学好数学物理方程与特殊函数。
下面是给大家的数学物理方程与特殊函数试题及答案,欢送大家学习参考。
1.对于一般的二阶线性偏微分方程0(1) 它的特征方程为,假设在域内ACB那么此域内称(1) 椭圆型假设在域内B那么此域内称(1)为抛物型假设在域内 B 那么此域内称(1)为双曲型。
2. 第一类格林公式第二类格林公式 . 已那么 ;而函数按1xP的展开式4.一维热传导方程可用差分方程似代替。
二维拉普拉斯方程可用差分方0 近似代替。
5. 勒让德多项式的正交性???。
二.用别离变量法求?的解。
(15分) 解:用别离变量法求解,先设满足边界条件且是变量被别离形式的特解为tTxXtxu?代入方程(1)上式左端不含有x,右端不含有t,从而得到两个线性常微分方程解(6)得 x由(2)得,及相应的固有函数为xlnBxXnn?sin? 7?? ,再由(5)得,? 由(7),(8)得由(1),(3)得又由(3) 得所以,原定解问题的解为?三.求方程? 的解。
(15分) 解:对(1)两端积分的通解为任意二阶可导函数,令(4)满足(2),(3)得解之得6(5),(6)代入(4)得u 四.求柯西问题的解。
(12分) 解;先确定所给方程的特征线。
为此,写出它的特征方程 dy2-2dxdy-3dx20 它的两族积分曲线为作特征变换4?经过变换原方程化它的通解为中21ff 是两个任意二次连续可微的函数。
方程(1)的通解为由(2。
《数学物理方程》习题参考答案(A)

《数学物理方程》习题参考答案(A)习题一1.判断方程的类型,并将其化成标准形式:0212222=∂∂+∂∂+∂∂y uyu y x u . 解:⎪⎩⎪⎨⎧==><<>-=-≡∆.0,0. ,00,.0,02211212时,抛物型当椭圆型时当时,双曲型当y y y y a a a①当0<y 时,所给方程为双曲型,其特征方程为,0)()(22=+dx y dy 即 ,0])([)(22=--dx y dy就是 0))((=---+dx y dy dx y dy .积分之,得 c y x =-±2,此即两族相异的实特征线.作可逆自变量代换⎪⎩⎪⎨⎧--=-+=,2,2y x y x ηξ则.1 ,1 ,1 ,1yy yy x x -=∂∂--=∂∂=∂∂=∂∂ηξηξ,2 ,2222222ηηξξηξηηξξ∂∂+∂∂∂+∂∂=∂∂∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂u u u x u u u y u x u x u ),(1ηξ∂∂+∂∂--=∂∂u u yyu ).1)(2()(121 ]1)1( 1)1([1)()(12122222222222322y u u u u u y y yu yu yuy u y u u y y u -∂∂+∂∂∂-∂∂+∂∂+∂∂---=-∂∂+--∂∂∂++-∂∂∂---∂∂--+∂∂+∂∂--=∂∂ηηξξηξηξηηξξηξ将这些偏导数代入原方程,得附注:若令⎩⎨⎧=-⇒-==0 ,2,ηηξξηξu u y x 碰巧(双曲型的另一标准形),这是巧合.②当0>y 时,所给方程为椭圆型,其特征方程为0)()(22=+dx y dy即 .0))((=-+dx y i dy dx y i dy 其特征线为 )2 ( 2c ix y c y i x =±=±或.作可逆自变量代换 ⎩⎨⎧==,2,y x ηξ则, 1 , 0 , 0 ,1y y y x x =∂∂=∂∂=∂∂=∂∂ηξηξ, 1 , ηξ∂∂=∂∂∂∂=∂∂u y y u u x u . 1121 , 22222222ηηξ∂∂+∂∂-=∂∂∂∂=∂∂u y u y y yu u x u 将这些偏导数代入原方程,得, 021212222=∂∂+∂∂+∂∂-∂∂ηηηξuy u u y u , 0 2222=∂∂+∂∂∴ηξu u 此即(0>y 时)所求之标准形. ③0=y 时,原方程变为 , 02122=∂∂+∂∂y uxu 已是标准形了(不必再化).2.化标准形:. 0222222222222=∂∂∂+∂∂∂+∂∂∂+∂∂∂+∂∂+∂∂t z ut x u z x u y x u zu x u解: u Lu )2222(434131212321δδδδδδδδδδ+++++≡.这是 ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=t z y x4321δδδδδ 的二次型,于是 , u A Lu Tδδ=其中 010*********1111⎪⎪⎪⎪⎪⎭⎫⎝⎛=A 为实对称矩阵.则∃可逆矩阵M ,使 TMAM B = 为对角形. 令 , 'δδT M = 其中 , '4'3'2'1'''''⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂=δδδδδt z y x 则 u B u MAM Lu T T T '''')()(δδδδ==.M 的找法很多,可配方,可从矩阵入手等.取 ,11000110001100011-=⎪⎪⎪⎪⎪⎭⎫⎝⎛---=N M , 1000110011101111)(1⎪⎪⎪⎪⎪⎭⎫⎝⎛==-TT M N . , 1''''''⎪⎪⎪⎪⎪⎭⎫⎝⎛===⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==-t zy x M MX X N t z y x X N T δδ则.)( )( 2222'2'2'2'2'''tu z uy u x u u B uMAM u A Lu TT T T ∂∂-∂∂+∂∂-∂∂====δδδδδδ这是超双曲型方程的标准形式.习题二1.决定任意函数法:(1).求解第一问题(0))(0) ( ).(),( , 002ψϕψϕ=⎪⎩⎪⎨⎧======-x ux u u a u at x at x xx tt .解:所给方程为双曲型,其特征线为 c at x =±. 令⎩⎨⎧-=+=,,at x at x ηξ 则可将方程化为 0=ξηu .其一般解为)()(),(21at x f at x f t x u -++= (其中21,f f 为二次连续可微函数). 由定解条件有)0()0()0()0( ).()2()0(),()0()2(212121ψϕψϕ==+⇒⎩⎨⎧=+=+f f x x f f x f x f . 则 ⎪⎩⎪⎨⎧-=-=⇒⎩⎨⎧-=-=).0()2()(),0()2()( ),0()()2(),0()()2(12211221f Y Y f f X X f f x x f f x x f ψϕψϕ 故 )()(),(21at x f at x f t x u -++=).0()2()2()]0()0([)2()2(21ϕψϕψϕ--++=+--++=at x at x f f atx at x (2).求解第二问题 ))0()0( ( ).(),( ,101002ϕϕϕϕ=⎪⎩⎪⎨⎧=====x u x u u a u t at x xx tt解:泛定方程的一般解为)()(),(21at x f at x f t x u -++=由定解条件有 (0))(0)(0)( ).()()(),()0()2(021121021ϕϕϕ=+⎩⎨⎧=+=+f f x x f x f x f x f 则 ),0()2()(201f xx f -=ϕ).0()2()()()()(201112f x x x f x x f +-=-=ϕϕϕ故 )()(),(21at x f at x f t x u -++= ).()2()2(100at x atx at x -+--+=ϕϕϕ (3).证明方程22222)1(])1[(tu h x a x u h x x ∂∂-=∂∂-∂∂ 的解可以写成)]()([1),(21at x f at x f xh t x u -++-=. 由此求该方程满足Cauchy 条件 ⎩⎨⎧====)(),(00x u x u t t t ψϕ 的解.解:令 ),,()(),(t x u x h t x v -= 则 ),(t x v 满足方程 xx tt v a v 2=.)()(),( 21at x f at x f t x v -++=∴.故 )]()([1),(21at x f at x f xh t x u -++-=. 因),(t x v 满足 ⎪⎩⎪⎨⎧≡-=≡-====),()()(),()()( ,10002x x x h vx x x h v v a v t t t xx tt ψϕϕϕ由D'Alembert 公式,得⎰+-+-++=atx atx d a at x at x t x v ααψϕϕ)(21)]()([21),( )]())(()())([(2100at x at x h at x at x h ---+++-=ϕϕ+ααϕαd h a atx at x ⎰+--)()(211 故 ),(1),(t x v xh t x u -=[]⎭⎬⎫⎩⎨⎧-+---+++--=⎰+-atx atx d h a at x at x h at x at x h x h ααϕαϕϕ)()(21)())(()())((211100 即为所求之解.2.Poisson 公式及应用:(1).若),,,(t z y x u u =是初值问题 ⎪⎩⎪⎨⎧+=+=>++===)()( , )()(),0( )(002z y uy g x f u t u u u a u t t t zz yy xx tt ψϕ的解,试求解的表达式.解:IIIIIIu u u u ++=(线性叠加原理),其中IIIIII,,u u u 分别满足如下的初值问题:.0 ),(),0( )(:002I ⎪⎩⎪⎨⎧==>++===t t t zz yy xx tt ux f u t u u u a u u).( ),(),0( )(:002II ⎪⎩⎪⎨⎧==>++===y uy g u t u u u a u u t t t zz yy xx tt ϕ).( ,0),0( )(:002III ⎪⎩⎪⎨⎧==>++===z uu t u u u a u u t t t zz yy xx tt ψ由Poisson 公式,可得⎰⎰∂∂=MatS dS f t a t u ])( 41[2I ξπ)].()([21])(21[at x f at x f d f a t atx atx -++=∂∂=⎰+-ξξ.)(21)( 41.)(21)]()([21 ])( 41[)( 412III22II ⎰⎰⎰⎰⎰⎰⎰⎰+-+-==+-++=∂∂+=Mat M atMat S atz at z aty aty S S d a d t a ud aat y g at y g dS g t a t dS t a u ζζψζζψπηηϕηπηϕπ故IIIII I ),,,(u u u t z y x u ++=.)(21)(2a1)]()([21)]()([21 ⎰⎰+-+-++-+++-++=atz at z aty aty d a d at y g at y g at x f at x f ζζψηηϕ(2).求解初值问题 ⎪⎩⎪⎨⎧+==>-+++=== . ,00),(t )(2)(2002yz x u u z y u u u a u t t t zz yy xx tt解: IIIu u u +=,其中I u : ⎪⎩⎪⎨⎧+==>++=== . ,00),(t )(2002yz x u u u u u a u t t t zz yy xx ttII u : ⎪⎩⎪⎨⎧==>-+++===.0 ,00),(t )(2)(002t t t zz yy xx tt uu z y u u u a u由poisson 公式,得32222I 31)()( 41t a t yz x dS t a u Mat S ++=+=⎰⎰ηζξπ. 由Duhamel 原理,得.)( ])(2)( 41[);,,,(2020II)(t z y d dS t a d t z y x w u M t a S tt-=--==⎰⎰⎰⎰-τζητπτττ故 2322)(31)(),,,(t z y t a t yz x t z y x u -+++= 即为所求. 3.降维法:⎪⎩⎪⎨⎧==>++===.0 ,00),(t ),,()(002t t t yy xx tt uu t y x f u u a u 解:把所给初值问题的解),,(t y x u 看作),,,(t z y x 空间中的函数,即与y x ,平面垂直的直线上的函数值都相等:),,(),,,(*t y x u t z y x u =,则 ),,,(*t z y x u 应形式的满足⎪⎩⎪⎨⎧==>+++=== .0 ,00),(t ),,()(0*0****2*t t t zz yy xx tt u u t y x f u u u a u 由推迟势可得dV ra rt f a t z y x u atr ⎰⎰⎰≤-=),,( 41),,,(2*ηξπττηξτπτττηξπττd dS f t a d dS t f a tS tS M t a M t a ]),,([141]),,([ 410202)()(⎰⎰⎰⎰⎰⎰---=-=τηξτηξττηξτπτd y x t a d d t a f t a ty x M t a ])()()( )(),,(2[141222202),()9------∑-=⎰⎰⎰-τηξτηξτηξπτd y x t a d d f a tx M t a ])()()( ),,([ 212222),()(⎰⎰⎰∑-----=-.此即所求初值问题解的积分表达式.习题三1.求解特征值问题 ⎩⎨⎧=+=<<=+ . 0)()( ,0)0(),(0 0)()("''l X l X X l x x X x X λ 解:该特征值问题要有解0≥⇔λ.0>λ时,记2ωλ=,则 x B x A x X ωωsin cos )(+=.x B x A x X ωωωωcos sin )('+-=. 1(*) 由 0)0('=X ,有 0=B .从而 x A x X A ωcos )(,0=≠. 由 0sin cos ,0)()('=-=+l A l A l X l X ωωω有. ωω=l cot . 此即确定 ω(从而确定λ)的超越方程.由图解法,曲线 ωω==y l y cot 和 有无穷个交点,其横坐标<<<<<n ωωω210,从而 ),2,1( 2==n nn ωλ 便是非0特征值,相应的特征函数为2(*) ,2,1 , cos )( ==n x A x X n n n ω.)( , )( 0'A x XB Ax x X =+==时,λ由0)0('=X ,有0=A .由0)()('=+l X l X , 有 0=B .此时只有平凡解 0)(≡x X . 综上,所求特征值问题的解),2,1( , cos )( ==n x A x X n n n ω.其中n ω为超越方程 ωω=l cot 的正根.附注:下证特征函数系{}∞=1cos n n x ω是],0[l 上的正交系:事实上,设x x X n n ωcos )(=和x x X m m ωcos )(=分别是相应于不同特征值2n n ωλ=和2m m ωλ=的特征函数,即)(x X n 和)(x X m 分别满足).()(,0)0(,0)()(:)(''"⎩⎨⎧+==+l X l X X x X x X x X n n nn n n n λ (1) ⎩⎨⎧=+==+.0)()(,0)0(,0)()(:)(''"l X l X X x X x X x X m m m m m m m λ (2) 则[]0 )()2()()1(0=⋅-⋅⎰dx x X x Xln m,即 []⎰-+-=lm n m n n m m n dx x X x X x X x X x X x X"" )()()())()()()((0λλdx x X x X lm n m n ⎰-=0)()()(λλ若,m n λλ≠则 ),2,1,( 0)()(0==⎰m n dx x X x X lm n .即在],0[l 上,不同特征值所对应的特征函数彼此正交. 2.用分离变量法求波动方程混合问题⎪⎩⎪⎨⎧≤≤==>==><<+=== ),0( , ),0( ),( ,),0(),0 ,0( 20022l x x ux u t t t l u t t u t l x g u a u t t t x xx tt的形式解,其中g 为常数.解:(1).边界条件齐次化:令 ),,(),(),(t x Q t x v t x u +=使⎪⎩⎪⎨⎧====,,20t Q t Q l x x x (这不是定解问题),则取 2)(),(t t l x t x Q +-=即可. 这时),(t x v 满足 ⎪⎩⎪⎨⎧≤≤--==>==><<-+===).0( )( , 0),( 0),( ,0),0(),0 ,0( 2200t 2l x l x x vx v t t l v t v t l x g v a v t t x xx tt(2).“拆”——由线性叠加原理:IIIv v v +=,其中⎪⎩⎪⎨⎧+-====><<=== ., ,0),(),0(),0,0( :2002I l x x vx v t l v t v t l x v a v v t t t x xx tt ⎪⎩⎪⎨⎧====><<-+=== .0,0 ,0),(),0(),0,0( 2:002IIt t t x xx tt vv t l v t v t l x g v a v v (3).用分离变量法求得l x n l at n b l at n a t x v n n n 2 )12(cos 2 )12(sin 2 )12(cos ),(1Iπππ-⎥⎦⎤⎢⎣⎡-+-=∑∞=. 其中⎰⎰--=ll n d ln d ln a 022)12(cos2)12(cos 1ξπξξξπξ,ξπξξξξπξπd ln l d l n l a n b lln 2)12(cos )(2)12(cos 2 )12(122-+---=⎰⎰..,2,1 =n (n n b a ,都可算出来).(4).由Duhamel 原理: ττd t x w t x v t⎰=0II),,(),(,其中),,(τt x w 满足 ⎪⎩⎪⎨⎧-====><<=== . 2 , 0 ,0),( ,0),0( ),,(0 2g ww t l w t w t l x w a w t t t x xx tt τττ用分离变量法求得∑∞=---=12 )12(cos 2)( )12(sin),,(n n l xn l t a n c t x w πτπτ.其中 ξπξξπξπd ln g d l n l a n c lln 2)12(cos)2(2)12(cos 2 )12(12----=⎰⎰. ,3,2,1 =n (n c 可算出).综上: ),(),(),(),(),(),(III t x Q t x v t x v t x Q t x v t x u ++=+=.习题四1.用分离变量法求热方程混合问题⎪⎩⎪⎨⎧===><<-== )( ,0),(),0(),0,0( 022x u t l u t u t l x u b u a u t xx t ϕ 的形式解.解:这是齐次方程、齐次边界条件情形,直接分离变量: 令 )()(),(t T x X t x u =,代入泛定方程,得),( )(22'"λ-=+=a bTa T X X 从而 0)()()( , 0)()(2'"=++=+t T b a t T x X x X λλ. 由边界条件,得 ,0)()0(==l X X 于是,特征值问题为⎩⎨⎧==<<=+0.)((0))(0 , 0)()("l X X l x x X x X λ 特征值 2)(l n n πλ=, 特征函数为 x ln x X n πsin )(=,),2,1( =n . 而 )1,2,(n )(])[(22 ==+-t b lan n n eA t T π.取 11])[((*) . sin),(22x ln eA t x u n t b lan n ππ∑∞=+-=利用 ]0[ sinl x ln ,在⎭⎬⎫⎩⎨⎧π上的正交性,可定出 ⎰==ln n d ln l A 0),2,1( sin)(2 ξπξξϕ. 2(*) 1(*),2(*)给出所求混合问题的形式解.附注:若令 ),( ),,(),(2t x v t x v e t x u t b 则-=满足⎪⎩⎪⎨⎧===><<==== ).( ,0),0,0( 002x v v v t l x v a v t l x x xx t ϕ用分离变量法求得lxn eA t x v t lan n n sin),(2)(1ππ-∞=∑=. 而n A 同2(*),这恰与上面结果一致.习题五用Fourier 变换法求初值问题⎩⎨⎧=>++== .0),0( ),(202t xx t u t t x f tu u a u 的形式解.解:方程和初始条件两端关于x 做Fourier 变换(视t 为参数),并记),(~)],([ , ),(~)],([t f t x f F t u t x u F ξξ==.则原问题化为常微分方程的初值问题:⎪⎩⎪⎨⎧=>++-=)( .0)0,(~),0( ),(~~ 2~~22为参数ξξξξu t t f u t u a dtu d 其解为 ττξξτξτξd e f e e e t u a tt a t 2222220),(~),(~⋅⋅⋅=⎰--. 故 )],(~[),(1t uF t x u ξ-= ττξττξττξτξττξτξτξd e f F ee d ef e F e d e f e e e F ta t t a tt t t a t a t t ⎰⎰⎰-----------⋅⋅⋅=⋅⋅⋅=⎥⎦⎤⎢⎣⎡⋅⋅⋅=01)(0101]),(~[]),(~[),(~)(22222222222222ττπτττd et a F x f F F e e tt a x t]])(21[)],([[0)(412222⎰-----⋅⋅=ττπτττd et a x f F F e e tt a x t]])(21*),([[0)(412222⎰-----⋅=τξττξπτξτd d et f e a ett a x t ]1),([20)(4)(2222⎰⎰---∞∞---=即为所求.习题六1.求边值问题⎪⎪⎩⎪⎪⎨⎧≤≤=≤≤==<≤≤<≤=++=== )(0 )( ),0( 0),20 ,0( 01102αθθρπαθρρρραθθθθρρρf u l u u l u u u l 的形式解.解:用分离变量法:令 )()(θρΘ=R u ,代入泛定方程可得)( "'"2λρρ=ΘΘ-=+RR R ,因而 0)()("=Θ+Θθλθ,0)()()('"2=-+ρλρρρρR R R (Euler 方程).由边界条件 00====αθθu u,得 0)()0(=Θ=Θα.于是特征值问题为,0)()0(),0( 0)()("⎩⎨⎧=Θ=Θ<<=Θ+Θααθθλθ 特征值 2)(απλn n =,特征函数为 )1,2,( sin)( ==Θn n n θαπθ.而 Euler 方程 0'"2=-+R R R λρρ 的解 απαπρρρn n D C R -+=)(.为保证有界性应取 0=D ,从而 ),2,1( )( ==n C R n n n απρρ.取 ∑∑∞=∞==Θ=11sin)()(),(n n n n n n n C R u απθρθρθραπ. 1(*)由边界条件 )(θρf ul ==,应有 ∑∞==1sin )(n n n n lC f απθθαπ.由 ⎭⎬⎫⎩⎨⎧απθn sin在 ],0[α上的正交性,可得),2,1( sin)( 2==⎰n d n f l C n n ϕαπϕϕαααπ. 2(*)1(*) ,2(*)给出所求问题的形式解.2.用Green 函数法求解上半平面Dirichlet 问题⎪⎩⎪⎨⎧∞→+=>=+=. ),( ),0( 0220有界时,u y x x f u y u u y yy xx 解:根据二维Poisson 方程Dirichlet 问题⎩⎨⎧=∈-=+∂ ),(D.),( ),,(2y x f u y x y x u u Dyy xx πρ 解的积分表达式P PDDdl n M P G P f dxdy M M G M y x u M u ∂∂-==⎰⎰⎰∂),()(21),()(),()(00000πρ(其中0M 是D 内任一点,P n是边界D ∂上点P 的外法线方向). 其中 满足而 ),( ),,(1ln),(0000M M g M M g r M M G MM -=⎪⎩⎪⎨⎧∂∈=∈=∆).( 1ln ),g(),( 0),(000D P r M P D M M M g PM M),(0M M G 称为Green 函数,找),(0M M G 的问题归结为“特定装置下”找感应电荷所产生的电势),(0M M g -.对上半平面0>y 而言,若在0M 处放置单位正电荷,它在M 处产生的电势为01lnMM r ,则感应电荷应放在0M 关于0=y 的对称点'0M 处,电量为 -1,它于M 处产生的电势为'1lnMM r -,从而Green 函数为'1ln1ln),(0MM MM r r M M G -=20202020)()(ln )()(ln y y x x y y x x ++-+-+--=.故所求解为⎰⎰⎰⎰∞∞-=∞∞-=∞∞-=∞∞-+-=∂∂=-∂∂-=∂∂-=.)()()(21 )()(21)(21),(22000000dx yx x x f y dx yG x f dxy G x f dx n G x f y x u y y y ππππ。
华南理工大学期末考试数学物理方程卷A及答(08[1].6
![华南理工大学期末考试数学物理方程卷A及答(08[1].6](https://img.taocdn.com/s3/m/2100f7f6f90f76c661371adf.png)
x + at
y
(a
)da
)。
2
2a x-at
4. 由 泊 松 公 式 , 三 维 波 动 方 程 初 值 问 题
ì í î
utt = a2 (uxx + uyy + uzz ), -¥ u( x, y, z,0) = j (x, y, z),
<
x, y, z < ut (x, y,
+¥,t > 0 z,0) = 0
即 ust
=
t 2(s2 -
t2)
us
-
s 2(s2 -
t2)
ut
+
1 2
.
《
》试卷第 2 页 共 4 页
ì
ï
三.
(10 分)
求解问题
ï í
utt = a2uxx , (0 < x < l, t > 0), u(0, t) = 0, u(l, t) = 0,
。
ï ï u( î
x,
0)
=
sin
px l
学号
姓名
ìDu = 0, (x, y, z) Î W
6.
根据调
和函数
的
性质,
诺伊曼
问题
ï í
ïî
¶u ¶n |G =
f (x, y, z)
有解的必要条件是
( òò f ( x, y, z)dS = 0 )。
G
7 设函数 G(M , M0 ) =
1 4p rMM0
- v 为区域 W 上的格林函数,则 W 上的狄利克雷问题
òò ìDu = 0,
í î
u |G =
西安邮电大学期末数理方程试题+答案

数学物理方程与特殊函数09级试题选讲一、求解定解问题22200,0,(0,0)x x lt u u a t x u u x l t xx u x ===춶=ﶶﶶï==<<>í¶¶ïï=ïî)()(),(t T x X t x u =)()()()(2t T x X a t T x X ¢¢=¢22)()()()(b -=¢¢=¢x X x X t T a t T 0>b 设,代入原方程得,则)()(22=+¢t T a t T b 0)()(2=+¢¢x X x X b 则,0x x lu u xx==¶¶==¶¶'(0)'()0X X l Þ==又因为得固有值问题2()()0'(0)'()0X x X x X X l b ¢¢ì+=í==î22)(ln pb =()cos 0,1,2,n n n xX x A n lp ==则固有值固有函数,数学物理方程与特殊函数09级试题选讲)()()(2=+¢t T la n t T p 2()()n a tl n T t C ep -Þ=2()01(,)cosn a tln n n x u x t C C elp p ¥-==+å从而0t ux==有因为01cosnn n x x C C lp ¥==+å所以220022[(1)1]cos 12n ln l n x l C x dx l l nl C xdx lp p --====òò2()2212(1)1(,)cos 2n a ntln l l n xu x t enlp p p¥-=--=+å数学物理方程与特殊函数09级试题选讲二、求解定解问题2222,,0(),0(),0(0)(0)t x t x u ut x t t t x ux x u x x =-=춶=-<<>ﶶïï=F £íï=Y ³ïïF =Y î解:特征变换为x t x tx h =-ìí=+î2u x h¶=¶¶原方程化为12()()u f f x h =+则它的通解为00(),()()(),()()2222t xt x ux u x u u h x x h x h x h=-====F =Y +-Þ=F =F =Y =Y 又因为数学物理方程与特殊函数09级试题选讲1212(0)()()2()(0)()2f f f f h h xx +=Y +=F 2112()()(0)2()()(0)2f f f f h h x x ì=Y -ïïÞíï=F -ïî12()()((0)(0))22()()(0)22u f f x t x tx h=F +Y -+-+=F +Y -F 则它的解为三、求解定解问题)0,(,0,3,03202022222>+¥<<-¥ïïïîïïíì=¶¶==¶¶-¶¶¶+¶¶==y x y ux u y uy x u x u y y 解:原方程的特征方程为22()23()0dy dydx dx --=13C x y +=2C x y +-=,则特征线为3x y x yx h =-ìí=+î特征变换20ux h¶=¶¶原方程化为12()()u f f x h =+则它的通解为数学物理方程与特殊函数09级试题选讲12(,)(3)()u x y f x y f x y =-++即203,y y u ux y==¶==¶又因为21212(3)()3(3)()0f x f x xf x f x ì+=í¢¢-+=î则可得C x x f¢-=2149)3(C x x f ¢+=2243)(C x x f¢-=2141)(222234)(34)3(),(yx y x y x y x u +=++-=22()()C Du vv u u v d v u ds n n s ¶¶Ñ-Ñ=-¶¶òòò 四、证明平面上的格林公式其中n 为曲线的外法线向量。
数学物理方程期末试卷

数学物理方程期末试卷第一部分:选择题请在每个题目中选择仅一个正确答案并将字母填入括号内。
1.求解y″+y=0有解的方法是?A. 特征根法 ( )B. 系数法 ( )C. 齐次线性微分方程法 ( )D. 变量分离法 ( )2.求解 $\\frac{\\partial^2u}{\\partialx^2}+\\frac{\\partial^2u}{\\partial y^2}=0$ 有解的条件是?A. u在区域内为调和函数 ( )B. u在区域内为多项式函数 ( )C. 区域的边界条件为第一类边界条件 ( )D. 区域的边界条件为第二类边界条件 ( )3.解 $\\frac{\\partial u}{\\partial t}+2u=0$,u(x,0)=x,在t=1时,u(x,1)=?A. $\\frac{x}{2}$B. xe−2C. $\\frac{x}{e^2}$D. xe2 ( )4.对于一般的偏微分方程,逐步消去导数的方法称为?A. 特征线法 ( )B. 微分方程求解法 ( )C. 变量分离法 ( )D. 特征值法 ( )5.$y=A\\cos(x)-B\\sin(x)$ 是如下微分方程的?A. $y''+y=\\sin(x)$B. $y''-y=\\cos(x)$ ( )C. $y''+y=\\cos(x)$D. $y''-y=\\sin(x)$第二部分:填空题请在每个题目中填入恰当的答案。
1.y″−2y′+2y=0的通解为______。
2.$\\frac{\\partial^2 u}{\\partial t^2}-c^2\\frac{\\partial^2u}{\\partial x^2}=0$ 的波动方程,初始时刻条件为$u(x,0)=\\varphi(x)$,$u_t(x,0)=\\psi(x)$,其解为$u(x,t)=\\frac{1}{2}(f_1(x-ct)+f_2(x+ct))$,其中f1(x),f2(x)分别是u(x,0)和u t(x,0)的__________。
数学物理方程试卷及答案

数学物理⽅程试卷及答案参考解答:⼀、填空题1. A 定解 B 初值(或Cauchy 问题) C 存在性、唯⼀性和稳定性2. D 双曲3. E (1)(2)(4)4. F [x-3t,x+t] ,G 决定区域5. H 222(21)(1,2,)4n n L πλ-==L I(21)cos (1,2,)2n x X n Lπ-==L ⼆、解:⽆界区域上波动⽅程200,,0|(),|()tt tt t t t u a u x t u x u x ?ψ==?=-∞<<+∞>??==?? 的达朗贝尔公式为:22()()1(,)()22x atx at x at x at u x t d aψξξ+--++=+对于本题所给半⽆界区域上的⾃由端点定解问题,只需对初始条件作偶延拓,即令:2(),()||x x x x ?ψ==即可,2a = ,代⼊达朗贝尔公式得22222222(2)(2)1()||2224,25(4),24x tx tx t x t u x d x xt t x tx t x t ξξ+--++=+??++≥?=?+⼆、解:设(,)()()u x t X x T t =,则()''()4''()()X x T t X x T t =,分离变量成为''()''()4()()T t X x T t X x λ==-,则''()()0,'(0)'(1)0''()4()0X x X x X X T t T t λλ+===??+=?,解前⼀⽅程,得固有值22(0,1,2,)n n n λπ==L 和固有函数()cos X x n x π=,代⼊⽅程''()4()0T t T t λ+=中可得()cos 2sin 2T t A n t B n t ππ=+,1,2,3,)n =L (由叠加原理,原⽅程有解1(,)(cos 2sin 2)cos nnn u x t A n t Bn t n x πππ∞==+∑。
数学物理方法期末试题(5年试题含答案)

………密………封………线………以………内………答………题………无………效……附:拉普拉斯方程02=∇u 在柱坐标系和球坐标系下的表达式 柱坐标系:2222222110u u u uzρρρρϕ∂∂∂∂+++=∂∂∂∂球坐标系:2222222111sin 0sin sin u u ur r r r r r θθθθθϕ∂∂∂∂∂⎛⎫⎛⎫++= ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭一、填空题36分(每空2分)1、 数量场2322u x z y z =+在点(2, 0, -1)处沿2423x xy z =-+l i j k 方向的方向导数是。
2、 矢量场()xyz x y z ==+A r r i +j k 在点(1, 3, 3)处的散度为 。
3、 面单连域内设有矢量场A ,若其散度0∇⋅A =,则称此矢量场为 。
4、 高斯公式Sd ⋅=⎰⎰ A S ;斯托克斯公式ld ⋅=⎰ A l 。
5、 将泛定方程和 结合在一起,就构成了一个定解问题。
只有初始条件,没有边界条件的定解问题称为 ;只有边界条件,没有初始条件的定解问题称为 ;既有边界条件,又有初始条件的定解问题称为 。
………密………封………线………以………内………答………题………无………效……6、 ()l P x 是l 次勒让德多项式,则11()()l l P x P x +-''-= ; m n =时,11()()mn P x P x dx -=⎰。
7、 已知()n J x 和()n N x 分别为n 阶贝塞尔函数和n 阶诺依曼函数(其中n 为整数),那么可知(1)()n H x = 。
(2)()n H x = 。
8、 定解问题2222000(0,0)|0,||0,|0x x ay y bu ux a y b x y u u V u u ====⎧∂∂+=<<<<⎪∂∂⎪⎪==⎨⎪==⎪⎪⎩的本征函数为 ,本征值为 。
数理方程期末试题及答案

带入微分方程求解得:
k
a2
A 2
则得通解
T1
t
C1
cos
n l
a
t
D1
sin
n l
a
t
a2
A 2
sin t
带入初始条件得: C1
0,
D1
A a2 2
l a
则原定解问题的解为
u x,t
A a2 2
l sin a t cos
a l
l
x
2、 求解下列初值问题:(10 分)
uuttx,0u
xx
数; (3) 将形式解带入泛定方程以及初始条件,求解待定函数 Tn(t).
4、试述行波法的适用范围,并写出无限长弦自由振动的达朗贝尔公式。 答:行波法(特征线法)对双曲型方程是有效的,沿着双曲型方程两条特征线做
自变量替换总可以把双曲型方程化为可积形式,获得通解,由此行波法仅适用于
无界条件的波动方程。
3x x ,t sin x,ut x,0 x
0
解:应用达朗贝尔公式: u 1 (x at) (x at) 1
xat
( )d
其中
2
2a xat
,
x sin x, x x ,带入上式得:
u
1 2
sin
x
at
sin
x
at
1 2a
xat
d
xat
sin x cos at t
数学物理方程期末试题答案
一、 简述题:(每题 7 分,共 28 分) 1、 简述数学物理中的三类典型方程,并写出三类方程在一维情况下的具体形
式。
答:波动方程:
2u t 2
数学物理方法期末考试试题

数学物理方法期末考试试题# 数学物理方法期末考试试题## 第一部分:选择题(每题2分,共20分)1. 以下哪个不是数学物理中的常用方法?A. 傅里叶变换B. 拉普拉斯变换C. 泰勒级数展开D. 牛顿迭代法2. 求解偏微分方程时,分离变量法的基本思想是什么?A. 将偏微分方程转化为常微分方程B. 将偏微分方程分解为几个独立的方程C. 将偏微分方程转化为线性方程D. 将偏微分方程转化为积分方程3. 在数学物理中,格林函数通常用于解决什么问题?A. 线性代数问题B. 非线性偏微分方程C. 边界值问题D. 初始值问题4. 以下哪个是求解波动方程的典型方法?A. 特征线法B. 有限差分法C. 有限元法D. 蒙特卡洛方法5. 拉普拉斯方程在数学物理中通常描述了什么类型的物理现象?A. 波动现象B. 热传导现象C. 流体动力学问题D. 电磁场问题## 第二部分:简答题(每题10分,共30分)6. 简述傅里叶变换在数学物理中的应用。
7. 解释什么是边界层理论,并说明它在流体力学中的重要性。
8. 描述格林函数在求解偏微分方程中的作用。
## 第三部分:计算题(每题25分,共50分)9. 给定函数 \( f(x) = x^2 - 4x + 3 \),使用泰勒级数展开在\( x = 1 \) 处展开 \( f(x) \) 并求出展开式。
10. 考虑一个无限长直导体,在 \( x \) 轴上,导体的电势 \( V(x) \) 满足泊松方程 \( \nabla^2 V = -\rho/\varepsilon_0 \),其中\( \rho \) 是电荷密度,\( \varepsilon_0 \) 是真空电容率。
假设\( \rho \) 是常数,求解 \( V(x) \)。
## 第四部分:论述题(共30分)11. 论述数学物理方法在解决实际物理问题中的应用,并给出至少两个具体的例子。
请注意,以上内容仅为示例,实际的数学物理方法期末考试试题可能会包含不同的问题和要求。
数学物理方程试题

考生注意:所有答题务必书写在考场提供的答题纸上,写在本试题单上的答题一律无效(本题单不参与阅卷)。
一、(本题20分)。
设细杆因外界原因而产生纵振动,以(,)u x t 表示其静止时x 点处在时刻t 离开原位置的偏移,并假设振动过程中所发生的张力服从虎克定律,即x 处单位面积受到的张力(,)(,)u x t p x t E x
∂=∂,其中E 为细杆的杨氏模量.令()x ρ为细杆的密度,试写出该振动所满足的偏微分方程.
二、(本题20分)。
判定方程
0623222222=∂∂+∂∂+∂∂-∂∂∂+∂∂y u x u y y x u x u
的类型并化简.
三、(本题10分)。
设有圆域r R <上的Laplace 方程的第二边值问题
0sin [0,2]4r R
u u n θθπ=∇=⎧⎪∂⎨=∈⎪∂⎩ 请讨论此方程是否有解(其中,(r ,θ)是该园域所在的二维空间的极坐标表示).
四、(本题10分)。
试用齐次化原理导出平面非齐次波动方程2()(,,)tt xx yy u a u u f x y t -+=在齐次初
始条件0000
t t t u u ==⎧=⎪⎨=⎪⎩下的求解公式.
五、(本题10分)。
求解热传导方程的初值问题
0(,0)sin t xx u u u x x -=⎧⎨=⎩
六、(本题20分)。
求解下列弦振动方程的定解问题
()200,0(,0)0,(,0)()(0,)(,)0tt xx t u a u x l t u x u x x l x u t u l t ⎧-=<<<⎪==-⎨⎪==⎩。
山东大学物理学院 数学物理方法 2022-2023期末试题及解析
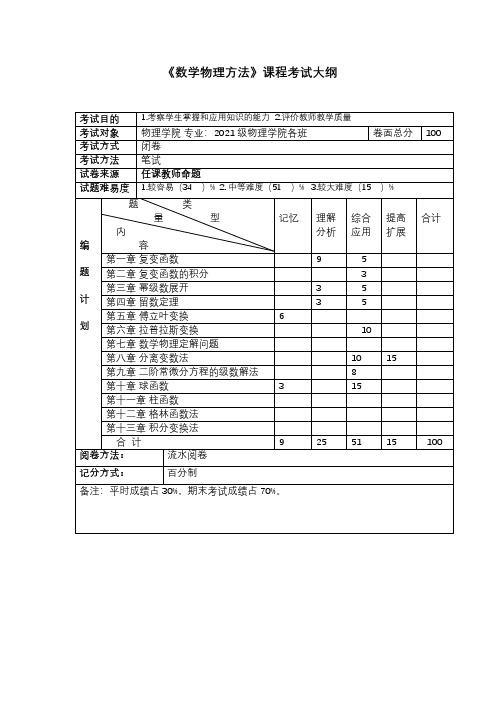
《数学物理方法》课程考试大纲2022-2023山东大学物理学院 数学物理方法期末试题一、 填空题(每题3分,共27分)1. 已知zz =cos (aa +iibb ),z 的代数表达式为________________2. 指出多值函数�(zz −aa )(zz −bb )的支点和阶数___________3. 已知级数∑aa nn xx nn ∞nn=0的收敛半径为A ,试问级数∑aa nn √1+bb nn nnxx nn ∞nn=0(|bb |<1)的收敛半径为_____________4.ssss nn 2zz zz 3的极点为_____,且为______ 阶极点5. 利用柯西公式计算∮zz 2−zz+1zz 2(zz−1)ddzz |zz |=2_______________6. 连带勒让德多项式的正交代数表达式为_______________7. 计算留数1(zz 2+1)2_________________________8. 从t=a 持续作用到t=b 的作用力ff (tt ),可以看作许多前后相继的瞬时力的总和,其数学表达形式为__________9. ∫3δδ(xx −ππ)[ee 2xx +cccccc xx ]ddxx 10−10=_________________ 二、 简算题(每题5分,共15分)1. 将函数ff (zz )=1zz 2−3zz+2,在区域0<|zz −1|<1上展开为洛朗级数 2. �cos mmxx(xx 2+aa 2)2d xx ∞−∞,m>03. 已知解析函数ff =uu +iiνν,而uu =xx 3−3xxyy 2,试求ff三、 (8分)用级数法解微分方程yy ′′+xxyy ′+yy =0四、 (10分)在圆域ρρ<ρρ0上求解泊松方程的边值问题�ΔΔuu =aa +bb (xx 2−yy 2)uu ρρ=pp 0=cc五、 (15分)设有一均匀球体,在球面上的温度为cos 2θθ,试在稳定状态下求球内的温度分布(已知,PP 0(xx )=1,PP 1(xx )=xx , PP 2(xx )=12(3xx 2−1))六、 (10分)利用拉普拉斯变换解RC 电路方程:�RRRR +1CC �RR dd tt tt=EE 0sin ωωttRR (0)=0七、 (15分)计算:⎩⎨⎧ðð2uu ððtt 2−aa 2ðð2uuððxx2=AA cos ππxx ll sin ωωttuu |xx=0=0, uu |xx=ll =0uu |tt=0=φφ(xx ), uu tt |tt=0=ψψ(xx )2022-2023 数学物理方法期末试题 参考答案一、 填空题(每题3分,共27分)1.【正解】 12(ee bb +ee −bb )cos aa +i2(ee −bb −ee bb )sin aa 【解析】cos (aa +i bb )=ee ss (aa+ss bb )+ee −ss (aa+ss bb )2=12(ee −bb ee ss aa+ee bb ee −ss aa )=12[e −bb(cos aa +isin aa )+e bb (cos aa −isin aa )]=12[(e bb+e −bb )cos aa +i(e −bb −e bb )sin aa ]=12(ee bb +ee −bb)cos aa +i 2(ee −bb−ee bb )sin aa 2.【正解】支点:z=a 、b 、∞;皆为一阶支点【解析】注意到函数为12次,且当z=a 、b 时函数置零,z=∞为熟知的支点,阶数皆为2−1=1 3.【正解】A【解析】由根值判别法,幂级数的收敛区间为ll ii ll nn→∞�aa nn ⋅(1+bb nn )nn⋅xxxx (−1,1)而|bb |<1⇒ll ii ll nn→∞√1+bb nn nn=1故收敛半径保持不变,仍为A 4.【正解】zz =0;一阶 【解析】ll ii llzz→0ssss nn 2zz zz 3→∞,且ll ii ll zz→0zz ⋅ssss nn 2zz zz 3=1故zz =0为一阶极点5.【正解】2πi注意到原函数的极点为zz =0和zz =1,且分别为2阶与一阶极点,故上述积分即为II =2ππii �Re cc�ff (zz ),0]+Re cc [ff (zz ),1]��而Re cc [ff (zz ),0]=ll ii ll zz→0dd �zz 2−zz +1zz −1�ddzz=0Re cc [ff (zz ),1]=ll ii ll zz→1zz 2−zz +1zz 2=1因此II =2ππii6.【正解】�PP ll mm (xx )⋅PP kk mm (xx )ddxx =01−1(ll ≠kk ) 7. 【正解】Re cc [ff (zz ),ii ]=ll ii ll zz→ss dd �1(zz +ii )2�ddzz=−2[2ii ]−3Re cc [ff (zz ),−ii ]=ll ii ll zz→−ss dd �1(zz −ii )2�ddzz=−2[−2ii ]−38.【正解】∫ff (ττ)1−1δδ(tt −ττ)ddττ 9.【正解】ee 2ππ−1【解析】由δδ函数的挑选性,上述积分即为 (ee 2xx +cccccc xx )|xx=ππ=ee 2ππ−1 二、 简算题(每题5分,共15分)1.【解析】在区域0<|zz −1|<1内ff (zz )=1zz 2−3zz +2=−12⋅11−zz 2−1zz −1=−12⋅11−zz 2−1zz ⋅11−1zzff (zz )=−�12kk+1zz kk ∞kk=0−�zz −(kk+1)∞kk=0 =−�zz kk−1kk=−∞−�12kk+1zz kk∞kk=02.【解析】由约旦引理,从上半平面的半圆弧补全围道,上半平面有一个二阶极点zz 0=iiaa ,该点的留数为RReeccff (zz 0) =limzz→zz 0d d zz e immzz(zz +aa i)2=lim zz→zz 0[i ll e immzz (zz +aa i)2−2e ss nn zz (zz +aa i)3] =−llaa +14aa 3ie −mmaaII =ππi ⋅(−llaa +14aa 3ie −mmaa )=llaa +14aa3ππe −mmaa 3.【解析】根据C-R 条件,有∂uu ∂xx =3xx 2−3yy 2=∂νν∂yy−∂uu ∂yy =6xxyy =∂νν∂xxddνν=−(−6xxyy )d xx +3(xx 2−yy 2)d yy =d(3xx 2yy −yy 3) 有νν=3xx 2yy −yy 3+CC ,代入得ff (zz )=xx 3−3xxyy 2+i(3xx 2yy −yy 3+CC ) =(xx +i yy )3+i CC =zz 3+i CC 0三、(8分)【解析】设 yy =�aa nn xx nn ∞nn=0 是方程的解,其中 aa 0,aa 1 是任意常数,则yy ′=�nnaa nn xx nn−1∞nn=1yy ′′=�nn (nn −1)aa nn xx nn−2∞nn=2=�(nn +2)(nn +1)aa nn+2xx nn ∞nn=0方程 yy ′′+xxyy ′+yy =0,得�[(nn +2)(nn +1)aa nn+2+nnaa nn +aa nn ]xx nn ∞nn=0=0故必有(nn +2)(nn +1)aa nn+2+(nn +1)aa nn =0即aa nn+2=−aa nnnn +2(nn =0,1,2,⋯ ) 可见,当 nn =2(kk −1) 时aa 2kk=(−12kk )aa 2kk−2=(−12kk )(−12kk −2)⋯(−12)aa 0=aa 0(−1)kkkk !2kk当nn =2kk −1时aa 2kk+1=(−12kk +1)aa 2kk−1=(−12kk +1)(−12kk −1)⋯(−13)aa 1=aa 1(−1)kk (2kk +1)!�aa 2nn xx 2nn ∞nn=0与�aa 2nn+1xx 2nn+1∞nn=0的收敛域均为(−∞,+∞) 故yy =�aa κκxx κκ∞κκ=0=�aa 2κκxx 2κκ∞κκ=0+�aa 2κκ+1xx 2κκ+1∞κκ=0=�aa 0(−1)nn nn !2nn xx 2nn∞nn=0+�aa 1(−1)nn (2nn +1)!xx 2nn+1∞ss=0即yy =aa 0e −xx 22+aa 1�(−1)nn (2nn +1)!xx 2nn+1∞nn=0,xx ∈(−∞,+∞)四、 (10分)【解析】 首先找到满足方程的特解vv =aa 4(xx 2+yy 2)+bb 12(xx 4−yy 4)=aa 4ρρ2+bb 12(xx 2+yy 2)(xx 2−yy 2) =aa 4ρρ2+bb 12ρρ4cos 2φφ 令uu =vv +ww =aa 4ρρ2+bb 12ρρ4cos 2φφ+ww对于齐次方程,且满足球心为有限值的泊松方程通解为ww (ρρ,φφ)=�ρρnn (AA mm cos ll φφ+BB nn sin llφφ)∞mm=0代入边界条件,有 �ρρ0nn (AA mmcos ll φφ+BB nn sin llφφ)∞mm=0=cc −aa 4ρρ02−bb 12ρρ04cos 2φφ比较系数解得uu =vv +ww =cc +aa 4(ρρ2−ρρ02)+bb 12ρρ2(ρρ2−ρρ02)cos 2φφ 五、(15分)【解析】对于满足球心处为有限值的拉普拉斯方程通解为uu (rr ,θθ)=�AA ll rr l P ll (cos θθ)∞ll=0代入边界条件有�AA ll rr 0l P ll (cos θθ)∞ll=0=cos 2θθ=xx 2由于P 2(xx ) =12(3xx 2−1) ,有xx 2=13[1+2P 2(xx )]=13P 0(xx )+23P 2(xx )即�AA ll rr 0lP ll (cos θθ)∞ll=0=cos 2θθ=xx 2=13P 0(xx )+23P 2(xx )对比系数可得uu (rr ,θθ)=13+23⋅1rr 02⋅rr 2P 2(cos θθ)六、(10分)【解析】对方程进行拉普拉斯变换,有jj ‾RR +jj ‾ppCC =EE 0ωωpp 2+ωω2 解得jj ‾=ωωEE 0(RR +1ppCC )(pp 2+ωω2)再进行反演RR (tt )=EE 0ωωRR (−RRCC e llRRRRωω2RR 2CC 2+1+RRCC cos ωωtt +ωωRR 2CC 2sin ωωtt ωω2RR 2CC 2+1) =EE 0RR 2+1/CC 2ωω2(RR sin ωωtt +1CCωωcos ωωtt )−EE 0/CCωωRR 2+1/CC 2ωω2e −tt /RRRR七、(15分)【解析】应用冲量定理法,先求解vv uu −aa 2vv xxxx =0ννxx ∣x=0=0,vv x ∣x=l =0vv ∣tt=ττ+0=0,vv t ∣t=ττ+0=AA cos ππxxllsin ωωττ根据通解的一般形式并代入边界条件,可得vv (xx ,tt ;ττ)=AAllππaasin ωωττsin ππaa (tt −ττ)ll cos ππxx ll uu (xx ,tt )=�vv (xx ,tt ;ττ)tt=AAll ππaa cos ππxx ll �sin ωωττsin ππaa (tt −ττ)ll d ττtt 0=AAll ππaa 1ωω2−ππ2aa 2/ll 2(ωωsin ππaa ll tt −ππaa ll sin ωωtt )cos ππxx ll。
数学物理方程试卷

数学物理方程试卷一、常微分方程(1)证明椭圆线方程$x^2+y^2=1$的曲率半径是无穷的证明:曲线的曲率半径R为曲线点处的法线与曲率半径的夹角$\frac{1}{R}$的反正切值,其表达式为$\frac{,y',}{\sqrt{1+y'^2}}$,其中$y'$为曲线其中一点处的导数值。
而椭圆线方程$x^2+y^2=1$的一阶导数分别为$\frac{dy}{dx}=\frac{-x}{y}$以及$\frac{dx}{dy}=\frac{x}{y}$,这里可以得到$y' = \frac{-x}{y}=\frac{-1}{x}$。
此时曲率半径表达式变为$\frac{x}{,x,\sqrt{1+\frac{1}{x^2}}}$,表达式中的$,x,$可以去掉,并且$x$取任意值,故椭圆线方程$x^2+y^2=1$的曲率半径是无穷的。
(2)证明球面$x^2+y^2+z^2=a^2$的曲率、曲率半径一致证明:根据曲线曲率的定义可知,球面$x^2+y^2+z^2=a^2$的曲率为$\kappa=\frac{,R_1\cdot R_2,}{R^3}$,其中$R_1$、$R_2$分别为曲线其中一点处的两个切线的曲率半径,$R$为曲线其中一点处的曲率半径。
而对于球面,它的两个曲率半径$R_1$和$R_2$是完全一样的,这是因为在球面其中一点的法线方向没有区别,故$R_1=R_2$。
此时曲率可以表示为$\kappa=\frac{R_1^2}{R^3}=\frac{R^2}{R^3}=\frac{1}{R}$,即曲率等于其曲率半径的倒数,也就是说球面$x^2+y^2+z^2=a^2$的曲率和曲率半径是一致的。
二、偏微分方程。
数学物理方程复习题

2.问初始条件)(x ϕ与)(x ψ满足怎样的条件时,齐次波动方程初值问题的解仅由右传播波组成?解:波动方程的通解为 u=F(x-at)+G(x+at)其中F ,G 由初始条件)(x ϕ与)(x ψ决定。
初值问题的解仅由右传播组成,必须且只须对 于任何t x ,有 G(x+at)≡常数. 即对任何x, G(x)≡C 0又 G (x )=⎰-+xx aC d ax 02)(21)(21ααψϕ所以)(),(x x ψϕ应满足 +)(x ϕ⎰=xx C d a1)(1ααψ(常数)或'ϕ(x)+)(1x aψ=03.利用传播波法,求解波动方程的特征问题(又称古尔沙问题)⎪⎪⎩⎪⎪⎨⎧==∂∂=∂∂=+=-).()(0022222x u x u x ua t u at x at x ψϕ ())0()0(ψϕ= 解:u(x,t)=F(x-at)+G(x+at) 令 x-at=0 得 )(x ϕ=F (0)+G (2x ) 令 x+at=0 得 )(x ψ=F (2x )+G(0)所以 F(x)=)2(x ψ-G(0). G (x )=)2(xϕ-F(0).且 F (0)+G(0)=).0()0(ψϕ= 所以 u(x,t)=(ϕ)2atx ++)2(at x -ψ-).0(ϕ即为古尔沙问题的解。
1. 用分离变量法求下列问题的解:(1)⎪⎪⎪⎩⎪⎪⎪⎨⎧==<<-=∂∂=∂∂=∂∂==0),(),0()0()1(,3sin 022222t l u t u l x x x t u l x u x u a t u ot t π解:边界条件齐次的且是第一类的,令)()(),(t T x X t x u =得固有函数x ln x X n πsin)(=,且 t lan B t lan A t T n n n ππsincos)(+=,)2,1( =n于是 ∑∞=+=1sin)sincos(),(n n n x ln t lan B t lan A t x u πππ今由始值确定常数n A 及n B ,由始值得 ∑∞==1s i n3s i nn n x ln A lx ππ∑∞==-1sin)(n n x ln B lan x l x ππ所以 ,13=A ,0=n A 当3≠n ⎰-=ln x d x ln x l x an B 0sin)(2ππ⎩⎨⎧ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+-=x l n x n l x l n n lx l n x n l l an πππππππcos sincos 22222)}))1(1(4cos2sin24430333222nlan lxln n lx ln n x l --=--πππππ因此所求解为∑∞=--+=1443s i ns i n)1(143s i n 3c o s ),(n nx ln t lan na lx l t l a t x u πππππ(2) ⎪⎪⎪⎩⎪⎪⎪⎨⎧=∂∂==∂∂==∂∂-∂∂0)0,(,)0,(0),(0),0(022222x tu x l h x u t l tu t u x ua t u 解:边界条件齐次的,令 )()(),(t T x X t x u =得:⎩⎨⎧='==+''0)(,0)0(0l X X X X λ (1)及 )2(02=+''X a T λ。
数学物理方法期末考试大题

2、 求解热传导问题
ut a 2u xx A sin t u x |x 0 0, u |x l 0 u | x t 0
3、 两端固定弦在点 x0 受谐变力 f t f0 sin t 作用而振动,求解振动情况。[提示: 外加力的线密度可表示为 f x, t f 0 sin t x x0 ]
4、 均匀的薄板占据区域 0 x a , 0 y b 。边界上的温度
u |x 0 0 , u |x a 0 , u | y 0 u0 , lim u 0
y
求解板的稳定温度分布。
三、非齐次方程的分离变数法(15 分) 1、 长为 l 的均匀细杆两端固定,杆上单位长度受有纵向外力 f 0 sin 2 x l cos t ,初始位 移为 sin x l ,初始速度为零,求解杆的纵振动。
4、 求解细杆导热问题。杆长 l ,初始温度均匀为 u0 ,两端分别保持温度 u1 和 u2 。
四、球函数(12 分) 1、一空心圆球区域,内半径为 r1 ,外半径为 r2 ,内球面上有恒定电势 u0 ,外球面上电势保 持为 u1 cos 2 , u0 、 u1 均为常数,试求内外球面之间空心圆球区域的电势分布。
数学物理方法期末考试大题数学物理方法判断题数学物理方法数学物理方法复习数学物理方法教材数学物理方法试卷数学物理方法课件数学物理方法pdf数学物理方法试题数学物理方法答案
一、拉普拉斯变换(8 分) 1、求积分 I t
0
cos tx dx x2 a2
二、齐次方程的分离变数法(15 分) 1、 求解细杆导热问题,杆长 l ,b 为常数,两端保持为零度,初始温度分布
数学物理方程题库

1
2) x 2 u xx + 2 xy u xy + y 2 u yy = 0 解 : 方 程 的 判 别 式 ∆ = a12 2 − a11 a 22 = ( xy ) − x 2 y 2 = 0. 所以方程为抛物型。 该方程的一组特征微分方程为 dy a12 y = = ,解 这 个 微 分 方 程 得 到 : dx a11 x
x
' 对上式积分得,a ⎡ f x − f x = − a ϕ ⎤ ( ) ( ) 1 2 ⎣ ⎦ ∫ ( x) dξ + c
x0
⎧ ϕ ( x) 1 x ' c − ∫ ϕ ( x) dξ + ⎪ f1 ( x) = 2 2 x0 2a ⎪ 于是得到, ⎨ x ⎪ f x = ϕ ( x) + 1 ϕ' x dξ − c ( ) ∫ ⎪ 2( ) 2 2 2a x0 ⎩ ⎧ ϕ ( x + at ) 1 x+at ' c f x + at = − ϕ x d ξ + ) ( ) ⎪ 1( ∫ 2 2 2a x0 ⎪ ⇒⎨ x0 c ⎪ f x − at = ϕ ( x − at ) + 1 ' ϕ x d ξ − ( ) ( ) ∫at ⎪ 2 2 2 2a x − ( ) ⎩ ⇒ u ( x,t) = f1 ( x + at ) + f2 ( x − at ) 1 1 = ⎡ ϕ x + at + ϕ x − at ⎤ − ϕ ' (ξ ) dξ ( ) ( ) ⎣ ⎦ ∫ 2 2 x−at = ϕ ( x − at )
2 ⎧ ⎪utt = a uxx ( −∞ < x < ∞) ⎨ ' u x ,0 = ϕ x , u x ,0 = − a ϕ ( ) ( ) ( ) ( x) ⎪ t ⎩ 根据题意,令u( x,t) = f1 ( x + at ) + f2 ( x − at )
数学物理方程期末考试题及答案

数学物理方程期末考试题及答案一、选择题(每题2分,共10分)1. 以下哪一项不是数学物理方程的特点?A. 连续性B. 离散性C. 线性D. 非线性答案:B2. 波方程是描述什么的方程?A. 热传导B. 电磁波C. 机械波D. 流体动力学答案:C3. 拉普拉斯方程通常出现在哪种物理现象中?A. 热传导B. 流体流动C. 电磁场D. 弹性力学答案:C4. 以下哪个不是偏微分方程的解的性质?A. 唯一性B. 线性C. 稳定性D. 离散性答案:D5. 波动方程的解通常表示什么?A. 温度分布B. 电荷分布C. 压力分布D. 位移分布答案:D二、填空题(每空2分,共20分)6. 波动方程的基本形式是 _______。
答案:\( \frac{\partial^2 u}{\partial t^2} = c^2 \nabla^2 u \)7. 热传导方程,也称为________方程。
答案:傅里叶8. 拉普拉斯方程 \( \nabla^2 \phi = 0 \) 在静电学中描述的是________。
答案:电势9. 边界条件通常分为________和________。
答案:狄利克雷边界条件;诺伊曼边界条件10. 波动方程的一般解可以表示为________和________的叠加。
答案:基频解;高阶谐波三、简答题(每题10分,共30分)11. 解释什么是边界层的概念,并给出一个实际应用的例子。
答案:边界层是流体力学中的一个概念,指的是流体靠近物体表面处的一层非常薄的流体,其中速度梯度很大。
在边界层内,流体的速度从物体表面的零速度逐渐增加到与外部流体速度相匹配。
一个实际应用的例子是飞机的机翼,边界层的厚度和特性对飞机的升力和阻力有重要影响。
12. 描述什么是格林函数,并解释它在解决偏微分方程中的作用。
答案:格林函数是一种数学工具,用于解决线性偏微分方程。
它是一个特定的函数,当它与方程的算子相乘时,结果是一个狄利克雷问题,其解是原始方程的一个解。
数学物理方程期末考试试题及答案

数学物理方程期末考试试题及答案一、求解方程(15分)⎧utt -a2uxx=0⎪⎨ux-at=0=ϕ(x)⎪u⎩x+at=0=ψ(x).其中ϕ(0)=ψ(0)。
⎧ξ=x-at解:设⎨则方程变为:η=x+at⎩uξη=0,u=F(x-at)+G(x+at)(8’)由边值条件可得:F(0)+G(2x)=ϕ(x),F(2x)+G(0)=ψ(x)由ϕ(0)=ψ(0)即得:u(x,t)=ϕ(x+at x-at)+ψ()-ϕ(0)。
22二、利用变量分离法求解方程。
(15分)⎧utt -a2uxx=0,(x,t)∈Q,⎪⎨ux=0=ux=l=0,t≥0,⎪u=ϕ(x),ut t=0=ψ(x)⎩t=0其中0≤x≤l。
a>0为常数解:设u=X(x)T(t)代于方程得:X''+λX=0,T''+λa2T=0(8’)X=C1cosλx+C2sinλx,T=C1cosλat+C2sinλat由边值条件得:C 1=0,λ=(∞n π2)ln πx lu =∑(B n cos λat +A n sin λat )sin n =1B n =2l n πx 2l n πx ,ϕ(x )sin dx A =ψ(x )sin dx n ⎰⎰00l l an πl2三.证明方程u t -a u xx -cu =0(c ≥0)具有狄利克雷边界条件的初边值问题解的唯一性与稳定性. (15分)证明:设v =e -ct u 代入方程:⎧v t-a 2v xx =0⎪⎨v t =0=ϕ(x )⎪v (0,t )=g (t ),v (l ,t )=g (t ).12⎩设v 1,v 2都是方程的解设v =v 1-v 2代入方程得:⎧v t-a 2v xx =0⎪⎨v t =0=0⎪v (0,t )=,v (l ,t )=0⎩由极值原理得v =0唯一性得证。
(8’)由v 1-v 2≤v 1-v 2得证。
τ≤ε,稳定性得证由v =e -ct u 知u 的唯一性稳定性四.求解二维调和方程在半平面上的狄利克雷问题(15分).∆u =u xx +u yy +u zz=0,z >0,u z =0=f (x ).解:设p (ξ,η,ζ)是上半平面内一点,在该点放置单位点电荷,其对称点p (ξ,η,-ς)格林函数:G (x ,y ,ξ,η)=-14π14π1(x -ξ)+(y -η)+(z -ς)1(x -ξ)+(y -η)+(z +ς)222222+∂G∂G=-∂n∂z z=0=ς2π[(x-ξ)+(y-η)+ς]2223/2方程的解:u(ξ,η)=ς2πϕ(x,y)⎰[(x-ξ)2+(y-η)2+ς2]3/2dx R2五、证明下列初边值问题解的唯一性.(20分)u utt-a2(uxx+uyy)=f(x,y,t) t=0=ϕ(x,y),=ψ(x,y),ut t=0uΓ=g(x,y,t).其中t>0,(x,y)∈Ω,Γ为Ω的边界.解:设u1,u2都是方程的解设u=u1-u2代入方程得:u tt -a(uxx+uyy)=0u u t t=02 =0=0 t=0uΓ=0.设E(t)=12222[u+a(u+u]dxdy t x y⎰⎰2ΩdE(t)=2⎰⎰[ut utt+a2(uxuxt+uyuyt)]dxdydtΩ=2[ut [utt-a(uxx+uyy)]dxdyΩ⎰⎰2=0(10’)E(t)=E(0)=0,u=C,由边值条件得:u=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学物理方程期末试卷2012学年第二学期数学与物理方程期末试卷出卷人:欧峥1、长度为 l 的弦左端开始时自由,以后受到强度为sin A t ω的力的作用,右端系在弹性系数为k 的弹性支承上面;初始位移为(),x ϕ初始速度为().x ψ试写出相应的定解问题。
(10分)2、长为l 的均匀杆,侧面绝热,一端温度为0度,另一端有已知的恒定热流进入,设单位时间流入单位截面积的热量为q ,杆的初始温度分布是()2x l x -,试写出其定解问题。
(10分)3、试用分离变量法求定解问题(10分):.⎪⎪⎪⎩⎪⎪⎪⎨⎧===><<∂∂=∂∂===x t x x ut u u u u t x x 2,0,00,40,040224、分离变量法求定解问题(10分)222sin cos ,(0,0)(0,)3,(,)64(,0)31,(,0)sin tt xxtu a u x x x l t l l u t u l t x u x u x x l l πππ⎧=+<<>⎪⎪⎪==⎨⎪⎛⎫⎪=+= ⎪⎪⎝⎭⎩5、利用行波法,求解波动方程的特征问题(又称古尔沙问题)(10分):⎪⎪⎩⎪⎪⎨⎧==∂∂=∂∂=+=-).()(0022222x ux u x u a t u at x at x ψϕ ())0()0(ψϕ=6、用达朗贝尔公式求解下列一维波动方程的初值问题(10分)⎪⎩⎪⎨⎧=∂∂=>+∞<<-∞+∂∂=∂∂==0,2sin 0,,cos 0022222t t t u x u t x x x u a t u7、用积分变换法求解定解问题(10分):⎪⎪⎩⎪⎪⎨⎧=+=>>=∂∂∂==,1,10,0,1002y x uy u y x y x u8、用积分变换法求解定解问题(10分):⎩⎨⎧==>∈=0)0,(,sin )0,(0,,2x u x x u t R x u a u t xx tt9、用格林函数法求解定解问题(10分):222200, y 0, () , .y u ux y u f x x =⎧∂∂+=<⎪∂∂⎨⎪=-∞<<+∞⎩10、写出格林函数公式(三维)及满足的条件,并解释其物理意义。
(10分)答案及分析1、解: 这是弦的自由振动,其位移函数(,)u x t 满足2,tt xx u a u = (2分) 其中2Ta ρ=.由于左端开始时自由,以后受到强度为sin A t ω的力的作用,所以(0,0)0,(0,)sin 0,0,x x u Tu t A t t ω=+=>因此 sin (0,),0.x A tu t t Tω=-≥ (2分) 又右端系在弹性系数为k 的弹性支承上面,所以 (,)(,)0,x Tu l t ku l t --= 即 (,)(,)0.x Tu l t ku l t += (2分) 而初始条件为 0(),().t tt ux u x ϕψ==== (2分)因此,相应的定解问题为200,0,0,sin (0,),(,)(,)0,0.(),().tt xx xx t t t u a u x l t A t u t Tu l t ku l t t T u x u x ωϕψ==⎧=<<>⎪⎪=-+=≥⎨⎪==⎪⎩ (2分)2、解:侧面绝热,方程为2,0,0t xx u a u x l t =<<> (3分)边界条件为 00,,0x xx lqu u t k====> (3分)初始条件为(),02t x l x ux l =-=<< (3分)因此,相应的定解问题为:(1分)3、解 令)()(),(t T x X t x u =(2分),代入原方程中得到两个常微分方程:0)()('=+t T t T λ,0)()(''=+x X x X λ(2分),由边界条件得到0)4()0(==X X ,对λ的情况讨论,只有当0>λ时才有非零解,令2βλ=,得到22224πβλn ==为特征值,特征函数4sin )(πn B x X n n =(1分),再解)(t T ,得到16;22)(t n n n e C t T π-=(2分),于是,4sin(),(16122xn eC t x u tn n n ππ-∞=∑=(1分)再由初始条件得到140)1(164sin 242+-==⎰n n n xdx n x C ππ(1分),所以原定解问题的解为,4sin)1(16),(161122xn e n t x u t n n n πππ-+∞=-=∑(1分)4、解:令(,)(,)()u x t V x t W x =+ (1分)将其代入定解问题可以得到:2,(0,0)(0,)0,(,)0.....(1)4(,0)31(),(,0)sin tt xx t V a V x l t V t V l t x V x W x V x x l l π⎧⎪=<<>⎪⎪==⎨⎪⎛⎫⎪=+-= ⎪⎪⎝⎭⎩(1分)222()sin cos 0(2)(0)3,()6a W x x x l l W W l ππ⎧''+=⎪⎨⎪==⎩ (1分)(2)的解为:2224()sin 3132l x W x x al l ππ⎛⎫=++ ⎪⎝⎭(2分)对于(1),由分离变量法可得一般解为1(,)cos sin sin n n n n at n at n x V x t a b l l l πππ+∞=⎛⎫=+ ⎪⎝⎭∑ (2分) 由初始条件可求得:222444(,)cos sin sin 324l a l at xV x t t a l a l l πππππ⎛⎫=-+ ⎪⎝⎭ (2分) 所以,原定解问题的解为:2222224444(,)cos sin sin sin 3132432l a l at x l x u x t t x a l a l l a l l πππππππ⎛⎫⎛⎫=-++++ ⎪ ⎪⎝⎭⎝⎭(1分)5、解:u(x,t)=F(x-at)+G(x+at)(2分) 令 x-at=0 得 )(x ϕ=F (0)+G (2x ) (2分) 令 x+at=0 得 )(x ψ=F (2x )+G(0)(2分)所以 F(x)=)2(x ψ-G(0). G (x )=)2(xϕ-F(0).(2分) 且 F (0)+G(0)=).0()0(ψϕ= (1分) 所以 u(x,t)=(ϕ)2at x ++)2(atx -ψ-).0(ϕ(1分)即为古尔沙问题的解。
6、解令)(),(),(x w t x v t x u +=(1分),代入原方程中,将方程齐次化,因此x a x w x x w a x x w x v a t v cos 1)(0cos )(cos )]([2''2''22222=⇒=+⇒++∂∂=∂∂(2分),再求定解问题⎪⎪⎩⎪⎪⎨⎧=∂∂-=>∂∂=∂∂==,0),(cos 12sin 0,02022222t t tvx xw a x t xv a t v v (2分)由达朗贝尔公式得到以上问题的解为atx a at x at x aat x at a a at x t x v cos cos 1cos sin 0)]cos(1)(2sin )cos(1)(2[sin 21),(222-=+---++-+= (4分)故.cos 1cos cos 1cos sin ),(22x a at x a at x t x u +-=(1分)7、解 对y 取拉普拉斯变换),()],([p x U y x u L =(1分),对方程和边界条件同时对y 取拉普拉斯变换得到p p U pdx dU px 11,120+===(3分),解这个微分方程得到p p x p p x U 111),(22++=(3分),再取拉普拉斯逆变换有1),(++=y yx y x u (2分)所以原问题的解为1),(++=y yx y x u .(1分) 8、解:对于初值问题关于x 作Fourier 变换,得:⎪⎩⎪⎨⎧==>∈+0)0,(ˆ),(sin )0,(ˆ0,),,(ˆd ),(ˆd 2222ωωωωωt u x F u t R x t u a t t u(2分) 该方程变为带参数ω的常微分方程的初值问题。
解得t ja t ja e C e C t uωωω-+=21),(ˆ (2分) 于是0)()0,(ˆ,)(sin )0,(ˆ2121=-=+==C C ja u C C x F u t ωωω(2分)则由)(sin 2121x F C C ==,得:))((sin 21),(ˆt ja t ja e e x F t u ωωω-+=。
(2分)作像函数),(ˆt uω的Fourier 逆变换 []at x at x at x e e x F F t uF t x u t ja t ja cos sin )]sin()[sin(21))((sin 21)],(ˆ[),(11=++-=+===---ωωω(2分)9、解:设),(000y x M 为下半平面中任意一点。
已知二维调和函数的积分表达式为dS n ur r n M u M u MM MM )1ln )1(ln )((21)(000∂∂-∂∂-=⎰Γπ (1分) 设v 为调和函数,则由第二格林公式知0)()(22=∂∂-∂∂=∇-∇⎰⎰⎰ΓΩdS nuv n v u d u v v u σ (2) (1)+(2)可得dS n uv r dS r n n v M u M u MM MM ])1ln 21(])1(ln 21)(([)(000⎰⎰ΓΓ∂∂-+∂∂-∂∂=ππ (2分) 若能求得v 满足⎪⎪⎩⎪⎪⎨⎧=<=∇==00201ln 210,0y MM y rv y v π (3)则定义格林函数v r M M G MM -=1ln 21),(0π,则有 dS nGM u M u ⎰Γ∂∂-=)()(0 (2分)由电象法可知,),(001y x M -为),(000y x M 的象点,故可取11ln21MM r v π=(1分)显然其满足(3)。
从而可得格林函数))()()()()()((21)1ln 1(ln 211ln211ln 21),(202002020001010y y x x y y y y x x y y r r y y G n G r r M M G MM MM MM MM ++-+-+-+---=-∂∂=∂∂=∂∂-=ππππ (3分) 故而ξξξπd f y x y dS n G M u M u ⎰⎰+∞∞-Γ+--=∂∂-=)()(1)()(202000 (1分)10、解:(1)格林函数公式(三维)为:11G (M ,M 0)=014MM r π— g (M ,M 0) M ∈Ω (2分)其中函数g 满足的条件为:001|4MM g M g r πΓΓ∆=∈Ω⎧⎪⎨=⎪⎩ 式中Γ为区域Ω的边界曲面(3分) (2)格林函数的物理意义:在某个闭合导电曲面Γ内M 0点处放一个单位正电荷,则有它在该导电曲面内一点M 处产生的电势为014MM r π(不考虑电介常数),将此闭合导电曲面接地,又静电平衡理论,则M 0将在该导电曲面上产生负感应电荷,其在M 处的电势— g (M ,M 0),并且导电面上的电势恒等于0,即有|g Γ=014MM r πΓ(5分)。
