简单几何体的面积和体积(基础+复习+习题+练习)
高中数学人教A版(2019)必修 第二册第八章 立体几何初步8.3简单几何体的表面积与体积

必修第二册 8.3 简单几何体的表面积与体积一、单选题1.如图,位于贵州黔南的“中国天眼”是具有我国自主知识产权、世界最大单口径、最灵敏的球面射电望远镜,其反射面的形状为球冠,球冠是球面被平面所截后剩下的曲面,截得的圆为球冠的底,与截面垂直的球体直径被截得的部分为球冠的高,设球冠所在球的半径为R ,球冠底的半径为r ,球冠的高为h ,球冠底面圆的周长为C .已知球冠的表面积公式为2S Rh π=,若65000,500S C ππ==,则球冠所在球的表面积为( )A .1620000πB .1690000πC .1720000πD .1790000π 2.已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)813.已知ABC O 的球面上,若球O 的体积为32π3,则O 到平面ABC 的距离为( )AB .32C .1D 4.已知A ,B 是球O 的球面上两点,90AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .128πD .144π5.如图,在棱长为a 的正方体1111ABCD A B C D -中,P 在线段1BD 上,且12BP PD =,M 为线段11B C 上的动点,则三棱锥M PBC -的体积为( )A .319aB .332aC .313aD .与点M 的位置有关6.已知正四棱锥P ABCD -的所有顶点都在球O 的球面上,且正四棱锥P ABCD -的底面面积为6,侧面积为,则球O 的表面积为( )A .323πBC .16πD .32π 7.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )AB C D 8.黄金分割是指将整体一分为二,较大部分与整体的比值等于较小部分与较大部分的,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金分割比,且它们的夹角的余弦值为黄金分割比值,那么这个三角形一定是直角三角形,这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,以短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,所得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以四棱锥的高为边长的正方形面积与该四棱锥的侧面积之比为( )A B C .1 D .149.阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径.若该球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π 10.平行四边形ABCD 中,AB BD ⊥,且2224AB BD +=,沿BD 将四边形折起成平面ABD ⊥平面BDC ,则三棱锥A BCD -外接球的表面积为( )A .2πB .2πC .4πD .16π 11.已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )A .122ππ+B .144ππ+C .12ππ+ D .142ππ+ 12.已知正四棱锥的底面边长和侧棱长均为2,则该正四棱锥的体积为( )A B .C D .二、填空题13.已知圆锥的侧面积(单位:2cm ) 为2π,且它的侧面积展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.14.一个正四棱锥的顶点都在同一球面上,若该棱锥的高为2,底面边长为2,则该球的表面积为______.15.已知圆柱的轴截面(经过圆柱的轴的截面)是一个边长为2的正方形,则此圆柱的体积为________.16.若球的大圆的面积为9π,则该球的体积为________17.若五棱台11111ABCDE A B C D E -的表面积是30,侧面积是25,则两底面面积的和为______.三、解答题18.圆台的母线长为2a ,母线与轴的夹角为30,一个底面的半径是另一个底面的半径的2倍,求两底面的半径及两底面面积之和.19.将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体,O 为11A C 的中点.(1)求证://OB 平面1ACD ;(2)求几何体111ACB A D 的体积.20.如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终在桌面上,设直径AB 所在直线与桌面所成的角为α.(1)求图①中圆柱的母线与液面所在平面所成的角(用α表示);(2)要使倾斜后容器内的溶液不会溢出,求α的最大值.21.“圆锥的两条母线所作的一切截面中,以轴截面的面积最大”是否成立?答案第1页,共1页 参考答案:1.B2.D3.C4.D5.A6.C7.C8.D9.C10.C11.A12.A13.114.9π15.2π16.36π17.518.圆台上底面半径为a ,下底面半径为2a ,两底面面积之和为25a π. 19.(1)见解析;(2)4.20.(1)2πα-;(2)45°﹒21.答案见解析。
第01讲 基本立体图形、简单几何体的表面积与体积 (精练)(教师版)

第01讲 基本立体图形、简单几何体的表面积与体积 (精练)A 夯实基础一、单选题1.(2022·广西玉林·高一期末)若一个圆锥的轴截面是边长为3的正三角形,则这个圆锥的表面积为( ) A .274π B .92πC .3πD .94π 【答案】A由题可知,该圆锥的底面半径为32,因此,该圆锥表面积为233273224πππ⎛⎫⨯+⨯⨯= ⎪⎝⎭故选:A2.(2022·广东梅州·高一期末)如图,A O B '''是水平放置的△AOB 的直观图,但部分图象被茶渍覆盖,已知O '为坐标原点,顶点A '、B '均在坐标轴上,且△AOB 的面积为12,则O B ''的长度为( )A .1B .2C .3D .4【答案】B画出△AOB 的原图为直角三角形,且6''==OA O A , 因为1122⨯=OB OA ,所以4OB =,所以122''==O B OB .故选:B.3.(2022·广东茂名·高二期末)储粮所用“钢板仓”,可以看成由圆锥和圆柱两部分组成的.现有一种“钢板仓”,其中圆锥与圆柱的高分别是1m 和3m ,轴截面中等腰三角形的顶角为120°,若要储存3003m 的水稻,则需要准备这种“钢板仓”的个数是( )A .6B .9C .10D .11【答案】C因为圆锥的高为1,轴截面中等腰三角形的顶角为120°, 所以圆锥的母线长为2所以一个“钢板仓”的体积为22313110m 3πππ⨯⨯+⨯⨯⨯=,因为3009.510π≈ 所以要储存3003m 的水稻,则需要准备这种“钢板仓”的个数为10个, 故选:C4.(2022·辽宁锦州·高一期末)正三棱锥S ABC -的高为则该三棱锥的侧棱长为( )A .B .C .D .4【答案】D依题意作上图,其中E 是BC 的中点,D 是正三角形ABC 的中心, 并且SD ⊥ 平面ABC ,SE BC ⊥ ,则有SD SE ==,在Rt SDE 中,3ED AE ED ==AB BC AE ∴===,在Rt SBE 中,4SB = ;故选:D.5.(2022·上海·复旦附中高二期末)小明同学用两个全等的六边形木板和六根长度相同的木棍搭成一个直六棱柱111111ABCDEF A B C D E F -,由于木棍和木板之间没有固定好,第二天他发现这个直六棱柱变成了斜六棱柱111111ABCDEF A B C D E F -,如图所示.设直棱柱的体积和侧面积分别为1V 和1S ,斜棱柱的体积和侧面积分别为2V 和2S ,则( ).A .1212V V S S > B .1212V V S S < C .1212V V S S = D .11V S 与22V S 的大小关系无法确定 【答案】A设底面面积为S ,底面周长为C , 则11V S AA =⋅,11S C AA =⋅,所以11V SS C=, 设斜棱柱的高为h ,则2V S h =⋅,2AB BC CD DE EF FA S AB h BC h CD h DE h EF h FA h =⨯+⨯+⨯+⨯+⨯+⨯ ()AB BC CD DE EF FA h Ch >+++++⨯=,所以2121V V Sh S S Ch C S <==. 故选:A6.(2022·湖南常德·则该圆锥的内切球体积为( ) A .4π B .43πC .πD .6π【答案】D轴截面如图所示,设内切球的半径为r ,则OD OE r ==, 由题意可得6OCD π∠=,CD =, 在Rt OCD △中,tan ODOCD CD∠=,所以1tan 2OD CD OCD =⋅∠==,即12r =,所以内切球体积为334413326r πππ⎛⎫== ⎪⎝⎭,故选:D7.(2022·河南驻马店·高一期末)已知平面四边形ABCD ,连接对角线BD ,得到等边三角形ABD 和直角三角形BCD ,且3AB =,π2BDC ∠=,BC =将平面四边形ABCD 沿对角线BD 翻折,得到四面体A BC D '',则当四面体A BC D ''的体积最大时,该四面体的外接球的表面积为( ) A .12π B .18π C .21π D .28π【答案】C因为底面A BD '为正三角形,所以底面A BD '面积为定值, 所以当C BD '⊥平面A BD '时,四面体ABCD 的体积最大.设A BD '外接圆圆心为1O ,则四面体ABCD 的外接球的球心O 满足1//OO C D ',且11322OO C D '==,三角形A BD '的外接圆半径为32sin 60r r =⇒︒因此外接球的半径R 满足222223321()()()224R r =+=+=从而外接球的表面积为2421R ππ=. 故选:C.8.(2022·重庆市第七中学校高一期末)如图所示,在平面四边形ABCD 中,AD CD ⊥,AC BC ⊥,60B ∠=︒,3AD CD ==.现将ACD △沿AC 折起,并连接BD ,当三棱锥D ABC -的体积最大时,其外接球的表面积为( )A .16π3B .C .32π3D .24π【答案】D因为ABC 的面积不变,要使体积最大,需 D 到平面ABC 的距离最大,即当平面ACD ⊥平面ABC 时,体积最大,因为ACD △等腰直角三角形,取AC 中点E ,则DE ⊥平面ABC ,高为DE AC =Rt ABC中,60B ︒∠=,BC ,AB =所以EB ,故Rt BDE 中BD 所以ABD △中222AD BD AB +=,即得空间中90ADB ACB ︒∠=∠=即AB 为球的直径,故半径22424R AB ==,所以外接球的表面积24π24πS R ==. 故选:D. 二、多选题9.(2022·重庆八中高一期末)某工厂生产出一种机械零件,如图所示零件的几何结构为圆台12O O ,在轴截面ABCD 中,AB =AD =BC =4cm ,CD =2AB ,则下列说法正确的有( )AB .该圆台轴截面面积为2C 3D .一只蚂蚁从点C 沿着该圆台的侧面爬行到AD 的中点,所经过的最短路程为10cm【答案】BCD如图,作BE CD ⊥交CD 于E ,易得22CD ABCE -==,则12224223B O E O ,则圆台的高为,A 错误;圆台的轴截面面积为21(48)2+⨯,B 正确;圆台的体积为31π(4168)cm 3=++⨯=V ,C 正确;将圆台一半侧面展开,如图中ABCD ,设P 为AD 中点,圆台对应的圆锥一半侧面展开为扇形COD ,由圆台补成圆锥,可得大圆锥的母线长为8cm ,底面半径为4cm ,侧面展开图的圆心角为2π4π8θ⋅==,连接CP ,可得∠COP =90°,OC =8,OP =4+2=6,则10CP =,所以沿着该圆台表面从点C 到AD 中点的最短距离为10cm ,故D 正确. 故选:BCD.10.(2022·安徽宣城·高一期末)已知正四面体的外接球、内切球的球面上各有一动点M 、N ,若线段MN) A .正四面体的棱长为6B .正四面体的内切球的表面积为6πC .正四面体的外接球的体积为D .线段MN 的最大值为【答案】ABD设这个四面体的棱长为a 的正方体截得的,所以四面体的外接球即为正方体的外接球,外接球直径为正方体的对角线长, 设外接球的半径为R ,内切球的半径为r ,则2R =,所以R =,四面体的高为h =,则等体积法可得 11433Sh Sr =⨯,所以14r h ==,由题意得R r -==6a = 所以A 正确,所以6R ==334433R ππ=⋅=⎝⎭,所以C 错误,因为内切球半径为6r ==22446r πππ=⋅=⎝⎭,所以B 正确,线段MN 的最大值为R r +=D 正确, 故选:ABD 三、填空题11.(2022·上海市青浦高级中学高一期末)设地球半径为R ,地球上北纬30°圈上有A ,B 两点,点A 在西经10°,点B 在东经110°,则点A 和B 两点东西方向的距离是___________.如图示,设O '为北纬30°圈的圆心,地球球心为O ,则60AOO '∠= ,故2AO R '=,即北纬30°R , 由题意可知2π1203AO B '∠==, 故点A 和B 两点东西方向的距离即为北纬30°圈上的AB 的长,故AB 的长为2π3=,12.(2022·广东·高二期末)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;将底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;将四个面均为直角三角形的四面体称为鳖孺.如图,在堑堵111ABC A B C -中,AC BC ⊥,2AC BC ==,11AA =,则鳖臑11A CBC -的外接球的表面积为__________.【答案】9π堑堵111ABC A B C -的外接球即为鳖臑11A CBC -外接球,又可将堑堵111ABC A B C -补成长方体,长方体的外接球即为堑堵111ABC A B C -的外接球,长方体的外接球直径为13A B ==, 所以鳖臑11A CBC -的外接球的半径为32, ∴鳖臑11A CBC -的外接球表面积为234π×=9π2S ⎛⎫= ⎪⎝⎭.故答案为:9π. 四、解答题13.(2022·广东佛山·高一期末)如图,一个高为8的三棱柱形容器中盛有水,若侧面11AA B B 水平放置时,水面恰好过AC ,BC ,11B C ,11A C 的中点E ,F ,G ,H .(1)直接写出直线FG 与直线1A H 的位置关系;(2)有人说有水的部分呈棱台形,你认为这种说法是否正确?并说明理由.(3)已知某三棱锥的底面与该三棱柱底面ABC 全等,若将这些水全部倒入此三棱锥形的容器中,则水恰好装满此三棱锥,求此三棱锥的高.【答案】(1)异面(2)不是棱台,理由见详解(3)18(1)因为水面恰好过AC ,BC ,11B C ,11A C 的中点E ,F ,G ,H , 所以111111//,//,,,22HG A B EF AB HG A B EF AB == 又11//,A B AB 且11,A B AB =因此//HG EF ,且HG EF =,所以四边形EFGH 是平行四边形, 故//FG EH ,而1A H EH H =,所以直线FG 与直线1A H 不可能平行,而面EFGH平面111A B C HG =,所以直线FG 与直线1A H 不可能是相交直线,所以直线FG 与直线1A H 是异面直线; (2)因为棱台各侧棱交于一点,易知1AE A H 无交点,所以该几何体不是棱台;(3)设此三棱锥的高为h ,底面面积为S , 容器中水的形状为棱柱,体积为3864SS ⨯= 所以有163S h S ⋅⋅=,解得18h =,即三棱锥的高为1814.(2022·重庆市巫山大昌中学校高一期末)如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5,3AB BC CD ===,(1)求该圆柱的表面积;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求ACD △的三边在旋转过程中所围成的几何体的体积. 【答案】(1)75π2(2)15π (1)由题意知AB 是圆柱OO '的一条母线,BC 过底面圆心O ,且5AB BC ==, 可得圆柱的底面圆的半径为52R =, 则圆柱的底面积为221525πππ24S R ⎛⎫==⨯= ⎪⎝⎭,圆柱的侧面积为252π2π525π2S Rl ==⨯⨯=所以圆柱的表面积为12257522π25ππ42S S S =+=⨯+=. (2)由线段AC 绕AB 旋转一周所得几何体为以BC 为底面半径,以AB 为高的圆锥, 线段AD 绕AB 旋转一周所得的几何体为BD 为底面半径,以AB 为高的圆锥, 所以以ACD △绕AB 旋转一周而成的封闭几何体的体积为: 22221111πππ55π4515π3333V BC AB BD AB =⋅⋅-⋅⋅=⋅⋅-⋅⋅=. B 能力提升1.(多选)(2022·海南·高一期末)已知正四棱台1111ABCD A B C D -,且1122AB A B ==,则( )A B .侧棱与底面所成的角为60︒C .正四棱台的侧面积为D 【答案】ABD设正四棱台的高为k ,由题意可知该四棱台的上下底面面积分别为1和4,则()11243V h =++=h =1A 作1A G ⊥底面ABCD ,易知点G 在线段AC 上,则1A G =又由11AC =AC =AG =,所以1AA =A 正确; 在1Rt A GA 中,111cos 2AG A AG A A ∠==,所以160A AG ∠=︒, 即侧棱与下底面所成的角为60︒,故B 正确;在梯形11ABB A 中,2AB =,111A B == 所以梯形11ABB A的面积为()1122⨯+=,4=,故C 错误; 设正方形ABCD 的中心为O ,易知1AA O 为等边三角形,11OA OA AA ==点O 到正四棱台的8则正四棱台的外接球体积为34π3⨯=,故D 正确. 故选:ABD2.(2022·江苏徐州·高一阶段练习)已知正方体1111ABCD A B C D -的棱长为6,E 、F 分别是11A D 、1AA 的中点,平面CEF 截正方体所得的截面为多边形,则此多边形的边数为___________,截面多边形的周长为___________.【答案】 五, +解:延长EF 交DA 的延长线于M ,连接MC 交AB 于N , 延长FE 与DD1的延长线相交于点P,连接PC 交C1D1于Q ,连接EQ, 则五边形EFNCQ 即为平面CEF 截正方体所得的截面.如图所示:则有A1F=FA=AM=3,又因为MAN∆与MDC∆相似,所以MA ANMD CD=,解得AN=2,所以FN NC同理可得:QD1=2,QC1=4,所以QC==EQ,又因为EF=所以五边形EFNCQ的周长为故答案为:五;C综合素养1.(2022·湖北·华中师大一附中高一期末)佩香囊是端午节传统习俗之一.香囊内通常填充一些中草药,有清香、驱虫、开窍的.因地方习俗的差异,香囊常用丝布做成各种不同的形状,形形色色,玲珑夺目.图1的平行四边形ABCD由六个边长为1的正三角形构成.将它沿虚线折起来,可得图2所示的六面体形状的香囊.那么在图2这个六面体中内切球半径为__________,体积为__________.【答案】 解:如图所示:易知该几何体是侧棱长为1,以边长为1的等边三角形ABD △为底的两个正三棱锥组成,O 为ABD △的中心,即内切球的球心,M 为FB 的中点,连接HM ,作ON HM ⊥,则ON 为内切球的半径,因为,,OM HM HO ====, 所以1122HOM S OH OM HM ON =⋅=⋅,所以内切球的半径为OH OM R ON HM ⋅===,内切球的体积为343V R ππ==,2.(2022·浙江宁波·高二期末)如图,D ,E ,F 分别是边长为4的正三角形三边,,CA AB BC 的中点,将ADE ,BEF ,CFD △分别沿,,DE EF FD 向上翻折至与平面DEF 均成直二面角,得到几何体ABC DEF -.则二面角C AB E --的余弦值为_____;几何体ABC DEF -的外接球表面积为_____.【答案】203π##203π 取DE 的中点P ,EF 的中点Q ,故,AP DE BQ EF ⊥⊥,根据面面垂直的性质可得AP ⊥平面DEF ,BQ ⊥平面DEF ,故//AP BQ ,且AP BQ =,故矩形APQB .所以112AB PQ FD ===.根据图形的对称性,易得ABC 为正三角形,取AB 中点G ,因为EA EB =,CA CB =,则CG AB ⊥,EG AB ⊥,则二面角C AB E --为CGE ∠,且GE GO PQ ⊥,易得GO AP ==CGE CGO OGE ∠=∠+∠,OE ===,故()cos cos 90sin CGE OGE OGE ∠=∠+=-∠==角C AB E --的余弦值为(2)设几何体ABC DEF -的外接球球心为O ,设ABC 中心为P ,DEF 中心为Q ,易得,,P O Q 共线,如图,设外接球半径OC OD R ==,根据正三角形中的关系,CP =DQ =.因为OP OQ PQ +==,=2214333R R -=+--2=253R =,故外接球表面积为22043S R ππ==故答案为:203π 3.(2022·山东菏泽·高一期中)在一个正方形1234PP P P 内有一个小正方形ABCD 和四个全等的等边三角形(如图1).将四个等边三角形折起来,使1P 、2P 、3P 、4P 重合于点P ,且折叠后的四棱锥P ABCD -(如图2)的外接球的表面积是64π,则四棱锥P ABCD -的侧棱PA 的长为______;若在四棱锥P ABCD -内放一个正方体,使正方体可以在四棱锥P ABCD -内任意转动,则该正方体棱长的最大值为______.【答案】 4343连接AC ,BD 交于点O ,则易得,APC BPD 是等腰直角三角形,则O 是正四棱锥外接球的球心,正四棱锥的所有棱都相等,设其为x ,则外接球的半径是OA ,所以2464x ππ⎫=⎪⎪⎝⎭,x =PA =因此PO OA ==4x =,故四棱锥P -ABCD 的体积22111284333x PO ⋅=⨯⨯=. 设四棱锥P -ABCD 的内切球半径为R ,四棱锥的表面积:((224432PAB ABCD S S S =+=+=, 所以四棱锥的体积12811()333S ABCD SAB ABCD V S S R SR -==+=, 则R ==, 在四棱锥P -ABCD 内放一个正方体的体对角线不超过内切球直径时,便可以在四棱锥内部任意转动,设放入四棱锥S -ABCD 内部的小正方体棱长为a ,24R ≤==,故4a ≤ 故a 最大为4343,故答案为:4343. 4.(2022·湖北·华中师大一附中高一期中)半正多面体(semiregularsolid )亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.以正方体每条棱的中点为顶点构造一个半正多面体,如图,它由八个正三角形和六个正方形构成,若它的所有棱长都为1,则该半正多面体外接球的表面积为___________;若该半正多面体可以在一个正四面体内任意转动,则该正四面体体积最小值为___________.【答案】 4π所以该半正多面体外接球的半径1R =,故其表面积为4π.若该半正多面体可以在一个正四面体内任意转动,则该半正多面体的外接球是正四面体的内切球时,该正四面体体积最小.此时,设正四面体的棱长为a ,考查轴截面,则有22211⎫⎫-=+⎪⎪⎪⎪⎝⎭⎝⎭,解得a =所以(2min 13V =⋅=⎝故答案为: 4π;。
简单几何体的面积与体积

例2.如图所示,在平行六面体ABCD—A1B1C1D1中,已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=3.(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;(2)求这个平行六面体的体积.题型2:锥体的体积和表面积例3.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60 ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60 ,求四棱锥P-ABCD的体积.例4. 在三棱锥S—ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=55.(1)证明:SC⊥BC;(2)求侧面SBC与底面ABC所成二面角的大小;(3)求三棱锥的体积V S-AB C.例5.ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GB垂直于正方形ABCD所在的平面,且GC=2,求点B到平面EFC的距离?例6.如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有()A .S 1<S 2B .S 1>S 2C .S 1=S 2D .S 1,S 2的大小关系不能确定题型3:棱台的体积、面积及其综合问题例7. 在多面体ABCD —A 1B 1C 1D 1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等, 侧棱延长后相交于E ,F 两点,上、下底面矩形的长、宽分别为c ,d 与a ,b ,且a >c ,b >d ,两底面间的距离为h .(1)求侧面ABB 1A 1与底面ABCD 所成二面角的大小;(2)证明:EF ∥面ABCD ;(3)在估测该多面体的体积时,经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是 V =6h(S 上底面+4S 中截面+S 下底面),试判断V 估与V 的大小关系,并加以证明.题型4:球的体积、表面积例8.已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半,且2AB BC CA ===,求球的表面积.例9. 如图,球面上有四个点P 、A 、B 、C ,如果PA ,PB ,PC 两两互相垂直,且PA=PB=PC=a ,求这个球的表面积.DBAOCEF例10. 如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,P 在球面上,如果 163P ABCD V -=,(1)求球O 的表面积;(2)半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方 体棱长为6,求球的表面积和体积.题型5:球的经纬度、球面距离问题例11. 我国首都靠近北纬40纬线,(1)求北纬40纬线的长度等于多少km ?(地球半径大约为6370km ) (2)在半径为13cm 的球面上有,,A B C 三点,12AB BC AC cm ===,求球心到经过这三点的截面的距离. 随堂练习 (一)选择题1. 如果棱台的两底面积分别是S 、S ′,中截面的面积是S 0,那么( ) A .S S S '+=02B .S S S '=0C .2S 0=S +S ′D .S 02=2S ′S2. 已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为( ) A .323B .283C .243D .2033. 一个长方体共一顶点的三个面的面积分别是6,3,2,这个长方体对角线的长是( ) A .23B .32C .6D .64. 将一个长方体沿从同一个顶点出发的三条棱截去一个棱锥,棱锥的体积与剩下的几何体的体积之比为( ) A .1:2 B .1:3 C .1:4 D .1:55. 如图,在多面体ABCDEF 中,已知四边形ABCD 是边长为1的正方形,且△ADE 、△BCF 均为正三角形,EF ∥AB ,EF=2,则该多面体的体积为( ) A .23B .33 C .43D .326. 已知几何体的三视图如图所示,它的表面积是( )A.42+ B.22+C.32+D.6(二)填空题7. 如图,三棱柱111CBAABC-中,若FE,分别为ACAB,的中点,平面11CEB将三棱柱分成体积为21,VV的两部分,那么21VV:= .8.已知三棱柱111CBAABC-的体积为V,E是棱CC1上一点,三棱锥E—ABC的体积是V1,则三棱锥E—A1B1C1 的体积是________.9. 已知某个几何体的三视图如,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是3cm.(三)解答题10. 如图在ABC∆中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.11.表面积为324π的球,其内接正四棱柱的高是14,(1)求这个正四棱柱的表面积.(2)正四面体ABCD的棱长为a,球O是内切球,球O1是与正四面体的三个面和球O都相切的一个小球,求球O1的体积.12.在北纬45圈上有,A B两点,设该纬度圈上,A B两点的劣弧长为24Rπ,求,A B两点间的球面距离.家庭作业(一)选择题1. 一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是()A.ππ221+B.ππ441+C.ππ21+D.ππ241+2.如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为()A. 1+ba且a+b>h B. 1+ba且a+b<hC. 1+ab且a+b>h D. 1+ab且a+b<h3. 设计一个杯子,其三视图如图所示,现在向杯中匀速注水,杯中水面的高度h随时间t变化的图象是()4. 在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图所示),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是()A.π29B.π27C.π25D.π235. 若一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的全面积是()A.π3 B.π33C.π6 D.π9(二)填空题6. 如图,一个底面半径为R的圆柱形量杯中装有适量的水.若放入一个半径为r的实心铁球,水面高度恰好升高r,则rR= .7.如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.8. 已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V=________. (三)解答题9. 在右图所示的几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=5,若该几何体的侧视图的面积为3.4(1)求证:PA⊥BC;(2)画出该几何体的正视图,并求其面积S;(3)求出多面体A—BMPC的体积V.10. 如图,AA1是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任意一点,A1A=AB=2. (1)求证:BC⊥平面A1AC;(2)求三棱锥A1-ABC的体积的最大值.参考答案 例题讲解例1.解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++24)(420)(2z y x zx yz xy ())2(1由(2)的平方得:x2+y2+z2+2xy+2yz+2xz=36(3) 由(3)-(1)得x2+y2+z2=16,即l2=16,所以l=4(cm).点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察.我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系. 例2.解析:(1)如图,连结A 1O ,则A 1O ⊥底面ABCD ,作OM ⊥AB 交AB 于M , 作ON ⊥AD 交AD 于N ,连结A 1M ,A 1N.由三垂线定得得A 1M ⊥AB ,A 1N ⊥AD.∵∠A 1AM=∠A 1AN ,∴Rt △A 1NA ≌Rt △A 1MA ,∴A 1M=A 1N ,从而OM=ON. ∴点O 在∠BAD 的平分线上. (2)∵AM=AA 1cos3π=3×21=23,∴AO=4cosπAM =223. 又在Rt △AOA 1中,A 1O 2=AA 12 – AO 2=9-29=29, ∴A 1O=223,平行六面体的体积为22345⨯⨯=V 230=. 例3. 解:(1)在四棱锥P-ABCD 中,由PO ⊥ABCD ,得∠PBO 是PB 与平面ABCD 所成的角, ∠PBO=60°.在Rt △AOB 中BO=ABsin30°=1, 由PO ⊥BO ,于是PO=BOtan60°=3,而底面菱形的面积为23. ∴四棱锥P -ABCD 的体积V=31×23×3=2. 点评:本小题重点考查线面垂直、面面垂直、二面角及其平面角、棱锥的体积.在能力方面主要考查空间想象能力. 例4. 解:(1)证明:∵∠SAB =∠SAC =90°,∴SA ⊥AB ,SA ⊥A C.又AB ∩AC =A ,∴SA ⊥平面AB C.由于∠ACB =90°,即BC ⊥AC ,由三垂线定理,得SC ⊥BC .(2)解:∵BC ⊥AC ,SC ⊥BC .∴∠SCA 是侧面SCB 与底面ABC 所成二面角的平面角.在Rt △SCB 中,BC =5,SB =55,得SC =22BC SB -=10.在Rt △SAC 中AC =5,SC =10,cos SCA =21105==SC AC , ∴∠SCA =60°,即侧面SBC 与底面ABC 所成的二面角的大小为60°. (3)解:在Rt △SAC 中,∵SA =755102222=-=-AC SC , S △ABC =21·AC ·BC =21×5×5=225,∴V S -ABC =31·S △ACB ·SA =631257522531=⨯⨯. 点评:本题较全面地考查了空间点、线、面的位置关系.要求对图形必须具备一定的洞察力,并进行一定的逻辑推理. 例5. 解:如图,取EF 的中点O ,连接GB 、GO 、CD 、FB 构造三棱锥B -EFG.设点B 到平面EFG 的距离为h ,BD =42,EF =22, CO =344232×=. G O C O G C =+=+=+=222232218422(). 而GC ⊥平面ABCD ,且GC =2. 由V V B E F G G E F B--=,得16EF GO h ··=13S E F B △·GC点评:该问题主要的求解思路是将点面的距离问题转化为体积问题来求解.构造以点B 为顶点,△EFG 为底面的三棱锥是解此题的关键,利用同一个三棱锥的体积的唯一性列方程是解这类题的方法,从而简化了运算. 例6. 解:连OA 、OB 、OC 、OD ,则V A -BEFD =V O -ABD +V O -ABE +V O -BEFDV A -EFC =V O -ADC +V O -AEC +V O -EFC 又V A -BEFD =V A -EFC , 而每个三棱锥的高都是原四面体的内切球的半径,故S ABD +S ABE +S BEFD =S ADC +S AEC +S EFC 又面AEF 公共,故选C点评:该题通过复合平面图形的分割过程,增加了题目处理的难度,求解棱锥的体积、表面积首先要转化好平面图形与空间几何体之间元素间的对应关系.例7.(1)解:过B 1C 1作底面ABCD 的垂直平面,交底面于PQ ,过B 1作B 1G ⊥PQ ,垂足为G .如图所示:∵平面ABCD ∥平面A 1B 1C 1D 1,∠A 1B 1C 1=90°, ∴AB ⊥PQ ,AB ⊥B 1P .∴∠B 1PG 为所求二面角的平面角.过C 1作C 1H ⊥PQ ,垂足为H .由于相对侧面与底面所成二面角的大小相等,故四边形B 1PQC 1为等腰梯形. ∴PG =21(b -d ),又B 1G =h ,∴tan B 1PG =d b h -2(b >d ),∴∠B 1PG =arctand b h -2,即所求二面角的大小为arctan db h-2. (2)证明:∵AB ,CD 是矩形ABCD 的一组对边,有AB ∥CD ,又CD 是面ABCD 与面CDEF 的交线,∴AB ∥面CDEF . ∵EF 是面ABFE 与面CDEF 的交线,∴AB ∥EF .∵AB 是平面ABCD 内的一条直线,EF 在平面ABCD 外,∴EF ∥面ABC D. (3)证明:∵a >c ,b >d ,∴V -V 估=h d b c a d b c a ab cd h 22)224(6+⋅+-+⋅+⋅++ =12h [2cd +2ab +2(a +c )(b +d )-3(a +c )(b +d )]=12h (a -c )(b -d )>0. ∴V 估<V .点评:该题背景较新颖,把求二面角的大小与证明线、面平行这一常规运算置于非规则几何体(拟柱体)中,能考查考生的应变能力和适应能力,而第三步研究拟柱体的近似计算公式与可精确计算体积的辛普生公式之间计算误差的问题,是极具实际意义的问题.考查了考生继续学习的潜能. 例8. 解:设截面圆心为O ',连结O A ',设球半径为R ,则23232323O A '=⨯⨯=, 在Rt O OA '∆中,222OA O A O O ''=+,∴222231()34R R =+, ∴43R =,∴26449S R ππ==. 点评: 正确应用球的表面积公式,建立平面圆与球的半径之间的关系.例9. 解析:如图,设过A 、B 、C 三点的球的截面圆半径为r ,圆心为O ′,球心到该圆面的距离为d.在三棱锥P —ABC 中,∵PA ,PB ,PC 两两互相垂直,且PA=PB=PC=a , ∴AB=BC=CA=2a ,且P 在△ABC 内的射影即是△ABC 的中心O ′. 由正弦定理,得︒60sin 2a =2r ,∴r=36a .又根据球的截面的性质,有OO ′⊥平面ABC ,而PO ′⊥平面ABC ,∴P 、O 、O ′共线,球的半径R=22d r +.又PO ′=22r PA -=2232a a -=33a , ∴OO ′=R -33a =d=22r R -,(R -33a )2=R 2 – (36a )2,解得R=23a , ∴S 球=4πR 2=3πa 2.点评:本题也可用补形法求解.将P —ABC 补成一个正方体,由对称性可知,正方体内接于球,则球的直径就是正方体的对角线,易得球半径R=23a . 例10. 解:(1)如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,PO ⊥底面ABCD ,PO=R ,22ABCD S R =,163P ABCD V -=, 所以2116233R R ⋅⋅=,R=2, 球O 的表面积是16π.(2)作轴截面如图所示,6CC '=,2623AC =⋅=,设球半径为R ,则222R OC CC '=+22(6)(3)9=+=∴3R =,∴2436S R ππ==球,34363V R ππ==球. 点评:本题重点考查球截面的性质以及球面积公式,解题的关键是将多面体的几何要素转化成球的几何要素. 例11. 解:(1)如图,A 是北纬40上一点,AK 是它的半径,∴OK AK ⊥, 设C 是北纬40的纬线长,∵40AOB OAK ∠=∠=,∴22cos 2cos 40C AK OA OAK OA πππ=⋅=⋅⋅∠=⋅⋅42 3.1463700.7660 3.06610()km ≈⨯⨯⨯≈⨯所以北纬40纬线长约等于43.06610km ⨯.(2)解:设经过,,A B C 三点的截面为⊙O ',设球心为O ,连结OO ',则OO '⊥平面ABC ,∵32124323AO '=⨯⨯=,∴2211OO OA OA ''=-=, 所以,球心到截面距离为11cm .随堂练习(一)选择题1. 解析:设该棱台为正棱台来解即可,答案为A ;2. 解析:正六棱台上下底面面积分别为:S 上=6·43·22=63,S 下=6·43·42=243, V 台=328)(31=+⋅+下下上上S S S S h ,答案B.3. 解析:设长方体共一顶点的三边长分别为a =1,b =2,c =3,则对角线l 的长为l =6222=++c b a ;答案D.4. 解析:设长方体同一顶点引出的三条棱长分别是a ,b ,c ,则棱锥的体积V1=13×12abc=16abc.长方体的体积V=abc ,剩下的几何体的体积为V2=abc-1566abc =abc ,所以V1:V2=1:5,故选D. 5. 解析:将几何体割成一个三棱柱和两个相同的三棱锥.在梯形ABFE 中,易知BN=32, ∴S △BCN=12BC·HN=12×1×22.24=故该几何体体积为24×1+2×1212,3423=⨯⨯选A. 6. 解析:该几何体为直三棱柱,其表面积为2×12×1×1+2×12+2×1=3+2,选C.(二)填空题7. 解:设三棱柱的高为h ,上下底的面积为S ,体积为V ,则V=V 1+V 2=Sh.∵E 、F 分别为AB 、AC 的中点,∴S △AEF =41S , V 1=31h(S+41S+41⋅S )=127Sh ,V 2=Sh-V 1=125Sh , ∴V 1∶V 2=7∶5.点评:解题的关键是棱柱、棱台间的转化关系,建立起求解体积的几何元素之间的对应关系.最后用统一的量建立比值得到结论即可.8. 解析:如图,过E 作AC 、BC 的平行线EF 、EG ,分别与AA1、BB1交于F 、G ,连接FG.∵三棱锥E —ABC 的体积是V1,∴三棱柱EFG —CAB 的体积是3V1,∴三棱柱EFG —C1A1B1的体积是V-3V1,∵VE —A1B1C1=13VEFG —C1A1B1, ∴VE —A1B1C1=13 (V-3V1)=3V -V1, 答案:3V -V1 9.解析:该几何体由半个圆柱和一个正方体构成的组合体.其体积为23+12×π×2=(8+π) cm3,答案:8+π (三)解答题 10. 解:如图所示,所得旋转体是两个底面重合的圆锥,高的和为AB=5.底面半径等于CO=125AC BC AB =,所以所得旋转体的表面积 S=π·OC·(AC+BC)=π·125·(3+4)=845π; 其体积V=13·π·OC2·AO+13·π·OC2·BO=13·π·OC2·AB=485π. 评析:求一些组合体的表面积和体积时,首先要弄清楚它由哪些基本几何体构成,再通过轴截面分析和解决问题.11. 解:(1)设球半径为R ,正四棱柱底面边长为a ,则作轴截面如图,14AA '=,2AC a =, 又∵24324R ππ=,∴9R =,∴2282AC AC CC ''=-=, ∴8a =,∴6423214576S =⨯+⨯=表(2)如图,设球O 半径为R ,球O 1的半径为r ,E 为CD 中点,球O 与平面ACD 、BCD切于点F 、G ,球O 1与平面ACD 切于点H .由题设a GE AE AG 3622=-= ∵ △AOF ∽△AEG∴ a R a a R 233663-=,得a R 126= ∵ △AO 1H ∽△AOF∴ R r R a r R a =---36236,得a r 246= ∴ 3331728624634341a a r V O =⎪⎪⎭⎫ ⎝⎛==ππ球 点评:正四面体的内切球与各面的切点是面的中心,球心到各面的距离相等.12. 解:设北纬45圈的半径为r ,则24r R =,设O '为北纬45圈的圆心,α=∠B AO ', ∴24r R απ=,∴2224R R απ=, ∴2πα=,∴2AB r R ==,∴ABC ∆中,3AOB π∠=,所以,,A B 两点的球面距离等于3R π.点评:要求两点的球面距离,必须先求出两点的直线距离,再求出这两点的球心角,进而求出这两点的球面距离. 家庭作业(一)选择题1. 解析:设圆柱的底面半径为r ,高为h ,则由题设知h =2πr .∴S 全=2πr 2+(2πr )2=2πr 2(1+2π).S 侧=h 2=4π2r 2,∴ππ221+=侧全S S .答案为A. 点评:本题考查圆柱的侧面展开图、侧面积和全面积等知识. 2. 解析:设酒瓶下底面面积为S ,则酒的体积为Sa ,酒瓶的体积为Sa+Sb ,故体积之比为1+,b a 显然有a<a′,又a′+b=h ,故a+b<h.选B.3. 解析:由三视图可知杯子是圆柱形的,由于圆柱形的杯子上下大小相同,所以当向杯中匀速注水时,其高度随时 间的变化是相同的,反映在图象上,选项B 符合题意.故选B.4. 解析:如图所示,该旋转体的体积为圆锥C —ADE 与圆锥B —ADE 体积之差,又∵求得AB =1.∴23133125331πππ=⋅⋅⋅-⋅⋅⋅=-=--ADE B ADE C V V V ,答案D. 5. 解析:∵S =21ab sin θ,∴21a 2sin60°=3,∴a 2=4,a =2,a =2r , ∴r =1,S 全=2πr +πr 2=2π+π=3π,答案A.(二)填空题6. 解析:水面高度升高r ,则圆柱体积增加πR 2·r .恰好是半径为r 的实心铁球的体积,因此有34πr 3=πR 2r . 故 332=r R .答案为332. 点评:本题主要考查旋转体的基础知识以及计算能力和分析、解决问题的能力.7. 解析:由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P —ABCD(如图),其中PD ⊥平面ABCD , 因此该四棱锥的体积V=13×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要216372=个这样 的几何体,才能拼成一个棱长为6的正方体. 答案:3评析:几何体的展开与折叠问题是近几年高考的一个热点内容,通过折叠与展开问题,可以很好地考查学生的空间想象能力以及推理能力.解决折叠与展开问题时,关键是弄清楚折叠与展开前后,位置关系和数量关系变化的情况,画出准确的图形解决问题.8. 解析:该几何体形状如图所示,是一个正方体与正四棱锥的组合体,正方体的体积是1,正四棱锥的体积是2,6故该凸多面体的体积为216+.点评:通过识图、想图、画图的角度考查了空间想象能力.而对空间图形的处理能力是空间想象力深化的标志,是高考从深层上考查空间想象能力的主要方向.(三)解答题9.解:(1)证明:AC=1,BC=2,AB=5,∴AC2+BC2=AB2.∴AC⊥BC.又∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,∴BC⊥平面PAC.又∵PA⊂平面PAC,∴PA⊥BC.(2)设几何体的正视图如图所示:∵PA=PC,取AC的中点D,连接PD,则PD⊥AC.又平面PAC⊥平面ABC,∴PD⊥平面ABC.∴几何体侧视图的面积=12AC·PD=12×1×PD=34.∴PD=32.易知△PAC是边长为1的正三角形.∴正视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积.∴S=12333.224=⨯+(3)取PC的中点N,连接AN,由△PAC是边长为1的正三角形,可知AN⊥PC,由(1)知BC⊥平面PAC,∴AN⊥BC,∴AN⊥平面PCBM.∴AN是四棱锥A—PCBM的高,且AN=3.2由BC⊥平面PAC,可知BC⊥PC.由PM∥BC,可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形.其面积S′=32,∴V=13S′·AN=3.410. 解:(1)证明:∵C是底面圆周上异于A、B的任意一点,且AB是圆柱底面圆的直径,∴BC⊥AC.∵AA 1⊥平面ABC ,BC平面ABC ,∴AA 1⊥BC . ∵AA 1∩AC =A ,AA 1平面AA 1C ,AC 平面AA 1C ,∴BC ⊥平面AA 1C .(2)设AC =x ,在Rt △ABC 中,BC =AB 2-AC 2=4-x 2(0<x <2),故VA 1-ABC =13S △ABC ·AA 1=13·12·AC ·BC ·AA 1=13x 4-x 2(0<x <2), 即VA 1-ABC =13x 4-x 2=13x 2(4-x 2)=13-(x 2-2)2+4. ∵0<x <2,0<x 2<4,∴当x 2=2,即x =2时,三棱锥A 1-ABC 的体积最大,其最大值为23.。
高中数学 第八章 立体几何初步 8.3.1 棱柱、棱锥、棱台的表面积和体积习题(含解析)新人教A版必

8.3简单几何体的表面积与体积8.3.1棱柱、棱锥、棱台的表面积和体积课后篇巩固提升基础达标练1.(多选题)长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,则()A.长方体的表面积为20B.长方体的体积为6C.沿长方体的表面从A到C1的最短距离为3D.沿长方体的表面从A到C1的最短距离为22×(3×2+3×1+2×1)=22,A错误.长方体的体积为3×2×1=6,B正确.如图①所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1.在表面上求最短距离可把几何体展开成平面图形,如图②所示,将侧面ABB1A1和侧面BCC1B1展开,则有AC1=,即当经过侧面ABB1A1和侧面BCC1B1时的最短距离是;如图③所示,将侧面ABB1A1和底面A1B1C1D1展开,则有AC1==3,即当经过侧面ABB1A1和底面A1B1C1D1时的最短距离是3;如图④所示,将侧面ADD1A1和底面A1B1C1D1展开,则有AC1==2,即当经过侧面ADD1A1和底面A1B1C1D1时的最短距离是2.因为3<2,所以沿长方体表面从A到C1的最短距离是3,C正确,D不正确.2.如图所示,正方体ABCD-A1B1C1D1的棱长为1,则三棱锥D-ACD1的体积是()A. B. C. D.1D-ACD1的体积等于三棱锥D1-ACD的体积,三棱锥D1-ACD的底面ACD是直角边长为1的等腰直角三角形,高D1D=1,∴三棱锥D-ACD1的体积为V=×1×1×1=.3.一个正四棱锥的底面边长为2,高为,则该正四棱锥的表面积为()A.8B.12C.16D.20=2,所以该四棱锥的表面积为22+4××2×2=12.4.正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.3πB.C.πD.1,由图可知,该几何体由两个四棱锥构成,并且这两个四棱锥体积相等.四棱锥的底面为正方形,且边长为,故底面积为()2=2;四棱锥的高为1,则四棱锥的体积为×2×1=.故几何体的体积为2×.5.正三棱锥的底面周长为6,侧面都是直角三角形,则此棱锥的体积为()A. B. C. D.,正三棱锥的底面周长为6,所以正三棱锥的底面边长为2,侧面均为直角三角形,可知侧棱长均为,三条侧棱两两垂直,所以此三棱锥的体积为.6.(2020全国高一课时练习)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是.ABCD-A1B1C1D1的体积为120,所以AB·BC·CC1=120,因为E为CC1的中点,所以CE=CC1,由长方体的性质知CC1⊥底面ABCD,所以CE是三棱锥E-BCD的底面BCD上的高,所以三棱锥E-BCD的体积V=AB·BC·CE=AB·BC·CC1=×120=10.7.正四棱柱的一条体对角线长为9,表面积为144,适合这些条件的正四棱柱有个.a,高为h,由题意得这个方程组有两个解,所以适合条件的正四棱柱有2个.8.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是,表面积是.V=4×6×3+×4×3×3=90,表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.9.在正四棱锥S-ABCD中,点O是底面中心,SO=2,侧棱SA=2,则该棱锥的体积为.侧棱SA=2,高SO=2,∴AO==2,因此,底面正方形的边长AB=AO=4,底面积为AB2=16.该棱锥的体积为V=AB2·SO=×16×2=.10.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40 cm,则它的深度为 cm.S',S.由V=(S++S')h,得h==75(cm).能力提升练1.(2020某某某某检测)我国古代名著《X丘建算经》中记载:“今有方锥下广二丈,高三丈,欲斩末为方亭,令上方六尺,问亭方几何?”大致意思为“有一个正四棱锥下底面边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台状方亭,且正四棱台的上底面边长为六尺,问该正四棱台的体积是多少立方尺?”(注:1丈=10尺)()A.1 946立方尺B.3 892立方尺C.7 784立方尺D.11 676立方尺,正四棱锥的高为30,所截得正四棱台的下底面棱长为20,上底面棱长为6, 设棱台的高为OO1=h,由△PA1O1∽△PAO可得,解得h=21,可得正四棱台的体积为×21×(62+202+6×20)=3892(立方尺),故选B.2.(2020某某某某检测)如图所示,在上、下底面对应边的比为1∶2的三棱台中,过上底面的一边A1B1和AC,BC的中点F,E作一个平面A1B1EF,记平面分三棱台两部分的体积为V1(三棱柱A1B1C1-FEC),V2两部分,那么V1∶V2=.h,上底面的面积是S,则下底面的面积是4S,∴V棱台=h(S+4S+2S)=Sh,V1=Sh,∴.∶43.(2020全国高一课时练习)如图,AA1,BB1,CC1相交于点O,形成两个顶点相对、底面水平的三棱锥容器,AO=A1O,BO=B1O,CO=C1O.设三棱锥高均为1,若上面三棱锥中装有高度为0.5的液体,且液体能流入下面的三棱锥,则液体流下去后液面高度为.,流下去后,液体上方空出的三棱锥的体积为三棱锥体积的.设空出的三棱锥的高为x,则,所以x=,所以液面高度为1-.-4.已知一个三棱柱的三视图如图所示,求这个三棱柱的侧面积.,该三棱柱的底面为正三角形,各侧面为矩形,侧棱长为4cm,如图所示.因为正三角形ABC和正三角形A'B'C'的高为2cm,所以正三角形ABC的边长AB==4(cm).故三棱柱的侧面积为S侧=4×4×3=48(cm2).5.一个正三棱锥P-ABC的底面边长为a,高为h.一个正三棱柱A1B1C1-A0B0C0的顶点A1,B1,C1分别在三条棱上,A0,B0,C0分别在底面△ABC上,何时此三棱柱的侧面积取到最大值?O,连接PO,图略,则PO为三棱锥的高,设A1,B1,C1所在的底面与PO交于O1点,则,令A1B1=x,而PO=h,则PO1=x,于是OO1=h-PO1=h-x=h.所以所求三棱柱的侧面积为S=3x·h(a-x)x=.当x=时,S有最大值为ah,此时O1为PO的中点,即A1,B1,C1分别是三条棱的中点.素养培优练在正三棱台ABC-A1B1C1中,已知AB=10,棱台一个侧面梯形的面积为,O1,O分别为上、下底面正三角形的中心,连接A1O1,AO并延长,分别交B1C1,BC于点D1,D,∠D1DA=60°,求上底面的边长.AB=10,∴AD=AB=5,OD=AD=.设上底面的边长为x(x>0),则O1D1=x.如图所示,连接O1O,过D1作D1H⊥AD于点H,则四边形OHD1O1为矩形,且OH=O1D1=x.∴DH=OD-OH=x,在Rt△D1DH中,D1D==2x.∵四边形B1C1CB的面积为(B1C1+BC)·D1D,∴(x+10)×2x,即40=(x+10)(10-x),∴x=2,故上底面的边长为2.。
简单几何体的表面积和体积(含答案)

简单几何体的表面积和体积[基础知识]1.旋转体的侧面积名称 图形侧面积公式 圆柱侧面积:S 侧=______圆锥侧面积:S 侧=______圆台侧面积:S 侧=________ 2.直棱柱、正棱锥、正棱台的侧面积S 直棱柱侧=______(c 为底面周长,h 为高) S 正棱锥侧=______(c 为底面周长,h ′为斜高)S 正棱台侧=12(c +c ′)h ′(c ′,c 分别为上、下底面周长,h ′为斜高)3.体积公式(1)柱体:柱体的底面面积为S ,高为h ,则V =____.(2)锥体:锥体的底面面积为S ,高为h ,则V =_____(3)台体:台体的上、下底面面积分别为S ′、S ,高为h ,则V =13(S ′+S ′S +S)h .[基础练习]1.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )A .8B .8πC .4πD .2π2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比为( )A .1+2π2πB .1+4π4πC .1+2ππD .1+4π2π3.中心角为135°,面积为B 的扇形围成一个圆锥,若圆锥的全面积为A ,则A ∶B 等于( )A .11∶8B .3∶8C .8∶3D .13∶84.已知直角三角形的两直角边长为a 、b ,分别以这两条直角边所在直线为轴,旋转所形成的几何体的体积之比为( )A .a ∶bB .b ∶aC .a 2∶b 2D .b 2∶a 25.有一个几何体的三视图及其尺寸如图(单位:cm ),则该几何体的表面积和体积分别为( )A .24π cm 2,12π cm 3B .15π cm 2,12π cm 3C .24π cm 2,36π cm 3D .以上都不正确 6.三视图如图所示的几何体的全面积是( )A .7+ 2B .112+ 2C .7+ 3D .32[典型例题]例1. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 的中点,沿图中虚线将边长为2的正方形折起来,围成一个三棱锥,求此三棱锥的体积.练1.如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若截面△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.例2.已知五棱台的上、下底面均是正五边形,边长分别是8 cm和18 cm,侧面是全等的等腰梯形,侧棱长是13 cm,求它的侧面积.练2.圆台上底的面积为16π cm2,下底半径为6 cm,母线长为10 cm,那么,圆台的侧面积和体积各是多少?例3.如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米);(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出用于制作灯笼的三视图(作图时,不需考虑骨架等因素).练3.圆柱形容器内盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是______cm.例4.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.练4.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?简单几何体的表面积和体积活页作业一、选择题1.圆柱的侧面展开图是一个边长为6π和4π的矩形,则圆柱的全面积为( )A .6π(4π+3)B .8π(3π+1)C .6π(4π+3)或8π(3π+1)D .6π(4π+1)或8π(3π+2)2.正棱锥的高缩小为原来的12,底面外接圆半径扩大为原来的3倍,则它的体积是原来体积的( )A.32B.92C.34D.943.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.8π3B.82π3 C .82π D.32π34.如图是一个几何体的三视图,根据图中的数据可得该几何体的表面积为( )A .18πB .30πC .33πD .40π 5.(2011·福州质检)某几何体的三视图如图所示,则该几何体的体积等于( )A.283πB.163πC.43π+8 D .12π 6.将边长为a 的正方形ABCD 沿对角线AC 折起,使BD =a ,则三棱锥D -ABC 的体积为( )A.a 36B. a 312C.312a 3D.212a 3 7.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是( )A.233πB .23π C.736πD.733π8.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是323π,那么这个三棱柱的体积是( )A .96 3B .16 3C .24 3D .48 3二、填空题9.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,O 为底面正方形ABCD 的中心, 则三棱锥B 1-BCO 的体积为________.10.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是________.11.已知球O 的表面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC , DA =AB =BC =3,则球O 的体积等于________.12. 如图所示是一个几何体的三视图,根据图中标出的尺寸(单位:cm),可得该几何体的表面积为________cm 2. 三、解答题13.如图所示,以圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,则该圆锥与圆柱等底等高.若圆锥的轴截面是一个正三角形,求圆柱的侧面积与圆锥的侧面积之比.14如图,如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体15.有一个圆锥的侧面展开图是一个半径为5、圆心角为6π5的扇形,在这个圆锥中内接一个高为x 的圆柱.(1)求圆锥的体积.(2)当x 为何值时,圆柱的侧面积最大?16.如图所示,从三棱锥P -ABC 的顶点P 沿着三条侧棱P A 、PB 、PC 剪开成平面图形得到△P 1P 2P 3,且P 2P 1=P 2P 3.(1)在三棱锥P -ABC 中,求证:P A ⊥BC .(2)若P 1P 2=26,P 1P 3=20,求三棱锥P -ABC 的体积.简单几何体的表面积和体积答案[基础知识]1.旋转体的侧面积名称 图形侧面积公式 圆柱侧面积:S 侧=______圆锥侧面积:S 侧=______圆台侧面积:S 侧=________ 2.直棱柱、正棱锥、正棱台的侧面积S 直棱柱侧=______(c 为底面周长,h 为高) S 正棱锥侧=______(c 为底面周长,h ′为斜高)S 正棱台侧=12(c +c ′)h ′(c ′,c 分别为上、下底面周长,h ′为斜高)3.体积公式(1)柱体:柱体的底面面积为S ,高为h ,则V =____.(2)锥体:锥体的底面面积为S ,高为h ,则V =_____(3)台体:台体的上、下底面面积分别为S ′、S ,高为h ,则V =13(S ′+S ′S +S)h .答案:1.名称 图形 侧面积公式圆柱侧面积:S 侧=2πrl圆锥侧面积:S 侧=πrl 圆台侧面积:S 侧=π(r 1+r 2)l 2.ch 12ch ′ 3.(1)Sh (2)13Sh[基础练习]1.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )A .8B .8πC .4πD .2π2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比为( )A .1+2π2πB .1+4π4πC .1+2ππD .1+4π2π3.中心角为135°,面积为B 的扇形围成一个圆锥,若圆锥的全面积为A ,则A ∶B 等于( ) A .11∶8 B .3∶8 C .8∶3 D .13∶84.已知直角三角形的两直角边长为a 、b ,分别以这两条直角边所在直线为轴,旋转所形成的几何体的体积之比为( )A .a ∶bB .b ∶aC .a 2∶b 2D .b 2∶a 25.有一个几何体的三视图及其尺寸如图(单位:cm ),则该几何体的表面积和体积分别为( )A .24π cm 2,12π cm 3B .15π cm 2,12π cm 3C .24π cm 2,36π cm 3D .以上都不正确 6.三视图如图所示的几何体的全面积是( )A .7+ 2B .112+ 2C .7+ 3D .32答案:1.B [易知2πr =4,则2r =4π,所以轴截面面积=4π×2=8π.]2.A [设底面半径为r ,侧面积=4π2r 2,全面积为=2πr 2+4π2r 2,其比为:1+2π2π.] 3.A [设圆锥的底面半径为r ,母线长为l ,则2πr =34πl ,则l =83r ,所以A =83πr 2+πr 2=113πr 2,B =83πr 2,得A ∶B =11∶8.]4.B [以长为a 的直角边所在直线旋转得到圆锥体积V =13πb 2a ,以长为b 的直角边所在直线旋转得到圆锥体积V =13πa 2b .]5.A [该几何体是底面半径为3,母线长为5的圆锥,易得高为4,表面积和体积分别为24π cm 2,12π cm 3.]6.A [图中的几何体可看成是一个底面为直角梯形的直棱柱.直角梯形的上底为1,下底为2,高为1,棱柱的高为1.可求得直角梯形的四条边的长度为1,1,2,2,表面积S 表面=2S 底+S 侧面=12(1+2)×1×2+(1+1+2+2)×1=7+2.][典型例题]例1. 如图,E 、F 分别为正方形ABCD 的边BC 、CD 的中点,沿图中虚线将边长为2的正方形折起来,围成一个三棱锥,求此三棱锥的体积.解析:折叠起来后,B 、D 、C 三点重合为S 点,则围成的三棱锥为S -AEF ,这时SA ⊥SE ,SA ⊥SF ,SE ⊥SF ,且SA =2,SE =SF =1,所以此三棱锥的体积V =13·12·1·1·2=13.练1. (2011·昆山模拟)如图,在正三棱柱ABC -A 1B 1C 1中,D 为棱AA 1的中点,若截面△BC 1D 是面积为6的直角三角形,则此三棱柱的体积为________.解析:由题意,设AB =a ,AA 1=b ,再由12BD ·DC 1=6可得a 2+b 24=12.又由BC 2+CC 21=BC 21, 得a 2+b 2=24, 可得a =22,b =4, ∴V =34×(22)2×4=8 3. 答案:8 3例2. 已知五棱台的上、下底面均是正五边形,边长分别是8 cm 和18 cm ,侧面是全等的等腰梯形,侧棱长是13 cm ,求它的侧面积.解析:如图所示的是五棱台的一个侧面,它是一个上、下底的边长分别为8 cm 和18 cm ,且腰长为13 cm 的等腰梯形,由点A 向BC 作垂线,垂足为点E ;由点D 向BC 作垂线,垂足为点F .∵四边形ABCD 为等腰梯形,∴BE =CF =12(BC -AD )=12(18-8)=5 cm.在Rt △ABE 中,AB =13 cm ,BE =5 cm ,∴AE =12 cm ,∴S 四边形ABCD =12(AD +BC )·AE =12×(8+18)×12=156(cm 2).∴S 五棱台侧=5×156=780(cm 2).即此五棱台的侧面积为780 cm 2.练2. 圆台上底的面积为16π cm 2,下底半径为6 cm ,母线长为10 cm ,那么,圆台的侧面积和体积各是多少?解析:首先,圆台的上底的半径为4 cm ,于是S 圆台侧=π(r +r ′)l =100π(cm 2). 其次,如图,圆台的高h =BC=BD 2-OD -AB 2=102-6-42=46(cm),所以V 圆台=13h (S +SS ′+S ′)=13×46×(16π+16π×36π+36π) =3046π3(cm 3). 例3. 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面). (1)当圆柱底面半径r 取何值时,S 取得最大值?并求出该最大值(结果精确到0.01平方米); (2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出用于制作灯笼的三视图(作图时,不需考虑骨架等因素).解析:由题意可知矩形的高即圆柱的母线长为9.6-8×2r8=1.2-2r ,∴塑料片面积S =πr 2+2πr (1.2-2r ) =πr 2+2.4πr -4πr 2=-3πr 2+2.4πr =-3π(r 2-0.8r )=-3π(r -0.4)2+0.48π.∴当r =0.4时,S 有最大值0.48π,约为1.51平方米.(2)若灯笼底面半径为0.3米,则高为1.2-2×0.3=0.6(米).制作灯笼的三视图如图.练3. 圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是______cm .解析:设球的半径为r cm ,则πr 2×8+43πr 3×3=πr 2×6r .解得r =4 (cm 3).例4.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解析:由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.根据切线性质知,当球在容器内时,水深为3r ,水面的半径为3r ,则容器内水的体积为V =V 圆锥-V球=13π·(3r )2·3r -43πr 3=53πr 3,而将球取出后,设容器内水的深度为h ,则水面圆的半径为33h ,从而容器内水的体积是V ′=13π·(33h )2·h =19πh 3,由V =V ′,得h =315r .即容器中水的深度为315r .练4. 如图所示,一个圆锥形的空杯子上放着一个直径为8 cm 的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?解析: 要使冰淇淋融化后不会溢出杯子,则必须V 圆锥≥V 半球,V 半球=12×43πr 3=12×43π×43,V 圆锥=13Sh =13πr 2h =13π×42×h .依题意:13π×42×h ≥12×43π×43,解得h ≥8.即当圆锥形杯子杯口直径为8 cm ,高大于或等于8 cm 时,冰淇淋融化后不会溢出杯子. 又因为S 圆锥侧=πrl =πrh 2+r 2,当圆锥高取最小值8时,S 圆锥侧最小,所以高为8 cm 时,制造的杯子最省材料.简单几何体的表面积和体积活页作业答案一、选择题1.圆柱的侧面展开图是一个边长为6π和4π的矩形,则圆柱的全面积为( )A .6π(4π+3)B .8π(3π+1)C .6π(4π+3)或8π(3π+1)D .6π(4π+1)或8π(3π+2)解析: 设圆柱的底面半径为r ,母线为l ,则⎩⎪⎨⎪⎧ 2πr =4πl =6π或⎩⎪⎨⎪⎧2πr =6πl =4π, ∴⎩⎪⎨⎪⎧ r =2l =6π或⎩⎪⎨⎪⎧r =3l =4π, ∴圆柱的全面积为24π2+8π或24π2+18π,即8π(3π+1)或6π(4π+3).答案: C2.正棱锥的高缩小为原来的12,底面外接圆半径扩大为原来的3倍,则它的体积是原来体积的( )A.32B.92C.34D.94解析: 设原棱锥高为h ,底面面积为S ,则V =13Sh ,新棱锥的高为h2,底面面积为9S ,∴V ′=13·9S ·h2,∴V ′V =92.答案: B3.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.8π3B.82π3 C .82π D.32π3 答案: B解析: S 圆=πr 2=1⇒r =1,而截面圆圆心与球心的距离d =1,∴球的半径为R =r 2+d 2=2,∴V=43πR 3=82π3,故选B.4.如图是一个几何体的三视图,根据图中的数据可得该几何体的表面积为( )A .18πB .30πC .33πD .40π解析: 由三视图知该几何体由圆锥和半球组成.球半径和圆锥底面半径都等于3,圆锥的母线长等于5,所以该几何体的表面积S =2π×32+π×3×5=33π.答案: C 5.(2011·福州质检)某几何体的三视图如图所示,则该几何体的体积等于( )A.283πB.163πC.43π+8 D .12π解析: 由三视图可知,该几何体为底面半径是2,高为2的圆柱体和半径为1的球体的组合体,则该几何体的体积为π×22×2+43π=283π.答案: A6.将边长为a 的正方形ABCD 沿对角线AC 折起,使BD =a ,则三棱锥D -ABC 的体积为( )A.a 36B. a 312C.312a 3D.212a 3 解析: 设正方形ABCD 的对角线AC 、BD 相交于点E ,沿AC 折起后,依题意得:当BD =a 时,BE ⊥DE ,∴DE ⊥面ABC ,∴三棱锥D -ABC 的高为DE =22a , ∴V D -ABC =13·12a 2·22a =212a 3.答案: D7.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是( )A.233πB .23πC.736πD.733π解析:上底半径r =1,下底半径R =2.∵S 侧=6π,设母线长为l ,则π(1+2)·l =6π,∴l =2,∴高h =l 2-(R -r )2=3,∴V =13π·3(1+1×2+2×2)=733π.答案:D8.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是323π,那么这个三棱柱的体积是( )A .96 3B .16 3C .24 3D .48 3解析:由43πR 3=323π,∴R =2,∴正三棱柱的高h =4,设其底面边长为a ,则13·32a =2,∴a =43,∴V =34(43)2·4=48 3. 答案:D二、填空题9.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,O 为底面正方形ABCD 的中心,则三棱锥B 1-BCO 的体积为________.解析: V =13S △BOC ·B 1B =13×12BO ·BC ·sin 45°·B 1B =16×2×2×22×2=23.答案: 2310.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是________.解析: 由三视图可知,该几何体为底面半径为1,母线长为2的圆锥的一半,所以圆锥的高为3,因此所求体积V =12×13×π×12×3=36π.答案: 36π11.已知球O 的表面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA =AB =BC =3,则球O 的体积等于________. 解析: 如图, 易知球心O 为DC 中点,由题意可求出CD =3,所以球O 的半径为32,故球O 的体积为43π×⎝⎛⎭⎫323=9π2. 答案: 9π212.如图所示是一个几何体的三视图,根据图中标出的尺寸(单位:cm),可得该几何体的表面积为________cm 2.答案 36解析 由三视图可知,此几何体是一个以AA ′=2,AD =4,AB =2为棱的长方体被平面A ′C ′B 截去一个角后得到的,在△A ′C ′B 中,因为A ′C ′=BC ′=25,BA ′=22,所以S △A ′C ′B =12×22×(25)2-(2)2=6,故几何体表面积为2×4×2+2×2+12×4×2×2+12×2×2+6=36.三、解答题13.如图所示,以圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,则该圆锥与圆柱等底等高.若圆锥的轴截面是一个正三角形,求圆柱的侧面积与圆锥的侧面积之比.解析: 设圆锥底面半径为r ,则母线为2r ,高为3r ,∴圆柱的底面半径为r ,高为3r ,∴S 圆柱侧S 圆锥侧=2πr ·3r πr ·2r = 3. 14如图,如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体解析:(1)如图所示.(2)所求多面体体积V =V 长方体-V 正三棱锥=446-131222⎛⎫⨯⨯ ⎪⎝⎭2=2843(cm 3).15.有一个圆锥的侧面展开图是一个半径为5、圆心角为6π5的扇形,在这个圆锥中内接一个高为x 的圆柱. (1)求圆锥的体积.(2)当x 为何值时,圆柱的侧面积最大?解析: (1)因为圆锥侧面展开图的半径为5,所以圆锥的母线长为5.设圆锥的底面半径为r ,则2πr =5×6π5,解得r =3. 所以圆锥的高为4.从而圆锥的体积V =13πr 2×4=12π.(2)右图为轴截面图,这个图为等腰三角形中内接一个矩形.设圆柱的底面半径为a ,则3-a 3=x 4,从而a =3-34x . 圆柱的侧面积S (x )=2π(3-34x )x =32π(4x -x 2) =32π[4-(x -2)2](0<x <4). 当x =2时,S (x )有最大值6π.所以当圆柱的高为2时,圆柱有最大侧面积为6π.16.如图所示,从三棱锥P -ABC 的顶点P 沿着三条侧棱P A 、PB 、PC 剪开成平面图形得到△P 1P 2P 3,且P 2P 1=P 2P 3. (1)在三棱锥P -ABC 中,求证:P A ⊥BC .(2)若P 1P 2=26,P 1P 3=20,求三棱锥P -ABC 的体积.解析: (1)证明:由题设知A 、B 、C 分别是P 1P 3,P 1P 2,P 2P 3的中点,且P 2P 1=P 2P 3,从而PB =PC ,AB =AC ,取BC 的中点D ,连AD 、PD ,则AD ⊥BC ,PD ⊥BC ,∴BC ⊥面P AD .故P A ⊥BC .(2)由题设有AB =AC =12P 1P 2=13,P A =P 1A =BC =10, PB =PC =P 1B =13,∴AD =PD =AB 2-BD 2=12,在等腰三角形DP A 中, 底边P A 上的高h =AD 2-⎝⎛⎭⎫12P A 2=119, ∴S △DP A =12P A ·h =5119,又BC ⊥面P AD , ∴V P -ABC =V B -PDA +V C -PDA=13BD ·S △DP A +13DC ·S △PDA =13BC ·S △PDA =13×10×5119 =503119.。
简单几何体的表面积与体积 测试题

简单几何体的表面积与体积测试题
1、有一个长方体,长为10cm,宽为6cm,高为15cm,求它的表面积和体积?
表面积=2×(10×6+10×15+6×15)=660平方厘米
体积=10×6×15=900立方厘米
2、有一个圆柱体,底面半径为5cm,高为10cm,求它的表面积和体积?
表面积=2×3.14×5×10+2×3.14×52=942.0平方厘米
体积=3.14×52×10=7850.0立方厘米
3、有一个圆锥体,底面半径为3cm,高为8cm,求它的表面积和体积?
表面积=2×3.14×3×8+2×3.14×32=150.72平方厘米
体积=3.14×32×8/3=75.36立方厘米
4、有一个长方体,长为12cm,宽为9cm,高为6cm,求它的表面积和体积?
表面积=2×(12×9+12×6+9×6)=432平方厘米
体积=12×9×6=648立方厘米
5、有一个正方体,边长为10cm,求它的表面积和体积?
表面积=6×102=600平方厘米
体积=103=1000立方厘米。
高中数学新教材必修第二册第八章 立体几何初步 8.3 简单几何体的表面积与体积(南开题库含详解)

第八章 立体几何初步 8.3 简单几何体的表面积与体积一、选择题(共40小题;共200分)1. 一个四面体的所有棱长都为 √2 ,四个顶点在同一球面上,则此球的表面积为 ( ) A. 3πB. 4πC. 3√3πD. 6π2. 有一个几何体的三视图及其尺寸如图(单位:cm ),该几何体的表面积和体积为 ( )A. 24π,12πB. 15π,12πC. 24π,36πD. 以上都不正确3. 已知下列三个命题:①若一个球的半径缩小到原来的 12,则其体积缩小到原来的 18; ②若两组数据的平均数相等,则它们的标准差也相等; ③直线 x +y +1=0 与圆 x 2+y 2=12 相切.其中真命题的序号是 ( ) A. ①②③B. ①②C. ①③D. ②③4. 如图,是一个几何体的三视图,其主视图、左视图是直角边长为 2 的等腰直角三角形,俯视图为边长为 2 的正方形,则此几何体的表面积为 ( )A. 8+4√2B. 8+4√3C. 6+6√2D. 8+2√2+2√35. 一个四棱锥的三视图如图所示,其侧视图是等边三角形.则该四棱锥的体积等于 ( )A. 8√3B. 16√3C. 24√3D. 48√36. 如图,在长方体ABCD−A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC,A1D1的两个平行截面将长方体分成三部分,其体积分别记为V1=V AEA1−DFD1,V2=V EBE1A1−FCF1D1,V3=V B1E1B−C1F1C.若V1:V2:V3=1:4:1,则截面A1EFD1的面积为( )A. 4√10B. 8√3C. 4√13D. 167. 一个几何体的三视图如图所示,则该几何体的体积(单位:cm3)为( )A. π+√33B. 2π+√33C. 2π+√3D. π+√38. 一个几何体的三视图如图所示,则该几何体的体积是( )A. 64B. 72C. 80D. 1129. 在△ABC中,AB=2,BC=1.5,∠ABC=120∘,若使该三角形绕直线BC旋转一周,则所形成的几何体的体积是( )A. 32π B. 52π C. 72π D. 92π10. 某空间几何体的三视图如图所示,则该几何体的表面积为( )A. 180B. 240C. 276D. 30011. 已知某四棱锥的三视图,如图所示.则此四棱锥的体积为( )A. 6B. 5C. 4D. 312. 正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是( )A. π3a B. π2a C. 2πa D. 3πa13. 一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )A. √3+√6B. √3+√5C. √2+√6D. √2+√514. 某几何体的三视图如图所示,则该几何体的体积为( )A. 8−2πB. 8−πC. 8−π2D. 8−π415. 直三棱柱ABC−A1B1C1的直观图及三视图如下图所示,D为AC的中点,则下列命题是假命题的是( )A. AB1∥平面BDC1B. A1C⊥平面BDC1C. 直三棱柱的体积V=4D. 直三棱柱的外接球的表面积为4π16. 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A. 9πB. 10πC. 11πD. 12π17. 一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )A. 1+2π2πB. 1+4π4πC. 1+2ππD. 1+4π2π18. 一个几何体的三视图如图所示,则该几何体的体积是( )A. 23π+4 B. 2π+4 C. π+4 D. π+219. 在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A. 2π3B. 4π3C. 5π3D. 2π20. 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )A. √23B. √33C. 43D. 3221. 小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )A. 16+8πB. 64+8πC. 64+8π3D. 16+8π322. 正三棱锥的底面边长为a,高为√66a,则此棱锥的侧面积为( )A. 34a2 B. 32a2 C. 3√34a2 D. 3√32a223. 已知正方形ABCD的边长为6,空间有一点M(不在平面ABCD内)满足∣MA∣+∣MB∣=10,则三棱锥A−BCM的体积的最大值是( )A. 48B. 36C. 30D. 2424. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A. 18B. 17C. 16D. 1525. 棱长为a的正方体中,连接相邻面的中心,以这些线段为棱的八面体的体积为( )A. a33B. a34C. a36D. a31226. 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A. 2√23π B. 4√2π3C. 2√2πD. 4√2π27. 已知A,B是球O的球面上两点,∠AOB=90∘,C为该球面上的动点,若三棱锥O−ABC体积的最大值为36,则球O的表面积为( )A. 36πB. 64πC. 144πD. 256π28. 某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )A. 2B. 92C. 32D. 329. 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A. 500π3cm3 B. 866π3cm3 C. 1372π3cm3 D. 2048π3cm330. 一个棱锥三个侧面两两互相垂直,它们的面积分别为12cm2,8cm2,6cm2,那么这个三棱锥的体积为( )A. 8√2πB. 8√23C. 24√2D. 8√231. E,F分别是边长为1的正方形ABCD边BC,CD的中点,沿线AF,AE,EF折起来,则所围成的三棱锥的体积为( )A. 13B. 16C. 112D. 12432. 如图,三棱柱ABC−A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )A. 2:3B. 1:1C. 3:2D. 3:433. 正方体的全面积为a2,它的顶点都在同一个球面上,这个球的半径是( )A. √36a B. √24a C. √22a D. √32a34. 如图,△ABC为正三角形,AA1∥BB1∥CC1,CC1⊥底面△ABC,若BB1=2AA1=2,AB=CC1=3AA1,则多面体ABC−A1B1C1在平面A1ABB1上的投影的面积为( )A. 274B. 92C. 9D. 27235. 如图,已知直三棱柱ABC−A1B1C1,点P,Q分别在侧棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )A. 2:1B. 3:1C. 3:2D. 4:336. 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )A. 1B. 2C. 4D. 837. 如图所示,正方体ABCD−AʹBʹCʹDʹ的棱长为1,E,F分别是棱AAʹ,CCʹ的中点,过直线E F的平面分别与棱BBʹ,DDʹ交于M,N,设BM=x,x∈[0,1],给出以下四个命题:①平面MENF⊥平面BDDʹBʹ;②当且仅当x=12时,四边形MENF的面积最小;③四边形MENF周长L=f(x),x∈[0,1]是单调函数;④四棱锥Cʹ−MENF的体积V=ℎ(x)为常函数.以上命题中假命题的序号为( )A. ①④B. ②C. ③D. ③④38. 如图,正方体ABCD−A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=√33.给出下列四个结论:①CE⊥BD;②三棱锥E−BCF的体积为定值;③△BEF在底面ABCD内的正投影是面积为定值的三角形;④在平面ABCD内存在无数条与平面DEA1平行的直线.其中,正确结论的个数是( )A. 1B. 2C. 3D. 439. 已知正方体ABCD−A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P−ABC的体积为( )A. 124B. 118C. 19D. 11240. 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )A. √5+3√3π2+3π2+1 B. 2√5+3√3π+3π2+1C. √5+3√3π2+3π2D. √5+3√3π2+π2+1二、填空题(共40小题;共200分)41. 已知某球体的体积与其表面积的数值相等,则此球体的半径为.42. 若一个球的体积为4√3π,则它的表面积为.43. 一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为.44. 一个正方体的各顶点均在同一球的球面上,若该球的体积为4√3π,则该正方体的表面积为.45. 某几何体的三视图如图所示,则该几何体的体积是.46. 已知某几何体的三视图如图所示,则该几何体的体积为.47. 一个几何体的三视图如图所示,则该几何体的体积为.48. 已知一个正方体的所有顶点在一个球面上,若球的体积为9π,则正方体的棱长为.249. 如图是一个几何体的三视图.若它的体积是3√3,则a=.50. 某空间几何体的三视图如图所示,则该几何体的体积为.51. 用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积是.52. 用一张长为12米,宽为8米的矩形铁皮围成圆柱的侧面,则这个圆柱的体积为.53. 有一个几何体的三视图及其尺寸(单位cm)如下图所示,则该几何体的表面积为:.54. 一个几何体的三视图如图所示(单位:m),则这个几何体的体积为m3.55. 底面是正方形,容积为256的无盖水箱,它的高为时最省材料.56. 某几何体的三视图如图所示,则该几何体的体积为.57. 一个几何体的三视图如图所示(单位:cm),则该几何体的体积为cm3.58. 已知一个四棱锥的三视图如图所示,则此四棱锥的体积为.59. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.60. 某几何体的三视图如图所示,则该几何体的体积为.61. 一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.62. 几何体的三视图如图所示,其侧视图是一个等边三角形,则这个几何体的体积是.63. 一空间几何体的三视图如图所示,则该几何体的体积为.64. 用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积为.65. 已知一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.66. 如图是一个几何体的三视图,则这个几何体的体积为.,则正视图与侧视图中x的值67. 一空间几何体的三视图如右图所示,该几何体的体积为12π+8√53为.68. 如图是—个几何体的三视图,则该几何体的表面积为.69. 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为.70. 如图所示,一款冰淇淋甜筒的三视图中俯视图是以3为半径的圆,则该甜筒的表面积为.71. ―个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.72. 正方体ABCD−A1B1C1D1的棱长为2√3,则四面体A−B1CD1的外接球的体积为.73. 已知正方体ABCD−A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M−EFGH的体积为.74. 如图,已知正方体ABCD−A1B1C1D1的棱长为1,则四棱锥A1−BB1D1D的体积为.75. 已知某三棱锥的三视图如图所示,则它的外接球体积为.76. 如图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:cm)可知该几何体的表面积为.77. 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,该几何体的外接球表面积为cm278. 一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.79. 一个圆锥体被过其顶点的平面截去一部分,余下的几何体的三视图如图所示(单位:cm),则余下的几何体的体积为cm3.80. 棱长为1的正四面体内有一点P,由点P向各面引垂线,垂线段长度分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为.三、解答题(共20小题;共260分)81. 如图,长方体ABCD−A1B1C1D1中AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由);(2)求平面α把该长方体分成的两部分体积的比值.82. 三棱锥S−ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,求四棱锥S−BCED的体积.83. 在单位正方体AC1中,点E,F分别是棱BC,CD的中点.(1)求证:D1E⊥平面AB1F;(2)求三棱锥E−AB1F的体积;(3)设直线B1E,B1D1与平面AB1F所成的角分别为α,β,求cos(α+β)的值.84. 如图,三棱锥S−ABC内接于一个圆锥(有公共顶点和底面,侧棱与圆锥母线重合).已知AB=5cm,BC=3cm,AC=4cm,SA=SB=SC=10cm,(1)求圆锥的侧面积及侧面展开图的中心角;(2)求A经过圆锥的侧面到B点的最短距离.85. 如图,四棱锥P−ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且AMMD =PNNC=4.(1)求证:MN∥平面PAB;(2)求三棱锥P−AMN的体积.86. 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45∘,AB=2AD=2,∠BAD=60∘.(1)求证:BD⊥平面ADG;(2)求此多面体的全面积.87. 养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12(m),高4(m),养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4(m)(高不变);二是高度增加4(m)(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?88. 如图,ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,Eʹ和Fʹ是平面ABCD内的两点,EʹE和FʹF都与平面ABCD垂直.(1)证明:直线EʹFʹ垂直且平分线段AD.(2)若∠EAD=∠EAB=60∘,EF=2,求多面体ABCDEF的体积.89. 如图,三棱锥A−BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A−MBC的体积.90. 如图,四棱锥 P −ABCD 中,底面是以 O 为中心的菱形,PO ⊥ 底面 ABCD ,AB =2,∠BAD =π3,M 为 BC 上一点,且 BM =12.(1)证明:BC ⊥ 平面 POM ; (2)若 MP ⊥AP ,求四棱锥 P −ABMO 的体积.91. 如图,平行四边形 ABCD 中,∠DAB =60∘,AB =2,AD =4,将 △CBD 沿 BD 折起到 △EBD的位置,使平面 EBD ⊥ 平面 ABD .(1)求证:AB ⊥DE ; (2)求三棱锥 E −ABD 的侧面积.92. 养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为 12 m ,高 4 m .养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大 4 m (高不变);二是高度增加 4 m (底面直径不变). (1)分别计算按这两种方案所建的仓库的体积; (2)分别计算按这两种方案所建的仓库的侧面积; (3)哪个方案更经济些?93. 如图所示,三棱柱 ABC −A 1B 1C 1 中,AA 1⊥平面ABC ,D ,E 分别为 A 1B 1,AA 1 的中点,点 F在棱 AB 上,且 AF =14AB .(1)求证:EF ∥平面BC 1D ;(2)在棱 AC 上是否存在一个点 G ,使得平面 EFG 将三棱柱分割成的两部分体积之比为 1:15,若存在,指出点 G 的位置;若不存在,请说明理由.94. 如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求四面体N−BCM的体积.95. 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;,求该三棱锥的侧面积.(2)若∠ABC=120∘,AE⊥EC,三棱锥E−ACD的体积为√6396. 如图,在斜三棱柱ABC−A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120∘,E、F分别是棱B1C1、A1A的中点.(1)求A1A与底面ABC所成的角;(2)证明A1E∥平面B1FC;(3)求经过A1、A、B、C四点的球的体积.97. 如图1,∠ACB=45∘,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90∘(如图2所示).(1)当BD的长为多少时,三棱锥A−BCD的体积最大;(2)当三棱锥A−BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小.98. 如图,四棱锥P−ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D−AE−C为60∘,AP=1,AD=√3,求三棱锥E−ACD的体积.99. 如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.(1)证明:BD⊥PC;(2)若AD=4,BC=2,直线PD与平面PAC所成的角为30∘,求四棱锥P−ABCD的体积.100. 如图,已知正方体ABCD−A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上的点,且AM= AN=1.(1)证明:M,N,C,D1四点共面;(2)平面MNCD1将此正方体分为两部分,求这两部分的体积之比.答案第一部分1. A2. A3. C4. A 【解析】由三视图知,该几何体是底面为正方形的四棱锥,其直观图如下图.所以其表面积为2×2+2×(12×2×2)+2×(12×2×2√2)=8+4√2.5. A【解析】由三视图可以看出,该几何体为四棱锥,所以V=13×12(2+4)×4×2√3=8√3.6. C7. A8. C 【解析】该几何体是由一个正方体和一个四棱锥组合而成,V=4×4×4+13×4×4×3=80.9. A 【解析】如图:△ABC中,绕直线BC旋转一周,则所形成的几何体是以ACD为轴截面的圆锥中挖去了一个以ABD为轴截面的小圆锥后剩余的部分.因为AB=2,BC=1.5,∠ABC=120∘,所以AE=ABsin60∘=√3,BE=ABcos60∘=1,设V1是以ACD为轴截面的圆锥的体积,V2是以ABD为轴截面的圆锥的体积.V1=13π⋅AE2⋅CE=52π,V2=13π⋅AE2⋅BE=π,所以V=V1−V2=32π.10. B【解析】由三视图可知,该几何体是由一个四棱锥和一个正方体组成,所以表面积=4×12×6×5+ 5×62=240.11. C 【解析】V=13×12×(2+4)×2×2=412. B 【解析】设球的半径为R,则正方体的对角线长为2R,依题意知43R2=16a,即R2=18a,所以S球=4πR2=4π⋅18a=π2a.13. C 【解析】由三视图可得:该几何体是四棱锥(如图所示),所以BA=BC=√2,BP=1,PA=PC=√3,PD=√5,可得PA⊥AD;S△PBC=S△PBA=1 2×√2×1=√22,S△PDC=S△PDA=12×√2×√3=√62,所以该几何体的侧面积S=2S△PBC+2S△PDC=√2+√6.14. B 【解析】该几何体为一个棱长为2的正方体在两端各削去一个14圆柱,V=2×2×2−2×14×(π×12×2)=8−π.15. D16. D17. A18. C19. C 【解析】提示:分析知,围成的几何体为如图所示一个圆柱挖去一个圆锥.20. A【解析】提示:如图,作AM⊥EF于点M,BN⊥EF于点N,则可将原多面体分成一个直三棱柱和两个三棱锥,然后去求其体积.21. C 【解析】由三视图可知,该建筑物由一个圆锥、一个圆柱以及一个正方体拼接而成,故所求几何体的体积V=13×π×12×2+π×12×2+4×4×4=64+8π3.22. A 【解析】利用高、底面正三角形的边心距和斜高组成的直角三角形可得斜高为√(√66a)2+(13×√32a)2=12a,于是侧面积S=3×12×a×12a=34a2.23. D24. D25. C【解析】提示:算出一个正四棱锥的体积再乘2即可.26. B27. C 【解析】在三棱锥O−ABC中,底面OAB的面积确定,所以要使O−ABC的体积最大,则C到平面OAB的距离最大,即为球的半径.设球半径为R,则三棱锥O−ABC的体积V max=13×12×R2×R=36,解得R=6,此时球的表面积S=4πR2=144π.28. D29. A30. D31. D 【解析】设AF,AE,EF折起交于点P,因为AP⊥PF,AP⊥PE,所以AP⊥面PEF,所以V P−AEF=V A−PEF=13×1×12×12×12=124.32. B【解析】不妨设此三棱柱为正三棱柱,AB=1,AA1=2,则正三棱柱的体积V=√34×2=√32,V下面部分=13×√32×32=√34,所以V上面部分=√34,所以上下两部分的体积的比为1:133. B 【解析】由正方体外接球的直径2R等于正方体的体对角线的长,得2R=√3⋅√a26,所以R=√24a.34. A35. A【解析】设B到AC的距离为m,AC=x,棱柱的高为ℎ,可得V四棱锥B−ACQP =16xℎm,V三棱柱ABC−A1B1C1=12xℎm,V四棱锥B−ACQPV三棱柱ABC−A1B1C1=13,所以平面BPQ把三棱柱分成两部分的体积比为1:2.36. B 【解析】提示:此组合体是过圆柱对称轴的平面截圆柱所得的半个圆柱和一个半球组成的组合体.37. C 【解析】因为EF⊥BD,EF⊥面BDDʹBʹ,EF⊂面EMFN,所以平面MENF⊥平面BDDʹBʹ成立;又因为四边形EMFN为菱形,∣MN∣2=(1−2x)2+2,所以S MENF=12∣EF∣×∣MN∣=1 2×√2×√4x2−4x+3,当x=12时,面积最小,所以②成立;四边形MENF的周长L=f(x)=4√4x 2−4x +3,在 (0,12) 上是单调递减函数,在 (12,1) 上是单调递增函数,所以命题③不正确;V Cʹ−MENF =2V Cʹ−MNF =2V M−CʹNF =16,所以 V =ℎ(x ) 为常函数.38. D 【解析】因为在正方体 ABCD −A 1B 1C 1D 1 中,BD ⊥平面AA 1CC 1,CE ⊂平面AA 1CC 1,所以 BD ⊥CE ,①正确;EF =√33,而 C 到 EF 的距离即为 C 到 AC 1 的距离,所以 △EFC 面积为定值,又 B点到 平面EFC 的距离为定值,所以三棱锥 E −BCF 的体积为定值,②正确;因为 EF 为定值,且在体对角线 AC 1 上,所以 EF 在底面上的投影为定值,而点 B 到 AC 的距离为定值,所以 △BEF 在底面 ABCD 内的正投影是面积为定值的三角形,③正确;因为平面 ABCD 与平面 DEA 1 不重合,显然在平面 ABCD 内存在无数条与平面 DEA 1 平行的直线,④正确.39. B 【解析】设 AP =CP =a ,在 △PAC 中,利用余弦定理有 cos∠APC =a 2+a 2−22a 2=1−1a 2,又因为当 AP ⊥BD 1 时,AP 最小,当 P 与点 D 1 重合时最大,所以 a ∈[√63,√2],所以当 AP ⊥BD 1 时,∠APC 最大,在 △BDD 1 中,BP =√33,则 P 到面 ABC 的距离为 √33√3=13.所以 V P−ABC =12×1×1×13×13=118.40. A【解析】圆锥母线为 l =√(√5)2+1=√6,高为 ℎ=√(√5)2−1=2,圆锥底面半径为 r =√l 2−ℎ2=√2,截去的底面弧的圆心角为直角,截去的弧长是底面圆周的 14,圆锥侧面剩余 34,即为 S 1=34⋅π⋅rl =34π⋅√2×√6=3√32π,截面三角形的面积为 S 2=12×2×√5=√5,底面剩余部分为S 3=34πr 2+12×√2×√2=1+3π2,所以被截后该几何体的表面积为 S =3π2+3√3π2+√5+1.第二部分 41. 3 42. 12π【解析】提示:球的半径为 √3. 43. 14π 44. 24【解析】球的半径为 √3 ,则正方体的体对角线长为 2√3 ,从而正方体的棱长为 2 ,表面积为 6×22=24 . 45. 16π−16 46. 12π【解析】提示:由三视图可知,该几何体是由左右两个相同的圆柱(底面圆半径为2,高为1)与中间一个圆柱(底面圆半径为1,高为4)组合而成.47. 12+π【解析】该几何体是一个长方体和一个圆柱的组合体.由三视图可知长方体的长、宽、高分别为4、3、1,圆柱的底面半径为1,高为1,故该组合体的体积为V=4×3×1+π×1×1=12+π.48. √349. √3【解析】三视图对应的空间几何体是以2为底、高为a的三角形作为底面,以3为高的卧放的一个三棱柱.50. 2π+2√3351. 9√3π52. 288πcm3或192πcm3.53. 24πcm2【解析】由三视图可知:该几何体是一个圆锥,其母线长是5cm,底面直径是6cm.所以该三棱锥的表面积S=π×32+12×6π×5=24πcm2.54. 6+π【解析】如图:该几何体为一个棱柱与一个圆锥的组合体.所以V=3×2×1+13π×12×3=6+π.55. 456. 108+3π【解析】由三视图可知,该几何体由两个长方体和一个圆柱组成.所以V=2×6×6×32+π×12×3=108+3π.57. 48【解析】由三视图可知,该几何体为四棱锥,所以V=13×62×4=48.58. 5359. 9π260. 13【解析】由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A−BCDE的高为1,四边形BCDE是边长为1的正方形,则V=13×1×1×1=13.61. 20π3【解析】三视图可得该几何体是组合体,上面是底面圆的半径为2m、高为2m的圆锥,下面是底面圆的半径为1m、高为4m的圆柱,所以该几何体的体积是13×4π×2+4π=20π3(m3).62. 8√3+4√3π3【解析】由三视图可知,该几何体是由半个圆锥和一个四棱锥组成,所以体积为12×13×π×22×2√3+13×3×4×2√3=8√3+4√33π.63. 16+8π【解析】由三视图可知,该几何体是由一个长方体和半个圆柱形成,所以体积为V=2×2×4+ 12π×22×4=16+8π.64. 9√3π【解析】如下图所示:PO=√62−32=3√3,所以体积为13⋅3√3⋅π⋅32=9√3π.65. 20π3【解析】该几何体的体积为π⋅4+13π⋅22⋅2=20π3m3.66. 3【解析】由三视图可知,该几何体为上面一个三棱柱,下方一个四棱柱.故V上=12×1×1×2=1,V下=2×1×1=2,所以V=1+2=3.67. 3【解析】由三视图可以看出,该几何体是由一个四棱锥和一个圆柱组成.体积为13×(2√2)2×√5+π×22x=12π+8√53,所以x=3.68. 9π【解析】由三视图可知,该几何体的侧面积为2π×1×3=6π,下底面面积为π×12=π,顶部为半个球的表面积12×4π×12=2π,所以该几何体的表面积为9π.69. 7π【解析】由三视图可知该几何体是由一个圆柱和半个球组成,所以表面积为π×12+2π×1×2+12×4π×12=7π.70. 33π【解析】上半部分为半个球,表面积为12×4πr2=18π.下半部分为圆锥,侧面积为12×2πr×母线=15π.所以表面积为33π.71. 18+9π【解析】由三视图可知,该几何体为两个相切的球上方加了一个长方体组成的组合体,所以其体积为V=3×6×1+2×43π×(32)3=18+9π(m3).72. 36π.73. 11274. 1375. 43π【解析】由俯视图可知,直角三角形的斜边中线等于斜边的一半,根据射影定理,球心为斜边中点,半径为1,所以球的体积为43πr3=43π.76. (18+2√3)cm2.77. 77π【解析】提示:依题意得20=13×12×5×6×ℎ,解出ℎ=4.可算出外接球半径为√772,所以外接球表面积为77π.78. 83π【解析】由三视图知该几何体由两个相同的圆锥和一个圆柱组成.其中,圆锥的底面半径和圆柱的底面半径均为1m,圆锥的高均为1m,圆柱的高为2m.因此该几何体的体积为V=2×13π×12×1+π×12×2=83πm3.79. 16π9+2√33【解析】由三视图可知,该几何体由23个圆锥和一个三棱锥组成,所以体积为23×13π×22×2+13×12×2√3×1×2=16π9+2√33.80. √63【解析】提示:设这个棱长为1的正四面体的四个顶点分别为A、B、C、D,可求得其高为ℎ=√63,设每个面面积为S,则V A−BCD =V P−ABC +V P−ACD +V P−ABD +V P−BCD ,所以13ℎS =13d 1S +13d 2S +13d 3S +13d 4S, 得 d 1+d 2+d 3+d 4=ℎ=√63. 第三部分81. (1) 交线围成的正方形 EHGF 如图.(2) 作 EM ⊥AB ,垂足为 M ,则 AM =A 1E =4,EB 1=12,EM =AA 1=8. 因为四边形 EHGF 为正方形,所以 EH =EF =BC =10. 于是 MH =√EH 2−EM 2=6,AH =10,HB =6.故 S 四边形A 1EHA =12×(4+10)×8=56,S 四边形EB 1BH =12×(12+6)×8=72. 因为长方体被平面 α 分为两个高为 10 的直棱柱,所以其体积的比值为 97(79 也正确). 82. ∵ D ,E 分别是 AB ,AC 中点, ∴ S △ADE =14S △ABC ,∴ V 三棱锥S−ADE =14V 三棱锥S−ABC ,∴ V 四棱锥S−BCED =V 三棱锥S−ABC −V 三棱锥S−ADE =34V 三棱锥S−ABC .∵ 三棱锥 S −ABC 的三条侧棱两两垂直,∴ V 三棱锥S−ABC =16⋅SA ⋅SB ⋅SC =16×5×4×3=10,∴ V 四棱锥S−BCED =34V 三棱锥S−ABC =34×10=152.83. (1) 因为点 E ,F 分别是棱 BC ,CD 的中点,所以AF ⊥DE又AF ⊥DD 1DE ∩DD 1=D}⇒AF ⊥面EDD 1⇒AF ⊥D 1E 又C 1D ∥B 1A C 1D ⊥面BCD 1}⇒D 1E ⊥B 1AB 1A ∩AF =A }}⇒D 1E ⊥面AB 1F.(2) V E−AB 1F =V B 1−AEF =13⋅1⋅38=18.(3) 由⑴可知:D 1E ⊥ 平面 AB 1F ,直线 B 1E ,B 1D 1 与平面 AB 1F 所成的角分别为 α,β,即 α+β=∠EB 1D 1,所以cos(α+β)=cos∠EB1D1=54+2−(14+1+1)2×√52×√2=√1010.84. (1)因为AB=5cm,BC=3cm,AC=4cm,所以∠ACB=90∘⇒AB为底面圆的直径⇒S侧=12⋅10⋅π⋅5=25π.圆锥的侧面展开图是一个扇形,设此扇形的中心角为θ,弧长为l,则l=10θ,所以2π×52=10θ,所以θ=π2.(2)沿着圆锥的侧棱SA展开,在展开图△ABS中,∠ASB=45∘,SA=SB=10,⇒AB2= SA2+SB2−2SA⋅SB⋅cos∠ASB⇒AB=10√2−√2.85. (1)在AC上取一点Q,使得AQQC=4,连接MQ,QN,则AMMD =AQQC=PNNC,所以QN∥AP,MQ∥CD,又CD∥AB,所以MQ∥AB.又因为AB⊂平面PAB,PA⊂平面PAB,MQ⊂平面MNQ,NQ⊂平面MNQ,所以平面PAB∥平面MNQ,又因为MN⊂平面MNQ,MN⊄平面PAB,所以MN∥平面PAB.(2)因为AB=3,BC=5,AC=4,所以AB⊥AC.过C作CH⊥AD,垂足为H,则CH=3×45=125,因为PA⊥平面ABCD,CH⊂平面ABCD,所以PA⊥CH,又CH⊥AD,PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,所以CH⊥平面PAD,因为PC=√PA2+AC2=√41,PNNC=4,所以N到平面PAD的距离ℎ=45CH=4825,所以V P−AMN=V N−PAM=13S△PAM⋅ℎ=13×12×5×4×4825=325.86. (1)在△BAD中,因为AB=2AD=2,∠BAD=60∘,所以由余弦定理可得BD=√3.AB2=AD2+BD2,所以AD⊥BD.又在直平行六面体中,GD⊥平面ABCD,BD⊂平面ABCD,所以GD⊥BD.又AD∩GD=D,所以BD⊥平面ADG.(2)由已知可得AG∥EF,AE∥GF,四边形AEFG是平行四边形.GD=AD=1,所以EF=AG=√2.EB=AB=2,所以GF=AE=2√2.过G作GM∥DC交CF于H,得FH=2,所以FC=3.过G作GM∥DB交BE于M,得GM=DB=√3,ME=1,所以GE=2.cos∠GAE=2×2√2×√2=34,所以sin∠GAE=√74.S AEFG=2×12×√2×2√2×√74=√7.该几何体的全面积S=√7+2×12×1×√3+12×1×1+12×2×2+12×(1+3)×2+12×(2+3)×1=√7+√3+9.87. (1)如果按方案一,仓库的底面直径变成16m,则仓库的体积V1=13Sℎ=13×π×(162)2×4=2563π(m3),如果按方案二,仓库的高变成8m,则仓库的体积V2=13Sℎ=13×π×(122)2×8=2883π(m3).(2)如果按方案一,仓库的底面直径变成16m,半径为8m.棱锥的母线长为l=√82+42=4√5,则仓库的表面积S1=π×8×4√5=32√5π(m2),如果按方案二,仓库的高变成8m.棱锥的母线长为l=√82+62=10,则仓库的表面积S2=π×6×10=60π(m2).(3)∵V2>V1,S2<S1,∴方案二比方案一更加经济.88. (1)因为EA=ED且EEʹ⊥平面ABCD,所以EʹD=EʹA,所以点Eʹ在线段AD的垂直平分线上,同理点Fʹ在线段BC的垂直平分线上.又ABCD是正方形,所以线段BC的垂直平分线也就是线段AD的垂直平分线即点EʹFʹ都居线段AD的垂直平分线上,所以直线E′F′垂直平分线段AD.(2)连接EB,EC,设AD中点为M,由题意知,AB=2,∠EAD=∠EAB=60∘,EF=2,所以ME=√3,BE=FC=2,则多面体ABCDEF可分割成正四棱锥E−ABCD和正四面体E−BCF两部分,在Rt△MEEʹ中,由于MEʹ=1,ME=√3,所以EEʹ=√2,所以V E−ABCD=13S正方形ABCD⋅EEʹ=13×4×√2=4√23.V E−BCF=V C−BEF=V C−BEA=V E−ABC=13S△ABC⋅EEʹ=13×12×4×√2=23√2,所以多面体ABCDEF的体积为V E−BCF+V E−ABCD=2√2.89. (1)在三棱锥A−BCD中,∵AB⊥平面BCD,又∵CD⊂平面BCD,∴AB⊥CD.又∵BD⊥CD,且BD∩AB=B,∴CD⊥平面ABD.(2)法一:由AB⊥平面BCD,得AB⊥BD,∵AB=BD=1,∴S△ABD=12.∵M是AD中点,∴S△ABM=12S△ABD=14.由(1)知,CD⊥平面ABD,∴三棱锥C−ABM的高ℎ=CD=1,因此三棱锥A−MBC的体积为V A−MBC=V C−ABM=13S△ABM⋅ℎ=112.法二:由AB⊥平面BCD知,平面ABD⊥平面BCD,又平面ABD∩平面BCD=BD,如图,过点M作MN⊥BD交BD于点N,则MN⊥平面BCD,且MN=12AB=12,又CD⊥BD,BD=CD=1,所以S△BCD=1 2 ,∴三棱锥A−MBC的体积V A−MBC=V A−BCD −V M−BCD =13AB ⋅S △BCD −13MN ⋅S △BCD=112.90. (1) 如图,因 ABCD 为菱形,O 为菱形中心,连接 OB ,则 AO ⊥OB ,因为 ∠BAD =π3,故OB =AB ⋅sin∠OAB =2sinπ6=1. 又因为 BM =12,且 ∠OBM =π3,在 △OBM 中OM 2=OB 2+BM 2−2OB ⋅BM ⋅cos∠OBM=12+(12)2−2×1×12×cos π3=34,所以OB 2=OM 2+BM 2,故 OM ⊥BM .又 PO ⊥ 底面 ABCD ,所以 PO ⊥BC ,从而 BC 与平面 POM 内两条相交直线 OM ,PO 都垂直, 所以 BC ⊥ 平面 POM .(2)由(1)可知,OA =AB ⋅cos∠OAB =2⋅cosπ6=√3, 设 PO =a ,由 PO ⊥ 底面 ABCD 知,△POA 为直角三角形,故PA 2=PO 2+OA 2=a 2+3,由 △POM 也是直角三角形,故PM 2=PO 2+OM 2=a 2+34,连接 AM ,在 △ABM 中,AM 2=AB 2+BM 2−2AB ⋅BM ⋅cos∠ABM=22+(12)2−2⋅2⋅12⋅cos 2π3=214,由已知MP⊥AP,故△APM为直角三角形,则PA2+PM2=AM2,即a2+3+a2+34=214,得a=√32,a=−√32(舍去),即PO=√32,此时S ABMO=S△AOB+S△OMB=12⋅AO⋅OB+12⋅BM⋅OM=12⋅√3⋅1+12⋅12⋅√32=5√3 8,所以四棱锥P−ABMO的体积V P−ABMO=13⋅S ABMO⋅PO=13⋅5√38⋅√32=5 16.91. (1)在△ABD中,因为AB=2,AD=4,∠DAB=60∘,所以BD=√AB2+AD2−2AB⋅ADcos∠DAB=2√3.所以AB2+BD2=AD2,所以AB⊥BD.又因为平面EBD⊥平面ABD.平面EBD∩平面ABD=BD,AB⊂平面ABD,所以AB⊥平面EBD.结合DE⊂平面EBD,可得AB⊥DE.(2)由(1)知AB⊥BD,因为CD∥AB,所以CD⊥BD,从而DE⊥BD.在Rt△DBE中,因为DB=2√3,DE=DC=AB=2,所以S△DBE=12DB⋅DE=2√3.又AB⊥平面EBD,BE⊂平面EBD,所以AB⊥BE.因为BE=BC=AD=4,所以S△ABE=12AB⋅BE=4.又DE⊥BD,平面EBD⊥平面ABD,故得到ED⊥平面ABD.而AD⊂平面ABD,所以ED⊥AD,因此S△ADE=12AD⋅DE=4.综上,三棱锥E−ABD的侧面积S=8+2√3.92. (1)如果按方案一,仓库的底面直径变成16m,则仓库的体积V1=13S⋅ℎ=13×π×(162)2×4=2563π(m3)如果按方案二,仓库的高变成8m,则仓库的体积V2=13S⋅ℎ=13×π×(122)2×8=2883π(m3)(2)如果按方案一,仓库的底面直径变成16m,半径为8m.圆锥的母线长为l1=√82+42=4√5(m),则仓库的侧面积S1=π×8×4√5=32√5π(m2);如果按方案二,仓库的高变成8m,圆锥的母线长为l2=√82+62=10(m),则仓库的侧面积S2=π×6×10=60π(m2).(3)因为V2>V1,S2<S1.所以方案二比方案一更加经济.93. (1)取AB的中点M,连接A1M.因为AF=14AB,所以F为AM的中点.。
高中数学8-3简单几何体的表体积第1课时柱体锥体台体的表面积与体积课后提能训练新人教A版必修第二册

第八章 8.3 第1课时A 级——基础过关练1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )A .4πB .3πC .2πD .π【答案】C【解析】底面圆半径为1,高为1,侧面积S =2πrh =2π×1×1=2π.故选C. 2.(2021年银川月考)已知正六棱柱的高为6,底面边长为4,则它的表面积为( ) A .48(3+3) B .48(3+23) C .24(6+2) D .144【答案】A【解析】由题意,知侧面积为6×6×4=144,两底面积之和为2×34×42×6=483,所以表面积S =48(3+3).3.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( ) A .π B .2π C .4π D .8π【答案】B【解析】设圆柱的底面半径为r ,则圆柱的母线长为2r ,由题意得S 圆柱侧=2πr ×2r =4πr 2=4π,所以r =1,所以V 圆柱=πr 2×2r =2πr 3=2π.故选B.4.(2021年郑州模拟)如图,ABC -A ′B ′C ′是体积为1的三棱柱,则四棱锥C -AA ′B ′B 的体积是( )A .13B .12 C .23 D .34【答案】C【解析】∵V 三棱锥C -A ′B ′C ′=13V 三棱柱ABC -A ′B ′C ′=13,∴V 四棱锥C -AA ′B ′B =1-13=23.5.将一个正方体截去四个角后,得到一个四面体,这个四面体的体积是原正方体体积的( )A .23B .12 C .13 D .14【答案】C【解析】将正方体ABCD -A ′B ′C ′D ′截去四个角后得到一个四面体B -DA ′C ′.设正方体的棱长为a ,则V 三棱锥B -B ′A ′C ′=V 三棱锥A ′-ABD =V 三棱锥C ′-BCD =V 三棱锥D -A ′C ′D ′=13×12×a ×a ×a=a 36,∴四面体B -DA ′C ′的体积V =V 正方体ABCD -A ′B ′C ′D ′-4V 三棱锥B -B ′A ′C ′=a 3-2a 33=a33,∴这个四面体的体积是原正方体体积的13.故选C.6.表面积为3π的圆锥,它的侧面展开图是一个半圆面,则该圆锥的底面直径为________.【答案】2【解析】设圆锥的母线为l ,圆锥底面半径为r ,由题意可知,πrl +πr 2=3π,且πl =2πr ,解得r =1,即直径为2.7.已知棱长为1,各面均为等边三角形的四面体,则它的表面积是________,体积是________.【答案】 3212【解析】S 表=4×34×12=3,V 体=13×34×12×12-⎝ ⎛⎭⎪⎫332=212.8.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.【答案】168π【解析】先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,则它的母线长为l =h 2+(R -r )2=(4r )2+(3r )2=5r =10,所以r =2,R =8.故S 侧=π(R +r )l =π(8+2)×10=100π,S 表=S 侧+πr 2+πR 2=100π+4π+64π=168π.9.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积. 解:设圆锥的底面半径为r ,母线为l , 则2πr =13πl ,得l =6r .又S 锥=πr 2+πr ·6r =7πr 2=15π,得r =157, 圆锥的高h =35×157, V =13πr 2h =13π×157×35×157=2537π. 10.在长方体ABCD -A 1B 1C 1D 1中,截下一个棱锥C -A 1DD 1,求棱锥C -A 1DD 1的体积与剩余部分的体积之比.解:已知长方体可以看成直四棱柱,设它的底面ADD 1A 1的面积为S ,高为h ,则它的体积为V =Sh .而棱锥C -A 1DD 1的底面积为12S ,高为h ,故三棱锥C -A 1DD 1的体积VC -A 1DD 1=13·⎝ ⎛⎭⎪⎫12S h =16Sh ,余下部分体积为Sh -16Sh =56Sh .所以棱锥C -A 1DD 1的体积与剩余部分的体积之比1∶5.B 级——能力提升练11.(2020年株洲期末)《九章算术》卷5《商功》记载一个问题“今有圆堡壔(d ǎo),周四丈八尺,高一丈-尺,文积几何?”意思是:今有圆柱形土筑小城堡,底面周长为4丈8尺,高1丈1尺,问它的体积是多少立方尺?这个问题的答案是(π≈3,1丈=10尺)( )A .2 112B .2 111C .4 224D .4 222【答案】A【解析】由已知,圆柱底面圆的周长为48尺,圆柱的高为11尺,∴底面半径r =482π=8(尺),∴它的体积V =11πr 2=2 112(立方尺).故选A.12.(2021年哈尔滨月考)鲁班锁起源于中国古代建筑的榫卯结构.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.图1是一个鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁玩具的表面积为( )A .8(6+62+3)B .6(8+82+3)C .8(6+63+2)D .6(8+83+2)【答案】A【解析】由题图,可知该鲁班锁玩具可以看成是由一个棱长为2(1+2)的正方体截去了8个正三棱锥而得到的,且被截去的正三棱锥的底面边长为2,侧棱长为2,则该鲁班锁玩具的表面积为6×4×(1+2)2-4×12×2×2+8×12×2×3=8(6+62+3).故选A.13.(2021年武汉模拟)已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.【答案】90 138【解析】该几何体的体积V =4×6×3+12×4×3×3=90,表面积S =2(4×6+4×3+6×3)-3×3+12×4×3×2+32+42×3+3×4=138.14.用一张正方形的纸把一个棱长为1的正方体礼品盒完全包住,不将纸撕开,则所需纸的最小面积是________.【答案】8【解析】如图1为棱长为1的正方体礼品盒,先把正方体的表面按图所示方式展开成平面图形,再把平面图形尽可能拼成面积较小的正方形,如图2所示,由图知正方形的边长为22,其面积为8.图1 图215.降水量是指水平平面上单位面积降水的深度,现用上口直径为38 cm 、底面直径为24 cm 、深度为35 cm 的圆台形水桶(轴截面如图所示)来测量降水量.如果在一次降雨过程中,此桶盛得的雨水正好是桶深的17,求本次降雨的降水量是多少毫米(精确到1 mm).解:因为这次降雨的雨水正好是桶深的17,所以水深为17×35=5(cm).如图,设水面半径为r cm ,在△ABC 中,AC A ′C ′=CB C ′B ,所以7r -12=7,r =13.所以V 水=13×(π×122+π×122×π×132+π×132)×5=2 3453π(cm 3).水桶的上口面积是S =π×192=361π(cm 2), 所以V 水S =2 3453π361π×10≈22(mm).故此次降雨的降水量约是22 mm.16.已知一个圆锥的底面半径为R ,高为H ,在其内部有一个高为x 的内接圆柱. (1)求圆柱的侧面积;(2)x 为何值时,圆柱的侧面积最大?解:(1)作圆锥的轴截面,如图所示.设圆柱底面半径为r ,因为r R =H -x H ,所以r =R -RHx .所以S 圆柱侧=2πrx =2πRx -2πRHx 2(0<x <H ).(2)因为-2πR H <0,所以当x =2πR 4πR H=H 2时,S圆柱侧最大.故当x =H2时,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.C 级——探索创新练17.一个封闭的正三棱柱容器,高为3,内装水若干(如图1,底面处于水平状态).将容器放倒(如图2,一个侧面处于水平状态),这时水面所在的平面与各棱交点E ,F ,F 1,E 1分别为所在棱的中点,则图1中水面的高度为( )A . 3B .2C .332D .94【答案】D【解析】设正三棱柱的底面积为S ,则VABC -A 1B 1C 1=3S . ∵E ,F ,F 1,E 1分别为所在棱的中点.∴S AEF S =14,即S AEF =14S .∴S BCEF =34S .∴VBCFE -B 1C 1F 1E 1=3×34S =94S .则图1中水面的高度为94.故选D.。
高考复习 第8篇 第1讲 空间几何体及其表面积与体积知识点+例题+练习 含答案
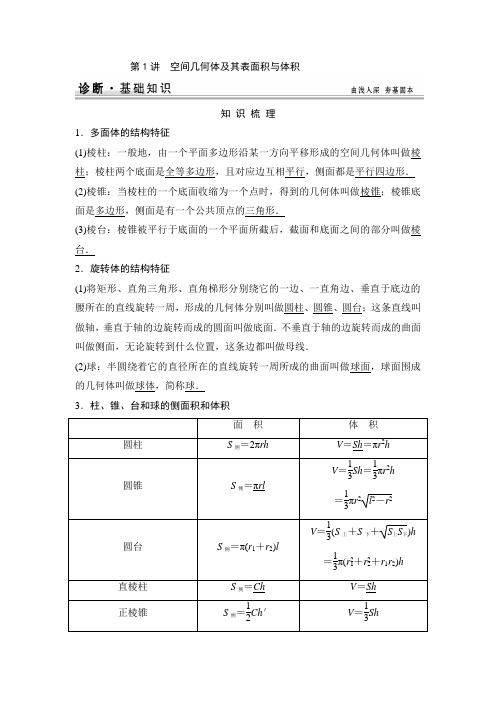
第1讲空间几何体及其表面积与体积知识梳理1.多面体的结构特征(1)棱柱:一般地,由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱;棱柱两个底面是全等多边形,且对应边互相平行,侧面都是平行四边形.(2)棱锥:当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥;棱锥底面是多边形,侧面是有一个公共顶点的三角形.(3)棱台:棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台.2.旋转体的结构特征(1)将矩形、直角三角形、直角梯形分别绕它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台;这条直线叫做轴,垂直于轴的边旋转而成的圆面叫做底面.不垂直于轴的边旋转而成的曲面叫做侧面,无论旋转到什么位置,这条边都叫做母线.(2)球:半圆绕着它的直径所在的直线旋转一周所成的曲面叫做球面,球面围成的几何体叫做球体,简称球.3.柱、锥、台和球的侧面积和体积面积体积圆柱S侧=2πrh V=Sh=πr2h圆锥S侧=πrlV=13Sh=13πr2h=13πr2l2-r2圆台S侧=π(r1+r2)lV=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h直棱柱S侧=Ch V=Sh正棱锥S侧=12Ch′V=13Sh续表4.(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和.辨析感悟1.柱体、锥体、台体与球的面积(1)圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是2πS.(×)(2)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为3πa2.(×)2.柱体、锥体、台体的体积(3)(教材练习改编)若一个球的体积为43π,则它的表面积为12π.(√)(4)在△ABC中,AB=2,BC=3,∠ABC=120°,使△ABC绕直线BC旋转一周所形成的几何体的体积为9π.(×)3.柱体、锥体、台体的展开与折叠(5)将圆心角为2π3,面积为3π的扇形作为圆锥的侧面,则圆锥的表面积等于4π.(√)(6)(2014·青州模拟改编)将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为312a3.(×)[感悟·提升]两点注意一是求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.二是几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.考点一空间几何体的结构特征【例1】给出下列四个命题:①有两个侧面是矩形的棱柱是直棱柱②侧面都是等腰三角形的棱锥是正棱锥③侧面都是矩形的直四棱柱是长方体④底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱其中不正确的命题为________.解析对于①,平行六面体的两个相对侧面也可能是矩形,故①错;对于②,对等腰三角形的腰是否为侧棱未作说明(如图),故②错;对于③,若底面不是矩形,则③错;④正确.答案①②③规律方法解决该类题目需准确理解几何体的定义,要真正把握几何体的结构特征,并且学会通过举反例对概念进行辨析,即要说明一个命题是错误的,设法举出一个反例即可.【训练1】设有以下四个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体;④棱台的相对侧棱延长后必交于一点.其中真命题的序号是________.解析命题①符合平行六面体的定义,故命题①是正确的.底面是矩形的平行六面体的侧棱可能与底面不垂直,故命题②是错误的.因为直四棱柱的底面不一定是平行四边形,故命题③是错误的.命题④由棱台的定义知是正确的. 答案 ①④考点二 几何体的表面积与体积【例2】 如图所示,四棱锥P -ABCD 的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,∠ABD =60°,∠BDC =45°, △ADP ∽△BAD . (1)求线段PD 的长;(2)若PC =11R ,求三棱锥P -ABC 的体积. 解 (1)∵BD 是圆的直径,∴∠BAD =90°, 又∵△ADP ∽△BAD ,∴AD BA =DP AD , ∠PDA =∠BAD =90°, DP =AD 2BA =(BD sin 60°)2BD sin 30°=4R 2×342R ×12=3R . ∴DP 的长为3R .(2)在Rt △BCD 中,BC =CD =BD cos 45°=2R , ∵PD 2+CD 2=9R 2+2R 2=11R 2=PC 2,∴PD ⊥CD , 又∠PDA =90°,AD ∩CD =D ,∴PD ⊥底面ABCD , 则S △ABC =12AB ·BC sin(60°+45°) =12R ·2R ⎝ ⎛⎭⎪⎫32×22+12×22=3+14R 2.所以三棱锥P -ABC 的体积为V P -ABC =13·S △ABC ·PD =13·3+14R 2·3R =3+14R 3.规律方法 求几何体的体积问题,可以多角度、全方位地考虑问题,常采用的方法有“换底法”、“分割法”、“补体法”等,尤其是“等积转化”的数学思想方法应高度重视.【训练2】 (2014·苏州模拟)一个正三棱台的上、下底面边长分别是3 cm 和6 cm ,高是32 cm.(1)求三棱台的斜高;(2)求三棱台的侧面积和表面积. 解(1)设O 1、O 分别为正三棱台ABC -A 1B 1C 1的上、下底面正三角形的中心,如图所示,则O 1O =32,过O 1作O 1D 1⊥B 1C 1,OD ⊥BC ,则D 1D 为三棱台的斜高;过D 1作D 1E ⊥AD 于E ,则D 1E =O 1O =32, 因O 1D 1=36×3=32,OD =36×6=3,则DE =OD -O 1D 1=3-32=32.在Rt △D 1DE 中, D 1D =D 1E 2+ED 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322=3(cm). (2)设c 、c ′分别为上、下底的周长,h ′为斜高, S 侧=12(c +c ′)h ′=12(3×3+3×6)×3=2732(cm 2),S 表=S 侧+S 上+S 下=2732+34×32+34×62=9934(cm 2).故三棱台斜高为 3 cm ,侧面积为2732 cm 2,表面积为9934 cm 2.考点三 球与空间几何体的接、切问题【例3】 (1)(2013·新课标全国Ⅱ卷)已知正四棱锥O -ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.(2)(2013·辽宁卷改编)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为________.审题路线 (1)根据正四棱锥的体积求高⇒求底面正方形的对角线长⇒由勾股定理求OA ⇒由球的表面积公式求解.(2)BC 为过底面ABC 的截面圆的直径⇒取BC 中点D ,则球心在BC 的垂直平分线上,再由对称性求解. 解析 (1)设正四棱锥的高为h , 则13×(3)2×h =322,解得h =322. 又底面正方形的对角线长为2×3= 6. 所以OA =⎝ ⎛⎭⎪⎫3222+⎝ ⎛⎭⎪⎫622= 6. 故球的表面积为S 球=4π×(6)2=24π.(2)因为在直三棱柱中AB =3,AC =4,AA 1=12,AB ⊥AC ,所以BC =5,且BC 为过底面ABC 的截面圆的直径,取BC 中点D ,则OD ⊥底面ABC ,则O 在侧面BCC 1B 1内,矩形BCC 1B 1的对角线长即为球的直径,所以2r =122+52=13,即r =132.答案 (1)24π (2)132规律方法 解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.【训练3】(2012·辽宁卷)已知点P,A,B,C,D是球O表面上的点,P A⊥平面ABCD,四边形ABCD是边长为23的正方形.若P A=26,则△OAB的面积为________.解析根据球的内接四棱锥的性质求解.如图所示,线段PC就是球的直径,设球的半径为R,因为AB=BC=23,所以AC=2 6.又P A=26,所以PC2=P A2+AC2=24+24=48,所以PC=43,所以OA=OB=23,所以△AOB是正三角形,所以S=12×23×23×32=3 3.答案3 3考点四几何体的展开与折叠问题【例4】(1)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC,OD折叠,使OA,OB重合,则以A,B,C,D,O为顶点的四面体的体积为________.(2)如图所示,在直三棱柱ABC-A1B1C1中,△ABC为直角三角形,∠ACB=90°,AC=4,BC=CC1=3.P是BC1上一动点,沿棱柱表面使CP+P A1最小,则最小值为________.解析 (1)折叠后的四面体如图所示.OA ,OC ,OD 两两相互垂直,且OA =OC =OD =22,体积V =13 S △OCD ·OA =13×12×(22)3=823.(2)由题意知,A 1P 在几何体内部,把面BB 1C 1C 沿BB 1展开与面AA 1B 1B 在一个平面上,如图所示,连接A 1C 即可. 则A 1、P 、C 三点共线时,CP +P A 1最小, ∵∠ACB =90°,AC =4,BC =C 1C =3,∴A 1B 1=AB =42+32=5,∴A 1C 1=5+3=8,∴A 1C =82+32=73.故CP +P A 1的最小值为73.答案 (1)823 (2)73规律方法 (1)有关折叠问题,一定要分清折叠前后两图形(折前的平面图形和折叠后的空间图形)各元素间的位置和数量关系,哪些变,哪些不变.(2)研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.【训练4】如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q共线,点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.解析由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图所示),其中PD⊥平面ABCD,因此该四棱锥的体积V=13×6×6×6=72,而棱长为6=3个这样的几何体,才能拼成的正方体的体积V=6×6×6=216,故需要21672一个棱长为6的正方体.答案 31.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决.2.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.3.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.方法优化5——特殊点在求解几何体的体积中的应用【典例】 (2012·山东卷)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为________.[一般解法] 三棱锥D 1-EDF 的体积即为三棱锥F -DD 1E 的体积.因为E ,F 分别为AA 1,B 1C 上的点,所以在正方体ABCD -A 1B 1C 1D 1中△EDD 1的面积为定值12,F 到平面AA 1D 1D 的距离为定值1,所以VF -DD 1E =13×12×1=16. [优美解法] E 点移到A 点,F 点移到C 点,则VD 1-EDF =VD 1-ADC =13×12×1×1×1=16. [答案] 16[反思感悟] (1)一般解法利用了转化思想,把三棱锥D 1-EDF 的体积转化为三棱锥F -DD 1E 的体积,但这种解法还是难度稍大,不如采用特殊点的解法易理解、也简单易求.(2)在求几何体体积时还经常用到等积法、割补法. 【自主体验】 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为________.解析补形法将三棱柱补成四棱柱,如图所示.记A1到平面BCC1B1的距离为d,则d=2.则V三棱柱=12V四棱柱=12S四边形BCC1B1·d=12×4×2=4.答案 4基础巩固题组(建议用时:40分钟)一、填空题1.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④一个平面截圆锥,得到一个圆锥和一个圆台.其中正确命题的个数是________.解析命题①错,因为这条边若是直角三角形的斜边,则得不到圆锥.命题②题,因这条腰必须是垂直于两底的腰.命题③对.命题④错,必须用平行于圆锥底面的平面截圆锥才行.答案 12.在正方体上任意选择4个顶点,它们可能是如下各种几何形体的四个顶点,这些几何形体是________(写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.解析①显然可能;②不可能;③取一个顶点处的三条棱,连接各棱端点构成的四面体;④取正方体中对面上的两条异面对角线的四个端点构成的几何体;⑤正方体ABCD-A1B1C1D1中,三棱锥D1-DBC满足条件.答案①③④⑤3.在三棱锥S-ABC中,面SAB,SBC,SAC都是以S为直角顶点的等腰直角三角形,且AB=BC=CA=2,则三棱锥S-ABC的表面积是________.解析设侧棱长为a,则2a=2,a=2,侧面积为3×12×a2=3,底面积为34×22=3,表面积为3+ 3.答案3+ 34.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为________.解析 设圆锥的底面圆半径为r ,高为h ,母线长为l ,则⎩⎪⎨⎪⎧ πrl =2π,πr 2=π,∴⎩⎪⎨⎪⎧r =1,l =2.∴h =l 2-r 2=22-12= 3.∴圆锥的体积V =13π·12·3=33π. 答案 33π5.(2012·新课标全国卷改编)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为________. 解析如图,设截面圆的圆心为O ′,M 为截面圆上任一点,则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3,∴V =43π(3)3=43π.答案 43π 6.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 答案 267.(2013·天津卷)已知一个正方体的所有顶点在一个球面上,若球的体积为9π2,则正方体的棱长为________.解析 设正方体的棱长为a ,外接球的半径为R ,由题意知43πR 3=9π2,∴R 3=278,而R =32.由于3a 2=4R 2,∴a 2=43R 2=43×⎝ ⎛⎭⎪⎫322=3,∴a = 3.答案 38.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为________.解析 如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,容易求得EG =HF =12,AG =GD =BH =HC =32,∴S △AGD =S △BHC =12×22×1=24,∴V =V E -ADG +V F -BHC +V AGD -BHC =2V E -ADG +V AGD -BHC =13×24×12×2+24×1=23. 答案 23 二、解答题 9.如图,在三棱锥P -ABC 中,AC =BC =2,∠ACB =90°,AP =BP =AB ,PC ⊥AC .(1)求证:PC ⊥AB ;(2)求点C 到平面APB 的距离. (1)证明 取AB 中点D ,连接PD ,CD .因为AP =BP ,所以PD ⊥AB , 因为AC =BC ,所以CD ⊥AB .因为PD ∩CD =D ,所以AB ⊥平面PCD .因为PC ⊂平面PCD ,所以PC ⊥AB . (2)解 设C 到平面APB 的距离为h ,则由题意,得AP =PB =AB =AC 2+BC 2=22, 所以PC =AP 2-AC 2=2.因为CD =12AB =2,PD =32PB =6, 所以PC 2+CD 2=PD 2,所以PC ⊥CD .由(1)得AB ⊥平面PCD ,于是由V C -APB =V A -PDC +V B -PDC , 得13·h ·S △APB =13AB ·S △PDC ,所以h =AB ·S △PDCS △APB=22×12×2×234×(22)2=233.故点C 到平面APB 的距离为233.10.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解 如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r ,水面半径BC 的长为3r ,则容器内水的体积为 V =V 圆锥-V 球=13π(3r )2·3r - 43πr 3=53πr 3,将球取出后,设容器中水的深度为h , 则水面圆的半径为33h ,从而容器内水的体积为 V ′=13π⎝ ⎛⎭⎪⎫33h 2h =19πh 3,由V =V ′,得h =315r .能力提升题组 (建议用时:25分钟)一、填空题1.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S -ABC 的体积为________.解析 由题意知,如图所示,在棱锥S -ABC 中,△SAC ,△SBC 都是有一个角为30°的直角三角形,其中AB =3,SC =4,所以SA =SB =23,AC =BC =2,作BD ⊥SC 于D 点,连接AD ,易证SC ⊥平面ABD ,因此V S -ABC =13×34×(3)2×4= 3. 答案 32.(2014·南京模拟)如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,BC =2,AC =5,AA 1=3,M 为线段B 1B 上的一动点,则当AM +MC 1最小时,△AMC 1的面积为________.解析 如图,当AM +MC 1最小时,BM =1,所以AM 2=2,C 1M 2=8,AC 21=14,于是由余弦定理,得cos ∠AMC 1=AM 2+MC 21-AC 212AM ·MC 1=-12,所以sin ∠AMC 1=32,S △AMC 1=12×2×22×32= 3. 答案 33.如图,已知正三棱柱ABC -A 1B 1C 1的底面边长为2 cm 、高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为________cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 cm.答案 13 二、解答题4.如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D -ABC ,如图2所示.(1)求证:BC ⊥平面ACD ; (2)求几何体D -ABC 的体积.(1)证明 在图中,可得AC =BC =22, 从而AC 2+BC 2=AB 2, 故AC ⊥BC ,又平面ADC ⊥平面ABC , 平面ADC ∩平面ABC =AC , BC ⊂平面ABC , ∴BC ⊥平面ACD .(2)解 由(1)可知,BC 为三棱锥B -ACD 的高,BC =22,S △ACD =2,∴V B -ACD =13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体D -ABC 的体积为423.。
简单几何体的表面积和体积 (教师版)

简单几何体的表面积和体积1 柱体①棱柱体积:V=sℎ(其中ℎ是棱柱的高)②圆柱(1) 侧面积:S=2πrℎ(2) 全面积:S=2πrℎ+2πr2(3) 体积:V=Sℎ=πr2ℎ(其中r为底圆的半径,ℎ为圆柱的高)2 锥体①棱锥棱锥体积:V=13Sℎ(其中ℎ为圆柱的高);②圆锥(1) 圆锥侧面积:S=πrl(2) 圆锥全面积:S=πr(r+l)(其中r为底圆的半径,l为圆锥母线)(3) 圆锥体积:V=13Sℎ=13πr2ℎ(其中r为底圆的半径,ℎ为圆柱的高)3台体①圆台表面积S=π (r′2+r′2+r′l+rl)其中r′是上底面圆的半径,r是下底面圆的半径,l是母线的长度.②台体体积V=13(S′+√SS′ +S) ℎ其中S , S′分别为上,下底面面积,ℎ为圆台的高.4 球体面积S=4πR2,体积V=43πR3(其中R为球的半径)【题型一】几何体的表面积【典题1】已知正四棱柱ABCD-A1B1C1D1中AB=2,AA1=3,O为上底面中心.设正四棱柱ABCD-A1B1C1D1与正四棱锥O-A1B1C1D1的侧面积分别为S1,S2,则S2S1=.【解析】如图,正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,则正四棱柱ABCD-A1B1C1D1的侧面积分别为S1=4×2×3=24;正四棱锥O-A1B1C1D1的斜高为√12+32=√10.∴正四棱锥O-A1B1C1D1的侧面积S2=4×12×2×√10=4√10.∴S2S1=4√1024=√106.【点拨】注意侧面积和全面积的区别.【典题2】一个底面半径为2,高为4的圆锥中有一个内接圆柱,该圆柱侧面积的最大值为()A.2π B.3πC.4πD.5π【解析】圆锥的底面半径为2,高为4,∴内接圆柱的底面半径为x时,它的上底面截圆锥得小圆锥的高为2x因此,内接圆柱的高 ℎ=4−2x;∴圆柱的侧面积为:S=2πx(4−2x)=4 π(2x−x2)(0<x<2)令t=2x−x2,当x=1时t max=1;所以当x=1时,S max=4π.即圆柱的底面半径为1时,圆柱的侧面积最大,最大值为4π.故选:C .【点拨】① 圆柱的侧面积S =2πrℎ,则需要知道圆柱的高ℎ与底圆半径r ;② 在处理圆锥、圆柱问题时,要清楚母线、高、底圆的半径之间的关系,则要看轴截面(如下图),此时由相似三角形的性质可以得到每个量的关系.【典题3】 一个圆台上、下底面半径分别为r 、R ,高为ℎ,若其侧面积等于两底面面积之和,则下列关系正确的是( )A .2ℎ=1R +1rB .1ℎ=1R +1rC .1r =1R +1ℎD .2R =1r +1ℎ 【解析】设圆台的母线长为l ,根据题意可得圆台的上底面面积为S 上=πr 2,圆台的下底面面积为S 下=πR 2,∵圆台的侧面面积等于两底面面积之和,∴侧面积S 侧=π(r 2+R 2)=π(r +R)l ,解之得l =r 2+R 2r+R ∵l =√ℎ2+(R −r)2∴r 2+R 2r+R =√ℎ2+(R −r)2,∴(r 2+R 2r +R )2=ℎ2+(R -r)2 ∴2ℎ=1R +1r .故选 A . 【点拨】在处理圆台问题时,要清楚母线、上底圆半径、下底圆半径、高之间的关系,则要看轴截面(如下图),有 l =√ℎ2+(R −r)2.【题型二】几何体的体积【典题1】正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧DB̂分成三部分,绕AD旋转,所得旋转体的体积V1、V2、V3之比是()A.2: 1: 1B.1∶2: 1C.1∶1∶1D.2∶2: 1【解析】设正方形ABCD的边长为1,可得图1旋转所得旋转体为以AD为轴的圆锥体,高AD=1且底面半径r=1∴该圆锥的体积为V1=13π×AB2×AD=13π;图2旋转所得旋转体,是以AD为半径的一个半球,减去图1旋转所得圆锥体而形成,∴该圆锥的体积为V2=V半球−V1=12×43π×AD2-V1=13π;图3旋转所得旋转体,是以AD为轴的圆柱体,减去图2旋转所得半球而形成,∴该圆锥的体积为V3=π×AB2×AD-V半球=π-23π=13π综上所述V1=V2=V3=13π,由此可得图中1、2、3三部分旋转所得旋转体的体积之比为1∶1∶1.故选 C.【点拨】①圆锥是由直角三角形以某一直角边为轴旋转得到;圆柱是由矩形以某一边为轴旋转得到;球是由半圆以直径为轴旋转得到;②求解不规则图形可用“割补法”.【典题2】如图,圆锥形容器的高为ℎ,圆锥内水面的高为ℎ1,且ℎ1=13ℎ,若将圆锥的倒置,水面高为ℎ2,则ℎ2等于()A.23ℎB.1927ℎC.√633ℎD.√1933ℎ【解析】方法一设圆锥形容器的底面积为S,则未倒置前液面的面积为49S.∴水的体积V =13Sℎ-13×49S ×(ℎ−ℎ1)=1981Sℎ. 设倒置后液面面积为S′,则S′S =(ℎ2ℎ)2,∴S′=Sℎ22ℎ2.∴水的体积V =13S′ℎ2=Sℎ233ℎ2. ∴1981Sℎ=Sℎ233ℎ2,解得ℎ2=√193ℎ3. 故选 D .方法二 设容器为圆锥1,高为ℎ,体积为V ;倒置前液面上的锥体为圆锥2,高为ℎ′=ℎ−ℎ1,体积为V 1;倒置后液面以下的锥体为圆锥3,高为ℎ2,体积为V 2.∵ℎ1ℎ=13 ∴ℎ′ℎ=23 ∴V−V 水V =(23)3=827⇒V 水V =1927, 在倒置后,又有V 水V =(ℎ2ℎ)3 ∴(ℎ2ℎ)3=1927⇒ℎ2=√193ℎ3【点拨】 ① 涉及圆台的表面积和体积,可把圆台补全为圆锥;② 两个相似几何体,若相似比为a ,则对应线段比为a ,对应的平面面积比为a 2,对应的几何体体积比是a 3.【典题3】 已知球的直径SC =4,A ,B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则棱锥S −ABC 的体积V = .【解析】由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,如图所示,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥SABD 和CABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DBC =∠DAC =45°,所以在△BDC 中,BD =4-x ,所以x =4-x ,解得x =2,所以AD =BD =2,所以 ABD 为正三角形,所以V =13S △ABD ×4=4√33.【点拨】① 圆内直径所对的圆周角为90°;② 若垂直于三棱锥的某棱长的截面面积为S ,棱长长ℎ,则三棱锥的体积为13Sℎ.【题型三】与球有关的切、接问题【典题1】 已知三棱锥D −ABC 的四个顶点在球O 的球面上,若AB =AC =BC =DB =DC =1,当三棱锥D -ABC 的体积取到最大值时,球O 的表面积为( )A. 5π3B. 2 πC. 5 πD. 20π3【解析】 如图,当三棱锥D −ABC 的体积取到最大值时,则平面ABC ⊥平面DBC ,取BC 的中点G ,连接AG ,DG ,则AG ⊥BC ,DG ⊥BC ,分别取△ABC 与△DBC 的外心E ,F ,分别过E ,F 作平面ABC 与平面DBC 的垂线,相交于O ,则O 为四面体ABCD 的球心,由AB =AC =BC =DB =DC =1,得正方形OEGF 的边长为√36,则OG =√66∴四面体A −BCD 的外接球的半径R =√OG 2+B G 2=√(√66)2+(12)2=√512 ∴球O 的表面积为=4 π×(√512)2=5π3,故选:A .【典题2】 如图,在一个底面边长为2,侧棱长为√10的正四棱锥P -ABCD 中,大球O 1内切于该四棱锥,小球O 2与大球O 1及四棱锥的四个侧面相切,则小球O 2的体积为 .【解析】设O为正方形ABCD的中心,AB的中点为M,连接PM,OM,PO,则OM=1,PM=√PA2−AM2=√10−1=3,PO=√9−1=2√2,如图,在截面PMO中,设N为球O1与平面PAB的切点,则N在PM上,且O1N⊥PM,设球O1的半径为R,则O1N=R,因为sin∠MPO=OMPM =13,所以NO1PO1=13,则PO1=3R,PO=PO1+OO1=4R=2√2,所以R=√22,设球O1与球O2相切与点Q,则PQ=PO-2R=2R,设球O2的半径为r,同理可得PQ=4r,所以r=R2=√24,故小球O2的体积V=43πr3=√224π,故答案为√224π.巩固练习1(★)如图1所示,一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计),圆柱形水桶的底面直径与母线长相等,现将该水桶水平放置后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S1、S2,则S1与S2的大小关系是()A.S1≤S2B.S1<S2C.S1>S2D.S1≥S2【答案】B【解析】设圆柱的底面半径为r,图1水的表面积为 S1=2πr2+2πr•r=4πr2.对于图2,上面的矩形的面积的长是2r,宽是2r.则面积是4r2.曲面展开后的矩形长是πr,宽是2r.则面积是2πr2.上下底面的面积的和是π×r2.图2水的表面积S2=(4+3π)r2.显然S1<S2.故选B.2(★) 若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为()A.πB.3π2C.2π3D.π2【答案】A【解析】设圆锥的底面圆半径为r,高为ℎ;由圆锥的母线长为4,所以圆锥的侧面积为πr•4=4πr;又圆锥的轴截面面积为12•2r•ℎ=rℎ,所以4πr=4rℎ,解得ℎ=π;所以该圆锥的高为π.故选:A.3(★★) 某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则该几何体共有个面;如果被截正方体的棱长是50cm,那么石凳的表面积是cm2.【答案】14,10000【解析】由题意知,截去的八个四面体是全等的正三棱锥,8个底面三角形,再加上6个小正方形,所以该几何体共有14个面;如果被截正方体的棱长是50cm,那么石凳的表面积是S表面积=8×12×25√2×25√2×sin60°+6×25√2×25√2=10000(cm2).故答案为:14,10000.4(★★) 直角梯形的上、下底和不垂直于底的腰的长度之比为12√3,那么以垂直于底的腰所在的直线为轴,将梯形旋转一周,所得的圆台上、下底面积和侧面面积之比是.【答案】1: 4: 3√3【解析】由题意可设直角梯形上底、下底和不垂直于底的腰为x,2x,√3x;则圆台的上、下底半径和母线长分别为x,2x,√3x,如图所示;所以上底面的面积为S上底=π•x2;下底面的面积为S下底=π•(2x)2=4πx2;侧面积为S侧面=π(x+2x)•√3x=3√3πx2;所以圆台的上底、下底面积和侧面面积之比是πx2∶4πx2: 3√3πx2=1: 4: 3√3.5(★★) 如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是.【答案】2√2π3【解析】如图所示,过点P 作PE ⊥平面ABC ,E 为垂足,点E 为的等边三角形ABC 的中心.AE =23AD ,AD =√32. ∴AE =23×√32=√33.∴PE =√PA 2−AE 2=√63.设圆柱底面半径为R ,则2R =1sin60°=2√3, ∴圆柱的侧面积=2πR •PE =√3π×√63=2√2π3,6(★★) 一竖立在地面上的圆锥形物体的母线长为4m ,侧面展开图的圆心角为2π3,则这个圆锥的体积等于 . 【答案】128√281πm 3【解析】设圆锥的底面半径为r ,圆锥形物体的母线长l =4m ,侧面展开图的圆心角为2π3,故2πr =2π3,解得 r =43m , 故圆锥的高ℎ=√l 2−r 2=83√2m ,故圆锥的体积V =13πr 2ℎ=128√281πm 3.7(★★) 如图①,一个圆锥形容器的高为a ,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为a2(如图②),则图①中的水面高度为 .【答案】(1−√732)a【解析】 令圆锥倒置时水的体积为V ′,圆锥体积为V ,则v′v =(a 2)3÷a 3=18,∴V 空V 锥=78,倒置后 V 水=18V , 设此时水高为ℎ,则ℎ3 a 3=78,∴ℎ=(1−√732)a . 故原来水面的高度为(1−√732)a .8(★★★) 半径为2的球O 内有一个内接正三棱柱,则正三棱柱的侧面积的最大值为 .【答案】12√3【解析】如图所示,设正三棱柱上下底面的中心分别为O 1,O 2,底面边长与高分别为x ,ℎ,则O 2A =√33x ,在Rt △OAO 2中,ℎ24+x 23=4, 化为ℎ2=16−43x 2,∵S 侧=3xℎ,∴S 侧2=9x 2ℎ2=12x 2(12−x 2)≤12(x 2+12−x 22)2=432.当且仅当x 2=12-x 2,即x =√6时取等号,此时S 侧=12√3.9(★★★) 如图所示,在边长为5+√2的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M 、N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,则圆锥的全面积与体积分别是 与 .【答案】10π,2√303π【解析】设圆锥的母线长为l ,底面半径为r ,高为ℎ,由已知条件可得{l+r+√2r=(5+√2)×√22πrl=π2,解得r=√2,l=4√2,∴S=πrl+πr2=10π,又∵h=√l2−r2=√30,∴V=13πr2ℎ=2√303π.故答案为10π,2√303π10(★★★) 已知四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,现将四面体ABCD放入一个主视图为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,则圆锥侧面积的最小值为.【答案】27π4【解析】因为四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,所以可以把其放到长宽高分别为a,b,c的长方体中,四面体的棱长是长方体的面对角线,∴a2+b2=22,①;b2+c2=22,②;c2+a2=12,③故四面体的外接球半径R满足:8R2=22+22+12=9;∴R2=98.∵四面体ABCD放入一个主视图为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,要想圆锥的侧面积最小;故需满足四面体的外接球恰好是圆锥的内切球;作圆锥的轴截面,如图:设BE=r,则AB=2r,AE=√3r;可得:OB2=OE2+EB2;∴R2=(√3r-R)2+r2⇒r=√3R;故圆锥侧面积的最小值为:πrl=2πr2=2π•3R2=27π4.故答案为:27π4.11(★★★) 在直三棱柱ABC-A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为.【答案】1110【解析】由AB=3,BC=4,AC=5,得AB2+BC2=AC2,∴AB⊥BC.将平面ABB1A1与平面BCC1B1放在一个平面内,连接AC1,与BB1的交点即为M,此时BM=3,设四棱锥A-BCC1M的体积为V1,则V1=13×12×(3+7)×4×3=20,三棱柱ABC-A1B1C1的体积V=12×4×3×7=42.∴当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为V−V1V1=1110.12(★★★) 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为.【答案】13【解析】将直三棱柱ABC-A1B1C1展开成矩形ACC1A1,如图,连结AC1,交BB1于D,此时AD+DC1最小,∵AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点,∴当AD +DC 1最小时,BD =1,此时三棱锥D -ABC 1的体积V D−ABC 1=V C 1−ABD =13×S △ABD ×B 1C 1=13×12×AB ×BD ×B 1C 1=13×12×1×1×2=13.13(★★★) 已知△SAB 是边长为2的等边三角形,∠ACB =45°,当三棱锥S -ABC 体积最大时,其外接球的表面积为 .【答案】28π3【解析】由题可知,平面CAB ⊥平面SAB ,且CA =CB 时,三棱锥S -ABC 体积达到最大,如右图所示, 则点D ,点E 分别为△ASB ,△ACB 的外心,并过两个三角形的外心作所在三角形面的垂线,两垂直交于点O .∴点O 是此三棱锥外接球的球心,AO 即为球的半径.在△ACB 中,AB =2,∠ACB =45°⇒∠AEB =90°,由正弦定理可知,AB sin∠ACB =2AE ,∴AE =EB =EC =√2,延长CE 交AB 于点F ,延长SD 交AB 于点F ,∴四边形EFDO 是矩形,且OE ⊥平面ACB ,则有OE ⊥AE ,又∵OE =DF =13SF =13×√32AB =√33, ∴OA =√OE 2+AE 2=√73.∴S 球表面积=4πR 2=4π×( √73)2=28π3.14(★★★)如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是 .【答案】12【解析】如图,M是AC的中点.①当AD=t <AM=√3时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AE,DM=√3-t,由△ADE∽△BDM,可得ℎ1=√(√3−t)2+1,∴ℎ=√(√3−t)2+1,V=13⋅12⋅(2√3−t)⋅1⋅√(√3−t)2+1=16√3−t)2√(√3−t)2+1,t∈(0,√3)②当AD=t>AM=√3时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AH,DM=t-√3,由等面积,可得12⋅AD⋅BM=12⋅BD⋅AH,∴1 2⋅t⋅1=12√(t−√3)2+1,∴ℎ=√(√3−t)2+1,∴V=13⋅12⋅(2√3−t)⋅1√(√3−t)2+1=16⋅√3−t)2√(√3−t)2+1,t∈(√3,2√3)综上所述,V=16√3−t)2√(√3−t)2+1,t∈(0,2√3)令m=√(√3−t)2+1∈[1,2),则V=16⋅4−m2m,∴m=1时,V max=12.故答案为12.。
专题8.2 简单几何体的表面积与体积(A卷基础篇)高一数学必修第二册同步单元卷(新教材人教A版)

专题8.2 简单几何体的表面积与体积(A 卷基础篇)(浙江专用)参考答案与试题解析第Ⅰ卷(选择题)一.选择题(共10小题,满分50分,每小题5分)1.(2021·浙江绍兴市·高二期末)已知球O 的体积为36π,则该球的表面积为( )A .6πB .9πC .12πD .36π 【答案】D【解析】根据球的体积公式求出半径,即可求出表面积.【详解】设球的体积为R ,则由题可得34363R ππ=,解得3R =,则该球的表面积为24336ππ⨯=.故选:D.2.(2021·安徽滁州市·高二期末(理))一个圆柱的轴截面是一个面积为16的正方形,则该圆柱的体积是( ) A .64πB .32πC .16πD .8π 【答案】C【解析】根据题意,求得圆柱的底面直径和高,代入公式,即可求得答案.【详解】因为轴截面的面积为16,所以圆柱的底面直径和高均为4,所以圆柱的体积22416V ππ=⋅⨯=.故选:C3.(2021·河南洛阳市·高一期末)如图网格中是某几何体的三视图(网格中每个小正方形的边长为1),则该几何体的体积为( )A .2B .5C .4D .25【答案】A【解析】根据三视图还原几何体,计算体积即可.【详解】还原几何体如图,为四棱柱,底面积为11⨯,高为2故体积为:2故选:A4.(2021·浙江舟山市·高二期末)已知圆锥的正视图是边长为2的等边三角形,则它的表面积是( )A .2πB .3πC .4πD .5π【答案】B【解析】根据圆锥的正视图,求得圆锥的底面半径和母线长,结合侧面积和圆的面积公式,即可求解.【详解】设圆柱的底面半径为r ,母线长为l ,因为圆柱的正视图为边长为2的等边三角形,可得22,2r l ==,所以1r =,所以圆锥的表面积为221213S S S rl r πππππ=+=+=⨯⨯+⨯=侧底.故选:B.5.(2021·湖南省平江县第一中学高二月考)体积为8的正方体的顶点都在同一个球面上,则该球的表面积为()A.8πB.12πC.16πD.32 3π【答案】B【解析】根据正方体的体对角线长等于其外接球直径可求出外接球半径,再根据球的表面积公式即可求出.【详解】因为正方体的体积为8,即其棱长为2,体对角线长为3233,所以其外接球的表面积为24312ππ⨯=.故选:B.6.(2021·陕西咸阳市·高三一模(理))已知某圆锥的轴截面是边长为4的正三角形,则它的体积为().A 23B43C83D.3π【答案】C【解析】根据题意,求得圆锥的高和底面圆的半径,代入公式,即可求得答案. 【详解】如图所示:ABC 为边长为4的正三角形,所以AB=AC=BC =4,取BC 中点为O ,则224223AO -= 所以圆锥的体积21832333V ππ=⨯⨯⨯=. 故选:C7.(2021·全国高一课时练习)若一个球的直径为2,则此球的表面积为( )A .2πB .16πC .8πD .4π 【答案】D【解析】得出球的半径,直接由球的表面积公式即可得结果.【详解】因为球的直径为2,即球的半径为1,所以球的表面积为2414ππ⨯=,故选:D.8.(2020·长春市第二十九中学高二月考(理))圆锥的表面积为12π,母线长为4,则该圆锥的底面半径为( )A .2B .3C .1D 3 【答案】A【解析】设圆锥的底面半径为r ,根据圆锥的表面积为12π,母线长为4,由212S r rl πππ=+=求解.【详解】设圆锥的底面半径为r ,因为圆锥的表面积为12π,母线长为4,所以212S r rl πππ=+=,即 24120r r +-=,解得 2r或 6r =-(舍去)故选:A9.(2020·四川成都市·高三其他模拟(理))一个多面体的三视图如图所示,其正视图、侧视图都是全等的等腰直角三角形,俯视图为边长为2的正方形,则其体积为( )A .83B .43C .8D .4【答案】A【解析】 由三视图知:该几何体是一条侧棱垂直与底面,底面是边长为2的正方形,高为2的倒立的四棱锥,然后利用锥体体积公式求解.【详解】 如图所示:由三视图知:该几何体是一个倒立的四棱锥S ABCD -,其中SA ⊥底面ABCD ,底面为正方形, 所以四棱锥S ABCD -的底面积为4,高为2,所以四棱锥S ABCD -的体积为: 184233V =⨯⨯=,故选:A10.(2020·陕西高三月考(文))一个长方体的长,宽、高分别为5,3则该长方体的外接球的表面积为( )A .36πB .40πC .45πD .70π 【答案】B【解析】根据长方体的外接球半径为长方体的体对角线的一半,再结合球的表面积公式,求出结果.【详解】该长方体的外接球的半径R 为体对角线的一半,则R === 则该长方体的外接球的表面积为:2440R ππ=.故选:B. 第Ⅱ卷(非选择题)二.填空题(共7小题,单空每小题4分,两空每小题6分,共36分)11.(2021·全国高一课时练习)已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为8π,则圆柱的高为________.【答案】4【解析】根据圆柱侧面积公式直径求解.【详解】设圆柱的高为h ,有28h ππ=,得4h =.故答案为:4.12.(2021·重庆北碚区·西南大学附中高二期末)一圆锥高为2,底面半径为1,则它的侧面积为___________.【解析】首先计算母线长,再根据侧面积公式计算结果.【详解】由条件可知圆锥的高2h =,和底面圆的半径1r =,则母线长l =,则圆锥的侧面积S rl π==.故答案为:5π13.(2021·陕西咸阳市·高一期末)张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为610的正方体,利用张衡的结论可得该正方体的内切球的体积为______.【答案】3600【解析】 设正方体的棱长为a ,内切球的半径为r ,由a =2r ,求得半径,再代入球的体积公式求解. 【详解】设正方体的棱长为a ,内切球的半径为r , 则a =2r ,因为a =10所以310r =10π=所以球的体积为(334410310360033V r π===,故答案为:360014.(2021·浙江高二开学考试)将半径为4的半圆卷成一个圆锥,则圆锥底面半径为________,圆锥的体积为________.【答案】2,83π 【解析】根据侧面展开图列方程计算圆锥的底面半径,根据勾股定理计算圆锥的高,代入体积公式计算即可.【详解】显然圆锥的母线长为 4,l = 设圆锥的底面半径为r ,则24,r ππ= 即2r, 所以圆锥的高2223,h l r =-=圆锥的体积 2118342333V r h πππ=⋅⋅=⨯⨯=故答案为:215.(2020·台州市洪家中学高二月考)正方体1111ABCD A B C D -的棱长为1,则其表面积为___________;其内切球的体积为___________.【答案】66π 【解析】正方体的表面积为6个面的面积和;球内切与正方体,则球的直径与正方体的棱长相等,即可得到球的半径,利用公式求体积即可.【详解】易得:616S =⨯=,因为球内切于棱长为1的正方体,所以球的直径等于正方体的棱长, 所以球的半径为12, 所以该球的体积为341()326ππ⨯=, 故答案为:6;6π. 16.(2020·全国高一课时练习)(1)已知一圆台上底面的半径为2,下底面的半径为3,截得此圆台的圆锥的高为6,则此圆台的体积为________.(2)圆台的上、下底面半径分别为10cm ,20cm ,它的侧面展开图扇环的圆心角为180°,则圆台的表面积为______2cm .(结果中保留π) 【答案】383π 1100π 【解析】(1)先利用圆台的轴截面求出圆台的高,再利用圆台的体积公式求解即可;(2)根据条件先求出侧面展开的扇环的半径,再根据圆台表面积公式求解即可.【详解】解析:(1)作出圆台的轴截面,如图,设圆台的高为h ,则2636h -=,所以2h =, 所以圆台的体积为()221382233233V π=+⨯+⨯=π. (2)如图所示,设圆台的上底面周长为lcm ,因为扇环的圆心角是180°,故210l SA ππ=⋅=⨯,所以20SA cm =.同理可得40SB cm =,所以20AB SB SA cm =-=,所以表面积()222(1020)2010201100mS c ππππ=+⨯+⨯+⨯=. 故圆台的表面积为21100cm π.答案:(1)383π(2)1100π. 17.(2011·全国高三专题练习)某地球仪上北纬030纬线的长度为12()cm π,该地球仪的半径是__________cm ,表面积是______________cm 2. 【答案】3 192π.【解析】先利用圆周长公式,求出小圆的半径,根据球的截面性质,可求出球的半径,进而求出球的表面积.【详解】设北纬030所在圆面的关系为r ,由题可得:212r ππ=解得6r =,设地球仪的半径为0643cos30R ==地球仪表面积为24192R ππ=.三.解答题(共5小题,满分64分,18--20每小题12分,21,22每小题14分)18.(2021·海原县第一中学高一期末)如图是边长为1的正方体,H 、G 、F 分别是棱AB 、AD 、1AA 的中点,现在沿三角形GFH 所在平面锯掉正方体的一个角,问锯掉的这块的体积是原正方体的几分之几?【答案】148. 【解析】 根据三棱锥和柱体的体积公式,即可求解.【详解】由题意,边长为1的正方体,H 、G 、F 分别是棱AB 、AD 、1AA 的中点, 锯掉的三棱锥的体积11111113222248V =⨯⨯⨯⨯=. 正方体的体积1111V =⨯⨯=. 锯掉的这块的体积是原正方体的148. 故答案为:148. 19.(2021·安徽池州市·高二期末(文))已知圆台上、下底面的底面积分别为16π,81π,且母线长为13. (1)求圆台的高;(2)求圆台的侧面积.【答案】(1)12;(2)169π.【解析】(1)依题意利用勾股定理计算可得;(2)利用圆台的侧面积公式()12S r r l π=+计算可得;【详解】解:(1)依题意,圆台的上底面半径14r =,下底面半径29r =,故圆台的高()22139412h =--=;(2)圆台的侧面积413913169S πππ=⨯⨯+⨯⨯=.20.(2020·福建三明市·高二期中)如图,某几何体的下部分是长、宽均为8,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:(1)该几何体的体积;(2)该几何体的表面积.【答案】(1)256;(2)240.【解析】(1)按照公式求出长方体和四棱锥的体积,求和即可;(2)先找到四棱锥侧面的高,然后可求出四棱锥的侧面积,继而求长方体的表面积,求和即可.【详解】连接11A C ,11B D 交于点O ,取11B C 的中点E ,连接PO ,OE ,PE(1)883192V =⨯⨯=长方体11111883643P A B C D V -=⨯⨯⨯= ∴19264256V =+=总(2)∵3PO =,4OE =∴225PE PO OE =+=1485802S =⨯⨯⨯=四棱椎侧 48388160S =⨯⨯+⨯=长方体80160240S =+=总21.(2020·湖北高二月考)有一堆规格相同的铁制(铁的密度为37.8g /cm )六角螺帽共重6kg ,已知该种规格的螺帽底面是正六边形,边长是12mm ,内孔直径为10mm ,高为10mm ,(1)求一个六角螺帽的体积;(精确到30.001cm )(2)问这堆六角螺帽大约有多少个?(参考数据:3 1.73,2.9527.823,1.0837.88.45π==⨯≈⨯≈)【答案】(1)()32.952cm;(2)261个. 【解析】(1)利用六棱柱的体积减去圆柱的体积即得解;(2)计算61000(7.8 2.952)⨯÷⨯即得解.【详解】 (1)由题得22310(12)610 3.141042V ⎛⎫=⨯⨯-⨯⨯ ⎪⎝⎭ 3736.8785=-()()332951.82952mm 2.952cm =≈=(2)这堆螺帽的个数为:61000(7.8 2.952)261⨯÷⨯≈(个)答:每个螺帽的体积为32.952cm ,共有261个螺帽.22.(2020·全国高三专题练习)已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,求该四棱台的表面积.【答案】804815+【解析】首先求出四棱台上、下底面面积与侧面面积,然后求出表面积即可.【详解】如图,在四棱台1111ABCD A B C D -中,过1B 作1B F BC ⊥,垂足为F ,在1Rt B FB 中,1(84)22BF =⨯-=,18B B =, 故22182215B F =-= 所以111(84)21512152BB C C S =⨯+⨯=梯形 故四棱台的侧面积412154815S =⨯=侧, 所以四棱台的表面积48154488804815S =⨯+⨯=+表。
高中数学必修二 8 简单几何体的表面积与体积(精练)(含答案)

8.3 简单几何体的表面积与体积(精练)【题组一 旋转体的体积】1.(2021·吉林·延边二中高一期中)阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径.若该球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π【答案】C 【解析】因为该球的体积为36π,设球的半径为R ,则34363R ππ=,解得3R =。
所以圆柱的体积为:23654V ππ=⨯⨯=,故选:C.2.(2021·河北·保定市第二十八中学高一月考)唐朝的狩猎景象浮雕银杯如图1所示,其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度)如图2所示,设酒杯上部分(圆柱)的体积为1V ,下部分(半球)的体积为2V ,若122V V =,则半球的半径与圆柱的高之比为( )A .4:3B .3:4C .1:2D .5:3【答案】B 【解析】设圆柱的高为h ,半径为r ,则圆柱的体积为21=V r h π.而半球的体积为332412==323V r r ππ⨯. 因为122V V =,所以324=3r r h ππ,所以3=4r h . 故选:B3(2021·全国·高一课时练习)如图所示,半径为R 的半圆内(其中∠BAC =30°)的阴影部分以直径AB 所在直线为轴,旋转一周得到一个几何体,则该几何体的表面积为_____,体积为_____.2R 356R π 【解析】如图所示,过C 作CO 1⊥AB 于O 1,在半圆中可得∠BCA =90°,又∠BAC =30°,AB =2R ,∴AC ,BC =R ,CO 1,∴1AO S 圆锥侧=π=32πR 2,1BO S 圆锥侧=π×R R 2,∴S 几何体表=S 球+11AO BO S S +=圆锥侧圆锥侧R 2,πR 2. 又V 球=43πR 3,∴V 几何体=V 球-(11AO BO V V +圆锥圆锥)=43πR 3-13×AB ×π×C 2143O =πR 3-22536R π⎫⨯=⎪⎪⎝⎭πR 3.2R ;356R π4.(2021·全国·高一课时练习)若圆锥的侧面展开图为一个半径为2的半圆,则圆锥的体积是__________.【解析】设圆锥的底面半径为r ,则22ππ=r ,所以1r =,圆锥的高h = 所以圆锥的体积213V r h π=5.(2021·全国·高一课时练习)若一个圆锥的底面直径和高都与一个球的直径相等,那么这个圆锥的体积与球的体积之比为________. 【答案】12【解析】解析:设球体的半径为R 2312=2=33R V R R ππ⋅圆锥,343V R π球=,33213==423R V R V ππ圆锥球. 故答案为:12【题组二 旋转体的表面积】 1.(2021·全国·高一课时练习)如图,在四边形ABCD 中,∠DAB=90°,∠ADC=135°,AB=5,CD=AD=2,则四边形ABCD 绕AD 所在直线旋转一周所成几何体的表面积为( )A .(60+πB .(60+)π C .(56+πD .(56+)π【答案】A 【解析】四边形ABCD 绕AD 所在直线旋转一周所成的几何体为一个圆台挖去一个圆锥,如图所示:因为25r AB ==,所以圆台下底面面积125S π=,又因为CD =,135ACD ∠=,所以12ED r ==,25l ==,所以圆台的侧面积()()212225535S r r l πππ=+=+⨯=.圆锥的侧面积3111122222S r l ππ=⨯⨯=⨯⨯⨯.所以几何体的表面积为(123253560S S S S πππ=++=++=+.故选:A2.(2021·山东邹城·高一期中)如图是底面半径为3的圆锥,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点S 滚动,当这个圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( )A .圆锥的母线长为18B .圆锥的表面积为27πC .圆锥的侧面展开图扇形圆心角为60°D .圆锥的体积为【答案】D【解析】设圆锥的母线长为l ,以S 为圆心,SA 为半径的圆的面积为2S l π=,又圆锥的侧面积3S rl l ππ==圆锥侧,因为圆锥在平面内转到原位置时,圆锥本身滚动了3周,所以233l l ππ=⨯,解得9l =,所以圆锥的母线长为9,故选项A 错误;圆锥的表面积239336S S S πππ=+=⨯⨯+⨯=圆锥侧底,故选项B 错误;因为圆锥的底面周长为236ππ⨯=,设圆锥的侧面展开图扇形圆心角为α,则69πα=⋅,解得23πα=, 所以圆锥的侧面展开图扇形圆心角为120°,故选项C 错误;圆锥的高h =所以圆锥的体积为2133V π=⨯⨯⨯=,故选项D 正确. 故选:D .3.(2021·重庆·垫江第五中学校高一月考)如图,圆锥的母线长为4,点M 为母线AB 的中点,从点M 处拉一条绳子,绕圆锥的侧面转一周达到B 点,这条绳子的长度最短值为则此圆锥的表面积为__________【答案】5π【解析】将圆锥侧面沿母线AB 剪开,其侧面展开图为扇形,如图,从点M 处拉一条绳子,绕圆锥的侧面转一周达到B 点,最短距离即为线段BM 长,则有BM = 而M 是线段AB '中点,又母线长为4,于是得22220AM AB BM +==,即2BAB π'∠=,设圆锥底面圆半径为r ,从而有:242r ππ=⋅,解得1r =,所以圆锥的表面积为25S r r AB πππ=+⋅=.故答案为:5π4(2021·全国·高一课时练习)已知一块正方形薄铁片的边长为8cm ,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),若用这块扇形铁片围成一个无底的圆锥,则这个无底的圆锥的表面积为多少平方厘米?【答案】()216cm π 【解析】由已知,可得这个无底的圆锥的母线长为8cm ,设圆锥的底面半径为cm r ,则282r ππ=⨯,所以2cm r =,所以圆锥的表面积即侧面积()22816cm S rl πππ==⨯=侧. 【题组三 多面体的体积】1.(2021·上海外国语大学闵行外国语中学高二期中)在三棱锥P ABC -中,已知5PA BC PB AC PC AB ======,则该三棱锥的体积为___________.【答案】8【解析】如图,设长方体的三条棱长为,,a b c ,由题得22220a b +==;2213a c +=;222525b c +==, 解之得2224,16,9a b c ===.所以2,4,3a b c ===. 所以该三棱锥的体积为112344243=832⨯⨯-⨯⨯⨯⨯⨯.故答案为:82(2021·全国·高一课时练习)已知一个空间几何体的所有棱长均为1 cm ,其表面展开图如图所示,则该空间几何体的体积V =________cm 3.【答案】【解析】依题意,原几何体是由一个正方体上面接一个正四棱锥组成,其中正方体的棱长为1cm ,正方体的体积为1cm 3,正四棱锥的底面边长和侧棱长均为1cm ,体积为2113⨯=3),所以该空间几何体的体积为(1V =cm 3.故答案为:3.(2021·全国·高一课时练习)球O 的球心为点O ,球O 3的圆锥,三棱锥V ABC -内接于球O ,已知,OA OB AC BC ⊥⊥,则三棱锥V ABC -的体积的最大值为_______.【解析】=O 的半径为r=,解得1r =, ,1OA OB OA OB ⊥==,AB ∴=AC BC ⊥,∴C 在以AB 为直径的圆上,∴平面OAB ⊥平面ABC ,∴O 到平面ABC 2,故V 到平面ABC 1+,又C 到AB∴三棱锥V ABC -的体积的最大值为,111)32⨯4.(2021·全国·高一课时练习)如图所示,△ABC 和△A ′B ′C ′的对应顶点的连线AA ′,BB ′,CC ′交于同一点O ,且12AO BO CO A O B O C O =''==',则O ABC O A B C V V --'''=___________. 【答案】18【解析】如题干图,12AO BO CO A O B O C O =''==', 可证AB //A ′B ′,AC //A ′C ′,BC //B ′C ′.所以平面//ABC 平面A B C '''三棱锥O ABC -和三棱锥O A B C '''-高之比也为12,由等角定理得∠CAB =∠C ′A ′B ′,∠ACB =∠A ′C ′B ′,所以△ABC ∽△A ′B ′C ′, 由12AO BO CO A O B O C O =''==', 可得211()24ABC A B C S S '''==, 所以O ABC O A B C V V --'''==111428⨯=. 故答案为:185.(2021·山东·日照神州天立高级中学有限责任公司高一月考)如图是边长为1的正方体,H 、G 、F 分别是棱AB 、AD 、1AA 的中点,现在沿三角形GFH 所在平面锯掉正方体的一个角,问锯掉的这块的体积是原正方体的______.【答案】148【解析】1111113222248A FGH V -=⨯⨯⨯⨯=,所以148A FGH V V -=正方体, 故答案为:148. 6.(2021·黑龙江·哈师大附中高一期中)如图,在四面体ABCD 中作截面PQR ,其中14AR AD =,13AP AC =,12AQ AB =,则:A PQR D BCPQ V V --=______.【答案】1:20【解析】作RG ⊥平面ABC ,作DH ⊥平面ABC ,则GH 共线,由14AR AD =,则14RG DH =, 由12AQ AB =,13AP AC =,则16APQ ABC S S =, 所以15APQBCPQ S S =, 所以11113:154203APQ R APQA PQR D BCPQ D BCPQ BCPQ S RG V V V V S DH ----⋅===⨯=⋅,故答案为:1:20【题组四 多面体的表面积】1.(2021·上海市控江中学高二期中)若正四棱台的上底边长为2,下底边长为8,高为4,则它的侧面积为___________.【答案】100【解析】因正四棱台的上底边长为2,下底边长为8,高为4,则该正四棱台上底、下底面边心距分别为1,4,而正四棱台的高、斜高、两底面对应边心距构成直角梯形,于是得斜高5h '=, 因此,侧面积28451002S +=⨯⨯=, 所以所求的侧面积为100.故答案为:1002(2021·上海外国语大学闵行外国语中学高二期中)已知正三棱锥O ABC -的底面边长为4,高为2,则此三棱锥的侧面积为___________.【答案】【解析】由题意作出图形如图:因为三棱锥P ABC -是正三棱锥,顶点在底面上的射影D 是底面的中心,在三角PDF 中, 2PD =,DF =,PF ∴==则这个棱锥的侧面积为1342⨯⨯=故答案为:3.(2021·全国·高一课时练习)已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________.【答案】80+【解析】如图,在四棱台1111ABCD A B C D -中,过点1B 作1B F BC ⊥,垂足为点F ,在1Rt B FB 中1(84)22BF =⨯-=,18B B =,故1B F =所以111(84)2BB C C S =⨯+⨯=梯形故四棱台的侧面积4S =⨯=侧,所以448880S =⨯+⨯=+表故答案为:80+4.(2021·全国·高一课时练习)已知正四棱台两底面边长分别为4cm,8cm ,侧棱长为8cm ,则它的侧面积为_______2cm .【答案】【解析】作出正四棱台的一个侧面如图,设,E F 分别为,AD BC 的中点,过D 作DG BC ⊥于点G .由题知4cm,8cm,8cm AD BC CD ===,得2cm,4cm DE FC ==,解得2cm GC =,在Rt DGC △中,DG =,即斜高为,所以所求侧面积为)21(1632)cm 2⨯+⨯=.答案:5.(2021·全国·高一课时练习)若五棱台11111ABCDE A B C D E -的表面积是30,侧面积是25,则两底面面积的和为______.【答案】5【解析】S S S =+表侧两底,则30255S S S =-=-=两底表侧.故答案为:5.6(2021·全国·高一课时练习)如图,已知正三棱锥S ABC -的侧面积是底面积的2倍,正三棱锥的高3SO =,则此正三棱锥的表面积为___________.【答案】【解析】如图,设正三棱锥的底面边长为a ,斜高为h ',侧面积、底面积分别为12,S S ,过点O 作OE AB ⊥,与AB 交于点E ,连接SE ,则,SE AB SE h '⊥=.由21 2S S =,即21322a h '⋅⋅=⨯,可得a '.由SO OE ⊥,则222SO OE SE +=,即2223h ⎫''+=⎪⎪⎝⎭.h '∴=6a =.222 6S ∴=== 1 S =∴表面积 1 2 S S S =+==故答案为:【题组五 有关球的计算】1.(2021·新疆·新和县实验中学高一期末)若三个球的表面积之比是1:2:3,则它们的体积之比是( )A .1:B .1:C .2:4:9D .【答案】A【解析】设三个球的半径分别为1R ,2R ,3R ,因为三个球的表面积之比为1:2:3,所以2221234π:4π:4π1:2:3R R R =,所以123::R R R =所以它们的体积之比为3333331231234π4π4π::::1:333R R R R R R == 故选:A.2.(2021·山东邹城·高一期中)已知长方体1111ABCD A B C D -的长、宽、高分别为2、1、1,且其顶点都在球面上,则该球的体积是( )AB .6πC .36πD .【答案】A【解析】长方体1111ABCD A B C D -=长方体1111ABCD A B C D -343π⨯=⎝⎭. 故选:A .3.(2021·全国·高一课时练习)两个半径为1的实心铁球,熔化成一个大球,这个大球的半径是________.【解析】设大球的半径为R ,则有3334421,233R R ππ=⨯⨯=,所以R =4.(2021·全国·高一课时练习)一个底面直径是32cm 的圆柱形水桶装入一些水,将一个球放入桶内完全淹没,水面上升了9cm 且无溢出,则这个球的表面积是________.【答案】2576cm π【解析】由题意,上升的水的体积即为球的体积,若球的半径为R ,即23324923R ππ⎛⎫⨯= ⎪⎝⎭,解得12R =, 故这个球的表面积224412576S R πππ=⨯=⨯=.故答案为:2576cm π5.(2021·全国·高一课时练习)如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为3,则该半球的表面积为________.【答案】6π【解析】如图,连接AC ,BD 交点为O ,设球的半径为r ,由题意知:SO AO OC OD OB r =====.则AB =,四棱锥的体积为21)3V r =⨯⨯=r = ∴该半球的表面积为22214362S r r r ππππ=⨯+==.故答案为:6π6.(2021·全国·高一课时练习)在四棱锥S ABCD -中,底面ABCD 是边长为为【答案】48π【解析】因为四棱锥S ABCD -中,底面ABCD 是边长为 所以该四棱锥是正四棱锥,取正方形ABCD 的中心1O ,连接1SO ,AC ,则点1O 为AC 的中点,如图,则球心O 在1SO 上,因为正方形ABCD 边长为6AC ==,所以13AO =,因为SA =,所以1SO ==设四棱锥S ABCD -外接球的半径为r ,则11OO SO SO r =-,在1Rt AOO 中,22211AO AO OO =+,即)2223r r =+,解得:r =所以该四棱锥外接球的表面积为(224π4π48πr =⨯=.【题组六 综合运用】1(2021·全国·高一课时练习)如图,已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个高为x 的圆柱.(1)求出此圆锥的侧面积;(2)用x 表示此圆柱的侧面积表达式;(3)当此圆柱的侧面积最大时,求此圆柱的体积.【答案】(1);(2)224(02)S x x x ππ=-+<<圆柱侧;(3)π.【解析】(1)圆锥的底面半径R 与高H 均为2,则圆锥的母线长为L =2S RL ππ==⨯⨯=圆锥侧.(2)设圆柱的半径为r , 则222r x -=,解得2r x =-,且02x <<; 所以圆柱的侧面积为222(2)24(02)S rx x x x x x ππππ==-=-+<<圆柱侧.(3)22242(1)1S x x x πππ⎡⎤=-+=--+⎣⎦圆柱侧,02x <<;当1x =时,S 圆柱侧取得最大值为2π,此时1r =,圆柱的体积为2211V r x πππ==⋅⋅=圆柱.2.(2021·贵州·高一月考)在长方体1111ABCD A B C D -中,AB =6,BC =8,16AA =.(1)求三棱锥1D ABC -的体积;(2)在三棱柱111ABC A B C -内放一个体积为V 的球,求V 的最大值.【答案】(1)48;(2)323π. 【解析】(1)由长方体的几何特征知,1D 到平面ABC 的距离为116DD AA ==, 又1242ABC S AB BC =⋅=,所以11112464833D ABC ABC V S DD -=⋅=⨯⨯=; (2)设球的半径为R ,若该球与三棱柱111ABC A B C -的三个侧面均相切,则R 为ABC 的内切圆的半径,则()1242R AB AC BC ++=, 又=6+10+8=24AB AC BC ++,此时2R =;若该球与三棱柱111ABC A B C -的上下底面均相切,此时126R AA ==,3R =;所以在三棱柱111ABC A B C -内放一个体积为V 的球,该球半径最大为2,3max 4=2=3323V ππ⨯.3.(2021·浙江路桥·高一月考)如图所示,在平面五边形ABCDE 中,2AB AE CD ===,1BC =,DE =90ABC ∠=︒,90AED ∠=︒,分别沿AC ,AD 将ABC 与ADE 折起使得B ,E 重合于点P .试求:(1)三棱锥A PCD -的体积;(2)三棱锥A PCD -的外接球的表面积.【答案】(2)8π.【解析】(1)PD =1PC =,2CD =,则222 PC PD CD PC PD +=⇒⊥,又AP PD ⊥,AP PC ⊥,PC PD D ⋂=,AP ⊥平面PCD .所以111111233232A PCD PCD V S AP PC PD PA -=⋅=⨯⋅⋅⋅=⨯⨯=△ (2)将三棱锥补成长方体知三棱锥A PCD -的外接球的直径即为长方体的体对角线长,即2R R ==,所以球的表面积为24π8πR =. 4.(2021·河北定州·高一期中)定州市某广场设置了一些多面体形或球形的石凳供市民休息.如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是3160000cm 3(1)求正方体石块的棱长;(2)为争创全国文明城市,现将表面脏污,棱角轻微磨损的多面形石凳(图(1))打磨成一个球形的石凳,并用一种环保底漆全面粉刷.已知这种底漆一瓶的净含量为235克,可粉刷21.5m 左右,求此球形石凳最大时,一瓶环保底漆大约可以粉刷几个球形石凳?(精确到1)(π按3.14算)【答案】(1)40cm ;(2)3个.【解析】(1)设正方体石块的棱长为a , 则每个截去的四面体的体积为3113222248a a a a ⨯⨯⨯⨯=. 由题意可得331600008483a a ⨯+=, 解得40a =.故正方体石块的棱长为40cm ;(2)当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大.此时正方体的棱长正好是球的直径,∴球形石凳的表面积224041600cm 2S ππ⎛⎫=⨯= ⎪⎝⎭. 41.51031600π⨯≈, 所以一瓶环保底漆大约可以粉刷3个球形石凳.5.(2021·湖北孝感·高一期中)如下图1,一个正三棱柱形容器中盛有水,底面三角形ABC 的边长为2cm ,侧棱14cm AA =,若侧面11AA B B 水平放置时(如下图2),水面恰好过AC ,BC ,11A C ,11B C 的中点.(1)求容器中水的体积;(2)当容器底面ABC 水平放置时(如图1),求容器内水面的高度.【答案】(1))3cm ;(2)3cm .【解析】(1)在图2中,水所占部分为四棱柱.四棱柱底面积为)222112sin 601sin 6022S cm =⨯⨯︒-⨯⨯︒=,又高为4cm所以水的体积为)34V cm ==,(2)设图1中水高度为cm h ,则212sin 602V h =⨯⨯︒⨯=3h =. 所以当容器底面ABC 水平放置时,容器内水面的高度为3cm .6.(2021·福建宁德·高一期中)如图所示是在圆锥内部挖去一正四棱柱所形成的几何体,该正四棱柱上底面的四顶点在圆锥侧面上,下底面落在圆锥底面内,已知圆锥侧面积为15π,底面半径为3r =.(Ⅰ)若正四棱柱的底面边长为a =(Ⅱ)求该几何体内正四棱柱侧面积的最大值.【答案】(Ⅰ)16123π-;(Ⅱ)【解析】设圆锥母线长为l ,高为h ,正四棱柱的高为1h(Ⅰ)由S rl π=圆锥侧,有315l ππ=,故5l =,由222h r l +=,故4h =,所以圆锥体积为2211341233V r h πππ==⨯⨯=圆锥由a =2, 由图可得11h r h r -=,所以11318433r h h r --==⨯=, 故正四棱柱的体积为21816233V a h ==⨯=正四棱柱 所以该几何体的体积为16123V V π-=-圆锥正四棱柱 (Ⅱ)由图可得12r h h r =,即13243h =,即1312h +=由13h +≥,当且仅当136h ==时左式等号成立,有112h a ⇒≤12h =,a =故正四棱柱侧面积14S h a =≤侧12h =,a =所以该几何体内正四棱柱侧面积的最大值为7.(2021·福建福州·高一期中)如图所示的圆锥,顶点为O ,底面半径是5cm ,用一与底面平行的平面截得一圆台,圆台的上底半径为2.5cm ,这个平面与母线OA 交于点B ,线段AB 的长为10cm .(提示:本题的数据有长度单位)(1)求圆台的体积和圆台的侧面积;(2)把一根绳从线段AB 的中点M 开始到点A ,沿着侧面卷绕.使它成为最短时候,求这根绳的长度;【答案】cm 3,75πcm 2;(2)25cm. 【解析】(1)作出圆锥的轴截面和沿OA 剪开的侧面展开图,如下图由下底面半径是5cm ,上底半径为2.5cm ,AB 的长为10 cm ,可得:10OB =cm ,因此圆台的体积为:223115 2.5(33cm )V ππ=⨯⨯⨯=, 侧面积为:2520 2.510)75cm (S πππ=⨯⨯-⨯⨯=.(2)由圆锥的底面周长可得侧面展开图的弧长为10π, 所以,侧面展开图的圆心角为2π,在直角三角形MOA '中15OM =,可得25(cm)MA '=,所以最短时候,绳长为25cm。
高中数学必修二 8 3 简单几何体的表面积与体积(精练)(含答案)

8.3 简单几何体的表面积与体积(精练)【题组一 多面体表面积】1.(2020·全国高一课时练习)长方体的高为2,底面积等于12,过不相邻两侧棱的截面(对角面)的面积为10,则此长方体的侧面积为( )A .12B .24C .28D .32 【答案】C【解析】设长方体底面矩形的长与宽分别为,a b ,则12ab =.210=,解得4,3a b ==或3,4a b ==.故长方体的侧面积为()243228⨯+⨯=.故选:C.2.(2021·江苏南通市)一个正四棱锥的底面边长为2A .8B .12C .16D .20 【答案】B, 所以该四棱锥的全面积为212+422=122⋅⋅⋅. 故选B3.(2020·全国高一课时练习)若正三棱台上、下底面边长分别是a 和2a ,棱台的高为6a ,则此正三棱台的侧面积为( )A .2aB .212aC .292aD .232a 【答案】C 【解析】如图,1,O O 分别为上、下底面的中心,1,D D 分别是AC ,11A C 的中点,过1D 作1D E OD ⊥于点E .在直角梯形11ODD O 中,12323OD a a =⨯⨯=,111326O D a a =⨯⨯=,116DE OD O D a ∴=-=.在1Rt DED 中,16D E a =,则1D D =a ==. 2193(2)22S a a a a ∴=⨯+=侧.故选:C4.(2020·河北沧州市一中高一月考)正四棱锥底面正方形的边长为4,高与斜高的夹角为30,则该四棱锥的侧面积( )A .32B .48C .64D .323【答案】A【解析】如图:正四棱锥的高PO ,斜高PE ,底面边心距OE 组成直角△POE .∵OE =2cm ,∠OPE =30°,∴斜高h ′=PE =4sin 30o OE =,∴S 正棱锥侧=114443222ch =⨯⨯⨯=' 故选:A5.(2020·全国高一课时练习)已知正四棱锥的底面边长是2,则该正四棱锥的表面积为( )A B .12 C .8 D .【答案】B【解析】如图所示,在正四棱锥S ABCD -中,取BC 中点E ,连接SE ,则SBE △为直角三角形,所以2SE ==, 所以表面积1422422122SBC ABCD S S S =+⨯=⨯+⨯⨯⨯=正方形△.故选:B.6.(2021·内蒙古包头市·高三期末(文))已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)81 【答案】D【解析】正四棱锥如图,设四棱锥的高OE h =,由底面边长为4,可知2OF =,斜高EF故2142h =⨯2=2h +故侧面积为(214448812h ⨯⨯==+=+, 故选:D. 7.(2020·山西吕梁市)已知,AB CD 是某一棱长为2的正方体展开图中的两条线段,则原正方体中几何体ABCD 的表面积为( )A .2+B .2+C .2+D .2+【答案】A 【解析】由所给正方体的展开图得到直观图,如图:则此三棱锥的表面积为:△△△△+++=BCD ABC ADC ABD S S S S1111222222222⨯⨯+⨯⨯⨯⨯⨯=+故选:A8.(2020·黑龙江哈师大青冈实验中学)长方体一个顶点上的三条棱长分别为3,4,a ,表面积为108,则a 等于( )A .2B .3C .5D .6 【答案】D【解析】长方体一个顶点上的三条棱长分别为3,4,a ,则长方体的表面积为342+2423108a a ⨯⨯⨯+⨯=,解得a =6,故选:D9.(2020·湖北省汉川市第一高级中学高一期末)一个正四棱柱的各个顶点都在一个半径为2cm 的球面上,如果正四棱柱的底面边长为2cm ,那么该棱柱的表面积为( )A .2(2+B .2(4+C .2(8+D .2(16+ 【答案】C【解析】∵一个正四棱柱的各个顶点都在一个半径为2cm 的球面上,正四棱柱的底面边长为2cm , ∴球的直径为正四棱柱的体对角线∴正四棱柱的体对角线为4,正四棱柱的底面对角线长为= ∴该棱柱的表面积为2×22+4×2×+(2cm ),故选:C【题组二 多面体台体积】1.(2021·扶风县法门高中)正方体的全面积为18cm 2,则它的体积是_________ 3cm【答案】【解析】设该正方体的棱长为a cm ,由题意可得,2618a =,解得a =所以该正方体的体积为3V a ==3cm .故答案为:2.(2021·湖南长沙市)如图,在长方体1AC 中,棱锥1A ABCD -的体积与长方体的体积之比为( )A .2∶3B .1∶3C .1∶4D .3∶4【答案】B 【解析】设长方体过同一顶点的棱长分别为,,a b c则长方体的体积为1V abc =,四棱锥1A ABCD -的体轵为213V abc =, 所以棱锥1A ABCD -的体积与长方体1AC 的体积的比值为13. 故选:B.3.(2020·浙江高一期末)由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21 米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .324276mD .312138m【答案】A 【解析】如图正四棱锥P ABCD -中,34AB BC ==,21PO =,所以正四棱锥P ABCD -的体积为311343421809233ABCD S PO m ⨯⨯=⨯⨯⨯=, 故选:A4.(2020·辽宁沈阳市·沈阳二中高一期末)《九章算术》问题十:今有方亭,下方五丈,上方四丈.高五丈.问积几何(今译:已知正四棱台体建筑物(方亭)如图,下底边长5a =丈,上底边长4b =丈.高5h =丈.问它的体积是多少立方丈?( )A .75B .3053C .3203D .4003 【答案】B【解析】(()2211+=33V S S h a b h '=+⋅ ()2211305545615333=⨯=⨯⨯=. 故选:B 5.(2021·浙江高一期末)出华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧楼长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .32427mD .312138m【答案】A【解析】如图正四棱锥P ABCD -中,PO ⊥底面ABCD ,21PO =,34AB =,底面正方形的面积为234341156S m =⨯=,则正四棱锥P ABCD -的体积为311115621809233S PO m ⨯⨯=⨯⨯=, 故选:A6.(2020·济南市·山东师范大学附中高一月考)如图,在棱长为2的正方体1111ABCD A B C D -中,截去三棱锥1A ABD -,求(1)截去的三棱锥1A ABD -的表面积;(2)剩余的几何体1111A B C D DBC -的体积.【答案】(1)6+;(2)203【解析】(1)由正方体的特点可知三棱锥1A ABD -中,1A BD 是边长为1A AD 、1A AB 、ABD △都是直角边为2的等腰直角三角形,所以截去的三棱锥1A ABD -的表面积(111231322642A BD A AD A AB ABD S S S S S =+++=⨯+⨯⨯⨯=+(2)正方体的体积为328=,三棱锥1A ABD -的体积为111142223323ABD SAA ⨯⨯=⨯⨯⨯⨯=, 所以剩余的几何体1111A B C D DBC -的体积为420833-=. 【题组三 旋转体的表面积】1.(2021·浙江丽水市)经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的侧面积是( )A .B .4πC .D .2π 【答案】C【解析】设圆锥的底面半径为r ,母线长为l ,则l =,由题可知)2122⨯=,∴2r l ==,侧面积为rl π=,故选:C.2.(2020·全国高一课时练习)某圆台的上、下底半径和高的比为1:4:4,母线长为10,则该圆台的表面积为( )A .81πB .100πC .168πD .169π 【答案】C【解析】该圆台的轴截面如图所示.设圆台的上底面半径为r ,则下底面半径4r r '=,高4h r =则它的母线长510l r ====∴2r,8r '=. ∴()(82)10100S r r l πππ'=+=+⨯=侧,22100464168S S r r ππππππ'=++=++=表侧.故选:C3.(2020·全国高一课时练习)用一个平行于圆锥底面的平面截这个圆锥,截得圆台上下底面半径的比是1:4,且该圆台的母线长为9,则截去的圆锥的母线长为( )A .94B .3C .12D .36【答案】B【解析】根据题意,设圆台的上、下底面的半径分别为r 、R ,设圆锥的母线长为L ,截得小圆锥的母线长为l ,∵圆台的上、下底面互相平行 ∴14l r L R ==,可得L=4l ∵圆台的母线长9,可得L ﹣l =9 ∴3L 4=9,解得L=12, ∴截去的圆锥的母线长为12-9=3故选B4.(2020·全国高一课时练习)圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )A .3B .5C .6D .7 【答案】D【解析】设圆台较小底面圆的半径为r ,由已知有另一底面圆的半径为3r ,而圆台的侧面积公式为(3)4384,7r r l r r πππ+=⨯⨯==,选D.5.(2020·江苏淮安市·淮阴中学高一期末)圆柱底面半径为1,母线长为2,则圆柱侧面积为( )A .4πB .3πC .5πD .2π 【答案】A【解析】圆柱底面半径为1,母线长为2,圆柱侧面积为224S rl =π=π⨯1⨯2=π ,故选:A6.(2021·广西河池市·高一期末)已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为8π,则圆柱的高为________.【答案】4【解析】设圆柱的高为h ,有28h ππ=,得4h =.故答案为:4.7.(2021·河南焦作市·高一期末)已知圆锥的底面半径为2,高为4,在圆锥内部有一个圆柱,则圆柱的侧面积的最大值为______.【答案】4π【解析】如图是圆锥与圆柱的轴截面,设内接圆柱的高为a ,圆柱的底面半径为r ()02r <<,则由224r a-=,可得42a r =-,所以圆柱的侧面积()22242484(1)4S r r r r r πππππ=⋅-=-+=--+,所以1r =时,该圆柱的侧面职取最大值4π. 故答案为:4π.8.(2020·北京高一期末)将底面直径为8,高为最大值为______.【答案】【解析】欲使圆柱侧面积最大,需使圆柱内接于圆锥; 设圆柱的高为h ,底面半径为r ,4r =,解得2h r =;所以()2224S rh r r r ππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧;当2r时,S 圆柱侧取得最大值为故答案为:. 【点睛】本题考查了求圆柱侧面积的最值,考查空间想象能力,将问题转化为函数求最值,属于中档题.9.(2021·陕西西安市·西安中学高一期末)若圆锥的侧面展开图是圆心角为90︒的扇形,则该圆锥的侧面积与底面积之比为___________. 【答案】4:1【解析】设圆锥的底面半径为r ,母线长为l , 由题意得:22l r ππ=,即4l r ,所以其侧面积是214S rl r ππ==,底面积是22S r π=,所以该圆锥的侧面积与底面积之比为4:1 故答案为:4:1【题组四 旋转体的体积】1.(2020·山东菏泽市·高一期末)若圆锥的底面半径为3cm ,侧面积为215cm π,则该圆锥的体积为( ) A .4π3cm B .9π3cmC .12π3cmD .36π3cm【答案】C【解析】设圆锥母线长为l ,则侧面积为123152S l r l πππ=⋅==,故5l =.故圆锥的高4h =,圆锥体积为21123V r h ππ==3cm .故选:C.2.(2021·黑龙江双鸭山市·双鸭山一中)现用一半径为10cm ,面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为__________3cm . 【答案】128π【解析】设铁皮扇形的半径和弧长分别为R 、l ,圆锥形容器的高和底面半径分别为h 、r , 则由题意得R=10,由1802Rl π=,得16l π=, 由2lr π=得8r =.由222R r h =+可得6h =.∴()231164612833V r h cm πππ==⋅⋅=∴该容器的容积为3128cm π.故答案为128π.3.(2020·湖南长沙市·高一期末)圆锥的母线与底面所成的角为60︒,侧面积为8π,则其体积为________.【答案】3【解析】如图所示,圆锥的母线与其底面所成角的大小为60︒,60SAO ∴∠=︒,由题意设圆锥的底面半径为r ,则母线长为2l r =,高为h =圆锥的侧面积为8π,2228S rl r r r ππππ∴==⋅⋅==侧面积,解得2r ,h =∴圆锥的体积为2211233V r h ππ=⋅⋅=⨯⨯=圆锥.故答案为:3.4.(2020·江苏南京市·高一期末)把一个棱长为2的正方体木块,切出一个最大体积的圆柱,则该圆柱的体积为( ) A .23πB .πC .2πD .4π【答案】C【解析】正方体棱长为2,所以正方体底面正方形的内切圆半径为1,面积为21ππ⨯=,以此内切圆为底、高为2的圆柱是可切出的最大圆柱.且该圆柱的体积为22ππ⨯=. 故选:C5.(2020·山东日照市·高一期末)《五曹算经》是我国南北朝时期数学家甄驾为各级政府的行政人员编撰的一部实用算术书,其第四卷第九题如下:“今有平地聚粟,下周三丈,高四尺,问粟几何”?其意思为场院内有圆锥形稻谷堆,底面周长3丈,高4尺,那么这堆稻谷有多少斛?已知1丈等于10尺,1斛稻谷的体积约为1.62立方尺,圆周率约为3,估算堆放的稻谷约有多少斛(保留两位小数)( ) A .61.73 B .61.71C .61.70D .61.69【答案】A【解析】设圆锥的底面半径为r ,高为h ,体积为V , 则230r π=,所以=5r , 故221135410033V r h π==⨯⨯⨯=(立方尺), 因此10061.731.62V =≈(斛). 故选:A.6.(2020·江苏无锡市·高一期末)某养路处有一圆锥形仓库用于储藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米,为存放更多的食盐,养路处拟重建仓库,将其高度增加4米,底面直径不变,则新建仓库比原仓库能多储藏食盐的体积为( ) A .24π米3 B .48π米3C .96π米3D .192π米3【答案】B【解析】原仓库圆锥的底面半径为6米,高为4米,则容积为21614483V ππ=⨯⨯⨯=立方米; 仓库的高增加4米,底面直径不变,则仓库的容积为22618963V ππ=⨯⨯⨯=立方米. 所以新建仓库比原仓库能多储藏食盐的体积为2148V V π-=立方米. 故选:B. 【题组五 球】1.(2021·天津滨海新区)在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为外接球的体积为( )A . BC .D .【答案】B【解析】设正方体的棱长为a ,则111111B D AC AB AD B C D C ======,由于三棱锥11A B CD -的表面积为所以)121442AB CS S==⨯=a ==,所以正方体的外接球的体积为34632π⎛⎫= ⎪ ⎪⎝⎭故选:B .2.(2020·广东高二期末)在长方体1111ABCD A B C D -中,22AB BC ==,若此长方体的八个顶点都在体积为92π的球面上,则此长方体的表面积为( ) A .16 B .18C .20D .22【答案】A【解析】根据长方体的结构特征可得,长方体外接球直径等于长方体体对角线的长, 因为长方体外接球的体积为92π,设外接球半径为R , 则33924R ππ=,解得32R =,因此2R =22AB BC ==,所以3=12BB =,因此长方体的表面积为:1122248416S AB BC AB BB BC BB =⨯⨯+⨯⨯+⨯⨯=++=. 故选:A.3.(2020的内切球,则此棱柱的体积是( ).A .3B .354cmC .327cmD .3【答案】B的内切球,则正三棱柱的高为,,设底面正三角形的边长为a cm,13⨯=6a =cm ,∴正三棱柱的底面面积为16622⨯⨯⨯=2,故此正三棱柱的体积V =54=cm 3. 故选:B .4.(2021·全国高一)如图所示,球内切于正方体.如果该正方体的棱长为a ,那么球的体积为( )A .343a π B .3aC 3aD .316a π【答案】D【解析】因为球内切于正方体,所以球的半径等于正方体棱长的12, 所以球的半径为2a ,所以球的体积为334326a a ππ⎛⎫= ⎪⎝⎭,故选:D.5.(2021·湖南邵阳市·高一期末)一个球的体积为36π,则这个球的表面积为( ) A .12π B .36πC .108πD .4π【答案】B【解析】设球的半径为R ,球的体积为3436=3R ππ,解得3R =,则球的表面积244936R πππ=⨯=, 故选:B6.(2020·浙江高一期末)已知正方体外接球的体积是323π,那么该正方体的内切球的表面积为_____________. 【答案】163π【解析】设正方体棱长为a ,则3432323ππ⎛⎫⨯= ⎪ ⎪⎝⎭,解得a =∴内切球半径为23a r ==,表面积为21643S ππ=⨯=⎝⎭. 故答案为:163π.【题组六 组合体的体积表面积】1.(2020·全国高一课时练习)如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有________个面,其体积为________.【答案】20 323-【解析】由图形观察可知,几何体的面共有2(242)20⨯⨯+=个, 该几何体的直观图如图所示,该几何体的体积为两个四棱柱的体积和减去两个四棱柱交叉部分的体积. 两个四棱柱的体积和为222432V =⨯⨯⨯=. 交叉部分的体积为四棱锥S ABCD -的体积的2倍.在等腰ABS 中,SB SB =边上的高为2,则SA =由该几何体前后,左右上下均对称,知四边形ABCD 的菱形. 设AC 的中点为H ,连接,BH SH 易证SH 即为四棱锥S ABCD -的高,在Rt ABH 中, 2.BH ==又AC SB ==所以 1222ABCDS=⨯⨯=因为BH SH =,所以112233ABCDS ABCD V S -=⨯=⨯=四棱柱所以求体积为3223233-⨯=-故答案为:20;323-2.(2020·新疆巴音郭楞蒙古自治州·高一期末)如图,直三棱柱,高为6,底边三角形的边长分别为3、4、5,以上下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积.【答案】366π-【解析】因为222345+=,所以底面是直角三角形, 所以上、下底面内切圆半径34512r +-==, 所以剩余部分几何体的体积21346163662V ππ=⨯⨯⨯⨯=-⨯-, 所以剩余部分几何体的体积为366π-.3.(2021·江西九江市)在底面半径为2,高为面积之比为1:4,求圆柱的表面积.【答案】1)π【解析】由圆柱的底面积与圆锥的底面积之比为1:4,知:底面半径比为1:2,即圆柱底面半径1r =,若设圆柱的高为h 12=,即h = ∴由圆柱的表面积等于侧面积加上两底面的面积,即:2221)S rh r πππ=+=.。
专题8.3 简单几何体的表面积与体积(解析版)

专题8.3 简单几何的表面积与体积运用一 体积【例1】(1)(2019·北京高二学业考试)如图,在直三棱柱111ABC A B C -中,AB AC ⊥,如果3AB =,1AC =,12AA =,那么直三棱柱111ABC A B C -的体积为( )A.2B.3C.4D.6(2)(2019·云南省玉溪第一中学高二月考)一个四棱锥的三视图如图所示,则该四棱锥的体积为( )B.D.(3)某几何体的三视图如图所示,该几何体的体积是( )A.1123B.1363C.48D.56【答案】(1)B (2)A (3)C 【解析】(1)因为AB AC ⊥,所以322ABCAB AC S ⋅==; 所以11113232ABC A B C ABC V SAA -=⨯=⨯=,故选:B.(2)由三视图知,该几何体是一个直四棱锥,底面是一个直角梯形,底面积为()122+=,高为2,因此,这个四棱锥的体积为1232⨯=,故选:A.(3)根据三视图知,该几何体是平放的四棱柱,如图所示,且该四棱柱的底面为等腰梯形, 棱柱的高为4,它的体积为()12444482V Sh ==⨯+⨯⨯=.故选:C .【举一反三】1.(2019·北京高一期末)已知圆柱的侧面展开图是一个边长为2π的正方形,则这个圆柱的体积是( ) A .22π B .2πC .22π D .23π【答案】A【解析】底面圆周长22l r ππ==,1r = ,2S r ππ==所以222V Sh πππ==⨯= 故选:A2.(2019·河北高三月考(理))圆锥的母线长是4,侧面积是4π,则该圆锥的高为( )A B .4C .3D .2【答案】A【解析】设母线为l ,底面半径为r ,高为h ,则4rl ππ=,1r =,所以h =.答案选A3.设正六棱锥的底面边长为1 )A. C. D.2【答案】B【解析】由底面边长为12h ==.又因为底面积16222S =⨯⨯=112332V Sh ==⨯⨯=.故选B.4.已知圆台上、下底面的面积分别为π,4π,侧面积为6π,则这个圆台的体积为( ).A .14πB .143πC .3D .【答案】C【解析】依题意知圆台上底面半径为1r = ,下底面半径为2R =如图所示圆台展开为一个圆环的一部分即ABCD ,其小扇形弧长2AD π=,大扇形弧长4BC π=, 由2BC AD=知道OA AB l == ,则圆台的侧面积11622S BC OB AD OA π=-=2l ⇒= 所以高h =圆台的体积221()3V h r rR R π=++= 故选C 5.(2019·四川绵阳中学高一月考)圆台上底半径为2,下底半径为6,母线长为5,则圆台的体积为( ) A.40π B.52πC.50πD.2123π 【答案】B【解析】作出圆台的轴截面如图所示:上底面半径2MD =,下底面半径6NC =,过D 做DE 垂直NC , 则624EC =-=由5CD =故3DE =即圆台的高为3,所以圆台的体积为2213(26523V πππ=⋅⋅⋅+⋅+=.故选:B . 运用二 表面积【例2】(1)(2019·山西高二月考(文))已知圆柱的轴截面为正方形,且圆柱的体积为54π,则该圆柱的侧面积为() A.27πB.36πC.54πD.81π(2)(2019·福建高三月考(文))《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图所示,则它的表面积为( )A .2B .4+C .4+D .6+(3)(2019·安徽高二期末(文))如图,长度为1的正方形网格纸中的实线图形是一个多面体的三视图,则该多面体表面积为( )A .16+B .16+C .12+D .12+【答案】(1)B(2)D(3)D【解析】(1)设圆柱的底面半径为r .因为圆柱的轴截面为正方形,所以该圆柱的高为2r .因为该圆柱的体积为54π,23π2π54πr h r ==,解得3r =,所以该圆柱的侧面积为2π236r r ⨯=π.(2),斜边是2,且侧棱与底面垂直,侧棱长是2,∴几何体的表面积12222262S =⨯+⨯⨯=+故选:D . (3)由三视图还原原几何体如图,该几何体为四棱锥,底面是矩形,AD =4,AB =2,四棱锥的高为2.则其表面积为S 111424222412222=⨯+⨯⨯+⨯⨯⨯⨯⨯=+.故选:D . 【举一反三】1.(2019·湖南高一期末)已知一个圆柱的高是底面圆半径的2倍,则该圆柱的侧面积与表面积的比值为( ) A.14B.12C.23D.45【答案】C【解析】设圆柱底面圆的半径为r ,则高2h r =,该圆柱的侧面积为224r h r ππ⋅=,表面积为222426r r r πππ+=,故该圆柱的侧面积与表面积的比值为224263r r ππ=. 2.(2019·湖南高三期末(文))一个几何体的三视图如图所示,则该几何体的表面积为( )A .B .C .D .5【答案】A【解析】1234511122222S S S S S S =++++=++++=+ 故答案选A3.若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )A 倍B .3倍C .2倍D .5倍【答案】C【解析】由题意可知,如下图所示,设OC r =,则2AC r =所以圆锥的底面积为21S r π=,圆锥的侧面积为()2212222S r r r ππ=⋅= 即圆锥的侧面积是底面积的22212=2S r S rππ=倍故答案选C 运用三 球【例3】(1)由球O 的球面上一点P 作球的两两互相垂直的三条弦PA ,PB ,PC .已知3cm PA =,PB =,PC =,求球O 的表面积和体积.(2)(2019·四川石室中学高三月考(文))已知球O 的内接圆锥体积为23π,其底面半径为1,则球O 的表面积为__________.(3)正方体的外接球与内切球的半径之比为( ) ABC .2:1D .3:1【答案】(1)()236cmπ,()336cm π(2)254π(3)B 【解析】(1)以点P 为一个顶点,PA ,PB ,PC 为三条相邻棱,构造长方体PADB CEFG -.由于点P ,A ,B ,C 都在球O 的球面上,显然长方体PADB CEFG -内接于球O ,其对角线PF 长就是球O 的直径,所以()26cm R ==,3cm R =.()22436cm S R ππ∴==球,()33436cm 3V R ππ==球.(2)由圆锥体积为23π,其底面半径为1,设圆锥高为h 则221133h ππ=⨯⨯,可求得2h = 设球半径为R ,可得方程:()2221R R --=,解得:54R =25254=164S ππ∴=⨯本题正确结果:254π(3)设正方体的边长为1,画出图像如下图所示,设O 为正方体体对角线的交点,1O 为上底ABCD 的中心,所以正方体外接球的半径为122AC OA ===,正方体内切球的半径为111122OO CC ==,故正方体的外接球与内切球的半径之比为1:22=,故选B.【举一反三】1.已知一个高为16的圆锥内接于一个体积为972π的球,在圆锥内又有一个内切球.求: (1)圆锥的侧面积. (2)圆锥内切球的体积.【答案】(1)侧面积96S π=;(2)2563V π=【解析】(1)作出轴截面, 如下图所示:则等腰三角形CAB 内接于圆O ,而圆1O 内切于CAB ∆,设圆O 的半径为R ,由题意,得349723R ππ=,3729R ∴=, 918R CE =∴=; 已知162CD ED =∴=,连接AE ,CE 是直径,CA AE ∴⊥,21816288CA CD CE =⋅=⨯=,CA ∴=,AB CD ⊥, ,216232AD CD DE ∴=⋅=⨯=,AD ∴=,所以圆锥的侧面积96S AD CA πππ=⨯⨯=⨯=; (2)设圆锥的内切球1O 的半径为r ,也即CAB ∆的内切圆的半径为r ,ABC ∆的周长为c ==,111622ABC S AB CD ∆∴=⨯⨯=⨯=,又三角形的面积12ABC S c r ∆=⨯⨯,所以12r ⨯= 4r ∴=;∴圆锥的内切球1O 的体积3425633V r ππ==.2.(2019·广东实验中学高三月考(理))三棱锥P ABC -的底面ABC 是等腰三角形,120C ∠=,侧面PAB 是等边三角形且与底面ABC 垂直,2AC =,则该三棱锥的外接球表面积为__________.【答案】20π【解析】由题意,由余弦定理2221AB =2+2-222-2⎛⎫⨯⨯⨯∴ ⎪⎝⎭,ABC 的外接圆半径21,R R =∴=等边三角形PAB 的高为3,设球的半径为,r 球心到底面的距离为x ,则22222r 2x 13x =+=+-(),所以x 1=,所以该三棱锥的外接球的表面积为24r 20ππ=. 故答案为:20π.3.已知棱长为a 的正方体,甲球是正方体的内切球,乙球是正方体的外接球,丙球与正方体的各棱都相切,则甲、乙、丙三球的表面积之比为( ).A .91:3:4B .1:3:2C .D .31:2【答案】B【解析】由已知得甲球是正方体的内切球,示意图如下图1,从中截面可以看出甲球的直径等于正方体的棱长,设甲球的半径为1R ,则12R a =,所以12a R =,所以甲球的表面积为22211442a S R a πππ⎛⎫=== ⎪⎝⎭; 乙球是正方体的外接球,示意图如下图2, 从中截面可以看出乙球的直径等于正方体的体对角线长,设乙球的半径为2R ,则22R ==,所以2R =,所以乙球的表面积为222224432S R aπππ⎛⎫===⎪⎪⎝⎭;丙球与正方体的各条棱相切,示意图如下图3, 从中截面可以看出丙球的直径等于正方体的面对角线长,设丙球的半径为3R,则32R==,所以32R=,所以丙球的表面积为222334422S R aπππ⎛⎫===⎪⎪⎝⎭;所以()()()222123:::3:21:3:2S S S a a aπππ==,故选:B.1.(2019·四川棠湖中学高二月考)一个棱长为2的正方体被一个平面截去部分后,余下部分的三视图如图所示,则截去部分与剩余部分体积的比为()A .1:3B .1:4C .1:5D .1:6【答案】A【解析】由题意可知:几何体被平面ABCD 平面分为上下两部分,设正方体的棱长为2,上部棱柱的体积为:121222⨯⨯⨯=; 下部为:22226⨯⨯-=,截去部分与剩余部分体积的比为:13.故选:A . 2.(2019·全国高三月考(理))某几何体的三视图如图所示,则该几何体的体积是()A.23B.43C.83D.163【答案】C【解析】根据三视图可得对应的几何体为四棱锥P ABCD - , 它是正方体中去掉一个三棱锥和三棱柱,又2ABCD S ==矩形,P 到底面ABCD ,故1833V =⨯=, 故选C.3.(2019·天水市第一中学高三月考(理))已知一个简单几何体的三视图如图所示,则该几何体的体积为A.36π+B.66π+C.312π+D.12【答案】A【解析】由三视图知,该几何体有四分之一圆锥与三棱锥构成,故体积为211113433436,4332V ππ=⨯⨯⨯⨯+⨯⨯⨯⨯=+,故选A.4.(2019·安徽省泗县第一中学高二期末(文))某几何体的三视图如图所示,则该几何体的体积等于()A .12B .15C .18D .21【答案】B【解析】根据三视图可得出该几何体为底面为直角梯形的直棱柱,底面积1(23)252S =⨯+⨯=,故该几何体的体积5315V =⨯=,故选:B .5(2019·广东高一期末)已知圆柱的轴截面为正方形,且该圆柱的侧面积为36π,则该圆柱的体积为 A.27π B.36πC.54πD.81π【答案】C【解析】设圆柱的底面半径r .因为圆柱的轴截面为正方形,所以该圆柱的高为2r 因为该圆柱的侧面积为36π,所以2236r r ππ⨯=,解得3r =, 故该圆柱的体积为2232354r h πππ=⨯⨯⨯=.故答案选C6.(2019·江西上高二中高二月考(理))圆锥的母线长为4,侧面展开图为一个半圆,则该圆锥表面积为( ) A .10π B .12πC .16πD .18π【答案】B【解析】一个圆锥的母线长为4,它的侧面展开图为半圆, 半圆的弧长为12442l ππ=⨯⨯=,即圆锥的底面周长为4π, 设圆锥的底面半径是r ,则得到24r ππ=,解得2r =,这个圆锥的底面半径是2,∴圆锥的表面积为242212S πππ=⋅⋅+⋅=.故选:B .7.(2019·江苏高一期末)已知圆锥的底面半径为1,母线与底面所成的角为3π,则此圆锥的侧面积为( )A. B.2πD.π【答案】B【解析】由于圆锥的底面半径1r =,母线与底面所成的角为3π, 所以母线长121cos32r l π=== ,故圆锥的侧面积=2S rl ππ=;故答案选B 8.(2019·河北高一月考)如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的表面积之比为( )A.6:1):4+ B.64 C.5:1):4+D.5:4【答案】A【解析】设球的半径为R ,圆柱的表面积2221S 246R R R πππ=+=。
新高考数学复习专题-专题十三 简单几何体的结构特征、表面积与体积(原卷版)

专题十三 简单几何体的结构特征、表面积与体积一、单选题1.(2021·浙江高一期末)如图所示是水平放置的三角形的直观图,2,,AB BC AB BC ==分别与y '轴、x '轴平行,则ABC 在原图中对应三角形的面积为( )A .2B .1C .2D .4 2.(2021·山东日照市·高三一模)已知直三棱柱111ABC A B C -的侧棱长为2,AB BC ⊥,2AB BC ==.过AB 、1BB 的中点E 、F 作平面α与平面11AAC C 垂直,则所得截面周长为( )A .+BC .D .3.(2021·全国高三其他模拟)如图是千里淮河第一闸——王家坝闸下游,蒙洼蓄洪区内特色居民生活区域——庄台的示意图.忽略其他因素不妨假设庄台的底部建筑(不含地面上建筑)恰好为一个正四棱台,若该正四棱台的上底面边长为a ,下底面边长为b ,上底面中心处高为h 的旗杆顶点恰好为该正四棱台四条侧棱的交点,则该正四棱台的高为( )A .ah b B .bh a C .()b a h b - D .()b a h a- 4.(2021·广东肇庆市·高三二模)牙雕套球又称“鬼工球”,取鬼斧神工的意思,制作相当繁复,工艺要求极高.明代曹昭在《格古要论·珍奇·鬼工毬》中写道:“尝有象牙圆毬儿一箇,中直通一窍,内车数重,皆可转动,故谓之鬼工毬”.现有某“鬼工球”,由外及里是两层表面积分别为2100cm π和264cm π的同心球(球壁的厚度忽略不计),在外球表面上有一点A ,在内球表面上有一点B ,连接线段AB .若线段AB 不穿过小球内部,则线段AB 长度的最大值是( )A B .9cm C .3cm D .2cm 5.(2021·浙江高二开学考试)一个几何体的三视图如图所示,其中正视图和俯视图均为等腰直角三角形,该几何体的体积为( )A.8 B.83C.4 D.436.(2021·江苏高一课时练习)关于斜二测画法所得直观图,以下说法正确的是()A.等腰三角形的直观图仍是等腰三角形B.正方形的直观图为平行四边形C.梯形的直观图不是梯形D.正三角形的直观图一定为等腰三角形7.(2021·甘肃兰州市·高三其他模拟(文))《九章算术》卷五《商功》中有如下问题:“今有委粟平地,下周一十二丈,高四丈.”意思是:今将粟放在平地,谷堆下周长12丈,高4丈.将该谷堆模型看作一个圆锥, 取近似值3,则该圆锥外接球的表面积约为()A.55平方丈B.75平方丈C.110平方丈D.150平方丈8.(2021·甘肃高三一模(理))玉琮是一种内圆外方的筒型玉器,它与玉璧、玉圭、玉璋、玉璜、玉琥被称为“六器”,是古人用于祭祀神祇的一种礼器.《周礼》中载有“以玉作六器,以礼天地四方,以苍璧礼天,以黄琮礼地”等文.如图为齐家文化玉琮,该玉琮中方内空,形状对称,圆筒内径2.0cm,外径2.4cm,筒高6.0cm,方高4.0cm,则其体积约为(单位:3cm)()A .23.04 3.92π-B .34.56 3.92π-C .34.56 3.12π-D .23.04 3.12π- 9.(2021·全国高三月考(理))已知三棱锥P ABC -中,ABC 是等腰直角三角形,AB AC ⊥,AB =PA =PAB PAC ∠=∠,三棱锥P ABC -的体积为1,则三棱锥P ABC -外接球的表面积为( )A .36πB .32πC .24πD .16π 10.(2021·全国高三专题练习(理))设ABC 为等腰三角形,2AB AC ==,3A π∠=,AD 为BC 边上的高,将ADC 沿AD 翻折成ADC ',若四面体ABC D '的外接球半,则线段BC '的长度为( )A .2B .1CD 11.(2021·全国高三专题练习(理))在棱长为2的正方体1111ABCD A B C D -中,O 为正方形1111D C B A 的中心,P ,M ,N 分别为1DD ,AB ,BC 的中点,则四面体OPMN 的体积为( )A .512B .56C .12D .612.(2021·全国高三专题练习(理))在正方体1111ABCD A B C D -中,三棱锥11A BC D -的内切球的表面积为16π,则正方体外接球的体积为( )A .81πB .288πC .36πD . 13.(2021·浙江高三专题练习)已知某几何体的三视图如图所示,则该几何体的体积为( )A .3π8B .π4C .5π24D .7π2414.(2021·浙江高一期末)圆台的上,下底面半径分别为3和4,母线长为6.则其表面积等于( )A .72B .42πC .67πD .72π 15.(2021·全国高三开学考试(文))如图,“蘑菇”形状的几何体是由半个球体和一个圆柱体组成,球的半径为2,圆柱的底面半径为1,高为3,则该几何体的表面积为( )A .18πB .20πC .223πD .26π16.(2021·江苏苏州市·高三开学考试)我国南北朝时期的数学家祖暅在计算球的体积时,提出了一个原理(祖暅原理):“幂势既同,则积不容异”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.图1是一种“四脚帐篷”的示意图,其中曲线AOC 和BOD 均是以1为半径的半圆,平面AOC 和平面BOD 均垂直于平面ABCD ,用任意平行于帐篷底面ABCD 的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为( )A .23B .43C .3πD .23π 17.(2021·山西晋中市·高三二模(理))如图,一个四棱柱形容器中盛有水,在底面ABCD 中,//AB CD ,3AB =,1CD =,侧棱14AA =,若侧面11AA B B 水平放置时,水面恰好过1111,,,AD BC B C A D 的中点,那么当底面ABCD 水平放置时,水面高为( )A .2B .52C .3D .7218.(2021·广西梧州市·高三其他模拟(理))在等腰三角形ABC 中,2AB AC ==,顶角为120,以底边BC 所在直线为轴旋转围成的封闭几何体内装有一球,则球的最大体积为( )A .2B .2C .12π D .3二、多选题19.(2021·广东韶关市·高三一模)如图三棱锥P ABC -,平面PBC ⊥平面ABC ,已知PBC 是等腰三角形,ABC 是等腰直角三角形,若2AB BC ==,PB PC ==球O 是三棱锥P ABC -的外接球,则( )A .球心到平面PBC 的距离是32B .球心到平面ABC 的距离是34C .球的表面积是414πD .球的体积是320.(2021·山东青岛市·高三一模)在南方不少地区,经常看到人们头戴一种用木片、竹篾或苇蒿等材料制作的斗笠,用来遮阳或避雨,随着旅游和文化交流活动的开展,斗笠也逐渐成为一种时尚旅游产品.有一种外形为圆锥形的斗笠,称为“灯罩斗笠”,根据人的体型、高矮等制作成大小不一的型号供人选择使用,不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量,现有一个“灯罩斗笠”,帽坡长20厘米,帽底宽 )A .斗笠轴截面(过顶点和底面中心的截面图形)的顶角为120B .过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为平方厘米C .若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为1600π平方厘米D .此斗笠放在平面上,可以盖住的球(保持斗笠不变形)的最大半径为30厘米21.(2021·山东德州市·高三一模)如图,在边长为4的正方形ABCD 中,点E 、F 分别在边AB 、BC 上(不含端点)且BE BF =,将AED ,DCF 分别沿DE ,DF 折起,使A 、C 两点重合于点1A ,则下列结论正确的有( ).A .1A D EF ⊥B .当12BE BF BC ==时,三棱锥1A F DE -C .当14BE BF BC ==时,三棱锥1A F DE -的体积为3D .当14BE BF BC ==时,点1A 到平面DEF 的距离为7第II 卷(非选择题) 请点击修改第II 卷的文字说明三、填空题22.(2021·浙江高一期末)圆锥底面半径为1,母线长为4,轴截面为PAB ,如图,从A 点拉一绳子绕圆锥侧面一周回到A 点,则最短绳长为_________.23.(2021·吉林长春市·高三二模(文))“中国天眼”是我国具有自主知识产权、世界最大单口径、最灵敏的球面射电望远镜(如图,其反射面的形状为球冠(球冠是球面被平面所截后剩下的曲面,截得的圆为底,垂直于圆面的直径被截得的部分为高,设球冠底的半径为r ,球冠的高为h ,则球的半径R =______________.24.(2020·江苏省苏州中学园区校高二期中)如图所示为水平放置的正方形ABCO ,在平面直角坐标系xOy 中点B 的坐标为()2,2,用斜二测画法画出它的直观图A B C O '''',则四边形A B C O ''''的面积为___________.25.(2021·江苏高一课时练习)从正方体ABCD -A 1B 1C 1D 1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.其中正确结论的个数为________.26.(2021·山东德州市·高三一模)已知三棱锥P ABC -中,AP 、AB 、AC 三条棱两两垂直,且长度均为P 为球心,4为半径作一个球,则该球面被三棱锥四个表面截得的所有弧长之和为______.27.(2021·江苏省天一中学高三二模)《九章算术》是古代中国的第一部自成体系的数学专著,与古希腊欧几里得的《几何原本》并称现代数学的两大源泉.《九章算术》卷五记载:“今有刍甍,下广三丈,表四丈,上袤二丈,无广,高一丈.问积几何?”译文:今有如图所示的屋脊状楔体PQ ABCD -,下底面ABCD 是矩形,假设屋脊没有歪斜,即PQ 的中点R 在底面ABCD 上的投影为矩形ABCD 的中心点O ,//PQ AB ,4AB =,3AD =,2PQ =,1OR =(长度单位:丈).则楔体PQ ABCD -的体积为___________(体积单位:立方丈).28.(2020·苏州市第三中学校高二月考)已知球O 的半径为3,正三棱锥S ABC -的四个顶点都在球O 的表面上,且2SA =,则正三棱锥S ABC -的体积为___________. 29.(2021·河南高三月考(理))棱长为2的正方体1111ABCD A B C D -中,M 、N 、P 、Q 分别是11A D 、11C D 、11B C 、11A B 的中点,沿平面AMQ 、BQP 、CPN 、DMN 截去4个小三棱锥后,所得多面体体积为______.30.(2021·全国高三专题练习(文))已知直三棱柱111ABC A B C -,14AB BC AA ===,AC =P 是上底面111A B C 所在平面内一动点,若三棱锥P ABC -的外接球表面积恰为41π,则此时点P 构成的图形面积为________.31.(2021·山东济宁市·高三一模)在长方体1111ABCD A B C D -中,3AB =,14A D A A ==,E ,F ,G 分别是棱AB ,BC ,1CC 的中点,P 是底面ABCD 内一动点,若直线1D P 与平面EFG 平行,当三角形1BB P 的面积最小时,三棱锥1A BB P -的外接球的体积是______.32.(2021·河北张家口市·高三一模)早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把sin36︒按35计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于___________.33.(2021·云南高三其他模拟(理))如图,已知面积为4的正方形ABCD 的四个顶点均在球O 的球面上,1O 为正方形ABCD 的外接圆,1AO O △为等腰直角三角形,则球O 的体积为___________.34.(2021·浙江高二开学考试)如图,过球的一条半径OP 的中点1O ,作垂直于该半径的平面,所得截面圆的面积与球的表面积之比为________.35.(2021·湖北高三月考)已知球O 的半径为4,3点,,,A B C D 均在球面上,若ABC则三棱锥D ABC -的最大体积是___________.四、解答题36.(2021·全国高三专题练习(文))设某几何体的三视图如图(尺寸的长度单位为cm ),(1)用斜二测画法画出该几何体的直观图(不写画法); (2)求该几何体最长的棱长.37.(2021·江苏高一课时练习)如图,在三棱锥V ABC -中,4VA VB VC ===,30AVB AVC BVC ∠=∠=∠=,过点A 作截面AEF ,求AEF 周长的最小值.38.(2021·江西高三其他模拟(文))如图,已知三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=︒,11AA =,AB =2AC =,E ,F 分别为棱1CC ,BC 的中点.(1)求异面直线EF 与1A B 所成角的大小;(2)若G 为线段1AA 的中点,试在图中作出过E ,F ,G 三点的平面截该棱柱所得的多边形,并求该截面分三棱柱成两部分(较小部分与较大部分)的体积的比值. 39.(2021·全国高三月考(文))如图,直三棱柱111ABC A B C -中,平面ABC 是边长为2的等边三角形,14BB =,E 为棱11A C 的中点,F 为棱11A B 的中点,11BC B C O =.(1)证明:1//A B 平面EFO ; (2)求三棱锥111B ACC -的体积.40.(2021·湖南高三月考(文))图1是由正方形ABCD ,Rt ABE △,Rt CDF △组成的一个平面图形,其中1AB AE DF ===,将其沿AB 、CD 折起使得点E 与点F 重合,如图2.(1)证明:图2中的平面ABE 与平面ECD 的交线平行于底面ABCD ; (2)求图2中几何体A BCE -的体积.41.(2021·全国高三专题练习(文))在四棱锥P ABCD -中,PD ⊥平面ABCD ,1,2PD PN ND ==.四边形ABCD 为梯形,//,224,120AD BC BC AD DC ADC ===∠=︒.(1)求证://PB 平面ACN ; (2)求三棱锥N PBC -的体积.42.(2021·全国高三专题练习(文))在等腰梯形ABCD 中,//,2,AB CD AB DC E =为AB 的中点,将ADE 与BEC △分别沿ED CE 、向上折起,使A B 、重合于点.P(1)在折后的三棱锥P DCE -中,证明:PE CD ⊥;(2)若60DEC ∠=,且折后的三棱锥P DCE -求三棱锥P DCE -的体积.43.(2021·全国高三专题练习(文))如图,在四棱锥S ABCD -中,SD ⊥平面ABCD ,四边形ABCD 是直角梯形,90ADC DAB ∠=∠=︒,2SD AD ==,1DC =,CB =.(1)证明:平面SAD ⊥平面SAB ; (2)求三棱锥C SAB -的体积.44.(2021·全国高三专题练习(文))如图,在四校锥P ABCD -中,四边形ABCD 为直角梯形,//AD BC ,90ADC ︒∠=,平面PAD ⊥平面ABCD ,Q ,M 分别为AD ,PC 的中点,22PA PD AD CD BC =====.(1)求证:BC ⊥平面PQB ; (2)求三棱锥P AMQ -的体积.45.(2021·河南高一月考)如图,在长方体1111ABCD A B C D -中,2AB BC ==,13AA =.(1)求证:直线1//A B 平面1ACD ; (2)求三棱锥1D BCD 的外接球的体积.五、双空题46.(2021·广东广州市·高三一模)已知三棱锥P ABC -的底面ABC 是边长为6的等边三角形,PA PB PC ===,先在三棱锥P ABC -内放入一个内切球1O ,然后再放入一个球2O ,使得球2O 与球1O 及三棱锥P ABC -的三个侧面都相切,则球1O 的体积为________,球2O 的表面积为__________.18原创精品资源学科网独家享有版权,侵权必究!。
《简单几何体的表面积与体积》考点讲解复习与同步训练
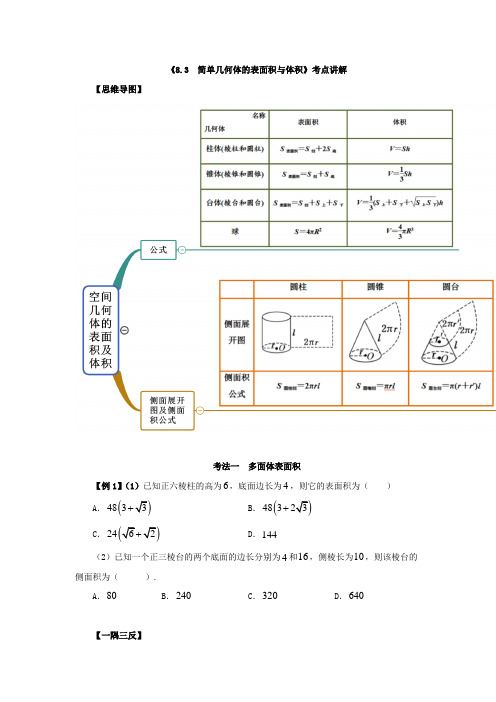
《8.3 简单几何体的表面积与体积》考点讲解【思维导图】考法一多面体表面积【例1】(1)已知正六棱柱的高为6,底面边长为4,则它的表面积为()A.(483B.(483+C.24D.144(2)已知一个正三棱台的两个底面的边长分别为4和16,侧棱长为10,则该棱台的侧面积为().A.80B.240C.320D.640【一隅三反】1.已知正四棱柱(即底面是正方形的直棱柱)的底面边长为3cm ,侧面的对角线长是,则这个正四棱柱的表面积为( )A .290cmB .2C .272cmD .254cm2.棱长为1的正四面体的表面积为( )AB .C .D .3.正三棱锥底面边长为a ,高为6a ,则此正三棱锥的侧面积为( )A .234a B .232a C 2D 2考法二 多面体台体积【例2】底面边长为2,高为1的正三棱柱的体积是( )A B .1C .2D .13【一隅三反】1.如图,已知高为3的棱柱111ABC A B C -的底面是边长为1的正三角形,则三棱锥1B ABC -的体积为( )A .14B .12C .62.正四棱锥的底面边长和高都等于2,则该四棱锥的体积为( )A B C.83D.83.已知棱长均为4,底面为正方形的四棱锥S ABCD-如图所示,求它的体积.4.如图,正三棱锥P ABC-的底面边长为2,侧棱长为3.(1)求正三棱锥P ABC-的表面积;(2)求正三棱锥P ABC-的体积.考法三旋转体的表面积【例3】若圆锥的轴截面是顶角为120的等腰三角形,且圆锥的母线长为2,则该圆锥的侧面积为()A B.2πC.D.【一隅三反】1.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比值是()A.142ππ+B.122ππ+C.12ππ+D.142ππ+2把一个半径为20的半圆卷成圆锥的侧面,则这个圆锥的高为( )A .10B .C .D .3.一个圆柱内接于一个底面半径为2,高为4的圆锥,则内接圆柱侧面积的最大值是( )A .32π B .3π C .5π D .4π考法四 旋转体的体积【例4】已知圆锥的母线长为5,底面周长为6π,则它的体积为( ) A .10π B .12πC .15πD .36π【一隅三反】1.将半径为3,圆心角为23π的扇形作为侧面围成一个圆锥,则该圆锥的体积为( )A .πB .C .3πD .32.古代将圆台称为“圆亭”,《九章算术》中“今有圆亭,下周三丈,上周二丈,高一丈,问积几何?”即一圆台形建筑物,下底周长3丈,上底周长2丈,高1丈,则它的体积为( )A .198π立方丈 B .1912π立方丈 C .198π立方丈 D .19π12立方丈3.已知圆锥的表面积为9π,它的侧面展开图是一个半圆,则此圆锥的体积为( ) A .3B .3πC .9D .9π考法五 球【例5】(1)已知一个正方体的8个顶点都在同一个球面上,则球的表面积与这个正方体的表面积之比为( )A .3π B .2π C D (2).已知一个正三棱锥的四个顶点都在一个球的球面上,且这个正三棱锥的所有棱长都为 )A .4πB .8πC .12πD .24π【一隅三反】1.若一个球的直径为2,则此球的表面积为( ) A .2πB .16πC .8πD .4π2.棱长为2的正方体的外接球的表面积为( )A .4πB .43π C .12πD .3.已知一个正方体的体积为8,求此正方体内切球的表面积为( ) A .43π B .8πC .4πD .16π4.将一个棱长为3cm 的正方体铁块磨成一个球体零件,则可能制作的最大零件的体积为( )A .39cm πB .39m 2c πC .3cmD 3cm考法六 组合体的体积表面积【例6】如图,一个无盖的器皿是由棱长为3的正方体木料从顶部挖掉一个直径为2的半球而成(半球的底面圆在正方体的上底面,球心为上底面的中心),则该器皿的表面积S 为( )A .54B .542π+C .54π+D .543π+【一隅三反】1.某组合体如图所示,上半部分是正四棱锥P EFGH -,下半部分是长方体ABCD EFGH -.正四棱锥P EFGH -,2EF =,1AE =,则该组合体的表面积为( )A .20B .12C .16D .82.鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图1,这是一种常见的鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )A .8(6+B .6(8+C .8(6+D .6(8+3.如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化后正好盛满杯子,则杯子高h =_______cm .《8.3 简单几何体的表面积与体积》考点讲解答案解析考法一 多面体表面积【例1】(1)已知正六棱柱的高为6,底面边长为4,则它的表面积为( )A .(483B .(483+C .24D .144(2)已知一个正三棱台的两个底面的边长分别为4和16,侧棱长为10,则该棱台的侧面积为( ).A .80B .240C .320D .640【答案】(1)A (2)B【解析】(1)由题知侧面积为664144⨯⨯=,两底面积之和为22464⨯⨯=所以表面积(483S =.故选:A.(2)由题意可知,该棱台的侧面为上下底边长为4和16,腰长为10的等腰梯形∴8= 等腰梯形的面积为:()14168802S '=⨯+⨯=∴棱台的侧面积为:3380240S S '==⨯=本题正确选项:B 【一隅三反】1.已知正四棱柱(即底面是正方形的直棱柱)的底面边长为3cm ,侧面的对角线长是,则这个正四棱柱的表面积为( )A .290cmB .2C .272cmD .254cm【答案】A6=.所以表面积为:224362390()S cm =⨯⨯+⨯=.故选:A.2.棱长为1的正四面体的表面积为( )A B .C .D .【答案】A 【解析】如图由正四面体的概念可知,其四个面均是全等的等边三角形,由其棱长为1,所以13sin 6024ABCSAB AC =⋅⋅=,所以可知:正四面体的表面积为4ABCS = 故选:A3.正三棱锥底面边长为a ,高为6a ,则此正三棱锥的侧面积为( )A .234a B .232a C .24a D .22a 【答案】Aa 23⨯=,且,所以利用直角三角形勾股定理可得侧棱长为22632632a a a ,2221222aa a ,所以侧面积为21133224S a a a .选A.考法二 多面体台体积【例2】底面边长为2,高为1的正三棱柱的体积是( )A 3B .1C D .13【答案】A【解析】底面边长为2,高为1的正三棱柱的体积是22)1⨯= A 【一隅三反】1.如图,已知高为3的棱柱111ABC A B C -的底面是边长为1的正三角形,则三棱锥1B ABC -的体积为( )A .14 B .12 C .6【答案】C【解析】三棱锥1B ABC -的体积为:111113332ABCSh ⋅⋅=⨯⨯⨯=故选:C 2.正四棱锥的底面边长和高都等于2,则该四棱锥的体积为( )A B C .83D .8【答案】C【解析】∵正四棱锥的底面边长和高都等于2, ∴该四棱锥的体积211822333V Sh ==⨯⨯=.故选:C . 3.已知棱长均为4,底面为正方形的四棱锥S ABCD -如图所示,求它的体积.【答案】3【解析】如图所示:连接AC ,BD 交于点O ,连接SO , 因为四棱锥的棱长均为4,所以SO ⊥平面ABCD ,即SO 为四棱锥的高,所以4,SA OA ==,所以SO ,所以114433V AB AD SO =⨯⨯⨯=⨯⨯⨯=.4.如图,正三棱锥P ABC -的底面边长为2,侧棱长为3.(1)求正三棱锥P ABC -的表面积; (2)求正三棱锥P ABC -的体积.【答案】(1);(2)3. 【解析】(1)取BC 的中点D ,连接PD ,在Rt PBD △中,可得PD ==∴12PBC S BC PD =⋅=△.∵正三棱锥的三个侧面是全等的等腰三角形,∴正三棱锥P ABC -的侧面积是3PBC S =△∵正三棱锥的底面是边长为2的正三角形,∴122sin 602ABC S =⨯⨯⨯︒=△.则正三棱锥P ABC -的表面积为;(2)连接AD ,设O 为正三角形ABC 的中心,则PO ⊥底面ABC .且133OD AD ==.在Rt POD 中,PO ==.∴正三棱锥P ABC -的体积为13ABC S PO ⋅=△考法三 旋转体的表面积【例3】若圆锥的轴截面是顶角为120的等腰三角形,且圆锥的母线长为2,则该圆锥的侧面积为( )A B .2πC .D .【答案】C【解析】如图圆锥的轴截面是顶角为120,即60APO ∠=,2AP =,90POA ∠=,所以AO =AO PA π⨯⨯=.故选:C.【一隅三反】1.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比值是( ) A .142ππ+ B .122ππ+ C .12ππ+ D .142ππ+ 【答案】B【解析】设圆柱的底面半径为r ,圆柱的高为h , 圆柱的侧面展开图是一个正方形, 2r h π∴=,∴圆柱的侧面积为2224rh r ππ=,圆柱的两个底面积为22r π,∴圆柱的表面积为22222224r rh r r ππππ+=+,∴圆柱的表面积与侧面积的比为:22222241242r r r πππππ++=,故选:B .2.把一个半径为20的半圆卷成圆锥的侧面,则这个圆锥的高为( )A .10B .C .D .【答案】B【解析】半径为20的半圆卷成圆锥的侧面,则圆锥的底面圆周长为220r ππ=⨯, 所以底面圆的半径为r =10,所以圆锥的高为h ==. 故选:B3.一个圆柱内接于一个底面半径为2,高为4的圆锥,则内接圆柱侧面积的最大值是( )A .32π B .3π C .5π D .4π【答案】D 【解析】圆锥的底面半径为2,高为4, 设内接圆柱的底面半径为x , 则它的上底面截圆锥得小圆锥的高为422xx ⨯=, 因此,内接圆柱的高42h x =-;∴圆柱的侧面积为()()224242S x x x x ππ=-=-(02)x <<,令()22121==-+--t x x x ,当1x =时,1max t =; 所以当1x =时,4max S π=,即圆柱的底面半径为1时,圆柱的侧面积最大,最大值为4π. 故选:D.考法四 旋转体的体积【例4】已知圆锥的母线长为5,底面周长为6π,则它的体积为( ) A .10π B .12πC .15πD .36π【答案】B【解析】设圆锥的底面半径为r ,高为h ,因为底面周长为6π,所以26r ππ=,解得3r =,又因为母线长为5,所以h =4,所以圆锥的体积是21123V r h ππ==故选:B 【一隅三反】1.将半径为3,圆心角为23π的扇形作为侧面围成一个圆锥,则该圆锥的体积为( )A .πB .C .3πD .3【答案】D【解析】由扇形弧长公式可求得弧长2323L ππ=⨯=,∴圆锥底面周长为2π, ∴圆锥底面半径1r =,∴圆锥的高h =∴圆锥的体积2133V r h π=⋅=.故选:D .2.古代将圆台称为“圆亭”,《九章算术》中“今有圆亭,下周三丈,上周二丈,高一丈,问积几何?”即一圆台形建筑物,下底周长3丈,上底周长2丈,高1丈,则它的体积为( )A .198π立方丈 B .1912π立方丈 C .198π立方丈 D .19π12立方丈 【答案】B【解析】由题意得,下底半径32R π=(丈),上底半径212r ππ==(丈),高1h =(丈),所以它的体积为()222211313113322V h R r Rr ππππππ⎡⎤⎛⎫⎛⎫=++=⨯⨯++⨯⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦所以19V =12π(立方丈).故选:B. 3.已知圆锥的表面积为9π,它的侧面展开图是一个半圆,则此圆锥的体积为( ) A .3 B .3πC .9D .9π【答案】B【解析】设圆锥的底面半径为r ,高为h ,则母线长为l则圆柱的侧面积为()2221122r r h ππ=+, 故表面积为()222192r h r πππ++=,得2231922r h +=①,又底面圆周长等于侧面展开半圆的弧长,故2r π=2r =得223h r =②,联立①②得:r =,3h =.故该圆锥的体积为2113333V Sh ππ==⨯⨯⨯=.故选:B.考法五 球【例5】(1)已知一个正方体的8个顶点都在同一个球面上,则球的表面积与这个正方体的表面积之比为( )A .3πB .2π CD.12(2).已知一个正三棱锥的四个顶点都在一个球的球面上,且这个正三棱锥的所有棱长都为 )A .4πB .8πC .12πD .24π【答案】(1)B (2)C【解析】(1)设正方体的棱长为a ,球的半径为R,则22R R a =⇒=,球的表面积为22214432S R a a πππ⎛⎫==⨯= ⎪ ⎪⎝⎭,正方体的表面积为226S a =, ∴2122362S a S a ππ==.故选:B (2)设该正三棱锥为A BCD -,将三棱锥A BCD -补成正方体AEBF GCHD -,如下图所示:则正方体AEBF GCHD -2=,该正方体的体对角线长为所以,正三棱锥A BCD -的外接球直径为2R =R , 该球的表面积为2412S R ππ==. 故选:C. 【一隅三反】1.若一个球的直径为2,则此球的表面积为( ) A .2π B .16πC .8πD .4π【答案】D【解析】因为球的直径为2,即球的半径为1,所以球的表面积为2414ππ⨯=,故选:D.2.棱长为2的正方体的外接球的表面积为( )A .4πB .43π C .12πD .【答案】C【解析】因为正方体的外接球的直径为正方体的体对角线的长,所以2R =R =所以球的表面积为:2412S R ππ==.故选:C3.已知一个正方体的体积为8,求此正方体内切球的表面积为( ) A .43π B .8πC .4πD .16π【答案】C【解析】正方体的体积为8,故边长为2,内切球的半径为1,则表面积244S R ππ==,故选:C.4.将一个棱长为3cm 的正方体铁块磨成一个球体零件,则可能制作的最大零件的体积为( )A .39cm πB .39m 2c πC .3cmD 3cm 【答案】B【解析】正方体的棱长为3cm ,所以球体最大体积的半径32r cm =, 所以球的体积:334932V r cm ππ==.故选:B考法六 组合体的体积表面积【例6】如图,一个无盖的器皿是由棱长为3的正方体木料从顶部挖掉一个直径为2的半球而成(半球的底面圆在正方体的上底面,球心为上底面的中心),则该器皿的表面积S 为( )A .54B .542π+C .54π+D .543π+【答案】C【解析】器皿的表面积是棱长为3的正方体的表面积减去半径为1的圆的面积,再加上半径为1的半球的表面积,即器皿的表面积()()221633141542542S πππππ=⨯⨯-⨯+⨯⨯=-+=+.故选:C . 【一隅三反】1.某组合体如图所示,上半部分是正四棱锥P EFGH -,下半部分是长方体ABCD EFGH -.正四棱锥P EFGH -,2EF =,1AE =,则该组合体的表面积为( )A .20B .12C .16D .8【答案】A【解析】由题意,正四棱锥P EFGH -2=,该组合体的表面积为122421422202⨯+⨯⨯+⨯⨯⨯=.故选:A2.鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图1,这是一种常见的鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )A .8(6+B .6(8+C .8(6+D .6(8+【答案】A【解析】由题图可知,该鲁班锁玩具可以看成是一个棱长为2+的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为2,则该几何体的表面积为2116(248222S ⎡=⨯+-⨯+⨯⨯⎢⎣8(6=+.故选:A.3.如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化后正好盛满杯子,则杯子高h =_______cm .【答案】8【解析】由题意得半球的半径和圆锥底面圆的半径4r =, 如果冰淇淋融化后正好盛满杯子,则半球的体积等于圆锥的体积 所以()32141448233h h ππ⨯⨯=⨯⨯⇒= 故答案为:8《8.3 简单几何体的表面积与体积(精练)》同步练习【题组一 多面体表面积】1.长方体的高为2,底面积等于12,过不相邻两侧棱的截面(对角面)的面积为10,则此长方体的侧面积为( )A .12B .24C .28D .322.一个正四棱锥的底面边长为2,则该正四棱锥的全面积为 A .8B .12C .16D .203.若正三棱台上、下底面边长分别是a 和2a ,棱台的高为6a ,则此正三棱台的侧面积为( )A .2aB .212a C .292a D .232a 4.正四棱锥底面正方形的边长为4,高与斜高的夹角为30,则该四棱锥的侧面积( ) A .32B .48C .64D .3235.已知正四棱锥的底面边长是2 )AB .12C .8D .6.已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)817.已知,AB CD 是某一棱长为2的正方体展开图中的两条线段,则原正方体中几何体ABCD 的表面积为( )A .2+B .2+C .2+D .2+8.长方体一个顶点上的三条棱长分别为3,4,a ,表面积为108,则a 等于( ) A .2B .3C .5D .69.一个正四棱柱的各个顶点都在一个半径为2cm 的球面上,如果正四棱柱的底面边长为2cm ,那么该棱柱的表面积为( )A .2(2+B .2(4+C .2(8+D .2(16+【题组二 多面体台体积】1.正方体的全面积为18cm 2,则它的体积是_________ 3cm2.如图,在长方体1AC 中,棱锥1A ABCD -的体积与长方体的体积之比为( )A .2∶3B .1∶3C .1∶4D .3∶43.由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21 米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .324276mD .312138m4.《九章算术》问题十:今有方亭,下方五丈,上方四丈.高五丈.问积几何(今译:已知正四棱台体建筑物(方亭)如图,下底边长5a =丈,上底边长4b =丈.高5h =丈.问它的体积是多少立方丈?( )A .75B .3053C .3203D .40035.出华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧楼长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .32427mD .312138m6.如图,在棱长为2的正方体1111ABCD A B C D -中,截去三棱锥1A ABD -,求(1)截去的三棱锥1A ABD -的表面积;(2)剩余的几何体1111A B C D DBC -的体积.【题组三 旋转体的表面积】1.经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的侧面积是( )A .B .4πC .D .2π2.某圆台的上、下底半径和高的比为1:4:4,母线长为10,则该圆台的表面积为( )A .81πB .100πC .168πD .169π3.用一个平行于圆锥底面的平面截这个圆锥,截得圆台上下底面半径的比是1:4,且该圆台的母线长为9,则截去的圆锥的母线长为( )A .94B .3C .12D .364.圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )A .3B .5C .6D .75.圆柱底面半径为1,母线长为2,则圆柱侧面积为( )A .4πB .3πC .5πD .2π6.已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为8π,则圆柱的高为________.7.已知圆锥的底面半径为2,高为4,在圆锥内部有一个圆柱,则圆柱的侧面积的最大值为______.8.将底面直径为8,高为值为______.9.若圆锥的侧面展开图是圆心角为90︒的扇形,则该圆锥的侧面积与底面积之比为___________.【题组四 旋转体的体积】1.若圆锥的底面半径为3cm ,侧面积为215cm π,则该圆锥的体积为( )A .4π3cmB .9π3cmC .12π3cmD .36π3cm2.现用一半径为10cm ,面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为__________3cm .3.圆锥的母线与底面所成的角为60︒,侧面积为8π,则其体积为________.4.把一个棱长为2的正方体木块,切出一个最大体积的圆柱,则该圆柱的体积为( )A .23πB .πC .2πD .4π5.《五曹算经》是我国南北朝时期数学家甄驾为各级政府的行政人员编撰的一部实用算术书,其第四卷第九题如下:“今有平地聚粟,下周三丈,高四尺,问粟几何”?其意思为场院内有圆锥形稻谷堆,底面周长3丈,高4尺,那么这堆稻谷有多少斛?已知1丈等于10尺,1斛稻谷的体积约为1.62立方尺,圆周率约为3,估算堆放的稻谷约有多少斛(保留两位小数)( )A .61.73B .61.71C .61.70D .61.696.某养路处有一圆锥形仓库用于储藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米,为存放更多的食盐,养路处拟重建仓库,将其高度增加4米,底面直径不变,则新建仓库比原仓库能多储藏食盐的体积为( )A .24π米3B .48π米3C .96π米3D .192π米3【题组五 球】1.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为接球的体积为( )A .BC .D .2.在长方体1111ABCD A B C D -中,22AB BC ==,若此长方体的八个顶点都在体积为92π的球面上,则此长方体的表面积为( ) A .16 B .18 C .20 D .223的内切球,则此棱柱的体积是( ).A .3B .354cmC .327cmD .34.如图所示,球内切于正方体.如果该正方体的棱长为a ,那么球的体积为( )A .343a π B .3a C 3a D .316a π 5.一个球的体积为36π,则这个球的表面积为( )A .12πB .36πC .108πD .4π6.已知正方体外接球的体积是323π,那么该正方体的内切球的表面积为______. 【题组六 组合体的体积表面积】1.如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有________个面,其体积为________.2.如图,直三棱柱,高为6,底边三角形的边长分别为3、4、5,以上下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积.3.在底面半径为2,高为积之比为1:4,求圆柱的表面积.《8.3 简单几何体的表面积与体积(精练)》同步练习答案解析【题组一 多面体表面积】1.长方体的高为2,底面积等于12,过不相邻两侧棱的截面(对角面)的面积为10,则此长方体的侧面积为( )A .12B .24C .28D .32 【答案】C【解析】设长方体底面矩形的长与宽分别为,a b ,则12ab =.210=,解得4,3a b ==或3,4a b ==.故长方体的侧面积为()243228⨯+⨯=.故选:C.2.一个正四棱锥的底面边长为2,则该正四棱锥的全面积为A .8B .12C .16D .20 【答案】B, 所以该四棱锥的全面积为212+422=122⋅⋅⋅. 故选B3.若正三棱台上、下底面边长分别是a 和2a ,则此正三棱台的侧面积为( )A .2aB .212aC .292aD .232a 【答案】C 【解析】如图,1,O O 分别为上、下底面的中心,1,D D 分别是AC ,11A C 的中点,过1D作1D E OD ⊥于点E .在直角梯形11ODD O 中,123OD a ==,111326O D a a =⨯=,116DE OD O D ∴=-=.在1Rt DED 中,1D E =,则1D D =a ==. 2193(2)22S a a a a ∴=⨯+=侧.故选:C4.正四棱锥底面正方形的边长为4,高与斜高的夹角为30,则该四棱锥的侧面积( )A .32B .48C .64D .323【答案】A【解析】如图:正四棱锥的高PO ,斜高PE ,底面边心距OE 组成直角△POE .∵OE =2cm ,∠OPE =30°,∴斜高h ′=PE =4sin 30oOE =, ∴S 正棱锥侧=114443222ch =⨯⨯⨯='故选:A5.已知正四棱锥的底面边长是2 )AB .12C .8D .【答案】B【解析】如图所示,在正四棱锥S ABCD -中,取BC 中点E ,连接SE ,则SBE △为直角三角形,所以2SE ===, 所以表面积1422422122SBC ABCD S S S =+⨯=⨯+⨯⨯⨯=正方形△.故选:B.6.已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)81 【答案】D【解析】正四棱锥如图,设四棱锥的高OE h =,由底面边长为4,可知2OF =,斜高EF =故2142h =⨯,解得2=2h +故侧面积为(214448812h ⨯⨯==+=+, 故选:D. 7.已知,AB CD 是某一棱长为2的正方体展开图中的两条线段,则原正方体中几何体ABCD 的表面积为( )A .2+B .2+C .2+D .2+【答案】A 【解析】由所给正方体的展开图得到直观图,如图:则此三棱锥的表面积为:△△△△+++=BCD ABC ADC ABD S S S S11112222222222⨯⨯+⨯⨯⨯⨯⨯=+ 故选:A8.长方体一个顶点上的三条棱长分别为3,4,a ,表面积为108,则a 等于( )A .2B .3C .5D .6【答案】D 【解析】长方体一个顶点上的三条棱长分别为3,4,a ,则长方体的表面积为342+2423108a a ⨯⨯⨯+⨯=,解得a =6,故选:D9.一个正四棱柱的各个顶点都在一个半径为2cm 的球面上,如果正四棱柱的底面边长为2cm ,那么该棱柱的表面积为( )A .2(2+B .2(4+C .2(8+D .2(16+【答案】C【解析】∵一个正四棱柱的各个顶点都在一个半径为2cm 的球面上,正四棱柱的底面边长为2cm , ∴球的直径为正四棱柱的体对角线∴正四棱柱的体对角线为4,正四棱柱的底面对角线长为=∴该棱柱的表面积为2×22+4×2×+(2cm ),故选:C【题组二 多面体台体积】1.正方体的全面积为18cm 2,则它的体积是_________ 3cm【答案】【解析】设该正方体的棱长为a cm ,由题意可得,2618a =,解得a =所以该正方体的体积为3V a ==3cm .故答案为:2.如图,在长方体1AC 中,棱锥1A ABCD -的体积与长方体的体积之比为( )A .2∶3B .1∶3C .1∶4D .3∶4【答案】B【解析】设长方体过同一顶点的棱长分别为,,a b c 则长方体的体积为1V abc =, 四棱锥1A ABCD -的体轵为213V abc =, 所以棱锥1A ABCD -的体积与长方体1AC 的体积的比值为13. 故选:B.3.由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21 米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .324276mD .312138m【答案】A【解析】如图正四棱锥P ABCD -中,34AB BC ==,21PO =, 所以正四棱锥P ABCD -的体积为311343421809233ABCD S PO m ⨯⨯=⨯⨯⨯=, 故选:A4.《九章算术》问题十:今有方亭,下方五丈,上方四丈.高五丈.问积几何(今译:已知正四棱台体建筑物(方亭)如图,下底边长5a =丈,上底边长4b =丈.高5h =丈.问它的体积是多少立方丈?( )A .75B .3053C .3203D .4003【答案】B【解析】(()2211+=33V S S h a b h '=⋅ ()2211305545615333=+⨯=⨯⨯=. 故选:B 5.出华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧楼长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21米,底宽34米,则该金字塔的体积为( )A .38092mB .34046mC .32427mD .312138m【答案】A【解析】如图正四棱锥P ABCD -中,PO ⊥底面ABCD ,21PO =,34AB =, 底面正方形的面积为234341156S m =⨯=, 则正四棱锥P ABCD -的体积为311115621809233S PO m ⨯⨯=⨯⨯=, 故选:A6.如图,在棱长为2的正方体1111ABCD A B C D -中,截去三棱锥1A ABD -,求(1)截去的三棱锥1A ABD -的表面积; (2)剩余的几何体1111A B C D DBC -的体积.【答案】(1)6+(2)203【解析】(1)由正方体的特点可知三棱锥1A ABD -中,1A BD 是边长为三角形,1A AD 、1A AB 、ABD △都是直角边为2的等腰直角三角形,所以截去的三棱锥1A ABD -的表面积(111231322642A BD A AD A AB ABDS SS S S=+++=+⨯⨯⨯=+(2)正方体的体积为328=,三棱锥1A ABD -的体积为111142223323ABD S AA ⨯⨯=⨯⨯⨯⨯=, 所以剩余的几何体1111A B C D DBC -的体积为420833-=.【题组三 旋转体的表面积】1.经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的侧面积是( )A .B .4πC .D .2π【答案】C【解析】设圆锥的底面半径为r ,母线长为l ,则l =,由题可知)2122⨯=,∴2r l ==,侧面积为rl π=, 故选:C.2.某圆台的上、下底半径和高的比为1:4:4,母线长为10,则该圆台的表面积为( ) A .81π B .100π C .168π D .169π【答案】C【解析】该圆台的轴截面如图所示.设圆台的上底面半径为r ,则下底面半径4r r '=,高4h r =则它的母线长510l r ====∴2r,8r '=.∴()(82)10100S r r l πππ'=+=+⨯=侧,22100464168S S r r ππππππ'=++=++=表侧.故选:C3.用一个平行于圆锥底面的平面截这个圆锥,截得圆台上下底面半径的比是1:4,且该圆台的母线长为9,则截去的圆锥的母线长为( )A .94B .3C .12D .36【答案】B【解析】根据题意,设圆台的上、下底面的半径分别为r 、R , 设圆锥的母线长为L ,截得小圆锥的母线长为l , ∵圆台的上、下底面互相平行 ∴14l r L R ==,可得L=4l ∵圆台的母线长9,可得L ﹣l =9 ∴3L 4=9,解得L=12, ∴截去的圆锥的母线长为12-9=3 故选B4.圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )A .3B .5C .6D .7【答案】D【解析】设圆台较小底面圆的半径为r ,由已知有另一底面圆的半径为3r ,而圆台的侧面积公式为(3)4384,7r r l r r πππ+=⨯⨯==,选D.5.圆柱底面半径为1,母线长为2,则圆柱侧面积为( ) A .4π B .3πC .5πD .2π【答案】A【解析】圆柱底面半径为1,母线长为2, 圆柱侧面积为224S rl =π=π⨯1⨯2=π ,故选:A6.已知圆柱的底面半径为1,若圆柱的侧面展开图的面积为8π,则圆柱的高为_____. 【答案】4【解析】设圆柱的高为h ,有28h ππ=,得4h =.故答案为:4.7.已知圆锥的底面半径为2,高为4,在圆锥内部有一个圆柱,则圆柱的侧面积的最大值为______.【答案】4π【解析】如图是圆锥与圆柱的轴截面,设内接圆柱的高为a ,圆柱的底面半径为r()02r <<,则由224r a-=,可得42a r =-,所以圆柱的侧面积()22242484(1)4S r r r r r πππππ=⋅-=-+=--+,所以1r =时,该圆柱的侧面职取最大值4π. 故答案为:4π.8.将底面直径为8,高为值为______.【答案】【解析】欲使圆柱侧面积最大,需使圆柱内接于圆锥; 设圆柱的高为h ,底面半径为r ,4r =,解得h =;所以()22242S rh r r r r ππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧;当2r时,S 圆柱侧取得最大值为故答案为:. 【点睛】本题考查了求圆柱侧面积的最值,考查空间想象能力,将问题转化为函数求最值,属于中档题.9.若圆锥的侧面展开图是圆心角为90︒的扇形,则该圆锥的侧面积与底面积之比为___________.【答案】4:1【解析】设圆锥的底面半径为r ,母线长为l , 由题意得:22l r ππ=,即4l r ,所以其侧面积是214S rl r ππ==,底面积是22S r π=,所以该圆锥的侧面积与底面积之比为4:1 故答案为:4:1【题组四 旋转体的体积】1.若圆锥的底面半径为3cm ,侧面积为215cm π,则该圆锥的体积为( ) A .4π3cm B .9π3cmC .12π3cmD .36π3cm【答案】C【解析】设圆锥母线长为l ,则侧面积为123152S l r l πππ=⋅==,故5l =.故圆锥的高4h ==,圆锥体积为21123V r h ππ==3cm .故选:C.2.现用一半径为10cm ,面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为__________3cm .【答案】128π【解析】设铁皮扇形的半径和弧长分别为R 、l ,圆锥形容器的高和底面半径分别为h 、r ,则由题意得R=10,由1802Rl π=,得16l π=, 由2lr π=得8r =.由222R r h =+可得6h =.∴()231164612833V r h cm πππ==⋅⋅=。
创优课堂秋数学北师大必修练习:单元测试三 简单几何体的面积和体积 含解析

单元测试三 简单几何体的面积和体积 班级____ 姓名____ 考号____ 分数____本试卷满分100分,考试时间90分钟.一、选择题:本大题共10小题,每小题4分,共40分.在下列各题的四个选项中,只有一个选项是符合题目要求的.1.两个半径为1的铁球,熔化成一个球,这个大球的半径为( )A .2B . 2C .32 D .1234答案:C解析:根据体积不变:43π×13×2=43πr 3,解得r =32.2.长方体一个顶点上的三条棱长分别为3,4,x ,表面积为108,则x 等于( ) A .2 B .3 C .5 D .6 答案:D解析:该长方体的表面积为2(3×4+3x +4x)=108,x =6.3.设等腰梯形ABCD 是圆台的一个轴截面,且AD ∥BC ,AB =3,AD =2,BC =4,则圆台的侧面积为( )A .9πB .10πC .14πD .18π 答案:A解析:由圆台的轴截面及相关数据知圆台的底面半径分别为1,2,母线长为3,则圆台的侧面积为π(r 1+r 2)l =π(1+2)×3=9π.4.过圆锥的轴的平面截圆锥所得三角形是边长为2的等边三角形,则该圆锥的体积为( )A .π3B .3π3C .2π3D .23π3 答案:A解析:正方体的对角线长等于球的直径,该球的半径为R ,则3a =2R ,所以球的表面积为S =4πR 2=π·(2R)2=3πa 2=3π,a =1.5.某几何体的三视图如图所示,根据图中数据,可得该几何体的体积是( )A .3 2+ 3B .2+3 3C .2 2+3 3D .3 2+2 3 答案:B解析:该几何体是上面是正四棱锥,下面为正方体的组合体,体积为V =(3)3+13×(3)2×2=3 3+ 2.6.一个棱长为a 的正方体的顶点都在一个球面上,该球的表面积为3π,则a 等于( ) A .1 B . 2 C . 3 D .2 答案:A解析:正方体的对角线长等于球的直径,该球的半径为R ,则3a =2R ,所以球的表面积为S =4πR 2=π·(2R)2=3πa 2=3π,a =1.7.两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积比是( )A .1:2:3B .1:7:19C .3:4:5D .1:9:27 答案:B解析:考查几何体的体积.可以直接求,也可以用间接法.本题还可以选取特例或特殊值.根据锥体的平行截面性质,如图所示,三个圆锥高的比是1:2:3,从而它们的体积比是1:8:27.圆锥被分成的三部分的体积的比是1:7:19.8.如图所示,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是边长为2的正方形,高为1,M 为线段AB 的中点,则三棱锥C -MC 1D 1的体积为( )A .12B .13C .1D .23答案:D解析:S △C 1D 1C =12×1×2=1,∴VC -MC 1D 1=VM -C 1D 1C =13S △C 1DC·h =13×1×2=23. 9.已知轴截面是正方形的圆柱,高与球的直径相等,则圆柱的表面积和球的表面积的比是( )A .6 5B .5 4C .4 3D .3 2 答案:D解析:设球半径为R ,则圆柱的高为2R ,底面圆的半径为R ,S 柱S 球=2πR 2+2πR·2R 4πR 2=32.10.球面上有A ,B ,C 三点,AB =AC =2,BC =2 2,球心到平面ABC 的距离为1,则球的表面积为( )A .4πB .6πC .12πD .4 3π 答案:C解析:由题意知AB 2+AC 2=BC 2,所以△ABC 为直角三角形,故△ABC 所在圆的圆心在斜边BC 的中点处,则有R 2=12+(2)2=3,所以S 球=4πR 2=4π×3=12π,故选C .二、填空题:本大题共3小题,每小题4分,共12分.把答案填在题中横线上. 11.一个球的表面积是144πcm 2,它的体积是________. 答案:288πcm 3解析:由公式得S =4πR 2=144π,故R =6.则V =4π3R 3=4π3×63=288π.12.已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V =________.答案:1+26解析:该凸多面体由一个正方体及一个正四棱锥组成,体积V =1+13×1×22=1+26.13.现要建造一个长方体形状的仓库,其内部的高为3m ,长和宽的和为20m ,那么仓库的容积的最大值是________m 3.答案:300解析:设仓库的长为x ,则仓库容积为3x(20-x)=-3x 2+60x =-3(x -10)2+300,所以当仓库底面为一边长为10m 的正方形时,容积最大为300m 3.三、解答题:本大题共5小题,共48分,其中第14小题8分,第15~18小题各10分.解答应写出文字说明、证明过程或演算步骤.14.已知圆台的上、下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.解:设圆台的上、下底面半径为r 、R ,母线为l ,则有πr 2+πR 2=π(r +R)l ,所以l =πr 2+πR 2π(r +R )=22+522+5=297.即该圆台的母线长为297.15.长、宽、高分别为80 cm,60 cm,50 cm 的水槽中有水216 000 cm 3. (1)求水槽中水面高度;(2)现在水槽中放入一个直径为30 cm 的铁球,求此时水面的高度(结果保留一位小数). 解:设水面高度为x cm ,(1)由80×60x =216 000得x =45,所以水面高度为45 cm .(2)球体积为43πr 3=4 500π,水槽体积为80×60×50=240 000,由于240 000-216 000=24 000>4 500π,所以80×60x =216 000+4 500π,x =45+1516π≈47.9此时水面高度约为47.9 cm .16.已知三棱柱三个侧面都是矩形,若底面的一边长为2 cm ,另两边长都为3 cm ,侧棱长为4 cm ,求它的体积和表面积.解:由题意设AB =AC =3,BC =2,AA ′=4,则底面BC 边上的高为32-1=22,所以体积为V =12×2×22×4=8 2 cm 3,表面积为S =2×12×2×22+(3+3+2)×4=42+32(cm 2).17.一个高为16的圆锥内接于一个体积为972π的球,在圆锥内又有一个内切球,求: (1)圆锥的侧面积;(2)圆锥的内切球的体积. 解:(1)如图所示,作轴截面,⊙O 1内切于△ABC.设⊙O 的半径为R ,由题意,得43πR 3=972π,R 3=729,R =9,∴CE =18.由已知CD =16,故ED =2.连结AE ,∵CE 是⊙O 的直径,∴CA ⊥AE ,又AB ⊥CE ,∴CA 2=CD·CE =16×18=288,CA =12 2.AD 2=CD·DE =16×2=32,AD =4 2.于是S 圆锥侧=π×4 2×12 2=96π. (2)设内切球半径为r.∵△ABC 的周长为2×(12 2+4 2)=32 2, ∴12r ×32 2=12×8 2×16. ∴r =4,于是V 内切球=43πr 3=2563π.18.斜三棱柱ABC -A 1B 1C 1的底面是边长为2的正三角形,顶点A 1在底面ABC 的射影O 是△ABC 的中心,AA 1与AB 的夹角为45°.(1)求证:AA 1⊥面A 1BC ; (2)求此棱柱的侧面积; (3)求此棱柱的体积. 解:(1)如图所示,∵底面△ABC 为正三角形,点A 1在面ABC 上的射影点O 为△ABC 的中心, ∴点O 在AD 上,(D 为BC 中点). ∵AD ⊥BC ,∴BC ⊥AA 1.又∵A 1点在面ABC 上射影点O 为△ABC 的中心,而△ABC 为正三角形,OA =OB , ∴A 1A =A 1B.又∵∠A 1AB =45°,∴△A 1AB 为等腰直角三角形,即AA 1⊥A 1B. ∵AA 1⊥BC ,A 1B ∩BC =B , ∴AA 1⊥面A 1BC.(2)∵底面△ABC 为正三角形,且点A 1在面ABC 上的射影点O 为△ABC 的中心, ∴侧面AA 1B 1B 与侧面AA 1C 1C 全等,由(1)知侧面BB 1C 1C 为矩形. ∵AB =2,∴S ▱AA 1C 1C =2S △AA 1B=2×(2)2×12=2,S ▱BB 1C 1C =2×2=2 2. ∴S 侧=2×2+2 2=4+2 2.(3)∵A 1O =AA 21-AO 2=(2)2-(233)2=63,∴V 棱柱=Sh =34·AB 2·63=34×4×63= 2.。
练习08 简单几何体的表面积和体积 (原卷版)

专题练习08 简单几何体的表面积和体积一、选择题1.棱长为2的正四面体的表面积是()A.B.C.D.【分析】根据棱长为2的正四面体的表面积是四个边长为2的正三角形面积之和,求出即可.【解答】解:棱长为2的正四面体的表面积是四个边长为2的正三角形面积之和,所以表面积为S=4××2×=4.故选:D.2.已知圆柱的高为2,它的两个底面的圆周在直径为的同一个球的球面上,则圆柱的表面积为()A.B.C.D.【分析】设球的半径为R,圆柱的底面所在的圆的半径为r,由勾股定理可求出r的值,而圆柱的表面积S=2πr2+2×2πr,代入r的值即可得解.【解答】解:设球的半径为R=,圆柱的底面所在的圆的半径为r,则r==.所以圆柱的表面积S=2πr2+2×2πr=10π+4π=(10+4)π.故选:D.3.若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为()A.πB.C.D.【分析】设圆锥的底面圆半径为r,高为h,求出圆锥的侧面积和轴截面面积,列方程求得圆锥的高.【解答】解:设圆锥的底面圆半径为r,高为h;由圆锥的母线长为4,所以圆锥的侧面积为πr•4=4πr;又圆锥的轴截面面积为•2r•h=rh,所以4πr=4rh,解得h=π;所以该圆锥的高为π.故选:A.4.已知一个圆柱的侧面积等于表面积的,且其轴截面的周长是16,则该圆柱的体积是()A.54πB.36πC.27πD.16π【分析】设圆柱的底面半径为r,高为h,由题意列关于r与h的方程组,求得r与h的值,代入圆柱体积公式求解.【解答】解:设圆柱的底面半径为r,高为h,由题意可得,,解得.∴该圆柱的体积是πr2h=16π.故选:D.5.正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,则棱台的侧面积为()A.4B.8C.4D.8【分析】利用已知条件求出斜高,然后求解棱台的侧面积即可.【解答】解:正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,所以棱台的斜高为:=.所以棱台的侧面积是:4××=8.故选:D.6.已知某圆柱的底面周长为4,体积为,矩形ABCD是该圆柱的轴截面,则在此圆柱的侧面上,从B到D的路径中,最短路径的长度为()A.2B.C.D.【分析】设圆柱的底面半径为r,高为h,则解得h.进而考点此圆柱的侧面上从B到D的最短路径长度.【解答】解:设圆柱的底面半径为r,高为h,则解得h=2.故圆柱的侧面展开图是长为4,宽为2的矩形,则在此圆柱的侧面上从B到D的最短路径长度为.故选:D.7.设P为单位立方体ABCD﹣A1B1C1D1上的一点,则P A1+PC1的最小值为()A.B.C.2﹣D.前三个答案都不对【分析】直线结合三角形的两边之和大于第三边即可求解.【解答】解:因为P A 1+PC1≥,当且仅当P在线段A1C1上时等号成立,所以P A1+PC1的最小值为,故选:D.8.四面体ABCD中,△ABD和△CBD均为正三角形,且它们所在平面互相垂直,已知AB=2,则四面体ABCD外接球的表面积为()A.12πB.C.D.16π【分析】先确定球心的位置,然后结合球的性质R2=r2+d2求出R,再利用球的表面积公式可求.【解答】解:设三角形BCD外接圆半径r,圆心F,球的半径R,球心O,取BD中点M,由△ABD和△CBD均为正三角形,且它们所在平面互相垂直可得AM⊥BD,CM⊥BD,AM⊥平面BCD,过F作平面BCD的垂线,过A作MF的平行线,两直线交于E,则四边形AMCE为矩形,O在EF上,EF=PM=,由正弦定理得=2r,即r=,故MF=,设OF=d,则所以R2==()2+()2,解得d=,R2=,则四面体ABCD外接球的表面积S=4πR2=.故选:C.二、填空题9.已知边长为1的正△ABC的三点都在球O的球面上,AO的延长线与球面的交点为S,若三棱锥S﹣ABC的体积为,则球O的体积为.【分析】根据题意作出图形,欲求球O的表面积,只须求球的半径r.利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.【解答】解:设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,作SD⊥平面ABC交CO1的延长线与D.OO1==,∴高SD=2OO1,∵△ABC是边长为1的正三角形,三棱锥S﹣ABC的体积为,∴S△ABC=,∴V三棱锥S﹣ABC=,h=,∴=,∴R=1.则球O的体积为=,故答案为:.10.一个漏斗的上半部分是一个长方体,下半部分是一个四棱锥,两部分的高都为米,公共的底面是边长为1米的正方形,那么这个漏斗的容积为米.【分析】由已知分别求出长方体与棱锥的体积,作和得答案.【解答】解:由长方体体积公式可得,容器上半部分的体积,由棱锥体积公式可得,容器上半部分的体积.则这个漏斗的容积为V=.故答案为:.11.将一个斜边长为4的等腰直角三角形以其一直角边所在直线为旋转轴旋转一周,所得几何体的表面积为.【分析】先求出等腰直角三角形的直角边长,进而求出旋转体圆锥的底面半径和母线,再利用圆锥的表面积公式即可求出结果.【解答】解:∵等腰直角三角形的斜边长为4,∴直角边长为2,由题意可知所得几何体是圆锥,其底面圆的半径r=,母线长l=4,则其表面积为,故答案为:.12.如图,在圆锥SO中,AB为底面圆O的直径,AB=6,且cos∠BSA=,则圆锥SO的侧面积为15π.【分析】连接SO,由圆锥的对称性可知cos∠ASO=,再利用同角三角函数间的基本关系可得sin∠ASO=,所以SA=5,再利用圆锥的侧面积公式,即可求出结果.【解答】解:连接SO,,由题意知∠ASO=,所以cos∠BSA=2cos2∠ASO﹣1=,所以cos∠ASO=,所以sin∠ASO==,易知AO=3,所以SA=5,所以圆锥SO的侧面积为π×3×5=15π.故答案为:15π.13.如图,在三棱锥A﹣BCD中,BC=CD=BD=2,AB=AC=AD=2a,若该三棱锥的侧面积是底面积的倍,则该三棱锥外接球的表面积为12π.【分析】取BC边的中点E,连结AE,如图所示,△BCD外接圆的圆心为F,三棱锥A﹣BCD外接球的球心为O,求出侧面积和底面积,从而可求出a的值,再利用球的几何性质结合勾股定理,求出球的半径,利用球的表面积公式求解即可.【解答】解:取BC边的中点E,连结AE,如图所示,△BCD外接圆的圆心为F,三棱锥A﹣BCD外接球的球心为O,因为AB=AC且点E为BC的中点,所以,由此可知该三棱锥的侧面积,底面△BCD的面积为,所以,解得a=1,设三棱锥A﹣BCD外接球半径为R,OF=x,因为AB=AC=AD=2,所以点A在底面BCD上的射影为点F,因为AB<BC,故三棱锥外接球球心O在直线AF的延长线上,BF为△BCD外接圆的半径,所以,在Rt△ABF中,由勾股定理可得①,在Rt△OBF中,由勾股定理可得②,由①②解得,所以外接球的表面积S=4πR2=12π.故答案为:12π.三、解答题14.用斜二测画法画一个底面边长为4cm,高为3cm的正四棱锥P﹣ABCD的直观图,点P在底面的投影是正方形的中心O,计算它的表面积.【分析】正四棱锥P﹣ABCD的直观图的高不变,还是3,底面正方形的直观图变成了平行四边形,此平行四边形的长为4,宽为2,一个锐角等于45°,求出中心O到平行四边形各边的距离,勾股定理求出各侧面三角形的高,表面积等于底面面积和四个侧面的面积之和.【解答】解:正四棱锥P﹣ABCD的直观图的高不变,还是3,底面正方形的直观图变成了平行四边形,此平行四边形的长为4,宽为2,一个锐角等于45°,故底面的面积为4×=4.正方形的中心O到平行四边形较长的边的距离为,故以平行四边形较长的边为底边的侧面三角形的高为=,正方形的中心O到平行四边形较短的边的距离为,故以平行四边形较短的边为底边的侧面三角形的高为=,故直观图的表面积等于4+2×(4×)+2×(2×)=4+2+2.15.已知某圆锥的轴截面是面积为的等边三角形,球O内切于该圆锥.(1)求该圆锥的高;(2)求内切球O的体积.【分析】(1)作出该圆锥的轴截面,求解BC,然后求解圆锥的高.(2)通过Rt△AOE~Rt△ACD,设OE=R,求出R,然后求解圆锥的内切球体积即可.【解答】解:作出该圆锥的轴截面如图所示:(1)依题意,,解得BC=2,故BD=CD=1,,即该圆锥的高为;(2)依题意,Rt△AOE~Rt△ACD,故;设OE=R,则,故,故,故圆锥的内切球体积.16.已知正四棱台ABCD﹣A1B1C1D1上、下底面的边长分别为4、10,侧棱长为6.(1)求正四棱台的表面积;(2)求三棱锥B﹣AC1D的体积.【分析】(1)由已知求得正四棱台的斜高,然后利用正方形面积公式及梯形面积公式求正四棱台的表面积;(2)求出正四棱台的高,利用等体积法求三棱锥B﹣AC1D的体积.【解答】解:(1)如图,ABCD﹣A1B1C1D1为正四棱台,AB=4,A1B1=10,AA1=6.在等腰梯形A1B1BA中,过A作AE⊥A1B1,可得,求得,∴正四棱台的表面积;(2)连接AC,A 1C1,可得,,过A作AG⊥A1C1,可得,∴,则==.。
新必修二-第八章.立体几何初步-8.3简单几何体的表面积与体积(知识点五:多面体和旋转体表面上的最短距离问

8.3简单几何体的表面积与体积(知识点五:多面体和旋转体表面上的最短距离问题)一.选择题(共30小题)1.在棱长为1的正方体ABCD﹣A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为()A.B.C.D.2.如图,在正三棱锥P﹣ABC中,∠APB=∠BPC=∠CP A=30°,P A=PB=PC=2一只虫子从A点出发,绕三棱锥的三个侧面爬行一周后,又回到A点,则虫子爬行的最短距离是()A.B.C.D.3.圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A.cm B.5cm C.cm D.7cm4.已知某圆柱的底面周长为12,高为2,矩形ABCD是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为()A.B.C.3D.25.如图,圆锥顶点为P,底面圆心为O,过轴PO的截面P AB,C为P A中点,P A=4,PO=6,则从点C经圆锥侧面到点B的最短距离为()A.2B.2C.6D.26.如图,一个无盖的正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,则蚂蚁爬行的最短距离是()A.B.1C.D.2+7.如图所示,在棱长为1的正方体ABCD﹣A1B1C1D1中,P是A1B上一动点,则AP+D1P的最小值为()A.2B.C.D.8.如图,一竖立在水平地面上的圆锥形物体的母线长为4m,底面半径为1m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为()A.4B.4m C.2D.2m9.如图,已知正三棱柱ABC﹣A1B1C1的底面边长为2cm,高为5cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为()A.5 cm B.12 cm C.13 cm D.25 cm10.古代数学名著《数学九章》中有云:“有木长三丈,围之八尺,葛生其下,缠木两周,上与木齐,问葛长几何?”意思为:圆木长3丈,圆周为8尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:1丈即10尺)()A.32尺B.34尺C.36尺D.38尺11.若圆锥的母线长是定值l,记顶角为θ,过顶点的最大截面积为S,则S=f(θ)的图象是()A.B.C.D.12.有一长方体木块,其顶点为ABCD﹣A1B1C1D1,AB=3,BC=2,AA1=1,一小虫从长方体木块的一顶点A绕其表面爬行到另一顶点C1,则小虫爬行的最短距离为()A.B.3C.2D.13.如图,S﹣ABC是正三棱锥且侧棱长为a,E,F分别是SA,SC上的动点,三角形BEF 的周长的最小值为,则侧棱SA,SC的夹角为()A.30°B.60°C.20°D.90°14.在长方体ABCD﹣A1B1C1D1中,AA1=3,AD=4,AB=5,由A在表面到达C1的最短行程为()A.12B.C.D.15.小蚂蚁的家住在长方体ABCD﹣A1B1C1D1的A处,小蚂蚁的奶奶家住在C1处,三条棱长分别是AA1=1,AB=2,AD=3,小蚂蚁从A点出发,沿长方体的表面到小蚂蚁奶奶家C1的最短距离是()A.B.C.D.16.如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有()条.A.40B.60C.80D.12017.圆柱的轴截面(经过圆柱的轴所作的截面)是边长为5cm的正方形ABCD,则圆柱侧面上从A到C的最短距离为()A.10cm B.cm C.5cm D.5cm 18.如图,长方体长AB=5cm,宽BC=4cm,高CC′=3cm,一只蚂蚁要从长方体的一个顶点A沿表面爬行到顶点C′处觅食,则最短路径为()A.3B.4C.D.519.在正方体ABCD﹣A1B1C1D1,点P在线段A1D1上运动,点Q在线段AB上运动,则线段PQ的中点轨迹是()A.线段B.三角形C.正方形D.由正方形围成的区域(含边界)20.如图,在四棱锥P﹣ABCD中,AB⊥AD,BC∥AD,P A=AD=4,AB=BC=2,P A⊥平面ABCD,点E是线段AB的中点,点F在线段P A上,且EF∥平面PCD,PD与平面CEF交于点H,则线段CH的长度为()A.B.2C.2D.221.已知正三棱柱ABC﹣A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为()A.4cm B.12cm C.2cm D.13cm22.点M为棱长是2的正方体ABCD﹣A1B1C1D1的内切球O球面上的动点,点N为B1C1的中点,若满足DM⊥BN,则动点M的轨迹的长度为()A.B.C.D.23.已知底面为边长为2的正方形,侧棱长为1的直四棱柱ABCD﹣A1B1C1D1中,P是面A1B1C1D1上的动点.给出以下四个结论中,正确的个数是()①与点D距离为的点P形成一条曲线,则该曲线的长度是;②若DP∥面ACB1,则DP与面ACC1A1所成角的正切值取值范围是;③若,则DP在该四棱柱六个面上的正投影长度之和的最大值为.A.0B.1C.2D.324.如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=,点E为棱AB上的动点,则D1E+CE的最小值为()A.B.C.D.25.如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是()A.B.π+1C.D.26.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:1丈等于10尺)()A.29尺B.24尺C.26尺D.30尺27.已知正三棱柱ABC﹣A1B1C1的底面边长为2,高为5,则一质点自A点出发,沿着三棱柱的侧面绕行一周到达点A1的最短路线的长为()A.10B.C.6D.28.圆锥的底面半径为1,母线长为2,顶点为S,轴截面为△SAB,C为SB的中点.若由A点绕侧面至点C,则最短路线长为()A.B.3C.D.29.在长方体ABCD﹣A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为()A.3B.4C.D.530.在正四棱柱ABCD﹣A1B1C1D1中,AB=,AA1=2,设四棱柱的外接球的球心为O,动点P在正方形ABCD的边上,射线OP交球O的表面于点M,现点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径长为()A.B.2πC.D.4π二.填空题(共20小题)31.已知长方体ABCD﹣A'B'C'D'的棱长分别为3、4、5,一只蚂蚁由长方体的顶点A'出发,沿长方体表面爬行到点C,则蚂蚁爬行的最短路程长为.32.已知圆台上底面半径为,下底面半径为,母线长为2,AB为圆台母线,一只蚂蚁从点A出发绕圆台侧面一圈到点B,则蚂蚁经过的最短路径长度为.33.在三棱柱ABC﹣A1B1C1中,若AB=4,BC=3,AA1=12.且AB⊥BC,AA1⊥底面ABC,E为AA1的中点,从E拉一条绳子绕过侧棱CC1到达B点的最短绳长为34.已知正四棱锥P﹣ABCD的棱长为2a,侧面等腰三角形的顶角为30°,则从点A出发,环绕侧面一周后回到A点的最短路程等于.35.已知三棱锥P﹣ABC,P A=2,M为棱BC的中点,N是三棱锥P﹣ABC面P AC上的动点,且MN∥平面P AB,则N点轨迹长度为.36.P是棱长为4的正方体ABCD﹣A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点P的最短路程是37.圆锥底面半径为10,母线长为30,从底面圆周上一点,绕侧面一周再回到该点的最短路线的长度是.38.圆锥底面半径为1,高为,点P是底面圆周上一点,则一动点从点P出发,绕圆锥侧面一圈之后回到点P,则绕行的最短距离是.39.已知在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是线段A1B1上的动点,点F是线段BC上的动点,则AE+EF的最小值是.40.如图,直三棱柱ABC﹣A1B1C1中,AB=1,BC=2,AC=,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,△AMC1的面积为.41.如图,已知正三棱柱ABC﹣A1B1C1中,AB=,AA1=4,若点P从点A出发,沿着正三棱柱的表面,经过棱A1B1运动到点C1,则点P运动的最短路程为.42.如图,已知正方体ABCD﹣A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1,在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长,则当点P运动时,|HP|2的范围是.43.在三棱锥P﹣ABC中,AP,AB,AC两两垂直,且AP=AB=AC=.若点D,E分别在棱PB,PC上运动(都不含端点),则AD+DE+EA的最小值为.44.正方体ABCD﹣A1B1C1D1的棱长为1,P是线段A1B上的一点,则AP+D1P的最小值是.45.如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=6,BC=CC1=,P是B1C 上的一个动点,则AP+PC1的最小值为.46.已知侧棱长为8的正三棱锥S﹣ABC如图所示,其侧面是顶角为20°的等腰三角形,一只蚂蚁从点A出发,围绕棱锥侧面爬行两周后又回到点A,则蚂蚁爬行的最短路程为.47.如图,圆锥顶点为P,底面圆心为O,过轴PO的截面△P AB,C为P A中点,P A=,PO=6,则从点C经圆锥侧面到点B的最短距离为.48.如图,已知圆柱体底面圆的半径为cm,高为2cm,AB、CD分别是两底面的直径,AD、BC是母线.若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是cm(结果保留根式).49.如图,长方体ABCD﹣A1B l∁l D1中,AD=3,AA l=4,AB=5,则从A点沿表面到∁l的最短距离为.50.如图,某圆柱的高为4,底面周长为16,∠AOB=90°,则在此圆柱侧面上,从B到C 的路径中,最短路径的长度为.8.3简单几何体的表面积与体积(知识点五:多面体和旋转体表面上的最短距离问题)参考答案与试题解析一.选择题(共30小题)1.【分析】连接BC1,得出点P、E、F在平面BC1D1中,问题转化为在平面内直线BD1上取一点P,求点P到定点E的距离与到定直线的距离的和的最小值问题,利用平面直角坐标系,求出点E关于直线BD1的坐标即可.【解答】解:连接BC1,则BC1∩B1C=E,点P、E、F在平面BC1D1中,且BC1⊥C1D1,C1D1=1,BC1=,如图1所示;在Rt△BC1D1中,以C1D1为x轴,C1B为y轴,建立平面直角坐标系,如图2所示;则D1(1,0),B(0,),E(0,);设点E关于直线BD1的对称点为E′,∵BD1的方程为x+=1①,∴k EE′=﹣=,∴直线EE′的方程为y=x+②,由①②组成方程组,解得,直线EE′与BD1的交点M(,);所以对称点E′(,),∴PE+PF=PE′+PF≥E′F=.故选:D.【点评】本题考查了空间几何体中距离和的计算问题,解题的关键是把空间问题转化为平面问题解答,是难题.2.【分析】将三棱锥的侧面展开,从A点虫子爬行绕三棱锥侧面一圈回到点A的距离中,虫子爬行的最短距离,可转化为求AA1的长度,利用勾股定理即可得到答案.【解答】解:设过点A作截面AEF与PB、PC侧棱分别交于E、F两点,将三棱锥由P A 展开,则∠AP A1=90°,AA1虫子爬行从点A沿侧面到棱PB上的点E处,再到棱PC上的点F处,然后回到点A 的最短距离,∵P A=2,∴由勾股定理可得AA1==2.虫子爬行的最短距离2.故选:D.【点评】本题考查的知识点是多面体和旋转体表面上的最短距离问题,其中将三棱锥的侧面展开,将空间问题转化为平面上两点间距离问题,是解答本题的关键.3.【分析】利用圆柱的侧面展开图是矩形,结合题意即可求出最短距离.【解答】解:如图所示,圆柱的底面周长为6cm,则侧面展开图的一半为A′CBD,高BC=6cm,所以PC=BC=4cm,A′C=3cm;所以从A点沿着圆柱体的表面到点P的最短距离为=5(cm).故选:B.【点评】本题考查了圆柱的侧面展开图应用问题,是基础题.4.【分析】由圆柱的侧面展开图是矩形,利用勾股定理求解.【解答】解:圆柱的侧面展开图如图,圆柱的侧面展开图是矩形,且矩形的长为12,宽为2,则在此圆柱侧面上从A到C的最短路径为线段AC,AC=.故选:A.【点评】本题考查圆柱侧面展开图中的最短距离问题,是基础题.5.【分析】由题意画出图形,得到圆锥沿母线剪开再展开的图形,由勾股定理求解.【解答】解:如图,沿圆锥母线P A剪开再展开,∵P A=4,PO=6,∴OA=,则圆锥底面周长为,展开后所得扇形为半圆,B到B′处,则从点C经圆锥侧面到点B的最短距离为.故选:A.【点评】本题考查旋转体表面上的最短距离问题,考查弧长公式的应用,是基础题.6.【分析】一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,蚂蚁爬行的最短距离是如图所示的BM的长,利用勾股定理能求出结果.【解答】解:∵一只蚂蚁从盒外的B点沿正方形的表面爬到盒内的M点,∴蚂蚁爬行的最短距离是如图所示的BM的长,∵无盖的正方体盒子的棱长为2,BC的中点为M,∴A1B=2+2=4,A1M=1,∴BM==.∴蚂蚁爬行的最短距离是.故选:C.【点评】本题考查蚂蚁爬行的最短距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.7.【分析】把对角面A1C绕A1B旋转,使其与△AA1B在同一平面上,连接AD1并求出,根据平面内两点之间线段最短,可知就是最小值.【解答】解:把对角面A1C绕A1B旋转,使其与△AA1B在同一平面上,连接AD1,则在△AA1D中,AD1==为所求的最小值.故选:D.【点评】本题的考点是点、线、面间的距离计算,主要考查考查棱柱的结构特征,考查平面内两点之间线段,最短考查计算能力,空间想象能力,是基础题.8.【分析】把圆锥沿P点所在母线剪开,然后展开,利用圆锥底面周长等于扇形弧长求得扇形的圆心角,求解三角形得答案.【解答】解:把圆锥沿P点所在母线剪开,然后展开如图,设展开后所得扇形的圆心角的弧度数为θ,则2π×1=4θ,得θ=.在Rt△POP′中,由OP=OP′=4,可得小虫爬行的最短路程为.故选:A.【点评】本题考查旋转体表面上的最短距离问题,考查弧长公式的应用,是基础题.9.【分析】将三棱柱展开两次如图,不难发现最短距离是六个矩形对角线的连线,正好相当于绕三棱柱转两次的最短路径.【解答】解:将正三棱柱ABC﹣A1B1C1沿侧棱展开,再拼接一次,其侧面展开图如图所示,在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6×2=12,宽等于5,由勾股定理d=.故选:C.【点评】本题考查棱柱的结构特征,考查空间想象能力和思维能力,考查数学转化思想方法,是中档题.10.【分析】根据题意知圆柱的侧面展开图是矩形,葛藤长是两个矩形相连所成对角线的长.【解答】解:由题意,圆柱的侧面展开图是矩形,如图所示;一条直角边(即圆木的高)长30尺,另一条直角边长8×2=16尺,因此葛藤长为=34(尺).故选:B.【点评】本题考查了旋转体侧面上的最短距离计算问题,正确运用圆柱的侧面展开图是解题的关键.11.【分析】通过顶角的范围,求出截面最大值的面积的表达式,判断图象即可.【解答】解:当0<θ≤时,S=f(θ)=l2sinθ;当<θ<π时,S=f(θ)=l2.故选:D.【点评】本题考查圆锥的截面图象的面积的最值的求法,考查分类讨论思想以及分析问题解决问题的能力.12.【分析】分三种情况,将两个平面展成一个平面后,对角线长最短,比较谁更小,即可.【解答】解:分三种情况:①当小虫沿表面经过棱BB1时,将平面A1ABB1和平面B1BCC1展成一个平面,则小虫沿对角线AC1爬,最短.此时最短距离为=;②当小虫沿着表面经过棱A1B1时,将平面A1ABB1和平面A1B1C1D1展成一个平面,则小虫沿对角线AC爬,最短距离为:3;③当小虫沿着表面经过棱BC时,将平面ABCD和平面1BBCC1展成一个平面,则小虫沿对角线AC1爬,最短距离为:2,比较,3,2的大小可知,3最小.故选:B.【点评】本题考查了多面体和旋转体表面上的最短距离.属中档题.13.【分析】由题意,三角形BEF的周长的最小值为,即沿多面体表面从B到B经过的长度的最小值为,可将此几何体沿SB剪开,变多面体表面上的轨迹长度问题为平面上的两点间距离问题,展开后得到等腰三角形SBB',可求得此时∠BSB'=90°,再由正三棱锥的性质得SA,SC的夹角为30°,选出正确选项【解答】解:把正三棱锥沿SB剪开,并展开,形成三个全等的等腰三角形,△SBC、△SCA、△SAB',连接BB',交SC于F,交SA于E,则线段BB′就是△BEF的最小周长,BB'=a,又SB=SB'=a,根据勾股定理,SB2+SB'2=BB'2=2a2,△SBB'是等腰直角三角形,∴∠BSB'=90°,∴∠ASC=90°×=30°,∴侧棱SA,SC的夹角为30°故选:A.【点评】本题考查了多面体表面上的距离问题及线线夹角求法问题,解题的关键是将多面体展开,将多面体表面上的轨迹长度问题变化为平面上的两点间距离问题研究,这里用到了几何中常用的降维的技巧,化体为面是一个重要的技巧.本题易因为没有把立体问题转化为平面问题研究而导致无法求解.14.【分析】从A点沿不同的表面到C1,其距离可采用将长方体展开的方式求得.【解答】解:从A点沿不同的表面到C1,其距离可采用将长方体展开的方式求得,分别是=,=4,=3∴从A点沿表面到C1的最短距离为.故选:B.【点评】本题考查从A点沿表面到C1的最短距离的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.15.【分析】根据题意知蚂蚁所走的路线有三种情况,利用勾股定理能求出小蚂蚁从A点出发,沿长方体的表面到小蚂蚁奶奶家C1的最短距离.【解答】解:根据题意知:蚂蚁所走的路线有三种情况,如下图所示①②③,由勾股定理得:图①中,AC1==3,图②中,AC1==,图③中,AC1==2.故小蚂蚁从A点出发,沿长方体的表面到小蚂蚁奶奶家C1的最短距离是3.故选:B.【点评】本题考查最短距离的求法,考查长方体的性质、结构特征等基础知识,考查学生分析解决问题的能力,是中档题.16.【分析】由题意,从A到C最短路径有C53=10条,由点C沿着置于水平面的长方体的棱爬行至顶点B,最短路径有C42=6条,即可求出它可以爬行的不同的最短路径.【解答】解:由题意,从A到C最短路径有C53=10条,由点C沿着置于水平面的长方体的棱爬行至顶点B,最短路径有C42=6条,∴它可以爬行的不同的最短路径有10×6=60条,故选:B.【点评】本题考查最短路径问题,考查组合知识,属于中档题.17.【分析】把圆柱沿着一条母线剪开后展开,然后利用直角三角形中的勾股定理求解从A 到C的最短距离.【解答】解:如图,∵圆柱的轴截面是边长为5cm的正方形,展开后为矩形ABA′B′,BC为圆柱底面圆的周长的一半,等于,AB=5,∴圆柱侧面上从A到C的最短距离为==(cm).故选:B.【点评】本题考查旋转体中的最短距离问题,关键在于对旋转体的剪展,考查运算求解能力,考查函数与方程思想,是中档题.18.【分析】由题意展开长方体,能求出结果.【解答】解:如图(1),AC′==,如图(2),AC′==,如图(3),AC′==4,∴AC′的最小值为.故选:C.【点评】本题考查最短路径的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.19.【分析】分别固定点P、Q,移动点Q、P,可得PQ的中点轨迹.【解答】解:如图,当P与A1重合,Q在AB上运动时,PQ中点为线段EF,当P与D1重合,Q在AB上运动时,PQ中点为线段HG,Q与A重合,P在A1D1上运动时,PQ中点为线段EH,Q与B重合,P在A1D1上运动时,PQ中点为线段FG.∴线段PQ的中点轨迹是正方形EFGH.故选:C.【点评】本题考查轨迹方程,考查立体几何与解析几何的综合,体现动与不动思想方法的运用,是中档题.20.【分析】取P A的中点M,PD的中点Nl,则BM∥平面PCD,故而H为PD的中点,证明PC⊥CD得出CH=PD.【解答】解:取P A的中点M,PD的中点N,由中位线定理可得MN AD BC,∴四边形BCNM是平行四边形,∴BM∥CN,∴BM∥平面PCD,又EF∥平面PCD,∴BM∥EF,即F为AM的中点,∵PD与平面CEF交于点H,∴H与N重合,即H为PD的中点,∵P A=AD=4,AB=BC=2,∴PD=4,AC=2,PC=2,由直角梯形知识可知CD=2,∴PC2+CD2=PD2,即PC⊥CD,∴CH=PD=2.故选:C.【点评】本题考查了线面平行的性质与判定,属于中档题.21.【分析】将三棱柱展开,不难发现最短距离是3个矩形对角线的连线,正好相当于绕三棱柱转1次的最短路径.【解答】解:将正三棱柱ABC﹣A1B1C1沿侧棱展开,在展开图中,最短距离是6个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于12,宽等于4,由勾股定理d==4.故选:A.【点评】本题考查棱柱的结构特征,空间想象能力,几何体的展开与折叠,体现了转化(空间问题转化为平面问题,化曲为直)的思想方法.22.【分析】取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,可得NB⊥面DCH,即动点M的轨迹就是平面DCH与内切球O的交线,求得截面圆的半径r=,动点M的轨迹的长度为截面圆的周长2πr【解答】解:如图,正方体ABCD﹣A1B1C1D1的内切球O的半径R=,由题意,取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,∴NB⊥面DCH,∴动点M的轨迹就是平面DCH与内切球O的交线,∵正方体ABCD﹣A1B1C1D1的棱长是2,∴O到平面DCH的距离为d=,截面圆的半径r=,动点M的轨迹的长度为截面圆的周长2πr=.故选:D【点评】本题考查了空间动点轨迹问题,弄清动点的轨迹是解题关键,属于难题.23.【分析】①与点D距离为的点P形成以D1为圆心,半径为的圆弧MN,利用弧长公式,可得结论;②当P在A1(或C1)时,DP与面ACC1A1所成角∠DA1O(或∠DC1O)的正切值为最小,当P在O1时,DP与面ACC1A1所成角∠DO1O的正切值为最大,可得正切值取值范围是;③设P(x,y,1),则x2+y2+1=3,即x2+y2=2,可得DP在前后、左右、上下面上的正投影长,即可求出六个面上的正投影长度之和.【解答】解:如图,①错误,与点D距离为的点P形成以D1为圆心,半径为的圆弧MN,长度为=;②错误,因为面A1DC1∥面ACB1,所以点P必须在面对角线A1C1上运动,当P在A1(或C1)时,DP与面ACC1A1所成角∠DA1O(或∠DC1O)的正切值为最小,当P 在O1时,DP与面ACC1A1所成角∠DO1O的正切值为最大,所以正切值取值范围是;③正确,设P(x,y,1),则x2+y2+1=3,即x2+y2=2,DP在前后、左右、上下面上的正投影长分别为,所以六个面上的正投影长度之和为,当且仅当P在O1时取等号.故选:B.【点评】本题以命题的真假判断为载体,考查了轨迹问题、线面角、正投影等知识点,综合性强,难度较大.24.【分析】连结D1A,延长至G,使得AG=AD,连结C1B,延长至F,使得BF=BC,连结EF,连结D1F,则D1F为D1E+CE的最小值,由此能求出D1E+CE的最小值.【解答】解:画出几何体的图形,连结D1A,延长至G,使得AG=AD,连结C1B,延长至F,使得BF=BC,连结EF,则ABFG为正方形,连结D1F,则D1F为D1E+CE的最小值,D1F==.∴D1E+CE取最小值.故选:B.【点评】本题考查线段和的最小值的求法,考查学生分析解决问题的能力,正确转化是关键,是中档题.25.【分析】画出圆柱的侧面展开图,根据对称性,求出AQ+PQ的最小值就是AE的长,求解即可.【解答】解:侧面展开后得矩形ABCD,其中AB=π,AD=2问题转化为在CD上找一点Q使AQ+PQ最短作P关于CD的对称点E,连接AE,令AE与CD交于点Q,则得AQ+PQ的最小值就是AE为.故选:D.【点评】本题考查求曲面上最短路程问题,通常考虑侧面展开,考查转化思想,计算能力,是中档题.26.【分析】由题意,圆柱的侧面展开图是矩形,一条直角边(即木棍的高)长24尺,另一条直角边长5×2=10(尺),利用勾股定理,可得结论.【解答】解:由题意,圆柱的侧面展开图是矩形,一条直角边(即木棍的高)长24尺,另一条直角边长5×2=10(尺),因此葛藤长=26(尺).故选:C.【点评】本题考查旋转体表面上的最短距离问题,考查学生的计算能力,正确运用圆柱的侧面展开图是关键.27.【分析】将三棱柱展开,不难发现最短距离是3个矩形对角线的连线,正好相当于绕三棱柱转1次的最短路径.【解答】解:将正三棱柱ABC﹣A1B1C1沿侧棱展开,在展开图中,最短距离是3个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于3×2=6,宽等于5,由勾股定理d==故选:D.【点评】本题考查棱柱的结构特征,空间想象能力,几何体的展开与折叠,体现了转化(空间问题转化为平面问题,化曲为直)的思想方法.28.【分析】求出圆锥底面圆的周长,则以SA为一边,将圆锥展开,就得到一个以S为圆心,以SA为半径的扇形,根据弧长公式求出展开后扇形的圆心角,根据勾股定理求出结论.【解答】解:圆锥底面是以AB为直径的圆,圆的周长是2π,以SA为一边,将圆锥展开,就得到一个以S为圆心,以SA为半径的扇形,弧长是l=2π,母线长为2,展开后的圆心角是π,则由A点绕侧面至点C,最短路线长为=,故选:C.【点评】本题考查了圆锥的计算,平面展开﹣最短路线问题,勾股定理,弧长公式等知识点的应用,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.29.【分析】由题意画出图形,把问题转化为从小长方体PMNG﹣A1HQD1的一个顶点P到另一顶点的表面最短距离问题.分类剪展求出最小值,求最小值中的最小者得答案.【解答】解:如图,∵P,Q分别为棱AA1,C1D1的中点,∴问题可转化为从小长方体PMNG﹣A1HQD1的一个顶点P到另一顶点的表面最短距离问题.共有三种剪展方法:沿QH剪开再展开,此时最短距离为l=;沿QN剪开再展开,此时最短距离为l=;沿QD1剪开再展开,此时最短距离为l=.∴从点P出发,沿长方体表面到达点Q的最短路径的长度为.故选:B.【点评】本题考查多面体表面上的最短距离问题,考查分类讨论和数形结合的解题思想方法,想到剪展的所有情况是解题的关键,是中档题.30.【分析】由题意,点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径是四段大圆上的相等的弧,求出,∠AOB=,利用弧长公式,即可得出结论.【解答】解:由题意,点P从点A出发,沿着A→B→C→D→A运动一次,则点M经过的路径是四段大圆上的相等的弧.∵正四棱柱ABCD﹣A1B1C1D1中,AB=,AA1=2,∴四棱柱的外接球的直径为其对角线,长度为=2,∴四棱柱的外接球的半径为,∴∠AOB=,∴AB所在大圆,所对的弧长为=,∴点M经过的路径长为.故选:A.【点评】本题考查弧长公式,考查学生的计算能力,确定点M经过的路径是四段大圆上的相等的弧是关键.二.填空题(共20小题)31.【分析】根据题意知从A′沿表面运动到C有三种方案,结合图形求出它们可能的路程长度,比较即可.【解答】解:从长方体一条对角线的一个端点A′出发,沿表面运动到另一个端点C,有三种方案,如图是它们的三种部分侧面展开图;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题3.如图所示,三棱锥中,,
,, 求三棱锥的体积(要求用四中不同的方法).
考点三 组合体的表面积和体积
问题3.正三棱柱的底面边长为,高为,则它的外接球的表面积为
_____
(届高三黑龙江双鸭山一中期中文(在长方体中,棱的长度分别为,若 长方体的各顶点都在球的表面上,则球的表面积为
考点四 几何体表面折线段长的最值
课题:简单几何体的面积和体积
考纲要求:了解球、棱柱、棱锥、台的表面积和体积的计算公式 教材复习
,,,, , ,, 球的体积公式:,表面积公式:; 正方体和长方体的外接球的直径等与其体对角线长.
基本知识方法
解决有关球、棱柱、棱锥、台的表面积和体积的计算的关键认清几何体 的类别,然后按有关公式计算; 组合几何体及有关几何体的切、接问 题关键是弄清切、接的几何元素的位置关系和数量关系.体积的计算五 种方法:直接、转换、分割、补形和几何体体积间的关系.
(宁夏)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱 柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为,则这个 球的体积为
(福建)若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的 表面积是
(北京)某三棱锥的三视图如图所示, 该三梭锥的表面积是
问题4.(江西)如图,在直三棱柱中,底面为直角三角形,,,,
是上一动点,则的最小值
是
课后作业:
长方体的过一个顶点的三条棱长的比是∶∶,对角线长为,则这个长方
体的 体积是
一个正三棱台的上、下底面边长分别是和,高是. 求三棱台的斜高;求三棱台的侧面积和表面积.
三棱锥一条侧棱长为,和这条棱相对的棱长是,其余四条棱长都是,求 棱锥的体积.
典例分析:
考点一 简单几何体的表面积
问题1.一个长方体全面积是,所有棱长的和是,求长方体的对角线长.
一个长方体共一顶点的三个面的面积分别是
,求这个长方体对角线的长.
考点二 简单几何体的体积
问题2.如图,三棱柱中,若、分别
为、 的中点,平面将三棱柱分成体积 为、的两部分,那么:
如图所示,在棱长为的正方体中,是上一点,且,则多面体的体积为
(天津)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三 条棱的长分别为,则此球的表面积为
(江苏)在平面上,若两个正三角形的边长的比为:,则它们的面积比 为:,类似地,在空间,若两个正四面体的棱长的比为:,则它ห้องสมุดไป่ตู้的体 积比为
(江西文)体积为的一个正方体,其全面积与球的表面积相等,则球的 体积等于
走向高考:
(新课标全国) 已知三棱锥 的所有顶点都在球 的求面上, 是边长为 的正三角形, 为球 的直径,且 ;则此棱锥的体积为
(江苏)如图,在三棱柱中,
分别是的中点,设三棱 锥的体积为,三棱柱的 体积为,则
(陕西)若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多 面体的体积为高.考.资 .源 .
