波的能量密度
波的能流密度强度公式

波的能流密度强度公式全文共四篇示例,供读者参考第一篇示例:波的能流密度强度公式是描述波动能量传播和传递速率的重要公式。
能流密度强度是指单位面积上通过的波动能量流量,可以用来衡量波在介质中传播的强度和速率。
在物理学和工程学中,波动现象是非常常见的,因此研究波的能流密度强度公式对于理解和控制波动现象非常重要。
波的能流密度强度公式可以根据不同类型的波以及波动现象的特性而有所不同,但一般情况下,波的能流密度强度与波的振幅和频率有关。
在传统的经典力学中,波的能流密度强度可以通过以下公式来表示:\[ P = \frac{1}{2} \sqrt{\frac{u}{\rho}} v^2 \]P表示能流密度强度,u表示波的线密度或者表面密度,ρ表示介质的密度,ν表示波的速度。
在这个公式中,波的振幅对于能流密度强度的影响体现在速度的平方项上。
速度越大,波的振幅对应的能流密度强度就越大。
介质的密度和波的线密度或者表面密度也对能流密度强度起到重要作用。
需要特别说明的是,对于不同类型的波,能流密度强度公式可能需要做适当的修正。
比如对于声波,由于声波是在气体、液体或固体介质中传播的,因此介质密度对于声波的传播会产生不同的影响。
而对于电磁波,介质的电磁性质对于能流密度强度也可能会有所影响。
因此在具体应用中,需要根据波的特性和介质性质做出相应的修正和调整。
在工程学和实际应用中,波的能流密度强度公式可以用来优化波动传输系统的设计,提高能量传播效率,加速数据传输速率,改善声音等波动现象的传播质量。
比如在声学领域中,通过调节声波的振幅和频率,可以控制声音的传播距离和声音质量,进而提高音响设备的性能。
在无线通信领域中,通过优化电磁波的能流密度强度,可以提高无线通信网络的覆盖范围和传输速率。
波的能流密度强度公式是描述波动能量传播和传递速率的重要工具,对于理解和应用波动现象具有重要意义。
在实际应用中,根据波的特性和介质性质,可以对能流密度强度公式进行适当的调整和修正,从而实现对波动现象的优化和控制。
大学物理 波的能量能流密度
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明:w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说,不断从波源方向的介质中吸收能
量,又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式,且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
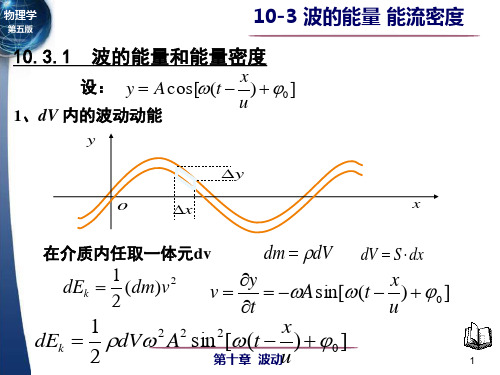
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中,产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
16-3 波的能量 能流密度

讨论 1)在波动传播的媒质中,任一体积元的动能、 )在波动传播的媒质中,任一体积元的动能、 势能、总机械能均随x, 作周期性变化 且变化是同 作周期性变化, 势能、总机械能均随 t作周期性变化,且变化是同 相位的 相位的. 体积元在平衡位置时,动能、 体积元在平衡位置时,动能、势能和总机械能 均最大. 均最大 体积元的位移最大时,三者均为零. 体积元的位移最大时,三者均为零
第十六章 机械波动理论 弹性势能
16-3 波的能量 能流密度 16O O
1 2 dW P = k (dy ) 2 dy F 胡克定律 =Y S dx
x
F
dx
SY k= F = YS dx dx 2 1 1 Y dy 2 dW P = k (d y ) = YS d x u= 2 2 ρ dx ∂y ω 1 dy 2 x 2 = ρu dV ( ) = A sin ω (t − ) 2 dx ∂x u u 1 x 2 2 2 = ρdVA ω sin ω (t − ) 2 u
16-3 波的能量 能流密度 16-
s2
s1
r1
r2
即
w 1 uS1 = w 2 uS2 1 1 2 2 2 ρ A1 ω u 4π r1 = ρ A22ω 2 u 4π r22 2 2 A0 r0 r A1 r2 y= cos ω (t − ) = r u A2 r1
处的振幅。 式中r为离开波源的距离, 式中 为离开波源的距离,A0为r=r0处的振幅。 为离开波源的距离
O O
x
dx
x
y + dy
y
x
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
O O
x
10-3 波的能量能流密度

平均能量密度
一个周期内能量密度的平均值。 一个周期内能量密度的平均值。
第十章 波动
5
物理学
第五版
1010-3 波的能量 能流密度
1 T 1 T x 2 2 2 w = ∫ wdt = ∫0 ρA ω sin ω( t − u )dt T 0 T T 1 x 2 2 2π ρA ω ∫0 sin ( t − )dt = T =π ω T T u T 1 1 x π 2 2 2 2 2π w = ρA ω = ρA ω ∫0 sin ( t − )d( t ) π T u T 2
1 A2ω2 x 2 = YSdx sin [ω(t − )] 2 2 u u
1 x 2 2 2 Wp = ρ A ω sin [ω(t − )]∆V = W k 2 u
第十章 波动
3
物理学
第五版
1010-3 波的能量 能流密度 体积中质点的总能量: 考虑 ∆V 体积中质点的总能量:
2 2 2
x W = Wk +Wp= ρA ω sin ω( t − )∆V u 说明: 说明:
∫
π
0
sin 2 θ ⋅ dθ = π 2
第十章 波动
6
物理学
第五版
1010-3 波的能量 能流密度 二、波的能流和能流密度 波的能流和能流密度
u
∆S
能流: 能流:单位时间内通过介质中某一 截面的能量。 截面的能量。 p = wu∆S 平均能流:在一个周期内能流的平均值。 平均能流:在一个周期内能流的平均值。
物理学
第五版
一、波的能量 波的能量
1010-3 波的能量 能流密度
波动是振动状态的传播过程, 波动是振动状态的传播过程,伴随着振动能量 的传播。 的传播。 振动动能 + 形变势能 = 波的能量 以纵波为例: 以纵波为例:
3波的能量 能流密度
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
讨 论 (1)介质中,任一体积元的动能、势能、总
机械能均随 x,t 作周期性变化,且变化是同相位的。
dW
2dWp
2dWk
dVA22 sin2 (t
x) u
体积元在平衡位置时,动能、势能和总机械能均 最大。因为 y Acos(t x )余弦为零,正弦达到最大。
P wuS
u
2、平均能流: P wuS
3、能流密度 ( 波的强度 )
通过垂直于波传播方向
S udt
的单位面积的平均能流。
I P w幅的平方、角频率的平方、
波速以及介质密度成正比。
波动
2、能量密度:单位体积介质中的波动能量
w dW A2 2 sin 2 (t x)
dV
u
3、平均能量密度:能量密度在一个周期内
的平均值:
w 1 T wdt 1 2 A2
T0
2
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
二、能流和能流密度
1、能流:单位时间内垂直通过某一面积的能量.
3、波的能量 能流密度
波动
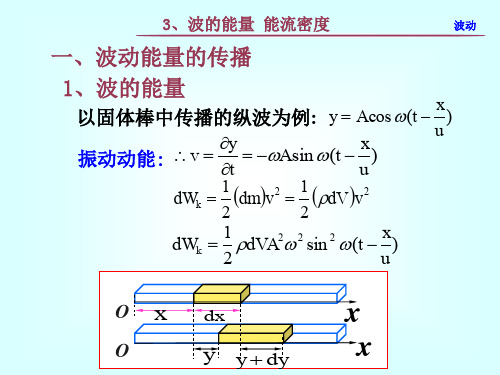
一、波动能量的传播
1、波的能量
以固体棒中传播的纵波为例:
y Acos(t x )
u
振动动能: v y Asin(t x )
t
u
dWk
1 2
dmv 2
1 2
dV
v 2
dWk
大学物理-波的能量 能流密度

2πr2
)
(1
2πr1
)
如果2 1即相干波源S1、S2同位相
则
2π
r1
r2
2π
r1 r2 称为波程差(波走过的路程之差)
水
的 衍
波 的 衍
射
射
19
三 波的干涉
1 波的叠加原理 波传播的独立性:两列波在某区域相遇
后再分开,传播情况与未相遇时相同,互不 干扰.
波的叠加性:在相遇区,任一质点的振 动为二波单独在该点引起的振动的合成.
20
2 波的干涉
频率相同、振动 方向平行、相位相同 或相位差恒定的两列 波相遇时,使某些地 方振动始终加强,而 使另一些地方振动始 终减弱的现象,称为 波的干涉现象.
波是如何传播的? 传播又有什么现象? 这些现象有什么规律?
一 惠更斯原理
介质中波动传播到的各点都可以看作是 发射子波的波源,而在其后的任意时刻,这 些子波的包络就是新的波前.
ut
平
球
面
面
R1
O
R2
波
波
18
二 波的衍射
波在传播过程中遇到障碍物,能绕过障 碍物的边缘,在障碍物的阴影区内继续传播.
波
一 波动能量的传播
1 波Байду номын сангаас能量
波的传播是能量的传播,传播过程中,
介质中的质点运动,具有动能
W
,介质形变
k
具有势能 W p .
1
以棒dW中k 哪哪传12播里里d的m最最v纵大小2 波,?12为例dV分v析2 波y 动A能co量s的(t 传ux播) .
v y Asin(t x )
t
u
振动动能
物理波的能量

=
3
cos
4πt
(2)以距a点5m处的b点为坐标原 点写出波动方程。
b.
u .a 5m
x
解:(1)以a点为原点在x轴上任取一点P,坐标为x
ya = 3 cos 4πt y =3 cos 4πt +
x
20
(2)以b点为坐标原点
wk
wp
2 A2
sin
2 [ (t
x )] u
平均能量密度(对时间平均)
w 1 T A2 2 sin 2[(t x)]dt
T0
u
w
=
1 2
ρAω2
2
三、波的强度
能流P :单位时间内垂直通过某一截面的 P = w S u 能量称为波通过该截面的能流,或叫能通量。
显然能流是随时间周期性变化的。但它总为正值
(t+
d u
)
π
2
]
y
=
A cos[ω
(
t
+
d u
x u
)
π
2
]
例6、波速 u =400m/s, t = 0 s时刻的波形如图所示。
{ 写出波动方程。
t= 0 (o点)
得:
y 0
=
2
=
A
2
v0
>0 0=
π
3
2
o
y(m)
4 5
p
u
x (m)
{ t =0
(p点)
2π
=
y 0
=
0
v0< 0
p
0
d
λ
得:
平均能流P : 能流在一个周期内的平均值。 P = S w u 波的强度 I(能流密度):
大学物理-波的能量能流密度

04
电磁波中的能量传播
电磁波概述
电磁波定义
电磁波是由电场和磁场交替变化而产生 的一种波动现象,可以在真空中或物质 中传播。
VS
电磁波分类
根据频率和波长的不同,电磁波可分为无 线电波、红外线、可见光、紫外线、X射线、 γ射线等。
电磁波中电场和磁场能量关系
电场能量
电磁波中电场能量与电场强度的平方成正比,即$W_e = frac{1}{2} epsilon_0 E^2$,其中 $epsilon_0$为真空介电常数,$E$为电场强度。
行波
与驻波不同,行波是向前传播的波形 。在行波中,质点的振动方向与波的 传播方向垂直(横波)或平行(纵波 )。行波传递能量和动量。
02
能量传播与能流密度
能量传播方式
机械波
通过介质中质点的振动和相互作用传播能量,如声波、水波 等。
电磁波
通过电场和磁场的交替变化传播能量,如光波、无线电波等 。
能流密度定义及表达式
磁场能量
电磁波中磁场能量与磁场强度的平方成正比,即$W_m = frac{1}{2} mu_0 H^2$,其中 $mu_0$为真空磁导率,$H$为磁场强度。
总能量
电磁波的总能量等于电场能量和磁场能量之和,即$W = W_e + W_m$。
电磁波中能量传播特点
01
能流密度矢量
电磁波中的能量传播可以用能流密度矢量$vec{S}$来描述 ,其方向垂直于电磁波的传播方向,大小等于单位时间内 通过单位面积的能量。
光学领域应用
光的传播
01
光波的能量能流密度决定了光的亮度、颜色和温度等特性,是
光学研究的基础。
激光技术
Hale Waihona Puke 02激光具有高能量能流密度的特点,被广泛应用于切割、焊接、
波的能量密度

波的能量密度一、引言波是自然界中广泛存在的物理现象,其能量密度是描述波能量分布的重要参数。
本文将介绍波的能量密度的概念、计算方法以及应用领域。
二、波的能量密度的概念1.定义波的能量密度是指单位体积内所包含的波动能量。
在电磁学中,电磁场中每个点上单位时间内通过单位面积传递的电磁能量称为辐射通量密度,而辐射通量密度除以光速就可以得到电磁场中每个点上单位体积内所包含的电磁辐射能量,即电磁场中的辐射能密度。
2.单位波的能量密度通常用J/m³或者W/m³来表示。
三、计算方法1.机械波对于机械波,其能量密度可以表示为:u = 1/2ρv²其中,u为机械波在介质中传播时所具有的单位体积内储存的总功率;ρ为介质的质量密度;v为机械波在介质中传播时所具有的速率。
2.电磁波对于电磁波,其能量密度可以表示为:u = εE²/2 + 1/2μB²其中,u为电磁波在介质中传播时所具有的单位体积内储存的总功率;ε为介质的介电常数;E为电场强度;μ为介质的磁导率;B为磁感应强度。
四、应用领域1.辐射治疗医学上常用的X射线、γ射线等电离辐射对人体组织产生伤害,而这些伤害与辐射通量密度和能量密度有关。
因此,在医学上,需要精确测量出辐射通量密度和能量密度,以便控制辐射剂量。
2.光学领域在光学领域中,波的能量密度是描述光强的重要参数。
例如,在太阳能电池中,需要精确测量出太阳光的能量密度以确定其转换效率。
3.声学领域在声学领域中,波的能量密度是描述声音强度的重要参数。
例如,在音频设备中,需要精确测量出声音波的能量密度以确定其音质和音响效果。
五、结论波的能量密度是描述波能量分布的重要参数,其计算方法不同于不同类型的波。
在医学、光学和声学领域中,波的能量密度被广泛应用于测量和控制波的强度和剂量。
波的能流密度

10
超声波、 • 超声波、次声波
* 次声波
特点一 频率在10 频率在 -4~20赫芝之间 赫芝之间 的机械波,人耳听不到。 的机械波,人耳听不到。 特点二 由于它具有衰减极小的特点, 由于它具有衰减极小的特点, 衰减极小的特点 具有远距离传播的突出特点。 具有远距离传播的突出特点。 已形成现代声学的一个新的 分支—次声学 次声学。 分支 次声学。 因为大气湍流、火山爆发、地震、 因为大气湍流、火山爆发、地震、 陨石落地、雷暴、 陨石落地、雷暴、磁暴等大规模自 用途 然活动中,都有次声波产生,因此, 然活动中,都有次声波产生,因此, 它是研究地球、海洋、 它是研究地球、海洋、大气等大规 模运动的有力的工具。 模运动的有力的工具。
y
∆y
A B
o o
A
∆x
B
2
质元形变: 质元形变:
2
∂y 1 ∂y [(∆x) + (∆y) ] − ∆x = ∆x1+ − ∆x ≈ 2 ∂x ∂x 质元的形变势能: 质元的形变势能: 2 1 ∂y = 1 FdxA 2 k 2 sin 2 (ω t − kx ) dE p ≈ F × 2 ∂x 2 ∂x
1 ε = T
∫
T
0
εdt =
ρA2ω 2
T
∫
T
0
1 sin (ω t − kx)dt = ρA 2ω 2 2
2
4
二、波的能流密度 波的强度 单位时间内通过截面 单位时间内通过截面 S 的能量等于体积 uS中的 中的 能量,称为能流 能流。 能量,称为能流。 E = ε uS 单位时间内通过垂直于波的传播方向的 通过垂直于波的传播方向的单位面 单位时间内通过垂直于波的传播方向的单位面 上的能量叫做能流密度 能流密度。 积上的能量叫做能流密度。 r dE 写成矢量式: J= = ε u 写成矢量式: J = ε u dS 一个周期内能流密度大小的平均值称为波的强度 波的强度。 一个周期内能流密度大小的平均值称为波的强度。
§9.4 波的能量 平均能流密度

波是振动状态的传播,相位的传播,同时 也是能量的传播.
波在弹性媒质中传播时,各质元都在振动。 每个质元,有振动速度而具有振动动能;因发生 形变而具有形变势能, 两者之和称此媒质中弹性 波的能量。 对于“流动着”的能量,要由能量密度和 能流密度两个概念来描述。
弹性体的剪切形变
切应变:
y A x sin ( t ) x u u
2 1 1 体元势能:dE p G 2dV GA2 2 sin2 (t x )dV 2 2 u u x 2 2 2 2 1 2 A sin ( t )dV (u G ) u x 体元总能: dE dEk dE p 2 A2 sin 2 ( t )dV u
二、平均能流密度
能流:单位时间内垂直通过某一面积的能量. 平均能流:
P uS
u
平均能流密度 (波的强度 ): 通过垂直于波传播方向的单 位面积的平均能流.
P 1 I u A2 2 u S 2 1 2 2 I 不吸收能量, 显然:
x 位移:y A cos ( t ) u
振动速度:
v y x A sin ( t ) t u
1 2 2 1 2 2 2 2
x 体元动能: dEk dVv A sin ( t )dV u
一、波的能量分布
x 位移:y A cos ( t ) u
2、能量密度与平均能量密度 能量密度:单位体积介质中的波动能量.
dE x 2 2 2 A sin (t ) dV u
平均能量密度:能量密度在一个周期内的平均值.
1 1 x 2 2 2 dt A sin (t )dt T0 T0 u
电磁波能量计算公式

电磁波能量计算公式
电磁波的能量计算公式可以通过不同的角度来进行解释和推导。
首先,我们可以从电磁波的能量密度出发,能量密度是指单位体积
或单位面积内的能量。
对于电磁波,其能量密度可以表示为能量传
播的强度。
电磁波的能量密度(u)与其电场强度(E)和磁场强度(H)有关,其计算公式为u = 0.5 (ε E^2 + 1/μ H^2),其
中ε为介电常数,μ为磁导率。
这个公式可以用来计算电磁波在
空间中的能量分布情况。
另外,我们还可以从电磁波的频率和波长出发来计算其能量。
根据普朗克的量子理论,电磁波的能量与其频率有关,能量E与频
率f之间的关系可以用公式E = hf来表示,其中h为普朗克常数。
此外,电磁波的能量也与其波长λ有关,能量E与波长λ之间的
关系可以用公式E = hc/λ来表示,其中c为光速。
这两个公式可
以用来计算电磁波的能量,同时也可以通过频率和波长的关系相互
推导。
此外,还可以从电磁波的功率出发来计算其能量。
电磁波的功
率可以表示为单位时间内通过某个面积的能量流量,功率P与电场
强度(E)和磁场强度(H)的关系可以用公式P = 0.5 (E H)来
表示。
通过功率和时间的关系,可以计算出电磁波的能量。
综上所述,电磁波的能量计算可以从能量密度、频率和波长、功率等多个角度来进行推导和计算。
不同的方法可以用于不同的情况和问题,从而全面而准确地描述电磁波的能量特性。
波的能流密度

波的能流密度波是一种能量的传递方式,具有能量和动量的特征。
在波传播过程中,波的能量被传递到介质之中,形成波的能流。
能流密度是描述波能量传递特性的重要物理量,它表示单位时间内通过介质单位面积的能量所述。
因此,能流密度反映了波能量传递的强度和方向性。
本文将介绍波的能流密度及其在物理学中的应用。
在光学、声学、电磁学等领域,波是一种能量的传递方式。
这些波在传播过程中,会将能量传递到介质中。
假设在介质中某一时刻的某一点处,波的能量为E,波的传播速度为v,波的通过单位面积的时间为t,则单位时间内通过该点的能量为:W=E/t其中,t是单位时间,W是单位时间内通过该点的能量。
但一个点的能量不一定向同一方向传播,因此,需要确定能量传递的方向,才能说明这个点的能流。
能量可以看作是以某种形式储存在介质中的物理量,当波通过介质时,能量也会随之传递,从而形成所谓的“能流”现象。
能流密度(S)定义为单位时间内能量通过单位面积的量,即:其中,v是波在介质中的传播速度。
能流密度是衡量介质中能量传递强度的物理量,它表示了单位面积的介质内在某一方向上的能量传递强度。
在电磁学中,电磁波的能流密度可以表示为:S=cε0E^2其中,c是光速,ε0是真空介电常数,E是电场强度。
这个公式说明了电磁波的能量强度和传递方向取决于电场强度。
S=ρvA^2能流密度的概念和应用,是物理学中重要的概念。
在各种实际应用中,能流密度都有着广泛的应用,下面将介绍几个具体的例子。
在光学中,光的能量可以表示为电场与磁场的电磁波的组合,因此,能流密度可以表示为光的强度密度和光速的积:其中,E是电场强度。
由于光的传递速度很快,因此光的能流密度可以在很短的时间内在物质中传递能量。
能流密度常常用来计算光的强度分布和光的传输效率。
例如,在光纤光通信中,能流密度是一个重要的概念,因为能流密度可以用来描述光在光纤中的能量传递效率。
光纤中的能流密度越大,表示光在光纤中的传输效率就越高,这对于提高光通信传输速率非常重要。
物理实践:波的功率和能量密度

计算公式: E = ρ c ² u ²/ 2 , 其 中 E为能量密度,ρ 为介质密度,c为 波速,u为振动 速度
与功率的关系: 能量密度与功率 成正比,即能量 密度越大,功率 越高
功率是单位时间内波所传递的能量, 表示波的强度。
功率和能量密度之间存在一定的关 系,通常功率越高的波具有越高的 能量密度。
波的功率和能量密度对环境的影响 波的传播对生态系统的破坏 波的能量密度对气候变化的影响 波的功率和能量密度对人类生活的影响
波的功率和能量密度在通信技术中的应用 波的能量密度对能源利用的影响 波的功率和能量密度在医疗领域的应用 波的功率和能量密度在军事领域的应用
波的功率和能量密 度未来发展趋势
波的功率和能量密 度对人类生活的影 响
电磁波对生物体的潜在危害
波的功率和能量密度对人体 的辐射影响
微波辐射对人体的伤害 高强度声波对听力的损伤
无线电波:传输 信号,实现远距 离通信
微波:用于卫星 通信和移动通信 网络
光纤:高速、大 容量的信息传输, 提高通信质量
电磁波:用于雷达、 导航和探测等军事 和民用领域
激光雷达技术:利用激光雷达技术实现高精度、高分辨率的波源测量和定位 微波源技术:利用微波源技术实现高效率、高可靠性的波源产生和控制 声波源技术:利用声波源技术实现低成本、高稳定性的波源产生和应用 电磁波源技术:利用电磁波源技术实现高速、高带宽的波源传输和通信
物联网技术:实现波的功率和能量 密度的远程监控和管理
激光技术:利用高能激光束产生高功率和能量密度的光束,可用于医疗、军事等领域。
核聚变技术:通过核聚变反应产生高能量密度,可用于未来能源领域。
纳米技术:利用纳米材料和纳米结构提高能量密度,可用于电池、传感器等领域。
波的能量能流密度

1.波动的动能
以固体棒中传播的纵波为例分析波动能量的传播.
O O
波函数
x
dx
x
y dy
y
x
x y x y A cos ( t ) v A si n ( t ) t u u
•质元的动能
1 1 2 dWk dm v dV v 2 2 2
1 x 2 2 2 dWk dVA si n ( t ) 2 u
① 任一时刻介质元的动能等于势能,且相位相同,与振动系 统的动能与势能总有π/2相位差不同。 ② 振动系统的机械能守恒,而波动过程中,能量不守恒。波 动过程中,沿波的传播方向,介质元不断地通过振动由后面的 质元获得能量,又不断地把能量传播给前面的质元,波是能量 传递的一种形式。 ③ 在平衡位置时质元具有最大动能和势能,在最大振幅处动 能和势能为零。在回到平衡位置时从相邻质元吸收能量,离开 时放出能量。
1 x 2 2 2 dWk dWp dVA si n ( t ) 2 u 表明:质元的总能量随时间作周期性变 3.波动的能量 化,时而达到最大值,时而为零 x dW dWk dWp dVA2 2 si n2 ( t ) u 4.结论 意味着:在由波传播的细棒中有能量在传播
2.波动的势能
弹性势能 O
1 2 dWP k dy 2
F l E S l
F
弹性模量
x
dx
O
y y dy
u E
x x
ES l l
1 1 dy 2 2 dWP k dy ESdx( ) 2 2 dx
SE k dx
1 dy 2 y A si n ( t x ) 2 u dV ( ) x u u 2 dx 1 x 2 2 2 dVA si n ( t ) 2 u
机械波的能量与能流密度

一、波场中质元的动能和势能
dEk
dEP
1 2
(dV )A2 2
sin2 (t
x) u
1、对给定(x 一定)质元,在波的传播过程中,其动能与
势能随 t 同步周期性变化,且在任何时刻两者相等。
u
x = x0
dEk
dEp
T
O
t
y
振动曲线
dEk 、dEp在平衡位置处最大; 在最大位移处为零。
一、波场中质元的动能和势能
二、波场中的能量密度和能流密度
讨论 (2) 球面波的振幅
若介质不吸收能量
通过两个球面的平均能流相等
设S1与S2的波振幅分别为A1、A2
1 2
2 A12u4πr12
1 2
2 A22u4πr22
r2
p1 p2
O r1 S1
波源
得
A1 r2 A2 r1
A(r) A A等于离开波源单位
r
距离处波的振幅。
球面简谐波的波函数
y A cos(t r )
r
u
三、波的吸收
对吸收媒质,实验表明:
dA A( x)dx
——介质吸收系数
A( x) A0ex
I ( x) I0e 2x
I0
I
O
x
A A-dA
O
dx
I I0
O
x
随堂练习
1.图示为一平面简谐机械波在t时刻的波形曲线。若此时 A点处媒质质元的振动动能在增大,则:
(1) 能量高、定向性好; (2) 对导体、液体(水)有较强的穿透力。
例 100kHz : 8.5105 / m
声强减少到 1 倍,水:5.9km;空气:5.8m。 e
光波的能量密度

光波的能量密度
光波的能量密度
光是视觉中最常见的自然现象,它有着令人惊叹的特征,既可以像水一样流淌,又能带来温暖的拥抱,是我们生活中不可或缺的重要元素。
就其能量密度而言,光可以理解为拥有一定能量的集合,这些能量能够进入物质中,并引发一些反应,如蒸发等。
光波的能量密度定义为每平方厘米表面所发射出的光能量。
对于看得见的光来说,有红色、绿色和蓝色三种,因此称为可见光。
其中,红色,偏色最大,能量密度也最大;绿色依次下降;蓝色最小,能量密度最低。
同样,还有可见光之外的其它频谱的光,如:X射线、紫外线等,它们的能量密度要比可见光都高得多。
由于光产生的能量密度差别,它们对物质也有不同的影响。
可见光由于能量密
度较低,因此不易对物质造成破坏,但能够照明物质,还可以促进植物的生长发育。
而X射线和紫外线的能量密度大于可见光,因此具有一定的穿透性,如:检查物体的内部结构、提取影像等;但太强的X射线或紫外线也会对生物体造成影响,或致癌,从而愈发强调了它的危害性。
总的来说,光波的能量密度和波长大小很大程度上决定了它们的影响,它们给
我们带来了美、利两方面的福音,我们应该在合理运用它们上起到谨慎作用,在发掘其用处的同时注意安全,以免耽误了人类的发展和幸福。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
2
(3) 振幅 A=1 mm,则振动速度的幅值为
vm A 1.88 103 cm/s 18.8 m/s
振动速度是交变的,其幅值为18.8 m/s,远小于波速。
返回 退出
§11-2 平面简谐波的波函数
一、波函数
(r,
t)
f
(r,t)
f
( x,
y, z,t)
波函数表示任一时刻物理量 在空间的分布情况。
返回 退出
(3)波函数反映了波的时间、空间双重周期性
T 时间周期性 空间周期性
同一质点在先后时刻的相位差:
2π t t
T
不同质点在同一时刻的相位差:
2π x k x
返回 退出
利用关系式 2π T 2π 和 uT ,可得
其他形式的平面简谐波波函数:
π 2
(5) t =0.0021 s时的波形为
y
0.110
3
cos
25
10
3
π
0.0021
5
x 10
3
0.1103 sin 5πx (m)
返回 退出
例11-3 一横波沿一弦线传播。设已知t =0时的波形曲 线如图中的虚线所示。波速 u=12 m/s,求:(1)振幅; (2)波长;(3)波的周期;(4)弦上任一质点的最大速率; (5)图中a、b两点的相位差;(6)3T/4时的波形曲线。
y( x, t )
Acos
2π
t T
x
0
y( x, t )
Acos
2πt
x
0
y(x,t) Acos( t k x 0 )
其中角波数 k 2π
返回 退出
例11-2 频率为=12.5 kHz的平面余弦纵波沿细长的金
cos
25
10 3
π t
x 5 10 3
(m)
式中x 以m计,t 以s 计。
(3)离原点10 cm处质点的振动表达式
y
0.103
cos
25
10 3
π
t
5
1 10
4
(m)
返回 退出
(4)该两点间的距离
x 10cm 0.10m 4
相应的相位差为
解:(1) 波的周期: T 1 1 s
3000
波长: u 0.52 m 52cm
返回 退出
B点比A点落后的时间为
0.13 1.56 103
1 (s) 12000
即T 4
(2) A、B 两点相差13cm , B点比A点落后的相位差为
4
2π π
纵波:质点的振动方向和波动的传播方向相平行。 波形特征:存在相间的稀疏和稠密区域, 如声波。
返回 退出
弹簧中的纵波
返回 退出
三、波阵面和波(射)线
波阵面:振动相位相同的点所构成的面。 波前:最前面的那个波阵面。 波线:表示波的传播方向的有向线段。
波面
波
线
平面波
球面波
远离波源处,很小区域内的波阵面可看作平面波。
属棒传播,波速为 5000 m/s。如以棒上某点取为坐标原 点,已知原点处质点振动的振幅为A =0.1 mm,试求: (1)原点处质点的振动表式;(2)波函数;(3)离原点10 cm 处质点的振动表式;(4)离原点20 cm和30 cm两点处质 点振动的相位差;(5)在原点振动0.0021 s时的波形。
初相: 随着x 值的增大,即在传播方向上,各质点的相位 依次落后。这是波动的一个基本特征。
返回 退出
(2)当 t 给定时:若t=t1,波动式表示t1 时的波形
y( x, t1 )
Acos[
(t1
x u
)
0
]
f (x)
y
u
t1
t2 t1 t
O
x
ut
t1 时刻的波形经t 时间沿波的传播方向移动了 ut 的距离,波函数反映了波形的传播——行波。
§11-1 机械波的产生和传播 一、机械波产生的条件
机械波: 机械振动(波源)在弹性介质中的传播过程 y
x
机械波产生的两个条件:波源,介质 传播特征: 由近及远传播振动状态。
返回 退出
如: 振动沿一细绳的传播。
返回 退出
二、横波与纵波 横波:质点的振动方向和波动的传播方向垂直。 波形特征:存在波峰和波谷, 如细绳上的波。
解:
波长:
u ν
5.0103 12 .5 10 3
0.40(m)
周期: T 1 ν 8105 s
返回 退出
(1)原点处质点的振动表达式
y0 Acost 0.1103 cos 25 103 πt (m)
(2)波函数
y Acost x u
0.110 3
各向同性介质中,波线与波阵面处处垂直。
返回 退出
四、波长、频率和波速间的关系
1. 波长:沿波的传播方向两相邻同相位点之间的距离
2. 周期T :波前进一个波长
的距离所需的时间。
等于波源的振动周期。
频率: ν 1 T
角频率: 2πν 2π
T
3. 波速 u (相速):振动状态或相位在空间的传播速度。
返回 退出
二、平面简谐波的波函数 简谐波:简谐振动在介质中传播形成的波。 如果波阵面为平面,则为平面简谐波。 平面波的特点:任一时刻在同一波阵面上的各点 有相同的相位。只要研究其中任一条波线上波的 传播规律,就能知道整个平面波的传播规律。
返回 退出
设一平面余弦波,在无吸收的均匀无限介质中沿
x 轴的正方向传播,波速为u 。取任意一条波线为x 轴, 取O 作为x 轴的原点。
O点处质点的振动表式为
y0(t) Acos( t 0 )
P点的振动状态在时间上落后于O点: t x u
平面简谐波的波函数:
返回 退出
平面简谐波的波函数:(沿x 轴正向传播)
沿x 轴负向传播的平面简谐波的波函数:
返回 退出
• 波函数的意义:
(1)当 x 给定时:若x=x1, 波动式成为x1 处质点的振动式
u ν
T
u 一般取决于介质的 性质(弹性和惯性)。
返回 退出
例11-1 频率为3000 Hz的声波,以1560 m/s的传播速度 沿一波线传播,经过波线上的A点后,再经13 cm而传 至B点。求:(1) B点的振动比A 点落后的时间。(2) 波 在A、B两点振动时的相位差是多少?(3) 设波源做简 谐振动,振幅为1 mm,求振动速度
