如何使用excel计算概率论一些题目
如何使用excel进行概率统计

数理统计实验1Excel基本操作1.1单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮.C. 单击“函数”下拉列表框右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按ENTER 键.1.2几种常见的统计函数1.2.1均值Excel计算平均数使用AVERAGE函数,其格式如下:AVERAGE(参数1,参数2,…,参数30)范例:AVERAGE(12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用AVERAGE(A1:B20).1.2.2标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel计算样本标准差采用无偏估计式,STDEV函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用VAR 函数,格式如下:VAR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 VAR(A1:B20). 范例:VAR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用VARP 函数,格式如下:VARP (参数1,参数2,…,参数30)范例:VAR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0.841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0.841345,360,40)得到结果为400,即P{X≤400}=0.841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).Φ=P{X<2}.输入公式范例:已知X~N(0,1), 计算(2)=NORMSDIST(2)Φ=0.97725.得到0.97725,即(2)范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T服从t(n-1)分布,样本数为25,求P(T>1.711).已知t=1.711,n=25,采用单侧,则T分布的值:=TDIST(1.711,24,1)得到0.05,即P(T>1.711)=0.05.若采用双侧,则T分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值.范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1 2已知时的置信区间 置信区间为22x u x u n n αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.141.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米). 步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,=0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025). 2.1.2 2未知时的置信区间置信区间为 22((x t n x t n n n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) =average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) 计算结果为(1.133695, 1.172555).2.1.3未知时2的置信区间:置信区间为2222122(1)(1),(1)(1)n nn ns sααχχ-⎛⎫ ⎪--⎪--⎪⎝⎭.例3从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=VAR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当12 =22 =2但未知时1-2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=AVERAGE(A2:A6),在单元格B12中输入公式=AVERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=VAR(A2:A6),=VAR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.21和未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4,19.8, 18.3, 20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5,23.5, 23.9, 25.3, 23.5, 22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5,20.9, 22.1, 22.7, 23.6, 24.5, 23.6, 21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8,21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1单个正态总体均值μ的检验3.1.12已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0(2)本地平均产量μ是否比原产地的平均产量μ=800kg高.0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=AVERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0.05).3.1.22未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=AVERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H:μ>250.1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得025.0到t检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2两个正态总体参数的假设检验3.2.1当12 =22 =2但未知时μ-μ的检验12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H:μ1>μ2.1操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显著差异?欲检验假设H0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
常用分布概率计算的Excel应用

上机实习常用分布概率计算的Excel应用利用Excel中的统计函数工具,可以计算二项分布、泊松分布、正态分布等常用概率分布的概率值、累积(分布)概率等。
这里我们主要介绍如何用Excel来计算二项分布的概率值与累积概率,其他常用分布的概率计算等处理与此类似。
§3.1 二项分布的概率计算一、二项分布的(累积)概率值计算用Excel来计算二项分布的概率值P n(k)、累积概率F n(k),需要用BINOMDIST函数,其格式为:BINOMDIST (number_s,trials, probability_s, cumulative)其中 number_s:试验成功的次数k;trials:独立试验的总次数n;probability_s:一次试验中成功的概率p;cumulative:为一逻辑值,若取0或FALSE时,计算概率值P n(k);若取1或TRUE时,则计算累积概率F n(k),。
即对二项分布B(n,p)的概率值P n(k)和累积概率F n(k),有P n(k)=BINOMDIST(k,n,p,0);F n(k)= BINOMDIST(k,n,p,1)现结合下列机床维修问题的概率计算来稀疏现象(小概率事件)发生次数说明计算二项分布概率的具体步骤。
例3.1某车间有各自独立运行的机床若干台,设每台机床发生故障的概率为0.01,每台机床的故障需要一名维修工来排除,试求在下列两种情形下机床发生故障而得不到及时维修的概率:(1)一人负责15台机床的维修;(2)3人共同负责80台机床的维修。
原解:(1)依题意,维修人员是否能及时维修机床,取决于同一时刻发生故障的机床数。
设X表示15台机床中同一时刻发生故障的台数,则X服从n=15,p=0.01的二项分布:X~B(15,0.01),而 P(X= k)= C15k(0.01)k(0.99)15-k,k = 0, 1, …, 15故所求概率为P(X≥2)=1-P(X≤1)=1-P(X=0)-P(X=1)=1-(0.99)15-15×0.01×(0.99)14=1-0.8600-0.1303=0.0097(2)当3人共同负责80台机床的维修时,设Y表示80台机床中同一时刻发生故障的台数,则Y服从n=80、p=0.01的二项分布,即Y~B(80,0.01)此时因为 n=80≥30, p=0.01≤0.2所以可以利用泊松近似公式:当n很大,p较小时(一般只要n≥30,p≤0.2时),对任一确定的k,有(其中 =np)λλ--≈e k qp C k k n k k n !来计算。
excel 概率计算表格

在Excel中,你可以使用一些内置的函数来计算概率。
以下是一个简单的概率计算表格的例子:
事件概率
A0.2
B0.3
C0.15
D0.25
假设你有一个事件列表,每个事件都有一个对应的概率。
你可以在Excel中创建一个表格,其中一列是事件名称,另一列是对应的概率。
如果你想计算某个事件发生的概率,你可以将该事件的概率相加。
例如,如果你想计算事件A和B同时发生的概率,你可以将A的概率和B的概率相加:0.2 + 0.3 = 0.5。
对于更复杂的概率计算,如条件概率、联合概率等,你可能需要使用Excel中的其他函数,如IF函数、SUM函数、COUNTIF函数等。
具体的使用方法可以参考Excel的官方文档或相关的教程。
常用概率函数在EXCEL中实现

常用概率函数在EXCEL中实现在Excel中,常用的概率函数可以使用内置函数进行实现。
下面将介绍四个常用的概率函数以及它们在Excel中的实现方法。
1.正态分布函数(NORM.DIST)正态分布函数可以用于计算一个随机变量处于指定范围内的概率。
在Excel中,可以使用NORM.DIST函数来计算正态分布的概率。
语法:NORM.DIST(x,mean,standard_dev,cumulative)-x:要计算概率的数值。
- mean:正态分布函数的均值。
- standard_dev:正态分布函数的标准差。
- cumulative:一个逻辑值,指定概率函数是累积函数(TRUE)还是密度函数(FALSE)。
例如,要计算一个随机变量X的值小于等于5的概率,该随机变量服从均值为10,标准差为2的正态分布,可以使用以下公式:=NORM.DIST(5,10,2,TRUE)2.标准正态分布函数(NORM.S.DIST)标准正态分布函数可以用于计算一个随机变量在标准正态分布中的概率。
在Excel中,可以使用NORM.S.DIST函数来计算标准正态分布的概率。
语法:NORM.S.DIST(z,cumulative)-z:要计算概率的数值。
- cumulative:一个逻辑值,指定概率函数是累积函数(TRUE)还是密度函数(FALSE)。
例如,要计算一个随机变量Z的值小于等于1的概率,可以使用以下公式:=NORM.S.DIST(1,TRUE)3.卡方分布函数(CHISQ.DIST)卡方分布函数可以用于计算一个随机变量处于指定范围内的概率。
在Excel中,可以使用CHISQ.DIST函数来计算卡方分布的概率。
语法:CHISQ.DIST(x,deg_freedom,cumulative)-x:要计算概率的数值。
- deg_freedom:卡方分布的自由度。
- cumulative:一个逻辑值,指定概率函数是累积函数(TRUE)还是密度函数(FALSE)。
excel中的概率统计

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况就是间断的单元格选取.选取方法就是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况就是间断的单元格范围选取.选取方法就是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认.、如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式就是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法与乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 与F5 中数值的与.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面就是等号(=),后面就是参与计算的元素(运算数)与运算符.每个运算数可以就是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果就是6),然后再加上 5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用5 加上2,再用其结果乘以 3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以 5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母与行数字.例如,D50 引用了列 D 与行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)与区域右下角单元格的引用.下面就是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数就是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总与,但就是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面就是左圆括号、以逗号隔开的参数与右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A、单击需要输入公式的单元格.B、如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C 、 单击“函数”下拉列表框 右端的下拉箭头.D 、 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查瞧其它函数列表.E 、 输入参数.F 、 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE(参数1,参数2,…,参数30)范例:A VERAGE(12、6,13、4,11、9,12、8,13、0)=12、74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1、35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP(参数1,参数2,…,参数30)范例:STDEVP(3,5,6,4,6,7,5)=1、251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR(参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR(3,5,6,4,6,7,5)=1、81(2)总体方差S 2=n x x i ∑-2)(Excel计算总体方差使用V ARP函数,格式如下:V ARP(参数1,参数2,…,参数30)范例:V AR(3,5,6,4,6,7,5)=1、551.2.4正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0、158655,即P{X≤500}=0、158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0、841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0、841345,360,40)得到结果为400,即P{X≤400}=0、841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).Φ=P{X<2}.输入公式范例:已知X~N(0,1), 计算(2)=NORMSDIST(2)Φ=0、97725.得到0、97725,即(2)范例:输入公式=NORMSINV(0、97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1、711).已知t =1、711,n =25,采用单侧,则T 分布的值:=TDIST(1、711,24,1)得到0、05,即P (T >1、711)=0、05.若采用双侧,则T 分布的值:=TDIST(1、711,24,2)得到0、1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV(双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0、05,求t 205.0(10).输入公式=TINV(0、05,10)得到2、2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0、05,求t 0、05 (10).输入公式=TINV(0、1,10)得到1、812462,即t 0、05 (10)= 1、812462. 1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2、9)的值.输入公式=FDIST(2、9,5,15)得到值为0、05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0、05,求其上侧0、05分位点F 0、05(9,9).输入公式=FINV(0、05,9,9)得到值为3、178897,即F 0、05(9,9)= 3、178897.若求单侧百分位点F 0、025(9,9),F 0、975(9,9).可使用公式=FINV(0、025,9,9)=FINV(0、975,9,9)得到两个临界值4、025992与0、248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5、226)的值.输入公式=CHIDIST(5、226,12)得到0、95,即1(5.226)F -=0、95或(5.226)F =0、05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV(上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0、95,12)得到值为5、226,即20.95(12)χ=5、226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE,为泊松分布函数值;若FALSE,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0、104196与0、889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT,与函数SUM ,等等.关于这些函数的具体用法,可以查瞧Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质就是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m)为:1、14 1、10 1、13 1、15 1、20 1、12 1、17 1、19 1、15 1、12 1、14 1、20 1、23 1、11 1、14 1、16.设苗高服从正态分布,求总体均值μ的0、95的置信区间.已知σ =0、01(米). 步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限与置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0、5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0、5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α与标准差σ就是具体的数值而不就是符号.本例中,α =0、05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0、975)*0、01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0、975)*0、01/sqrt(count(b3:g5))计算结果为(1、148225, 1、158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝.例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0、05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) =average(b3:g5)-tinv(0、05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) 计算结果为(1、133695, 1、172555).2.1.3μ未知时σ2的置信区间:置信区间为22 22122(1)(1),(1)(1)n nn ns sααχχ-⎛⎫⎪--⎪--⎪⎝⎭.例3从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50、7 54、9 54、3 44、8 42、2 69、8 53、4 66、1 48、1 34、5试求总体方差2σ的0、9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0、1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0、1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0、1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5与7,分析其蛋白质含量为甲:12、6 13、4 11、9 12、8 13、0乙:13、1 13、4 12、8 13、5 13、3 12、7 12、4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0、05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组与乙组样本均值.(3)分别在单元格C11与C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11与D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0、05输入到单元格E11中.(6)分别在单元格B13与B14输入=B11-B12-TINV(0、025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)与=B11-B12+TINV(0、025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限与上限.2.2.2μ1与μ2未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,她们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别就是SA=0、5419,SB=0、6065.设σ2A与σ2B分别就是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0、95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4与B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))与=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组与B组的方差比的置信区间上限与下限.2.3 练习题1、已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22、3, 21、2, 19、2, 16、6, 23、1, 23、9, 24、8, 26、4, 26、6, 24、8, 23、9, 23、2, 23、3, 21、4, 19、8, 18、3, 20、0, 21、5, 18、7, 22、4, 26、6, 23、9, 24、8, 18、8, 27、1,20、6, 25、0, 22、5, 23、5, 23、9, 25、3, 23、5, 22、6, 21、5, 20、6, 25、8, 24、0, 23、5, 22、6, 21、8, 20、8, 19、5, 20、9, 22、1, 22、7, 23、6, 24、5, 23、6, 21、0, 21、3,22、4,18、7, 21、3, 15、4, 22、9, 17、8, 21、7, 19、1, 20、3, 19、8试以0、95的可靠性,对于该林地上全部林木的平均高进行估计.2、从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50、7,54、9,54、3,44、8,42、2,69、8,53、4,66、1,48、1,34、5.试求总体方差的0、9的置信区间(设总体为正态).3、已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区: 62 57 65 60 63 58 57 60 60 58第二实验区: 56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值与未施以磷肥的玉米产量均值之差的范围(α=0、05) 3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法与操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别就是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0(2)本地平均产量μ就是否比原产地的平均产量μ=800kg高.0(3)本地平均产量μ就是否比原产地的平均产量μ=800kg低.0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0、975);(6)根据算出的数值作出推论.本例中,U的检验值1、341641小于临界值1、959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0、95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0、05).3.1.2σ2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0、025时,就是否与她的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1、06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0、05, D10-1)、欲检验假设H0:μ=250;H1:μ>250.=2、093.由上面计算得到t检已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t.0025验统计量的值1、06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当σ12 = σ22 = σ2但未知时12在此情况下,采用t检验.例试验及观测数据同11、2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H1:μ1>μ2.操作步骤:(1)(2)(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0、05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3、03,“t单尾临界”值为1、734063.由于3、03>1、73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组与第2组测验结果如下:第1组: 91 88 76 98 94 92 90 87 100 69第2组: 90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别就是57与53,取α =0、05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0、05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0、21106(即u统计量的值),其绝对值小于“z双尾临界”值1、959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0、19 0、18 0、21 0、30 0、41 0、12 0、27处理后:0、15 0、13 0、07 0、24 0、19 0、06 0、08 0、12问处理前后含脂率的标准差就是否有显著差异?欲检验假设H0:σ21=σ22; H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0、025. (8)在“输出区域”框输入D1.(9)选择“确定”,得到结果如图所示.计算出F 值2、35049小于“F 单尾临界”值5、118579,且P(F<=f)=0、144119>0、025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i in np np χ=-=∑, (11、1) i i n np k 其中为实测频数,为理论频数,为分组数。
概率函数在EXCEL中的使用方法

概率函数在EXCEL中的使用方法在Excel中,概率函数被称为统计函数,用于计算概率分布函数(Probability Distribution Function,简称PDF)和累积分布函数(Cumulative Distribution Function,简称CDF)的值。
概率函数在统计分析和数据建模中非常有用,可以帮助我们计算出特定事件发生的可能性。
下面将介绍Excel中一些常用的概率函数的使用方法。
1.概率密度函数(PDF):在Excel中,我们可以使用函数DENSITY函数来计算概率密度函数的值。
这个函数的语法如下:DENSITY(x, mean, standard_dev, cumulative)其中,x是要计算PDF的数值;mean是概率分布的平均值;standard_dev是概率分布的标准偏差;cumulative是一个逻辑值,用于指示是否计算累积分布函数(CDF)的值。
如果cumulative为TRUE(默认值),则计算CDF的值;如果为FALSE,则计算PDF的值。
2.累积分布函数(CDF):在Excel中,我们可以使用函数NORM.DIST来计算累积分布函数的值。
这个函数的语法如下:NORM.DIST(x, mean, standard_dev, cumulative)其中,x是要计算CDF的数值;mean是概率分布的平均值;standard_dev是概率分布的标准偏差;cumulative是一个逻辑值,指示是否计算累积分布函数(CDF)的值。
如果cumulative为TRUE(默认值),则计算CDF的值;如果为FALSE,则计算PDF的值。
3.正态分布:在Excel中,正态分布是一种非常常见的概率分布,可以使用NORM.DIST函数来计算正态分布的概率密度函数(PDF)和累积分布函数(CDF)的值。
4.t-分布:在Excel中,t-分布是一种常用的概率分布,用于小样本的假设检验。
概率论与数理统计实验_用Excel软件解决数理统计问题

用Excel 软件解决数理统计问题一 实验目的学习、掌握用Excel 中求置信区间,作假设检验,作方差分析和回归分析.二 实验的准备在微软Office 的Excel 中有许多函数用于数据处理, 其中有些涉及数理统计, 使用非常方便.Excel 在原安装中可能没有“数据分析”菜单,建立“数据分析”的步骤是:由“工具”菜单中选择“加载宏”,在弹出的加载宏对话框中选定“分析工具库”和“分析数据库-VBA 函数”,确定后“工具”菜单中增加了“数据分析”子菜单. 其中有“描述统计”,“协方差”,“相关系数”,“回归”,“方差分析”,“Z -检验”,“T -检验”,“F -检验”等工具.三 实验内容1. 一般统计a) 平均数Excel 计算平均数用AVERAGE 函数,其格式如下:=AVERAGE(数据1,数据2,…,数据30)例如输入=A VERAGE(1,2,3,4,5)则得到平均数3. 若要得到位于工作表中E3至E12这组数据的平均数,则输入=A VERAGE(E3:E12)b) 样本标准差样本标准差的定义是1)(2--=∑n x xs iExcel 计算样本标准差的函数是STDEV ,其格式如下=STDEV(数据1,数据2,…,数据30)例如输入=STDEV(3,5,6,4,6,7,5)则得到这组数据的样本标准差1.35. 输入=STDEV(E3:E12)则得到位于E3至E12的这组数据的样本标准差.c) 样本方差样本方差的定义是1)(22--=∑n x x s iExcel 计算样本方差使用VAR 函数,格式为=VAR(数据1,数据2,…,数据30)例如输入=V AR(3,5,6,4,6,7,5)则得到这组数据的样本方差1.81. 输入=V AR(E3:E12)则得到位于E3至E12的这组数据的样本方差.2. 区间估计a) 估计均值已知方差, 估计均值时, 使用函数CONFIDENCE, 它的格式是:CONFIDENCE (显著性水平α, 总体标准差, 样本容量) 计算结果是nz σα2/. 再用样本均值加减这个值, 即得总体均值的置信区间.如果已知方差, 则先用函数SQRT 计算平方根, 得标准差, 再代入.如果已知一组样本值, 则还要用函数AVERAGE 计算样本均值, 然后才能计算置信区间. 例1 已知样本容量25=n , 总体的标准差100=σ, 样本均值950=X .取05.0=α. 求均值的置信区间.解 在Excel 的一个单元 (例如A1) 内输入=CONFIDENCE(0.05, 100, 25) 用鼠标点击其它任意单元, 则公式所在单元显示39.19922. 这就是nz σα2/的值. 然后,在另一个单元格中输入=950-A1则显示910.8008. 这是置信区间的左端点. 同样方法可计算置信区间的右端点, 即得均值的置信区间.例2 对某种钢材的抗剪强度进行了10次测试,测得结果如下(单位: MPa)578, 572, 570, 568, 572, 570, 570, 596, 584, 572. 若已知抗剪强度服从正态分布),(2σμN ,且252=σ,求μ的95%的置信区间.解 打开Excel 的一个新工作表. 在单元格B2,C2,…,K2内分别输入数据:578,572,570,…,572. 在单元格B3内输入=A VERAGE(B2: K2) 得到输出2.575=X . 在单元格B4内输入=STDEV(B2: K2)得到输出702.8=S . 在单元格B5内输入=CONFIDENCE(0.05, 5, 10)得到输出nz σα2/=5.394. 在单元格B6内输入=B3-B5得到置信下限为572.101,在单元格B7内输入=B3+B5得到置信上限为578.299. 因此置信区间为(572.101, 578.299)未知方差, 估计均值时, 没有这样的可以直接计算的函数, 需要一步一步计算. 例3 设总体服从正态分布. 已知样本容量16=n , 样本均值75.503=X ,样本标准差2022.6=S . 取05.0=α. 求均值μ的区间估计.解 打开Excel 的一个新工作表. 先用函数TINV 求T 分布的分位点, 它的格式是=TINV(显著性水平α,自由度1-n )在单元格B2内输入=TINV(0.05, 15)则这个单元将显示2.131451. 这就是)15()1(025.02/t n t =-α的值. 在单元格B3内输入 =B2*6.2022/SQRT(16) 显示3.304921. 这是nSn t )1(2/-α的值.在单元格B4内输入=503.75-B3得到置信下限为500.4451, 在单元格B3内输入=503.75+B3得到置信上限为507.0549.因此置信区间为(500.4451, 507.0549)例4 在例2中,设方差未知,求μ的95%的置信区间.解 在例2中已经算得2.575=x , 702.8=S .而样本容量为10. 沿用例2中的工作表. 在单元格E4中输入=TINV(0.05, 9)得到)9()1(025.02/t n t =-α=2.26216, 在单元格E5中输入=E4*B4/SQRT(10)得到nS n t )1(2/-α=6.22539, 在单元格E6中输入=B3-E5得到置信下限为568.975,在单元格E7中输入=B3+E5得到置信上限为581.425.因此置信区间为(568.975, 581.425).注意: TINV(n ,α)给出的是T 分布的上2/α分位点.b) 估计方差估计方差时,要用到2χ分布或F 分布 求2χ分布的上α分位点的函数为CHIINV, 它的格式为=CHIINV(2/α或者2/1α-,自由度1-n )例5 设总体服从正态分布. 已知样本容量9=n . 样本标准差007.0=S . 取05.0=α. 求总体方差的区间估计.解 打开Excel 的一个新工作表,在单元格B2中输入=CHIINV(0.025,8) 显示17.53454()8(2025.0χ=). 在单元格C2中输入=CHIINV(0.975,8)显示 2.179725()8(2975.0χ=). 然后用公式⎪⎪⎭⎫ ⎝⎛-----)1()1(,)1()1(22/1222/2n S n n S n ααχχ计算置信区间. 在单元格B3中输入=8*0.007^2/B2显示0.00002236,在单元格C3中输入=8*0.007^2/C2显示0.0001798,因此总体方差的置信区间为(0.00002236,0.0001798).此外, 函数FINV 可以计算F 分布的上α分位点, 从而求方差比的置信区间.3. 假设检验a) 单个正态总体方差未知时均值的t 检验由于没有一个函数一次完成单个正态总体方差未知时均值的检验,需要分几步计算.所用的检验统计量为nS/X T 0μ-=可以用一般统计中介绍的方法计算检验统计量T 的观察值,再用区间估计中介绍的方法得到T 分布的上2/α分位点(双边检验时),比较统计量T 的观察值t 和T 分布的上2/α分位点(拒绝域为:2/||αt t >),便可得到检验结果.例 6 设某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行使速度如下:250 238 265 242 248 258 255 236 245 261 254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度每小时高于250km ,请问样本数据在显著性水平为0.025时是否和他的声明相抵触?解 (1) 打开Excel 的一个新工作表. 在单元格B3:F6输入样本数据,如下表(2)计算样本平均速度,在单元格D8中输入公式:=A VERAGE(B3:F6)得到平均速度252.05.(3)计算标准差,在单元格D9中输入公式:=STDEV(B3:F6)得到标准差8.64185.(4)在单元格D10中输入样本数20.(5)在单元格D12中输入T 检验值的计算公式:=(D8-250)/(D9/SQRT(D10))得到t 的值为1.06087.(6)在单元格D13中输入公式=TINV(0.05,19)得到025.0t 的值为2.093.现在的检验问题是:250:0=μH ; 250:1>μH .拒绝域为025.0t t >,由上面的计算得到093.206087.1025.0=<=t t ,因此检验的结果是不拒绝原假设. 即无充分证据显示支持引擎制造商声明.b) 两个正态总体方差相等时均值差的t 检验为检验两个正态总体方差相等(但未知)时均值之差的假设:0210:d H =-μμ021:d H a ≠-μμ所用的检验统计量为2102111)(n n S d x x t w +--=(自由度为21n n +-2的t 分布)Excel 在计算时,使用“工具”,“数据分析”,“t-检验:双样本等方差假设”,就得到输出结果.例7 某化工试验中要考虑温度对产品断裂韧度的影响,在C 070,C 080条件下分别作了8次重复试验,侧得断裂韧度的数据如下:(单位:Mpa/m 2)C 070时 20.5 18.8 19.8 20.9 21.5 19.5 21.0 21.2 C 080时 17.7 2.03 20.0 18.8 19.0 20.1 20.2 19.1断裂韧度可以认为服从正态分布. 若已知两种温度的方差相等,1. 问数学期望是否可以认为相等(05.0=α)?2. 求两种温度时的数学期望差的置信区间(05.0=α).解 1.(1) 打开Excel 的一个新工作表. 在单元格A1中输入标记“70oC ”,在单元格B1中输入标记“80o C ”. 从A2到A9输入70o C 时的数据,从B2到B9输入80oC 时的数据.(2) 选定“工具”、“数据分析…”.(3) 选定“t-检验:双样本等方差假设”. (4) 选择“确定”,显示一个对话框. (5) 在“变量1区域”输入A1:A9. (6) 在“变量2区域”输入B1:B9. (7) 选中“输出区域”,并在框内输入D2,表示输出结果将放置于D2右下方的单元格中.(8) 打开“标志”复选框. 如果在“变量1区域”输入A2:A9,在“变量2区域”输入B2:B9,则不打开“标志”复选框. (9) 在“)(A α”内填临界值α为0.05.(10) 在“假设平均差”内填0. (11) 选择“确定”,得到结果如下表所示:在单元格E11中,显示统计量t 的值为2.160247,而在单元格E15中显示了临界值为2.14479,由于2.160247>2.14479,表示拒绝原假设: 认为两种温度下的数学期望不相等.2.利用上图所示的结果,也可以得到两个正态总体方差未知(但相等)时均值差的区间估计.由于检验统计量2111n n S YX T w +-=,现在已知Y X T ,,的值,因此T Y X n n S w -=+2111. 在单元格H5中输入=(E5-F5)/E11显示0.46291(=2111n n S w+),再在单元格H6中输入 =H5*E15显示0.9928442(=)2(11212/21-+⋅+n n t n n S wα),再在单元格H8中输入 =E5-F5-H6显示0.0071558(置信下限),再在单元格H9中输入=E5-F5+H6显示1.9928442(置信上限),因此得到均值差的置信区间为(0.0071558,1.9928442).注解 在本例的Excel 输出表中,单元格E12给出了单边检验时的p 值:0.0242901,单元格E14给出了双边检验时的p 值:0.0485803. P-值的定义是:在原假设成立的条件下,检验统计量取其观察值及比观察值更极端的值(沿着对立假设方向)的概率. P-值也称作“观察”到的显著性水平. P-值越小,反对原假设的证据越强. 通常若P 低于5%,称此结果为统计显著;若P 低于1%,称此结果为高度显著.c) 两个正态总体方差是否相等的F 检验假设两总体服从正态分布,在均值未知时作两样本方差是否相等的检验:22210:σσ=H 22210:σσ≠H 检验统计量为222121)1,1(s s n n F =--(自由度为(1,121--n n )的F 分布)Excel 在计算时,使用“工具”,“数据分析”,“F-检验:双样本方差”,就得到输出结果.例8 由一台自动机床加工某型号零件,现在分别从同一月份上旬和下旬的产品中随意各取若干件,测定其直径,得如下数据(单位:mm)上旬产品:20.5 19.8 19.7 20.4 20.1 20.0 19.0 19.9 下旬产品:19.7 20.8 20.5 19.8 19.4 20.6 19.2假设刀具磨损是引起变化的唯一原因. 问检验结果是否表明加工精度显著降低了(=α0.05)?解 (1) 打开Excel 的一个新工作表. 在单元格A1输入“上旬产品”,在单元格B1输入“下旬产品”. 从单元格A2至A9输入上旬产品的数据,从单元格B2至B8输入下旬产品的数据.(2) 选取“工具”、“数据分析…”(3) 选取“F-检验:双样本方差”,选择“确定”. (4) “在变量1的区域”输入A1:A9. (5) “在变量2的区域”输入B1:B8. (6) 选中“输出区域”,并在框内输入D2,表示输出结果将放置于D2右下方的单元格中.(7) 打开“标志”复选框. 如果在“变量1区域”输入A2:A9,在“变量2区域”输入B2:B8,则不打开“标志”复选框. (8) 在“)(A α”内填临界值α为0.05. (9) 选择“确定”,得到结果如下表:计算出的F 值为0.455618(=2221/S S ),注意单元格E11中给出的“F 单尾临界”值为0.258668,它是)6,7(95.0F 的查表值. 因为0.455618>0.258668,所以不拒绝原假设22210:σσ≥H . 因此检验结果认为下旬产品的加工精度未显著降低.4. 单因素方差分析用Excel 作单因素方差分析的步骤见下例.例9解 (1) 打开Excel 的一个新工作表. 在单元格A1输入标记“同学甲”,在单元格B1输入标记“同学乙”,在单元格C1输入标记“同学丙”. 从单元格A2至A5输入同学甲的100m 成绩,从单元格B2至B5输入同学乙的100m 成绩,从单元格C2至C5输入同学丙的100m 成绩. (2) 选取“工具”、“数据分析…”. (3) 选定“单因素方差分析”. (4) 选择“确定”,显示“单因素方差分析”对话框. (5) 在“输入区域”框输入A1:C5. (6) 在“分组方式”框选定“逐列”. (7) 选中“标志位于第一行(L )”.(8) 显著性水平“α”采用0.05.(9) 在输出选项中选中“输出区域)(O ”,在“输出区域”框中输入A7. (10) 选择“确定”,输出结果如下表所示.单元格A16:G21中显示的是方差分析表. 17行还有一些符号没有汉化. 符号“df ”表示“自由度”,“SS ”表示“偏差平方和”,“MS ”表示“方差”,“F ”为统计量F 的值,“P-value"为统计量F 的P-值. “F crit ”为统计量F 的临界值.从方差分析表知:05.0=α的临界值256.4)9,2(05.0=F . 因计算所得的统计量F 的值<=5263.2F 256.4)9,2(05.0=F ,故接收原假设. 不认为三个同学的100m 成绩有显著不同.5. 无重复双因素方差分析双因素无重复试验是不能区分交互作用的. 双因素无重复试验方差分析的试验数据(1)打开Excel 后在选定的工作表中设定和输入数据阵. (2)选取“工具”、“数据分析…”.(3)选定“方差分析:无重复双因素分析”选项. (4)填写“输入区域”框. (5)打开“标记”复选框(O). (6)填写显著性水平α(A)的值. (7)填写“输出区域”框. (8)选择“确定”,得到输出结果.解 (1)在单元格B1, C1, D1, E1分别输入地区1,地区2,地区3,地区4. 在单元格A2, A3, A4, A5分别输入季度一, 季度二, 季度三, 季度四.(2)在单元格B2, C2, D2, E2分别输入季度一的数据118,200,150,140; 在单元格B3, C3, D3, E3分别输入季度二的数据120,205,148,135; 在单元格B4, C4, D4, E4分别输入季度三的数据115,200,148,138; 在单元格B5, C5, D5, E5分别输入季度四的数据118,202,148,136.(3) 选取“工具”、“数据分析…”.(4) 选定“方差分析:无重复双因素分析”. (5) 在“输入区域”框填写A1:E5. (6) 选中“标记”复选框(有对勾). (7) 选定显著性水平α的值:0.05.(8) 在输出选项中选中输出区域(O):A8. (9) 选择“确定”,得到输出结果:由输出结果行间产生的离差平方和为8.6875(单元格B24), 自由度为3(单元格C24),所以均方和MSR=8.6875/3=2.895833(单元格D24), F 检验的统计量的值为0.675851, 这个检验统计量的P 值为0.588334(单元格E24), 它太大了. 而临界值为3.862539(单元格G24), 因此不否定原假设: 季度这个因素(行间)对结果无显著差异.又由列间产生离差平方和为15504.19(单元格B25), 自由度为3(单元格C25), 均方和MSC=15504.19/3= 5168.063(单元格D25), F 检验的统计量的值为1206.16(单元格E25), 检验统计量的P 值为4.881210-⨯(单元格F25), 而临界值为3.862539(单元格G25), 因此强烈地否定原假设: 地区这个因素(列间)对结果有显著差异.6. 一元线性回归在理解了一元线性回归的概念以后,可以用Excel 直接进行回归分析. 因此避免了复杂的计算过程. 例1较详细地说明了作线性回归的方法和步骤.(1)画出散点图. (2)求线性回归方程x b a y+=. (3)求的方差σ的无偏估计. (4)检验假设0:0=b H ,0:1≠b H . (5)若回归效果显著,求b 的置信水平为0.95的置信区间. 解 (1) 打开Excel 的一个新工作表. 在单元格A1输入标记“碳含量x ”,在单元格B1输入标记“电阻y ”. 从单元格A2至A8输入碳含量的值:0.10,0.30,...,0.95. 从单元格B2至B8输入电阻的值:15,18, (26)(2) 选取“工具”、“数据分析…”. (3) 选定“回归”. (4) 选择“确定”,显示“回归”对话框. (5) 在“Y 值输入区域”输入B1:B8. (6) 在“X 值输入区域”输入A1:A8. (7) 选中“标志L ”,不选中“常数为零”. (8) 选中“置信度F ”,在框内确定置信度为95%. (9) 选中“输出区域O ”,在框内填入A10. (10) 选中“线性拟合图”. (11) 选择“确定”,得到如下的输出表:在上面的输出表中,省略了“残差输出”和“概率输出”的内容.首先单元格A10:B17中的输出为回归分析的摘要表. 单元格A19:F23中的输出为线性回归的方差分析表. 符号“df ”表示“自由度”,“SS ”表示“偏差平方和”,“MS ”表示“方差”,“F ”为统计量F 的值,“Significance F"为统计量F 的P-值.其次,单元格A25:I27中显示的是回归系数的估计与检验. “Coefficient s ”表示“系数”,“Intercept ”表示“截距”,“t Stat ”表示统计量t 的观察值.现在来回答本题中提出的5个问题. (1)在线性回归的方差分析表的右边,可以找到一幅名为“含碳量x Line Fit Plot ”的图形,它就是散点图(图20.1).(2)从“Coefficient s ”的下面两格读出回归直线的截距为13.95839,斜率为12.55034.因此线性回归方程为x y 55034.1295839.13ˆ+=.(3)从方差分析表中的单元格D22读出ε的方差2σ的无偏估计为2ˆσ=0.043195. (4)因为单元格E27中显示出统计量t 的P-值很小(71014.1-⨯),所以回归效果显著.(5)由单元格H27读出b 的置信下限为11.81796,单元格I27读出b 的置信上限为 13.28271,所以b 的置信水平为0.95的置信区间为(11.82,13.28).。
excel均匀分布函数计算概率

一、概述Excel是一款功能强大的电子表格软件,广泛应用于数据分析、统计计算等领域。
在使用Excel进行数据分析时,经常需要计算概率分布,以便进行概率统计和决策分析。
Excel提供了多种函数来计算不同类型的概率分布,其中包括均匀分布函数。
本文将详细介绍如何使用Excel 的均匀分布函数来计算概率,帮助读者更好地掌握Excel在统计计算中的应用。
二、均匀分布概念及特点1. 均匀分布概念均匀分布是概率论中常见的一种连续概率分布,它的概率密度函数在一定区间内具有相同的取值,即概率密度函数呈现为水平的直线。
均匀分布的特点是在给定区间内各个取值的概率是相等的,因此也被称为等概率分布。
2. 均匀分布特点- 概率密度函数在一定区间内呈水平直线,各取值的概率相等;- 均匀分布的期望值等于区间的中点,方差等于区间长度的平方除以12。
三、Excel中均匀分布函数在Excel中,可以使用UNIFORM.DIST函数来计算均匀分布的概率。
UNIFORM.DIST函数的语法如下:UNIFORM.DIST(x, min, max, cumulative)- x:表示要计算概率的数值;- min:表示区间的下限;- max:表示区间的上限;- cumulative:表示是否计算累积概率,可以为TRUE或FALSE。
四、使用Excel计算均匀分布概率1. 计算概率密度要使用Excel计算均匀分布的概率密度,可以利用UNIFORM.DIST函数。
以下是一个示例:假设区间是[3, 7],要计算x=5的概率密度,可以使用以下公式: =UNIFORM.DIST(5, 3, 7, FALSE)函数的返回值为0.25,表示在区间[3, 7]中取值为5的概率密度为0.25。
2. 计算累积概率如果需要计算均匀分布的累积概率,可以将UNIFORM.DIST函数的cumulative参数设置为TRUE。
以下是一个示例:假设区间是[3, 7],要计算x小于等于6的累积概率,可以使用以下公式:=UNIFORM.DIST(6, 3, 7, TRUE)函数的返回值为0.75,表示在区间[3, 7]中取值小于等于6的累积概率为0.75。
excel中的概率统计(非常好的资料).

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C. 单击“函数”下拉列表框 右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE (参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P {X ≤400}=0.841345.注意:(1) NORMDIST 函数的反函数NORMINV 用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P {X <2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值u α(n ),则使用公式=NORMSINV(1-α).1.2.6 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2χ(n),则使用公式=CHIINV(α, n).1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭. 例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7) 计算出置信区间的下限和上限.2.2.2μ1和μ2未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3,20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5,22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U 检验下侧的临界值=NORMSINV(0.05).3.1.2 2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设:μ>250.H0:μ=250;H1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得到t025.0检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当σ12 = σ22 = σ2但未知时12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设:μ1>μ2.H0:μ1=μ2;H1操作步骤:(1)(2)(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3 两个正态总体的方差齐性的F检验例5 羊毛在处理前与后分别抽样分析其含脂率如下: 处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12 问处理前后含脂率的标准差是否有显著差异? 欲检验假设H 0:σ21=σ22; H 1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”. (4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i in np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
excel 随机计算题

excel 随机计算题一、概述Excel是一款功能强大的电子表格软件,它提供了许多工具和功能,可以帮助用户进行数据分析和统计。
为了提高Excel的使用技巧和思维能力,我们特地设计了一些随机计算题,供大家练习和挑战。
二、题目设计以下是我们设计的几个随机计算题,难度适中,覆盖了Excel的多个功能和应用场景。
请根据实际情况,选择适合的难度和题目进行解答。
1.概率计算题:在一张10人的员工名单中,随机抽取两人进行面试。
问这两个人来自不同部门的概率是多少?2.统计图表题:统计公司各部门员工的工资情况,并将数据制成图表。
要求使用Excel的图表功能,将各部门工资情况进行对比和分析。
3.函数应用题:根据销售数据,计算销售额环比增长率。
需要使用Excel的SUMPRODUCT函数和INT函数,以及对数据的有效处理和格式化。
4.数据透视题:对销售数据进行分析,使用数据透视表功能,按地区、产品类别等进行分类统计,并生成各种报表和图表。
5.条件格式题:根据库存数据,使用Excel的条件格式功能,将低于安全库存的产品标记为红色,以便及时处理和调整库存。
三、解题步骤以下是对上述题目的一些解题步骤和思路,供大家参考和参考:1.概率计算题:首先需要确定抽样的总人数和部门数量,再根据独立事件的概率计算方法,计算出这两个人来自不同部门的概率。
2.统计图表题:首先需要将数据录入Excel表格中,并进行格式化处理。
然后使用Excel的图表功能,将各部门工资情况进行对比和分析。
需要注意图表类型、数据源、标签和标题等细节问题。
3.函数应用题:需要先根据销售数据计算出环比增长基数,再使用SUMPRODUCT函数和INT函数进行计算。
需要注意函数的参数和使用方法,以及对数据的有效处理和格式化。
4.数据透视题:需要使用数据透视表的功能,将数据按照地区和产品类别进行分类和统计。
需要注意数据源的整理和筛选,以及报表和图表的生成。
5.条件格式题:需要使用Excel的条件格式功能,将库存数据低于安全库存的部分标记出来。
Excel在概率论和数理统计应用的举例

Excel在概率论与数理统计中应用的举例理优078 10074399 赵晨一.概率计算1.二项分布概率的计算例2.54(保险业务)今有2500名同一类型的人参加保险公司的人寿保险,参加者每年参保费为1200元,一年中若死亡,保险公司赔偿200000元,据生命表统计这类人员每年死亡率为2‰,试求:⑴保险公司获益的概率α;⑵保险公司获益不少于1000000元的概率β.(P62页)解:现拟用二项分布计算,设ξ~B(2500,0.002),由题意知需解出ξ<15的概率,用Excel 函数计算的步骤如下:操作步骤:①.单击要存放结果的单元格B2②.单击“插入函数”按钮,选择“BINOMDIST”函数,在弹出“函数参数”的对话框中依次输入参数14,2500,0.002,true,如下图所示。
Number_s:求解的试验的成功次数;Trials:独立试验的次数;Probability_s:每次试验的成功概率;Cumulative:如果为“true”,函数BINOMDIST返回P{X≤k(Number_s)}的概率;如果为“false”函数BINOMDIST返回P{X=k(Number_s)}的概率③.单击“确定”按钮,Excel计算的二项分布概率为:0.99982.泊松分布的概率计算例:假设某电话总机交换台每分钟收到的呼唤次数服从参数为3的泊松分布,则在1分钟内恰有2次呼唤的概率是多少?解操作步骤:1.单击要存放结果的单元格B22.单击“插入函数”按钮,选择“POISSON”函数,在弹出“函数参数”的对话框中依次输入参数2,3,false,如下图所示。
X:事件出现的次数Mean:期望值(λ)Cumulative:如果为“true”,函数POISSON返回P{X≤k(X)}的概率;如果为“false”函数POISSON返回P{X=k(X)}的概率3.单击“确定”按钮,Excel计算的泊松分布概率为:0.2243.超几何分布概率的计算例:在52张扑克牌中抽取7张,其中有一张黑桃的概率是多少?解操作步骤:1.单击要存放结果的单元格B22.单击“插入函数”按钮,选择“HYPGEOMDIST”函数,在弹出“函数参数”的对话框中依次输入参数1,13,7,52,如下图所示。
概率在EXCEL中的应用

概率在EXCEL中的应用
投掷硬币,每次的结果是正面和反面, 因为我们可以说正面和反面出现的概率 分别是0.5、0.5。 投掷筛子,我们我们这样描述样本空间 和样本点: S={1,2,3,4,5,6} P(1)=1/6 P(2)=1/6 P(3)=1/6 ……
基本的概率关系
两事件的交P(A B)பைடு நூலகம்
A B
两事件的并 P(AUB)
A B
加法公式-两事件并的概率
P(AUB)=P(A)+P(B)-P(A B)
A
B
有50名工人的小型装配厂。每个工人都必须按时完成 50名工人的小型装配厂。 名工人的小型装配厂 工作配额,并且使所装配的产品通过最终检验。 工作配额,并且使所装配的产品通过最终检验。有些 时候,一些工人没有达到工作标准, 时候,一些工人没有达到工作标准,因为他们没有能 够按时完成工作,或者因为装配的产品不合格。 够按时完成工作,或者因为装配的产品不合格。在期 末的绩效评估中,一名生产经理发现在50名工人中有5 50名工人中有 末的绩效评估中,一名生产经理发现在50名工人中有5 人未能按时完成工作; 人装配的产品不合格; 人未能按时完成工作;6人装配的产品不合格;2人即 没能按时完成工作又存在产品不合格的问题。 没能按时完成工作又存在产品不合格的问题。那么该 经理对工人给予低的评估的概率有多少呢? 经理对工人给予低的评估的概率有多少呢?
5/50+6/50-2/50=0.08
乘法公式-两事件交的概率
A
B
假设某报社的发行部已知在某社区有84%的住户 假设某报社的发行部已知在某社区有84%的住户 84% 订阅了该报社的日报。我们用D来表示事件“ 订阅了该报社的日报。我们用D来表示事件“某 住户订阅了日报” P(D)=0.84。此外, 住户订阅了日报”,P(D)=0.84。此外,还知道 某个已经订阅日报的住户订阅其周刊(事件S 某个已经订阅日报的住户订阅其周刊(事件S) 的概率为0.75 0.75, S/D)=0.75。 的概率为0.75,即P(S/D)=0.75。则某住户既 订阅了日报,又订阅了周刊的概率有多少? 订阅了日报,又订阅了周刊的概率有多少?利 用乘法公式我们可以计算如下: 用乘法公式我们可以计算如下: P(S D)=P(D)*P(S/D)=0.84*0.75=0.63 某住户既订阅了日报,又订阅了周刊的概率是63% 某住户既订阅了日报,又订阅了周刊的概率是63%。
excel已知概率密度求均值方差

excel已知概率密度求均值方差标题,Excel中使用已知概率密度求均值和方差。
在统计学和概率论中,均值和方差是两个重要的统计量,它们
可以帮助我们了解数据的分布和变化情况。
在Excel中,我们可以
使用已知概率密度函数来计算数据的均值和方差。
首先,让我们假设有一组数据,我们已经知道了它们的概率密
度函数。
在Excel中,我们可以使用内置的函数来计算这些数据的
均值和方差。
假设我们有一组数据,它们的概率密度函数为f(x),
我们可以使用下面的公式来计算均值和方差:
均值μ = ∫xf(x)dx.
方差σ^2 = ∫(x-μ)^2f(x)dx.
在Excel中,我们可以使用积分函数来计算上述的积分。
首先,我们需要将概率密度函数离散化,即将连续的概率密度函数转换为
离散的数据点。
然后,我们可以使用Excel的SUMPRODUCT函数来计
算均值和方差。
假设我们已经将概率密度函数离散化为一组数据点,并将它们存储在单元格A1:A10中。
我们可以使用下面的公式来计算均值和方差:
均值μ = SUMPRODUCT(A1:A10, B1:B10)。
方差σ^2 = SUMPRODUCT((B1:B10-μ)^2, A1:A10)。
其中B1:B10是对应的数据点的取值。
通过这些公式,我们可以在Excel中轻松地计算出已知概率密度函数的数据的均值和方差。
总之,Excel提供了丰富的函数和工具,可以帮助我们计算已知概率密度函数的数据的均值和方差。
通过使用这些函数,我们可以更好地了解数据的分布和变化情况,为进一步的分析和决策提供支持。
excel中的概率统计

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况就是间断的单元格选取.选取方法就是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况就是间断的单元格范围选取.选取方法就是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认.、如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式就是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法与乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 与F5 中数值的与.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面就是等号(=),后面就是参与计算的元素(运算数)与运算符.每个运算数可以就是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果就是6),然后再加上 5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用5 加上2,再用其结果乘以 3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以 5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母与行数字.例如,D50 引用了列 D 与行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)与区域右下角单元格的引用.下面就是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数就是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总与,但就是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面就是左圆括号、以逗号隔开的参数与右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A、单击需要输入公式的单元格.B、如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C 、 单击“函数”下拉列表框 右端的下拉箭头.D 、 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查瞧其它函数列表.E 、 输入参数.F 、 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE(参数1,参数2,…,参数30)范例:A VERAGE(12、6,13、4,11、9,12、8,13、0)=12、74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1、35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP(参数1,参数2,…,参数30)范例:STDEVP(3,5,6,4,6,7,5)=1、251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR(参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR(3,5,6,4,6,7,5)=1、81(2)总体方差S 2=n x x i ∑-2)(Excel计算总体方差使用V ARP函数,格式如下:V ARP(参数1,参数2,…,参数30)范例:V AR(3,5,6,4,6,7,5)=1、551.2.4正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0、158655,即P{X≤500}=0、158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0、841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0、841345,360,40)得到结果为400,即P{X≤400}=0、841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).Φ=P{X<2}.输入公式范例:已知X~N(0,1), 计算(2)=NORMSDIST(2)Φ=0、97725.得到0、97725,即(2)范例:输入公式=NORMSINV(0、97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1、711).已知t =1、711,n =25,采用单侧,则T 分布的值:=TDIST(1、711,24,1)得到0、05,即P (T >1、711)=0、05.若采用双侧,则T 分布的值:=TDIST(1、711,24,2)得到0、1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV(双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0、05,求t 205.0(10).输入公式=TINV(0、05,10)得到2、2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0、05,求t 0、05 (10).输入公式=TINV(0、1,10)得到1、812462,即t 0、05 (10)= 1、812462. 1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2、9)的值.输入公式=FDIST(2、9,5,15)得到值为0、05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0、05,求其上侧0、05分位点F 0、05(9,9).输入公式=FINV(0、05,9,9)得到值为3、178897,即F 0、05(9,9)= 3、178897.若求单侧百分位点F 0、025(9,9),F 0、975(9,9).可使用公式=FINV(0、025,9,9)=FINV(0、975,9,9)得到两个临界值4、025992与0、248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5、226)的值.输入公式=CHIDIST(5、226,12)得到0、95,即1(5.226)F -=0、95或(5.226)F =0、05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV(上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0、95,12)得到值为5、226,即20.95(12)χ=5、226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE,为泊松分布函数值;若FALSE,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0、104196与0、889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT,与函数SUM ,等等.关于这些函数的具体用法,可以查瞧Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质就是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m)为:1、14 1、10 1、13 1、15 1、20 1、12 1、17 1、19 1、15 1、12 1、14 1、20 1、23 1、11 1、14 1、16.设苗高服从正态分布,求总体均值μ的0、95的置信区间.已知σ =0、01(米). 步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限与置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0、5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0、5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α与标准差σ就是具体的数值而不就是符号.本例中,α =0、05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0、975)*0、01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0、975)*0、01/sqrt(count(b3:g5))计算结果为(1、148225, 1、158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝.例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0、05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) =average(b3:g5)-tinv(0、05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) 计算结果为(1、133695, 1、172555).2.1.3μ未知时σ2的置信区间:置信区间为22 22122(1)(1),(1)(1)n nn ns sααχχ-⎛⎫⎪--⎪--⎪⎝⎭.例3从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50、7 54、9 54、3 44、8 42、2 69、8 53、4 66、1 48、1 34、5试求总体方差2σ的0、9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0、1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0、1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0、1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5与7,分析其蛋白质含量为甲:12、6 13、4 11、9 12、8 13、0乙:13、1 13、4 12、8 13、5 13、3 12、7 12、4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0、05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组与乙组样本均值.(3)分别在单元格C11与C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11与D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0、05输入到单元格E11中.(6)分别在单元格B13与B14输入=B11-B12-TINV(0、025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)与=B11-B12+TINV(0、025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限与上限.2.2.2μ1与μ2未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,她们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别就是SA=0、5419,SB=0、6065.设σ2A与σ2B分别就是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0、95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4与B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))与=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组与B组的方差比的置信区间上限与下限.2.3 练习题1、已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22、3, 21、2, 19、2, 16、6, 23、1, 23、9, 24、8, 26、4, 26、6, 24、8, 23、9, 23、2, 23、3, 21、4, 19、8, 18、3, 20、0, 21、5, 18、7, 22、4, 26、6, 23、9, 24、8, 18、8, 27、1,20、6, 25、0, 22、5, 23、5, 23、9, 25、3, 23、5, 22、6, 21、5, 20、6, 25、8, 24、0, 23、5, 22、6, 21、8, 20、8, 19、5, 20、9, 22、1, 22、7, 23、6, 24、5, 23、6, 21、0, 21、3,22、4,18、7, 21、3, 15、4, 22、9, 17、8, 21、7, 19、1, 20、3, 19、8试以0、95的可靠性,对于该林地上全部林木的平均高进行估计.2、从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50、7,54、9,54、3,44、8,42、2,69、8,53、4,66、1,48、1,34、5.试求总体方差的0、9的置信区间(设总体为正态).3、已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区: 62 57 65 60 63 58 57 60 60 58第二实验区: 56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值与未施以磷肥的玉米产量均值之差的范围(α=0、05) 3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法与操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别就是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0(2)本地平均产量μ就是否比原产地的平均产量μ=800kg高.0(3)本地平均产量μ就是否比原产地的平均产量μ=800kg低.0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0、975);(6)根据算出的数值作出推论.本例中,U的检验值1、341641小于临界值1、959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0、95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0、05).3.1.2σ2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0、025时,就是否与她的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1、06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0、05, D10-1)、欲检验假设H0:μ=250;H1:μ>250.=2、093.由上面计算得到t检已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t.0025验统计量的值1、06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当σ12 = σ22 = σ2但未知时12在此情况下,采用t检验.例试验及观测数据同11、2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H1:μ1>μ2.操作步骤:(1)(2)(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0、05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3、03,“t单尾临界”值为1、734063.由于3、03>1、73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组与第2组测验结果如下:第1组: 91 88 76 98 94 92 90 87 100 69第2组: 90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别就是57与53,取α =0、05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0、05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0、21106(即u统计量的值),其绝对值小于“z双尾临界”值1、959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0、19 0、18 0、21 0、30 0、41 0、12 0、27处理后:0、15 0、13 0、07 0、24 0、19 0、06 0、08 0、12问处理前后含脂率的标准差就是否有显著差异?欲检验假设H0:σ21=σ22; H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0、025. (8)在“输出区域”框输入D1.(9)选择“确定”,得到结果如图所示.计算出F 值2、35049小于“F 单尾临界”值5、118579,且P(F<=f)=0、144119>0、025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i in np np χ=-=∑, (11、1) i i n np k 其中为实测频数,为理论频数,为分组数。
如何使用excel计算概率论一些题目

如何使用excel 计算概率论一些题目简单介绍一些1.1.1 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.1.2 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.1.3 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.1.4 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.1.5 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.1.6 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.1.7 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.13 1.151.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭. 例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在。
ecel中的概率统计非常好的资料

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按 CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格 B4 中的数值加上 25,再除以单元格 D5、E5 和 F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为 11,将 2 乘以 3(结果是 6),然后再加上 5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上 2,再用其结果乘以 3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格 B15 中的数值乘以 5.每当单元格 B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用 A1 引用类型.这种类型用字母标志列(从 A 到IV ,共 256 列),用数字标志行(从 1 到 65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列 D 和行 50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮.C. 单击“函数”下拉列表框右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值Excel计算平均数使用AVERAGE函数,其格式如下:AVERAGE(参数1,参数2,…,参数30)范例:AVERAGE(12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 AVERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用VAR 函数,格式如下:VAR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 VAR(A1:B20). 范例:VAR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用VARP 函数,格式如下:VARP (参数1,参数2,…,参数30)范例:VAR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P{X≤400}=0.841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P{X<2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T服从t(n-1)分布,样本数为25,求P(T>1.711).已知t=1.711,n=25,采用单侧,则T分布的值:=TDIST(1.711,24,1)得到0.05,即P(T>1.711)=0.05.若采用双侧,则T分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=.1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F-=0.95或(5.226)F=0.05.1.2.11卡方分布的反函数Excel使用CHIINV函数得到卡方分布的反函数,即临界值2()nαχ.格式为:CHIINV(上侧概率值α,自由度n)范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n).1.2.12泊松分布计算泊松分布使用POISSON函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE,为泊松分布函数值;若FALSE,则为泊松分布概率分布值.范例:设X服从参数为4的泊松分布,计算P{X=6}及P{X≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT,开平方函数SQRT,和函数SUM,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1 σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.101.13 1.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.231.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间: 置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间 (单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=VAR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=AVERAGE(A2:A6),在单元格B12中输入公式=AVERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=VAR(A2:A6),=VAR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.2μ1和μ2未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的 0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2,23.3, 21.4, 19.8, 18.3, 20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8,27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5, 22.6, 21.5, 20.6, 25.8,24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8 试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区: 62 57 65 60 63 58 57 60 60 58第二实验区: 56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1σ2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显 (1)若方差未变,本地平均产量μ与原产地的平均产量μ0著变化.=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=AVERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U 检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0.05).3.1.2σ2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=AVERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1). 欲检验假设H0:μ=250;H1:μ>250.已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t025.0=2.093.由上面计算得到t检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验3.2.1当σ12 = σ22 = σ2但未知时12μ-μ的检验在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H1:μ1>μ2.操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“ t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组: 91 88 76 98 94 92 90 87 100 69第2组: 90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显著差异?欲检验假设H 0:σ21=σ22; H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表: (2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值 2.35049小于“F 单尾临界”值 5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
利用Excel估计概率分布

一、计算频数、绘制频数图1.计算一组数据的最大值、最小值、极差、分组数和分组组距最大值:= MAX ( )最小值:= MIN ( )极差:= 最大值—最小值分组数:=ROUNDUP (SQRT(COUNT( )),0)分组组距:极差/分组数2.按下图所示分好组3.计算频数:=COUNTIFS ($A$2:$A$10, “>=”&F2, $A$2:$A$10,“<”&F3)4.绘制频数图二、制作正态分布图1. 获取正态分布概率密度正态分布概率密度正态分布函数“NORMDIST”获取该函数的语法格式为:NORMDIST (x, mean, standard_dev, cumulative)其中各参数功能如下:X 为需要计算其分布的数值Mean分布的算术平均值Standard_dev分布的标准偏差Cumulative为一逻辑值,指明函数的形式。
如果cumulative 为TRUE,函数NORMDIST 返回累积分布函数;如果为FALSE,返回概率密度函数具体操作如下:在这里是以分组边界值为“X”来计算:Mean=AVERAGE(A:A)(数据算术平均)Standard_dev=STDEV(A:A)(数据的标准方差)Cumulative=0(概率密度函数)2. 向下填充3.在直方图中增加正态分布曲线图(1)在直方图内右键→选择数据→添加→(2)系列名称:选中H1单元格(3)系列值:选中H2:H21(4)确定、确定4. 修整图形(1)在图表区柱形较下方选中正态分布曲线数据,(正态分布密度值和频率数值相比太小了,实在看不清,多试几次,选中后如图,同时正态分布曲线那数数据处于选中状态)。
(2)右键→设置数据列格式→系列绘制在→次坐标轴;关闭,如图5. 更改系列图表类型(1)选中正态分布柱形图→右键→更改系列图表类型(2)选中“拆线图”(3)确定(4)平滑正态分布图选中正态分布曲线→右键→设置数据列格式→线型→勾选“平滑线”→关闭大功告成!!!。
xls函数概率
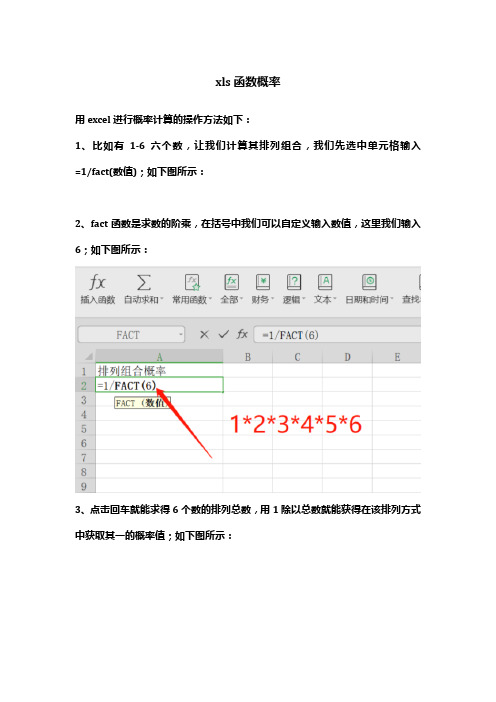
xls函数概率
用excel进行概率计算的操作方法如下:
1、比如有1-6六个数,让我们计算其排列组合,我们先选中单元格输入=1/fact(数值);如下图所示:
2、fact函数是求数的阶乘,在括号中我们可以自定义输入数值,这里我们输入6;如下图所示:
3、点击回车就能求得6个数的排列总数,用1除以总数就能获得在该排列方式中获取其一的概率值;如下图所示:
4、返回给定集合中选取若干对象的排列值(最常见的是彩票中的11选5)。
如下图所示:
5、我们在单元格中输入=1/permut()公式;如下图所示:
6、permut()中参数分别为对象总数,每个排列的对象数,比如5选2,我们就输入5和2,点击回车这样就能求得其排列方式总和;用1处以总数就能获得其概率值。
如下图所示:。
Excel中怎样计算概率

Excel中怎样计算概率?
最佳答案
一、FACT函数求组合
FACT函数是求组合的函数。
例1、1至9中组成不包含重复数的9位数,有几种组合方式呢,可以用下列公式 =FACT(9)。
二、PERMUT求排列计算11选5的概率
例2,11选5共有多少种排列方式呢,一个公式就可以求出? =PERMUT(11,5)。
也可以用FACT函数求得这个结果,公式为=FACT(11)/FACT(11-5)。
三、COMBIN函数计算福彩双色球中头奖概率
福彩双色球当中有33个红球,16个蓝球,要在红球中选择6个,蓝球中选择1个,因此中头奖的概率用公式表示就是=1/COMBIN(33,6)/COMBIN(16,1)。
要在单元格中设置一下小数点的显示数。
四、结果就出来了。
元才能中头奖。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何使用excel 计算概率论一些题目
简单介绍一些
1.1.1 t 分布
Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:
TDIST (变量,自由度,侧数)
其中:
变量(t ):为判断分布的数值;
自由度(v ):以整数表明的自由度;
侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.
范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).
已知t =1.711,n =25,采用单侧,则T 分布的值:
=TDIST(1.711,24,1)
得到0.05,即P (T >1.711)=0.05.
若采用双侧,则T 分布的值:
=TDIST(1.711,24,2)
得到0.1,即()
1.7110.1P T >=. 1.1.2 t 分布的反函数
Excel 使用TINV 函数得到t 分布的反函数,格式如下:
TINV (双侧概率,自由度)
范例:已知随机变量服从t (10)分布,置信度为0.05,求t 2
05.0(10).输入公式
=TINV(0.05,10)
得到2.2281,即()
2.22810.05P T >=.
若求临界值t α(n ),则使用公式=TINV(2*α, n ).
范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式
=TINV(0.1,10)
得到1.812462,即t 0.05 (10)= 1.812462.
1.1.3 F 分布
Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:
FDIST(变量,自由度1,自由度2)
其中:
变量(x ):判断函数的变量值;
自由度1(1n ):代表第1个样本的自由度;
自由度2(2n ):代表第2个样本的自由度.
范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式
=FDIST(2.9,5,15)
得到值为0.05,相当于临界值α.
1.1.4 F 分布的反函数
Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:
FINV(上侧概率,自由度1,自由度2)
范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式
=FINV(0.05,9,9)
得到值为3.178897,即F 0.05(9,9)= 3.178897.
若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式
=FINV(0.025,9,9)
=FINV(0.975,9,9)
得到两个临界值4.025992和0.248386.
若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).
1.1.5 卡方分布
Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:
CHIDIST(数值,自由度)
其中:
数值(x ):要判断分布的数值;
自由度(v ):指明自由度的数字.
范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式
=CHIDIST(5.226,12)
得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.
1.1.6 卡方分布的反函数
Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:
CHIINV (上侧概率值α,自由度n )
范例:下面的公式计算卡方分布的反函数:
=CHIINV(0.95,12)
得到值为5.226,即2
0.95(12)χ=5.226.
若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.1.7 泊松分布
计算泊松分布使用POISSON 函数,格式如下:
POISSON(变量,参数,累计)
其中:变量:表示事件发生的次数;
参数:泊松分布的参数值;
累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式
=POISSON(6,4,FALSE)
=POISSON(6,4,TRUE)
得到概率0.104196和0.889326.
在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.
2 区间估计实验
计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.
2.1 单个正态总体均值与方差的区间估计:
2.1.1
σ2已知时μ的置信区间 置信区间为
22x u x u αα
⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.13 1.15
1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).
步骤:
(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.
(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:
=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))
=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))
上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为
=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))
=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))
计算结果为(1.148225, 1.158025).
2.1.2 σ2未知时μ的置信区间
置信区间为
22
((x t n x t n αα⎛
⎫--+- ⎝. 例2 同例1,但σ未知.
输入公式为:
=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))
=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))
计算结果为(1.133695, 1.172555).
2.1.3 μ未知时σ2的置信区间:
置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪
⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间
(单位:s)如下:
50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5
试求总体方差2σ的0.9的置信区间(设总体为正态).
操作步骤:
(1)在单元格B3:C7分别输入样本数据;
(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);
(3)在单元格C10中输入置信水平0.1.
(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)
(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)
(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12
(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.
当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:
=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)
=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)
2.2 两正态总体均值差与方差比的区间估计
2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间
置信区间为 ()12122
11(2)w x y t n n S n n α⎛
⎫-±+-+ ⎪ ⎪⎝⎭. 例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为
甲:12.6 13.4 11.9 12.8 13.0
乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4
蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ
1-μ
2
所在。
