数学人教版八年级下册正方形课件
合集下载
新人教版数学初中八年级下册18.2.3《正方形》公开课优质课课件

且
的四边形是正方形; 的四边形是
且有三个角是
三、应用新知 解决问 题:
相交于点O,
例1 已知:如图,四边形ABCD是正方形,对角线AC、BD
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三
角形.
证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO. ∴△ABO,△BCO,△CDO,△DAO都是等腰直 角三角形, △ABO≌△BCO≌△CDO≌△DAO.
人民教育出版社 八年级 | 下册
第十八章 · 平行四边
18.2.3 正方 形
形
一、创设情境 引入新知:
活动1:把一张长方形的纸片(如图)中,如何通过折纸的方法, 截出正方形纸片,你有几种方法? 如果是长方形木板,又怎样从中截出面积最大的 正方形木板呢?
一、创设情境 引入新知:
活动2:如图,某一拉门在完全关闭时,其相应的菱形变成正 方形.请说说图中∠1的变化过程.
一、创设情境 引入新知:
小结:正方形既是矩形, 又是菱形. 有一组邻边相等的矩形是 正方形;
有一个角是直角的菱形是 正方形.
二、回顾思考 梳理关系:
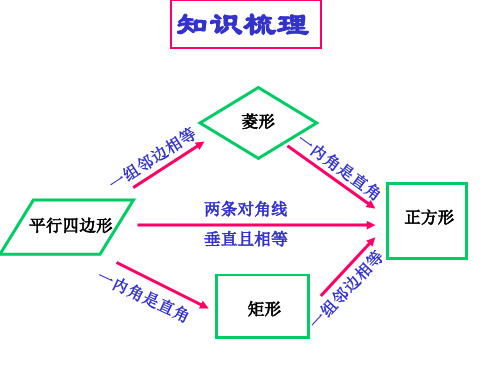
1.通过前面的探究,我们知道正方形既是矩形,又是菱形,还是 平行四边形,它们之间的关系如图:
二、回顾思考 梳理关系:
2.理解上面的关系图,填写下面的表格: 图形 平行四 边形 矩形 菱形 对边 平行、相等 平行、相等 平行、 四条边 都相等 平行、 四条边 都相等 对角 相等 四个角 都是直 角 相等 对角线 互相平分 对称性
不是轴对称图形
正方形
轴对称图 互相平分且相等 形,有两条对 互相垂直且 称轴 轴对称图形, 平分,每条对 有两条对称 角线平分一 轴 组对角 互相垂直、 四个角都 轴对称图形, 平分且相等, 是直角 有四条对称轴 每条对角线 平分一组对
八年级数学下册教学课件《正方形的性质》

情境导入
仔细观察下列实际生活中的图片,你会发现这些都 是正方形的形象.
正方形是我们熟悉的图形,你还能列举出正方形在 生活中应用的其他例子吗?
情境导入
结合已有经验,类比菱形与矩形,正方形的概念是怎 样的呢?
正方形可以定义为有一组邻边相等并且有一个角 是直角的平行四边形.
下面我们一起来探讨一下正方形的性质吧!
解:有多种方法:只要两条小路 交于正方形对角线的交点且两条 小路互相垂直,则满足条件.
课后作业
5. 如图为某城市部分街道示意图,四边形ABCD为正方
形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,
小敏行走的路线为B A G E,小聪行走的路线为B A
D E F,若小敏行走的路程为3100m,则小聪行走的路程
∴C(b,d)
课后作业
2.(2)如图,四边形ABCD是菱形,C,D两点的
坐标分别是(c,0),(0,d).点A , B的在坐标轴上.求A ,
B两点的坐标.【选自教材P61,习题18.2第12题】
y
(2)∵四边形ABCD是菱形,
D
∴AO=CO,BO=DO.
A
O
Cx
Hale Waihona Puke ∵C(c,0),∴A(-c,0)
B
∵D(0,d),∴B(0,-d)
由勾股定理得BC= EC2 EB2 900 100 20 2 (m).
在Rt△ABC中,∠B=90°,AB=BC= 20 2 m,
A
D
由勾股定理得AC= AB2 BC 2 800 800 40(m).
2
S正方形ABCD BC 2 20 2 800
E
∴这块场地的面积为800m2,对角线长40m.
仔细观察下列实际生活中的图片,你会发现这些都 是正方形的形象.
正方形是我们熟悉的图形,你还能列举出正方形在 生活中应用的其他例子吗?
情境导入
结合已有经验,类比菱形与矩形,正方形的概念是怎 样的呢?
正方形可以定义为有一组邻边相等并且有一个角 是直角的平行四边形.
下面我们一起来探讨一下正方形的性质吧!
解:有多种方法:只要两条小路 交于正方形对角线的交点且两条 小路互相垂直,则满足条件.
课后作业
5. 如图为某城市部分街道示意图,四边形ABCD为正方
形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,
小敏行走的路线为B A G E,小聪行走的路线为B A
D E F,若小敏行走的路程为3100m,则小聪行走的路程
∴C(b,d)
课后作业
2.(2)如图,四边形ABCD是菱形,C,D两点的
坐标分别是(c,0),(0,d).点A , B的在坐标轴上.求A ,
B两点的坐标.【选自教材P61,习题18.2第12题】
y
(2)∵四边形ABCD是菱形,
D
∴AO=CO,BO=DO.
A
O
Cx
Hale Waihona Puke ∵C(c,0),∴A(-c,0)
B
∵D(0,d),∴B(0,-d)
由勾股定理得BC= EC2 EB2 900 100 20 2 (m).
在Rt△ABC中,∠B=90°,AB=BC= 20 2 m,
A
D
由勾股定理得AC= AB2 BC 2 800 800 40(m).
2
S正方形ABCD BC 2 20 2 800
E
∴这块场地的面积为800m2,对角线长40m.
18.2.3正方形 正方形的判定(教学课件)-人教版数学八年级下册

探究点
正方形的判定
归纳总结:
(1)四条边相等、四个角都是直角的四边形是正方形 从四边形出发
(2)对角线互相垂直平分且相等的四边形是正方形 (1)有一组邻边相等并且有一个角是直角的平行四边 从平行四边形 形是正方形 出发 (2)对角线互相垂直且相等的平行四边形是正方形 从矩形出发 对角线互相垂直的矩形是正方形 从菱形出发 对角线相等的菱形是正方形
A
D
∴AB=BC=CD=DA,∠A=∠C,∠B=∠D.
又∠A=90°,
ቤተ መጻሕፍቲ ባይዱ
B
C
∴易得∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是正方形.
归纳总结:有一个角是直角的菱形是正方形
探究点
正方形的判定
在上面的证明过程中,是分别从矩形、菱形出 发,添加边或角的条件后得到正方形,那么还有没 有通过添加边、角、对角线的条件可以得到其他 判定正方形的方法呢? 大家想一想.
课堂总结
知识结构
四边形
平行四边形
正 矩形 方 菱形
形
课堂总结
知识结构
课堂总结
1. 教材P62习题18.2第13题.
课后作业
1. 如图,E,F,M,N 分别是正方形ABCD四条边上的
点,且AE=BF=CM=DN,试判断四边形EFMN是什么
图形,并证明你的结论. 【选自教材P62,习题18.2第13题】
把能活动的菱形木框的一个角变为直角(如图),
能否得到正方形?
探究点
正方形的判定
2. 有一个角是直角的菱形是正方形
正方形
可以看到,这个变化过程中只要改变菱形的一 个角,就能得到正方形.
下面我们进行证明:
探究点
人教版八年级下册数学《正方形》平行四边形研讨复习说课教学课件

A
B
O
D
C
阶段归纳
正方形判定的常用方法:
+
一个角是直角 或对角线相等
先判定菱形
矩形条件(二选一)
先判定矩形
+
一组邻边相等, 或对角线垂直
菱形条件(二选一)
正方形 正方形
阶段归纳
平行四边形、矩形、菱形、正方形的判定总结
矩形
5种判定方法 四边形
平行四边形
一个角是直角且一组邻边相等
正方形
菱形
当堂练习
6.对角线互相平分,垂直,相等的四边形是正方形
几何语言表示 ∵AC⊥BD,AC平分BD,BD平分AC,AC=BD, ∴四边形ABCD是正方形
知识点四:正方形,菱形矩形平行四边形之间的关系
归纳总结:正方形是特殊的平行四边形,还是特殊的矩
形、特殊的菱形,因此正方形具有这些图形的所有性质. 判定正方形有两个思路:(1)先判定四边形是矩形,再判定
这个矩形是菱形;(2)先判定四边形是菱形,再判定这个菱形 是矩形.
例1 求证:正方形的两条对角线把这个正方形分成四个全等的 等腰直角三角形.
已知:如图,正方形ABCD中,对角线AC、BD相交于O。 求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形。
证明:∵四边形ABCD是正方形。
知识点二:正方形的性质(从边,角,对角线,对称性四个方面研究)
1.角:正方形的四个角都是直角; 几何语言表示:在正方形ABCD中,∠ABC=∠BCD=∠CDA=∠DAB=90° 2.边:正方形的四条边都相等;对边平行。
几何语言表示:在正方形ABCD中,AB=BC=CD=DA,AB∥CD,AD∥BC
证一证
对角线互相垂直的矩形是正方形.
八年级数学19.3-6正方形的判定ppt课件

一个角是直角且一组邻边相等
判断对错
1. 四边相等的四边形是正方形
2.四角相等的四边形是正方形
3.对角线垂直的平行四边形是正方形 4.对角线互相垂直平分且相等的四边形 是正方形 5.四条边相等且有一个角是直角的四边 形是正方形
1、正方形具有而菱形不一定具有的性质是( D) (A)四条边相等 (B)对角线互相垂直平分 (C)对角线平分一组对角 (D)对角线相等 2、正方形具有而矩形不一定具有的性质是( B) (A)四个角相等 (B)对角线互相垂直平分 (C)对角线相等 (D)对角互补 3、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长 A D 为 7.5 cm。
A
N
E M F
D
B
C
:2、已知:如图矩形ABCD,对角线 AC、BD相交于点O,AE平分∠BAD交 BC于点E,连接OE,若∠EAO=150, 求∠BOE的度数。
A O
B C D
E
3、如图,正方形ABCD的边长为8, M在DC上,且DM=2,N是AC上一个动 点,求DN+MN的最小值。
A
N D M
在数学的天地里,重要的不是我们知道什么, 而是我们怎么知道。 ——毕达哥拉斯
矩形
两组 对边 四边形
分别 平行
平行四 边形 菱 形
• 什么样的四边形叫做正方形呢?
1、 有一组邻边相等的矩形叫做正方形 2、 有一个角是直角的菱形叫做正方形 3、 有一组邻边相等且一个角是直角的
平行四边形叫做正方形
正方形是特殊的平行四 边形,也是特殊的矩形,也 是特殊的菱形。 正方形的性质=
A D
A`
D 1如图,在Rt△ABC中,∠ACB=90°,CD 平分∠ACB,DE⊥AC,DF⊥BC,垂足分 别为E、F,试说明四边形DECF是正方形.
人教版八年级数学下册第十八章《正方形》优课件(共17张PPT)

(1) AB=AD;
A
(2) AC=BD;
(3) ∠BAD=90;
(4) AC⊥BD。
B
D O
C
判断对错
1. 四边相等的四边形是正方形 2.四角相等的四边形是正方形 3.四条边相等且有一个角是直角的四边 形是正方形 4.对角线互相垂直平分且相等的四边形 是正方形 5.对角线垂直的平行四边形是正方形
判断对错
6.对角线互相垂直且相等的四边形是正 方形。 7.对角线互相垂直的矩形是正方形。 8.对角线相等的菱形是正方形。
活动
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验 一下方巾是否是正方形的。
1.已知:正例方形题AB解CD中析,点E、F、G 、H
正方形
菱形
这一 样个 的人 人所 才受 有的 学教 问育 。超
过 了 自 己 的 智 力 ,
You made my day!
我们,还在路上……
每一条对角线平分一组对角
对称性---- 是轴对称图形.
D O
C
根据图形所具有的性质,在下表相应的空格中打 ”√”
对边平行且相 等
四边都相等
四个角都是直 角
对角线互相平 分
对角线互相垂 直
对角线相等
平行四边 形
√
√
矩形
√
√ √
√
菱形
√ √
√ √
正方形
√ √ √ √ √ √
你觉得什么样的四 边形是正方形呢?
分别是AB 、BC 、CD 、DA的中点,试判断四
边形EFGH是正方形吗?为什么?
正方形及其性质八年级人教版数学下册习题课件

(2)设 AD=a,当四边形 EGFH 是正方形时,求矩形 ABCD 12.【中考·天门】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分
线CG于点G,连接GF,求证: 解:设CD=BC=x,则CM=x-3,CN=x-2,
的面积. 把△ADN绕点A顺时针旋转90°得到△ABE.
(2)若BM=3,DN=2,求正方形ABCD的边长.
解:设CD=BC=x,则CM=x-3,CN=x-2, ∵△AEM≌△ANM,∴EM=MN. ∵BE=DN,∴MN=EM=BM+BE=BM+DN=5. ∵∠C=90°,∴MN2=CM2+CN2. 即52=(x-3)2+(x-2)2,解得x=6或-1(舍去), ∴正方形ABCD的边长为6.
证明:∵把△ ADN 绕点 A 顺时针旋转 90°得到△ ABE,∴△ADN≌△ABE, ∴∠DAN=∠BAE,DN=BE,AN=AE.
由题易知 E 在 CB 的延长线上. ∵∠DAB=90°,∠MAN=45°, ∴∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°. ∴∠MAE=∠MAN. 又∵MA=MA,AN=AE, ∴△AEM≌△ANM.
3.【中考·天津】如图,四边形OBCD是正方形,O,D两 点的坐标分别是(0,0),(0,6),点C在第一象限,则 点C的坐标是( D ) A.(6,3) B.(3,6) C.(0,6) D.(6,6)
4.【中考·北京】把图①中的菱形沿对角线分成四个全等的直角 三角形,将这四个直角三角形分别拼成如图②、图③所示的 正方形,则图①中菱形的面积为___1_2____.
∵正方形 ABCD 的边长为 4, ∴AD=AB=4,∠DAB=90°. ∵点 E 在 AB 上且 BE=1,∴AE=3. ∴DE= AD2+AE2= 42+32=5. ∴DE+BE=5+1=6,即△ BFE 周长的最小值为 6. 【答案】B
线CG于点G,连接GF,求证: 解:设CD=BC=x,则CM=x-3,CN=x-2,
的面积. 把△ADN绕点A顺时针旋转90°得到△ABE.
(2)若BM=3,DN=2,求正方形ABCD的边长.
解:设CD=BC=x,则CM=x-3,CN=x-2, ∵△AEM≌△ANM,∴EM=MN. ∵BE=DN,∴MN=EM=BM+BE=BM+DN=5. ∵∠C=90°,∴MN2=CM2+CN2. 即52=(x-3)2+(x-2)2,解得x=6或-1(舍去), ∴正方形ABCD的边长为6.
证明:∵把△ ADN 绕点 A 顺时针旋转 90°得到△ ABE,∴△ADN≌△ABE, ∴∠DAN=∠BAE,DN=BE,AN=AE.
由题易知 E 在 CB 的延长线上. ∵∠DAB=90°,∠MAN=45°, ∴∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°. ∴∠MAE=∠MAN. 又∵MA=MA,AN=AE, ∴△AEM≌△ANM.
3.【中考·天津】如图,四边形OBCD是正方形,O,D两 点的坐标分别是(0,0),(0,6),点C在第一象限,则 点C的坐标是( D ) A.(6,3) B.(3,6) C.(0,6) D.(6,6)
4.【中考·北京】把图①中的菱形沿对角线分成四个全等的直角 三角形,将这四个直角三角形分别拼成如图②、图③所示的 正方形,则图①中菱形的面积为___1_2____.
∵正方形 ABCD 的边长为 4, ∴AD=AB=4,∠DAB=90°. ∵点 E 在 AB 上且 BE=1,∴AE=3. ∴DE= AD2+AE2= 42+32=5. ∴DE+BE=5+1=6,即△ BFE 周长的最小值为 6. 【答案】B
18.2.3.1正方形的性质(同步课件)-八年级数学下册同步精品课堂(人教版)

如图,在正方形 ABCD 中,点 F 为对角线 AC 上一点,连接 BF, DF. 你能找出图中的全等三角形吗?选择其中一对进行证明.
全等三角形有:△ AFD ≌ △AFB,
D
△CFD ≌ △CFB,△ACD ≌ △ABD.
证明:∵四边形 ABCD 为正方形,
∴AD = AB ( 正方形的四条边都相等 ).
∴∠FCE=90°, AC垂直平分BD, ∴AP=PC. 又∵PE⊥BC , PF⊥DC,
∴四边形PECF是矩形, ∴PC=EF. ∴AP=EF.
A
D
PF
B
EC
用直尺和量角器测量正方形的四条边长度、四个角度数、对角线的长度及 夹角度数和OA、OB、OC、OD的长度,并记录测量结果.
AB BC CD AD
∠ABC ∠BCD ∠ADC ∠BAD
AC BD
∠AOB OA OB OC OD
根据测量的结果,你有什么猜想?
A
D
O
B
C
已知:如图,四边形ABCD是正方形.
解:∵四边形ABCD是正方形, ∴AC⊥BD,OA=OD=2. 在Rt△AOD中,由勾股定理,得 AD AO2 OD2 2 2, ∴正方形的周长为4AD= 8 2, 面积为AD2=8.
13.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
解: 连接PC,AC. ∵四边形ABCD是正方形,
证明:∵正方形ABCD是矩形, ∴AO=BO=CO=DO. ∵正方形ABCD是菱形. ∴AC⊥BD.
A
D
O
B
C
图中有 8 个等腰直角三角形.
请同学们拿出准备好的正方形纸片,折一折,观察并思考. 正方形 是不是轴对称图形?如果是,那么对称轴有几条?
【最新】人教版八年级数学下册第十八章《18-2正方形的判定》公开课课件.ppt

• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线)
AEຫໍສະໝຸດ FBDC
练习2:正方形ABCD中,对角线AC和 BD交于点O,点A`,B`,C`,D`分别是A O,BO,CO,DO的中点,判断四边形A` B`C`D`的形状。说明原因
A
D
A`
D`
O
B`
C`
B
C
3.正方形ABCD中,对角线AC和BD交于点 O,点A`,B`,C`,D`分别在AC、BD上, 且AA`=BB`=CC`=DD`. 判断四边形A`B`C`D`的形状
•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/112021/1/112021/1/112021/1/11
谢谢观看
(填上一个条件即可)
矩形
平行四边形
有一组邻边相等 有一个角是直角
正方形
菱形
判断对错
1. 四边相等的四边形是正方形 2.四角相等的四边形是正方形 3.对角线垂直的平行四边形是正方形 4.对角线互相垂直平分且相等的四边形 是正方形 5.四条边相等且有一个角是直角的四边 形是正方形
新课标人教版初中数学八年级下册第十九章19.2特殊的平行四边形--正方形的判定-精品课件
∴∠CEA=∠ABG
练习1:判断 (1)四个角都相等的四边形是正方形 (2)四条边都相等的四边形是正方形 (3)对角线相等的菱形正方形 (4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是 正方形
例2 已知:在正方形ABCD中,A′、B ′、C ′、 D ′分别从顶点A、B、C、D沿AB、BC、CD、 DA方向同时以同样速度向B、C、D、A移动。
D
M
A
E
F
C
N
B
练习2(2019年山东省济南市中考试题)如图,是 一块在电脑屏幕上出现的矩形色块图,由5种颜色 不同的正方形组成。设中间最小的一个正方形边 长为1,则这个矩形的面积是
练习4 (2019年陕西省中考题)如图,在矩形 ABCD中,点E、F分别在AB、CD上,BF平行 于DE。若AD=12cm,AB=7cm,且AE:EB=5: 2,求阴影部分的面积。
例题3:已知正方形ABCD中,Q在CD上,且 DQ=QC,P在BC上,AP=CD+CP; 求证:AQ 平分∠DAP.
证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形, ∴AD=CD,AD∥CD;
A
D
∴∠D=∠QCE,∠DAQ=∠E, 又∵DQ=CQ,
Q
∴⊿ADQ≌⊿ECQ (AAS).
∴∴ACDD==CCEE,,又∴AADP==CCDD,+CP=CE+CP=EPB.
①AE与BF相等吗?为什么?
②AE与BF是否垂直?说明你的理由。
A
D
F G
BE
C
练习7:如图,已知正方形ABCD中,
E、F分别为BC和DC上的点,且
练习1:判断 (1)四个角都相等的四边形是正方形 (2)四条边都相等的四边形是正方形 (3)对角线相等的菱形正方形 (4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是 正方形
例2 已知:在正方形ABCD中,A′、B ′、C ′、 D ′分别从顶点A、B、C、D沿AB、BC、CD、 DA方向同时以同样速度向B、C、D、A移动。
D
M
A
E
F
C
N
B
练习2(2019年山东省济南市中考试题)如图,是 一块在电脑屏幕上出现的矩形色块图,由5种颜色 不同的正方形组成。设中间最小的一个正方形边 长为1,则这个矩形的面积是
练习4 (2019年陕西省中考题)如图,在矩形 ABCD中,点E、F分别在AB、CD上,BF平行 于DE。若AD=12cm,AB=7cm,且AE:EB=5: 2,求阴影部分的面积。
例题3:已知正方形ABCD中,Q在CD上,且 DQ=QC,P在BC上,AP=CD+CP; 求证:AQ 平分∠DAP.
证明:延长AQ交BC延长线与E,
∵四边形ABCD是正方形, ∴AD=CD,AD∥CD;
A
D
∴∠D=∠QCE,∠DAQ=∠E, 又∵DQ=CQ,
Q
∴⊿ADQ≌⊿ECQ (AAS).
∴∴ACDD==CCEE,,又∴AADP==CCDD,+CP=CE+CP=EPB.
①AE与BF相等吗?为什么?
②AE与BF是否垂直?说明你的理由。
A
D
F G
BE
C
练习7:如图,已知正方形ABCD中,
E、F分别为BC和DC上的点,且
人教版八年级数学下册第十八章《18.2.3 正方形》优质公开课课件

角三角形.
A
D
思考:图中共有__四____个
O
等腰直角三
B
C
证明:∵四边形ABCD是_正__方__形_____,
∴AC=_B_D___,AC__⊥__BD,AO=_C_O___=_B_O___=_D_O___. ∴△ABO、△_B__C_O__、△_C_D__O__、△_D_A_O___是等腰直角三角 形,且△ABO≌△BCO__≌___△CDO__≌___△DAO.
“引导学生读懂数学书”课题 研究成果配套课件
新课引入 展示目标 研读课文 归纳小结 强化训练
第十课时 § 18.2.3 正方形
一、新课引入
矩形
1.四个角都___相__等___ 性 质
2.对角线__互__相__平__分__
1.有一个角是_直__角___的 __平__行__四__边__形_
判 2.有三个角是_直__角__的 定 ___四__边__形__
_______________
五、强化训练
已知:如图,△ABC中,∠C=90°,CD平分
∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
C
解:∵∠C=90°,DE⊥BC于E,
DF⊥AC于F
E
∴四边形CEDF有三个直角F,
它是矩形
A
又∵CD平分∠ACB
D
B
根据角平分线上的点都两边的距离相等,可知
二
2、正方形与平行四边形、矩形、菱形之间的关系有怎样的
包含关系?请填入下图中.
正
方
平行四边形
形
的 性
菱形
正方形 矩形
质
三、研读课文
例5 求证:正方形的两条对角线把这个正方形分成四个全
人教版(五四制)八年级下册数学:2特殊的平行四边形丰富多彩的正方形课件

10
步骤1:计算正方形的面积、边长
10 5 10 5 10
步骤2:找出正方形的边 步骤3:找出分割方案
20 200
100 20
正方形面积S=200+100+200=500 200 20 正方形边长= 500=10 5
10 5
10 5
10
剪拼后大正方形的边长= a2 b2
B
a Cb E B
a
C b E 你能找到长度等于 a2 b2的线段吗?
方案一
方案二
将两个边长不等的正方形分割——重拼成一个正方形.
方案三
a
a2 b2
b
工人师傅将一块如图所示的铝板,经过适当的剪切拼接,焊接成
一块正方形铝板,请画出剪切方法,并将剪切后的铝板拼成一个面积 与本来图形面积一样的正方形。
请你在图中添加两条直线,将一块正方形分割成面积 相等的四个部分, 设计出分割方案.
请你当设计师
AE
1
3
G
2
D
B H O
4
FC
证明:连接OA、OD O
∵∠GOF=∠GDF=90 O
∴∠4+∠DGO=180 O
∵∠3+∠DGO=180
∴∠3=∠4
在△OAG和△ODF中
∠3=∠4
∠1=∠2
OA=OD
∴ △OAG ≌△ODF(AAS)
∴S △OAG =S △ODF
1
∵
S
△OAD=
4
S正方形ABCD
1
∴ S四边形OGDF= 4 S正方形ABCD
上述分割方法有什么共同点? 1、两条直线都经过正方形的中心 2、两条直线互相垂直
小结:经过正方形对角线的交点O,且互相垂直的 两条直线将正方形分割成等面积的四部分.
八年级数学下册课件: 正方形(第课时) 公开课一等奖课件

高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校:
北京大学光华管理学院
北京市理科状元杨蕙心
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
zx``x````````k
6
六、应用新知
已知:点E、F、G、 H分别是正方形ABCD四 条边上的中点,并且E、F、 G、H分别是AB、BC、 CD、AD的中点.求证:四 边形EFGH是正方形.
A E B
H
D G
F
C
7
七、小结
1.正方形的判定方法. 2.了解正方形、矩形、菱形之间的联系与 区别,体验事物之间是相互联系但又有区别的 辩证唯物主义观点.
青 春 风 采
高考总分:
692分(含20分加分) 语文131分 数学145分 英语141分 文综255分
最新整理人教版八年级数学下册第十八章《特殊的平行四边形 正方形》优质课件(2课时)

矩形
中心对称图形 (对角线的交点)
即是中心对称图形, 又是轴对称图形(两条)
菱形
正方形
即是中心对称图形,
即是中心对称图形,
又是轴对称图形(两条) 又是轴对称图形(四条)
探究新知
18.2 特殊的平行四边形/
平行四边形、矩形、菱形、正方形之间关系:
平行四 边形
(1)
矩形 (3) 有一组邻边相等且 有一个角是直角
D
?E
∴AB=BC,∠1=∠2=45°,
又∵BE=BE ∴△ABE≌△CBE ∴AE=CE.
1 2
B
?
C
探究新知
18.2 特殊的平行四边形/
素养考点 2 利用正方形的性质求角度 例2 如图,在正方形ABCD中, ΔBEC是等边三角形,
求证: ∠EAD=∠EDA=15° . 证明:∵ ΔBEC是等边三角形,
问题1:图中CD在平移时,这个图形始终是怎样的图形?
问题2:当CD移动到CD位置,此时AD =AB,四边形
ABCD还是矩形吗? 正方形是特殊的矩形
探究新知
18.2 特殊的平行四边形/
【思考】1. 矩形一组邻边相等时变成怎样的图形呢?
〃
正方形矩 形
探究新知
【思考】2.菱 形有一个角是 直角时变成怎 样的图形呢?
探究新知
18.2 特殊的平行四边形/
已知:如图,四边形ABCD是正方形. 求证:正方形ABCD四边都相等,四个角都是直角.
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=BC (正方形的定义).
又∵正方形是平行四边形.
A
D
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
八年级数学下册特殊的平形四边形中的正方形3课件人教版

A
D O
• •
边----- 四条边都相等 角----- 四个角都是直角
B
C
•对角线----- 相等、互相垂直且平分、平分一组对角
二、正方形的性质
性质定理1: 正方形的四个角都是直角,四条边都相等 性质定理2: 正方形的两条对角线相等,并且互相垂直 平分、每条对角线平分一组对角
三、正方形的判定
1、 定义法: 有一组邻边相等并且有一个角是直角 的平行四边形是正方形。 矩形菱形法: 既是矩形又是菱形的四边形是正方形。 2、 3、 对角线法: 两条对角线互相垂直平分且相等的四 边形是正方形。
正方形的判定
1、定义法 2、矩形菱形法 3、对角线法
形成性测试题
1、选择题: ①、下列判断中正确的是( ) A、四边相等的四边形是正方形 B、四角相等的四边形是正方形 C、对角线垂直的平行四边形是正方形 D、对角线互相垂直平分且相等的四边形是正方形
②、在四边形ABCD中O是对角线的交点,能判定 这个四边形是正方形的是( ) D A、AC = BD,AB∥CD,AB = CD F B、AD∥BC,∠A =∠ C G C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
2、如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG A
C
E B
一、正方形的定义
正方形:有一组邻边相等并且有一个角是直角的平 行四边形是正方形。 ①、正方形既是邻边相等的特殊矩形,又是有一个 角是直角的特殊菱形。 ②、正方形既具有矩形的性质有具有菱形的性质。
平行四边形 矩 形 正 方 形 菱 形
想一想
①、图中有哪些相等的线段?有 哪些相等的角? ②、图中有那些等腰直角三角形?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版 八年级下册
18.2 正方形
导入新课
平行四边形
有一个角为直角 矩形 邻边相等
?
菱形
是什么?
新课学习
正方形
两组互相垂直的平行线围成矩形ABCD
A
D
A
D
B
C
B
C
正方形是特殊的矩形
邻边相等的矩形。
新课学习
正方形
★正方形是特殊的菱形 一个角是直角的菱形。
新课学习
பைடு நூலகம்
正方形的性质
轴对称图形,有4条对称轴 四边相等 AB=BC=CD=DA
1、对称性 2、边
A O
D(B)
3、角
四角相等 ∠A=∠B=∠C=∠D=90°
B
C(A)
4、对角线
相等,且互相垂直平分,每条对角线平分一组对角。
新课学习
正方形的判定
1、定义法
A D A D
平行四边形
B
C
一组邻边相等
一个内角是直角
B
正方 形
C
∵ □ABCD中,AB=BC且∠A=90°, ∴ABCD为正方形
因此AG⊥CF。
达标检测
5.如图,在△ABC中,∠BAC=90°,AB=AC,点D是 BC的中点,DE⊥AB,DF⊥AC垂足分别为E,F.求 证:四边形DEAF是正方形
达标检测 解析:∵DE⊥AB,DF⊥AC
∴∠AED=90°,∠AFD=90°
∵∠BAC=90°∴∠EDF=90°∴□AEDF是矩形 在△BDE和△CDF中 ∵AB=AC∴∠ABC=∠ACB ∵DE⊥AB,DF⊥AC ∴∠DEB=∠DFC 又∵D是BC的中点∴BD=DC∴△BDE≌△CDF
达标检测
A
分析:阴影部分的面积=S△ACD-S△MEC,△ACD和△MEC都 是等腰直角三角形,利用面积公式即可求解.
达标检测
3.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,
BE与AC相交于点M,则∠AMD的度数是( B ) A.75° C.54° B.60° D.67.5°
分析:连接BD,根据BD,AC为正方形的两条对角线可知AC
相等,且互相垂直平分,每条对角线平分一组对角。 正方形的判定
达标检测 1.如图,有一平行四边形ABCD与一正方形CEFG,其中E 点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为 何?( C ) A.50B.55C.70D.75 分析:由平角的定义求出∠CED的度数,由三角形内角和定理求 出∠D的度数,再由平行四边形的对角相等即可得出结果.
为BD的垂直平分线,所以∠AMD=AMB,要求∠AMD,求
∠AMB即可.
达标检测
4.已知正方形ABCD,E为BC上任一点延长AB至F,使 BF=BE,连AE并延长交CF于G,求证:AG⊥CF.
达标检测
解析:如图, ∵BE=BF,∴∠BFE=45°
∵∠CAB=45°,
∴FH⊥AC,
又CB⊥AF,
∴E是△ACF的垂心,
∴四边形ABCD是正方形;
知识巩固 解:(2)如图2所示:
已知:四边形ABCD是矩形,对角线AC⊥BD;
求证:四边形ABCD是正方形; 证明:∵四边形ABCD是矩形,对角线AC⊥BD, ∴∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形, ∴AB=BC=CD=DA,
∴四边形ABCD是正方形.
知识巩固 3.已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F. (1)四边形AEDF是什么四边形? (2)当△ABC满足什么条件时,四边形AEDF是矩形? (3)当线段AD满足什么条件时,四边形AEDF是菱形?
(4)当△ABC满足什么条件时,四边形AEDF是正方形?
知识巩固 解:(1)∵DE∥AC,DF∥AB ∴四边形AEDF是平行四边形;
∴DE=DF∴□AEDF是正方形
(2)由矩形的性质和已知条件得出
∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形, 得出AB=BC=CD=DA,即可得出结论.
知识巩固 解:(1)如图1所示:
已知:四边形ABCD是菱形,∠A=90°;
求证:四边形ABCD是正方形; 证明:∵四边形ABCD是菱形,∠A=90°, ∴AB=CD=BC=DA,四边形ABCD是矩形, ∴∠A=∠B=∠C=∠D=90°,
新课学习
2、菱形法
A B
菱形
C
一内角是直角
D
A
D
B
正方 形
C
∵ 菱形ABCD中,∠A=90°,
∴ABCD为正方形
新课学习
3、矩形法
A D A D
矩形
B C
一组邻边相等
B
正方形
C
∵ 矩形ABCD中,AB=BC,
∴ABCD为正方形.
新课学习 例5 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.
知识巩固 解析:(1)连接AF
在Rt△AEF和Rt△ABF中,
∵AF=AF,AE=AB, ∴Rt△AEF≌Rt△ABF, ∴BF=EF;
知识巩固
2.证明:
(1)有一个角是直角的菱形是正方形; (2)对角线垂直的矩形是正方形。 分析:(1)由菱形的性质和已知条件得出AB=CD=BC=DA, 四边形ABCD是矩形,得出∠A=∠B=∠C=∠D=90°,即可得 出结论;
结论很重要!
新课学习
矩形
平行四边形
有一组邻边相等且有一个角是直角
正方形
菱形
新课学习
平行四边形 正
矩形
方
形
菱形
知识巩固 1.在正方形ABCD的对角线AC上点E,使AE=AB,过E作 EF⊥AC交BC于F, 求证:(1)BF=EF;(2)BF=CE。
分析:连接AF,要求BF=EF,求证△AEF≌△ABF,可以求证EF=BF (2)根据(1)的结论,要求BF=CE,求证△CEF为等腰直角三角 形即可
(2)∵一个角为直角的平行四边形为矩形,
∴∠BAC=90°时,四边形AEDF是矩形; (3)∵菱形对角线互相垂直, ∴当AD⊥EF时,四边形AEDF是菱形; (4)∵正方形既是菱形又是矩形,
∴∠BAC=90°且AD⊥BC时,四边形AEDF是正方形.
课堂小结 正方形的性质 轴对称图形,有4条对称轴
四边相等 四角相等
已知:如图四边形ABCD是正方形,
A
D
对角线AC、BD交于点O。
求证: △ ABO、 △ BCO、 △ CDO、 △ DAO是全等的等腰直角三角形。
O B
C
新课学习
证明:∵四边形ABCD是正方形, ∠B=90°
∴AC=BD,AC ⊥ BD,AO=BO=CO=DO
∴△ ABO、 △ BCO、 △ CDO、 △ DAO是等腰 直角三角形,且△ABO≌△BCO≌ △ CDO ≌ △ DAO
18.2 正方形
导入新课
平行四边形
有一个角为直角 矩形 邻边相等
?
菱形
是什么?
新课学习
正方形
两组互相垂直的平行线围成矩形ABCD
A
D
A
D
B
C
B
C
正方形是特殊的矩形
邻边相等的矩形。
新课学习
正方形
★正方形是特殊的菱形 一个角是直角的菱形。
新课学习
பைடு நூலகம்
正方形的性质
轴对称图形,有4条对称轴 四边相等 AB=BC=CD=DA
1、对称性 2、边
A O
D(B)
3、角
四角相等 ∠A=∠B=∠C=∠D=90°
B
C(A)
4、对角线
相等,且互相垂直平分,每条对角线平分一组对角。
新课学习
正方形的判定
1、定义法
A D A D
平行四边形
B
C
一组邻边相等
一个内角是直角
B
正方 形
C
∵ □ABCD中,AB=BC且∠A=90°, ∴ABCD为正方形
因此AG⊥CF。
达标检测
5.如图,在△ABC中,∠BAC=90°,AB=AC,点D是 BC的中点,DE⊥AB,DF⊥AC垂足分别为E,F.求 证:四边形DEAF是正方形
达标检测 解析:∵DE⊥AB,DF⊥AC
∴∠AED=90°,∠AFD=90°
∵∠BAC=90°∴∠EDF=90°∴□AEDF是矩形 在△BDE和△CDF中 ∵AB=AC∴∠ABC=∠ACB ∵DE⊥AB,DF⊥AC ∴∠DEB=∠DFC 又∵D是BC的中点∴BD=DC∴△BDE≌△CDF
达标检测
A
分析:阴影部分的面积=S△ACD-S△MEC,△ACD和△MEC都 是等腰直角三角形,利用面积公式即可求解.
达标检测
3.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,
BE与AC相交于点M,则∠AMD的度数是( B ) A.75° C.54° B.60° D.67.5°
分析:连接BD,根据BD,AC为正方形的两条对角线可知AC
相等,且互相垂直平分,每条对角线平分一组对角。 正方形的判定
达标检测 1.如图,有一平行四边形ABCD与一正方形CEFG,其中E 点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为 何?( C ) A.50B.55C.70D.75 分析:由平角的定义求出∠CED的度数,由三角形内角和定理求 出∠D的度数,再由平行四边形的对角相等即可得出结果.
为BD的垂直平分线,所以∠AMD=AMB,要求∠AMD,求
∠AMB即可.
达标检测
4.已知正方形ABCD,E为BC上任一点延长AB至F,使 BF=BE,连AE并延长交CF于G,求证:AG⊥CF.
达标检测
解析:如图, ∵BE=BF,∴∠BFE=45°
∵∠CAB=45°,
∴FH⊥AC,
又CB⊥AF,
∴E是△ACF的垂心,
∴四边形ABCD是正方形;
知识巩固 解:(2)如图2所示:
已知:四边形ABCD是矩形,对角线AC⊥BD;
求证:四边形ABCD是正方形; 证明:∵四边形ABCD是矩形,对角线AC⊥BD, ∴∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形, ∴AB=BC=CD=DA,
∴四边形ABCD是正方形.
知识巩固 3.已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F. (1)四边形AEDF是什么四边形? (2)当△ABC满足什么条件时,四边形AEDF是矩形? (3)当线段AD满足什么条件时,四边形AEDF是菱形?
(4)当△ABC满足什么条件时,四边形AEDF是正方形?
知识巩固 解:(1)∵DE∥AC,DF∥AB ∴四边形AEDF是平行四边形;
∴DE=DF∴□AEDF是正方形
(2)由矩形的性质和已知条件得出
∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形, 得出AB=BC=CD=DA,即可得出结论.
知识巩固 解:(1)如图1所示:
已知:四边形ABCD是菱形,∠A=90°;
求证:四边形ABCD是正方形; 证明:∵四边形ABCD是菱形,∠A=90°, ∴AB=CD=BC=DA,四边形ABCD是矩形, ∴∠A=∠B=∠C=∠D=90°,
新课学习
2、菱形法
A B
菱形
C
一内角是直角
D
A
D
B
正方 形
C
∵ 菱形ABCD中,∠A=90°,
∴ABCD为正方形
新课学习
3、矩形法
A D A D
矩形
B C
一组邻边相等
B
正方形
C
∵ 矩形ABCD中,AB=BC,
∴ABCD为正方形.
新课学习 例5 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.
知识巩固 解析:(1)连接AF
在Rt△AEF和Rt△ABF中,
∵AF=AF,AE=AB, ∴Rt△AEF≌Rt△ABF, ∴BF=EF;
知识巩固
2.证明:
(1)有一个角是直角的菱形是正方形; (2)对角线垂直的矩形是正方形。 分析:(1)由菱形的性质和已知条件得出AB=CD=BC=DA, 四边形ABCD是矩形,得出∠A=∠B=∠C=∠D=90°,即可得 出结论;
结论很重要!
新课学习
矩形
平行四边形
有一组邻边相等且有一个角是直角
正方形
菱形
新课学习
平行四边形 正
矩形
方
形
菱形
知识巩固 1.在正方形ABCD的对角线AC上点E,使AE=AB,过E作 EF⊥AC交BC于F, 求证:(1)BF=EF;(2)BF=CE。
分析:连接AF,要求BF=EF,求证△AEF≌△ABF,可以求证EF=BF (2)根据(1)的结论,要求BF=CE,求证△CEF为等腰直角三角 形即可
(2)∵一个角为直角的平行四边形为矩形,
∴∠BAC=90°时,四边形AEDF是矩形; (3)∵菱形对角线互相垂直, ∴当AD⊥EF时,四边形AEDF是菱形; (4)∵正方形既是菱形又是矩形,
∴∠BAC=90°且AD⊥BC时,四边形AEDF是正方形.
课堂小结 正方形的性质 轴对称图形,有4条对称轴
四边相等 四角相等
已知:如图四边形ABCD是正方形,
A
D
对角线AC、BD交于点O。
求证: △ ABO、 △ BCO、 △ CDO、 △ DAO是全等的等腰直角三角形。
O B
C
新课学习
证明:∵四边形ABCD是正方形, ∠B=90°
∴AC=BD,AC ⊥ BD,AO=BO=CO=DO
∴△ ABO、 △ BCO、 △ CDO、 △ DAO是等腰 直角三角形,且△ABO≌△BCO≌ △ CDO ≌ △ DAO
