最短路径matlab计算机仿真
matlab避障最短路径

matlab避障最短路径一、引言随着机器人技术的发展,自动化导航成为一个重要的研究领域。
在许多应用中,机器人需要通过复杂的环境中,避开障碍物并找到最短路径。
Matlab作为一种强大的数学计算工具,为我们提供了实现这一目标的丰富功能和工具。
二、建立环境模型在开始编写避障算法之前,首先需要建立机器人所在环境的模型。
可以使用Matlab的图形界面工具来实现,也可以通过编程方式来创建。
这里我们选择使用编程方式来建立环境模型。
在Matlab中,可以使用矩阵来表示环境模型。
假设我们的环境是一个网格,每个网格可以是空地、障碍物或起点/终点。
我们可以用不同的数值来表示不同的状态,例如0表示空地,1表示障碍物,2表示起点,3表示终点。
三、编写避障算法在建立环境模型之后,我们可以开始编写避障算法了。
这里我们使用A*算法来寻找最短路径。
A*算法是一种常用的启发式搜索算法,它通过估计当前节点到目标节点的代价来选择下一个节点,从而找到一条最短路径。
具体来说,A*算法通过维护一个开放列表和一个关闭列表来搜索最短路径。
初始时,将起点加入开放列表。
然后,重复以下步骤直到找到终点或开放列表为空:1. 从开放列表中选择代价最小的节点作为当前节点。
2. 如果当前节点是终点,搜索结束,返回最短路径。
3. 否则,将当前节点加入关闭列表,并计算其相邻节点的代价。
4. 对于每个相邻节点,如果它不在关闭列表中并且不是障碍物,则更新其代价,并将其加入开放列表。
四、Matlab实现在Matlab中,可以使用自定义函数来实现A*算法。
下面是一个简单的示例代码:```matlabfunction path = astar(start, goal, map)% 初始化开放列表和关闭列表openList = start;closeList = [];% 初始化起点的代价为0start.g = 0;while ~isempty(openList)% 选择开放列表中代价最小的节点作为当前节点[~, index] = min([openList.f]);current = openList(index);% 如果当前节点是终点,搜索结束if current == goalpath = reconstructPath(current);return;end% 将当前节点加入关闭列表closeList = [closeList, current];openList(index) = [];% 对当前节点的相邻节点进行处理neighbors = findNeighbors(current, map);for i = 1:length(neighbors)neighbor = neighbors(i);% 如果相邻节点在关闭列表中或是障碍物,跳过if ismember(neighbor, closeList) || map(neighbor) == 1continue;end% 计算相邻节点的代价g = current.g + 1;h = heuristic(neighbor, goal);f =g + h;% 如果相邻节点不在开放列表中,或其代价更小if ~ismember(neighbor, openList) || g < neighbor.gneighbor.g = g;neighbor.f = f;neighbor.parent = current;% 如果相邻节点不在开放列表中,加入if ~ismember(neighbor, openList)openList = [openList, neighbor];endendendend% 如果开放列表为空,搜索失败error('No path found.');endfunction path = reconstructPath(node)path = [];while ~isempty(node.parent)path = [node, path];node = node.parent;endendfunction neighbors = findNeighbors(node, map)% 根据当前节点的位置和地图大小,找到相邻节点[row, col] = size(map);neighbors = [];% 上方节点if node.row > 1neighbors = [neighbors, struct('row', node.row-1, 'col', node.col)];end% 下方节点if node.row < rowneighbors = [neighbors, struct('row', node.row+1, 'col', node.col)];end% 左方节点if node.col > 1neighbors = [neighbors, struct('row', node.row, 'col', node.col-1)];end% 右方节点if node.col < colneighbors = [neighbors, struct('row', node.row, 'col', node.col+1)];endendfunction h = heuristic(node, goal)% 使用曼哈顿距离作为启发函数h = abs(node.row-goal.row) + abs(node.col-goal.col);end```以上代码实现了A*算法,并提供了辅助函数来计算相邻节点、启发函数和重构最短路径。
最短路径 dijkstra算法的matlab代码实现

最短路径dijkstra算法的matlab代码实现如何用Matlab实现Dijkstra算法求解最短路径问题?Dijkstra算法是一种用于计算图中的最短路径的经典算法。
该算法以一个起始节点为基础,通过不断更新节点到其他节点的最短距离,直到找到最短路径为止。
本文将一步一步地回答如何使用Matlab实现Dijkstra算法,以及如何在Matlab中构建图并求解最短路径。
第一步:构建图Dijkstra算法是基于图的算法,因此我们首先需要在Matlab中构建一个图。
图可以用邻接矩阵或邻接表等方式表示。
这里我们选择使用邻接矩阵来表示图。
在Matlab中,可以使用矩阵来表示邻接矩阵。
假设我们的图有n个节点,我们可以创建一个n×n的矩阵来表示图的邻接矩阵。
如果节点i和节点j 之间有一条边,则将邻接矩阵中的第i行第j列的元素设置为边的权重,如果没有边相连,则将元素设置为一个较大的值(例如无穷大)表示不可达。
现在,我们可以开始构建邻接矩阵。
这里以一个具体的例子来说明。
假设我们有一个包含6个节点的无向图,如下所示:0 1 2 3 4 5-0 0 4 3 0 0 01 4 0 1 4 0 02 3 1 0 2 1 03 04 2 0 3 24 0 0 1 3 0 25 0 0 0 2 2 0在Matlab中,可以将邻接矩阵表示为一个n×n的矩阵。
在这个例子中,我们可以这样定义邻接矩阵:G = [0 4 3 0 0 0;4 0 1 4 0 0;3 1 0 2 1 0;0 4 2 0 3 2;0 0 1 3 0 2;0 0 0 2 2 0];第二步:实现Dijkstra算法在Matlab中,我们可以使用一些循环和条件语句来实现Dijkstra算法。
下面是一个基本的Dijkstra算法的实现流程:1. 创建一个数组dist,用于存储从起始节点到其他节点的最短距离。
初始时,将起始节点到自身的距离设置为0,其他节点的距离设置为无穷大。
matlab最短路径实验报告

matlab最短路径实验报告一、实验目的本实验的目的是通过使用Matlab软件来实现最短路径算法,掌握最短路径算法的基本思路和实现方法,加深对图论知识的理解和应用能力。
二、实验原理最短路径算法是图论中一个重要的问题,它是指在一个加权有向图或无向图中从一个顶点到另一个顶点之间经过的边权值之和最小的路径。
常见的最短路径算法有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
本次实验采用Dijkstra算法来求解最短路径。
Dijkstra算法是一种贪心算法,它通过维护一个集合S来不断扩展已知最短路径集合S中所有节点到未知节点v之间的距离,并选取其中距离最小的节点u加入S中,直到所有节点都被加入S为止。
三、实验步骤1. 构建图首先需要构建一个加权有向图或无向图。
本次实验采用无向图,并使用邻接矩阵表示。
具体步骤如下:(1)定义节点数n和边数m;(2)定义邻接矩阵A(n*n),其中A(i,j)表示从i到j是否有边,如果有则为边的权值,如果没有则为无穷大。
2. 初始化(1)定义两个数组dist和visited,其中dist(i)表示从起点到节点i 的最短距离,visited(i)表示节点i是否已经加入集合S中;(2)将起点加入集合S中,并将visited数组对应位置设为1;(3)初始化dist数组,将所有非起点节点的距离设为无穷大。
3. 迭代更新(1)遍历集合S中所有节点u的邻居节点v,如果v未被加入集合S 中,则更新dist(v)的值。
具体而言,如果dist(u)+A(u,v)<dist(v),则更新dist(v)=dist(u)+A(u,v);(2)在所有未加入集合S中的节点中选取距离最小的节点u,并将其加入集合S中。
4. 输出结果输出起点到各个终点的最短路径长度和路径。
四、实验结果与分析本次实验构建了一个无向图,并使用Dijkstra算法求解了最短路径。
具体实现过程如下:1. 构建图构建了一个6个节点、8条边的无向图,邻接矩阵如下:0 6 4 Inf Inf Inf6 0 1 5 Inf Inf4 1 0 Inf Inf InfInf5InfInf0 Inf 1InfInfInf Inf0 2InfInfInf 1 2 0其中,Inf表示两个节点之间没有边。
matlab最短路径案例

matlab最短路径案例在实际生活和工作中,我们经常会遇到需要找到最短路径的问题,例如在物流配送中,我们需要计算货物从出发地到目的地的最短路线,以提高效率和节约成本。
在这种情况下,MATLAB是一种非常有效的工具,可以帮助我们快速计算出最短路径。
最短路径问题是计算图中两个节点之间最短路径的问题。
在MATLAB中,我们可以使用Graph和Dijkstra算法来实现最短路径的计算。
首先,我们需要构建一个图,用来表示节点和边。
在MATLAB中,我们可以使用Graph对象来表示图,并且可以使用addnode和addedge函数来添加节点和边。
G = graph();G = addnode(G, 5); % 添加5个节点G = addedge(G, 1, 2, 10); % 添加边,每条边都有一个权重G = addedge(G, 1, 3, 15);G = addedge(G, 2, 3, 8);G = addedge(G, 2, 4, 2);G = addedge(G, 3, 4, 6);G = addedge(G, 4, 5, 12);上面的代码创建了一个图,其中包含5个节点和6条边。
每条边都有一个权重,代表两个节点之间的距离。
接下来,我们可以使用dijkstra函数来计算最短路径。
这个函数需要指定图、起始节点和目标节点。
[start_node, end_node, shortest_dist] = shortestpath(G, 1, 5);上面的代码计算了图G中从节点1到节点5的最短路径,并且返回了起始节点、终止节点和最短路径的长度。
最后,我们可以使用plot函数将最短路径可视化。
plot(G, 'EdgeLabel', G.Edges.Weight) % 可视化图highlight(G, shortest_path, 'EdgeColor', 'r') % 高亮显示最短路径通过以上步骤,我们可以使用MATLAB计算并可视化最短路径。
MATLAB解决最短路径问题代码

默认是Dijkstra 算法是有权的, 我想如果把权都赋1的话, 就相当于没权的了参数是带权的稀疏矩阵及结点看看这两个例子(一个有向一个无向), 或许你能找到你想知道的% Create a directed graph with 6 nodes and 11 edgesW = [.41 .99 .51 .32 .15 .45 .38 .32 .36 .29 .21]; %这是权DG = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],W) %有权的有向图h = view(biograph(DG,[],'ShowWeights','on')) %画图, 这个好玩% Find shortest path from 1 to 6[dist,path,pred] = graphshortestpath(DG,1,6) %找顶点1到6的最短路径% Mark the nodes and edges of the shortest pathset(h.Nodes(path),'Color',[1 0.4 0.4]) %上色edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));set(edges,'LineColor',[1 0 0]) %上色set(edges,'LineWidth',1.5) %上色下面是无向图的例子% % Solving the previous problem for an undirected graph% UG = tril(DG + DG')% h = view(biograph(UG,[],'ShowArrows','off','ShowWeights','on')) % % Find the shortest path between node 1 and 6% [dist,path,pred] = graphshortestpath(UG,1,6,'directed',false)% % Mark the nodes and edges of the shortest path% set(h.Nodes(path),'Color',[1 0.4 0.4])% fowEdges = getedgesbynodeid(h,get(h.Nodes(path),'ID'));% revEdges = getedgesbynodeid(h,get(h.Nodes(fliplr(path)),'ID')); % edges = [fowEdges;revEdges];% set(edges,'LineColor',[1 0 0])% set(edges,'LineWidth',1.5)clc;close all; clear;load data;% global quyu;quyu = [2,3];%一片区域z_jl = lxjl(jdxx,lxxh);%计算路线的距离z = qyxz(jdxx,quyu,z_jl);% 根据节点信息,从z中将y区域的节点和路线选出所有点的信息hzlx(z);%绘制Z的图像[qypt, nqypt] = ptxzm(xjpt,quyu);changdu = length(bhxz(jdxx,1:6));%选出x中y区的标号,只是分区域,求长度并绘制它tt = z(:,[1,2,end])';k = min(min(tt(1:2,:)));%求两次最小值t = tt(1:2,:) ;xsjz = sparse(t(2,:),t(1,:),tt(3,:),changdu,changdu);%产生稀疏矩阵[dist, path, pred] = zdljxz(xsjz, qypt, k );%三个原包矩阵通过zdljxz计算得到最短路径hold onfor j = 1:nqyptcolors = rand(1,3);%产生随机数并用颜色标记hzptxc(path{j},jdxx,colors)endhold offaxis equal%把坐标轴单位设为相等zjd = jdfgd( path, quyu);function z = lxjl(x, y)%计算路线的距离[m n] = size(y);for i = 1:myy(i,1:2) = x(y(i,1),2:3);yy(i,3:4) = x(y(i,2),2:3);endz = sqrt((yy(:,3) - yy(:,1)).^2 + (yy(:,2) - yy(:,4)).^2);y = sort(y');y = y';z = [y yy z];z = sortrows(z);function [z lz] = ptxz(xjpt,y)pt = xjpt(:,2);wei = ismember(xjpt(:,1),y);z = pt(wei);lz = length(z);unction hzptxc(path,jdxx,colors)n = length(path);% hold onfor i = 1:nhzptjd(jdxx, path{i},colors)end% hold offunction hzptjd(jdxx,x,colors)% m = length(x);% x = x';hold onplot(jdxx(x,2),jdxx(x,3),'o','LineStyle' ,'-' ,...'Color',colors,'MarkerEdgeColor',colors)plot(jdxx(x(1),2),jdxx(x(1),3),'*','MarkerFaceColor',colors)hold offfunction hzlx(x)%绘制x的图像[m n] = size(x);hold onfor i = 1:mplot([x(i,3) x(i,5)],[x(i,4) x(i,6)],'k:')endhold offfunction z = bhxz(x,y)%选出x中y区的标号,只是分区域xzq = x(:,4);xzr = ismember(xzq,y);z = x(xzr,:);z = z(:,1);。
利用Matlab编程计算最短路径及中位点选址

139§19. 利用Matlab 编程计算最短路径及中位点选址1、最短路问题两个指定顶点之间的最短路径。
例如,给出了一个连接若干个城镇的铁路网络,在这个网络的两个指定城镇间,找一条最短铁路线。
以各城镇为图G 的顶点,两城镇间的直通铁路为图G 相应两顶点间的边,得图G 。
对G 的每一边e ,赋以一个实数)(e w —直通铁路的长度,称为e 的权,得到赋权图G 。
G 的子图的权是指子图的各边的权和。
问题就是求赋权图G 中指定的两个顶点00,v u 间的具最小权的轨。
这条轨叫做00,v u 间的最短路,它的权叫做00,v u 间的距离,亦记作),(00v u d 。
求最短路已有成熟的算法:迪克斯特拉(Dijkstra )算法,其基本思想是按距0u 从近到远为顺序,依次求得0u 到G 的各顶点的最短路和距离,直至0v (或直至G 的所有顶点),算法结束。
为避免重复并保留每一步的计算信息,采用了标号算法。
下面是该算法。
(i) 令0)(0=u l ,对0u v ≠,令∞=)(v l ,}{00u S =,0=i 。
(ii) 对每个i S v ∈(i i S V S \=),用)}()(),({min uv w u l v l iS u +∈代替)(v l 。
计算)}({min v l iS v ∈,把达到这个最小值的一个顶点记为1+i u ,令140}{11++=i i i u S S 。
(iii). 若1||-=V i ,停止;若1||-<V i ,用1+i 代替i ,转(ii)。
算法结束时,从0u 到各顶点v 的距离由v 的最后一次的标号)(v l 给出。
在v 进入i S 之前的标号)(v l 叫T 标号,v 进入i S 时的标号)(v l 叫P 标号。
算法就是不断修改各项点的T 标号,直至获得P 标号。
若在算法运行过程中,将每一顶点获得P 标号所由来的边在图上标明,则算法结束时,0u 至各项点的最短路也在图上标示出来了。
最短路径问题matlab求解详尽版

最短路径问题m a t l a b求解详尽版Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】MATLAB 求最短路径利用graphshortestpath 可以求最短路径,具体用法参考MATLAB帮助Examples:S=[1 1 2 2 3 3 4 4 4 4 5 6 6 7 8]; %起始节点向量E=[2 3 5 4 4 6 5 7 8 6 7 8 9 9 9]; %终止节点向量W=[1 2 12 6 3 4 4 15 7 2 7 7 15 3 10]; %边权值向量,有向图,G(9,9)=0; 9个节点G=sparse(S,E,W); %关联矩阵的稀疏矩阵表示G(9,9)=0;P=biograph(G,[],'ShowWeights','on');%建立有向图对象PH=view(P);%显示各个路径权值[Dist,Path]=graphshortestpath(G,1,9,'Method','Dijkstra') %求节点1到节点9的最短路径set(Path),'Color',[1 ]);%以下三条语句用红色修饰最短路径edges=getedgesbynodeid(H,get(Path),'ID'));set(edges,'LineColor',[1 0 0]);set(edges,'LineWidth',;%以下是运行结果,节点1到节点9的最短路径为19Dist =19Path =1 3 4 5 7 9利用graphallshortestpaths可以求出所有最短路径Dists=graphallshortestpaths(G) %求所有最短路径Dists =0 1 2 5 9 6 16 12 19Inf 0 Inf 6 10 8 17 13 20Inf Inf 0 3 7 4 14 10 17Inf Inf Inf 0 4 2 11 7 14Inf Inf Inf Inf 0 Inf 7 Inf 10Inf Inf Inf Inf Inf 0 Inf 7 15Inf Inf Inf Inf Inf Inf 0 Inf 3Inf Inf Inf Inf Inf Inf Inf 0 10Inf Inf Inf Inf Inf Inf Inf Inf 0。
matlab 单源最短路径

matlab 单源最短路径Matlab单源最短路径算法是计算机科学中非常重要的算法之一,该算法可以解决许多实际问题。
本文将针对Matlab单源最短路径,进行详细介绍。
1.问题的定义:对于一个带权无向图,如何从其中的某一节点出发,找到到其他节点的最短路径?2.算法思想:Dijkstra算法是解决单源最短路径问题的一个经典算法。
该算法基于贪心思想,每次选择当前距离源点最近的一个没有确定最短路径的点作为下一步的目标,并依据这个点来更新其余点到源点的距离。
3.算法流程(1)初始化:将源点标记为已确定最短路径,将源点到其余点的距离赋值给初始路径。
(2)迭代:对于未确定最短路径的点,选择距离源点最近的点标记为已确定最短路径,更新其余点到源点的距离。
(3)结束条件:当所有节点都被标记为最短路径或者无法到达时,算法结束。
4.算法实现:以一个典型的图作为例子,展示Dijkstra算法在Matlab中的实现过程。
由于在Matlab中没有提供图数据结构,我们需要手动定义节点和边的信息。
这里我们采用数组来存储节点和边的信息,如下:G = sparse([1 1 1 2 2 3 3 4],... %边所连接的节点[2 3 4 3 4 4 5 5],...[2 1 5 3 2 3 1 3],... %边的权值5,5); %定义图的大小此时,G表示一个含有5个节点和8条边的无向图,权值保存在3行中。
接下来,定义源点、初始路径、标记点位,并进行循环计算。
在每一次循环中,找到当前未标记节点中距离源点最短的节点,将其标记,更新其余节点到源点的距离,并赋值到路径变量中。
5.算法应用:Matlab的单源最短路径算法可应用于很多实际问题中。
除了传统的路由算法,也可应用于社交网络中的用户推荐、电子商务中的商品推荐等多个领域。
综上所述,Matlab单源最短路径算法是计算机科学中非常重要的算法之一,具有广泛的应用场景。
如果读者想要深入学习该算法,可以通过Matlab提供的简单实例进行探索。
matlab最短路径问题标号法

一、介绍MATLAB是一种非常流行的数学建模和仿真软件,被广泛应用于工程、科学和金融领域。
在MATLAB中,最短路径问题是一个常见的优化问题,通常会涉及到图论、线性代数和优化算法等知识。
在解决最短路径问题时,我们常常需要使用标号法来求解,本文将对MATLAB中最短路径问题的标号法进行介绍。
二、什么是最短路径问题最短路径问题是指在一个加权有向图或无向图中寻找两个顶点之间的最短路径。
在实际应用中,最短路径问题通常涉及到网络规划、路线规划、物流配送等方面。
我们需要求解城市之间的最短路径来设计公交线路,或者求解货物在仓库之间的最短路径来优化物流方案。
三、最短路径问题的标号法在MATLAB中,我们可以使用标号法(Label Correcting Algorithm)来求解最短路径问题。
标号法是一种基于节点标号的启发式算法,它通过不断更新节点的标号信息来逐步搜索最短路径。
下面是标号法的基本思路:1. 初始化:我们需要对图中的节点进行初始化,设置起点的标号为0,其他节点的标号为无穷大。
2. 标号更新:我们开始不断更新节点的标号。
对于每个节点,我们计算通过它能够到达的节点的距离,并将这些距离与当前节点的标号进行比较。
如果通过当前节点到达某个邻居节点的路径距离更短,则更新该邻居节点的标号为当前节点的标号加上当前节点到邻居节点的距离。
3. 节点选择:在标号更新的过程中,我们需要选择一个未加入最短路径的节点,并将其标记为已加入最短路径。
这个过程通常会涉及到优先级队列等数据结构的使用,以便快速找到最短路径的下一个节点。
4. 终止条件:当所有节点都已加入最短路径,或者找到目标节点时,算法终止,最短路径即为标号信息所指示的路径。
四、MATLAB实现最短路径问题的标号法在MATLAB中,我们可以利用图论工具箱和优化工具箱来实现最短路径问题的标号法。
下面是一个简单的MATLAB示例:```matlab创建图N = 5; 节点数E = [1, 2; 1, 3; 2, 3; 2, 4; 3, 4; 3, 5; 4, 5]; 边集L = [1, 2, 3, 4, 5]; 标号W = [1, 2, 3, 4, 5, 6, 7]; 权重G = digraph(E(:, 1), E(:, 2), W);最短路径求解[s, t] = deal(1, N); 起点和终点[P, D] = graphshortestpath(G, s, t, 'Method', 'positive');```在这个例子中,我们首先创建了一个有向图G,并指定了节点数N、边集E、节点标号L和边权重W。
蚁群算法最短路径通用Matlab程序(附图)

if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);%用细胞结构存储每一代的每一只蚂蚁的爬行路线PL=zeros(K,M);%用矩阵存储每一代的每一只蚂蚁的爬行路线长度%% -----------启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁-------------------- for k=1:Kdisp(k);for m=1:M%% 第一步:状态初始化W=S;%当前节点初始化为起始点Path=S;%爬行路线初始化PLkm=0;%爬行路线长度初始化TABUkm=ones(1,N);%禁忌表初始化TABUkm(S)=0;%已经在初始点了,因此要排除DD=D;%邻接矩阵初始化%% 第二步:下一步可以前往的节点DW=DD(W,:);DW1=find(DWfor j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数%% 觅食停止条件:蚂蚁未遇到食物或者陷入死胡同while W~=E&&Len_LJD>=1%% 第三步:转轮赌法选择下一步怎么走PP=zeros(1,Len_LJD);for i=1:Len_LJDPP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);endPP=PP/(sum(PP));%建立概率分布Pcum=cumsum(PP);Select=find(Pcum>=rand);%% 第四步:状态更新和记录Path=[Path,to_visit];%路径增加PLkm=PLkm+DD(W,to_visit);%路径长度增加W=to_visit;%蚂蚁移到下一个节点for kk=1:Nif TABUkm(kk)==0DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;%已访问过的节点从禁忌表中删除for j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数end%% 第五步:记下每一代每一只蚂蚁的觅食路线和路线长度ROUTES{k,m}=Path;if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endend%% 第六步:更新信息素Delta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m) ROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分end%% ---------------------------绘图-------------------------------- plotif=1;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLKPLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)');xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendhold onROUT=ROUTES{K,M};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=1;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));将上述算法应用于机器人路径规划,优化效果如下图所示。
matlab dijkstra算法求解最短路径例题

matlab dijkstra算法求解最短路径例题Dijkstra算法是一种用于在带有非负权值的图中找到单源最短路径的算法。
以下是一个用MATLAB实现Dijkstra算法求解最短路径的简单例子:function [shortestDistances, predecessors] = dijkstra(graph, startNode)% 输入参数:% - graph: 表示图的邻接矩阵,graph(i, j) 表示节点i 到节点 j 的权值,如果没有直接连接则为 inf。
% - startNode: 起始节点的索引。
numNodes = size(graph, 1);% 初始化距离数组,表示从起始节点到每个节点的最短距离 shortestDistances = inf(1, numNodes);shortestDistances(startNode) = 0;% 初始化前驱节点数组predecessors = zeros(1, numNodes);% 未访问的节点集合unvisitedNodes = 1:numNodes;while ~isempty(unvisitedNodes)% 选择当前最短距离的节点[~, currentNodeIndex] = min(shortestDistances(unvisitedNodes));currentNode = unvisitedNodes(currentNodeIndex);% 从未访问节点集合中移除当前节点unvisitedNodes(currentNodeIndex) = [];% 更新与当前节点相邻节点的距离for neighbor = unvisitedNodesif graph(currentNode, neighbor) + shortestDistances(currentNode) < shortestDistances(neighbor) shortestDistances(neighbor) = graph(currentNode, neighbor) + shortestDistances(currentNode);predecessors(neighbor) = currentNode;endendendend现在,让我们使用一个简单的例子来测试这个算法:% 创建一个邻接矩阵表示图graph = [0, 2, 0, 4, 0;2, 0, 3, 7, 0;0, 3, 0, 1, 0;4, 7, 1, 0, 5;0, 0, 0, 5, 0];startNode = 1; % 起始节点% 调用Dijkstra算法[shortestDistances, predecessors] = dijkstra(graph, startNode);% 显示结果disp('最短距离:');disp(shortestDistances);disp('前驱节点:');disp(predecessors);这个例子中,graph 表示一个带有权值的图的邻接矩阵,startNode 是起始节点的索引。
matlab两点间最短路径

matlab两点间最短路径Matlab是一款基于高级编程语言的软件,适用于科学计算、数据分析和可视化等多个领域。
在Matlab中,求两点间最短路径可以使用多种算法实现,例如Dijkstra算法和Floyd算法等。
下面,我们针对最常见的Dijkstra算法进行介绍。
Dijkstra算法是一种基于贪心思想的单源最短路径算法,其具体步骤如下:1. 初始化:将起点到所有节点的距离都设为无穷大,将起点到自身的距离设为0。
2. 选择起点:从起点开始,首先将起点标记为“已访问”。
3. 更新距离:遍历起点可以到达的所有节点,计算起点到这些节点的距离,并更新距离数组。
如果通过起点到当前节点的距离比之前的更短,就更新距离数组。
4. 标记节点:从未标记为“已访问”的节点中,选择距离起点最近的节点,并将其标记为“已访问”。
5. 重复以上步骤:重复以上步骤,直到所有节点都被标记为“已访问”,或者到达目标节点为止。
6. 回溯路径:最后,根据更新的距离数组和前驱节点数组,可以回溯出起点到目标点的最短路径。
在Matlab中,可以使用以下代码实现Dijkstra算法:```matlabfunction [dist,prev] = dijkstra(adj,start)n = size(adj,1);dist = inf(1,n);prev = zeros(1,n);visited = zeros(1,n);dist(start) = 0;for i=1:n[mindist,index] = min(dist);if (mindist == inf)break;endvisited(index) = 1;for j=1:nif (visited(j) == 0 && adj(index,j) ~= inf)newdist = mindist + adj(index,j);if (newdist < dist(j))dist(j) = newdist;prev(j) = index;endendendendend```其中,adj为节点之间的邻接矩阵,start为起点位置,dist为从起点到各点的最短距离数组,prev为各点的前驱节点数组。
Dijkstra算法,最短路径路由算法matlab代码

Dijkstra算法,最短路径路由算法matlab代码Dijkstra算法是⼀种最短路径路由算法,⽤于计算⼀个节点到其他所有节点的最短路径。
主要特点是以起始点为中⼼向外层层扩展,直到扩展到终点为⽌。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率较低。
算法详细解释各⽹站都有,不太难。
下边是对下图从D开始到A节点寻找最短路径的matlab代码,个⼈原创。
%% Dijkstra算法%by Jubobolv369 at 2022/1/22clc;clear;close all;%% 初始化带权邻接矩阵,起点、终点等initRoute=[0 12 inf inf inf 16 14;12 0 10 inf inf 7 inf;inf 10 0 3 5 6 inf;inf inf 3 0 4 inf inf;inf inf 5 4 0 2 8;16 7 6 inf 2 0 9;14 inf inf inf 8 9 0;];[row,column]=size(initRoute);start_node=4;end_node=1;close_list=[];open_list=[];%closelist中加⼊初始节点close_list=[start_node,start_node,0];%% 如果closelist中没有终点,则遍历节点,通过⽐较逐渐加⼊节点到closelist。
while isempty(find(close_list(:,1) == end_node))[last1,~]=size(close_list);%获取closelist的最后⼀⾏的索引now_node=close_list(last1,1);%当前节点编号now_length=close_list(last1,3);%当前最优长度[last2,~]=size(open_list); %%获取openlist的最后⼀⾏的索引now_list=initRoute(now_node,:); %从原始矩阵中取初当前节点的边权值i=1;%% 更新openlistfor j=1:column%如果第j个节点可达、不是⾃⾝且不在close_list中,该点可能需要改动或添加到openlist中if now_list(j)~=inf && now_list(j)~=0 && isempty(find(close_list(:,1) == j))if last1==1open_list(i,1)=j;open_list(i,2)=now_node;open_list(i,3)=now_list(j);i=i+1;%如果不在openlist中,就将其添加到其中,否则将通过当前⽗节点到此节点的权值与之前的作⽐较elsek=find(open_list(:,1) == j);if isempty(k)open_list(last2+i,1)=j;open_list(last2+i,2)=now_node;open_list(last2+i,3)=now_list(j)+now_length;i=i+1;elseif open_list(k,3)>(now_list(j)+now_length) %若現在的路徑⾧度⼩,則更新路徑open_list(k,1)=j;open_list(k,1)=j;open_list(k,2)=now_node;open_list(k,3)=now_list(j)+now_length;endendendend%% 更新closelist和openlist。
最短路径的Floyd算法的Matlab程序

每对顶点之间的最短路径计算赋权图中各对顶点之间最短路径,显然可以调用Dijkstra 算法。
具体方法是:每次以不同的顶点作为起点,用Dijkstra 算法求出从该起点到其余顶点的最短路径,反复执行n 次这样的操作,就可得到从每一个顶点到其它顶点的最短路径。
这种算法的时间复杂度为)(3n O 。
第二种解决这一问题的方法是由Floyd R W 提出的算法,称之为Floyd 算法。
假设图G 权的邻接矩阵为0A ,1112121222012n n n n nn a a a a a a A a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 来存放各边长度,其中: 0=ii a 1,2,,i n =; ∞=ij a j i ,之间没有边,在程序中以各边都不可能达到的充分大的数代替; ij ij w a = ij w 是j i ,之间边的长度,,1,2,,i j n =。
对于无向图,0A 是对称矩阵,ji ij a a =。
Floyd 算法的基本思想是:递推产生一个矩阵序列01,,,,,k n A A A A ,其中),(j i A k 表示从顶点i v 到顶点j v 的路径上所经过的顶点序号不大于k 的最短路径长度。
计算时用迭代公式:)),(),(),,(m in(),(111j k A k i A j i A j i A k k k k ---+=k 是迭代次数,,,1,2,,i j k n =。
最后,当n k =时,n A 即是各顶点之间的最短通路值。
例 某公司在六个城市126,,,c c c 中有分公司,从i c 到j c 的直接航程票价记在下述矩阵的),(j i 位置上。
(∞表示无直接航路),请帮助该公司设计一张任意两个城市间的票价最便宜的路线图。
⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∞∞∞∞∞∞055252510550102025251001020402010015252015050102540500矩阵path 用来存放每对顶点之间最短路径上所经过的顶点的序号。
最短路径算法 matlab程序

算法描述:输入图G,源点v0,输出源点到各点的最短距离D中间变量v0保存当前已经处理到的顶点集合,v1保存剩余的集合1.初始化v1,D2.计算v0到v1各点的最短距离,保存到Dfor each i in v0;D(j)=min[D(j),G(v0(1),i)+G(i,j)] ,where j in v13.将D中最小的那一项加入到v0,并且从v1删除这一项。
4.转到2,直到v0包含所有顶点。
%dijsk最短路径算法clear,clcG=[inf inf 10 inf 30 100;inf inf 5 inf inf inf;inf 5 inf 50 inf inf;inf inf inf inf inf 10;inf inf inf 20 inf 60;inf inf inf inf inf inf;]; %邻接矩阵N=size(G,1); %顶点数v0=1; %源点v1=ones(1,N); %除去原点后的集合v1(v0)=0;%计算和源点最近的点D=G(v0,:);while 1D2=D;for i=1:Nif v1(i)==0D2(i)=inf;endendD2[Dmin id]=min(D2);if isinf(Dmin),error,endv0=[v0 id] %将最近的点加入v0集合,并从v1集合中删除v1(id)=0;if size(v0,2)==N,break;end%计算v0(1)到v1各点的最近距离fprintf('计算v0(1)到v1各点的最近距离\n');v0,v1id=0;for j=1:N %计算到j的最近距离if v1(j)for i=1:Nif ~v1(i) %i在vo中D(j)=min(D(j),D(i)+G(i,j));endD(j)=min(D(j),G(v0(1),i)+G(i,j));endendendfprintf('最近距离\n');Dif isinf(Dmin),error,endendv0%>> v0%v0 =% 1 3 5 4 6。
基于遗传算法的最短路径问题及其MATLAB实现(1)
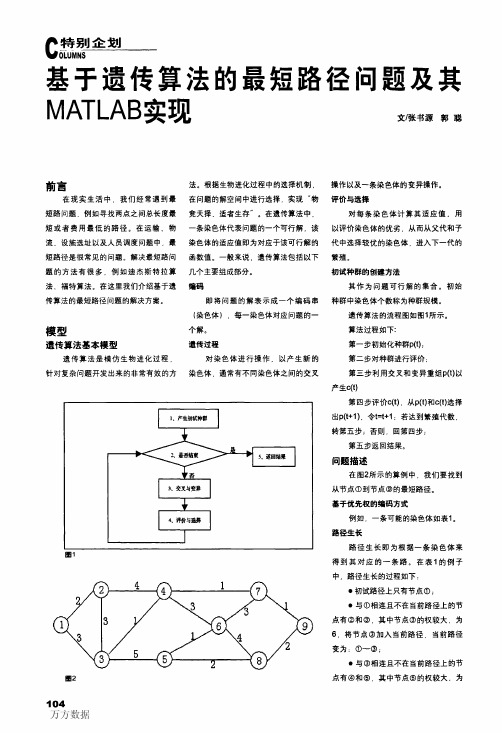
子代l 父代2
父代l
子代2 父代2
田3
父代
子代
圈4
结论
将以上算法用maUab实现(程序见 附录).我们找到对应于我们算例的最 短路为:①一③一④一⑦一⑨.路径总 长度为6。
此外.不难发现,使用遗传算法 来进行全局寻优.基本上不需要关于问 题本身的信息.这使得遗传算法的应用 可以扩展到模拟技术.非线性规划问题 等领域,具有广阔的前景。6
其作为问题可行解的集合。初始 种群中染色体个数称为种群规模。
遗传算法的流程图如图1所示。 算法过程如下: 第一步初始化种群p(t); 第二步对种群进行评价; 第三步利用交叉和变异重组p(t)以 产生c(t) 第四步评价c(t).从p(t)和c(t)选择 出p(t+1),令t=t+l:若达到繁殖代数, 转第五步;否则,回第四步: 第五步返回结果。 问题描述 在图2所示的算例中.我们要找到 从节点①到节点⑨的最短路径。 基于优先权的编码方式 例如.一条可能的染色体如表1。 路径生长 路径生长即为根据一条染色体来 得到其对应的一条路。在表1的例子 中,路径生长的过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③,其中节点③的权较大.为 6.将节点③加入当前路径,当前路径 变为:①~③; ·与③相连且不在当前路径上的节 点有④和⑤.其中节点⑤的权较大.为
路径生长过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③.其中节点②的权较大,为 6,将节点②加入当前路径.当前路径 变为:①一②; 重复此过程.我们会找到路径 ①一②一④一@一⑤一③.已经没有与 ③相连且不在当前路径的节点,从而找 不到从①到⑨的一条路。当出现这种情 况时.我们抛弃这条染色体.用一条合 法染色体去取代它。 染色体的适应值 染色体的适应值是我们选择较优 染色体的依据。这里染色体的适应值即 为我们得到的路径长度。由于我们得到 的路径为①一③一⑤一⑨一⑨,因此该 染色体的适应值即为此路径的长度:
matlab两点间最短路径

matlab两点间最短路径两点间最短路径是指在一个图中,找出连接两个给定节点的最短路径,即路径上的边权重之和最小。
在Matlab中,我们可以使用图论算法来解决这个问题。
本文将介绍如何使用Matlab来计算两点间的最短路径,以及一些应用场景和实例。
我们需要创建一个图对象,并定义节点和边的信息。
在Matlab中,可以使用graph函数来创建一个图对象。
假设我们有一个包含n个节点的图,节点之间的连接关系可以用一个邻接矩阵来表示。
邻接矩阵A的第i行第j列的元素表示节点i和节点j之间的边权重。
如果节点i和节点j之间没有边,则对应的元素为0。
接下来,我们可以使用图对象的shortestpath函数来计算两点间的最短路径。
该函数的输入参数包括图对象、起始节点和目标节点。
函数将返回一个包含最短路径节点索引的数组。
如果不存在连接起始节点和目标节点的路径,则返回空数组。
下面是一个简单的示例,演示如何使用Matlab计算两点间的最短路径:```% 创建一个包含5个节点的图对象G = graph([1 1 2 2 3 4 4 5], [2 3 3 4 5 1 5 3]);% 计算节点1到节点5的最短路径path = shortestpath(G, 1, 5);% 打印最短路径节点索引disp(path);```上述示例中,我们创建了一个包含5个节点的图对象G。
然后,我们使用shortestpath函数计算节点1到节点5的最短路径。
最后,我们将结果打印出来。
除了计算两点间的最短路径,Matlab还提供了其他一些与图相关的函数和工具。
例如,我们可以使用graphallshortestpaths函数来计算图中所有节点对之间的最短路径。
我们还可以使用plot函数将图对象可视化,以便更直观地理解图的结构和节点之间的连接关系。
两点间最短路径在实际应用中有很多用途。
例如,在交通网络中,我们可以使用最短路径算法来计算从一个地点到另一个地点的最短驾驶路径。
遗产算法最短路径问题matlab

遗产算法最短路径问题matlab 下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!遗传算法在最短路径问题中的应用引言遗传算法是一种模拟自然界生物进化过程的优化算法,近年来在解决各种优化问题中展现出了强大的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机仿真期末作业
姓名:吴隐奎 班级:04601 学号:041751 日期:2007-6-15
题目:Floyd 算法实现和分析
内容:用MATLAB 仿真工具实现Floyd 算法,求任意两端间的最短路径。
要求:尽可能用M 函数分别实现算法的关键部分,用M 脚本来进行算法结果验证;分别用以下两个图(用初始距离矩阵表示)进行算法验证:
图一:(0)0 100 100 1.2 9.2 100 0.5100 0 100 5 100 3.1 2100 100 0 100 100 4 1.51.2 5 100 0 6.7 100 1009.2 100 100 6.7 0 15.6 100100 3.1 4 100 15.6 0 1000.5 2 1.5 100 100 100 0]W ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
图二:(0)
0 0.5 2 1.5 100 100 1000.5 0 100 100 1.2 9.2 1002 100 0 100 5 100 3.11.5 100 100 0 100 100 4100 1.2 5 100 0 6.7 100100 9.2 100 100 6.7 0 15.6100 100 3.1 4 100 15.6 0W ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
算法:给定图G 及其边(,)i j 的权,(1,1)i j w i n j n ≤≤≤
≤ F0:初始化距离矩阵(0)W
和路由矩阵(0)R 。
其中: (0)0ij ij ij ij w e E w e E i j ∈⎧⎪=∞∉⎨⎪=⎩ 若(有边) 若(无边)
若(对角线元素)
(0)(0)w 0,ij ij
j r ⎧≠∞=⎨⎩ 若 其它 F1:已求得(-1)k W 和(-1)k R ,依据下面的迭代求()k W 和()k R
()(1)(1)(-1),,,,min(,)k k k k i j i j i k k j w w w w --=+
(1)()(1),,,(),(1)()(1),,,k k k i k i j i j k i j k k k i j i j i j
r w w r r w w ----⎧<⎪=⎨=⎪⎩ 若 若 F2:若k<n ,重复F1;若k=n ,终止。
仿真:
用四个m 文件来实现仿真,其中main 为主函数,首先测试出矩阵的长度,然后赋给n ,作为循环的次数;然后调用func1实现路由矩阵的初始化,把第k-1次的值付给a 后,调用func2函数来迭代求出k 次的w 值,调用func3函数,根据a (实际上为k-1次w 值)值和k 次w 值来求出k 次r 值。
迭代循环n 次。
主要程序:
n=length(w);
r=func1(w,n);
for k=1:n
a=w;
w=func2(w,n,k);
r=func3(a,w,r,n,k);
end;
Func1实现路由矩阵的初始化
主要程序
for i=1:1:n
for j=1:1:n
if x(i,j)==100
r0(i,j)=0;
else
r0(i,j)=j;
end,
end;
end;
Fuuc2该函数实现的功能是根据k-1次w 的值迭代求k 次w 的值
主要程序
for i=1:n
for j=1:n
w(i,j)=min(s(i,j),s(i,k)+s(k,j));
end
end
Func3来根据k-1次w 值和k 次w 值的大小求k 次R 的值
主要程序:
for i=1:n
for j=1:n
if i==j
r(i,j)=0;
elseif w(i,j)<a(i,j)
r(i,j)=r(i,k);
else
r(i,j)=r(i,j);
end
end
end
结果:
图一的结果:
w=
0 2.5000 2.0000 1.2000 7.9000 5.6000 0.5000
2.5000 0
3.5000 3.7000 10.4000 3.1000 2.0000
2.0000
3.5000 0 3.2000 9.9000
4.0000 1.5000
1.2000 3.7000 3.2000 0 6.7000 6.8000 1.7000
7.9000 10.4000 9.9000 6.7000 0 13.5000 8.4000
5.6000 3.1000 4.0000
6.8000 13.5000 0 5.1000
0.5000 2.0000 1.5000 1.7000 8.4000 5.1000 0
r=
0 7 7 4 4 7 7
7 0 7 7 7 6 7
7 7 0 7 7 6 7
1 1 1 0 5 1 1
4 4 4 4 0 4 4
2 2
3 2 2 0 2
1 2 3 1 1 2 0
可以看出:V4和V6之间最短距离是6.8,最短路由是V4—>V1—>V7—>V2—>V6 V3和V4之间最短距离是3.2,最短路由是V3—>V7—>V1—>V4
图二的结果:
w =
0 0.5000 2.0000 1.5000 1.7000 8.4000 5.1000
0.5000 0 2.5000 2.0000 1.2000 7.9000 5.6000
2.0000 2.5000 0
3.5000 3.7000 10.4000 3.1000
1.5000
2.0000
3.5000 0 3.2000 9.9000
4.0000
1.7000 1.2000 3.7000 3.2000 0 6.7000 6.8000
8.4000 7.9000 10.4000 9.9000 6.7000 0 13.5000
5.1000 5.6000 3.1000 4.0000
6.8000 13.5000 0
r =
0 2 3 4 2 2 3
1 0 1 1 5 5 1
1 1 0 1 1 1 7
1 1 1 0 1 1 7
2 2 2 2 0 6 2
5 5 5 5 5 0 5
3 3 3
4 3 3 0
端点对V1和V7之间最短距离是5.1,最短路由是V1—>V3—>V7
端点对V3和V5之间最短距离是3.7,最短路由是V3—>V1—>V2—>V5
端点对V1和V6之间最短距离是8.4,最短路由是V1—>V2—>V5—>V6
总结:通过一个学期计算机仿真课的学习,我现在已经能很熟练的使用的仿真工具matlab来进行一些简单的系统仿真,系统的仿真,能很好的帮助我们去理解各种模型,验证书本上的理论知识,而且仿真在系统设计中也有很重要的应用,通过仿真,可以节约成本和时间。
所以这门课的学习,对我以后的学习和工作有很大的帮助。
