数字电路 加法器共29页
第8讲 数电 中规模 加法器..
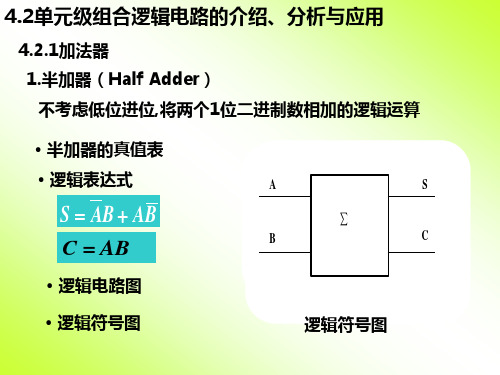
真值表 A
0 0 0 0 1 1 1 1
B
0 0 1 1 0 0 1 1
CI
0 1 0 1 0 1 0 1
CO F 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1
分析: (3)分析逻辑功能 :
A B
0
=1 =1
0
& &
0
0 0
& =1
0
F
0
0
0
CI
0
输入有奇数个1时,F=1;
0
CO F 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1
1位全加器的逻辑符号
Bi C i-1
∑
CO
CI
F A B CI
CO ( A B) CI AB
用异或门构成全加器
CI =1 F A B
=1
&
>1 CO
&
F A B CI
CO ( A B) CI AB
4位全加器的逻辑符号为全加器实现的是二进制数的加法因此若某一逻辑函数的输出恰巧等于输入代码所表示的数加上另一常数或另一组输入代码时适合用全加器实现
4.2单元级组合逻辑电路的介绍、分析与应用
4.2.1加法器 1.半加器(Half Adder)
不考虑低位进位,将两个1位二进制数相加的逻辑运算 • 半加器的真值表
4位全加器的逻辑符号为
0
3
CO
}
0
}
}
0
P
Q
3
3
CI
全加器实现的是二进制数的加法,因此若某一逻辑函数 的输出恰巧等于输入代码所表示的数加上另一常数或另 一组输入代码时,适合用全加器实现。全加器一般可以 构成代码转换电路、加减运算电路等。
数字电路 全加器

目录摘要 (2)ABSTRACT (3)数字电路-全加器 (4)1 一位全加器的设计 (4)1.1一位全加器的原理 (4)1.2一位全加器的逻辑电路图 (4)1.3用S IMULINK创建全加器电路模块 (5)1.4一位全加器的子系统图 (5)2.四位全加器的设计 (6)2.1四位全加器电路图 (6)2.2仿真波形及与理论值的比较 (7)小结与体会 (10)参考文献 (11)摘要Simulink是从底层开发的一个完整的仿真环境和图形界面,它把MATLAB的许多功能都设计成一个个直观的功能模块,把需要的功能模块连接起来就可以实现所需要的仿真功能。
Simulink仿真应用于数字电路、数字信号处理、通信仿真、电力系统仿真、宇航仿真等领域。
由于数字系统中高低电平分别用0和1表示,因此数字电路问题往往可以转化为一个数字上的逻辑问题。
MATLAB提供了逻辑运算模块和各种触发器模块,可以方便的进行数字电路的设计和仿真。
借助于组合电路仿真常用模块Logic and Bit Operations子库中的Local Operator模块,将其拖到所建的untitled窗口中,然后鼠标左键双击该模块弹出的Block Parameters/Logical Operator对话框,按Operator栏后的黑三角来选择所需要的门电路标识符,如:AND、OR、NAND、NOR、XOR、NOT中的一个,并依次设置所需的输入、输出端子个数,之后按OK键确定。
利用这些基本门电路组成全加器逻辑电路。
关键词:MATLAB Simulink仿真全加器AbstractFrom the bottom of the development of Simulink a complete simulation environment and graphic interface, it put many of the functions are design MATLAB as an intuitive function module, the need to connect the function module can be achieved need simulation function. Simulink used in the digital circuit, digital signal processing, communication simulation, electric power system simulation, the space simulation, etc. As digital system in high and low level respectively with 0 and 1 said, so the digital circuit problems are often can be converted into a number of problems on logic. MATLAB provides logic operation module and various trigger module, easy to digital circuit design and simulation. Combined with the simulation module circuit commonly used Logic and Bit Operations son in the library Local Operator module, will drag the building untitled window, and then the mouse left click on the module of the pop-up Block Parameters/Logical Operator dialog box, press the black triangle Operator bar to select the desired a gate identifier, such as: and, OR, NAND, NOR, XOR, NOT of a, and were set to the desired input and output terminals number, then press OK sure. Using these basic of gate adder logic circuit.Keywords: MATLAB Simulink QuanJia device数字电路-全加器1 一位全加器的设计1.1 一位全加器的原理所谓全加器,就是带进位输入和进位输出的加法器。
数字逻辑 第三章 加法器.ppt

四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1.外部特性
图中,A4、A3、A2、A1 ------- 二进制被加数; B4、B3、 B2、B1 ------- 二进制加数; F4、 F3、 F2、 F1 ------相加产生的和数; C0 --------------------来自低位的进位输入; FC4 -------------------向高位的进位输出。
a3b1
+) 乘积 Z5 a3b2 Z4 a2b2 Z3
a2b1
a1b2 Z2
a1b1
Z1
因为: ☆1位二进制数乘法 法则和逻辑“与”运算法 则相同,“积”项aibj(i =1,2,3;j=1,2)可用 两输入与门实现。 ☆对部分积求和可用 并行加法器实现。 所以:该乘法运算电 路可由6个两输入与门和1 b2 个4位二进制并行加法器构 成。逻辑电路图如右图所 示。
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。 1) 输入端A4、A3、A2、 A1输入8421码;
2) 而从另一输入端B4、 B3、B2、B1输入二进 制数0011; 3) 进位输入端C0接上“0”;
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对
应的余3码。
四位二进制并行加法器
Z5 Z4 Z3 Z 2 Z1
F4 F3 F2 F 1 FC4 T 693 C0
0
A4 A3 A2 A1
B4 B 3 B2 B1
&
&
&
&
&
&
b1
a3
a2
a1 0 a 3
a2
a1
FA4
F3 C3
FA3
F2
加法器

八位二进制加法器摘要:加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
在不同的场合使用的加法器对其要求也不同,有的要求速度更快,有的要求面积更小。
常见的加法器有串行进位加法器、74LS283超前进位加法器等,因此可以通过选取合适的器件设计一个加法器。
本次设计主要是如何实现8位二进制数的相加,即两个000到255之间的数相加,由于在实际中输入的往往是三位十进制数,因此,被加数和加数是两个三位十进制数,范围在000到255之间.当输入十进制数的时候,8421BCD码编码器先开始工作,编码器先将十进制数转换成四位二进制数,输出的四位二进制数直接到达8421BCD码加法器的输入端,我们可以使用71LS185加法器构成的一位8421BCD码的加法器,8421BCD码是用4位二进制数表示1位十进制数,4位二进制数内部为二进制,8421BCD码之间是十进制,即逢十进一。
而四位二进制加法器是按四位二进制数进行运算,即逢十六进一。
二者进位关系不同。
当四位二进制数加法器74LS283完成这个加法运算时,要用两片74LS283。
第一片完成加法运算,第二片完成修正运算。
8421BCD码加法器工作时,8421BCD码的加法运算为十进制运算,而当和数大于9时,8421BCD码就产生进位,而此时十六进制则不一定产生进位,因此需要对二进制和数进行修正,即加上6(0110),让其产生一个进位。
当和数小于等于9时,则不需要修正或者说加上0。
因此我们可以通过三个8421BCD码加法器的相连组成一个三位串行进位并行加法器,这样通过低位向高位产生进位进行十进制的加法运算,最后通过连接数码管显示所得的结果。
当输入二进制数的时候,两个串接的74LS283四位加法器进行加法运算,产生的八位二进制数通过集成芯片转换成三位十进制数,最后通过数码管显示。
另外,本次设计不仅可以适用加数和被加数是000到255的数字,同时也适用于加数和被加数是000到999的任何一个数,这是本次设计的创新之处。
全加器逻辑电路图

全加器逻辑电路图全加器英语名称为full-adder,是用门电路实现两个二进制数相加并求出和的组合线路,称为一位全加器。
一位全加器可以处理低位进位,并输出本位加法进位。
多个一位全加器进行级联可以得到多位全加器。
常用二进制四位全加器74LS283。
一位全加器:全加器是能够计算低位进位的二进制加法电路一位全加器(FA)的逻辑表达式为:S=A⊕B⊕CinCo=AB+BCin+ACin其中A,B为要相加的数,Cin为进位输入;S为和,Co是进位输出;如果要实现多位加法可以进行级联,就是串起来使用;比如32位+32位,就需要32个全加器;这种级联就是串行结构速度慢,如果要并行快速相加可以用超前进位加法,超前进位加法前查阅相关资料;如果将全加器的输入置换成A和B的组合函数Xi和Y(S0…S3控制),然后再将X,Y和进位数通过全加器进行全加,就是ALU的逻辑结构结构。
即X=f(A,B)Y=f(A,B)不同的控制参数可以得到不同的组合函数,因而能够实现多种算术运算和逻辑运算。
半加器、全加器、数据选择器及数据分配器一、实验目的1.验证半加器、全加器、数据选择器、数据分配器的逻辑功能。
2.学习半加器、全加器、数据选择器的使用。
3.用与非门、非门设计半加器、全加器。
4.掌握数据选择器、数据分配器扩展方法。
二、实验原理1.半加器和全加器根据组合电路设计方法,列出半加器的真值表,见表7。
逻辑表达式为:S=AB+AB=A⊕BC=AB半加器的逻辑电路图如图17所示。
用两个半加器可组成全加器,原理图如图18所示。
在实验过程中,我们可以选异或门74LS86及与门74LS08来实现半加器的逻辑功能;也可用全与非门如74LS00、反相器74LS04组成半加器。
这里全加器不用门电路构成,而选用集成的双全加器74LS183。
其管脚排列和逻辑功能表分别见图19和表4.9所示(a)用异或门组成的半加器(b)用与非门组成的半加器图17半加器逻辑电路图图18由二个半加器组成的全加器图1974LS183双全加器管脚排列图2.数据选择器和数据分配器数据选择器又叫多路开关,其基本功能相当于单刀多位开关,其集成电路有“四选一”、“八选一”、“十六选一”等多种类型。
数字电路实验报告实验三加法器

实验三加法器一、实验目的1、掌握用SSI器件实现全加器的方法。
2、掌握用MSI组合逻辑器件实现全加器的方法。
3、掌握集成加法器的应用。
二、实验设备及器件1、数字逻辑电路实验板1块2、74HC(LS)00(四二输入与非门)1片3、74HC(LS)86(四二输入异或门)1片4、74HC(LS)153(双四选一数据选择器)1片5、74HC(LS)283(4位二进制全加器)1片6、万用表1块三、实验原理组合逻辑电路是数字电路中最常见的逻辑电路之一。
组合逻辑电路的特点,就是在任意时刻电路的输出仅取决于该时刻的输入信号,而与信号作用前电路所处的状态无关。
本实验是根据给定的逻辑功能,设计出实现这些功能的组合逻辑电路。
不考虑低位进位,只本位相加,称半加。
实现半加的电路,为半加器。
考虑低位进位的加法称为全加。
实现全加的电路,为全加器。
实现三个输入变量(一位二进制数)全加运算功能的电路称为1位全加器。
实现多位二进制数相加有串行多位加法和并行多位加法两种形式,其中比较简单的一种电路是采用多个1位全加器并行相加,逐位进位的方式。
实验用器件管脚介绍:1、74HC(LS)00(四二输入与非门)管脚如下图所示。
2、74HC(LS)86(四二输入异或门)管脚如下图所示。
3、74HC(LS)153(双四选一数据选择器)管脚如下图所示。
4、74HC(LS)283(4位二进制全加器)管脚如下图所示。
四、 实验内容与步骤1、用门电路实现全加器(基本命题)参照表达式i i i i C B A S ⊕⊕=,i i i i i i B A C B A C +⊕=+)(1,其中i S 为本位和,i C 为低位向本位的进位,1+i C 为本位向高位进位,设计用与非门74HC(LS)00及异或门74HC(LS)86实现1位全加器的实验电路图,搭接电路,用LED 显示其输出,并记录结果在下表中。
1.1电路图1.2实验结果(基本命题)2、用数选器实现全加器输出Sn参照和实验内容与步骤1完全相同的逻辑功能,设计用与非门74HC(LS)00和数选器74HC(LS)153实现1位全加器输出S n的实验电路图,搭接电路,用LED显示其输出,观察电路的逻辑功能是否与设计功能一致。
加法器电路

加法器电路概述:加法器电路是一种基本的数字电路,用于将两个二进制数相加。
它是数字计算机中常用的关键部件之一。
在本文中,我们将探讨加法器电路的原理、分类、设计和应用。
一、原理加法器电路的原理基于基本的二进制加法规则。
在二进制加法中,相加的两个数字(0或1)称为位,而进位(carry)表示相邻位之间的进位情况。
加法器电路的任务是将这两个输入位和进位位相加,并产生正确的输出位和输出进位。
加法器电路的实现有多种方法,包括半加器、全加器和并行加法器。
1. 半加器:半加器是最基本的加法器电路,用于实现单个位的相加。
它有两个输入,即要相加的两个位(A和B),以及一个进位输入(Carry In)。
半加器的输出包括两个部分:和(Sum)和进位(Carry)。
和位表示两个输入位相加的结果,进位位表示进位情况。
半加器电路可以用逻辑门实现,如异或门和与门。
2. 全加器:全加器扩展了半加器的功能,用于实现两个位和一个进位位的相加。
除了输入位(A和B)和进位输入(Carry In),全加器还有一个输出进位(Carry Out)。
当两个输入位和进位位相加时,全加器产生两个输出:和位(Sum)和进位位(Carry Out)。
全加器电路可以通过组合多个半加器电路来实现。
3. 并行加法器:并行加法器是多位加法器的一种形式,用于实现多位的二进制数相加。
它在每一位上使用全加器电路,并将进位位连接在各个全加器之间。
并行加法器通过同时处理多个位来实现快速的二进制加法,因此在计算机中得到广泛应用。
二、分类根据多位加法器的输入和输出方式,加法器电路可以分为串行加法器和并行加法器。
1. 串行加法器:串行加法器按位进行计算,即逐个位地相加和产生进位。
它的输入和输出仅在单个位上进行。
串行加法器的优点是简单且成本低廉,但它的运算速度较慢。
2. 并行加法器:并行加法器可以同时处理多个位的相加和进位。
它的输入和输出可以同时进行,并且每一位之间可以并行操作。
天津大学数字集成电路第十讲加法器

A0
&
B0
clk
!C0
G P !C4
G P
G P
G P
!C3
!C2
!C1
S3
S2
S1
S0
TJU. ASIC Center---Arnold Shi
曼彻斯特进位链的动态实现
3 Ci,4 P3 1 3 P2 2 3 P1 3 3 P0 4 3
clk
1
2
G3 2
3
G2 3
4
G1 4
5
G0 5
TJU. ASIC Center---Arnold Shi
CBEA-Compliant处理器
TJU. ASIC Center---Arnold Shi
Cell内部有一条 768bit位宽的“EIB单元互联总线 环(Element Interconnect BUS Ring,EIB Ring)”,它实际上是一个强大的内部总线控制 逻辑—Cell内所有的功能单元都通过EIB总线环连 接在一起,包括PPE、八个SPE、XDR内存控制 器以及外部总线接口,它们所采用的无一例外都 是全双工的128bit连接总线。若Cell工作在4GHz 频率上,Cell内部的各个功能单元便都拥有 4GHz×128bit/Hz×2(全双工)÷8Byte/bit= 128GBps带宽
asiccenterarnoldshi逐位行波进位与旁路进位carrybypass比较增加进位旁路一般使面积增加10至20进位旁路加法器的总进位传播时间仍与位数n成正比但比例系数较逐位进位加法较小时旁路的额外开销使采用旁路进位的收益不大一般n之间采用旁路进位
VLSI
数字电路第4章(5加法器)_2

2. 全加器
CI
01
11
10
输 入 A B CI 0 0 0 0 0 1
输 出 S CO 0 0 1 0
0 0 1 1 1 1
1 1 0 01 0 1 0 1
0 1 0 1 0 1
1 0 1 11 0 1 0 1
0 1 0 10 1 10 1
1
1
1
S (ABCI AB CI ABCI ABCI) CO (AB BCI ACI)
Σ
Σ
A0 B 0
A1
B1
C1 为A1 B0 + A0 B1的进位位。 C2 为A1 B1 + C1的进位位。
思考:为什么片1的Ci 、片2的B 要接地?
例2. 将BCD的8421码转换为余3码 解:其真值表如右表所示,则
Y3Y2Y1Y0 DCBA 0011
D
输
C 0 0 0 0 1 0 0 0 0 0
1、实现两个一位8421BCD加法电路 于9 时对结果加0110,小于等于 9 时加0000。 2、产生修正控制信号 F 3、完成加 6 修正 8421输入 四 位 全 加 器 加0修正 修正控 加6修正 制信号 结果错误 结果正确 四 位 全 加 器
8421输出
8421输入
十进制数 二进制数相加的“和数 ” 进位Co S3 S2 S1 S0
0
1
2 3 4 11 12 13
4 8
9 10 11 12
1
0 0
0 1
0 1
1 0
1 0
1 0
1 1
1 1
1 1
1 1
0 0
1 1
0 1
0 1
加法器(Adder) 数电课件

2. 分析
半加器有两个输入:加数 、被加数Ai ;两个输出:B和i 输出 、进位输出 。
Si
Ci
3. 真值表
半加器的真值表如表4.2.1—1所示。
表4.2.1—1
4. 逻辑函数表达式
半加器的逻辑函数表达式为
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
5. 逻辑电路图
定
。
An1 An、2 L A2 A1 A0 Cn1Cn2 L C2C1C0
B和n1Bn给2出L,B便2可B1以B直0 接C确01
方法二
C0 P0C01 G0
C1 P1C0 G1
P1 P0C01 G0 G1
C2 P2C1 G2
P2 P1 P0C01 G0 G1 G2
图4.2.5—3 Ⅰ. 加减控制输入为0时,该电路实现加法运算; Ⅱ. 加减控制输入为1时,该电路实现减法运算(补码加法)。
返回
半加器的逻辑函数表达式为
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
5. 逻辑电路图
半加器的逻辑电路图如图4.2.1—1所示。
(公式4.2.1) (公式4.2.2)
图4.2.1—1
6. 逻辑符号
半加器的逻辑符号如图4.2.1—2所示。
图4.2.1—2
二、全加器(Full Adder)
依次递推可知,只要
定
。
An1 An、2 L A2 A1 A0 Cn1Cn2 L C2C1C0
B和n1Bn给2出L,B便2可B1以B直0 接C确01
四位超前进位加法器的逻辑电路图如图4.2.3—2所示。 图4.2.3—2
四、中规模集成加法器
数字逻辑课件——加法器

综上所述,接法如图3-3-23(b)所示。与方法1比 较,多用了一个与非门,却省去两个“四选一” 选择器。“选择输入”端A1,A0,可接C,D, 也可接A,B或A,C或B,D或A,D或B,C, 相应的卡诺图略加变动,所得的D0,D1, D2, D3的表达式各不相同。经过各种方案的比较, 可得最佳的简化结构。
例3-6 用74153实现逻辑函数Z F (A, B) m(1, 3)
解:由最小项表达式得该函数的真值表,如表 3-3-12所示,用半片74153即可实现该逻辑函数, 接法如图3-3-20。
输入变量A,B分别送选择输入端A1,A0选通输 入,ST 应接0,数据输入D0,D1,D2,D3根据 真值表分别接0,1,0,1。这样,74153的输 出端Y 即逻辑函数Z。
逻辑图可以看出,数据输出Y 的逻辑表达 式为
Y ST[D0 ( A1 A0 ) D1( A1 A0 ) D2 ( A1 A0 ) D3 ( A1 A0 )]
即当选通输入 ST 0 时,若将选择输入A1,
A0分别为00,01,10,11则相应地把D0,D1,
D2,D3送到数据输出端Y去, 当
图3-3-21 例3-7图
25
①B当C BC =00时,Z = D0 ;由卡诺图可见,Z 此时 不②不A管管当01 AAB0000等 等C 于 于=01110001或 或时111011,, ,Z1ZZ001 =都都D等等1 于于;01由,,卡因因B0C 诺此此图以以S可AAT0110 输 输见D012入 入,7DY411DD此53D012。 。时D3
从图3-3-22可以发现,下层的片0和片3, 输出分别恒为0和1,故可省去片0和片3, 同时,片4的D0和D3分别改接0和1。因此, 在用74153实现逻辑函数时,必须根据具 体情况考虑简化结构的可能性。
02-16.1 加法器工作原理-课件
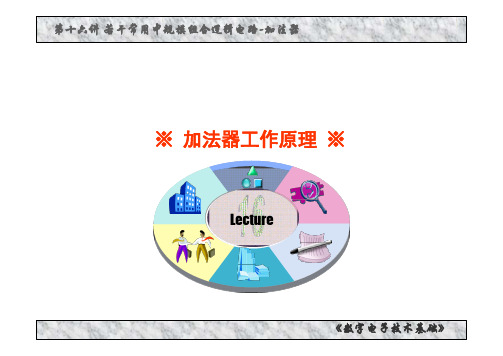
依次代入 展开:
第i位的和为:
(CO )i Gi Pi Gi 1 Pi Pi 1Gi 2 K
Pi Pi 1 K P G1
0
PP
(CIi )
i i
1
(KCOP1C) i10
S i Ai Bi (CI )i
《数字电子技术基础》
第十六讲 若干常用中规模组合逻辑电路-加法器
★ 超前进位加法器示例
█ 4位串行进位全加器的Verilog-HDL设计
//4位串行进位全加器设计 full_add1 f0
(a[0],b[0],cin,sum[0],cin1);
module add4_1
full_add1 f1
(sum,cout,a,b,cin); (a[1],b[1],cin1,sum[1],cin2);
目前,常用加法器分类如下:
1位加法器 加
法
器
多位加法器
半加器 全加器 串行进位加法器 超前进位加法器
《数字电子技术基础》
第十六讲 若干常用中规模组合逻辑电路-加法器
█ 1位全加器
◆ 半加器(Half-adder)
若不考虑有来自低位的进位将两个1位二进制数相加, 称为半加。实现半加运算的电路叫做半加器。
output cout; output[3:0] sum; input[3:0] a,b; input cin;
full_add1 f2 (a[2],b[2],cin2,sum[2],cin3); full_add1 f3 (a[3],b[3],cin3,sum[3],cout);
endmodule
下图示出了4位 超前进位加法 器74LS283的电 路图:
图2 74LS283的逻辑电路图
数字电路加法器原理

数字电路加法器原理数字电路加法器是一种用于实现数字加法运算的电路。
它可以将两个二进制数相加,并输出其和。
在计算机和其他数字系统中,加法器是非常基础且重要的组件之一。
数字电路加法器的原理主要基于二进制加法的规则。
在二进制加法中,每一位的相加结果有四种可能:0+0=0,0+1=1,1+0=1,1+1=0(产生进位)。
这四种情况可以通过逻辑门来实现。
一个简单的加法器可以由多个半加器和一个全加器组成。
半加器用于计算两个输入位的和与进位,而全加器则用于计算包括上一位进位的三个输入位的和与进位。
通过级联多个半加器和全加器,可以构建出实现任意位数加法的加法器。
在加法器中,输入通常为两个二进制数和一个进位输入。
输出为两个二进制数相加的和和一个进位输出。
当两个输入数的每一位和进位输入都经过相应的逻辑运算后,得到了相应的输出结果。
在实际应用中,加法器常常是与其他数字电路组合使用的。
例如,在计算机的中央处理器中,加法器被用于实现整数加法、浮点数加法以及其他一些运算。
此外,加法器还可以用于实现其他数字运算,如减法、乘法和除法等。
除了基本的加法器,还有一些其他类型的加法器。
比如带有进位输入的全加器,可以通过输入一个外部进位信号来实现多位数的加法。
还有带有进位输出的全加器,可以将多个全加器级联,实现多位数相加时的进位传递。
在设计和实现加法器时,需要考虑到许多因素。
例如,加法器的延迟时间、功耗、面积等。
为了提高加法器的性能,可以使用一些优化技术,如并行加法器、流水线加法器和超前进位加法器等。
数字电路加法器是实现数字加法运算的基础组件。
它通过逻辑门的组合实现了二进制加法的规则,可以广泛应用于计算机和其他数字系统中。
加法器的设计和实现是数字电路设计中的重要内容,对于提高计算机的性能和效率具有重要意义。
逻辑电路的设计加法器PPT课件
请同学们思考以下两个问题:
1、各位上的运算有何不同之处?
2、只考虑某一位数相加,用逻辑电路实现,分别有几个 输入端和输出端?
——加法器
加法器
加法运算的基本规则:
(1)逢二进一。 (2)最低位是两个数最低位的叠加,不需
考虑进位。 (3)其余各位都是三个数相加,包括加数
例2:利用四位全加器实现四位全减器。
两个多位数相减,可以用补码相加来实现。
A-B=A+B补=A+B反+1
差
A4A3A2A1 N4N3N2N1
借位 1
S4
S3
S2
C4
S1 C0
A4A3A2A1 N4N3N2N1 1 “1”
A4 A3 A2 A1 B4 B3 B2 B1
被减数
1 1 11
• 由于4位二进制数相加是逢十六进一,而 8421码相加是逢十进一,用4位全加器构成 8421码加法器时,必须解决“逢十六进一 变成逢十进一”的问题。
“逢十六进一变成逢十进一”
6+7=13
加
6修正
非法码
8+9=17
加6
需要加6修正情况:①:和在10—15之间,② :有进位Co。
•BCD(8421)码加法器电路设计
Bn
Cn
Cn-1
F3
F2
F1
F0
加法器
C3
C0
B3 A3 B2 A2
B1 A1 B0 A0
74LS83
加法器(5)
多位加法器
串行进位加法器 并行进位加法器
例:四位串行进位加法器
数字电路中加法器和减法器逻辑图分析

数字电路中加法器和减法器逻辑图分析1.加法器,减法器都是从一位的二进制数开始进行例题讲解,逐渐扩展到多位二进制位数之间的运算。
在设计逻辑电路的过程中,根据所描述的功能构建好真值表。
出题者喜欢要求读者用与或门,与或非门构建函数表达式。
它的原因在于依据真值表写函数表达式,最标准的就是最小项表达式。
以下小图的逻辑图来看与或门,我们的头脑中不能老是思维定势,认为输入就是两个,在实际生活中,输入应该非常多,远非两个,在逻辑符号中,要清楚地认识与非门的多输入的画法,将与门分成了好几格,每一格代表一个与门电路。
下小图可以写成AB+CD+EF(不认真考虑前面的输入),由细小的门集成为更大的门,将某一部分单独来看,它们就是一个整体,如(AB+CD+EF),体现在逻辑图中就是一个角。
如果从全图的角度看,在最后一级门电路中,每一个小整体代表着输出。
最后一级的与门中,有两个输入,有三个输入,这都是可以的,最多输入的个数是依照初始的输入的个数来定,不可能超过这个数,只可能少于这个数,因为对于某一输出而言,并非所有的输入对它都是有效的。
从最左边的所有输入,经过逻辑电路图,在最右边得到了所有的输出。
还有一点,这是与或表达式的逻辑图,如果在写逻辑表达式,包括化简变化函数式时,采用了不同于与或形式的表达式,那么最终得到的逻辑图就和下面的与或形式的逻辑图完全不一样。
2.一位的全减器是指,两个一位的二进制数之间进行减法运算。
全减器的特例就是半减器。
多位二进制减法器,是由加法电路构成的;在加法电路的基础上,减法与加法采用同一套电路,实现加减法共用。
3.这里的多位二进制数的减法,是指无符号数,为什么?将减法运算转换为加法运算,采用的是补数的方法完成的。
这就解释了为什么两者能共用一套电路,是不是减法在转换时,我们需要在加法电路的基础上进行一些小的扩展,来进行减法的补码转换?N反是每一位都取反,没有符号位,下式当中,A-B是减法,通过形式转化,将-B化为B反+1-2n,B是正数,A和B均为无符号数,通过补码的转变,我们成功的将-B变为了固定的-2n,但是这还是有减号,该怎么解决?仔细观察下面这张图,A和B是两个四位二进制数相减。
