六年级奥数试题-等积变形(学生版)
六年级等积变形应用题

六年级等积变形应用题
六年级的学生们学习了等积变形的概念后,接下来他们将应用这个概念来解决一些实际问题。
等积变形是指图形或物体的形状改变,但其面积不变。
在这个阶段,学生们将学会如何应用等积变形来解决一些日常生活中的问题。
例如,他们可能会遇到这样的问题:某个矩形花坛的面积为16平方米,长是3米,那么宽是多少米?学生们可以通过等积变形来解决这个问题。
他们可以将长和宽分别表示为x和y,根据等积变形的原则,有xy=16。
已知x=3,所以可以通过等式求得y的值,从而得到花坛的宽度。
另一个例子是关于房间布局的问题。
假设学生们需要重新布置一个矩形房间的家具,但是要保持房间的面积不变。
他们可以使用等积变形的原理,将房间的长度和宽度表示为x和y,然后设置一个新的长和宽,即x+2和y+1。
通过等积变形,他们可以设置方程xy=(x+2)(y+1),解这个方程可以得到新的房间尺寸。
此外,学生们还可以应用等积变形来解决有关体积的问题。
他们可以考虑一个长方体的体积为24立方厘米,长为4厘米,那么宽和高各是多少厘米?通过等积变形的原理,他们可以设置方程4xy=24,其中x表示宽,y表示高。
通过解这个方程,他们可以得到宽和高的值。
通过这些应用题,学生们可以更好地理解等积变形的概念,并将其应用到实际问题中。
这不仅可以帮助他们提高解决问题的能力,还可以培养他们的逻辑思维和数学推理能力。
小学数学《三角形的等积变形》练习题(含答案)

三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
而四边形CEFH是它们的公共部分,
所以三角形DHF的面积=三角形BCH的面积,
进而可得阴影面积=三角形BDF的面积=三角形BCD的面积= 10×10÷2=50(平方厘米)。
法2:连接CF,那么CF平行BD,
所以,阴影面积=三角形BDF的面积=三角形BCD的面积=50(平方厘米)。
附加题目
【附1】 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
巩固理解结论:两个三角形等底时,面积的倍数=高的倍数
【例3】用两种不同的方法,把任意一个三角形分成四个面积相等的三角形.
分析:法1:如图(1),将BC边四等分,连接各等分点,则△ABD、△ADE、△AEF、△AFC面积相等。
法2:如图(2),D是BC的二等分点,E、F是AC、AB的中点,从而得到四个等积三角形△ADF、△BDF、△DCE、△ADE.
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
分析:
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
分析:连结AE、BF、CD(如右下图).由于三角形AEB与三角ABC的高相等,而底边EB=2BC,所以三角形AEB的面积是2.同理,三角形CBF的面积是3,三角形ACD的面积是1.
六年级奥数第3讲等积变形

六年级奥数第3讲等积变形
引言
本文档将介绍六年级奥数第3讲的等积变形。
通过本讲的研究,学生将能够更深入地理解等积变形的概念和方法,并能够应用于相
关问题的解决。
等积变形的定义
等积变形是指在保持图形面积不变的前提下,通过改变形状、
角度或尺寸等方式进行变换的过程。
在等积变形中,图形的比例关
系和形状特征保持不变。
例题解析
以下是一些关于等积变形的例题解析,以帮助学生更好地理解
和掌握相关知识。
例题1
已知一个长方形的长为12cm,宽为8cm,将其等比例缩小为
原来的一半,请计算缩小后长方形的长和宽分别是多少?
解析:由于题目要求等比例缩小为原来的一半,可以将长和宽都除以2来计算。
因此,缩小后的长方形的长为6cm,宽为4cm。
例题2
一个三角形的底边长为10cm,高为8cm。
将该三角形的底边长保持不变,将高等比例放大为原来的2倍,请计算放大后三角形的高和面积分别是多少?
解析:根据等积变形的性质,底边长不变,高放大为原来的2倍意味着面积放大为原来的2倍。
因此,放大后三角形的高为
16cm,面积为80平方厘米。
总结
通过学习本讲的等积变形概念和例题解析,我们了解到等积变形是指在保持图形面积不变的前提下进行变换的过程。
在计算等积变形时,可以利用比例关系和形状特征来解决相关问题。
希望同学们通过本讲的学习,能够更熟练地运用等积变形的方法解决各类数学问题。
等积变形--小升初专项训练 学生版
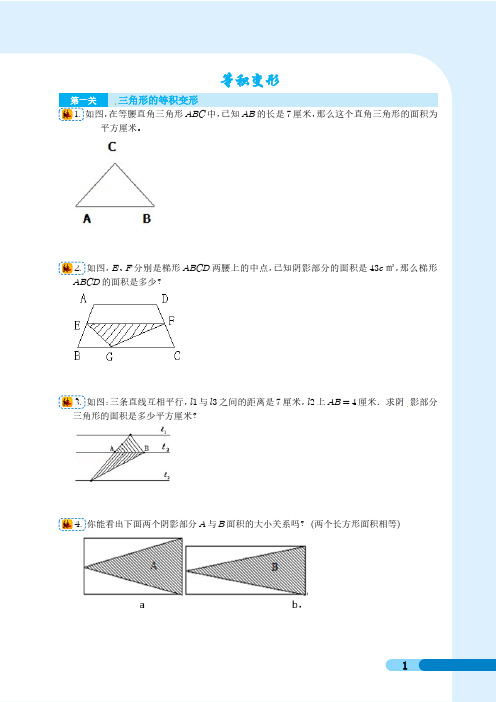
等积变形第一关三角形的等积变形1.如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
2.如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD的面积是多少?3.如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 4.你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)5.如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.6.如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?7.如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?8.下图中阴影部分甲的面积与阴影部分乙的面积哪个大?9.如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC 的面积为1,那么图中两个阴影三角形面积之和是多少?10.已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.11.如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的23.请问:阴影部分的总面积是多少?12.如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
13.(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?14.如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?15.如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?16.由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?17.如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
等积变形(附答案)

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积三角形面积==底×高÷底×高÷2 2这个公式告诉我们:这个公式告诉我们:三角形面积的大小,三角形面积的大小,三角形面积的大小,取决于三角形底和高的乘积.取决于三角形底和高的乘积.取决于三角形底和高的乘积.如如果三角形的底不变,果三角形的底不变,高越大高越大高越大((小),三角形面积也就越大三角形面积也就越大((小).同样若三角形的高不变,底越大高不变,底越大((小),三角形面积也就越大,三角形面积也就越大((小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.它的底和高之中至少有一个要发生变化.但是,但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:同时也告诉我们:一个三角形在面积不改变的情况下,一个三角形在面积不改变的情况下,一个三角形在面积不改变的情况下,可以有无数多个不可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高③若两个三角形的高((或底或底))相等,其中一个三角形的底其中一个三角形的底((或高或高))是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.它们所对的顶点同为A 点,(也就是它们的高相等也就是它们的高相等))那么这两个三角形的面积相等.同时也可以知道△同时也可以知道△ABC ABC 的面积是△的面积是△ABD ABD 或△或△AEC AEC 面积的3倍.例如在图中,△例如在图中,△ABC ABC 与△与△DBC DBC 的底相同的底相同((它们的底都是BC)BC),它所对的两个顶点,它所对的两个顶点A 、D 在与底BC 平行的直线上,平行的直线上,((也就是它们的高相等也就是它们的高相等)),那么这两个三角形的面积相等.例如图中,△例如图中,△ABC ABC 与△与△DBC DBC 的底相同的底相同((它们的底都是BC)BC),△,△,△ABC ABC 的高是△的高是△DBC DBC 高的2倍(D 是AB 中点,AB=2BD AB=2BD,,有AH=2DE)AH=2DE),,则△则△ABC ABC 的面积是△的面积是△DBC DBC 面积的2倍.倍.上述结论,是我们研究三角形等积变形的重要依据.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法2:如右图,先将BC 二等分,分点D 、连结AD AD,得到两个等积三角,得到两个等积三角形,即△形,即△ABD ABD 与△与△ADC ADC 等积.然后取AC AC、、AB 中点E 、F ,并连结DE DE、、DF DF.以而.以而得到四个等积三角形,即△得到四个等积三角形,即△ADF ADF ADF、△、△、△BDF BDF BDF、△、△、△DCE DCE DCE、△、△、△ADE ADE 等积.等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.方法方法 1 1 1:如下左图,将:如下左图,将BC 边八等分,取1∶3∶4的分点D 、E ,连结AD AD、、AE AE,从而得到△,从而得到△,从而得到△ABD ABD ABD、△、△、△ADE ADE ADE、△、△、△AEC AEC 的面积比为1∶3∶4.DE DE,从而得到三个三角形:△,从而得到三个三角形:△,从而得到三个三角形:△ADE ADE ADE、△、△、△BDE BDE BDE、△、△、△ACD ACD ACD.其面积比为.其面积比为1∶3∶4.当然本题还有许多种其他分法,同学们可以自己寻找解决.当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD 中,中,AC AC 与BD 是对角线,其交点O ,求证:△,求证:△AOB AOB 与△COD 面积相等.面积相等.证明:∵△证明:∵△ABC ABC 与△与△DBC DBC 等底等高,等底等高,∴S △ABC =S △DBC又∵又∵ S S △AOB =S △ABC —S △BOCS △DOC =S △DBC —S △BOC ∴S △AOB =S △COD .例4、如图,把四边形ABCD 改成一个等积的三角形.改成一个等积的三角形.分析分析 本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A 移到CB 的延长线上的A ′处,△′处,△A A ′BD 与△与△ABD ABD 面积相等,从而△A ′DC 面积与原四边形ABCD 面积也相等.这样就把四边形ABCD 等积地改成了三角形△了三角形△A A ′DC DC.问题是.问题是A ′位置的选择是依据三角形等积变形原则.过A 作一条和DB 平行的直线与CB 的延长线交于A ′点.′点.解:①连结BD BD;;②过A 作BD 的平行线,与CB 的延长线交于A ′.′. ③连结A ′D ,则△,则△A A ′CD 与四边形ABCD 等积.等积.例5、如图,已知在△、如图,已知在△ABC ABC 中,中,BE=3AE BE=3AE BE=3AE,,CD=2AD CD=2AD.若△.若△.若△ADE ADE 的面积为1平方厘米.求三角形ABC 的面积.的面积.解法1:连结BD BD,在△,在△,在△ABD ABD 中∵ BE=3AE BE=3AE,,∴ S △ABD =4S △ADE =4(=4(平方厘米平方厘米平方厘米)). 在△在△ABC ABC 中,∵中,∵CD=2AD CD=2AD CD=2AD,,∴ S △ABC =3S △ABD =3=3××4=12(4=12(平方厘米平方厘米平方厘米)).解法2:连结CE CE,如右图所示,在△,如右图所示,在△,如右图所示,在△ACE ACE 中,中,∵ CD=2AD CD=2AD,,∴ S △ACE =3S △ADE =3(=3(平方厘米平方厘米平方厘米)).在△在△ABC ABC 中,∵中,∵BE=3AE BE=3AE∴ S △ABC =4S △ACE=4=4××3=12(3=12(平方厘米平方厘米平方厘米)).例6、如下图,在△、如下图,在△ABC ABC 中,中,BD=2AD BD=2AD BD=2AD,,AG=2CG AG=2CG,,BE=EF=FC=解:连结BG BG,在△,在△,在△ABG ABG 中,中,∴ S △ADG +S △BDE +S △CFG例7、如右图,、如右图,ABCD ABCD 为平行四边形,为平行四边形,EF EF 平行AC AC,如果△,如果△,如果△ADE ADE 的面积为4平方厘米.求三角形CDF 的面积.的面积.解:连结AF AF、、CE CE,∴,∴,∴S S △ADE =S △ACE ;S △CDF =S △ACF ;又∵;又∵AC AC 与EF 平行,∴平行,∴S S △ACE =S △ACF ;∴ S △ADE =S △CDF =4(=4(平方厘米平方厘米平方厘米)).例8、如右图,四边形ABCD 面积为1,且AB=AE AB=AE,,BC=BF BC=BF,,DC=CG DC=CG,,AD=DH AD=DH.求.求四边形EFGH 的面积.的面积.解:连结BD BD,将四边形,将四边形ABCD 分成两个部分S 1与S 2.连结FD FD,有,有S △FBD =S △DBC =S 1 所以S △CGF =S △DFC =2S 1.同理同理 S S △AEH =2S 2,因此S △AEH +S △CGF =2S 1+2S 2=2(S 1+S 2)=2)=2××1=21=2..同理,连结AC 之后,可求出S △HGD +S △EBF =2所以四边形EFGH 的面积为2+2+1=5(2+2+1=5(平方单位平方单位平方单位)).例9、如右图,在平行四边形ABCD 中,直线CF 交AB 于E ,交DA 延长线于F ,若S △ADE=1ADE=1,求△,求△,求△BEF BEF 的面积.的面积.解:连结AC AC,∵,∵,∵AB//CD AB//CD AB//CD,∴,∴,∴S S △ADE =S △ACE又∵又∵AD//BC AD//BC AD//BC,∴,∴,∴S S △ACF =S △ABF而 S △ACF =S △ACE +S △AEF ∶S △ABF =S △BEF +S △AEF ∴ S △ACE =S △BEF ∴S △BEF =S △ADE =1=1..。
六年级奥数优胜教育第3讲:等积变形含答案

第三讲等积变形例1:如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例2:长方形ABCD的面积为36cm2,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?A H DE GB F C例3:如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为.A DE OGB F C例4:已知ABC为等边三角形,面积为400,D、E、F分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)例5:如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是.A AC D E F G C D E FGB B例6:如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB=2:5,AE:AC=4:7,△S ADE=16平方厘米,求△ABC的面积.AAD DE EB C B C例7:如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△S ADE=12平方厘米,求△ABC的面积.DAEB CDAEB C例8:如图,平行四边形ABCD,BE=AB,C F=2CB,G D=3DC,HA=4A D,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比.H HA B E A B EG D C G D CF例9:如图所示的四边形的面积等于多少?FC O131213D1312131212AB例10:如图所示,∆ABC中,∠ABC=90︒,AB=3,BC=5,以AC为一边向∆ABC外作正方形ACDE,中心为O,求∆OBC的面积.EEO DODA3B5CA3B5C F A1.如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?_E_E_A_B_A_B_F_F_D_G_C_D_G_C2.在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.A D A(P)D A DP PB C B C B CC C甲乙3.如图,长方形ABCD的面积是36,E是AD的三等分点,AE=2ED,则阴影部分的面积为.A E DA E DMNO OB B4.如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?A AD E DEB C B C5.如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4,B E=3,AE=6,乙部分面积是甲部分面积的几倍?A AE B甲乙D C BED CB6.如图,以正方形的边AB为斜边在正方形内作直角三角形ABE,∠AEB=90︒,AC、B D 交于O.已知AE、BE的长分别为3cm、5cm,求三角形OBE的面积.C B C BO E OEFD A D A7.如下图,六边形ABCDEF中,AB=ED,AF=CD,BC=EF,且有AB平行于ED,AF 平行于CD,BC平行于EF,对角线FD垂直于BD,已知F D=24厘米,BD=18厘米,请问六边形ABCDEF的面积是多少平方厘米?B G BAC ACF D F DE E角形 BCD 的面积的 ,且 AO = 2 ,DO = 3 ,那么 CO 的长度是 DO 的长度的_________倍.EBE8.如图,三角形 ABC 的面积是 1 , E 是 AC 的中点,点 D 在 BC 上,且 BD : DC = 1: 2 , AD 与 BE 交于点 F .则四边形 DFEC 的面积等于 .AEBDFC9.如图,长方形 ABCD 的面积是 2 平方厘米, EC = 2DE , F 是 DG 的中点.阴影部分的面积是多少平方厘米?AD ADBGFECBxF x y Gy EC10.四边形 ABCD 的对角线 AC 与 BD 交于点 O (如图所示).如果三角形 ABD 的面积等于三13ADOBCC11.如图,平行四边形 ABCD 的对角线交于 O 点,△CEF 、△OEF 、△ODF 、△BOE 的面 积依次是 2、4、4 和 6.求:⑴求 △OCF 的面积;⑵求 △GCE 的面积.ADOF GBEC12.如图,长方形 ABCD 中, BE : EC = 2:3 , DF : FC = 1: 2 ,三角形 DFG 的面积为 2 平方 厘米,求长方形 ABCD 的面积.AGDFAGDFBCC13.如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.B CGA M D14.在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.A DFB E C15.已知ABCD是平行四边形,BC:CE3:2,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.A DA DO OB C E B C E1.右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.A D A D992121O44B E B E CCDA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数 ,那么,2.右图中 ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米), 阴影部分的面积是 平方厘米.AD AD881616O 2 2BEC BEC3.如图,长方形 ABCD 被 CE 、 DF 分成四块,已知其中 3 块的面积分别为 2、5、8 平方厘 米,那么余下的四边形 OFBC 的面积为___________平方厘米.A EFB A EFB225O ?5O ?88DC D C4.如图, ∆ABC 是等腰直角三角形, DEFG 是正方形,线段 AB 与 CD 相交于 K 点.已知正 方形 DEFG 的面积 48, AK : KB = 1:3 ,则 ∆BKD 的面积是多少?DA G DA GKKBEF C B E M F C5.下图中,四边形 ABCD 都是边长为 1 的正方形,E 、F 、G 、H 分别是 AB ,BC ,CD ,mn(m + n ) 的值等于.AH D A H DEG E GBFC BFC1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.2.用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及 1∶3∶4.3.如右图,在梯形 ABCD 中,AC 与 BD 是对角线,其交点 △O ,求证:AOB 与△COD 面积相等.4.如右图,把四边形 ABCD 改成一个等积的三角形.5.如右图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为 1 平方厘米.求三角形 ABC的面积.6.如下页图,在△ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC=面积的几分之几?1 3BC ,求阴影部分面积占三角形 A BC7.如右图,ABCD 为平行四边形,EF 平行 △A C ,如果 ADE 的面积为 4 平方厘米.求三角形 CDF的面积.8.如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.9.如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若△S ADE=1,求△BEF的面积.△S ACD = △S BCD ,则可知直线 AB 平行于 CD .E第三讲 等积变形1.等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 S : S = a : b12③夹在一组平行线之间的等积变形,如图 △S ACD = △S BCD ;反之,如果④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于 它们的高之比. 2.鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在 △ABC 中,D , E 分别是 AB, AC 上的点如图 ⑴(或 D 在 BA 的延长线上, 在 AC 上),则S△ABC :S△ADE=(AB⨯AC):(AD⨯AE)3.蝶形定理任意四边形中的比例关系(“蝶形定理”):①S:S=S:S或者S⨯S=S⨯S②AO:OC=(S+S):(S+S)124313241243蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.DAS2S1OS4S3B C梯形中比例关系(“梯形蝶形定理”):①S:S=a2:b213②S:S:S:S=a2:b2:ab:ab;1324③S的对应份数为(a+b)2.4.相似模型(一)金字塔模型(二)沙漏模型A E F DAD F EB GC B G C①AD AE DE AF===AB AC BC AG;②:=AF2:AG2.△S ADE△S ABC所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.5.共边定理(燕尾模型和风筝模型)共边定理:若直线AO和BC相交于D(有四种情形),则有S∆ABO :S∆ACO=BD:DC在三角形ABC中,AD,BE,CF相交于同一点O,那么S:S=BD:DC.∆ABO∆ACO上述定理给出了一个新的转化面积比与线段比的手段,因为∆ABO和∆ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.AFEBOD C1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
等积变形 小学数学 习题集
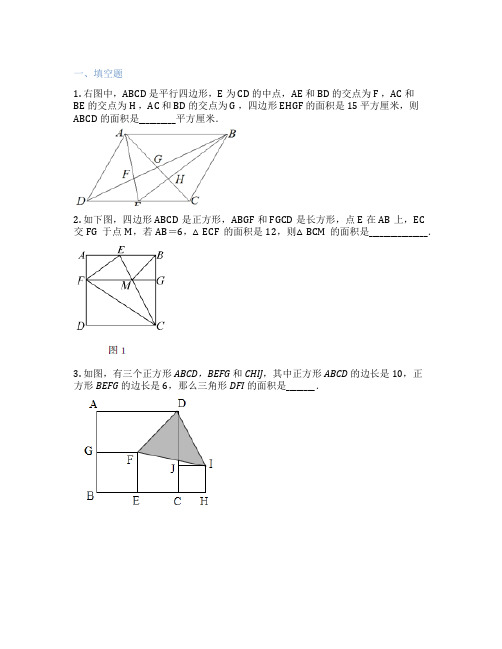
一、填空题
1. 右图中,ABCD 是平行四边形,E 为 CD 的中点,AE 和 BD 的交点为 F ,AC 和
BE 的交点为 H ,AC 和 BD 的交点为 G ,四边形 EHGF 的面积是 15 平方厘米,则ABCD 的面积是__________平方厘米.
2. 如下图,四边形ABCD是正方形,ABGF和FGCD是长方形,点E在AB上,EC
交FG于点M,若AB=6,△ECF的面积是12,则△BCM的面积是________________.3. 如图,有三个正方形ABCD,BEFG和CHIJ,其中正方形ABCD的边长是10,正
方形BEFG的边长是6,那么三角形DFI的面积是________.
4. 如图所示,,则阴影部分的面积=________.
5. 如图,△ABC中,点AD=CD,点E是BC上一点,且EC=2BE,BD与AE相交于点F,若△ABC的面积为12,则S△ADF-S△BEF=_______.
二、解答题
6. 如图,在长方形中,是的中点,是的中点,如果厘米,
厘米,求三角形的面积.
7. 如图,在三角形ABC中, BC=8厘米,AD=6厘米,E、F分别为AB和AC的中点。
那么三角形EBF的面积是多少平方厘米?
8. 图中是一个各条边分别为5厘米、12厘米、13厘米的直角三角形.将它的短直角边对折到斜边上去与斜边相重合,那么图中的阴影部分(即未被盖住的部分)的面
积是多少平方厘米?
9. 如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?。
【思维拓展】数学六年级思维拓展之等积变形(附答案)必考知识点

面积是三角形 AEF 面积的 2 倍,所以三角形 ABC 面积是三角形 AEF 面积的 3
倍;又因为平行四边形的面积是三角形 ABC 面积的 2 倍,所以平行四边形的面
积是三角形 AFE 面积的(3×2)=6 倍。因此,平行四边形的面积为 8 ×6=48(平
方厘米)。
6
10.【解答】连结 AE、BF、CD(如图)。由于三角形 AEB 与三角
PQRS。因此四块阴影的面积和就等于四边形 PQRS 的面积,即阴影部分与四边
形 PQRS 的面积之比为 1:1。
8. 【解答】连接 BD .设 SDCB S1, SDAB S2
∵ CB BF ,
∴ SCDF
CB BF CB
SCDB
2SCDB ,
又∵ DC CG ,
∴ SCFG SCDF 2S1 ,
4. 如图,在三角形 ABC 中,BC=8 厘米,AD=6 厘米,E、F 分别为 AB 和 AC
的中点,那么三角形 EBF 的面积是多少平方厘米?
A
E
F
B
C
1
5. 如图,已知三角形 ABC 面积为 1,延长 AB 至 D ,使 BD AB ;延长 BC 至 E , 使 CE 2BC ;延长 CA 至 F ,使 AF 3AC ,求三角形 DEF 的面积。
于是三角形 DEF 的面积等于三角形 ABC、AEB、CBF、ACD、AED、BEF、CFD
的面积之和,即 1+2+3+1+2+6+3=18。
11.【解答】连接辅 C 助线 E。
(三角形 BCE 的面积)︰(三角形 DCE 的面积)=BC﹕CD=1﹕1,
所以三角形 BCE 的面积等于三角形 DCE 的面积。
小学奥数等积变形2

奥数拓展:等积变形2【例1】重叠面积中的等积变形1.如图是有两个相同的直角梯形重叠而成(单位:厘米),阴影部分的面积是()平方厘米.2.如图,两个完全一样的直角三角形重叠一部分,图中阴影部分面积是()平方厘米.A.90 B.75 C.52 D.30【例2】等积变形的灵活运用1.如图,长方形ABCD的面积是56平方厘米,点E、F、G分别是长方形ABCD边上的中点,H为AD边上的任意一点,求阴影部分的面积.2.将三角形ABC的BA边延长1倍到D;CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于2,那么三角形DEF的面积是_____。
备用图1 备用图23.如图直角三角形中的空白部分是正方形,正方形的一个顶点将这个直角三角形的斜边分成两部分,阴影部分的面积是6 平方厘米,DB长厘米.EBA三.出门考1. 一个等腰三角形的两条边长分别是51米和21米,这个三角形的周长是( )米。
2. 如下图,ABCD 为平行四边形,E 、F 分别为AD 、DC 的中点,如果△BFC 的面积为4平方厘米,则△AEB 的面积是( )平方厘米.3. 如图是由两个相同的直角梯形重叠而成的,图中只标出三个数据(单位:厘米),图中阴影部分的面积是多少平方厘米?4*.如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)四.课后作业1. 计算,能简算的要简算。
435177-- 4847157+- 74512712⎛⎫-- ⎪⎝⎭ 4357910910+++ 41327373-+-2. 一根长2米的绳子,先用去41米,又用去21米,这根绳子短了多少米?3. 光明小学拥有一块公顷的菜地,其中青菜占菜地的,黄瓜占菜地的.剩下的种西红柿,西红柿占菜地的几分之几?4. 光明小学拥有一块公顷的菜地,其中种青菜的有公顷,种黄瓜的有公顷.剩下的种西红柿,西红柿有多少公顷?5. 如图将△ABC 的AB 边延长到D ,BC 边延长到E ,CA 边延长到F ,使DB=AB ,EC=2BC ,FA=2AC ,如果三角形ABC 的面积是5平方厘米,那么三角形DEF 的面积是平方厘米.6. 探索规律并计算=-4131 =-5131 =-6151 =-8151 =+4131 =+5131 =+6151 =+8151 我发现每日一练第一天:周天(5月20日)1. 三根电线共长87米,第一根和第二根共长43米,第二根和第三根共长31米。
奥数等积变形题目

奥数等积变形题目一、一个长方体水箱,长、宽、高分别为3米、2米、1米。
若将其变形为正方体,且体积保持不变,则正方体的边长为多少米?A. 1米B. 2米C. 3米D. 根号6米(答案)B二、有一个圆柱体,底面半径为2厘米,高为5厘米。
若将其等体积变形为圆锥体,且底面半径保持不变,则圆锥体的高为多少厘米?A. 5厘米B. 10厘米C. 15厘米D. 20厘米(答案)C三、一个正方体纸盒,棱长为4厘米。
若将其等体积变形为长方体,且新长方体的长、宽、高均为整数,则新长方体的可能的长、宽、高组合为?A. 1厘米、2厘米、8厘米B. 2厘米、2厘米、4厘米C. 1厘米、4厘米、4厘米D. 3厘米、3厘米、3厘米(答案)A四、有一个圆锥体,底面半径为3厘米,高为4厘米。
若将其等体积变形为圆柱体,且圆柱体的高为2厘米,则圆柱体的底面半径为多少厘米?A. 3厘米B. 4厘米C. 5厘米D. 6厘米(答案)A五、一个长方体水槽,长、宽、高分别为6分米、4分米、2分米。
若将其等体积变形为正方体水槽,则新水槽的表面积比原水槽的表面积减少了多少平方分米?A. 16平方分米B. 32平方分米C. 48平方分米D. 64平方分米(答案)C六、一个圆柱体,底面半径为1厘米,高为10厘米。
若将其等体积变形为圆锥体,且圆锥体的高保持不变,则圆锥体的底面半径为多少厘米?A. 1厘米B. 根号3厘米C. 2厘米D. 3厘米(答案)B七、有一个正方体,棱长为5厘米。
若将其切割成若干个小正方体,且小正方体的棱长均为整数,这些小正方体的体积之和最大为多少立方厘米?(小正方体可以大小不同)A. 125立方厘米B. 100立方厘米C. 75立方厘米D. 50立方厘米(答案)A八、一个圆锥体,底面半径为4厘米,高为6厘米。
若将其等体积变形为圆柱体,且圆柱体的底面半径为2厘米,则圆柱体的高为多少厘米?A. 6厘米B. 8厘米C. 12厘米D. 24厘米(答案)D。
2022-2023学年六年级数学上册典型例题之第一单元等积变化问题专项练习

20222023学年六年级数学上册典型例题系列之第一单元:等积变化问题专项练习(解析版)1.在一个长20厘米,宽8厘米,高10厘米的密封玻璃缸中,测得水深6厘米。
然后将它的左侧面朝上,这时水深多少厘米?【答案】12厘米【分析】先利用“长方体的体积=长×宽×高”求出水的体积,翻转后,体积不变,底面积变成长为10厘米,宽为8厘米,再根据“高=长方体的体积÷底面积”求出水的深度,据此解答。
【详解】20×8×6÷(10×8)=160×6÷80=960÷80=12(厘米)答:这时水深12厘米。
【点睛】理解水的体积不变并熟练掌握长方体的体积计算公式是解答题目的关键。
2.晶晶家的厨房里有一个长方体容器,从里面量,长20厘米、宽16厘米、高10厘米,平放时水面高8厘米,如图(1)。
如果把这个容器封闭并竖起来放,如图(2),请你算一算,水面的高度会是多少厘米?【答案】16厘米【分析】根据“长方体的体积=长×宽×高”求出图(1)长方体容器中水的体积,再利用“高=长方体的体积÷(长×宽)”求出图(2)长方体容器中水面的高度。
【详解】20×16×8÷(16×10)=20×16×8÷160=320×8÷160=2560÷160=16(厘米)答:水面高度是16厘米。
【点睛】熟练运用长方体的体积计算公式是解答题目的关键。
3.有一个正方体水箱,从里面量得棱长4分米。
如果把一满箱水倒入一个长8分米、宽2.5分米的长方体水池内,水深多少分米?【答案】3.2分米【分析】利用正方体的体积公式:V=a3,求出一满箱水的体积,根据长方体的体积公式:V=Sh可知,用水的体积除以长方体的底面积,即可求出水的深度。
小学六年级奥数-等积变形

小学六年级奥数等积变形(5)
【题目1】如图,四边形ABCD的对角线AC和BD相交于点O,BO:DO=3:2,三角形ABC的面积是18,求三角形ACD的面积。
.
【题目2】如图,梯形ABCD的面积是64平方厘米,上底AD和下底BC的长度比是3:5,求三角形BOC的面积是多少平方厘米?
【题目3】如图,正方形ABCD的边长是10厘米,E、F分别是AB、BC的中点,求四边形BFGE的面积是多少平方厘米?
【题目4】如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC 的中点,求四边形BGHF的面积是多少平方厘米?
【题目5】如图,平行四边形ABCD的面积是60平方厘米,BE=2AE,BF:FC=5:3,四边形ADGE的面积是多少平方厘米?
【题目6】如图,在三角形ABC中,G是AC的中点,D、E、F是BC的四等分点,且三角形ABD的面积比四边形CFNG的面积大6平方厘米,求三角形ABC的面积。
【题目7】如图,如图,在三角形ABC中,G是AC的中点,D、E、F是BC的四等分点,且三角形ABM的面积比四边形CFNG的面积大6平方厘米,求三角形ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲等积变形
1.等积模型
2.鸟头定理
3.蝶形定理
4.相似模型
5.共边定理(燕尾模型和风筝模型)
1.了解三角形的底、高与面积的关系,会通过分析以上关系解题。
2.能在解题中发现题目中所涉及的几何模型。
例1:如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .
例2:长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?
例3:如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .
例4:已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC )
例5:如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .
E
B
例6:如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.
例7:如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,
:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.
例8:如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.
例9:如图所示的四边形的面积等于多少?
G
F
E D
C B
A
A
B
C D
E F
G
E
D
C
B
A
E
D
C
B
A
E
D
C
B
A
E
D
C
B A
H
G
A
B C
D E
F
H
G
A
B C
D E
F
例10:如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.
A
1.如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?
2.在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.
O
D
C
B
A
13
13
12
12
13
13
12
12
5
3O
A B
C
D
E
F
53
O
A B C D
E
P D
C
B
A
A B
C
D
(P )
P
D
C
B
A
_ A _ B
_ G
_ C _E _F
_ D
_ A _ B
_ G
_ C
_E
_F
_ D
3.如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积
为 .
4.如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等
于1,那么三角形ABC 的面积是多少?
5.如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,
乙部分面积是甲部分面积的几倍?
B
6.如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.
7.如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?
B
B
E
D
C
B
A A
B C
D
E
乙甲
E D
C
B
A A
B C D E
甲
乙
F
F
E
A
B
D
C
G
F
E
A
B
D
C
8.如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .
9.如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面
积是多少平方厘米?
10.四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三
角形BCD 的面积的1
3
,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.
C
11.如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.
12.如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.
F
E
D C
B
A
x y
y x A
B
C
D E F
G
E D C
B
A
A
B
C
D
O
O
G
F
E
D
C
B
A
A
B
C
D E
F G
A
B
C
D E
F G
13.如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.
14.在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.
15.已知ABCD 是平行四边形,:3:2BC CE ,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.
1.右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.
B
A
A B
C
D
E
F B
B
B
B
2.右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.
3.如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.
4.如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?
5.下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,
DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m
n
,那么,
()m n +的值等于 .
B
B
8
5
2O A B C
D
E
F
?
8
5
2O A B
C
D E
F
B
B
E
E
1.用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.
2.用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.
3.如右图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.
4.如右图,把四边形ABCD改成一个等积的三角形.
5.如右图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC 的面积.
6.如下页图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=1
3
BC,求阴影部分面积占三角形ABC
面积的几分之几?
7.如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF 的面积.
8.如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
9.如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.
小学数学文化知识
圆田术
刘徽(大约1700年前)是我国魏晋时期的数学家,他在《九章算
术》方田章“圆田术”注中提出把割圆术作为计算圆的周长、面积以
及圆周率的基础。
刘徽从圆内接六边形开始,将倍数逐次加倍,得到的圆内接正多边形就逐步逼近圆。
查票
老教授搭乘火车旅行,列车长前来查票时,他竟找不到票,老教授急得满头大汗,列车长说:找不到就算了,再补张票好了。
老教授:这怎么可以,找不到那张票,我就不知道我要去哪里啊!。
