线索二叉树课程设计说明书格式
数据结构课程设计_线索二叉树的生成及其遍历

数据结构课程设计题目: 线索二叉树的生成及其遍历学院:班级:学生姓名:学生学号:指导教师:2012 年12月5日课程设计任务书摘要针对以二叉链表作为存储结构时,只能找到结点的左、右孩子的信息,而得不到结点的前驱与后继信息,为了使这种信息只有在遍历的动态过程中才能得到。
增设两个指针分别指示其前驱和后继,但会使得结构的存储密度降低;并且利用结点的空链域存放(线索链表),方便。
同时为了记下遍历过程中访问结点的先后关系,附设一个指针pre始终指向刚刚访问过的结点,若指针 p 指向当前访问的结点,则 pre指向它的前驱。
由此得到中序遍历建立中序线索化链表的算法本文通过建立二叉树,实现二叉树的中序线索化并实现中序线索二叉树的遍历。
实现对已生成的二叉树进行中序线索化并利用中序线索实现对二叉树的遍历的效果。
关键词二叉树,中序线索二叉树,中序线索二叉树的遍历目录摘要 ............................................. 错误!未定义书签。
第一章,需求分析.................................. 错误!未定义书签。
第二章,概要设计.. (1)第三章,详细设计 (2)第四章,调试分析 (5)第五章,用户使用说明 (5)第六章,测试结果 (5)第七章,绪论 (6)第八章,附录参考文献 (7)线索二叉树的生成及其遍历第一章需求分析以二叉链表作为存储结构时,只能找到结点的左、右孩子的信息,而得不到结点的前驱与后继信息,为了使这种信息只有在遍历的动态过程中才能得到。
增设两个指针分别指示其前驱和后继,但会使得结构的存储密度降低;并且利用结点的空链域存放(线索链表),方便。
同时为了记下遍历过程中访问结点的先后关系,附设一个指针pre始终指向刚刚访问过的结点,若指针 p 指向当前访问的结点,则 pre指向它的前驱。
由此得到中序遍历建立中序线索化链表的算法本文通过建立二叉树,实现二叉树的中序线索化并实现中序线索二叉树的遍历。
线索二叉树

6·4 线索二叉树1、线索二叉树的结点结构二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。
对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。
为了容易找到前驱和后继,有两种方法。
一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。
现将二叉树的结点结构重新定义如下:其中:ltag=0 时ltag=1 时lchild指向前驱;rtag=0 时rchild指向左子女;rtag=1 时rchild指向后继;以这种结点结构构成的二叉链表作为二叉树的存储结构,叫做线索链表,指向前驱和后继的指针叫线索,加上线索的二叉树叫线索二叉树,对二叉树进行某种形式遍历使其变为线索二叉树的过程叫线索化。
学习线索化时,有三点必须注意:一是何种“序”的线索化,是先序、中序还是后序;二是要“前驱”线索化、“后继”线索化还是“全”线索化(前驱后继都要);三是只有空指针处才能加线索。
2、对二叉树进行中序线索化的算法bithptr *pre; /* 全程变量*/void INTHREAD(bithptr *p){if(p!=NULL){ INTHREAD(p->lchild); /* 左子树线索化*/if(p->lchild==NULL) { p->ltag=1;p->lchild=pre;}if(p->rchild==NULL) p->rtag=1;if(pre!=NULL && pre->rtag==1) pre->rchild=p;pre=p; /* 前驱指向当前结点*/INTHREAD(p->rchild); /* 右子树线索化*/}3、在线索二叉树上查找前驱和后继(1)中序线索二叉树:若结点的ltag=1,lchild指向其前驱;否则,该结点的前驱是以该结点为根的左子树上按中序遍历的最后一个结点。
线索二叉树课程设计说明书-模板

数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码:题目: 线索二叉树的应用年级/专业/班: 2010级软件1班学生姓名:学号: 1127开始时间:2011 年12 月9 日完成时间:2011 年12 月23 日课程设计成绩:1指导教师签名:年月日摘要首先是对需求分析的简要阐述,说明系统要完成的任务和相应的分析,并给出测试数据。
其次是概要设计,说明所有抽象数据类型的定义、主程序的流程以及各程序模块之间的层次关系,以及ADT描述。
然后是详细设计,描述实现概要设计中定义的基本功操作和所有数据类型,以及函数的功能及代码实现。
再次是对系统的调试分析说明,以及遇到的问题和解决问题的方法。
然后是用户使用说明书的阐述,然后是测试的数据和结果的分析,最后是对本次课程设计的结论。
关键词:线索化;先序遍历;中序遍历;后续遍历线索二叉树的运用引言数据结构是计算机专业重要的专业基础课程与核心课程之一,在计算机领域应用广泛,计算机离不开数据结构。
数据结构课程设计为了能使我们掌握所学习的知识并有应用到实际的设计中的能力,对于掌握这门课程的学习方法有极大的意义。
本课程设计的题目为“线索二叉树的应用”,完成将二叉树转化成线索二叉树,采用前序、中序或后序线索二叉树的操作。
本课程设计采用的编程环境为Microsoft Visual Stdio 2008。
目录1需求分析 (3)2开发及运行平台 (4)3 概要设计 (5)4 详细设计 (7)5 调试分析 (12)6 测试结果 (13)7 结论 (18)致谢 (19)参考文献 (20)附录 (21)1、需求分析为了能更熟练精准的掌握二叉树的各种算法和操作,同时也为了开拓视野,综合运用所学的知识。
为此,需要将二叉树转化成线索二叉树,采用前序、中序或后序线索二叉树,以实现线索树建立、插入、删除、恢复线索等。
1.1任务与分析中次系统要实现对二叉树的建立,以及线索化该二叉树,同时实现对其先序、中序、后序线索话的并输出结果。
数据结构课程设计报告之线索二叉树

线索二叉树一目的程序从文件中读取每个结点的信息,然后建立一个二叉树。
通过菜单的形式,选择不同的线索化方式,然后再对线索化的二叉树经行遍历并输出对应的结果。
二需求分析1、文件的读入程序首先要从一个文件中读入结点的信息。
故需建立一个文件,在文件中,给出每个结点的信息。
2、菜单的实现由于需要建立两种不同的线索二叉树,故需要一个菜单,来选择需要进行的操作,并输出操作的结果。
3、树的建立从文件中,读入每个结点的信息。
然后建立起树,然后再对已建立的树进行相应的线索化。
4、树的线索化根据菜单的选择,对已建立的树经行相对应的线索化。
5、输出遍历的结果对每种不同的线索化的的树,给出相对应的算法。
然后,根据算法把每种遍历的结果输出。
三概要设计1、主程序模块(1)主程序模块int main(){welcome(); //通过welcome()模块来让用户控制,做线索化的工作。
return 0;}(2)可线索化单元模块—实现各种线索化的抽象数据类型;通过welcome()模块来调用每个线索化模块。
2、建立二叉树的模块bool CreatBinTree();函数会根据用户输入的文件名,打开一个存储了树中每个结点的文件,且是用广义表的形式给出结点信息的文件。
操作结果:根据文件中广义表的形式,建立相对应的二叉树,该树的根节点为root。
3、线索化的抽象数据类型void CreatInThread();void CreatInThread(Node *current,Node *&front)current是中序遍历下,当前遍历的结点的指针。
front是中序遍历下,current结点的前驱的指针。
操作结果:对建立的二叉树完成中序线索化。
void CreatPostThread();void CreatPostThread(Node *current,Node *&front)current是后续遍历下,当前遍历的结点的指针。
二叉树数据结构课程设计报告

数据结构课程设计报告题目:线索二叉树的应用院(系):计算机工程学院专业:嵌入式系统软件设计方向班级:嵌入式109(1)学生:黄江彬指导教师:寇海洲殷路邱军林孙成富2010年12月目录1.设计目的 (3)2.总体设计 (3)2.1首先创建一个线索二叉树 (3)2.2功能函数的实现 (4)3.调试分析 (7)4.测试结果 (7)5课程设计小结. (10)1.设计目的线索二叉树的应用:创建线索二叉树,实现二叉树的建立,插入,删除,恢复线索的算法。
2.总体设计实现过程和步骤提示:2.1首先创建一个线索二叉树2.1.1功能说明:程序首先显示创建线索二叉树的界面,并等待用户输入命令(见图1-1所示)。
假如用户输入ABCE##F##D##G##,程序将在显示屏上输出运算结果(见图1-2所示)。
图1-1图1-22.1.2创建线索二叉树的程序代码://创建二叉树ABD#GJ##K##E##C#FH##IL### ABCD##E###F#GH##I#J#K## void Creat(Bitree *p) //指向指针的指针{char ch=getchar();if(ch=='#')(*p)=NULL;else{//Bitree k;*p=(Bitreenode *)malloc(sizeof(Bitreenode));(*p)->data=ch;Creat(&(*p)->lchild);Creat(&(*p)->rchild);}//return 1;}2.1.3创建线索二叉树系统菜单实现提示:(1).遇“#”则该结点为空;(2).直接从键盘获取字符串.2.2功能函数的实现2.2.1二叉树的遍历2.2.1.1功能说明:对用户输入的二叉树进行遍历2.2.1.2二叉树的遍历程序代码://先序遍历void First(Bitree p){if(p){printf("%2c",p->data);First(p->lchild);First(p->rchild);}}//中序遍历void Middle(Bitree p){if(p){Middle(p->lchild);printf("%2c",p->data);Middle(p->child);}//后序遍历void Last(Bitree p){if(p){Last(p->lchild);Last(p->rchild);printf("%2c",p->data);}}2.2.1.3遍历二叉树功能实现提示:(1).用户输入二叉树后函数自动对所输入二叉树进行遍历。
二叉树后序线索化

输出二叉树的结构
printf("%d\t %d\ n",i++,bt->data); if(bt->lchild!=null) outbtree(bt->lchild); if(bt->rchild!=null) outbtree(bt->rchild);
int k
if(bt==null)
N
对二叉树后序化 POSTREAD(T->lchild); POSTREAD(T->rchild);
scanf("%d",&a);
bt=BThead(a,null,null); /*建立二叉树根结点*/
bttree(bt);
/*建立二叉树的各个结点*/
goto start;
/*返回主菜单*/
}
cif(bt==null)
{
printf(" **************************************\n"); printf(" 二叉树不存在,请重新建立二叉树。 \n");
中序遍历线索化二叉树算法的设计与实现实验报告参考模板

数学与计算科学学院实验报告实验项目名称中序遍历线索化二叉树算法的设计与实现所属课程名称数据结构A实验类型设计型实验日期2014.11.26班级信计1302班学号201353100216姓名危志鹏成绩一、实验概述:【实验目的】1.掌握二叉链表及线索二叉链表的特点及基本运算。
【实验原理】//-----二叉树的二叉线索存储表示-----Typedef enum PointerTag{Link,Thread};Typedef struct BiThrNode{TElemType data;Struct BiThrNode *lchild, *rchild;PointerTag LTag,RTag;}BiThrNode, *BiThrTree;【实验环境】VC++ 6.0二、实验内容:【实验方案】在VC++环境下,编写二叉树的线索链表存储结构,中序遍历二叉线索树T的非递归算法,以及将二叉树T的中序线索化算法,对每个数据元素均调用函数Visit。
最后设计主函数,调用以上算法,验证算法的正确性,调试运行,得出结果。
【实验过程】(实验步骤、记录、数据、分析)1.运行VC++ 6.0,建立新的命令文件;2.将程序输入,如下,发现一个错误。
3.经过查找,发现一个错误,然后改正如下4.然后进行调试,发现调试出错。
【实验结论】(结果)【实验小结】(收获体会)这次实验又出现了和上次一样的错误:程序无错误,但结果不能运行。
经过多次的检查终于解决了问题,相信这样的错误不会再有第三次了。
三、指导教师评语及成绩:评语评语等级优良中及不及格附录1:源程序友情提示:范文可能无法思考和涵盖全面,供参考!最好找专业人士起草或审核后使用,感谢您的下载!。
线索二叉树的实现

线索⼆叉树的实现数据结构课程设计设计说明书线索⼆叉树的实现学⽣姓名学号班级成绩指导教师曹记东计算机科学与技术系2010年9⽉10⽇数据结构课程设计评阅书题⽬线索⼆叉树的实现学⽣姓名学号指导教师评语及成绩指导教师签名:年⽉⽇答辩评语及成绩答辩教师签名:年⽉⽇教研室意见总成绩:室主任签名:年⽉⽇课程设计任务书2010—2011学年第1学期专业:计算机科学与技术学号:姓名:课程设计名称:数据结构课程设计设计题⽬:线索⼆叉树的实现完成期限:⾃2010 年8 ⽉30 ⽇⾄2010 年9 ⽉10 ⽇共 2 周设计内容:n个结点的⼆叉链表中含有n+1个空指针域。
利⽤⼆叉链表中的空指针域,存放指向结点在某种遍历次序下的前趋和后继结点的指针(这种附加的指针称为"线索")。
这种加上了线索的⼆叉树称为线索⼆叉树(Threaded BinaryTree)。
对⼀棵⾮线索⼆叉运⽤VC++编写⼀个程序实现前序线索⼆叉树、中序线索⼆叉树和后序线索⼆叉树,其中遍历要求⽤先左后右的递归或⾮递归算法来实现。
要求:1)阐述设计思想,画出流程图;2)任意建⽴⼀棵⼆叉树,采⽤前序、中序、后序三种⽅法线索化⼆叉树;3)说明测试⽅法,写出完整的运⾏结果;4)从时间、空间对算法分析;5)较好的界⾯设计;6)编写课程设计报告。
以上要求中第⼀个阶段的任务完成后,先将设计说明书的草稿交指导⽼师⾯审,审查合格后⽅可进⼊后续阶段的⼯作。
设计⼯作结束后,经指导⽼师验收合格后将设计说明书打印装订,并进⾏答辩。
指导教师(签字):教研室主任(签字):批准⽇期:年⽉⽇摘要设计了⼀个对线索⼆叉树实现遍历的软件,该软件可以实现对线索⼆叉树分别进⾏先序遍历、中序遍历、后序遍历。
这种遍历⽅法是以线索为根本,利⽤该软件,⽤户可以⽅便的查找树中任意结点的前驱和后继,给⽤户带来了⽅便。
该软件采⽤了VC6.0作为软件开发环境,实现对线索⼆叉树的遍历。
操作简单,界⾯清晰,易于⽤户接受。
二叉排序树问题说明书

摘要二叉排序树又称二叉查找树,亦称二叉搜索树。
它或者是一棵空树;或者是具有下列性质的二叉树:若左子树不空,则左子树上所有结点的值均小于它的根结点的值;若右子树不空,则右子树上所有结点的值均大于它的根结点的值;左、右子树也分别为二叉排序树;本次课程设计,程序中的数据采用“二叉树结构”。
具体采用的是“二叉排序树”,并且使用“二叉链表”作为其存储结构。
运用链表所特有的动态开辟分配删除内存的特点,可以完成结点动态建立,形成一棵排序树。
再通过链表中结点之间的连接,进行相应的操作,如算平均查找长度等。
但是在使用链表的指针对数据进行操作中,首位结点的妥善处理是很细微的,也是很关键与相对烦琐的,对与链表的头结点的使用一般避免不了,但是我们在链表的循环中可以通过链表中结点数来控制开始与停止,这样可以避免链表尾结点next带来的不便。
这样便要求我们每时每刻都要得到链表中结点数的准确值,对于这我们可以通过全局变量来解决。
本课程设计实现了二叉排序树的创建、查找、插入、删除,中序遍历输出等基本操作,完美地实现了二叉排序树的大部分功能。
关键词:二叉链表;二叉排序树;插入结点;中序遍历输出AbstractTwo binary sort tree also known as two binary search tree, also known as two binary search tree. It is either a hollow tree; or has the following properties of the two fork tree: if the left sub tree is not empty, then the left sub tree of all node values are less than the root node of its value; if the right subtree is not empty, then the right subtree all node values are greater than the root node of it value; left, right subtree is respectively two binary sort tree; the curriculum design, process data using the "two tree structure". Specific uses is "two binary sort tree", and "two binary list" as its storage structure.The use of dynamic linked list open characteristic distribution delete memory, can complete the dynamic node set, forming a sort of tree. Then the connection between the linked list node through, corresponding to the operation, such as the average search length.But in using pointer linked list for data operation, properly handle the first node is very slight, but also very critical and relatively cumbersome to use, and list the first node generally cannot avoid, but we are in the list of the cycle can start and stop node number in the list, so that you can avoid list tail node next inconvenience. This will require us to obtain the accurate value of every node in the linked list number, for which we can solve the global variables.This course is designed to achieve the two binary sort tree to create, find, insert, delete, traversal of output and other basic operations, the perfect realization of the most functional two binary sort tree.Key words:The data structure of binary tree; two binary sort tree; insert node traversal output目录1 概述 (1)1.1题目内容 (1)1.2设计要求及目的 (2)2 概要设计 (3)3 详细设计 (5)3.1 主函数流程图 (5)3.2 创建二叉排序树模块流程图 (8)3.3 查找并删除结点模块流程图 (13)3.4 二叉树遍历模块流程图 (15)3.5 插入结点模块流程图 (16)3.6 判断是否为平衡二叉树模块流程图 (18)4调试分析 (17)4.1调试结果 (17)4.1.1 主界面 (17)4.1.2 创建二叉排序树界面 (18)4.1.3 输出排序树界面 (18)4.1.4 查找并删除结点界面 (19)4.1.5 二叉树遍历界面 (19)4.1.6 插入结点界面 (23)4.1.7 判断是否为平衡二叉树界面 (23)5 总结 (24)参考文献 (25)致谢 (23)1 概述1.1题目内容数据结构是一门理论性强、思维抽象、难度较大的课程,是基础课和专业课之间的桥梁。
(完整word版)线索二叉树课程设计说明书格式

中北大学课程设计说明书学院、系:软件学院专业:软件工程班级:15140X04学生姓名:张航学号:1514040423设计题目:线索二叉树的应用起迄日期:2016年12月16日~2016年12月29日指导教师:付东来日期: 2016年12月29日1 设计目的《数据结构》课程主要介绍最常用的数据结构,阐明各种数据结构内在的逻辑关系,讨论其在计算机中的存储表示,以及在其上进行各种运算时的实现算法,并对算法的效率进行简单的分析和讨论.进行数据结构课程设计要达到以下目的:⏹了解并掌握数据结构与算法的设计方法,具备初步的独立分析和设计能力;⏹初步掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能;⏹提高综合运用所学的理论知识和方法独立分析和解决问题的能力;训练用系统的观点和软件开发一般规范进行软件开发,培养软件工作者所应具备的科学的工作方法和作风。
2 任务概述设计内容:(1)建立线索二叉树,实现插入、删除操作。
(2)线索二叉树的遍历(本程序中使用中序遍历方法)设计要求:实现线索树建立、插入、删除、恢复线索任务分析:该任务是关于线索二叉树的运算,其中的基本运算应基于二叉树,但又有所不同,首先应了解问题有:(1)线索二叉树如何建立:是通过二叉树来实现线索化,还是直接进行线索化的输入。
若由二叉树建立而来,该二叉树应如何输入,对具体的二叉树应该使初次使用者明白使用的格式。
(2)该程序重点内容是有关二叉树的插入、删除和查找前驱后继,在进行具体操作时,该如何实现查找到相应结点,线索应该如何改变才能不破坏线索二叉树的结构。
重点在于插入删除是分清楚插入删除位置的双亲结点与被插入删除的结点的孩子关系.3 模块划分(1)定义数据结构模块:typedef struct BiThrNode{ElemType data;struct BiThrNode *lchild,*rchild;int LTag,RTag;}BiThrNode,*BiThrTree;(2)功能函数:二叉树的建立函数:void CreateBiTree(BiThrTree &T)询二叉树深度函数:int Depth(BiThrTree T)带头结点的二叉树中序线索化函数:void InOrderThreading(BiThrTree &Thrt,BiThrTree T)以结点T为根的子树中序线索化:void InThreading(BiThrTree &T)中序遍历函数:void InOrderTraverse_Thr(BiThrTree Thrt)查找某结点函数:BiThrTree Search(BiThrTree T,ElemType key)查找某结点函数:BiThrTree SearchPre(BiThrTree point,BiThrTree child)插入函数:Status InsertTree(BiThrTree T)删除函数:Status DeleteTree(BiThrTree T)主函数:main()整体结构图:4 主要函数说明及其N—S图4.1详细设计思想建立二叉树(即指在内存中建立二叉树的存储结构),建立一个二叉链表,需按某种顺序一次输入二叉树中的结点,且输入顺序必须隐含结点间的逻辑结构信息。
线索二叉树课程设计说明书格式

中北大学课程设计说明书学院、系:软件学院专业:软件工程班级:15140X04学生姓名:张航学号:1514040423 设计题目:线索二叉树的应用起迄日期: 2016年12月16日~2016年12月29日指导教师:付东来日期: 2016年12月29日1 设计目的《数据结构》课程主要介绍最常用的数据结构,阐明各种数据结构内在的逻辑关系,讨论其在计算机中的存储表示,以及在其上进行各种运算时的实现算法,并对算法的效率进行简单的分析和讨论。
进行数据结构课程设计要达到以下目的:⏹了解并掌握数据结构与算法的设计方法,具备初步的独立分析和设计能力;⏹初步掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能;⏹提高综合运用所学的理论知识和方法独立分析和解决问题的能力;训练用系统的观点和软件开发一般规范进行软件开发,培养软件工作者所应具备的科学的工作方法和作风。
2 任务概述设计内容:(1)建立线索二叉树,实现插入、删除操作。
(2)线索二叉树的遍历(本程序中使用中序遍历方法)设计要求:实现线索树建立、插入、删除、恢复线索任务分析:该任务是关于线索二叉树的运算,其中的基本运算应基于二叉树,但又有所不同,首先应了解问题有:(1)线索二叉树如何建立:是通过二叉树来实现线索化,还是直接进行线索化的输入。
若由二叉树建立而来,该二叉树应如何输入,对具体的二叉树应该使初次使用者明白使用的格式。
(2)该程序重点内容是有关二叉树的插入、删除和查找前驱后继,在进行具体操作时,该如何实现查找到相应结点,线索应该如何改变才能不破坏线索二叉树的结构。
重点在于插入删除是分清楚插入删除位置的双亲结点与被插入删除的结点的孩子关系。
3 模块划分(1)定义数据结构模块:typedef struct BiThrNode{ElemType data;struct BiThrNode *lchild,*rchild;int LTag,RTag;}BiThrNode,*BiThrTree;(2)功能函数:二叉树的建立函数:void CreateBiTree(BiThrTree &T)询二叉树深度函数:int Depth(BiThrTree T)带头结点的二叉树中序线索化函数:void InOrderThreading(BiThrTree &Thrt,BiThrTree T) 以结点T为根的子树中序线索化:void InThreading(BiThrTree &T)中序遍历函数:void InOrderTraverse_Thr(BiThrTree Thrt)查找某结点函数:BiThrTree Search(BiThrTree T,ElemType key)查找某结点函数:BiThrTree SearchPre(BiThrTree point,BiThrTree child)插入函数:Status InsertTree(BiThrTree T)删除函数:Status DeleteTree(BiThrTree T)主函数:main()整体结构图:4 主要函数说明及其N-S图4.1详细设计思想建立二叉树(即指在内存中建立二叉树的存储结构),建立一个二叉链表,需按某种顺序一次输入二叉树中的结点,且输入顺序必须隐含结点间的逻辑结构信息。
二叉排序树的操作课程设计报告

然后返回主菜单。 BSTree *SearchKey(root,key) 初始条件:二叉排序树不为空,存在根节点; 操作结果:输入一个字符型数据,先寻找二叉排序树中是否有此数 据的,有则返回次数据项的地址给指针变量,没有则就返回该数据按照 二叉排序树规则,应该插入位置的父节点地址。 void DeleteKey(root,key); 初始条件:二叉排序树不为空,存在根节点; 操作结果:输入一个字符型数据,调用BSTree *SearchKey(root,key)函数,先寻找二叉排序树中是否有此数据的,有 则返回次数据项的地址给指针变量,然后就此节点的特征分为四类:删 除叶子节点;删除只有右孩子的节点;删除只有左孩子的节点;删除左 右孩子都有的节点,根据结点类型进入不同删除模块,删除结点,修改 相应二叉树结点指针,返回主菜单;没有则就返回提示语句“没有找到 该数据”。 void ChainTree_LDR(root) 初始条件:二叉排序树不为空,存在根节点; 操作结果:按照中序遍历并输出有序的数据序列。 } ADT BT
.4 功能需求
创建二叉排序树 输出二叉排序树 在二叉排序树中查找给定值 在二叉排序树中插入新结点 在二叉排序树中删除给定值 并设计主函数测试该类(或类模板)。
.5 任务计划
主程序流程图 算法:主程序主要用运了switch结构,使得主程序更加方便的调用成员 函数,各个成员函数间的关系也清晰明了。
输入与功能相对应的序号 执行功能 是否存在 开始 结束
.2 添加模块设计
if(root==NULL) { cout<<"空树!!!禁止操作!!!"; cout<<endl; } else{ cout<<"请输入你要添加的结点数目:"; cin>>n; fflush(stdin); for(i=0;i<n;i++) { cout<<"请输入你要添加的结点数据:"; cin>>key; a.Inserter(root,key); fflush(stdin); } }
二叉搜索树课程设计

二叉搜索树课程设计一、课程目标知识目标:1. 学生能理解二叉搜索树的定义、性质和基本操作。
2. 学生能掌握二叉搜索树的插入、删除和查找算法。
3. 学生能了解二叉搜索树的中序遍历、前序遍历和后序遍历算法。
技能目标:1. 学生能运用所学知识,实现二叉搜索树的构建和操作。
2. 学生能通过编程实践,解决与二叉搜索树相关的问题。
3. 学生能分析二叉搜索树在实际应用中的优缺点,并进行优化。
情感态度价值观目标:1. 学生培养对数据结构和算法的兴趣,增强计算机科学素养。
2. 学生培养团队协作意识,学会与他人共同解决问题。
3. 学生通过学习二叉搜索树,认识到数据结构在实际应用中的重要性,激发学习动力。
课程性质:本课程为计算机科学领域的数据结构与算法课程,以二叉搜索树为研究对象,结合编程实践,提高学生的数据分析和问题解决能力。
学生特点:学生已具备基本的编程能力,对数据结构有一定了解,但可能对二叉搜索树的具体应用和实现细节掌握不足。
教学要求:注重理论与实践相结合,通过讲解、示例、编程实践等环节,使学生掌握二叉搜索树的相关知识,提高编程能力。
同时,关注学生的情感态度价值观培养,激发学习兴趣。
在教学过程中,将课程目标分解为具体的学习成果,便于教学设计和评估。
二、教学内容1. 二叉搜索树的定义及性质- 理解二叉搜索树的定义- 掌握二叉搜索树的性质:左子树所有节点小于根节点,右子树所有节点大于根节点2. 二叉搜索树的插入、删除和查找操作- 学习插入算法,包括递归和非递归实现- 学习删除算法,包括三种情况的处理:删除叶子节点、删除只有一个子节点的节点、删除有两个子节点的节点- 学习查找算法,掌握如何在二叉搜索树中查找特定值3. 二叉搜索树的遍历算法- 学习中序遍历、前序遍历和后序遍历的原理及实现- 分析遍历算法在实际应用中的用途4. 二叉搜索树的应用及优化- 探讨二叉搜索树在实际编程中的应用场景- 分析二叉搜索树的性能,了解平衡二叉搜索树的概念及优势5. 编程实践- 结合教材,完成二叉搜索树的构建、插入、删除、查找等操作的编程实践- 实现二叉搜索树的中序、前序、后序遍历算法- 分析编程实践中遇到的问题,进行优化和改进教学内容安排和进度:第一课时:二叉搜索树的定义及性质,插入算法第二课时:删除算法,查找算法第三课时:遍历算法,应用及优化第四课时:编程实践与讨论教材章节关联:《数据结构与算法分析》第四章:二叉树《算法导论》第三章:二叉树和红黑树三、教学方法1. 讲授法:- 采用引导式讲授,通过问题驱动的形式,激发学生对二叉搜索树知识的探究欲望。
二叉树的课程设计
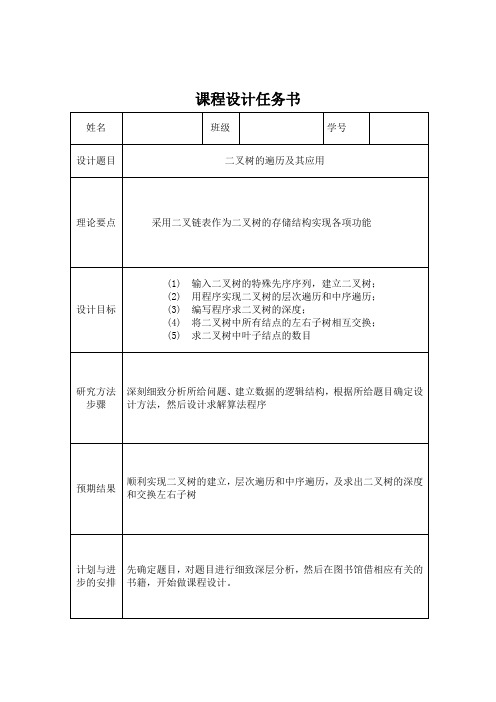
课程设计任务书摘要针对现实世界中许多关系复杂的数据,如人类社会的家谱,各种社会组织机构,博弈交通等复杂事物或过程以及客观世界中广泛存在的具有分支关系或层次特性的对象.如操作系统的文件构成、人工智能和算法分析的模型表示以及数据库系统的信息组织形式等,用线性结构难以把其中的逻辑关系表达出来,必须借助于数和图这样的非线性结构,因此在以模拟客观世界问题,解决客观世界问题为主要任务的计算机领域中树型结构是信息的一种重要组织形式,树有着广泛应用。
在树型结构的应用中又以二叉树最为常用。
二叉树是一种非常重要的非线性结构,所描述的数据有明显的层次关系,其中的每个元素只有一个前驱,二叉树是最为常用的数据结构,它的实际应用非常广泛,二叉树的遍历方式有三种,前序遍历,中序遍历,后序遍历,先序遍历的顺序为:NLR先根结点,然后左子树,右子树;中序遍历顺序为;LNR先左子树,然后根结点,右子树;后序遍历顺序为:LRN先左子树,然后右子树,根结点。
由前序和中序遍历,有中序和后序遍历序列可以唯一确定一棵二叉树对于给几个数据的排序或在已知的几个数据中进行查找,二叉树均能提供一种十分有效的方法,比如在查找问题上,任何借助于比较法查找长度为Ⅳ的一个序表的算法,都可以表示成一株二叉树。
反之,任何二叉树都对应一个查找有序表的有效方法根据树的数学理论,对于算法分析的某些最有启发性的应用,是与给出用于计算各种类型中不同树的数目的公式有关的。
本文对二叉树以及二叉树的各种功能做介绍以及写出一些基本的程序,让读者对二叉树的理解有更好的效果。
关键词:二叉树,左子树,右子树,二叉树的遍历,二叉树的深度等目录摘要 (I)1 课程设计题目及题目基本理论 (1)2 概要设计 (1)3 详细设计 (2)3.1 建立二叉树 (2)3.2二叉树的层次遍历和中序遍历 (2)3.3 求二叉树的深度 (3)3.4将二叉树中所有结点的左右子树相互交换 (4)3.5求二叉树中叶子结点的数目 (5)4 调试分析 (7)5 用户使用说明 (8)6 结论 (9)7 参考文献 (10)二叉树的遍历及其应用基本理论(1)建立二叉树的操作就是用递归算法以先序遍历的次序从根结点开始建立一棵二叉树,(2)利用栈的非递归算法对二叉树进行遍历,从二叉树的根结点开始,自顶向下,同层自左往右访问树中的每个结点,此时,保存结点的顺序和访问的顺序刚好一致(3)用递归算法求出左右子树的深度1 需求分析(1)输入二叉树的特殊先序序列,建立二叉树;(2)实现二叉树的层次遍历和中序遍历;(3)求二叉树的深度;(4)将二叉树中所有结点的左右子树相互交换;(5)求二叉树中叶子结点的数目2 概要设计CreatBinTree(&T):建立一棵二叉树,Value(T,e):查找值为e的二叉树结点,并返回该结点的地址。
线索二叉树课程设计

#include<iostream.h>#include <stdio.h>#include <stdlib.h>typedef struct node {char data;struct node *lchild,*rchild;//}BiTNode,*BiTree;void CreatBiTree(BiTree &T){char ch;ch=getchar();if (ch == ' ')T = 0;else {T=(BiTNode*)malloc(sizeof(BiTNode)); T->data=ch;//生成根节点CreatBiTree(T->lchild);//构造左子树CreatBiTree(T->rchild);//构造右子树}}void preorder(BiTree T)//前序遍历{if (T!=NULL){printf ("%c",T->data);preorder(T->lchild);preorder(T->rchild);}}void inorder(BiTree T)//中序遍历{if (T!=NULL){inorder(T->lchild);printf ("%c",T->data);inorder(T->rchild);}}void postorder(BiTree T)//后序遍历{if (T!=NULL){postorder(T->lchild);postorder(T->rchild);printf ("%c",T->data);}}void main (){cout<<"请输入要创建的二叉树包括空格:"<<endl ; BiTree T;CreatBiTree(T);//创建二叉树cout<<"前序遍历的结果为:"<<endl;preorder(T);cout<<endl;cout<<"中序遍历的结果为:"<<endl;inorder(T);cout<<endl;cout<<"后序遍历的结果为:"<<endl;postorder(T);}。
数据结构课程设计-二叉树

《数据结构》课程设计说明书二叉平衡树算法实现班级组别:二指导老师:完成时间:2019.6.19 组长:学号:05 组员1:学号:33 组员2:学号:组员3:学号:成绩:目录目录一、课题设计任务 (2)二、任务分析 (2)1. 数据逻辑结构(算法描述) (2)2. 关键算法思想 (3)三、概要设计(总体设计) (3)四、详细设计 (4)1. 数据存储结构 (4)2. 各模块流程图及算法 (5)3. 算法效率分析 (9)五、测试 (10)1. 删除 (10)2. 查找 (10)3. 遍历 (10)六、课程设计心得 (10)七、参考文献 (11)八、附录 (11)一、课题设计任务针对给定的序列建立存储结构,实现各种遍历;实现树的生成,实现数据的查找、插入、删除,输出各种遍历。
二、任务分析1.数据逻辑结构(算法描述)//中序--递归void InorderTra(PNode root) {if (root) {InorderTra(root->leftChild); //中序遍历左子树printf("%d\t", root->keyValue); //访问根节点InorderTra(root->rightChild); //中序遍历右子数}}//前序--递归void PreOrderTra(PNode root) {if (root != NULL) {printf("%d\t", root->keyValue); //访问根节点PreOrderTra(root->leftChild); //前序遍历左子树PreOrderTra(root->rightChild); //前序遍历右子数}}//后序--递归void PostOrderTra(PNode root) {if (root) {PostOrderTra(root->leftChild); //后序遍历左子树PostOrderTra(root->rightChild); //后序遍历右子树printf("%d\t", root->keyValue); //访问根节点}}//求树的最大深度int getDeep(PNode root) {if (!root) {return 0;}int leftDeep = getDeep(root->leftChild) + 1;int rightDeep = getDeep(root->rightChild) + 1;return leftDeep > rightDeep ? leftDeep : rightDeep;}//从根节点开始打印出所有层void printByLevel(PNode root, int deep) {for (int i = 0; i < deep; i++) {LevelOrderTra(root, i);}printf("\n");}2.关键算法思想树的生成过程保持左右平衡,插入删除过程中保证树的平衡。
线索二叉树实验

实验名称:线索二叉树一、实验目的和要求∶(1)掌握线索二叉树的有关知识。
(2)掌握求解线索二叉树中结点前趋和后继的算法以及以相应次序遍历线索二叉树的算法。
(3)掌握二叉树的线索化算法的设计。
二、实验环境和仪器设备∶Windows xp/Ubuntu VC++6.0三、实验任务∶<1>按先序次序遍历先序线索二叉树。
<2>按中序次序遍历中序线索二叉树。
<3>将值为x的结点作为先序线索二叉树T的左子树的(先序)最后一个结点的右孩子插入进去。
<4>按中序次序线索化二叉树。
<5>按后序次序线索化二叉树。
四、实验内容(步骤)∶<1>设计二叉树的数据结构,并根据数据结构设计算法实现。
<2>编写源代码<3>上机调试<4>总结五、实验程序#include <iostream>#include <fstream>using namespace std;enum Thread{notThreaded,preThreaded,midThreaded,postThreaded };template <class Element_type>struct BiThrNode{Element_type data;BiThrNode * lchild , * rchild;bool ltag , rtag;};template <class Element_type>class BiThrTree{public: BiThrTree ();BiThrTree (const char * filename); //根据文件构造二叉树~BiThrTree (); //析构函数void Build( const char * filename); //根据文件创建二叉树void PreOrder () ; //先序遍历二叉树void MidOrder () ; //中序遍历二叉树void PostOrder () ; //后序遍历二叉树BiThrNode <Element_type> * PreSuc ( BiThrNode <Element_type> * node ) const; //先序后继BiThrNode <Element_type> * MidSuc ( BiThrNode <Element_type> * node ) const; //中序后继BiThrNode <Element_type> * PostUsher( BiThrNode <Element_type> * node ) const; //后序前驱void PostPrint(); //输出后序遍历二叉树void PostPrint( BiThrNode <Element_type> * node);void PreThread (); //先序线索化void PreThread ( BiThrNode <Element_type> * node );void MidThread (); //中序线索化void MidThread (BiThrNode <Element_type> * node );void PostThread (); //后序线索化void PostThread (BiThrNode <Element_type> * node);void InsertAtL ( Element_type data); //插入为左子树先序最后一个结点的右孩子void Clear (); //删除二叉树void Clear ( BiThrNode <Element_type> * node);void Visit (BiThrNode <Element_type> * node ); //访问结点private:void CreatNode( BiThrNode <Element_type> * node);BiThrNode <Element_type> * root;ifstream file;Thread status;BiThrNode <Element_type> * pre;};template <class Element_type>BiThrTree<Element_type> :: BiThrTree(){root=NULL;status=notThreaded;}template <class Element_type>BiThrTree<Element_type> :: BiThrTree( const char * filename ){root=NULL;Build(filename);}template <class Element_type>BiThrTree<Element_type> :: ~BiThrTree (){Clear();root=NULL;}template <class Element_type>void BiThrTree <Element_type> :: Build ( const char * filename ){ if(root!=NULL)Clear();Element_type data;char tree[40];int child;file.open( filename );file>>tree>>child;if( child == 0 ){file>>data;root=new BiThrNode <Element_type> ;root->data=data;root->lchild=NULL;root->rchild=NULL;root->ltag=false;root->rtag=false;CreatNode(root);}else root=NULL;status=notThreaded;}template <class Element_type>void BiThrTree <Element_type> :: PreOrder () {if(status==notThreaded)PreThread();BiThrNode <Element_type> * te=root;while ( te!=NULL ){Visit (te) ;te=PreSuc (te);}}template <class Element_type>void BiThrTree <Element_type> :: MidOrder () {if(status==notThreaded)MidThread();BiThrNode <Element_type> * te=root;if (te==NULL)return ;while( te->lchild !=NULL )te=te->lchild;while ( te!=NULL ){Visit (te) ;te=MidSuc (te);}}template <class Element_type>void BiThrTree<Element_type>::PostOrder (){if (status==notThreaded){PostThread();PostPrint();}}template <class Element_type>BiThrNode <Element_type> * BiThrTree <Element_type> :: PreSuc ( BiThrNode <Element_type> * node ) const{if (!node->ltag)return node ->lchild;else return node ->rchild;}template <class Element_type>BiThrNode <Element_type> * BiThrTree <Element_type> :: MidSuc ( BiThrNode <Element_type> * node ) const{if( node->rtag )return node->rchild;BiThrNode <Element_type> * te=node->rchild;if (te==NULL)return te;while (!te->ltag )te=te->lchild;return te;}template <class Element_type>BiThrNode <Element_type> * BiThrTree <Element_type> :: PostUsher( BiThrNode <Element_type> * node ) const{if (!node->rtag)return node->rchild;elsereturn node->lchild;}template <class Element_type>void BiThrTree <Element_type> :: PostPrint(){PostPrint(root);}template <class Element_type>void BiThrTree <Element_type> :: PostPrint( BiThrNode <Element_type> * node){ if (node==NULL)return;PostPrint (PostUsher(node));cout<<node->data<<" ";}template <class Element_type>void BiThrTree <Element_type> :: PreThread (){if( status==notThreaded){pre=NULL;if ( root!=NULL)PreThread ( root );pre=NULL;status=preThreaded;}}template <class Element_type>void BiThrTree <Element_type> :: PreThread ( BiThrNode <Element_type> * node ){ if (node==NULL)return;BiThrNode <Element_type> * te=pre;pre=node;PreThread( node->lchild );PreThread( node->rchild );if (node->lchild==NULL){node->ltag=true;node->lchild=te;}if (te!=NULL&&te->rchild==NULL){te->rtag=true;te->rchild=node;}}template <class Element_type>void BiThrTree <Element_type> :: MidThread (){if (status==notThreaded){BiThrNode <Element_type> * te;te=root;pre=NULL;if (te==NULL)return ;MidThread(te);pre=NULL;status=midThreaded;}else cout<<"this tree is threaded/n";}template <class Element_type>void BiThrTree <Element_type> :: MidThread (BiThrNode <Element_type> * node){ if (node==NULL)return;MidThread( node->lchild );BiThrNode <Element_type> * te=pre;pre=node;if (node->lchild==NULL){node->ltag=true;node->lchild=te;}if (te!=NULL&&te->rchild==NULL){te->rtag=true;te->rchild=node;}MidThread( node->rchild );}template <class Element_type>void BiThrTree <Element_type> :: PostThread (){if( status==notThreaded){BiThrNode <Element_type> * te=root;pre=NULL;if ( te==NULL )return ;/* while( te->lchild!=NULL ){te=te->lchild;}*/PostThread (te);pre=NULL;status=postThreaded;}}template <class Element_type>void BiThrTree <Element_type> :: PostThread (BiThrNode <Element_type> * node){ if ( node==NULL )return ;PostThread ( node->lchild );PostThread ( node->rchild );node->ltag=true;node->lchild=pre;}if( pre!=NULL && pre->rchild == NULL){pre->rtag=true;pre->rchild=node;}pre=node;}template <class Element_type>void BiThrTree <Element_type> :: InsertAtL ( Element_type data ){ BiThrNode <Element_type> * node=new BiThrNode <Element_type>;BiThrNode <Element_type> * end , *te, *pre;node->data=data;node->lchild=NULL;node->rchild=NULL;node->ltag=false;node->rtag=false;if (root->rtag)end=NULL;else end=root->rchild;pre=root;te=PreSuc(pre);while (te!=end){pre=te;te=PreSuc(te);}pre->rtag=false;pre->rchild=node;node->ltag=true;node->lchild=pre;node->rtag=true;node->rchild=end;}template <class Element_type>void BiThrTree <Element_type> :: Clear (){if( status==notThreaded){Clear(root);root=NULL;}else{BiThrNode <Element_type> * node, *te;node=root;te=node;switch ( status ){case preThreaded:node=PreSuc(node);break;case midThreaded:node=MidSuc(node);break;case postThreaded:node=PostUsher(node);break;default:return;}delete (te);}}}template <class Element_type>void BiThrTree <Element_type> :: Clear ( BiThrNode <Element_type> * node){ if ( node == NULL)return ;Clear ( node->lchild);node->lchild=NULL;Clear ( node->rchild);node->rchild =NULL;delete node;}template <class Element_type>void BiThrTree <Element_type> :: Visit (BiThrNode <Element_type> * node ){ cout<< node->data<<" ";}template <class Element_type>void BiThrTree <Element_type> :: CreatNode( BiThrNode <Element_type> * node){ Element_type data;int lchild,rchild;BiThrNode <Element_type> * te;file>>lchild>>rchild;if(lchild==0){file>>data;node->lchild=new BiThrNode <Element_type> ;te=node->lchild;te->data=data;te->lchild=NULL;te->rchild=NULL;te->ltag=false;te->rtag=false;CreatNode(te);}if(rchild==0){file>>data;node->rchild=new BiThrNode <Element_type> ;te=node->rchild;te->data=data;te->lchild=NULL;te->rchild=NULL;te->ltag=false;te->rtag=false;CreatNode(te);}}void part1( const char * file){cout<<"树"<<file<<"\n";BiThrTree <char > tree(file);cout<<"树的先序遍历:\n";tree.PreOrder();cout<<"\n\n";}void part2( const char * file){cout<<"树"<<file<<"\n";BiThrTree <char > tree(file);cout<<"树的中序遍历:\n";tree.MidOrder();cout<<"\n\n";}void part3( const char * file){cout<<"树"<<file<<"\n";BiThrTree <char > tree(file);cout<<"树的后序遍历:\n";tree.PostOrder();cout<<"\n\n";}void part4( const char * file){cout<<"树"<<file<<"\n";BiThrTree <char > tree(file);cout<<"先序遍历最初的树\n";tree.PreOrder();cout<<endl;cout<<"插入结点X:\n";tree.InsertAtL('X');cout<<"结果(先序遍历):\n";tree.PreOrder();cout<<"\n\n";}int main (){part1("FULL41.CBT");part1("LETTER.CBT");cout<<"\n\n";part2("FULL41.CBT");part2("LETTER.CBT");cout<<"\n\n";part3("FULL41.CBT");part3("LETTER.CBT");cout<<"\n\n";part4("FULL41.CBT");part4("LETTER.CBT");cout<<"\n\n";system("pause");return 0;}六、完整的实验结果记录∶(为了方便,将此次试验重新分为四个部分)<1>先序线索化二叉树,再先序遍历二叉树预期结果:Full41.cbt:ABCDEFGHIJKLMNLetter.cbt:abcdefghijklmnopqrstuvwxyz<2>中序线索化二叉树,再中序遍历二叉树预期结果:FULL41.CBT:DCEBGFHAKJLINMO LETTER.CBT:dfgeihjclkmbonpartsuqwxvyz<3>后序线索化二叉树,再后序遍历二叉树预期结果:FULL41.CBT:DECGHFBKLJNOMLETTER.CBT:gfijhedlmkcopnbtusrxwzyvqa<4>将值为x的结点作为先序线索二叉树T的左子树的(先序)最后一个结点的右孩子插入进去。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中北大学课程设计说明书学院、系:软件学院专业:软件工程班级:15140X04学生姓名:航学号:1514040423 设计题目:线索二叉树的应用起迄日期: 2016年12月16日~2016年12月29日指导教师:付东来日期: 2016年12月29日1 设计目的《数据结构》课程主要介绍最常用的数据结构,阐明各种数据结构在的逻辑关系,讨论其在计算机中的存储表示,以及在其上进行各种运算时的实现算法,并对算法的效率进行简单的分析和讨论。
进行数据结构课程设计要达到以下目的:⏹了解并掌握数据结构与算法的设计方法,具备初步的独立分析和设计能力;⏹初步掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能;⏹提高综合运用所学的理论知识和方法独立分析和解决问题的能力;训练用系统的观点和软件开发一般规进行软件开发,培养软件工作者所应具备的科学的工作方法和作风。
2 任务概述设计容:(1)建立线索二叉树,实现插入、删除操作。
(2)线索二叉树的遍历(本程序中使用中序遍历方法)设计要求:实现线索树建立、插入、删除、恢复线索任务分析:该任务是关于线索二叉树的运算,其中的基本运算应基于二叉树,但又有所不同,首先应了解问题有:(1)线索二叉树如何建立:是通过二叉树来实现线索化,还是直接进行线索化的输入。
若由二叉树建立而来,该二叉树应如何输入,对具体的二叉树应该使初次使用者明白使用的格式。
(2)该程序重点容是有关二叉树的插入、删除和查找前驱后继,在进行具体操作时,该如何实现查找到相应结点,线索应该如何改变才能不破坏线索二叉树的结构。
重点在于插入删除是分清楚插入删除位置的双亲结点与被插入删除的结点的孩子关系。
3 模块划分(1)定义数据结构模块:typedef struct BiThrNode{ElemType data;struct BiThrNode *lchild,*rchild;int LTag,RTag;}BiThrNode,*BiThrTree;(2)功能函数:二叉树的建立函数:void CreateBiTree(BiThrTree &T)询二叉树深度函数:int Depth(BiThrTree T)带头结点的二叉树中序线索化函数:void InOrderThreading(BiThrTree &Thrt,BiThrTree T)以结点T为根的子树中序线索化:void InThreading(BiThrTree &T)中序遍历函数:void InOrderTraverse_Thr(BiThrTree Thrt)查找某结点函数:BiThrTree Search(BiThrTree T,ElemType key)查找某结点函数:BiThrTree SearchPre(BiThrTree point,BiThrTree child)插入函数:Status InsertTree(BiThrTree T)删除函数:Status DeleteTree(BiThrTree T)主函数:main()整体结构图:4 主要函数说明及其N-S图4.1详细设计思想建立二叉树(即指在存中建立二叉树的存储结构),建立一个二叉链表,需按某种顺序一次输入二叉树中的结点,且输入顺序必须隐含结点间的逻辑结构信息。
对于一般的二叉树,需添加虚结点,使其成为完全二叉树。
二叉树的中序线索化算法与中序遍历算法类似。
只需要将遍历算法中访问结点的操作具体化为建立正在访问的结点与其非空中序前趋结点间线索。
该算法应附设一个指针pre始终指向刚刚访问过的结点(pre的初值应为NULL),而指针p指示当前正在访问的结点。
结点*pre是结点*p的前趋,而*p是*pre的后继。
结点插入算法:由线索二叉树的定义易知插入的节点定是个叶子节点,需注意线索的修改,可分为两种情况:(1):插入的节点t是右儿子,t的中序后继是其父亲的中序后继,中序前驱是其父亲。
(2):插入的节点t是左儿子,t的中序前驱是其父亲的中序前驱,中序后继是其父亲。
结点删除算法:删除的情况与搜索二叉树的删除的类似(1):删除的节点p是叶子节点,直接删除,修改其父亲的线索。
(2):删除的节点p有一个儿子,p有一个左儿子,以p为根的左子树中的具有最大值节点的t中序后继是p的中序后继,中序前驱不变;p有一个右儿子,以p为根的右子中的具有最小值节点t中序前驱是p的中序前驱,中序后继不变。
(3):删除的节点p有二个儿子,转化为叶子节点或只有一个儿子节点的删除。
4.2各功能函数流程图图4.1 :创建二叉树图4.2 :查询二叉树深度图4.3 :中序线索化二叉树图4.4 :中序遍历输出二叉树图4.5 :查询结点图4.6 :查询结点的双亲结点.图4.7 :插入结点图4.8 :删除结点5 程序运行数据及其结果1_按中序输入一课二叉树,建树并实现线索化2_建树完成后进入主菜单,可执行相应插入、删除、打印操作3_选择操作1,以中序遍历输出线索二叉树4_选择操作2,在线索二叉树中插入新结点5_选择操作3,删除二叉树中的结点6 课程设计心得通过这次做课程设计,发现了学习中的很多问题,平时学习的东西在做起来时有很大的困难,独立构思一个程序很难,不仅仅是要实现某个功能,而且还要把这些功能结合起来,成为一个能良好运行的程序,需要对错误输入提示,需要排除debug,需要设计每个使用界面等等。
刚开始的时候是先写了一部分代码,后来就发觉应该先把函数的功能需要弄清楚,整理出一个大框架。
再此基础上完善程序的功能。
这次的线索二叉树的插入和删除课本上没有相应的容,为了完成课设,在网络上一直翻看别人的博客,先看明白思想,在尽量看懂人家的代码。
最后是借鉴了别人的思想,自己画图,才把代码实现出来。
其间废了好大的力气。
而且虽说是实现了,但函数的语句还是显得有些乱,自己为了看懂还加了一大堆注释。
不便于和同学交流。
一直以来,觉得自己数据结构学的还行,起码概念那些都能理解,知道说了些什么,也大致知道怎么个原理,考完试也感觉良好,但是一到课程设计,看的题目挺简单,二叉树,可是一去上手做了去无从下手,一点都不会,只会纸上谈兵,我也知道变成这东西是需要多实践的,但没想到真的坐到那儿去编时,却怎么也下不了手,于是很失落的回宿舍查阅书籍以及上网百度资料,仔细的参读了很长时间后,自己不停的磨合,终于完成个大概,不可避免调试中又出些问题,经过好几遍的查错,一点一点的改,最终终于完成现在的程序。
通过这段时间的课程设计,我认识到数据结构是一门比较难的课程,但同时有时一门基础切极为重要的课程。
需要多花时间上机练习。
这次的程序训练培养了我实际分析问题、编程和动手能力,使我掌握了程序设计的基本技能,提高了我适应实际,实践编程的能力。
总的来说,这次课程设计让我获益匪浅,对数据结构也有了进一步的理解和认识。
附录:#include<stdio.h>#include<stdlib.h>#include<math.h>#include<windows.h>//windows自带函数库:Sleep()函数#define ERROR 0#define OK 1typedef char ElemType;//二叉树结点数据域可随时修改数据类型typedef int Status;typedef struct BiThrNode{//二叉树的存储结构ElemType data;struct BiThrNode *lchild,*rchild;int LTag,RTag;}BiThrNode,*BiThrTree;//BiThrTree用来声明指针类型变量static BiThrTree pre = (BiThrTree)malloc(sizeof(BiThrNode));void CreateBiTree(BiThrTree &T){//前序创建char ch;ch = getchar();if(ch == '#') T = NULL;else{T = (BiThrTree)malloc(sizeof(BiThrNode));T->data = ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}}void InThreading(BiThrTree &T){//以T为根节点的二叉树线索化if(T){InThreading(T->lchild);if(!(T->lchild)){T->LTag = 1;T->lchild = pre;}else T->LTag = 0;if(!(pre->rchild)){//pre被定义为全局变量pre->RTag = 1;pre->rchild = T;}else T->RTag = 0;pre = T;InThreading(T->rchild);}}void InOrderThreading(BiThrTree &Thrt,BiThrTree T){//带头结点的二叉树中序线索化Thrt = (BiThrTree)malloc(sizeof(BiThrNode));Thrt->LTag = 0;Thrt->RTag = 1;Thrt->rchild = Thrt;if(!T) Thrt->lchild = Thrt;else{Thrt->lchild = T;pre = Thrt;InThreading(T);pre->rchild = Thrt;pre->RTag = 1;Thrt->rchild = pre;}}void InOrderTraverse_Thr(BiThrTree Thrt){//中序遍历线索二叉树BiThrTree p = (BiThrTree)malloc(sizeof(BiThrNode));p = Thrt->lchild;printf("二叉树中序遍历结果为:");while(p!=Thrt){while(p->LTag==0) p = p->lchild;printf(" -> %c",p->data);while(p->RTag==1&&p->rchild!=Thrt){p = p->rchild;printf(" -> %c",p->data);}p = p->rchild;}puts("");//回车换行}BiThrTree Search(BiThrTree T,ElemType key){//查找data == key 的结点,并返回该节点的指针地址BiThrTree p = (BiThrTree)malloc(sizeof(BiThrNode));p = T->lchild;while(p!=T){while(p->LTag==0) p = p->lchild;if(p->data==key) return p;while(p->RTag ==1&&p->rchild!=T){p = p->rchild;if(p->data==key) return p;}p = p->rchild;}return NULL;}BiThrTree SearchPre(BiThrTree point,BiThrTree child) // 查找以point为根,child的双亲结点{BiThrTree p1,p2;if(point!=NULL){if((point->LTag!=1&&point->lchild==child)||(point->RTag!=1&&point->rchild==child)) return point;//找到则返回elseif(point->LTag!=1){p1=SearchPre(point->lchild,child);if(p1!=NULL) return p1;}if(point->RTag!=1){p2=SearchPre(point->rchild,child);if(p2!=NULL) return p2;}return NULL;}else return NULL;}Status InsertTree(BiThrTree T){//线索二叉树的插入函数BiThrTree p = (BiThrTree)malloc(sizeof(BiThrNode));//新结点,要插入的结点BiThrTree t ;//要插入结点的父母结点ElemType key;int n = 1,temp = 0;while(temp==0){n = 1;t = NULL;InOrderTraverse_Thr(T);//遍历输出线索二叉树printf("请输入新结点的值:");scanf("%c",&(p->data));getchar();printf("请问新结点的父母结点为:");scanf("%c",&key);getchar();printf("请问新结点是%c结点的左孩子or右孩子:(0-左,1-右)",key);while(1){//循环执行scanf("%d",&n);getchar();if(n==0||n==1) break;puts("输入的值应为0或1,请重新输入!");}t = Search(T,key);if(!t) puts("输入的父母结点不存在于树中,查找失败!");else{if(n == 0){//插入左子树p->RTag = 1;p->rchild = t;//父母结点的前驱p->LTag = t->LTag;p->lchild = t->lchild;t->LTag = 0;t->lchild = p;t = p;if(p->LTag==0){//找到p的左子树的最右结点,改为自己前驱p = p->lchild;while(p->RTag == 0)p = p->rchild;p->rchild = t;}}else{ //插入右子树p->LTag = 1;p->lchild = t;p->RTag = t->RTag;p->rchild = t->rchild;t->RTag = 0;t->rchild = p;t = p;if(p->RTag==0){p = p->rchild;while(p->LTag == 0)p = p->lchild;p->lchild = t;}}}printf("继续插入结点请按—0 返回主界面—请按1:");while(1){scanf("%d",&temp);getchar();if(temp == 1) break;else if(temp == 0) break;else puts("输入错误,应输入0-继续插入1-主界面:");}}return OK;}Status DeleteTree(BiThrTree T){//线索二叉树的删除函数BiThrTree t,pre,save;//pre_待删结点的双亲,屏蔽了全局变量pre save_保留要删除的结点,用以free(save);ElemType key;int n = -1,temp = 0;//temp 用来判断是否循环,继续使用删除结点函数while(temp == 0){InOrderTraverse_Thr(T);//遍历输出printf("请输入要删除的结点:");scanf("%c",&key);getchar();t = Search(T,key);//在头结点为T的树中找到key结点的位置if(!t) puts("所要删除的结点不存在!!");else{.pre = SearchPre(T,t);save = t;if(t->LTag==1&&t->RTag==1){//要删除的结点没有孩子if(pre->lchild==t){pre->LTag = t->LTag;pre->lchild = t->lchild;}else if(pre->rchild==t){pre->RTag = t->RTag;pre->rchild = t->rchild;} else puts("查找双亲结点可能有误1");}else if(t->LTag==1&&t->RTag==0){//要删除的结点仅有右孩子if(pre->lchild==t){//被删结点是双亲的左孩子pre->lchild = t->rchild;pre = t;t = t->rchild;while(t->LTag==0) t = t->lchild;t->lchild = pre->lchild;}else if(pre->rchild==t){//被删结点是双亲的右结点pre->rchild = t->rchild;t = t->rchild;while(t->LTag==0) t = t->lchild;t->lchild = pre;}else puts("查找双亲结点可能有误2");}else if(t->LTag==0&&t->RTag==1){//要删除的结点仅有左孩子if(pre->lchild==t){//被删结点是双亲的左孩子pre->lchild = t->lchild;pre = t;pre = pre->lchild;//修改pre为待删结点的左孩子while(pre->RTag==0) pre = pre->rchild;pre->rchild = t->rchild;}else if(pre->rchild==t){//被删结点是双亲的右孩子pre->rchild = t->lchild;pre = t;pre = pre->lchild;while(pre->RTag) pre = pre->rchild;pre->rchild = t->rchild;}else puts("查找双亲结点可能有误3");}else{//要删除的结点有两个孩子if(pre->lchild==t){pre->lchild = t->lchild;//被删除结点的左树作为根节点pre = t->lchild;//开始查找t的前驱while(pre->RTag==0) pre = pre->rchild;pre->RTag = 0;pre->rchild = t->rchild;t = t->rchild;//开始查找t的后继while(t->LTag==0) t = t->lchild;t->LTag = 1;t->lchild = pre;}else if(pre->rchild==t){pre->rchild = t->lchild;pre = t->lchild;//开始查找t的前驱while(pre->RTag==0) pre = pre->rchild;pre->RTag = 0;pre->rchild = t->rchild;t = t->rchild;//开始查找t的后继while(t->LTag==0) t = t->lchild;t->LTag = 1;t->lchild = pre;}else puts("查找双亲结点可能有误4");}free(save);}printf("继续删除结点—请按0 返回主界面—请按1:");while(1){scanf("%d",&temp);getchar();if(temp == 1) break;else if(temp == 0) break;else puts("输入错误,应输入0-继续插入1-主界面:");}}return OK;}main(){BiThrTree T = NULL;pre->rchild = NULL;//初始化preBiThrTree Thrt;int Temp = -1;puts("请输入字符串以建立二叉树,输入# 表示空树。
