各种短路向量分析
故障录波录波图分析word版

故障录波录波图分析各类故障情形下的波行特点:单相接地故障,故障相电流和零序电流大小相等且同相位,故障相电压有必然程度减小,同时有零序电压显现。
两相之间故障,两个故障相的电流大小相等,方向相反,没有零序电流。
两相接地故障,两个故障相的电流突变增大,但两个电流之间的相位有角度差,转变范围随过渡电阻的不同在60°-180°之间转变,但有零序电流显现。
三相接地故障或不接地故障,三相电流同步增大,没有零序电流和零序电压。
故障进程中的波形特点:➢故障相电流有明显突变增大,电压有必然程度减小,同时有零序电压和零序电流显现➢在故障切除后,电流通道变成一根直线。
若是是线路PT,在线路两头故障均切除后故障相电压变成0,零序电流变得很小或为0,但有专门大的零序电压。
重合成功。
三相电流恢复正常负荷电流,三相电压恢复对称。
依照故障录波图能够取得的信息1、发生故障的电气元件和故障类型2、爱惜动作时刻和故障切除时刻3、故障电流和故障电压4、重合时刻和是不是重合成功5、详细的爱惜动作情形6、完成附属功能(测距、阻抗轨迹、相量和谐波分析等)7、直流是不是正常,是不是接地、短路8、高频是不是发信在咱们的日常生产中常常需要通过录波图来分析电力系统到底发生了什么样的故障?爱惜装置的动作行为是不是正确?二次回路接线是不是正确?CT、PT 极性是不是正确等等问题。
接下来我就先讲一下分析录波图的大体方式:一、当咱们拿到一张录波图后,第一要通过前面所学的知识大致判定系统发生了什么故障,故障持续了多长时刻。
二、以某一相电压或电流的过零点为相位基准,查看故障前电流电压相位关系是不是正确,是不是为正相序?负荷角为多少度?3、以故障相电压或电流的过零点为相位基准,确信故障态各相电流电压的相位关系。
(注意选取相位基准时应躲开故障初始及故障终止部份,因为这两个区间一是非周期分量较大,二是电压电流夹角由负荷角转换为线路阻抗角跳跃较大,容易造成错误分析)4、绘制向量图,进行分析。
故障分析电压向量图

一般规律
单电源系统采用各种不同类型短路时,各序电压有效值的分布具有一定的普遍性: 越靠近电源,正序电压数值越大。 越靠近短路点,正序电压数值越小。 越靠近短路点,负序、零序电压数值越大。 越靠近电源点,负序和零序电压数值越低。
断线故障
短路计算是用从故障点对地看入的阻抗,称横向综合阻抗;断线计算是用从断线两端看入的阻抗,称纵向综合 阻抗,因此短路又称横向故障,断线又称纵向故障。
3.计算各种不对称短路的短路电流 ➢ 单相接地短路
➢
I(1) a1 两相短路
X1
E1 X2
X0
Id
1.67
120
kA0.43kA
➢
两相短I路k(1接)地1m.3(1)I0a(.118) 530.10.64
5 3k
3115 A1.29kA
Ia (1 2)X 1 E 1 X 2Id1.3 1 .6 0.8 7 5
断线计算是用从断线两端看入的阻抗称纵向综合阻抗因此短路又称横向故障断线又称纵向故横向两相断线故障纵向单相短路接地故障50纵向不对称故障的两种极端状态即一相或两相断开的运行状态单相断开两相断开分相检修线路或开关设备以及开关断路器三相触头合分闸不同期51断口处三相电流电压不对称可应用对称分量值进行分解其计算方法和步骤与短路计算基解相同
2
•
UR [1 (cos2 j sin 2 ]
两相直接短路接地故障电流相量图
Ib a2Ia1aIa2Ia0 a2XX22aXX00Ia1
Ic aIa1a2Ia2
短路电
Ia0
流
的 a绝 XX22对 aX 2X0值 0Ia: 1
I
a
1
I(1.1) k
Ib
Ic
关于变电站内短路电流分流系数实测和分析

关于变电站内短路电流分流系数实测和分析摘要:变电站内发生单相短路接地故障后,真正引发安全问题的是入地电流部分,而不是总的短路故障电流。
入地电流部分所占比重越大,其引发的安全问题也更严重。
分流系数表征了接地网或架空地线对故障电流的分流能力,可以用于分析短路电流的分布情况。
对某变电站内的单相短路接地故障电流的分布情况进行现场实测,并与模拟计算结果进行了对比。
实测与模拟计算结果相一致,地线分流系数较大。
模拟计算可以用于分析变电站内发生短路故障时的地线分流系数,为工程实际提供参考,应用该算法分析了影响地线分流系数的主要因素和影响规律。
结果表明,当变电站接地电阻较大或出线数量较少时,地线分流系数较大。
关键词:变电站;短路故障;短路电流;分流系数变电站的良好接地是电力系统安全运行的根本保障。
随着现代大电网向超高压、大容量和远距离方向的发展,系统发生短路时的故障电流越来越大,对于电力系统安全、稳定及经济运行的提出了更高的要求。
电力系统中,短路故障一般分为变电站站内短路和站外短路两种类型。
与站外短路相比,站内短路对变电站安全运行有更大的危害,更容易引起事故。
1、分流系数定义变电站站内短路时,电流分布如图1所示。
图1中变压器左侧连接架空线,右侧连接电缆,设在右侧发生站内单相对地短路故障,短路电流为Io。
该电流由两侧的远方电源提供。
根据基尔霍夫定律,这些短路电流终将流回两侧的电源。
由于是站内短路,因此部分电流Ig会直接通过接地系统由大地流向无穷远端的电源;同时,部分电流会沿着左侧架空地线和右侧电缆金属护层流回电源,这2部分电流分别为Iw和I0 , IN为通过变压器中性点流出接地网的电流。
这部分电流一般比较小,一般可以忽略不计I0。
定义接地网的分流系数K,定义中Ig、Io均为电流的有效值。
本文中分流系数如不加说明均采用这种定义。
在实际工程中,入地电流IR对变电站的安全运行造成较大威胁。
不仅接地系统接地电阻的安全限定值由Ig决定,网孔电压、地电位升、接触电压、跨步电压等也与入地故障电流成正比。
电力系统接地短路故障种类及接地保护方式直观分析
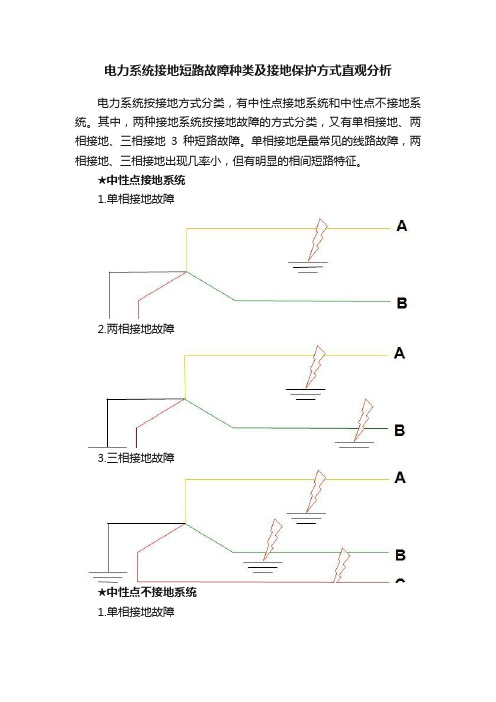
电力系统接地短路故障种类及接地保护方式直观分析电力系统按接地方式分类,有中性点接地系统和中性点不接地系统。
其中,两种接地系统按接地故障的方式分类,又有单相接地、两相接地、三相接地3种短路故障。
单相接地是最常见的线路故障,两相接地、三相接地出现几率小,但有明显的相间短路特征。
★中性点接地系统1.单相接地故障2.两相接地故障3.三相接地故障★中性点不接地系统1.单相接地故障2.单相接地故障3.三相接地故障☆单相接地故障特点:1.一相电流增大,一相电压降低;出现零序电流、零序电压。
2.电流增大、电压降低为同一相别。
3.零序电流相位与故障相电流同向,零序电压与故障相电压反向。
4.故障相电压超前故障相电流约80度左右(短路阻抗角,又叫线路阻抗角);零序电流超前零序电压约110度左右。
☆两相短路故障特点:1.两相电流增大,两相电压降低;没有零序电流、零序电压。
2.电流增大、电压降低为相同两个相别。
3.两个故障相电流基本反向。
4.故障相间电压超前故障相间电流约80度左右。
☆两相接地短路故障特点:1.两相电流增大,两相电压降低;出现零序电流、零序电压。
2.电流增大、电压降低为相同两个相别。
3.零序电流向量为位于故障两相电流间。
4.故障相间电压超前故障相间电流约80度左右;零序电流超前零序电压约110度左右。
☆三相短路故障特点:1.三相电流增大,三相电压降低;没有零序电流、零序电压。
2.故障相电压超前故障相电流约80度左右;故障相间电压超前故障相间电流同样约80度左右。
★电力系统工作接地(接地保护)变压器或发电机中性点通过接地装置与大地连接,称为工作接地。
工作接地分为直接接地与非直接接地(包括不接地或经消弧线圈接地)两类,工作接地的接地电阻不超过4?为合格。
☆电网中性点运行方式:大接地电流系统(110kV及以上)1.直接接地,又称为有效接地2.经低电阻接地大接地电流系统(35kV及以下)1.不接地,又称为中性点绝缘2.经消弧线圈接地3.经高阻接地煤矿电网中性点接地方式1.井下3300、1140、660V系统采用中性点不接地方式2.6、10kV主要采用中性点经消弧线圈接地方式3.35kV采用中性点不接地方式4.110kV采用中性点直接接地方式举例:中性点经消弧线圈接地和中性点直接接地★接地保护系统的型式文字代号☆第一个字母表示电力系统的对地关系:T--直接接地I--所有带电部分与地绝缘,或一点经阻抗接地。
对称分量法(正序、负序、零序)

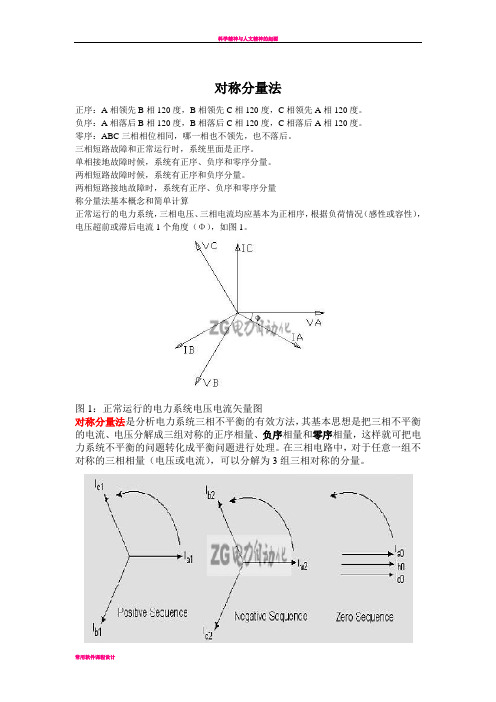
对称分量法正序:A相领先B相120度,B相领先C相120度,C相领先A相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后。
三相短路故障和正常运行时,系统里面是正序.单相接地故障时候,系统有正序、负序和零序分量。
两相短路故障时候,系统有正序和负序分量.两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1。
图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法,其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理.在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为3组三相对称的分量.图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0式中,α为运算子,α=1∠120°有α2=1∠240°, α3=1,α+α2+1=0由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义(方法)求解。
接触网分相处短路故障的分析与判断方法

接触网分相处短路故障的分析与判断方法李文起;孙晓薇【摘要】Two fault trips of the same kind occurred in Yanhui and Jingnan substations on Shijiazhuang-Taiyuan railway. The paper carried out theoretical and qualitative analysis and vector diagram quantitative analysis on the short circuit faults occurred on two points of phase segragation along overhead contact line in supply arms in the power substatios. It found out the causes of abnormal operation of relay protection and abnormal calibration device indications. Effective ways were put forward to identify the short-circuit fault trips on two points of phase segragation along overhead contact line in supply arms in the power substation. Suggestions for the operation maintenance are put forward to the computer protection device manufacturer and catenary operation sectors of substations.%以发生在石太线岩会、井南两个变电所两次同性质的故障跳闸为例,对变电所两个供电臂接触网分相处发生短路故障进行理论定性分析及向量图定量分析,找出保护动作、故障标定装置指示不正常的原因,提出判断变电所两个供电臂接触网分相处发生短路故障的有效方法,对微机保护装置生产企业和供电段接触网运行工区的运营维护提出建议.【期刊名称】《铁道标准设计》【年(卷),期】2011(000)009【总页数】4页(P105-108)【关键词】牵引变电所;供电臂;接触网;分相;故障判断分析【作者】李文起;孙晓薇【作者单位】北京铁路局石家庄供电段,石家庄050000;北京铁路局石家庄供电段,石家庄050000【正文语种】中文【中图分类】U226.8+l在牵引变电所微机馈线保护中,设有电流保护、阻抗保护、增量保护和故障标定装置。
电气工程概论第六章

a I a a Ib I 1 c
2
运算子
ae
j120
第五节
简单不对称短路计算
暂态
由上式可以得出正序、负序、零序三组对称分量
矩阵形式 可以用反变换求出 三相不对称的相量
I120 SIabc
Iabc S I120
1
第五节
简单不对称短路计算
暂态
第一节
概述
暂态
短路电流对电力系统将产生极大的危害,主 要有以下方面:
(1)短路电流的热效应使设备急剧发热,持续时间过长就可 能导致设备过热损坏; (2)短路电流将产生很大的电动力,可能使设备永久变形或 严重损坏; (3)短路将引起系统电压大幅度下降,严重影响用户的正常 工作; (4) 短路情况严重时,可能使电力系统的运行失去稳定, 造成电力系统解列,甚至崩溃,引起大面积停电; (5)不对称短路产生的不平衡磁场,会对附近的通讯系统及 弱电设备产生电磁干扰,影响正常工作。
暂态
在标幺制中,三相电路计算公式与单 相电路的计算公式完全相同。
工程计算中,通常选定功率基准值Sd和电压 基准值Ud,这时,电流和阻抗的基准值分别为
2 Ud Ud Zd 3I d S d Sd Id 3U d
S U I U Z I
第二节
标幺值
暂态
电力系统计算中有时采用一些物理量的相对 值来进行计算,这些相对值就叫作标幺值。
一、标幺值
有名值(任意单位) 标幺值 基准值(与有名值同单 位)
Z Z Z d ( R j X ) Z d R j X U U U d I I I d S S Sd ( P j Q) Sd P j Q
对称分量法(正序、负序、零序)
对称分量法正序:A相领先B相120度,B相领先C相120度,C相领先A相120度。
负序:A相落后B相120度,B相落后C相120度,C相落后A相120度。
零序:ABC三相相位相同,哪一相也不领先,也不落后。
三相短路故障和正常运行时,系统里面是正序。
单相接地故障时候,系统有正序、负序和零序分量。
两相短路故障时候,系统有正序和负序分量。
两相短路接地故障时,系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序,根据负荷情况(感性或容性),电压超前或滞后电流1个角度(Φ),如图1。
图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法,其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理。
在三相电路中,对于任意一组不对称的三相相量(电压或电流),可以分解为3组三相对称的分量。
图2:正序相量、负序相量和零序相量(以电流为例)当选择A相作为基准相时,三相相量与其对称分量之间的关系(如电流)为:IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量:Ib2=αIa2 ,Ic2=α2Ia2对于零序分量:Ia0= Ib0 = Ic0式中,α为运算子,α=1∠120°有α2=1∠240°, α3=1, α+α2+1=0由各相电流求电流序分量:I1=Ia1= 1/3(IA +αIB +α2 IC)I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义(方法)求解。
短路电流预测方法综述

文章编号:1004-289X(2024)02-0001-09短路电流预测方法综述李嘉敏1ꎬ庄胜斌1ꎬ杨广辉1ꎬ唐玲玲2(1.福州大学电气工程与自动化学院ꎬ福建㊀福州㊀350108ꎻ2.福建电力职业技术学院ꎬ福建㊀泉州㊀362008)摘㊀要:随着用电负荷与新型电力系统容量的不断增大ꎬ短路保护如何与之适配的技术难题日渐突出ꎮ系统发生短路故障时ꎬ可对短路电流发展进行预测ꎬ并根据该规律制定最佳保护与控制方案ꎬ力求安全前提下ꎬ使得短路造成的停电范围㊁设施损害最小ꎮ因此ꎬ短路电流预测方法被广泛研究ꎮ首先对短路电流进行了数学分析ꎬ得出其主要特征与影响因素ꎻ其次ꎬ以不同短路电流预测应用场景为分类依据ꎬ将国内外主要相关贡献归纳为节点预测㊁零点预测和峰值预测共三种研究类型ꎬ并总结了各类型预测方法的优缺点ꎻ最后ꎬ对短路电流预测方法进一步的研究方向和趋势进行了展望ꎮ关键词:短路电流预测ꎻ节点预测ꎻ过零预测ꎻ峰值预测中图分类号:TM71㊀㊀㊀㊀㊀文献标识码:BASummaryoftheShortCircuitCurrentPredictionMethodLIJia ̄min1ꎬZHUANGSheng ̄bin1ꎬYANGGuang ̄hui1ꎬTANGLing ̄ling2(1.CollegeofElectricalEngineeringandAutomationꎬFuzhouUniversityꎬFuzhou350108ꎬChinaꎻ2.FujianVocational ̄technicalSchoolofElectricPowerꎬQuanzhou362008ꎬChina)Abstract:Withthecontinuousexpansionofpowerloadandnewpowersystemcapacityꎬthetechnicalproblemthatadaptingshort ̄circuitprotectiontowhichhasbecomeincreasinglyprominent.Whenashort ̄circuitfaultoccursinthesystemꎬtheshort ̄circuitcurrentdevelopmentcanbepredicted.Accordingtotheregularityꎬthebestprotectionandcontrolschemecanbeformulatedsoastonarrowpoweroutageareaandreducefacilitydamagecausedbytheshortcircuitundersafety.Thereforeꎬshort ̄circuitcurrentpredictionmethodshavebeenwidelystudied.Inthispa ̄perꎬtheshort ̄circuitcurrentismathematicallyanalyzedꎬanditsmaincharacteristicsandinfluencingfactorsareob ̄tained.Secondlyꎬbasedondifferentapplicationscenariosofshort ̄circuitcurrentpredictionꎬthemainrelevantcontri ̄butionsathomeandabroadaresummarizedintothreeresearchtypes:nodepredictionꎬzeropredictionandpeakpre ̄diction.Theadvantagesanddisadvantagesofeachtypeofpredictionmethodaresummarized.Finallyꎬthefurtherre ̄searchdirectionsandtrendsofshort ̄circuitcurrentpredictionmethodsareprospected.Keywords:predictionofshortcircuitcurrentꎻnodepredictionꎻzero ̄crossingpredictionꎻpeakprediction1㊀引言随着分布式新能源和储能的大规模不断并网与区域电网的不断互联ꎬ电力系统短路电流水平不断提高[1ꎬ2]ꎮ部分电网出现由于更换不及时造成短路电流水平已接近或超出保护设备的额定分断能力ꎬ且无限提升设备的短路承载力是不现实的ꎮ短路电流的发展预测ꎬ可为短路故障电流早期抑制与选择性保护提供科学的决策依据ꎬ同时也是指导电网规划与建设㊁继电保护设计的主要技术手段[3]ꎮ因此ꎬ快速准确的短路故障电流预测技术研究对电网安全运行有着十分重要的意义ꎮ㊀㊀近年来ꎬ国内外提出的短路电流预测可分为三类:(1)节点预测短路电流方法ꎻ(2)过零预测短路电流方法ꎻ(3)峰值预测短路电流方法ꎬ如图1所示ꎮ以上三种短路电流预测方法适应不同的应用场景ꎮ节点预测方法ꎬ即从电力系统的网络拓扑结构及分布式电源㊁储能㊁负荷或潮流分布的角度出发ꎬ通过仿真电路计算或已训练的神经网络模型对特定网络节点的短路电流水平进行预估ꎬ以便在网架改造或建设初期配置合理的继电保护设备ꎻ过零预测方法则是在电网发生短路故障时ꎬ实时㊁快速㊁准确地进行短路电流特征参数估计并预测出过零时刻ꎬ以实现断路器相位控制开断ꎬ适当协调不断增大的系统短路容量与断路器分断能力提升困难且浪费之间的矛盾ꎻ峰值预测方法ꎬ是在短路故障保护在故障发生后时刻进行动作ꎬ该时间内故障电流激增ꎬ若提前预测出峰值便可指导限流与分断措施实施ꎮ同时ꎬ若在系统规划建设时利用短路故障信号数学模型及人工智能算法进行短路电流峰值预测ꎬ有利于实现系统全局选择性㊁经济协调保护方案设计ꎮ图1㊀短路电流预测分类图㊀㊀算法快速性与准确性的恰当配合是短路电流预测方法有效作用的关键ꎬ不同应用场景对于预测算法性能的要求也不尽相同ꎮ国内外学者从不同角度出发对短路电流预测方法做了大量研究ꎬ本文在此基础上对各类预测方法加以详细分类总结ꎬ客观分析了现有方法存在的问题和不足ꎬ并对短路电流预测方法的未来发展趋势进行展望ꎮ2㊀短路故障特性分析电流与电压信号可以直观反映电力系统的运行状态ꎬ当发生短路故障时ꎬ电压下跌而电流剧增ꎮ然而电压信号易受到干扰及噪声的影响并不稳定ꎬ从保护的角度出发一般更多以短路故障电流信号作为关键信息依据ꎬ因此ꎬ大量文献针对短路电流剧增现象进行故障检测研究[4-6]ꎮ系统发生短路故障时的简化电路如图2所示ꎬ假设电源等效为无穷大㊁理想系统ꎮ图2㊀简化短路故障等效电路图㊀㊀图2中R1㊁L1为电源侧等效电阻及电感ꎬR2㊁L2为等效负载电阻及电感ꎬu(t)为等效电源ꎬisc为线路电流ꎮ假设系统在t=0时刻发生短路故障ꎬ故障发生后系统等效阻抗由(R1+R2)+jw(L1+L2)(R1+R2)+(jωL1+jωL2)突然变为R1+jwL1R1+jωL1()ꎮ由基尔霍夫定律可得:L1disc(t)dt+Risc(t)=Umsin(wt+α)(1)㊀㊀对式(1)求解可得线路短路电流的瞬时公式ꎬ即isc(t)=Imsin(wt+α-φ)+[Im(sin(α-φ0)-sin(α-φ))]e-tτ(2)㊀㊀式中ꎬIm=Um/Zk为短路电流周期分量峰值ꎻIm0=Um/Z为短路前的电流峰值ꎻα为故障电压初相角ꎻϕ为短路回路阻抗角ꎻϕ0为短路前回路阻抗角ꎻτ=L1/R1为衰减时间常数ꎮ在不同故障初相角下ꎬ即不同短路故障发生时刻的短路电流如图3所示ꎮ图3㊀不同故障初相角下电流随时间变化曲线㊀㊀由式(2)与图3分析可得:㊀㊀(1)故障初相角对短路电流第一峰值有显著影响ꎮ在0ʎ故障初相角下ꎬ短路电流第一峰值接近短路电流最大峰值ꎬ随着故障初相角增大至180ʎꎬ短路电流第一峰值减小至接近0ꎮ(2)不同故障初相角下的短路电流上升速率有明显不同ꎮ在90ʎ故障初相角附近ꎬ短路电流上升速率最大ꎬ畸变特征最为明显ꎻ在0ʎ及180ʎ故障初相角附近ꎬ短路电流上升速率最小ꎬ畸变特征最不明显ꎮ㊀㊀(3)短路故障发生后短路电流呈现明显的非周期性ꎬ非周期性分量按照指数规律衰减ꎬ衰减的速度由时间常数决定ꎬ则与短路阻抗有关ꎮ3㊀短路电流的节点预测3.1㊀节点预测概述㊀㊀随着电网分布式电源数量的快速增长与充电桩等新型电力电子设施的大规模接入ꎬ导致电网结构越来越趋于复杂化ꎬ电网负荷水平持续增加㊁负荷特性日益多样ꎬ短路电流情况也愈复杂ꎬ传统的短路电流计算方法已经难以满足电网安全稳定运行的要求ꎮ基于逐渐升高的电网信息化程度ꎬ利用在电力网络中采集的海量数据与人工智能算法相结合ꎬ对短路电流进行短期㊁超短期的预测能够起到良好的效果ꎮ网络节点预测法是先构建各节点电路短路模态ꎬ然后通过分析短路电流水平预估可能发生短路故障的节点位置ꎮ与传统的短路电流计算方法相比ꎬ网络节点预测法在通过减少数据的输入量来提高计算速度的同时ꎬ还能保证预测精度[7]ꎮ3.2㊀节点预测法分类㊀㊀网络节点预测法主要可以分为两类:第一类是特征提取法ꎬ通过快速提取和分析短路电流的暂态特征分量ꎬ根据暂态特征的分量的变化ꎬ来实现短路电流预测[8-10]ꎻ第二类是机器学习法ꎬ建立考虑各种因素对短路电流的影响ꎬ确定预测模型的输入特征量ꎬ采用神经网络等机器学习方法训练历史数据ꎬ建立电力网络短路电流水平的预测模型[7-11]ꎮ其预测依据与特点如表1所示ꎮ表1㊀网络节点预测法中不同方法的比较预测方法预测依据特点特征提取法短路电流关于特征分量的数字表达式对历史数据需求低ꎬ预测精度高ꎬ数据处理量少ꎬ运算量小ꎬ程序运行速度快等优势ꎬ有利于在硬件系统上的实时实现机器学习法神经网络对历史数据的训练需要大量历史数据并对数据进行预处理ꎬ拟合程度强ꎬ但容易陷入局部最优ꎬ需引入其他算法来优化参数㊀㊀文献[12]通过设定220kV电厂接入的分布模型ꎬ得到该电厂短路电流与接入发电机容量之间的关系ꎬ由此建立了系统最大供电规模与220kV电网的短路电流关系ꎮ文献[13]选用三次B样条区数为小波函数ꎬ对短路电流实施二进小波变换ꎬ获得各尺度小波变换的平滑分量及小波分量ꎬ将小波分量变化作为短路故障信息特征对峰值电流进行预测ꎮ文献[14]在短路故障早期诊断基础上ꎬ提出一种基于最小二乘法的低压配电系统短路电流峰值预测计算方法ꎬ利用少量电流数据与故障电压初相角进行曲线拟合ꎬ预测短路电流发展趋势及峰值ꎮ㊀㊀文献[10]通过大量的历史数据的训练得到隐含层与输出层的权值ꎬ即可利用训练好的模型对未知的短路电流值进行预测ꎬ无需知道具体输入输出量之间的表达式ꎬ但存在过学习和易陷入局部最优解的缺陷ꎮ为解决上述不足ꎬ文献[11]将故障发生后0.2ms的电流值和故障初始相位角作为多层神经网络的输入特征向量来预测低压分布式系统短路电流的大小ꎮ文献[15]提出一种将小波变换短路故障早期检测技术与极端学习机相结合的短路电流预测方法ꎬ将特征提取法与机器学习法结合在一起ꎬ结合二者优势从而提高了预测精度ꎮ㊀㊀综上所述ꎬ网络节点预测法是在电网架构相对稳定的前提下ꎬ通过对电网节点的短路水平进行预测㊁辨识ꎬ对合理平衡电网短路容量和输电容量的资源㊁减少设备投资具有指导意义ꎻ同时对电网可能出现的短路故障进行预测分析ꎬ为电力系统的规划设计和运行工作提供有效依据[3]ꎮ4㊀短路故障电流过零点预测4.1㊀电流过零预测概述㊀㊀新能源渗透比例与用电需求持续上升ꎬ带来低压交流系统短路容量增大ꎬ对保护电器的短路分断能力也提出了较高要求ꎮ现有断路器产品的最大开断性能已无法匹配部分区域电网的短路电流ꎬ而大批量地更换高分断能力开关是不经济且不可持续的ꎬ因此有必要对短路电流过零预测进行研究ꎬ使开关可在短路电流过零时将故障隔离ꎬ实现小电弧能量开断ꎬ减小短路故障分断时对开关设备的损害ꎮ但由于短路故障的多样性和直流衰减分量的影响ꎬ故障电流并非周期性过零ꎬ因此快速提取故障电流的特征参数并准确估计故障电流零点是短路电流相控开断技术的关键基础ꎮ㊀㊀故障电流选相控制技术可缩短断路器动作时灭弧室的燃弧时间ꎬ降低触头间隙电弧能量ꎬ减小触头电侵蚀ꎬ能够有效提高断路器的开断容量和寿命[16-17]ꎮ相控分断是通过对短路电流波形的拟合重构ꎬ在短路故障发生后ꎬ通过零点预测算法精确预测一个目标过零点ꎬ根据开关机构固有分闸动作时间ꎬ延迟一定时刻触发断路器分闸ꎬ使得断路器触头在时刻分离后ꎬ经过最佳燃弧时间ꎬ在目标电流自然过零点处熄弧ꎬ这样燃弧时间短而能量积累少ꎬ有利于绝缘介质恢复ꎬ从而避免电弧重燃㊁实现短路故障开断[18]ꎬ如图4所示ꎮ㊀㊀断路器相控开断时序如图5所示ꎬ其中tzpr为零点预测算法响应时间ꎻtwait为零点预测结束到发出分闸动作信号之间的等待时间ꎻtcbo为操动机构固有动作时间ꎻtarc为燃弧时间ꎻto为从接受分闸动作信号到电弧熄灭的总时间ꎬ即为开关分闸动作总时间ꎮ图4㊀相控分断流程图5㊀故障电流相控分断时序4.2㊀零点预测法分类㊀㊀国内外关于利用短路电流离散采样数据估算短路特征参数预测目标过零点以实现提前发出断路器分断指令的预测算法主要可分为基于傅里叶算法的零点预测法㊁基于最小二乘算法的零点预测法与其他预测法三大类ꎮ4.2.1㊀基于傅里叶算法的零点预测法㊀㊀傅立叶算法在电力系统谐波分析㊁故障诊断等领域中应用广泛[19]ꎬ在短路电流零点预测领域中已有研究的包括全波傅立叶算法和半波傅立叶算法[20-23]ꎮ基于傅氏算法的预测流程如图6所示ꎬ该算法对于只含有奇数次谐波分量的信号处理效果很好ꎬ能够保证零点预测的速度与准确度ꎬ但在直流衰减分量或者偶数次谐波含量较大时的信号时预测精度不佳[24]ꎮ㊀㊀文献[25]采用改进快速傅里叶算法对6个采样数据长度的窗口对短路电流进行分解计算ꎬ但实验为理想状态ꎬ实际会出现的谐波分量并未充分考虑ꎮ文献[26]对比了最小二乘参数辨识与改进快速傅里叶变换两种方法在短路电流含有不同噪声㊁采样不同期情况下的过零预测效果ꎬ最终得出:理想状态下改进快速傅里叶算法预测精度高ꎬ但在受到采样采集系统的噪声和电网频率的较大波动影响时ꎬ最小二乘参数辨识算法可靠性与准确度更高ꎮ图6㊀基于傅氏算法的预测流程图4.2.2㊀基于最小二乘算法的零点预测法㊀㊀最小二乘法是一种通过求解估计值与实际值之间的误差平方和最小问题从而找到最符合样本数据的函数的经典方法ꎬ计算简单ꎬ具有灵活的数据窗口ꎬ但其提取参数的过程常常将短路电流中的衰减直流分量表达式用泰勒级数展开式的前两项近似代替[27]ꎬ该截断误差使得其采样窗长通常需超过半个周波(10ms)才能对参数进行有效提取ꎮ基于最小二乘算法的预测流程如图7所示ꎮ㊀㊀文献[28]提出一种基于加权最小二乘法的零点预测法ꎬ对电流参数进行估计ꎬ可以在10ms内实现短路电流过零点的预测ꎬ预测误差在ʃ1ms以内ꎬ但采用相位角替换会产生随机误差ꎻ文献[27]提出一种能够消除直流衰减分量影响的递推最小二乘校正算法ꎬ利用递推原理对计算过程进行分解以提高计算速度ꎮ文献[29-30]提出了补偿时间常数的改进递推最小二乘法ꎬ该算法具有可变的数据窗ꎬ参数估计精度高ꎬ收敛速度快ꎬ计算简便ꎬ且对高频分量的滤波能力强ꎬ在故障电流含有谐波时仍然有效ꎬ但是部分工况下算法预测时间较长ꎮ文献[31]提出了带有遗忘因子的最小二乘法来提高算法对频率偏移问题的耐受能力ꎬ提升了预测初始阶段的零点精度ꎬ但是随着时间推移ꎬ零点预测误差仍会逐渐增大ꎮ图7㊀基于最小二乘法的预测流程4.2.3㊀其他零点预测方法㊀㊀小波分析法在时频域分析时可以聚焦原始信号细节处ꎬ能够自动划分信号频段ꎮ但小波变换会有 边界效应 的缺陷ꎬ须经过较长时间的采样数据过渡ꎬ实际应用在零点预测时需事先启动计算ꎬ耗费单片机算力资源[32]ꎮ㊀㊀文献[33]提出了一种 安全点算法 以预测短路电流过零时刻ꎮ该算法为简化计算模型ꎬ做出 电流中的直流分量并不衰减 的假设与利用故障电流基波分量的过零时刻为 安全点 替代实际波形过零点ꎮ该算法在直流含量较低㊁衰减缓慢的场合可实现准确快速的预测ꎬ然而简化模型的同时也导致当谐波含量较大时预测精度不足ꎮ㊀㊀Thomas等人[34-35]针对 安全点算法 存在的缺陷ꎬ提出了 自适应算法 ꎬ该算法对电流中的衰减直流分量进行泰勒展开[28ꎬ36]ꎬ且能够自适应地变换采样窗长以更好地实现故障判断ꎮ自适应算法考虑了直流分量的衰减特性ꎬ但是该算法模型的拟合阶数增加ꎬ需要在线进行矩阵和除法运算ꎬ计算量大ꎬ难以满足快速性的技术要求ꎮ文献[37]提出了基于自适应神经元的短路电流参数提取算法ꎬ当矩阵维数较大时ꎬ计算量大不利于短路故障的快速隔离ꎮ㊀㊀Prony算法模型将短路电流的周期分量和直流衰减分量综合进行考虑ꎬ直接利用采样信号得到电流的特征参数ꎬ且在参数求解时应用最小二乘拟合ꎬ对测量过程中带来的噪声有所消除[36ꎬ38]ꎮProny算法可在时域内直接得到待分析信号的幅值㊁相位㊁频率和衰减因子ꎬ计算量小ꎬ适合分析按照指数规律变化的信号ꎬ但仅适合离线计算[39]ꎮ㊀㊀文献[40]将支持向量机(SVM)应用于短路电流零点预测ꎬ该算法原理简单ꎬ对大量数据进行离线训练后即可得到预测结果ꎬ目前只在特定的短路故障中可应用ꎬ实时性和通用性还有待提高ꎮ文献[41]基于神经网络模型提出了一种电力系统谐波频率的分析方法ꎬ整次谐波的求解精度较高ꎬ但是该算法可能受网络本身收敛系数的影响而出现难以收敛的现象ꎮ㊀㊀文献[42]通过长度为3的电流数据采样滑动窗口不断求解更新短路电流的周期分量幅值和衰减时间常数ꎬ并根据计算参数重构短路故障电流波形ꎬ进而预测故障电流过零点㊁实现断路器相位控制开断ꎮ该预测方法故障辨识参数计算准确㊁计算量小㊁预测短路电流与实际波形吻合度高ꎬ与改进递推最小二乘法相比ꎬ其具有快速㊁精度高的优点ꎮ㊀㊀综上所述ꎬ现有方法均通过数字信号分析算法实现零点预测ꎮ目前所研究算法存在模型简化带来误差与模型完整带来求解复杂的矛盾ꎮ这些算法虽然较传统傅里叶㊁最小二乘拟合等方法已有诸多改善ꎬ但由于硬件电流传感器对模拟信号采集调理放大环节的信噪比和短路工况下电路频率稳定性等因素的制约ꎬ难以同时满足现场预测精度与实时性的要求ꎮ如何将不同算法组合起来进行目标过零点预测ꎬ兼顾预测精度与短耗时ꎬ是未来研究热门方向且具有开阔的应用前景ꎮ5㊀短路电流的峰值预测5.1㊀峰值预测概述㊀㊀为解决如何根据短时故障信息精准采取最佳的抗短路故障的技术措施这一难题ꎬ有必要进行短路电流峰值预测与发展规律研究ꎮ依托故障信息的短时辨识ꎬ结合轻量化峰值预测算法ꎬ可实现短路电流尚未 成熟 时预知电流发展规律ꎬ继而可根据该规律制定选择性限制㊁分断保护策略ꎬ以保证短路故障下低压配电网全范围的最优保供电服务ꎮ5.2㊀电流峰值预测方法分类㊀㊀目前关于短路电流峰值预测的方法主要可分为两类:一类是从短路电流的数学模型出发ꎬ采集短路故障早期的电流(电压)信号ꎬ计算出模型的特征参数ꎬ进行曲线拟合ꎬ可在时间序列上对短路电流的发展趋势进行外推预测ꎬ称为趋势外推预测法ꎻ另一类是以人工智能算法为工具ꎬ以故障后某个时刻的电流㊁故障电压初相角或其他电气量为输入特征量ꎬ以短路电流峰值为输出结果ꎬ建立短路电流峰值预测模型并加以训练及测试ꎬ称为人工智能预测法[43]ꎮ5.2.1㊀趋势外推预测法㊀㊀趋势外推预测法的主要实现过程包括确立短路电流随时间的数学模型㊁利用实时(历史)数据求出模型的特征参数㊁在时间序列上进行递推预测ꎬ其关键在于数学模型建立的有效性与特征参数提取的准确性ꎮ傅氏算法㊁最小二乘法㊁灰色算法等多种算法均可在线提取短路电流的特征参数ꎮ㊀㊀傅氏算法是目前应用最广泛的峰值预测法ꎬ它的预测精度高ꎬ滤波效果好ꎬ但至少需要采样半个周波(10ms)的数据量ꎬ检测时间过长ꎮ为解决傅氏算法的滤波效果与响应速度之间的矛盾ꎬ文献[44]提出一种可根据需要滤除指定谐波分量的数字信号处理算法ꎬ为短窗傅氏算法在微机继电保护中的应用提供了理论基础ꎮ随后ꎬ文献[43]采用短窗傅氏算法ꎬ建立五元滤波矩阵对短路电流信号进行分解ꎬ通过基本四则运算求出周期分量与直流衰减分量的特征参数ꎬ最终确定电流离散表达式ꎬ实现短路电流趋势的预测ꎮ㊀㊀文献[45]结合短路电流的一阶微分方程ꎬ提出将灰色理论应用于低压配电系统的短路电流预测ꎮ文献[46]提出等维信息递推预测算法可缩短总体预测时间ꎬ并通过调整初始迭代点㊁选择合适的外推因子等方式提高预测精度ꎮ文献[10]在实现低压配电系统短路故障早期检测的基础上ꎬ采用最小二乘法将故障电压初相角和少量已采集到的短路电流数据进行曲线拟合ꎬ并对其进行残差修正以得到更好的预测效果ꎮ㊀㊀趋势外推预测法的模型简单ꎬ易于在线实现ꎬ且在参数提取过程中具有数据窗口灵活㊁计算过程简单的优点ꎮ但是趋势外推法必须经过一定的数据窗口对信号进行采样ꎬ导致其在预测速度上有所滞后ꎬ难以满足实际工程应用中短路电流峰值预测的实时性要求ꎮ5.2.2㊀人工智能预测法㊀㊀人工智能预测法是通过算法模拟人类的思考㊁学习方式ꎬ根据历史数据和模型算法ꎬ对未来事件㊁趋势㊁情况进行预测和分析从而得到预测条件与待预测量之间的关系ꎮ目前用于短路电流峰值预测的人工智能算法有人工神经网络(ANN)㊁BP神经网络㊁遗传算法(GA)㊁支持向量机(SVM)㊁极端学习机(ELM)和二维云模型等ꎮ㊀㊀2011年ꎬ文献[47]首次提出将人工神经网络应用于短路电流峰值预测ꎬ以故障电压初相角及故障后0.2ms的短路电流瞬时值作为预测模型输入特征量ꎬ利用仿真模型得到的短路电流数据进行训练与预测ꎬ验证了ANN算法的可行性ꎮ文献[15]直接采用极端学习机算法ꎬ以故障后0.2ms的短路电流瞬时值及故障电压初相角为输入ꎬ经离线训练后应用于NICompact-RIO硬件上ꎬ实现短路电流的在线预测ꎮ㊀㊀文献[48]提出可充分动态应用新数据且相对误差最小的灰色BP神经网络动态预测模型ꎬ改进了传统灰色预测模型数据迭代不合理的问题ꎬ适用于原始样本点少㊁非线性和随机性强的复杂系统ꎮ其以短路电流㊁故障初相角㊁灰色模型预测结果和结果相对残差作为BP神经网络的输入参数对灰色模型训练ꎬ得到能快速准确地进行短路电流峰值预测的模型ꎮ灰色BP神经网络模型预测流程如图8所示ꎮ㊀㊀文献[49]利用粒子群优化算法去改善传统ELM短路电流峰值预测准确性低和效果不稳定的缺点ꎬ通过故障点位置不确定下的全相角故障数据建立预测模型ꎬ并分析了粒子群算法在不同适应度函数ꎬ即平均相对误差㊁均方根误差和灰色绝对关联度下的精度与预测实时性ꎬ得出灰色绝对关联度做适应度函数的短路电流峰值预测模型最佳的结论ꎮ㊀㊀人工智能预测中不同方法的比较ꎬ如表2所示ꎮ人工智能预测法最主要的优点在于它能够自动学习并发现历史数据中的规律和模式ꎬ即可通过数据训练建立预测模型ꎬ无需计算出输入与输出之间的表达式ꎮ人工神经网络的学习能力非常强大ꎬ能充分逼近复杂的非线性关系ꎬ具有鲁棒性和容错能力ꎬ然而一个完善的人工神经网络需要具有大量的历史数据和时间来训练ꎬ且有可能会陷入局部最优解ꎮ支持向量机适用于小样本和非线性数据的预测ꎬ能够避免过拟合和局部最小值问题ꎬ但核函数计算复杂ꎬ对缺失数据敏感ꎬ并且求解支持向量所需时间较长ꎮ极端学习机参数设置简单ꎬ学习速度快ꎬ泛化能力强ꎬ但可能产生无效的隐层节点ꎬ且精度和速度具有随机性ꎮ二维云模型预测过程中兼顾模糊性和随机性ꎬ虽然每次预测的精度不尽相同ꎬ但都能够集中在一定范围之内[50]ꎬ能够使得预测结果更加合理ꎬ然而其预测速度未得到实际验证ꎬ且通过硬件实现也相对困难ꎮ图8㊀灰色BP神经网络模型预测流程图表2㊀AI短路电流峰值预测方法对比文献[]AI类型预测耗时/ms预测峰值偏差/100%[15]极限学习机1.903.2[48]BP神经网络0.06(迭代次数为3时)1.93[50]二维云模型/1.71[49]粒子群优化极限学习机2.901.36。
4-3电路定律的向量形式
I
u i
U
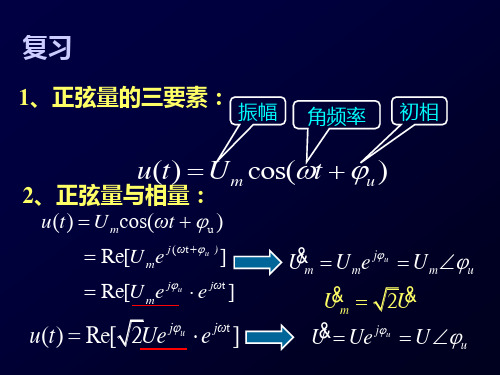
3)电阻的uR (t )的相位 iR (t ) 的相位同相;
4 ) 振幅关系 U Rm RI Rm
u (t )
i (t )
R
时域模型
例2:在正弦稳态电路中,
i ( t ) 2cos(100t 30 )A 流过10Ω电阻的电流
求: u (t )
10 2 cos(100t 30 )V
k 1 k
n
对于线性时不变的正弦稳态电路(单一频率激 励)各支路电压、电流为同频率的正弦量。 设:
n
jωt ik (t ) I km cos(ωt ik ) Re[ I km e ]
n
n jωt jωt ik (t ) Re[I km e ] Re I kme k 1 k 1 k 1
0 I
元件 电阻 电感 相量模型
I
0 U
伏安关系 相量图
R
U
I
jL
U
I
1 jC
电容
U
例 4:
u (t )
4H电感端电压 u (t ) 8 2cos(t 50 )V 100rad/s 求 i (t )
i(t )
解:1)画出电路的相量模型
i3
i1 i2
求:
i3 (t )
解:方法1)由KCL的时域形式: 1060
0
6.236.2
10 60 5 90 I3 I1 I 2
5 90
相量图
10 cos 60 10 j sin 60 j5
5 j3.66 6.236.2 A
最新《电力系统故障分析》复习题(学员)

电力系统故障分析复习题一、填空:1.在实际工程计算中,常用(标么值)进行,使计算过程简化,这称为(标么制)。
2.采用标么制,应选定基准值,基准值有(电压基准值)、(电流基准值)、(功率基准值)和(阻抗基准值)。
3.求解不对称短路问题,一般采用对称(分量法),即将故障点的不对称三相电压分解为(正序)、(负序)和(零序)电压。
4.电力系统的元件分为(旋转元件)、(静止元件)两大类。
5.输电线路是(静止元件),所以(正序阻抗)和(零序阻抗)相等。
6.“导线——大地”回路的自阻抗,由(电阻)和(电抗)两部分组成。
7.为防止雷击过电压,架空线路杆塔顶上通常装有一根或多根避雷线,避雷线也称(架空地线)。
8.电力系统中的实际负荷,是由不同性质的负荷组合而成的,这称为(综合负荷)。
9.异步电机是(旋转)元件,其负序阻抗(不等于)正序阻抗。
10.在某一时刻短路电流可以达到最大值,将短路电流最大可能的(瞬时)值称为(冲击电流)。
11.在工程计算中,常利用(计算曲线)来确定短路后任意指定时刻短路电流的周期分量。
12.(计算曲线)的方法对短路点的总电流和在短路点邻近支路的电流分布计算具有足够的准确度。
13.两相短路、两相接地短路、单相接地短路称为(横向不对称短路故障)。
14.分析短路点的电压、故障支路电流的方法有(解析法)和(复合序网法)。
15.电力系统的非全相运行不会引起(过电压)、(大电流),但会出现(负序)和(零序)分量。
16.电力系统的非全相运行中的负序分量影响(输出功率),零序分量影响(通讯)。
17.根据(对称分量合成公式)可以求出断相处各相电流和电压。
18.当两部分等值电动势的夹角摇摆范围没有超过180度,经若干摇摆后恢复同步运行的情况称为(稳定振荡)或(同步振荡)。
19.线路一侧序电流的正方向规定由(母线)指向(被保护线路)。
20.规定负序电压的正方向是由(母线)指向(零电位点)。
判断题:1.由于变压器是静止元件,所以其负序等值电路和负序电抗分别与正序等值电路和正序电抗相同.(√)2.变压器的等值电路表征了一相一、二次绕组间的电磁关系。
Y△-11接线变压器常见故障两侧电流电压特征分析

现代发电厂大型变压器多采用Y/△-11接线方式,我厂主变和励磁变也均采用该种接线方式。
当正常运行中一次系统发生故障时,如果对故障情况下,变压器两侧的电流电压特征有所了解掌握,继保人员就可以迅速准确地判断出故障类型和故障点大致位置,对故障排除和系统恢复有很大的帮助。
本文对Y/△-11变压器集中常见的故障时,用两种方法两侧的电流电压特征进行分析总结。
为方便分析,对于Y/△-11接线变压器常见故障分析的几点前提及假设:(1)由于负荷电流相对于故障电流很小,可以忽略不计,因此分析时不考虑负荷电流;(2)本文仅对变压器故障时两侧的电流特征进行定性分析,假设变压器的变比为1,两侧的CT、PT 变比相同;(3)对于变压器两侧的零序分量传变,由Y/△-11变压器零序等值电路,两侧的零序分量电流、电压相互独立,不能从一侧传变到另一侧;(4)对于变压器两侧的正序分量传变,设Y 侧用下标A、B、C 表示,△侧用下标a、b、c 表示,两侧正序电流量关系为:İA1=I ̇a1e -j30°、I ̇a1=I ̇A1ej30°;两侧的正序电压关系,应计及变压器阻抗上压降的影响,两侧的正序电压关系有:U̇A1=(U ̇a1+jI ̇a1X T1)e -j30°、U ̇A1=(U ̇A1+jI ̇A1X T1)e j30°。
为了方便定性分析,假设变压器的变比为1且不考虑变压器正序阻抗的影响,即有:U̇A1=U a1e -j30°、U ̇a1=U ̇A1e j30°。
(5)同样,对于变压器两侧的负序分量传变,两侧负序电流量关系为:İA2=I ̇a2e j30°、I ̇a2=I ̇A2e -j30°两侧的负序电压关系,应计及变压器阻抗上压降的影响,两侧的负序电压关系有:U̇A2=(U ̇a2+jI ̇a2X T1)e j30°、U ̇a2=(U ̇A2+jI ̇A2X T1)e -j30°同样也不考虑变压器正序阻抗的影响则有:U̇A2=U ̇a2e j30°、U ̇a2=U ̇A2e -j30°1变压器△侧两相短路故障,以AB 相短路为例分析故障时忽略负荷电流则有AB 相短路时的边界条件为:I c =0,I c0=0由此可得:I c =0,I c1+I c2=0U a =U b 由此可得:U c1=U c2设△侧短路电流为I a =-I b =I k ,因为没有零序电流,故I a1=I a2=I k /3√,因此可得到△侧电流向量图为:由İA1=I a1e -j30°、I ̇a1=I ̇A1e j30°、I ̇A2=I ̇a2e j30°、I ̇a2=I ̇a2e -j30°可得Y 侧的电流向量图如下:两侧的电压特征分析:△侧U a =U b 由此可得:U c1=U c2,则有:△侧电压为:Y 侧电压为:综上:△侧两相短路故障时,变压器两侧的电压电流特征为:Y 侧各相电流的分布与故障相别有关,其规律为:与△侧故障相对应的两相中滞后相的电流最大(如△侧ab 两相短路,Y 侧B 相电流最大),数值上为故障相电流的2/3√倍,其他两相电流相等、方向相同,在数值上为故障相电流的1/3√倍,方向与电流最大一相相反;不计变压器内部电抗压降,Y 侧与△侧两故障相对应的两相中的滞后相电压最低,为0,其他两相电压大小相等,方向相反。
一起非典型10kV相间短路故障分析

一起非典型 10kV相间短路故障分析[摘要] 针对一起10kV线路因箱变进入小动物导致跳闸的非典型故障,深入分析了其不同时刻的故障类型、故障过程、故障波形、保护动作行为等。
[关键词] 继电保护;相间短路;接地故障过流保护;非典型故障1.故障简介2021年11月11日,某大型水电站(简称A水电站)10kV系统厂外10kV配电室馈线发生AB相间短路故障,导致10kV馈线开关跳闸。
1.故障现象通过调取馈线保护装置报文获取信息如下:2021年11月11日00:24:43启动;故障类型:AB;故障电流4.52A(折算到一次为542.4A,变比600/5);过流Ⅱ段保护动作;馈线保护装置整定定值:过流Ⅰ段定值:4.33A,过流Ⅰ段时间:0.2s过流Ⅱ段定值:2.17A,过流Ⅱ段时间:0.4s;故障电流已达到过流Ⅰ段保护定值,但过流Ⅰ段保护未动作。
1.故障录波波形分析因本馈线为厂外配电室负荷,并未将信号和故障录波接入厂内监控系统,但厂外配电室电源取自厂内10kV厂用电系统905M,因此可借助厂内故障录波、CCS报文辅助分析。
图1 A水电站站内监控画面报文图2 A水电站站内#5高厂变低压侧波形图图3故障初始时刻向量图故障状态一:根据故障初始时刻波形分析1.A、B相电压出现小幅度降低,C相几乎无变化,电压相位关系几乎不变;2.A、B相电流出现增大,由正常时刻的36A增大为293A,C相电流几乎无变化,A、B相电流反向;3.无零序电压、零序电流出现;4.故障电流与故障电压之间相位关系:∠UAB =∠UA-∠UB=117.839°,∠IAB=∠IA-∠IB=183.734°,故障相间电压超前故障电流约70°;结论:由上判断此刻发生较为轻微的相间短路故障,并无接地发生。
图4故障发展时刻向量图故障状态二:根据跳闸时刻波形分析1.B相电压出现大幅度降低,A、C相电压升高;2.有零序电压、零序电流产生,零序电流相位与故障电流同向,零序电压与故障电压反向。
两相相间短路故障仿真分析(AC)

1.2Matlab软件简介
MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
SimPowerSystems(电力系统元件库)涵盖了电路分析、电力电子、电力系统等电气工程学科中基本元件的仿真模型。它包括:Electrical Sources(电力元件),Elements(线路元件),Power Electronics(电力电子元件),Machines(电机元件),Connectors(连接器元件),Measurements(电路测量仪器),Extras(附加元件),Demos(演示教程)和Powergui(电力图形用户接口)等元件。
1.3电力系统发展前景
目前电力系统市场发展中的自动控制技术趋向于控制策略的日益优化,呈现出适应性强、协调控制完善、智能优势明显、区域分布日益平衡的发展趋势。在设计层面电力自动化系统更注重对多机模型的问题处理,且广泛借助现代控制理论及工具实现综合高效的控制。在实践控制手段的运用中合理引入了大量的计算机、电子器件及远程通信应用技术。而在研究人员的组合构建中电力企业本着精益求精、综合适用的原则强调基于多功能人才的联合作战模式。在整体电力系统中,其工作方式由原有的开环监测合理向闭环控制不断发展,且实现了由高电压等级主体向低电压丰富扩展的安全、合理性过度,例如从能量管理系统向配电管理系统合理转变等。再者电力系统自动化实现了由单个元件到部分甚至全系统区域的广泛发展,例如实现了全过程的监测控制及综合数据采集发展、区域电力系统的稳定控制发展等。相应的其单一功能也实现了向多元化、一体化综合功能的发展,例如综合变电站实现了自动化发展与提升。系统中富含的装置性功能更是向着灵活、快速及数字化的方向发展;系统继电保护技术实现了全面更新及优势发展等。依据以上创新发展趋势电力系统自动化市场的发展目标更加趋于优化、协调与智能的发展,令潮流及励磁控制成为市场新一轮的发展研究目标。因此我们只有在实践发展中不仅提升系统的安全运行性、经济合理性、高效科学性,同时还应注重向自动化服务及管理的合理转变,引入诸如管理信息系统等高效自动化服务控制体系,才能最终令电力系统自动化市场的科学发展之路走的更远。
电力系统三相短路的分析计算

d q
X did X qiq
X adi f
f X adid X f i f
X X
d f
X ad X ad
Xa X f
∴
d q
( Xa X ad )id X qiq
X adi f
X aid
X ad (i f
id )
电力系统中某一处发生短路和 断相故障的情况
两个以上简单故障的组合
电力系统 短路故障
电力系统 断相故障
1.三相对称短路 2.单相接地短路 3.两相短路 4.两相接地短路
1.断一相故障 2.断两相故障
属
于
在各种短路故障中,单相
不
接地占大多数(65%),三
对
相短路的机会最少(5%).
称
但三相短路的短路电流最
当电源距短路点的电气距离较远时,内阻抗相对于外阻抗要小得多,且 由短路而引起的电源送出功率的变化远小于电源的容量,这时认为电源的 电压幅值和频率都不发生变化。这样,可以将该电源视为恒定电势源或无 限大容量电源。
二、恒定电势源的三相短路
2.1、三相短路的暂态过程
短路前,系统中的A相电压和电流分别为
e Em sin(t ) i Im sin(t )
因此,在有限容量系统突然发生三相短路时,短路电流的 初值将大大超过稳态短路电流。
实际电机的绕组中都存在电阻,励磁绕组中的直流分量将衰减至零。 与该分量对应的定子电流中的自由分量也将逐步衰减,定子电流最终为 稳态短路电流。
三、同步发电机三相短路的暂态过程
同步发电机的暂态电势和暂态电抗
为了便于描述同步电机突然短路的暂态过程,需要确定一个短路瞬间不突 变的电势—交轴暂态电势 (通常以暂态后电势 代替)。
电力系统的短路分析与故障测距

3.2 故障测距的概念及种类 3.2.1 故障测距的概念 故障测距又称故障定位,对于输电线路来说,是指在线路发生故障后, 根据不同的故障特征,迅速准确地测定出故障点的位置。现有的故障测 距算法按其工作原理可以分为行波法、阻抗法、故障分析法、智能化测 距法。由于阻抗法和故障分析法本质上没有区别,都是分析短路后的故 障特征量,利用短路计算的逆运算求解故障距离。因此把阻抗法和故障 分析法统称为故障分析法。 3.2.2 故障测距的分类
3.3.
参数线路模型
1. 集中参数模型:
图1 集中参数线路模型 假设线路三相完全对称,图1给出了集中参数线路模型,其中:
Zs是线路相自阻抗; Zm是线路相间互阻抗; Ys是线路相自导纳; Ym是线路相间互导纳。
§ 3.3
参数线路模型
是M侧母线电压向量;
是M侧母线a、b、c相电压相量;
2. 分布参数模型:
3.2
故障测距的概念及种类
2 故障分析法 故障分析法依据电压电流的测量值,通过故障分析根据各种特征构造各种原 理(如阻抗与距离成正比,用两端数据计算到的故障点电压相等,过渡电阻 的纯阻性等)的测距方程,进行故障测距。事实上,在线路参数已知的情况 下,输电线路某处发生故障时,线路两端的电压电流均为故障距离的函数, 其实质是短路电流的逆运算。 故障分析法由于简单易行,对设备要求较低, 投资小,获得了广泛的运用。早起的故障分析方法主要是利用单端电气量的 测距算法,常见的单端算法主要有工频阻抗法解微方程算法,零序电流相位 修正法,故障电流相位修正法,解二次方程法,对称分量法,解一次方程法, 网孔方程法。上述单端测距算法都无法从原理上同时消除过渡电阻和对侧系 统阻抗的影响。制约了单端测距的发展。随着通道的发展,能够较为容易的 获得对侧的电压电流,因此双端测距方法逐渐发展起来。
故障分析解析PPT课件

电力系统典型故障分析的一般方法:
• 1、选取特殊相进行分析。 • 2、由故障特征确定故障边界条件。 • 3、由故障边界条件,通过对称分量法求取
特殊相各序分量。 • 4、由各序分量关系,绘制特殊相序网图。
对称分量法Байду номын сангаас
序网图的绘制方法
• 在序网图中,只有正序网络图包含电源 电势,负、零序网络图中没有电源电势。
电力系统典型故障的类型:
• 1、短路故障(横向故障): • 相间短路: • 两相短路故障 : 用K(2)表示 • 三相短路故障:用K(3)表示 • 接地短路: • 单相接地短路故障:用K(1)表示 • 两相接地短路:用K(1.1)表示 • 2、断线故障(纵向故障): • 单相断线故障(两相运行) :用F(1.1)表示 • 两相断线故障(单相运行) :用F(1)表示
出现零序电流、零序电压。 2、电流增大、电压降低为相同两个
相别。 3、零序电流向量为位于故障两相电
流间。 4、故障相间电压超前故障相间电流
约80度左右;零序电流超前零序 电压约110度左右。
电流电压的相位关系。(注意选取相位基准时应躲开故障初 始及故障结束部分,因为这两个区间一是非周期分量较大, 二是电压电流夹角由负荷角转换为线路阻抗角跳跃较大,容 易造成错误分析) 4、绘制向量图,进行分析。
三相短路故障录波图分析
分析三相短路故障录波图要点: 1、三相电流增大,三相电压降低;
没有零序电流、零序电压。 2、故障相电压超前故障相电流约80
两相短路保护安装处相量图
单相接地短路故障的特点
1、出现负、零序分量; 2、序网构成中正、负、零序分量串联,也即在正序的基础上串入了X∑2+X∑0 阻抗; 3、接地故障必然产生零序分量; 4、不对称故障必然产生负序分量; 5、短路点非故障相电流为零,对于单电源网络保护安装处非故障相电流也为零, 对于双电源网络当各序分量阻抗分配系数C1=C2=C0 即X1N/(X1M+X1N)=X2N/(X2M+X2N)=X0N/(X0M+X0N)时保护安装处 非故障相电流为零;不等时不为零。(此处所说的是故障分量,不包括故障前 的负荷电流) 6、故障相电压超前故障相电流一个线路阻抗角。 7、负、零序电流超前负、零序电压(180度减一个线路阻抗角)约105度。
电力系统不对称故障的分析-PPT

a1
.
Uc
.
.
aU a1 a 2 U a2
.
U a1
jX 2
. I a1
短路点得电流、电压相量图
Ua
IC
Ia2 Ia1 0
Ub Uc Ua
电压向量图
Ib
电流向量图
三、两相短路接地
Ua Ub Uc
a b c
Ia
Ib
Ic
jX f
➢短路点得边界条件为
U
b U c
Ia 0 j(Ib
.
Ib
.
I a0 a2
.
I a1 a
.
I a2
(a2
X 2 aX 0 X2 X0
)
.
I
a1
.
Ic.Leabharlann I a0.a I a1
a2
.
I a2
(a
X 2
a2 X0
. ) I a1
X2 X0
.
.
.
.
.
U a U a0 U a1 U a2 3U a1 j3
X 2 X 0
.
I a1
X 2 X 0
X 0 X1
E1
1.5
X 0 X1
2
X 0 X1
j
3 2
E1
Uc
j [(a
a2 ) X1
(a 1) X 0 ]
E12 j (2 X1
X0 )
(a
a2) 2
(a 1)
X 0 X1
X 0 X1
E1
1.5
X 0 X1
2 X0 X1
j
3 2
E1
➢非故障相电压得绝对值为
第二章的第二节多侧电源网络相间短路的方向性电流保护

第⼆章的第⼆节多侧电源⽹络相间短路的⽅向性电流保护第⼆节多侧电源⽹络相间短路的⽅向性电流保护⼀、⽅向性电流保护的⼯作原理实际的电⼒系统是由很多电源组成的复杂⽹络,此时,采⽤第⼀节中介绍的三段式电流保护不能满⾜选择性的要求。
图2-13 双侧电源⽹络接线及保护动作⽅向的规定(a )1d 点短路时的电流分布;(b )2d 点短路时的电流分布;(c )各保护动作⽅向的规定;例如在图2—13所⽰的双侧电源⽹络接线中,每条线路的两侧均需装设断路器和保护装置。
因为当线路上发⽣短路故障时,线路两侧分别流过各侧电源提供的短路电流,如果只在线路的⼀侧装设断路器和保护装置,实际上并不能真正切除故障。
假设保护1、2、3、4的电流速断仍按第⼀节中的整定原则,其起动电流依据电源1E 单独存在情况下整定;保护5、6、7、8的电流速断依据电源∏E 单独存在情况下整定。
在图2-13(a )中1d 点发⽣短路时,按照选择性的要求应该由距故障点最近的保护2和6动作切除故障。
然⽽,由电源∏E 供给的短路电流1d I ''也将通过保护1,如果1d I ''⼤于保护1电流速断的起动电流1.dz I ',则保护1的电流速断就要误动作。
因此,可以得出这样的结论:在双侧或多侧电源的复杂⽹络中,采⽤电流速断不能满⾜选择性的要求。
那么,此类⽹络中能否采⽤定时限过电流保护呢?结论也是否定的。
因为当1d 点短路时,要求25t t >;但是,当2d 点短路时,⼜要求52t t >。
这两个要求是不可能同时得到满⾜的。
对误动作的保护进⾏分析可知,误动作的原因是由对侧电源供给的短路电流引起的;此时误动作保护的实际短路功率⽅向是由线路流向母线的。
因此,为了消除双侧电源或多侧电源中三段式电流保护的⽆选择动作,需要在可能误动作的保护上增设⼀个功率⽅向闭锁元件。
该元件当短路功率⽅向由母线流向线路时动作,开放电流保护;⽽当短路功率⽅向由线路流向母线时不动作,闭锁电流保护。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、三相Байду номын сангаас路
故障点边界条件为
I kA I kB I kC 0;U kA U kB U kC
以对称分量法表示,则
.
.
.
.
.
.
I k 0 0;U kA1 0;U kA 2 0
三相短路电流向量图如下:
.
.
.
即短路电流向量仍然保持平衡,各项短路电压为零。
三、两相短路
故障点的边界条件为
I kA 0; I kB I kC ;U kB U kC
以对称分量形式表示故障点电压、电流边界条件:
.
.
.
.
.
I kA 0; I kA1 I kA 2 ;U kA1 U kA 2
向量图如下:
.
.
.
.
.
由向量图可知,A 相电流为零,B、C 相电流增大;A 相电压增大,B、C 相电压减小。
二、B、C 相接地短路。
故障点边界条件为
I kA 0;U kB 0;U kC 0
同上用对称分量表示,则
.
.
.
I kA1 I kA 2 I k 0 0
.
.
.
1 U kA1 U kA 2 U k 0 U kA 3
. . .
相量图如下:
有向量图可知, A相 电流为零,B、C 相电流 增大;A 相电压增大,B、C 相电压为零。
一、单相(A 相)接地短路
故障点边界条件
U kA 0; I kB 0; I kC 0
即
.
.
.
U kA U kA1 U kA 2 U kA0 0
. . 1 . 1. 2 I kA1 ( I kA a I kB a I kC ) I kA 3 3 .
. . . 1 . 1. I kA 2 ( I kA a 2 I kB a I kC ) I kA 3 3
.
.
.
.
又
I k0
.
. . 1 . 1. ( I kA I kB I kC ) I kA 3 3
kA1 kA 2 k0 所以 以上就是以对称分量形式表示的故障点电压和电流的边界条件。
I
.
I
.
I
.
向量图如下:
由向量图可知 A 相电流增大,B、C 相电流为零,A 相电压为零,B、C 相电压增大。
