用excel进行方差分析的实验报告
实验四 用EXCEL进行方差分析

实验四用EXCEL进行方差分析一、单因素方差分析例题1:某鞋厂为了比较几种不同材质的鞋跟耐磨程度,随机选取了十个人试穿一双鞋跟厚度相同的新鞋,分别用A、B、C三种不同的材质做成,试穿一个月后测量每个人所穿的两只鞋的鞋跟厚度,测得如下数据:试分析,在0.05的显著性水平下,三种材质的鞋跟质量有无显著性差别。
提出原假设:不同材料的鞋跟没有显著性差异表1.1单因素方差分析的汇总表组观测数求和平均方差材料A 10 38.5 3.85 0.196111材料B 10 36.4 3.64 0.202667材料C 10 38.3 3.83 0.189从各组的均值看,最低为3.64cm,最高为3.85cm。
从各组的方差看最小的为0.189,最大的等于0.202667。
表1.2单因素方差分析的方差分析表差异源SS df MS F P-value F crit组间0.268667 2 0.134333 0.685633 0.512328 3.354131组内 5.29 27 0.195926总计 5.558667 29由结果可知P值为0.512328,大于显著性水平0.05,因此接受原假设,即材料的不同并没有导致鞋跟质量有显著性差异。
二、用Excel进行无重复双因素方差分析例题2:假设四名工人操作机器A、B、C各一天,其日产量,分析在0.05的显著性水平下,机器或不同工人对日产量是否有显著影响。
原假设1:机器对日产量没有显著影响;原假设2:不同工人对日产量没有显著影响。
在数据分析中选择:无重复双因素分析得到如下所示结由分析结果可知:行因素的P值为0.014445,小于显著性水平0.05,即应拒绝原假设,可以认为机器对日产量有显著影响;列因素的P值为0.230838,大于显著性水平0.05,即应接受原假设,认为不同工人对日产量没有显著影响。
三、用Excel进行有重复双因素方差分析例题3:为考察通电方法和液温对某零件质量的影响,通电方法有3种A、B、C,液温选取两种水平(现行温度或增加10度)。
实验四用EXCEL实现方差分析

《田间试验设计与统计》实验
例4.3 将A1、 A2 、 A3 、 A4 四 种 生 长 素 , 并 用 B1 、 B2 、 B3 三 种 时 间 浸渍菜用大豆品 种 种 子 , 45 天 后 测得各处理的平 均 单 株 干 物 重 (g) 于 表 4.3 , 试 作 分 析。
用EXCEL实现方差分析
对于多重比较的EXCEL方法请参考前述有关内容, 在此不再赘述;而其它试验设计方法所获得的试验结 果的方差分析方法,请大家参考其它有关书籍自行学 习掌握。
而不同的试验设计方法所产生的变异来源不同完全随机设计可分为处理间变异和误差变异两部分随机区组设计则可分为处理间变异区组间变异和误差变异三部分而拉丁方设计则可以分为处理间变异横向区组间变异纵向区组间变异以及误差变异四个部分
《田间试验设计与统计》实验
用EXCEL实现方差分析
实验四 用EXCEL进行方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=IF(E35>=D$32,FIXED(E35,1)&”**”,IF(E35>=D$31,FIXED(E 35,1)&”*”,FIXED(E35,1)))”,并按住填充柄向左填充
第十步: 将梯形表中右 下角的无用数 据清除后,再 复制一次梯形 表,在第二个 梯形表中删除 所有差数,并 编制公式进行 填充,以获得 差异显著性。
《田间试验设计与统计》实验
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
▼注意修正公式中的单元 格引用,使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(D36>=D$32,FIXED(D36,1)&”**”,IF(D36>=D$31,FIXED(D 1)&”*”,FIXED(D36,1)))”,同理按住填充柄向左填充
实验四用EXCEL实现方差分析

实验四用EXCEL实现方差分析方差分析(Analysis of Variance, ANOVA)是一种用于比较两个或更多个样本均值是否显著不同的统计方法。
它通过比较各样本的方差是否相等来推断样本均值是否有显著差异。
本实验将使用EXCEL软件来实现方差分析。
1.实验目的掌握用EXCEL实现方差分析的方法,能够对不同样本的均值进行比较,并判断是否有显著差异。
2.实验原理方差分析是通过计算组间与组内的均方差(mean square)与自由度(degree of freedom)来推断是否存在差异显著的方法。
在EXCEL中使用方差分析的步骤主要包括数据录入、数据分析工具的使用、方差分析表的解读和结果的判断。
3.实验步骤Step 1: 数据录入首先将要分析的数据录入到EXCEL的工作表中,每组数据占用一列或一行,例如:组1:67,75,62,71,73组2:82,79,85,80,87组3:91,85,89,95,93Step 2: 数据分析工具的使用选择数据分析工具,依次点击"数据"-"数据分析",弹出数据分析对话框,选择"方差分析",点击"确定"。
Step 3: 填写方差分析对话框参数Step 4: 方差分析结果解读与判断EXCEL会生成方差分析表,其中包括组间均方(MSb),组内均方(MSw),总均方(MSt),标准误差(Sb),F值,自由度(df),P值等数据。
根据F值和P值来判断是否有显著差异。
通常,如果P值小于显著性水平(0.05),则拒绝原假设,即表示组间均值有显著差异。
4.实验注意事项(1)确保数据录入准确无误,符合方差分析的前提条件。
(2)需事先安装加载数据分析工具,具体操作方法可参考EXCEL软件帮助手册。
(3)在解读结果时,除了判断P值是否小于显著性水平之外,还要注意观察各组的均值和方差大小关系。
5.结论通过上述步骤,在EXCEL中可以快速实现方差分析,并得到方差分析表。
实验四用EXCEL实现方差分析

实验四用EXCEL实现方差分析方差分析(Analysis of Variance,简称ANOVA)是一种用于比较两个或多个组之间均值差异是否显著的统计方法。
在统计学中,方差分析被广泛应用于各个领域,如医学、社会科学、经济学等。
方差分析的基本原理是通过比较组间方差与组内方差的大小来推断均值之间的差异是否显著。
在进行方差分析之前,我们首先要明确研究对象和目的。
假设我们要分析一个实验的结果,该实验包含三个组,每个组有若干个样本。
我们的目标是确定这三个组的均值是否有显著差异。
在EXCEL中进行方差分析,首先需要收集所需的数据,并将其整理成适合进行分析的形式。
我们将每个组的数据放在一个列中,列的顶部标有组的名称。
接下来,我们将这些数据输入到EXCEL的数据分析工具中。
1.打开EXCEL,并选中数据分析工具。
在EXCEL的菜单栏中,选择“数据”选项卡,然后选择“数据分析”。
如果未能找到“数据分析”选项,则需要先启用此选项。
点击“文件”选项卡,在“选项”中选择“增益”选项,然后勾选“数据分析”选项。
2.选择方差分析工具。
在数据分析工具中,选择“方差分析”选项,然后点击“确定”。
3.输入数据范围。
在方差分析工具的对话框中,输入数据范围,即每个组的数据所在的列。
确认输入范围后,点击“确定”。
4.设置其它参数。
方差分析工具还提供了一些可选参数,如方差齐性检验、置信水平等。
如果不需要使用这些参数,可以直接点击“确定”。
5.分析结果。
EXCEL将自动生成方差分析报告,报告包含了各个组的均值、方差、自由度、F值、P值等统计指标。
通过分析这些指标,我们可以判断各个组之间的均值差异是否显著。
方差分析的结论要根据P值的显著性确定。
如果P值小于设定的显著性水平(通常为0.05),则说明各个组之间的均值差异是显著的;反之,如果P值大于显著性水平,则说明各组之间的均值差异不显著。
需要注意的是,方差分析只能用于比较两个或多个组之间的均值差异,不能确定具体是哪个组之间存在差异。
EXCEL中方差分析
方差分析1、单因素方差分析例1:一家管理咨询公司为不同的客户进行人力资源管理讲座。
每次讲座的内容基本上是一样的,但讲座的听课者有时是高级管理者,有时是中级管理者,有时是低级管理者。
该咨询公司认为,不同层次的管理者对讲座的满意度是不同的。
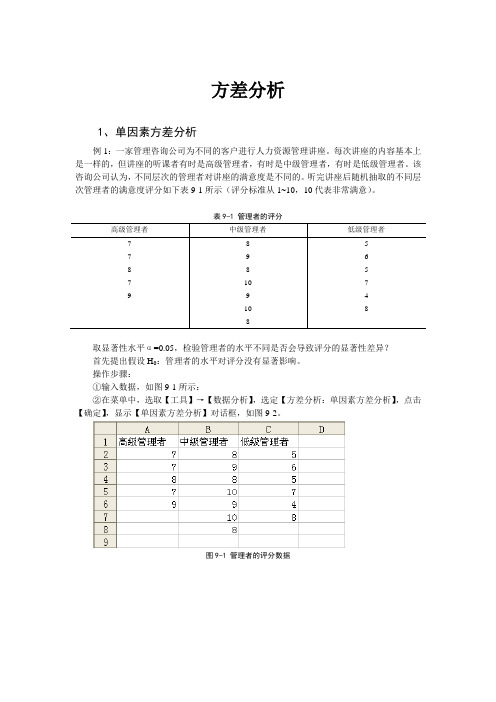
听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1所示(评分标准从1~10,10代表非常满意)。
表9-1 管理者的评分高级管理者中级管理者低级管理者7 8 57 9 68 8 57 10 79 9 410 88取显著性水平α=0.05,检验管理者的水平不同是否会导致评分的显著性差异?首先提出假设H0:管理者的水平对评分没有显著影响。
操作步骤:①输入数据,如图9-1所示:②在菜单中,选取【工具】→【数据分析】,选定【方差分析:单因素方差分析】,点击【确定】,显示【单因素方差分析】对话框,如图9-2。
图9-1 管理者的评分数据图9-2 单因素方差分析对话框③在“输入区域”框输入数据矩阵(首坐标:尾坐标),可选为“A1:C8”,点选“标志位于第一行”,在“分组方式”框选定“列”,指定显著水平α=0.05,输出选项的输出区域可为工作表的任何位置,本例选择在I4处。
④点击【确定】,则得输出结果,如下图9-3所示。
图9-3 单因素方差分析结果图9-3是一个单因素方差分析结果的报告。
第一个表是有关各样本的一些描述统计量,它可以作为方差分析的参考信息。
第二个表是方差分析结果。
其中SS 表示平方和,df 为自由度,MS 表示均方,F 为检验的统计量,P-value 为用于检验的P 值,F crit 为给定α水平下的临界值。
从方差分析表可以看到,由于68232.375573.11=>=αF F ,所以拒绝原假设,即管理者的水平对评分的影响是显著的。
在进行决策时,可以直接利用方差分析表中的P 值与显著性水平α的值进行比较,若 P <α,则拒绝原假设;若P >α,则不能拒绝原假设。
Excel中的单因素方差分析

Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题,需要应用方差分析。
方差分析是把试验看成一个整体,分解各种变异的原因。
从总的方差中,将可能的变异原因逐个分出,并用误差的方法作为判断其他方差是否显著的标准,如果已知变异原因的方差比误差方差大得多,那么,该方差就不是随机产生的,试验的处理间的差异不会是由于误差原因造成的,这时处理的效应是应该肯定的。
通过学习Excel中方差分析,掌握基本的分析操作,能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法2、例:在五个硼肥试验处理中测得苹果叶内硼含量(ppm),试比较各处理苹果叶内平均含硼量的差异显著性。
3、操作步骤:在Excel统计中,完全随机试验设计的方差分析,只须经过单因素方差分析即可得出结果,具体步骤如下:①打开Excel,向单元格中输入文字与数字,建立表格;②单击“工具”,在出现的对话框中,选择“数据分析”,选取“方差分析: 单因素方差分析”;③单击“确定”,单击“输入区域:”框右边的按钮,用鼠标选中数据,再次单击按钮;其他设置选择a为0.05。
分组方式:行。
点选标志位于第一列④单击“确定”,即可输出单因素方差分析结果。
4、方差分析输出结果: SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.55、多重比较:由方差分析的结果,采用新复极差测验法,再稍加计算比较处理, 即可得出:新复极差测验的LSR值6结论:由方差分析结果F=94.17>F o.o5=Fcrit=2.76,可知5种喷硼处理间差异显著,并可知除E与B二处理间无极显著差异外,其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析,是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题,如各组之间有显著差异,说明这个因素(分类变量)对因变量是有显著影响的,因素的不同水平会影响到因变量的取值。
试验六、 用excel进行方差分析

地区A 方案B B1
A1
354 336
B2
385 392
B3
360 371
A2
342 367
390 377
353 374
A3
330 352
388 380
378 359
数据转换 反正旋转换:
处理 对照
1
2
3
97
95
93
70
91Biblioteka 777868
82
72
75
66
85
64
76
49
78
56
63
55
77
68
71
64
练习:课本122页 例6.14。 127-129页所有的习题 实验报告:P128习题6.9
库”) -------“单因素方差分析”-------点 击确定,根据要求,输入数据,得到结
果。
例:某公司对新销售人员进行不同的销售培训。 为了比较培训课程的有效性,随机选择了三组销 售人员,每组五人,一组接受A课程训练,一组接 受B课程训练,另一组C不接受任何训练。当前两 组的训练课程结束时,收集训练后两个星期内各 组销售人员的销售记录,进行方差分析。
实验六 运用EXCEL进行方差分析 实验目的:熟练掌握运用EXCEl进 行方差分析。 实验材料:计算机,EXCEL软件 实验地点:机房 实验内容:
单向分组资料方差分析
• 此类资料由完全随机试验获得
• 步骤:
•
输入数据-------从菜单中找到“工
具”------- 选择“数据分析”(如没有,
选择“加载宏”,然后选择“分析工具
A课程
2058 2176 3449 2517 944
实验三 用Excel进行方差分析实验报告

3种课程训练平均销售记录多重比较表
课程 B课程 A课程 C课程
平均数 x i 2928 2228.8 1951.6
x i 1951 6 . 976.4 277.2
x i 2228.8 699.2
因为MSe 3992323, n 5, 所以标准误 x 为 . s
的提高无显著影响,不 同改革方
q0.01 6.93 5.95 5.41
LSR0.05 1.6996 1.5288 1.4280
LSR0.01 3.0356 2.6063 2.3698
进一步对改革方案各水 平平均经
3.多重比较
品种小麦收获量极显著高于B4品种,但B1、B2和B3品
方案
B2 B3
B1
式为
F值 1.61 20.49**
自由度df 均方MS 4 3.5245 3 44.8818 12 2.1902 19
SS B
1 1 x2j C 3 2 (20 an
2415655 2411208 444
SSAB SSAB SSA SSB 469
因为MSe 3992323, n 5, 所以标准误 x 为 . s
s x MSe / n 3992323 / 5 282.5712 .
q值与LSR值
dfe
12
秩次距 2 3
q0.05 3.08 3.77
q0.01 4.32 5.05
LSR0.05 870.3193 1065.2934
A2
单个观测值试验资料。A因素有5个水平,即a=5
b=5× 4=20个观测值。方差分析如下:
实验六协方差分析(Excel)

如何运用统计方法对数据进行分析和解释。
实验不足与改进
数据预处理不足
在实验过程中,我们可能没有对原始数据进行充分的预处理,导致分析结果受到异常值或 离群点的影响。在未来的实验中,应更加注重数据预处理环节,确保数据的准确性和可靠 性。
实验操作不够熟练
由于本次实验是首次接触协方差分析,我们在操作过程中可能存在一些不熟练的情况,导 致分析过程出现误差。未来可以通过多加练习和熟悉操作来提高实验操作的准确性。
分析协方差值的大小和正负,判 断变量之间的关联程度和方向。
结果应用
根据协方差分析的结果,可以进一步探讨变量之间的关系,以及它们对目标变量的 影响。
可以利用协方差分析的结果进行更深入的数据挖掘和统计分析,例如回归分析、因 子分析等。
将协方差分析的结果应用于实际问题的解决,例如市场调查、经济预测、医学研究 等领域。
Excel软件准备
安装Excel软件
确保计算机上已安装Microsoft Excel 软件。
打开Excel
设置工作表
在工作簿中设置一个工作表用于输入 数据和进行统计分析。
打开Excel软件,创建一个新的工作簿。
实验环境准备
安静的环境
确保实验环境安静,避免 干扰,以便专注于实验过 程。
充足的时间
根据实验复杂度和数据量, 预留充足的时间进行实验 操作和分析。
04
实验总结
实验收获
掌握Excel协方差分析工具的使用
01
通过本次实验,我们学会了使用Excel的协方差分析工具,了解
了如何利用该工具进行数据的协方差分析。
理解协方差分析原理
02
在实验过程中,我们深入学习了协方差分析的基本原理,理解
统计学实验报告
《统计学》实验一一、实验名称:数据的图表处理二、实验日期:三、实验地点:管理学院实验室四、实验目的和要求目的:培养学生处理数据的基本能力。
通过本实验,熟练掌握利用Excel,完成对数据进行输入、定义、数据的分类与整理。
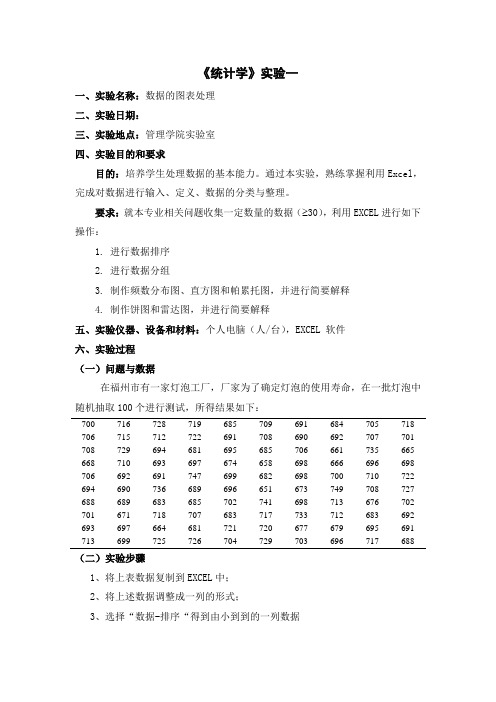
要求:就本专业相关问题收集一定数量的数据( 30),利用EXCEL进行如下操作:1.进行数据排序2.进行数据分组3.制作频数分布图、直方图和帕累托图,并进行简要解释4. 制作饼图和雷达图,并进行简要解释五、实验仪器、设备和材料:个人电脑(人/台),EXCEL 软件六、实验过程(一)问题与数据在福州市有一家灯泡工厂,厂家为了确定灯泡的使用寿命,在一批灯泡中随机抽取100个进行测试,所得结果如下:700716728719685709691684705718 706715712722691708690692707701 708729694681695685706661735665 668710693697674658698666696698 706692691747699682698700710722 694690736689696651673749708727 688689683685702741698713676702 701671718707683717733712683692 693697664681721720677679695691 713699725726704729703696717688(二)实验步骤1、将上表数据复制到EXCEL中;2、将上述数据调整成一列的形式;3、选择“数据-排序“得到由小到到的一列数据4、选择“插入-函数(fx)-数学与三角函数-LOG10”计算lg100/lg2=6.7,从而确定组数为K=1+ lg100/lg2=8,这里为了方便取为10组;确定组距为:(max-min)/K=(749-651)/10=9.8 取为10;5、确定接受界限为 659 669 679 689 699 709 719 729 739 749,分别键入EXCEL 表格中,形成一列接受区域;6、选“工具——数据分析——直方图”得到如下频数分布图和直方图表1 灯泡使用寿命的频数分布表图1 灯泡使用寿命的直方图(帕累托图)7、将其他这行删除,将表格调整为:表2 灯泡使用寿命的新频数分布表8、选择“插入——图表——柱图——子图标类型1”,在数据区域选入接收与频率两列,在数据显示值前打钩,标题处键入图的名称图2 带组限的灯泡使用寿命直方图9、双击上述直方图的任一根柱子,将分类间距改为0,得到新的图图2 带组限的灯泡使用寿命直方图图3 分类间距为0的灯泡使用寿命直方图10、选择“插入——图表——饼图”,得到:图4 灯泡使用寿命分组饼图11、选择“插入——图表——雷达图”,得到(三)实验结果分析:从以上直方图可以发现灯泡使用寿命近似呈对称分布,690-700出现的频次最多,690-700的数量最多,说明大多数处于从饼图和饼图也能够清晰地看出结果。
实验 利用EXCEL软件进行方差分析(一)
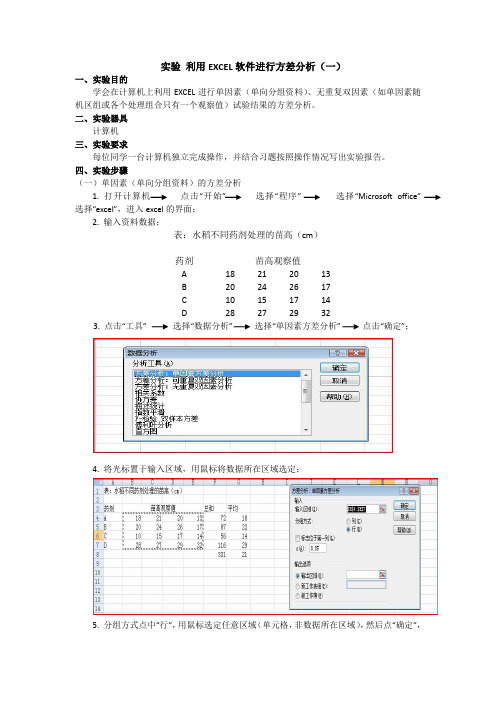
实验利用EXCEL软件进行方差分析(一)一、实验目的学会在计算机上利用EXCEL进行单因素(单向分组资料)、无重复双因素(如单因素随机区组或各个处理组合只有一个观察值)试验结果的方差分析。
二、实验器具计算机三、实验要求每位同学一台计算机独立完成操作,并结合习题按照操作情况写出实验报告。
四、实验步骤(一)单因素(单向分组资料)的方差分析1. 打开计算机点击“开始” 选择“程序” 选择“Microsoft office” 选择“excel”,进入excel的界面;2. 输入资料数据;表:水稻不同药剂处理的苗高(cm)药剂苗高观察值A 18 21 20 13B 20 24 26 17C 10 15 17 14D 28 27 29 323. 点击“工具” 选择“数据分析” 选择“单因素方差分析” 点击“确定”;4. 将光标置于输入区域,用鼠标将数据所在区域选定;5. 分组方式点中“行”,用鼠标选定任意区域(单元格,非数据所在区域),然后点“确定”,即可得到结果。
(二)无重复双因素(如单因素随机区组或各个处理组合只有一个观察值)试验结果的方差分析1. 打开计算机点击“开始” 选择“程序” 选择“Microsoft office” 选择“excel”,进入excel的界面;2. 输入资料数据,例如;表:小麦品比试验(随机区组)的产量结果(kg)品种区组T t ⅠⅡⅢA 10.9 9.1 12.2 32.2B 10.8 12.3 14.0 37.1C 11.1 12.5 10.5 34.1D 9.1 10.7 10.1 29.9E 11.8 13.9 16.8 42.5F 10.1 10.6 11.8 32.5G 10.0 11.5 14.1 35.6H 9.3 10.4 14.4 34.13. 点击“工具” 选择“数据分析” 选择“无重复双因素方差分析” 点击“确定”;4. 将光标置于输入区域,用鼠标将数据所在区域选定;5. 将光标置于输出区域,用鼠标选定任意区域(单元格,非数据所在区域),然后点“确定”,即可得到结果。
实验七 方差分析的EXCEL应用

作业
• 1.用四种不同的分析方法测定同一药物的某种成分 的含量,测得数据如下:试判断这四种方法的测量 的含量,测得数据如下: 结果有无显著性差异。(α=0.05) 。(α 结果有无显著性差异。( =0.05)
检验结果作出合理的解释。 检验结果作出合理的解释。
方差分析的EXCEL应用 实验七 方差分析的 应用
二、实验内容
单因素试验
组内观测值数目相等 组内观测值数目不等
两因素试验
无重复观测值 有重复观测值
方差分析的基本原理
自由度和平方和的分解
SSt、SSe 、 DFt、DFe 、
F测验 测验
变异来源 处理间 误差 总
• 例7.1 考察催化剂对某药得率的影响,现用4种不同的 考察催化剂对某药得率的影响,现用4 催化剂独立地在相同条件下进行试验,每种催化剂各做 催化剂独立地在相同条件下进行试验, 5次试验,得到的该药得率如下表所示。 次试验,得到的该药得率如下表所示。 • 试问不同的催化剂是否对该药的得率有显著影响? 试问不同的催化剂是否对该药的得率有显著影响?
实验七 方差分析的EXCEL 方差分析的EXCEL 应用
实验七 方差分析的EXCEL应用 方差分析的EXCEL EXCEL应用
一、实验目的 • ① 通过本实验掌握单因素方差分析和双因素
方差分析的方法; 方差分析的方法; • ② 利用EXCEL软件独立进行方差分析, 利用EXCEL软件独立进行方差分析,并对 EXCEL软件独立进行方差分析
DF
实验六 协方差分析(Excel)

实验名称、时间、地点 实验内容 主要方法 关键运算结果 讨论 比较协方差分析和方差分析有何异同
所有练习结果
软盘
t
yi ( x x ) y j ( x x ) sD
df k (n 1) 1
方法:
利用Excel函数
SUM () AVERAGE() DEVSQ() SUMPRODUCT() SUMSQ() FINV () TINV ()
实验报告Leabharlann 书面
实验六
协方差分析
内容:
回归模型
统计控制
将未加或难以控制的因素x对y的影响看做协变量,建立y依x而变
化的线性回归方程
将各个y值都矫正到x在同样水平时,比较 y i ( xi x )
差异显著性
相关模型
计算遗传参数
回归模型
平方和、乘积和及自由度剖分
SUMSQ()、DEVSQ()、 SUMPRODUCT () 或COVAR()*n
检验x和y是否存在直线关系
F=U/(Q/n-2)
矫正平均数间差异是否存在
F=处理间/处理内(矫正后)
多重比较
类似于回归截距间的比较
矫正平均数间的多重比较
yi ( x x ) yi b( xi x )
2 1 1 ( xi x j ) sD MSe[ ] n1 n2 SS( e ) x
用excel进行方差分析的实验报告

用excel进行方差分析的实验报告实验四:用excel进行方差分析的实验报告实验目的:学会在计算机上利用excel进行单因素方差分析和有交互的双因素分析以及无交互的双因素分析,实验背景:方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
一个复杂的事物,其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显著影响的因素,各因素之间的交互作用,以及显著影响因素的最佳水平等。
方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
对变差的度量,采用离差平方和。
实验内容:实验(1):单因素方差分析条件:单因素方差分析是对成组设计的多个样本均数比较,所以对数据格式有特殊要求,因素的不同水平作为表格的列(或行),在不同水平下的重复次数作为行(或列)。
例1:以下数据来自2009年中国统计年鉴,各地区农村居民家庭平均每人生活消费支出,按不同项目分组的不同地区:其中,1代表生活消费支出合计,2代表食品,3代表衣着,4代表居住, 5代表家庭设施及服务, 6代表交通和通讯, 7代表文教娱乐用品及服务,8代表医疗保健, 9代表其他商品及服务各地区农村居民家庭平均每人生活消费支出 (2009年)单位:元地区项目地区生活消费食品衣着居住家庭设备交通和文教娱乐医疗保健其他品支出合计及服务通讯用品及服务及务地区 1 2 3 4 5 6 7 8北京8897.59 2808.92 654.36 1798.88 528 1132.09 960.41 867.87 14天津4273.15 1848.11 324.63 674.67 187.83 481.27 371.85 299.79 8河北3349.74 1195.65 217.82 796.62 170.4 350.92 263.53 289.27 6山西3304.76 1224.6 283.2 584.07 156.27 324.89 416.94 240.94 7内蒙古3968.42 1578.57 271.88 609.29 148.03 466.34 390.85 416.87 8辽宁4254.03 1563.33 335.93 793.91 185.5 416.41 437.79 409.64 11吉林3902.9 1371.12 286.97 737.07 168.36 355.99 376.76 511.5 9黑龙江4241.27 1331.07 345.69 946.84 161.03 427.35 496.42 434.25 9上海9804.37 3639.14 496.14 2102.96 480.62 1212.38 942.76 738.94 19江苏5804.45 2275.28 306.62 969.76 286.37 691.56 818.45 322.99 13浙江7731.7 2812.39 473.11 1488.95 374.31 968.17 843.34 609.07 16安徽3655.02 1494.19 203.37 813.12 229.66 302.23 312.05 227.1 福建5015.72 2304.14 291.72 821.21 260.68 570.24 421.69 219.02 12江西3532.66 1609.2 162.58 725.11 181.91 295.76 254.77 232.78 7山东4417.18 1618.66 265.59 945.81 273.77 533.55 399.95301.55河南3388.47 1220.36 225.64 875.83 203.81 310.11 234.01 242.87 7湖北3725.24 1668.35 195.45 702.62 229.32 307.22 281.68 236.31 10步骤:(1)、在excel的分析工具库中中选择“方差分析:单因素方差分析”指定相应的数据区域和显著性水平,点击“确定”后输出最终输出结果:表一方差分析:单因素方差分析SUMMARY组观测数求和平均方差列 1 32 129281.5 4040.048 3465440列 2 32 52249.75 1632.805 428309.6列 3 32 7951.16 248.4738 15408.02列 4 32 25251.6 789.1125 162323.1列 5 32 6519.28 203.7275 10263列 6 32 13547.29 423.3528 66285.85列 7 32 11279.63 352.4884 55136列 8 32 9809.81 306.5566 31281.44列 9 32 2716.05 84.87656 1665.067 表一是各组数据的描述统计指标。
基于Excel2003软件的单因素方差分析实验报告
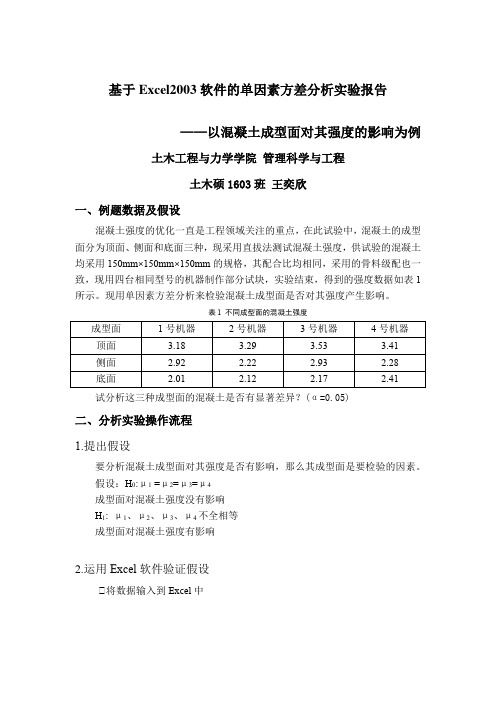
基于Excel2003软件的单因素方差分析实验报告——以混凝土成型面对其强度的影响为例土木工程与力学学院管理科学与工程土木硕1603班王奕欣一、例题数据及假设混凝土强度的优化一直是工程领域关注的重点,在此试验中,混凝土的成型面分为顶面、侧面和底面三种,现采用直拔法测试混凝土强度,供试验的混凝土均采用150mm×150mm×150mm的规格,其配合比均相同,采用的骨料级配也一致,现用四台相同型号的机器制作部分试块,实验结束,得到的强度数据如表1所示。
现用单因素方差分析来检验混凝土成型面是否对其强度产生影响。
表1 不同成型面的混凝土强度试分析这三种成型面的混凝土是否有显著差异?(α=0.05)二、分析实验操作流程1.提出假设要分析混凝土成型面对其强度是否有影响,那么其成型面是要检验的因素。
假设:H0:μ1 =μ2=μ3=μ4成型面对混凝土强度没有影响H1: μ1、μ2、μ3、μ4不全相等成型面对混凝土强度有影响2.运用Excel软件验证假设①将数据输入到Excel中图1 输入数据②在工具栏点击加载宏选项,跳出对话框,如图2,勾选分析工具库,选中后点击确定。
图2 加载宏③再次在工具栏点击数据分析选项,跳出对话框如图3,选择“方差分析:单因素方差分析”选项,选中后点击确定。
图3 选择分析方法④开始选择数据,以行分组,如图4,点击输入区域框右侧的图标,开始在工作簿上划定区域,或者直接输入数据所在的行、列范围,如$B$2:$E$4,所选范围边界呈虚线状,并会显示区域范围名称,如图5。
图4 选择数据图5 区域选择完成⑤点击enter键后,跳出对话框如图6,确认数据输入区域,检查置信水平α,是否符合要求,不符合的话可以输入更改,本题的显著性水平为0.05。
选择分析结果输出在新的工作簿上。
(也可以如上一步操作一样在现有的工作簿上划区域选择分析结果输出的范围),点击确定。
图6 输出选择⑥输出结果如图7图7 输出结果3.得出结果由上图可知,因为:F=20.94075>4.256496,所以拒绝H不同成型面的混凝土平均强度有显著差异,有理由认为混凝土成型面对混凝土的强度有显著影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四:用excel进行方差分析的实验报告实验目的:学会在计算机上利用excel进行单因素方差分析和有交互的双因素分析以及无交互的双因素分析,实验背景:方差分析是从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
一个复杂的事物,其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显著影响的因素,各因素之间的交互作用,以及显著影响因素的最佳水平等。
方差分析是在可比较的数组中,把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
对变差的度量,采用离差平方和。
实验内容:实验(1):单因素方差分析条件:单因素方差分析是对成组设计的多个样本均数比较,所以对数据格式有特殊要求,因素的不同水平作为表格的列(或行),在不同水平下的重复次数作为行(或列)。
例1:以下数据来自2009年中国统计年鉴,各地区农村居民家庭平均每人生活消费支出,按不同项目分组的不同地区:其中,1代表生活消费支出合计,2代表食品,3代表衣着,4代表居住, 5代表家庭设施及服务, 6代表交通和通讯, 7代表文教娱乐用品及服务,8代表医疗保健, 9代表其他商品及服务各地区农村居民家庭平均每人生活消费支出 (2009年)单位:元地区项目地区生活消费食品衣着居住家庭设备交通和文教娱乐医疗保健其他品支出合计及服务通讯用品及服务及务地区 1 2 3 4 5 6 7 8北京8897.59 2808.92 654.36 1798.88 528 1132.09 960.41 867.87 14天津4273.15 1848.11 324.63 674.67 187.83 481.27 371.85 299.79 8河北3349.74 1195.65 217.82 796.62 170.4 350.92 263.53 289.27 6山西3304.76 1224.6 283.2 584.07 156.27 324.89 416.94 240.94 7内蒙古3968.42 1578.57 271.88 609.29 148.03 466.34 390.85 416.87 8辽宁4254.03 1563.33 335.93 793.91 185.5 416.41 437.79 409.64 11吉林3902.9 1371.12 286.97 737.07 168.36 355.99 376.76 511.5 9黑龙江4241.27 1331.07 345.69 946.84 161.03 427.35 496.42 434.25 9上海9804.37 3639.14 496.14 2102.96 480.62 1212.38 942.76 738.94 19江苏5804.45 2275.28 306.62 969.76 286.37 691.56 818.45 322.99 13浙江7731.7 2812.39 473.11 1488.95 374.31 968.17 843.34 609.07 16安徽3655.02 1494.19 203.37 813.12 229.66 302.23 312.05 227.1福建5015.72 2304.14 291.72 821.21 260.68 570.24 421.69 219.02 12江西3532.66 1609.2 162.58 725.11 181.91 295.76 254.77 232.78 7山东4417.18 1618.66 265.59 945.81 273.77 533.55 399.95 301.55河南3388.47 1220.36 225.64 875.83 203.81 310.11 234.01 242.87 7湖北3725.24 1668.35 195.45 702.62 229.32 307.22 281.68 236.31 10步骤:(1)、在excel的分析工具库中中选择“方差分析:单因素方差分析”指定相应的数据区域和显著性水平,点击“确定”后输出最终输出结果:表一方差分析:单因素方差分析SUMMARY组观测数求和平均方差列 1 32 129281.5 4040.048 3465440列 2 32 52249.75 1632.805 428309.6列 3 32 7951.16 248.4738 15408.02列 4 32 25251.6 789.1125 162323.1列 5 32 6519.28 203.7275 10263列 6 32 13547.29 423.3528 66285.85列 7 32 11279.63 352.4884 55136列 8 32 9809.81 306.5566 31281.44列 9 32 2716.05 84.87656 1665.067 表一是各组数据的描述统计指标。
从各组的均值看,最低的为84.87656,最高的为4040.048。
从各组的方差看最小的为1665.067,最大的等于3465440。
判断数据是否符合同法差假设的一个经验方法是:如果各组织中最大的方差与最小方差之比不超过4,就可以认为是同法差。
此例子中的比值明显大于4,可能违背了同方差假设。
表2方差分析差异源SS df MS F P-value F crit组间 4.12E+08 8 51448014 109.3059 2.13E-81 1.971665组内 1.31E+08 279 470679.1总计 5.43E+08 287如果假设数据是同方差的,则方差分析中得到的p值2.13E-81小于0.05,因此拒绝零假设,检验的结论是以上项目对家庭平均每人生活消费支出有显著影响。
实验(2)进行无重复双因素方差分析无重复方差分析是分析两个因素对观测变量的独立影响。
例2:分析不同品种、不同施肥量对农作物产量的影响时,可将农作物产量作为观测变量,品种和施肥量作为控制变量。
利用双因素方差分析方法,研究不同品种、不同施肥量是如何影响农作物产量的,并进一步研究哪种品种与哪种水平的施肥量是提高农作物产量的最优组合。
如表所示为不同品种、不同施肥量对每亩农作物产量的影响单位(吨)。
施肥量(g)氮肥磷肥钾肥混合肥料1 0.256752 0.482131 0.475753 0.2850122 0.394818 0.591235 0.547889 0.4789273 0.780786 0.834162 0.099826 0.391984 0.951811 0.510636 0.450697 0.6657925 0.857387 0.466231 0.333811 0.9033786 0.429975 0.139531 0.107242 0.8754337 0.324168 0.050702 0.125126 0.7958018 0.152196 0.03456 0.04181 0.5709719 0.002747 0.000123 0.001456 0.47322步骤:在excel的分析工具库中中选择“方差分析:无重复双因素方差分析”指定相应的数据区域和显著性水平,点击“确定”后输出结果显示如下:方差分析:无重复双因素分析SUMMARY 观测数求和平均方差1 4 1.499649 0.374912 0.014572 4 2.012869 0.503217 0.0073613 4 2.106754 0.526688 0.1198214 4 2.578936 0.644734 0.0501245 4 2.560808 0.640202 0.0801916 4 1.552181 0.388045 0.1266387 4 1.295796 0.323949 0.112288 4 0.799537 0.199884 0.06419 4 0.477546 0.119387 0.055645氮肥9 4.150639 0.461182 0.108927 磷肥9 3.109312 0.345479 0.088124 钾肥9 2.183611 0.242623 0.04377 混合肥料9 5.440514 0.604502 0.048056方差分析差异源SS df MS F P-value F crit 行 1.072058 8 0.134007 2.595867 0.033646 2.355081 列0.653227 3 0.217742 4.217908 0.015714 3.008787 误差 1.23896 24 0.051623总计 2.964245 35从分析结果可以看出,行因素即不同品种的肥料的p值为0.033646小于0.05,列因素,即施肥量的p值为0.015714,也小于0.05,可见不同品种、不同施肥量农作物的产量有显著何影响。
所以提醒农民在种植农作物是要合理施肥,并不是施肥越多越好。
实验(3)进行有重复双因素方差分析与无重复的双因素方差分析方法不同,有重复的双因素方差分析可以分为有交互作用和无交互作用两种情况,无交互作用的双因素方差分析,它假定因素A和因素B的效应之间是相互独立的,不存在相互关系;有交互作用的双因素方差分析,它假定因素A和因素B的结合会产生出一种新的效应。
但excel只能分析有交互作用的情况。
例3:假定不同地区的消费者对某种颜色有与其他地区消费者不同的特殊偏爱,一家饮料公司在A、B、C、D、E五个地区销售茶饮料、营养快线、果汁三种饮料。
为了比较不同颜色的包装(红、黄、蓝)对销售额的影响,收集了一些数据,假设数据是正态分布和等方差的。
在0、05的显著性水平下,分析各因素及其交互作用是否显著。
如下图所示地区A B C D E产品类别茶饮料33.33383 28.2232 38.37822 33.59415 26.2789222.49046 4.670718 22.12519 25.45866 21.8648934.06555 43.30196 36.38367 41.65873 42.91192 营养快线32.20557 27.69192 32.42379 34.77793 34.5581216.12655 18.47858 22.37859 26.37849 34.8748936.14277 37.18354 26.45575 23.36641 30.36626果汁34.34963 40.78914 22.40878 33.49535 26.99414 39.82528 29.81375 26.38293 29.1184 42.51924 28.92406 26.879 29.69658 21.56876 17.35989步骤:在excel的分析工具库中中选择“方差分析:可重复双因素方差分析”指定相应的数据区域和显著性水平,并指明每种处理重复的次数,然后点击“确定”后输出输出结果如下:方差分析:可重复双因素分析SUMMARY A B C D E 总计茶饮料观测数 3 3 3 3 3 15求和89.88984 76.19588 96.88708 100.7115 91.05573 454.7401平均29.96328 25.39863 32.29569 33.57051 30.35191 30.316方差42.01611 379.0769 78.57396 65.61105 123.1864 106.67营养快线观测数 3 3 3 3 3 15求和84.4749 83.35404 81.25814 84.52284 99.79928 433.4092平均28.1583 27.78468 27.08605 28.17428 33.26643 28.89395方差112.4476 87.47538 25.52448 34.97431 6.333295 43.39572 果汁观测数 3 3 3 3 3 15求和103.099 97.48189 78.48829 84.1825 86.87327 450.1249平均34.36632 32.49396 26.16276 28.06083 28.95776 30.00833方差29.70937 53.76061 13.31434 36.3997 161.1401 51.65815 总计观测数9 9 9 9 9求和277.4637 257.0318 256.6335 269.4169 277.7283平均30.8293 28.55909 28.51483 29.93521 30.8587方差53.6913 139.855 37.5539 41.68236 76.29028方差分析差异源SS df MS F P-value F crit样本16.79379 2 8.396897 0.1008 0.904419 3.31583列48.34576 4 12.08644 0.14509 0.963768 2.689628交互276.7021 8 34.58777 0.415205 0.902686 2.266163内部2499.087 30 83.3029总计2840.929 44从分析结果可以看出,样本因素,即产品类别的P值为0.904419,大于0.05,则说明产品类别对销售收入没有显著影响,列因素颜色的P值也大于0.05,列因素地区的P 值也大于0.05,都说明地区、颜色对销售收入没有显著影响,这与现实意义不符合,这说明公司的调查人员在统计时,没有履行公正、客观、诚实的原则,数据的可靠性与真实性不高。
