静电场之均匀带电线段的电场
基于Matlab的静电场电场线和等势线(面)的数值模拟

基于Matlab的静电场电场线和等势线(面)的数值模拟作者:王红兵来源:《教育教学论坛》2017年第49期摘要:利用Matlab软件模拟描绘了静电场的电场线和等势线(面),以电偶极子、均匀带电线段和等量异号平行直线电荷为例,导出了电场线和等势线方程并给出了数值模拟的相应结果,使教学内容更形象和直观,也更深刻地揭示了物理现象的内涵。
关键词:大学物理;Matlab;电场线;等势线(面);数值模拟中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2017)49-0193-03在大学物理的教学中,除理论分析、实验研究外,计算机数值模拟也是一种很重要的研究方法。
Matlab是一套高性能的数值计算和可视化数学软件,集数值分析、矩阵运算、信号处理和图形显示等功能于一体[1]。
其丰富的数学函数使得用Matlab进行数值模拟时程序变得简洁易懂,不像其他高级语言那样要从底层开始编写复杂的程序[2]。
在研究如电磁学等的同类问题时,只需将Matlab代码稍加改动即可,类似的代码可重复使用,减轻了编程工作量。
Matlab 强大的功能为大学物理教学的数值化和可视化提供了强有力的手段。
用这种语言编程可以方便地用图形、图像、动画等形象直观地描述物理过程和物理现象,有助于学生对物理问题的深刻理解[3]。
本文用Matlab软件在大学物理电磁学的教学中进行了一些有益的尝试,用这种软件以电偶极子、均匀带电线段和等量异号平行直线电荷的静电场为例分析了数值模拟的过程并给出了模拟的结果。
一、电偶极子的电场如图1所示为两个相距为2a的等量异号点电荷+q和-q组成的点电荷系,称为电偶极子。
由点电荷的电势公式及电势的叠加原理,可求得场点P(x,y)处产生的电势为V= - ,式中,r 和r 是场点P到两点电荷的距离r = ,r = 。
若取a为坐标单位,且令V = ,x′= ,y′= (V 为点电荷q在原点处产生的电势),则电势可表示为V=V ( - ),当场点P到电偶极子的距离比两点电荷的间距大得多时,即x>>a,则有r ≈r+acosθ,r ≈r-acosθ。
静电场之均匀带电圆环-圆盘和圆圈在轴线上的电场共17页文档

31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确
静电场之均匀带电圆柱面圆柱体和圆柱壳的电场

电场的唯一性定理
在给定的边界条件下,对于一个封闭的静电场,其电场分布 是唯一的。
唯一性定理是静电场的基本性质之一,它确保了在给定电荷 分布和边界条件下,电场分布的唯一性和确定性。
THANKS FOR WATCHING
感谢您的观看
电场强度与电荷密度的关系
电场强度与电荷密度成正比,即电荷 密度越大,电场强度越大。
在均匀带电圆柱面中,电场强度的大 小与电荷密度的大小成正比,比例系 数为介电常数。
电场分布的几何解释
电场分布的几何解释可以通过高斯定理来理解,高斯定理表明,在静电场中,穿过任意闭合曲面的电场强度通量等于该闭合 曲面内所包围的电荷量。
电场线的疏密
由于电场强度与距离成反比,因此电 场线在靠近圆柱体的一侧较为密集, 远离圆柱体的一侧较为稀疏。
04
均匀带电圆柱壳的电场
均匀带电圆柱壳的电场分布
圆柱壳内
电场强度为零,因为内部没有电荷分布。
圆柱壳外
电场强度与电荷密度成正比,方向垂直于圆柱壳表面。
电场强度与电荷密度的关系
电场强度E与电荷密度ρ成正比,即E=kρ,其中k是常数。 电场强度的大小与电荷密度的分布范围有关,电荷密度越大,电场强度越高。
对于均匀带电圆柱面,由于电场分布是轴对称的,因此可以通过计算垂直于轴线的任意一个圆环上的电场强度通量来理解整 个圆柱面的电场分布。
03
均匀带电圆柱体的电场
均匀带电圆柱体的电场分布
圆柱体电荷分布
假设圆柱体长度Biblioteka L,半径为R,电荷线密度为λ,则电荷均匀分布在圆柱体的轴线 上。
电场分布
根据高斯定理,圆柱体外部的电场线与圆柱体轴线平行,且电场强度E与距离圆柱体 轴线的距离r成反比,即E=λ/2πrε0。
静电场复习

解:(1)
4o r 2 1 q 2 we o E 2 4 2 32 o r
2
E
q
+ -
+ R3 -
dV 4 r U V V E d
电场力的功与电势能:E
E
W
q0
E d
V
E q0
W
q 0 ( V ) qUab V
qq E 点电荷q的电场中某处另一点电荷的电势能: 4 r E qV
关于电势与电场强度关系的讨论
在电场中任一点,场强等于该点处电势梯度的负值, 即电场强度的大小与电势变化率的最大值对应。
(2)
W2 we dV
q
2 2
R3
8o r
dr
W2
q
2
8o R3
8.1105 ( J )
例6、内半径为R1,外半径为R2的圆柱形电容器( R2 <2 R1 ),中间充以两种不同介质,相对介电常数分别 为r1和r2 = r1/2,分界面半径为r。两介质的介电强 度都是EM 。问:当电压升高时,哪层介质先被击穿 ?最大电压为多少? r2 解:
x
a 0dx dx a o o
0
U 外2
a Edx 0dx dx x x a o o
0 a 0
x U内 dx x o o
0
( a x a)
+
-
-a
a o
静电场之均匀带电球面球体和球壳的电场精选全文完整版

UC
UC UC
(R3 R03 ) 3 0 r
kQ r
(R ≤ r)
C点的场强大小为
EC
dUC dr
kQ r2
可见:C点的电势和场强等效于全部电荷集中在球心产生的。
{范例9.6} 均匀带电球面、球体和球壳的电场
UA
3kQ(R 2(R2 RR0
R0 ) R02 )
EA = 0 (r ≤ R0)
球体的全部体积为VR=4πR3/3, 电荷的体密度为ρ = Q/VR,
取一条从P2开始的电场线作
为积分路径,则P2的电势为
R
高斯面内的体积为Vr = 4πr3/3, U E ds Edr Edr
r
r
R
高斯面内的电量为q = ρVr = QVr/VR = Qr3/R3, kQ (R2 r2 ) kQ
空腔内的电势是常数,球壳中的电 势随距离的增加而加速减小,球壳 外电势随距离的增加而减速减小。
U
r
E
ds
R r
E
ds
R
E
ds
0
R
Edr
R
kQ r2
dr
kQ R
U0 (r
<
R)
球面内任何一点的电势都与表面的
电势相同,球内空腔是一个等势体。
{范例9.6} 均匀带电球面、球体和球壳的电场
对于均匀带电球体,球体外 的电场强度和电势与均匀带 电球面的公式是相同的。
在球体内取一个高斯面, 高斯面内有电荷,并且电 荷的体密度处处相等。
(r < R)
{范例9.6} 均匀带电球面、球体和球壳的电场
U R3 (r > R)
(3R2 r2 )
9.0静电场之基本内容

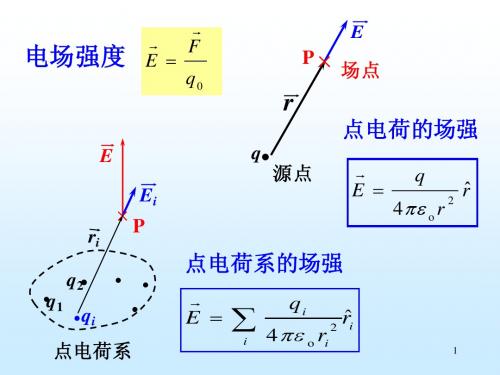
空间某点的所产生的场强等于各个 ri是电荷Qi到场点P的矢径。 点电荷在该点产生场强的矢量和 当电荷连续分布时,可将带电体分成许 dE = dq 3 r 4πε 0 r 多点电荷,每个点电荷产生的场强为 全部电荷产生 E = 1 dq r 4πε 0 ∫ r 3 的合场强为 点电荷dq可根据线密度λ, 面密度σ或体密度ρ决定 dq = λdl,dq = σdS和dq = ρdV。
4.典型源电荷的电场 (1)点电荷 E = 1 Q r 4πε 0 r 3 的电场为 其中r是点电荷 Q到场点的矢径。 Q>0 Q<0 r r P E EP
点电荷产生的场强与其电量Q成正比, 与场点到点电荷的距离的平方成反比, 方向在场点到点电荷的连线上。 正点电荷产生场强的方向沿径向向外, 负点电荷产生场强的方向沿径向向内。 (2)无限长均匀带 E = λ r 2 ε 2 π r 电直线的场强为 0
n
θ
E
∫
S
E ⋅ dS 对于封闭的曲面,通常取外
法线方向为曲面的正方向。
7.高斯定理:在静电场中,通过任一闭合曲面(称为高 斯面)的电通量等于该曲面包围的电量的代数和除以ε0
ΦE =
∫
S
E ⋅ dS =
1
ε0
高斯定理说明电场是有源场,正电荷 q ∑ i
i
是电场的源头,负电荷是电场的汇尾。
注意:任何一点的场强E是所有电荷在 该处产生的,而 ∑ qi 是高斯面内的电 i 荷,不包括高斯面外的电荷,因为高 斯面外的电荷产生的电通量为零。
湖南大学物电院周群益第九章第九章静电场静电场基本内容基本内容范例范例92电偶极子的电场电偶极子的电场范例范例93均匀带电线段的电场均匀带电线段的电场范例范例91点电荷的电场点电荷的电场范例范例94平行直线电荷的电场平行直线电荷的电场范例范例95均匀带电圆环圆盘和圆圈在轴线上的电场均匀带电圆环圆盘和圆圈在轴线上的电场范例范例98直线电荷与共面带电线段之间的作用力直线电荷与共面带电线段之间的作用力范例范例97均匀带电圆柱面圆柱体和圆柱壳的电场均匀带电圆柱面圆柱体和圆柱壳的电场范例范例99直线电荷与共面圆弧电荷之间的作用力直线电荷与共面圆弧电荷之间的作用力范例范例910点电荷在有孔带电平面轴线上的运动规律点电荷在有孔带电平面轴线上的运动规律范例范例96均匀带电球面球体以及球壳的电场均匀带电球面球体以及球壳的电场基本内容基本内容1
静电场2
8
3)求积分 3)求积分
E = Exi
y
dq Q
E x = ∫ dE x
R
r
o
θ
p
x
dEy
dEx dE
x
dEx = dE cos θ cos θ =
Ex = ∫ dEx =
z
2
x x +R
2
,
xλ
dE =
l 3
1
1
λ dl
2 2
4πε 0 x + R
0 2
1
4πε 0 ( x 2 + R 2 )
2
P
E
dS⊥
dN ∝ EdS⊥
静电场中电场线的性质: 静电场中电场线的性质: 中电场线的性质 有头(源)有尾, 由+(或∞)指向(或∞) 有头( 有尾, +(或 指向 无电荷处不中断 不闭合, 不相交 不闭合,
dN → E∝ dS⊥
18
线分布: 几种电荷的 E 线分布:
带正电的点电荷
电偶极子
均匀带电的直线段
一个点电荷所产生的电场, 一个点电荷所产生的电场,在以点电荷为 中心的任意球面的电通量等于 q
ε0
25
点电荷q被 点电荷 被 任意曲面 曲面包围 任意曲面包围
q dS ' q r dS q dΦE = = = d 2 2 4πε 0 r 4πε 0 r 4πε 0
对整个闭合面S有 对整个闭合面 有
p
dE x E
α
x
θ1
dE y
dE
λ Ex = 2πε 0 a
Ey = 0
θ2 → π , θ1 → 0 , 有
17
静电场公式整理

221rq q k F =r r q q Fˆ412210πε= rr q E ˆ420πε=304d d rqr E πε =⎰=E Edq F E =E qF ii ⋅=∑0E dqF Q ⋅=⎰0电通量:0d cos εθiSq S E S E Φ∑=⋅=⋅=⎰⎰(高斯定理)点电荷在高斯面外,0d =⋅=⎰⎰SS E Φ有限长均匀带电直线:j E i E E y x+=??==y x E E 无限长均匀带电直线:r rEˆ20πελ=均匀带电圆环轴线上:23220)(4R x iqx E +=πε无限大均匀带电平面:02εσ=E 垂直于带电面 =+=-+E E E0εσ平行板内的场强:0εσ=E 板间电势差:Ed V =平行板的的静电能:Sd E VQ W e 22121ε==半径为R 带电为q 的均匀带电球面的电场:24d επq r E S E S∑=⋅=⋅⎰204r qE πε∑=∴r < R 时,高斯面无电荷,0=E ;r > R 时,高斯面包围电荷q ,204rq πε=E两平行板间 两平行板外侧半径为R 带电量为Q 的均匀带电球体的电场:R r r 30<ερ=ER r r 13R 203>ερ无限长均匀带电圆柱面圆柱半径为R 沿轴线方向单位长度带电量为λ的电场:⎰⎰⎰⋅+⋅=⋅上下底面侧面S d E S d E S d E srl E π2⋅=2επ∑=⋅q rl Er < R 时,l q λ=∑ ,rE 02πελ=r > R 时,0=∑q ,0=E静电场力所做的功:)11( π4d π40020末初末初r r qq r r qq W r r -==⎰εεBA B A U q V q V q 000-=-=单位:V静电场力做功与路径无关电势零点选择方法:对于有限长带电体以无穷远为电势零点,实际问题中常选择地球电势为零;对于无限长均匀带电直线,只能选有限远点为电势零点;对无限大均匀带点平面,也只能选有限远点为电势零点。
静电场之均匀带电线段的电场

若带电线为无限长,则电场强度为 E=Q/2πr。
若带电线电荷分布不均匀,则需 对每段线段分别计算电场强度再 求和。
电场能量的分布
电场能量密度与电场强度成 正比,即w=0.5εE^2。
带电线全部电荷量集中在带电线 的中心轴线上,其周围电场能量 最大。
带电线周围的电场能量密度分布 不均匀,离带电线越近,能量密 度越大。
位移
带电线段的位移随时间变化,可以 通过速度和时间的关系计算,即$x = vt + frac{1}{2}at^{2}$。
电场与带电线段的能量交换
电场力做功
当带电线段在电场中移动时,电场力 对带电线段做功,将电能转化为带电 线段的动能。
带电线段能量变化
带电线段的能量随速度和位置的变化 而变化,可以通过动能定理计算,即 $Delta E_{k} = W_{k}$。
05
均匀带电线段电场的实际应 用
电场在电子设备中的应用
01
02
03
电子设备中的电场
在电子设备中,如晶体管、 集成电路等,电场被用来 控制电子的运动,实现信 号的传输和处理。
半导体电场效应
在半导体中,电场可以改 变半导体的导电性能,从 而实现电子设备的开关和 放大功能。
集成电路中的电场
在集成电路中,电场被用 来将电路中的各个元件相 互连接,实现信号的传递 和运算。
02 电场的对称性有助于简化电场计算和分析,使得 问题处理更为简便。
03 在实际应用中,利用电场的对称性可以设计出更 为高效和稳定的电子设备和电磁系统。
电场的周期性
在某些情况下,均匀带电线段的电场分布可能呈现出周期性变化的特点。
电场的周期性可能与带电线的长度、形状以及周围介质的性质等因素有关。 电场的周期性对于深入理解电磁波传播和散射等复杂现象具有重要的意义, 也为电磁波的调控和应用提供了新的思路。
例题之无限长均匀带电线的电场
如果要使r>R2的空间内无电场,对两带电柱面有什么要求?
第五章 静电场
2
第五章 静电场
1
物理学
第五版
5-4 电场强度通量
高斯定理
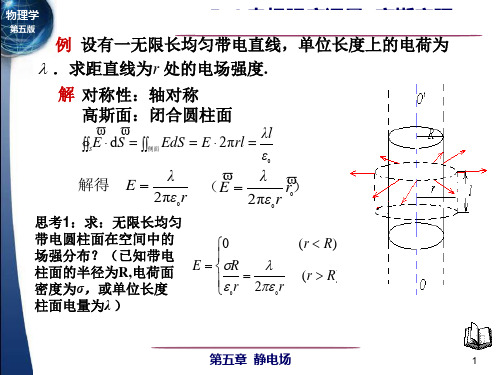
思考2:两个共轴的无限长均匀带电圆柱面,半径分别为R1,R2; 单位长度电量分别为λ1,λ2.求在空间中的场强分布.
0 ( r R ) R r R ) ( 2 r E ( r R ) 2 r
0
(E
பைடு நூலகம்
+
2 πε r
0
思考1:求:无限长均匀 带电圆柱面在空间中的 0 ( r R ) 场强分布?(已知带电 E R 柱面的半径为R,电荷面 R ) (r r 2 r 密度为σ,或单位长度 柱面电量为λ )
0 0
l
r
+ + +
物理学
第五版
5-4 电场强度通量
高斯定理
例 设有一无限长均匀带电直线,单位长度上的电荷为 .求距直线为r 处的电场强度. 解 对称性:轴对称 高斯面:闭合圆柱面
E d S
S 侧面
EdS E 2 π rl
λ
λl ε
λ
0
+
r)
0
E
解得 E
2 πε r
08.3静电场的环路定理、电势

b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理, 的电势为 由电势叠加原理,P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差(电压) 电势之差(电压)
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、
均匀带电导体棒的电场

均匀带电导体棒的电场
均匀带电导体棒的电场是指在均匀带电的导体棒周围产生的电场。
当导体棒被充电时,电荷会均匀分布在导体棒的表面上,从而产生一个电场。
这个电场的大小和方向取决于导体棒的形状、电荷量和周围介质的电性质。
如果导体棒是长直的,那么它周围的电场可以近似为一个均匀电场。
在这种情况下,电场的大小可以通过库仑定律计算:$E=\frac{kQ}{r^2}$,其中$k$是库仑常数,$Q$是导体棒上的电荷量,$r$是到导体棒中心的距离。
如果导体棒是弯曲的,那么它周围的电场就会变得更加复杂。
在这种情况下,需要使用数值计算方法来求解电场。
一种常见的方法是使用有限元方法,将导体棒分成许多小的单元,然后计算每个单元周围的电场。
高中物理静电场与电场力的计算方法

高中物理静电场与电场力的计算方法静电场和电场力是高中物理中重要的概念和计算题型。
本文将详细介绍静电场和电场力的计算方法,并通过具体题目的举例,说明其考点和解题技巧。
一、静电场的计算方法静电场是指电荷周围的电场,可以通过电场强度来描述。
电场强度的计算方法如下:1. 对于点电荷:点电荷产生的电场强度与距离的关系由库仑定律给出,即E = kQ/r^2,其中E表示电场强度,k为电场常量,Q为电荷量,r为距离。
2. 对于均匀带电球壳:带电球壳产生的电场强度在球壳外部是与距离成反比的,即E = kQ/r^2,其中E表示电场强度,k为电场常量,Q为球壳上的总电荷量,r为距离。
3. 对于均匀带电平板:带电平板产生的电场强度在平板两侧是均匀的,大小为E = σ/2ε0,其中E表示电场强度,σ为平板上的电荷面密度,ε0为真空介电常数。
通过以上计算方法,可以求解不同情况下的电场强度,进而帮助解决与电场相关的问题。
二、电场力的计算方法电场力是电荷在电场中受到的力,可以通过库仑定律来计算。
电场力的计算方法如下:1. 对于点电荷:电荷在电场中受到的电场力与电场强度和电荷量的乘积成正比,即F = qE,其中F表示电场力,q为电荷量,E为电场强度。
2. 对于带电球壳:电荷在带电球壳电场中受到的电场力为零。
这是因为带电球壳内部的电场强度为零,所以电荷在球壳内部不受力。
3. 对于带电平板:电荷在带电平板电场中受到的电场力与电荷量和电场强度的乘积成正比,即F = qE,其中F表示电场力,q为电荷量,E为电场强度。
通过以上计算方法,可以求解不同情况下电荷在电场中受到的电场力,进而帮助解决与电场力相关的问题。
三、题目举例及解析1. 题目:一个点电荷Q在距离它r的地方产生的电场强度大小为E,求点电荷Q的电荷量。
解析:根据电场强度的计算方法E = kQ/r^2,可以求解出点电荷Q的电荷量。
2. 题目:一个带有电荷量Q的均匀带电球壳半径为R,求球壳外某点的电场强度。
静电场2-例题

r1
o
-r2 a
o′
9
例题6 两同心均匀带电球面,半径为R 例题 两同心均匀带电球面,半径为 1和R2,分 别带电q 求空间电场分布。 别带电 1和q2, 求空间电场分布。 由对称性可知,电场方向是沿径向向外的。 解 由对称性可知,电场方向是沿径向向外的。 由球对称中的高斯定理
∫
∑
εo ∑
即
∑q E=
4πεor
内 2
∑
r是场点到球心的距离。 是场点到球心的距离。 是场点到球心的距离 q内是以 为半径的球面内电荷的代数和。 是以r为半径的球面内电荷的代数和 为半径的球面内电荷的代数和。
6
∑q E=
r<R :
4πεor
内 2
r R
E1 =
4πr 3 ρ 3
4πεor 2 ρr q r = = 3εo 4πεo R3
ρ
o
p
r1
+
p r2 -ρ o′
ρ
=
o
P o′
a
ρr 由上题的结果,球体内: 由上题的结果,球体内: E = 3εo
8
p
ρ
o
r1
ρr E= 3εo
+
p r2 -ρ o′
ρ
=
o
P o′
a 空腔中任一点P的电场为 空腔中任一点 的电场为
ρa ρ ρr2 ρr1 [r1 + (r2 )] = = + E= 3εo 3εo 3εo 3εo
dE =
4πεor
2
(3)分析问题的对称性。 分析问题的对称性。 分析问题的对称性 由于不同位置的电荷元在 P点产生的场强 方向不同 点产生的场强dE方向不同 点产生的场强 方向不同, 故应将dE向 轴和 轴和y轴方向投 故应将 向x轴和 轴方向投 影,于是有 于是有
无限长均匀带电直线电场的电势分布

“无限长”直线如图放置,其上电荷线密度为λ。
分析如下: 如图所示建立直角坐标系。
将导线所在的位置定义为 OY轴,我们可以在OX轴上距直线为 r 处任取一点 P ,求出 P点的电势。
由高斯定理可知, “无限长”均匀带电直线周围任一点电场强度的大小:E讨论: 1. 若选择无限远处为电势零点,则带电直线外任一点P的电势为是发散的, 即电势值为无限大,是不合理的,因此在“无限长”均匀带点直线的电场中不能选无限远处为电势零点。
2. 若选择轴线上 r=0处为电势零点,则 V p , l n 0也是无意义的,因此电势零点选在轴线上也无法计算出电场中的电势分布。
3. 若选择电场中任一点 p 0( 到带电直线的距离为 r 0) 为电势零点,如图所示,距离直线为 r 的 p 点的电势为 V p ,r( 2) r 0 取( 0, ∞) 的任意值,就可以计算出对应的 P 点的电势值。
由此可见,在计算“无限长”均匀带电直线在周围空间激发的电势时,既不能选取无限远处为电势零点,也不能选取带电直线上一点为电势零点,而只能选在带点直线外一个距离带电直线有限远的确定点上。
( 2) 式中,由于 r 0 ( 0, ∞) ,可选取 r 0 =1m ,则 l n 1 =0,也就是说将电势零点选在距带电直线为 1m 处,则 p点的电势为:V p ,此时电势的表达式为最简。
由上式看出,若细线带正电(λ> 0) ,当场点到细线的垂直距离 r<1m 时,由于 l n r<0,故该区域各点的电势 V P>0; 显然,在 r>1m的区域,各点的电势 V P<0。
可见,电势值是相对的,根据电势零点的不同而变化,但是两点之间的电势差是绝对的,不随电势零点的选取而变化,所以我们选择了合适的电势零点以后就可以由电势差算出各点的电势值。
关于静电场电势零点的选取由以上例题可以看出,虽然从理论上讲,在计算电势时,电势零点的选取是任意的,但是要具体问题具体分析,注意以下几点: ( 1) 在“无限长”均匀带电直线和“无限大”均匀带电平面的电场中,计算电势时,电势零点不能选取在无限远处,而只能选在有限远处适当的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k x L
xL
Ey
[ y
(x L)2 y2
] (x L)2 y2
②当y→0时,可得
Ex
k(
|
x
1
L|
|
x
1
L
) |
如果x > L,则
Ex
k(
x
1
L1 x) L源自2kLx2 L2根据二项式定理可证Ey→0。
可知:合场强沿x轴正向。
如果x < -L,则
Ex
k[ 1
(x
L)
1 (x
(x L) / y [(x L) / y]2 1
如果取无穷远处为电势零点,则C = 0。
保持y不变,当x趋于无穷大时也可得出同一结果。 当C = 0时,可得 U k ln x / L 1 (x / L 1)2 ( y / L)2
x / L 1 (x / L 1)2 ( y / L)2
当线段延伸到无穷远处,即L→∞,就会有U→∞的结果。
] L)
2k L
x2 L2
同理可得Ey→0。 合场强沿x轴负向。
当x→L时,场强Ex→∞。
当x→-L时,场强Ex→-∞。 如果|x| < L,可证场强Ey→∞。
场强的x分量在线段两个端点附近较大,其 他部分较小,左右两端场强的方向相反。
场强的y分量在线段附近较大,其他部分 比较小,前后两侧的场强方向相反。
O
r
(x l)2 y2
-L
l dl L x
根据电势叠加原
L
U k
理,P点的电势为
L
dl
L
k
(x l)2 y2
L
d(x l) (x l)2 y2
根据积分公式
可得
[
du
ln(u
u2 a2 ) C] U k ln x L
(x L)2 y2 C
u2 a2
x L (x L)2 y2
中垂线上的电势
L2 y2 L
当y→0时,电势U→∞。
由于λ = Q/2L,所以
kQ ln( L2 y2 L)-ln( L2 y2 -L) U
2
L
如果L→0 根据罗必塔法则可得
U kQ [ L/
向在第一象限沿着x轴和y轴的正向。
r
如果λ < 0,则电场强度的方向相反。 θ1 -L
在线段的l处取线元dl,电荷元
O
θ θ2
l dl L
x
为dq = λdl,到P点的距离为 r (x l)2 y2
由于x – l = ycotθ,这里,x和y是场点的 坐标,l和θ变量,可得dl = ydθ/sin2θ。
k ln{
2
a2 / 2L} k ln{a2 (1 x )}
y2 / 2(L x) 2
y2 L
即 U 2k ln a ln a 这就是无限长带电
y 2π0 y 直线的电势公式。
[讨论] U k ln x L (x L)2 y2
x L (x L)2 y2
①当x = 0时,可得 U k ln L2 y2 L
(L x)2 y2 L x
L2 a2 L}
(L x)2 y2 (L x) L2 a2 L
当线段趋于无 限长时可得
U k ln{
(1 x / L)2 ( y / L)2 1 x / L L( 1 a2 / L2 1)} (L x)[ 1 y2 /(L x)2 1] 1 (a / L)2 1
说明:对于无限长的带电直线来 说,不能取无限远处为电势零点。
x L (x L)2 y2
U k ln
C
x L (x L)2 y2
如果取(0,a)点为零势点,将x = 0, y = a和U = 0代入上式得
0 k ln L2 a2 L C
L2 a2 L
因 此
U k ln{
Ex k[
1
(x L)2 y2
1 ]
(x L)2 y2
Ey
k
y
[
xL (x L)2 y2
xL ]
(x L)2 y2
可见:均匀带电线段的电场强度是坐标的函数。
[讨论]
Ex k[
1
(x L)2 y2
1 ]
(x L)2 y2
Ey
k
y
[
xL (x L)2 y2
xL ]
(x L)2 y2
合场强呈“高墙”状,距离带电线段较近 的地方电场强度特别大,然后陡然减小。
合场强的方向角随极角的增加而增加, 当方向角达到180°时就向-180°跃变。
(2)求任一点的电势,电势分布曲面的规律 y 是什么?电场线和等势线是如何分布的?
P
[解析](2)电荷元dq在P点产生的电势为
r
dU kdq kdl
y
Ey
E α
E
Ex2
Ey2
k y
2 2cos(2
场强的方向角的正切为
1)
2k y
sin
2
1 2 θ1
O
tan Ey cos2 cos1 tan 2 1
Ex sin1 sin2
2
-L
即 2 1
2
P Ex θ2 Lx
用角度表示的场强公式十分简单,但不便于计算。
根据角度与坐标的关系,场强的分量可用坐标表示
均匀带电线段的电场
电量均匀分布在长2L的线段上,单位长度上的电荷密度为λ。
(1)求任一点的电场强度,电场强度分布曲面的规律是什么?
(2)求任一点的电势,电势分布曲面的规律是什么?电场线和
等势线是如何分布的? [解析](1)如图所示,建立坐标系。 如果λ > 0,则可确定电场强度的方
y
dEy
P
dE dθEx
①当x = 0时,可得中垂线上的场强
Ex 0
Ey
y
2k L
L2 y2
如果L→∞,则得
由于λ = Q/2L,所以
Ey y
kQ L2 y2
Ey
2k
y
2π0 y
如果L→0,可得
Ey
kQ y2
这是无限长带电
直线的场强公式。
这是点电荷的场强公式。
[讨论]
Ex k[
1
(x L)2 y2
1
]
(x L)2 y2
其中,C是积分常数,由零势点的坐标决定。
均匀带电线段的电势是坐标的函数。 电势关于原点的分布是对称的。
均匀带电线段的电场
U k ln x L
(x L)2 y2 C
x L (x L)2 y2
保持x不变,当y趋于 无穷大时,可得
U k ln (x L) / y [(x L) / y]2 1 C k ln1 C C
又因为r = y/sinθ,所 以场强的大小为
dE k d
y
由于场强的方向 随θ角变化,所以 不能直接由上式 积分求合场强。
场强的 分量为
dEx
积分得 Ex
dE cos k cosd
k
y
(sin 2
y sin 1 )
Ey
dEy dE sin
k
y
(cos1
k
y
cos
sin
2)
d
利用三角函数很容易计算合场强
