基于MATLAB的泊松分布的仿真
一种基于MATLAB的节点分布仿真研究

2 遗传算法流程和实现方法
- 57
遗传算法是一种模拟生物自然选择的方法。遗传操作的目的就是将群体中的个体按对环境的适应度进行 一定的操作来完成寻求最优解的进化过程[11]。 它包括三个基本的遗传算子(Genetic Operator): 选择(Selection)、 交叉(Crossover)、变异(Mutation) 。
- 59
pop--生成的初始种群 x--求得的最优解 endPop--最终得到的种群 bPop--最优种群的一个搜索轨迹
3 WSN 节点定位仿真
3.1 WSN 节点模型分析
(1)简单节点模型 在无线传感器节点定位中,锚点坐标和待测节点与锚点之间的距离 d 是已知的,因此可以通过遗传算法 来实现。 (2)复杂节点模型 由于测距的不稳定,d 往往不准确。在本文的仿真中,数据用 generate.m 文件生成,用噪声干扰来模拟 实际测量中的误差。又考虑到实际,锚点坐标为整数,服从区域内的 2 维均匀分布(可改) ;待测节点具有 随机性,服从 2 维正态分布(可改) 。
(6)
3.3 遗传算子的设计及 MATLAB 仿真
适应度计算:对适应度函数进行线性评估计算出适应度值,适应度最高的个体不通过选择直接进入下一 代个体本文中选择。 选择算子:采用随机遍历采样法。 交叉算子:采用单点交叉,交叉率为 0.7。 变异算子:采用离散变异。 重组算子:将适应度最高的个体与通过选择、交叉、变异得到的个体进行重组,形成新一代种群。 交叉、变异均采用 2 进制编码,编码长度为 20 位,x、y 各十位,可以提高计算结果的精度[12,13]。初始 种群大小为 40,遗传代数 100 代。 以下程序生成图 3。
- 58
多目标规划有两个或两个以上的目标函数,且目标函数与约束条件都为线性函数,它的数学模型为: z1 c11 x1 c12 x2 c1n xn z c21 x1 c22 x2 c2 n xn (1) max 2 zr cr1 x1 cr 2 x2 crn xn 约束条件是:
通过编程实现poisson过程的模拟
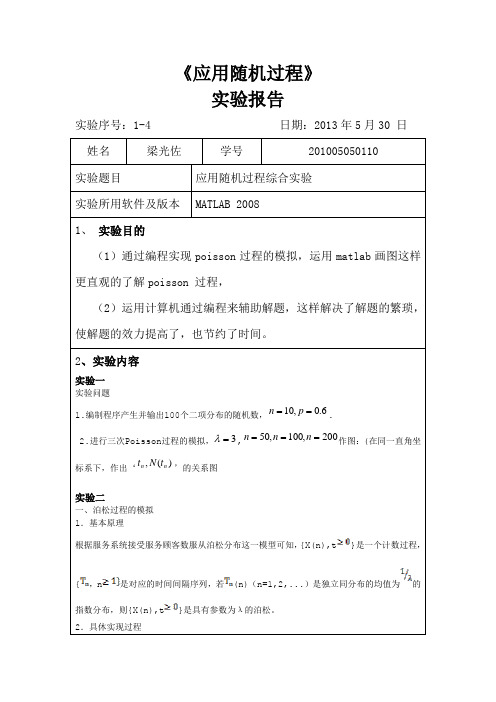
《应用随机过程》实验报告实验序号:1-4 日期:2013年5月30 日 姓名梁光佐 学号 201005050110 实验题目 应用随机过程综合实验实验所用软件及版本 MATLAB 20081、 实验目的(1)通过编程实现poisson 过程的模拟,运用matlab 画图这样更直观的了解poisson 过程,(2)运用计算机通过编程来辅助解题,这样解决了解题的繁琐, 使解题的效力提高了,也节约了时间。
2、实验内容实验一实验问题1.编制程序产生并输出100个二项分布的随机数,6.0,10==p n .2.进行三次Poisson 过程的模拟,3=λ,200,100,50===n n n 作图:(在同一直角坐标系下,作出‘)(,n n t N t ’的关系图实验二一、泊松过程的模拟1.基本原理根据服务系统接受服务顾客数服从泊松分布这一模型可知,{X(n),t }是一个计数过程,{,n 是对应的时间间隔序列,若(n)(n=1,2,...)是独立同分布的均值为的指数分布,则{X(n),t}是具有参数为λ的泊松。
2.具休实现过程实现步骤如下:(1).由函数random(‘exponential’,lamda)构造服从指数分布的序列。
(2).根据服务系统模型,=+。
(3).对任意t(,),X(t)=n,由此得到泊松过程的模拟。
3.过程模拟验证(1)设定t=0时刻,计数为0,满足X(0)=0这一条件。
(2) 是由random(‘exponential’,lamda)生成,间相互独立。
二、泊松过程的检验1.检验方法Kolmogorov-Smirnov检验(柯尔莫哥洛夫-斯摩洛夫),亦称拟合优度检验法,用来检用来检验模拟所得的数据的分布是不是符合一个理论的已知分布。
检验步骤及过程:(1)条件设定:H1:实验产生模拟泊松分布数据的总体分布服从泊松分布。
H0:实验产生模拟泊松分布数据的总体分布不服从泊松分布。
(2)检验准备:对于H1,已经假定所产生模拟泊松过程数据()X n服从泊松分布,而强度λ未知,利用函数poissfit(x,alpha)估算出模拟泊松过程的强度λ,再利用函数poisscdf(x,lamda)得到泊松分布的累积分布函数P。
数学试验四概率论一用MATLAB计算随机变量的分布1用

数学实验四(概率论)一.用MATLAB 计算随机变量的分布1.用MA TLAB 计算二项分布当随变量(),X B n p 时,在MATLAB 中用命令函数(,,)Px binopdf X n p =计算某事件发生的概率为p 的n 重贝努利试验中,该事件发生的次数为X 的概率。
例1 在一级品率为0.2的大批产品中,随机地抽取20个产品,求其中有2个一级品的概率。
解 在MATLAB 中,输入 >>clear>> Px=binopdf(2,20,0.2) Px =0.1369即所求概率为0.1369。
2.用MA TLAB 计算泊松分布当随变量()X P λ 时,在MATLAB 中用命令函数(,)P poisspdf x lambda =计算服从参数为lambda 的泊松分布的随机变量取值x 的概率。
用命令函数(,)P poisscdf x lambda =计算服从参数为lambda 的泊松分布的随机变量在[]0,x 取值的概率。
例2 用MATLAB 计算:保险公司售出某种寿险保单2500份.已知此项寿险每单需交保费120元,当被保人一年内死亡时,其家属可以从保险公司获得2万元的赔偿(即保额为2万元).若此类被保人一年内死亡的概率0.002,试求:(1)保险公司的此项寿险亏损的概率;(2)保险公司从此项寿险获利不少于10万元的概率; (3)获利不少于20万元的概率.利用泊松分布计算. 25000.0025np λ==⋅= (1) P(保险公司亏本)=()()15250025000(3020)1(15)10.0020.998kkk k P X P X C -=-<=-≤=-⋅∑=155051!k k e k -=-∑在MATLAB 中,输入 >> clear>> P1=poisscdf(15,5) P1 =0. 9999即 15505!k k e k -=∑= P1 =0.9999故 P(保险公司亏本)=1-0.9999=0.0001 (2) P(获利不少于10万元)=()()10102500250025000(30210)(10)0.0020.998k kk kk k P X P X CC -==-≥=≤=⋅≈∑∑ =10505!k k e k -=∑ 在MATLAB 中,输入 >>P=poisscdf(10,5) P =0.9863即 10505!k k e k -=∑=0.9863(3) P(获利不少于20万元)=()()525002500(30220)(5)0.0020.998k kk k P X P X C-=-≥=≤=⋅∑ =5505!k k e k -=∑ 在MATLAB 中,输入 >>P=poisscdf(5,5) P =0.6160即 5505!k k e k -=∑= 0.61603.用MA TLAB 计算均匀分布当随机变量(),X U a b 时,在MATLAB 中用命令函数(),,P unifpdf x a b =计算在区间[],a b 服从均匀分布的随机变量的概率密度在x 处的值。
概率-matlab上机实验

数学实验-概率学院:理学院班级:xxxx姓名:xxxx学号:xxxx指导教师:xxxxx实验名称:概率试验目的:1)通过对mathematica软件的练习与运用,进一步熟悉和掌握mathematica软件的用法与功能。
2)通过试验过程与结果将随机实验可视化,直观理解概率论中的一些基本概念,并初步体验随机模拟方法。
实验步骤:1)打开数学应用软件——Mathematica ,单击new打开Mathematica 编辑窗口;2)根据各种问题编写程序文件;3)运行程序文件并调试;4)观察运行结果(数值或图形);5)根据观察到的结果写出实验报告,并析谈学习心和体会。
实验内容:1)概率的统计定义2)古典概型3)几种重要分布1)二项分布2)泊松分布4)概率问题的应用(一)概率的统计定义我们以抛掷骰子为例,按古典概率的定义,我们要假设各面出现的机会是等可能的,这就要假设:(1)骰子的质料绝对均匀;(2)骰子是绝对的正方体:(3)掷骰子时离地面有充分的高度。
但在实际问题中是不可能达到这些要求的,假设我们要计算在一次抛掷中出现一点这样一个事件 的概率为多少,这时,已无法仅通过一种理论的考虑来确定,但我们可以通过试验的方法来得到事件 概率:设反复地将骰子抛掷大量的次数,例如n 次,若在n 次抛掷中一点共发生了 次,则称是 这个事件在这n 次试验中的频率,概率的统计定义就是将 作为事件 的概率P( )的估计。
这个概念的直观背景是:当一个事件发生的可能性大(小)时,如果在同样条件下反复重复这个实验时,则该事件发生的频繁程度就大(小)。
同时,我们在数学上可以证明:对几何任何一组试验,当n 趋向无穷时,频率 趋向同一个数。
<练习一>模拟掷一颗均匀的骰子,可用产生1-6的随机整数来模拟实验结果1) 作n=200组实验,统计出现各点的次数,计算相应频率并与概率值1/6比较;2) 模拟n=1000,2000,3000组掷骰子试验,观察出现3点的频率随试验次数n 变化的情形,从中体会频率和概率的关系。
在Matlab中进行模拟和仿真

在Matlab中进行模拟和仿真Matlab是一种功能强大的数学软件,广泛应用于科学研究、工程设计和数据分析等领域。
它不仅拥有丰富的数学函数库和绘图工具,还提供了一套强大的仿真和模拟功能,使用户能够更加方便地进行系统建模和性能评估。
本文将以Matlab中的模拟和仿真为主题,介绍其应用和原理,希望能为读者提供一些有用的参考和指导。
一、模拟与仿真的基本概念模拟和仿真是现代科学和工程中常用的研究方法,通过对实际系统进行数学建模和计算机模拟,可以在不进行实际试验的情况下,预测和评估系统的性能和行为。
模拟和仿真能够节省时间和成本,提高研究效率,使得科学家和工程师能够更快地了解和优化系统。
在Matlab中,模拟和仿真一般包括以下几个步骤:首先,确定系统的数学模型,即建立数学方程或差分方程描述系统的动态行为。
其次,选择仿真方法和算法,根据系统的特点和需求,确定合适的模拟算法,如欧拉法、龙格-库塔法等。
然后,设定仿真参数,包括仿真时间、步长等,这些参数将影响仿真结果的准确性和计算效率。
最后,执行仿真,并对仿真结果进行分析和评估。
二、Matlab中的模拟功能在Matlab中,模拟功能是通过内置的仿真工具和函数库来实现的。
Matlab提供了一系列用于数学建模和仿真分析的函数、工具箱和工具。
例如,Simulink是Matlab中最常用的仿真工具之一,它基于图形化仿真模型,可以快速搭建各种系统的模型,并进行仿真和分析。
Simulink提供了丰富的模块和工具箱,能够满足不同系统的建模和仿真需求。
用户可以通过拖放模块、连接信号线的方式,构建系统模型,并设置参数、仿真时间等。
Simulink还支持自定义模块和函数,用户可以根据具体需要,编写自己的模块和函数,以满足特定的仿真需求。
除了Simulink之外,Matlab还提供了其他一些实用的仿真函数和工具,如ode45函数用于解非刚性系统的常微分方程,ode15s函数用于解刚性系统的常微分方程等。
(完整版)基于MATLAB的泊松分布的仿真

(完整版)基于MATLAB的泊松分布的仿真泊松过程样本轨道的MATLAB 仿真⼀、 Poisson Process 定义若有⼀个随机过程{:0}t N N t =≥是参数为λ>0的Poisson 过程,它满⾜下列条件: 1、0N = 0;2、对任意的时间指标0s t ≤<,增量()()t s N N t s ω-ωλ(-)服从参数为泊松分布。
3、对任意的⾃然数n ≥2和任意的时间指标0120n t t t t =<<12110,,n n t t t t t t N N N N N N --?,--是相互独⽴的随机变量。
⼆、从泊松过程的定义可知1、泊松过程具有平稳独⽴增量性。
2、时间指标集合为[ 0 , +∞],状态空间为*S=N 。
3、泊松过程是⼀个连续时间离散状态的随机过程。
三、MATLAB 仿真泊松过程的思想1、若定义i T 为泊松过程的到达时间,1,n n n T T n τ=+-∈N 为到达时间间隔。
那么泊松过程N 的到达时间间隔{:}n n N τ∈是相互独⽴且同服从于参数为λ的指数分布。
2、若U 是服从于[0,1]的均匀分布,则1()E Ln U =-λ服从于参数为λ的指数分布。
利⽤随机变量分布函数的定义很容易证明这条性质。
3、由于1、和2、中的条件成⽴,现在我们考虑11[()]n n n T T Ln U n τ=+=--λ那么就可以推出11[()]n n T T Ln U n +=-λ在MATLAB 中我们可以⽤rand(1,K)产⽣⼀个具有K 个值的随机序列,它们在[0,1]上服从于均匀分布,利⽤上式计算出 n T ,在每⼀个到达时间 n T 处,N 的值从n-1变成n 。
⽤plot 函数就可以将样本轨道画出了。
四、MATLAB 程序1、⾸先我们建⽴⼀个poisson 函数,即poisson.m:function poisson(m)%This function can help us to simulate poisson processes. %If you give m a integer like 1 2 3 and so on ,then you will get %a figure to illustrate the m sample traces of the process. %rand('state',0); %复位伪随机序列发⽣器为0状态 K=10; %设置计数值为10%m=6; %设置样本个数color=char('r+','b+','g+','m+','y+','c+'); %不同的轨道采⽤不同的颜⾊表⽰lambda=1; %设置到达速率为1for n=1:mu=rand(1,K); %产⽣服从均匀分布的序列T=zeros(1,K+1); %长⽣K+1维随机时间全零向量k=zeros(1,K+1); %产⽣K+1维随机变量全零向量for j=1:Kk(j+1)=j;T(j+1)=T(j)-log(u(j))/lambda; %计算到达时间endfor i=1:Kplot([T(i):0.001:T(i+1)],[k(i):k(i)],color(n,[1,2])); hold on;endend2、下⾯我们在命令窗⼝键⼊以下命令:clear;poisson(1);就可以得到⼀条样本轨道,如下所⽰:键⼊poisson(2),得到的图如下:键⼊poisson(3),得到的图如下:键⼊poisson(4),仿真结果:键⼊poisson(5),仿真结果:键⼊poisson1(6),仿真结果:。
概率论与数理统计MATLAB上机实验报告

《概率论与数理统计》MATLAB上机实验实验报告一、实验目的1、熟悉matlab的操作。
了解用matlab解决概率相关问题的方法。
2、增强动手能力,通过完成实验内容增强自己动手能力。
二、实验内容1、列出常见分布的概率密度及分布函数的命令,并操作。
概率密度函数分布函数(累积分布函数) 正态分布normpdf(x,mu,sigma) cd f(‘Normal’,x, mu,sigma);均匀分布(连续)unifpdf(x,a,b) cdf(‘Uniform’,x,a,b);均匀分布(离散)unidpdf(x,n) cdf(‘Discrete Uniform’,x,n);指数分布exppdf(x,a) cdf(‘Exponential’,x,a);几何分布geopdf(x,p) cdf(‘Geometric’,x,p);二项分布binopdf(x,n,p) cdf(‘Binomial’,x,n,p);泊松分布poisspdf(x,n) cdf(‘Poisson’,x,n);2、掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X(1) 试计算X=45的概率和X≤45 的概率;(2) 绘制分布函数图形和概率分布律图形。
答:(1)P(x=45)=pd =3.0945e-07P(x<=45)=cd =5.2943e-07(2)3、用Matlab软件生成服从二项分布的随机数,并验证泊松定理。
用matlab依次生成(n=300,p=0.5),(n=3000,p=0.05),(n=30000,p=0.005)的二项分布随机数,以及参数λ=150的泊松分布,并作出图线如下。
由此可以见得,随着n的增大,二项分布与泊松分布的概率密度函数几乎重合。
因此当n足够大时,可以认为泊松分布与二项分布一致。
4、 设22221),(y x e y x f +−=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
matlab在球体表面按泊松分布生成点

matlab在球体表面按泊松分布生成点敬爱的读者:今天我想和你分享的主题是“matlab在球体表面按泊松分布生成点”。
这是一个非常有趣并且具有挑战性的话题,通过本文,我希望能够带你深入探讨这个主题,并且加深你对它的理解。
1. 背景介绍在开始深入讨论之前,我想先给你介绍一下什么是泊松分布以及Matlab的基本原理。
泊松分布是描述在一个固定时间或空间范围内事件发生次数的概率分布。
而Matlab是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
它可以让你进行矩阵操作、函数曲线绘制、数据算法实现以及创建用户界面等。
了解这些基本概念将有助于我们更好地理解如何在球体表面按照泊松分布生成点。
2. 泊松分布在球体表面的应用现在让我们来深入探讨如何在球体表面按照泊松分布生成点。
我们需要明确如何在球体表面定义一个均匀的分布。
这将涉及到球面上的参数化表示以及如何根据泊松分布在球面上生成点。
在Matlab中,我们可以利用球面的参数化方程和随机数生成函数来实现这一目标。
当然,在实际操作中,我们还需要考虑如何控制点的密度、分布范围以及如何对生成的点进行可视化等问题。
3. 实际操作与案例分析接下来,让我们通过一个实际的案例来加深对这个主题的理解。
我们可以选择一个特定的球体参数化表示,然后利用Matlab中的相关函数来生成符合泊松分布的点集。
在生成点集之后,我们可以通过可视化工具来观察点的分布情况,并且对比理论分布和实际生成的点集之间的差异。
通过这样的案例分析,我们可以更好地理解在球体表面按照泊松分布生成点的具体步骤和方法,并且掌握如何在Matlab中进行实际操作。
4. 总结与展望通过本文的探讨,相信你已经对在球体表面按泊松分布生成点有了更深入的理解。
无论是理论知识还是实际操作,这个主题都具有一定的挑战性和深度。
在未来,我们可以进一步探讨如何在其他几何形状的表面上实现类似的点分布生成,并且结合更多实际应用场景来加深对这一主题的理解。
基于MATLAB的泊松分布的仿真

泊松过程样本轨道的MATLAB 仿真一、 Poisson Process 定义若有一个随机过程{:0}t N N t =≥是参数为λ>0的Poisson 过程,它满足下列条件: 1、0N = 0;2、对任意的时间指标0s t ≤<,增量()()t s N N t s ω-ωλ(-)服从参数为泊松分布。
3、对任意的自然数n ≥2和任意的时间指标0120n t t t t =<<<⋯<<⋯,n 个增量12110,,n n t t t t t t N N N N N N --⋯,--是相互独立的随机变量。
二、从泊松过程的定义可知1、泊松过程具有平稳独立增量性。
2、时间指标集合为[ 0 , +∞],状态空间为*S=N 。
3、泊松过程是一个连续时间离散状态的随机过程。
三、MATLAB 仿真泊松过程的思想1、若定义i T 为泊松过程的到达时间,1,n n n T T n τ=+-∈N 为到达时间间隔。
那么泊松过程N 的到达时间间隔{:}n n N τ∈是相互独立且同服从于参数为λ的指数分布。
2、若U 是服从于[0,1]的均匀分布,则1()E Ln U =-λ服从于参数为λ的指数分布。
利用随机变量分布函数的定义很容易证明这条性质。
3、由于1、和2、中的条件成立,现在我们考虑11[()]n n n T T Ln U n τ=+=--λ那么就可以推出11[()]n n T T Ln U n +=-λ在MATLAB 中我们可以用rand(1,K)产生一个具有K 个值的随机序列,它们在[0,1]上服从于均匀分布,利用上式计算出 n T ,在每一个到达时间 n T 处,N 的值从n-1变成n 。
用plot 函数就可以将样本轨道画出了。
四、MATLAB 程序1、首先我们建立一个poisson 函数,即poisson.m:function poisson(m)%This function can help us to simulate poisson processes. %If you give m a integer like 1 2 3 and so on ,then you will get %a figure to illustrate the m sample traces of the process. %rand('state',0); %复位伪随机序列发生器为0状态 K=10; %设置计数值为10%m=6; %设置样本个数color=char('r+','b+','g+','m+','y+','c+'); %不同的轨道采用不同的颜色表示lambda=1; %设置到达速率为1for n=1:mu=rand(1,K); %产生服从均匀分布的序列T=zeros(1,K+1); %长生K+1维随机时间全零向量k=zeros(1,K+1); %产生K+1维随机变量全零向量for j=1:Kk(j+1)=j;T(j+1)=T(j)-log(u(j))/lambda; %计算到达时间endfor i=1:Kplot([T(i):0.001:T(i+1)],[k(i):k(i)],color(n,[1,2]));hold on;endend2、下面我们在命令窗口键入以下命令:clear;poisson(1);就可以得到一条样本轨道,如下所示:键入poisson(2),得到的图如下:键入poisson(3),得到的图如下:键入poisson(4),仿真结果:键入poisson(5),仿真结果:键入poisson1(6),仿真结果:。
泊松回归预测matlab

泊松回归预测matlab
泊松回归是一种用于计数数据的回归分析方法,常用于预测事
件发生的次数。
在MATLAB中,可以使用统计工具箱中的函数来进行
泊松回归分析和预测。
首先,你需要准备好你的计数数据和预测变量。
然后,使用MATLAB中的`fitglm`函数来拟合泊松回归模型。
这个函数可以指定
泊松分布作为误差分布,并且可以选择预测变量来建立模型。
接下来,你可以使用拟合好的模型来进行预测。
使用`predict`
函数可以根据你的预测变量得到对应的计数数据的预测值。
除了预测,你还可以使用泊松回归模型来进行参数估计和推断。
可以使用`coefTest`函数来进行参数的显著性检验,以及使用
`coefCI`函数来获得参数的置信区间。
另外,你还可以使用交叉验证等方法来评估泊松回归模型的性能,以及进行模型的选择和比较。
总之,在MATLAB中,你可以使用统计工具箱中的函数来进行泊
松回归分析和预测,这些函数提供了丰富的功能和选项,可以帮助你进行全面的分析和预测。
matlab中服从泊松过程的到达时间序列生成

Matlab中服从泊松过程的到达时间序列生成泊松过程是一种常见的随机过程,描述了事件在给定时间段内的到达规律。
在实际应用中,我们经常需要生成服从泊松过程的到达时间序列,以便进行仿真、建模和分析。
在Matlab中,我们可以通过一些方法来生成服从泊松过程的到达时间序列。
一、生成泊松过程到达时间序列的基本原理泊松过程的到达时间间隔服从指数分布,而指数分布可以通过指数分布的累积分布函数的逆函数来生成。
在Matlab中,我们可以使用rand函数生成服从均匀分布的随机数,再通过指数分布的累积分布函数的逆函数,即负指数分布的逆函数,来得到服从指数分布的随机数。
我们可以将这些随机数累积相加,即可得到泊松过程的到达时间序列。
二、Matlab代码实现以下是一段简单的Matlab代码,用于生成服从泊松过程的到达时间序列:```matlablambda = 10; % 泊松过程的到达率T = 100; % 时间段的长度N = poissrnd(lambda*T); % 生成总到达次数interarrival_times = exprnd(1/lambda, 1, N); % 生成到达时间间隔arrival_times = cumsum(interarrival_times); % 生成到达时间序列```在这段代码中,我们首先指定了泊松过程的到达率lambda和时间段的长度T。
我们使用poissrnd函数生成服从泊松分布的随机数N,表示在时间段内的总到达次数。
我们使用exprnd函数生成服从指数分布的随机数,表示到达时间间隔。
通过cumsum函数累积相加,得到服从泊松过程的到达时间序列。
三、代码分析和有效性验证这段代码的有效性可以通过对生成的到达时间序列进行统计分析来验证。
我们可以计算到达时间间隔的均值和方差,并与指数分布的理论均值和方差进行比较。
我们还可以绘制到达时间序列的直方图和间隔时间的概率密度函数,以直观地观察其分布特征。
泊松自回归模型matlab

泊松自回归模型matlab全文共四篇示例,供读者参考第一篇示例:泊松自回归模型(Poisson Autoregressive Model)是一种用于计数数据分析的统计模型,常用于分析时间序列数据中的计数变量。
该模型主要用于描述某一时间点上计数变量的取值与之前时间点计数变量的取值之间的关系,并且考虑到计数数据的离散性和非负性。
在实际应用中,泊松自回归模型通常被应用于疾病发生率、环境污染、人口增长等领域的数据分析中,用来建立计数变量和时间相关性的模型,预测未来的计数值。
在本文中,我们将介绍如何使用Matlab软件来实现泊松自回归模型。
一、泊松分布简介泊松分布是概率论中常用的一种分布,用于描述单位时间或单位面积内随机事件的次数。
泊松分布的概率质量函数为:P(X=k) = (λ^k * e^(-λ)) / k!λ是随机事件在单位时间或单位面积上的平均发生率,k是随机事件发生的次数。
二、泊松自回归模型的定义泊松自回归模型是一种基于泊松分布的时间序列模型,用于描述计数变量在时间上的自回归关系。
泊松自回归模型的一般形式为:Y(t) = α + β1 * Y(t-1) + β2 * Y(t-2) + ... + βp * Y(t-p) + ε(t)Y(t)是在时间t上的计数变量的取值,α是截距,β1,β2,...,βp 是模型的回归系数,p是自回归阶数,ε(t)是误差项。
三、使用Matlab实现泊松自回归模型在Matlab中,可以使用泊松回归函数fitglm()来实现泊松自回归模型的拟合。
以下是一个简单的示例代码:```matlab% 生成模拟数据t = 1:100;Y = poissrnd(5,100,1);% 构建泊松自回归模型mdl = fitglm(t,Y,'poisson','Distribution','poisson');% 查看模型参数disp(mdl)```在上述代码中,首先生成了一个包含100个计数变量的模拟数据Y,然后使用fitglm()函数来拟合泊松自回归模型,指定分布类型为poisson。
如何使用Matlab进行随机过程建模与仿真

如何使用Matlab进行随机过程建模与仿真使用Matlab进行随机过程建模与仿真随机过程是概率论的重要分支,它用于描述随机事件在时间或空间维度上的演变规律。
在工程与科学领域中,随机过程建模与仿真是十分重要的工具,它可以帮助我们预测未来的状态、优化系统设计以及进行风险评估等。
Matlab作为一种功能强大的数值计算和科学数据可视化工具,提供了丰富的函数和工具箱,使得随机过程的建模与仿真变得更加简便高效。
本文将介绍如何使用Matlab进行随机过程建模与仿真,并结合实际案例进行说明。
一、随机过程的基本概念在开始使用Matlab进行随机过程建模与仿真之前,我们首先需要了解随机过程的基本概念。
随机过程可以看作是一组随机变量的集合,它的演变具有一定的随机性。
常见的随机过程包括马尔可夫过程、泊松过程、布朗运动等。
在建模随机过程时,我们通常需要确定其状态集合、状态转移概率和初始状态等。
这些概念的理解对于后续的建模与仿真工作非常重要。
二、随机过程建模在使用Matlab建模随机过程时,我们需要选择合适的模型以及提取合适的参数。
Matlab提供了多种用于随机过程建模的函数和工具箱,例如Stochastic Process Toolbox和Statistics and Machine Learning Toolbox等。
我们可以利用这些工具来创建各种类型的随机过程模型,也可以自定义模型。
这些模型可以用来描述各种实际问题,比如金融市场的波动、传感器数据的变化等。
以布朗运动为例,我们可以使用Matlab创建一个布朗运动模型并进行仿真。
布朗运动是一种连续时间、连续状态的随机过程,其在单位时间内的状态增量是服从正态分布的。
在Matlab中,我们可以使用"brownian"函数来生成布朗运动的仿真数据。
首先,我们需要确定布朗运动的参数,例如时间步长、仿真时长、起始状态等。
然后,通过调用"brownian"函数,可以获得仿真数据,并进行可视化分析。
柏松过程matlab程序

Nm=((numda.*m).^k).*exp((-1).*numda.*m)./(factorial(k));
sum=0;
for i=1:1:n
sum=sum+Nm(i);
end
ENm=sum/n;
%随机生成随机过程Ns,并求其数学期望
s=unifrnd(0,99);%随机产生时间s
%求方差
ssum=0;
for i=1:1:n
ssum=ssum+(Nt(i)-ENt)*(Nt(i)-ENt);
end
DNt=ssum/n;
%随机生成随机过程Nm,并求其数学期望
m=unifrnd(0,99);%随机产生时间m
k=poissrnd(lambda,1,n);%产生柏松随机数
%求Nt的自协方差
ssum=0;
for Байду номын сангаас=1:1:n
ssum=ssum+(Nm(i)-ENm)*(Ns(i)-ENs);
end
Cx=ssum/n;
k=poissrnd(lambda,1,n);%产生柏松随机数
Ns=zeros(1,100);
Ns=((numda.*s).^k).*exp((-1).*numda.*s)./(factorial(k));
sum=0;
for i=1:1:n
sum=sum+Ns(i);
end
ENs=sum/n;
%画Nt-t图
plot(t,Nt,'-k');
xlabel('时间/t');
Matlab仿真应用详解 讲义

《Matlab仿真应用详解》一、基本概念1.1、什么是计算机仿真1、仿真定义基本思想:仿真的基本思想是利用物理的或数学的模型来类比模仿现实过程,以寻求过程和规律。
它的基础是相似现象,相似性一般表现为两类:几何相似性和数学相似性。
当两个系统的数学方程相似,只是符号变换或物理含义不同时,这两个系统被称为“数学同构”。
仿真的方法可以分为三类:(1)实物仿真。
它是对实际行为和过程进行仿真,早期的仿真大多属于这一类。
物理仿真的优点是直观、形象,至今在航天、建筑、船舶和汽车等许多工业系统的实验研究中心仍然可以见到。
比如:用沙盘仿真作战,利用风洞对导弹或飞机的模型进行空气动力学实验、用图纸和模型模拟建筑群等都是物理仿真。
但是要为系统构造一套物理模型,不是一件简单的事,尤其是十分复杂的系统,将耗费很大的投资,周期也很长。
此外,在物理模型上做实验,很难改变系统参数,改变系统结构也比较困难。
至于复杂的社会、经济系统和生态系统就更无法用实物来做实验了。
(2)数学仿真。
就是用数学的语言、方法去近似地刻画实际问题,这种刻画的数学表述就是一个数学模型。
从某种意义上,欧几里德几何、牛顿运动定律和微积分都是对客观世界的数学仿真。
数学仿真把研究对象(系统)的主要特征或输入、输出关系抽象成一种数学表达式来进行研究。
数学模型可分为:●解析模型(用公式、方程反映系统过程);●统计模型(蒙特卡罗方法);●表上作业演练模型然而数学仿真也面临一些问题,主要表现在以下几个方面:●现实问题可能无法用数学模型来表达,即刻画实际问题的表达式不存在或找不到;●找到的数学模型由于太复杂而无法求解;●求出的解不正确,可能是由模型的不正确或过多的简化近似导致的。
(3)混合仿真。
又称为数学—物理仿真,或半实物仿真,就是把物理模型和数学模型以及实物联合在一起进行实验的方法,这样往往可以获得较好的效果。
2、计算机仿真计算机仿真也称为计算机模拟,就是利用计算机对所研究系统的结构、功能和行为以及参与系统控制的主动者——人的思维过程和行为,进行动态性的比较和模仿,利用建立的仿真模型对系统进行研究和分析,并可将系统过程演示出来。
matlab编程求解2维泊素叶流动的速度分布

文章主题:使用Matlab编程求解2维泊松叶流动的速度分布在流体力学中,泊松叶流动是一种经典的流体流动问题,它描述了在一个受到外界力场作用下的流体中,流体粒子所具有的速度分布。
这是一个非常复杂的问题,需要借助数值计算方法进行求解。
在本文中,我们将使用Matlab编程来求解2维泊松叶流动的速度分布,通过深入的分析和全面的讨论,将帮助你更深入地理解这一流体力学问题。
### 1. 问题概述让我们从问题的概述开始。
泊松叶流动问题描述了一个在二维平面上受到外力作用的黏性流体的速度场分布问题。
在这个问题中,我们需要求解流体速度的二维分布,以及流体的压力分布。
这是一个经典的流体力学问题,在工程实践中有着广泛的应用。
### 2. 相关理论在进入Matlab编程求解之前,我们需要对相关的理论知识进行深入的理解和学习。
泊松叶流动问题涉及到了流体力学、数值计算方法等多个领域的知识,需要我们对Navier-Stokes方程、有限元方法等进行全面的学习和理解,才能够准确地求解问题。
### 3. Matlab编程求解在这一部分,我们将详细讨论如何使用Matlab编程来求解2维泊松叶流动的速度分布。
我们将从建立数学模型开始,逐步介绍编写程序的方法和技巧,以及求解过程中需要注意的问题。
通过实际的编程实例,我们将逐步展示程序的运行结果和求解过程,帮助你更好地理解这一流体力学问题。
### 4. 结果分析在这一部分,我们将对Matlab编程求解的结果进行深入的分析和讨论。
我们将探讨速度分布的特点,流体的压力分布等问题,帮助你更全面地理解泊松叶流动问题的解析过程和结果。
通过对结果的分析,我们将进一步加深对这一经典问题的理解。
### 5. 个人观点与总结在文章的结尾部分,我将共享我对这一问题的个人观点和理解。
我会总结文章中的内容,让你对泊松叶流动问题有一个全面、深刻和灵活的理解。
希望通过本文的阅读,你能对这一经典的流体力学问题有更深入的理解和认识。
概率分布简介及其matlab实现

几种常见的概率分布简介及其matlab 实现1.二项分布在n 次独立重复的伯努利试验中,设每次试验中事件A 发生的概率为p 。
用X 表示n 重伯努利试验中事件A 发生的次数,则X 的可能取值为0,1,…,n,且对每一个k (0≤k ≤n ),事件{X=k}即为“n 次试验中事件A 恰好发生k 次”,随机变量X 的离散概率分布即为二项分布(Binomial Distribution )如果(也就是说,X 是服从二项分布的随机变量),那么X 的期望值为:E(X)=np X 的方差为:D(X)=np(1-p)Matlab 程序实现:clear all;clc;x=1:30;y=binopdf(x,300,0.05);%产生一个n=300,p=0.05的二项分布;figure;plot(x,y,'r*');title('二项分布(n=300,p=0.05)');程序运行结果:2.泊松分布泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的概率函数为:()01k P X k e ,k ,,...k !λλ-===泊松分布的期望和方差均为λ。
Matlab 程序实现:clear all;clc;x=1:50;y=poisspdf(x,25); %泊松分布,其lambda=25figure;plot(x,y,'r+');title('泊松分布');程序运行结果:3.几何分布几何分布(Geometric distribution )是离散型概率分布。
其中一种定义为:在n 次伯努利试验中,试验k 次才得到第一次成功的机率。
详细地说,是:前k-1次皆失败,第k 次成功的概率。
几何分布是帕斯卡分布当r=1时的特例。
在伯努利试验中,成功的概率为p ,若ξ表示出现首次成功时的试验次数,则ξ是离散型随机变量,它只取正整数,且有P(ξ=k)=(1-p)的(k-1)次方乘以p (k=1,2,…,0<p<1),此时称随机变量ξ服从几何分布。
matlab蒙特卡洛方法求解泊松方程

一、概述在数学和工程领域中,泊松方程是一种常见的偏微分方程,描述了物质的扩散和漂移现象。
求解泊松方程在科学计算、工程建模和数据分析等领域中具有重要意义。
而蒙特卡洛方法是一种常用的随机模拟方法,适用于复杂问题的数值求解。
本文将以matlab编程语言为工具,探讨使用蒙特卡洛方法求解泊松方程的过程和实现。
二、泊松方程的数学描述泊松方程是描述标量场\( u(\mathbf{x})\)对应点源(或“蒙古支数”)的引力,在三维笛卡尔坐标系下可表示为:\[ \nabla^2 u = -f(\mathbf{x}) \]其中\( \nabla^2 \)是拉普拉斯算子,\( f(\mathbf{x}) \)表示引力的分布。
对于给定的边界条件和引力分布,求解泊松方程即可得到标量场\( u(\mathbf{x})\)的解析表达式。
三、蒙特卡洛方法的基本原理蒙特卡洛方法是一种基于随机采样的数值求解方法,通过大量的随机样本来估计数学问题的解。
对于求解泊松方程,可以利用蒙特卡洛方法进行随机采样,通过统计分析获得近似解。
四、matlab实现蒙特卡洛方法求解泊松方程的步骤1. 生成随机采样点在matlab中生成满足特定分布的随机采样点。
可以使用rand函数生成均匀分布的随机样本,也可以使用normrnd函数生成正态分布的随机样本。
这些随机采样点将作为泊松方程中的点源,用于估计标量场的解。
2. 计算引力分布根据生成的随机采样点,计算每个点源对应的引力分布。
可以根据点源与其他位置的距离来计算引力的大小,通常可以使用高斯函数或牛顿引力定律来描述点源的引力分布。
3. 统计估计解利用生成的随机采样点和对应的引力分布,通过统计分析来估计标量场的解。
可以计算每个采样点对标量场的贡献,并对这些贡献进行平均或加权平均,从而得到标量场的近似解。
五、示例代码```matlab生成随机采样点N = 1000; 采样点数x = rand(1, N); 生成均匀分布的随机样本计算引力分布f = zeros(size(x)); 初始化引力分布for i = 1:N计算第i个点源对应的引力分布...end统计估计解u = sum(f) / N; 估计标量场的解```六、优缺点分析蒙特卡洛方法求解泊松方程的优点在于能够处理复杂的引力分布,适用于高维空间和非线性问题。
泊松分布近似计算二项分布实验报告

** 实验 名称 问题背景描述: 在同一条件下重复做 n 次独立试验,每次试验只可能有两种互斥的结果:A 或非 A 之一,并设在同一次试验中 A 发生的概率是 P(A)=p,0<p<1,P( A )=1-p, 在 n 次独立试验中,出现 A 的次数 k 是一个随机变量,并且
实验所用软件及版本: Matlab R2012b
主要内容(要点) : 1. 了解二项分布和泊松分布; 2. 利用泊松分布近似计算二项分布的值; 3. 作图比较泊松分布近似值与二项分布值。
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等) : 基本步骤: 1. 利用泊松分布近似计算二项分布的值; 2. 作图比较泊松分布近似值与二项分布值 主要程序: n=100; p=0.01; lamda=n*p; B=zeros(1,21); P=zeros(1,21); for k=0:20 temp=nchoosek(n,k); B(k+1)=temp*(p^k)*(1-p)^(n-k); P(k+1)=(lamda^k)*exp(-lamda)/prod(1:k); end k=0:1:20; plot(k,B,'-b.','LineWidth',2); hold on; plot(k,P,'-r+','LineWidth',2); xlabel('k'); legend('二项分布','泊松分布')
实验结果报告与实验总结: 当 n=100,p=0.01,lamda=1 时:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泊松过程样本轨道的MATLAB 仿真
一、 Poisson Process 定义
若有一个随机过程{:0}t N N t =≥是参数为λ>0的Poisson 过程,它满足下列条件: 1、0N = 0;
2、对任意的时间指标0s t ≤<,增量()()t s N N t s ω-ωλ(-)服从参数为泊松分布。
3、对任意的自然数n ≥2和任意的时间指标0120n t t t t =<<<⋯<<⋯,n 个增量
12110,,n n t t t t t t N N N N N N --⋯,--
是相互独立的随机变量。
二、从泊松过程的定义可知
1、泊松过程具有平稳独立增量性。
2、时间指标集合为[ 0 , +∞],状态空间为*
S=N 。
3、泊松过程是一个连续时间离散状态的随机过程。
三、MATLAB 仿真泊松过程的思想
1、若定义i T 为泊松过程的到达时间,1,n n n T T n τ=+-∈N 为到达时间间隔。
那么泊松过程N 的到达时间间隔{:}n n N τ∈是相互独立且同服从于参数为λ的指数分布。
2、若U 是服从于[0,1]的均匀分布,则
1
()E Ln U =-λ
服从于参数为λ的指数分布。
利用随机变量分布函数的定义很容易证明这条性质。
3、由于1、和2、中的条件成立,现在我们考虑
11[()]n n n T T Ln U n τ=+=--λ
那么就可以推出
11
[()]n n T T Ln U n +=-
λ
在MATLAB 中我们可以用rand(1,K)产生一个具有K 个值的随机序列,它们在[0,1]上服从于均匀分布,利用上式计算出 n T ,在每一个到达时间 n T 处,N 的值从n-1变成n 。
用plot 函数就可以将样本轨道画出了。
四、MATLAB 程序
1、首先我们建立一个poisson 函数,即poisson.m:
function poisson(m)
%This function can help us to simulate poisson processes. %If you give m a integer like 1 2 3 and so on ,then you will get %a figure to illustrate the m sample traces of the process. %
rand('state',0); %复位伪随机序列发生器为0状态 K=10; %设置计数值为10
%m=6; %设置样本个数
color=char('r+','b+','g+','m+','y+','c+'); %不同的轨道采用不同的颜色表示lambda=1; %设置到达速率为1
for n=1:m
u=rand(1,K); %产生服从均匀分布的序列
T=zeros(1,K+1); %长生K+1维随机时间全零向量
k=zeros(1,K+1); %产生K+1维随机变量全零向量
for j=1:K
k(j+1)=j;
T(j+1)=T(j)-log(u(j))/lambda; %计算到达时间
end
for i=1:K
plot([T(i):0.001:T(i+1)],[k(i):k(i)],color(n,[1,2]));
hold on;
end
end
2、下面我们在命令窗口键入以下命令:
clear;
poisson(1);
就可以得到一条样本轨道,如下所示:
键入poisson(2),得到的图如下:
键入poisson(3),得到的图如下:
键入poisson(4),仿真结果:
键入poisson(5),仿真结果:
键入poisson1(6),仿真结果:
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
