2011-2012数学物理方程-B卷
河南理工大学 2011-2012 学年第 2 学期高等数学试卷b2

河南理工大学 2011-2012 学年第 2 学期《高等数学b 》试卷(A 卷)1. 已知1=a,2=b,a 与b 的夹角为4π,则=+b a( ).(A )5 (B ) 21+ (C ) 2(D ) 12.曲线⎪⎩⎪⎨⎧==22x z yx 上点()1,1,1-处的法平面方程为( ). (A ) 342-=--z y x (B ) 0542=---z y x (C ) 0742=-+-z y x (D ) 0542=+--z x y3.积分()⎰⎰θπρρθρθρθcos 020sin ,cos d f d 可以写为( ). (A ) ()⎰⎰-y y dx y x f dy 2010, (B )()⎰⎰-21010,y dx y x f dy (C )()⎰⎰1010,dy y x f dx (D ) ()⎰⎰-210,xx dy y x f dx4.若D :4122≤+≤y x ,则=⎰⎰Ddxdy ( ).(A ) π4 (B ) π15 (C )π (D ) π35.下列级数中条件收敛的是( ).(A ) ()∑∞=+-111n nn n(B )()∑∞=-111n nn(C ) ()∑∞=-1211n nn (D )()∑∞=-111n nnn6. 方程x e y y y x 2cos 2=-'-''的特解形式为( ).(A ) x a x e x 2c o s (B ) x b x e x a x e xx 2s i n 2c o s + (C ) x be x ae xx2sin 2cos + (D ) x e bx x e ax xx2sin 2cos 22+ 1.设函数y x z =,则函数yx z =的全微分=dz .2.点()0,1,2到平面0543=++z y x 的距离=d . 3.若()z y u 3sin +=,而z 由方程342-=--z y x 确定,则=∂∂==01y x xu .4.已知∑:22y x z +=(10≤≤z ),则=+⎰⎰∑ds z 41 .5. 级数()∑∞=-13n nnx 的收敛域是 .1.(本题8分)求过点()4,3,1-M 且与直线L :21331zy x =-=+垂直相交的直线方程.一、选择题(每小题4分,共24分)三、试解下列各题 (共51分)2. (本题8分)已知函数()22ln z y x u ++=(1)求该函数在点()1,0,1A 处的梯度;(2)求该函数在点()1,0,1A 处沿从点()1,0,1A 到点()2,2,3-B 的方向的方向导数.3. (本题8分)计算⎰⎰⎰Ωxdxdydz ,其中Ω是由三坐标面及平面12=++z y x 所围成的闭区域.4.(本题8分)设连续函数()x ϕ满足方程()()⎰+=+xx tdt t x x 01sin 2cos ϕϕ,求()x ϕ.5. (本题9分)计算()()()⎰Γ-+-+-dz y x dy z x dx y z ,其中Γ是有向曲线⎩⎨⎧=+-=+2122z y x y x ,从z 轴正向往z 轴负向看,Γ的方向为逆时针.6. (本题10分)设周期为π2的函数()⎩⎨⎧≤≤<≤-=.0 ,;0,0ππx x x x f 的傅里叶级数为()∑∞=++10sin cos 2n n n nx b nx a a ,求: (1)系数n a (0≥n );(2)求傅里叶级数的和函数()x s 在ππ≤<-x 时的表达式.。
数学物理方程试卷

数学物理方程试卷一、选择题1.在一个匀速运动中,物体的速度v与物体的位移s的关系是:A.v=s/tB.v=s/t^2C.v=s*tD.v=s*t^22.以下哪个物理量属于标量?A.速度B.力C.加速度D.距离3.物体质量为m,重力加速度为g,物体所受重力的大小为:A. mgB. mg/2C. 2mgD. mg^24.物体自由落体下落t秒后的位移s与时间t的关系为:A. s=gtB. s=gt^2C. s=gt^3D. s=1/gt5.以下哪个物理量属于矢量?A.面积B.速度C.力D.质量二、填空题1.一辆车以10m/s的速度匀速行驶了20秒,那么它的位移是_____________米。
2.物体在一个小时内匀速运动40千米,速度为_____________米每秒。
3.物体在水平地面上受到10牛的推力,质量为2千克,加速度为_____________。
4.一个物体从100米高的地方自由落体,下落10秒后的速度是_____________米每秒。
5.物体质量为5千克,重力加速度为10米每秒的平方,所受重力的大小是_____________牛。
三、解答题1.用物理公式解释为什么月亮绕地球运动?答:根据万有引力定律,任意两个物体之间都存在引力。
月球的质量相对较小,在地球的引力作用下,它会受到向地心的引力,从而绕着地球进行运动。
2.一个物体以10m/s的速度沿水平方向运动,另一个物体以5m/s的速度沿同一方向追赶第一个物体,如果第二个物体和第一个物体质量相同,两个物体发生碰撞后,它们的速度是多少?答:根据动量守恒定律,两个物体的总动量在碰撞前后保持不变。
因此,第一个物体的动量为10 kg·m/s,第二个物体的动量为5 kg·m/s。
由于两个物体质量相同,碰撞后它们的速度将相等。
设碰撞后的速度为v,则第一个物体的动量为10v kg·m/s,第二个物体的动量为5v kg·m/s。
北京理工大学 数理方程2013年B卷

课程编号: 07000125 北京理工大学2012-2013学年第二学期2011级数学物理方程与特殊函数期末试题(B 卷)班级_______________学号_______________姓名______________成绩_____________一、简答下列各题(直接写出结果,无需推导求解,每题5分,共计15分):1. 设Ω是二维空间中一物体,闭曲线S 是其边界,物体表面绝热。
请写出稳恒状态下物体的温度分布所满足的定解问题。
2.长度为1的均匀细弦作自由振动,两端固定,弦的初始位移为()f x ,初始速度为()g x . 请写出该振动的定解问题。
3.半径为R 的薄圆盘侧面绝热,圆盘边界上的温度保持为零度,初始温度为21r R ⎛⎫- ⎪⎝⎭, 其中r 为圆盘内任一点的极半径。
试写出极坐标系下圆盘的温度分布规律。
二、(15分)用分离变量法求解如下定解问题:222202cos , 0, 0,0,0.x x x x l t t t u u xx l t t x l u u u u π====⎧∂∂=+<<>⎪∂∂⎪⎨==⎪⎪==⎩三、(15分)用特征线法解下列定解问题:2222200540, , 0,|0, 2.y y u u ux y x x y y u u x y ==⎧∂∂∂++=-∞<<+∞>⎪∂∂∂∂⎪⎨∂⎪==⎪∂⎩四、(15分)用积分变换法求解如下定解问题:2200,0,,|().t u ut x t x u x ϕ=⎧∂∂-=>-∞<<+∞⎪∂∂⎨⎪=⎩24x a t-的傅里叶变换为22a teω-, 其中a 为常数。
五、(15分)求拉普拉斯方程第一边值问题在半空间x a >内的格林函数,并求解定解问题:0,()().xx yy zz u u u x a u a y z f y z y z ++=>⎧⎨=-∞<<+∞⎩,,,,, ,六、(15分) 设 (1,2,3,)i i α= 是零阶贝塞尔函数0()J x 的正零点,请将函数2()(01)f x x x =≤≤ 展开成贝塞尔函数0()i J x α的级数。
数学物理方程练习题

σf 4dSdt.
根据热量平衡有 故所求边界条件为
−k
∂u ∂n
dSdt
=
σu4dSdt
−
σf
4dSdt.
−k
∂u ∂n
=
σ(u4
− f 4).
齐海涛 (SDU)
数学物理方程
2012-10-3 12 / 49
1. 热传导方程及其定解问题的导出 2. 初边值问题的分离变量法 3. 柯西问题 4. 极值原理、定解问题解的唯一性和稳定性 5. 解的渐近性态
dQ = −βQ, dt Q(0) = Q0,
⇒ Q(t) = Q0e−βt.
易知 t1 到 t2 时刻, 砼内任一区域 Ω 中的热量的增加等于从 Ω 外部流入 Ω 的热量及砼中的水化热之和, 即
齐海涛 (SDU)
数学物理方程
2012-10-3 7 / 49
热传导方程及其定解问题的导出
∫ t2 cρ ∂u dtdxdydz =
.
热传导方程
.
Heat Equations
齐海涛
山东大学(威海)数学与统计学院
htqisdu@
齐海涛 (SDU)
数学物理方程
2012-10-3 1 / 49
目录
1. 热传导方程及其定解问题的导出 2. 初边值问题的分离变量法 3. 柯西问题 4. 极值原理、定解问题解的唯一性和稳定性 5. 解的渐近性态
热传导方程及其定解问题的导出
.E.xample 1.2
.试直接推导扩散过程所满足的微分方程.
解: 设 N(x, y, z, t) 表示在时刻 t, (x, y, z) 点处扩散物质的浓度, D(x, y, z) 为 扩散系数, 在无穷小时间段 dt 内, 通过无穷小曲面块 dS 的质量为
2011-2012数学物理方程-B卷-答案

u ( x0 , y 0 ) = −
1 ∂ 1 1 ∂u u ln − ln ds , ∫ 2π Γ ∂n r r ∂n r
其中 ( x0 , y 0 ) 为平面有界区域 Ω 内任一点,Γ 是区域 Ω 的边界曲线, 且光滑,n 为 Γ 的外法向量, ds 是弧微分; (2)证明格林函数的性质:
∂G( M , M 0 ) ds M = −1 。 ∫∫ ∂ n Γ
1 ∂ 1 1 ∂u u ln − ln ds , ∫ 2π Γ ∂n r r ∂n r
证: (1)证明: = −
其中 ( x 0 , y 0 ) 为平面有界区域 Ω 内任一点,Γ 是区域 Ω 的边界曲线, 且光滑,n 为 Γ 的外法向量, ds 是弧微分; 证:记 M 0 ( x 0 , y 0 ) , K ε :以 M 0 为中心半径为 ε 的圆且包含在 Ω 内,
u tt = a 2 u xx , 0 < x < π , t > 0, t ≥ 0, ; u (0, t ) = u x (π , t ) = 0, 3 u ( x,0 ) = x , u t ( x,0 ) = 0, 0 ≤ x ≤ π .
解:分析知,其形式解
u ( x, t ) = ∑ sin
sin
nπ x l
再由初始值得
f ( x) − u 0 = ∑ An sin
n =1
l
∞
nπ x l
5分
故
2 nπ An = ∫ [ f ( x) − u 0 ] sin xdx l 0 l u ( x, t ) = u 0 + v( x, t )e − βt
∞ l
因此
数学物理方程期末试卷

数学物理方程期末试卷2012学年第二学期数学与物理方程期末试卷出卷人:欧峥1、长度为 l 的弦左端开始时自由,以后受到强度为sin A t ω的力的作用,右端系在弹性系数为k 的弹性支承上面;初始位移为(),x ϕ初始速度为().x ψ试写出相应的定解问题。
(10分)2、长为l 的均匀杆,侧面绝热,一端温度为0度,另一端有已知的恒定热流进入,设单位时间流入单位截面积的热量为q ,杆的初始温度分布是()2x l x -,试写出其定解问题。
(10分)3、试用分离变量法求定解问题(10分):.⎪⎪⎪⎩⎪⎪⎪⎨⎧===><<∂∂=∂∂===x t x x ut u u u u t x x 2,0,00,40,040224、分离变量法求定解问题(10分)222sin cos ,(0,0)(0,)3,(,)64(,0)31,(,0)sin tt xxtu a u x x x l t l l u t u l t x u x u x x l l πππ⎧=+<<>⎪⎪⎪==⎨⎪⎛⎫⎪=+= ⎪⎪⎝⎭⎩5、利用行波法,求解波动方程的特征问题(又称古尔沙问题)(10分):⎪⎪⎩⎪⎪⎨⎧==∂∂=∂∂=+=-).()(0022222x ux u x u a t u at x at x ψϕ ())0()0(ψϕ=6、用达朗贝尔公式求解下列一维波动方程的初值问题(10分)⎪⎩⎪⎨⎧=∂∂=>+∞<<-∞+∂∂=∂∂==0,2sin 0,,cos 0022222t t t u x u t x x x u a t u7、用积分变换法求解定解问题(10分):⎪⎪⎩⎪⎪⎨⎧=+=>>=∂∂∂==,1,10,0,1002y x uy u y x y x u8、用积分变换法求解定解问题(10分):⎩⎨⎧==>∈=0)0,(,sin )0,(0,,2x u x x u t R x u a u t xx tt9、用格林函数法求解定解问题(10分):222200, y 0, () , .y u ux y u f x x =⎧∂∂+=<⎪∂∂⎨⎪=-∞<<+∞⎩10、写出格林函数公式(三维)及满足的条件,并解释其物理意义。
2011-2012第二学期期末数学试卷和答案

石家庄市2011~2012学年度第二学期期末考试试卷高一数学(B 卷)(时间l20分钟,满分150分)注意事项:本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.号填写在答题卡上. 参考公式:柱体体积V 柱体=Sh(S 为底面面积,h 为高)锥体体积V 锥体=31Sh(S 为底面面积,h 为高)台体体积V 台体=31(S '+S S '+S)h (S ',S 分别为上、下底面面积,h 为台体高)圆柱的表面积S=2πr(r+l ) (其中r 为底面半径,l 为母线长)圆锥的表面积S=πr(r+l ) (其中r 为底面半径,l 为母线长)圆台的表面积S=π(r '2+r 2+r 'l +r l ) (其中r ',r 为上、下底面半径,l 为母线长) 球的表面积、体积公式S=4πR 2,V=34πR 3,(其中R 为球的半径) 第I 卷(选择题,共60分)一、选择题:本大题共l2小题,每小题5分。
在每小题给出的四个选项中.只有一项是符合题目要求的.1.若直线l 的斜率为l ,则l 的倾斜角为A .90°B .60°C .45°D .135° 。
2.在等差数列{a n }中,若a 4+a 6 =12,则a 5= A .12 B .6 C .5 D .43.直线y=-2x+3与直线y=kx-5互相垂直,则实数k 的值为 A .21B.2 C .-2 D .-l 4.设a>b>0,c ∈R,则下列不等式恒成立的是 A .a|c|>b|c| B .ac 2>bc 2C .a 2c>b 2c D .a 1<b1 5.设l 、m 是两条不同的直线,α是一个平面,则下列命题正确的是 A .若l ⊥m ,l ⊂α,则l ⊥α B .若l ⊥α,l ∥m ,则m ⊥α C .若l ∥α,m ⊂α,则l ∥m D .若l ∥α,m ∥α,则l ∥m 1石一4y 一<-3,6.已知x ,y 满足不等式组 则z=2x+y 的最大值为A .14B .12C .13D .3 7.从一个棱长为l 的正方体中切去一部分,得到一个 几何体,其三视图如右图,则该几何体的体积为 A .87 B .85 C .65 D .43 8.在△ASC 中,若lgsinA-lgcosB-lgsinC=lg2,贝△ABC 的形状是A .直角三角形B .等边三角形C .等腰三角形D .不能确定9.将边长为2的正△ABC 沿BC 边上的高AD 折成直二面角B-AD-C ,则三棱锥B-ACD 的 外接球的表面积为A .4πB .5πC .12πD .8π10.已知M 是△ABC 内的一点,且·=23,∠ABC=30°,若△MBC ,△MCA ,△MAB 的面积分别为21、x 、y ,则x 1+y4的最小值为 A .20 B .19 C .18 D .1611.已知函数f(x)=2mx 2-2(4-m)x+1,g(x)=mx ,若对于任意一个实数x ,f(x)与g(x)至少有 一个为正数,则实数m 的取值范围是A .(0,2)B .(0,8)C .(2,8)D .(-∞,0)12.设S n 为等差数列{a n }的前n 项和,若对于任意的n ∈N *,不等式21222a nS a n n λ≥+(1a ≠0)恒成立,则λ的最大值为 A .0 B .51 C. 21D .1二、填空题:本大题共4小题,每小题5分,共20分. 13.已知等比数列{ a n },a 2 =2,a 5 =41,则公比q 为 . 14.一辆汽车原来每天行驶x 公里,如果它每天多行驶l9公里,那么在8天内它的行程就 超过2200公里;如果它每天比原来少行驶l2公里,那么行驶同样的路程所需要的时间 就超过9天.列出上述问题中未知数x 所满足的不等式(或不等式组) .15.已知a 、b 、c 分别是△ABC 的三个内角A 、B 、C 所对的边长,若a=1,b=3,A+C=2B ,则 sinC 的值为16.如图:已知正方体ABCD -A 1B 1C 1D 1,点P 在BC 1上运动, 则下列四个命题:①三棱锥A-D1PC的体积不变;②A1P∥面ACD1;⑧ DP⊥BC l;④面PDB1⊥面ACD l.其中正确的命题的序号是三、解答题:本大题共6小题,共70分.解答应写出文字说明17.(本小题满分10分)某几何体的三视图如右图,其中正视图是等边三角形,俯视图为半圆(数据如图所示),求该几何体的表面积.18.(本小题满分12分)公差不为零的等差数列{ a n}的前5项和为-20,数列{ b n}为等比数列,且b n= a1, b2= a3,b3= a4 .(I)求数列{ a n}的通项公式;(Ⅱ)求数列{ b n}前n项和.19.(本小题满分12分)如图,一辆汽车在一条水平的公路上向正西行驶,在A处测得公路北侧远处一山顶D在西偏北角度为α的方向上,行驶a km后到达B处,测得此山顶在西偏北角度为β的方向上,仰角为γ,求此山高CD (单位:km) 20.(本小题满分12分)已知△ABC的顶点A(1,3),AB边上的中线CM所在的直线方程为2x-3y+2=0,AC边上的高BH所在的直线方程为2x+3y-9=0.(I)求顶点C的坐标;(II)求直线BC的方程.21.(本小题满分12分)如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD 为直角梯形,且AB∥CD,AB⊥AD,AB=AD=21CD=1(I)若M为ED的中点,求证:AM∥平面BEC;(Ⅱ)Q是DC中点,问在EB上是否存在点P使得平面EBQ⊥平面ADP,若存在指出点P的位置,并证明;若不存在,请说明理由.22.(本小题满分12分)已知f(x)=422+xx.(I)若关于x的不等式f(x)>k的解集是{x|x<-4,或x>-1},求实数k的值;(Ⅱ)设g(x)=322+=mxx,x∈[1,3],若对任意的x l>0,总存在x2∈[l,3]使得f(x l)<g(x2)成立,求实数m的取值范围.附加题:(本小题满分10分)(各校可根据本校的情况酌情选择本题)已知半径为5的圆与直线4x+3y-29=0相切,且圆心在x轴上,其横坐标为整数.(I)求圆的方程;(II)设直线ax-y+5=0(a>O)与圆相交于A,B两点,求实数a的取值范围.石家庄市2011~2012学年度高一第二学期期末考试试卷(B 卷答案)一、选择题:本大题共12小题,每小题5分. 1-5 CBADB 6-10 BCCBC 11-12 BB 二、填空题: 本大题共4小题,每小题5分.13. 12 14. (19)82200,(19)89.12x x x +⨯>⎧⎪+⨯⎨>⎪-⎩ 15. 1 16.; ①②④ 三、解答题17.(本小题满分12分) 解:由题中三视图可得,该几何体为圆锥的一半.则该几何体的表面积为该圆锥表面积的一半与轴截面面积的和 . ………………2分 又圆锥侧面展开图为扇形21=2222s a a a ππ∴⨯⨯=扇.…………4分 底面积为2=s a π∴底 . ………………6分 轴截面面积为21=2222s a a ∴⨯⨯⨯=轴 . ………………8分2232S a π∴=该几何体表面积为 . ……………12分18. (本小题满分12分)解:(Ⅰ)设数列{}n a 的,首项为 1a ,公差为d ,数列{}n b 的公比为q , 由 520S =- , 1,34,a a a 成等比,1211154520,2(2)(3).a d a d a a d ⨯⎧+=-⎪⎨⎪+=+⎩…………………3分 18,2,a d ∴=-=210n a n ∴=-.………………6分(Ⅱ)依题意128,4,b b ∴=-=-所以12q =,……………8分 所以数列{}n b 前n 项和为18[1()]2112n n T --∴=-…………10分 41162n -=-.……………12分 19. (本小题满分12分)解:依题意,,CAB ACB αβα∠=∠=-,,DBC γ∠= …………3分 由正弦定理得 又因为sin sin BC ABCAB ACB =∠∠ ………………6分 sin sin ,sin sin()AB CAB a BC ACB αβα∠∴==∠-……………9分sin tan tan sin()a CD BC DBC αγβα∴=⨯∠=-.所以此山高为sin tan sin()a αγβα-(km) .……………12分20. (本小题满分12分)解:(Ⅰ)依题意知:直线AC 的斜率为32, 可得AC 所在的直线方程为0323=+-y x ,…………3分 又AB 边上的中线CM 所在直线方程为0232=+-y x ,由3230,2320.x y x y -+=⎧⎨-+=⎩ 得C (-1,0),所以顶点C 的坐标为(-1,0).……………6分(Ⅱ)设B (a,b ),又A (1,3), M 是AB 的中点 ,则M ()23,21++b a , 由已知得2390,132320.22a b a b +-=⎧⎪⎨++⋅-⋅+=⎪⎩ 得B (3,1).………………10分 又C (-1,0) ,得直线BC 的方程为014=+-y x .……………12分21.(本小题满分12分)(Ⅰ)证明:取EC 中点N ,连结BN MN ,. 在△EDC 中,,M N 分别为,EC ED 的中点, 所以MN ∥CD ,且12MN CD =.…………2分 由已知AB ∥CD ,12AB CD =, 所以MN ∥AB ,且MN AB =.所以四边形ABNM 为平行四边形. 所以BN ∥AM . 又因为⊂BN 平面BEC ,且⊄AM 平面BEC , 所以AM ∥平面BEC .………………5分(Ⅱ)存在这样的点P,此时P 点为EB 中点.…………6分 证明:取EQ 中点K,连结PK,DK,AP.可知PK//BQ,BQ//AD,所以PK//AD,所以A,P,K,D 四点共面. 由已知AD ⊥ED,AD ⊥DC,所以AD ⊥面EDC EQ ⊂面EDC ,所以AD ⊥EQ ①………………8分因为ED=DQ=1,K 为EQ 中点,所以DK ⊥EQ ②………………10分 由①,②可知EQ ⊥平面APKD,EQ ⊂面EBQ,所以平面EBQ ⊥平面ADP.………………12分 22 (本小题满分12分) 解:(Ⅰ)由()f x k >,得224xk x >+, 即2240kx x k -+< , ……………2分 其解集为{}14x x x >-<-或.则-1,-4是方程2240kx x k -+=的两根 ,25k ∴-=, 25k ∴=- .……………5分 (Ⅱ)0x >时 ,222()44x f x x x x==++ ,又444,2x x x x x+≥===当且仅当即等号成立,max 1()2f x ∴=,……………7分又对任意10x >,总存在[]21,3x ∈使得 12()()f x g x < 成立, 所以当[]1,3x ∈时 函数2()23g x x mx =-+的最大值大于12,…………9分 函数2()23g x x mx =-+的对称轴0x m =,221196312322m m m m ≤>⎧⎧⎪⎪∴⎨⎨-+>-+>⎪⎪⎩⎩或,2312m ∴<.………………12分 附加题:(本小题满分10分)解:(Ⅰ)设圆心为(, 0)M m (m ∈Z ).由于圆与直线43290x y +-=相切,且半径为5,所以42955m -=,…………………2分 即42925m -=.因为m 为整数,故1m =.故所求圆的方程为22(1)25x y -+=. ………………………… 5分 (Ⅱ)将直线50ax y -+=代入圆的方程中得:22(1)2(51)10a x a x ++-+=,………………7分由于直线与圆交于A 、 B 两点,所以224(51)4(1)0a a ∆=--+>, 即21250a a -> 又0a >. 512a ∴>所以实数a 的取值范围是5(,)12+∞ . ……………10分。
北京理工大学2011-2012学年第二学期数学物理方程与特殊函数期末试题(A卷)
课程编号: 07000125 北京理工大学2011-2012学年第二学期2010级数学物理方程与特殊函数期末试题(A 卷)班级_______________学号_______________姓名______________成绩_____________一、简答下列各题(直接写出结果,无需推导求解,每题5分,共计15分)1.设正方形薄板上下两面绝热,板的两边(0x =,x a =)始终保持零度,另外两边(0y =,y a =)的温度分别为()f x 和()g x ,请写出板内稳恒状态下的温度分布所满足的定解问题。
2. 长为1的均匀细杆侧表面绝热,0x =端有恒定热流q 进入,1x =端绝热,杆的初始温度为()f x , 试写出杆内温度分布的定解问题。
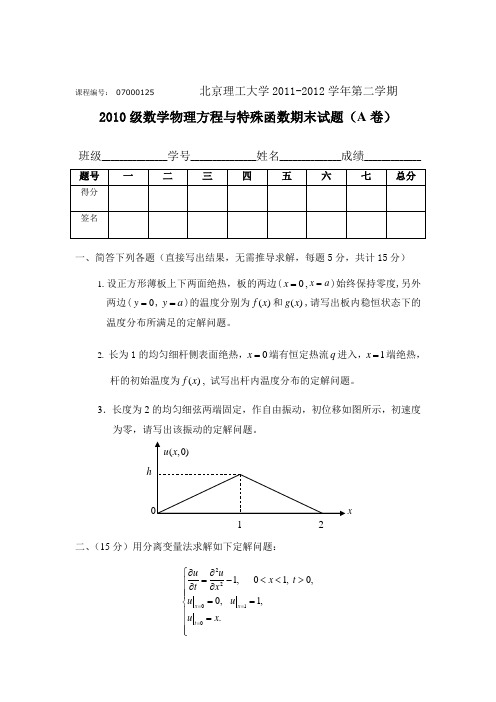
3.长度为2的均匀细弦两端固定,作自由振动,初位移如图所示,初速度为零,请写出该振动的定解问题。
hx1 2二、(15分)用分离变量法求解如下定解问题:220101, 01, 0,0, 1,.x x t u ux t t x u u u x ===⎧∂∂=-<<>⎪∂∂⎪⎪==⎨⎪=⎪⎪⎩三、(15分)用特征线法解下列定解问题:0020, , 0,|sin , |0.tt xt xx t t t u u u x t u x u ==+-=-∞<<+∞>⎧⎨==⎩四、(15分)用积分变换法求解如下定解问题:001,0,0,|1,| 1.xy x y u x y u y u ===>>⎧⎪=+⎨⎪=⎩附:常用的拉普拉斯变换五、(15分)求拉普拉斯方程第一边值问题在半空间1y >-内的格林函数,并求解定解问题:01,(1)().xx yy zz u u u y u x z f x z x z ++=>-⎧⎨-=-∞<<+∞⎩,,,,, ,六、(15分) 设(1,2,)i i α= 是一阶贝塞尔函数1()J x 的正零点,将函数3()(01)f x x x =≤≤ 展开成贝塞尔函数1()i J x α的级数。
数学物理方程考试试题及解答

数学物理方程试题(一)一、填空题(每小题5分,共20分)1.长为π的两端固定的弦的自由振动,如果初始位移为x sin 2x ,初始速度为cos2x 。
则其定解条件是2.方程∂u ∂u -3=0的通解为∂t ∂x⎧X "(x )+λX (x )=03.已知边值问题⎨',则其固有函数X n(x )=⎩X (0)=X (π)=04.方程x y +xy +(αx -n )y =0的通解为2"'222二.单项选择题(每小题5分,共15分)∂2u ∂2u1.拉普拉斯方程2+2=0的一个解是()∂x ∂y (A )u (x ,y )=e sin xy (B )u (x ,y )=(C )u (x ,y )=x x 2+y 2x 2+y 21x 2+y 2(D )u (x ,y )=ln2.一细杆中每点都在发散热量,其热流密度为F (x ,t ),热传导系数为k ,侧面绝热,体密度为ρ,比热为c ,则热传导方程是()∂2u F (x ,t )∂u ∂2u F (x ,t )2(A )(B )=a 2+=a +22∂t c ρc ρ∂x ∂t ∂x 2222∂F∂F u (x ,t )∂F ∂F u (x ,t )(其中2k )22(C )(D)=a +=a +a =222c ρ∂t c ρc ρ∂t ∂x ∂x 2⎧∂2u 2∂u =a ⎪⎪∂t 2∂x 23.理想传输线上电压问题⎨⎪u (x ,0)=A cos ωx ,∂u ⎪∂t ⎩∂2ut =0=aA ωsin ωx(其中a 2=1)的解为()L C(A )u (x ,t )=A cos ω(x +at )(B )u (x ,t )=A cos ωx cos a ωt(C )u (x ,t )=A cos ωx sin a ωt (D )u (x ,t )=A cos ω(x -at )三.解下列问题1.∂u ⎧∂u+3=0⎪(本题8分)求问题⎨∂x 的解∂y3x⎪⎩u (x ,0)=8e ⎧∂2u=6x 2y ⎪⎪∂x ∂y(本题8分)⎨⎪u (x ,0)=1-cos x ,u (0,y )=y 2⎪⎩2⎧∂2u 2∂u ⎪2=a 2⎪∂t ∂x 3 . (本题8分)求问题⎨⎪u (x ,0)=sin 2x ,∂u ⎪∂t ⎩2.的解t =0=3x 2四.用适当的方法解下列问题2⎧∂u 2∂u=a ⎪(本题8分)解问题⎨∂t ∂x 2⎪u (x ,0)=1-2x +3x 2⎩2⎧∂2u ∂2u ∂2u2∂u =a (2+2+2)⎪2⎪∂t ∂x ∂y ∂z (本题8分)解问题⎨2∂u 2⎪u t =0=2y +3xz ,=6y t =0⎪∂t 2⎩1. 2.2⎧∂u2∂u⎪∂t =a 2∂x ⎪⎪五.(本题10分)解混合问题:⎨u (0,t )=u (1,t )=0⎪u (x ,0)=2sin πx⎪⎪⎩六.(本题15分)用分离变量法解下列混合问题:2⎧∂2u 2∂u =a ⎪2∂x 2⎪∂t ⎪⎨u (0,t )=u (π,t )=0⎪∂u ⎪u (x ,0)=2x (π-x ),∂t ⎪⎩t =0=3sin 2x一.单项选择题(每小题4分,共20分)1.(D )2.(B )3.(D )4.(D )二.填空题(每空4分,共24分)⎧u (0,t )=u (2π,t )=0⎪1.x +y =C 1,2x +y =C22.⎨,∂u (x ,0)=x ,t =0=2x ⎪∂t ⎩3.u (x ,t )=x +f (3x +2y ),4.X n (x )=B n cos n πx,(n =0,1,2,3,)25.通解为u (x ,t )=322x y +f (x )+g (y )2三.解下列问题(本题7分)∂u ⎧∂u+3=0⎪1.求问题⎨∂x的解∂y 3x⎪⎩u (x ,0)=8e 解:设u (x ,t )代入方程,(8e =8e 3x +m y(2分))⨯3+3⋅(8e 3x +m y )⨯m=03x +m y 3m +3=0,m =-1(6分)所以解为u (x ,t )=8e 3x -y(7分)2.2⎧∂2u ∂u 2⎪2=a 2⎪∂t ∂x (本题7分)求问题⎨⎪u (x ,0)=sin 2x ,∂u ⎪∂t ⎩的解t =0=3x 2解:由达朗贝尔公式,得11x +at2u (x ,t )=[sin 2(x +at )+sin 2(x -at )]+3ξd ξ(3分)⎰x -at22a =cos 2at sin 2x +3x 2t +a 2t 3(7分)四.用适当的方法解下列问题2⎧∂u 2∂u=a ⎪1.(本题7分)解问题⎨∂t ∂x 2⎪u (x ,0)=1-2x +3x 2⎩解:设u (x ,t )=1-2x +3x 2+At代入方程,A =a 2[0-0+6+A ''t ]+6x⎧A ''=0令⎨显然成立2⎩A =6a +6x解为u (x ,t )=1-2x +3x 2+6a 2t +6xt2∂2u ∂2u ∂2u2∂u =a (2+2+2)2∂t ∂x ∂y ∂z 2∂u2=6y t =0=x +2y +3yz ,t =0∂t 22.⎧⎪⎪(本题7分)解问题⎨⎪u ⎪⎩解:设u=[x 2+2y 2+3yz +At 2]+[6x 2t +Bt 3](2分)代入方程2A +6Bt =a 2[(2+12y +∆At 2)+(12t +∆Bt 3)](4分)⎧∆B =0令,⎨显然成立,解为2⎩6B =12a u (x ,t )=x +2y +3yz +a 2t 2+6y 2t +2a 2t 3五.(本题7分)解混合问题:2⎧∂u 2∂u ⎪∂t =a ∂x 2⎪⎪⎨u (0,t )=u (1,t )=0⎪u (x ,0)=2sin πx ⎪⎪⎩解u (x ,t )=L -1{U (x ,s )}=2e -a πt sin πx22六.(本题15分)用分离变量法解下列混合问题:2⎧∂2u 2∂u=a ⎪22∂t ∂x ⎪⎪⎨u (0,t )=u (π,t )=0⎪∂u ⎪u (x ,0)=2x (π-)x ,∂t ⎪⎩t =0=3sin 2x解:设u (x ,t )=X (x )T (t )代入方程及边界⎧T ''+λa 2T =0n π2⎪λ=()=n 2,X n=sin nx''⎨X +λX =0nπ⎪X (0)=X (π)=0⎩u n=(C ncos ant +D nsin ant )sin nxu (x ,t )=∑(C ncos ant +D nsin ant )sin nxn =1∞其中C n =2π⎰π08[1-(-1)n ]x (π-x )sin nxdx =n 3πD n =2π⎰π0⎧0(n ≠2)⎪3sin 2x sin nxdx =⎨3(n =2)⎪⎩a∞38[1-(-1)n ]cos ant sin nx 所以解为u (x ,t )=sin 2at sin 2x +∑3a n πn =12009-2010学年第一学期数学物理方程试题一、填空题(每小题4分,共24分)∂2u ∂2u ∂2u 1.方程2-3+22=sin(x 2+y 2)的特征线为∂x ∂y ∂x ∂y 2.长为l 的弦做微小的横振动,x =0、x =l 两端固定,且在初始时刻处于水平状态,初始速度为2x ,则其定解条件是3.方程∂u ∂u +3=2x 的通解为∂x ∂y⎧X "(x )+λX (x )=04.已知边值问题⎨,则其固有函数⎩X '(0)=X '(2)=0X n(x )=5.方程x y +xy +(25x -64)y =0的通解为6.2⎰x J 1(x )dx = .2"'2二.单项选择题(每小题4分,共20分)1.微分方程uxxx+uxyy-sin u =ln(1+x 2)是()(A )三阶线性偏微分方程(B )三阶非线性偏微分方程(C )三阶线性齐次常微分方程(D )三阶非线性常微分方程∂2u ∂2u2.拉普拉斯方程2+2=0的一个解是()∂x ∂y (A )u (x ,y )=e sin xy (B )u (x ,y )=(C )u (x ,y )=x x 2+y 2x 2+y 21x 2+y 2(D )u (x ,y )=ln3.一细杆中每点都在发散热量,其热流密度为F (x ,t ),热传导系数为k ,侧面绝热,体密度为ρ,比热为c ,则热传导方程是()∂2u F (x ,t )∂u ∂2u F (x ,t )2(A )(B )=a 2+=a +22∂t c ρc ρ∂x ∂t ∂x 2222∂F∂F u (x ,t )∂F ∂F u (x ,t )(其中2k )22(C )(D)=a +=a +a =222c ρ∂t c ρc ρ∂t ∂x ∂x 2⎧∂2u 2∂u=a ⎪2⎪∂t ∂x 24.理想传输线上电压问题⎨⎪u (x ,0)=A cos ωx ,∂u ⎪∂t ⎩∂2ut =0=aA ωsin ωx(A )u (x ,t )=A cos ω(x +at )(B )u (x ,t )=A cos ωx cos a ωt(C )u (x ,t )=A cos ωx sin a ωt (D )u (x ,t )=A cos ω(x -at )5.单位半径的圆板的热传导混合问题2⎧∂u 1∂u2∂u =a (2+)(ρ<1)⎪⎨有形如()的级数解。
数学物理方程 第三章练习题

齐海涛
(SDU)
数学物理方程
2012-10-3
11 / 69
建立方程、定解条件
方法二: 同上题, 在柱面坐标系下 q1 = r, q2 = θ, q3 = z, 则 ds2 = dr2 + r2 dθ2 + dz2 , H1 = 1, H2 = r, H3 = 1,
代入 (1.4) 即得柱面坐标下 Laplace 算子的表达式.
.
第三章
.
调和方程
Laplace Equations
齐 海 涛
山东大学(威海)数学与统计学院
htqisdu@
齐海涛
(SDU)
数学物理方程
2012-10-3
1 / 69
目录
. 1 . 2 . 3 . 4
建立方程、定解条件 格林公式及其应用 格林函数 强极值原理、第二边值问题解的唯一性
对上式两边积分即得结论.
齐海涛
(SDU)
数学物理方程
2012-10-3
4 / 69
建立方程、定解条件
.
Example 1.2
. 证明: 拉普拉斯算子在球面坐标 (r, θ, φ) 下可以写成 ( ) ( ) 1 ∂ 2 ∂u 1 ∂ ∂u 1 ∂2 u △u = 2 r + 2 sin θ + . r ∂r ∂r r sin θ ∂θ ∂θ r2 sin2 θ ∂φ2 .
∂2 u ∂2 u ∂2 u sin θ cos θ ∂2 u sin2 θ ∂u sin2 θ ∂u sin 2θ = 2 cos2 θ − 2 · + 2 2 + + , 2 ∂x ∂r ∂r∂θ r ∂θ r ∂r r ∂θ r2 ∂2 u ∂2 u 2 ∂2 u sin θ cos θ ∂2 u cos2 θ ∂u cos2 θ ∂u sin 2θ · + 2 2 + − = sin θ + 2 , ∂y2 ∂r2 ∂r∂θ r ∂θ r ∂r r ∂θ r2 将最后两式相加, 并加以整理, 即得到所需结果.
文档:数学物理方程B答案

解:对上述两个等式进行傅里叶变换,并利用傅里叶变换求导性质可得:
(2分)
其中 .解之得:
.(3分)
对上式进行傅里叶逆变换,可得
,
(2分)
.
(3分)
一、(每小题15分,共30分)用分离变量法求解下列两个定解问题:
(1)
解:上述问题的解的表达式为: ,(2分)
代入泛定方程可得: . (2分)
其解为: , (2分)
.(2分)
,
; (3分)
又 , .(3分)
综上即知:
.(1分)
(2)
福州大学2012~2013学年第二学期考试B卷答案
解:上述问题的解的表达式为: .(2分)
代入泛定方程可得: , (2分)
其解为 . (3分)
由边值条件 ,可得 ,
从而 . (3分)
,
(4分)
. (1分)
二、(每15分,共30分)用球函数法求解下列问题:
(1)
其中未知函数 且定义域为 。
解:设问题的解
(1分)
由边界条件可知 中含 阶勒让德多项式,则
(2分)
当 , (2分)
当 , (2分)
比较系数可得 (2分)
解得 (3分)
故 (3分)
(2)
其中未知函数 且其定义域为 。
解:由于 ,故上述问题的解的表达式为:
. (2分)代入边值条Βιβλιοθήκη 可得: , (2分)(2分)
(2分)
,(1分)
(2分)
. (2分)
(2分)
三、(15分)请利用格林函数法推导下列定解问题的积分形式的解:
其中未知函数 且定义域为 。
数学物理方程第三章练习题

2012-10-3 3 / 69
建立方程、定解条件
∂2u ∂x2i
=
x2i r2
f
′′(r)
+
( 1 r
−
x2i r3
)
f
′(r),
(i = 1, 2, . . . , n)
将上式代入调和方程得
f
′′(r)
+
n
−
1 f
′(r)
=
0,
r
即
f ′′(r) f ′(r)
=
−n
− r
1.
对上式两边积分即得结论.
πx a
,
u(x, b)
=
0.
齐海涛 (SDU)
数学物理方程
2012-10-3 17 / 69
建立方程、定解条件
.E.xample 1.6
用分离变量法求解由下述调和方程的第一边值问题所描述的矩形平板 (0 ≤ x ≤ a, 0 ≤ y ≤ b) 上的稳定温度分布:
.
uxx + uyy = 0,
u(0, y) = u(a, y) = 0,
,
∂r ∂R
=
sin θ,
∂θ ∂R
=
cos θ . r
由 (1.2) 及 (1.3) 知
(1.3)
∂2u ∂z2
=
cos2
θ
∂2u ∂r2
+
sin2 r2
θ
∂2u ∂θ2
+
sin2 r
θ
∂u ∂r
+
sin 2θ r2
∂u ∂θ
−
sin 2θ r
∂2u ∂r∂θ
,
(完整版)南昌大学2011-2012历年数学物理方法期末试卷ABC套卷(附所有答案)

—南昌大学考试试卷—
【适用时间:2011 ~2012 学年第二学期试卷类型:[B]卷】
2. 考查下面的无限长弦的振动问题:
其中,。
这是一个达朗贝尔公式定解问题。
(1)首先给出达朗贝尔公式及相应定解问题的一般形式;
(2)利用达朗贝尔公式求解。
3. 已知矩形区域上的函数满足方程和
齐次边界条件,按以下步骤求解:
(1)分离变数并找到本问题中包含的本征值问题;
(2)求解此本征值问题,确定本征值和本征函数;
(3)给出满足上述方程和条件的的一般解。
—南昌大学考试试卷—
【适用时间:2011 ~2012 学年第二学期试卷类型:[C]卷】
—南昌大学考试试卷—
【适用时间:2011 ~2012 学年第二学期试卷类型:[A]卷】
—南昌大学考试试卷—
【适用时间:2011 ~2012 学年第二学期试卷类型:[A]卷】答案
—南昌大学考试试卷参考答案及评分标准—【适用时间:20 11 ~20 12 学年第二学期试卷类型:[ B ]卷】。
2011-2012第二学期期末物理试卷及答案

石家庄市2011~2012学年度第二学期期末考试试卷高一物理(B 卷)注意事项:1.本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.时间90分钟,满分100分。
3.请在答题卡上做答。
第I 卷(选择题)一、选择题(本题共l2小题;每小题4分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确,全部选对的得4分,选不全的得2分,有选错或不答的得0分) 1.在物理学发展的过程中,许多科学家的发现推动了人类历史的进步。
以下关于几位科学 家所作贡献的叙述正确的是( )A .牛顿测出了万有引力常量B .哥白尼提出了“地心说”C .爱因斯坦建立了狭义相对论D .伽利略发现了太阳系行星运动三大定律2.两个可视为点电荷的相同带电小球固定在绝缘架上,相距r ,带电荷量大小分别为-Q 和+3Q , 相互间库仑力大小为F. 现将两个带电小球相接触,然后分开且其距离变为2r,则它们之间的 库仑力大小变为( ) A .F 121 B. F 43 C. F 34D. F 123.玩陀螺是省会石家庄陀螺爱好者的一项健身活动。
如图所示为一个玩具陀螺,a,b 、c 是陀螺上的三个点。
当陀螺绕垂直于地面的轴线以角速 度ω稳定旋转时,下列判断正确的是( ) A .a 点的角速度比b 点的大 B .a 点的线速度比b 点的小C .a 、b 、c 三点的线速度大小相等D .a 、b 、c 三点的角速度相等4.在高速公路的拐弯处,通常路面都是外高内低,如图所示。
汽车的运动可看作是做半径为R 的匀速圆周运动。
设内外路面高度差为h ,路基的水平宽度为d ,路面的宽度为L ,已知重力加速度为g 。
要使汽车所受的重力与支持力的合力提供向心力,则汽车转弯时的车速应等于( )5.空间存在一匀强电场,如图所示,平行虚线a 、b 、c 、d 表示该电场中的四个等势面。
若在 此电场中一个带电粒子仅受电场力的作用,运动轨迹如图中曲线AB 所示,则下列说法中正确的是( )A .四个等势面中。
《数学物理方法》第十二章--11级-2012解析

将C(k,t) 代入式(12.2.17) 可得
在式(12.2.18)中令 t = 0 得 再与式(12.2.16)联立得 代入式(12.2.18)即有
(12.2.18)
60
(3)作像函数的傅里叶逆变换
61
利用奇,偶函数的性质及定积分公式(例4.2.7)p90
62
本题不利用卷积定理,在傅里叶的逆变换公式中对 指数作配方运算后,再利用定积分公式计算也可以 得到相同的结果。
上两式称为傅里叶余弦变换及其逆变换.
18
3. 三维傅里叶变换
正如由式(12.1.7)可以得到式(12.1.14),式 (12.1.15)一样,由式(12.1.10)可得
19
【例12.1.1】求 的傅里叶变换
解
20
【例12.1.2】求f(x)=exp[2ax2] 的傅里叶变换, 其中a为正数 解 由傅里叶变换的定义出发,并利用4.2节
耐心+坚持+努力 ≈成功
第十二章 积分变换法
积分变换法是物理学与其他应用科学中 求解数学物理方程的一种重要方法, 它适用于求解无界区域及半无界区域的 定解问题。
积分变换法是
通过对数理方程的积分变换,减少自变量的个数, 直至化为常微分方程,使求解问题大为简化。
此外,积分变换法还可以用来计算定积分,求解常 微分方程和积分方程.
49
§12.2 傅里叶变换法
傅里叶变换法广泛地应用于求解无界区 域的定解问题中.求解步骤为 ①对定解问题作傅里叶变换; ②求像函数; ③对像函数作傅里叶逆变换, 得解
对于半无界区域的定解问题
可采用傅里叶正弦变换(第一类边界条件),或傅里 叶余弦变换(第二类边界条件);也可将边界条件齐 次化后,采用延拓法,最后用傅里叶变换求解.
数学物理方程 练习题

数学物理方程
2012-10-3 14 / 39
二阶线性方程的特征理论
(3)
∂u ∂t
=
∂2u ∂x2
−
∂2u ∂y2
齐海涛 (SDU)
数学物理方程
2012-10-3 15 / 39
二阶线性方程的特征理论
(3)
∂u ∂t
=
∂2u ∂x2
−
∂2u ∂y2
解: 特征方程:
α21 − α22 = 0.
特征方向 l 满足:
2012-10-3 13 / 39
二阶线性方程的特征理论
∂2u ∂2u ∂2u ∂2u (2) ∂t2 = ∂x21 + ∂x22 + ∂x23
齐海涛 (SDU)
数学物理方程
2012-10-3 14 / 39
二阶线性方程的特征理论
∂2u ∂2u ∂2u ∂2u (2) ∂t2 = ∂x21 + ∂x22 + ∂x23
解: 特征方程:
α20 = α21 + α22 + α23.
特征方向 l 满足:
α20 = α21 + α22 + α23,
α20 + α21 + α22 + α23 = 1.
√√
√
√
解得:
l
=
(±
2 2
,
2 2
sin
θ
sin
β,
2 2
sin
θ
cos
β,
2 2
cos
θ),
其中
θ,
β
为任意参数.
齐海涛 (SDU)
(1.2)
ξ = α1x + α2y, η = α3x + α4y,
2011-2012学年第二学期石家庄期末高一数学B卷答案

石家庄市2011~2012学年度高一第二学期期末考试试卷(B 卷答案)一、选择题:本大题共12小题,每小题5分.1-5 CBADB 6-10 BCCBC 11-12 BB二、填空题: 本大题共4小题,每小题5分.13. 1214. (19)82200,(19)89.12x x x +⨯>⎧⎪+⨯⎨>⎪-⎩ 15. 1 16.; ①②④ 三、解答题 17.(本小题满分12分)解:由题中三视图可得,该几何体为圆锥的一半.则该几何体的表面积为该圆锥表面积的一半与轴截面面积的和 . ………………2分又 圆锥侧面展开图为扇形21=2222s a a a ππ∴⨯⨯=扇.…………4分 底面积为2=s a π∴底 . ………………6分轴截面面积为21=222s a a ∴⨯⨯=轴 . ………………8分2232S a π∴=+该几何体表面积为 . ……………12分 18. (本小题满分12分)解:(Ⅰ)设数列{}n a 的,首项为 1a ,公差为d ,数列{}n b 的公比为q ,由 520S =- , 1,34,a a a 成等比,1211154520,2(2)(3).a d a d a a d ⨯⎧+=-⎪⎨⎪+=+⎩…………………3分 18,2,a d ∴=-=210n a n ∴=-.………………6分(Ⅱ)依题意128,4,b b ∴=-=- 所以12q =,……………8分所以数列{}n b 前n 项和为 18[1()]2112n n T --∴=-…………10分 41162n -=-.……………12分 19. (本小题满分12分)解:依题意,,CAB ACB αβα∠=∠=-,,DBC γ∠= …………3分由正弦定理得又因为 sin sin BC AB CAB ACB=∠∠ ………………6分 sin sin ,sin sin()AB CAB a BC ACB αβα∠∴==∠- ……………9分sin tan tan sin()a CD BC DBC αγβα∴=⨯∠=-.所以此山高为sin tan sin()a αγβα-(km) .……………12分20. (本小题满分12分)解:(Ⅰ)依题意知:直线AC 的斜率为32, 可得AC 所在的直线方程为0323=+-y x ,…………3分又AB 边上的中线CM 所在直线方程为0232=+-y x ,由3230,2320.x y x y -+=⎧⎨-+=⎩得C (-1,0), 所以顶点C 的坐标为(-1,0).……………6分 (Ⅱ)设B (a,b ),又A (1,3), M 是AB 的中点 ,则M ()23,21++b a , 由已知得2390,132320.22a b a b +-=⎧⎪⎨++⋅-⋅+=⎪⎩ 得B (3,1).………………10分 又C (-1,0) ,得直线BC 的方程为014=+-y x .……………12分21.(本小题满分12分)(Ⅰ)证明:取EC 中点N ,连结BN MN ,.在△EDC 中,,M N 分别为,EC ED 的中点,所以MN ∥CD , 且12MN CD =.…………2分 由已知AB ∥CD ,12AB CD =, 所以MN ∥AB ,且MN AB =.所以四边形ABNM 为平行四边形. 所以BN ∥AM .又因为⊂BN 平面BEC ,且⊄AM 平面BEC ,所以AM ∥平面BEC .………………5分 (Ⅱ)存在这样的点P,此时P 点为EB 中点.…………6分证明:取EQ 中点K,连结PK,DK,AP.可知PK//BQ,BQ//AD,所以PK//AD,所以A,P,K,D 四点共面.由已知AD ⊥ED,AD ⊥DC,所以AD ⊥面EDCEQ ⊂面EDC ,所以AD ⊥EQ ①………………8分因为ED=DQ=1,K 为EQ 中点,所以DK ⊥EQ ②………………10分由①,②可知EQ ⊥平面APKD,EQ ⊂面EBQ,所以平面EBQ ⊥平面ADP.………………12分22 (本小题满分12分)解:(Ⅰ)由()f x k >,得224x k x >+, 即2240kx x k -+< , ……………2分其解集为{}14x x x >-<-或.则-1,-4是方程2240kx x k -+=的两根 , 25k ∴-=, 25k ∴=- .……………5分 (Ⅱ)0x >时 ,222()44x f x x x x==++ , 又44244,2x x x x x+≥===当且仅当即等号成立, max 1()2f x ∴=,……………7分 又对任意10x >,总存在[]21,3x ∈使得 12()()f x g x < 成立,所以当[]1,3x ∈时 函数2()23g x x mx =-+的最大值大于12,…………9分 函数2()23g x x mx =-+的对称轴0x m =,221196312322m m m m ≤>⎧⎧⎪⎪∴⎨⎨-+>-+>⎪⎪⎩⎩或, 2312m ∴<.………………12分 附加题:(本小题满分10分)解:(Ⅰ)设圆心为(, 0)M m (m ∈Z ).由于圆与直线43290x y +-=相切,且半径为5,所以 42955m -=,…………………2分 即42925m -=.因为m 为整数,故1m =.故所求圆的方程为22(1)25x y -+=. ………………………… 5分(Ⅱ)将直线50ax y -+=代入圆的方程中得: 22(1)2(51)10a x a x ++-+=,………………7分由于直线与圆交于A 、 B 两点,所以224(51)4(1)0a a ∆=--+>,即21250a a -> 又0a >. 512a ∴> 所以实数a 的取值范围是5(,)12+∞ . ……………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名
(a > 0)的傅立叶变换;
2
(3)判定方程 u xx + ( x + y ) u yy = 0; 的类型; (4)将方程 u xx + yu yy = 0 化为标准形式。 三、计算题( 计算题(20 分) (1)求解波动方程的初边值问题。
u tt = a 2 u xx , 0 < x < π , t > 0, t ≥ 0, ; u (0, t ) = u x (π , t ) = 0, 3 u ( x,0 ) = x , u t ( x,0 ) = 0, 0 ≤ x ≤ π .
四、证明题( 证明题(20 分) (1) 设受摩擦力作用的固定端点的有界弦振动,满足方程
专业 专业年 年级
utt = a 2 u xx − cut
证明其能量是减少的; (2)证明调和方程狄利克莱外问题的稳定性。 五、证明题( 证明题(20 分) (1)证明:二维调和函数的积分表达式为:
u ( x0 , y 0 ) = −
1 ∂ 1 1 ∂u u ln − ln ds , ∫ 2π Γ ∂n r r ∂n
r
其中 ( x0 , y 0 ) 为平面有界区域 Ω 内任一点,Γ 是区域 Ω 的边界曲线, 且光滑,n 为
Γ 的外法向量, ds 是弧微分;
(2)证明格林函数的性质:
∫∫
3 2 −1 的解将一致地趋向于零,其趋于零的阶数为 t 。其中, ϕ ∈ C ,ψ ∈ C 。
授课教师命题教师或 院系负责人签字 命题负责人签字 201 2011 年 12 月 日 年 月 日
共 2 页 第 2 页
授课教师
一、简答题( 简答题(12 分) (1)以热传导过程为例,如果物体的边界温度及其初始温度都不超过某值 M,而且 物体内部没有热源,则这物体内就不可能产生大于 M 的温度。和这个事实相对应, 叙述对齐次热传导方程的极值原理?(6 分) (2)弦振动方程中初始条件指的是什么?(3 分) ; (3)弦振动方程中具体指出第三类边界条件?(3 分) ; 二、解答题( 解答题(20 分) (1)试直接推导扩散过程所满足的微分方程; (2)求函数 e
Γ
∂G( M , M 0 ) ds M = −1 。 ∂n
六、证明题( 证明题(8 分) 证明如果初始资料具有紧支集,那么当 t → ∞ 时,三维波动方程的柯西问题:
u tt = a 2 ∆u , u ( x, y, z ,0) = ϕ ( x, y, z ) u ( x, y, z ,0) = ψ ( x, y, z ) t
(2)在 t > 0, 0 < x < l 区域中求解如下的定解问题:
学号
∂u ∂ 2u = α 2 2 2 − β (u − u0 ), ∂t ∂ x
u (0, t ) = u (l , t ) = u0 , u ( x, 0) = f ( x) 其中 α , β , u 0 均为常数, f ( x) 均为已知函数。
数学科学
中国海洋大学 2011 秋季学期 秋季学期 期末考试 期末考试试卷 考试试卷 学院 《数学物理方程》课程试题(B 卷) 共 2 页 第 1 页 文具,满分为:100 分。
考试说明:本课程为闭卷考试,可携带 考试说明 座号
题号
一
二
三
ቤተ መጻሕፍቲ ባይዱ
四
五
六
七
总分
得分
----------------装 装----------------订 订----------------线 线----------------
