电路基本定律(基尔霍夫定律)
电路基本定律 基尔霍夫定律

电路基本定律基尔霍夫定律
基尔霍夫定律是电路中电压和电流所遵循的基本规律,是分析和计算较为复杂电路的基础,1845年由德国物理学家G.R.基尔霍夫提出。
基尔霍夫(电路)定律包括基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)。
基尔霍夫(电路)定律既可以用于直流电路的分析,也可以用于交流电路的分析,还可以用于含有电子元件的非线性电路的分析。
基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上,在稳恒电流条件下严格成立。
当基尔霍夫第一、第二方程组联合使用时,可正确迅速地计算出电路中各支路的电流值。
由于似稳电流(低频交流电) 具有的电磁波长远大于电路的尺度,所以它在电路中每一瞬间的电流与电压均能在足够好的程度上满足基尔霍夫定律。
因此,基尔霍夫定律的应用范围亦可扩展到交流电路之中。
电路理论 基尔霍夫定律

n
uk 0
k 1
列写KVL方程时,需要先指定回 路的绕行方向或路径的方向,且 规定参考方向与绕行方向一致的 电压变量前取正号,反之取负号。
例:沿图示绕行方向有:
u1 u2 u3 u4 0
+ u1 -
+ 1+
u4 4
-
+
3
u3
-
2 u2
-
u1 u2 u3 u4 0 移项得: u1 u2 u3 u4
a
+
+
b=3
US1 _ 1
US2 3 1 _ 22
3 R3
n=2
R1
R2
l=3
m=2
b
二、基尔霍夫电流定律(KCL)
a’
a
1d
表述1:对于集总参数电路中的任一节
i1 i2 i3
点,在任何时刻通过该节点所有支路电
3
2
流的代数和恒等于0
4 b
对某节点 ∑i=0
对右图节点a: i1 i2 i3 0
解:对节点①,有 i2=i1+ic=51ic 对回路Ⅰ,有
-us+R1i1+R2i2=0 代入数值得
10 i1 51.5103 A
U3=-R3ic=-2×103×50i1=-19.4V
例3 如图所示,求R为何值时电流i为零。
(清华大学研究生招生考试试题)
2A 6Ω
ai +
4V
R
-
2Ω
b
解:由题意,有
④ KVL不仅适用于闭合回路,对不闭合的回路(闭 合节点序列)也适用。
推论:电路中任意两点间的电压等于两点间任一
条路径经过的各元件电压的代数和。
基尔霍夫定律

-
4V
+ -
-
+
3i 4 5 i 3A
u 5 7 12V
5. +
10V
I1 10
I =? 1A
6.
10A
4V +
+
2
+
I
3I2 U =?
3A
5
-10V 7. +
I =0
-
I2 5 5
10V
+
-
-
-
+ U=? 2I2
+
8.
I1 R1 I1 R2 US
解 + U=? -
例
i1 i4 i6 0 i2 i4 i5 0 i 3 i5 i6 0
1
i1
i2
1
i4
2
i6
三式相加得: i
i2 i3 0
表明KCL可推广应用于电路中包 围多个结点的任一闭合面
i3
3
i5
三、基尔霍夫电压定律 (KVL):在任何集总参数电路中,在任 一时刻,沿任一闭合路径( 按固定绕向 ), 各支路电压的 代数和为零。 即
U R2 I1
I1 I1 U S R1
+ -
US I1 R1 (1 )
R2U S U R1 (1 )
2 US PS U S I1 R )
2 US Po R2 2 2 2 R1 (1 )
电路的两类约束关系
1.元件的特性约束:元件的VCR
2.拓扑约束(结构约束):基尔霍夫定律
uS1
+
+ uS2 1 R2 _ 2 3 R3
基尔霍夫定律
基尔霍夫定律
若⽤ I表⽰电路本⾝的最⼤线性尺⼨,⽤λ表⽰电压或电流的波长,若满⾜l<0.1*λ,电路便可视为集总参数电路,否则便需作为分布参数电路处理
基尔霍夫定律是任何集总参数电路都适⽤的基本定律
电路的⼏个名词:
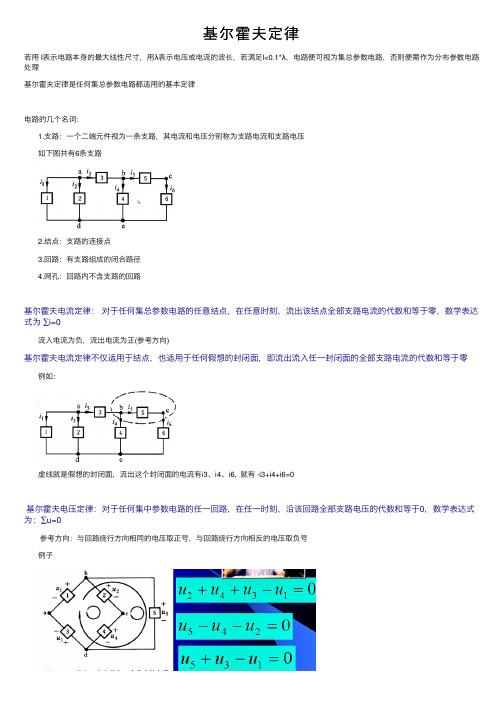
1.⽀路:⼀个⼆端元件视为⼀条⽀路,其电流和电压分别称为⽀路电流和⽀路电压
如下图共有6条⽀路
2.结点:⽀路的连接点
3.回路:有⽀路组成的闭合路径
4.⽹孔:回路内不含⽀路的回路
基尔霍夫电流定律:对于任何集总参数电路的任意结点,在任意时刻,流出该结点全部⽀路电流的代数和等于零,数学表达式为 ∑i=0
流⼊电流为负,流出电流为正(参考⽅向)
基尔霍夫电流定律不仅适⽤于结点,也适⽤于任何假想的封闭⾯,即流出流⼊任⼀封闭⾯的全部⽀路电流的代数和等于零
例如:
虚线就是假想的封闭⾯,流出这个封闭⾯的电流有i3、i4、i6, 就有 -i3+i4+i6=0
基尔霍夫电压定律:对于任何集中参数电路的任⼀回路,在任⼀时刻,沿该回路全部⽀路电压的代数和等于0,数学表达式为:∑u=0
参考⽅向:与回路绕⾏⽅向相同的电压取正号,与回路绕⾏⽅向相反的电压取负号
例⼦
基尔霍夫电压定律不仅适⽤于回路,也适⽤于任何闭合结点序列
天⼦骄龙。
基尔霍夫定律是电路的基本定律

基尔霍夫定律是电路的基本定律基尔霍夫定律是电路学中最基本的定律之一,由德国物理学家基尔霍夫于19世纪提出。
它是描述电路中电流和电压分布的定律,被广泛应用于电路分析和设计中。
基尔霍夫定律包括两个方面:基尔霍夫第一定律和基尔霍夫第二定律。
基尔霍夫第一定律,也称为电流守恒定律,指出在任何一个电路节点处,进入该节点的电流等于离开该节点的电流之和。
简单来说,电流在电路中的分布是守恒的,不会凭空消失或增加。
基尔霍夫第一定律的数学表达式为ΣI_in = ΣI_out,其中Σ表示求和,I_in表示进入节点的电流,I_out表示离开节点的电流。
这个定律可以帮助我们分析电路中各个节点处的电流分布情况。
基尔霍夫第二定律,也称为电压环路定律,指出在闭合电路中,沿着任意一条回路的电压之和等于零。
简单来说,电压在电路中的分布是平衡的,总和为零。
基尔霍夫第二定律的数学表达式为ΣV = 0,其中Σ表示求和,V表示电压。
这个定律可以帮助我们分析电路中各个回路的电压分布情况。
基尔霍夫定律的应用非常广泛。
在电路分析中,我们可以利用基尔霍夫定律来计算电路中各个节点和回路的电流和电压分布情况,从而帮助我们理解电路的工作原理和性能。
例如,当我们需要计算一个复杂电路中某个节点处的电流时,可以利用基尔霍夫第一定律,将进入该节点的电流和离开该节点的电流进行求和,从而得到该节点处的电流值。
另外,当我们需要计算一个闭合电路中某个回路的电压时,可以利用基尔霍夫第二定律,将沿着该回路的电压进行求和,从而得到该回路的电压值。
基尔霍夫定律的应用不仅限于理论分析,还可以用于电路设计和故障排除。
在电路设计中,我们可以根据基尔霍夫定律来选择合适的电阻、电容和电感等元件,以满足电路的要求。
在故障排除中,我们可以利用基尔霍夫定律来分析电路中的问题,找出故障的原因并进行修复。
总之,基尔霍夫定律是电路学中最基本的定律之一,它描述了电路中电流和电压的分布情况。
通过应用基尔霍夫定律,我们可以更好地理解和分析电路的工作原理,从而提高电路设计和故障排除的能力。
电路基尔霍夫定律

电路基尔霍夫定律
基尔霍夫定律是求解复杂电路的电学基本定律。
从19世纪40年代,由于电气技术发展的十分迅速,电路变得愈来愈复杂。
某些电路呈现出网络形状,并且网络中还存在一些由3条或3条以上支路形成的交点(节点)。
这种复杂电路不是串、并联电路的公式所能解决的。
基尔霍夫电流定律又称为基尔霍夫第一定律,规定在电路中所有进入某节点的电流的总和等于所有离开这节点的电流的总和。
或者说,假设进入某节点的电流为正值,离开这节点的电流为负值,则所有涉及这节点的电流的代数和等于零.以方程式表达,对于电路的任意节点,有
n
∑I k
k=1
其中,I k是第k个进入或离开这节点的电流,是流过与这节点相连接的第k 个支路的电流,可以是实数或复数。
基尔霍夫三大定律公式

基尔霍夫三大定律公式
基尔霍夫定律公式是∑I(流入)=∑I(流出) ∑I=0。
基尔霍夫电流定律指出在任意时刻,对电路中的任何一节点,流经该节点的电流代数和恒为零。
即在直流电路中ΣI=0;在交流电路中Σi=0。
容是电路中任一个节点上,在任一时刻,流入节点的电流之和等于流出节点的电流之和。
相关信息:
基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上,在稳恒电流条件下严格成立。
当基尔霍夫第一、第二方程组联合使用时,可正确迅速地计算出电路中各支路的电流值。
由于似稳电流具有的电磁波长远大于电路的尺度,所以它在电路中每一瞬间的电流与电压均能在足够好的程度上满足基尔霍夫定律。
基尔霍夫定律百科

基尔霍夫定律百科基尔霍夫定律是电路分析中非常重要的基本定律,它由德国物理学家基尔霍夫于1845年提出。
基尔霍夫定律是电路中电流和电压的基本关系,可以用来描述电路中电流的分布和电压的变化。
基尔霍夫定律包括两个定律:基尔霍夫第一定律(电流定律)和基尔霍夫第二定律(电压定律)。
基尔霍夫第一定律,也称为电流定律,是指在电路中,电流在节点处的总和等于零。
简单来说,就是电流流入节点的总和等于电流流出节点的总和。
这个定律是基于电荷守恒定律的基础上发展起来的。
电流定律可以用来解决电路中复杂的电流分布问题,例如电流的分流、合流等情况。
基尔霍夫第二定律,也称为电压定律,是指在电路中,沿着闭合回路的任意一条路径,电压的代数和等于零。
简单来说,就是电压上升等于电压下降。
这个定律是基于能量守恒定律的基础上发展起来的。
电压定律可以用来解决电路中复杂的电压分布问题,例如电压的分配、降压、升压等情况。
基尔霍夫定律的应用非常广泛,几乎所有的电路分析都离不开它。
无论是简单的串联电路还是复杂的并联电路,都可以通过基尔霍夫定律来进行分析和计算。
基尔霍夫定律的应用可以帮助我们理解电路中的电流和电压分布,从而设计和优化电路。
在实际应用中,我们可以通过基尔霍夫定律解决各种电路问题。
例如,当我们需要计算一个电路中某个分支的电流时,可以通过基尔霍夫定律来计算。
首先,我们需要选择一个合适的节点,然后根据电流定律,将流入节点和流出节点的电流进行求和,得到等式。
然后,根据电压定律,在回路中选择一条路径,将沿途的电压进行代数和计算,得到等式。
最后,通过解这个方程组,可以求解出所需的电流值。
除了用于解决电路问题,基尔霍夫定律还可以应用于其他领域。
例如,在热传导中,可以用基尔霍夫定律来描述热流的传递和分布。
在流体力学中,可以用基尔霍夫定律来描述流体的流动和压力变化。
在金融领域中,可以用基尔霍夫定律来描述资金的流动和分配。
基尔霍夫定律是电路分析中非常重要的基本定律,它可以帮助我们理解电路中的电流和电压分布,解决各种电路问题。
基尔霍夫kcl定律

基尔霍夫kcl定律基尔霍夫的电流定律(KCL)是电路分析中的一个重要定律,它指出在集总电路中,任何时刻,对任一节点,所有支路电流的代数和恒等于零,即∑i=0。
KCL具有以下特点:1、KCL是集总电路的基本定律,适用于任何集总参数电路。
2、KCL适用于线性电路和非线性电路。
3、KCL与电路元件的性质和参数大小无关。
4、KCL只与电路的元件和结构有关,与电路元件的性质和参数无关。
KCL的验证方法有多种,其中一种是通过测量各支路电流的方法来验证。
假设有三个支路电流分别为I1、I2和I3,流入节点的支路电流为-I1、-I2,流出节点的支路电流为I3。
根据KCL,有I1+I2+I3=0。
通过测量各支路电流,可以验证KCL是否成立。
除了通过测量各支路电流的方法来验证KCL外,还可以通过其他方法来验证。
例如,可以通过计算各支路电流的方法来验证KCL。
假设有两个支路电流分别为I1和I2,流入节点的支路电流为-I1,流出节点的支路电流为I2。
根据KCL,有I1+I2=0。
通过计算各支路电流,可以验证KCL是否成立。
另外,还可以通过实验的方法来验证KCL。
例如,可以使用电源、电阻器、电容器、电感器和开关等元件搭建一个简单的电路,通过观察各支路电流的变化情况,可以验证KCL是否成立。
总之,基尔霍夫的电流定律(KCL)是电路分析中的一个重要定律,它适用于任何集总参数电路,与电路元件的性质和参数无关。
可以通过多种方法来验证KCL是否成立,例如测量各支路电流、计算各支路电流和实验等方法。
在实际应用中,应该根据具体的情况选择合适的方法来验证KCL是否成立。
电子通用课件(基尔霍夫定律)

01
02
03
电源
提供稳定的直流电源,以 供电路使用。
测量仪表
包括电流表、电压表和欧 姆表,用于测量电路中的 电流、电压和电阻等参数 。
电路板和元件
包括电阻、电容、电感等 电子元件,以及连接线和 焊台等工具,用于搭建电 路。
实验步骤与操作
实验准备
搭建电路
根据实验要求选择合适的元件和仪表,搭 建电路前应先设计好电路图,并确保元件 的质量和规格符合要求。
实验目的与要求
验证基尔霍夫定律的正确性
通过实验测量和数据分析,验证基尔霍夫定律在电路中的适用性 和正确性。
培养实验技能
通过实验操作,培养学生的实验设计、操作、数据分析和处理等方 面的技能。
理解电路基本原理
通过实验,加深学生对电路基本原理和电子技术的理解,为后续课 程的学习打下基础。
实验设备与材料
电子通用课件(基尔霍夫 定律)
• 基尔霍夫定律简介 • 基尔霍夫定律的内容 • 基尔霍夫定律的应用 • 基尔霍夫定律的验证与实验 • 基尔霍夫定律的扩展与深化 • 习题与思考题
01
基尔霍夫定律简介
什么是基尔霍夫定律
01
基尔霍夫定律是电路分析中的基 本定律之一,它包括基尔霍夫电 流定律(KCL)和基尔霍夫电压 定律(KVL)。
在物理教学中的应用
帮助学生理解物理概念
通过应用基尔霍夫定律,可以帮助学 生更好地理解电流、电压、电阻等物 理概念,以及它们之间的关系。
提高学生解决问题能力
通过解决基于基尔霍夫定律的实际问 题,可以提高学生的问题解决能力和 实践技能,同时也可以培养学生的逻 辑思维和分析能力。
04
基尔霍夫定律的验证与实验
详细描述
基尔霍夫定律公式

基尔霍夫定律公式基尔霍夫定律(Kirchhoff's laws)是电路分析中最基本的定律之一、它是由德国物理学家叶夫·基尔霍夫(Gustav Kirchhoff)在19世纪提出的,用来描述电路中电流和电压的关系。
基尔霍夫定律包括基尔霍夫第一定律和基尔霍夫第二定律。
基尔霍夫第一定律,也称为节点定律,表明在任何一个电路节点中,进入该节点的电流总和等于离开该节点的电流总和。
换句话说,电流在一个节点中守恒。
这个定律是基于电流的连续性原理得出的。
如果一个节点是一个电流的分裂点,进入该节点的电流之和将等于离开该节点的电流之和。
数学上可以表示为:∑I_in = ∑I_out其中,∑I_in表示进入节点的电流之和,∑I_out表示离开节点的电流之和。
节点电流的方向可以根据约定定为正或负。
基尔霍夫第二定律,也称为回路定律,表明在一个电路回路中,环绕回路的电压之和等于零。
这个定律是基于电压的闭合性原理推导得出的。
在一个电路中,沿着一个回路的电压的总和必须为零。
这个定律适用于任何电路中的任何封闭回路,包括简单电路和复杂电路。
数学上可以表示为:∑V=0其中,∑V表示回路中的电压之和。
电压的符号取决于电流的方向。
基尔霍夫定律是电路分析的基础,可以用来解决复杂电路中的电流和电压分布的问题。
通过将电路划分为不同的节点和回路,可以使用基尔霍夫定律来建立一系列的方程来求解电路中未知的电流和电压。
一旦这些方程被解算出来,就可以得到完整的电路分析结果。
为了更好地理解基尔霍夫定律的应用,以下是一个简单的电路分析的示例:假设有一个由两个电源和三个电阻组成的串联电路。
电源1的电动势为E1,电源2的电动势为E2,电阻1的阻值为R1,电阻2的阻值为R2,电阻3的阻值为R3、我们需要求解电阻1、电阻2和电阻3上的电压。
首先,将电路进行标记,选择适当的节点和回路。
在本电路中,我们可以选择两个节点(节点A和节点B)和一个回路(环绕电阻1、电阻2和电压源E2)。
基尔霍夫定律

三、基尔霍夫电压定律
基尔霍夫电压定律(Kirchhoff's Voltage Law),简写为 基尔霍夫电压定律 , KVL,陈述为: ,陈述为: 对于任何集总参数电路的任一回路,在任一时刻, 对于任何集总参数电路的任一回路,在任一时刻,沿 该回路全部支路电压的代数和等于零,其数学表达式为 该回路全部支路电压的代数和等于零,
− i5 + i6 = 0 → i6 = i5 = 5A
此例说明,根据 此例说明,根据KCL,可以从一些电流求出另一些电流。 ,可以从一些电流求出另一些电流。
KCL不仅适用于结点 , 也适用于任何假想的封闭面 , 不仅适用于结点, 也适用于任何假想的封闭面, 不仅适用于结点 即流出任一封闭面的全部支路电流的代数和等于零。 即流出任一封闭面的全部支路电流的代数和等于零。例如对 图示电路中虚线表示的封闭面,写出的 图示电路中虚线表示的封闭面,写出的KCL方程为 方程为
∑u = 0
取负号。 取负号。
(1−10)
在列写回路KVL方程时,其电压参考方向与回路绕行 方程时, 在列写回路 方程时 方向相同的支路电压取正号, 方向相同的支路电压取正号,与绕行方向相反的支路电压
例如对图1- 电路的三个回路 电路的三个回路, 例如对图 -11电路的三个回路,沿顺时针方向绕行回 路一周,写出的 方程为: 路一周,写出的KVL方程为: 方程为
− i3 + i4 + i6 = 0
从以上叙述可见: 从以上叙述可见: KCL的一个重要应用是:根据电路中已知的某些支路 的一个重要应用是: 的一个重要应用是 电流,求出另外一些支路电流, 电流,求出另外一些支路电流,即 集总参数电路中任一支路电流等于与其连接到同一结 点(或封闭面 的其余支路电流的代数和,即 或封闭面)的其余支路电流的代数和 或封闭面 的其余支路电流的代数和,
基尔霍夫基本定律

基尔霍夫基本定律
基尔霍夫基本定律,又称为基尔霍夫定律,是电路理论中最重要的基础理论之一。
该定律是由德国物理学家基尔霍夫于
1845年发现的,用于描述电路中电流和电压的关系,是电路
分析的重要基础。
基尔霍夫基本定律分为两种:基尔霍夫第一定律和基尔霍夫第二定律。
基尔霍夫第一定律是说:在任何一个电路中,电流进入某个节点的总和等于电流离开该节点的总和。
这个定律可以用数学公式表示为:Σi=0,即所有进入该节点的电流之和等于所有离开该节点的电流之和。
这个定律的重要性在于:它为电路的分析提供了一个基本的基础,自然界中总的能量是守恒的,电路中的电流也是如此,所以这个定律可以保证电路中所有电流都是平衡的。
基尔霍夫第二定律是说:在任何一个电路中,一个电流的总和等于所有电动势(电压源)与电阻之间的电势降之和。
这个定律可以用一个简单的数学公式表示为:ΣUk=ΣiRi,即
所有电动势与电阻之间的电势降之和等于电路中所有电流之和。
这个定律的重要性在于:它可以对电路进行精细的分析,以了解在任何情况下电路的电流和电压分布。
它也可以帮助我们更
好地理解一些电路的重要性,例如电源和电阻的大小对电路的影响等。
基尔霍夫基本定律可以应用于各种电路分析中,例如直流电路、交流电路、复杂电路等。
仔细研究它可以提高我们的电路分析技能和问题解决能力。
总的来说,基尔霍夫基本定律是电路分析的基础理论之一,是我们理解电路运行机制的关键。
可以说,电路分析与设计的基本原理都是依据基尔霍夫基本定律展开的,没有它就不可能有我们现在的电子技术。
基尔霍夫定律 电路

基尔霍夫定律电路基尔霍夫定律(Kirchhoff's laws)是电路分析中非常重要的定律之一,它由德国物理学家叶夫·基尔霍夫于1845年提出。
基尔霍夫定律是研究电路中电流和电压分布的基础,它能够帮助我们理解电路中的电流和电压关系,为电路设计和故障排除提供了有力的工具。
基尔霍夫定律包括两个部分:基尔霍夫第一定律(电流定律)和基尔霍夫第二定律(电压定律)。
基尔霍夫第一定律,也称为电流定律,是基于电荷守恒定律的基础上提出的。
它表明,在任何一个电路中,流入某个节点的电流等于流出该节点的电流的总和。
换句话说,电流在一个闭合回路中是守恒的。
这个定律可以用一个简单的方程来表示:ΣI_in = ΣI_out,其中Σ表示总和,I_in表示流入节点的电流,I_out表示流出节点的电流。
基尔霍夫第二定律,也称为电压定律,是基于能量守恒定律的基础上提出的。
它表明,在一个闭合回路中,电压的总和等于零。
这个定律可以用一个简单的方程来表示:ΣV = 0,其中Σ表示总和,V 表示电压。
通过基尔霍夫定律,我们可以解决各种复杂的电路问题。
例如,我们可以通过应用基尔霍夫第一定律来计算电路中各个节点的电流分布情况。
通过应用基尔霍夫第二定律,我们可以计算电路中各个元件之间的电压关系。
同时,基尔霍夫定律还可以帮助我们理解电路中元件的连接方式以及元件之间的相互作用。
在实际应用中,基尔霍夫定律可以用于解决各种电路问题,如电路中的电流分布、电压分布、电阻的计算等。
它广泛应用于电子工程、电力系统、通信工程等领域。
需要注意的是,基尔霍夫定律是基于一些假设前提的。
首先,基尔霍夫定律假设电路是稳态的,即电路中的电流和电压不随时间变化。
其次,基尔霍夫定律假设电路中没有电磁辐射和电磁感应等非理想因素的影响。
因此,在实际应用中,我们需要根据具体情况进行合理的近似和简化,以保证基尔霍夫定律的适用性。
基尔霍夫定律是电路分析中的重要工具,它能够帮助我们理解电路中的电流和电压关系,解决各种复杂的电路问题。
(完整版)电工基础-基尔霍夫定律
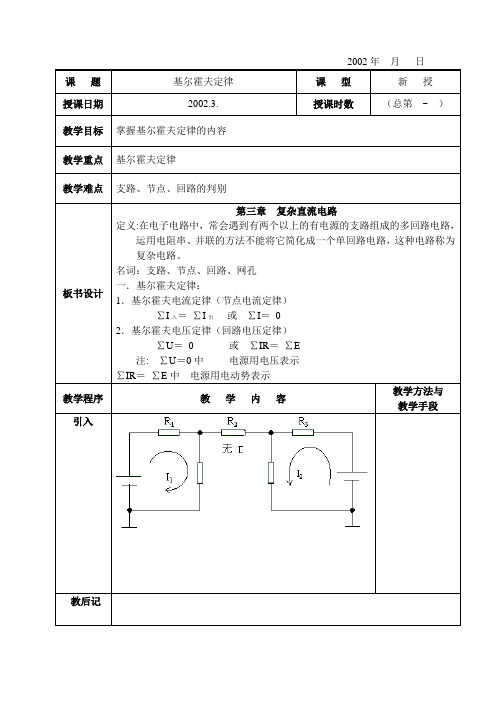
课题基尔霍夫定律课型新授授课日期2002.3. 授课时数(总第~ )教学目标掌握基尔霍夫定律的内容教学重点基尔霍夫定律教学难点支路、节点、回路的判别板书设计第三章复杂直流电路定义:在电子电路中,常会遇到有两个以上的有电源的支路组成的多回路电路,运用电阻串、并联的方法不能将它简化成一个单回路电路,这种电路称为复杂电路。
名词:支路、节点、回路、网孔一.基尔霍夫定律:1.基尔霍夫电流定律(节点电流定律)∑I入=∑I出或∑I=02.基尔霍夫电压定律(回路电压定律)∑U=0 或∑IR=∑E注: ∑U=0中电源用电压表示∑IR=∑E中电源用电动势表示教学程序教学内容教学方法与教学手段引入教后记教学手段新授[例]复杂直流电路第三章复杂直流电路定义:有两个以上的有电源支路组成的多回路电路,运用电阻的串、并联不能简化成一个单回路电路。
基本定律:基尔霍夫定律叠加原理戴维南定理名词解释:支路:由一个或几个元件首尾相接的无分支(判别)节点:三条或三条以上支路汇聚的点回路:任意的闭合电路网孔:最简单的闭合电路一、基尔霍夫定律:电流定律、电压定律1.基尔霍夫电流定律(节点电流定律):电路中任意一个节点上,流入节点的电流之和等于流出节点的电流之和。
(∑I入=∑I出)P.48图3-1教后记教学手段推广[例]图3-2 (a)图3-2 (b)还可写成:∑I=0(规定:流入为正,流出为负)任意假定的封闭面(节点),流入封闭面的电流之和等于流出封闭面的电流之和。
P.49 图3-3P.49 [例]图示电路中,方框代表电源或电阻各支路上电流的参考方向如图,I3 = -4A, I4 = 2A, 则I1 = I2 =教后记教学手段注:(1)假设电流方向正―对负-实际方向与假设方向相反练习P.65 1如图所示,求I1、、I2的大小。
2.基尔霍夫电压定律:(回路电压定律)从一点出发绕回路一周回到流点时,各段电压的代数和等于零。
(∑U=0 )教后记教学手段[例]小结:作业:P.50 图3-6还可写成∑IR=∑E注:(1)电压和电动势指的是代数和,必须考虑正负,当∑U=0时,电源作电压看;当∑IR=∑E时,电源作电动势。
基尔霍夫定律

基本信息基尔霍夫定律Kirchhoff laws是电路中电压和电流所遵循的基本规律,是分析和计算较为复杂电路的基础,1845年由德国物理学家G.R.基尔霍夫(Gustav Robert Kirchhoff,1824~1887)提出。
它既可以用于直流电路的分析,也可以用于交流电路的分析,还可以用于含有电子元件的非线性电路的分析。
运用基尔霍夫定律进行电路分析时,仅与电路的连接方式有关,而与构成该电路的元器件具有什么样的性质无关。
基尔霍夫定律包括电流定律和电压定律。
发现背景基尔霍夫定律是求解复杂电路的电学基本定律。
从19世纪40年代,由于电气技术发展的十分迅速,电路变得愈来愈复杂。
某些电路呈现出网络形状,并且网络中还存在一些由3条或3条以上支路形成的交点(节点)。
这种复杂电路不是串、并联电路的公式所能解决的,刚从德国哥尼斯堡大学毕业,年仅21岁的基尔霍夫在他的第1篇论文中提出了适用于这种网络状电路计算的两个定律,即著名的基尔霍夫定律。
该定律能够迅速地求解任何复杂电路,从而成功地解决了这个阻碍电气技术发展的难题。
基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上,在稳恒电流条件下严格成立。
当基尔霍夫第一、第二方程组联合使用时,可正确迅速地计算出电路中各支路的电流值。
由于似稳电流(低频交流电)具有的电磁波长远大于电路的尺度,所以它在电路中每一瞬间的电流与电压均能在足够好的程度上满足基尔霍夫定律。
因此,基尔霍夫定律的应用范围亦可扩展到交流电路之中。
基本概念1、支路:(1)每个元件就是一条支路,如图ab、bd;基尔霍夫定律(2)串联的元件我们视它为一条支路,如图aec;(3)流入等于流出的电流的支路。
2、节点:(1)支路与支路的连接点;(2)两条以上的支路的连接点,如图a,b,c,d;(3)广义节点(任意闭合面)。
3、回路:(1)闭合的支路,如abda,bcdb;(2)闭合节点的集合。
4、网孔:(1)其内部不包含任何支路的回路如abcea;(2)网孔一定是回路,但回路不一定是网孔如abcda主要内容基尔霍夫第一定律第一定律又称基尔霍夫电流定律,简记为KCL,是电流的连续性在集总参数电路上的体现,其物理背景是电荷守恒公理。
基尔霍夫定律是什么电路的基本定律

基尔霍夫定律是什么电路的基本定律嘿,朋友们,今天咱们聊聊基尔霍夫定律。
这可是电路里的“大Boss”,没它可真是寸步难行啊。
想象一下,一个电路就像是一条热闹的街道,电流就像街上的小车,大家都在赶路,可是要是没有交通规则,真是一片混乱。
基尔霍夫定律就是这个街道上的交通警察,让一切井然有序。
有两个主要的定律,分别叫电流定律和电压定律。
电流定律嘛,简单来说就是在一个节点上,流进来的电流总和等于流出去的电流总和。
想象一下,街角有三个路口,A、B、C,大家都在这儿匆匆而过,A路口进来了三辆车,B路口出去了两辆车,那么C路口就得出去一辆车,才能保证不堵车。
你想,电流也得遵守这个道理,要是进得多,出得少,那可真是要出大事了。
再说电压定律,这个就像是在说一条路的“高度”。
每个电器都需要一定的电压,才能正常运转,就像汽车需要加油才能开动。
电压定律告诉我们,环路中的电压升降总和是零,也就是说,电池提供的电压减去电阻带来的电压损失,最后得出的结果是零。
这就好比你开车从A地到B地,路上爬坡和下坡,最后还是得回到原点,要是不平衡,车可就不听话了。
想象一下,如果没有基尔霍夫定律,电流就像是小孩子们放学后奔向游乐场,完全没有方向可言,互相推搡,最后都不知道去哪儿了。
电路里的电压和电流,就像是他们的老师,要告诉他们,哪里是安全的、哪里是能玩的。
没了这些定律,电器们就像无头苍蝇,随便乱转,哪儿也到不了。
基尔霍夫定律不仅仅是电路中的玩意儿,在生活中处处都有它的影子。
你想想,一个团队工作,如果每个人都在自己的小角落里忙活,而不考虑其他人,那真是乱成一团。
而基尔霍夫定律就像团队里的协作精神,大家一起出力,才能达到目标。
电流和电压相互作用的关系,恰好反映了我们日常生活中人与人之间的关系。
谁来、谁去,都是需要有个平衡的,才能让生活这条大船行稳致远。
咱们还得提一提,基尔霍夫定律在电路设计中的重要性。
你想象一下,一个电路设计师,要是没遵循这些基本定律,那可真是要被同行们笑掉大牙。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1847年发表的两个电路定律 (基尔霍夫电压定律和基尔霍夫电流 定律), 发展了欧姆定律,对电路理论有重大 作用。
基尔霍夫电流定律 (Kirchhoff 's Current Law,KCL) 基尔霍夫电压定律 (Kirchhoff 's Voltage Law,KVL)
常用术语
一、复杂电路中的基本概念
1.支路:由一个或几个元件首尾 相接构成的无分支电路。 右图中有 3 条支路: E1和R1串联构成一条支路 E2和R2串联构成一条支路 R3单独构成另一条支路
思考
B E1 E2 R3
A
R1
R2
同一支路中的电流有什么关系?
I4
I1
2.节点:三条或三条以上支路的会聚的点。 下图中 a为节点。 上图中A 和 B 为节点;
-4mA:电流的实际 计算结
果为正值,电流的实际方向与参考方 向相同;结果为负值,电流的实际方 向与参考方向相反
基尔霍夫第二定律——回路电压定律
1、内容:在任一时刻,对任一闭合回路,沿回路绕行方 电工基础教程 向上各段电压代数和等于零。 2、公式:
教学难点:式中括号外正负号是由基尔霍夫第一定律根
据电流 的参考方向确定的,括号内数字前的负号则是 表示实际电流方向和参考方向相反。
电路如下图所示,求电流 I 3。
I1
R1
A
I3
I2
R2
R3
B
I4
R4
I5
R5
U s1
U s2
对A节点 I1 - I 2 - I 3 0 因为 I1 I 2 所以 I3 0 同理,对B节点: I 4 - I5 + I 3 0 因为 I 4 I 5 也得 I3 0
U1
R1
-
I3
R2 R3 b
+
-
U2
I1+I2 = I3 对节点 a:
(一)基尔霍夫电流定律(KCL) 1.内容:电路中任意一个节点上,在任意时刻,流入节电的 电流之和等于流出节点的电流之和。 2.表达式:根据右图写出节点电流定律的数学表达式 I1+I3=I2+I4+I5 变形得:I1+I3+(-I2)+(-I4)+(-I5)=0 如果规定流入节点的电流为正,流出 节点的电流为负,则可得出下面的结论:
10A
I2
A I1 B 2A
解: 对节点A I1=3A+10A+5A =18A 对节点B 5A=I2+2A+10A 整理: I2=5A-2A-10A =-7A 可知:I1的方向与参考方向相同,
3A
5A
10A
I2的实际方向是向下的
注意:应用基尔霍夫电流定 律时必须首先假设电流的参 考方向,若求出电流为负值, 则说明该电流实际方向与假 设的参考方向相反。
U 0
请用基尔霍夫第二定律 列出右图回路电压方程
电源电动势之和 = 电路电压降之和
攀登总高度 = 下降总高度
方法:
1、先设下回路的绕行方向。可顺时针,也可逆。
2、确定各段电压的参考方向。电阻上电压的参考 方向与所取电流的一致,电源部分的电压方向由电 源的正极指向负极。 3、凡是参考方向与绕行方向一致的电压取正,反 之取负。 4、电阻上电压的大小等于该电阻阻值与流经该电 阻的电流的乘积;电源部分的电压等于该电源的电 动势。 5、沿回路绕行一周,列出KVL方程。
电路基本定律-- 基尔霍夫定律
三、电压定律
KVL
第5节
比较以下两个电路的不同
1.电路中只有1个电源 2.可以用电阻的串并联化简
1.电路中有2个电源 2.不能用电阻的串并联化简
分析方法
分析方法
基尔霍夫简介
古斯塔夫· 罗伯特· 基尔霍夫 (Gustav Robert Kirchhoff,1824 —1887 ) 德国物理学家,柏林科学院院士
E2 I 2 R2 + I3 R3
电
整理得联立方程
I 2 I 3 - I1 2 I1 + 5 I 3 17 I 2 + 5 I 3 17
流 方 向 和 假 设 方 向 相 同
3、解联立方程得
I1 1 A I2 2A I3 3A
注意: 1.列方程前标注回路绕行方向(顺时针);
实例进阶
已知I1 = 25 mA,I3 = 16 mA,I4 = 12 mA,试
求其余电阻中的电流I2、I5、I6 解:节点a:I1=I2+I3 则
I2=I1-I3=25 -16=9mA 节点d:I1=I4+I5 则 I5=I1-I4=25 -12=13mA 节点b:I2=I6+I5 I6=I2 -I5= 9 -13= -4mA 则
I5 I1
a
I4
I2 I3
∑I=0
即:在任一电路的任一节点上,电流的代数和永远等于零。
【例1】如图所示电桥电路,已知I1 = 2A,I2 = -3A,I3 =- 2 A,
试求电流I4。
I1
I2
I3
方法: 1、先确定各支路电流方向。 2、列写KCL方程。 3、有N个节点,可列出N个方程。
I4
由基尔霍夫第一定律可知 I1 - I 2 + I 3 - I 4 0 代入已知值 2 - (-3) + (-2) - I 4 0 可得: I 4 3 A
作业:找出电路中的节点、支路、回路、网孔。
列写KCL、KVL方程.
a
I4
I2 I3
一、复杂电路中的基本概念
3.回路:电路中从任一点出发,经过 一定路径又回到该点形成的闭合路径。 考虑:图中共有 3 个回路, 分别是: A B D M A A N C B A M N C D M 4.网孔:最简单的、不可再分的回路。 思考
网孔和回路有什么关系? 上述的回路中哪些是网孔?
E1
M
E2
A
N
R3 R1 R2
D
B
C
支路:由一个或几个元件串联组成的无分支电 路。
1、支路:三条
节点:三条或三条以上支路的汇交点叫节点。
2、节点:b、e
回路:电路中任一闭合路径。
3、回路:abeda、 bcfeb、 abcfeda
网孔:内部不含有支路的回路。
4、网孔: abeda、 bcfeb
2.应用 U = 0列方程时,等号右边写0,左边要注意
电压的符号: 对于电源:从正极到负极取+号,反之取-号。 对于电阻:电流方向与绕行方向相同取+号,反之取-号 3. 开口电压可按回路处理 B + + + 对回路1: U1 U2 U=0 – – 1 UBE R I2R2 – U2 + UBE = 0 R2 I2 _ 1 E
帮 助
支路:6条 节点:4个 回路:7个 网孔:3个
例 1:
I1
a
I2
IG
d G
I3
b
I4
I
支路:ab、bc、ca、… (共6条) 结点:a、 b、c、d c (共4个) 回路:abda、abca、 adbca … (共7 个)
+
E
–
基尔霍夫电流定律(KCL定律)
1.定律 在任一瞬间,流向任一结点的电流等于流出该结 点的电流。 即: I入= I 出 I1 I2 a +
由此可知,没有构成闭合回路的单支路电流为零
基尔霍夫电流定律的应用
试一试
1、电路如图所示,求I1、I2的大小。
10A
A B
I2
3A I1
5A
10A 2A
例:求电路中的电流I1和I2
分析:电路中有两个节点,为A、B I1为节点A一支路电流,其它支路电流已知 I2为节点A一支路电流,其它支路电流已知 可以利用基尔霍夫电流定律求解
下图电路中,E1 = E2 = 17V,R1 = 2Ω, R2 = 1Ω,R3 = 5Ω,求各支路电流。
1.标出各支路电流参考方向和独立回路的绕行方向,应
用基尔霍夫第一定律列出节点电流方程.
I1 + I 2 I 3
2. 应用基尔霍夫第二定律列出回路电压方程 对于回路1有 对于回路2有
E1 I1R1 + I 3 R3
