四参数计算的操作流程及投影转换流程

四参数坐标转换方法

四参数坐标转换⽅法
⼯程应⽤上，免不了不同坐标系统之间的转换，对于⼯程测量，⼀般范围不够⼤的时候，⼤多数采⽤四参数转换。

四参数坐标转换的公式为：
X2=（1+p）*（X1*COSA+Y*SINA）+X
Y2=（1+p）*（-X1*SINA+Y*COSA）+Y
其中，四参数分别为：平⾯位移量X、Y，旋转因⼦A，⽐例因⼦P。

在excel中，C1、D1单元格分别X1、Y1，那么
D1中输⼊“=(1+p/1000000)*(C1*COS(A)+D1*SIN(A))+X”
F1中输⼊“=(1+p/1000000)*(-C1*SIN(A)+D1*COS(A))+Y”
即得到四参数转换后的结果。

四参数坐标转换的根本是要得到四参数，⼀般，可能已经给出，那么带⼊上述公式求解即可；如果没有给出四参数，但是有2套系统之间的公共点坐标，就需要先求解四参数。

四参数的求解，可⽤的软件⽐较多，⼀般的免费软件“笑脸”，“经天测绘坐标转换”等，在选定公共点的时候，点位越多越均匀，那么转换精度则越⾼，越可靠。

ps：
1、“经天测绘坐标转换”免费版软件，在四参数求解的时候，需要注意，旋转因⼦R，需要增加⼀个负号。

估计是因为免费版本的原因，作者有意增加⼀个错误，已正权益。

2、七参数换椭球，四参数换同椭球⾥不同坐标。

在同⼀椭球⾥，四参数转换精度⼀般能满⾜要求，不同的椭球，则需要先转为空间直⾓坐标，再投影为平⾯坐标。

空间直⾓坐标，在不同椭球⾥，有严密的计算公式。

不同椭球的空间直⾓坐标，需要七参数转换。

3、在同⼀个椭球⾥坐标转换，需要先换到同⼀中央⼦午线，再在各坐标系统间转换。

三参数、四参数、七参数等坐标系转换参数求解 -回复

三参数、四参数、七参数等坐标系转换参数求解-回复在地理信息系统（GIS）和空间数据处理中，经常需要进行不同坐标系之间的转换。

常见的坐标系转换方法包括三参数、四参数和七参数等。

本文将一步一步地讲解这些坐标系转换参数的求解方法。

1. 三参数坐标系转换参数求解三参数坐标系转换是一种基本的坐标系转换方法，适用于同一地区内的小范围转换。

这种方法使用三个参数来描述转换，分别是平移参数（delta X 和delta Y）和旋转参数（delta Z）。

其数学模型可以表示为：X_new = X_old + delta X + delta Z * Y_oldY_new = Y_old + delta Y - delta Z * X_oldZ_new = Z_old要求解这三个参数，通常需要至少三对已知的坐标点。

已知的坐标点可以是在两个不同坐标系中测量得到的。

下面是求解三参数坐标系转换参数的步骤：步骤1：选择至少三对已知的坐标点，并在两个不同坐标系中用坐标系A 和坐标系B表示。

步骤2：通过观察坐标系A和坐标系B之间的关系，将数学模型中的公式改写为总体误差最小的形式。

步骤3：将已知坐标点的坐标值代入改写后的数学模型，得到带有未知参数的方程组。

步骤4：通过数学方法求解方程组，得到三个参数的近似解。

步骤5：对参数的近似解进行迭代计算，直到满足预设的误差限度。

2. 四参数坐标系转换参数求解四参数坐标系转换是在三参数的基础上增加了一个尺度参数（scale factor）。

尺度参数描述了坐标系统之间的比例差异，通常用ppm（百万分之一）表示。

其数学模型可以表示为：X_new = X_old + delta X + ppm * Y_oldY_new = Y_old + delta Y - ppm * X_oldZ_new = Z_old与三参数的求解类似，四参数的求解也需要至少三对已知的坐标点。

下面是求解四参数坐标系转换参数的步骤：步骤1：选择至少三对已知的坐标点，并在两个不同坐标系中用坐标系A 和坐标系B表示。

七参数四参数转化

七参数四参数转化七参数和四参数是地图投影参数的两种主要形式。

七参数转化为四参数意味着从包含更多参数的转换模型向包含更少参数的模型转换。

下面将详细介绍七参数和四参数的概念以及它们之间的转换方法。

1.七参数转换模型：七参数是指地图投影转换过程中需要考虑的七个参数，它们分别是平移X、平移Y、平移Z、旋转角度α、β、γ和尺度因子k。

这些参数用来描述两个坐标系之间的平移、旋转和尺度变换关系。

七参数转换模型的数学表达形式为：X' = X + tx + (-rz * Y) + (ry * Z) + dxY' = Y + rz * X + (-tx * Z) + dyZ' = Z + (-ry * X) + (tx * Y) + dz其中，(X', Y', Z')为转换坐标系中的坐标，在这个坐标系中，X轴指向东方，Y轴指向北方，Z轴指向上方。

而(X, Y, Z)为原始坐标系中的坐标，原始坐标系的坐标轴方向可能与转换坐标系不一致。

tx、ty、tz 为平移参数，表示坐标系之间的平移关系。

rx、ry、rz为旋转参数，表示坐标系之间的旋转关系。

dx、dy、dz为尺度参数，表示坐标系之间的尺度变换关系。

2.四参数转换模型：四参数是指地图投影转换过程中只需考虑的四个参数，它们分别是平移dx、dy、旋转角度θ和尺度因子m。

这些参数也用于描述两个坐标系之间的平移、旋转和尺度变换关系。

四参数转换模型的数学表达形式为：X' = m * (X * cosθ - Y * sinθ) + dxY' = m * (X * sinθ + Y * cosθ) + dy其中，(X', Y')为转换坐标系中的坐标，在这个坐标系中，X轴指向东方，Y轴指向北方。

而(X, Y)为原始坐标系中的坐标，原始坐标系的坐标轴方向可能与转换坐标系不一致。

dx、dy为平移参数，表示坐标系之间的平移关系。

如何进行参数计算（四参数高程拟合）？

如何进行参数计算（四参数高程拟合）？定义：四参数是指两个平面坐标系之间的平移（DX、DY），旋转（α），缩放参数（κ）。

四参数是RTK常用的一种坐标转换模式，通过四参数完成WGS84平面到当地平面的转换，通过高程拟合完成WGS84椭球高到当地水准的拟合。

要求：至少两个任意同一坐标系的坐标（通用方法）使用环境：适用于大部分的普通工程测量，工程放样简要步骤1）仪器工作模式设置2）采集控制点坐标3）求解参数4）坐标检核计算参数的详尽流程1、设置基站与移动站（可以选择手机卡或者电台模式），使移动台最终达到固定解；2、采集控制点坐标（如“交186”与“y265”为控制点）在碎部测量中，分别对控制点进行“交186”和“y265”采集坐标（使用平滑采集对控制点进行采集），分别保存为“交186”与“y265”。

3、求解参数1）进入参数求解界面2）、添加控制点对如图操作，分别添加“交186”与“y265”两个点对。

其中源点为刚才采集的坐标，目标点为控制点的已知坐标（需要自己手动添加，或者提前输到控制点库中，再调用）。

3）计算参数点击计算，得到“四参数+高程拟合”的结果点击应用后，即可完成操作。

A为高程固定差改正的差值。

注意：尺度的数据为0.999……或者1.000……4、进行坐标检核找一个控制点进行碎部测量（最好找第三个控制点），对比采集的（N,E,Z）与已知坐标（N,E,Z）检核坐标的正确性。

注意：1、这里的“四参数+高程拟合”计算是针对于基站而言的。

在计算“四参数+高程拟合”之前，必须保证坐标系统中的基准面的“转换模型”，平面转换的“转换模型”，高程拟合“转换模型”均为“无”；2、一个项目只能求解一次参数计算，或者说一个项目求参数前，必须满足前一点条件；3、计算参数的两个点数据必须是接收同一个基站信号采集的固定解坐标；用于计算参数的两个点的已知坐标必须是同一个坐标系统，即计算的尺度（k）为0.999……或者1.000……。

坐标转换四参数范文

坐标转换四参数范文坐标转换是指将一个空间坐标系中的点坐标转换到另一个空间坐标系中的点坐标的过程。

常见的坐标转换方法有七参数转换和四参数转换。

四参数转换是一种常用的二维坐标转换方法，也称为仿射变换。

四参数转换可以将一个平面坐标系中的点坐标转换到另一个平面坐标系中的点坐标。

四参数转换的基本原理是通过平移、旋转、缩放和翻转等变换操作来实现坐标的转换。

四参数转换的数学模型可以表示为：x’ = x * cosθ + y * sinθ + Dxy’ = -x * sinθ + y * cosθ + Dy其中，x和y是源坐标系中的点坐标，x’和y’是目标坐标系中的点坐标，θ是旋转角度，Dx和Dy是平移量。

四参数转换的步骤如下：1.确定源坐标系和目标坐标系。

2.收集样本点坐标，这些样本点坐标同时在源坐标系和目标坐标系中已知。

3.根据样本点坐标，求解旋转角度θ、平移量Dx和Dy的数值。

4.利用求解出的参数，进行坐标转换，计算目标坐标系中的点坐标。

5.验证坐标转换结果，查看转换后的坐标是否与目标坐标系中的样本点坐标一致。

6.在需要的情况下，优化四参数转换的结果。

四参数转换的优点是计算简单、效率高，适用于二维平面坐标系的转换。

但是，四参数转换只能实现平移、旋转、缩放和翻转等刚性变换，不能处理非刚性变换。

对于需要进行非刚性变换的情况，可以利用其他的坐标转换方法，如七参数转换。

在实际应用中，四参数转换被广泛应用于地理信息系统（GIS）中的地图投影、坐标转换、地图叠加和地图的符号绘制等方面。

通过四参数转换，可以将不同地理坐标系下的地图数据进行叠加和转换，实现地图数据的整合和共享。

需要注意的是，四参数转换在坐标转换中只是一种方法，具体的坐标转换过程还需要根据具体的应用需求和数据特点来确定。

在实际应用中，还需要考虑数据的准确性、精度要求和误差评定等因素，综合选择合适的坐标转换方法和参数进行数据的转换和处理。

matlab坐标转换四参数法

matlab坐标转换四参数法1.引言1.1 概述在地理信息系统和测绘学中，坐标转换是一项重要的任务。

由于不同的坐标系统具有不同的基准和投影方式，因此需要进行坐标转换才能将一个点的坐标从一个坐标系统转换到另一个坐标系统。

本文将介绍一种常用的坐标转换方法——四参数法。

四参数法是一种简单而有效的坐标转换方法，通过使用四个参数进行坐标的平移和旋转，实现坐标的转换。

本文的目的是为读者介绍四参数法的原理、应用和优势。

通过深入理解四参数法的原理，读者将能够准确地将坐标在不同的坐标系统之间进行转换。

本文的结构如下：首先，将介绍坐标转换的背景，包括不同坐标系统的特点和应用领域。

其次，将详细介绍四参数法的原理，包括参数的意义和计算方法。

最后，将探讨四参数法在坐标转换中的应用，并对整个文章的内容进行总结。

通过阅读本文，读者将能够全面了解四参数法在坐标转换中的作用，掌握使用四参数法进行坐标转换的基本技巧和要点。

希望本文能够对地理信息系统和测绘学领域的专业人士和学生提供有益的参考和借鉴。

1.2文章结构文章结构部分的内容如下：1.2 文章结构本文分为引言、正文和结论三部分。

每个部分都包含了多个章节，以便清晰地呈现出Matlab坐标转换四参数法的相关内容。

在正文部分，我们将首先介绍坐标转换的背景，包括为什么需要进行坐标转换以及坐标转换的重要性。

然后，我们将详细解释四参数法的原理，包括如何使用四个参数来进行坐标转换，并且说明其适用性和局限性。

在结论部分，我们将探讨四参数法在坐标转换中的实际应用，包括它在地理信息系统和测量等领域中的重要性和实用性。

最后，我们将对整篇文章进行总结，并提出一些展望和未来的研究方向。

通过这种结构，读者将能够系统地了解Matlab坐标转换四参数法的相关知识和应用，同时也可以深入研究并拓展该方法的更多可能性。

1.3 目的本文的目的是介绍和讨论在Matlab中使用四参数法进行坐标转换的方法。

坐标转换是在地理信息系统（GIS）和测量工程中常用的技术，用于在不同的坐标系统或参考框架之间转换地理位置信息。

四参数计算的操作流程及投影转换流程

四参数计算的操作流程及投影转换流程
四参数计算的操作流程
1）打开坐标转换软件，在坐标转换里，找到计算四参数，双击，进入
2）在输入用PDA采集的WGS84坐标系，在里，输入控制点坐标（已知80坐标），两坐标均为平面坐标
3）第一个点输入完成后，选择，按照同样的方法，输入第二个点的
WGS84坐标和80坐标，并选择
4）点击按钮，右上角出现四参。

将其导出，并保存
投影带转换的操作流程
1.从程序里找到，双击打开，进入程序界面
2.在程序界面左侧找到需要注入的文件，展开，如图1.找到
，然后点右键在出现的下拉菜单中找到，点击进入，如图2
图 1 图2 3.在弹出的对话框中选择“select ”，进入。

如图3
选择，进入。

如图4
图4
在上面的对话框中点选，进入，弹出对话框如图5
图5
在上面的对话框中选择，点击进入，如图6
图6
选择，双击，出现图7
图7
选择“确认”即可。

4.打开ArcMAP。

在左侧的Layer点击右键，如图8
图8
选择进入，选择想要的工作底图，如图9
图9.
双击所需要图形，即可
5.打开刚才的Catalog软件，将采集的GPS点位信息直接拖入Arcmap的底图中，即可实现比对，如图10。

三维四参数空间直角坐标转换计算方法

一、引言在地图制图、航空航天、导航定位等领域，经常需要进行三维空间直角坐标的转换计算。

在进行这类计算时，常常会涉及到三维四参数空间直角坐标的转换。

本文将介绍三维四参数空间直角坐标转换的计算方法及其应用。

二、三维四参数空间直角坐标的定义三维空间中，直角坐标系通常用(x, y, z)表示。

在进行坐标转换时，需要考虑到可能存在的平移、旋转、缩放等变换。

三维四参数空间直角坐标则包括了平移在x、y、z三个方向上的位移和绕某个轴的旋转角度。

三、三维四参数空间直角坐标转换的计算方法1. 平移变换的计算方法平移变换是指在x、y、z三个方向上的位移。

假设平移量分别为tx、ty、tz，那么进行平移变换后的坐标可以表示为：x' = x + txy' = y + tyz' = z + tz2. 旋转变换的计算方法绕某个轴的旋转变换通常用旋转矩阵来表示。

以绕z轴的旋转为例，旋转角度为θ，那么进行旋转变换后的坐标可以表示为：x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθz' = z3. 综合变换的计算方法综合平移和旋转变换后，坐标的变换可以表示为：x' = (x - xs)*cosθ - (y - ys)*sinθ + xty' = (x - xs)*sinθ + (y - ys)*cosθ + ytz' = z + zt四、三维四参数空间直角坐标转换的应用在实际应用中，三维四参数空间直角坐标转换通常用于地图制图、航空航天、导航定位等领域。

在地图制图中，需要将世界坐标系中的地理坐标转换为局部坐标系中的平面坐标，就需要进行三维四参数空间直角坐标的转换。

在航空航天领域，导航定位系统也需要进行三维坐标的转换计算，以确定飞行器的位置和姿态。

五、结论三维四参数空间直角坐标转换是现代科学技术中常见的数学计算方法，具有广泛的应用价值。

四参数坐标转换步骤

四参数坐标转换步骤1. 引言四参数坐标转换是一种常用的地理信息处理方法，用于将不同坐标系下的地理数据进行转换。

本文将介绍四参数坐标转换的基本原理和步骤。

2. 坐标系的基本概念在开始了解四参数坐标转换之前，需要了解一些基本概念。

地理坐标系是用来描述地球表面位置的一种坐标系统。

常见的地理坐标系有经纬度坐标系和投影坐标系。

经纬度坐标系使用经度和纬度来表示地球上的点，而投影坐标系是将地球表面投影到一个平面上，并使用x和y坐标来表示点的位置。

3. 四参数坐标转换的原理四参数坐标转换是一种简化的投影坐标转换方法，它通过四个参数来描述两个坐标系之间的转换关系。

这四个参数分别是平移、旋转、比例因子和误差。

平移参数表示两个坐标系的原点之间的偏移量，旋转参数表示两个坐标系之间的旋转角度，比例因子表示两个坐标系之间的比例关系，误差参数用来补偿转换过程中的误差。

4. 四参数坐标转换的步骤四参数坐标转换的步骤如下：4.1 数据准备首先需要准备两个坐标系下的地理数据，包括源坐标系和目标坐标系下的点的坐标。

这些坐标可以通过GPS测量或其他地理信息系统获取。

4.2 坐标系匹配将源坐标系和目标坐标系进行匹配，确定它们之间的关系。

这个过程需要使用一些参考点来进行匹配，比如在源坐标系下测量一些点的坐标，在目标坐标系下测量同样的点的坐标，并将这些点进行对应。

4.3 参数计算通过匹配点的坐标，可以计算出四个参数的值。

平移参数可以通过计算两个坐标系的原点之间的偏移量得到，旋转参数可以通过计算两个坐标系之间的旋转角度得到，比例因子可以通过计算两个坐标系之间的比例关系得到，误差参数可以通过计算两个坐标系之间的坐标差得到。

4.4 坐标转换根据计算得到的四个参数，将源坐标系下的点的坐标转换到目标坐标系下。

这个过程可以通过矩阵运算来实现，将源坐标系下的点的坐标乘以一个转换矩阵，得到目标坐标系下的点的坐标。

4.5 检验精度转换完成后，需要检验转换的精度。

四参数转换

四参数转换介绍四参数转换是一种数学模型，常用于处理地理坐标转换的问题。

它是基于一组数学方程，通过将一个坐标系统的坐标转换为另一个坐标系统的坐标来实现的。

四参数转换常用于地理测量、地图投影、GPS定位等领域。

原理四参数转换基于以下原理：将一个坐标系的坐标转换为另一个坐标系的坐标，需要考虑两个坐标系之间的平移量和旋转角度。

平移量表示两个坐标系之间在水平和垂直方向上的平移关系，旋转角度表示两个坐标系之间的旋转关系。

参数四参数转换涉及四个参数，分别为平移参数X、平移参数Y、旋转参数α和比例参数s。

其中平移参数X和Y表示两个坐标系之间的平移量，旋转参数α表示两个坐标系之间的旋转角度，比例参数s表示两个坐标系之间的尺度变换关系。

应用领域四参数转换广泛应用于地理测量、地图投影和GPS定位等领域。

在地理测量中，常使用四参数转换将平面坐标系转换为大地坐标系，以实现对地球表面的测量。

在地图投影中，四参数转换可以将一个地图投影系统的坐标转换为另一个地图投影系统的坐标，以实现地图的拼接和叠加。

在GPS定位中，四参数转换可以将GPS接收器接收到的经纬度坐标转换为目标坐标系的坐标，以实现目标的定位和导航。

使用方法进行四参数转换的具体步骤如下：1.收集输入数据：需要收集两个坐标系的坐标数据，以及对应的控制点。

2.确定参数：根据输入数据，使用数学方法计算出四个参数的值。

3.坐标转换：将源坐标系的坐标通过四参数转换公式转换为目标坐标系的坐标。

4.验证数据：将转换得到的坐标与实际数据进行比较，验证四参数转换的准确性。

实例分析以下通过一个实例来展示四参数转换的具体应用。

输入数据假设有两个坐标系A和B，坐标系A的控制点数据如下：点名坐标X(A) 坐标Y(A)A 100 200B 300 400C 500 600坐标系B的控制点数据如下：点名坐标X(B) 坐标Y(B)A 150 180B 320 380C 480 590计算参数根据输入数据，可以计算出四个参数的值。

四参数计算过程

四参数计算过程四参数计算过程是一种常用的统计分析方法，它通过四个参数来描述一组数据的分布情况。

这四个参数分别是均值、方差、偏度和峰度。

下面将详细介绍四参数计算过程的具体步骤。

一、均值计算均值是数据集中的所有数据的平均值，用来描述数据的集中趋势。

计算均值的方法是将所有数据相加，然后除以数据的个数。

二、方差计算方差是数据集中各个数据与均值之差的平方的平均值，用来描述数据的离散程度。

计算方差的方法是将每个数据与均值之差的平方相加，然后除以数据的个数。

三、偏度计算偏度是数据集分布偏斜程度的度量，用来描述数据分布的不对称性。

偏度为正表示数据分布的右侧较重尾，偏度为负表示数据分布的左侧较重尾，偏度为零表示数据分布基本对称。

计算偏度的方法是将每个数据与均值之差的立方相加，然后除以方差的三分之二次方。

四、峰度计算峰度是数据集分布峰态的度量，用来描述数据分布的陡峭程度。

峰度大于零表示数据分布相对于正态分布更陡峭，峰度小于零表示数据分布相对于正态分布更平坦，峰度等于零表示数据分布与正态分布具有相同的陡峭程度。

计算峰度的方法是将每个数据与均值之差的四次方相加，然后除以方差的四次方。

通过这四个参数的计算，可以全面地描述一组数据的分布情况。

均值和方差可以告诉我们数据的集中程度和离散程度，偏度可以告诉我们数据分布的偏斜程度，峰度可以告诉我们数据分布的陡峭程度。

四参数计算过程是统计分析中常用的方法之一，它可以帮助我们更好地理解和解释数据。

在实际应用中，我们可以根据数据的四个参数来判断数据是否服从正态分布，以及进行进一步的数据分析和预测。

四参数计算过程是一种简单而有效的统计分析方法，通过计算数据的均值、方差、偏度和峰度，可以全面地描述数据的分布情况。

这些参数可以帮助我们更好地理解和解释数据，为后续的数据分析和预测提供依据。

计算转换参数方法

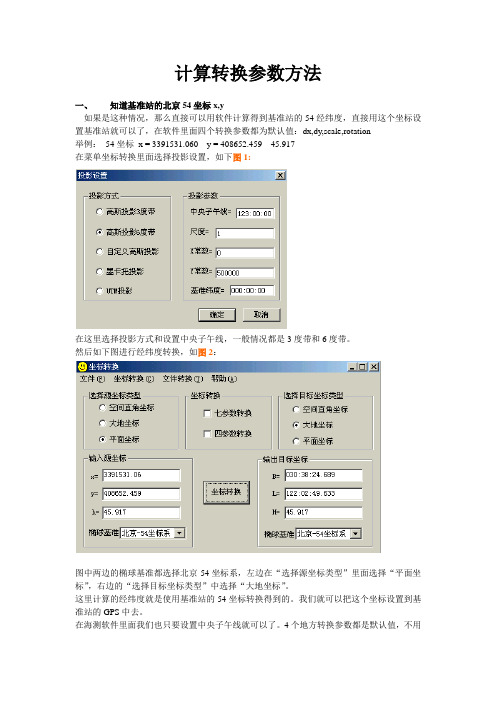
计算转换参数方法一、知道基准站的北京54坐标x,y如果是这种情况，那么直接可以用软件计算得到基准站的54经纬度，直接用这个坐标设置基准站就可以了，在软件里面四个转换参数都为默认值：dx,dy,scale,rotation举例：54坐标x = 3391531.060 y = 408652.459 45.917在菜单坐标转换里面选择投影设置，如下图1:在这里选择投影方式和设置中央子午线，一般情况都是3度带和6度带。

然后如下图进行经纬度转换，如图2：图中两边的椭球基准都选择北京-54坐标系，左边在“选择源坐标类型”里面选择“平面坐标”，右边的“选择目标坐标类型”中选择“大地坐标”。

这里计算的经纬度就是使用基准站的54坐标转换得到的。

我们就可以把这个坐标设置到基准站的GPS中去。

在海测软件里面我们也只要设置中央子午线就可以了。

4个地方转换参数都是默认值，不用设置。

二、知道两个wgs84坐标和两个地方坐标，其中一个是基准站的坐标这时候，我们可以很方便的设置基准站，但是在流动站的船上，我们必须设置相关的坐标转换参数。

现在我们在软件里面设计了输入地方坐标转换参数的对话框。

主要的工作就是要求出这四个转换参数。

需要有几个步骤，但是对于一个工程来说，只要在工作前花半个小时就可以了。

具体步骤和图示如下：1、84经纬度转换成54投影坐标如图1设置投影带和中央子午线2、把两个点的经纬度转换成54投影坐标，如下图如上图的设置，在左边的椭球基准选择WGS-84坐标系，右边也是相同的坐标系。

举例已知的两组数据如下：点一B = 030:38:26.645L = 122:02:49.556地方坐标x’ = -65839.283y’ = 55680.371点二B = 030:37:59.928L = 122:03:07.031地方坐标x’ = -66659.526y’ = 56150.074分别得到高斯平面投影坐标点一x = 3391469.448y = 408651.927点二x = 3390704.294y = 409110.864通过计算得到的平面投影坐标和已知的地方坐标可以计算得到四个转换参数。

arcgis四参数转换坐标

arcgis四参数转换坐标1. 引言地理信息系统（GIS）是一种用于处理地理空间数据的工具。

在GIS中，经纬度是常见的地理坐标系统，但在实际应用中可能需要将坐标转换到其他坐标系统，如百度坐标、腾讯坐标等。

本文将介绍如何使用ArcGIS软件进行四参数转换坐标操作，以满足特定需求。

2. 四参数转换坐标的原理四参数转换坐标是一种常用的坐标转换方法，它通过平移、旋转、缩放和长轴旋转等操作，将一个坐标系统的坐标转换为另一个坐标系统的坐标。

在ArcGIS软件中，可以通过指定四个参数的值来完成坐标转换。

下面将详细介绍四个参数的含义和作用：2.1 平移参数平移参数用于将原始坐标系统的原点移动到目标坐标系统的原点。

平移参数由两个值组成，分别表示在X轴和Y轴上的平移量。

通过平移参数的调整，可以将原始坐标系统的原点平移到目标坐标系统的原点，实现两个坐标系统之间的空间对齐。

2.2 旋转参数旋转参数用于将原始坐标系统中的坐标旋转一定的角度，使其与目标坐标系统之间的方向一致。

旋转参数由一个角度值组成，表示坐标的旋转角度。

通过旋转参数的调整，可以实现原始坐标系统中坐标的旋转，以适应目标坐标系统的方向要求。

2.3 缩放参数缩放参数用于将原始坐标系统中的坐标进行缩放，使其与目标坐标系统之间的比例一致。

缩放参数由一个比例值组成，表示坐标的缩放比例。

通过缩放参数的调整，可以实现原始坐标系统中坐标的缩放，以适应目标坐标系统的比例要求。

2.4 长轴旋转参数长轴旋转参数用于将原始坐标系统中的坐标绕原点旋转一定的角度，使其与目标坐标系统之间的方向一致。

长轴旋转参数由一个角度值组成，表示坐标的旋转角度。

通过长轴旋转参数的调整，可以实现原始坐标系统中坐标的旋转，以适应目标坐标系统的方向要求。

3. 使用ArcGIS进行四参数转换坐标的步骤使用ArcGIS软件进行四参数转换坐标操作的步骤如下：3.1 准备数据首先，需要准备原始坐标系统和目标坐标系统的坐标数据，以及四个参数的值。

坐标转换四参数解算

坐标转换四参数解算
分享⼀个前段时间项⽬中遇到的⼀个姿势点，就是求解平⾯坐标四参数转换的转换参数；当时学渣⼩编还是花了些时间研究，其实原理很Easy，过程也很Easy，理解起来更Easy。

废话不多说，下⾯开整
已知：
转换前坐标点（x1,y1）,转换后坐标点（x2,y2）；
⼆维四参数转换模型:
求解：平移参数、旋转参数、尺度参数。

开始求解：
Step1:为了简化计算公式，我们先设定：
以上转换模型公式表达为：
Step2:经过矩阵运算变化，将我们要求解的参数变换到同⼀个矩阵中：
Step3:利⽤间接平差法得到以下计算公式：
Step4:计算旋转参数和尺度参数：
　⾄此，我们要求解的参数已经全部计算出来了，很Easy吧。

当然实际⽣产中，我们的坐标是坐标点对，可以结合上述计算公式利⽤最⼩⼆乘法来进⾏计算，同时也可以计算误差。

四参数坐标转换原理和程序设计

四参数坐标转换原理和程序设计摘要:四参数在平面坐标转换中被广泛应用,如何正确和科学地使用四参数显得尤为重要。

通过分析四参数的原理,提出用VB编程求解四参数的方法,并结合工程实例,分析和判断如何选取公共点,满足了测绘和施工的要求。

关键词:四参数坐标转换RMS坐标转换是是从一种坐标系统变换到另一种坐标系统的过程,通过建立两个坐标系统之间一一对应关系来实现,它是各种比例尺地图测量和编绘中建立地图数学基础必不可少的步骤。

坐标转换一般有两种意义,一是地图投影变换,即从一种地图投影转换到另一种地图投影,地图上各点坐标均发生变化；另一是量测系统坐标转换,即从大地坐标系到地图坐标系、数字化仪坐标系、绘图仪坐标系或显示器坐标系之间的坐标转换。

在测绘和施工中,常常会遇到不同坐标系统间坐标转换的问题,目前国内常见的转换有以下3种:大地坐标和平面直角坐标的相互转换、不同椭球坐标系间的相互转换和平面坐标系间的相互转换。

常用的方法有四参数法、三参数法和七参数法。

本文主要介绍了利用自编的坐标转换软件对四参数转换原理和方法做详细的讲解。

1 四参数坐标转换的原理在我国平面坐标系中以1954北京坐标系为主,除此之外各地又建有相应的地方独立坐标系统。

在测绘和项目施工中,我们常常需将1954北京坐标和地方独立坐标进行互相转换。

该类型的转换为同一个椭球系统的不同坐标系中的转换,对于这样的转换至少需要两个公共点求取转换参数,如图1所示,设xoy为1954北京坐标系,x′o′y′为地方独立坐标系,xo、yo为地方独立坐标系的原点O′在1954北京坐标系中的坐标,α为地方独立坐标系的纵轴o′x′在1954北京坐标系中的坐标方位角。

设已知P点的地方独立坐标为(x′p、y′p),则可按下式将其换算为1954北京坐标(xp、yp),其转换公式为:Xp=△x+X′p×K×cosα-Y′p×K×sinαYp=△y+X′p×K×sinα+Y′p×K×cosα式中K为尺度因子,α为旋转角度,△x,△y为相对应的平移。

如何使用RTK手簿求坐标转换参数（四参数七参数）

如何使用RTK手簿求坐标转换参数（四参数七参数）手簿：南方H5安卓手簿；软件：工程之星5.01、四参数示例：2000坐标系转地方坐标系准备材料：2个以上的已知点坐标步骤：1.1 打开求转换参数操作：“输入”→“求转换参数”1.2 设置四参数在求转换参数界面首先点击右上角的设置按钮，将“坐标转换方法”改为“一步法”，点击“确定”，则可以开始四参数的设置。

1.3 添加坐标参数“一步法”设置完成后，在求转换参数界面点击“添加”1.4 输入坐标参数平面坐标输入已知点坐标，大地坐标输入RTK测的已知点的坐标。

大地坐标可以点击更多获取方式，里面有“定位获取”和“点库获取”，输入完成以后，点击“确定”，添加完第一个坐标Pt1。

然后以同样的方法输入第二个坐标Pt2，如下图所示：1.5 计算四参数并应用如果Pt1或Pt2不小心输入错误，单击改点可进行编辑或者删除。

坐标输入无误后，点击“计算”即可获得2000坐标系转当地坐标系的四参数，再点击“应用”即可，再进行点测量时，获取的坐标就是当地坐标系了。

需要主要的是，四参数覆盖范围较少，一般推荐使用七参数。

2、七参数示例说明：2000坐标系转地方坐标系准备材料：3个以上的已知点坐标2.1 打开求转换参数操作：“输入”→“求转换参数”2.2 设置七参数在求转换参数界面首先点击右上角的设置按钮，将“坐标转换方法”改为“七参数”，点击“确定”，则可以开始七参数的设置。

2.3 添加坐标参数“七参数”设置完成后，在求转换参数界面点击“添加”2.4 输入坐标参数坐标输入方法同四参数一样，但是需要至少输入3个已知点坐标。

输入完成后点击“计算”即可获得2000坐标系转当地坐标系的七参数，最后点击应用即可。

华测手簿：HCE320、HCE300等；软件：测地通LandStar7七参数1.1 打开参数计算操作：在主界面依次点击“工具”→“参数计算”1.2 设置七参数将计算类型设置为七参数1.3 添加坐标点击左下角“添加”按钮，添加已知点坐标。

中海达RTK两个控制点如何计算四参数之欧阳地创编

中海达RTK两个控制点如何计算四参数？摘要中海达RTK两个控制点计算四参数(转换参数)流程：1.把两个控制点输入控制点库；2.平滑采集两个控制点坐标；3.计算参数。

注意：使用两个点计算四参数前，请确保坐标系统里“平面转换和高程拟合”为无！否则会造成参数叠加，怎么算都是错误的！---------------------------------------------------------中海达RTK两个点求转换参数参数流程：1、把两个控制点（GPS01\GPS05）输入控制点库2、采集两个控制点坐标（GPS01\GPS05）3、计算参数1、把控制点输入到控制点库进坐标数据，选择控制点，添加，把GPS01\GPS05依次添加进去。

2、采集控制点坐标进碎步测量用平滑采集依次采集GPS01和GPS05点，输入点名GPS01、GPS05，杆高保存。

①碎步测量②点显示隐藏图标采集控制点GPS01，把移动站放在控制点GPS01上，气泡水平居中。

点平滑采集图标开始采集，平滑采集10次，输入点名（GPS01）、杆高（1.8）。

平滑采集，每秒采集一次，采集10次求平均，精度较高！③重复以上操作，采集控制点GPS05，把移动站放在控制点GPS05上，气泡水平居中，点平滑采集图标开始采集，平滑采集10次，输入点名（GPS05）、杆高（1.8）3、计算参数①进计算参数②默认计算类型“四参数+高程拟合”，点添加依次添加GPS01和GPS05。

④添加 GPS01，源点进点库从坐标点库选择GPS01，目标点——进点库从控制点库选择GPS01，保存。

⑤同样添加 GPS05，保存⑥添加结果⑦计算⑧计算结果：四参数平移北：—平移东：—旋转：—尺度K：无限接近1，即0.999xxxxxxx < K<1.000xxxxxxx高程拟合改正值A:XX.XXXX注意：尺度K<0.999，尺度K>1.000应该考虑操作错误或控制点有问题，必须检查错误重新计算！⑨点击应用！4、检核精度参数计算完后，必须对所计算的参数进行精度检核，检核方法有两种：①进碎步测量，测任意控制点坐标(N，E，Z)与已知坐标(N，E，Z)对比。

平面四参数转换

平面四参数转换引言：我们求出四参数到底有什么意义呢？假如我们用C#写一个画图的程序，比如在picturebox中画一个某一边是尖头的矩形。

我们知道，picturebox的坐标系的原点在它的左上角，X轴是向指向右边的，Y轴是指向下边的。

而测量坐标系中，X是指向上边的（北），Y是指向右边的（东），原点在左下角，为了方便用户设计图形，我们就用测量的坐标系来设计。

在船体坐标系中，如下图3（新坐标系，用户定义的坐标系）：我们知道四参数后，就可以把测量坐标系的几个点转换成picturebox坐标，然后画出来。

当然也可以改变picturebox控件的坐标，但是这样效率很低，也不容易理解，特别是图形旋转的话也很难弄。

原始坐标系是: Xo-Yo 经过尺度缩放，坐标系旋转，然后再平移，变成了Xt-Yt 坐标系。

如《控制测量》上的图1：图1中，我们要注意的是:1. X的方向是向右的，Y是向上的。

2. 旋转角是以顺时针方向为正的这两点非常重要。

如果X是向上的，那么四参数将会不一样；而如果旋转角是逆时针方向为正的，四参数也不一样。

X有可能是向左或者向下的甚至是向任意方向的，所以关键是我们一定要能画出图形，并且推导出公式。

如《控制测量》书上的推导图就很典型可以做为参考，如图2：这个图的优点就在于，它的源坐标系旋转后就成为水平和垂直的轴线，非常便于平移理解。

需要注意的是，图2中，源坐标系X向任意方向，Y轴的正方向和X轴的正方向逆时针旋转90度的方向一致，定义旋转角顺时针方向为正时。

其实应该有4种情况，图上是下面提到的情况C。

假如源坐标系的X是向上的(其实X轴向哪个方向都没有关系，只要Y轴的正方向和X轴的正方向顺时针旋转90度的方向一致)，Y是向右的，定义的旋转角逆时针旋转是正的，平面转换四参数的计算公式如下（公式1）：其中为新坐标，为两个平移参数，(1+m)为尺度，为旋转角，为原坐标。

这就是下面提到的情况A。

公式1也可以用在情况C。

四参数计算.ppt

为简化书写，常引入以下符号和两个辅助函数：
c a2 ,t tan B, 2 e2 cos2 B
b
W 1 e2 sin2 B,V 1 e2 cos2 B
式中，W 第一基本纬度函数，V 第二基本纬度函数。
6
克拉索夫斯基椭球
1975国际椭球
WGS-84系椭球
a
6378245
966
588
e’2 0.006738525414 0.006739501819 0.0067394967422
683
473
7
我国所采用的的1954年北京坐标系应用的是克
拉索夫斯基椭球参数；以后采用的1980国家大地坐
标系应用的是1975国际椭球参数；而GPS应用的是
WGS-84系椭球参数。
7
高斯投影的一般公式
x X l 2 N sin B cosB l 4 N sin B cos3 B(5 t 2 9 2 4 4 )
2
24
l 6 N sin B cos5 B(61 58t 2 t 4 ) 720
y lN cosB l 3 N cos3 B(1 t 2 2 )
6378140
6378137
b 6356863.018773 6356755.288157
0473
5287
6356752.3142
c 6399698.901782 6399596.651988
7110
0105
6399593.6258
1/298.3
1/298.257
1/298.257223563
e2 0.006693421622 0.006694384999 0.0066943799013

四参数计算的操作流程及投影转换流程

四参数坐标转换方法

三参数、四参数、七参数等坐标系转换参数求解 -回复

七参数四参数转化

如何进行参数计算（四参数高程拟合）？

坐标转换四参数范文

matlab坐标转换四参数法

四参数计算的操作流程及投影转换流程

三维四参数空间直角坐标转换计算方法

四参数坐标转换步骤

四参数转换

四参数计算过程

计算转换参数方法

arcgis四参数转换坐标

最新IHAND手薄四参数简易操作(精)

坐标转换四参数解算

四参数坐标转换原理和程序设计

如何使用RTK手簿求坐标转换参数（四参数七参数）

中海达RTK两个控制点如何计算四参数之欧阳地创编

平面四参数转换

四参数计算.ppt