物理学第四章
大学物理第四章--功和能

a
l
xdx
2l
前已得出:
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时:
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例1一水平放置的弹簧,其一端固定,另一端系一小球,求小
球的位置由A到B的过程中弹力对它所做的功。(在O处弹簧无 形变)
解:根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上.在该质点从坐标原点运动到(0,2R)位
置过程中,力
F
对它所作的功为多少?
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图,水平桌面上有质点 m ,桌面的摩 擦系数为μ 求:两种情况下摩擦力作的功
大学物理第四章刚体转动

进动和章动在自然界中实例
陀螺仪
地球极移
陀螺仪的工作原理即为进动现象。当 陀螺仪受到外力矩作用时,其自转轴 将绕某固定点作进动,通过测量进动 的角速度可以得知外力矩的大小和方 向。
地球极移是指地球自转轴在地球表面 上的移动现象,其产生原因与章动现 象类似。地球极移的周期约为18.6年 ,且极移的幅度会受到地球内部和外 部因素的影响。
天体运动
许多天体的运动都涉及到进动和章动 现象。例如,月球绕地球运动时,其 自转轴会发生进动,导致月球表面的 某些特征(如月海)在地球上观察时 会发生周期性的变化。同时,行星绕 太阳运动时也会发生章动现象,导致 行星的自转轴在空间中的指向发生变 化。
感谢观看
THANKS
02
刚体定轴转动动力学
转动惯量定义及计算
转动惯量定义
刚体绕定轴转动时,其惯性大小的量度称为转动惯量,用字母$J$表示。它是一个与刚体质量分布和转轴位置有 关的物理量。
转动惯量计算
对于形状规则的均质刚体,可以直接套用公式计算其转动惯量;对于形状不规则的刚体,则需要采用间接方法, 如分割法、填补法等,将其转化为规则形状进行计算。
刚体性质
刚体是一个理想模型,它在力的作用 下,只会发生平动和转动,不会发生 形变。
转动运动描述方式
01
02
03
定轴转动
平面平行运动
ห้องสมุดไป่ตู้
定点转动
物体绕一固定直线(轴)作转动。
物体上各点都绕同一固定直线作 不同半径的圆周运动,同时物体 又沿该固定直线作平动。
物体绕一固定点作转动。此时物 体上各点的运动轨迹都是绕该固 定点的圆周。
非惯性系下刚体转动描述方法
欧拉角描述法
大学物理——第4章-振动和波

合成初相 与计时起始时刻有关.
v A 2
ω
v A
2
O
x2
1
v A 1
x1
xx
分振动初相差2 1与计时起始时刻无关,但它对合成振幅 是相长还是相消合成起决定作用.
20
讨 论
2 A = A2 + A2 + 2A A2 cos(2 1) 1 1
F = kx
3
l0
k
m
A
F = kx = ma
k 令ω = m
2
A x = Acos(ωt +)
o
x
积分常数,根据初始条件确定
a = ω2 x
dx = ω2 x dt 2
2
dx υ = = Aω sin( ωt +) dt
dx 2 a = 2 = Aω cos(ωt +) dt
4
2
x = Acos(ωt +)
15
π
例 4-3 有两个完全相同的弹簧振子 A 和 B,并排的放在光滑 的水平面上,测得它们的周期都是 2s ,现将两个物体从平衡 位置向右拉开 5cm,然后先释放 A 振子,经过 0.5s 后,再释 放 B 振子,如图所示,如以 B 释放的瞬时作为时间的起点, (1)分别写出两个物体的振动方程; (2)它们的相位差是多少?分别画出它们的 x—t 图.
5cm
O
x
16
解: (1)振动方程←初始条件
x0 = 0.05m, υ0 = 0 , T = 2s
2π ω= = π rad/s T
2 υ0 2 A = x0 + 2 = 0.05m ω υ0 对B振子: tan B = = 0 B = 0 x0ω
大学物理第四章习题解

第四章 刚体的定轴转动4–1 半径为20cm 的主动轮,通过皮带拖动半径为50cm 的被动轮转动,皮带与轮之间无相对滑动,主动轮从静止开始作匀角加速度转动,在4s 内被动轮的角速度达到π/s 8,则主动轮在这段时间内转过了 圈。
解:被动轮边缘上一点的线速度为πm/s 45.0π8222=⨯==r ωv在4s 内主动轮的角速度为πrad/s 202.0π412111====r r v v ω主动轮的角速度为2011πrad/s 540π2==∆-=tωωα在4s 内主动轮转过圈数为20π520ππ2(π212π212121=⨯==αωN (圈)4–2绕定轴转动的飞轮均匀地减速,t =0时角速度为0ω=5rad/s ,t =20s 时角速度为08.0ωω=,则飞轮的角加速度α= ,t =0到t =100s 时间内飞轮所转过的角度θ= 。
解:由于飞轮作匀变速转动,故飞轮的角加速度为20s /rad 05.020558.0-=-⨯=-=tωωα t =0到t =100s 时间内飞轮所转过的角度为rad 250100)05.0(21100521220=⨯-⨯+⨯=+=t t αωθ4–3 转动惯量是物体 量度,决定刚体的转动惯量的因素有 。
解:转动惯性大小,刚体的形状、质量分布及转轴的位置。
4–4 如图4-1,在轻杆的b 处与3b 处各系质量为2m 和m 的质点,可绕O 轴转动,则质点系的转动惯量为 。
解:由分离质点的转动惯量的定义得221i i i r m J ∆=∑=22)3(2b m mb +=211mb =4–5 一飞轮以600r/min 的转速旋转,转动惯量为·m 2,现加一恒定的制动力矩使飞轮在1s 内停止转动,则该恒定制动力矩的大小M =_________。
解:飞轮的角加速度为20s /rad 20160/π26000-=⨯-=-=tωωα制动力矩的大小为m N π50π)20(5.2⋅-=-⨯==αJ M负号表示力矩为阻力矩。
大学物理复习第四章知识点总结

大学物理复习第四章知识点总结大学物理复习第四章知识点总结一.静电场:1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式:Fk122err适用范围:真空中静止的两个点电荷F⑵电场强度定义式:Eqo⑶电场线:是引入描述电场强度分布的曲线。
曲线上任一点的切线方向表示该点的场强方向,曲线疏密表示场强的大小。
静电场电场线性质:电场线起于正电荷或无穷远,止于负电荷或无穷远,不闭合,在没有电荷的地方不中断,任意两条电场线不相交。
⑷电通量:通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理:eSoEdSqi1int只能适用于高度对称性的问题:球对称、轴对称、面对称应用举例:球对称:0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称:无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称:无限大均匀带电平面EE⑹安培环路定理:dl0l2o★重点:电场强度、电势的计算电场强度的计算方法:①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法:①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式:UAAPEdl(UP0)B电势差的定义式:UABUAUBA电势能:WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。
Ⅱ.导体表面紧邻处的电场强度垂直于导体表面,即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布:只分布在导体外表面上。
Ⅱ.空腔有电荷时的分布(空腔本身不带电,内部放一个带电量为q的点电荷):静电平衡时,空腔内表面带-q电荷,空腔外表面带+q。
3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质,电介质中的场强为:E⑵有电介质存在时的高斯定理:SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后,电容为CrC0★重点:静电场的能量计算①电容:②孤立导体的电容C4R电容器的电容公式C0QQUUU举例:平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场:1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度:大小BF方向:小磁针的N极指向的方向qvsin⑵磁感应线:是引入描述磁感应强度分布的曲线。
大学物理第四章题解

第四章 经典质点动力学4-1.已知质量为2kg 的质点的运动学方程为22(61)(341)r t i t t j =-+++(国际制单位),求证质点所受合力为恒力.证 对运动学方程求时间导数()d 1264d r v t i t j t==++ 22d d 126d d v r a i j t t ===+ 2(126)=2412(N)F ma i j i j ==⨯++可见质点所受合力为恒力.4-2.已知质量为1kg 的质点,在合力128(N)F t i j =+作用下运动.已知1t =s 时,质点位于2x =m 、0y =处,并以速率3m s 沿y 轴正向运动.求质点运动学方程.解 由mr F =,知12x t =,8y =.可得d 12d x t t = ,d 8d y t =积分 01d 12d xt x t t =⎰⎰ ,31d 8d y ty t =⎰⎰ 求出 266x t =- ,85y t =-再根据 2d (66)d x t t =- ,d (85)d y t t =-再积分 221d (66)d xt x t t =-⎰⎰ ,01d (85)d y ty t t =-⎰⎰ 质点运动学方程为 3266x t t =-+ ,2451y t t =-+4-3.跳水运动员沿竖直方向入水,刚入水时速率为0v ,以入水点为O 点,y 轴竖直向下,运动员入水后浮力与重力抵消,受水的阻力与速度平方成正比,比例系数为k ,求入水后运动员速度随时间的变化规律.解 以运动员为质点,根据牛顿第二定律有 2d d yy v m kv t =- ,即2d d y y v k v t m =- 分离变量并积分 020d d y v t y v y v k t v m =-⎰⎰即可求出 011y k t v v m -= 也可以表示为 00y mv v m kv t=+4-4.跳水运动员由高处下落,设运动员入水后重力与浮力抵消,受水的阻力与速度平方成正比,比例系数0.4k m =(m 为运动员质量).求运动员速率减为入水速率的110时,其入水深度(均为国际制单位).解 以入水点为O 点,y 轴竖直向下,以运动员为质点,根据牛顿第二定律有2d 0.4d yy v m mv t =-做变量变换,得 2d d d 0.4d d d y y y y v v y v v y t y ==- 即 d 0.4d y y v v y=- 分离变量并积分 00100d 0.4d v y y v y v y v =-⎰⎰ 0010ln |0.4v y v v y =- 可知运动员速率减为入水速率的110时,其入水深度ln1004576(m)y ..==.4-5.质量为m 的小球系在一不可伸长的轻绳之一端,可在水平光滑桌面上滑动.绳的另一端穿过桌面上一小孔,握在一人手中使它以匀速率a 向下运动.设初始时绳是拉直的,小球与小孔的距离为R ,初速度在垂直于绳的方向上的分量为0v .试求小球运动和绳子的张力.解 小球m 视为质点,作为研究对象,受力分析如图.以桌面小孔为坐标原点O ,建立极坐标系如图,根据牛顿第二定律,有T N T ma F F mg F =++=在极坐标系中的投影方程为2()T m r r F θ-=- (1)(2)0m r r θθ+= (2)由题意可知 r a =- (3)由(3)式得0d d r tR r a t =-⎰⎰ 所以r R at =-,代入(2)式,得 ()20R at a θθ--= ,即 d ()2d R at a tθθ-= 初始时00R v θ=,即00v R θ=,把上式分离变量且积分 000d 2d d()2tt v R a t R at R at R at θθθ-==---⎰⎰⎰220ln 2ln ln ()R R at R v R R at θ-=-=- 所以 02d d ()v R t R at θθ==- 把上式分离变量且积分 0200d()d ()t v R R at a R at θθ-=--⎰⎰ 所以 0011()v R v t a R at R R atθ=-=-- 小球的运动学方程为r R at =-,0v t R atθ=-.由(1)式得 222220023()()[]()()T v R mv R F m r r mr m R at R at R at θθ=-==-=--4-6.已知质点所受合力为sin cos e tF t i t j k =++,求在0t =到2t π=时间内合力对质点的冲量.(国际制单位.)解 0t =到2t π=时间内合力对质点的冲量为 200d (sin cos e )d t t I F t t i t j k t π==++⎰⎰22000(sin d )(cos d )(d )t t t i t t j e t k πππ=++⎰⎰⎰ 222000(cos |)(sin |)(|)t t i t j e k πππ=-++2(e 1)i j k π=++-(国际制单位)4-7.用棒打击质量为0.5kg 、从西沿水平方向以速率20m 飞来的球,球落到棒的西面80m 处,球上升的最大高度为20m ,打击时间为0.05s ,打击时可略去重力,取210m s g =.求:(1)棒对球的冲量;(2)棒给予球的平均冲力.解 建立坐标系Oxy ,Ox 轴沿水平方向自东向西,Oy 轴竖直向上.先讨论球被棒打击后的运动,球仅受重力,可知2012y y v t gt =- ,0y y v v gt =- 当0y v =时球达到最大高度m 20m y =.根据0010y v t =-求出0010y t .v =,代入202050y v t .t =-得到 22200020010005005y y y .v .v .v =-=因00y v >,略去020y v =-,可求出020m s y v =.进而求出2s t =.由于球沿Ox 方向作匀速率运动,到4s t =时向西运动了80m ,所以020m x v =. 在碰撞中根据动量定理 21I mv mv =- 由于120v i =-,2002020x y v v i v j i j =+=+,所以棒对球的冲量2010(N s)I i j =+⋅平均冲力 2010400200 (N)0.05I i j F i j t +===+∆4-8.从高出枰盘 4.9m h =处,将每个质量m 均为0.02kg 的橡皮泥块,以每秒100n =个的速率注入枰盘,橡皮泥块落入枰盘后均黏附在盘上.以开始注入时为0t =,求10s t =时枰的读数.解 橡皮泥块在下落过程中只受重力,橡皮泥块落入枰盘的速率98(m v .=在橡皮泥块落入秤盘的过程中,对秤盘的平均冲力为(向上为正方向)21()100002[0(9.8)]196(N)F n mv mv ..=-=⨯⨯--=由于橡皮泥块由 4.9m h =处下落,由22119.8 4.922gt t =⨯⨯= 可知下落的时间1s t =.所以10s t =时枰盘内橡皮泥块受到的总重力g (10-1)1009002981764(N)F n mg ...==⨯⨯⨯=因此秤的读数为 g 1961764196(N)F F ..+=+=4-9.对例题4-4-2(见图),判断以下说法的正误:(1)质点对O 点角动量守恒;(2)质点对O '点角动量守恒;(3)质点对z 轴角动量守恒;(4)质点对x 轴角动量守恒.解 (1)摆锤所受合力指向O 点,摆锤所受合力对O 点力矩为零,所以质点对O 点角动量守恒.(2)合力对O'点力矩不为零,质点对O'点角动量不受恒.(3)质点所受合力的作用线过Oz 轴,对Oz 轴合力矩为零,所以质点对Oz 轴角动量守恒.(4)质点对O 点角动量守恒,所以质点对Ox 轴角动量守恒.4-10.在一直角坐标系Oxyz 中,一质点位于点(3m,4m,5m)处,并受一作用力7N 8N 9N F i i i =++,求:(1)力F 对O 点的力矩;(2)力F 对x 轴的力矩.解 345r i j k =++,所以(345)(789)484(N m)O M r F i j k i j k i j k =⨯=++⨯++=-+-⋅4N m x O M M i =⋅=-⋅4-11.在直角坐标系Oxyz 中,质点质量为2kg ,其速度1242(m s )v i j tk -=+-⋅,并已知0t =时位置矢量02(m)r i =.求:(1)质点对O 点的角动量;(2)质点对y 轴的角动量;(3)质点所受合力对O 点和y 轴的力矩.解 因为d d r v t=,d d r v t =,所以00d d r t r r v t =⎰⎰,即 00002(2d )(4d )(2d )t t tr r r i t i t j t t k -=-=+-⎰⎰⎰ 所以 2(22)4r t i tj t k =++- (1) 22[(22)4](242)O L r mv t i tj t k i j tk =⨯=⨯++-⨯+-22218(48)16(kg m s )t i t t j k -=-+++⋅⋅(2) 22148(kg m s )y O L L j t t -=⋅=+⋅⋅(3) d 16(88)(N m)d O O L M t i t j t==-++⋅ d 88(N m)d y y L M t t==+⋅4-12.设质点在Oxy 平面内运动,试判断以下论述是否正确:(1)若质点动量守恒,则对z 轴角动量守恒;(2)若质点对z 轴角动量守恒,则动量守恒;(3)若质点对z 轴角动量守恒,则动量的大小保持不变;(4)若质点对z 轴角动量守恒,则质点不可能作直线运动.解 (1)正确.质点动量守恒,则质点所受合力为零,质点所受合力对Oz 轴力矩为零,所以对Oz 轴角动量守恒.(2)不对.比如,质点在Oxy 平面内、绕O 点做匀速圆周运动,对Oz 轴角动量守恒,但是动量并不守恒.(3)不对.比如例题4-5-2,质点在Oxy 平面内做椭圆运动,它所受的合力是有心力,始终指向O 点,所以对Oz 轴的角动量守恒,但是动量的大小不断变化.(4)不对.在Oxy 平面内做匀速直线运动的质点对Oz 轴角动量守恒.4-13.质量为m 的质点在Oxy 平面内运动,其运动学方程为cos x a t ω=,sin y b t ω=,a 、b 、ω均为常量.求:(1)质点对z 轴的角动量;(2)质点所受对z 轴的合力矩.解 (1)对运动学方程cos sin r a ti b tj ωω=+求时间导数,可得 d sin cos d r v a ti b t j t ωωωω==-+ 所以 (cos sin )(sin cos )O L r mv a ti b tj m a ti b t j ωωωωωω=⨯=+⨯-+22(cos sin )m ab t ab t k mab k ωωωωω=+=z O L L k abm ω=⋅=(2)因z L 为常量,由对Oz 的角动量定理,可知质点所受对Oz 轴的合力矩d 0d z z L M t==4-14.如图,刚性转动系统放在盛有液体的容器内,长为l 的细杆一端固定一质量为m 的小球,另一端垂直地固定于转轴z .小球受液体阻力与小球质量及系统转动角速度的大小成正比,即F km ω=,k 为比例常量.z 轴及细杆的质量及所受阻力均忽略不计,问:经过多长时间系统的角速度的大小变为初始值0ω的1e .解 由题意知z M lkm ω=-,2z L ml ω=,根据d d z z L M t=,得 2d d ml lkm tωω=- 分离变量并积分 d d k t lωω=-⎰⎰ ln k t C lω=-+ 由0t =时0ωω=定出积分常数,0ln C ω=,则 0e kt l ωω-=所以,当0e ωω=时l t k=.4-15.如图所示,小球m 系于不可伸长的轻绳的一端,绳经O 点穿入竖直小管.开始时小球绕管在水平面内做半径为R 的圆周运动,每分钟转120转.由绳的A 端将绳拉入小管,拉绳后小球绕管在水平面内做半径为2R 的圆周运动.求:(1)拉绳以后小球每分钟之转数;(2)拉绳过程中小球对O 点角动量是否守恒?为什么?解 (1)在拉绳过程中,因为小球所受重力与OA 轴平行、绳拉力与OA 轴相交,对OA 轴力矩均为零,所以在拉绳过程中小球对OA 轴角动量守恒02R mvmv R = 拉绳前,每秒转两转,022R v π⋅=.设拉绳后,每秒转n 转,22R n v π⋅=.把04v R π=和v n R π=代入角动量守恒方程,得 42R mn R m R R ππ=⋅ 即可求出拉绳后小球每秒转8n =转,即每分钟480转.(2)因为小球所受合力对O 点力矩不为零,所以小球对O 点角动量不守恒.4-16.试判断以下说法是否正确:(1)静摩擦力一定不做功;(2)滑动摩擦力一定做负功;(3)摩擦力总是阻碍物体运动;(4)运动质点如受摩擦力作用,则能量一定减小.答 均不正确.4-17.试证明2(3sin e )(N)x F x x i =++是保守力.质点在F 作用下由0x =运动到1m x =,试用两种方法计算力F 对质点做的功.解 由于2(3sin e )(N)x F x x i =++在位移d r 中所做元功2d (3sin )(d d d )x F r x x e i xi yj zk ⋅=++⋅++2(3sin e )d x x x x =++3d(cos e )xx x =-+可以表示为只与位置有关的标量函数3()cos e x U x x x =-+的微分,所以此力为保守力.方法一:质点沿Ox 轴由0x =运动到1x =,F 对质点所做的功为 120d (3sin e )d x W F r x x x =⋅=++⎰⎰310(cos e )|x x x =-+ 1cos1e 11=-++-1cos1e =-+ 方法二:因F 为保守力,引入势能3p (cos e )x E U C x x C =-+=--++,则p2p1()W E E =--1cos1e 11=-++-1cos1e =-+4-18.如图,一劲度系数为k 的弹簧,一端固定于A 点,另一端与质量为m 的质点相连.弹簧处于自由伸张状态时,质点位于竖直面与半径为R 的半圆柱面的交界处B .质点在力F 的作用下,由B 点从静止开始运动到光滑半圆柱面的顶点C ,到达C 点时质点速率为C v .求力F 对质点所做的功.解 在质点由B 到C 点的过程中,所受重力和弹簧弹性力为保守力,以B 点为重力势能及弹性势能零点.质点受面的支撑力不做功,设力F 做功为F A .由质点的机械能定理k p k p ()()C C B B F E E E E A +-+=可得 22111[(R)](00)222F C A mv mgR k π=++-+ 2221128C mv mgR k R π=++4-19.接题4-18,质点到达C 点后,力F 被撤除,求质点运动到AB 之间的平衡位置时的速率.解 质点平衡时mg k l =∆,mg l k ∆=,即质点的平衡位置位于B 点下方mg k处. 在质点由C 到平衡位置的过程中,由于所受重力和弹簧弹性力为保守力,受面的支撑力不做功,所以机械能守恒.以B 点为重力势能及弹性势能零点,则()2222211112822C mv mgR k R mv mg l k l π++=-∆+∆ 22222122m g m g mv k k =-+222122m g mv k=- 即可求出质点运动到AB 之间的平衡位置时的速率2222121(2)4C k R mg v v gR m kπ=+++4-20.如题4-15图之装置.设小球质量0.5g m =,初态管外绳长12m l =,绳与竖直方向夹角130θ=,速度为1v .末态绳与竖直方向夹角260θ=,速度为2v .求:(1)1v 、2v ;(2)绳对小球所做的功.解 视小球为质点,受重力W 和绳的张力T F 如图.初态小球做水平圆周运动,合力T F W F =+指向圆轨道圆心,由牛顿第二定律2211111tg sin v v m m mg R l θθ== 所以 21111sin 1298238m s cos 23v l g ..θθ==⨯⨯= 设末态2l l =,小球做水平圆周运动,有22222tg sin v m mg l θθ= ,222222sin cos v l g θθ= 可知 22111212222122sin cos 1cos sin 33v l l v l l θθθθ== (1) 在由初态到末态的过程中,小球所受合力对竖直轴AB 的力矩为零,所以小球对轴AB 的角动量守恒111222sin sin mv l mv l θθ=所以 12222111sin 3sin v l l v l l θθ== (2) (1)(2)⨯得 313213v v = 可求出 13213343m s v v .==2(1)(2)得 313293l l = 13211()080m 93l l .== 由机械能定理,以O 点为势能零点,绳对小球所做的功为k p W E E =∆+∆2221121()(cos30cos60)2m v v mg l l =-+-000805J .=4-21.质量为0.2kg 的小球B 以弹性绳在光滑水平面上与固定点A 相连.弹性绳劲度系数为8N m ,其自由伸张长度为0.6m .小球初位置和速度0v 如图所示.当小球速率变为v 时,它与A 点距离最大且等于0.8m .求初态与末态之速率0v 和v .解 小球在水平面上仅受弹性绳弹性力,弹性力作用线过A ,所以小球在运动过程中对过A 的竖直轴角动量守恒;注意到小球与A 点距离最大时其速度与弹性绳垂直;则004sin3008.mv .mv =小球在水平面内仅受弹性绳弹性力,弹性力为保守力,因此小球在运动过程中机械能守恒,以弹性绳自由伸张时为弹性势能零点;则2220111(0806)222mv mv k ..=+- 所以 04v v = ,22016v v .-=联立求解上述二式即可求出0131m s v .=,033m s v .=.4-22.如图,在升降机内有一和升降机固定的光滑斜面,斜面相对水平方向的倾角为θ.当升降机以匀加速度a 沿竖直方向上升时,质量为m 的物体沿斜面下滑,试以升降机为参考系,求:(1)物体相对升降机的加速度;(2)物体对斜面的压力;(3)物体对地面的加速度.解 以升降机为非惯性参考系,建立与斜面固连的坐标系Oxy 如图.视物体为质点,受重力mg 、支承力N F 和惯性力I F ma =-,物体在非惯性系中的动力学方程为()sin m g a mx θ+=()N cos 0F m g a θ-+=所以,物体相对升降机的加速度()sin a x i g a i θ'==+物体对斜面的压力()NN cos F F m g a j θ'=-=-+ 物体对地面的加速度sin cos ()sin sin cos a a a a i a j g a i g i a j θθθθθ'=+=-+++=+地4-23.如图,一理想定滑轮固定于升降机上,一不可伸长之轻绳跨过滑轮后,两端各悬挂一物体,物体质量为1m 和2m ,12m m ≠.升降机以加速度a 沿竖直方向下降时,试以升降机为参考系,求:两个物体相对地面的加速度及绳内张力.解 以升降机为非惯性参考系,建立与升降机固连的坐标系Ox 如图.视二物体为质点,物体受重力、绳张力和惯性力I11F m a =-、I22F m a =-,在非惯性系中的动力学方程为1T1111m g F m a m x --=2T2222m g F m a m x --=绳不可伸长 12x x =-根据牛顿第三定律 T1T2T F F F ==所以 12211212()()m m g m m a x x m m -+-=-=+ 绳内张力 12T 122()m m F g a m m =-+ 两个物体相对地面的加速度为1221122111212()()()2m m g m m a m m g m a a a x i ai i i m m m m -+--+=+=+=++ 1221211121212()()()2m m g m m a m m g m a a a x i ai i i m m m m -+--+=+=-=++ 4-24.如图所示有一绕竖直z 轴以角速度k ωω=作匀角速度定轴转动的光滑水平大转台.在距z 轴R 的A 处立一竖直杆,杆端有一长度为l 的不可伸长的轻绳,绳末端挂一质量为m 的小球.当绳与竖直杆夹角θ保持不变时,以转台为参考系,求θ与ω的关系.解 以转台为非惯性参考系,视小球为质点,小球受重力mg ,绳的拉力T F ,惯性离心力It F ,2It (sin )F m R l ωθ=+.小球在非惯性系中受三个力平衡,水平方向的平衡方程为2(sin )tan m R l mg ωθθ+=所以 12tan ()sin g R l θωθ=+ 4-25.接题4-24,有人试图从O 点以初速0v 沿台面抛出一小球,而使小球沿转台上的直线OA 运动,此人的目的能否达到?试在转台参考系中加以说明.解 以转台为非惯性参考系,小球相对于转台具有速度,所以小球除受重力、支持力和惯性离心力以外,还受科里奥利力作用.由于科里奥利力与小球运动方向垂直,所以小球不可能沿转台上的直线OA 运动.(第四章题解结束)。
大学物理第四章

解:利用功能原理:
A=DE
q
kF
m
Fl0tgq
=
1 2
k (l0 setq
- l0 )2
1 2
mv2
F
m
解得:
v=
2 m
Fl0tgq
-
1 m
k (l0 setq
-
l0
)2
[例13] 作业、p-55 功和能 自-20
一质量为m的球,从质量为M的圆弧
形槽中由A位置静止滑下,设圆弧形槽的半
径为R,(如图)。所有摩擦都略,试求:
+12 MV2
l
L
解得:
vr=
2(m +M) gR M
V= m
2gR M(m +M)
(2)小球到最低点B处时,槽滑行的距离。
∵ SFx = 0 ∴ DPx = 0
mvx = MVx
Am
m vxdt = M Vxdt
R
ml=ML
MB
l+L=R
L
=
mR m+M
lL
(3)小球在最低点B处时,槽对球的作用力;
1、动量: P
P = mv 2、第二定律:
F
=
dP dt
= ma
3、冲量: I
I
=
F t 2
t1
dt
4、动量原理
I = DP
5、力矩 M M = r × F
6、动量矩 L
L = r × P = r × mv
7、角动量原理:
t 2 t1
M dt
=
ω ω
2 1
J
dω
= Jω 2
大学物理课后答案第四章

第四章 气体动理论一、基本要求1.理解平衡态的概念。
2.了解气体分子热运动图像和理想气体分子的微观模型,能从宏观和统计意义上理解压强、温度、内能等概念。
3.初步掌握气体动理论的研究方法,了解系统的宏观性质是微观运动的统计表现。
4.理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义,理解气体分子运动的最概然速率、平均速率、方均根速率的意义,了解玻尔兹曼能量分布律。
5.理解能量按自由度均分定理及内能的概念,会用能量均分定理计算理想气体的内能。
6.了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。
二、基本内容1. 平衡态在不受外界影响的条件下,一个系统的宏观性质不随时间改变的状态。
2. 理想气体状态方程在平衡态下,理想气体各参量之间满足关系式pV vRT =或 n k T p =式中v 为气体摩尔数,R 为摩尔气体常量 118.31R J mol K --=⋅⋅,k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质,在微观统计上32t kT ε=5. 能量均分定理在平衡态下,分子热运动的每个自由度的平均动能都相等,且等于2kT 。
以i 表示分子热运动的总自由度,则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p =≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间(粒子能量为ε)的粒子数正比于kT e /ε-。
重力场中粒子数密度按高度的分布(温度均匀):kT m gh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型,对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=, 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触,经过足够长的时间后,系统也可以达到一个宏观性质不随时间变化的状态。
物理学第四章知识点总结

物理学第四章知识点总结第四章主要内容是力和压力第一节力1、力的概念力是一种相互作用,是一种可以改变物体形态或状态的物理量,是物体之间的相互作用。
2、力的性质(1) 力的作用是相互的。
(2) 力有大小和方向。
(3) 力可以使物体产生变化,而且是物理量。
(4) 力是矢量,有大小和方向。
3、力的计算力的大小和方向都是有实际意义的,力是矢量,有大小和方向。
力的计算要按照力的平行四边形法则来计算。
4、万有引力任何两个物体之间都有万有引力。
万有引力的大小与质量有关系。
5、弹力当物体受到变形时,产生弹性形变所产生的力叫做弹力。
6、弹性力和非弹性力(1) 弹性力:弹性形变所产生的力。
弹性形变是指在物体内部弹性变形,而不改变其形状的变形。
(2) 非弹性力:非弹性形变所产生的力。
非弹性形变是指在物体内部非弹性变形,而改变其形状的变形。
7、摩擦力摩擦力是两个物体相互接触时,在相互接触面上出现的一个与运动方向相反的力。
8、力的平行四边形法则如果一个物体受到一组几个共静力的作用,那么它受到的合外力等于这些力合成的结果。
第二节压力1、压力的概念压力是单位面积上的力。
形象地说:压力是对物体的作用力,是单位面积上的力。
2、压力的计算压力=力/面积3、万有引力产生的压力任何两个物体间都有万有引力,所以产生了压力。
4、液体的压力液体中任一点受到来自各个方向的压力,是由于这点上液体分子对这点的作用力的结果。
5、压强压强是单位面积上的压力。
在常见的情况下,常常用单位面积上的力叫做压力,叫做单位面积上的压力,叫做压强。
6、静液压当液体被加在容器中,液体将充分自动的塞满整个容器,液体在容器的作用是将容器的每个部分都用均能。
这种现象叫做静液压。
7、动液压动液压装置是用被通向,有较大压力的流体来传送运动能。
第三节力的组合1、力的平行或反向关系共静力----平行关系缠绕力----交叉关系対立力----反向关系2、单握条件的合外力如果所有的合外力平行,并且在同一线上,那么力的合成为这些力的代数和。
大学物理第四章 波动光学(1)

169第4章 波动光学(Ⅰ)——光的干涉一.基本要求1.理解光的相干条件、光程的概念、干涉加强和干涉减弱的条件以及光强分布; 2.理解获得相干光的分波面法,掌握杨氏双缝干涉;3.理解获得相干光的分振幅法,掌握波膜干涉、劈尖干涉和牛顿环干涉;4.了解光的非单色性对干涉条纹的影响,了解空间相干性和时间相干性的概念;5.了解Michel son 干涉仪原理。
二.内容提要和学习指导(一)光的相干叠加概述1.光源的发光特性:普通光源发光是自发辐射,所发的光相干性差;激光光源发光是受激辐射,所发的光相干性好;2.光的相干叠加:①振幅平方:ϕ∆++=cos 22122212A A A A A ; ②光强分布:ϕ∆++=cos 22121I I I I I ; ③干涉加强和减弱的条件(相位差表述):πϕk 2=∆时,干涉加强;πϕ)12(+=∆k 时,干涉减弱;④干涉加强和减弱的条件(光程差表述):光程的定义L n L '=,其物理意义是将光在介质中的路程折算为真空路程。
22L kλ∆=时,干涉加强;(21)2L k λ∆=+时,干涉减弱; (二)分波阵面干涉1. Young 双缝干涉明纹中心:λd kD x ±= ⋅⋅⋅⋅=,,,321k ;暗纹中心:λd Dk x 2)12(-±= ⋅⋅⋅⋅=,,,321k 条纹间距:λdD x =∆;光强分布:)(cos 420x D dI I λπ=2.菲涅耳(Fresnel )双棱镜实验; 3.菲涅耳(Fresnel )双面镜实验 4.洛埃(Lloyd )镜实验(三)分振幅干涉之一:等倾干涉1.明、暗条纹条件:2/2(1,2,3,)2/2(21)/2(0,1,2,)k k k k λλλ=⎧=⎨+=⎩ 暗明2.条纹是内疏外密的同心圆环;3.每冒出(缩进)一个亮斑,就意味着薄膜厚度增加(缩小)了n e 2/λ=∆4.由光源上不同点发出的光线,凡有相同倾角的,其强度相加,因而明暗对比更为鲜明,所以观察等倾条纹时应使用面光源。
八年级上册物理笫四章知识点

八年级上册物理笫四章知识点
八年级上册物理第四章的知识点主要有以下内容:
1. 电流:电流是电荷在导体中的流动,它的单位是安培(A),符号是I。
电流的大小等于单位时间内通过导体横截面的电荷量。
2. 电路的基本要素:电路包括电源、导体和负载。
电源提供电流,导体传输电流,负载将电能转化为其他形式的能量。
3. 静电场和静电力:电荷之间的相互作用力称为静电力,它与电荷之间的距离和电荷的大小有关。
静电力遵循库仑定律,即静电力正比于两个电荷的乘积,反比于它们之间的距离的平方。
4. 电阻和电阻率:导体中电流的流动受到阻碍,这种阻碍称为电阻。
电阻的大小与导体的材料有关,用电阻率来表示。
电阻的单位是欧姆(Ω)。
5. 欧姆定律:欧姆定律描述了电流、电压和电阻之间的关系。
根据欧姆定律,电流等于电压与电阻的比值,即I=U/R,其中I代表电流,U代表电压,R代表电阻。
6. 串联电路和并联电路:在串联电路中,电流沿着一条路径依次通过各个电阻。
在并联电路中,电流通过分支,再汇集在一起。
7. 电功和功率:电功表示电能的转化或传递,它等于电流乘以电压乘以时间。
电功的单位是焦耳(J)。
功率表示单位时间内的电功,它等于电功与时间的比值,单位是瓦特(W)。
这些是八年级上册物理第四章的主要知识点,通过学习这些内容,可以理解电流、电路的基本要素、静电力、电阻和欧姆定律等物理概念和原理。
人教版八年级物理第四章《光现象》单元复习说课稿

2.教学难点
(1)光的折射现象的理解,尤其是凸透镜成像规律的应用;
(2)光的颜色合成与分解原理在物体颜色形成中的应用;
(3)学生在解决实际问题时,对光学知识的应用和综合分析能力的培养。
二、学情分析导
(一)学生特点
本节课面向的是八年级学生,这个年龄段的学生正处于青春期,思维活跃,好奇心强,对于新鲜事物有较高的探索欲望。他们的认知水平已经有了较好的基础,具备一定的逻辑思维能力和抽象思维能力,但在理解抽象的光学原理时仍可能感到困难。在学习兴趣方面,学生对实验、游戏等互动性强的学习方式更感兴趣,而对于传统的讲授式教学则可能缺乏耐心。此外,学生们的学习习惯各异,需要教师在教学中加以引导和培养。
4.对学生的进步和表现给予及时的表扬和鼓励,增强他们的自信心,激发学习动力。
三、教学方法与手段
(一)教学策略
我将采用的主要教学方法包括实验法、情境教学法、问题导向法和小组合作学习法。选择这些方法的理论依据如下:
1.实验法:通过亲自动手实验,学生可以直观地感受光现象,加深对光学知识的理解,符合建构主义学习理论;
(三)学习动机
为了激发学生的学习兴趣和动机,我拟采取以下策略和活动:
1.设计有趣的实验和互动游戏,让学生在动手操作中感受光现象,提高学习兴趣;
2.创设生活情境,引导学生运用光学知识解释日常生活中的现象,增强学习的实用性和现实意义;
3.开展小组合作学习,鼓励学生互相交流、分享心得,提高团队协作能力和学习积极性;
2.情境教学法:创设生活情境,让学生在具体情境中学习光学知识,有助于提高学习的现实意义和兴趣,符合情境认知理论;
3.问题导向法:以问题为驱动,引导学生主动探究光学原理,培养学生的问题解决能力,符合认知心理学原理;
大学物理第四章

二、平动和转动
1、平动 当刚体运动时,如果刚体内任何一条给定的直
线,在运动中始终保持它的方向不变,这种运动叫 平动(translation)。
平动时,刚体内各质点在任一时 刻具有相同的速度和加速度。
刚体内任何一个质点的运动,都可代表整个刚体的 运动,如质心。
可以用质点动力学的方法来处理刚体的平动问题。
如:车轮的滚动。
返回 退出
3、刚体的定轴转动 定轴转动时,刚体上各点都绕同一固定转轴作
不同半径的圆周运动。
在同一时间内,各点转过的圆弧长度不同,但 在相同时间内转过的角度相同,称为角位移,它可 以用来描述整个刚体的转动。
作定轴转动时,刚体内各点具 有相同的角量,包括角位移、角速 度和角加速度。但不同位置的质点 具有不同的线量,包括位移、速度 和加速度。
直角坐标系中,采用用 、 ,如图所示:
最后,刚体绕定轴转动时,需
要一个坐标来描述,选定参考方 z
向后,转动位置用表示。
p
总的说来,刚体共有6个自由
度,其中3个平动自由度,3个转 动自由度。
y
物体有几个自由度,它
o
的运动定律可归结为几个
独立的方程。
x
返回 退出
返回 退出
§4-2 力矩 转动惯量 定轴转动定律 一、力矩
v r
返回 退出
三、定轴转动定律
对刚体中任一质量元
mi
受外力 Fi 和内力 fi
应用牛顿第二定律,可得:
F ifi m ia i
采用自然坐标系,上式切向分量式为:
F isii n fisi i n m ia it m ir i
F ir isiin fir isiin m ir i2
大学物理_第四章__动量和角动量

d (mv ) dm d v dm dv 0 F m v dt m dt dt dt dt ma
物理意义:物体所受合外力的冲量等于物体动量的增量。
I mv2 mv1
——质点的动量定理
I x mvx 2 mvx1 I y mvy 2 mvy1 直角坐标分量式为 I z mvz 2 mvz1 注意: t2 1. I Fdt P2 P1 为矢量式,使用中
I x px mvBx mv Ax
mvB mv A cos45
vB
O
B
vA
x
0.683kg m s
1
A
I y p y mvBy mv Ay mv A sin45 0.283kg m s1
总冲量: 大小 I
2 0.739 N s Ix I2 y
球与棒脱离到飞至最高点过程机械能守恒
1 2 mv 2 mgh 2
v2 2 gh
2.据动量原理作矢量图:
3.解析式:
p2
2 2 I P P2 P 1
p I
7.3 (N S) 2 1 P 0 tan 1 34.99 P I 7.3 365N F 0.02 t
v1 0 P 1 0
l
2
T
m
1
mg
EP 0
v2 ?
1 2 机械能守恒 1 2 m 2gl(1 cos ) mv 2 mgl (1 cos ) 2
I合
P2 m v2
例2.一重锤从高度h=1.5m处自静止下落,锤与被加工的 工件碰撞后末速为0。若打击时间 t 为 10 1 s、 10 -2 s、 10 -3 s 和10 -4 s ,试计算这几种情形下平均冲击力与重力的比值.
物理学教程(第二版)马文蔚主编第四章

物理学教程 (第二版)
0 2π
1
6
dt
e
t /
0 2π
1
Байду номын сангаас
6
m (1 e t / ) d t 344
t / 2
(3)
d dt
m
540 π e
rad s
2
(角加速度 指数衰减)
第四章 刚体转动
2) 任一质点运动 , , 均相同,但 v , a 不同;
3) 运动描述仅需一个坐标 .
第四章 刚体转动
4 – 1 刚体的定轴转动 2 匀变速转动公式
物理学教程 (第二版)
当刚体绕定轴转动的角加速度为恒量时,刚体做 匀变速转动 . 刚体匀变速转动与质点匀变速直线运动公式对比 质点匀变速直线运动
物理学教程 (第二版)
d dt
d dt
d
2
a
an r
d t
2
v r et
a t r a n r
2
at
et v
2 a r et r en
第四章 刚体转动
4 – 1 刚体的定轴转动
物理学教程 (第二版)
例1 一飞轮半径为 0.2m、 转速为150r· -1, 因 min 受制动而均匀减速,经 30 s 停止转动 . 试求:(1)角加速度和在此时间内飞轮所转的圈数; 0 5 π rad s 1 , t = 30 s 时, 0 . 解 (1) 设 t = 0 s 时, 0 0 .飞轮做匀减速运动
第四章 刚体转动
质点运动
4 – 1 刚体的定轴转动
大学物理第四章课后答案

υ2 l
9. 解: m 下降到斜面瞬间满足机械能守恒: 1 则 mgh = mυ 0 2 2 M 与 m 碰撞后无机械能损失: 1 1 1 mυ 0 2 = Mυ 2 + mυ ′ 2 2 2 2 水平方向 M 与 m 组成的系统动量守恒, 总动量 为 0, Mυ = m υ ′ 解得: υ = 2m 2 gh M ( M + m)
如图所示在一铅直面内有一光滑的轨道左边是一个上升的曲线右边是足够长的水平直线两者平滑连接现有b两个质点b在水平轨道上静止a在曲线部分高h处由静止滑下与b发生完全弹性碰撞碰后a仍可返回上升到曲线轨道某处并再度滑下已知ab两质点的质量a分别为和
自治区精品课程—大学物理学
题库
第四章 动量定理
一、 填空 1. 2. 3. 4. 是表示力在空间上累积作用的物理量, 是表示力在时间上累 积作用的物理量。 质点动量定理的微分形式是 。 质点动量定理的积分形式是 。 对于质点系来说,内力 ( “改变”或“不改变” )质点系中各个质点 的动量,但 ( “改变”或“不改变” )质点系的总动量。 若质点系沿某坐标方向所受的合外力为零,则 守恒。 如果两物体碰撞过程中,动能完全没有损失,这种碰撞称为 ,否则 就称为 ;如果碰撞后两物体以相同的速度运动,这种碰撞称 为 。 , 其中 υ10 ,υ1 是某一物
-1-
自治区精品课程—大学物理学
题库
上,如图所示。求链条下落在地面的长度为 l 瞬时,地面所受链条的作用力的大 小。 4. 质量为 M 的人,手里拿着一个质量为 m 的物体,此人以与地平面成 α 角的速 度 υ0 向前方跳起,当他达到最高点时,将物体以相对速度 µ 水平向后抛出,由 于物体的抛出,人跳的距离增加多少?假设空气阻力不计。 5. 速度为 υ0 的物体甲和一个质量为甲的 2 倍的静止物体乙作对心碰撞,碰撞后 1 甲物体以 υ 0 的速度沿原路径弹回,求: 3 (1)乙物体碰撞后的速度,问这碰撞是完全弹性碰撞吗? (2) 如果碰撞是完全非弹性碰撞, 碰撞后两物体的速度为多大?动能损失多少? 6. 如图所示,质量为 m 的物体从斜面上高度为 h 的 A 点处由静止开始下滑,滑至水平段 B 点 停止,今有一质量 m 的子弹射入物体中,使物 体恰好能返回到斜面上的 A 点处。求子弹的速 度( AB 段摩擦因数为恒量) 。 7. 如图所示,劲度系数 k = 100 N m 的弹簧, 一 段固 定于 O 点, 另一端 与一 质量 为
大学物理第四章习题及答案

大学物理第四章习题及答案大学物理第四章习题及答案第四章是大学物理课程中的重要章节,主要涉及力学和运动学的内容。
在这一章中,学生将学习到关于运动的基本概念和原理,以及如何应用这些知识解决实际问题。
为了帮助学生更好地理解和掌握这一章节的知识,以下是一些常见的习题及其答案。
习题一:一个物体以10 m/s的速度从10 m高的斜面上滑下,滑到底部时的速度是多少?解答:根据能量守恒定律,物体在滑下过程中,其机械能守恒。
由于没有外力做功,物体的机械能在滑下过程中保持不变。
因此,物体在滑到底部时的机械能等于初始机械能。
初始机械能 = 动能 + 重力势能= 1/2 mv^2 + mgh根据题目给出的条件,可得:1/2 mv^2 + mgh = 1/2 m(10)^2 + m(10)(10)= 50m + 100m= 150m因此,滑到底部时的速度为10 m/s。
习题二:一个物体以10 m/s的速度从斜面上滑下,滑到底部时的时间是多少?解答:根据运动学中的运动方程,可以求解物体滑下斜面所用的时间。
在这个问题中,物体的初速度为0,加速度为重力加速度g,位移为斜面的长度L。
根据运动方程:S = ut + 1/2 at^2L = 0 + 1/2 gt^22L = gt^2t^2 = 2L/gt = sqrt(2L/g)根据题目给出的条件,斜面的长度L为10 m,重力加速度g为10 m/s^2,代入上述公式可得:t = sqrt(2(10)/10)= sqrt(2)≈ 1.414 s因此,滑到底部时的时间约为1.414秒。
习题三:一个物体以10 m/s的速度从斜面上滑下,滑到底部时的加速度是多少?解答:根据牛顿第二定律,物体在斜面上滑动时受到的合力等于物体的质量乘以加速度。
在这个问题中,物体的质量为m,斜面的倾角为θ,重力加速度为g。
合力 = m * 加速度m * g * sinθ = m * 加速度加速度= g * sinθ根据题目给出的条件,斜面的倾角θ为30度,重力加速度g为10 m/s^2,代入上述公式可得:加速度= 10 * sin(30°)≈ 5 m/s^2因此,滑到底部时的加速度约为5 m/s^2。
大学物理学(课后答案)第4章

第4章 刚体的定轴转动习 题一 选择题4-1 有两个力作用在一个有固定转轴的刚体下,对此有以下几种说法:(1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.对L 述说法下述判断正确的是[ ](A )只有(l )是正确的 (B )(1)、(2)正确,(3)、(4)错误 (C )(1)、(2)、(3)都正确 (D )(1)、(2)、(3)、(4)都正确 解析:力矩是描述力对刚体转动的作用,=⨯M r F 。
因此合力为零时,合力矩不一定为零;合力矩为零时,合力也不一定为零。
两者并没有一一对应的关系。
答案选B 。
4-2 有A 、B 两半径相同,质量相同的细圆环。
A 环的质量均匀分布,B 环的质量不均匀分布,设它们对过环心的中心轴的转动惯量分别为A I 和B I ,则有[ ](A )A B I I > (B )A B I I < (C )无法确定哪个大 (D )A B I I = 解析:转动惯量2i i iI m r =∆∑,由于A 、B 两细圆环半径相同,质量相同,所以转动惯量相同2A B I I mR ==,而与质量分布均匀与否无关。
选D 。
4-3 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图4-3所示.今使棒从水平位置由静止开始自由下落,在棒摆到竖直位置的过程中,下述说法正确的是[ ](A )角速度从小到大,角加速度不变 (B )角速度从小到大,角加速度从小到大(C )角速度从小到大,角加速度从大到小 (D )角速度不变,角加速度为零解析:在棒摆到竖直位置的过程中,重力势能和转动动能相互转化,因此转速越来越大,即角速度从小到大。
整个过程中棒只受到重力矩的作用,211cos 23M mg l J ml θαα===,所以3cos 2gl αθ=,随着转角θ逐渐增大,角加速度α由大变小。
大学物理热学 第四章 (热力学第一定律)

理学院 物理系 陈强
第四章 热力学第一定律
四. 理想气体的内能和CV、Cp
对理想气体, 内能仅是温度T的函数, 是状态函数.
U U (T )
所以, 不论对等体或等压过程均有:
dU dU dU dT dT V dT p
理想气体的定容摩尔热容为
Q L 4 . 06 10 J
4
外界对系统作功为
W p ( V g V l ) ... 3 . 05 10 J
3
Q
由热力学第一定律, 水的内能增量为
U Q W 3 . 75 10 J
4
16
理学院 物理系 陈强
第四章 热力学第一定律
绝热
• 微观本质不同:作功 有序; 传热 无序
8
理学院 物理系 陈强
第四章 热力学第一定律
准静态过程中功的计算 如图,dW pSdx pdV
dW:外界对系统作的元功
dV 0 膨胀 , dW 0
S p dx
dV 0 压缩 ,
dW 0
从状态I(p1,V1,T1)变化到状态II (p2,V2,T2)
T1+dT
系统T1 T2
T1+2dT
T1+3dT
5
例1:气体被压缩的过程
例2:系统的加热过程
理学院 物理系 陈强
第四章 热力学第一定律
对一定量气体,任何一个平衡态都对应于状态图(如 P-V图,P-T图或V-T图)中的一点。反之亦然;
一定量气体的任何一个准静态过程都可用系统的 状态图(如P-V图,P-T图或V-T图)中一条光滑连 续曲线表示,反之亦如此。
大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量
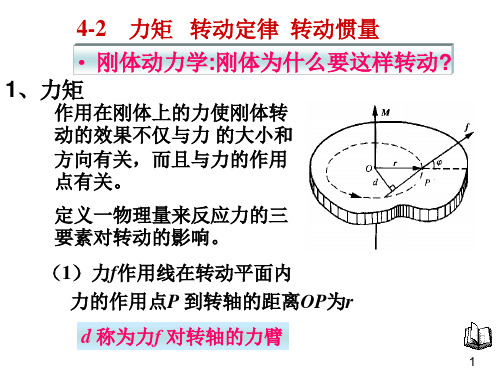
} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性,J 反映刚体的转动惯性。 反映质点的平动惯性, 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m,长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ,长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ?
飞轮的质量为什么 大都分布于外轮缘? 大都分布于外轮缘?
(3) )
1 2 对M: T2 r − T1r = J α = M r α : 2
4、运动学: 运动学:
rα = a
(4) )
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因: 原因:
' 1
' (1)若:T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1(补充例题):一个转动惯量为2.5 kg⋅m2 、 (补充例题) 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮,正以 的飞轮,正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求: 闸瓦与飞轮之间的摩擦系数为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、声强级
声强每增加10倍,人耳听觉才改变1倍左右; (采用对数来表示声强的等级)
标准参考声强:I0=10-12W/m2
声强级:
定义P67
L lg I I0
单位:贝尔(B)
L 10lg I I0
单位:分贝(dB)
1000HZ的听觉区域: L = 0 ~ 12 B L = 0 ~ 物理学第四章 120 dB
熟悉 听阈和听阈曲线 痛阈和痛阈曲线 听觉区域
了解 超声波的特性及其生物效应,脉冲超声波
的产生与探测;超声波成像的基本原理;超声在
医学中的应用。
物理学第四章
声波:频率在20Hz—20000Hz之间
的机械波(纵波),能引起人的听觉。
超声波 (Ultrasonic wave):频率高于20000Hz 次声波 (Infrasonic wave):频率低于20Hz
1B=10dB
L 10lg I I0
听域: I 1012W/2m;
I
1012
L10lg I0
10lg101210lg10(dB)
痛域: I 1W/2m L10lg1101210lg101212(0dB)
物理学第四章
几种声音的声强和声强级
声源种类
几乎不能察觉的声音 树叶的沙沙声
耳语 医院 闹市 地铁或汽车 喷气飞机 火箭发射场
物理学第四章
二、响度级:人耳主观感觉到的声音的响亮程度。
等响曲线:
在听觉域中把不同 频率、不同声强, 但响度相同的点连 成一条曲线.
声 强 120 级 (dB)100
80
60
40
响度级(单位:方) 20
0
痛阈 听阈
120方 100方 80方 60方 40方 20方 0方
声强(W/m2) 1 10-2 10-4 10-6 10-8 10-10 10-12
声阻抗ρu (kg/m2s) 4.28×102 4.16×102 1.48×106 1.36×106 1.63×106 6.12×106 39.4×106
人体组织可分为:低声物阻理学抗第四、章中等声阻抗、高声阻抗
三.声强(声波的强度)
声强:单位时间内通过垂直于声波传播方向的 单位面积的声波能量.
I
声强( W/m2) 10-12 10-11 10-10 10-8
10-6~ 10-5 10-3 103 106
物理学第四章
声强(dB)
0 10 20 30 60~70 90 140 170
例题1、某马达开动时产生的噪声声强为10-7 W/m2,求
①开动一台马达,其噪声声强级为多少dB?
②
同时开动两台马达,其噪声声强级为多少dB?
p v
y
t
声压方程
物理学第四章
pdp dy
二.声特性阻抗
介质质点振动速度幅值: m A
声特性阻抗: 声压幅值Pm与速度幅值 m 之比。
Z Pm uA u
m
A
Z u 单位:kgm2s1 或 Pasm1
或 1瑞利 10kgm2s1
是表征介质声学特性的一个物理量。
物理学第四章
几种介质的声速和声阻抗
第四章 声波 (Sound wave)
第一节:声波基本性质 第二节:声强级与响度级 第三节:多普勒效应 第四节:超声波及其医学上的应用
作业:1、2、4、5、6、 8 、9 、10、11、12、14
物理学第四章
教学大纲
掌握: 概念:声波、声压、声特性阻抗、声强、 声强级、响度级
公式:多普勒效应及公式的应用
1 u2A2
2
1 2
Zm2
Pm2 2Z
单位:J﹒s-1 ﹒ m-2 = W ﹒ m-2
描写声场 的物理量
Pm uA
Z u I 1 u2A2
2 物理学第四章
第二节 声强级与响度级
引起人耳听觉的声波: 与频率有关(声调)(20--20 kHz)
与声强有关(响度)(10-12--1 W/m2) 听觉区域:
听阈:能引起听觉的最低声强(最低可闻声强).
如:1000Hz的听阈为10-12 W/m2
痛阈:人耳能忍受的最高声强.
如:1000Hz的听阈为1 W/m2
物理学第四章
听阈曲线和痛阈曲线
痛阈
声
声
强
强
级
听觉域
(W/m2)
(dB)
听阈
频率(HZ)
1000HZ的听觉域:物理I学=第四1章0-12 ~ 100 W/m2
物理学第四章
次声波 特点:频率低、能量损失少、穿透能力强。
如火山爆发、地震、大气湍流等都有次声波产生. 某些动物的信息交流也采用次声波. 军事上有次声弹.
超声波在医学的治疗与物理诊学第断四章当中有重要的应用.
一、声压
P x
声压:在某一时刻,介质中某一点的压强与无声波 通过时的压强之差: ppi p0
L10lg I 80 I0
I0=10-12w/m2
I=10-4w/m2
E=I. t .s
L10lg2I 83dB I0
解:①∵ I1= I = 10-7 W/m2 ,I0= 10-12 W/m2 ∴ L110lgII0 10lg110 017250(dB)
②∵ I2=2 I ∴ L 21l0 g 2 I0 I1l0 g 21l0 gII035(0dB)
声强具有可加性,而声强级不能直接相加
物理学第四章
同声强级但人耳的听觉不同,为此引入一个新概念---
20 100
1K 2K 5K 10K
响度相同的声音具有相同的响度级。
①1000HZ纯音响度级与声强级(dB)数值相同 ②同一等响曲线具有相物同理学的第四响章度级
例题 面积为1平方米的窗户开向街道,街中有频率为
1000Hz的声源在窗口 的声强级为80 dB,则每秒钟 传入窗口声波的能量为( )J,若街中有两个频率 为1000Hz的声源在窗口 的声强级各为80 dB,则这 两个声源同时传到窗口的响度 级 为 ( )方。
简谐声波的声压表达式: PuAcos(t [x)]
u2
声压幅值: PmuA 单位:N·m-2
有效声压:
Pe
pm 2
(实际中测量值)
物理学第四章
声波在空气中以 纵波的形式传播:
yAcos(tx)
u
p
F i ma
F i t
dp dy dv dt
介质
空气(0 ℃) 空气(20℃) 水(20 ℃)
脂肪 肌肉 密质骨
钢
声速 u (m/s) 3.32×102 3.44×102 14.8×102 14.0×102 15.7×102 36.0×102 50.5×102
密度ρ (kg/m3)
1.29 1.21 988.2 970 1040 1700 7800
