4.8 岩石的蠕变
岩石材料的蠕变实验及本构模型研究

岩石材料的蠕变实验及本构模型研究蠕变是指材料在一定温度和应力条件下,随着时间的推移发生的持续变形。
在地质和工程领域,岩石是一种典型的蠕变材料。
岩石的蠕变行为对工程结构的长期稳定性和可靠性具有重要影响。
因此,对岩石材料的蠕变实验及本构模型研究具有重要的理论和实际意义。
岩石材料的蠕变实验主要分为应力松弛实验和恒定应力蠕变实验两种。
应力松弛实验是通过对材料施加一定的应力后,观察材料的应力随时间的变化,以及应变随时间的变化。
这种实验常常用来研究岩石材料的蠕变速率和蠕变变形的领导指数。
恒定应力蠕变实验则是在一定的应力水平下,观察材料的应变随时间的变化,并且通过实验数据拟合来得到本构模型。
岩石材料的蠕变行为可以通过多种本构模型来描述,其中最常用的是Norton、Burgers、Power-law以及Generalized Kelvin-Voigt模型。
这些模型可以通过实验数据进行参数拟合,从而得到对应的本构关系。
这些本构关系可以用来预测岩石材料在不同应力和温度下的蠕变行为。
此外,还可以通过拟合这些本构模型的参数,来研究岩石材料的蠕变机制。
研究表明,岩石材料的蠕变行为是由多种因素共同影响的,包括温度、应力水平、孔隙水压力、孔隙率等。
因此,在进行蠕变实验时,需要对这些因素进行控制和监测,以保证实验数据的可靠性。
同时,还需要考虑到实际工程环境中的应力和温度条件,从而得到更准确的本构关系。
总之,岩石材料的蠕变实验及本构模型研究对于预测岩石在地下工程中的蠕变行为具有重要的理论和实际意义。
通过研究岩石材料的蠕变行为及其本构关系,可以为地质和工程领域提供重要的科学依据,从而保证工程结构的长期稳定性和可靠性。
岩石材料的蠕变实验及本构模型研究

岩石材料的蠕变实验及本构模型研究引言:岩石是地球上最基础的构造材料之一,其性质的研究对于地质科学以及岩土工程领域具有重要意义。
岩石在地壳中扮演着起支撑与保护作用,因此了解岩石的变形行为以及蠕变性质对于地质灾害的预测与评估具有重要的指导意义。
本文将就岩石材料的蠕变实验及本构模型研究进行详细阐述。
一、岩石材料的蠕变实验蠕变是指物质在长时间内受到持续应力下的变形现象。
岩石材料由于具有多种类型的孔隙和裂隙,因此其蠕变行为比一般材料更为复杂。
蠕变实验是研究岩石材料蠕变性质的主要手段之一,其目的是了解岩石在不同应力、不同温度和不同时间下的蠕变特性。
1.实验设备蠕变实验一般需要使用蠕变试验机,该仪器能够提供连续加载并测量样品的应力和应变,同时控制温度。
实验所需的试样通常需要根据具体需要制备。
此外,还需要一些测量设备,如蠕变计和应变测量仪等。
2.实验过程蠕变实验的过程包括准备试样、加载试样、施加应力、保持应力和测量应变等步骤。
首先,需要根据实验要求制备符合标准的试样。
然后,将试样放置在蠕变试验机上,施加适当的负载并开始加载。
在加载过程中,需要保持恒定的应力并测量试样的应变,常用的应变测量方法有外部应变计和内部传感器等。
最后,根据实验结果绘制蠕变曲线,分析蠕变行为。
本构模型是描述材料力学性质的数学模型,通过建立岩石材料的本构模型,可以预测岩石的变形行为并进行力学仿真研究。
目前常用的岩石本构模型有线性弹性模型、弹塑性模型和粘弹性模型等。
1.线性弹性模型线性弹性模型是最简单的本构模型,它假设岩石材料的应力应变关系是线性的,即满足胡克定律。
这种模型适用于小应变范围内的岩石变形,但无法描述岩石的时间依赖性和非线性特性。
2.弹塑性模型弹塑性模型考虑了岩石在加载时的弹性变形和塑性变形,常用的模型有Mohr-Coulomb模型、Drucker-Prager模型等。
这些模型能够更准确地描述岩石的变形行为,但在蠕变时间很长的情况下,塑性本构模型可能会失效。
岩石流变理论中的蠕变现象

岩石流变理论中的蠕变现象作者:石喜梅来源:《青年与社会》2014年第29期【摘要】流变学研究内容是各种材料的蠕变和应力松弛的现象、屈服值以及材料的流变模型和本构方程。
在土木工程中,建筑的土地基的变形可延续数十年之久。
地下隧道竣工数十年后,仍可出现蠕变断裂。
因此,土流变性能和岩石流变性能的研究日益受到重视。
【关键词】岩石;蠕变;流变理论蠕变是指材料在恒定载荷作用下,变形随时间而增大的过程。
蠕变是由材料的分子和原子结构的重新调整引起的,这一过程可用延滞时间来表征。
当卸去载荷时,材料的变形部分地回复或完全地回复到起始状态,这就是结构重新调整的另一现象。
材料在恒定应变下,应力随着时间的变化而减小至某个有限值,这一过程称为应力松弛。
这是材料的结构重新调整的另一种现象。
蠕变和应力松弛是物质内部结构变化的外部显现。
这种可观测的物理性质取决于材料分子(或原子)结构的统计特性。
因此在一定应力范围内,单个分子(或原子)的位置虽会有改变,但材料结构的统计特征却可能不会变化。
一、流变理论在岩石的流变理论中常见四种现象。
流变:指材料的应力-应变关系与时间因素有关的性质,材料变形过程中具有时间效应的现象称为流变现象。
蠕变:当应力不变时,变形随时间增加而增长的现象。
松弛:当应变不变时,应力随时间增加而减小的现象。
弹性后效:加载或卸载时,弹性应变滞后于应力的现象。
这四种现象构成了岩石流变理论中的基础,是研究岩石流变理论不可或缺的理论基础。
二、流变理论中的蠕变(一)蠕变试验岩石蠕变现象通常通过蠕变试验的曲线来确定。
图1所示为某岩石进行岩石蠕变试验的岩石蠕变曲线示意图。
图1 岩石蠕变曲线示意图该蠕变试验表明:1. 当岩石在某一较小的恒定荷载持续作用下,其变形量虽然随时间增长有所增加,但蠕变变形的速率则随时间增长而减少,最后变形趋于一个稳定的极限值,这种蠕变称为稳定蠕变。
2. 当荷载较大时,abcd 曲线所示,蠕变不能稳定于某一极限值,而是无限增长直到破坏,这种蠕变称为不稳定蠕变。
岩石蠕变的变形机制及其地质意义

岩石蠕变的变形机制及其地质意义岩石是地壳的主要组成部分,它们在地壳运动中起着重要的作用。
岩石的变形是地质活动的重要表现形式之一,而岩石蠕变则是岩石变形的一种重要机制。
本文将探讨岩石蠕变的变形机制及其在地质研究中的意义。
一、岩石蠕变的概念和表现形式岩石蠕变是指岩石在长期作用下出现持续缓慢变形的现象。
蠕变是一种时间依赖性的现象,其发生需要较长的时间。
岩石蠕变的主要表现形式有蠕变流动、蠕变滑动和蠕变脆性破裂等。
二、岩石蠕变的机制1. 组分改变岩石蠕变过程中,岩石的成分会发生改变。
矿物的晶体结构可能发生变化,新的矿物相形成。
不同的成分改变对蠕变的机制有着重要的影响。
2. 晶体结构变化岩石蠕变过程中晶体结构会发生变化,主要是晶界运动和晶粒内的位错运动。
晶界运动是指晶界的移动和重构,而位错运动是指晶粒内部位错的滑移和传播。
3. 矿物形态变化岩石蠕变过程中,矿物的形态和组织可能会发生变化。
有些矿物会发生晶界迁移和重构,形成新的结构。
这些变化会导致岩石整体的形态和结构发生变化。
三、岩石蠕变的意义岩石蠕变在地质研究中具有重要的意义。
1. 岩石蠕变是地震活动的重要前兆之一岩石蠕变的发生会伴随着能量的积累,当岩石受到足够的应力时,就会引发地震活动。
因此,研究岩石蠕变有助于预测地震的发生,为地震灾害的防范提供科学依据。
2. 岩石蠕变对巨型工程建设有重要影响岩石蠕变的发生会导致岩石的变形和破裂,对于巨型工程建设如水坝、隧道等有着重要的影响。
因此,在工程建设中对岩石蠕变进行充分的研究和评估,对保证工程安全具有重要意义。
3. 岩石蠕变对地质资源的勘查和开发有指导意义岩石蠕变对地质矿产资源的分布和形成有重要影响。
研究岩石蠕变可以了解地壳中不同岩石中矿物形态和组织的变化规律,为地质资源的勘查和开发提供科学依据。
4. 岩石蠕变对地形变的影响岩石蠕变是地壳运动的重要表现形式之一,它对地形变化有重要的影响。
通过研究岩石蠕变,可以了解地壳的变形规律,对地质灾害的预测和防范具有重要意义。
岩石的蠕变

EFG下降,最后e 应变为零。其中EF曲线为瞬时弹性应变 之恢复曲线,
而FG曲线表示应变随时间逐渐恢复为零。 由于卸载后应力立刻消失,而应变却随时间逐渐恢复,所以应力
与应变的恢复不是同步的,即应变总是落后于应力。具有这种特性的 弹性变形称为滞弹性或弹性后效。
5.3 蠕变模型
γ
τ
γ
τ
η η
ηη 1 1
τ τ
b
b
γ
γ
η2η2
cc
γ
ττ
γ
ηη 1 1 η1
η1
γ
ττγΒιβλιοθήκη dde) e)ττ
η2 η2
γ
γ
图5-5 线性粘弹性模型及其蠕变曲线 (a)马科斯威尔模型;(b)伏埃特模型;(c)广义的马科斯威尔模型;
(d)广义的伏埃特模型;(e)鲍格斯模型
5.3 蠕变模型
1(t) A1 exp(ct)
式中,A、C均为实验常数。 第一阶段蠕变应变公式更复杂些也可采用:
1(t) A1 exp(c1t) B1 exp(c2t)
式中,A、B、C1、C2 均为实验常数。
5.2 岩石蠕变经验公式
第二阶段蠕 变经验公式有:
1 ) Nadai (1963) 提出的:
.0 exp( / 0 )
石油工程中的流变现象: 在石油钻井过程中,当钻遇盐膏层时,会发生缩径现象;油田开发过程 中,由于注水,泥页岩部位的套管会受到非均匀外载的作用等都与岩层蠕变 有关。
5.1 蠕变概念和蠕变曲线
蠕变的定义: 岩石在恒定载荷持续作用下,其变形随时间逐渐缓慢 地增长现象称为蠕变(Creep)。 应力松弛的定义: 若控制变形保持不变,应力随时间的延长而逐渐减少 的现象称松驰(Relaxation)或称应力松驰。
岩石蠕变性能和徐变性能测试方法与分析

岩石蠕变性能和徐变性能测试方法与分析岩石是地壳中的基本构造材料,其性能对于地下工程的设计和施工起着至关重要的作用。
岩石的蠕变性能和徐变性能是研究岩石长期稳定性和变形特性的重要指标。
本文将对岩石蠕变性能和徐变性能的测试方法和分析进行介绍和探讨。
一、岩石蠕变性能的测试方法与分析1. 岩石蠕变性能的定义及重要性岩石蠕变性是指在恒定的应力条件下,岩石随时间的延续而发生的不可逆性变形。
蠕变性能是岩石长期稳定性的重要指标之一,对于地下工程的安全运营和设计起着至关重要的作用。
2. 岩石蠕变性能的测试方法(1)直接剪切试验法:通过对岩石样品施加恒定剪切应力,观察岩石的剪切应变随时间的变化,以评估岩石的蠕变性能。
(2)恒定应力压缩试验法:通过施加恒定应力对岩石样品进行压缩,观察岩石的应变随时间的变化,以评估岩石的蠕变性能。
(3)恒定应力拉伸试验法:通过施加恒定应力对岩石样品进行拉伸,观察岩石的应变随时间的变化,以评估岩石的蠕变性能。
3. 岩石蠕变性能的分析方法(1)蠕变曲线分析:根据岩石蠕变性能测试获得的实验数据,构建蠕变曲线,分析曲线的特征,如蠕变速率、蠕变应变等,以评估岩石的蠕变性能。
(2)蠕变模型分析:将蠕变性能的实验数据输入到合适的蠕变模型中,通过模型仿真分析,得到岩石的蠕变特性和变形规律,以评估岩石的蠕变性能。
二、岩石徐变性能的测试方法与分析1. 岩石徐变性能的定义及重要性岩石徐变性是指在恒定应力条件下,岩石随时间的延续而发生的可逆性变形。
徐变性能是评估岩石短期变形特性和应力松弛程度的指标。
2. 岩石徐变性能的测试方法(1)应力松弛试验法:通过施加恒定应力,观察岩石应变随时间的变化,以评估岩石的徐变性能。
(2)弛豫试验法:通过施加瞬时应力,观察岩石应变随时间的变化,再施加恒定应力,观察应变的进一步变化,以评估岩石的徐变性能。
3. 岩石徐变性能的分析方法(1)弛豫-徐变模型分析:根据弛豫试验与徐变试验的实验数据,将其输入到合适的模型中,通过模型分析得到岩石的徐变特性和变形规律,以评估岩石的徐变性能。
岩土力学 作业三答案.

岩土力学 作业三答案说明:本次作业对应于文字教材7至9章,应按相应教学进度完成。
一、单项选择题 (每小题2分,共计10分)1.岩石内结晶晶格错位的结果,引起岩石的 (b ) a 、晚性破坏 b 、塑性破坏 c 、弱面剪切破坏2.岩石的单轴抗压强度一般与单轴抗拉强度间成下列哪种关系: (b)a.Rc=(1-4)Rtb. Rc=(4-10)Rtc. Rt=(1-4)Rcd. Rt=(1-4)Rc 3.下面岩体的那种应力状态是稳定状态 (a)a.ϕσσσσcctg 23131++- <sin α b. ϕσσσσcctg 23131++- >sin αc.ϕσσσσcctg 23131++- =sin α4.广义虎克定律中岩石的剪切模量G 为 (a )a.)1(2μ+=E G ,b. )1(2μ-=E G ,c. )1(2μ+=ME G ,d. )1(2μ-=MEG5. 岩石的变形(弹性)模量可表示为 (c )a. yr p E )1(μ+=,b.yr p E )1(μ-=,c.y pr E )1(μ+=,d.ypr E )1(μ-= 二、填空题 (每空1分,共计20分)1.岩石的破坏形式:脆性破坏、延性破坏、弱面剪切破坏。
2.岩石的力学强度是工程设计中最重要的力学指标,分别是单轴抗压强度,抗拉强度、抗剪强度。
3.岩石的抗压强度就是岩石试件在单轴压力(无围压)作用下,抗压破坏的极限能力。
4.岩石的抗剪强度就是指岩石抵抗剪切破坏(滑力)的能力,用凝聚力C 和内摩擦角Φ来表示。
5. 岩石的变形是指岩石在任何物理因素作用下形状和体积大小的变化。
岩石的变形特性常用弹性模量E 和泊松比μ两个指标来表示;6. 岩石的蠕变是指岩石在应力σ不变的情况下岩石变形 ε随着时间t 而增加的现象,一般而言,典型的岩石蠕变曲线可分为三个阶段:初期蠕变,二次蠕变(稳态蠕变),(加建蠕变)第三期蠕变。
7. 天然应力(或初始应力)是习惯上常将工程施工前就存在于岩体中的地应力,称为初始应力。
岩块的变形与强度性质

岩块的力学属性:1.弹性(elasticity):在一定的应力范围内,物体受外力产生的全部变形当去除外力后能够立即恢复其原有的形状和大小的性质。
2.塑性(plasticity):物体受力后产生变形,在外力去除(卸荷)后不能完全恢复原状的性质。
不能恢复的变形叫塑性变形或永久变形、残余变形。
3.粘性(viscosity):物体受力后变形不能在瞬时完成,且应变速率随应力增加而增加的性质。
应变速率随应力变化的变形叫流动变形。
4.脆性(brittle):物质受力后,变形很小时就发生破裂的性质。
5.延性(ductile):物体能承受较大塑性变形而不丧失其承载力的性质。
第一节岩块的变形性质一、单轴压缩条件下的岩块变形性质1.连续加载下的变形性质(1)加载方式:单调加载(等加载速率加载和等应变速率加载)循环加载(逐级循环加载和反复循环加载)(2)四个阶段:①Ⅰ:OA段,孔隙裂隙压密阶段;②Ⅱ:AC段,弹性变形至微破裂稳定发展阶段(AB段和BC段)弹性极限→屈服极限③Ⅲ:CD段,非稳定破裂发展阶段(累进破裂阶段)→“扩容”现象发生“扩容”:在岩石的单轴压缩试验中,当压力达到一定程度以后,岩石中的破裂(裂纹)继续发生和扩展,岩石的体积应变增量由压缩转为膨胀的力学过程。
—峰值强度或单轴抗压强度④Ⅳ:D点以后阶段,破坏后阶段(残余强度)以上说明:岩块在外荷作用下变形→破坏的全过程,具有明显的阶段性,总体上可分为两个阶段:1)峰值前阶段(前区)2)峰值后阶段(后区)(3)峰值前岩块的变形特征(Miller,1965)①应力—应变曲线类型米勒(Miller,1965)6类(σ—εL曲线),如图4.3所示:Ⅰ:近似直线型(坚硬、极坚硬岩石):如玄武岩、石英岩等;Ⅱ:下凹型(较坚硬、少裂隙岩石):如石灰岩、砂砾岩;Ⅲ:上凹型(坚硬有裂隙发育):如花岗岩、砂岩;Ⅳ:陡“S”型(坚硬变质岩):如大理岩、片麻岩;Ⅴ:缓“S”型(压缩性较高的岩石):如片岩;Ⅵ:下凹型(极软岩)。
《岩石力学》期末试卷及答案

《岩石力学》期末试卷及答案姓名 学号 成绩一、 选择题(每题1分,共20分)1. 已知岩样的容重为γ,天然含水量为0w ,比重为s G ,40C 时水的容重为w γ,则该岩样的饱和容重m γ为( A )A 。
()()w s s G w G γγ++-011 B. ()()w s s G w G γγ+++011 C 。
()()γγ++-s s w G w G 011 D. ()()w s s G w G γγ+--0112。
岩石中细微裂隙的发生和发展结果引起岩石的( A )A .脆性破坏B 。
塑性破坏C 。
弱面剪切破坏 D. 拉伸破坏3. 同一种岩石其单轴抗压强度为c R ,单轴抗拉强度t R ,抗剪强度f τ之间一般关系为( C )A 。
f c t R R τ<< B. f t c R R τ<< C 。
c f t R R <<τ D 。
t f c R R <<τ4。
岩石的蠕变是指( D )A 。
应力不变时,应变也不变;B 。
应力变化时,应变不变化;C. 应力变化时,应变呈线性随之变化;D. 应力不变时应变随时间而增长5。
模量比是指(A )A .岩石的单轴抗压强度和它的弹性模量之比B 。
岩石的 弹性模量和它的单轴抗压强度之比C .岩体的 单轴抗压强度和它的弹性模量之比D .岩体的 弹性模量和它的单轴抗压强度之比6。
对于均质岩体而言,下面岩体的那种应力状态是稳定状态( A ) A.ϕϕσσσσsin 23131<++-cctg B.ϕϕσσσσsin 23131>++-cctg C 。
ϕϕσσσσsin 23131=++-cctg D.ϕϕσσσσsin 23131≤++-cctg 7. 用RMR 法对岩体进行分类时,需要首先确定RMR 的初始值,依据是( D )A .完整岩石的声波速度、RQD 值、节理间距、节理状态与地下水状况B. 完整岩石的强度、RQD 值、节理间距、节理状态与不支护自稳时间C. 完整岩石的弹性模量、RQD 值、节理间距、节理状态与地下水状况D. 完整岩石的强度、RQD 值、节理间距、节理状态与地下水状况8。
第四章 岩石得蠕变
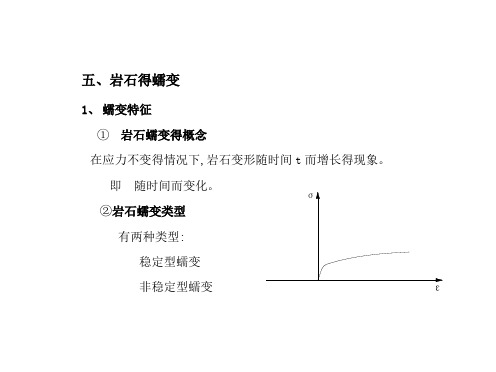
五、岩石得蠕变1、蠕变特征①岩石蠕变得概念在应力不变得情况下,岩石变形随时间t而增长得现象。
②岩石蠕变类型有两种类型:稳定型蠕变非稳定型蠕变a、稳定型蠕变:应力作用下,随时间递减,零,即,一般在较小应力或硬岩中。
b、非稳定型蠕变:岩石在恒定应力作用下,岩石变形随时间不断增长,直至破坏。
一般为软弱岩石或应力较大。
③蠕变曲线变化特征三个阶段:Ⅰ阶段:初期蠕变。
曲,属弹性变形。
Ⅱ阶段:等速蠕变。
应变-时间曲线近似直线,应变随时间呈近于等速增长。
出现塑性。
Ⅲ阶段:加速蠕变。
应变-时间曲线向上弯曲,其应变速率加快直至破坏。
应指出,并非所有得蠕变都能出现等速蠕变阶段,只有蠕变过程中结构得软化与硬化达到动平衡,蠕变速率才能保持不变。
在Ⅰ阶段,如果应力骤降到零,则-t曲线具有PQR形式,曲线从P点骤变到Q点,PQ=为瞬时弹性变形,而后随时间慢慢退到应变为零,这时无永久变形,材料仍保持弹性。
在Ⅱ阶段,如果把应力骤降到零,则会出现永久变形,其中TU=。
变速度变化缓慢,稳定。
应力增大时率增大。
高应力时速,蠕变速率越大,反之愈小。
岩石长期强度:指岩石由稳定蠕变转为非稳定蠕变时得应力分界值。
即,岩石在长期荷载作用下经蠕变破坏得最小应力值(或)岩石极限长期强度:指长期荷载作用下岩石得强度。
2、蠕变经验公式由于岩石蠕变包括瞬时弹性变形、初始蠕变、等速蠕变与加速蠕变,则在荷载长期作用下,岩石蠕变得变形可用经验公式表示为: =+++-瞬时变形;-初始蠕变;-等速蠕变;-加速蠕变。
对于前两个阶段,目前得经验公式主要有三种:①幂函数取第一阶段:;第二阶段:,>、就是试验常数,其值取决于应力水平、材料特性以及温度条件。
②对数函数:B、D就是与应力有关得常数。
③指数函数,或A为试验常数,就是时间t得函数伊文思(Evans)对花岗岩、砂岩与板岩得研究:,C为试验常数,n=0、4; 而哈迪(Hardy)给出经验方程,,A、C为试验常数。
3、蠕变理论模型(理论公式)(1)基本模型由于岩石材料具有弹性、刚性、粘性与塑性,目前采用简单得机械模型来模拟材料得某种性状。
常见岩石力学参数

常见岩石力学参数岩石力学参数是指描述岩石在外力作用下的力学行为的物理性质,包括弹性模量、剪切模量、泊松比、抗压强度、抗拉强度、抗剪强度等。
这些参数对于岩石的力学性质和工程应用具有重要意义。
本文将详细介绍这些常见的岩石力学参数。
1. 弹性模量(Young's modulus):弹性模量是衡量岩石弹性性质的一个重要参数,表示岩石在外力作用下产生弹性变形的能力。
弹性模量越大,岩石的刚度越大,抗弯和抗变形能力越强。
2. 剪切模量(Shear modulus):剪切模量是衡量岩石抗剪切性质的参数,表示岩石在剪切应力作用下产生剪切变形的能力。
剪切模量越大,岩石的抗剪强度越高,稳定性越好。
3. 泊松比(Poisson's ratio):泊松比是衡量岩石体积变形性质的参数,表示岩石在受到压缩应力时,横向收缩的程度。
泊松比一般介于0.1到0.4之间,数值越大,岩石的蠕变性越强。
5. 抗拉强度(Tensile strength):抗拉强度是衡量岩石抗拉性质的参数,表示岩石在受到拉伸应力时的最大承载能力。
抗拉强度一般比抗压强度要小,岩石在受到拉伸时易发生断裂。
6. 抗剪强度(Shear strength):抗剪强度是衡量岩石抗剪切性质的参数,表示岩石在受到剪切应力时的最大承载能力。
抗剪强度主要与岩石内部的粘聚力和内摩擦角有关。
除了上述常见的岩石力学参数外,还有一些与岩石稳定性有关的参数:7. 断裂韧性(Fracture toughness):断裂韧性是衡量岩石抗断裂性质的参数,表示岩石在受到裂纹扩展时的抵抗能力,能够反映岩石的破坏扩展能力。
8. 孔隙度(Porosity):孔隙度是衡量岩石孔隙结构的参数,表示岩石内部的孔隙空间占总体积的比例。
孔隙度能够影响岩石的密实程度和渗透性,对工程建筑的渗流和稳定性有重要影响。
9. 饱和度(Saturation):饱和度是衡量岩石孔隙中被水、气体或其他流体填充的程度。
岩石材料的蠕变实验及本构模型研究

岩石材料的蠕变实验及本构模型研究流变学作为力学的一个分支,主要研究材料在应力、应变、温度、辐射等条件下与时间因素有关的变形规律,所涉及的内容包括蠕变、应力松弛和弹性后效等。
蠕变是影响岩体稳定性的一个重要因素。
软弱岩石在受到较低水平的应力作用时,就会产生明显的蠕变现象,如软岩巷道中的底鼓,即使是很坚硬的岩体,在高应力作用下同样会产生蠕变,从而影响到工程的功能和使用。
因此,需要对岩石材料的蠕变行为进行深入研究,力求从本质上揭示其蠕变行为的特征。
本文通过实验研究和理论分析,得到了盐岩的基本力学参数,并研究了盐岩在不同应力条件下的力学特性和蠕变行为。
以经典蠕变模型为基础,结合分数阶微积分理论,构建了一个新的蠕变模型,并利用盐岩、泥岩和煤岩的蠕变实验数据对其进行了验证。
(1)对盐岩材料进行了多组单轴和三轴压缩实验,并在每组实验中选取三个试样重复进行实验,以此来降低实验的随机性和试样个体的差异性。
结果三个试样的测试结果比较接近,此批试样的个体差异性较小。
此外,常规压缩实验的结果还表明随着围压的增大,抗压强度和最大应变会随之增大。
(2)在单轴蠕变实验中,选取了四个轴压水平来进行实验,分析了不同轴压对蠕变的影响。
当轴压水平越大时,加速蠕变阶段就会越早地出现,并且稳定蠕变应变率也会越大。
与单轴蠕变相比,当材料受到一个较小的围压作用时,其蠕变行为也会发生巨大的变化,例如蠕变应变率大幅下降、蠕变时间大幅增长、加速蠕变阶段缺失等。
(3)通过分析不同应力条件下的蠕变应变率可以发现,稳定蠕变应变率与轴压大小呈线性关系,加速蠕变应变率与轴压大小也呈现出正相关性。
此外,蠕变等时曲线表明随着时间的延长,轴压大小对蠕变的影响会越来越明显。
相反,围压会明显地降低蠕变应变率并抑制蠕变行为的发展。
(4)结合分数阶微积分理论构建了一个新的非线性蠕变模型,并利用广义塑性力学理论和张量分析理论对新模型在三轴应力状态下的蠕变方程进行了推导。
以盐岩实验数据为基础,对蠕变模型的参数进行了辨识,并验证了模型的准确性。
岩体蠕变试验

岩体蠕变试验
岩体弯曲蠕变试验的原理及其结论
岩体弯曲蠕变试验的原理
蠕变试验对材料施加一个恒定的应力状态, 然后保持该应力状态不变,观测应变状态 随时间的变化过程,通过自制重力驱动偏 心轮式杠杆扩力加载式流变仪以及弯曲蠕 变系统,研究了红砂岩梁和油页岩梁的弯曲 蠕变及其扰动效应问题。
弯曲蠕变曲线
根据应变速率不同,其蠕变过程可以分为三 个阶段: 第一蠕变阶段:如曲线中ab段所示,蠕变速 二蠕变阶段:如曲线中bc段所示,应变速 率保持不变,故称为等速蠕变阶段。 第三蠕变阶段:如曲线中cd段所示,应变速 率迅速增加直到岩石破坏,故称为加速蠕 变阶段。
岩石弯曲蠕变曲线
• 岩石蠕变曲线
试验结论
• 未受到冲击扰动的岩梁试件断口形态比较 整齐,断口开裂部位位于岩梁载荷集中部位, 裂纹开裂始于中性面。 • 受到扰动载荷的岩梁试件断口形态不整齐, 断口开裂部位偏离岩梁中性面。 • 考虑粘弹性蠕变特性,在一定扰动载荷水平 的作用下,经历一段时间后岩梁可出现延迟 性蠕变失稳。 • 扰动载荷超出一定的范围时,岩梁将发生突 然失稳。
岩石蠕变曲线三个特征阶段

岩石蠕变曲线三个特征阶段岩石蠕变是指一种地质现象,它描述了岩石在地下长期受到地质应力作用下的变形和演化过程。
岩石蠕变曲线是用来描述这个变形过程的工具,它可以帮助我们更好地理解岩石在应力作用下的行为,并为地质学家和工程师提供重要的参考。
在岩石蠕变曲线中,我们可以分为三个主要的特征阶段:初级蠕变、次级蠕变和三次蠕变。
每个阶段都有其独特的特征和行为,一起来探讨一下吧。
1. 初级蠕变初级蠕变是岩石蠕变曲线的第一个阶段,也是最明显的阶段。
在初级蠕变阶段,岩石会迅速发生塑性变形,形成明显的蠕变曲线。
这是因为岩石受到应力后,内部的微观结构会发生变化,其晶体结构开始发生位移和滑动,导致整体的形变。
在初级蠕变阶段,岩石的应力与应变之间呈现出非线性关系。
具体来说,初级蠕变曲线呈现为一个指数增长的曲线,应力逐渐增加,岩石的变形也随之增加,但增幅逐渐减小。
这是因为在初级蠕变阶段,岩石中的微观结构发生变化的速率较快,但随着时间的推移,速率逐渐减慢。
初级蠕变还有一个重要的特征是弹性回复。
当应力移除后,岩石会部分地恢复到初始状态,这被称为弹性回复。
然而,需要注意的是,岩石在经历过初级蠕变后,弹性回复的程度会降低,这是因为岩石中的微观结构已经发生了较大的改变。
2. 次级蠕变次级蠕变是岩石蠕变曲线的第二个阶段。
在初级蠕变之后,如果还存在应力的作用,岩石将进入次级蠕变阶段。
在次级蠕变阶段,岩石的变形速率会明显降低,相对稳定地保持在一个较小的水平。
在次级蠕变阶段,岩石中的微观结构仍在发生变化,但速率较初级蠕变时要慢得多。
次级蠕变曲线呈现为一个逐渐平稳的曲线,应力和应变之间存在一个较小的线性关系。
这是因为在次级蠕变阶段,岩石中的微观结构已经部分地调整和重新排列,导致变形速率减缓。
除了变形速率的减缓外,次级蠕变还有一个特征是持续时间的延长。
相较于初级蠕变,次级蠕变可以持续更长的时间,甚至可以维持数小时、数天甚至数年,这取决于岩石的性质和应力的作用。
(完整版)岩石力学试卷二及答案

20~20学年第学期级专业试题学号:姓名:……………………………………密…………封……………线…………………………………1、岩石的常用物理指标有哪些?它们与岩石的强度之间大致有什么关系?(5分)2、现场测定岩体变形指标的试验方法有哪些?(5分)3、简述水对岩石强度的影响。
(5分)4、影响岩石应力-应变曲线主要因素有哪些?是如何影响的?(5分)5、什么是岩体初始应力场?岩体内产生应力的原因有哪些?(5分)第1页共6 页20~20学年第学期级专业试题学号:姓名:……………………………………密…………封……………线…………………………………6、何谓喷锚支护,它与传统的老式支护有何区别?(5分)二、作图题(5分)什么是岩石的蠕变?试作图说明岩石流变三阶段的特点:三、填空题: (0.5/空)(共20分)1、岩石力学是研究岩石的,是探讨岩石对。
岩石力学研究的主要领域可概括为、、。
研究方法主要有、、、。
2、岩石的破坏形式:、、。
3、影响岩石抗压强度的主要因素一般有:、和、、、、、、、等。
4、格里菲斯理论把岩石看作为有材料,岩石之所以破坏是由于在引起细小裂隙的发生发展所致。
修正的格里菲斯理论则认为岩石破坏除拉第2页共6 页20~20学年第学期级专业试题应力集中所致外,还可以是引起裂隙沿裂隙长轴方向发生 。
5、已知材料的弹性模量E 和泊松比μ,用它们来表示G:λ:、K:。
6、在1=o k 的四周等压地应力场rH v h ==σσ作用下,围岩中的径向应力r σ都岩体中的初始应力;切向应力θσ则岩体中的初始应力,在洞壁上达最大值。
由理论上可以证明,开挖洞室的影响范围是。
7、岩压力是由于洞室开挖后岩体和而形成的。
由于岩体而对支护或衬砌的压力,称为“变形压力”;将由于岩体而而对支护或衬砌的压力,称为“松动压力”。
8、按压力拱理论分析,在可形成压力拱的洞室内,压力拱的高度是 ,洞室顶部的最大垂直压力在拱轴线上大小为,洞室任何其它点的垂直山岩压力等于。
岩石的蠕变2 [修复的]-其他蠕变模型
![岩石的蠕变2 [修复的]-其他蠕变模型](https://img.taocdn.com/s3/m/e974c7ff5ef7ba0d4a733bf2.png)
一、弹性模型(弹性单元)
理想的弹性体:线性弹性模型; 完全服从虎克定律,也称虎克物质;
用刚度为G的弹簧表示。
K
弹性模型
1
5.3 蠕变模型
二、粘性模型(粘性单元)
理想粘性体(牛顿流体);
完全服从牛顿粘性定律应力与应变速率成比例;
用充满粘性液体的圆筒形容器内的有孔活塞表示。
5.4 岩石蠕变性态的影响因素
应力大小 性质
围压
周期性载荷
温度
湿度以及岩石的结构
8
5.4 岩石蠕变性态的影响因素
雪花石膏在不同应力水平下的蠕变曲线
9
5.4 岩石蠕变性态的影响因素
二、围压、温度对岩石蠕变性态的影响
Griggs(1936)对Solenhofen石灰岩试件,在围压500MPa下采用不同的 轴向压应力进行蠕变实验
增长到一定值时,剪应变就趋于零。
伏埃特模型及其蠕变曲线
4
5.3 蠕变模型
五、广义马克斯威尔模型
模型由伏埃特模型与粘性单元串联而成; 剪应变开始以指数速率增长,逐渐趋近于常速率。
广义马克斯威尔模型及其蠕变曲线
5
5.3 蠕变模型
六、广义的伏埃特(Voigt)模型(开尔文模型)
将弹性元件与弹性元件串联而成的模型,
开始时产生瞬时应变,随后剪应变以指数递减速率增长,
最终应变速率趋于零,应变不再增长。
广义的伏埃特模型及其蠕变曲线
6
5.3 蠕变模型
七、柏格斯模型
麦克斯韦尔模型与开尔文模型串联形成的组合模型。 蠕变曲线上开始有瞬时变形,然后剪应变以指数递减的速 率增长,最后趋于不变速率增长。
最新第四章 3 岩石的蠕变

第四章3岩石的蠕变仅供学习交流五、岩石的蠕变1、 蠕变特征 ①岩石蠕变的概念在应力σ不变的情况下,岩石变形随时间t 而增长的现象。
即dtd ε随时间而变化。
②岩石蠕变类型有两种类型:稳定型蠕变非稳定型蠕变a、稳定型蠕变最终趋于零,即dε=dt定。
一般在较小应力下或硬岩中。
仅供学习交流b、非稳定型蠕变:岩石在恒定应力作用下,岩石变形随时间不断增长,直至破坏。
③蠕变曲线变化特征三个阶段:Ⅰ阶段:初期蠕变。
d曲,应变速率dt仅供学习交流小。
属弹性变形。
Ⅱ阶段:等速蠕变。
应变-时间曲线近似直线,应变随时间呈近于等速增长。
出现塑性。
Ⅲ阶段:加速蠕变。
应变-时间曲线向上弯曲,其应变速率加快直至破坏。
应指出,并非所有的蠕变都能出现等速蠕变阶段,只有蠕变过程中结构的软化和硬化达到动平衡,蠕变速率才能保持不变。
仅供学习交流在Ⅰ阶段,如果应力骤降到零,则ε-t 曲线具有PQR 形式,曲线从P 点骤变到Q 点,PQ =e ε为瞬时弹性变形,而后随时间慢慢退到应变为零,这时无永久变形,材料仍保持弹性。
在Ⅱ阶段,如果把应力骤降到零,则会出现永久变形,其中TU =e ε。
仅供学习交流应变速度变化缓慢,逐渐趋于稳定。
应力增大时,应变速率增大。
高应力时,蠕变加速,直至破坏。
应力越大,蠕变速率越大,反之愈小。
岩石长期强度:指 岩石由稳定蠕变转为非稳定蠕变时的应力分界值。
即,岩石在长期荷载作用下经蠕变破坏的最小应力值(∞σ或∞τ) 岩石极限长期强度:指长期荷载作用下岩石的强度。
2、 蠕变经验公式仅供学习交流由于岩石蠕变包括瞬时弹性变形、初始蠕变、等速蠕变和加速蠕变,则在荷载长期作用下,岩石蠕变的变形ε可用经验公式表示为:ε=e ε+)(t ε+t M +)(t T εe ε-瞬时变形;)(t ε-初始蠕变;t M -等速蠕变;)(t T ε-加速蠕变。
对于前两个阶段,目前的经验公式主要有三种: ①幂函数取n t A t ⋅=)(ε仅供学习交流第一阶段:n e t A ⋅+=εε;第二阶段:)(11t t M t A n e -+⋅+=εε,t >1tA、n 是试验常数,其值取决于应力水平、材料特性以及温度条件。
05岩石的蠕变

2
15
第21页,共22页。
B×1048 5.2 18 5.9 12 6.6 42 4.7
21
★
思考题
什么是岩石的蠕变?岩石蠕变分哪三个阶段?画出 岩石蠕变的典型曲线。
22
第22页,共22页。
第5章 岩石的蠕变
5.1 蠕变概念和蠕变曲线 5.2 岩石蠕变经验公式 5.3 蠕变模型 5.4 岩石蠕变性态的影响因素(加) 5.5 粘弹性常数的室内测定
1 第1页,共22页。
本节教学内容
蠕变的概念 蠕变曲线 岩石蠕变的经验公式
2
第2页,共22页。
本节教学目标
掌握岩石蠕变的概念
掌握典型蠕变曲线含义
5.2 岩石蠕变经验公式
4)Menzel及Schrelner(1975)经验公式
Menzel及Schrelner(1975)在杂盐岩蠕变实验中得出:
恒定应力下的经验公式为:
1
s
B
1 •
S 1
r s 1
1
• t s1
E
在恒定应变速率下的经验公式为:
1
1
s
B
1 •
S 1
r s 1
南喀1井盐层侧钻6次,损失1.2 亿;
套管变形破坏,导致油 井报废
引起固井、完井等复 杂问题
高效钻穿盐膏岩地层是油气藏开发的关键
8
第8页,共22页。
5.1 蠕变概念和蠕变曲线
二、岩石的蠕变性态的实验研究
单轴或三轴压缩蠕变实验 实验表明;在恒定载荷作用下,只要有充分长的
时间,应力低于或高于弹性极限均能产生蠕变现象。 但在不同的恒定载荷下,变形随时间增长的蠕变曲线 却有差异。
应力松弛:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹性后效概念:
加载或卸载时,弹性应变滞后于应力的现象。
2. 影响蠕变的因素 岩性 应力 温度、湿度
长期强度概念:时间→∞的强度(σ∞)
/瞬时强度(σc ) σ∞/ σc : 一般岩石为 0.4-0.8 中、软岩为 0.4-0.6 硬岩为 0.7-0.8
应力
时间
3. 蠕变模型及本构方程
(1)理想物体基本模型
4.8
岩石的蠕变
γ
2
蠕变模型
τ
(1)马克斯威尔(Maxwell)模型: 这种模型是用弹性单元和
γ
η
γ
粘性单元串联而成,见图4-11(a)。
当剪应力骤然施加并保持为常量时, τ 变形以常速率不断发展。这个模型用 两个常数G和来描述。
τ
b
γ
a b
a b
η
τ
η 1 图4-11 线性粘弹性模型及其蠕变曲线 c
弹性元件(弹簧)
粘性元件(阻尼器)
E
,如 G
塑性元件(摩擦片)
0 t
s时,=0
s时,
4.8
岩石的蠕变
2 蠕变模型
2)粘性模型
或称粘性单元
这种模型完全服从牛顿粘性定律,它表示应力与 应变速率成比例,例如剪应力与剪应变速率的关系 为:
6
图3 试件P3剪切位移与剪切时间的关系曲
试件分别在0.3Mp、0.35Mp、0.45Mp剪切应力作用 下,剪切位移与剪切时间关系曲线发生转折点,由等 速蠕变转变为加速蠕变。因此,试件P1、P2、P3的长 期剪切蠕变强度分别为0.3Mp、0.35Mp、0.45Mp。
根据法向应力和对应的长期剪切蠕变强度的关系曲 线求出长期抗剪强度参数为71.2Kpa,为20.8。
0.15Mpa 0.2Mpa 0.25Mpa 0.3Mpa 0.35Mpa
3 剪切历时t(d)
4
5
6
图2
14 12
试件P2剪切位移与剪切时间的关系曲线
0.25Mpa 0.3Mpa 0.35Mpa 0.4Mpa 0.45Mpa
剪切位移(mm)
10 8 6 4 2 0 0 1 2
3 剪切历时t(d)
4
5
γ
4.8 岩石的蠕变 b
η
τ
η 1
η 2
c
2 蠕变模型
γ
τ 伏埃特模型:见图4-11(d),模 η 2 型由伏埃特模型与弹性单元串联 η 1 c 而成,用三个常数G1、G2和表示 该种材料的性状。开始时产生瞬 时应变,随后剪应变以指数递减 τ 速率增长,最终应变速率趋于零, 应变不再增长。 d η 1 τ
三、岩石的流变特性
岩 石 变 形
与时间无关的变形
弹性(可恢复) 塑性(不恢复)
与时间有关的—流变
蠕变
松弛
岩石的时间效 应
蠕变:应力恒定,岩石应变随时间增大,所产生的变形称 为蠕变(又称为流变)。 松驰:应变恒定,岩石中的应力随时间减少,这种现象称 “松驰”。
4.8
岩石的蠕变
1蠕变概念和蠕变曲线
岩石的蠕变就是指在应力不变的情况下岩石变形(或应 变)随着时间t而增长的现象。工程实践发现,在岩石开挖洞 室以后一段很长的时间内,支护或衬砌上的压力一直在变化 的,这可解释为由蠕变的结果。因此,研究岩石的蠕变对于 洞室特别是深埋洞室围岩的变形,有着重要意义。
四、长期强度的的确方法
由蠕变试验曲线确定岩石的长时强度
扎哈卓尔露天矿边坡软岩进行直剪蠕变试验
表1 垂直应力和剪切应力分级表 试件编号 垂直应力(Mpa) 剪切应力(Mpa)
0.1 0.15
P1
0.6
0.2
0.25 0.3
0.15
0.2 P2 0.8 0.25 0.3
0.35
0.25 0.3
P3
Kelvin 模型
1 2 1 2 1 E1 E d 2 d 2 dt dt d E o dt
o
E
(1 e
E t
)
o o t E
其他模型
γ
γ
4.8 岩石的蠕变
2 蠕变模型
τ
η
b
γ
τ
γ
τ
η 1
η
c
3)广义马克斯威尔模型:见 b η 图4-11(c),该模型由伏埃特 模型与粘性单元串联而成。用 τ 三个常数G、和描述。剪应变 η 2 η 1 开始以指数速率增长,逐渐趋 c 近于常速率。
(
γ
γ
τ
η 1
d
τ
τ 图4-11 线性粘弹性模型及其蠕变曲线 η 2 γ η 1 e) (c)广义的马科斯威尔模型;
γ
η 2
τ
b
(a)马科斯威尔模型;
γ
4.8
岩石的蠕变
2 蠕变模型
γ
η
γ
(2)伏埃特(Voigt)模型: 该模型又称凯尔文模型,它由 τ
τ
b
弹性单元和粘性单元并联而成,
见图4-11(b)。当剪应力骤然施加时, 剪应变速率随着时间逐渐递减,在增 τ 长到一定值时,剪应变就趋于零。这 γ η 2 个模型用两个常数G和来描述。由于并 η 1 τ c 联,介质上的剪应力是弹性单元与粘 b 性单元剪应力之和,由下列方程给出: η 图4-11 线性粘弹性模型及其蠕变曲线 d G (b)伏埃特模型 dt
1.0
0.35
0.4 0.45
9 8 7 6 5 4 3 2 1 0 0 1 2
剪切位移(mm)
0.1Mpa 0.15Mpa 0.2Mpa 0.25Mpa 0.3Mpa
3 剪切历时t(d)
4
5
6
图1 试件P1剪切位移与剪切时间的关系曲线
9 8 7
剪切位移(mm)
6 5 4 3 2 1 0 0 1 2
τ
η 1
d
γ
τ
η 1 η 2
e)
(d)广义的伏埃特模型;
图4-11 线性粘弹性模型及其蠕变曲线 γ
c
τ
η1
γ
d
4.4
岩石的蠕变
τ (5)鲍格斯(Burgers)模型:
2 蠕变模型
τ
η2 η1 这种模型由伏埃特模型与 η 1 d e) 马克斯威尔模型串联而组成,见 图4-11(e)。模型用4个常数G1、 γ τ G2、和来描述。蠕变曲线上开始 η 2 有瞬时变形,然后剪应变以指数 η 1 e) 递减的速率增长,最后趋于不变 图4-11 线性粘弹性模型及其蠕变曲线 速率增长。 (e)鲍格斯模型
加载、卸载岩石变形分析
• 岩石开挖 • 岩基 • 实验室受力
d dt
(2)组合模型 Maxwall 模型
1 2 1 2 d 1 1 d 对于弹性元件1 E dt E dt d 对于粘性元件 2 dt d 1 d dt E dt d d o o 0 dt dt
8 页岩 6
ε (10-5)
4 2 2 页岩 花岗岩 4 6 8 10 12
4.8 岩石的蠕变性质
在外部条件不变的情况下,岩石的变形或应力随 时间而变化的现象叫流变,主要包括蠕变、松弛。 蠕变(creep)是指岩石在恒定的荷载作用下,变形随时间 逐渐增大的性质。 1. 蠕变曲线特征(三个阶段)
AB段-初始蠕变阶段 BC段-等速蠕变阶段 CD段-加速蠕变阶段
