第十章图形操作
华师大版七年级数学下册第十章《10.5 图形的全等》优质课件

课后作业
1.教材P136习题10.5第1、2、3题; 2.完成练习册本课时的习题.
学习如果想有成效,就必须专 心。学习本身是一件艰苦的事,只 有付出艰苦的劳动,才会有相应的 收获。 —— 谷超豪
这一 样个 的人 人所 才受 有的 学教 问育 。超
过 了 自 己 的 智 力 ,
随堂演练
1. 下列说法正确的是(C )
①用一张像纸冲洗出来的10张1寸像片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个
B.2个
C.3个
D.4个
2.对于两个图形,给出下列结论:①两个图形的周长
相等;②两个图形的面积相等;③两个图形的周长
【归纳结论】
能够完全重合的两个图形 叫做全等图形.
P133做一做:观察图中的平面图形,你能发现哪两个 图形是全等图形吗?
【归纳结论】
图形的翻折、旋转、平 移是图形的三种基本的运动. 图 形经过这样的运动,位置虽然 发生了变化,但形状、大小却 没有改变,前后两个图形是全 等的.反过来,两个全等的图形 经过这样的运动一定能够重合.
P134思考:观察下图中的两对多边形,其中的一个可以 经过怎样的运动和另一个图形重合?
上面的两对多边形都是全等图形,也称为全等多边 形.两个全等的多边形,经过运动而重合,相互重合的 顶点叫做对应顶点,相互重合的边叫做对应边,相互 重合的角叫做对应角.
如下图中的两个五边形是全等的,记作五边形 ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表 示全等,读作“全等于”.).点A与A′,B与B′,C 与C′,D与D′,E与E′分别是对应顶点.
图形的输入输出与打印

第四节 打 印 创建完图形后,通常要将图形打印到图纸上。 AutoCAD 2005提供的打印功能可以将图 形输出到绘图仪、打印机或图形文件中。 启动方式 菜单栏:“文件”→“打印”。 工具栏:“打印”按钮 。 命令行:PLOT。
图10.4.1 “打印局-地下 室平面图”对话框
执行打印命令后,系统弹 出“打印-地下室平面图” 对话框,如图所示。
习题:将“轴测图” 模型空间进行打印, 并用“完全预览”的 方式预览打印效果。 执行Plot命令,系统 将打开如图所示的 “打印-模型”对话框。
图10.4.3 “打印-模 型”对话框
01
在“打印机/绘图仪” 选项区中选择“打印 机(可打印)\HP”。
04
在“打印偏移”选 项区中选中“局中
打印”复选项。
“图纸尺寸”下拉列表框:用于选择图纸的尺寸 大小。 “打印区域”选项区:用于选择图纸的有效打印区域。在 “打印范围”下拉列表框中可以选择布局、窗口、范围和显 示。 “打印偏移”选项区:用于显示相对于介质源左下角的打印 偏移值的设置。一般情况下,打印原点位置在图纸的左下方, 用户可以分别在X和Y文本框中输入偏移量,如果选中“局中 打印”复选框,则可以自动计算输入的偏移值以便居中打印。
习题十 填空题 AutoCAD可以输入的文件类型包括_________、_________、 _________、_________、_________和_________。 设置图形的打印范围有_________、_________、_________和 _________4种方式。
题图 10.1
图10.4.2 “添加页面设置”对话框
该对话框与“页面设置-地下室平面图” 中的内容基本相同,用户可以设置其他 的选项。 “页面设置”选项区:在该选项区中可 以选择打印设置。单击右侧的“添加” 按钮,系统弹出“添加页面设置”对话 框,如图所示,通过该对话框可以添加 新的页面设置。
华师版七年级数学下册精品课件(HS) 第10章 轴对称、平移与旋转 专题课堂(十) 图形变换的应用

6.(原创题)如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点 A与CB延长线上的点E重合.
(1)三角尺旋转了多少度? (2)连结CD,试判断△CBD的形状; (3)在等腰三角形中存在“两个底角相等”的事实,请用这个结论,求∠BDC的度 数. 解:(1)因为∠ABC=30°,所以∠ABE=180°-∠ABC=180°-30°=150°, 即三角尺旋转了150° (2)因为由旋转的特征可知BC=BD,所以△CBD是等腰三角形 (3)因为△BCD是等腰三角形,所以∠BCD=∠BDC.∴∠DBE=∠BCD+∠BDC= 2∠BDC.又因为由平移的特征知∠DBE=∠CBA=30°,所以2∠BDC=30°,所以 ∠BDC=15°
(3)略
(3)选择图③,④中的一种说明理由.
解:(2)画图如下:
(3)略
分析:(1)由平移的特征可知∠C=∠BED=45°,根据三角形的内角和求出∠A; (2)由平移的特征可得 DE=AF,DE=FC,则 AF=CF=DE=12 AC,可求出 DE; (3)由(2)即可得出结论.
解:(1)∠A=65°,∠C=45° (2)DE=6 cm (3)成立,理由:由平移可得 DE=AF,DE=FC,所以 DE=AF=FC,所以 2DE=AF+FC,所以 2DE=AC, 所以 DE=12 AC
点E处,若∠A=25°,则∠CDE的度数为( C ) A.50° B.65° C.70° D.75°
3.如图,在Rt△ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,
中文版AutoCAD 2019基础教程 第10章 绘制三维图形

中文版AutoCAD 2019基础教程
10.1.2三维视图
创建三维模型时,常常需要从不同的方向观察模型。当用户设定某个查看方向 后,AutoCAD将显示出对应的3D视图。具有立体感的3D视图将有助于用户正 确理解模型的空间结构 。
中文版AutoCAD 2019基础教程
10.1.3创建三维用户坐标系
10.1三维绘图基础知识
在使用AutoCAD绘制三维图形之前,首先应切换至“三维建模”空间,并掌握 三维绘图的基础知识,例如绘制三维模型时经常使用的三维坐标系、三维视图 等。
中文版AutoCAD 2019基础教程
10.1.1三维绘图的术语
三维实体模型需要在三维实体坐标系下进行描述。在三维坐标系下,可以使用 直角坐标或极坐标方法来定义点。此外,在绘制三维图形时,还可以使用柱坐 标和球坐标来定义点。在创建三维实体模型前,应先了解下面的一些基本术 语。
中文版AutoCAD 2019基础教程
10.5.4将二维图形放样成实体
在快捷工具栏选择“显示菜单栏”命令,在弹出的菜单中选择“绘 图”|“建模”|“放样”命令(LOFT),可以将二维图形放样成实体 。
中文版AutoCAD 2019基础教程
10.5.5根据标高和厚度绘制实体
在AutoCAD中,用户可以为将要绘制的对象设置标高和延伸厚度。一旦设 置了标高和延伸厚度,就可以用二维绘图的方法得到三维图形。使用AutoCAD 绘制二维图形时,绘图面应是当前UCS的XY面或与其平行的平面。标高就是 用来确定这个面的位置,它用绘图面与当前UCS的XY面的距离表示。厚度则 是所绘二维图形沿当前UCS的Z轴方向延伸的距离 。
中文版AutoCAD 2019基础教程
10.2.3绘制三维样条曲线和三维螺旋线
新华东师大版七年级数学下册《10章 轴对称、平移与旋转 10.4 中心对称》教案_19

教学内容:义务教育课程标准华东师大版教科书七年级下册第十章中心对称第二单元中心对称一、内容和内容解析1.内容中心对称概念、性质和中心对称图形的概念.2.内容解析中心对称是旋转角为180°的旋转,是一种特殊的旋转.中心对称在生活中广泛存在,而中心对称图形是对轴对称图形,旋转知识的延伸与拓展,学生通过本节课再次体会旋转变化,认识中心对称和中心对称图形,同时也进一步完善初中学习中对“对称图形”知识的认识.本节课从旋转变化引入中心对称的概念,先让学生从旋转的角度观察两个图形之间的关系,类比旋转得出中心对称的定义,在此基础上,通过探索成中心对称的两个图形的对称中心与对应点所连线段之间的关系获得性质,并能运用中心对称的性质画出一个图像关于某一点的对称图形,以画出的图形用描述的方式给出了中心对称图形的概念,类比中心对称得出中心对称图形的定义,渗透了从一般到特殊的数学思想方法,要求会判断一个图形是否为中心对称图形,在此基础上,通过对比中心对称和中心对称图形的概念、轴对称图形和中心对称图形,加深知识间的区别和联系.基于以上分析,确定本节课的教学重点是:中心对称概念、性质和中心对称图形的概念.二、目标和目标解析1.目标了解中心对称、中心对称图形的概念,会画一个简单几何体关于某一点对称的图形,会判断一个图形是否为中心对称图形.通过操作、观察、归纳中心对称的性质,经历由具体到抽象认识问题的过程.知道中心对称和中心对称图形联系与区别.感悟类比方法在研究数学问题中的作用.2.目标解析达成目标(1)的标志:学生能根据两个图形的特殊关系的到中心对称是旋转角为180°的旋转,类比旋转的定义得出中心对称的概念,用运动的观点观察和认识图形的过程中渗透旋转变化的思想.抽象出中心对称图形的特征,能正确识别简单的中心对称图形.达成目标(2)的标志:学生知道中心对称是旋转角为180°的旋转,进而得出中心对称的两个图形是全等图形,对称中心到两个对称点的距离相等.知道中心对称图形是一个图形,它绕一个点旋转180°后能与自身完全重合.中心对称反映了两个图形的位置关系,这两个图形绕着某一点旋转180°后能够重合;一个中心对称图形沿对称中心可以分成中心对称的两个图形,成中心对称的两个图形也可以看成是一个中心对称图形.中心对称图形和轴对称图形都是具有某种性质的一个图形.而中心对称图形有一个对称中心,图形绕中心旋转180°,轴对称图形有一条对称轴,图形沿轴对折.三、学生学情诊断学生学过轴对称图形,旋转的概念及性质,这是本节课的知识基础,在此基础上得出中心对称和中心对称图形的概念不难,但是需认识到中心对称的旋转角度必须是180°,而且这使得对称点和对称中心三点共线.而中心对称图形渗透了旋转变换思想,学生学习静态图形已成习惯,对运动变化不适应,教学时,老师要充分利用具体图形,让学生获得感性认识,进而归纳出中心对称图形满足的条件.基于以上分析,本节课的教学难点是:中心对称性质的探索、中心对称图形和中心对称的区别与联系.四、教学策略分析自然界和日常生活中有很多具有中心对称性质的事物,为学生的学习奠定了感性认识;经过轴对称图形的探索,学生具备了观察、归纳的能力;旋转的学习也为学生积累了探索的经验.因此,本节课采用演示、观察法,借助多媒体辅助教学.引导学生类比分析,通过自主探究、合作交流的方式,获取知识,掌握方法.五、教学过程前面我们研究了旋转及其性质,现在研究一类特殊的旋转--中心对称及其性质.1.了解中心对称的概念问题1 (1)如左图,把其中一个图案绕点O旋转180°,你有什么发现?图1 图2 (2)如右图,线段AC,BD相交于点O,OA=OC,OB=OD,把△OCD绕点O旋转180°,你有什么发现?师生活动:教师展示两组图形,演示旋转过程,学生观察后回答问题(两个图形重合).设计意图:让学生通过观察图形,感知中心对称的特征,为得出中心对称的概念作铺垫.从旋转变化的角度让学生从几何图形中体会中心对称是特殊的旋转.问题2 你能说说上述两个旋转的共同点吗?师生活动:学生独立思考后进行交流,然后学生代表发言.教师根据学生回答情况进行评价,如果学生有困难,可以适时追问.教师追问1:图形中旋转中心是哪个点?教师追问2:旋转的角度是多少?教师追问3:两个图形的关系是什么?师生活动:师生共同归纳得出:把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心(简称中心).设计意图:进一步明确中心对称的共同点:(1)两个图形;(2)(选定)一个点;(3)旋转角是180°(4)两个图形重合.发现两个图形成中心对称图形的特征,进而概括出中心对称的概念.问题3 中心对称与旋转的联系和区别是什么?师生活动:学生思考并相互交流,发现其联系——中心对称和旋转都是绕着某一点进行旋转后两图形重合;区别--中心对称的旋转角都是180°,旋转的旋转角度不固定,中心对称是特殊的旋转.设计意图:进一步明确中心对称是特殊的旋转,为探索中心对称的性质作铺垫.问题4 对称中心和对称点事如何确定的?你还能指出图2中其他的对称点吗?师生活动:学生思考并回答.设计意图:明晰概念,让学生结合图1、图2理解定义中的“某一点”,明确对称中心和对称点的关系,为探索中心对称的性质作铺垫.2.探索中心对称的性质问题5 中心对称是特殊的旋转,它会有哪些性质?师生活动:教师引导学生动手操作,完成教科书64-65页的画图(图3):旋转三角尺,画关于O对称的两个三角形;利用画好的图形,分别连接对应点AA′,BB′,CC′.图3教师追问1:点O在线段AA′上吗?如果在,在什么位置?教师追问2:△ABC与△A′B′C′有什么关系?教师追问3:你能从以上过程中得到什么结论?师生活动:学生思考讨论并发表自己的看法.设计意图:让学生利用具体图形,获得感性认识,进而归纳出中心对称的性质.教师追问4:中心对称是特殊的旋转,你能从旋转的性质出发总结(演绎、类比)出中心对称的性质吗?师生活动:学生独立思考后进行交流,然后学生代表发言.教师根据学生回答情况进行评价,如果学生有困难,可以适时提出以下问题.教师追问5:中心对称的旋转角度是180°,这使得对称点和对称中心这三点有怎样的特殊位置关系?师生活动:师生共同归纳出中心对称的性质:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(2)关于中心对称的两个图形是全等图形.设计意图:通过中心对称性质的归纳总结让学生体会演绎和类比等方法在研究数学问题中的重要作用.清楚“三点共线”这一几何事实的表述方式.3.应用中心对称性质画图例(1)如下图4,选择点O为对称中心,画出点A关于点O的对称点A′;(2)如下图5,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.图4 图5 师生活动:学生依据中心对称的性质动手画图,学生代表在黑板上画图.待学生完成作图后,教师进一步追问.教师追问1:为什么这样作出的点A′就是点A关于点O的对称点?教师追问2:怎样画出△ABC关于点O对称的△A′B′C′?师生活动:学生思考并回答:要画一个多边形关于已知点的对称图形,只要画出这个多边形的各个顶点关于已知点的对称点,再顺次连接各点即可.设计意图:利用中心对称的性质画图,加强对中心对称性质的理解,为学习中心对称图形的学习作铺垫.4.了解中心对称图形的概念问题1:(1)图4我们已经画出点A关于点O的对称点A′,那么我们观察画出的图形整体有什么特点?(2)图5我们也观察画出的图形整体有什么特点?设计意图:让学生通过观察及动手操作,感知中心对称图形的特征,为得出中心对称图形的概念作铺垫.教师追问1:旋转的对象都是几个图形?教师追问2:图形都是绕着什么旋转?教师追问3:旋转的角度是多少?教师追问4:旋转后的图形与原图形有什么关系?师生活动:师生共同归纳出:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.(板书:中心对称图形的定义)设计意图:进一步明确中心对称图形的共同点:(1)一个图形;(2)绕着某一个点;(3)旋转角是180°;(4)与本身重合.发现中心对称图形的特征,从而概括出中心对称图形的概念.问题2:在我们学过的图形中,有哪些是中心对称图形?学生活动:以小组为单位,操作手中的学具,归纳出初中阶段常见的中心对称图形.设计意图:学生实际操作,让学生更深刻的理解中心对称图形的特征.中心对称图形的形状通常匀称美观,我们在自然界中可以看到许多美丽的中心对称图形,如雪花.在很多建筑物和工艺品中也常采用中心对称图形作装饰图案,如地毯.另外,由于具有中心对称图形形状的物体,能够在所在的平面内绕对称中心平稳地旋转,所以在各种机器中要旋转的零部件的形状常设计成中心对称图形,如水泵叶轮等.问题3:现实生活中你还见过哪些中心对称图形?师生活动:学生独立思考,给足够的时间小组交流归纳,看看哪个小组说出的图形最多.教师及时点评,课件展示生活中的一些中心对称图形及常见中心对称图形的几何图案.设计意图:加深了对中心对称图形这一概念的理解,培养了学生的识图能力和分析问题的能力,同时又让学生欣赏到了中心对称图形在生活中的应用和数学的美.5.小结反思(1)引导学生从数学知识和思想方法两个角度对本节课进行回顾小结.本节课应掌握:(1)中心对称的概念及性质、中心对称图形的概念.(2)根据性质作图.设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的两个核心知识点:中心对称图形的概念,中心对称图形和中心对称的区别与联系.(2)课堂检测.六、课堂检测题必做题1.(10分)在下列图形中,既是轴对称图形,又是中心对称图形的是( )A.等边三角形 B.等腰三角形 C.平行四边形 D.正方形2.(10分)下列图形中,是中心对称图形,但不一定是轴对称图形的是( )A.正方形B.矩形C.菱形 D.平行四边形3.(10分)下列汽车标志图案中属于中心对称图形的是()A B C D4.(10分)下列标志中,既是轴对称图形,又是中心对称图形的是()A B C D5.(10分)下列图形中,既是轴对称图形,又是中心对称图形的是()A B C D6.(20分)如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师解除蒙具后,看到张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过,则应该是( )A .方块4B .黑桃 5C .梅花6D .红桃77.(30分)在①线段,②角,③等腰三角形,④等腰梯形,⑤平行四边形,⑥矩形,⑦菱形,⑧正方形,⑨圆中,是轴对称图形的有_______________ ,是中心对称图形的有_______________ ,既是轴对称图形又是中心对称图形的有______________.选做题为班级设计一个成中心对称图形的班徽.。
10第十章-感觉功能评定PPT课件

.
26
(三)视觉模拟评分(VAS)
1.直线法:被评定者根据自己的实际感觉在直线上 标出疼痛的程度表。
2.数字评分法(NRS):以无痛的0的11个点来描 述疼痛强度,0表示无疼痛,10表示最剧烈的疼 痛。
3.注意事项
1)间歇评定。
2)周期性动态评分不宜过度频繁。(以免加重患者 焦虑)
(一)感觉评定的设备 1.大头钉若干个(一端尖、一端钝)。 2.两支测试管及试管架。 3.一些棉花、纸巾或软刷。 4.4~5件常见物:钥匙、钱币、铅笔、汤勺等。 5.感觉丧失测量器,或心电图测径器头、纸夹和 尺子。 6.一套形状、大小、重量相同的物件。 7.几块不同质地的布。 8.音叉(256Hz)、耳机或耳塞。
有限的急性发作。
.
22
三、常用的评定方法
(一)压力测痛法
1.压力测痛法 适用于肌肉骨骼系统疼痛。 2.评定方法 找准痛点将压力测痛器的探头对准痛点
逐渐施加压力并观察和听取评定者反应,记录被评 定者诱发疼痛第一次出现所需的压力强度和最高疼 痛耐受限度所需的压力强度。
3.注意事项 (1)合适体位以提高检查准确性。 (2)测痛器探头须平稳地放在待测部位。
.
28
( 五 ) 简 化 McGill 疼 痛 问 卷 ( SF-MPQ )
SF-MPQ疼痛问卷在临床应用上具有 简便、快速等特点适用于对疼痛特性进 行评定的评定者和存在疼痛心理问题者。
.
29
(六)疼痛日记评定法
1.适用范围:适用对疼痛发展过程的评定, 特别适于癌性疼痛的镇痛治疗应用。
2.评定记录:由评定者、评定者亲属或护士 记录。以日或小时为时间段记录与疼痛有 关的活动、使用药物名称及剂量、疼痛的 强度等。疼痛强度用0~10的数字量级来表 示。睡眠过程按无疼痛记分。
第10章平面图形的几何性质ppt课件

如:
1.静矩
n
Sx
yd A
ydA
A n
A1 An n
i 1
Ai
yd A
S xi Ai yCi A yC
i 1
i 1
n
n
S y S yi Ai xCi A xC
i 1
i 1
y
xC C yC
x O
2.形心
n
Ai xCi
Ix0
Ix
Iy 2
1 2
Ix Iy
2
4
I
2 xy
I y0
Ix
Iy 2
1 2
Ix
Iy
2
4
I
2 xy
极大值Imax 极小值Imin
例 计算所示图形的形心 主惯性矩.
120 40 z 20
25 20 10
解:该图形形心C的位置已
确定,如图所示.
过形心C选一对座标轴
C
y
y z 轴,计算其惯性矩(积).
1.5d (2d )3 3d 2(0.177d )2 [πd 4 πd 2 (0.5d 0.177d )2 ]
12
64 4
2d
0.685d 4
I zC I矩zC I圆zC
(1.5d )3 2d πd 4 0.513d 4
12
64
I yC zC 0
所以 yCzC 便是形心主轴
——反映平面图形的形状与尺寸的几何量
如:
在轴向拉(压)中:
FN A
l FNl EA
本章介绍:平面图形几何性质的定义、计算方法和性质
§10.1 静矩与形心
华师大版七年级数学下册第十章《图形的全等》优质课课件

探究性问题
4.判断下列说法是否正确,不正确的请改正. ①所有的等边三角形都全等. ②所有的正方形都全等.
对应角分别对应相等的两 个多边形不一定全等
反馈训练
找一找
1.观察下图,从中找出全等图形,与同学交流。
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
全等图形有①和⑨; ②和⑧; ③和⑥.
反馈训练
想一想
2.如图,四边形ABCD ≌四边形A′B′C′D′, ∠A=__7_0_°_,∠B=__8_5_°__,B′C′=__1_2___,AD=__6____, A′B′=__1_0___,CD=__8____,四边形A′B′C′D′的 周长为__3_6_____.
(1)
实验台
(2)
探究性问题
3.全等多边形除了对应边相等,对应角相等之外,还有什
么相等呢?如下图, 五边形ABCDE≌五边形
A´B´C´D´E´,请结合A图形加以说明.
A'
E
E'
B
B'
C
D
C'
D'
◆ S五边形ABCDE=S五边形A´B´C´D´E´; ◆ C五边形ABCDE=C五边形A´B´C´D´E´; ◆ ∠CAD=∠C´A´D´, ∠DAE=∠D´A´E´; ◆ AC=A´C´,AD=A´D´;……
◆知识与能力:知道全等图形、全等多边形、全等三角 形的概念和性质;能找出全等多边形、全等三角形的对 应元素,会利用图形的全等解决一些简单的问题. ◆过程与方法:培养学生动手操作能力;培养学生观察 、探索、分析与归纳能力. ◆情感、态度、价值观:在学生动手操作的过程中,激 发学生学习数学的积极性,培养学生主动探索,敢于实 践的科学精神,培养学生交流合作和创新意识.
第十章 第10课时 图形的位似

第10课时图形的位似预学目标1.通过课本中的“数学实验室”感受点光源的位置对投影的影响,尝试探索变化的原因.2.通过课本中的“实践”体会相似三角形性质的应用,初步了解如何将图形放大或缩小.3.结合“实践”,尝试“思考”,阅读位似形的相关概念,体会位似与相似的关系.知识梳理1.位似形的相关概念如果两个图形________,而且______________________相交于一点,那么这两个图形叫做位似形,这个交点叫做____________.说明:位似形一定是相似形,但相似形不一定是位似形.2.位似形的意义及画法(1)意义:利用位似形可以将一个图形________或________.(2)画法:以△ABC为例,将△ABC扩大n倍(或缩小1n),得到△A'B'C'.①确定位似中心O,连接OA、OB、OC;②延长(或反向延长)OA、OB、OC;③在延长线(或反向延长线)OA上取OA'=n·OA,在延长线(或反向延长线)OB 上取OB'=n·OB,在延长线(或反向延长线)OC上取OC'=n·OC;④顺次连接A'B'、B'C'、C'A',则△A'B'C'就是所画的图形.3.位似形的性质如图,若△A'B'C'与△ABC位似,相似比为k.(1)因为''OA OCOA OC=,∠A'OC'=∠AOC,所以△________∽△________.所以''''OA OC A COA OC AC===________,同理,'OBOB=________.归纳:在位似形中,各对应点到位似中心的距离之比等于________(注意:对应点重合除外).(2)因为''OA OCOA OC=,∠A'OC'=∠AOC,所以△________∽△________.所以∠________=∠________.所以A'C'____AC.同理,B'C'____BC,A'B'_____AB.归纳:在位似形中,各对应边____________(注意:对应边所在的直线重合除外).例题精讲例1 画一个三角形,使它与△ABC (如图①)相似,且原三角形与所画三角形的相似比为2:1.提示:本题中没有明确指出位似中心,故方法有多种,解答:方法一:如图②,任意取一点O ,连接OA 、OB 、OC ,并分别取OA 、OB 、OC 的中点A'、B'、C',连接A'B'、A'C'、B'C',则△A'B'C'即为所求.方法二:如图③,以点A 为位似中心,取AB 的中点D ,取AC 的中点E ,连接DE ,则△ADE 即为所求.方法三:如图④,以点C 为位似中心,延长BC 至点B',使CB'=12BC ,延长AC 至点C',使CC'=12AC ,连接B'C',则△C'B'C 即为所求. 点评:解决本题的方法还有很多,同学们不妨再想一想,试一试.例2 如图,正方形OEFG 和正方形ABCD 是位似形,点F 的坐标为(1,1),点C 的坐标为(4,2),则这两个正方形的位似中心的坐标为________.提示:首先要找出位似中心,连接DG 并延长,交x 轴于点H ,则易知点H 是位似中心.由点F 和点C 的坐标,正方形OEFG 的边长为1.正方形ABCD 的边长为2,且OA =2,易知OG 是△HAD 的中位线,则HA =OA =2,即点H 的坐标为(-2,0),故这两个正方形的位似中心是(-2,0).解答:(-2,0).点评:要求位似中心的坐标,首先要找出位似中心,位似中心找到了,再运用所学的知识来求.热身练习1.如图,五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形,且PA 1=23PA ,则11AB A B 为( ) A .23 B .32 C .35 D .532.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a ,b ),那么大“鱼”上对应“顶点”的坐标为 ( )A .(-a ,-2b )B .(-2a ,-b )C .(-2a ,-2b )D .(-2b ,-2a )3.如图,△EFH 和△MNK 是位似图形,那么它们的位似中心是点________ (填A 、B 、C 或D).4.如图,在正方形ABCD 和正方形OEFG 中,点A 和点F 的坐标分别为(3,2)、(-1,-1),则两个正方形的位似中心是________.5.如图,以点A 为位似中心,将五角星缩小为原来的12.6.如图,在矩形ABCD 中,以对角线AC 、BD 的交点O 为位似中心,解答以下问题:(1)按新图与已知图形的相似比为12和2作两个矩形A 1B 1C 1D 1和A 2B 2C 2D 2 (2)求△OA 1B 1和四边形A 1D 1D 2A 2的面积之比.参考答案1.B 2.C 3.B 4.(1,0) 5.略 6.(1)略 (2)1:15。
AutoCAD 2017基础教程第10章绘制三维图形

10-11所示。其命令执行过程如下:
命令: _helix
圈数 = 3.0000 扭曲=CCW
指定底面的中心点: 0,0,0∥指定中心位置
指定底面半径或 [直径(D)] <50.0000>: 80↙
指定顶面半径或 [直径(D)] <30.0000>: 60↙
指定螺旋高度或 [轴端点(A)/圈数(T)/圈高(H)/扭曲(W)] <80.0000>: 120↙
与XY平面的角度。例如,坐标“10<45<60”表示一个点,它与当前UCS原
点的距离为10个单位,在XY平面的投影与X轴的夹角为45°,该点与XY平面
的夹角为60°,如图10-2所示。
同样地,圆柱坐标的相对形式表明了某点与上个输入点的距离,二者
连线在XY平面上的投影与X轴的角度及二者连线与XY平面的角度。
10.4.2 绘制三维面与多边三维面
三维面是三维空间的表面,它没有厚度,也没有质量属性。 【执行方法】 (1)执行“绘图”→“建模”→“网格”→“三维面”菜单命令。 (2)在命令行中输入3DFACE并按Enter键。 【执行过程】 执行上述操作,根据命令行提示绘制三维面,如图10-15所示;利用绘制 三维面的命令绘制出多边三维面,如图10-16所示。
10.2.3使用“三维视图”菜单设置视点
使用“三维视图”菜单设置 视点,可以从多个方向来观察图 形。
【执行方法】: (1)执行“视图”→“三维视 图”菜单命令,在其子菜单中选 择不同的视点,如图10-5所示。 (2)在“视图”工具栏中设置 视点,如图10-6所示。
图10-5 “三维视图”子菜单
图10-6“视图”工具栏
图10-11 绘制圆锥弹簧
数值分析及其MATLAB实现》第四篇书稿图形第十章图形
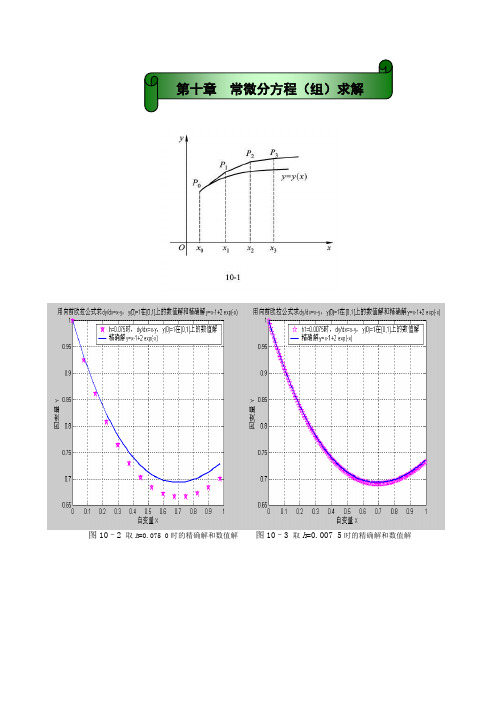
第十章常微分方程(组)求解图10–4 n =10,100时,1)0(,783=-+-=y x y dxdy 在[0,1]上的数值解和精确解图10–5a 40=n ,用向前欧拉公式和一、四阶泰勒逼近法及double 求初值问题的图图10–5b 40=n ,用向前欧拉公式和一、四阶泰勒逼近法及double 求初值问题的图图10–6 取80=n 时,用向前欧拉公式和一、四阶泰勒逼近法及double 求初值问题的图图10–7 取10010,=n 时,用向前欧拉公式求初值问题数值解和精确解的图形图10–8 取精度为110-时,用向前欧拉公式求初值问题和精确值的图形图10–10 取h=0.05时,用向后欧拉公式求初值问题的数值解和精确解的图形图10–11用梯形公式求解区间]2,0[上的初值问题1)0(,783=-+-=y x y dxdy图10–12 自适应梯形公式和向前欧拉公式求解初值问题1)0(,783=-+-=y x y dxdy图10–13用梯形和改进的欧拉公式求解1)0(,783=-+-=y x y dxdy的图形图10–14 用二阶龙格—库塔方法求初值问题图10–15 常用的三阶龙格-库塔公式求初值问题图10–16用常用的四阶龙格-库塔公式求初值问题图10–17 用二阶龙格-库塔方法计算d y/d x=2x/(3y2),y(0)=1的数值解图10–18a 精确解和用ode15s求数值解的图图10–18b 精确解和用ode45求数值解的图图10–19 用四阶龙格-库塔公式和四阶亚当斯显式公式求解常微分方程初值问题图10–20 用四阶龙格-库塔公式和四阶亚当斯隐式公式求解常微分方程初值问题图10–21 用改进的亚当斯方法求解常微分方程初值问题图10–22 米尔恩公式、改进的亚当斯方法及常用的四阶龙格-库塔公式求数值解图10–23 米尔恩方法、米尔恩公式、改进的亚当斯方法和龙格-库塔公式求解图10–24a 取21 h ,用汉明公式、米尔恩公式、改进的四阶亚当斯方法和常用的四阶龙格-库塔公式求初值问题图10–24b 取h =1/20时,用四种方法求初值问题图10–25 单环节的Adams预测-校正公式四阶Adams显式公式和四阶Adams隐式公式.图10–26图10–27例10.7.2用ode15s 计算 图10–28例10.7.3用RK 4z 计算图10–29微分方程07)21(5'4''=+--y y y y 的解图10–30方程组05'''=-xz y ,05'''=+xy z 的解图10–31方程组xy z cy z z y b y yz ax x 3),2(,'''--=--=+-=的解图10–33单摆运动初始角010)0(=θ,030的数值解和数值解图10–35 例10.8.1的数值解和精确解的图形图10–36 n =6 时数值解和精确解的图形 图10–37 n =36 时数值解和精确解的图形图10–38 0"=+y y 在 [0,4]上满足0)0(=y 和2)4(-=y 的数值解图10–39图10–40(注:本资料素材和资料部分来自网络,仅供参考。
华师大版七年级数学下册第十章《画轴对称图形》优课件

3.画轴对称图形
新课导入
1、提问:如果给出一个图形和一条直线, 那么如何画出这个图形关于这条直线的对称 图形呢?
2、请同学们尝试解决以下的问题。 如图实线所构成的图形为已知图形,虚线为对
称轴,请画出已知图形的轴对称图形.
(1)
(2)
3、画完之后,请同学们思考下面两个问题: (1)你可以通过什么方法来验证你画得是否正确. (折叠) (2)和其他同学比较一下,你的方法是最简单吗?
谢谢观赏
You made my day!
我们,还在路上……
在格点图中,大家会很容易画出已知图形的轴对称 图形,如果没有格点图,我们还能比较准确地画出 已知图形的轴对称图形吗?
新课推进
让我们先从简单的图开始吧!
如图,已知点A和直线l ,试画出点A关于直线
的对称点。
请一位同学说说他的画l 法。(其他同不补充)
A
l
作法:(1)从点A出发画直线l的垂 线,与l交于O点;
ቤተ መጻሕፍቲ ባይዱ
3.画轴对称图形的基础是画已知图形各点的 轴对称点。
4.用尺规法画已知图中各点关于直线l的对称 点,将对称点连结得到对称线段,对称线 段组成的的图形就是对称图形。
课后作业
1.教材P109习题10.1第6题; 2.完成练习册本课时的习题.
在寻求真理的长河中,唯有学习,不断 地学习,勤奋地学习,有创造性地学习, 才能越重山跨峻岭。 —— 华罗庚
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月14日星期一2022/2/142022/2/142022/2/14 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/142022/2/142022/2/142/14/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/142022/2/14February 14, 2022 •4、享受阅读快乐,提高生活质量。2022/2/142022/2/142022/2/142022/2/14
华师大版七年级数学下册第十章《图形的旋转8》优课件

例:如图,边长为4的正方形ABCD绕D点旋 转30°后能与四边形A’B’C’D’重合.
(1)旋转中心在哪一点?
(2)四边形A’B’C’D’ 是怎样的图形/面积是多少?
A
D
(3)求∠C’DC和∠CDA’的度数;
A'
(4)连结AA’,求∠DAA’的度数.
B
C
C'
B'
随堂练习:本图案可以看做是一个菱形通过
观察下列转动的现象
学习目标
▪ 通过本节课的学习,学会分析图形中的 旋转现象,确定旋转中心和旋转角,以 及旋转不改变图形的形状、大小等几何 性质。
讨论
▪ 1.这些运动在我们的生活中常见吗?它和平移运 动相比较有什么不同之处?
▪ 2.它们有什么共同的特征? ▪ 3.这些物体在转动的过程中,其形状、大小、位
点B的对应点是
点A的对应点是
E
AC的对应线段是 AB的对应线段是
A
D
∠AEB的对应角是
旋转角度是
B
C
旋转方向是
议一议
如图,四边形AOBC,它绕O点旋转得到四边形DOEF. 在这 个旋转过程中:
(1)旋转中心是什么? 旋转中心是O (2)经过旋转,点A、B分别移动到什么位置?点D和点E的位置 (3)旋转角是什么? ∠AOD和∠BOE都是旋转角 (4)AO与DO的长有什么关系? AO=DO
几次旋转得到的?每次旋转了多少度?
5次
600, 1200, 1800, 2400, 3000
也可以看做是二个相邻菱 形通过几次旋转得到的? 每次旋转了多少度?
2次 1200 , 2400
还可以看做是几个菱形通 过几次旋转得到的?每次 旋转了多少度?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向Y轴正向走50的点。
Line(150,250) - Step(150,50) 等同于:Line(150,250) - (300,300)
例4:画一个左上角在(20,40),右下角在(150,200)
的矩形,注意在color 参数省略时,逗号并不省 略。 Line (20,40) - (150,200) , , B
线条控件的主要属性:
BorderStyle属性:设置线条的类型。
BorderWidth属性:设置线条的宽度,
即线条的粗细。
BorderColor属性设置线条的颜色。
BorderStyle属性的设置值 0 1 2 3 4 5 6 — — — — — — — 透明线 实心线 虚线 点线 点划线 点点相间的长划线 内部实线
例5:用红色从(20,40)到(70,110)画一个实心的矩
形。 Line(20,40)- Step(50,70), RGB(255,0,0), BF
例:使用Line方法,画出一个三角形和一个矩形。 Private Sub Form_Click() Form1.Scale(0,0)-(9,9) ' 定义新的坐标系 Form1.ForeColor=QBColor(1) '窗体的前景色为蓝色 Line(0, 6)-Step(4, 0) '画直线 Line -Step(-2, -4) '以第一条直线的终点为起点再画一直线 Line -Step(-2,4) '以第二条直线的终点为起点再画一直线 Line(5,2)-(8,6), , BF ‘画矩形并填充 end sub
Circle方法的使用:
Form1.Circle (-0.2, 0), 0.5, vbRed Circle (-0.2, 0), 0.5, vbBlue, , , 0.5
Circle (-0.2, 0), 0.5, , 0.5, 2.6
Circle (-0.2, 0), 0.5, vbGreen, -0.5, 2.6 Circle (-0.2, 0), 0.5, vbMagenta, -2.5, 0.6
RGB(red, green, blue)
说明: red, green, blue3种颜色,从0~255之间 的一个亮度值(0表示亮度最低,而255表示 亮度最高)。 例:Form1.BackColor = RGB(255, 0, 0)
'设定背景红色
二、使用QBColor函数
QBColor函数可返回一个Long值,用来表 示所对应颜色值的RGB颜色码。其使用格式 如下:
2. 使用Scale属性建立自己的坐标系 第一:重新定义坐标原点
属性ScaleTop,ScaleLeft的值用于控制对象左上角 坐标,所有对象的ScaleTop,ScaleLeft属性的缺省值为 0,坐标原点在对象的左上角。
= N,表示将X轴向Y轴的负方向平移N个单位
ScaleTop
= -N,表示X轴向Y轴的正方向平移N个单位
QBColor(color)
说明: color参数是一个界于0~15的整型数, 分别代表16种颜色。0-黑,1-蓝,2-绿, 3-青,4-红,等等。
三、使用系统定义的颜色常数
在VB系统中已经预先定义了常用颜色的 颜 色 常 数 , 如 常 数 vbRed 就 代 表 红 色 , vbGreen代表绿色等等。可在“对象浏览 器”中查询常数列表。 例如,要将窗体的背景色设为红色。则可使用 如下语句: Form1.BackColor = vbRed
返回
使用绘图方法绘图
当前坐标:CurrentX,CurrentY属性给出窗
体或图片框在绘图时的当前坐标。 在调用与绘图有关的方法时,currentx与 currenty的值会自动改变。 变化情况如下: Pset方法:当前坐标用来指向画出的点。 Line方法:当前坐标指向画出线的终点。 Circle方法:当前坐标指向画出圆形的中心。 Cls:当前坐标指向坐标原点。
Line直线控件
使用线条控件的操作步骤: (1)单击工具箱中的Line图标; (2)移动鼠标到要画线的起始位置: (3)按下鼠标左键并拖曳鼠标到要画线的结 束处,放开鼠标左键。 (4)打开属性窗口,设置线条属性,如线条 风格、线条颜色等。 (5)需要对设置好的线条进行调整时,可再 单击该线条,通过鼠标的拖动来改变线条的 大小或位置,或通过属性窗口来改变属性值。
(x2,y2)
可在程序中使用Scale方法改变坐标系统。当Scale方法不 带参数时,取消用户定义的坐标系,采用缺省坐标系。
使用控件绘图 ( Shape和Line控件 )
Shape控件可以用来画矩形、正方形、
椭圆、圆、圆角矩形及圆角正方形。
Line控件用于在窗体、图片框和框架
中画各种直线段
Shape形状控件
Circle方法
Circle方法用于画圆、椭圆、圆弧和扇形。
格式如下: [对象].Circle [Step] (x,y) ,<半径>[,[颜色][, [起始角][,[终止角][,[<纵横比>]]]]] 半径:要绘制的圆形,圆弧或扇形的圆心半径,若绘制的 为椭圆,则为长半轴的长度 颜色:所绘制图形的边框颜色,缺省时为当前容器的前 景色 起始角:所绘制圆弧或扇形的起始角度,弧度为单位 终止角:要绘制圆弧或扇形的终止角度,弧度为单位 纵横比:要绘制的椭圆形长半轴和短半轴的比值,>1时 为椭圆,<1,为椭圆,=1 为圆
在Visual Basic系统中,所有的颜色属性都 由一个Long整数表示。 在代码中可使用4种方式给颜色赋值: 使用RGB函数。
使用QBColor函数。
使用系统提供的颜色常量。 直接使用Long型颜色值。
一、使用RGB函数
RGB函数可返回一个Long整数,用来表示一 个RGB颜色值。其使用格式如下:
4
5
圆角矩形
圆角正方形
Vbshaperoundrectangle
vbshaperoundedsquare
形状控件的FillStyle属性
FillStyle 属性值 0 1 2 3 4 5 6 7 描述 实心 透明 水平线 垂直线 左上对角线 右下对角线 交叉线 对角交叉线 对应的符号常量 Vbfssolid Vbfstransparent Vbhorizontalline Vbverticalline Vbupwarddiagonal Vbdownwarddiagonal Vbcross vbdiagonalcross
X ( 0, 0 )
Y
用户自定义坐标系统
1.用户可用ScaleMode属性设置坐标系统的刻度 单位。ScaleMode属性的取值及含义见表。
说明:
1.当设置容器对象的ScaleMode属性值>0, 将使容器对象的ScaleLeft 和 ScaleTop 自 动 设 置 为 0 , ScaleHeight 和 ScaleWidth 的度量单位也将发生改变。 2.用ScaleMode属性只能改变刻度单位,不 能改变坐标原点及坐标轴的方向。
FillStyle属性:设置图形填充样式,
可以构成不同的填充效果。
Fillcolor:设置图形填充色
Bordercolor:设置图形边框色 Borderwidth:设置图形边框宽度
形状控件的Shape属性
Shape属性值 0 1 2 3 描述 矩形 正方形 椭圆 圆 对应的符号常量 vbshaperectangle Vbshapesquare vbshapeoval vbshapecircle
例:颜色的渐变过程。
Private Sub Form_Click() Dim j As Integer Dim x As Single Dim y As Single y = Form1.ScaleHeight x = Form1.ScaleWidth sp = 255 / y For j = 0 To y Line(0,j)-(x,j),RGB(j*sp,j*sp,j*sp) Next j End Sub
例:随机产生多条彩色射线。
Private Sub Form_Click() Dim i%, x%, y% Form1.Scale (-100, 100)-(100, -100) For i = 1 To 100 x = 100 * Rnd If Rnd < 0.5 Then x = -x y = 100 * Rnd If Rnd < 0.5 Then y = -y Line (0, 0)-(x, y), QBColor(15 * Rnd) Next i 思考:如果没有两条 if语句, End Sub 产生的射线在什么范围?
注意:各参数可根据实际要求进行取舍,但如 果舍去的是 中间参数,参数的位置分隔符不 能舍去。
例1:画一条从(250,300)到(400,500)点的直线。
Line (250,300)-(400,500) 例2:从当前位置画到(400,500)点的直线。 Line - (400,500) 例3:出发点是(150,250),终点是向X轴正向走150,
第五章
坐标系统
图形设计
使用控件绘图(Line控件和Shape控件) 使 用 绘 图 方 法 绘 图 ( Pset 、 Line 、 Circle方法) AutoRedraw属性和Paint事件
坐标系统
默认的坐标系统
每个容器都有一个坐标系,构成一个坐标系, 需要三个要素:坐标原点、坐标度量单位、X轴和 Y轴的方向。坐标度量单位由容器对象的 ScaleMode属性决定。缺省时为Twip。
Pset方法:
[对象].Pset 其中: [Step] (X,Y) [<颜色>]
在指定位置用指定颜色画点。其语法格式如下:
Step:可选参数,使用此参数表明所画的点位于 相对当前坐标点的(X,Y)处;缺省时,(X,Y) 为点相对于当前坐标系的的位置坐标; Co1or:参数可选,用于设置点的颜色。
