二次函数双图像问题
二次函数y=ax2的图像和性质

教案教学内容二次函数y=ax²的图象和性质一、学习目标:1.会用描点法画出二次函数y=ax2的图象;2.根据对特殊函数图象的观察,归纳得出二次函数y=ax2的性质;3.进一步理解二次函数和抛物线的有关知识,并能解决一些简单的应用问题;4.领悟数形结合的数学思想方法,培养观察能力、分析能力和归纳能力.二、知识回顾:1.画函数图象的一般步骤:(1)列表;(2)描点;(3)连线.2.什么是一次函数?怎么画一次函数y=-x+2的图象?形如y=kx+b(k≠0)的函数叫做一次函数.(1)列表:(2)描点;(3)连线.3.什么叫二次函数?一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数,其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.想一想:怎么画二次函数的图象?二次函数有哪些性质?三、知识梳理:1.二次函数y=ax2的图象的画法画二次函数y=ax2的图象,一般用描点法,具体步骤如下:(1)列表:以坐标原点(0,0)为中心,在其左右两边均匀地选取一些便于计算的x值,并计算出对应的y的值,列出表格;(2)描点:把每对x与y的值分别作为点的横坐标和纵坐标,在平面直角坐标系内描出相应的点;(3)连线:按自变量的取值由小到大(或由大到小)的顺序,用平滑的曲线连接各点,即可得到二次函数的大致图像。
【例1】在同一平面直角坐标系中,画出函数y= -2x2,y=x2,y=2x2的图象。
2.二次函数y=ax²的图象和性质:二次函数y=ax²的图象是一条关于y轴对称的抛物线.其图象与性质如下图所示:a的符号a>0 a<0 图象开口方向开口向上开口向下a 的绝对值越大,开口越小顶点坐标(0,0)顶点是最低点顶点是最高点对称轴y轴增减性x>0时,y随x的增大而增大;x<0时,y随x的增大而减小x>0时,y随x的增大而减小;x<0时,y随x的增大而增大最值x =0时,y有最小值0 x =0时,y有最大值0【例2】函数y=(k+1)x2(k+1≠0)的图象的顶点是,对称轴是,当k 时,图象的开口向上,这时函数有最值;当k ,时,图象的开口向下,这时函数有最值。
二次函数的图像和性质(共82张PPT)

y=ax2
向上
y轴 (0,0)
向下
y轴 (0,0)
4、二次函数y=2x2+1的图象与二次函数y=
2x2的图象开口方向、对称轴和顶点坐标是否相
同?它们有什么关系?我们应该采取什么方法
来研究这个问题?
画出函数y=2x2和函数y= 2x2+1的图象, 并加以比较
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y 1 x2 ··· 2
8
4.5
2 0.5 0 0.5 2 4.5
8
···
x
·· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
y 2x2 · 8 4.5 2 0.5 0 0.5 2 4.5 8
·· ·
y y x2 8
y 2x2
···
6
y 1 x2
4
2
2
-4
-2 O
24
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),
再沿对称轴整体上(下)平移|
|个单位 (当
>0时向上平移;当 <0时,向下平移)得到的.
y 1 x2
y1
1 3
x2
2
3
y2
1 3
x2
2
的图像
在同一直角坐标系中
画出函数 y 1 x2 5 y
y1
1 3
x2
2
3
y2
的图像
二次函数y=ax2+bx+c的图像与性质

◆本节课内容一、二次函数y=ax2+bx+c1、二次函数y=ax2+bx+c可以用配方法转化为y=a(x-h)2+k的形式:2、二次函数y=ax2+bx+c的图像的作法:二次函数y=ax2+bx+c的图像是一条对称轴平行于y轴的抛物线。
它的图像常见作法有两种:五点法和平移法。
方法一:五点法先用配方法将y=ax2+bx+c(a≠0)化为y=a(x-h)2+k(a≠0)的形式,确定抛物线的顶点、开口方向、再以顶点为中心,在对称轴的两侧对称地各取两对值进行列表,最后描点画图。
方法二:平移法利用平移法作二次函数y=ax2+bx+c的图像的一般步骤如下:(1)利用配方法将二次函数y=ax2+bx+c化为y=a(x-h)2+k的形式,确定其顶点为(h,k);(2)作出二次函数y=ax2的图像;(3)将函数y=ax2的图像平移,使其顶点(0,0)平移到(h,k),平移后的图像即是二次函数y=ax2+bx+c的图像。
3、二次函数y=ax2+bx+c的图像及性质如下表:二、二次函数y=ax2+bx+c(a≠0)的图像特征与系数a,b,c的符号关系注意:(1)b的符号由a的符号和对称轴的位置来决定(2)a+b+c(或a-b+c)可以看成是x=1(或x=-1)时的函数值。
三、二次函数解析式的求法求二次函数的解析式y=ax2+bx+c,需求出a,b,c的值。
由已知条件(如二次函数图像上三点的坐标)列出关于a,b,c的方程组,求出a,b,c的值,就可以写出二次函数的解析式。
◆课堂练习题型一利用公式法直接求抛物线的顶点、对称轴及最值1、求二次函数y=(x+5)(x-1)的对称轴、顶点及最值。
题型二、由抛物线的顶点、对称轴及最值求字母或代数式的取值范围2、二次函数y=ax2+bx+1(a≠0)的图像的顶点在第一象限,且过点(-1,0)。
设t=a+b+1,则t 的取值范围是()A、0<t<1B、0<t<2C、1<t<2D、-1<t<1题型三、二次函数图像平移规律的直接应用3、抛物线y=-2x2-4x-5经过平移得到抛物线y=-2x2,平移的方法是()A、向左平移1个单位,再向下平移3个单位B、向左平移1个单位,再向上平移3个单位C、向右平移1个单位,再向下平移3个单位D、向右平移1个单位,再向上平移3个单位题型四、根据抛物线的平移求字母的值4、已知抛物线y=x2+4x+1向上平移m(m>0)个单位得到的新抛物线过点(1,8),求m的值1题型五、利用二次函数y=ax2+bx+c的图像判断各项系数的符号5、二次函数y=ax2+bx+c的图像如图,那么abc,2a+b,a+b+c这3个代数式中,值为正数的有( c )A、3个B、2个C、1个D、0个题型六、利用二次函数的性质比较函数值得大小6、若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图像上的三点,则y1,y 2,y3的大小关系是()题型七、利用二次函数的增减性求字母的取值范围7、已知二次函数y=x2-(m+1)x+1,当x≥1时,y随x的增大而增大,求m的取值范围。
二次函数图像中的几何问题

以抛物线上的三个点为顶点的三角形称为抛物线的内接三角形。已知内接三角形的三个顶点的坐标可以求出抛物线的表达式。
例2、已知抛物线与x轴交于点A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3),抛物线顶点为D,联结AD、AC、CD。
(1)求该抛物线的表达式;
(2)△ACD与△COB是否相似?如果相似,请给予证明;如果不相似,请说明理由。
(1)求A、B两点的坐标;(用m的代数式表示)
(2)如果平行四边行ABCD的顶点D在上述二次函数的图像上,求m的值。
四、综合问题
函数图像中的几何问题已成为历年中考的热门考题,而二次函数的图像与几何图形的结合更是考查的重点,因此,熟悉这类问题的解题思路是必须具备的能力。
下面的例题是抛物线与平行四边、相似三角形的综合。
为。
7、抛物线的顶点为M(2,3),且经过点A(0,-1),若该抛物线上另有点B(m,-1),则m的值为。
8、若抛物线 与x轴交于点A、B,与y轴交于点C,且△ABC是等腰直角三角形,则a、c之间的数量关系是。
9、若抛物线的顶点A在x轴上,且抛物线经过B(0,2),△AOB为等腰三角形,则该抛物线的表达式
(3)若直线AB交y轴于点E,在直线AB上找点F,使△CEF∽△AOM,求点F的坐标。
小结:本题涉及的几何图形是:内接于抛物线与直线之间的平行四边形和相似三角形。解题的关键是:(1)函数 图像上的点的坐标可以表示为P(x,f(x)),即用解析式来代替纵坐标;(2)用垂直于x轴的直线去截函数 和 图像,则截得的线段长PQ=∣f(x)-g(x)∣(其中x为点P或点Q的横坐标)。
精练12+1:
1、若抛物线 与x轴相交于点A、B,顶点为P,则△PAB是()
培思数学-------“二次函数图像形状相同” 问题

培思数学-------“二次函数图像形状相同” 问题
1、如果把一个二次函数的图像向上平移a 49个单位(a>0),再向左平移2
5个单位,就得到第二个二次函数2y ax =的图像。
(1)、写出第二个二次函数定点的坐标(可用a 表示);
(2)若第一个二次函数图像经过A(x 1, 0), B(x 2, 0), C (0, y 3)三点,其中x 1<x 2, 且y 3是x 1与x 2的比例中项,求函数解析式。
2,将抛物线 542y 2+-=x x 作下列移动后,求得到新的抛物线方程。
(1)向左平移2个单位,再向下平移3个单位;
(2)顶点不动,将原抛物线开口反向;
(3)以x 轴为对称轴,将原抛物线开口反向。
2、已知抛物线 c bx x a ++=2y 的形状与抛物线 32
1y 2+=x 相同,它的对称轴是x=-2, 它与x 轴两个交点距离为2,求:(1)图像与x 轴两交点坐标; (2)确定二次函数的解析式。
初中数学课件 2二次函数y=ax2的图象

当x ≠ 0时,y<0.
活动三、应用迁移
例1.
(1)若抛物线y=(2-m)xm2-3有最低点,则m=---------------
(2)点A(-3,y1),B(-2,y2),C(-1,y3)在抛物线
y=ax (a<0)上,则y ,y ,y 的大小关系是 2
x>0时,y随x增大而增大 x>0时,y随x增大而减小
做一做
(1)抛物线y=5x 的顶点坐标是(0,0) ,开口 向上 2 -------------------------对称轴是 y轴 ,在对称轴 右 侧,y随着x的增大而增 大;在对称轴左 侧,y随着x的增大而减小,当x= 0 时,函数y的值最小,最小值是 0 ,抛物线y=5x2在x轴 的_上___方(除顶点外). (2)抛物线 y 2 x2 当x<0时,y随着x的 增大而增大 ; 3 当x >0 ,y随着x的增大而减小; ------------------
作业:金榜行动 P4第1-10题,选做P5第6、8题
活动三、应用迁移
例3.已知正方形周长为Ccm,面积为Scm2; (1)求S和C之间的函数关系式,并画出图像; (2)根据图像,求出S=1cm2时,正方形的周长; (3)根据图像,求出C取何值时,S≥4cm2 .
结束寄语
下课了!
只有不断的思考,才会 有新的发现;只有量的 变化,才会有质的进步.
∴x的值可取负数、零、正数
(2)为了计算和描点方便,x取整数.且以1为 间距取值,取有代表性的7对值
画函数y=x2的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
二次函数图像问题
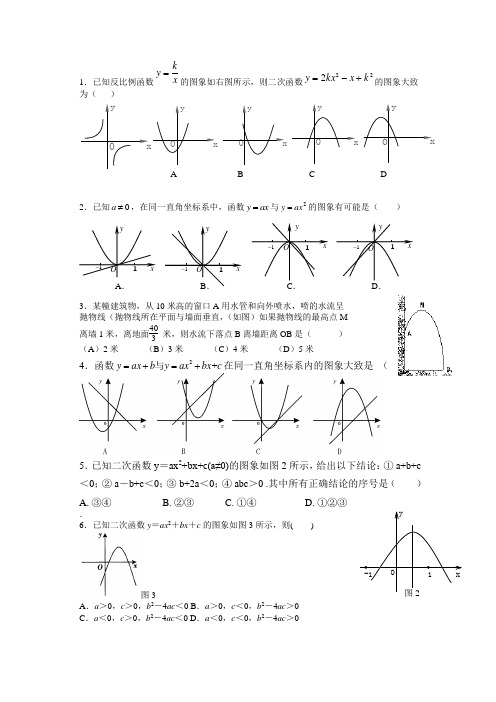
1.已知反比例函数x k
y =
的图象如右图所示,则二次函数2
2
2k x kx y +-=的图象大致为( )
2.已知0≠a ,在同一直角坐标系中,函数ax y =与2ax y =的图象有可能是( )
3.某幢建筑物,从10米高的窗口A 用水管和向外喷水,喷的水流呈 抛物线(抛物线所在平面与墙面垂直,
(如图)如果抛物线的最高点M
离墙1米,离地面40
3
米,则水流下落点B 离墙距离OB 是(
)
(A )2米 (B
)3米 (C )4米
(D )5米
4.函数2
+y ax b y ax bx c =
+=+与在同一直角坐标系内的图象大致是 (
)
5
.已知二次函数y =ax 2+bx+c(a≠0)的图象如图2所示,给出以下结论:① a+b+c
<0;② a -b+c <0;③ b+2a <0;④ abc >0 .其中所有正确结论的序号是( )
A. ③④
B. ②③
C. ①④
D. ①②③
.
6.已知二次函数y =ax 2
+bx +c 的图象如图3所示,则(
)
图3
A .a >0,c >0,b 2-4ac <0
B .a >0,c <0,b 2-4ac >0
C .a <0,c >0,b 2-4ac <0
D .a <0,c <0,b 2
-4ac >0
A . A
B
C D。
图像法解二次函数问题例析
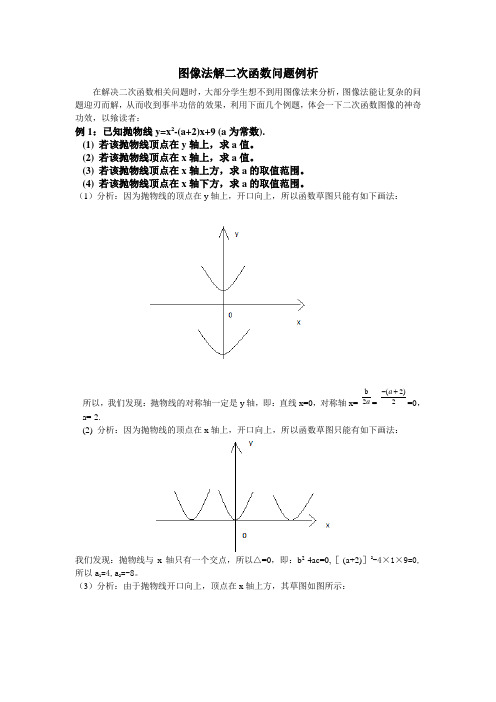
图像法解二次函数问题例析在解决二次函数相关问题时,大部分学生想不到用图像法来分析,图像法能让复杂的问题迎刃而解,从而收到事半功倍的效果,利用下面几个例题,体会一下二次函数图像的神奇功效,以飨读者:例1:已知抛物线y=x2-(a+2)x+9 (a为常数).(1)若该抛物线顶点在y轴上,求a值。
(2)若该抛物线顶点在x轴上,求a值。
(3)若该抛物线顶点在x轴上方,求a的取值范围。
(4)若该抛物线顶点在x轴下方,求a的取值范围。
(1)分析:因为抛物线的顶点在y轴上,开口向上,所以函数草图只能有如下画法:所以,我们发现:抛物线的对称轴一定是y轴,即:直线x=0,对称轴x=-b2a=-(2)2a-+=0,a=-2.(2) 分析:因为抛物线的顶点在x轴上,开口向上,所以函数草图只能有如下画法:我们发现:抛物线与x轴只有一个交点,所以△=0,即:b2-4ac=0,[-(a+2)]2-4×1×9=0,所以a1=4,a2=-8。
(3)分析:由于抛物线开口向上,顶点在x轴上方,其草图如图所示:于是有:抛物线与x轴没有交点,△<0,△=b2-4ac=〔-(a+2)〕2-4×1×9<0,∴a的取值范围是-8<a<4.(4) 分析:由于抛物线开口向上,顶点在x轴下方,其草图如图所示:于是有:抛物线与x轴有两个交点,△>0,△=b2-4ac=〔-(a+2)〕2-4×1×9>0,∴a的取值范围是a<-8或a>4.例2:某二次函数图像经过点A(2,a)和点B(-4,a),则这个二次函数图像对称轴是直线。
分析:抛物线草图如图所示:因为:抛物线是轴对称图形,观察图像得:对称轴是直线x=422-+=-1,即x= -1.例3:已知抛物线y=x2-2x+c经过点A(-1,y1)和点B(2,y2),比较y1与y2的大小。
分析:根据解析式可得:对称轴为直线x=1,且开口向上,抛物线草图如图所示:观察图像得:y1 >y2.例4:若二次函数y=ax2+bx+c (a≠0)图像如图所示,当x=2时,y的值是。
中考压轴——二次函数图像中的动点、极值与存在问题

中考压轴——⼆次函数图像中的动点、极值与存在问题n两点,移,直到点O与点E(P)重合时停⽌,设运动的时间为t,平移后的△O1C1P1与△CEM的重叠部分的⾯积为S,求S与t之间的函数表达式.5.如图,抛物线C1:y=ax2+2ax+4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M为此抛物线的顶点,若△ABC的⾯积为12.(1)求此抛物线的函数解析式;(2)动直线l从与直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时终⽌运动,直线l与BC交于点D,P是线段AD 的中点.①直接写出点P所经过的路线长为;②点D与B、C不重合时,过点D作DE⊥AC于点E,作DF⊥AB于点F,连接PE、PF、EF,在旋转过程中,求EF的最⼩值;(3)将抛物线C1平移得到抛物线C2,已知抛物线C2的顶点为N,与直线AC交于E、F两点,若EF=AC,求直线MN的解析式.6.在平⾯直⾓坐标系xOy中,已知抛物线y=-49(x-2)2+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=255.(1)求此抛物线的函数表达式;(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂⾜分别为E,F,若HEHF =12时,求点P的坐标;(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的⼀动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由.7.已知,抛物线y=ax2+bx+4(a≠0)与x轴交于A(-2,0)、B(8,0)两点,与y轴交于点C.(1)求此抛物线的解析式;(2)如图1,点E是线段OB上⼀动点,过点E作DE⊥x轴,交抛物线于点D,若直线CD与以OE为直径的⊙M相切,试求出点E的坐标;(3)如图2,在抛物线上是否存在⼀点P,过点P作x轴的垂线,垂⾜为F,过点F作FG∥BC,交线段AC于点G,连接FC,使△BCF∽△CFG?若存在,求出点P的坐标;若不存在,请说明理由.8.已知:抛物线y=-(x+1)(x-k)(k>0)与x轴交于点A、B(点A在B的左侧),与y轴交于点C,点D是抛物线上位于第⼀象限上⼀动点,过D作DE⊥x轴于点E.(1)如图⼀,当OC=4时,求此抛物线解析式;(2)如图⼆,过点A作直线l⊥x轴,点F为x轴下⽅直线l上⼀点,连接EF、BD,当∠BDE=∠FEO时,求点F 的坐标.(3)如图三,在(1)的条件下,DE与BC交于点H,过D作DK⊥CH于点K,若点P为x轴上⽅抛物线上⼀动点,连接PC、PE,当DK=12CH,且∠PCO+∠PED=90°时,求点P的坐标.9.如图,在平⾯直⾓坐标系中,点O为坐标原点,直线y=-x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=-x+4交于另⼀点B,且点B的横坐标为1.(1)求抛物线的解析式;(2)点P是线段AB上⼀个动点(点P不与点A、B重合),过点P作PM∥OB交第⼀象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,①求MN与t之间的函数关系式(不要求写出⾃变量t的取值范围);②当MN取最⼤值时,连接ON,直接写出sin∠BON的值.10.如图,经过点A(0,-4)的抛物线y=12x2+bx+c与x轴相交于B(-2,0),C两点,O为坐标原点.(1)求抛物线的解析式;(2)将抛物线y=12x2+bx+c向上平移72个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,直接写出m的取值范围;(3)点P为x轴下⽅的抛物线上的⼀个动点,连接PA、PC,若所得△PAC的⾯积为S,求出当S取何值时,相应的点P有且只有2个?(4)设点M在x轴上,∠OMA+∠OAB=∠ACB,求BM的长.11.如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B、C三点的坐标;(2)在抛物线的对称轴上找到点P,使得△PBC的周长最⼩,并求出点P的坐标;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G为顶点四边形是平⾏四边形?如果存在,求出所有满⾜条件的F点坐标;如果不存在,请说明理由.12.如图,抛物线y=33x2+233x-3交x轴于点A、B,交y轴于点C.(1)求该抛物线的对称轴及△ABC的⾯积.(2)如图1,已知点Q(0,3),点P是直线AC下⽅抛物线上的⼀动点,连接PQ交直线AC于点K,连接BQ、BK,当点P使得△BQK周长最⼩时,请求出△BQK周长的最⼩值和此时点P的横坐标.(3)如图2,线段AC⽔平向右平移得线段FE(点A的对应点是F,点C的对应点是E),将△ACF沿CF翻折得△CFA′,连接A′E,是否存在点F,使得△CEA′是直⾓三⾓形?若存在,请求出点F的坐标;若不存在,请说明理由.13.如图,抛物线y=-12x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).(1)求抛物线的解析式和顶点坐标;(2)求直线BC的解析式;(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三⾓形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(4)点E时线段BC上的⼀个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的⾯积最⼤?求出△CBF的最⼤⾯积及此时E点的坐标.14.如图,在平⾯直⾓坐标系中,以A(3,0)为圆⼼,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D.(1)若抛物线y=ax2+bx+c经过B、C、D三点,求此抛物线的解析式,并写出抛物线与圆A的另⼀个交点E的坐标;(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正⽅向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,当t为何值时,MN?OP的值最⼤,并求出最⼤值;MN+OP(3)在(2)的条件下,若以P、C、M为顶点的三⾓形与△OCD相似,求实数t的值.15.如图,已知直线l:y=1x+2与y轴交于点D,过直线l上⼀点E作EC丄y轴于点C,且C点坐标为(0,4),过2x2+bx+c交x轴于A、B两点(点A在点B的左侧).C、E两点的抛物线y=-13(1)求抛物线的解析式:(2)动点Q从点C出发沿线段CE以1单位/秒的速度向终点E运动,过点Q作QF⊥ED于点F,交BD于点H,设点Q运动时间为t 秒,△DFH的⾯积为S,求出S与t的函数关系式(并直接写出⾃变量t的取值范围);(3)若动点P为直线CE上⽅抛物线上⼀点,连接PE,过点E作EM⊥PE交线段BD于点M,当△PEM是等腰直⾓三⾓形时,求四边形PMBE的⾯积.16.如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.(1)求抛物线的解析式和直线BC的解析式;(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直⾓三⾓形时,求m的值;(3)当以C、O、M、N为顶点的四边形是以OC为⼀边的平⾏四边形时,求m的值.17.如图所⽰,动点A、B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正⽅向运动,动点B沿y轴正⽅向运动,以OA、OB为邻边建⽴正⽅形OACB,抛物线y=-x2+bx+c经过B、C两点,假设A、B两点运动的时间为t秒:(1)直接写出直线OC的解析式;(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在⼀点D,使得S△BCD=6?若存在,求出点D 的坐标;若不存在,说明理由;(3)在(2)的条件下,有⼀条平⾏于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F 四个点构成的四边形是平⾏四边形,求点F的坐标;(4)在动点A、B运动的过程中,若正⽅形OACB内部有⼀个点P,且满⾜OP=2,CP=2,∠OPA=135°,直接写出此时AP的长度.18.如图,抛物线y=1x2+bx+c与y轴交于点C(0,-4),与x轴交于点A、B,且B点的坐标为(2,0).2(1)求抛物线的解析式;(2)若点P是AB上的⼀个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE⾯积的最⼤值;(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上⼀点,当△OMD为等腰三⾓形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,求点N的坐标,并判断点N是否在抛物线上.19.如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)(1)求这条抛物线所对应的函数关系式;(2)设点P在该抛物线上滑动,若使△PAB的⾯积为1,这样的点P有⼏个?并求出满⾜P点的坐标;(3)设抛物线交y轴于点C,在该抛物线对称轴上是否存在点M,使得△MAC的周长最⼩?若存在,求出点M的坐标;若不存在,请说明理由.20.抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)与y轴交于点C,抛物线的对称轴交x轴于点D,P是直线BC上⼀动点.(1)求抛物线的解析式;(2)过点P作y轴的平⾏线交直线BC下⽅的抛物线于点E,当PE达到最长时,求点P的坐标;(3)点Q是抛物线对称轴上⼀动点,当△PAQ是以PQ为斜边的等腰直⾓三⾓形时,求点P的坐标.21.如图,在平⾯直⾓坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂⾜为x2+bx+c过点O、A两点.A,OA=5,抛物线y=16(1)抛物线的解析式为;(2)点C是抛物线上的⼀点,且BC=10,连接AC交OB于点D,以BC为直径的⊙O1经过点D,连接DC,求证:OC是的⊙O1切线;(3)设点P是OB上的⼀个动点,是否存在⼀点P,使△PCD与△ABD相似,若存在,请求出点P的坐标;若不存在,请说明理由.22.如图,在平⾯直⾓坐标系xOy中,O为坐标系原点,AD为等腰三⾓形AOC底边OC上的⾼,直线OA的解析式为y=x,抛物线y=a(x-4)2+k的顶点为A,且经过坐标原点.(1)求此抛物线的解析式;(2)有⼀动点P从点O出发,沿射线OA⽅向以每秒2个单位长度的速度运动,连接PD,设△APD的⾯积为S,点P的运动时间为t秒,求S与t的解析式,并直接写出⾃变量t的取值范围;(3)在(2)的情况下,过点D作PD的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,问当t为何值时,CE的长为2,并求出此时点F的坐标.23.如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),点C为抛物线上⼀点,且点C的横坐标为2,抛物线的对称轴EF交x轴于点E,交直线AC于点F.(1)求点A、B 的坐标和直线AC的解析式;(2)若G是y轴上⼀个动点,当∠AGC=90°时,求点G的坐标;(3)在直线EF上是否存在点P,使⊙P与直线AC和y轴都相切,若存在,求出圆⼼P的坐标,若不存在,请说明理由.24.如图,O为坐标原点,点A在x正半轴上,OA=2,将线段OA绕点O逆时针旋转150°⾄OB的位置,若经过点A、O、B三点的抛物线的解析式为y=ax2+bx+c.(1)求经过A、O、B三点的抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三⾓形是等腰三⾓形?若存在,求出满⾜条件的所有点P的坐标;若不存在,请说明理由;(3)若点D是线段OB下⽅抛物线上的动点,求四边形ABDO⾯积的最⼤值.25.如图1,已知⼆次函数y=ax2+bx+c的图象经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H,(1)求⼆次函数的表达式;(2)如图2,若E是线段AD上的⼀个动点(E与A、D不重合),过E点作平⾏于y轴的直线交抛物线与点F,交x轴与点G,设点E的横坐标为m,△ADF的⾯积为S,①求S与m的函数表达式;②S是否存在最⼤值?若存在,求出最⼤值及此时点E的坐标;若不存在,请说明理由.26.如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)若M为对称轴上的点,且△MAB的⾯积是4,求M点的坐标;(3)设抛物线的顶点为D,在第⼀象限的抛物线上是否存在点N,使得△NCD是等腰三⾓形?若存在,求出符合条件的N点的坐标;若不存在,请说明理由.27.如图,抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,对称轴是直线x=52x-4经过B,C两点.(1)求该抛物线的关系式;(2)若在对称轴右侧的抛物线上有⼀点P,过点P作PD⊥直线BC,垂⾜为点D,当∠PBD=∠ACO时,求出点P的坐标;(3)如图2,过点C作CE∥x轴交抛物线于点E,连接AE,点F是线段CE上的动点,过点F作FG⊥x轴,交AE 于H,垂⾜为点G,将△EFH沿直线AE翻折,得到△EMH,连接GM,是否存在这样的点F,使△GHM是等腰三⾓形?若存在,求出对应的EF的长度;若不存在,请说明理由.28.已知:⼆次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.(1)求抛物线的解析式;(2)抛物线的对称轴上有⼀动点P,求出PA+PD的最⼩值;(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平⾏四边形?如果存在,求出所有满⾜条件的E点坐标;如果不存在,请说明理由.29.如图,在平⾯直⾓坐标系中,抛物线y=-x2+bx+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),抛物线的顶点为点D.(1)求抛物线和直线AD的解析式;(2)点Q是抛物线⼀象限内⼀动点,过点Q作QN∥AD交BC于N,QH⊥AB交BC于点M,交AB于点H(如图1),当点Q坐标为何值时,△QNM的周长最⼤,求点Q的坐标以及△QNM周长的最⼤值;(3)直线AD与y轴交于点F,点E是点C关于对称轴的对称点,点P是线段AE上⼀动点,将△AFP沿着FP所在的直线翻折得到△A′FP(如图2),当三⾓形A′FP与△AED重叠部分为直⾓三⾓形时,求AP的长.30.如图1,在平⾯直⾓坐标系中,抛物线y=ax2+bx+4与x轴交于A、B两点,与y轴交于点C,且OC=2OA,抛物线的对称轴为直线x=3,且与x轴相交于点D.(1)求该抛物线解析式;(2)点P是第⼀象限内抛物线上的⼀个动点,设点P的横坐标为m,记△PCD的⾯积为S,是否存在点P使得△PCD的⾯积最⼤?若存在,求出S的最⼤值及相应的m值;若不存在请说明理由.(3)如图2,连接CD得Rt△COD,将△COD沿x轴正⽅向以某⼀固定速度平移,记平移后的三⾓形为△C′O ′D′,当点D′到达B 时运动停⽌,直线BC与△C′O′D′的边C′O′、C′D′分别相交于G、H,在平移过程中,当△O ′GH变为以O′H为腰的等腰三⾓形时,求此时BD′的长.31.如图.在平⾯直⾓坐标系中,直线y=-12x+3的图象与x釉、y轴分别交于点A、点B.抛物线y=14图象经过点A,并且与直线相交于点C,已知点C的横坐标为-4.(1)求⼆次函数的解析式以及cos∠BAO的值;(2)点P是直线AC下⽅抛物线上⼀动点(不与点A、点C重合),过点P作PD⊥x轴于点D,交AC于点E,作PF⊥AC于点F.当△PEF的周长与△ADE的周长之⽐等于5:2时,求出点D的坐标并求出此时PEF的周长;(3)在(2)的条件下,将△ADE绕平⾯内⼀点M按顺时针⽅向旋转90°后得到△A1D1E1,点A、D、E的对应点分别是A1、D1、E1.若△A1D1E1的两个顶点恰好落在抛物线上,求出点A1的坐标.32.如图,在平⾯直⾓坐标系Oxy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=45.(1)求过A、C、D三点的抛物线的解析式.(2)设直线AB与(1)中抛物线的另⼀个交点为E,P点为抛物线上A、E两点之间的⼀个动点,当△PAE的⾯积最⼤时,求点P的坐标.(3)若过点F(-6,0)的直线L上有⼀动点M,当以A,D,M为顶点所作的直⾓三⾓形有且只有三个时,请直接写出点M的坐标.33.如图1,已知抛物线y=ax2-32x+c与x轴相交于A、B两点,并与直线y=12x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点,连接AC.(1)点B的坐标是;点C的坐标是;(2)求抛物线的解析式;(3)设点E是线段CB上的⼀个动点(不与点B、C重合),直线EF∥y轴,交抛物线与点F,问点E运动到何处时,线段EF的长最⼤?并求出EF的长的最⼤值;(4)如图2,点D是抛物线的顶点,判断直线CD是否是经过A、B、C三点的圆的切线,并说明理由.34.如图,⼆次函数y=ax2+bx+c的图象于x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D,连接BC、BD、AC、CD,将△AOC绕点O逆时针旋转90°得△MOB.(1)求抛物线解析式及直线BD的解析式;(2)①操作⼀:动点P从点M出发到x轴上的点N,⼜到抛物线的对称轴上的点Q,再回到y轴上的点C,当四边形MNQC的周长最⼩时,则四边形MNQC的最⼩周长为;此时,tan∠OMN=;②操作⼆:将△AOC旋转的过程中,A的对应点为A′C的对应点为C′,当OA′⊥AC时,求直线OC′与抛物线的交点坐标;(3)将△BOM沿y轴的负半轴以每秒1个单位的速度平移,当BM过点D时停⽌平移,设平移的时间为t秒,△BOM与△BCD的重叠部分的⾯积为S,请直接求出S与t的函数关系式及相应的t的取值范围.35.如图,抛物线经过A(-1,0),B(5,0),C(0,-5)三点,点P是直线BC下⽅2的抛物线上⼀动点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有⼀点M,使MA+MC的值最⼩,求点M的坐标;(3)当点P运动到什么位置时,△PBC的⾯积最⼤,并求出此时P点的坐标和△PBC的最⼤⾯积.36.如图,抛物线y=-x2+x+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.(1)求A、B、C、D的坐标;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三⾓形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E(m,n)是线段BC上的⼀个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的⾯积最⼤?求出△CBF的最⼤⾯积及此时E点的坐标.37.平⾯直⾓坐标系中,抛物线y=ax2+bx+c交x轴于A,B两点(点A在点B左侧),与y轴交于点C,点A,C的坐标分别为(-3,0),(0,3),对称轴直线x=-1交x轴于点E,点D为顶点.(1)求抛物线的解析式;(2)点K是直线AC下⽅的抛物线上⼀点,且S△KAC=S△DAC求点K的坐标;(3)如图2若点P是线段AC上的⼀个动点,∠DPM=30°,DP⊥DM,则点P的线段AC上运动时,D点不变,M点随之运动,求当点P从点A运动到点C时,点M运动的路径长.38.如图,在平⾯直⾓坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.(1)求抛物线的解析式;(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向⽽⾏,当点M到达原点时,点H⽴刻掉头并以每秒32个单位长度的速度向点B⽅向移动,当点M到达抛物线的对称轴时,两点停⽌运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的⾯积S的函数关系式,并求出S的最⼤值.39.如图,已知⼀次函数y1=12x+b的图象l与⼆次函数y2=-x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2-5,0).(1)求⼆次函数的最⼤值;(2)设使y2>y1成⽴的x取值的所有整数和为s,若s是关于x的⽅程(1+1a-1)x+3x-3=0的根,求a的值;(3)若点F、G在图象C′上,长度为5的线段DE在线段BC上移动,EF与DG始终平⾏于y轴,当四边形DEFG的⾯积最⼤时,在x轴上求点P,使PD+PE最⼩,求出点P的坐标.40.如图,已知抛物线y=ax 2+bx+4与x 轴交于A (-2,0)、B 两点,与y 轴交于C 点,其对称轴为直线x=1.(1)直接写出抛物线的解析式:;(2)把线段AC 沿x 轴向右平移,设平移后A 、C 的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;(3)除(2)中的点A′、C′外,在x 轴和抛物线上是否还分别存在点E 、F ,使得以A 、C 、E 、F 为顶点的四边形为平⾏四边形?若存在,求出E 、F 的坐标;若不存在,请说明理由.41.如图,已知抛物线经过点A (-2,0)、B (4,0)、C (0,-8).(1)求抛物线的解析式及其顶点D 的坐标;(2)直线CD 交x 轴于点E ,过抛物线上在对称轴的右边的点P ,作y 轴的平⾏线交x 轴于点F ,交直线CD 于M ,使PM=15EF ,请求出点P 的坐标;(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM 总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.42.如图,抛物线y=ax 2+bx+c 关于y 轴对称,它的顶点在坐标原点O ,点B (2,-43)和点C (-3,-3)两点均在抛物线上,点F (0,-34)在y 轴上,过点(0,34)作直线l 与x 轴平⾏.(1)求抛物线的解析式和线段BC 的解析式.(2)设点D (x ,y )是线段BC 上的⼀个动点(点D 不与B ,C 重合),过点D作x 轴的垂线,与抛物线交于点G .设线段GD 的长度为h ,求h 与x 之间的函数关系式,并求出当x 为何值时,线段GD 的长度h 最⼤,最⼤长度h 的值是多少?(3)若点P (m ,n )是抛物线上位于第三象限的⼀个动点,连接PF 并延长,交抛物线于另⼀点Q ,过点Q 作QS⊥l ,垂⾜为点S ,过点P 作PN⊥l ,垂⾜为点N ,试判断△FNS 的形状,并说明理由;(4)若点A (-2,t )在线段BC 上,点M 为抛物线上的⼀个动点,连接AF ,当点M 在何位置时,MF+MA 的值最⼩,请直接写出此时点M 的坐标与MF+MA 的最⼩值.43.如图,在平⾯直⾓坐标系中,顶点为(4,-1)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧),已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D ,如果以点C 为圆⼼的圆与直线BD相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的⼀个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,△PAC 的⾯积最⼤?并求出此时P 点的坐标和△PAC 的最⼤⾯积.。
二次函数双动点面积最值

二次函数双动点面积最值一、问题描述在平面直角坐标系内,给定二次函数 $y=ax^2+bx+c$,且 $a<0$。
定义该二次函数的双动点为其图像上两个不同的点 $(x_1,y_1)$ 和$(x_2,y_2)$,满足 $y=ax^2+bx+c$ 在区间 $(x_1,x_2)$ 内单调递减或单调递增。
现在要求求出所有可能的双动点,并计算出其对应的面积最大值。
二、解题思路本题需要分别考虑二次函数的凸性和双动点的性质。
具体来说,我们可以通过求导数来判断二次函数的凸性,并通过判别式来计算二次方程的根以确定双动点。
然后,我们可以利用双动点的性质,结合微积分知识求出面积最大值。
三、解题步骤1. 求解二次函数的凸性由于$a<0$,因此该二次函数开口向下。
此时,当且仅当$a>0$ 时,该二次函数在整个定义域内为凸函数;当且仅当 $a<0$ 时,该二次函数在整个定义域内为下凸函数。
因此,在本题中,我们可以通过判断 $a$ 的符号来确定该二次函数的凸性。
2. 计算二次方程的根由于$a<0$,因此该二次函数的图像是一个开口向下的抛物线。
此时,该二次函数的双动点必然是两个不同的零点,即 $ax^2+bx+c=0$ 的两个根。
根据二次方程求根公式可得:$$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$由于 $a<0$,因此 $\sqrt{b^2-4ac}$ 为实数。
因此,当 $b^2-4ac>0$ 时,该二次方程有两个不同的实根;当 $b^2-4ac=0$ 时,该二次方程有一个重根;当$b^2-4ac<0$ 时,该二次方程无实数解。
在本题中,我们需要计算出所有可能的双动点。
因此,在计算完根之后,我们需要对其进行判断:若两个根均在定义域内,则它们为一个双动点;若其中一个根在定义域内而另一个不在,则不存在双动点;若两个根均不在定义域内,则也不存在双动点。
二次函数图像及解析式问题

二次函数图像及解析式问题1.若二次函数的图象经过A(0,0),B(-1,-11),C(1,9)三点,求这个二次函数的解析式2.如果抛物线y =ax 2+bx +c 经过点(-1,12),(0,5)和(2,-3),求a +b +c 的值3.抛物线y =ax 2+bx +c 经过点(0,1),(1,3),(-1,1)三点,求这个二次函数的解析式4.抛物线顶点P(-1,-8),且过点A(0,-6),求这个二次函数的解析式5.已知二次函数y =ax 2+bx +c 的图象过(3,0),(2,-3)两点,并且以x =1为对称轴,求这个函数的解析式6.二次函数的图象的顶点在原点,且过点(2,4),求这个二次函数的关系式7.已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式8.已知抛物线的顶点是(2,-4),它与y 轴的一个交点的纵坐标为4,求函数的关系式9.已知二次函数当x =-3时,有最大值-1,且当x =0时,y =-3,求二次函数的关系式10.已知二次函数y =x 2+px +q 的图象的顶点坐标是(5,-2),求二次函数关系式11.已知抛物线的顶点坐标为(-1,-3),与y 轴交点为(0,-5),求二次函数的关系式12.函数y =x 2+px +q 的最小值是4,且当x =2时,y =5,求p 和q13.若抛物线y =-x 2+bx +c 的最高点为(-1,-3),求b 和c14.若二次函数y =(m +1)x 2+m 2-2m -3的图象经过原点,则m =______15.已知二次函数y =ax 2+bx +c 的图象经过A(0,1),B(-1,0),C(1,0),求此函数的关系式16.已知二次函数y =ax 2+bx +c 的图象过A(0,-5),B(5,0)两点,它的对称轴为直线x =2,求这个二次函数的关系式17.二次函数y =ax 2+bx +c 与x 轴的两交点的横坐标是-0.5,1.5,与x 轴交点的纵坐标是-5,求这个二次函数的关系式18.已知y=x 2+(m 2+4)x-2m 2-12,求证,不论m 取何实数图象总与x 轴有两个交点19.(1)已知二次函数y =ax 2+bx +c 的图象如图所示,求这个二次函数的关系式(2)已知二次函数y =ax 2+bx +c 的图象如图所示,求这个二次函数的关系式(3)根据图中的抛物线,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x 时,y 有最大值(4)已知二次函数y =ax 2+bx +c 的图像如图所示,下列结论:⑴a+b+c ﹤0 ⑵a-b+c ﹥0 ⑶abc ﹥0⑷b=2a (5)042ac b ,其中正确的结论的个数是( )A 1个 B 2个 C 3个 D 4个 (5)已知y=2x 2+8x+7的图象上有有点A 1(2)y ,,B 21(5)3y ,,C 31(1)5y ,,则 y 1、y 2、y 3的大小关系为( ) A . y 1 > y 2> y 3 B . y 2> y 1> y 3 C . y 2> y 3> y 1 D . y 3> y 2> y 120.(1)下列图象中,当ab >0时,函数y =ax 2与y =ax +b 的图象是( )(2)在同一直角坐标系中,一次函数y=ax+c 和二次函数y=ax 2+c 的图象大致为 ( )21.如图是抛物线拱桥,已知水位在AB位置时,水面宽46米,水位上升3米就达到警戒线CD,这时水面宽43米,若洪水到来时,水位以每小时0.25米速度上升,求水过警戒线后几小时淹到拱桥顶?22.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.(1)建立如图所示的直角坐标系,求抛物线的表达式;(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少.23.有一座圆弧形的拱桥,桥下水面宽度7.2m,拱顶高出水平面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过拱桥,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由24.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,问绳子的最低点距地面的距离是多少米.25.在平面直角坐标系中,ΔAOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1)。
二次函数的图像

汇报人:
二次函数图像的形状 二次函数图像的平移 二次函数图像的对称变换 二次函数图像的翻折 二次函数图像的交点 二次函数图像的综合应用
二次函数图像的形状
开口方向
向上开口:二次项系数大于0
垂直于x轴:二次项系数等于0
添加标题
添加标题
向下开口:二次项系数小于0
添加标题
添加标题
水平线:一次项系数等于0
抛物线与坐标轴交点的应 用
抛物线在实际问题中的建 模应用
在数学竞赛中的应用
二次函数图像的综合应用可以解决数学竞赛中的代数问题。 通过分析二次函数图像,可以解决几何问题。 利用二次函数图像的性质,可以解决数列问题。 二次函数图像的综合应用在数学竞赛中具有广泛的应用价值。
在高中数学中的重要性
二次函数图像是高中数学的重要知识点,是理解和掌握函数性质的关键。 通过二次函数图像的综合应用,可以解决各种实际问题,提高数学应用能力。 二次函数图像在高中数学中占有重要地位,是高考数学的必考内容之一。 掌握二次函数图像的综合应用,有助于提高学生的数学素养和思维能力。
变化规律:顶点不变,开口方 向相反,对称轴不变
举例:y=x^2沿x轴翻折后为 y=-x^2
应用:理解次函 数图像在y轴两侧 对称翻转
效果:改变开口 方向和顶点位置
公式:将二次函 数的一般形式 y=ax^2+bx+c 中的a替换为-a, 得到新的二次函 数
上平移和下平移对函数值的影响:上平移会使函数值增大,下平移会使函数值减小。
上平移和下平移的代数表示:向上平移a个单位,函数解析式变为y=f(x+a);向下平移 a个单位,函数解析式变为y=f(x-a)。
上平移和下平移的实际应用:在解决实际问题时,可以通过平移二次函数的图像来调整 参数,从而得到最优解。
浅谈二次函数图像问题的处理

浅谈二次函数图像问题的处理
二次函数图像是数学中最常见的几何图形之一,它的形状就像一个天花板或圆弧的形状(或凹)。
它们可以用来表示双曲线,弓形线,抛物线,及其他与几何图像相关的数学函数。
处理二次函数图像的方法有很多,它们的简单性使得使用这些方法变得更容易。
首先,了解二次函数的性质是处理它们的关键。
这需要临界点,最大值和最小值等等。
然后,利用椭圆体或其他几何形状来推导存在的约束条件,如果知道了约束条件,就可以用它们来进行下一步的求解,例如在给定的范围内求出可行的u,v取值。
接下来,要推导当函数取特定值时的极限,即求出最大值和最小值。
此外,根据函数和参数相关系数,可以求得几何形状,及其对应的定义域和值域。
最后,利用技术手段可以计算出函数的积分,从而可以用来归纳性地求解二次函数图像问题。
此外,还可以利用软件,如MATLAB,SPSS等绘制二次函数图像,从而能够更方便地求解函数的性质及形状。
总而言之,完全理解二次函数的基本性质及其求解方法是处理它们的关键,利用这些性质和技术手段,可以将抽象的数学概念映射到几何实体,有助于减小计算量和把握解决问题的过程。
二次函数图象和性质知识点总结

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式:①一般式:(a 、b 、c 为常数,a ≠0) ②顶点式:(a 、h 、k 为常数,a ≠0),其中(h ,k )为顶点坐标。
③交点式:,其中是抛物线与x 轴交点的横坐标,即一元二次方程的两个根,且a ≠0,(也叫两根式)。
2. 二次函数的图象 ①二次函数的图象是对称轴平行于(包括重合)y 轴的抛物线,几个不同的二次函数,如果a 相同,那么抛物线的开口方向,开口大小(即形状)完全相同,只是位置不同。
②任意抛物线可以由抛物线经过适当的平移得到,移动规律可简记为:[左加右减,上加下减],具体平移方法如下表所示。
③在画的图象时,可以先配方成的形式,然后将的图象上(下)左(右)平移得到所求图象,即平移法;也可用描点法:也是将配成的形式,这样可以确定开口方向,对称轴及顶点坐标。
然后取图象与y 轴的交点(0,c ),及此点关于对称轴对称的点(2h ,c );如果图象与x 轴有两个交点,就直接取这两个点(x 1,0),y ax bx c =++2y a x h k =-+()2y a x x x x =--()()12x x 12,ax bx c 20++=y ax bx c =++2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2(x 2,0)就行了;如果图象与x 轴只有一个交点或无交点,那应该在对称轴两侧取对称点,(这两点不是与y 轴交点及其对称点),一般画图象找5个点。
a >0 a <0 a >0 a <0(1)抛物线开口向上,(1)抛物线开口向下,(1)抛物线开口(1)抛物线开4. 求抛物线的顶点、对称轴和最值的方法①配方法:将解析式化为的形式,顶点坐标为y ax bx c =++2y a x h k =-+()2(h ,k ),对称轴为直线,若a >0,y 有最小值,当x =h 时,;若a <0,y 有最大值,当x =h 时,。
4.1 二次函数的图像(北师大版)

[思路点拨]
对每个函数列表、描点、连线作出相应
的图像,然后利用图像分析y=x2与y=2x2-4x的关系.
[精解详析]
(1)列表:
-2 4 2 16 -1 1 -1 6 0 0 -2 0 1 1 -1 2 4 2 0 3 9 7 6
x y=x2 y=x2-2 y=2x2-
一般式y=ax2+bx+c,a、b、c为常数,a≠0的形式.
(2)若已知二次函数图像的顶点坐标或对称轴方程与
最大(小)值,则设所求二次函数为顶点式y=a(x-h)2+k
(其中顶点(h,k),a为常数,a≠0).
(3)若已知二次函数图像与x轴的两个交点的坐标为 (x1,0),(x2,0),则设所求二次函数为两根式y=a(x-x1) (x-x2)(a为常数,且a≠0).
给定下面几个函数
f(x)=x2,f(x)=2x2,f(x)=2(x-1)2+1
问题1:由f(x)=x2的图像如何得到f(x)=2x2的图像?
提示:f(x)=x2的图像上各点横坐标不变,纵坐标变
为原来的2倍即可得到f(x)=2x2的图像.
问题2:由f(x)=2x2的图像如何得到f(x)=2(x-1)2+1的
[一点通]
任意抛物线y+h)2+k的形式,都可由y=ax2图像经过适当的平移得
到,具体平移方法,如图所示.
即上述平移规律“h值正、负,左、右移”,亦即“加时
左移,减时右移”;“k值正、负,上、下移”,即“加时上移,
减时下移”.
1.如何把y=2x2-4x的图像变换为y=x2的图像?
a-b-6=-4, 故 a+b-6=-6,
① ②
由①②可得 a=1,b=-1, 故该函数的解析式为 y=x2-x-6.
初三数学,二次函数(图像、性质、规律、实际问题)

y=ax^2 (0,0) x=0
y=ax^2+K (0,K) x=0
y=a(x-h)^2 (h,0) x=h
y=a(x-h)^2+k (h,k) x=h
y=ax^2+bx+c (-b/2a,4ac-b²/4a) x=-b/2a
(1)图象与y轴一定相交,交点坐标为(0,c);
(2)当△=b^2-4ac>0,图象与x轴交于两点A(x?,0)和B(x?,0),其中的x1,x2是一元二次方程ax^2+bx+c=0
(a≠0)的两根.这两点间的距离AB=|x?-x?| =√△/∣a∣(a绝对值分之根号下△)另外,抛物线上任何一对对称点的距离可以由|2×(-b/2a)-A |(A为其中一点的横坐标)
3。一般式,顶点式,交点式,等,区分对称轴,顶点,图像等的差异性。
4。联系实际对函数图像的理解。
5。计算时,看图像时切记取值范围。
二次函数的图像
在平面直角坐标系中作出二次函数y=2x的平方的图像,
可以看出,二次函数的图像是一条永无止境的抛物线。
不同的二次函数图像
顶点的横坐标,是取得最值时的自变量值,顶点的纵坐标,是最值的取值。
6.用待定系数法求二次函数的解析式
(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时,可设解析式为一般形式:
y=ax^2+bx+c(a≠0)。
(2)当题给条件为已知图象的顶点坐标或对称轴或极大(小)值时,可设解析式为顶点式:y=a(x-h)^2+k(a≠0)。
可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时
人教版九年级上册期末点对点攻关:二次函数图像问题综合(七)

人教版九年级上册期末点对点攻关:二次函数图像问题综合(七)1.如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac<b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是()A.①②③B.①②④C.②③④D.③④⑤2.二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为()A.1 B.2 C.3 D.43.抛物线y=ax2+bx+c过点(1,0)且对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc<0;②b+2a=0;③b2>4ac;④若点(﹣0.5,y1),(﹣2,y2)均在抛物上,则y1<y2;⑤13a﹣4b+c>0;⑥3a+2c<0,其中正确个数有()A.2 B.3 C.4 D.54.如图,在二次函数y=ax2+bx+c(a≠0)的图象中,小明同学观察得出了下面几条信息:①b2﹣4ac>0;②abc<0;③;④b2=4a(c﹣1);⑤关于x的一元二次方程ax2+bx+c=3无实数根,其中信息错误的个数为()A.4 B.3 C.2 D.15.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①abc>0;②4a+2b+c>0;③5a﹣b+c=0;④若方程a(x+5)(x﹣1)=﹣1有两个根x 1和x2,且x1<x2,则﹣5<x1<x2<1;⑤若方程|ax2+bx+c|=2有四个根,则这四个根的和为﹣4.其中正确的结论有()A.2个B.3个C.4个D.5个6.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b =0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是()A.1 B.2 C.3 D.47.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()A.a>0B.当﹣1<x<3时,y<0C.2a+b=0D.当x≥1时,y随x的增大而增大8.如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a﹣2b+c<0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>2.其中正确的有()A.4个B.3个C.2个D.1个9.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①abc>0;②b2﹣4ac<0;③4a﹣2b+c<0;④b=﹣2a.则其中结论正确的是()A.①③B.③④C.②③D.①④10.已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有()A.3个B.2个C.1个D.0个11.如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac≤b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是()A.①②③B.②④C.②③④D.③④⑤12.如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是()A.②④B.①③C.②③D.①④13.小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:(1)a <0;(2)c>1;(3)b>0;(4)a+b+c>0;(5)a﹣b+c>0.你认为其中正确信息的个数有()A.2个B.3个C.4个D.5个14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有()A.2个B.3个C.4个D.5个15.小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0,你认为其中正确信息的个数有()A.2个B.3个C.4个D.5个16.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c <0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是()A.1 B.2 C.3 D.417.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是()A.①④B.②④C.①②③D.①②③④18.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b).其中所有正确的结论是()A.①②③B.①③④C.①②③⑤D.①③⑤19.已知抛物线y=ax2+bx+c的图象如图所示,顶点为(4,6),则下列说法错误的是()A.b2>4acB.ax2+bx+c≤6C.若点(2,m)(5,n)在抛物线上,则m>nD.8a+b=020.从如图所示的二次函数y=ax2+bx+c的图象中,观察得出下面五条信息:①c<0;②abc >0;③a+b+c>0;④2a+3b=0;⑤c﹣8b>0.你认为其中正确信息的个数为()A.2个B.3个C.4个D.5个参考答案1.解:①由图象可知:a>0,c<0,∴ac<0,故①错误;②由于对称轴可知:<1,∴2a+b>0,故②正确;③由于抛物线与x轴有两个交点,∴△=b2﹣4ac>0,故③正确;④由图象可知:x=1时,y=a+b+c<0,故④正确;⑤当x>时,y随着x的增大而增大,故⑤错误;故选:C.2.解:①抛物线开口方向向下,则a<0.抛物线对称轴位于y轴右侧,则a、b异号,即ab<0.抛物线与y轴交于正半轴,则c>0所以abc<0.故①错误.②∵抛物线对称轴为直线x =﹣=1, ∴b =﹣2a ,即2a +b =0,故②正确;③∵抛物线对称轴为直线x =1,∴函数的最大值为:a +b +c ,∴当m ≠1时,a +b +c >am 2+bm +c ,即a +b >am 2+bm ,故③错误;④∵抛物线与x 轴的一个交点在(3,0)的左侧,而对称轴为直线x =1, ∴抛物线与x 轴的另一个交点在(﹣1,0)的右侧∴当x =﹣1时,y <0,∴a ﹣b +c <0,故④错误;⑤∵ax 12+bx 1=ax 22+bx 2,∴ax 12+bx 1﹣ax 22﹣bx 2=0,∴a (x 1+x 2)(x 1﹣x 2)+b (x 1﹣x 2)=0,∴(x 1﹣x 2)[a (x 1+x 2)+b ]=0,12∴a (x 1+x 2)+b =0,即x 1+x 2=﹣,∵b =﹣2a ,∴x 1+x 2=2,故⑤正确.综上所述,正确的有②⑤.故选:B .3.解:①由图象可知:a >0,c <0,由对称轴可知:<0,∴b >0, ∴abc <0,故①正确;②由对称轴可知:=﹣1,∴b ﹣2a =0,故②错误;③由图象可知:抛物线与x 轴有两个交点,∴△=b 2﹣4ac >0,故③正确;④∵(﹣0.5,y 1)关于直线x =﹣1的对称点为(,y 1),∵x <﹣1时,y 随着x 的增大而减少,∴y 1<y 2,故④正确;⑤∵抛物线经过(1,0),∴c=﹣3a,由于b=2a,∴13a﹣4b+c=13a﹣8a﹣3a=2a>0,故⑤正确;⑥3a+2c=3a﹣6a=﹣3a<0,故⑥正确;故选:D.4.解:①根据图象可知:△>0,∴b2﹣4ac>0,故①正确;②由图象可知:a<0,c>0,由对称轴可知:<0,∴b<0,∴abc>0,故②错误;③由图象可知:﹣1<<0,∴2a﹣b<0,当x=1时,y<0,∴a+b+c<0,∴>0,故③错误;④由图象可知:当x=时,y=1,∴=1,∴4ac﹣b2=4a,∴b2=4a(c﹣1),故④正确;⑤由于二次函数y=ax2+bx+c(a≠0)的最大值为1,∴关于x的一元二次方程ax2+bx+c=3无实数根,故⑤正确;故选:C.5.解:∵抛物线的开口向上,则a>0,对称轴在y轴的左侧,则b>0,交y轴的负半轴,则c<0,∴abc<0,所以①结论错误;∵抛物线的顶点坐标(﹣2,﹣9a),∴﹣=﹣2,=﹣9a,∴b=4a,c=﹣5a,∴抛物线的解析式为y=ax2+4ax﹣5a,∴4a+2b+c=4a+8a﹣5a=7a>0,所以②结论正确,5a﹣b+c=5a﹣4a﹣5a=﹣4a<0,故③结论错误,∵抛物线y=ax2+4ax﹣5a交x轴于(﹣5,0),(1,0),∴若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1,正确,故结论④正确,若方程|ax 2+bx +c |=1有四个根,设方程ax 2+bx +c =1的两根分别为x 1,x 2,则=﹣2,可得x 1+x 2=﹣4,设方程ax 2+bx +c =﹣1的两根分别为x 3,x 4,则=﹣2,可得x 3+x 4=﹣4, 所以这四个根的和为﹣8,故结论⑤错误,故选:A . 6.解:①由抛物线的对称轴可知:﹣>0,∴ab <0,∵抛物线与y 轴的交点在正半轴上,∴c >0,∴abc <0,故①正确;②∵﹣=1,∴b =﹣2a ,∴2a +b =0,故②正确.③∵(0,c )关于直线x =1的对称点为(2,c ),而x =0时,y =c >0,∴x =2时,y =c >0,∴y =4a +2b +c >0,故③正确;④由图象可知:△>0,∴b 2﹣4ac >0,故②正确;故选:D .7.解:(A)由图象可知:a<0,故A错误;(B)∵抛物线与x轴的一个交点为(﹣1,0),对称轴x=1,∴抛物线与x轴的另一个交点为(3,0),∴由图象知当﹣1<x<3时,y>0,故B错误;(C)由对称轴可知,可得2a+b=0,故C正确;(D)由图象可知当x≥1时,y随x的增大而减小,故D错误.故选:C.8.解:∵二次函数y=ax2+bx+c(a≠0)的对称轴为x=1,∴﹣=1,得2a+b=0,故①正确;当x=﹣2时,y=4a﹣2b+c<0,故②正确;该函数图象与x轴有两个交点,则b2﹣4ac>0,故③正确;∵二次函数y=ax2+bx+c(a≠0)的对称轴为x=1,点B坐标为(﹣1,0),∴点A(3,0),∴当y<0时,x<﹣1或x>3,故④错误;故选:B.9.解:由抛物线的开口向下,得到a<0,∵﹣>0,∴b>0,由抛物线与y轴交于正半轴,得到c>0,∴abc<0,选项①错误;又抛物线与x轴有2个交点,∴b2﹣4ac>0,选项②错误;∵x=﹣2时对应的函数值为负数,∴4a﹣2b+c<0,选项③正确;∵对称轴为直线x=1,∴﹣=1,即b=﹣2a,选项④正确,则其中正确的选项有③④.故选:B.10.解:根据图象可得:a>0,c<0,对称轴:x=﹣>0,①∵它与x轴的两个交点分别为(﹣1,0),(3,0),∴对称轴是x=1,∴﹣=1,∴b+2a=0,故①错误;②∵a>0,∴b<0,∵c<0,∴abc>0,故②错误;③∵a﹣b+c=0,∴c=b﹣a,∴a﹣2b+4c=a﹣2b+4(b﹣a)=2b﹣3a,又由①得b=﹣2a,∴a﹣2b+4c=﹣7a<0,故此选项正确;④根据图示知,当x=4时,y>0,∴16a+4b+c>0,由①知,b=﹣2a,∴8a+c>0;故④正确;故正确为:③④两个.故选:B.11.解:∵抛物线开口向上,∴a>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴ac<0,所以①错误;∵0<﹣<1,∴﹣b<2a,∴2a+b>0,所以②正确;∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,所以③错误;∵x=1时,y<0,∴a+b+c<0,所以④正确;在对称轴的左侧,y随x的增大而减小,所以⑤错误.故选:B.12.解:①图象与x轴有两个交点,则方程有两个不相等的实数根,b2﹣4ac>0,b2>4ac,正确;②因为开口向下,故a<0,有﹣>0,则b>0,又c>0,故bc>0,错误;③由对称轴x=﹣=1,得2a+b=0,正确;④当x=1时,a+b+c>0,错误;故①③正确.故选:B.13.解:(1)由抛物线的开口向下知a<0,故正确;(2)由抛物线与y轴的交点为在y轴的正半轴上且大于1,可推出c>1,故正确;(3)由图可知对称轴为x=>0,可推出a、b异号,又∵a<0,∴b>0,故正确;(4)因为抛物线与x轴的交点可以看出,当x=1时,y>0,所以a+b+c>0,故正确,(5)因为抛物线与x轴的交点可以看出,当x=﹣1时,y<0,所以a﹣b+c<0,错误.∴正确答案为4个.故选:C.14.解:开口向下,a<0;对称轴在y轴的右侧,a、b异号,则b>0;抛物线与y轴的交点在x轴的上方,c>0,则abc<0,所以①不正确;当x=﹣1时图象在x轴上,则y=a﹣b+c=0,即a+c=b,所以②不正确;对称轴为直线x=1,则x=2时图象在x轴上方,则y=4a+2b+c>0,所以③正确;x=﹣=1,则a=﹣b,而a﹣b+c=0,则﹣b﹣b+c=0,2c=3b,所以④不正确;开口向下,当x=1,y有最大值a+b+c;当x=m(m≠1)时,y=am2+bm+c,则a+b+c>am2+bm+c,即a+b>m(am+b)(m≠1),所以⑤正确.故选:A.15.解:∵抛物线开口方向向上,∴a>0,∵与y轴交点在x轴的下方,∴c<0,∵﹣,∵a>0,∴b<0,2a﹣3b>0,∴abc>0,∴①②是正确的,④对称轴x=﹣=,∴3b=﹣2a,∴2a+3b=0,∴④是错误的;当x=﹣1,y=a﹣b+c,而点(﹣1,a﹣b+c)在第二象限,∴a﹣b+c>0是正确的;当x=2时,y=4a+2b+c=2×(﹣3b)+2b+c=c﹣4b,而点(2,c﹣4b)在第一象限,∴c﹣4b>0.故选:C.16.解:∵图象与x轴有两个交点,∴方程ax2+bx+c=0有两个不相等的实数根,∴b2﹣4ac>0,∴4ac﹣b2<0,①正确;∵﹣=﹣1,∴b=2a,∵a+b+c<0,∴b+b+c<0,3b+2c<0,∴②是正确;∵当x=﹣2时,y>0,∴4a﹣2b+c>0,∴4a+c>2b,③错误;∵由图象可知x=﹣1时该二次函数取得最大值,∴a﹣b+c>am2+bm+c(m≠﹣1).∴m(am+b)<a﹣b.故④正确∴正确的有①②④三个,故选:C.17.解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a<0,∴ab<0,所以①正确;∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,所以②正确;∵x=1时,y<0,∴a+b+c<0,而c<0,∴a+b+2c<0,所以③正确;∵抛物线的对称轴为直线x=﹣=1,∴b=﹣2a,∴a+2a+c>0,所以④错误.故选:C.18.解:由抛物线的开口向下可得:a<0,根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,根据抛物线与y轴的交点在正半轴可得:c>0,∴abc>0,故①正确;直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣=﹣1,可得b=2a,a﹣2b+4c=a﹣4a+4c=﹣3a+4c,∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(,0),∴抛物线与x轴的另一个交点坐标为(﹣,0),当x=﹣时,y=0,即a(﹣)2﹣b+c=0,整理得:25a﹣10b+4c=0,故③正确;∵b=2a,a+b+c<0,∴b+b+c<0,即3b+2c<0,故④错误;∴a﹣b≥m(am﹣b),故⑤正确;故选:D.19.解:A、由抛物线与x轴有2个交点可知b2﹣4ac>0,即b2>4ac,故此选项正确;B、由抛物线的顶点坐标为(4,6)知函数的最大值为6,则ax2+bx+c≤6,故此选项正确;C、由抛物线对称轴为x=4且开口向下知离对称轴水平距离越大函数值越小,则m<n,故此选项错误;D、由对称轴x=﹣=4知,b=﹣8a,即8a+b=0,故此选项正确;故选:C.20.解:①由抛物线与y轴的交点可知:c<0,故①正确;②由抛物线的开口方向可知:a>0,﹣>0,∴b<0,∴abc>0,故②正确;③令x=1代入y=ax2+bx+c,∴y=a+b+c<0,故③错误;④由对称轴可知:﹣=,则2a+3b=0,故④正确⑤如图所示,当x=﹣2时,y>0.所以4a﹣2b+c>0,所以﹣8b+c>0.所以c﹣8b>0.故⑤正确;综上所述,正确的结论有4个.故选:C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数双图像问题 猿题库
单选题
1. 已知抛物线(
)的顶点为,点
,
,
在该抛
物线上,当
恒成立时,
的最小值为()。
A. B. C. D.
2. 如图,抛物线与轴交于点,,把抛物线在轴及其上方的部分记作
,将
向右平移
得
,
与轴交于点,,若与
共有个不同的交点,则的取值范围是()。
A. B. C.
D.
3. 二次函数,当
且
时,的最小值为
,最大值为
,则
的值为
()。
A.
B.
D.
C.
4.
5. 如图,垂直于轴的直线分别与抛物线
和抛物线
交于,两点,
过点作轴分别于轴和抛物线交于点,,过点作
轴分别与轴和抛物线
交于点
, ,则的值为()。
A. B.
C.
D.
6. 已知抛物线与轴交于、两点,将这条抛物线的顶点记为,连接、,则
的值为()。
A. B.
D.
C.
6. 如图,反比例函数
的图象经过二次函数
图象的顶点
(
),则有()。
1
A.
B.
C.
D.
7. 一次函数()、二次函数和反比例函数()在同一直角坐标系中
的图象如图所示,点的坐标为,则下列结论中,正确的是()。
A.
B.
C.
D.
8. 抛物线的图象如图所示,则反比例函数与一次函数在同
一坐标系内的图象大致是()。
9. 已知直线与坐标轴分别交于点,,点在抛物线上,能使
为等腰三角形的点的个数有()。
A. 个
B. 个
C. 个
D. 个
10. 如图,抛物线与交于点,过点作轴的平行线,分别交两条
抛物线于点,。
则以下结论:①无论取何值,的值总是正数;②;③当时,
;④;其中正确结论是()。
2
A. ①②
B. ②③
C. ③④
D. ①④
11. 已知二次函数与轴只有一个交点,且图象过,两点,则、的关
系为()。
A. B. C. D.
12. 给出下列命题及函数,和的图象:①如果,那么;②如果,
那么;③如果,那么;④如果时,那么。
则()。
A. 正确的命题是①④
B. 错误的命题是②③④
C. 正确的命题是①②
D. 错误的命题只有③
13. 如图,已知点,为坐标原点,是线段上任意一点(不含端点,),过、两点的二次
函数和过、两点的二次函数的图象开口均向下,它们的顶点分别为、,射线与相交于点。
当时,这两个二次函数的最大值之和等于()。
A.
B.
C.
D.
14. 如图,直线与轴交于点,与直线交于点,以为边向右作菱形,点恰
与原点重合,抛物线的顶点在直线上移动。
若抛物线与菱形的边、都
有公共点,则的取值范围是()。
3
A.
B.
C.
D.
15. 如图,抛物线与双曲线的交点的横坐标是,则关于的不等式的解集是
()。
A.
B.
C.
D.
16. 如图所示,抛物线()与轴交于点、。
直线与此抛物线
交于点,与轴交于点,在直线上取点,使。
连接、、、。
某同学根据
图象写出下列结论:①;②当时,;③四边形是菱形;
④。
你认为其中正确的是()。
A. ②③④
B. ①②④
C. ①③④
D. ①②③
17. 如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,则下列关系不正确的是
()。
A.
B.
C.
D. ,
4
二次函数双图像问题猿题库
18. 如图,抛物线与交于点,过点作轴的平行线,分别交两条
抛物线于两点,且分别为顶点.则下列结论:
①;②;③是等腰直角三角形;④当时,。
其中正确结论的个数是()。
A. 个
B. 个
C. 个
D. 个
19. 如图,把抛物线沿直线平移个单位后,其顶点在直线上的处,则平移后的抛物线解析
式是()。
A.
B.
C.
D.
20. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线
所围成的阴影部分的面积为()。
A.
B.
C.
D.
21. 如图,二次函数的图象过点。
它与反比例函数的图象交于点则这
个二次函数的解析式为()。
5。
