单因素、交互作用、简单效应分析
田间试验名词解释

实用标准文案精彩文档一、名词解释 1、保护区:在试验区四周种植的不计产的区域。
2、混合模型:当一个模型中除了总平均μ和随机误差ε外,还含有固定效应和随机效应,就称为..3、复相关系数:即为多元相关系数,是多元回归平方和与总变异平方和之比的平方根。
4、完全随机设计:设计上试验时,只应用了环境设计上的重复和随机排列两个原则的试验设计方法。
(特点:有重复,不设区组;优点:每个区组重复次数不相等;应用条件:试验单元一致,外界条件椅子)5、拉丁方设计:行和列互为区组,每个处理在每个行区组和列区组中都出现1次的试验设计方法。
6、同质性:方差分析中假定所有试验处理的误差方差都是相同的。
7、协方差分析:将方差分析和回归分析相结合而产生的统计方法。
(作用:进行试验条件矫正;统计分析)8、统计数:用样本的各个观察数值计算所得的能够反映样本特征的数值称…9、单因素试验:在同一试验中只研究某一因素不同水平的效果。
(缺点:效益低;优点:分析、涉及简单) 10、(1)观察值:每一个体某一性状的测定结果称为…(2)变数:同一性质的一群观察值总称为变数。
(3)参数:从总体的全部观察值计算所得的数值是能够表达总体特征的真值,如总体平均数称为参数(4)统计数:从样本中的各个观察值计算所得数值,反映样本的特征数,如样本平均数等称为统计数 11、概率:以重复次数充分大时事件A 发生的频率做为其概率的近似值。
12、水平:统计假设测验中否定无效假设的概率标准。
13、随机模型:将各个处理效应皆看成固定常数的数学模型。
14、因素水平:简称水平,一个试验因素内不同状态或不同数量级别。
15、总体:符合指定条件的研究对象的全体 16、(1)区间估计:指在一定概率保证下,由样本的结果估计相应的总体参数可能取值的一个范围或区间。
(保证总体在一定范围,并且伴随有一定置信概率)(2)这个区间称为置信区间(3)区间的上、下限成为置信限(4)置信度或置信系数:保证总体参数位于一定区间范围内的概率17、适应性测验:比较观察次数与某种理论次数是否相符的测验,称为适合性测试或称吻合度测试18、两向分组资料:观察值按两个因素交叉分组的资料称为…19、偏回归系数:在多元回归分析中,其余自变数保持不变时,反映某个自变数变化一个单位对依变数的平均数效应的统计数是…20、试验方案:根据试验目的与要求所拟定的进行比较的一组试验处理的总称。
方差分析中的名词解释

试验指标(experimental index):为衡量试验结果的好坏和处理效应的高低,在实验中具体测定的性状或观测的项目称为试验指标。
常用的试验指标有:身高、体重、日增重、酶活性、DNA含量等等。
试验因素(experimental factor):试验中所研究的影响试验指标的因素叫试验因素。
当试验中考察的因素只有一个时,称为单因素试验;若同时研究两个或两个以上因素对试验指标的影响时,则称为两因素或多因素试验。
因素水平(level of factor):试验因素所处的某种特定状态或数量等级称为因素水平,简称水平。
如研究3个品种奶牛产奶量的高低,这3个品种就是奶牛品种这个试验因素的3个水平。
试验处理(treatment):事先设计好的实施在实验单位上的具体项目就叫试验处理。
如进行饲料的比较试验时,实施在试验单位上的具体项目就是具体饲喂哪一种饲料。
试验单位(experimental unit ):在实验中能接受不同试验处理的独立的试验载体叫试验单位。
一只小白鼠,一条鱼,一定面积的小麦等都可以作为实验单位。
重复(repetition):在实验中,将一个处理实施在两个或两个以上的试验单位上,称为处理有重复;一处理实施的试验单位数称为处理的重复数。
例如,用某种饲料喂4头猪,就说这个处理(饲料)有4个重复。
方差:又叫均方,是标准差的平方,是表示变异的量。
试验误差:试验过程中偶然性因素的干扰和测量误差所致。
多重比较(multiple comparisons):要明确不同处理平均数两两间差异的显著性,每个处理的平均数都要与其他的处理进行比较,这种差异显著性的检验就叫多重比较。
因素(factor):也叫因子,是指对试验指标有影响,在研究中加以(控制)考虑的试验条件。
可控因子:在试验中可以人为地加以调控的因子浓度、温度等非控因子:不能人为调控的因素(气象、环境等)固定因素:指因素的水平是经过特意选择的随机因素:指因素的水平是从该因素水平总体中随机抽出的样本水平(level):每个因素的不同状态(从质或量方面分成不同的等级)处理:指对试验对象施以不同的措施固定效应(fixed effect):由固定因素所引起的效应。
心理学与教育研究中的多因素实验设计——————舒华

心理学与教育研究中的多因素实验设计——————舒华第二章 几种基本的实验设计一、 基本特点适用于:研究中有一个自变量,自变量有两个或多于两个水平。
方法:把被试随机分配给自变量的各个水平,每个水平被试只接受一个水平的处理。
二、 计算与举例(一) 检验的问题与实验设计 (二) 实验数据及其计算()()()()()22i 22j T 2j ij j ss ss X X NX X ss n nNss ss n S X ss ss X X ss X =+=-=-=∙-=-=∙=-∑∑∑∑∑∑∑∑∑∑∑∑总变异组间组内总变异组间组内总变异组间一、 基本特点适用于:研究中有一个变量,自变量有两个或多个水平(P ≥2),研究中还有一个无关变量,也有两个或多个水平(n ≥2);并且自变量的水平与无关变量的水平之间没有交互作用。
适合检验的假说:(1)处理水平的总体平均数相等或处理效应为零;(2)区组的总体平均数相等或区组效应为零。
二、计算ss ss ss (ss SS ss =+=++总变异组间组内组间区组残差)三、优点:从实验中分离出了一个无关变量的效应,从而减少了实验误差。
一、 基本特点定义:是一个含P 行、P 列、把P 个字母分配给方格的管理方案,其中每个字母在每行中只出现一次。
适用于:(1)研究中自变量与无关变量的水平平均≥2,一个无关变量的水平被分配给P行,另一个则给P列;(2)假定处理水平与无关变量水平之间没有交互作用, (3)随即分配处理水平给2P 个方格单元,每个处理水平仅在每行,每列中出现一次。
1c 2c 3c 4c无关变量C的四个水平 无关变量B的四个水平 1b 自变量A的四个水平 2b3b4bA B C SS SS SS SS SS SS SS SS =+=++++处理间总变异处理内残差单元内()一、 基本特点:(也叫被试内设计) 基本方法:实验中每个被试接受所有的处理水平目 的:利用被试自己做控制,使被试的各方面特点在所有的处理中保持恒定,以最大限度地控制由被试的个体差异带来的变异。
简单效应分析范文

简单效应分析范文简单效应分析(Simple Effect Analysis)是一种常用的统计分析方法,用于研究一些因素对于特定因变量的影响效应。
简单效应分析的目的是通过对不同组别进行对比,探究因素对效应的具体作用。
本文将从简单效应分析的定义和原理、应用领域、步骤、案例分析以及优缺点等方面进行详细介绍。
简单效应分析可广泛应用于社会科学研究的各个领域,如心理学、教育学、社会学等。
以心理学为例,简单效应分析可以用于研究不同干预措施对人们情绪、认知等心理变量的影响效果。
在教育学领域,研究者可以使用简单效应分析来探究不同教育方法对学生成绩的影响效应。
1.设计实验:确定实验对象、实验组别、自变量和因变量。
确保实验设计合理,能够将不同组别进行对比。
2.数据收集:收集实验所需的数据,可以通过实验、问卷调查等方式获得相关数据。
3.数据预处理:对所收集的数据进行预处理,包括数据清洗、缺失值处理等,确保数据的可靠性和准确性。
4.方差分析:使用方差分析进行数据分析,计算不同组别之间的差异。
5.简单效应分析:通过将不同组别进行对比,研究因素对效应的影响。
可以使用图表或描述统计等方式,展示不同组之间的差异。
6.结果解释:根据分析结果,对因素对效应的影响进行解释和讨论。
案例分析以一个心理学实验为例,假设我们想研究颜色对情绪的影响。
我们将参与者随机分为红色组和蓝色组,让他们观看不同颜色的图片,并记录他们的情绪反应。
通过简单效应分析,我们可以比较两组参与者之间的情绪差异,并判断颜色对情绪的影响是否显著。
在进行方差分析后,我们得出了以下结果:红色组的情绪得分显著高于蓝色组(F(1,98)=4.23,p<0.05)。
这意味着红色对情绪有显著的正向影响,而蓝色对情绪的影响不显著。
根据上述分析结果,我们可以得出结论:观看红色图片能够显著提高参与者的情绪,而观看蓝色图片对情绪的影响不明显。
1.可以研究因素对效应的具体作用:通过对不同组别进行对比,直观地了解因素对效应的影响。
【2024版】单因素交互作用简单效应分析

整理课件
12
结果
多重比较
整理课件
13
练习1
数据文件“自信心与社交苦恼” 任务1:在1总自信平均分上,男生与女生是否存
在显著差异; 任务2:在1总自信平均分上,各个年级间是否存
在显著差异
整理课件
14
8.2 单因素随机区组方差分析
Univariate
整理课件
15
因变量
绝大多数时候 自变量都应该 往里面选
左边整变理课量件的全选入右边
18
单击后出现一个对话框,用于设置在模型中包含哪些 主效应和交互因子,默认情况为Full factorial,即分 析所有的主效应和交互作用。
本例没有交互作用 可分析,所以要改
整理课件
19
例2:单因素随机区组设计
题目:文章的生字密度对学生阅读理解的影响
自变量:生字密度,含有4个水平 (5:1、10:1、15:1、20:1)
题目:当主题熟悉性不同时,生字密度对儿童阅读理 解的影响。
实验变量:
自变量A——文章类型,即熟悉的(a1)与不熟悉的(a2); 自变量B——生字密度,即5:1(b1)、10:1(b2)、
15:1(b3) 实验设计:两因素完全随机实验设计
被 试:24名五年级学生
实验程序:首先将自变A与B的水平结合成2×3即6 个实验处理;然后把选取的被试分成6组,每组4人, 分别接受一种实验处理水平的结合。
数边
缘应 即
()
际
主 效
平
均
整理课件
细效 即 格应 交 平互 均作 数用
27
Onece more
主效应 一个因素内各个水平的差异
交互作用
一个因素的各个水平在另一个因素的不同水平上变化趋 势不一致。
SPSS做方差分析交互作用的简单效应分析
SPSS做方差分析交互作用的简单效应分析两个试验因素如果他们的交互作用有统计学意义,此时还需继续考察一个因素在另一个因素各水平上的差异,或者说,要考察两个因素不同水平组合之间到底是哪些组合有统计学差异。
这项工作就是交互作用的两两比较,为了区别于主效应的两两比较,特将交互作用的两两比较叫做简单效应分析。
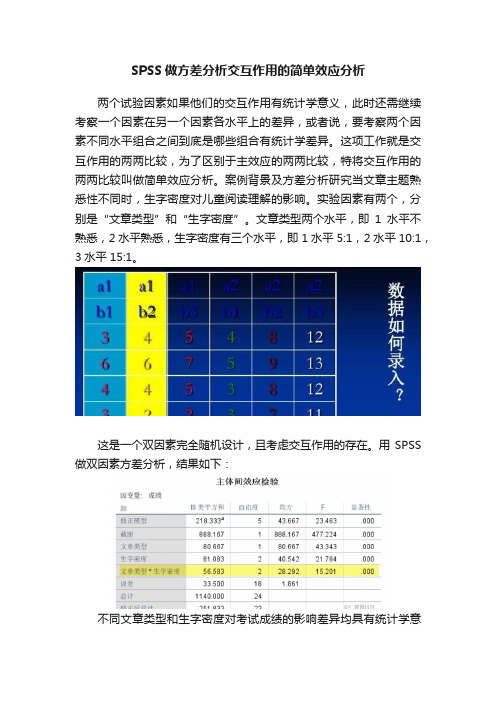
案例背景及方差分析研究当文章主题熟悉性不同时,生字密度对儿童阅读理解的影响。
实验因素有两个,分别是“文章类型”和“生字密度”。
文章类型两个水平,即1水平不熟悉,2水平熟悉,生字密度有三个水平,即1水平5:1,2水平10:1,3水平15:1。
这是一个双因素完全随机设计,且考虑交互作用的存在。
用SPSS 做双因素方差分析,结果如下:不同文章类型和生字密度对考试成绩的影响差异均具有统计学意义(P<0.05),各因素两两比较略,大家可以自己尝试。
文章类型和生字密度对成绩的影响存在交互作用,F(2,18)=15.2,P<0.05。
即当文章主题熟悉性不同时,生字密度对儿童阅读理解的影响有统计学差异。
正如交互效应图所示,当阅读的文章类型不熟悉时,不同生字密度下测试的成绩差距不大(见蓝色线条),而当熟悉文章的类型时,不同生字密度下测试的成绩相差很大(见红色线条)。
6个水平组合中,两两之间的差异到底如何呢?需要进行简单效应分析。
开始分析打开SPSS一般线性模型(单变量)菜单。
因变量“成绩”,固定因子“文章类型”、“生字密度”,打开模型对话框,创建两个因素的主效应加二者的交互作用模型项。
其他参数按软件默认即可,返回主对话框。
SPSS方差分析对话框中并没有内置简单效应参数选项,我们需要使用SPSS的语法代码。
此时在主对话框点击【粘贴】按钮,打开该过程的语法窗口。
如下所示。
请将以下这两行代码粘贴至已有代码中,建议放在最后一行之前。
/EMMEANS=TABLES(文章类型*生字密度)COMPARE(文章类型)ADJ(LSD)/EMMEANS=TABLES(文章类型*生字密度)COMPARE(生字密度)ADJ(LSD)其中:EMMEANSE是estimated marginal means subcommand的缩写,意思是估计边际平均数,TABLES函数以透视表格形式输出边际平均值;COMPARE指定要比较的分组变量;SPSS默认提供lsd ,bonferroni和sidak这三种两两比较方法,本例选择lsd法。
试验统计方法名词解释

一、名词解释1.试验方案:根据试验目的和要求所拟进行比较的一组试验处理的总称。
2.试验因素:被变动并设有比较的一组处理的因子。
简称因素或因子。
3.单因素实验:整个试验中只变更、比较一个试验因素的不同水平,其它作为试验条件的因素均严格控制一致的试验。
4.多因素试验:在同一试验方案中包含两个或两个以上的试验因素,各个因素都分为不同水平,其它试验条件均严格控制一致的试验。
5.处理组合:各因素不同水平的组合。
6.试验指标:用于衡量试验效果的指示性状。
7.试验效应:试验因素对试验指标所起的增加或减少的作用。
8.简单效应:在同一因素内两种水平间试验指标的相差。
9.平均效应:一个因素内各简单效应的平均数。
也称主要效应,简称主效。
10.交互作用效应:两个因素简单效应间的平均差异。
简称互作。
11.准确度:试验中某一性状的观察值与其理论值真值的接近程度。
12.精确度:试验中同一性状的重复观察值彼此接近的程度。
(即试验误差的大小)13.空白试验:在整个试验地上种植单一品种的作物。
14.田间试验设计:广义上指整个试验研究课题的设计,狭义上指小区技术。
15.试验小区:在田间试验中,安排处理的小块地段。
简称小区。
16.边际效应:小区两边或两端的植株,因占较大空间而表现的差异。
17.生长竞争:相邻小区种植不同品种或施用不同肥料时,由于株高、分蘖力或生长期的不同,通常有一行或更多行受到影响。
18.区组:将全部处理小区分配于具有相对同质的一块土地上。
19.完全区组:重复与区组相等,每一区组或重复包含有全套处理。
20.不完全区组:一个重复安排在几个区组上,每个区组只安排部分处理。
21.主区:在裂区设计中,按主处理划分的小区。
也称整区。
22.副区:裂区设计中,主区内按各副处理划分的小区。
也称裂区。
23.总体:具有共同性质的个体所组成的集团。
24.观察值:每一个体的某一性状、特性的测定数值。
25.变数:观察值的集合。
26.变量:观察值中的每个成员。
试验统计方法名词解释

一、名词解释1.试验方案:根据试验目的和要求所拟进行比较的一组试验处理的总称。
2.试验因素:被变动并设有比较的一组处理的因子。
简称因素或因子。
3.单因素实验:整个试验中只变更、比较一个试验因素的不同水平,其它作为试验条件的因素均严格控制一致的试验。
4.多因素试验:在同一试验方案中包含两个或两个以上的试验因素,各个因素都分为不同水平,其它试验条件均严格控制一致的试验。
5.处理组合:各因素不同水平的组合。
6.试验指标:用于衡量试验效果的指示性状。
7.试验效应:试验因素对试验指标所起的增加或减少的作用。
8.简单效应:在同一因素内两种水平间试验指标的相差。
9.平均效应:一个因素内各简单效应的平均数。
也称主要效应,简称主效。
10.交互作用效应:两个因素简单效应间的平均差异。
简称互作。
11.准确度:试验中某一性状的观察值与其理论值真值的接近程度。
12.精确度:试验中同一性状的重复观察值彼此接近的程度。
(即试验误差的大小)13.空白试验:在整个试验地上种植单一品种的作物。
14.田间试验设计:广义上指整个试验研究课题的设计,狭义上指小区技术。
15.试验小区:在田间试验中,安排处理的小块地段。
简称小区。
16.边际效应:小区两边或两端的植株,因占较大空间而表现的差异。
17.生长竞争:相邻小区种植不同品种或施用不同肥料时,由于株高、分蘖力或生长期的不同,通常有一行或更多行受到影响。
18.区组:将全部处理小区分配于具有相对同质的一块土地上。
19.完全区组:重复与区组相等,每一区组或重复包含有全套处理。
20.不完全区组:一个重复安排在几个区组上,每个区组只安排部分处理。
21.主区:在裂区设计中,按主处理划分的小区。
也称整区。
22.副区:裂区设计中,主区内按各副处理划分的小区。
也称裂区。
23.总体:具有共同性质的个体所组成的集团。
24.观察值:每一个体的某一性状、特性的测定数值。
25.变数:观察值的集合。
26.变量:观察值中的每个成员。
单因素交互作用简单效应分析

单因素交互作用简单效应分析一、单因素分析是一种最基本的统计方法,用于研究一个因素对一个变量的影响。
在单因素分析中,只有一个自变量(也被称为因素)和一个因变量。
通过对自变量的不同水平进行操作,观察因变量的变化情况,从而揭示二者之间的关系。
单因素分析可以通过方差分析(ANOVA)进行。
ANOVA是一种比较多个样本均值之间差异的统计方法,它可以判断这些差异是否具有统计学意义。
在实际应用中,可以将ANOVA分为单因素单水平、单因素多水平和多因素等不同类型。
单因素分析的一个重要应用是比较不同组别之间的均值差异。
例如,研究人员想要比较两个不同教学方法对学生成绩的影响,可以将学生分为两组,分别接受不同的教学方法,然后通过对比两组学生成绩的均值来判断两种教学方法是否有显著差异。
二、交互作用分析是用于研究两个或更多因素之间的相互作用效应。
在交互作用分析中,主要研究因素之间的相互作用是否对因变量产生了显著的影响。
与单因素分析不同,交互作用分析考虑了两个或多个因素的联合效应。
交互作用分析可以通过方差分析、回归分析等方法进行。
其中,方差分析多用于比较两个及以上的组别之间的差异,而回归分析则可以用于研究连续因变量和离散因变量之间的交互作用。
交互作用分析的一个重要应用是研究两个或多个因素对其中一种药物的疗效是否存在相互影响。
例如,研究人员可能想要探究不同性别和不同年龄群体对其中一种药物的疗效是否存在差异,通过分析性别和年龄之间的交互作用,可以评估这两个因素对药物疗效的相互影响。
三、简单效应分析是一种用于研究交互作用的方法,通过将因素分成不同的水平进行比较,以揭示因素对因变量的影响。
简单效应分析主要关注因素在不同情况下对因变量的差异。
简单效应分析可以通过t检验、方差分析等方法进行。
其中,t检验适用于比较两个组别之间的差异,而方差分析适用于比较两个以上组别之间的差异。
简单效应分析的一个重要应用是研究两个或多个因素对一些变量的影响是否存在差异。
单因素交互作用简单效应分析概要

单因素交互作用简单效应分析概要在数据分析过程中,单因素、交互作用和简单效应分析是常用的统计方法,用于探究变量之间的关系、影响和解释。
下面将对这些概念进行详细介绍。
1.单因素分析单因素分析是一种用于研究一个自变量对一个因变量的影响的统计方法。
它可以帮助我们了解一个变量的效应以及它对因变量的贡献。
在单因素分析中,我们控制其他可能影响因变量的变量,将自变量进行分类或相关指标进行比较,从而确定自变量对因变量的影响大小。
在实际应用中,单因素分析常用于实验和观察研究中。
例如,研究员想要了解不同教育水平对工资收入的影响,可以将参与者分为高中、本科和硕士研究生三组,然后比较不同组的平均收入。
单因素分析的结果通常通过方差分析(ANOVA)进行统计推断。
ANOVA可以帮助我们判断不同组的均值差异是否显著,并提供相应的统计指标,如F值和p值。
2.交互作用分析交互作用分析是一种用于检验两个或多个自变量之间是否存在相互作用的统计方法。
相互作用表示自变量之间的效应取决于其他自变量的水平。
换句话说,当自变量间存在交互作用时,它们一起对因变量产生的效应不是简单的加和,而是有相互作用的复杂效应。
交互作用的检验通常使用方差分析方法或回归分析中的交叉项(interaction term)来实现。
例如,在研究体重对性别和年龄的影响时,研究者可以使用卡方检验或线性回归模型来检验体重和性别、年龄之间的交互作用。
交互作用分析对于理解多个自变量之间的复杂关系非常重要。
它可以帮助我们识别变量间的非线性关系、探索特定子群体的差异以及设计并解释实验结果。
3.简单效应分析简单效应分析是一种用于解释交互作用的统计方法。
当我们在交互作用检验中发现存在交互作用时,简单效应分析可以帮助我们了解自变量间交互作用的具体性质和方向。
简单效应分析通过研究不同自变量水平对因变量的影响来实现。
对于存在交互作用的自变量组合,我们计算各组的平均值并进行比较,以确定其对因变量的影响差异。
简单交互效应和简单简单效应分析

between-subject designif three-way interaction is signifcant , compute the simple interaction effect.**********simple interaction effect******************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/design = gender*grade within depart(1)gender*grade within depart(2).if the simple interaction effect is not signifcant , compute the simple effect.如果简单交互效应不显著,那么就计算***************simple effect*********************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/design = grade within depart(1)gender within depart(1).**************multiple comparison s***************** manovatotal by gender (1,2) depart (1,2) grade(1,3)/contrast (grade) = special (1 1 1 1 -1 0 1 0 -1)/design = grade within depart(1).manovatotal by gender (1,2) depart (1,2) grade(1,3)/contrast (grade) = special (1 1 1 1 -1 0 0 1 -1)/design = grade within depart(1).if the simple interaction is significant ,compute the simple simple effect.简单交互效应显著,计算简单简单效应。
SPSS如何做交互作用后简单效应分析

SPSS如何做交互作用后简单效应分析当两个或多个因素之间出现交互作用时,就需要进行简单效应检验。
比如在两因素2A(a1,a2)*2B(b1,b2)的实验设计中,如果A和B之间有交互作用,可以用简单效应来查看A因素在B因素的各个水平上(b1,b2)的处理效应,或者B因素在A因素各个水平上(a1,a2)的处理效应。
SPSS里面需要自己写语句,但是挺简单的。
举两因素完全被试内设计的例子,可以这样写:manova A1B1 A1B2 A2B1 A2B2 %列出因素结合的变量名/wsfactor=A(2) B(2) %表明完全被试内设计/wsdesign=A within B(1)A within B(2). %计算A因素分别在B因素两个水平上的处理效应,别忘了最后那个点。
例如A和B是组内变量,C是组间变量,如果考察组内变量A在B和C某一水平结合上的处理效应,可以这样写:比如可以把组间变量C想象成性别(男,女),想分别看对于男被试,A因素在B1上的处理效应是否有差异。
manova A1B1 A1B2 A2B1 A2B2 BY C(1,2)/wsfactors = A(2)B(2)/wsdesin = A within B(1)/design = mwithin C(1).如果是三因素混合设计,其中F,S均是两个水平的组内自变量,A是三个水平的组间变量,现在想研究F*S的交互作用在A上的情况*THREE-FACTOR MIXED MEASURED EXPERIMENT ANOVA. *SIMPLE EFFECTS.MANOVA F1S1 F1S2 F2S1 F2S2 BY A(1,3)/WSFACTORS = F(2)S(2)/WSDESIGN = F WITHIN S(1)/DESIGN = MWITHIN A(1).。
三个变量的交互作用简单效应简单效应分析

三个变量的交互作用简单效应简单效应分析Main effect 一个因素的独立效应,即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较,不考虑其他因素。
Interaction 多个因素的联合效应,A因素的作用受到B因素的影响,即有交互——two-way interaction. 当一因素作用受到另外两个因素影响,即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用,A*B, A*R, B*R三重交互作用,A*B*C结果发现,A, B为被试间因素,交互作用SIG当二重交互作用SIG,需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG,需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上,R1 与 R2 差异在A1B2水平结合上,R1 与 R2 差异在A2B1水平结合上,R1 与 R2 差异在A2B2水平结合上,R1 与 R2 差异在A3B1水平结合上,R1 与 R2 差异在A3B2水平结合上,R1 与 R2 差异重复测量方差分析之后,如果三重交互作用显著,需要编辑语法,得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时,也会报告多重比较结果,会有更直观的对比结果。
如果三重交互作用SIG,需要进行简单简单效应检验。
固定某两个因素水平组合,考察研究者最感兴趣的那个变量的效应。
单因素交互作用简单效应分析

单因素交互作用简单效应分析单因素分析是研究一种因素对结果变量的影响的一种统计方法。
在进行单因素分析时,只考虑研究中的一个变量,其他变量保持不变。
这种分析可以帮助研究人员了解不同变量的影响程度,并且可以用于比较不同组别之间的差异。
交互作用是指在进行多因素分析时,不同因素之间的相互作用。
简单来说,当多个因素同时存在时,它们的效应可能不仅是各自的效应之和,而是相互叠加产生的新的效应。
交互作用的存在可以改变我们对因素效应的理解和解释。
简单效应分析是用于研究交互作用的一种方法。
在进行简单效应分析时,研究人员会将原始数据进行重新分组,然后对其中的每个组别进行单因素分析。
通过这种方法,研究人员可以更好地理解在交互作用下各个组别的效应。
为了更好地说明单因素、交互作用和简单效应分析的概念和应用,我们可以举一个具体的例子作为说明。
假设我们正在研究一种新的药物对其中一种疾病的治疗效果。
研究中有两个变量:药物剂量和患者的年龄。
我们希望了解药物剂量和年龄对治疗效果的影响。
首先,我们可以进行单因素分析来研究药物剂量对治疗效果的影响。
我们将患者分为两组,一组给予低剂量的药物,另一组给予高剂量的药物。
然后,我们比较两组患者的治疗效果,例如疾病的缓解程度或者生存率。
通过这种分析,我们可以评估药物剂量对治疗效果的影响。
接下来,我们可以使用交互作用来研究药物剂量和年龄对治疗效果的影响。
我们将年龄分为两组,一组为年轻患者,一组为老年患者。
然后,我们比较低剂量和高剂量药物在两个年龄组内的治疗效果。
如果交互作用是存在的,那么不同年龄组的药物剂量对治疗效果的影响可能是不同的。
最后,我们可以进行简单效应分析,通过比较不同年龄组内低剂量和高剂量药物的治疗效果,来进一步理解交互作用。
例如,我们可以发现对于年轻患者,高剂量药物的治疗效果更好;而对于老年患者,低剂量药物的治疗效果更好。
通过这种方式,我们可以更好地理解交互作用对治疗效果的影响。
总之,单因素分析、交互作用和简单效应分析是统计学中常用的方法,用于研究因素对结果变量的影响。
两因素实验设计中单纯主效应

A因素的两个水平在b1水平的方差,显然是不显著的。 A因素的两个水平在b2水平的方差,显然是显著的。
b2 b1
a1
a2
a1
a2
注意:必须在交互作用的前提下才可以讨论。
用例子说明在spss上的操作:
如果在文章生字密度的研究中,同时想探讨文 章熟悉性对阅读理解的影响,可以做一个两因 素完全随机实验设计。研究者预期,当文章主 题熟悉性不同时,生字密度对阅读理解的影响 可能产生变化。他选择了两种类型的文章:主 题是儿童不熟悉的(a1)例如激光技术,和主 题是儿童非常熟悉的(a2)例如春游。他使用 的三种生字密度是5:1(b1)、10:1(b2)和 20:1(b3)。这是一个两因素实验设计,实验中 有6种处理水平的结合。选择24名五年级学生, 将他们随机分为6组,每组接受一种水平的处 理。(数据下页)
弱
强
Байду номын сангаас
自学能力
传 统 教 学
集 教学方式 体 讨 论
交互作用:当一个因素的水平在另一个因素的不 同水平上变化趋势不一致时,我们称两个因素之 间存在交互作用。
A教学方式:a1传统教学a2集体讨论
B自学能力:b1能力强b2能力弱
学 习 成 绩 b1
b2
a1
a2
1.在b1水平,被试在a1,a2两种条件 下分数没有什么差别。在b2水平上, 被试在a1水平的分数远远高于a2水平 的分数。这表明:自学能力弱的同学 的分数受老师教学方式的影响非常大, 而自学能力强的人并没有因老师的教 学方式不同而有大的差异。所以,b1、 b2在A因素两个水平上的变化趋势是 不相同的,即学习能力这个因素受到 老师教学方式的影响非常大。因此我 们可以认为,学生的学习成绩是受到 老师教学方式和学习能力共同作用而 改变的,二者是有交互作用的。
主效应交互效应简单效应

主效应交互效应简单效应
主效应是指一个自变量或处理因素对因变量的影响。
例如,一个药物对疾病的治疗效果就是一个主效应。
交互效应是指两个或多个自变量或处理因素之间的相互作用对
因变量的影响。
例如,在评估一种新的药物疗法时,药物的剂量和病人的性别可能会互相影响。
简单效应是指当一个自变量或处理因素保持不变时,另一个自变量或处理因素对因变量的影响。
例如,在上述药物疗法的例子中,如果病人的性别被固定,那么药物剂量对治疗效果的影响就是简单效应。
对于一个实验设计和数据分析来说,理解主效应、交互效应和简单效应的概念非常重要,因为它们有助于解释因变量的变化和了解实验条件之间的关系。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Sig. .000
F值
p值
自由度 组内均方
研究报告中的方差分析结果
One-Way ANOVA通常用文字陈述结果
自由度、均方、F、P 因素较多时则用三线表呈现
自由度、均方、F 单因素而、交p值互作以用星、简号单的效形应分式析标注
毕业论文格式
结果
A NOVA
阅 读理 解 成 绩
Sum of Squares Between19G0r.o1u2p5s Within Gr7o8u.7p5s 0 Total 268.875
8.1 单因素完全随机方差分析
One-Way ANOVA
单因素、交互作用、简单效应分析
例1:单因素完全随机实验设计
目的:文章生字密度对学生阅读理解成绩的影响 自变量:生字密度,含4个水平
(5:1、10:1、15:1、20:1) 因变量:阅读测验的分数 被试及程序:32人,随机分为四组,每组接受一
单因素、交互作用、简单效应分析
生字密度对学生阅读理解的影响
(按智力测验成绩划分8个区组)
shuhua_p_45.sav
生字密度 5:1 10:1 15:1 20:1
阅 区组1 3
4
8
9
读 区组2 6
6
9
8
理 区组3 4
4
8
8
解 测 验
区组4 区组5
3 5
2 4
7
7
5
12
分 区组6 7
5
6
13
数 区组7 5
单击后出现一个对话框,用于设置在模型中包含哪些 主效应和交互因子,默认情况为Full factorial,即分 析所有的主效应和交互作用。
本例没有交互作用 可分析,所以要改
单因素、交互作用、简单效应分析
即 【custom 】
【Buil Term】【main effcts】 单因素、交左互边作用变、量简的单效全应选 3 63.37522.533
28 2.813 31
Sig. .000
由方差分析表可知, F(3,28)=22.533,p<.01, 学生对生字密度不同的文章的阅读理解有显著差异 生字密度对阅读理解成绩有影响。
单因素、交互作用、简单效应分析
结果
多重比较
单因素、交互作用、简单效应分析
单因素方差分析
General Linear Model
• Univariate
单因变量方差分析
• Multivariate
多因变量方差分析
• Repeated Measures 含有重复测量的方差分析
单因素、交互作用、简单效应分析
很常用
含有重 复测量 的数据
很少用, 因变量不 止一个时
单因素、交互作用、简单效应分析
20:1 9 8 8 7 12 13 12 11
即自变量
即多重比较 也称事后检 验
单因素、交互作用、简单效应分析
单因素、交互作用、简单效应分析
结果
Test of Homogeneity of V ariances
阅读 理解成 绩
Lev ene Stat ist ic
d f1
3 .23 5
3
d f2 28
单击后出现一个对话框,用于设置在模型中包含哪些 主效应和交互因子,默认情况为Full factorial,即分 析所有的主效应和交互作用。
本例没有交互作用 可分析,所以要改
单因素、交互作用、简单效应分析
例2:单因素随机区组设计
题目:文章的生字密度对学生阅读理解的影响 自变量:生字密度,含有4个水平
1 54 4. 00 0
S ig. .0 37
p值
由p=.037<.05可知, 边缘显著 可认为方差齐性
单因素、交互作用、简单效应分析
结果
组间均方
A NOVA
阅 读理 解 成 绩
Sum of Squares Between19G0r.o1u2p5s Within Gr7o8u.7p5s 0 Total 268.875
df Mean Square F 3 63.37522.533
练习1
• 数据文件“自信心与社交苦恼” • 任务1:在1总自信平均分上,男生与女生是否存
在显著差异; • 任务2:在1总自信平均分上,各个年级间是否存
在显著差异
单因素、交互作用、简单效应分析
8.2 单因素随机区组方差分析
Univariate
单因素、交互作用、简单效应分析
因变量
绝大多数时候 自变量都应该 往里面选 用于选入随机因素,如果你不明白,假装没 单因素、交互看作见用他、简就单是效了应分。析
df Me an Square F
10
21.600 8.579
Int erce pt
1 27 5. 12 5
1 1275.125 506.433
GRO UP
1 90 .1 25
3
63.375 25.170
IQ
2 5. 87 5
7
3.696 1.468
Erro r
5 2. 87 5
21
2 .5 18
T otal
单因素、交互作用、 简单效,应分析
单因素、交互作用、简单效应分析
方差分析的适用条件
• 变异的可加性 • 总体正态分布 • 方差齐性(总体方差相等)
实际应用中,对方差齐性要求较高,因此需要单独检验。
单因素、交互作用、简单效应分析
SPSS中的4个方差分析菜单
Compare Means
One-Way ANOVA
个自变量处理(即阅读一种生字密度的文章)
单因素、交互作用、简单效应分析
One Way ANOVA: 生字密度对学生阅读理解的影响
shuhua_p_39.sav
生字密度
阅 读 理 解 测 验 分 数
5:1 10:1
3
4
6
6
4
4
3
2
5
4
7
5
5
3
2 3 单因素、交互作用、简单效应分析
15:1 8 9 8 7 5 6 7 6
(5:1、10:1、15:1、20:1) 因变量:阅读测验的分数 无关变量:被试的智力水平
(区组变量) 实验设计:单因素随机区组实验设计 被试及程序:首先给32个学生做智力测验,并按测验分
数将被试分成8个组,每组4人(智力水平相等),然后 随机分配每个区组内的4个被试阅读一种生字密度的文 章。
3
7
12
区组8 2 3 单因素、交互作用、简单效应分析
6
11
数据录入
单因素、交互作用、简单效应分析
Test s of Bet ween-Subject s Effect s
Depe ndent V ariable : SCORE
T ype III Sum
S ou rc e
o f Squares
Corre ct ed Model 2 16 .0 00 a
