假设图G采用邻接表存储
信息学模拟试卷一

模拟试卷一一、单项选择题1.若某链表中最常用的操作是在最后一个结点之后插入一个结点和删除最后一个结点,则采用存储方式最节省运算时间。
(1)单链表 (2)双链表(3)单循环链表 (4)带头结点的双循环链表2.设一个栈的输入序列为A,B,C.,D,则借助一个栈所得到的输出序列不可能是(1)A,B,C,D (2)D,C,B,A (3)A,C,D,B (4)D,A,B,C3.串是。
(1)不少于一个字母的序列 (2)任意个字母的序列(3)不少于一个字符的序列 (4)有限个字符的序列4.链表不具有的特点是。
(1)可随机访问任一元素 (2)插入删除不需要移动元素(3)不必事先估计存储空间 (4)所需空间与线性表长度成正比5.在有n个叶子结点的哈夫曼树中,其结点总数为。
(1)不确定 (2)2n (3)2n+1 (4)2n-16.任何一个无向连通图的最小生成树(1)只有一棵 (2)有一棵或多棵 (3)一定有多棵 (4)可能不存在7.将一棵有100个结点的完全二叉树从根这一层开始,每一层上从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为。
(1)98 (2)99 (3)50 (4)488.下列序列中,是执行第一趟快速排序后得到的序列(排序的关键字类型是字符串)。
(1)[da,ax,eb,de,bb]ff[ha,gc] (2)[cd,eb,ax,da]ff[ha,gc,bb] (3)[gc,ax,eb,cd,bb]ff[da,ha] (4)[ax,bb,cd,da]ff[eb,gc,ha] 9.用n个键值构造一棵二叉排序树,最低高度为。
(1)n/2 (2)n (3)[log2n] (4)[log2n+1]10.二分查找法要求查找表中各元素的键值必须是排列。
(1)递增或递减 (2)递增 (3)递减 (4)无序11.对于键值序列(12,13,11,18,60,15,7,18,25,100),用筛选法建堆,必须从键值为的结点开始。
数据结构考试题2

else
break;
}
while (p!=NULL && q!=NULL && p->data==q->data)
{//当两者值相等时同步后移
p=p->next;
q=q->next;
}
if (q==NULL)//当B中节点比较完毕返回1
return 1;
else//否则返回0
return 0;
三
1.设A=(a1,a2,…,an),B=(b1,b2,…,bm)是两个递增有序的线性表(其中n、m均大于1),且所有数据元素均不相同。假设A、B均采用带头节点的单链表存放,设计一个尽可能高效的算法判断B是否为A的一个子序列,并分析你设计的算法的时间复杂度和空间复杂度。(15分)
2.假设二叉树b采用二叉链存储结构存储,试设计一个算法,输出该二叉树中从根节点出发的第一条最长的路径长度,并输出此路径上各节点的值。并分析你设计的算法的时间复杂度和空间复杂度。(15分)
{//pathlen和maxpathlen的初值均为0
int i;
if (b==NULL)
{if (pathlen>maxpathlen)//通过比较求最长路径
{for (i=pathlen-1;i>=0;i--)
maxpath[i]=path[i];
maxpathlen=pathlen;
}
}
else
}
}
A. O(n)B. O( )
C. O(nlog2n)D. O(log2n)
3.在一个双链表中,删除p所指节点(非首、尾节点)的操作是。
A.p->prior->next=p->next;p->next->prior=p->prior;
计算机学科专业基础综合数据结构-图(二)_真题-无答案

计算机学科专业基础综合数据结构-图(二)(总分100,考试时间90分钟)一、单项选择题(下列每题给出的4个选项中,只有一个最符合试题要求)1. 具有6个顶点的无向图至少应有______条边才能确保是一个连通图。
A.5 B.6 C.7 D.82. 设G是一个非连通无向图,有15条边,则该图至少有______个顶点。
A.5 B.6 C.7 D.83. 下列关于无向连通图特性的叙述中,正确的是______。
①所有顶点的度之和为偶数②边数大于顶点个数减1③至少有一个顶点的度为1A.只有① B.只有② C.①和② D.①和③4. 对于具有n(n>1)个顶点的强连通图,其有向边的条数至少是______。
A.n+1B.nC.n-1D.n-25. 下列有关图的说法中正确的是______。
A.在图结构中,顶点不可以没有任何前驱和后继 B.具有n个顶点的无向图最多有n(n-1)条边,最少有n-1条边 C.在无向图中,边的条数是结点度数之和 D.在有向图中,各顶点的入度之和等于各顶点的出度之和6. 对于一个具有n个顶点和e条边的无向图,若采用邻接矩阵表示,则该矩阵大小是______,矩阵中非零元素的个数是2e。
A.n B.(n-1)2 C.n-1 D.n27. 无向图的邻接矩阵是一个______。
A.对称矩阵 B.零矩阵 C.上三角矩阵 D.对角矩阵8. 从邻接矩阵可知,该图共有______个顶点。
如果是有向图,该图共有4条有向边;如果是无向图,则共有2条边。
A.9 B.3 C.6 D.1 E.5 F.4 G.2 H.09. 下列说法中正确的是______。
A.一个图的邻接矩阵表示是唯一的,邻接表表示也唯一 B.一个图的邻接矩阵表示是唯一的,邻接表表示不唯一 C.一个图的邻接矩阵表示不唯一,邻接表表示唯一 D.一个图的邻接矩阵表示不唯一,邻接表表示也不唯一10. 用邻接表存储图所用的空间大小______。
A.与图的顶点数和边数都有关 B.只与图的边数有关 C.只与图的顶点数有关 D.与边数的二次方有关11. 采用邻接表存储的图的深度优先搜索算法类似于二叉树的______,广度优先搜索算法类似于二叉树的层次序遍历。
山东专升本数据结构练习1

一、填空题:(每小题2分,共10分)1. 设有数据结构(D,R),其中D 是数据元素的有限集,R 是的有限集。
2. 深度为k 的二叉树其结点数至多有个。
3. 栈是一种特殊的线性表,它允许在表的一端进行操作。
4. 通常象交通、道路问题的数学模型是一种称为的数据结构。
5. 哈希表是一种查找表,可以根据哈希函数直接获得。
二、单项选择题:(每小题2分,共10分)对于下列各题,在备选答案中选出一个正确的,并将其编号填在“”位置上。
1. 若线性表最常用的操作是存取第i 个元素及其前驱元素的值,则采用存储方式最节省运算时间。
A. 单链表B. 双链表C. 单循环链表D. 顺序表2. 下列排序算法中,算法在进行一趟相应的排序处理结束后不一定能选出一个元素放到其最终位置上。
A. 直选择排序B. 冒泡排序C. 归并排序D. 堆排序3. 队列的操作原则是。
A. 先进后出B. 先进先出C. 只能进行插入D. 只能进行删除4. 在具有n 个结点的二叉链表中,非空的链域个数为。
A. n-1B. nC. n+1D. 不确定5. 对具有n 个元素的有序查找表采用折半查找算法查找一个键值,其最坏比较次数的数量级为。
A. O(log2n)B. O(n)C. O(nlog2n)D. O(n2)三、判断题:(每小题2分,共10分)判断下列各题是否正确,若正确,在题后的括号内填“T”,否则填“F”。
1. 在栈为空的情况下不能作出栈处理,否则,将产生下溢出。
()2. 如果有向图G=(V, E) 的拓扑序列唯一,则图中必定仅有一个顶点的入度为0、一个顶点的出度为0。
()3. 在大根堆中,必定满足每个结点的键值大于其左右子树中所有结点的键值。
()4. 在采用线性探测法处理冲突的散列表中所有同义词在表中相邻。
()5. 在索引顺序表中,对索引表既可采用顺序查找,也可采用二分查找。
()四、解答下列各题:(每题10分,共40分)1. 已知线性表L 采用带头结点的的单向循环链表表示,试给出它的存储结构类型描述及相应的示意图。
《数据结构》单元测试1(含答案)

《数据结构》单元测试1一、选择题(每题2分,共40分)1.数据的最小单位是( A)。
(A) 数据项(B) 数据类型(C) 数据元素(D) 数据变量2. 栈和队列的共同特点是( A )。
(A)只允许在端点处插入和删除元素(B)都是先进后出(C)都是先进先出(D)没有共同点3. 用链接方式存储的队列,在进行插入运算时( D )。
(A)仅修改头指针(B)头、尾指针都要修改(C)仅修改尾指针 (D)头、尾指针可能都要修改4. 以下数据结构中哪一个是非线性结构?( D )(A)队列(B)栈(C)线性表(D)二叉树5.函数substr(“DATASTRUCTURE”,5,9)的返回值为( A )。
(A) “STRUCTURE”(B) “DATA”(C) “ASTRUCTUR”(D) “DATASTRUCTURE”6.设一个有序的单链表中有n个结点,现要求插入一个新结点后使得单链表仍然保持有序,则该操作的时间复杂度为( D)。
(A) O(log2n) (B) O(1) (C) O(n2) (D) O(n)7.设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为Nl,……,度数为m的结点数为Nm,则N0=( B)。
(A) Nl+N2+……+Nm(B) 1+N2+2N3+3N4+……+(m-1)Nm(C) N2+2N3+3N4+……+(m-1)Nm (D) 2Nl+3N2+……+(m+1)Nm 8.设有序表中有1000个元素,则用二分查找查找元素X最多需要比较( B)次。
(A) 25 (B) 10 (C) 7 (D) 19. 二叉树的第k层的结点数最多为( D )。
(A)2k-1 (B) 2K+1 (C) 2K-1 (D)2k-110. 树最适合用来表示( C )。
(A)有序数据元素(B)无序数据元素(C)元素之间具有分支层次关系的数据 (D)元素之间无联系的数据个权构成一棵Huffman树,其节点总数为( A )。
数据结构期末复习题

练习题:一、填空题1、元素项是数据的最小单位,数据元素是讨论数据结构时涉及的最小数据单位。
2、设一棵完全二叉树具有100个结点,则此完全二叉树有49个度为2的结点。
3、在用于表示有向图的邻接矩阵中,对第i列的元素进行累加,可得到第i个顶点的出度。
4、已知一棵度为3的树有2个度为1的结点,3个度为2的结点,4个度为3的结点,则该树中有12个叶子的结点。
n=n0+n1+n2+…+nm (1)又有除根结点外,树中其他结点都有双亲结点,且是唯一的(由树中的分支表示),所以,有双亲的结点数为:n-1=0*n0+1*n1+2*n2+…+m*nm (2)联立(1)(2)方程组可得:叶子数为:n0=1+0*n1+1*n2+2*n3+...+(m-1)*nm5、有一个长度为20的有序表采用二分查找方法进行查找,共有4个元素的查找长度为3。
6、对于双向链表,在两个结点之间插入一个新结点需要修改的指针共4个。
删除一个结点需要修改的指针共2个。
7、已知广义表LS=(a,(b,c,d),e),它的深度是2,长度是3。
8、循环队列的引入是为了克服假溢出。
9、表达式a*(b+c)-d/f的后缀表达式是abc+*df/-。
10、数据结构中评价算法的两个重要指标是时间复杂度和空间复杂度。
11、设r指向单链表的最后一个结点,要在最后一个结点之后插入s所指的结点,需执行的三条语句是r->next=s; r=s; r->next=null;12、设有一个空栈,栈顶指针为1000H(十六进制),现有输入序列为1,2,3,4,5,经过PUSH,PUSH,POP,PUSH,POP,PUSH,PUSH之后,输出序列是23,而栈顶指针值是1012_H。
设栈为顺序栈,每个元素占4个字节。
13、模式串P=‘abaabcac’的next函数值序列为01122312。
14、任意连通图的连通分量只有一个,即是自身。
15、栈的特性是先进后出。
16、串的长度是包含的元素个数。
JAV数据库考题适用于大连东软信息学院

5.8 习题5.8.1 知识点:图的基本概念一、选择题1①n个顶点的连通图至少有( A )条边。
A.n-1 B.nC.n+1 D.02① 在无向图中定义顶点vi与vj之间的路径为从vi到达vj的一个(B )。
A .顶点序列B .边序列C.权值总和 D .边的条数3① 具有n个顶点的有向图最多可包含(D )条有向边。
A. n-1B. nC. n(n-1)/2D. n(n-1)4①在无向图中定义顶点的度为与它相关联的(B )的数目。
A .顶点B .边C.权 D .权值5①一个有N个顶点的无向图中,要连通全部顶点至少需要(C )条边。
A. NB. N+1C. N -1D. N/26② 含N个顶点的连通图中的任意一条简单路径,其长度不可能超过( C )。
A. 1B. N/2C. N -1D. N7② 设无向图的顶点个数为n,则该图最多有(B )条边。
【清华大学1998】【西安电子科技大1998】【北京航空航天大学1999】A. n-1B. n(n-1)/2C. n(n+1)/2D. n(n-1)8② 在一个无向图中,所有顶点的度数之和等于所有边数( B )倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的( C )倍。
【哈尔滨工业大学2001】A. 1/2B. 2C. 1D. 4二、填空题1②n (n> 0)个顶点的无向图中顶点的度的最大值为___n-1 ____ 。
2②n (n> 0)个顶点的无向图最少有___0 _______ 条边。
3②n (n> 0)个顶点的连通无向图各顶点的度之和最少为__2(n-1)__ 。
4② 具有n个顶点的无向完全图,边的总数为__n(n-1)/2 ___ 条;而具有n个顶点的有向完全图边的总数为__n(n-1) ____ 条。
5② 在有n个顶点的有向图中,每个顶点的度最大可达__2(n-1)____ 。
6② 在有n个顶点的有向图中,若要使任意两点间可以互相到达,则至少需要__n___条弧。
图练习与答案
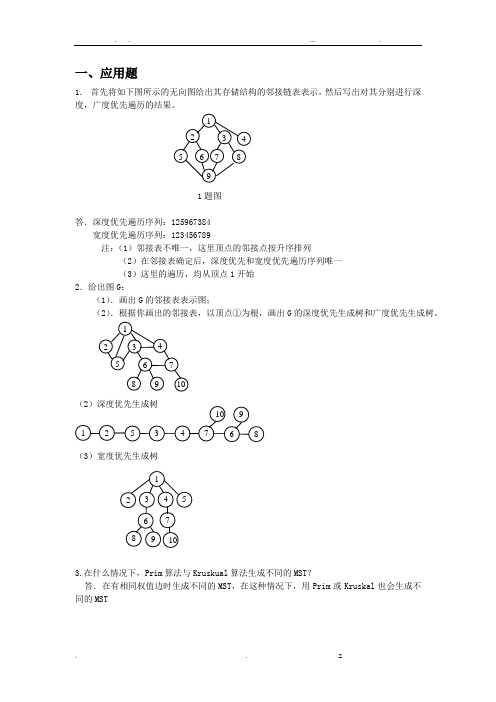
一、应用题1.首先将如下图所示的无向图给出其存储结构的邻接链表表示,然后写出对其分别进行深度,广度优先遍历的结果。
1题图答.深度优先遍历序列:125967384宽度优先遍历序列:123456789注:(1)邻接表不唯一,这里顶点的邻接点按升序排列(2)在邻接表确定后,深度优先和宽度优先遍历序列唯一(3)这里的遍历,均从顶点1开始2.给出图G:(1).画出G的邻接表表示图;(2).根据你画出的邻接表,以顶点①为根,画出G的深度优先生成树和广度优先生成树。
(3)宽度优先生成树3.在什么情况下,Prim算法与Kruskual算法生成不同的MST?答.在有相同权值边时生成不同的MST,在这种情况下,用Prim或Kruskal也会生成不同的MST4.已知一个无向图如下图所示,要求分别用Prim 和Kruskal 算法生成最小树(假设以①为起点,试画出构造过程)。
答.Prim 算法构造最小生成树的步骤如24题所示,为节省篇幅,这里仅用Kruskal 算法,构造最小生成树过程如下:(下图也可选(2,4)代替(3,4),(5,6)代替(1,5))5.G=(V,E)是一个带有权的连通图,则:(1).请回答什么是G 的最小生成树; (2).G 为下图所示,请找出G 的所有最小生成树。
28题图答.(1)最小生成树的定义见上面26题 (2)最小生成树有两棵。
(限于篇幅,下面的生成树只给出顶点集合和边集合,边以三元组(Vi,Vj,W )形式),其中W 代表权值。
V (G )={1,2,3,4,5} E1(G)={(4,5,2),(2,5,4),(2,3,5),(1,2,7)};E2(G)={(4,5,2),(2,4,4),(2,3,5),(1,2,7)}6.请看下边的无向加权图。
(1).写出它的邻接矩阵。
(2).按Prim 算法求其最小生成树,并给出构造最小生成树过程中辅助数组的各分量值。
辅助数组各分量值:7.已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa)、伦敦(L) 、东京(T) 、墨西哥(M),下表给定了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)(1).画出这六大城市的交通网络图;(2).画出该图的邻接表表示法;(3).画出该图按权值递增的顺序来构造的最小(代价)生成树.8.已知顶点1-6和输入边与权值的序列(如右图所示):每行三个数表示一条边的两个端点和其权值,共11行。
数据结构第7章-答案

一、单选题C01、在一个图中,所有顶点的度数之和等于图的边数的倍。
A)1/2 B)1 C)2 D)4B02、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A)1/2 B)1 C)2 D)4B03、有8个结点的无向图最多有条边。
A)14 B)28 C)56 D)112C04、有8个结点的无向连通图最少有条边。
A)5 B)6 C)7 D)8C05、有8个结点的有向完全图有条边。
A)14 B)28 C)56 D)112B06、用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A07、用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A08、一个含n个顶点和e条弧的有向图以邻接矩阵表示法为存储结构,则计算该有向图中某个顶点出度的时间复杂度为。
A)O(n) B)O(e) C)O(n+e) D)O(n2)C09、已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是。
A)0 2 4 3 1 5 6 B)0 1 3 6 5 4 2 C)0 1 3 4 2 5 6 D)0 3 6 1 5 4 2B10、已知图的邻接矩阵同上题,根据算法,则从顶点0出发,按广度优先遍历的结点序列是。
A)0 2 4 3 6 5 1 B)0 1 2 3 4 6 5 C)0 4 2 3 1 5 6 D)0 1 3 4 2 5 6D11、已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是。
A)0 1 3 2 B)0 2 3 1 C)0 3 2 1 D)0 1 2 3A12、已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是。
A)0 3 2 1 B)0 1 2 3 C)0 1 3 2 D)0 3 1 2A13、图的深度优先遍历类似于二叉树的。
A)先序遍历 B)中序遍历 C)后序遍历 D)层次遍历D14、图的广度优先遍历类似于二叉树的。
算法与数据结构重考复习题(0910)

i列1的元素之和 )。对于含n个顶点和e条边的图,采用邻接矩阵表示的空间复杂度为( O(n2) )。连通图
是指图中任意两个顶点之间(都连通的无向图 )。一个有n个顶点的无向连通图,它所包含的连通分量个数最
保持青春的秘诀,是有一颗不安分的心。
算法与数据结构重考复习题(0910)
一、单选题(斜体为答案)
1.数据结构被形式地定义为(D,R),其中D 是
A. 算法 B. 操作的集合 C. 数据元素的集合 D. 数据关系的集合
2.顺序表是线性表的
A. 顺序存储结构 B. 链式存储结构 C. 索引存储结构 D. 散列存储结构
5.已知栈的输入序列为1,2,3....,n,输出序列为a1,a2,...,an,a2=n的输出序列共有(n-1)种输出序列。
队列的特性是先入先出,栈的特性是(后入先出)。如果以链栈为存储结构,则出栈操作时必须判别(栈空 )。与顺序栈相比,链栈有一个明显的优势是( 不易出现栈满 )。
6.循环队列采用数组data[1..n]来存储元素的值,并用front和rear分别作为其头尾指针。为区分队列的满和空,约定:队中能够存放的元素个数最大为(n-l),也即至少有一个元素空间不用,则在任意时刻,至少可以知道一个空的元素的下标是(front) ;入队时,可用语句(rear=rear+1%n)求出新元素在数组data中的下标。
(3)双向链表:q=p->prior; temp=q->data; q->data=p->data;p->data=temp;
2.内存中一片连续空间(不妨设地址从1到m),提供给两个栈S1和S2使用,怎样分配这部分存储空间,使得对任意一个栈,仅当这部分全满时才发生上溢。(为了尽量利用空间,减少溢出的可能,可采用栈顶相向,栈底分设两端的存储方式,这样,对任何一个栈,仅当整个空间全满时才会发生上溢。)
北林 数据结构期末考试(三) 填空题

数据结构填空题天涯古巷 出品1. 向一个长度为n的向量的第i个元素(1≤i≤n+1)之前插入一个元素时,需向后移动 n-i+1 个元素。
2. 向一个长度为n的向量中删除第i个元素(1≤i≤n)时,需向前移动 n-i 个元素。
3. 在顺序表中访问任意一结点的时间复杂度均为 O(1) ,因此,顺序表也称为 随机存取 的数据结构。
4. 在单链表中,除了首元结点外,任一结点的存储位置由 其直接前驱结点的链域的值 指示。
5.对于一个具有n个结点的单链表,在已知的结点*p后插入一个新结点的时间复杂度为 O(1) ,在给定值为x的结点后插入一个新结点的时间复杂度为 O(n) 。
第三章1. 向量、栈和队列都是 线性 结构,可以在向量的 任何 位置插入和删除元素;对于栈只能在 栈顶 插入和删除元素;对于队列只能在 队尾 插入和 队首 删除元素。
2. 栈是一种特殊的线性表,允许插入和删除运算的一端称为 栈顶 。
不允许插入和删除运算的一端称为 栈底 。
3. 队列 是被限定为只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表。
4. 在具有n个单元的循环队列中,队满时共有 n-1 个元素。
第四章1. 不包含任何字符(长度为0)的串 称为空串。
2. 由一个或多个空格(仅由空格符)组成的串 称为空白串。
3. 设S=“A;/document/Mary.doc”,则strlen(s)= 20 , “/”的字符定位的位置为 3 。
4. 子串的定位运算称为串的模式匹配; 被匹配的主串 称为目标串, 子串 称为模式。
5. 设目标T=”abccdcdccbaa”,模式P=“cdcc”,则第 6 次匹配成功。
6. 若n为主串长,m为子串长,则串的古典(朴素)匹配算法最坏的情况下需要比较字符的总次数为 (n-m+1)*m 。
7.设数组a[1…60, 1…70]的基地址为2048,每个元素占2个存储单元,若以列序为主序顺序存储,则元素a[32,58]的存储地址为 8950 。
数据结构联考试卷1及答案

试卷一
一、单项选择题 (每小题 2 分,共 30 分)
1.算法的时间复杂度表征的是( A. 算法的难易程度 C. 执行算法所消耗的存储空间 )。 B. 算法的可读性 D. 执行算法所消耗的时间
7.可以惟一地转化为一棵树的二叉树的特点是( A.根结点没有孩子 C.根结点无左孩子
B.根结点只有一个孩子 D.根结点无右孩子 ) 。
8. 若采用邻接表存储结构, 则图的深度优先搜索类似于二叉树的 ( A.先序遍历 B表 A = (a,(b),(),(c,d,e,f))的长度为( A.3 B.4 C.5 D.6
10.用某种排序方法对关键字序列(25,82,20,45,16,27,66,34, 18)进行排序时,序列的变化情况如下: 18,16,20,25,45,27,66,34,82 16,18,20,25,34,27,45,66,82 16,18,20,25,27,34,45,66,82 则所采用的排序方法是( A.归并排序 ) 。 C.快速排序 D.希尔排序
2.在一个单链表中,若 p 所指结点不是尾元结点,s 指向已生成的新结 点,则在 p 之后插入 s 所指结点的正确操作是( A. s -> next = p -> next; p = s; B. p -> next = s -> next; s -> next = p; C. s -> next = p -> next; p -> next = s; D. s -> next = p; p -> next = s; 3.设循环队列的元素存放在一维数组 A[0..40]中,队列非空时,front 指示队首元素,rear 指示队尾元素的后一个位置。如果队列中元素的个 数为 15,front 的值为 33,则 rear 应指向的位置是( A. A[6] B. A[16] C. A[7] ) 。 D. A[17] ) 。 ) 。
数据结构单元8练习参考答案

单元练习8一.判断题〔以下各题,正确的请在前面的括号内打√;错误的打╳〕〔√〕〔1〕图可以没有边,但不能没有顶点。
〔ㄨ〕〔2〕在无向图中,〔V1,V2〕与〔V2,V1〕是两条不同的边。
〔ㄨ〕〔3〕邻接表只能用于有向图的存储。
〔√〕〔4〕一个图的邻接矩阵表示是唯一的。
〔ㄨ〕〔5〕用邻接矩阵法存储一个图时,所占用的存储空间大小与图中顶点个数无关,而只与图的边数有关。
〔ㄨ〕〔6〕有向图不能进展广度优先遍历。
〔√〕〔7〕假设一个无向图的以顶点V1为起点进展深度优先遍历,所得的遍历序列唯一,则可以唯一确定该图。
〔√〕〔8〕存储无向图的邻接矩阵是对称的,因此只要存储邻接矩阵的上三角〔或下三角〕局部就可以了。
〔ㄨ〕〔9〕用邻接表法存储图时,占用的存储空间大小只与图中的边数有关,而与结点的个数无关。
〔√〕〔10〕假设一个无向图中任一顶点出发,进展一次深度优先遍历,就可以访问图中所有的顶点,则该图一定是连通的。
二.填空题(1)图常用的存储方式有邻接矩阵和邻接表等。
(2)图的遍历有:深度优先搜和广度优先搜等方法。
(3)有n条边的无向图邻接矩阵中,1的个数是_2n____。
(4)有向图的边也称为_ 弧___。
(5)图的邻接矩阵表示法是表示__顶点____之间相邻关系的矩阵。
(6)有向图G用邻接矩阵存储,其第i行的所有元素之和等于顶点i的__出度____。
(7)n个顶点e条边的图假设采用邻接矩阵存储,则空间复杂度为: O〔n2〕。
(8)n个顶点e条边的图假设采用邻接表存储,则空间复杂度为: O〔n+e〕。
(9)设有一稀疏图G,则G采用_邻接表____存储比拟节省空间。
(10)设有一稠密图G,则G采用_邻接矩阵____存储比拟节省空间。
(11)图的逆邻接表存储构造只适用于__有向____图。
(12) n个顶点的完全无向图有 n(n-1)/2_ 条边。
(13)有向图的邻接表表示适于求顶点的出度。
(14)有向图的邻接矩阵表示中,第i列上非0元素的个数为顶点V i的入度。
数据结构教程李春葆课后答案第8章图

3
3
3
3 5 3
图 8.10 图 G
图 8.11 图 G 中的关键路径
14. 假设不带权有向图采用邻接矩阵 g 存储,设计实现以下功能的算法: (1)求出图中每个顶点的入度。 (2)求出图中每个顶点的出度。 (3)求出图中出度为0的顶点数。 解:利用邻接矩阵的特点和相关概念得到如下算法:
????????????????????????????????????????????0303034050640a图89邻接矩阵a10234545643331023454564333图810图g图811图g中的关键路径14
第8章 图
教材中练习题及参考答案
1. 图G是一个非连通图,共有28条边,则该图至少有多少个顶点? 答:由于G是一个非连通图,在边数固定时,顶点数最少的情况是该图由两个连通分 量构成,且其中之一只含一个顶点(没有边),另一个为完全无向图。设该完全无向图的 顶点数为n, 其边数为n(n-1)/2,即n(n-1)/2=28,得n=8。所以,这样的非连通图至少有1+8=9 个顶点。 2. 有一个如图 8.2(a)所示的有向图,给出其所有的强连通分量。 答:图中顶点0、1、2构成一个环,这个环一定是某个强连通分量的一部分。再考察顶 点3、4,它们到这个环中的顶点都有双向路径,所以将顶点3、4加入。考察顶点5、6,它 们各自构成一个强连通分量。该有向图的强连通分量有3个,如图8.2(b)所示。
2
数据结构教程学习指导
接表表示的有向图,图中的边数等于边结点的个数。 (2)对于邻接矩阵g表示的无向图,邻接矩阵数组元素g.edges[i][j]为1表示它们有边相 连,否则为无边相连。对于邻接矩阵g表示的有向图,邻接矩阵数组元素g.edges[i][j]为1表 示从顶点i到顶点j有边,g.edges[j][i]为1表示从顶点j到顶点i有边。 对于邻接表G表示的无向图,若从头结点G->adjlist[i]的单链表中找到编号为j的边表结 点,表示它们有边相连;否则为无边相连。对于邻接表 G 表示的有向图,若从头结点 G->adjlist[i] 的单链表中找到编号为 j的边表结点,表示从顶点 i到顶点 j有边。若从头结点 G->adjlist[j]的单链表中找到编号为i的边表结点,表示从顶点j到顶点i有边。 (3)对于邻接矩阵表示的无向图,顶点i的度等于第i行中元素为1的个数;对于邻接矩 阵表示的有向图,顶点i的出度等于第i行中元素为1的个数,入度等于第i列中元素为1的个 数,顶点i度等于它们之和。 对于邻接表G表示的无向图,顶点i的度等于G->adjlist[i]为头结点的单链表中边表结点 个数。 对于邻接表G表示的有向图,顶点i的出度等于G->adjlist[i]为头结点的单链表中边表结 点的个数;入度需要遍历所有的边结点,若G->adjlist[j]为头结点的单链表中存在编号为 i 的边结点,则顶点i的入度增1,顶点i的度等于入度和出度之和。 5. 对于如图 8.3 所示的一个无向图 G,给出以顶点 0 作为初始点的所有的深度优先遍 历序列和广度优先遍历序列。
数据结构_图_采用邻接矩阵存储,构造无向图

1.采用邻接矩阵(邻接表)存储,构造无向图(网)输入:顶点数、边数、顶点信息、边信息输出:图的顶点,图的边邻接矩阵(数组表示法)处理方法:用一个一维数组存储图中顶点的信息,用一个二维数组(称为邻接矩阵)存储图中各顶点之间的邻接关系。
假设图G=(V,E)有n个顶点,则邻接矩阵是一个n×n 的方阵,定义为:如果(vi,vj)属于边集,则edges[i][j]=1,否则edges[i][j]=0。
邻接表存储的处理方法:对于图的每个顶点vi,将所有邻接于vi的顶点链成一个单链表,称为顶点vi的边表(对于有向图则称为出边表),所有边表的头指针和存储顶点信息的一维数组构成了顶点表。
程序代码:#include<iostream>using namespace std;#define MAX_VERTEX_NUM 20 //最大顶点个数#define OK 1typedef int Status;//图的数组(邻接矩阵)存储表示typedef struct ArcCell { // 弧的定义int adj; // VRType是顶点关系类型。
// 对无权图,用1或0表示相邻否;// 对带权图,则为权值类型。
int *info; // 该弧相关信息的指针} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct { // 图的定义char vexs[MAX_VERTEX_NUM];//顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数、弧数} MGraph;int LocateV ex(MGraph G, char v){int a;for (int i = 0; i <= G.vexnum; i++){if (G.vexs[i] == v)a= i;}return a;}Status CreateUDN(MGraph &G) { //采用邻接矩阵表示法,构造无向网Gint i, j, k, w;char v1, v2;cout <<"输入顶点数,边数:"<< endl;cin >> G.vexnum >> G.arcnum;//IncInfo为0,表示各弧无信息cout <<"各顶点分别为:"<< endl;for (i = 0; i<G.vexnum; i++)cin >> G.vexs[i]; //构造顶点向量for (i = 0; i<G.vexnum; i++) //初始化邻接矩阵for (j = 0; j<G.vexnum; j++){G.arcs[i][j].adj =NULL;}cout <<"顶点信息、边信息:"<< endl;for (k = 0; k<G.arcnum; k++) { //构造邻接矩阵cin >> v1 >> v2 >> w; //输入一条边依附的顶点及权值i = LocateV ex(G, v1); j = LocateV ex(G, v2);G.arcs[i][j].adj = w;G.arcs[j][i] = G.arcs[i][j];} return OK;} //CreateUDN (p162 算法7.2)Status printf1(MGraph G){cout <<"该图的顶点分别为:";for (int i = 0; i<G.vexnum; i++)cout << G.vexs[i] <<"";return OK;}Status printf2(MGraph G){cout <<"该图的边为:";for (int i = 1; i<G.vexnum; i++) //初始化邻接矩阵for (int j = 0; j<i; j++){if (G.arcs[i][j].adj !=NULL)cout << G.vexs[j]<< G.vexs[i] <<"," ;}return OK;}int main(){MGraph G;CreateUDN(G);printf1(G);cout << endl;printf2(G);cout << endl;system("pause");return 0;}。
数据结构第7章图习题

第7章图一、单项选择题1.在一个无向图G中,所有顶点的度数之和等于所有边数之和的______倍。
A.l/2 B.1C.2 D.42.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的______倍。
A.l/2 B.1C.2 D.43.一个具有n个顶点的无向图最多包含______条边。
A.n B.n+1C.n-1 D.n(n-1)/24.一个具有n个顶点的无向完全图包含______条边。
A.n(n-l) B.n(n+l)C.n(n-l)/2 D.n(n-l)/25.一个具有n个顶点的有向完全图包含______条边。
A.n(n-1) B.n(n+l)C.n(n-l)/2 D.n(n+l)/26.对于具有n个顶点的图,若采用邻接矩阵表示,则该矩阵的大小为______。
A.nB.n×nC.n-1 D.(n-l)×(n-l)7.无向图的邻接矩阵是一个______。
A.对称矩阵B.零矩阵C.上三角矩阵D.对角矩阵8.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则表头向量的大小为______。
A.n B.eC.2n D.2e9.对于一个具有n个顶点和e条边的无(有)向图,若采用邻接表表示,则所有顶点邻接表中的结点总数为______。
A.n B.eC.2n D.2e10.在有向图的邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是入边也不是出边11.在有向图的逆邻接表中,每个顶点邻接表链接着该顶点所有______邻接点。
A.入边B.出边C.入边和出边D.不是人边也不是出边12.如果从无向图的任一顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是______。
A.完全图B.连通图C.有回路D.一棵树13.采用邻接表存储的图的深度优先遍历算法类似于二叉树的______算法。
A.先序遍历B.中序遍历C.后序遍历 D.按层遍历14.采用邻接表存储的图的广度优先遍历算法类似于二叉树的______算法。
中国农业大学_821数据结构_《数据结构》习题(7)

第7章图及应用一、问答题1. 在一个图中,所有顶点的度数之和等于所有边数的多少倍?2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的多少倍?3. 对图7-1(a)和(b)所示的有向图,试回答:(1) 每个顶点的入度和出度是多少;(2) 给出它们的邻接矩阵、邻接表、逆邻接表和十字链表表示。
图7-1 有向图4. 对图7-2所示的无向图,试回答:(1) 给出邻接矩阵和邻接表的表示;(2) 根据邻接表,给出从顶点v1作深度优先和广度优先遍历图中顶点的次序。
图7-2 无向图5. 对图7-3(a)和(b)所示的无向图,画出其深度优先生成树和广度优先生成树。
图7-3 无向图6. 对图7-4所示的带权无向图:(1) 按照普里姆算法,从顶点v1出发生成最小生成树,按生成次序写出各条边;(2) 按照克鲁斯卡尔算法,生成最小生成树,按生成次序写出各条边;(3) 画出其最小生成树,并求出它的权值。
图7-4 带权无向图7. 对图7-5所示的带权有向图,用迪杰斯特拉(Dijkstra)算法,试回答:(1) 带权邻接矩阵arcs是什么?(2) 从顶点v1到其他各顶点之间的最短路径是多少?并写出Dist数组的变化过程。
图7-5 带权有向图8. 对图7-6所示的带权有向图,用弗洛伊德(Floyd)算法,试回答:每一对顶点之间的最短路径试多少,并写出计算过程。
图7-6 带权有向图9. 已知有m个顶点的无向图,采用邻接矩阵结构存储,试回答:(1) 图中有多少边?(2) 任意两个顶点i和j之间是否有边相连?(3) 任意一个顶点的度是多少?10. 已知一个无向图,采用邻接表结构存储,试回答:(1) 图中有多少边,(2) 任意两个顶点i和j之间是否有边相连?(3) 任意一个顶点的度是多少?11. 对图7-7所示的AOE网所代表的一项计划,试回答:(1) 每一事件的最早开始时间和最迟开始时间是多少?(2) 该计划最早完成的时间是多少?图7-7 代表一项计划的AOE网12. 对图7-8所示的AOE网所代表的一项工程,试回答:(1) 每项活动的最早开始时间是多少?(2) 每项活动的最迟开始时间是多少?(3) 工程完成的最短时间是多少?(4) 关键活动是什么?图7-8 代表一项工程的AOE网二、填空题1. 在无权图G的邻接矩阵A中,若(i, j)或<i, j>属于图G的边集合,则对应元素A [i, j]等于、否则等于。
数据结构试题库

数据结构试题库一、单项选择题1.下列程序段所代表的算法的时间复杂度为(D)。
x=n;y=0;while(x>=(y+1)*(y+1))y++;(A)O(n)(B)O(n2)(C)O(log2n)(D)O(n)2345(B)。
6叉树中任一结点的平均查找长度最小,则应选择下面哪个序列输入(C)。
(A)45,24,53,12,37,96,30(B)30,24,12,37,45,96,53(C)37,24,12,30,53,45,96(D)12,24,30,37,45,53,967.有一组数值{5,12,9,20,3},用以构造哈夫曼树,则其带权路径长度WPL值为(D)。
(A)93(B)96(C)123(D)1038.已知一个有向图G的顶点v={v1,v2,v3,v4,v5,v6},其邻接表如下图所示,根据有向图的深度优先遍历算法,从顶点v1出发,所得到的顶点遍历序列是(B)。
(A)v1,v2,v3,v6,v4,v5(B)v1,v2,v3,v6,v5,v4 (C)v1,v2,v5,v6,v3,v4(D)v1,v2,v5,v3,v4,v69.设有10. 12. 13. D )存14. 一个带头结点head 的循环单链表为空的判断条件是(C )。
(A)head==NULL(B)head->next==NULL(C)head->next==head(D)head!=NULL15. 若链队列HQ 中只有一个结点,则队列的头指针和尾指针满足下列条件(D )。
(A)HQ->rear->next==HQ->front(B)HQ->front->next==HQ->rear->next(C)HQ->front==HQ->rear(D)HQ->front->next==HQ->rear16.从一个栈顶指针为HS的链栈中删除一个结点时,用x保存被删除结点的值,则应执行操作为(A)。
数据结构第7章 图习题

习题7 图7.1 单项选择题1.在一个图中,所有顶点的度数之和等于所有边数的____倍。
A. 1/2B. 1C. 2D. 42.任何一个无向连通图的最小生成树。
A.只有一棵B.有一棵或多棵C.一定有多棵D.可能不存在3.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的____倍。
A. 1/2B. 1C. 2D. 44.一个有n个顶点的无向图最多有____条边。
A. nB. n(n-1)C. n(n-1)/2D. 2n5.具有4个顶点的无向完全图有____条边。
A. 6B. 12C. 16D. 206.具有6个顶点的无向图至少应有____条边才能确保是一个连通图。
A. 5B. 6C. 7D. 87.在一个具有n个顶点的无向图中,要连通全部顶点至少需要____条边。
A. nB. n+1C. n-1D. n/28.对于一个具有n个顶点的无向图,若采用邻接矩阵表示,则该矩阵的大小是____。
A. nB. (n-1)2C. n-1D. n29.对于一个具有n个顶点和e条边的无向图,若采用邻接表表示,则表头向量的大小为_①___;所有邻接表中的接点总数是_②___。
①A. n B. n+1 C. n-1 D. n+e②A. e/2 B. e C.2e D. n+e10.已知一个图如图7.1所示,若从顶点a出发按深度搜索法进行遍历,则可能得到的一种顶点序列为__①__;按宽度搜索法进行遍历,则可能得到的一种顶点序列为__②__。
①A. a,b,e,c,d,f B. e,c,f,e,b,d C. a,e,b,c,f,d D. a,e,d,f,c,b②A. a,b,c,e,d,f B. a,b,c,e,f,d C. a,e,b,c,f,d D. a,c,f,d,e,b图 7.1 一个无向图11.已知一有向图的邻接表存储结构如图7.2所示。
图7.2 一个有向图的邻接表存储结构⑴根据有向图的深度优先遍历算法,从顶点v1出发,所得到的顶点序列是____。
2011年全国数据结构导论模拟试卷(五)

答案:B
15. 设有6个结点的无向图,该图至少应有()条边才能确保是一个连通图。 A. 5 B. 6 C. 7 D. 8
答案:A
二、填空题(本大题共13小题,每小题2分,共26分)请在每小题的空格中填上正确答 案。错填、不填均无分。
1. 程序段“i=1;while(i<=n)i=i*2;”的时间复杂度T(n)=___。
答案:B
4. 用某种排序方法对序列(25,84,21,47,15,27,68,35,20)进行排序,记录序列的变
化情况如下: 258421471527683520 201521254727683584 152021253527476884 152021252735476884 则采用的排序方法是()
答案:D
13. 索引顺序文件的记录,在逻辑上按关键字的顺序排列,但物理上不一定按关键字顺序存储
。对这种文件需建立一张指示逻辑记录和物理记录之间一一对应关系的(),它一般用树结构来组 织。
A. 符号表 B. 索引表 C. 交叉访问表 D. 链接表
更多试卷请登陆九州考苑()
答案:B
14. 设图G采用邻接表存储,则拓扑排序算法的时间复杂度为() A. O(n) B. O(n+e) C. O(n2) D. O(n×e)
答案:D
8. 下面关于线性表的叙述正确的是() A. 线性表采用顺序存储,必须占用一片连续的存储单元 B. 线性表采用顺序存储,便于进行插入和删除操作
更多试卷请登陆九州考苑()
C. 线性表采用链接存储,不必占用一片连续的存储单元D.线性表采用链接存储,不便于插
入和删除操作
D. 线性表采用链接存储,不便于插入和删除操作
答案:答案见图应用题29所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
typedef struct { // 图的定义
VertexType AdjMatrix // 顶点信息 arcs; // 弧的信息 vexs[MAX_VERTEX_NUM]; int vexnum, arcnum; // 顶点数,弧数
GraphKind kind;
} MGraph;
// 图的种类标志
第7章 图
教学重点: 图的定义、术语及其含义,各种图的邻接矩阵 表示法及其类型说明,图的按深度优先搜索遍 历方法和按广度优先搜索遍历方法,生成树和 最小生成树的概念, Prim 算法,拓扑序列和 拓扑排序的概念和算法思想,关键路径的算法 思想,最短路径的算法思想。 教学难点: 图的存储表示、关键路径,最短路径算法 。
引言
图(Graph)是一种较线性表和树更为复杂 的数据结构。 图形结构中,结点之间 的关系可以是任意的, 任意两个数据元素之间都可能相关。
应用广泛:
如电路网络分析、交通运输、管理与线路的 铺设、印刷电路板与集成电路的布线等众多直接 与图有关的问题,它们必须用图的有关方法进行 处理; 另外像工作的分配、工程进度的安排、课程表 的制订、关系数据库的设计等许多实际问题,如 果间接地用图来表示,处理起来比较方便。
第7章 图
二、教学要求:
1、理解图的基本概念,熟悉图的各种存储结构及其构 造算法; 2、熟练掌握图的两种搜索路径的遍历; 3、掌握构造最小生成树的方法,并理解算法; 4、掌握用Dijkstra方法求解单源最短路径问题,理解 Floyd(弗洛伊德)算法思想; 5、掌握求活动网络的拓扑排序的方法,并理解算法; 6、掌握求解关键路径的方法。
邻接表表示
图的邻接表存储方法是一种顺序分配与链式分配相结合 的存储方法,它包括两部分: 一部分是单链表,用来存 放边的信息;另一部分是数组,主要用来存放顶点本身 的数据信息。 表结点
adjvex nextarc info
指示下一条边 或弧的结点
信息可无
指示与顶点Vi邻接的 点在图中的位置
头结点
data firstarc
回答问题
1、什么是图形结构?它和线性结构、树 形结构有何区别? 2、以下图为例,理解图的相关术语,并 回答有关问题。
A BABE源自C G1 D C G2 D
回答问题
(1)G1中,A到D的路径是什么?路径长 度多少? (2)G2中,A到E的路径是什么?路径长 度多少? (3)G1是强连通图吗?若不是找出其强 连通分量? (4)写出G2的生成树; (5)写出G1的生成森林;
(3)矩阵中1的个数的一半为图中边的数目;
(4)很容易判断顶点i 和顶点j之间是否有边相 连(看矩阵中i行j列值是否为1)。
邻接矩阵存储表示特点
邻接矩阵法优点:
容易实现图的操作,如:求某顶点的度、判断顶点 之间是否有边(弧)、找顶点的邻接点等等。仅耗 费 O(1) 时间。
邻接矩阵法缺点:
n个顶点需要n*n个单元存储边(弧);空间效率为 O(n2)。对稀疏图而言尤其浪费空间。
typedef struct ArcCell { // 弧的定义
VRType adj; // VRType是顶点关系类型。 // 对无权图,用1或0表示相邻否; // 对带权图,则为权值类型。
InfoType *info; // 该弧相关信息的指针
} ArcCell,
AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
回答问题
(6)写出G1的邻接矩阵、邻接表和十字链表; (7)写出G2的邻接矩阵、邻接表和邻接多重表。 3、如下所示为一带权有向图,写出其邻接矩阵、 邻接表。
V1
10
40
V2
20
V3
50
V4
邻接矩阵的结构定义:
#define MAX_VERTEX_NUM 20 Typedef enum{DG,DN,UDG,UDN} Graphkind;
问题的提出
假设有”平顶山”、”郑州”、”洛阳”、”许昌”、”漯 河”五城市的交通图如下,完成如下要求: 1:对任意输入的两个城市,输出它们之间的直接距 离,有则输出实际距离,无则输出道路不直接相通。 2:对任意一个城市,输出都能够直接通达哪些城市, 平顶山 距离多少? 1
100 120
洛阳 郑州
3
第七章
图
第7章 图
一、教学内容:
1、图的基本概念 2、图的存储结构(邻接矩阵、邻接表); 3、图的遍历(深度优先搜索、广度优先搜索); 4、最小生成树(kruskul算法、prim算法); 5、最短路径(dijkstra算法、floyd算法); 6、AOV网络与拓扑排序; 7、AOE网络与关键路径。
150
150 200
5
漯河
2
4
180 许昌
第7章 图
7.1 图的定义和术语 7.2 图的存储结构 7.3 图的遍历操作 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
7.1 图的定义和术语
1、图的结构定义、图形结构特点 2、顶点、弧、边、弧头、弧尾 3、无向图和有向图 4、完全图和有向完全图 5、网、子图 6、顶点的度、入度和出度、 边、弧与各顶点度的关系
指示链表中 第一个结点
存储顶点Vi的 名或其他信息
邻接表表示
从无向图的邻接表可以得到如下结论:
(1)第i 个链表中结点数目为顶点i的度; (2)所有链表中结点数目的一半为图中边数;
(3)占用的存储单元数目为n+2e 。
从有向图的邻接矩阵可以得出如下结论
(1) 矩阵不一定是对称的;
(2) 第i 行中1的个数为顶点i 的出度;
(3) 第i列中1的个数为顶点 i的入度; (4) 矩阵中1的个数为图中弧的数目; (5) 很容易判断顶点i 和顶点j 是否有弧相连.
从无向图的邻接矩阵可以得出如下结论
(1)矩阵是对称的,可压缩存储(上(下)三角; (2)第i行或第i 列中1的个数为顶点i 的度;
7.1 图的定义和术语
7、路径、路径长度、回路(环)、简单 路径 8、连通、连通图、连通分量 9、强连通图、强连通分量 10、生成树、有向树、生成森林
7.2 图的存储表示
图的数组(邻接矩阵)存储表示(重点) 图的邻接表存储表示(重点) 有向图的十字链表存储表示 无向图的邻接多重表存储表示
