图的邻接表存储方式.
数据结构 邻接多重表

数据结构邻接多重表摘要:1.邻接多重表的定义和特点2.邻接多重表的存储方式3.邻接多重表的优缺点分析4.邻接多重表的应用实例正文:一、邻接多重表的定义和特点邻接多重表(Adjacency List)是一种用于表示有向图或无向图中顶点之间关系的数据结构。
它通过一个顶点表和一组边表来表示图的顶点和边。
邻接多重表具有以下特点:1.每个顶点对应一个边表,边表中存储与该顶点相邻的所有顶点。
2.如果两个顶点之间存在一条边,则它们在各自的边表中相互出现。
3.边表中的元素为顶点序号,而非顶点本身。
二、邻接多重表的存储方式邻接多重表的存储方式包括顺序存储和链式存储两种:1.顺序存储:将所有顶点及其边表按顺序排列在一个数组中。
这种存储方式的优点是访问速度快,但需要较大的存储空间。
2.链式存储:每个顶点对应一个链表,链表中存储与该顶点相邻的所有顶点。
这种存储方式的优点是节省存储空间,但访问速度较慢。
三、邻接多重表的优缺点分析邻接多重表的优点:1.表示简单,易于理解。
2.便于实现和操作。
3.可以灵活表示有向图和无向图。
邻接多重表的缺点:1.存储空间较大,尤其是当图规模较大时。
2.链式存储的访问速度较慢,可能影响算法效率。
四、邻接多重表的应用实例邻接多重表广泛应用于图论算法中,如深度优先搜索(DFS)、广度优先搜索(BFS)、最短路径算法(如Dijkstra 算法、Floyd-Warshall 算法等)等。
这些算法通常需要使用邻接多重表来表示图的顶点和边,并进行相应的操作。
总之,邻接多重表是一种重要的数据结构,用于表示图的顶点和边。
它具有表示简单、易于实现等优点,但也存在存储空间较大、访问速度较慢等缺点。
图的邻接矩阵和邻接表相互转换

图的邻接矩阵和邻接表相互转换图的邻接矩阵存储方法具有如下几个特征:1)无向图的邻接矩阵一定是一个对称矩阵。
2)对于无向图的邻接矩阵的第i 行非零元素的个数正好是第i 个顶点的度()i v TD 。
3)对于有向图,邻接矩阵的第i 行非零元素的个数正好是第i 个顶点的出度()i v OD (或入度()i v ID )。
4)用邻接矩阵方法存储图,很容易确定图中任意两个顶点之间是否有边相连;但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所发费得时间代价大。
邻接表是图的一种顺序存储与链式存储相结合的存储方法。
若无向图中有n 个顶点、e 条边,则它的邻接表需n 个头结点和2e 个表结点。
显然,在边稀疏的情况下,用邻接表表示图比邻接矩阵存储空间。
在无向图的邻接表中,顶点i v 的度恰好是第i 个链表中的结点数,而在有向图中,第i 个链表中结点个数是顶点i v 的出度。
在建立邻接表或邻逆接表时,若输入的顶点信息即为顶点的编号,则建立临接表的时间复杂度是)(e n O +;否则,需要通过查找才能得到顶点在图中位置,则时间复杂度为)*(e n O 。
在邻接表上容易找到任意一顶点的第一个邻接点和下一个邻接点,但要判断任意两个顶点之间是否有边或弧,则需要搜索第i 个或第j 个链表,因此,不及邻接矩阵方便。
邻接矩阵和邻接表相互转换程序代码如下:#include<iostream.h>#define MAX 20//图的邻接表存储表示typedef struct ArcNode{int adjvex; //弧的邻接定点 char info; //邻接点值struct ArcNode *nextarc; //指向下一条弧的指针}ArcNode;typedef struct Vnode{ //节点信息char data;ArcNode *link;}Vnode,AdjList[MAX];typedef struct{AdjList vertices;int vexnum; //节点数int arcnum; //边数}ALGraph;//图的邻接矩阵存储表示typedef struct{int n; //顶点个数char vexs[MAX]; //定点信息int arcs[MAX][MAX]; //边信息矩阵}AdjMatrix;/***_____________________________________________________***///函数名:AdjListToMatrix(AdjList g1,AdjListMatrix &gm,int n)//参数:(传入)AdjList g1图的邻接表,(传入)int n顶点个数,(传出)AdjMatrix gm图的邻接矩阵//功能:把图的邻接表表示转换成图的邻接矩阵表示void AdjListToAdjMatrix(ALGraph gl,AdjMatrix &gm){int i,j,k;ArcNode *p;gm.n=gl.vexnum;for(k=0;k<gl.vexnum;k++)gm.vexs[k]=gl.vertices[k].data;for(i=0;i<MAX;i++)for(j=0;j<MAX;j++)gm.arcs[i][j]=0;for(i=0;i<gl.vexnum;i++){p=gl.vertices[i].link; //取第一个邻接顶点while(p!=NULL){ //取下一个邻接顶点gm.arcs[i][p->adjvex]=1;p=p->nextarc;}}}/***________________________________________________***///函数名:AdjMatrixToAdjListvoid AdjMatrixToAdjList(AdjMatrix gm,ALGraph &gl){int i,j,k,choice;ArcNode *p;k=0;gl.vexnum=gm.n;cout<<"请选择所建立的图形是无向图或是有向图:";cin>>choice;for(i=0;i<gm.n;i++){gl.vertices[i].data=gm.vexs[i];gl.vertices[i].link=NULL;}for(i=0;i<gm.n;i++)for(j=0;j<gm.n;j++)if(gm.arcs[i][j]==1){k++;p=new ArcNode;p->adjvex=j;p->info=gm.vexs[j];p->nextarc=gl.vertices[i].link;gl.vertices[i].link=p;}if(choice==1)k=k/2;gl.arcnum=k;}void CreateAdjList(ALGraph &G){int i,s,d,choice;ArcNode *p;cout<<"请选择所建立的图形是有向图或是无向图:";cin>>choice;cout<<"请输入节点数和边数:"<<endl;cin>>G.vexnum>>G.arcnum;for(i=0;i<G.vexnum;i++){cout<<"第"<<i<<"个节点的信息:";cin>>G.vertices[i].data;G.vertices[i].link=NULL;}if(choice==1){for(i=0;i<2*(G.vexnum);i++){cout<<"边----起点序号,终点序号:";cin>>s>>d;p=new ArcNode;p->adjvex=d;p->info=G.vertices[d].data;p->nextarc=G.vertices[s].link;G.vertices[s].link=p;}}else{for(i=0;i<G.vexnum;i++){cout<<"边----起点序号,终点序号:";cin>>s>>d;p=new ArcNode;p->adjvex=d;p->info=G.vertices[d].data;p->nextarc=G.vertices[s].link;G.vertices[s].link=p;}}}void CreateAdjMatrix(AdjMatrix &M){int i,j,k,choice;cout<<"请输入顶点个数:";cin>>M.n;cout<<"请输入如顶点信息:"<<endl;for(k=0;k<M.n;k++)cin>>M.vexs[k];cout<<"请选择所建立的图形是无向图或是有向图:";cin>>choice;cout<<"请输入边信息:"<<endl;for(i=0;i<M.n;i++)for(j=0;j<M.n;j++)M.arcs[i][j]=0;switch(choice){case 1:{for(k=0;k<M.n;k++){cin>>i>>j;M.arcs[i][j]=M.arcs[j][i]=1;}};break;case 2:{for(k=0;k<M.n;k++){cin>>i>>j;M.arcs[i][j]=1;}};break;}}void OutPutAdjList(ALGraph &G){int i;ArcNode *p;cout<<"图的邻接表如下:"<<endl;for(i=0;i<G.vexnum;i++){cout<<G.vertices[i].data;p=G.vertices[i].link;while(p!=NULL){cout<<"---->("<<p->adjvex<<" "<<p->info<<")";p=p->nextarc;}cout<<endl;}}void OutPutAdjMatrix(AdjMatrix gm){cout<<"图的邻接矩阵如下:"<<endl;for(int i=0;i<gm.n;i++){。
实现图的邻接矩阵和邻接表存储

实现图的邻接矩阵和邻接表存储1.需求分析对于下图所示的有向图G,编写一个程序完成如下功能:1.建立G的邻接矩阵并输出之2.由G的邻接矩阵产生邻接表并输出之3.再由2的邻接表产生对应的邻接矩阵并输出之2.系统设计1.图的抽象数据类型定义:ADT Graph{数据对象V:V是具有相同特性的数据元素的集合,称为顶点集数据关系R:R={VR}VR={<v,w>|v,w∈V且P(v,w),<v,w>表示从v到w的弧,谓词P(v,w)定义了弧<v,w>的意义或信息}基本操作P:CreatGraph(&G,V,VR)初始条件:V是图的顶点集,VR是图中弧的集合操作结果:按V和VR的定义构造图GDestroyGraph(&G)初始条件:图G存在操作结果:销毁图GInsertVex(&G,v)初始条件:图G存在,v和图中顶点有相同特征操作结果:在图G中增添新顶点v……InsertArc(&G,v,w)初始条件:图G存在,v和w是G中两个顶点操作结果:在G中增添弧<v,w>,若G是无向的则还增添对称弧<w,v>……DFSTraverse(G,Visit())初始条件:图G存在,Visit是顶点的应用函数操作结果:对图进行深度优先遍历,在遍历过程中对每个顶点调用函数Visit一次且仅一次。
一旦Visit()失败,则操作失败BFSTraverse(G,Visit())初始条件:图G存在,Visit是顶点的应用函数操作结果:对图进行广度优先遍历,在遍历过程中对每个顶点调用函数Visit一次且仅一次。
一旦Visit()失败,则操作失败}ADT Graph2.主程序的流程:调用CreateMG函数创建邻接矩阵M;调用PrintMatrix函数输出邻接矩阵M调用CreateMGtoDN函数,由邻接矩阵M创建邻接表G调用PrintDN函数输出邻接表G调用CreateDNtoMG函数,由邻接表M创建邻接矩阵N调用PrintMatrix函数输出邻接矩阵N3.函数关系调用图:3.调试分析(1)在MGraph的定义中有枚举类型typedef enum{DG,DN,UDG,UDN}GraphKind;//{有向图,有向网,无向图,无向网}赋值语句G.kind(int)=M.kind(GraphKind);是正确的,而反过来M.kind=G.kind则是错误的,要加上那个强制转换M.kind=GraphKind(G.kind);枚举类型enum{DG,DN,UDG,UDN}会自动赋值DG=0;DN=1,UDG=2,UDN=3;可以自动从GraphKind类型转换到int型,但不会自动从int型转换到GraphKind类型(2)算法的时间复杂度分析:CreateMG、CreateMGtoDN、CreateDNtoMG、PrintMatrix、PrintDN的时间复杂度均为O(n2) n为图的顶点数,所以main:T(n)= O(n2)4.测试结果用需求分析中的测试数据输入:输出:5、用户手册(1)输入顶点数和弧数;(2)输入顶点内容;(3)按行序输入邻接矩阵,输入各弧相应权值(4)回车输出邻接矩阵M、邻接表G和邻接矩阵N6、附录源程序:#include <stdio.h>#include <stdlib.h>#define MAX_VERTEX_NUM 20typedef int VRType;typedef int InfoType;typedef int VertexType;typedef enum{DG,DN,UDG,UDN}GraphKind;//{有向图,有向网,无向图,无向网} typedef struct ArcCell{VRType adj;//VRType是顶点关系类型,对无权图用1或0表示是否相邻;//对带权图则为权值类型InfoType *info;//该弧相关信息的指针}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct{VertexType vexs[MAX_VERTEX_NUM];//顶点向量AdjMatrix arcs;//邻接矩阵int vexnum,arcnum;//图的当前顶点数和弧数GraphKind kind;//图的种类标志}MGraph;void CreateMG(MGraph &M){int i,j;M.kind=DN;printf("输入顶点数:");scanf("%d",&M.vexnum);printf("输入弧数:");scanf("%d",&M.arcnum);printf("输入顶点:\n");for(i=0;i<M.vexnum;i++)scanf("%d",&M.vexs[i]);printf("建立邻接矩阵:\n");for(i=0;i<M.vexnum;i++)for(j=0;j<M.vexnum;j++)scanf("%d",&M.arcs[i][j].adj);printf("输入相应权值:\n");for(i=0;i<M.vexnum;i++)for(j=0;j<M.vexnum;j++)if(M.arcs[i][j].adj){scanf("%d",&M.arcs[i][j].info);}}typedef struct ArcNode{int adjvex;//该弧所指向的顶点在数组中的下标struct ArcNode *nextarc;InfoType *info;//该弧相关信息的指针}ArcNode;typedef struct VNode{VertexType data;//顶点信息ArcNode *firstarc;//指向第一条依附该顶点的弧的指针}VNode,AdjList[MAX_VERTEX_NUM];typedef struct{AdjList vertices;int vexnum,arcnum;//图的当前顶点数和弧数int kind;//图的种类标志}ALGraph;void PrintDN(ALGraph G){int i;ArcNode *p;printf("顶点:\n");for(i=0;i<G.vexnum;++i)printf("%2d",G.vertices[i].data);printf("\n弧:\n");for(i=0;i<G.vexnum;++i){p=G.vertices[i].firstarc;while(p){printf("%d→%d(%d)\t",i,p->adjvex,p->info);p=p->nextarc;}printf("\n");}//for}void CreateMGtoDN(ALGraph &G,MGraph M){//采用邻接表存储表示,构造有向图G(G.kind=DN)int i,j;ArcNode *p;G.kind=M.kind;G.vexnum=M.vexnum;G.arcnum=M.arcnum;for(i=0;i<G.vexnum;++i){//构造表头向量G.vertices[i].data=M.vexs[i];G.vertices[i].firstarc=NULL;//初始化指针}for(i=0;i<G.vexnum;++i)for(j=0;j<G.vexnum;++j)if(M.arcs[i][j].adj==1){p=(ArcNode*)malloc(sizeof(ArcNode));p->adjvex=j;p->nextarc=G.vertices[i].firstarc;p->info=M.arcs[i][j].info;G.vertices[i].firstarc=p;}}void CreateDNtoMG(MGraph &M,ALGraph G){int i,j;ArcNode *p;M.kind=GraphKind(G.kind);M.vexnum=G.vexnum;M.arcnum=G.arcnum;for(i=0;i<M.vexnum;++i)M.vexs[i]=G.vertices[i].data;for(i=0;i<M.vexnum;++i){p=G.vertices[i].firstarc;while(p){M.arcs[i][p->adjvex].adj=1;p=p->nextarc;}//whilefor(j=0;j<M.vexnum;++j)if(M.arcs[i][j].adj!=1)M.arcs[i][j].adj=0;}//for}void PrintMatrix(MGraph M){ int i,j;for(i=0;i<M.vexnum;++i){for(j=0;j<M.vexnum;++j) printf("%2d",M.arcs[i][j].adj); printf("\n");}}void main(){MGraph M,N;ALGraph G; CreateMG(M);PrintMatrix(M); CreateMGtoDN(G,M); PrintDN(G); CreateDNtoMG(N,G); PrintMatrix(N);}。
图基本算法图的表示方法邻接矩阵邻接表

图基本算法图的表⽰⽅法邻接矩阵邻接表 要表⽰⼀个图G=(V,E),有两种标准的表⽰⽅法,即邻接表和邻接矩阵。
这两种表⽰法既可⽤于有向图,也可⽤于⽆向图。
通常采⽤邻接表表⽰法,因为⽤这种⽅法表⽰稀疏图(图中边数远⼩于点个数)⽐较紧凑。
但当遇到稠密图(|E|接近于|V|^2)或必须很快判别两个给定顶点⼿否存在连接边时,通常采⽤邻接矩阵表⽰法,例如求最短路径算法中,就采⽤邻接矩阵表⽰。
图G=<V,E>的邻接表表⽰是由⼀个包含|V|个列表的数组Adj所组成,其中每个列表对应于V中的⼀个顶点。
对于每⼀个u∈V,邻接表Adj[u]包含所有满⾜条件(u,v)∈E的顶点v。
亦即,Adj[u]包含图G中所有和顶点u相邻的顶点。
每个邻接表中的顶点⼀般以任意顺序存储。
如果G是⼀个有向图,则所有邻接表的长度之和为|E|,这是因为⼀条形如(u,v)的边是通过让v出现在Adj[u]中来表⽰的。
如果G是⼀个⽆向图,则所有邻接表的长度之和为2|E|,因为如果(u,v)是⼀条⽆向边,那么u会出现在v的邻接表中,反之亦然。
邻接表需要的存储空间为O(V+E)。
邻接表稍作变动,即可⽤来表⽰加权图,即每条边都有着相应权值的图,权值通常由加权函数w:E→R给出。
例如,设G=<V,E>是⼀个加权函数为w的加权图。
对每⼀条边(u,v)∈E,权值w(u,v)和顶点v⼀起存储在u的邻接表中。
邻接表C++实现:1 #include <iostream>2 #include <cstdio>3using namespace std;45#define maxn 100 //最⼤顶点个数6int n, m; //顶点数,边数78struct arcnode //边结点9 {10int vertex; //与表头结点相邻的顶点编号11int weight = 0; //连接两顶点的边的权值12 arcnode * next; //指向下⼀相邻接点13 arcnode() {}14 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}15 arcnode(int v):vertex(v),next(NULL) {}16 };1718struct vernode //顶点结点,为每⼀条邻接表的表头结点19 {20int vex; //当前定点编号21 arcnode * firarc; //与该顶点相连的第⼀个顶点组成的边22 }Ver[maxn];2324void Init() //建⽴图的邻接表需要先初始化,建⽴顶点结点25 {26for(int i = 1; i <= n; i++)27 {28 Ver[i].vex = i;29 Ver[i].firarc = NULL;30 }31 }3233void Insert(int a, int b, int w) //尾插法,插⼊以a为起点,b为终点,权为w的边,效率不如头插,但是可以去重边34 {35 arcnode * q = new arcnode(b, w);36if(Ver[a].firarc == NULL)37 Ver[a].firarc = q;38else39 {40 arcnode * p = Ver[a].firarc;41if(p->vertex == b) //如果不要去重边,去掉这⼀段42 {43if(p->weight < w)44 p->weight = w;45return ;46 }47while(p->next != NULL)48 {49if(p->next->vertex == b) //如果不要去重边,去掉这⼀段50 {51if(p->next->weight < w);52 p->next->weight = w;53return ;54 }55 p = p->next;56 }57 p->next = q;58 }59 }60void Insert2(int a, int b, int w) //头插法,效率更⾼,但不能去重边61 {62 arcnode * q = new arcnode(b, w);63if(Ver[a].firarc == NULL)64 Ver[a].firarc = q;65else66 {67 arcnode * p = Ver[a].firarc;68 q->next = p;69 Ver[a].firarc = q;70 }71 }7273void Insert(int a, int b) //尾插法,插⼊以a为起点,b为终点,⽆权的边,效率不如头插,但是可以去重边74 {75 arcnode * q = new arcnode(b);76if(Ver[a].firarc == NULL)77 Ver[a].firarc = q;78else79 {80 arcnode * p = Ver[a].firarc;81if(p->vertex == b) return; //去重边,如果不要去重边,去掉这⼀句82while(p->next != NULL)83 {84if(p->next->vertex == b) //去重边,如果不要去重边,去掉这⼀句85return;86 p = p->next;87 }88 p->next = q;89 }90 }91void Insert2(int a, int b) //头插法,效率跟⾼,但不能去重边92 {93 arcnode * q = new arcnode(b);94if(Ver[a].firarc == NULL)95 Ver[a].firarc = q;96else97 {98 arcnode * p = Ver[a].firarc;99 q->next = p;100 Ver[a].firarc = q;101 }102 }103void Delete(int a, int b) //删除以a为起点,b为终点的边104 {105 arcnode * p = Ver[a].firarc;106if(p->vertex == b)107 {108 Ver[a].firarc = p->next;109 delete p;110return ;111 }112while(p->next != NULL)113if(p->next->vertex == b)114 {115 p->next = p->next->next;116 delete p->next;117return ;118 }119 }120121void Show() //打印图的邻接表(有权值)122 {123for(int i = 1; i <= n; i++)124 {125 cout << Ver[i].vex;126 arcnode * p = Ver[i].firarc;127while(p != NULL)128 {129 cout << "->(" << p->vertex << "," << p->weight << ")";130 p = p->next;131 }132 cout << "->NULL" << endl;133 }134 }135136void Show2() //打印图的邻接表(⽆权值)137 {138for(int i = 1; i <= n; i++)140 cout << Ver[i].vex;141 arcnode * p = Ver[i].firarc;142while(p != NULL)143 {144 cout << "->" << p->vertex;145 p = p->next;146 }147 cout << "->NULL" << endl;148 }149 }150int main()151 {152int a, b, w;153 cout << "Enter n and m:";154 cin >> n >> m;155 Init();156while(m--)157 {158 cin >> a >> b >> w; //输⼊起点、终点159 Insert(a, b, w); //插⼊操作160 Insert(b, a, w); //如果是⽆向图还需要反向插⼊161 }162 Show();163return0;164 }View Code 邻接表表⽰法也有潜在的不⾜之处,即如果要确定图中边(u,v)是否存在,只能在顶点u邻接表Adj[u]中搜索v,除此之外没有其他更快的办法。
图的3种储存方式

图的3种储存⽅式图的储存⽅式有三种⼀。
邻接矩阵 优点:简洁明了,调⽤⽅便,简单易写; 缺点:内存占⽤⼤,⽽且没办法存重边(可能可以,但我不会),点的个数超过 3000 直接爆炸 适⽤范围:点的个数少,稠密图,⼀般结合floyed使⽤,可以传递闭包。
代码:scanf("%d%d",&u,&v,&w);a[u][v]=w;a[v][u]=w;// 双向边⼆。
邻接表 优点:占⽤空间⼩,可以快速查找每个点的出度,重边可以存,写着较为⽅便 缺点:查找和删除边很不⽅便,对于⽆向图,如果需要删除⼀条边,就需要在两个链表上查找并删除,⽤了STL,速度会慢 适⽤范围:⼤部分情况,不要求删除边就⾏ 代码:struct Edge{int v,w;};vector <Edge> edge[maxn];void addedge(int u,int v,int w){edge[u].push_back({v,w});edge[v].push_back({u,w});//双向边}三。
链式前向星 优点:⽐邻接表还省空间,可以解决某些卡空间的问题,删除边也很⽅便,只需要更改next指针的指向即可,速度也快 缺点:好像就是写的⿇烦,理解⿇烦,性能好像很猛 适⽤:需要删除边的题⽬,速度时间都要求⾼的题⽬ 代码:struct Edge{int to,w,next;}edge[maxn*2];int cnt,head[maxn],s,t,n,m;void addedge(int u,int v,int w){edge[++cnt].to=v;edge[cnt].w=w;edge[cnt].next=head[u];head[u]=cnt;}struct Pre{int v,edge;}pre[maxn]; 解释:这是⽐较难理解的⼀种⽅式,所以做⼀下解释,主要是看别⼈的博客看懂的 对于上图,输⼊为 1 2 2 3 3 4 1 3 4 1 1 5 4 5 对于上⾯的结构体, 其中edge[i].to表⽰第i条边的终点 ,edge[i].next表⽰与第i条边同起点的下⼀条边的存储位置, edge[i].w为边权值. 数组head[],它是⽤来表⽰以i为起点的第⼀条边存储的位置, head[]数组⼀般初始化为-1 实际上你会发现这⾥的第⼀条边存储的位置其实在以i为起点的所有边的最后输⼊的那个编号. 有了以i为起点的第⼀条边的储存位置和同起点下⼀条边的储存位置我们就可以便利这个i点的每⼀条边了 初始化cnt = 0,这样,现在我们还是按照上⾯的图和输⼊来模拟⼀下: edge[0].to = 2; edge[0].next = -1; head[1] = 0; edge[1].to = 3; edge[1].next = -1; head[2] = 1; edge[2].to = 4; edge[2],next = -1; head[3] = 2; edge[3].to = 3; edge[3].next = 0; head[1] = 3; edge[4].to = 1; edge[4].next = -1; head[4] = 4; edge[5].to = 5; edge[5].next = 3; head[1] = 5; edge[6].to = 5; edge[6].next = 4; head[4] = 6; 很明显,head[i]保存的是以i为起点的所有边中编号最⼤的那个,⽽把这个当作顶点i的第⼀条起始边的位置. 这样在遍历时是倒着遍历的,也就是说与输⼊顺序是相反的,不过这样不影响结果的正确性. ⽐如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5 ⽽head[1] = 5 我们在遍历以u节点为起始位置的所有边的时候是这样的: for(int i=head[u];~i;i=edge[i].next) 那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也就是编号0的边,可以看出是逆序的.。
使用MySQL进行图数据库存储和查询

使用MySQL进行图数据库存储和查询引言:在当今信息时代,数据的规模和复杂性不断增加,对于数据的存储和查询方式提出了更高的要求。
传统的关系型数据库虽然能够有效地存储和查询结构化的数据,但对于非结构化的数据、复杂的关系和网络结构并不擅长。
而图数据库作为一种新兴的数据库类型,能够有效地存储和查询图形结构的数据,被广泛应用于社交网络分析、推荐系统、知识图谱等领域。
本文将介绍如何使用MySQL进行图数据库的存储和查询,以及其优缺点和适用场景。
一、图数据库简介图数据库是一种以图形结构为基础,用于存储、表示和查询图数据的数据库。
它通过节点(node)和边(edge)来表示实体和实体之间的关系,并通过图的遍历和搜索算法来实现高效的查询操作。
与传统的关系型数据库相比,图数据库具有以下特点:1. 存储效率高:图数据库通过使用节点和边的方式来存储数据,能够减少存储空间的消耗,并提高数据的读取效率。
2. 查询灵活性高:图数据库能够通过遍历和搜索算法来查询图结构数据,特别适合处理非结构化和复杂关系的数据。
3. 内容和结构的一体性:图数据库将数据的结构和内容存储在一起,能够有效地保持数据的完整性和一致性。
二、使用MySQL进行图数据库存储MySQL是一种常用的关系型数据库管理系统,虽然它本身并不是专门用于存储和查询图形结构数据的数据库,但我们可以通过一些技术手段来实现图数据库的存储。
下面将介绍两种常用的方法。
1. 邻接表存储方式邻接表是一种以表格的形式存储图数据的方式,通过两个表分别存储节点和边的信息。
节点表中记录节点的唯一标识符和属性信息,边表中记录边的唯一标识符、起始节点和终止节点的标识符、以及边的属性信息。
通过关联查询,我们可以实现对图结构的查询操作。
2. 邻接矩阵存储方式邻接矩阵是一种以矩阵的形式存储图数据的方式,通过一个二维数组来表示节点之间的关系。
数组的行和列分别对应节点的标识符,数组的值表示节点之间的边的关系。
图的种类及储存方式

图的种类及储存⽅式⼀.图的种类(以下的分类不是并列的)1.有向图:图中边的⽅向是⼀定的,不能逆序⾛。
2.⽆向图:图中的边没有⽅向,可以逆序⾛。
没有正负⽅向3.完全图:完全图:对于顶中的每⼀个顶点,都与其他的点有边直接相连⽆向完全图:任意⼀个具有n个结点的⽆向简单图,其边数n*(n-1)/2;我们把边数恰好等于n*(n-1)/2的n个结点的称为完全图。
有向完全图:在⼀个n个结点的中,最⼤边数为n*(n-1)。
4.稀疏图和稠密图:⼀般的对于⼀个图来说,边的数⽬多的就是稠密图,边的数⽬少的就是稀疏图。
5.⼆部图与完全⼆部图(⼆部图也就是⼆分图)⼆分图的概念:简⽽⾔之,就是顶点集V可分割为两个互不相交的⼦集,并且图中每条边依附的两个顶点都分属于这两个互不相交的⼦集,两个⼦集内的顶点不相邻。
两个⼦集:A,B;性质满⾜:A∩B=∅,A∪B=V,这就是⼆分图。
6.图的⽣成树:把图中的n个点,和图中的n-1条边挑出来,如果这n-1条边能把这n个点连起来,那这就是图的⼀个⽣成树7.有向⽹,⽆向⽹:⽹就是加权的图8.活动⽹络:AOV图:顶点是活动,有向边表⽰活动之间的前驱后继关系--拓扑排序AOE图:E,也就是⽤边表⽰活动,⽤边表⽰的⽬的是利⽤边的权值,⽐如⽤边的权值表⽰最长时间--关键路径⼆:图的存储表⽰1. 邻接矩阵也就是⽤jz[i][j]表⽰i--j的连通情况,可以表⽰权值,也可以表⽰是否连通。
2.邻接表:就是把同⼀个顶点出发的边的链接储存在同⼀个边链表中,边链表的每⼀个结点代表⼀条边,称为边结点,边结点包括的信息可以⾃⼰确定。
⼀种⽅法:g[i][j]代表从i出发的第j条边的编号,对应着edge数组中的储存着边的信息,可以直接从g[i]得到从i出发的边的数⽬。
另⼀种就是边表了。
3.边表:就不介绍了,因为⼀直以来我都是⽤“邻接矩阵”和“边表”的,⽐较熟悉。
《图的存储结构》PPT课件

(4)网的邻接矩阵
网的邻接矩阵可定义为:
wi,j 若<vi, vj>或(vi, vj) ∈VR A[i][j] =
∞ 反之
例如,下图列出了一个有向网和它的邻接矩阵。
V1
5
V2
5 7
3
84
4
V6
79
V3
8 9 5 6
1
6
V5
5
5
5
V4
3 1
(a) 网N
精选ppt (b) 邻接矩阵
7
(5)图的构造
01
∧
2 1∧
精选ppt
2 0∧∧
0 2∧∧
19
(3)C语言描述
#define MAX_VERTEX_NUM 20
typedef struct ArcBox {
int
tailvex, headvex;
//该弧的尾和头顶点的位置
struct ArcBox * hlink, * tlink;
//分别为弧头相同和弧尾相同的弧的链域
精选ppt
14
在无向图的邻接表中, 顶点Vi的度恰为第i个
B
链表中的结点数。
A
0A 1 4
1B 0 4 5
F
2C 3 5
3D 2 5
4E 0 1
5F
1
2 3 精选ppt
C D
E
15
有向图的邻接表
A
B
E 0A
CF
1B
可见,在有向图的 2 C 邻接表中不易找到 3 D 指向该顶点的弧 4 E
精选ppt
精选ppt
9
7.2.2邻接表表示法(Adjacency List)
数据结构_图_采用邻接矩阵存储,构造无向图

1.采用邻接矩阵(邻接表)存储,构造无向图(网)输入:顶点数、边数、顶点信息、边信息输出:图的顶点,图的边邻接矩阵(数组表示法)处理方法:用一个一维数组存储图中顶点的信息,用一个二维数组(称为邻接矩阵)存储图中各顶点之间的邻接关系。
假设图G=(V,E)有n个顶点,则邻接矩阵是一个n×n 的方阵,定义为:如果(vi,vj)属于边集,则edges[i][j]=1,否则edges[i][j]=0。
邻接表存储的处理方法:对于图的每个顶点vi,将所有邻接于vi的顶点链成一个单链表,称为顶点vi的边表(对于有向图则称为出边表),所有边表的头指针和存储顶点信息的一维数组构成了顶点表。
程序代码:#include<iostream>using namespace std;#define MAX_VERTEX_NUM 20 //最大顶点个数#define OK 1typedef int Status;//图的数组(邻接矩阵)存储表示typedef struct ArcCell { // 弧的定义int adj; // VRType是顶点关系类型。
// 对无权图,用1或0表示相邻否;// 对带权图,则为权值类型。
int *info; // 该弧相关信息的指针} ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct { // 图的定义char vexs[MAX_VERTEX_NUM];//顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数、弧数} MGraph;int LocateV ex(MGraph G, char v){int a;for (int i = 0; i <= G.vexnum; i++){if (G.vexs[i] == v)a= i;}return a;}Status CreateUDN(MGraph &G) { //采用邻接矩阵表示法,构造无向网Gint i, j, k, w;char v1, v2;cout <<"输入顶点数,边数:"<< endl;cin >> G.vexnum >> G.arcnum;//IncInfo为0,表示各弧无信息cout <<"各顶点分别为:"<< endl;for (i = 0; i<G.vexnum; i++)cin >> G.vexs[i]; //构造顶点向量for (i = 0; i<G.vexnum; i++) //初始化邻接矩阵for (j = 0; j<G.vexnum; j++){G.arcs[i][j].adj =NULL;}cout <<"顶点信息、边信息:"<< endl;for (k = 0; k<G.arcnum; k++) { //构造邻接矩阵cin >> v1 >> v2 >> w; //输入一条边依附的顶点及权值i = LocateV ex(G, v1); j = LocateV ex(G, v2);G.arcs[i][j].adj = w;G.arcs[j][i] = G.arcs[i][j];} return OK;} //CreateUDN (p162 算法7.2)Status printf1(MGraph G){cout <<"该图的顶点分别为:";for (int i = 0; i<G.vexnum; i++)cout << G.vexs[i] <<"";return OK;}Status printf2(MGraph G){cout <<"该图的边为:";for (int i = 1; i<G.vexnum; i++) //初始化邻接矩阵for (int j = 0; j<i; j++){if (G.arcs[i][j].adj !=NULL)cout << G.vexs[j]<< G.vexs[i] <<"," ;}return OK;}int main(){MGraph G;CreateUDN(G);printf1(G);cout << endl;printf2(G);cout << endl;system("pause");return 0;}。
图的三种存储方式

图的三种存储⽅式⼀、邻接矩阵适⽤:稠密图,就是说点数的平⽅与边数接近的情况,换句话说就是边特别多。
不适⽤:稀疏图,就是点数的平⽅与边数差的特别多,边数少,但点数多,就不⾏了,因为空间占⽤太⼤了。
实现代码#include <bits/stdc++.h>using namespace std;const int N = 1010; //图的最⼤点数量int n;int v[N][N]; //邻接矩阵/*** 测试数据40 5 2 35 0 0 12 0 0 43 14 0*/int main() {cin >> n;//读⼊到邻接矩阵for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)cin >> v[i][j];//下⾯的代码将找到与点i有直接连接的每⼀个点以及那条边的长度for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)if (v[i][j]) cout << "edge from point "<< i << " to point " << j << " with length " << v[i][j] << endl;return 0;}⼆、邻接表#include <bits/stdc++.h>using namespace std;const int N = 1010; //图的最⼤点数量struct Edge { //记录边的终点,边权的结构体int to; //终点int value; //边权};int n, m; //表⽰图中有n个点,m条边vector<Edge> p[N]; //使⽤vector的邻接表/*** 测试数据4 62 1 11 3 24 1 42 4 64 2 33 4 5*/int main() {cin >> n >> m;//m条边for (int i = 1; i <= m; i++) {int u, v, l; //点u到点v有⼀条权值为l的边cin >> u >> v >> l;p[u].push_back({v, l});}//输出for (int i = 1; i <= n; i++) {printf("出发点:%d ", i);for (int j = 0; j < p[i].size(); j++)printf(" ⽬标点:%d,权值:%d;", p[i][j].to, p[i][j].value);puts("");}return 0;}三、链式前向星链式前向星是邻接表存图的第⼆种⽅法,它⾃⼰还有两种写法,⽐⽤向量存图的那种邻接表要快。
图的几种存储方式

之前几天把数据结构扔在一边,在看离散数学的图论部分,看了大部分,最后还是觉得纯数学的,有一些可能现在我刚接触图还不会觉得有什么用,所以就选择性的跳过一些,现在也决定先放下书,回到数据结构上,开始图的部分的学习。
图的存储通用的存储方式有邻接矩阵表示法、邻接表表示法。
为方便有向图的顶点的入度与出度的计算,有有向图的十字链表表示法。
为方便对无向图的边进行操作,有无向图的邻接多重表表示法。
邻接矩阵表示法应该算是最容易的一种表示法,一些简单的操作比如查找某顶点的指定邻接点等很容易实现。
邻接表表示在计算无向图顶点的度很方便,计算有向图的出度也很方便,但是计算入度的话就要从第一个结点开始遍历,比较麻烦,这时采用逆邻接表表示法的话,求有向图的入度就会很方便,相应的,出度就不方便了,所以要根据需要选择存储结构。
如果在程序中要统计有向图的度,那么最好的方式就是采用十字链表的存储方式。
邻接多重表可以看作是对无向图的邻接矩阵的一种压缩表示,当然这种结构在边的操作上会方便很多,但是我现在还没学到,所以暂时还不知道。
下面是几种表示方法的算法实现,逆邻接表和邻接表的实现方式几乎一样,所以就不贴出来了。
1.#define MAX_VERTEX_NUM 202.3.#include<iostream>4.#include<string>ing namespace std;6.7.template<class T>8.int Locate_Vex(T G,string x) //定位顶点位置9.{10.for(int k=0;G.vexs[k]!=x;k++);11.return k;12.}13.14.//邻接矩阵存储图15.struct MGraph16.{17. string vexs[MAX_VERTEX_NUM];//顶点数组18.int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接矩阵19.int vexnum;//顶点数目20.int arcnum;//边数目21.};22.23.void CreateUDN_MG(MGraph &G)24.{25.//采用邻接矩阵表示法,构造无向网26. cin>>G.vexnum>>G.arcnum;27.for(int i=0;i<G.vexnum;i++)28. cin>>vaxs[i];29.30.for(i=0;i<G.vexnum;i++)31.for(int j=0;j<G.vexnum;j++)32. G.arcs[i][j]=-1;33.//上面是初始化邻接矩阵,-1表示两点间边的权值为无穷大34.35.for(int k=0;k<G.arcnum;k++)36. {37. string v1,v2;38.int w;39. cin>>v1>>v2>>w;40. i=Locate_Vex(G,v1);41. j=Locate_Vex(G,v2);42.while(i<0|| i>G.vexnum-1 || j<0 || j>G.vexnum-1)43. {44. cout<<"结点位置输入错误,重新输入: ";45. cin>>v1>>v2>>w;46. i=Locate_Vex(G,v1);47. j=Locate_Vex(G,v2);48. }49. G.arcs[i][j]=w;50. G.arcs[j][i]=G.arcs[i][j]; //置对称边51. }52.}53.54.//邻接表存储图55.//表结点56.struct ArcNode57.{58.int adjvex; //弧所指向顶点的位置59. ArcNode *nextarc;// 指向下一条弧60.};61.62.//头结点63.typedef struct VNode64.{65. string data;//顶点名66. ArcNode *firstarc;//指向第一条关联顶点的弧67.}AdjList[MAX_VERTEX_NUM];68.69.struct ALGraph70.{71. AdjList vertices;//头结点数组72.int vexnum;73.int arcnum;74.};75.76.void CreateDG_ALG(ALGraph &G)77.{78.//采用邻接表存储表示,构造有向图G79. string v1,v2;80.int i,j,k;81. cin>>G.arcnum>>G.vexnum;82.83.//构造头结点数组84.for(i=0;i<G.vexnum;i++)85. {86. cin>>G.vertices[i].data;87. G.vertices[i].firstarc=NULL;88. }89.90.//输入各弧并构造邻接表91.for(k=0;k<G.arcnum;k++)92. {93. cin>>v1>>v2;94. i=Locate_Vex(G,v1);95. j=Locate_Vex(G,v2);96.while(i<0|| i>G.vexnum-1 || j<0 || j>G.vexnum-1)97. {98. cout<<"结点位置输入错误,重新输入: ";99. cin>>v1>>v2;100. i=Locate_Vex(G,v1);101. j=Locate_Vex(G,v2);102. }103.104. ArcNode *p=new ArcNode;105. p->adjvex=j;106. p->nextarc=NULL;107. p->nextarc=G.vertices[i].firstarc;108. G.vertices[i].firstarc=p;109. }110.}111.112.//十字链表方式存储有向图113.//弧结点114.struct ArcBox115.{116.int tailvex,headvex;//弧结点头尾结点位置117. ArcBox *hlink,*tlink;//弧头和弧尾相同的弧的链域118.};119.120.//顶点结点121.struct VexNode122.{123. string data;124. ArcBox *firstin,*firstout;//顶点第一条入弧和出弧125.};126.127.struct OLGraph128.{129. VexNode xlist[MAX_VERTEX_NUM];130.int vexnum;131.int arcnum;132.};133.134.void CreateDG_OLG(OLGraph &G)135.{136.//采用十字链表存储表示,构造有向图G137. string v1,v2;138.int i,j,k;139. cin>>G.vexnum>>G.arcnum;140.for(i=0;i<G.vexnum;i++)141. {142. cin>>G.xlist[i].data;143. G.xlist[i].firstin=NULL;144. G.xlist[i].firstout=NULL;145. }146.for(k=0;k<G.arcnum;k++)147. {148. cin>>v1>>v2;149. i=Locate_Vex(G,v1);150. j=Locate_Vex(G,v2);151.152.while(i<0|| i>G.vexnum-1 || j<0 || j>G.vexnum-1) 153. {154. cout<<"结点位置输入错误,重新输入: ";155. cin>>v1>>v2;156. i=Locate_Vex(G,v1);157. j=Locate_Vex(G,v2);158. }159.160. ArcBox *p=new ArcBox;161. p->tailvex=i;162. p->headvex=j;163. p->hlink=G.xlist[j].firstin;164. p->tlink=G.xlist[i].firstout;165. G.xlist[i].firstout=G.xlist[j].firstin=p;166. }167.}168.169.//邻接多重表存储170.//边结点171.struct EBox172.{173.int mark;//标志域,指示该边是否被访问过(0:没有 1:有) 174.int ivex,jvex;//该边关联的两个顶点的位置175. EBox *ilink,*jlink;//分别指向关联这两个顶点的下一条边176.};177.178.//顶点结点179.struct VexBox180.{181. string data;182. EBox *firstedge;//指向第一条关联该结点的边183.};184.185.struct AMLGraph186.{187. VexBox adjmulist[MAX_VERTEX_NUM];188.int vexnum;189.int arcnum;190.};191.192.void CreateUDG_AML(AMLGraph &G)193.{194.//用邻接多重表存储,构造无向图G195. string v1,v2;196.int i,j,k;197. cin>>G.vexnum>>G.arcnum;198.for(i=0;i<G.vexnum;i++)199. {200. cin>>G.adjmulist[i].data;201. G.adjmulist[i].firstedge=NULL;202. }203.204.for(k=0;k<G.arcnum;k++)205. {206. cin>>v1>>v2;207. i=Locate_Vex(G,v1);208. j=Locate_Vex(G,v2);209.210.while(i<0|| i>G.vexnum-1 || j<0 || j>G.vexnum-1) 211. {212. cout<<"结点位置输入错误,重新输入: ";213. cin>>v1>>v2;214. i=Locate_Vex(G,v1);215. j=Locate_Vex(G,v2);216. }217.218. EBox *p=new EBox;219. p->ivex=i;220. p->jvex=j;221. p->ilink=G.adjmulist[i].firstedge;222. p->jlink=G.adjmulist[j].firstedge;223. p->mark=0;224. G.adjmulist[i].firstedge=G.adjmulist[j].firstedge=p; 225. }226.}。
图的两种存储结构及基本算法

图的两种存储结构及基本算法第一篇:图的两种存储结构及基本算法一、图的邻接矩阵存储1.存储表示#definevexnum10typedefstruct{vextypevexs[vexnum];intarcs[vexnum][vexnum];}mgraph;2.建立无向图的邻接矩阵算法voidcreat(mgraph*g, inte){for(i=0;iscanf(“%c”,&g->vexs[i]);for(i=0;ifor(j=0;jg->arcs[i][j]=0;for(k=0;kscanf(“%d,%d”,&i,&j);g->arcs[i][j]=1;g->arcs[j][i]=1;} }3.建立有向图的邻接矩阵算法voidcreat(mgraph*g, inte){for(i=0;iscanf(“%c”,&g->vexs[i]);for(i=0;ifor(j=0;jg->arcs[i][j]=0;for(k=0;kscanf(“%d,%d,%d”,&i,&j,&w);g->arcs[i][j]=w;}}二、图的邻接表存储1.邻接表存储表示#definevexnum10typedefstructarcnode{intadjvex;structarcnode*nextarc;}Arcnode;typedefstructvnode{vextypedata;Arcnode*firstarc;}Vnode;typedefstruct{Vnodevertices[vexnum];intvexnum,arcnum;}algraph;2.建立无向图的邻接表算法:voidcreat(algraph*g, inte){for(i=0;iscanf(“%c”,&g->vertices[i]->data);g->vertices[i]->firstarc=NULL;}for(k=0;kscanf(“%d,%d”,&i,&j);q=(Arcnode*)malloc(sizeof(Arcnode));p=(Arcnode*)malloc(s izeof(Arcnode));p->adjvex=j;p->nextarc=g->vertices[i]->firstarc;g->vertices[i]->firstarc=p;q->adjvex=i;q->nextarc=g->vertices[j]->firstarc;g->vertices[j]->firstarc=q;}}3.建立有向图邻接表算法:voidcreat(algraph*g, inte){for(i=0;iscanf(“%c”,&g->vertices[i]->data);g->vertices[i]->firstarc=NULL;}for(k=0;kscanf(“%d,%d”,&i,&j);p=(Arcnode*)malloc(sizeof(Arcnode));p->adjvex=j; p->nextarc=g->vertices[i]->firstarc;g->vertices[i]->firstarc=p;}}三、图的遍历1.连通图的深度优先搜索遍历intvisited[vexnum]={0};voiddfs(mgraph*g, inti){printf(“%3c”,g->vexs[i]);visited[i]=1;for(j=0;jif((g->arcs[i][j]==1)&&(!visited[j]))dfs(g, j);}2.联通图的广度优先搜索遍历intvisited[vexnum]={0};voidbfs(mgraph*g, intk){intq[20], f, r;f=0;r=0;printf(“%3c”,g->vexs[k]);visited[k]=1;q[r]=k;r++;while(r!=f){i=q[f];f++;for(j=0;jif((g->arcs[i][j]==1)&&!visited[j]){printf(“%3c”,g->vexs[j]);visited[j]=1;q[r]=j;r++;}}}4.求图的联通分量intvisited[vexnum]={0};voidcomponent(mgraph*g){intcount=0;for(j=0;jif(!visited[j]){count++;printf(“n第%d个联通分量:”, count);dfs(g, j);} printf(“n 共有%d个联通分量。
邻接表的边结点概念

邻接表的边结点概念
邻接表的边结点
邻接表是一种用于存储图的数据结构,在邻接表中,每个顶点都对应一个链表,链表中存储着与该顶点相邻的顶点。
邻接表的边结点则是表示两个顶点之间的边的数据结构。
概念
邻接表的边结点是一个包含两个主要字段的数据结构:源顶点和目标顶点。
源顶点表示边的起始点,目标顶点表示边的终点。
除了这两个字段,边结点还可以包含其他字段,如权重和标志等。
相关内容
邻接表的边结点通过链表的形式连接起来,形成一个链表结构,每个链表头节点都对应一个顶点。
邻接表的边结点的存储方式可以是线性链表,也可以是其他数据结构,如数组或二叉搜索树等。
使用邻接表的边结点存储图的优点在于节省了存储空间。
对于稀疏图而言,邻接表的边结点仅存储有相邻顶点的边,而对于稠密图而言,邻接表的边结点所占用的存储空间会更小。
在使用邻接表的边结点表示图时,我们可以很方便地获得与指定顶点相邻的顶点列表,只需遍历该顶点对应的链表即可。
这种操作在很多图算法中都会用到,如广度优先搜索和最短路径算法等。
总结
邻接表的边结点是用于表示图中顶点之间连接关系的数据结构,通过链表的方式将顶点与边联系起来。
邻接表的边结点的存储方式节省了存储空间,并提供了快速访问与指定顶点相邻的顶点的能力。
在图算法中,邻接表的边结点是一个重要的数据结构。
图的存储方式

p→next=g[d].link;
g[d].link=p; /*将新结点插入顶点Vd边表的头部*/
}
}
返回
数据结构
do {
产生无向图邻接矩阵算法续
scanf (“%d,%d”,&v1,&v2); /*输入边*/ adjarray[v1][v2]=1; adjarray[v2][v1]=1; } while(v1!=0 && v2!=0); } else num=0; retrun num; }
1.2 邻接表
在每个链表设一表头结点,一般这些表头结 点本身以向量的形式存储。
对于无向图的邻接表来说,一条边对应两个 单链表结点,邻接表结点总数是边数的2倍。
在无向图的邻接表中,各顶点对应的单链表 的结点数(不算表头结点)就等于该顶点的 度数。
在有向图邻接表中,一条弧对应一个表结点, 表结点的数目和弧的数目相同。
邻接表是图的一种链接存储结构。
在邻接表结构中,对图中每个顶点建立 一个单链表,第i个单链表中的结点表示 依个附 结于 点表该示顶与点该Vi的顶边点,相即邻对接于的无一向个图顶每点; 对于有向图则表示以该顶点为起点的一 条边的终点。
一个图的邻接矩阵表示是唯一的,但其 邻接表表示是不唯一的。因为在邻接表 的每个单链表中,各结点的顺序是任意 的。
在有向图邻接表中,单链表的结点数就等于 相应顶点的出度数。
要求有向图中某顶点的入度数,需扫视邻接 表的所有单链表,统计与顶点标号相应的结 点个数。
邻接表存储结构定义
#define MAXVEX 30
struct edgenode
{
int adjvex ;
/*邻接点域*/
struct edgenode *next ; /*链域*/
名词解释—邻接表:

名词解释—邻接表
邻接表(Adjacency List)是一种常用的图数据结构,用于表示图中的顶点以及它们之间的连接关系。
在计算机科学中,图是由顶点和边组成的数据结构,可以用来表示各种复杂的网络关系,如社交网络、交通网络、电路等。
邻接表是表示图的一种有效方法,尤其适用于稀疏图(即边的数量相对较少的图)。
邻接表的核心思想是将每个顶点与其相邻的顶点列表相关联。
具体实现时,通常使用一个数组或链表来存储每个顶点的相邻顶点。
对于无向图,每个顶点都需要存储其相邻顶点的信息;对于有向图,只需要存储出度(从该顶点出发的边)或入度(指向该顶点的边)的相邻顶点信息。
邻接表的优点包括:
节省空间:邻接表仅存储实际存在的边,对于稀疏图来说非常节省空间。
便于添加和删除顶点:只需要修改相应的顶点列表即可。
便于查询邻接顶点:可以通过直接访问顶点的相邻顶点列表来查询邻接顶点。
数据库中图数据的存储与查询优化

数据库中图数据的存储与查询优化随着大数据时代的到来,图数据的存储和查询优化成为了数据管理的重要议题。
图数据是指由节点和边组成的复杂网络结构,如社交网络、知识图谱等。
为了高效地存储和查询图数据,数据库系统在数据结构和查询算法上进行了改进和优化。
本文将讨论数据库中图数据的存储和查询优化的相关技术和方法。
一、图数据存储图数据的存储方式对数据访问的效率和系统性能起着重要影响。
常见的图数据存储方式有邻接矩阵、邻接表和属性表三种。
1. 邻接矩阵邻接矩阵是一种以二维矩阵形式来表示图数据的方法,矩阵中的每个元素代表一个节点之间的边的关系。
对于一个有n 个节点的图,邻接矩阵的大小为n*n。
邻接矩阵的存储方式简单直观,查询两个节点之间的边关系也非常高效,但是对于稀疏图(边的数量较少)来说,邻接矩阵的存储空间可能会非常浪费。
2. 邻接表邻接表是一种以链表的形式来表示图数据的方法,每个节点维护一个链表,链表中的每个元素代表当前节点和其它节点之间的边关系。
相比邻接矩阵,邻接表可以有效地解决稀疏图的存储问题,但是查询两个节点之间的边关系会比较耗时,需要遍历链表来找到匹配的边。
3. 属性表属性表是一种以属性列矩阵的形式来存储图数据的方法,每个属性都会有一个列,每一行表示一个节点,每个节点的属性值会存储在相应的列中。
属性表适用于具有大量节点和节点属性的图数据,可以跨多个属性进行高效的查询。
但是属性表在处理节点之间的边关系时相对较慢。
综上所述,邻接矩阵适用于密集图,邻接表适用于稀疏图,而属性表适用于属性丰富的图数据。
二、图数据查询优化图数据的查询通常包括按条件过滤、路径查询和子图匹配等操作。
为了高效地进行图数据查询,数据库系统采用了以下优化策略。
1. 索引加速索引是加速图数据查询的常用技术之一。
数据库系统可以根据节点和边的属性值创建索引,使得查询时可以快速定位匹配的节点和边。
索引的选择和设计需要结合具体情况来确定,以最大程度地提高查询效率。
图的两种存储方式---邻接矩阵和邻接表

图的两种存储⽅式---邻接矩阵和邻接表图:图是⼀种数据结构,由顶点的有穷⾮空集合和顶点之间边的集合组成,表⽰为G(V,E),V表⽰为顶点的集合,E表⽰为边的集合。
⾸先肯定是要对图进⾏存储,然后进⾏⼀系列的操作,下⾯对图的两种存储⽅式邻接矩阵和邻接表尽⾏介绍。
(⼀)、邻接矩阵存储:⽤两个数组分别进⾏存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。
存储顶点:⽤⼀个连续的空间存储n个顶点。
存储顶点之间的边:将由n个顶点组成的边⽤⼀个n*n的矩阵来存储,如果两个顶点之间有边,则表⽰为1,否则表⽰为0。
下⾯⽤代码来实现邻接矩阵的存储:#define SIZE 10class Graph{public:Graph(){MaxVertices = SIZE;NumVertices = NumEdges = 0;VerticesList = new char[sizeof(char)*MaxVertices];Edge = new int*[sizeof(int*)*MaxVertices];int i,j;for(i = 0;i<MaxVertices;i++)Edge[i] = new int[sizeof(int)*MaxVertices];for(i = 0;i<MaxVertices;i++){for(j = 0;j<MaxVertices;++j)Edge[i][j] = 0;}}void ShowGraph(){int i,j;cout<<"";for(i = 0;i<NumVertices;i++)cout<<VerticesList[i]<<"";cout<<endl;for(i = 0;i<NumVertices;i++){cout<<VerticesList[i]<<"";for(j = 0;j<NumVertices;j++)cout<<Edge[i][j] <<"";cout<<endl;}cout<<endl;}int GetVertexPos(char v){int i;for(i = 0;i<NumVertices;i++){if(VerticesList[i] == v)return i;}return -1;}~Graph(){Destroy();}void Insert(char v){if(NumVertices < MaxVertices){VerticesList[NumVertices] = v;NumVertices++;}}void InsertEdge(char v1,char v2){int i,j;int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2 == -1)return ;Edge[p1][p2] = Edge[p2][p1] = 1;NumEdges++;}void RemoveEdge(char v1,char v2){int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2== -1)return;if(Edge[p1][p2] == 0)return;Edge[p1][p2] = Edge[p2][p1] = 0;NumEdges--;}void Destroy(){delete[] VerticesList;VerticesList = NULL;for(int i = 0;i<NumVertices;i++){delete Edge[i];Edge[i] = NULL;}delete[] Edge;Edge = NULL;MaxVertices = NumVertices = 0;}void RemoveVertex(char v){int i,j;int p = GetVertexPos(v);int reNum = 0;if(p == -1)return;for(i = p;i<NumVertices-1;i++){VerticesList[i] = VerticesList[i+1];}for(i = 0;i<NumVertices;i++){if(Edge[p][i] != 0)reNum++;}for(i = p;i<NumVertices-1;i++){for(j = 0;j<NumVertices;j++){Edge[i][j] = Edge[i+1][j];}}for(i = p;i<NumVertices;i++){for(j = 0;j<NumVertices;j++)Edge[j][i] = Edge[j][i+1];}NumVertices--;NumEdges = NumEdges - reNum;}private:int MaxVertices;int NumVertices;int NumEdges;char *VerticesList;int **Edge;};上⾯的类中的数据有定义最⼤的顶点的个数(MaxVertices),当前顶点的个数(NumVertices),当前边的个数(NumEdges),保存顶点的数组,保存边的数组。
图的存储实验报告

图的存储实验报告图的存储实验报告引言在计算机科学领域中,图是一种重要的数据结构,用于描述对象之间的关系。
图的存储方式对于图的遍历、搜索和其他操作有着重要的影响。
本实验旨在探究不同的图存储方式,并比较它们在不同操作下的性能差异。
一、邻接矩阵存储方式邻接矩阵是一种常见的图存储方式,它使用二维数组来表示图中各个顶点之间的关系。
在邻接矩阵中,行和列分别代表图中的顶点,矩阵中的元素表示两个顶点之间的边的关系。
实验中,我们通过一个简单的例子来说明邻接矩阵的存储方式。
假设有一个无向图,其中包含5个顶点和6条边。
我们可以使用一个5x5的矩阵来表示这个图,矩阵中的元素为1表示两个顶点之间存在边,为0表示不存在边。
邻接矩阵的优点是可以快速判断两个顶点之间是否存在边,时间复杂度为O(1)。
然而,邻接矩阵的缺点是当图中的边数较少时,会造成存储空间的浪费。
此外,在图中顶点的增加和删除操作时,需要重新调整矩阵的大小,开销较大。
二、邻接表存储方式邻接表是另一种常见的图存储方式,它使用链表来表示图中各个顶点之间的关系。
在邻接表中,每个顶点都有一个链表,链表中存储了与该顶点相邻的顶点。
实验中,我们同样以一个简单的例子来说明邻接表的存储方式。
假设有一个有向图,其中包含4个顶点和5条边。
我们可以使用一个包含4个链表的数组来表示这个图,数组中的每个元素表示一个顶点,链表中的元素表示与该顶点相邻的顶点。
邻接表的优点是在图中边的数量较少时,可以节省存储空间。
此外,在图中顶点的增加和删除操作时,开销较小。
然而,邻接表的缺点是判断两个顶点之间是否存在边的时间复杂度较高,需要遍历链表,时间复杂度为O(顶点的度数)。
三、性能比较与结论通过实验,我们对比了邻接矩阵和邻接表两种图存储方式在不同操作下的性能差异。
在判断两个顶点之间是否存在边的操作中,邻接矩阵的时间复杂度为O(1),而邻接表的时间复杂度为O(顶点的度数)。
因此,在此操作下,邻接矩阵的性能更优。
邻接表
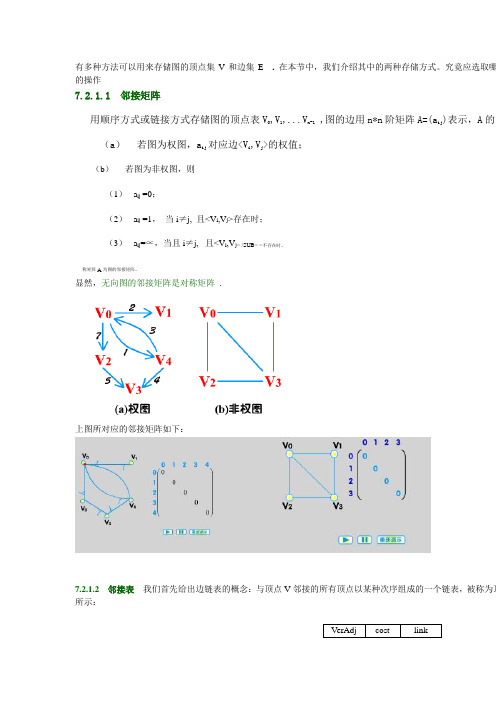
VerAdj cost
link
图 7.4 边结点 其中,VerAdj 域存放 V 的某个邻接顶点在顶点表中的序号;cost 域存放边<V,VerAdj>的权值;link 域存放指向 点显示的是边<V,VerAdj>的信息,因此称之为边结点。
对于无权图,边没有权值,边结点也就不需要包含 cost 域,所以边结点由两个域 VerAdj 和 l
(b) 若图为非权图,则 (1) aij =0; (2) aij =1, 当 i≠j, 且<Vi,Vj>存在时; (3) aij=∝,当且 i≠j, 且<Vi,Vj< /SUB> >不存在时。
称矩阵 A 为图的邻接矩阵。
显然,无向图的邻接矩阵是对称矩阵 .
上图所对应的邻接矩阵如下:
7.2.1.2 邻接表 我们首先给出边链表的概念:与顶点 V 邻接的所有顶点以某种次序组成的一个链表,被称为顶 所示:
对于无权图,边没有权值,边结点也就不需要包含 cost 域,所以边结点由两个域 VerAdj 和 l 用顺序存储方式存储图的顶点表 n-1,每个顶点的结构如图 7.5 所示
7.5 顶点结点
VerName adjacent
其中,VerName 域存放该顶点的名称,adjacent 域是指针域,存放指向 VerName 的边链表的头 adjacent 域存放的是顶点 VerName 的边链表的头指针。
info
头结点
data
firstarc
二、无向图的邻接表
ห้องสมุดไป่ตู้
图 7-5
三、有向图的邻接表和逆邻接表 (一)在有向图的邻接表中,第 i 个单链表链接的边都是顶点 i
发出的边。 (二)为了求第 i 个顶点的入度,需要遍历整个邻接表。因此可
图(Graph)是一种比线性表和树更为复杂的数据结构在图形....ppt

第七章
12
权、网、子图
在图的边或弧中给出相关的数,称
15 A 9
为权。 权可以代表一个顶点到另一个顶
11
点的距离、耗费等。带权的图通常称作 B 7 21
E
网。
3 C2F
假设有两个图G=(V,{VR}) 和 图 G=(V,{VR}), 如果 VV且 VRVR, 则称 G 为 G 的子图。
B B
C
A E
第七章
11
完全图、稀疏图、稠密图
假设图中有 n 个顶点,e 条边,则: ❖ 含有 n(n-1)/2 条边的无向图称作完全图; (无向图中边的取 值范围为0~n(n-1)/2) ❖ 含有 n(n-1) 条弧的有向图称作 有向完全图; (有向图中边 的取值范围为0~n(n-1))
❖ 若边或弧的个数 e<n*logn,则称作稀疏图,否则称作稠密 图。(当n很大时,n2>> n*log n)
❖ 生成树是对连通图而言的; ❖ 是连通图的极小连通子图; ❖ 包含图中的所有顶点; ❖ 有且仅有n-1条边。
B A
F
C D
E
第七章
19
7.2 图的存储结构
一、数组表示法(邻接矩阵) 二、邻接表存储表示 三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
第七章
20
一、数组表示法(邻接矩阵)
由顶点集和边集构成的图称作无向图(Undigraph)。
例如: G2=(V2, {R2})
B
C
V2={A, B, C, D, E, F} R2={(A,B), (A,E),
(B,E), (B,F),
(C,D), (C,F) ,
A
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图的邻接表存储方式——数组实现初探焦作市外国语中学岳卫华在图论中,图的存储结构最常用的就是就是邻接表和邻接矩阵。
一旦顶点的个数超过5000,邻接矩阵就会“爆掉”空间,那么就只能用邻接表来存储。
比如noip09的第三题,如果想过掉全部数据,就必须用邻接表来存储。
但是,在平时的教学中,发现用动态的链表来实现邻接表实现时,跟踪调试很困难,一些学生于是就觉得邻接表的存储方式很困难。
经过查找资料,发现,其实完全可以用静态的数组来实现邻接表。
本文就是对这种方式进行探讨。
我们知道,邻接表是用一个一维数组来存储顶点,并由顶点来扩展和其相邻的边。
具体表示如下图:其相应的类型定义如下:typepoint=^node;node=recordv:integer; //另一个顶点next:point; //下一条边end;vara:array[1..maxv]of point;而用数组实现邻接表,则需要定义两个数组:一个是顶点数组,一个是边集数组。
顶点编号结点相临边的总数s第一条邻接边next此边的另一邻接点边权值下一个邻接边对于上图来说,具体的邻接表就是:由上图我们可以知道,和编号为1的顶点相邻的有3条边,第一条边在边集数组里的编号是5,而和编号为5同一个顶点的下条边的编号为3,再往下的边的编号是1,那么和顶点1相邻的3条边的编号分别就是5,3,1。
同理和顶点3相邻的3条边的编号分别是11,8,4。
如果理解数组表示邻接表的原理,那么实现就很容易了。
类型定义如下:见图的代码和动态邻接表类似:下面提供一道例题邀请卡分发deliver.pas/c/cpp 【题目描述】AMS公司决定在元旦之夜举办一个盛大展览会,将广泛邀请各方人士参加。
现在公司决定在该城市中的每个汽车站派一名员工向过往的行人分发邀请卡。
但是,该城市的交通系统非常特别,每条公共汽车线路都是单向的,且只包含两个车站,即起点站与终点站,汽车从起点到终点站后空车返回。
假设AMS公司位于1号车站,每天早上,这些员工从公司出发,分别到达各自的岗位进行邀请卡的分发,晚上再回到公司。
请你帮AMS公司编一个程序,计算出每天要为这些分发邀请卡的员工付的交通费最少为多少?【输入文件】输入文件的第一行包含两个整数P和Q (1<=P<=10000,0<=Q<=20000)。
P为车站总数(包含AMS公司),Q为公共汽车线路数目。
接下来有Q行,每行表示一条线路,包含三个数:起点,终点和车费。
所有线路上的车费是正整数,且总和不超过1000000000。
并假设任何两个车站之间都可到达。
【输出文件】输出文件仅有一行为公司花在分发邀请卡员工交通上的最少费用。
【样例输入】Case1:2 21 2 132 1 33Case2:4 61 2 102 1 601 3 203 4 102 4 54 1 50【样例输出】Case1:46Case2:210【分析】此题是一道基本最短路径问题,但是如果想通过全部数据,10000个点,20000条边,必须用邻接表来实现。
下面给出此题目用dijkstra和 spfa两种算法的实现。
program delive_dijstrkalr;constinf='deliver.in';ouf='deliver.out';maxm=20000;maxn=10000;typenode=records,next:longint; //s为与第i个点相临的边有多少个,next为第一条边的编号为多少?end;edge=recordy,v,next:longint; // y为这条边的另一个顶点,v为权值,next为和第i个节点相临的另一条边,next为0 则表示结束。
end;vari,j,k,m,n,x1,y1,w1,ans:longint;a,a1:array[1..maxn] of node;e,e1:array[1..maxm] of edge;d,d1:array[1..maxn] of longint;procedure dij;vari,j,k,min,jj,kk:longint;f:array[1..maxn] of boolean;beginfillchar(d,sizeof(d),$7f);fillchar(f,sizeof(f),false);j:=a[1].next;for i:=1 to a[1].s dobegink:=e[j].y;d[k]:=e[j].v;j:=e[j].next;end;//用邻接表来找和第1个点相临的点,并给 d数组赋初值。
f[1]:=true; d[1]:=0;for i:=2 to n dobeginmin:=maxlongint; k:=0;for j:=1 to n doif (not f[j]) and (d[j]<min) thenbeginmin:=d[j]; k:=j;end;if k=0 then exit;f[k]:=true;jj:=a[k].next;for j:=1 to a[k].s dobeginkk:=e[jj].y;if (not f[kk]) and ( d[k]+e[jj].v<d[kk]) then d[kk]:=d[k]+e[jj].v;jj:=e[jj].next;end; //邻接表的使用,要好好注意。
end;end;beginassign(input,inf);reset(input);assign(output,ouf);rewrite(output);fillchar(a,sizeof(a),0);fillchar(e,sizeof(e),0);fillchar(a1,sizeof(a1),0);fillchar(e1,sizeof(e1),0);readln(n,m);for i:=1 to m dobeginreadln(x1,y1,w1);e[i].y:=y1; e[i].v:=w1;e[i].next:=a[x1].next; a[x1].next:=i;inc(a[x1].s);e1[i].y:=x1; e1[i].v:=w1;e1[i].next:=a1[y1].next; a1[y1].next:=i; inc(a1[y1].s);end;dij;d1:=d;a:=a1; e:=e1;dij;ans:=0;for i:=2 to n doans:=ans+d[i]+d1[i];writeln(ans);close(input);close(output);end.program deliver;constinf='deliver.in';ouf='deliver.out';maxm=20000;maxn=10000;typenode=records,next:longint; //s为与第i个点相临的边有多少个,next为第一条边的编号为多少?end;edge=recordy,v,next:longint; // y为这条边的另一个顶点,v为权值,next为和第i个节点相临的另一条边,next为0 则表示结束。
end;vari,j,k,m,n,x1,y1,w1,ans:longint;a,a1:array[1..maxn] of node;e,e1:array[1..maxm] of edge;d,d1:array[1..maxn] of longint;q:array[1..100000] of longint;procedure spfa; //spfa 是基于边的松弛操作的最短路径求法。
基本原理就是vari,j,k,now,min,t,w:longint;f:array[1..maxn] of boolean;beginfillchar(d,sizeof(d),$7f);fillchar(f,sizeof(f),false);fillchar(q,sizeof(q),0);d[1]:=0;t:=1;f[1]:=true;w:=1;q[t]:=1;repeatk:=q[t];j:=a[k].next;for i:=1 to a[k].s dobeginnow:=e[j].y;if d[now]>d[k]+e[j].v thenbegind[now]:=d[k]+e[j].v;if not f[now] thenbegininc(w);q[w]:=now;f[now]:=true;end;end;j:=e[j].next;end;f[k]:=false;inc(t);until t>w;end;beginassign(input,inf);reset(input);assign(output,ouf);rewrite(output); fillchar(a,sizeof(a),0);fillchar(e,sizeof(e),0);fillchar(a1,sizeof(a1),0);fillchar(e1,sizeof(e1),0);readln(n,m);for i:=1 to m dobeginreadln(x1,y1,w1);e[i].y:=y1; e[i].v:=w1;e[i].next:=a[x1].next; a[x1].next:=i;inc(a[x1].s);e1[i].y:=x1; e1[i].v:=w1;e1[i].next:=a1[y1].next; a1[y1].next:=i; inc(a1[y1].s);end;spfa;d1:=d;a:=a1; e:=e1;spfa;ans:=0;for i:=2 to n doans:=ans+d[i]+d1[i];writeln(ans);close(input);close(output);end.。
