常见定位方式定位误差的计算
2.4定位误差的分析与计算(一)

3.以圆孔定位时的定位误差计算
LOGO
Page 23
作业
LOGO
Page 24
复习
工件以圆柱面定位:
固定V型块:限制自由度(长4、短2) 标准化 活动V型块:限制自由度(短1) 标准化
定 位 套:限制自由度(长4、短2)
半 圆 套:限制自由度(长4、短2)
工件以特殊表面定位:
圆锥面定位:固定V型块定位,限制自由度(长4、短2) 锥度轴、套定位,限制自由度(长5、短3) 燕尾导轨定位:限制自由度(5) 齿面定位:限制自由度(长4、短2)
△Y =Xmax=TD + Td + Xmin
LOGO
2.4 定位误差的分析与计算
3.定位误差计算实例
1.
LOGO
Page 21
2.4 定位误差的分析与计算
2.
LOGO
Page 22
课堂小结
1.定位误差的概念
(1)基准不重合误差 △ B (2)基准位移误差 △Y
2.工件以平面定位误差计算
精基准平面定位时,一般认定△Y=0, △D=△B
LOGO
2.4 定位误差的分析与计算
基准不重合误差的计算公式
B i cos
i 1
n
i
——定位基准与工序基准间的尺寸链组成环的公差(包含位
置公差)(mm);
—— i 的方向与加工尺寸方向间的夹角(°)。
LOGO
2.4 定位误差的分析与计算
基准不重合误差练习
习题集P11-3 如图所示工件的加工工序 是镗D孔。如果定位基准分别 选择E、F、G,加工尺寸A的 定位误差分别是多少?
方向上的最大变动量,以“Δ D”表示。 成批加工工件时,夹具相对机床的位置及切削运动的行程调定后
定位误差的分析与计算

定位误差的分析与计算一、定位误差的概念和原因定位误差是指定位系统测量结果与真实位置之间的差异或偏差。
在现代生活中,定位系统广泛应用于导航系统、无人驾驶、无人飞行器等领域,而定位误差对于系统的准确性和可靠性至关重要。
1.信号传播误差:这是由于信号在传播过程中受到大气中的影响,如电离层、大气湿度等所产生的误差。
这种误差对于GPS系统尤为明显,导致多径效应、钟差误差等。
2.接收机误差:接收机的硬件和软件系统可能存在不同程度的误差。
硬件方面,接收机的时钟精度、天线阻抗匹配等问题都可能导致定位误差。
软件方面,接收机的算法、数据处理等也可能引入误差。
3.观测误差:观测误差是指由于测量设备的精度或不完善性所导致的误差。
例如,测量设备的精度限制了对信号强度、TOA(Time of Arrival)等参数的准确测量。
4.环境因素:环境因素也是定位误差产生的原因之一、比如,建筑物、树木、走廊等物体会对信号传播产生阻碍和衍射,从而影响接收机的测量结果。
5.多径效应:多径效应是指信号传播过程中,信号除了直射到达接收机外,还经历了反射,导致信号的多个传播路径同时到达接收机。
多径效应会产生明显的信号干扰和测量误差。
二、定位误差的计算方法1.位置误差计算:位置误差是指实际测量位置与真实位置之间的距离差异。
一种常见的计算方法是通过比较GPS测量点与参考点之间的差异来计算位置误差。
通过收集多个测量点的数据,可以使用最小二乘法进行曲线拟合,从而计算出测量点与真实位置之间的距离差异。
2.时间误差计算:时间误差是指实际测量时间与真实时间之间的差异。
在GPS系统中,时间误差主要由于卫星钟的钟差所引起。
通过GPS接收机接收到的卫星信号的时间戳和GPS接收机内部的时间戳之间的差异,可以计算出时间误差。
4.误差修正算法:为了减小定位误差,可以使用一些误差修正算法来对测量结果进行修正。
一种常见的方法是差分GPS技术,通过使用两个或多个接收机接收同一卫星信号,对测量结果进行差分处理,从而减小定位误差。
机械加工精度定位误差
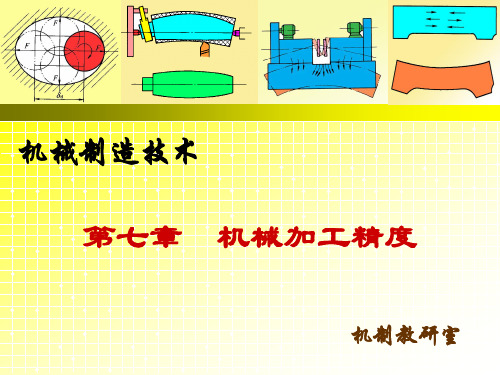
定位误差计算实例3
(3)工序尺寸A3 定 位 误 差 计 算 实 例
工序基准为孔的下母线,定位基准为孔的轴线 TD Td1 TD Y B 2 2 工序基准在定位基 面上,定位基面(孔) 变大,定位基准下移; 定位基准不动,工序基 准下移。 TD Td1 TD D Y B 2 2
定 位 误 差 计 算 实 例
故,ΔD=ΔB=0.15mm
平面定位时定位误差的计算
定位误差计算实例2
例2:如图所示,工件以内孔在定位销上定位铣槽, 要求保证加工尺寸,求其定位误差。 定 位 误 差 计 算 实 例
以内孔定位心轴垂直放置时定位误差的计算
定位误差计算实例2
解: 1)定位基准与工序基准重合,ΔB =0。 2)定位销垂直放置 ΔY=Xmax=Dmax-dmin=TD+Td 定 位 误 差 计 算 实 例 3)ΔD=ΔY=TD+Td
定位误差
圆孔 面
平面 及V型 面
二、常见定位方式的定位误差
定位方式
常 见 定 位 方 式 的 定 位 误 差
定位 基面
限位 基面
定位简图
定位误差
圆孔 面
V型面
二、常见定位方式的定位误差
定位方式
常 见 定 位 方 式 的 定 位 误 差
定位 基面
限位 基面
定位简图
定位误差
圆孔 面
V型面
二、常见定位方式的定位误差
定位 基面
限位 基面
定位简图
定位误差
圆孔 面
平面 及V型 面
二、常见定位方式的定位误差
定位方式
常 见 定 位 方 式 的 定 位 误 差
定位 基面
限位 基面
定位误差分析

(3)定位误差的计算由于定位误差ΔD是由基准不重合误差和基准位移误差组合而成的,因此在计算定位误差时,先分别算出Δ B和ΔY ,然后将两者组合而得ΔD。
组合时可有如下情况。
1)Δ Y ≠ 0,Δ B=O时Δ D= Δ B (4.8)2)ΔY =O,Δ B ≠ O时Δ D= Δ Y (4.9)3)Δ Y ≠ 0, Δ B ≠ O时如果工序基准不在定位基面上Δ D=Δ y + Δ B (4.10)如果工序基准在定位基面上Δ D=Δ y ±Δ B (4.11)“ + ” ,“—” 的判别方法为:①设定位基准是理想状态,当定位基面上尺寸由最大实体尺寸变为最小实体尺寸 (或由小变大)时,判断工序基准相对于定位基准的变动方向。
②② 设工序基准是理想状态,当定位基面上尺寸由最大实体尺寸变为最小实体尺寸 (或由小变大)时,判断定位基准相对其规定位置的变动方向。
③③ 若两者变动方向相同即取“ + ” ,两者变动方向相反即取“—”。
-、定位误差及其组成图9-21a图9-21 工件在V 形块上的定位误差分析工序基准和定位基准不重合而引起的基准不重合误差,以表示由于定位基准和定位元件本身的制造不准确而引起的定位基准位移误差,以表示。
定位误差是这两部分的矢量和。
二、定位误差分析计算(一)工件以外圆在v形块上定位时定位误差计算如图9-16a所示的铣键槽工序,工件在v 形块上定位,定位基准为圆柱轴心线。
如果忽略v形块的制造误差,则定位基准在垂直方向上的基准位移误差(9-3)对于9-16中的三种尺寸标注,下面分别计算其定位误差。
当尺寸标注为B1时,工序基准和定位基准重合,故基准不重合误差ΔB=0。
所以B1尺寸的定位误差为(9-4)当尺寸标注为B2时,工序基准为上母线。
此时存在基准不重合误差所以△D应为△B与Δy的矢量和。
由于当工件轴径由最大变到最小时,和Δy都是向下变化的,所以,它们的矢量和应是相加。
故(9-5)当尺寸标注为B3时,工序基准为下母线。
项目5:夹具设计中的定位误差分析

2
(3)以外圆在V形块上定位时的定位误差计算
b、合成法求解
d d-T d
O O1
O2 O A B C d-T d
A1
3
A3
α
图9-10工件以外圆在V形块上定位
M1
A2
d d-T d
由于Td的影响,使工件中心沿垂直 方向从O移至O1,即基准位移量:
A3
O O
1
O2
A B C α
Td OO1 O 2 sin( / 2)
【例9 】
如图是加工四个定位销 孔的工序图。已知双销 中心距59±0.02;圆柱 销直径 Φ12-0.006 ;菱形 -0.017 销直径 Φ12-0.008 ,求 -0.091 图中所标工序尺寸的定
位误差。
【例10 】如下图所示,为在半V块上定位铣轴上平面。试求工序尺寸A的
0
Y
1 ( TD Td ) 2
对于尺寸H2:
ΔB 1 TD 2
ΔDH2 ΔY ΔB
1 Td 2
d0 Td
对于尺寸H3:
ΔB 1 TD 2
ΔDH3 ΔY ΔB 1 1 1 ( TD Td ) TD TD Td 2 2 2
ΔD
对于尺寸H4:
ΔB 1 Td 2 1
d-T d
问:
当α=180°时,三种情况的定位误差是多大?
【例8
如图钻孔,保证A,用90°V形块定位,采用 a)~d)四种加工方案, 】试分别进行定位误差分析(外圆 0 )。 dT
d
方案 a b
ΔB
0 0.5Td
ΔY
0.707Td 0.707Td
ΔD
0.707Td 0.207Td
常见定位方式定位误差的计算
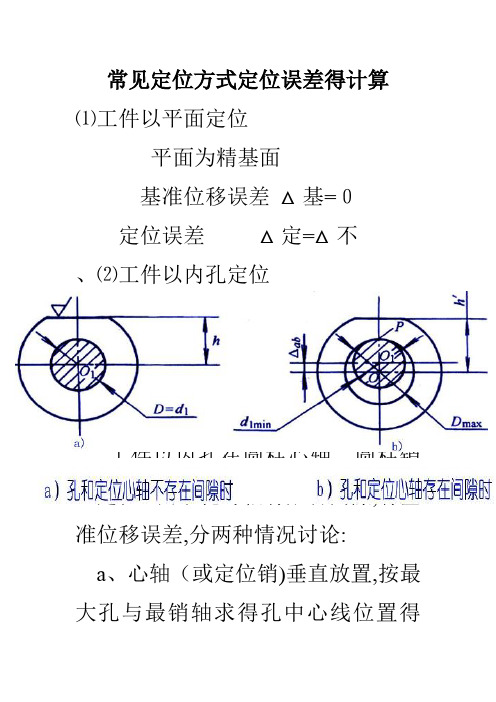
常见定位方式定位误差得计算⑴工件以平面定位平面为精基面基准位移误差△基=0定位误差△定=△不、⑵工件以内孔定位①工件孔与定位心轴(或销)采用间隙配合得定位误差计算△定= △不+ △基工件以内孔在圆柱心轴、圆柱销上定位。
由于孔与轴有配合间隙,有基准位移误差,分两种情况讨论:a、心轴(或定位销)垂直放置,按最大孔与最销轴求得孔中心线位置得变动量为:△基= δD+ δd+△min = △max =孔Dmax-轴dmin (最大间隙)b、心轴(或定位销)水平放置,孔中心线得最大变动量(在铅垂方向上)即为△定△基=OO'=1/2(δD+δd+△mi n)=△max/2或△基=(Dmax/2)-(dmin /2)=△max/2= (孔直径公差+轴直径公差) / 2②工件孔与定位心轴(销)过盈配合时(垂直或水平放置)时得定位误差此时,由于工件孔与心轴(销)为过盈配合,所以△基=0。
对H1尺寸:工序基准与定位基准重合,均为中心O,所以△不=0对H2尺寸:△不=δd/2⑶工件以外圆表面定位A、工件以外圆表面在V型块上定位由于V型块在水平方向有对中作用。
基准位移误差△基=0B.工件以外圆表面在定位套上定位定位误差得计算与工件以内孔在圆柱心轴、圆柱销上定位误差得计算相同。
⑷工件与"一面两孔"定位时得定位误差①“1”孔中心线在X,Y方向得最大位移为:△定(1x)=△定(1y)=δD1+δd 1+△1min=△1max(孔与销得最大间隙)②“2”孔中心线在X,Y方向得最大位移分别为:△定(2x)=△定(1x)+2δLd(两孔中心距公差)△定(2y)=δD2+δd2+△2min=△2max③两孔中心连线对两销中心连线得最大转角误差:△定(α)=2α=2tan-1[(△1max+△2max)/2L](其中L为两孔中心距)以上定位误差都属于基准位置误差,因为△不=0。
需要指出得就是定位误差一般总就是针对批量生产,并采用调整法加工得情况而言。
定位误差的分析与计算

答案:
1)若工件的工序基准为外圆的下母线时(相应的工序尺寸 为H1,参考图2-45a),C点至A点的距离为:
d
取全微分,并忽略V型块的角度误差(即将α视为常量), 可得到此种情况的定位误差:
(2-13)
40
18
合成时,若设计基准不在定位基面上(设计基准 与定位基面为两个独立的表面),即基准不重合误 差与基准位移误差无相关公共变量。
△定=△基+△不 合成时,若设计基准在定位基面上,即基准不重 合误差与基准位移误差有相关的公共变量。
△定=△基±△不
19
+ - 确定方法:
定位基准与限位基面接触,定位基面直径由小变 大(或由大变小),分析定位基准变动方向。
△基 =Δi 定位基准的变动方向与加工尺寸的方向不一致, 两者之间成夹角时,基准位移误差等于定位基准的 变动范围在加工尺寸方向上的投影。
△基=Δicosα
17
2.定位误差的计算
定位误差的常用计算方法是合成法。 定位误差应是基准不重合误差与基准位移 误差的合成。 计算时,可先算出基准不重合误差和基准 位移误差,然后将两者合成。则需满足以下条件: ①△总 ≤ δ 其中△总为多种原因产生的误差总和; δ是工件被加工尺寸的公差。 △总包括(1)夹具在机床上的装夹误差,(2)工件在
夹具中的定位误差和夹紧误差,(3)机床调整误 差,(4)工艺系统的弹性变形和热变形误差,(5) 机床和刀具的制造误差及磨损误差等 。
12
⑵基准位移误差△基
定位基准与限位基准不重合引起的误差。 工件定位面与夹具定位元件共同构成定位 副,由于定位副制造得不准确和定位副间的 配合间隙引起的工件最大位置变动量,也称 为定位副制造不准确误差。 这是由于定位基面和限位基面的制造公差 和间隙造成的。
机械制造工艺中的定位误差计算

机械加工定位误差分析(上)如前所述,为保证工件的加工精度,工件加工前必须正确的定位。
所谓正确的定位,除应限制必要的自由度、正确地选择定位基准和定位元件之外,还应使选择的定位方式所产生的误差在工件允许的误差范围以内。
本节即是定量地分析计算定位方式所产生的定位误差,以确定所选择的定位方式是否合理。
使用夹具时造成工件加工误差的因素包括如下四个方面:( 1)与工件在夹具上定位有关的误差,称为定位误差 D ;( 2)与夹具在机床上安装有关的误差,称为安装误差 A ;( 3)与刀具同夹具定位元件有关的误差,称为调整误差T ;( 4 )与加工过程有关的误差,称为过程误差 G 。
其中包括机床和刀具误差、变形误差和测量误差等。
为了保证工件的加工要求,上述误差合成后不应超出工件的加工公差δK,即D + A +T +G ≤δ K本节先分析与工件在夹具中定位有关的误差,即定位误差有关的内容。
由定位引起的同一批工件的设计基准在加工尺寸方向上的最大变动量,称为定位误差。
当定位误差 D ≤ 1/3δ K,一般认为选定的定位方式可行。
一、定位误差产生的原因及计算造成定位误差的原因有两个:一个是由于定位基准与设计基准不重合,称为基准不重合误差(基准不符误差);二是由于定位副制造误差而引起定位基准的位移,称为基准位移误差。
(一)基准不重合误差及计算由于定位基准与设计基准不重合而造成的定位误差称为基准不重合误差,以 B 来表示。
图 3 -61a 所示为零件简图,在工件上铣缺口,加工尺寸为 A 、B 。
图 3-61b 为加工示意图,工件以底面和E 面定位, C 为确定刀具与夹具相互位置的对刀尺寸,在一批工件的加工过程中C 的位置是不变的。
加工尺寸 A的设计基准是 F ,定位基准是 E ,两者不重合。
当一批工件逐个在夹具上定位时,受尺寸S±δ S /2的影响,工序基准 F 的位置是变动的, F 的变动影响 A 的大小,给 A 造成误差,这个误差就是基准不重合误差。
rtk点位中误差计算

rtk点位中误差计算RTK点位中误差计算RTK(Real-Time Kinematic)是一种实时运动定位技术,通过接收卫星导航系统的信号,利用测距原理实现对移动物体的精确定位。
在RTK定位中,误差是不可避免的,而误差的计算对于定位精度的评估和改进至关重要。
误差来源主要包括卫星信号误差、接收机误差、大气误差、多路径误差等。
为了准确计算RTK点位中的误差,我们需要了解各个误差来源,并采取相应的措施进行校正。
下面将详细介绍各个误差来源以及相应的误差计算方法。
1. 卫星信号误差卫星信号误差主要包括钟差误差、星历误差、轨道误差等。
这些误差会导致卫星定位信号与真实位置之间存在一定的偏差。
对于这些误差,我们可以通过接收多颗卫星的信号进行差分处理,消除或减小其影响。
2. 接收机误差接收机误差包括接收机的硬件误差和信号处理误差。
硬件误差主要来自于接收机内部的时钟精度、频率稳定性等因素,而信号处理误差则与接收机的算法和处理能力有关。
为了减小接收机误差,可以选择高精度的接收机设备,并进行相关的校准和调试。
3. 大气误差大气误差主要包括电离层延迟、对流层延迟等。
这些误差会导致卫星信号在穿过大气层时发生折射,从而影响定位的精度。
为了消除大气误差的影响,可以通过接收多颗卫星的信号进行差分定位,利用差分信号计算出大气误差,并进行相应的校正。
4. 多路径误差多路径误差是指卫星信号在传播过程中遇到障碍物后,发生反射、绕射等现象导致的误差。
这种误差会导致接收机接收到来自不同路径的信号,从而影响定位的准确性。
为了减小多路径误差,可以选择合适的接收机天线,避免信号的反射和绕射,或者通过信号处理算法进行多路径抑制。
对于以上各个误差来源,我们可以通过以下方法来计算RTK点位中的误差:1. 静态定位法静态定位法是通过静止不动的方式进行定位,利用接收到的卫星信号进行测量和计算。
通过记录一段时间内的观测数据,并进行差分处理,可以得到相对较为准确的定位结果。
定位误差计算

• 4)计算出的定位误差数值是指加工一批工件时某加工精度参 数可能产生的最大误差范围(加工精度参数最大值与最小值 之间的变动量)。它是个界限范围,而不是某一个工件定位 误差的具体值。 • 5)一批工件的工序基准(设计基准)相对定位基准、定位基 准相对对刀基准产生最大位置变动量是产生定位误差的原因, 而不一定就是定位误差的数值。
关键:找出同一批工件的工序基准在工序尺寸方向上可能的最大位移变动量
方法1—合成法:
先分别求出基准位移误差和基准不重 合误差,再求出其在加工尺寸方向上的矢 量合,即Δdw =Δjb +Δjw
•当 Δjb 和Δjw 由两个互不相关的变量引起时,用“+”;
•当Δjb 和Δjw 是同一变量引起时,要判断两者对Δdw 的影
响是否同向,方向相同时“+”,方向相反时“-”。
分析计算定位误差时应注意的问题:
• 1)定位误差是指工件某工序中某加工精度参数的定位误差。 它是该加工精度参数(尺寸、位置)的加工误差的一部分。 • 2)某工序的定位方案对本工序的多个不同加工精度参数产生 不同的定位误差,应分别逐一计算。 • 3)分析计算定位误差的前提是用夹具装夹加工一批工件,用 调整法保证加工要求。
定位误差计算实例
1. L1
Δdw= Δjw
2. L2
L2 的定位误差为两者的合成。两者都是由外圆直径的变化同时引 起的,所以要判断两者的方向特点。
要判断两者的方向特点。
当外圆直径从大到小时,工序基准M相对定位基准O是向O 方向即向下偏移的。 当放入V形块中后,当外圆直径由大变小时,定位基准相对 与理论也是向下偏移的。 综合起来两者合成方向相同。
dw T (d ) T (d ) jw jb 2 sin 2 2
第三节定位误差的分析与计算

位置(A) 2L工tg工 角度(A) tg工
2、一面二孔定位 工件底面为第一基准,两孔O1、O2为第二、第三基准
2、一面二孔定位 第一定位基准:底面 没有基准位置误差 两孔O1、O2为第 二、第三基准, 由于制造及装配 误差, 定位基准 O1、O2存在位置 误差。
TD Td1 2
+ Td 2
30H 7 30
第三节 定位误差的分析 与计算
一、定位误差及其计算方法
(一)定位误差的概念及其产生的原因
例:如图所示,要在套 筒上钻一通孔,保证尺 寸H-TH0.
根据六点定位原理,用 套筒端面和内圆表面定 位消除五个自由度,使 工件获得正确位置; 定位元件:带支承垫圈 的定位销; 定位基准: 工序基准:
虽然套筒已在夹具中的 位置确定了,但由于工 件的内孔、外圆及定位 销的直径不可能制造得 绝对准确,工件内孔与 定位销之间存在间隙, 所以工件的内孔中心线 和外圆下母线均在一定 范围内变动,加工后的 一批工件的工序尺寸也 不同。造成在工序尺寸 上的加工误差。
例2、P51
存在基准不重合误差,忽略第二基准B面位置变动
定位(L) 位置(AB)+ 不重(O )cos -) (
1
定位(L)=L L=O1O2 O1O2
2 ( 0+o1o1 cos -)= TL1 TL2 cos -) ( 2
定位(H 2) 位置(O) 不重(D)
o1o2 Td / 2 Td / 2sin 2 Td / 2
Td 2 1 ( sin 1)
2
(四)圆锥表面定位时的定位误差
工件定位基准的位置误差为0,但在轴线方向的尺寸产生 定位误差
第十六次、定位误差计算、夹紧

① 工序尺寸以H1标注,其定位误差为: Td 1 Δd=Δj= 2 sinα 2
基准重合的,只有一项位移误
(3)以外圆定位时的定位误差计算
工件在V形块上定位
② 工序尺寸以H2标注,其定位误差为基准不重合 与基准位移误差合成: Δd= Δb+ Δj Td 1 d-Td Td 1 + 1 d + 2 sinα - 2 sinα 2 2 2 2 = =
用的基准。
工件、夹具、刀具位置与标注尺寸的实现
• 工件通过六点定位完成了与夹具的结合,工件 与夹具的结合有误差; 总目标要求是△合≤ • 夹具安装在工作台上有误差; δ • 刀具与夹具对刀有误差; △定位≤ δ/3 • 加工过程有误差(刀、机床、变形、磨损); δ :工件被加工尺寸的公差 • 工件的定位基准选择是否合理,有“原罪”误 差; • 那么多误差均要影响到工件加工的尺寸误差上 去。
与工序基准不重
合而造成的定位
误差,称为基准 不重合误差,以
Δb表示 。ຫໍສະໝຸດ 基准不重合误差示例其大小△b等于工序基准与定位基准间联系尺寸在加工尺寸方 向上的变动量(公差)。
一次安装加工两孔A和B,孔B在X方向定位基 准C与工序基准A不重合。 基准不重合误差为联系尺寸22的公差0.2
基准重合与不重合误差示例
上定位相同)
2.4.2 工件在夹具中的定位
⑵工件以孔定位时的定位误差的计算 工件孔与定位心轴无间隙配合 如小锥度心轴和可胀心轴。这时工件孔的 轴心线始终与心轴的轴心线重合,这样就 不存在定位副不准确引起的定位误差,故 这种定位方式的定位精度较高。 工件单向靠紧定位 工件进行回转加工 工件孔与垂直放置的心轴(销)间隙配合
分析计算常见定位方式产生的定位误差
定位误差的分析与计算课件

按工件尺寸链计算定位误差
总结词
按工件尺寸链计算定位误差是一种基于工件 尺寸链的定位误差计算方法。通过分析工件 尺寸链中各尺寸之间的关系,可以计算出定 位误差的大小。
详细描述
工件尺寸链是加工过程中各相关尺寸之间的 相互关系。通过分析工件尺寸链中各尺寸之 间的关系,可以确定工件在夹具中的位置, 从而计算出定位误差。这种方法适用于具有 复杂尺寸关系的加工过程。
比较测量法
总结词
比较测量法是通过将工件与标准件进行比较来计算定位误差 的方法。
详细描述
比较测量法适用于具有较为复杂几何形状和尺寸的工件,通 过将工件与已知精度和尺寸的标准件进行比较,确定工件的 几何参数和定位误差。该方法精度较高,但需要高精度的标 准件作为参考。
间接测量法
总结词
间接测量法是通过测量工件上多个相关尺寸来计算定位误差的方法。
按夹具调整计算定位误差
总结词
按夹具调整计算定位误差是根据夹具调 整参数来计算定位误差的方法。通过调 整夹具的位置和角度,可以减小定位误 差对加工精度的影响。
VS
详细描述
在实际加工过程中,夹具的调整参数对工 件的定位精度有很大影响。通过调整夹具 的位置和角度,可以减小定位误差,提高 加工精度。这种方法需要经验丰富的操作 人员进行夹具调整,以保证加工精度。
定位误差的影响因素
工件与夹具的配合关系
工件与夹具之间的配合精度和装配关 系对定位误差有直接影响。
机床的几何精度
机床的导轨、主轴等部件的制造精度 和运动精度对定位误差有重要影响。
夹具的设计与制造精度
夹具的设计合理性、制造精度以及使 用过程中的磨损情况都会影响定位误 差。
工件的热变形
在加工过程中,由于工件受热而产生 的变形会导致工件位置的变化,从而 影响定位误差。
定位误差的计算方法解析

定位误差的计算方法:(1)合成法为基准不重合误差和基准位移误差之和; (2)极限位置法工序基准相对于刀具(机床)的两个极限位置间的距离就是定位误差; (3)微分法先用几何方法找出工序基准到定位元件上某一固定点的距离,然后对其全微分,用微小增量代替微分,将尺寸误差视为微小增量代入,就可以得到某一加工尺寸的定位误差。
注:基准不重合误差和基准位移误差它们在工序尺寸方向上的投影之和即为定位误差。
例如:用V 型块定位铣键槽,键槽尺寸标注是轴的中心到键槽底面的尺寸H 。
T D 为工件定位外圆的公差;α为V 型块夹角。
1. 工序基准为圆柱体的中心线。
表示一批工件依次放到V 型块上定位时所处的两个极端位置情形,当工件外圆直径尺寸为极大和极小时,其工件外圆中心线分别出于点O '和点O ''。
因此工序基准的最大位置变动量O O ''',便是对加工尺寸H 1所产生的定位误差: 故得:OE O E H H O O 11DH1''-'='-''='''=ε O A E Rt 1''∆中: max 1D 21A O ='' 2sin A O O E 1α''='O A E Rt 1''''∆中:min 1D 21A O ='''' 2sin A O O E 1α''''=''2sin 2T 2sin 2T 2sin A O A O O E O E D D11DH1α=α=α''''-''=''-'=ε2. 工序基准为圆柱体的下母线:工件加工表面以下母线C 为其工序基准时,工序基准的极限位置变动量C C '''就是加工尺寸H2所产生的定位误差。
定位误差计算方法

定位误差计算方法定位误差是指实际测量值与真实值之间的差异,用于衡量一个位置测量结果的准确性。
在现代定位技术中,定位误差是一个关键指标,其精度直接影响定位系统的可靠性和有效性。
本文将介绍几种常见的定位误差计算方法。
一、绝对误差绝对误差是指实际测量值与真实值之间的差异,通常以绝对值表示。
绝对误差可以直观地描述一个定位系统的精度,但不适用于不同测量结果之间的比较。
二、平均误差平均误差是指多次测量结果的平均值与真实值之间的差异。
平均误差可以通过下式计算:平均误差=Σ(测量值-真实值)/测量次数平均误差可以用来衡量一个定位系统的整体准确性,但不能反映观测数据的离散程度。
三、均方根误差均方根误差是指实际测量值与真实值之间的差异的平方的平均值的平方根,通常用RMSE表示。
均方根误差是一种常用的测量指标,可以综合考虑测量结果的离散程度和偏差。
均方根误差可以通过下式计算:RMSE = sqrt(Σ(测量值 - 真实值)² / 测量次数)均方根误差越小,定位系统的精度越高。
四、标准差标准差是一种常见的测量结果离散程度的度量方法,它表示一组测量结果相对于均值的分散程度。
标准差可以通过下式计算:标准差= sqrt(Σ(测量值 - 均值)² / 测量次数)标准差越小,定位系统的精度越高。
五、置信椭圆置信椭圆是一种用于描述定位误差的图形表示方式,能够直观地展示定位系统的误差分布情况。
置信椭圆的形状和大小可以通过计算定位误差的均值和方差来确定。
通常情况下,置信椭圆的中心为测量结果的平均值,长轴和短轴的长度与测量结果的方差相关。
六、相关误差相关误差是指多个测量结果之间的相关性误差。
相关误差可以通过计算测量结果之间的协方差来确定。
相关误差可以反映定位系统中不同观测量之间的相互影响程度。
综上所述,定位误差计算方法多种多样,常见的包括绝对误差、平均误差、均方根误差、标准差和置信椭圆等。
不同的误差计算方法适用于不同的情况,可以综合使用来评估一个定位系统的准确性和可靠性。
第四章第4节定位误差的分析与计算 (2)

例中由于工件的重力作用使 得工件向单一方向位移,故
j,y
TD
Td 2
X
(也叫定位副制造不准确误差)。
刀的位置不动
工序基准的位 置变化了 工件的线条已组合在一起,可在PPT编辑状态下移动黄色的线条进行演示。
上述两项定位误差是相 互独立存在的,所以对 于工序尺寸A总的定位 误差为
d (B) j,b(B) j,y(B) 0 2h tan 2h tan
例题
工件底面已加工过, △jy =0
图a为零件图,图 b 铣顶面工序中,H尺寸定 位基准与设计基准重合,不存在△jb。而图c 铣台阶面工序中,A尺寸由于基准不重合而 存在△jb,设计基准在H+TH与H-TH之间变 化,∴△jb=2TH 。
工件的定位基准(基面)和定位元件工作表面 本身存在制造误差会引起基准位移误差;
上述两种情况都会引起工件的工序基准偏 离理想位置,引起工序尺寸产生加工误差。
工件的工序基准沿工序尺寸方向上发生的
最大偏移量称为定位误差,用 d 表示。
(也叫定位副制造不准确误差)。
定位误差
定位误差 d 包括两个部分:
当心轴垂直放置时:
仍以上述工件钻孔为例,在立式钻床上钻孔并保证工 序尺寸A。从下图可看出,工序基准偏移范围,是以 心轴轴线为圆心,直径为最大配合间隙的圆。
工序基准为孔的轴线--图中 蓝色的点,它可以在粉色 的圆内任意位置处。 工序基准偏移的方向是向 四向方向的,也可以说成 是双向或多向的偏移。 在工序尺寸方向上的偏移 即图中的Z向(正反两个方 向)上的偏移,造成了基准 位移误差
d (H ) j,b(H ) j,y(H ) 0 0 0
对于工序尺寸B,它的工序 基准和定位基准都是K2平 面,由于平面K1与K2之间 存在垂直度误差( 90o ), 因此,在调整好的机床上加 工一批工件时,将引起工序 基准位置发生变化,故工序 尺寸B也随之产生加工误差, 其定位误差为:
常见定位方式定位误差的计算

常见定位方式定位误差的计算定位误差是指实际定位结果与真实位置之间的偏差。
常见的定位方式包括全球定位系统(GPS)、移动通信系统(如基站定位)、无线传感器网络、惯性测量单元等。
下面我将对其中几种常见的定位方式的定位误差计算进行介绍。
1.GPS定位误差计算:GPS是一种基于卫星信号的定位系统,它通过接收来自卫星的信号来测量和计算位置。
GPS定位误差的计算主要涉及到以下几个方面:-接收机定位误差:GPS接收机的性能和质量也会影响定位的精度。
定位误差可以通过接收机的接收灵敏度、信噪比和多路径效应等因素来计算。
-卫星时钟误差:GPS中的卫星时钟误差会对定位结果产生影响。
在定位的过程中,需要校正卫星的时钟误差,以提高定位的精度。
-接收机钟差:GPS接收机的内部时钟精度也会对定位结果产生影响。
为了减小时钟误差带来的影响,可以采用差分GPS的方法来校正时钟误差。
-多路径效应:在GPS信号的传输过程中,会经历多次反射和散射,导致接收机接收到多个不同路径上的信号。
这些多路径效应会对定位结果产生误差。
可以通过衡量同一卫星的信号在空间中的多路径效应来计算定位误差。
2.基站定位误差计算:基站定位是一种利用移动通信系统中的基站设备对移动终端进行定位的方式。
基站定位误差的计算主要涉及到以下几个方面:-平均距离误差(RTK错误):基站定位中常常使用差分定位技术,通过测量基站与移动终端之间的距离差,来对移动终端的位置进行计算。
平均距离误差是指多次测量的距离平均误差,可以通过对多组测量数据进行统计来计算。
3.无线传感器网络定位误差计算:无线传感器网络是由分布式传感节点组成的网络系统,用于采集和传输环境信息。
无线传感器网络定位误差的计算主要涉及到以下几个方面:-距离估计误差:无线传感器网络中的节点之间通常通过测量信号强度来估计节点之间的距离。
距离估计误差是指估计值与真实值之间的偏差,可以通过多组测量数据的均值和方差来计算。
-锚定节点误差:无线传感器网络中通常会设置一些已知位置的锚定节点,用于提供参考位置。
第四讲 定位误差的分析与计算(一

B s cos
由图1—32可知,基准位移误差应等于因定位基准与限位基准不重合 造成的加工尺寸的变动范围。 Y = Amax Amin imax imin i 式中
i
——定位基准的位移量;
i ——一批工件定位基准的变动范围。
图1—32
当定位基准的变动方向与加工尺寸的方向不一致,两者之间成夹 角α时 , Y = icosα
⒈工序基准为工件轴心线 此时为定位基准与工序基准重合,则基准不重合误差为零,而基准位 移的方向又与加工尺寸方向一致,所以加工尺寸B2的定位误差为
DB 2 Y
d
2 sin
2
⒉工序基准为外圆上母线 此时为定位基准与工序基准不重合。不仅有基准位移误差,而且还有 基准不重合,又定位尺寸与加工尺寸方向一致,所以尺寸B1的定位误差为
DB1 B1max B1min P 1P 2 P 1O2 O2 P 2
即
DB 1
d
2 sin
2
d
2
⒊工序基准为外圆下母线 此时亦为基准不重合,且基准位移和定位尺寸的方向均与加工尺寸方 向一致,故工序尺寸B3的定位误差为
DB 3 B3max B3min A1 A2 CA2 CA1
0.01 0.03 例1一1 在图1一32中,设 A 40 0.1 D= 500 d 0 = 500.04
求加工尺寸A的定位误差。 B =0。 解 1)定位基准与工序基准重合, 2)在 FJ 作用下,定位基准相对限位基准作单向移动,方向 与加工尺寸一致。
imax
X max
2
本讲小结: 一、产生定位误差的原因
Y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见定位方式定位误差的计算
⑴工件以平面定位
平面为精基面
基准位移误差△基=0 定位误差△定=△不
.⑵工件以内孔定位
①工件孔与定位心轴(或销)采用间隙配合的定位误差计算△定= △不+ △基
工件以内孔在圆柱心轴、圆柱销上定位。
由于孔与轴有配合间隙,有基准位移误差,分两种情况讨论:
a.心轴(或定位销)垂直放置,按最大孔和最销轴求得孔中心线位置的变动量为:
△基= δD + δd + △min = △max =孔Dmax-轴dmin (最大间隙)
b.心轴(或定位销)水平放置,孔中心线的最大变动量(在铅垂方向上)即为△定
△基=OO'=1/2(δD+δd+△min)=△max/2
或△基=(Dmax/2)-(dmin/2)=△max/2
= (孔直径公差+轴直径公差) / 2
②工件孔与定位心轴(销)过盈配合时(垂直或水平放置)时的定位误差
此时,由于工件孔与心轴(销)为过盈配合,
所以△基=0。
对H1尺寸:工序基准与定位基准重合,均为中心O ,所以△不=0
对H2尺寸:△不=δd/2
⑶工件以外圆表面定位
A、工件以外圆表面在V型块上定位
由于V型块在水平方向有对中作用。
基准位移误差△基=0
B.工件以外圆表面在定位套上定位定位误差的计算与工件以内孔在圆柱心轴、圆柱销上定位误差的计算相同。
⑷工件与"一面两孔"定位时的定位误差
①“1”孔中心线在X,Y方向的最大位移为:
△定(1x)=△定(1y)=δD1+δd1+△1min=△1max(孔与销的最大间隙)
②“2”孔中心线在X,Y方向的最大位移分别为:
△定(2x)=△定(1x)+2δLd(两孔中心距公差)
△定(2y)=δD2+δd2+△2min=△2max
③两孔中心连线对两销中心连线的最大转角误差:
△定(α)=2α=2tan-1[(△1max+△2max)/2L]
(其中L为两孔中心距)
以上定位误差都属于基准位置误差,因为△不=0。
需要指出的是定位误差一般总是针对批量生产,并采用调整法加工的情况而言。
在单件生产时,若采用调整法加工(采用样件或对刀规对刀),或在数控机床上加工时,同样存在定位误差问题。
但若采用试切法进行加工,则一般不考虑定位误差。
